Open Access Article
Open Access ArticleThe influence of random-coil chemical shifts on the assessment of structural propensities in folded proteins and IDPs†
Dániel Kovács
ab and
Andrea Bodor
 *a
*a
aELTE, Eötvös Loránd University, Institute of Chemistry, Analytical and BioNMR Laboratory, Pázmány Péter sétány 1/A, Budapest 1117, Hungary. E-mail: andrea.bodor@ttk.elte.hu
bEötvös Loránd University, Hevesy György PhD School of Chemistry, Pázmány Péter sétány 1/A, Budapest 1117, Hungary
First published on 31st March 2023
Abstract
In studying secondary structural propensities of proteins by nuclear magnetic resonance (NMR) spectroscopy, secondary chemical shifts (SCSs) serve as the primary atomic scale observables. For SCS calculation, the selection of an appropriate random coil chemical shift (RCCS) dataset is a crucial step, especially when investigating intrinsically disordered proteins (IDPs). The scientific literature is abundant in such datasets, however, the effect of choosing one over all the others in a concrete application has not yet been studied thoroughly and systematically. Hereby, we review the available RCCS prediction methods and to compare them, we conduct statistical inference by means of the nonparametric sum of ranking differences and comparison of ranks to random numbers (SRD-CRRN) method. We try to find the RCCS predictors best representing the general consensus regarding secondary structural propensities. The existence and the magnitude of resulting differences on secondary structure determination under varying sample conditions (temperature, pH) are demonstrated and discussed for globular proteins and especially IDPs.
1. Introduction
NMR spectroscopy is one of the few methods that can provide secondary structural information for proteins at atomic level resolution. In this respect, a crucial parameter is the chemical shift (CS) which reports on the local chemical environment of the corresponding atom. The first step of any NMR investigation is spectral assignment and as a result, chemical shift information is obtained for various atom types. Extraction of structural information from chemical shifts is a well-established practice.1–10 The method relies on calculating the secondary chemical shift (SCS), defined as the difference between the measured chemical shift and the appropriate random coil chemical shift (RCCS) value:| SCSAi = δAi,measured − RCCSAi | (1) |
Many IDPs/IDRs have been shown to play important biological roles11–14 and this created the need to study and assess their physical, chemical and biological behavior. An important goal is to make IDPs pharmaceutical targets.15–24 In this respect – despite its inefficiency – still the earlier sequence–structure–function paradigm is utilized as a starting point of the characterization.25 This means, that investigation is focused on finding remnants of structural features. Even though IDPs are generally disordered, they can exhibit inherent structural preferences26 that are referred to as secondary structural propensity, residual structure, transient structure. Apart from an inclination toward the well-known, another reason for identifying regions with structural propensities is that such regions are usually the ones involved in protein/protein or protein/membrane interactions. Typical sequential regions with detectable structural propensities are the so-called preformed interaction prone fragments, preformed structural motifs and short linear motifs which are generally crucial for the function of IDPs/IDRs.27–31 Thus, the regions of modest structural propensity are also expected to be key to understanding interactions and achieving the druggability of IDPs. For this, an efficient experimental characterization of these regions is necessary, which most tools of protein research are unable to accomplish. Due to the high flexibility of IDPs,32 attempts via classical methods, based on a rather rigid three-dimensional chemical structure, are inadequate.33 The necessity of describing IDPs in terms of structural ensembles instead of single structures especially calls for multiple sources of experimental data34 further increasing the importance of NMR. Consequently, the correct interpretation of the SCS is necessary.
A typical evaluation of the SCS values calculated based on eqn (1) is via the graphical representation as a function of the amino acid sequence. The positive or negative sign indicates the type of secondary structural propensity, while the amplitude shows the strength of this propensity. Data can also be interpreted indirectly via calculating some function of the SCSs, that can be (i) the probability of the presence of different secondary structural elements,35 (ii) the so-called CheZOD Z-score,36 (iii) the secondary structure propensity score (SSP),37 (iv) the neighbor-corrected structural propensity score,38 (v) the chemical shift index (CSI),39–42 (vi) the random coil index (RCI)43–45 and (vii) probability-based secondary structure identification (PSSI).46 Lately, attempts have been made to base disorder prediction exclusively on Z-score values, and thus exclusively on SCSs.47,48 Moreover, SCSs are used in the software such as SHIFTX,49 NMRView50 PESCADOR51 and DIPEND.52 The existence of such advanced methods indicates the importance of calculating SCS values appropriately. However, they are ambiguous quantities, where the ambiguity arises already from the definition (see eqn (1)), by the involvement of RCCSs. The real value of the RCCS of a given atom, for a given amino acid, under given experimental conditions is not well-defined. This is proved by the number of RCCS calculation methods that have been proposed in the last few decades by several authors.42,46,53–68 This lack of consensus on RCCS values causes the aforementioned ambiguity of SCSs. On the other hand, experimental aspects such as CS referencing, and signal assignment also contribute to the uncertainty of SCS values.69,70 Based on all this, the arising questions are: how much does the RCCS-related ambiguity influence secondary structure determination and what can be done to eliminate or at least reduce this effect? To address this problem, a comparative study of different RCCS datasets and calculation methods is necessary. Only very few works focus explicitly on the comparison of different RCCS prediction methods.71–75 Usually, such issues constitute marginal parts of the papers introducing new predictors.58,60,63–66,76
We intend to fill this gap and we propose to discuss RCCS predictor development as a calibration problem. We give an overview of the theoretical and experimental background of the presently available RCCS predictors, focusing on their differences. Further on, we provide case studies demonstrating how the different RCCS prediction methods influence the secondary structure or structural propensity assessment of a protein. As examples, we chose well-known and extensively studied proteins: the folded ubiquitin, and α-synuclein and the transactivation domain of p53 as IDPs, highlighting at the same time the effect of experimental conditions at various pH values and different temperatures. By means of statistical inference, we try to determine which RCCS predictor, if any, best represents the consensus of multiple predictors for a given experimental dataset. In the light of all these, one can choose and apply predictors simultaneously, a so far uncommon – but useful – practice.
2. Determining RCCSs: an ill-defined calibration problem
As purely computational approaches for determining RCCSs have been limited,77–81 producing an RCCS calculation method turns out to be a calibration process. Differences between RCCS prediction methods can be categorized as conceptual and experimental. The conceptual properties of the presently available RCCS calculation methods are: the type of example system(s) chosen (i.e. small peptides, IDRs, IDPs), factors that are included in calculating RCCSs, such as local sequence, pH, temperature, ionic strength, the form of the equations providing RCCS values and the method used to parametrize these equations. The experimental differences arise primarily from the actual example systems chosen and to a lesser extent from the measurement uncertainty of chemical shifts. It has been pointed out that already the random coil state of polypeptides has to be clarified.82Historically, two main conceptual approaches were considered for the calibration of RCCSs. One approach is based on designing small peptides whose behavior is assumed to best represent the most disordered state any polypeptide might adopt.53–56,58,64,68,76 The other approach involves compiling a protein chemical shift database followed by a statistical analysis of the data.42,46,57,59–63,65–67 This approach has become increasingly popular with the growing number of IDP-related datasets in the Biological Magnetic Resonance Databank (BMRB).
Following the choice of suitable model systems, another issue is how to take experimental conditions into account. So far, according to the literature, temperature and pH, have been directly and ionic strength indirectly considered.62,65,66,76,83 Besides these experimental parameters, the local amino acid sequence has an impact on the CSs of an individual residue in the polypeptide chain and has been accounted for in some methods.
The small peptide approach has the advantage that the tabulation of RCCSs is very straightforward and requires no or very little computation. Also, one has extensive control over experimental conditions as the respective values of pH, temperature and ionic strength may all be precisely adjusted. On the other hand, it is much more difficult to cover the local compositional space of proteins. For example, if 20 amino acids and only the nearest neighbors are considered, 203, meaning 800 combinations must be examined. Accounting for the neighboring ±2 amino acids, this number jumps to 3.2 million. As it would be very time-consuming and costly to produce so many different peptides, in studies done so far, authors designed a given polypeptide frame (for example Gly–Gly–Xxx–Ala–Gly–Gly)56 and varied a single amino acid in a central position. The sequential effect of the different amino acids on their neighboring partners is evaluated by their effect on the amino acids of the polypeptide frame, in the abovementioned case on glycines and alanine. On the other hand, the effect of a given amino acid on its neighbors depends also on the identity of the neighbors. Such pairwise and n-wise relationships are impossible to account for by the small peptide approaches utilized so far.
In contrast, database-related statistical approaches have the opposite strengths and weaknesses. With large numbers of CSs available for extensive numbers of proteins, the compositional space is much better covered than in peptide-based studies. The same local sequence may appear numerous times, therefore chemical shift values for all the involved amino acids are observed numerous times as well. A large enough database even enables the determination of pairwise or n-wise correction terms for the effect of the local sequence. The drawback is, that the effect of experimental conditions is generally difficult to account for, as these parameters usually vary from entry to entry. Also, since database approaches directly use chemical shifts of proteins for calibration, it could be argued that the resulting RCCS values are more appropriate for studying proteins than RCCSs originating from small peptide studies. However, even if chemical shift data of IDPs are used,63,65,66 it is not guaranteed that all CS are RCCSs because of residual structural motifs in IDPs.84 This requires authors to filter the data in some manner that decomposes the measured CSs into RCCSs and the different contributions of all the experimental conditions, the local sequence and, most importantly, residual structure.63,66,85,86 Loop regions, denatured proteins and even some peptides have been shown to not be completely disordered.87–102
In the light of the above, in Table 1 we summarize the works that have been carried out with the aim of calibrating RCCSs. One can observe that database-derived, statistical approaches have recently been gaining popularity. It is interesting to note, that, except for the work of Bundi et al.,54 systematic pH and temperature corrections only became available in the 2000's, while the effect of local sequence was already considered in the work of Braun et al.55 in 1994. Sequence corrections became more elaborate in later RCCS predictors.
| Method | Year | Ref. | Type of system | Corrections | Atom types | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sequence | Temperature | pH | HN | Hα | Cα | Cβ | C′ | N | ||||
| McDonald | 1969 | 53 | Free amino acids, different small peptides | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| Howarth | 1978 | 67 | Peptides and denatured proteins in D2O | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| Richarz | 1978 | 68 | Small peptide (GG-X-A) | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ |
| Bundi | 1979 | 83 | Small peptide (GG-X-A) | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ |
| CSI | 1992, 1994 | 41 and 42 | Globular proteins | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Braun | 1994 | 55 | Small peptide (GG-X-A) | ✓ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ |
| Wishart | 1995 | 56 | Small peptide (GG-X-A/P-GG) | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Lukin | 1997 | 57 | Database (BMRB and literature) | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Schwarzinger | 2000 | 58 | Small peptides, in acidic 8 M urea | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ |
| PSSI | 2002 | 59 | Database (selected BMRB) | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Wang | 2002 | 60 | Database (selected BMRB) | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| RefDB | 2003 | 61 | Selected BMRB data (database) | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Wang L. | 2006 | 46 | Proteins from refDB | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| Camcoil | 2009 | 62 | Loop regions of globular proteins (selected BMRB) | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| ncIDP | 2010 | 63 | IDPs (mostly BMRB) | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Kjaergaard | 2011 | 64 and 76 | Small peptides | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Prosecco | 2017 | 65 | IDPs (selected BMRB) | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Potenci | 2018 | 66 | IDPs (ncIDP extended) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
In this work, we focus on investigating free proteins in aqueous solutions and under the typical conditions of NMR studies. We are aware of works concerning RCCSs under high pressure,103–107 for phosphorylated,108 posttranslationally modified109 amino acids and in the presence of organic solvents,110,111 however we are not discussing these specialties here.
Below, we provide a brief overview of the approaches regarding RCCS corrections for the three aforementioned factors: local sequence, pH and temperature.
2.1. Sequence correction of RCCSs
Nearest neighbor-effects on the local structure and energetics of proteins is an extensively studied topic especially in the field of IDPs.112The first sequence corrections of RCCSs were suggested by Braun et al.55 Considering the Gly–Gly–Xxx–Ala and Gly–Gly–Gly–Ala sequences, corrections were defined as:
| ΔδX = δGGXAA,N − δGGGAA,N | (2) |
Although the calculation is very straightforward, this approach assumes that the local sequence effect experienced by alanine because of residues X is equal to what the remaining 19 amino acids would experience, which is not necessarily the case. Also, taking only the preceding residue into account might be plausible for amide nitrogen, but not for other atom-types of the peptide backbone.66
A similar approach was used in the work of Wishart et al.56 considering Gly–Gly–Xxx–Ala–Gly–Gly and Gly–Gly–Xxx–Pro–Gly–Gly hexapeptides. Sequence correction was given as:
| ΔX = δXA − δXP | (3) |
In 2000, Schwarzinger et al. used Gly–Gly–Xxx–Gly–Gly constructs and provided sequence correction terms for all four of the i − 2, i − 1, i + 1 and i + 2 positions.58 These correction terms were respectively calculated as the CS difference of Gly1, Gly2, Gly4 and Gly5 in the Gly–Gly–Xxx–Gly–Gly and the reference Gly–Gly–Gly–Gly–Gly peptide according to the set of equations below
| A = δ(G1) − δ(G1ref) | (4) |
| B = δ(G2) − δ(G2ref) | (5) |
| C = δ(G3) − δ(G3ref) | (6) |
| D = δ(G4) − δ(G4ref) | (7) |
| δR(corrected) = δrandom(R) + A + B + C + D | (8) |
The first statistical approach in sequence correction was given by Wang et al.60 They used more than 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemical shifts from BMRB to calibrate average random coil chemical shifts, pairwise sequence correction terms, average secondary structural chemical shift terms and terms for pairwise sequence effects in the random coil, β-strand and α-helical states. We note, that in this case the definition of RCCS heavily depends on the identification of residues in the random coil state by means of VADAR, DSSP and PSSI.59,116,117 Using this definition of disorder, parametrization of eqn (9) and (10) could be performed:
000 chemical shifts from BMRB to calibrate average random coil chemical shifts, pairwise sequence correction terms, average secondary structural chemical shift terms and terms for pairwise sequence effects in the random coil, β-strand and α-helical states. We note, that in this case the definition of RCCS heavily depends on the identification of residues in the random coil state by means of VADAR, DSSP and PSSI.59,116,117 Using this definition of disorder, parametrization of eqn (9) and (10) could be performed:
| Δ(XY)n,s = 〈δn,s(X)〉 − 〈δn,s(w/o X)〉 | (9) |
| Δ(YZ)n,s = 〈δn,s(Z)〉 − 〈δn,s(w/o Z)〉 | (10) |
The next method including sequence correction terms in RCCS calculation was Camcoil,62 published by De Simone et al. in 2009. Therein, a database of 1772 BMRB entries belonging to proteins possessing PDB entries was used. Residue specific RCCSs were calculated as the average CSs of the given residue found in the coil regions of the considered proteins. Pairwise correction contributions for the preceding and succeeding residue were calculated by averaging for CSs of the appropriate residue pairs in the database. Moreover, a set of atom-type dependent weight factors for these correction terms was proposed for the predicted RCCS of atom i of residue A in a BAC peptide triplet:
| δRCiA = δ0iA + α−iδ1iBA + α+iδ1iAC | (11) |
The ncIDP method by Tamiola et al., includes sequence corrections.63 This is achieved by solving a set of equations of the following form:
| δn(x,a,y,i) = δRCn(a) + Δ−1n(x) + Δ+1n(y) + εn(i) | (12) |
Here, the tripeptide xay is considered, and δn(x,a,y,i) is the CS of atom-type n of the i-th residue, δRCn(a) is the uncorrected RCCS of a, Δ−1n(x) and Δ+1n(y) are sequence correction terms for the preceding and succeeding residue, while the εn(i) term accounts for any deviation caused by pH, temperature or CS referencing of individual datasets. Thus, the resulting sequence correction terms – despite originating from a database approach – are not pairwise and depend only on the identity of the preceding and succeeding residue. In practice, ncIDP is available online.113
In 2011, Kjaergaard et al. provided an RCCS dataset including sequence correction terms derived from the investigation of Gln–Gln–Xxx–Gln–Gln peptides.64 The procedure of Schwarzinger et al. was adopted, however Gln–Gln–Gln–Gln–Gln was defined as the reference peptide. Correction terms for sequence positions i − 2, i − 1, i + 1 and i + 2 and for the HN, Hα, N, Cα, C′ and Cβ atom types were determined. RCCS calculation follows eqn (4)–(8) with the adjustment of the reference peptide. Problems mentioned earlier, regarding the validity of correction terms for the two terminal positions, are present here as well. This RCCS calculation method is also available as a web application.119
In the first attempt to apply an advanced machine learning approach for RCCS calibration, Sanz-Hernández and De Simone built the Prosecco neural network model, which uses sequence correction terms.65 A sufficiently large dataset of more than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CSs of IDPs and IDRs from BMRB was used, and determination of pairwise correction terms for the i − 2, i − 1, i + 1 and i + 2 positions was achieved. The calculation involved the use of smoothed empirical probability density functions of CSs derived by applying Gaussian kernels according to eqn (13).
000 CSs of IDPs and IDRs from BMRB was used, and determination of pairwise correction terms for the i − 2, i − 1, i + 1 and i + 2 positions was achieved. The calculation involved the use of smoothed empirical probability density functions of CSs derived by applying Gaussian kernels according to eqn (13).
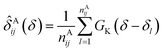 | (13) |
![[small delta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b1.gif) Aij(δ) is the resulting smoothed empirical probability density function of pairwise chemical shifts. From these empirical probability density functions, the corresponding ΔδAi,j sequence correction term is calculated as:
Aij(δ) is the resulting smoothed empirical probability density function of pairwise chemical shifts. From these empirical probability density functions, the corresponding ΔδAi,j sequence correction term is calculated as:| ΔδAi,j = δAi,j − δAi | (14) |
![[small delta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b1.gif) Aij(δ) empirical probability density function, δAi is the uncorrected RCCS of residue i, which is defined, similarly, as the expected value of the smoothed empirical probability density function of the chemical shifts of residue i in the database.
Aij(δ) empirical probability density function, δAi is the uncorrected RCCS of residue i, which is defined, similarly, as the expected value of the smoothed empirical probability density function of the chemical shifts of residue i in the database.
The correction terms of Prosecco are not used directly but are multiplied by weight factors wAi,k−2, wAi,j−1, wAi,l+1, wAi,m+2 defined as the corresponding empirical negative overlap integral of the corresponding primary and pairwise probability density functions of the CSs of the central amino acid in a quintuple of residues:
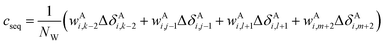 | (15) |
Presently the latest RCCS prediction method with sequence correction terms is Potenci by Nielsen and Mulder, published in 2018.66 The local sequence effect is accounted for from position i − 2 to position i + 2. The formulation of sequence correction terms combines an earlier idea with a novel one. As seen in both small peptide studies and the practical applications of the Wang method, general correction terms could theoretically be assigned to all 20 amino acids for all atom-types. Nielsen and Mulder determined a set of such general correction terms for all 6 canonical atom-types, and Hβ. Their novel idea was that the meticulous determination of pairwise correction terms can be neglected, instead, so-called correlated amino acid or second order contributions are determined. To achieve this, the 20 amino acids were divided into 7 groups according to the properties of the side-chain: G Gly, P Pro, r aromatics (Phe, Tyr, Trp), a aliphatics (Leu, Ile, Val, Met, Cys) and A, “+” positive (Lys, Arg), “-” negatives (Asp, Glu), while p polar residues (Asn, Gln, Ser, Thr, His). The direct neighbor correction and next-neighbor correction terms were defined using a principal component representation of amino acids suggested by Georgiev121 and corresponding wkj tunable weights:
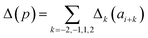 | (16) |
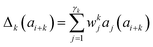 | (17) |
In determining correlated contribution terms, a similar approach was followed. For each atom-type, ωkl,m was defined as the contribution of residue type m to the CS of residue type l in position i when m is in relative position k with respect to i:
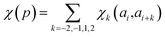 | (18) |
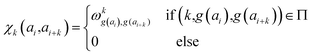 | (19) |
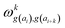 parameters if the given correlated contribution is significant, otherwise they are zero. Accordingly, Π denotes a certain set of values for k, g(ai) and g(ai+k). For any atom-type, theoretically 4 × 7 × 7 such parameters exist, as there are 4 relative positions (i − 2, i − 1, i + 1, i + 2) and seven groups of amino acids. In the optimization process, the number of such terms to be used was also treated as an adjustable parameter, and its ultimate value was smaller than the theoretical maximum for each atom type.
parameters if the given correlated contribution is significant, otherwise they are zero. Accordingly, Π denotes a certain set of values for k, g(ai) and g(ai+k). For any atom-type, theoretically 4 × 7 × 7 such parameters exist, as there are 4 relative positions (i − 2, i − 1, i + 1, i + 2) and seven groups of amino acids. In the optimization process, the number of such terms to be used was also treated as an adjustable parameter, and its ultimate value was smaller than the theoretical maximum for each atom type.
2.2. pH correction of RCCSs
The importance of pH was already noted in the earliest efforts for RCCS determination. Despite this, only a few RCCS predictors apply pH correction, even less treat the pH as a quasi-continuous variable. Generally, the non-structure related effect of pH on CSs is only important in the case of residues with titratable sidechains: glutamic acid, aspartic acid, histidine and their direct neighbors are affected in the acidic and neutral regime.122,123In 3 early works Richarz and Wüthrich,68 Bundi and Wüthrich54 and Braun et al.55 respectively published 1H, 13C and 15N chemical shifts of Gly–Gly–Xxx–Ala tetrapeptides. These three works established the first so-called binary pH-correction scheme for RCCSs. That is, respective pairs of RCCSs were proposed for Glu, Asp and His residues: one for pH values at least 1.5 smaller than the pKa of the given residue, and one for pH values at least 1.5 larger than the corresponding pKa. This is equivalent to providing an RCCS value for the completely protonated and the completely deprotonated state of the residue, respectively. For Asp and Glu residues, this might be a smaller issue as peptide and protein studies are either carried out under very acidic condition (pH < 3), where even the acidic sidechains of these two amino acids are almost completely protonated, or, at neutral pHs, where both are close to completely deprotonated.122–125 In contrast, histidine has typical pKa values between 6 and 7 and is therefore partially protonated under close to physiological conditions, making it fall into a “blind range” of binary pH-correction schemes.
Camcoil, published in 2009 (ref. 62) also has a binary pH-correction scheme. That is, spectra recorded under either acidic (pH < 2) or close to neutral (average pH = 6.1) conditions were used. The correction terms for acidic conditions, nominally pH = 2, were optimized by fitting chemical shifts of aspartic acid, glutamic acid and histidine residues of two BMRB entries acquired under denaturing conditions at acidic pH values.
In 2011, Kjaergaard et al. took a more sophisticated approach to performing pH-correction of RCCSs76 using Gly–Gly–Xxx–Gly–Gly pentapeptides similarly to Schwarzinger et al.58 In contrast to the original work, Kjaergaard et al. determined RCCS values at pH = 6.5 instead of pH = 2.5 in 8 M urea. Moreover, they performed pH-titration of the peptides with Xxx = Asp, Glu and His and determined the side chain pKa values of these residues by non-linear fitting of the titration curves. The equation for the δ(pH) pH-corrected RCCS is the linear combination shown by eqn (20).
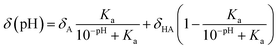 | (20) |
On the basis of eqn (20), originating from the classical equation for chemical equilibria, a continuous pH-correction is enabled.
Such an approach is dependent on the knowledge of side chain pKa values for individual residues in the protein.
Another limitation is that in practice, the pH-dependence of the chemical shifts of titratable residues in proteins often follows a Hill-model,122,124,126 including an extra parameter called the Hill-coefficient. The advantage is the lack of a “blind range” as opposed to the earlier, binary corrections.
The Prosecco server provides a binary pH-correction with the same parametrization of pH correction terms as Camcoil.62,65 In Prosecco, 6 BMRB entries were used to optimize the correction terms, with chemical shifts corresponding to nominal pH values of 2.8 and 6.4. During optimization the minimization of the absolute difference between calculated and experimentally determined chemical shifts of the 6 analyzed IDP entries was performed.
Being a very synthetic approach, the pH-correction of Potenci utilizes earlier ideas, but introduces some novelty to the field.66 Potenci's uncorrected RCCSs correspond to pH = 7.0. Therefore, pH-correction is only needed if the pH differs from this value. The correction considers a linear combination approach similar to eqn (20). The novelty is, that the Hill model is utilized, and the fHA relative concentration of the protonated side chain is calculated as in eqn (21).
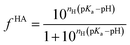 | (21) |
Further on, using the determined relative concentrations, the final pH-correction is acquired according to eqn (22).
| εk(ai+k,pKai+k,pH) = ΔδkHA–A(ai+k)(fHA(pH) − fHA(pH = 7)) | (22) |
2.3. Temperature correction of RCCSs
Although the effect of temperature on chemical shifts is well-known and widely studied,127–130 at present, there are only two RCCS calculation methods that explicitly take this effect into account by introducing correction terms. In the case of small peptide derived RCCS datasets, the temperature of the experiments is known precisely, so the RCCS values correspond to this temperature, however, it is not straightforward, how one should use such data for measurements that were carried out at different temperatures. On the contrary, for database-derived predictors the opposite is true. Although these works usually use measurement data covering a relatively wide range of temperature values, it is not clear, what temperature the acquired RCCSs correspond to. Usually, the average temperature of the different spectra is reported however, this still does not solve the problem of extrapolation.The first continuous temperature-correction terms in RCCS calculation were introduced by Kjaergaard et al.76 The chemical shifts of Gly–Gly–Xxx–Gly–Gly peptides were determined at 5, 15, 25, 35 and 45 °C. As in all cases, a linear dependence was observed, the slopes of the corresponding curves were obtained from linear fitting. Thus, temperature coefficients for the HN, Hα, N, Cα, C′ and Cβ atom types of the 20 amino acids are available and the temperature correction is performed as:
| dTcorr = a × (T − Tref) | (23) |
Once the reference temperature of any RCCS dataset is available, it is theoretically possible to transfer temperature coefficients from this RCCS prediction method to others – in stark contrast to sequence correction terms. Nielsen and Mulder performed such a transfer of temperature coefficients published by Kjaergaard et al. when developing Potenci. Accordingly, Potenci uses eqn (23) with Tref = 298 K for temperature correction.
3. Importance and non-equivalence of RCCS predictors in practical applications
We proposed to investigate how the selection of a given RCCS predictor influences the identification of secondary structural motifs and structural propensities. To test the performance of RCCS predictors we chose three well-studied proteins: the folded ubiquitin and two IDPs: α-synuclein and a 60-residue part of the transactivation domain (TAD) of p53. For ubiquitin and α-synuclein chemical shift data are available from the BMRB under codes 4769, 27348 and 18857, and these systems were tested in our lab, too. The p53TAD1-60 construct has been studied in detail by our group earlier.131,132 In the followings, from the available atom types, we limit ourselves to Cα environments. Chemical shifts of Cα are generally considered one of, if not the, most sensitive parameters to secondary structure and structural propensities and have been preferred over their counterparts in various cases.3,37,46,52,59,133–140 Out of the numerous RCCS predictors in Table 1, we selected those 8 which have at least some sort of local sequence correction, yield prediction for the Cα atom type and could theoretically be considered appropriate for studying IDPs in aqueous solutions.Comparison of RCCS predictors was performed in two different ways. First, by visual analysis of the calculated Cα SCS plots where one has to focus on regions showing meaningful differences depending on the RCCS predictor, and therefore leading to the controversial identification of secondary structural propensities. Second, via comparison of the predictors by a versatile non-parametric statistical tool: the sum of ranking differences and comparison of ranks to random numbers (SRD-CRRN) method augmented by one-way analysis of variance (ANOVA) with post hoc Bonferroni pair-wise tests.141–144
3.1. The visual comparison of RCCS predictors for Cα chemical shifts
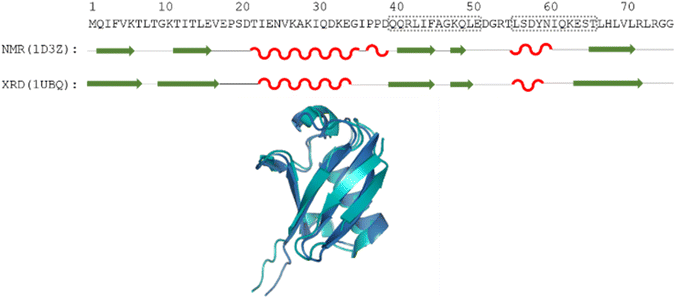 | ||
| Fig. 1 The amino acid sequence of human ubiquitin; structures determined by different methods, where secondary structural elements are represented by red wave (helix), green arrow (sheet) and black line (flexible loop) below the sequence; as well as the aligned 3D structures (PDB: 1D3Z, cyan, PDB: 1UBQ, dark blue). Regions Gln40–Glu51 and Leu56–Thr66 are highlighted by dotted grey boxes. | ||
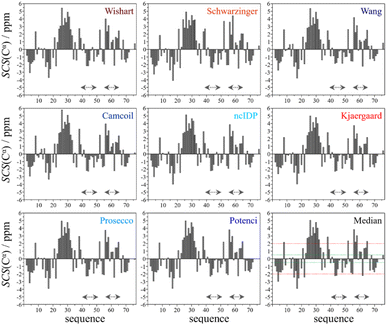
Using the chemical shift information, the secondary structural elements can be assessed, and for this purpose we prepared the Cα SCS plots of ubiquitin (BMRB: 4769) with the selected 8 predictors (see Fig. 2). A simple visual inspection shows that there is little discrepancy between the different methods, as also represented in the plot showing the median values. Regions with a given secondary structure have high (±2 ppm) Cα SCS values, while the mobile loop regions show ±0.5 ppm values, that are characteristic of the behavior of IDPs. We use the median instead of the mean to represent the general trend of the 8 selected RCCS predictors because the former is less sensitive to outliers. As will be shown later, outliers do appear when SCS values with different RCCS predictors are calculated, especially in the case of IDPs.
Still, despite the general similarity of plots in Fig. 2, some differences can be noticed. The Gln40–Glu51 region, which is highlighted on the sequence in Fig. 1, is suggested by structure elucidation to host two β-structures separated by a short loop. On the SCS plots, this structural motif is supported by most methods, appearing as an “inverse valley”, but this pattern is visually less well-defined for the Camcoil predictor. The discrepancy originates from the SCS values of Gly47 being either positive or very small negative by all predictors, but Camcoil yields a negative value of −0.40 ppm – leading to the interpretation that a single, unbroken β-structure is present. Moreover, differences arise in how pronounced the second β-motif is. The ncIDP and Wishart methods give very small amplitude SCSs for the Gln49 residue which makes noticing the motif more difficult compared to other predictors. The Wang and Schwarzinger methods give relatively larger negative SCSs for Arg42 of the first β-motif, suggesting an inclusion of Arg42 in the structure which is not as obvious with the other predictors. We note that even the two 3D structures of Fig. 1 agree on the presence of two β-structures separated by Ala46 and Gly47 but differ in the exact length.
Another region with spectacular differences is the Leu56–Thr66 part. Both 3D structures of Fig. 1 report a helix followed by a flexible loop. In the Cα SCS plots of Fig. 2, one can see relatively large, positive values for Leu56–Asp58, followed by positive values with differing amplitudes between Lys63–Thr66. In-between a set of SCSs is characteristic of a loop. Gln62 gives a relatively large negative value according to all methods, and such spikes are known to occur at the beginning and the end of well-defined structural elements. An interesting feature is that with the Schwarzinger method, SCS(Asp58) > SCS(Leu56). This is because the Schwarzinger method overestimates the SCS of aspartic acid at a close to neutral pH, due to its acidic calibration. The Camcoil method also features something very peculiar regarding this region. Similarly to the Wang method, Camcoil indicates a relatively high SCS for Thr66, suggesting a helix between Lys63–Thr66. With Camcoil, all SCS values between Leu56 and Thr66 are positive, with only the negative spike of Gln62 breaking the tendency. Therefore, one can assume that there is a single helical structure between Leu56–Thr66 and the experimentally determined CS of Gln 62 was assigned incorrectly. Such a conclusion would obviously call for a reinspection of spectral assignment on the part of a researcher using Camcoil, whereas none of the other methods indicate any need for such a procedure. One must be aware that the choice of an RCCS predictor might result in such ambiguities even in the case of globular proteins with well-defined secondary structural elements along the sequence.
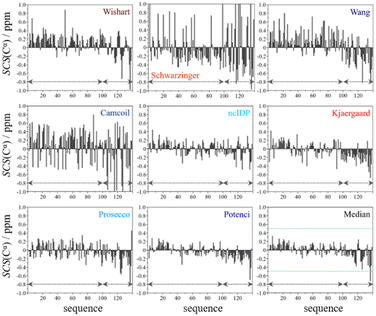
From the available chemical shift information (BMRB 27348) the SCS plots were constructed for each of the eight predictors and the median. The trends correspond to white noise with some added effects of residual structure. This is clearly shown by the fact that all but one value in the median plot in Fig. 4 are within the ±0.5 ppm range. Therefore, the importance of both the choice of an adequate RCCS predictor and the differences between RCCS prediction methods increases. As can be seen in Fig. 4, different structural tendencies may be proposed just by visual assessment of the Cα SCS plots. Obviously, all trends and related conclusions are much less sound than for structured proteins. However, in IDP research, this is the information that is available and that all advanced structural propensity calculation methods, irrespective of their varying degrees of sophistication, may rely on. While all the plots in Fig. 4 differ from each other to some extent, Cα SCS plots yielded by the Schwarzinger and Camcoil methods are especially unique. In the case of the Schwarzinger method, the spikes appearing at Glu and Asp residues result from the corresponding RCCS values having been recorded at pH = 2.3. The titratable side chains of these residues were completely or close to completely protonated under the circumstances of RCCS calibration, while the same side chains were completely deprotonated at pH = 6.5, where the data of BMRB entry 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348 were recorded. In the case of Camcoil, the surprising feature is that the average amplitude of the SCSs is generally larger than for the other methods, irrespective of residue type. We see no direct connection between this and the theoretical background of Camcoil. However, one must be aware of this feature when using SCSs calculated by Camcoil either directly or by deriving structural probabilities from them in the δ2D35,148 method.
348 were recorded. In the case of Camcoil, the surprising feature is that the average amplitude of the SCSs is generally larger than for the other methods, irrespective of residue type. We see no direct connection between this and the theoretical background of Camcoil. However, one must be aware of this feature when using SCSs calculated by Camcoil either directly or by deriving structural probabilities from them in the δ2D35,148 method.
For the other 6 Cα SCS plots of Fig. 4, a few general tendencies can be noticed. A set of predominantly negative values at the C-terminal of the protein are seen in the plot corresponding to the Kjaergaard method with a similar pattern being present in the Wang plot, the Prosecco plot and, to a smaller degree, in the Potenci plot, too. The Cα SCS plot made using the Wishart data set indicates some sets of consecutive negative values in this sequential region, but these are separated by short sets of consecutive positive values. The positive spike appearing in the Wishart plot belongs to His50 and can be attributed to the effect of pH. The Wishart data set was collected at pH = 5.0, where titratable side chain of histidine was close to completely protonated, while at pH = 6.5 the same side chain is already partially deprotonated, resulting in an inherent and uncorrected error of SCSs.
A part of the sequence, where a structural propensity could be assumed to be present, is the Ala18–Gly36 region according to Wishart and between Ala19–Glu28 according to the Kjaergaard method. Data obtained from the Potenci method could also be argued to mildly reinforce this tendency.
The Cα SCS plot based on the Wang method is peculiar even in itself. Up until residue Gln99, positive SCS values, many of which exceed 0.4 ppm, dominate the plot, with very few negative values of smaller than 0.2 ppm amplitude breaking the trend. From Gln99 onward, negative values, indicating β-sheet propensity dominate. Because of regular breaks in the trends and considerable variation in the amplitude of consecutive SCSs of the same sign, the Wang plot of α-synuclein is a typical example of a Cα SCS plot, which is very difficult to interpret, even qualitatively.
On the contrary, the Cα SCS plot of α-synuclein by ncIDP has amplitudes below 0.3 ppm almost exclusively, and no longer series of consecutive SCSs with the same sign are present. The plot is very similar to small amplitude white noise, as one would expect for a completely unstructured protein.
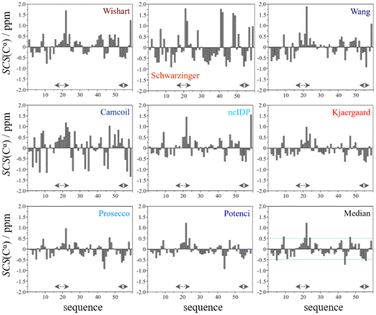
In the median Cα SCS plot of Fig. 6, the Gln16–Lys24 region of p53TAD1-60, has a set of consecutive positive values, suggesting a helical propensity. However, both the strength and exact localization of this propensity vary between the individual predictors. The strongest suggestion for residual helicity originates from Camcoil and the Wishart method, but even these two plots differ considerably in their patterns. With the Schwarzinger method there are only two positive spikes at Asp21 and Leu22, and no propensity can be supposed. The double spikes appearing at Asp41–Asp42 and Asp48–Asp49 because of the acidic calibration of the Schwarzinger method should also be noticed. In the Val31–Asp40 region neither glutamate nor aspartate residues are found, yet the Schwarzinger plot suggests a relatively convincing β-propensity. Neither of the remaining methods reinforces this tendency in comparable strength and length. Some β-motif could also be present close to the C-terminus between Trp53 and Asp57, according to the median plot, however the patterns of Camcoil and the Schwarzinger method differ from those of their peers considerably in this aspect.
Summarizing the visual inspection for all the above-mentioned biomolecules, in the case of folded ubiquitin differences between RCCS predictors are not crucial. Also, assessing α-synuclein and p53TAD1-60 to be fundamentally unstructured is possible using each of the eight RCCS predictors. However, assessment of the presence or absence of regions with secondary structural propensities – the primary aim of SCS analysis – is not at all clear. The eight selected methods differ in both the amplitudes of SCS values, and in the corresponding trends of the signs thereof. Thus, evaluation of secondary structural propensities according to this set of RCCS predictors is ambiguous, raising various questions. Which RCCS calculation method(s) is one supposed to use for a given experimental dataset? If each method has its own limitations, is there a way to use a set of different RCCS predictors to get a realistic idea about these mild propensities? Is there a single RCCS prediction method which generally best represents the consensus of all 8?
3.2. The statistical comparison of RCCS predictors for Cα chemical shifts
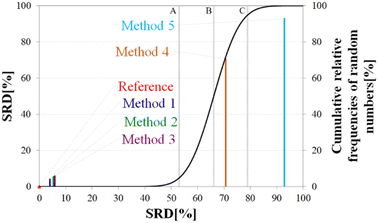
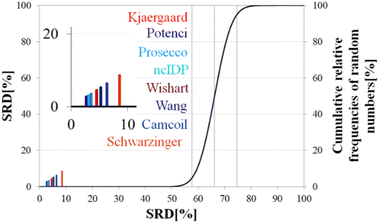
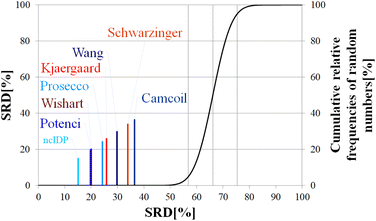
Above, we have shown examples for differences between RCCS predictors which might completely alter the visual identification of residual structure in IDPs. Below, we show that some differences are statistically significant, and we highlight how statistics can be used to find predictors best representing the consensus of a predictor ensemble.We illustrate the use of our approach on a model example, where five datasets were generated with thirty observations each. Note here, that for the SCS data, the only data pretreatment needed is the removal of missing SCS values for the missing assignments. The input data matrix contains the vectors corresponding to the methods to be compared. In the next step the SRD algorithm performs the comparison and validation by two built-in approaches. The first one is a comparison of SRD values to the SRD distribution of random vectors; and the second one is a 5-fold cross-validation. Running such an SRD-CRRN implementation results in a graph similar to the one in Fig. 7.
The theoretical cumulative distribution function of random vectors is represented by the black curve, and its numerical values are shown on the y-axis on the right. The curve is sigmoidal, as the SRD values of random vectors may be approximated by a normal distribution already for relatively small sample sizes (in our case thirty), as proved by Héberger and Kollár-Hunek.142 Lines A, B and C represent the 5th percentile, median and 95th percentile of this distribution, meaning the interval between A and C is the region of insignificance (insignificant region at α = 5% level of significance). The compared five methods from our example are represented by colorful sticks. The height of a given stick is equal to its x-coordinate, that is the SRD score of the corresponding method (i.e. 4.24 for method 1). This is the reason for the SRD score being shown on both the x and the left y-axis. In the chosen model example, the reference method also appears in the SRD-CRRN plot. Obviously, the SRD value of this is 0 by definition, as its ranking is identical to that of the reference vector, meaning itself. Generally, in the SRD-CRRN applications this is not shown. Further on, Fig. 7 shows, methods 1, 2 and 3 reproduce the reference ranking much better than random numbers, as the corresponding colorful sticks are close to zero and they are far away from the region of insignificance A–C. In contrast, method 4 falls in the insignificant region, meaning it is not linked to the reference vector by any deterministic relationship. Method 5 is related to the reference vector, but produces a ranking inversely correlated to the reference, and as a result it is situated closer to the value of 100 than to the median of the distribution of random numbers. In conclusion, Fig. 7 provides an ordering of the compared methods according to their performance. Still, one can observe that methods 1, 2 and 3 are close to each other but there is no indication whether one is significantly better than the other. This can be decided by applying ANOVA on the data provided by the built-in 5-fold cross-validation of the SRD algorithm. As p(ANOVA) in Table 2 is, <10−7, which is <5%, the test is significant, meaning not all methods perform equivalently well. This is highlighted by the mean SRD score of the methods shown in Table 2. These mean SRD score values correspond to the positions of the stick in Fig. 7. Which of the five methods are significantly better or worse can be checked by a Bonferroni post hoc test.144 The Bonferroni test provides a grouping pattern of the methods as shown in Table 2. In this example, the chosen five methods form four homogenous groups named G1, G2, G3 and G4. The grouping pattern highlights that method 1 and 2 are not differentiable at a 5% level of significance by the post hoc Bonferroni t-test. Similarly, method 2 and 3 can be treated as equivalent, however method 1 performs clearly better than Method 3 based on the Bonferroni test. Method 4 and 5 are significantly different from all other methods, therefore they form independent groups G4, G5. This model example was deliberately made to show that a method might belong to multiple homogenous groups as method 2 belongs to both groups G1 and G2; but it is also possible to have groups containing a single method like G3 and G4.
| p (ANOVA) | Method | Mean SRD score | G1 | G2 | G3 | G4 |
|---|---|---|---|---|---|---|
| <10−7 | Method 1 | 4.24 | **** | |||
| Method 2 | 5.56 | **** | **** | |||
| Method 3 | 6.14 | **** | ||||
| Method 4 | 70.21 | **** | ||||
| Method 5 | 92.78 | **** |
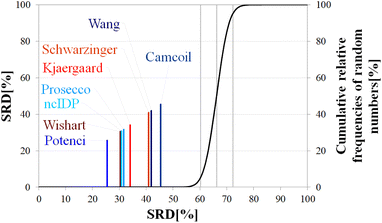
Still, the RCCS predictors align in a certain order and according to ANOVA they are, even if seemingly not very different, not all equivalent. The Bonferroni post hoc test indicates that the two best methods, Potenci and that of Kjaergaard are equivalent at a 5% level of significance (Table 3). All other methods are significantly different from each other. The Schwarzinger method falling visibly behind all the other predictors is explained by its calibration under acidic circumstances. This makes Schwarzinger SCS values for residues with titratable side chains like Asp21, Asp24 and Asp32 much larger than those given by the other predictors. This effect might go unnoticed in visual assessment of Fig. 2 but is highlighted by SRD-CRRN.
| p (ANOVA) | Method | Mean SRD score | G1 | G2 | G3 | G4 | G5 | G6 | G7 |
|---|---|---|---|---|---|---|---|---|---|
| <10−7 | Potenci | 2.71 | **** | ||||||
| Kjaergaard | 2.75 | **** | |||||||
| Prosecco | 3.14 | **** | |||||||
| ncIDP | 3.53 | **** | |||||||
| Wishart | 4.61 | **** | |||||||
| Wang | 5.31 | **** | |||||||
| Camcoil | 6.50 | **** | |||||||
| Schwarzinger | 8.71 | **** |
Another interesting observation is, that four more recent methods – three database-derived (Potenci, Prosecco, ncIDP) and one small peptide-based (Kjaergaard) perform best, and they are followed by the small peptide-based method of Wishart. Thus, the Wishart method, which is the oldest one here, ends up in front of three methods developed later (Camcoil, Wang, Schwarzinger) that could naively be considered improvements in the field.
A strongly phrased interpretation is that in the case of α-synuclein, although it is possible to find RCCS predictors which better reproduce the consensus of the eight considered methods, no single prediction is even close to being equivalent to this consensus SCS vector.
Differences in median SRD are larger, indicating a more pronounced ordering and grouping of the predictors. This is reinforced by the ANOVA post hoc analysis results (Table 4). Potenci performs best, finishing at first place, followed by the Wishart method, ncIDP and Prosecco. As for these three, at a 5% level of significance ncIDP – located in between – is indistinguishable from both the Wishart and Prosecco methods. In turn, these latter two are not equivalent according to the Bonferroni test. The remaining four methods form no homogenous groups but are all pairwise distinguishable from each other. This result highlights the usefulness of conducting ANOVA on the SRD data, as by a simple visual inspection of Fig. 9 one would consider the Wang and Schwarzinger methods equivalent. The ordering of the methods differs from that found for ubiquitin; however, one has to observe that the first five and last three methods are the same for both proteins. Similarly, in the case of α-synuclein no clear trend can be seen based on either time of introduction or the underlying principles of the methods. Potenci, the newest database derived RCCS predictor finishes first, but the oldest small peptide-base method is the next in line.
| p (ANOVA) | Method | Mean SRD score | G1 | G2 | G3 | G4 | G5 | G6 | G7 |
|---|---|---|---|---|---|---|---|---|---|
| <10−7 | Potenci | 25.66 | **** | ||||||
| Wishart | 30.49 | **** | |||||||
| ncIDP | 30.83 | **** | **** | ||||||
| Prosecco | 31.65 | **** | |||||||
| Kjaergaard | 34.19 | **** | |||||||
| Schwarzinger | 40.81 | **** | |||||||
| Wang | 41.87 | **** | |||||||
| Camcoil | 45.32 | **** |
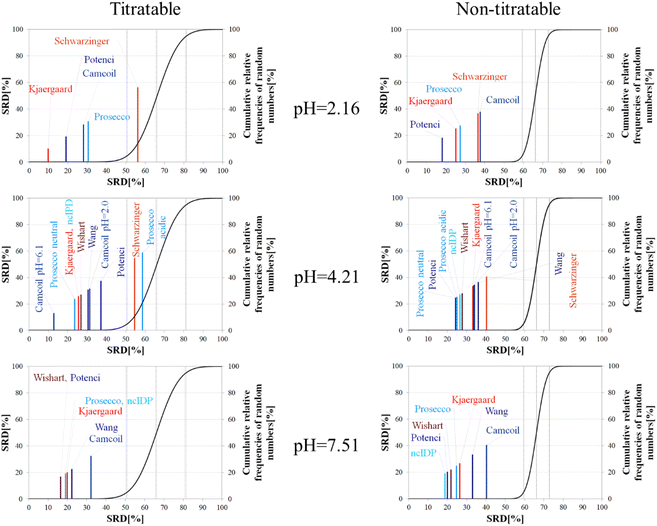
The importance of pH effects was highlighted in the comparison of RCCS predictors by the SRD-CRRN method even for folded ubiquitin. As some sort of pH correction is available in four of the eight studied predictors, we intended to investigate the effect of pH via SRD calculations. For this purpose, we used chemical shift data for α-synuclein, acquired at various pH and temperature values (BMRB: 18857). We classified the amino acid residues as titratable (including aspartic and glutamic acid) and all others as non-titratable. This way, according to the BMRB dataset out of the possible 140 residues 133 are assigned, yielding 22 titratable and 111 non-titratable residues in the 2.16–7.51 pH range, at 283 K. For the analysis we selected representative pH values of 2.16, 4.21 and 7.51. This enables us to see how the different pH-correction schemes deal with a pH value at which most of the titratable side chains are partially protonated, and what happens if the pH is close to the Asp, Glu sidechain pKa values. In order to avoid unnecessary outliers in SRD-CRRN calculations, at each pH we use only the suitable RCCS predictors. This means, for example, that the Schwarzinger method is excluded at pH = 7.51, as its RCCSs have clearly been calibrated under acidic conditions. Similarly, ncIDP and the methods of Wishart and Wang are excluded at pH = 2.16 values, as the Wishart dataset corresponds to pH = 5.0, while data recorded between pH values of 4.0 and 7.5 were used for the development of ncIDP. The Wang method was also developed for very mildly acidic and close to neutral conditions. The obtained pH-dependent SRD plots are shown in Fig. 10.
Considering the titratable residues of α-synuclein at pH = 2.16 the SRD results suggest that the Kjaergaard and Potenci methods – the two RCCS predictors with continuous pH correction schemes – perform the best. Quite surprisingly, the Schwarzinger method ends up in the in significant range and is the worst at reproducing the consensus of the five methods even under these conditions. Since the pH in this case is rather close to the calibration pH of the Schwarzinger dataset, this result is surprising. It is also interesting that the two small peptide methods (Kjaergaard and Schwarzinger) finish first and last, respectively. This confirms that it is generally not recommended to choose an RCCS prediction method solely based on its origin as datasets with very similar backgrounds can produce very different results under conditions at which both should be equally valid. The lack of consensuality between the Schwarzinger method and its peers might be explained by the small peptides used for calibration. The simple glycine frame harboring a glutamic or aspartic acid residue is extreme with respect to molecular mobility and intramolecular electronic interactions.
Regarding the non-titratable residues of α-synuclein at pH = 2.16, the order of the same five RCCS predictors is shuffled, and the grouping pattern is also different. In this case, Potenci is the most consensual of the five, while Camcoil finishes last. The Schwarzinger method is at the fourth position but is better than random numbers, indicating that the Schwarzinger method predicts more consensual RCCSs for non-titratable residues than for titratable ones under acidic conditions. The Kjaergaard method, which was the most consensual for the titratable residues, now finishes second with Prosecco closely following it. Interestingly, at pH = 2.16, all the above differences in SRD values are significant (Tables S1 and S2†).
At the intermediate pH of 4.21 and for titratable residues neutral generally neutral methods perform well, while the Schwarzinger method and the acidic version of Prosecco end up in the insignificant region (Fig. 10). The most interesting feature at this pH is the very pattern of the SRD-CRRN plots with titratable and non-titratable residues. In the latter case, all methods are grouped close to one another. This highlights that differences between RCCS predictors are generally much more pronounced for glutamic acid and aspartic acid residues than for the non-titratable amino acids. Note, that the general consensus of the predictors is generally worse at this pH, indicated by higher values SRD values. Also, at pH = 4.21, more predictors perform equivalently well based on post hoc Bonferroni test results shown in Tables S3 and S4.† Here, there are multiple homogenous groups containing more than one predictor.
For titratable residues at pH = 7.51, the Wishart and Potenci methods perform equivalently and are followed rather closely by the equivalently performing Prosecco, ncIDP and the Kjaergaard method (Table S5†). The Wang method is reasonably close to this cluster, while Camcoil is at the seventh position. Once again, Potenci as the newest database-derived method – shows similarity to the Wishart dataset which is the oldest of those used here and has been calibrated on a set of small peptides. It is also interesting that Potenci and ncIDP, where the former is an enhanced and more complete version of the latter, are not the closest to each other. Regarding the non-titratable residues at pH = 7.51 (Table S6†), ncIDP seems to be the most consensual, closely followed by Potenci and the Wishart method. Then, Prosecco and the Kjaergaard method perform rather similarly to each other with the Wang method and Camcoil loosely following them.
Generally, the consensus of RCCS predictors is weaker for Glu and Asp residues of α-synuclein, than for non-titratable ones. The identity of the most consensual predictors is dependent both upon pH and amino acid constitution of the protein.
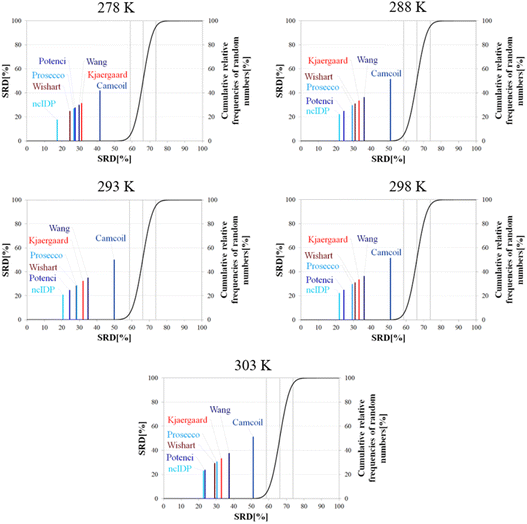
Besides pH, the other dominant factor affecting CSs and corrected for by some RCCS prediction methods is the temperature. To study its effect, we used the five datasets of BMRB entry 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 containing the experimental CSs of α-synuclein at 278, 288, 293, 298 and 303 K, at pH = 5.87. As the Schwarzinger method has been shown to be inappropriate at this pH especially for glutamate and aspartate residues making up more than 10% of amino acids in α-synuclein, we excluded this predictor from the analysis. The results of the SRD calculations for each temperature are shown in Fig. 11. The general pattern shows that ncIDP is the most consensual followed by a group comprising Potenci, Prosecco, and the methods of Wishart, Kjaergaard and Wang in varying order. Camcoil ends up at the seventh position in all cases. Most methods are usually significantly different from each other according to the Bonferroni post hoc test, however, there is usually a single pair of methods which are indifferentiable (Tables S7–S11†). At 278 K it is Potenci and Prosecco, at 288 K the Kjaergaard and Wang methods, at 293 and 298 K it is Prosecco and the Wishart method, while finally, at 303 K ncIDP and Potenci end up being indifferentiable at a 5% level of significance. We note that this set of methods shows considerable stability in SRD, namely, at 288 K and above the last three positions are occupied by the method of Kjaergaard, Wang and Camcoil in this exact order. Prosecco and the method of Wishart are close in all cases, switching places between 293 K and 298 K and then their earlier order is restored again at 303 K. Potenci, which performs ordinarily at 278 K, becomes very closely the most consensual method at 303 K.
857 containing the experimental CSs of α-synuclein at 278, 288, 293, 298 and 303 K, at pH = 5.87. As the Schwarzinger method has been shown to be inappropriate at this pH especially for glutamate and aspartate residues making up more than 10% of amino acids in α-synuclein, we excluded this predictor from the analysis. The results of the SRD calculations for each temperature are shown in Fig. 11. The general pattern shows that ncIDP is the most consensual followed by a group comprising Potenci, Prosecco, and the methods of Wishart, Kjaergaard and Wang in varying order. Camcoil ends up at the seventh position in all cases. Most methods are usually significantly different from each other according to the Bonferroni post hoc test, however, there is usually a single pair of methods which are indifferentiable (Tables S7–S11†). At 278 K it is Potenci and Prosecco, at 288 K the Kjaergaard and Wang methods, at 293 and 298 K it is Prosecco and the Wishart method, while finally, at 303 K ncIDP and Potenci end up being indifferentiable at a 5% level of significance. We note that this set of methods shows considerable stability in SRD, namely, at 288 K and above the last three positions are occupied by the method of Kjaergaard, Wang and Camcoil in this exact order. Prosecco and the method of Wishart are close in all cases, switching places between 293 K and 298 K and then their earlier order is restored again at 303 K. Potenci, which performs ordinarily at 278 K, becomes very closely the most consensual method at 303 K.
Since the changes in the experimental CSs of α-synuclein are apparently not related to any change in structural propensities in this temperature range, the data further highlight the fact that the degree of similarity of RCCS datasets provided by the different predictors is much dependent on the experimental conditions. This is true even despite some general tendencies in the SRD plots displaying stability. The individual changes in the consensuality of the seven methods indicates that in order to formulate a sound conclusion from SCS data, the simultaneous use of a carefully selected set of RCCS predictors is desirable.
| p (ANOVA) | Method | Mean SRD score | G1 | G2 | G 3 | G4 | G5 | G6 | G7 |
|---|---|---|---|---|---|---|---|---|---|
| <10−7 | ncIDP | 15.35 | **** | ||||||
| Potenci | 19.92 | **** | |||||||
| Wishart | 20.20 | **** | |||||||
| Prosecco | 24.49 | **** | |||||||
| Kjaergaard | 26.01 | **** | |||||||
| Wang | 30.05 | **** | |||||||
| Schwarzinger | 34.21 | **** | |||||||
| Camcoil | 36.51 | **** |
4. Conclusions
NMR chemical shifts and the calculated SCSs are the most important atomic-scale variables reporting on the secondary structural propensities of IDPs. This information can be further used for building databases of short linear motifs, and highlighting these regions is important in further interaction studies. On the other hand, SCS analysis is becoming a cornerstone for the possible targeting of IDPs and drug development. However, the SCS method suffers from the ambiguity of RCCSs which makes finding the proper RCCS values an important issue especially in IDP studies. Because of the continuous increase in the number of existing predictors, resulting from both new theoretical approaches and the growth of available experimental data in the field, RCCS prediction requires precaution when applying the SCS method.In this work we intended to give an overview with corresponding theoretical background of RCCS prediction, and special attention was paid to neighbor-, pH-, and temperature correction schemes. We attempted summarizing earlier work in a way that highlights fundamentals of different approaches and the temporal evolution of RCCS predictors in the last decades. We believe, such a review might be helpful for the experimental protein scientists to maximally exploit the acquired data for identifying secondary structural propensities of IDPs. Our approach of treating RCCS prediction as a somewhat ill-defined calibration problem is expected to give hints for computational and theoretical researchers for making developments in RCCS prediction.
Our selected set of eight RCCS predictors (most of them are also the ones most abundantly referenced in publications) can, in our opinion, be plausibly used. Performing a visual and statistical comparison of the selected RCCS predictors demonstrates how the choice of any single RCCS predictor might affect the structural conclusions. Even though we focus only on the Cα environment, and the conclusions reflect the behavior of this atom type, the chosen examples highlight general tendencies and are not compromised in validity. We introduce in this field and suggest the use of the very sensitive SRD-CRRN analysis coupled with post hoc complemented ANOVA. This approach can detect statistically significant differences even in the case of a folded protein with well-characterized structure. However, these differences only slightly affect secondary structural conclusions, as we show on the example of ubiquitin. Much more importantly, using α-synuclein and p53TAD1-60 as examples, we demonstrate that the slight differences – occurring exclusively as a consequence of choosing different RCCS predictors – can be crucial in the study of IDPs. The non-equivalence of RCCS predictors could clearly highlight or mask certain potential secondary structural tendencies. Relying on the pure review part of the present work, we discuss how these differences of RCCS predictors are related to the different theoretical backgrounds of the predictors, especially correction schemes and the molecular systems used in the calibration processes. These examples and explanations were aimed at highlighting the most general pitfalls to avoid during SCS analysis. We have demonstrated that amino acid sequence, pH and temperature mutually determine which RCCS predictors should be used. However, a trustworthy selection of RCCS predictors should be based on statistical analysis, rather than intuition or habit alone. Especially, applying SRD-CRRN – one of the up-and-coming tools of chemometrics – for SCS analysis and selection of RCCS predictors is an important methodological advance.
In case of IDPs the use of multiple RCCS predictors is beneficial. Noting their individual drawbacks and peculiarities, we recommend all eight predictors used in this study, if experimental conditions permit. However, we believe that there is a need for the development of at least one composite statistical method which is capable of incorporating the information content of multiple RCCS predictors. Until the underlying problem of ill-defined RCCS calibration is satisfactorily solved, such an approach to SCS analysis would be the best and most user-friendly option in the field.
Author contributions
Both D. K. and A. B. contributed to the writing of this manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support of the National Research, Development and Innovation Office, Hungary (grants NKFI K124900 and K137940) is highly acknowledged.Notes and references
- J. Glushka, M. Lee, S. Coffin and D. Cowburn, N-15 chemical-shifts of backbone amides in bovine pancreatic trypsin-inhibitor and apamin, J. Am. Chem. Soc., 1989, 111(20), 7716–7722 CrossRef CAS.
- D. S. Wishart, B. D. Sykes and F. M. Richards, Relationship between nuclear-magnetic-resonance chemical-shift and protein secondary structure, J. Mol. Biol., 1991, 222(2), 311–333 CrossRef CAS PubMed.
- S. Spera and A. Bax, Empirical correlation between protein backbone conformation and C-alpha and C-beta C-13 nuclear-magnetic-resonance chemical-shifts, J. Am. Chem. Soc., 1991, 113(14), 5490–5492 CrossRef CAS.
- S. Luca, D. V. Filippov, J. H. van Boom, H. Oschkinat, H. J. M. de Groot and M. Baldus, Secondary chemical shifts in immobilized peptides and proteins: A qualitative basis for structure refinement under Magic Angle Spinning, J. Biomol. NMR, 2001, 20(4), 325–331 CrossRef CAS PubMed.
- K. Modig, V. W. Jurgensen, K. Lindorff-Larsen, W. Fieber, H. G. Bohr and F. M. Poulsen, Detection of initiation sites in protein folding of the four helix bundle ACBP by chemical shift analysis, FEBS Lett., 2007, 581(25), 4965–4971 CrossRef CAS PubMed.
- R. P. Barnwal and K. V. R. Chary, An efficient method for secondary structure determination in polypeptides by NMR, Curr. Sci., 2008, 94(10), 1302–1306 CAS.
- J. A. Marsh and J. D. Forman-Kay, Structure and Disorder in an Unfolded State under Nondenaturing Conditions from Ensemble Models Consistent with a Large Number of Experimental Restraints, J. Mol. Biol., 2009, 391(2), 359–374 CrossRef CAS PubMed.
- W. Yu, W. Lee, S. Kim and I. Chang, Uncovering symmetry-breaking vector and reliability order for assigning secondary structures of proteins from atomic NMR chemical shifts in amino acids, J. Biomol. NMR, 2011, 51(4), 411–424 CrossRef CAS PubMed.
- A. Cavalli, R. W. Montalvao and M. Vendruscolo, Using Chemical Shifts to Determine Structural Changes in Proteins upon Complex Formation, J. Phys. Chem. B, 2011, 115(30), 9491–9494 CrossRef CAS PubMed.
- Y. Ono, M. Miyashita, H. Okazaki, S. Watanabe, N. Tochio and T. Kigawa, et al., Comparison of residual alpha- and beta-structures between two intrinsically disordered proteins by using NMR, Biochim. Biophys. Acta, Proteins Proteomics, 2015, 1854(3), 229–238 CrossRef CAS PubMed.
- Z. L. Peng, J. Yan, X. Fan, M. J. Mizianty, B. Xue and K. Wang, et al., Exceptionally abundant exceptions: comprehensive characterization of intrinsic disorder in all domains of life, Cell. Mol. Life Sci., 2015, 72(1), 137–151 CrossRef CAS PubMed.
- P. Tompa and A. Fersht, Structure and Function of Intrinsically Disordered Proteins, Chapman and Hall/CRC, 1st edn, 2009 Search PubMed.
- V. Weber, Intrinsically disordered proteins (IDPS): Structural characterization, therapeutic applications and future directions, 2016, vol. 1. pp. 1–107 Search PubMed.
- V. N. Uversky, Dancing protein clouds: Intrinsically disordered proteins in health and disease, Part A, Academic Press, 1st edn, 2019 Search PubMed.
- C. Y. C. Chen and W. L. Tou, How to design a drug for the disordered proteins, Drug Discovery Today, 2013, 18(19–20), 910–915 CrossRef CAS PubMed.
- S. Choudhary, M. Lopus and R. V. Hosur, Targeting disorders in unstructured and structured proteins in various diseases, Biophys. Chem., 2022, 281, 106742 CrossRef CAS PubMed.
- T. L. Blundell, M. N. Gupta and S. E. Hasnain, Intrinsic disorder in proteins: Relevance to protein assemblies, drug design and host-pathogen interactions, Prog. Biophys. Mol. Biol., 2020, 156, 34–42 CrossRef CAS PubMed.
- Y. G. Zhang, H. Q. Cao and Z. R. Liu, Binding cavities and druggability of intrinsically disordered proteins, Protein Sci., 2015, 24(5), 688–705 CrossRef CAS PubMed.
- P. Joshi and M. Vendruscolo, Druggability of Intrinsically Disordered Proteins, in Intrinsically Disordered Proteins Studied by Nmr Spectroscopy. Advances in Experimental Medicine and Biology, ed. I. C. Felli and R. Pierattelli, 2015, vol. 870, pp. 383–400 Search PubMed.
- G. Hu, Z. H. Wu, K. Wang, V. N. Uversky and L. Kurgan, Untapped Potential of Disordered Proteins in Current Druggable Human Proteome, Curr. Drug Targets, 2016, 17(10), 1198–1205 CrossRef CAS PubMed.
- B. K. Maity, Dynamics Based Drug Design for Intrinsically Disordered Proteins, Biophys. J., 2018, 114(3), 590A CrossRef.
- P. Santofimia-Castano, B. Rizzuti, Y. Xia, O. Abian, L. Peng and A. Velazquez-Campoy, et al., Designing and repurposing drugs to target intrinsically disordered proteins for cancer treatment: using NUPR1 as a paradigm, Mol. Cell. Oncol., 2019, 6(5), e1612678 CrossRef PubMed.
- H. Ruan, Q. Sun, W. L. Zhang, Y. Liu and L. H. Lai, Targeting intrinsically disordered proteins at the edge of chaos, Drug Discovery Today, 2019, 24(1), 217–227 CrossRef CAS PubMed.
- M. Ameri, N. Nezafat and S. Eskandari, The potential of intrinsically disordered regions in vaccine development, Expert Rev. Vaccines, 2022, 21(1), 1–3 CrossRef CAS PubMed.
- V. N. Uversky, Intrinsically Disordered Proteins, 1st edn, 2014 Search PubMed.
- V. Uversky and S. Longhi, Instrumental Analysis of Intrinsically Disordered Proteins: Assessing Structure and Conformation, 2010, vol. 9 Search PubMed.
- H. Kim and K. H. Han, PreSMo Target-Binding Signatures in Intrinsically Disordered Proteins, Mol. Cells, 2018, 41(10), 889–899 Search PubMed.
- N. E. Davey, K. Van Roey, R. J. Weatheritt, G. Toedt, B. Uyar and B. Altenberg, et al., Attributes of short linear motifs, Mol. BioSyst., 2012, 8(1), 268–281 RSC.
- V. N. Uversky, Intrinsically disordered proteins and novel strategies for drug discovery, Expert Opin. Drug Discovery, 2012, 7(6), 475–488 CrossRef CAS PubMed.
- L. Liu and Z. C. Zhang, Short Linear Motifs (SLiMs): New Functionally Diverse Modules Regulating Protein-protein Interactions, Prog. Biochem. Biophys., 2017, 44(2), 129–138 Search PubMed.
- T. J. Gibson, H. Dinkel, K. Van Roey and F. Diella, Experimental detection of short regulatory motifs in eukaryotic proteins: tips for good practice as well as for bad, Cell Commun. Signaling, 2015, 13, 42 CrossRef PubMed.
- A. B. Sigalov, A. V. Zhuravleva and V. Y. Orekhov, Binding of intrinsically disordered proteins is not necessarily accompanied by a structural transition to a folded form, Biochimie, 2007, 89(3), 419–421 CrossRef CAS PubMed.
- R. Tenchov and Q. A. Zhou, Intrinsically Disordered Proteins: Perspective on COVID-19 Infection and Drug Discovery, ACS Infect. Dis., 2022, 8(3), 422–432 CrossRef CAS PubMed.
- J. Lincoff, M. Haghighatlari, M. Krzeminski, J. M. C. Teixeira, G. N. W. Gomes and C. C. Gradinaru, et al., Extended experimental inferential structure determination method in determining the structural ensembles of disordered protein states, Commun. Chem., 2020, 3(1), 74 CrossRef CAS PubMed.
- C. Camilloni, A. De Simone, W. F. Vranken and M. Vendruscolo, Determination of Secondary Structure Populations in Disordered States of Proteins Using Nuclear Magnetic Resonance Chemical Shifts, Biochemistry, 2012, 51(11), 2224–2231 CrossRef CAS PubMed.
- J. T. Nielsen and F. A. A. Mulder, There is Diversity in Disorder -“In all Chaos there is a Cosmos, in all Disorder a Secret Order”, Front. Mol. Biosci., 2016, 3, 4 Search PubMed.
- J. A. Marsh, V. K. Singh, Z. C. Jia and J. D. Forman-Kay, Sensitivity of secondary structure propensities to sequence differences between alpha- and gamma-synuclein: Implications for fibrillation, Protein Sci., 2006, 15(12), 2795–2804 CrossRef CAS PubMed.
- K. Tamiola and F. A. A. Mulder, Using NMR chemical shifts to calculate the propensity for structural order and disorder in proteins, Biochem. Soc. Trans., 2012, 40, 1014–1020 CrossRef CAS PubMed.
- N. E. Hafsa and D. S. Wishart, CSI 2.0: a significantly improved version of the Chemical Shift Index, J. Biomol. NMR, 2014, 60(2–3), 131–146 CrossRef CAS PubMed.
- N. E. Hafsa, D. Arndt and D. S. Wishart, CSI 3.0: a web server for identifying secondary and super-secondary structure in proteins using NMR chemical shifts, Nucleic Acids Res., 2015, 43(W1), W370–W377 CrossRef CAS PubMed.
- D. S. Wishart, B. D. Sykes and F. M. Richards, The chemical shift index: a fast and simple method for the assignment of protein secondary structure through NMR spectroscopy, Biochemistry, 1992, 31(6), 1647–1651 CrossRef CAS PubMed.
- D. S. Wishart and B. D. Sykes, The 13C chemical-shift index: a simple method for the identification of protein secondary structure using 13C chemical-shift data, J. Biomol. NMR, 1994, 4(2), 171–180 CrossRef CAS PubMed.
- M. V. Berjanskii and D. S. Wishart, The RCI server: rapid and accurate calculation of protein flexibility using chemical shifts, Nucleic Acids Res., 2007, 35, W531–W537 CrossRef PubMed.
- M. V. Berjanskii and D. S. Wishart, Application of the random coil index to studying protein flexibility, J. Biomol. NMR, 2008, 40(1), 31–48 CrossRef CAS PubMed.
- M. Berjanskii and D. S. Wishart, NMR: prediction of protein flexibility, Nat. Protoc., 2006, 1(2), 683–688 CrossRef CAS PubMed.
- L. Y. Wang, H. R. Eghbalnia and J. L. Markley, Probabilistic approach to determining unbiased random-coil carbon-13 chemical shift values from the protein chemical shift database, J. Biomol. NMR, 2006, 35(3), 155–165 CrossRef CAS PubMed.
- R. Dass, F. A. A. Mulder and J. T. Nielsen, ODiNPred: comprehensive prediction of protein order and disorder, Sci. Rep., 2020, 10(1), 14780 CrossRef CAS PubMed.
- J. T. Nielsen and F. A. A. Mulder, CheSPI: chemical shift secondary structure population inference, J. Biomol. NMR, 2021, 75(6–7), 273–291 CrossRef CAS PubMed.
- S. Neal, A. M. Nip, H. Y. Zhang and D. S. Wishart, Rapid and accurate calculation of protein H-1, C-13 and N-15 chemical shifts, J. Biomol. NMR, 2003, 26(3), 215–240 CrossRef CAS PubMed.
- S. Schwarzinger, G. J. A. Kroon, T. R. Foss, P. E. Wright and H. J. Dyson, Random coil chemical shifts in acidic 8 M urea: Implementation of random coil shift data in NMRView, J. Biomol. NMR, 2000, 18(1), 43–48 CrossRef CAS PubMed.
- A. Pajon, W. F. Vranken, M. A. Jimenez, M. Rico and S. J. Wodak, PESCADOR: The PEptides in Solution ConformAtion Database: Online Resource, J. Biomol. NMR, 2002, 23(2), 85–102 CrossRef CAS PubMed.
- Z. Harmat, D. Dudola and Z. Gáspári, DIPEND: An Open-Source Pipeline to Generate Ensembles of Disordered Segments Using Neighbor-Dependent Backbone Preferences, Biomolecules, 2021, 11(10), 1505 CrossRef CAS PubMed.
- C. C. McDonald and W. D. Phillips, Proton magnetic resonance spectra of proteins in random-coil configurations, J. Am. Chem. Soc., 1969, 91(6), 1513–1521 CrossRef CAS PubMed.
- A. Bundi and K. Wüthrich, H-1-NMR parameters of the common amino-acid residues measured in aqueous-solutions of the linear tetrapeptides H-Gly-Gly-X-L-Ala-OH, Biopolymers, 1979, 18(2), 285–297 CrossRef CAS.
- D. Braun, G. Wider and K. Wüthrich, Sequence-corrected N-15 random coil chemical-shifts, J. Am. Chem. Soc., 1994, 116(19), 8466–8469 CrossRef CAS.
- D. S. Wishart, C. G. Bigam, A. Holm, R. S. Hodges and B. D. Sykes, H-1, C-13 and N-15 random coil nmr chemical-shifts of the common amino-acids. 1. Investigations of nearest-neighbor effects, J. Biomol. NMR, 1995, 5(1), 67–81 CrossRef CAS PubMed.
- J. A. Lukin, A. P. Gove, S. N. Talukdar and C. Ho, Automated probabilistic method for assigning backbone resonances of (C-13,N-15)-labeled proteins, J. Biomol. NMR, 1997, 9(2), 151–166 CrossRef CAS PubMed.
- S. Schwarzinger, G. J. A. Kroon, T. R. Foss, J. Chung, P. E. Wright and H. J. Dyson, Sequence-dependent correction of random coil NMR chemical shifts, J. Am. Chem. Soc., 2001, 123(13), 2970–2978 CrossRef CAS PubMed.
- Y. J. Wang and O. Jardetzky, Probability-based protein secondary structure identification using combined NMR chemical-shift data, Protein Sci., 2002, 11(4), 852–861 CrossRef CAS PubMed.
- Y. J. Wang and O. Jardetzky, Investigation of the neighboring residue effects on protein chemical shifts, J. Am. Chem. Soc., 2002, 124(47), 14075–14084 CrossRef CAS PubMed.
- H. Y. Zhang, S. Neal and D. S. Wishart, RefDB: A database of uniformly referenced protein chemical shifts, J. Biomol. NMR, 2003, 25(3), 173–195 CrossRef CAS PubMed.
- A. De Simone, A. Cavalli, S. T. D. Hsu, W. Vranken and M. Vendruscolo, Accurate Random Coil Chemical Shifts from an Analysis of Loop Regions in Native States of Proteins, J. Am. Chem. Soc., 2009, 131(45), 16332–+ CrossRef CAS PubMed.
- K. Tamiola, B. Acar and F. A. A. Mulder, Sequence-Specific Random Coil Chemical Shifts of Intrinsically Disordered Proteins, J. Am. Chem. Soc., 2010, 132(51), 18000–18003 CrossRef CAS PubMed.
- M. Kjaergaard and F. M. Poulsen, Sequence correction of random coil chemical shifts: correlation between neighbor correction factors and changes in the Ramachandran distribution, J. Biomol. NMR, 2011, 50(2), 157–165 CrossRef CAS PubMed.
- M. Sanz-Hernandez and A. De Simone, The PROSECCO server for chemical shift predictions in ordered and disordered proteins, J. Biomol. NMR, 2017, 69(3), 147–156 CrossRef CAS PubMed.
- J. T. Nielsen and F. A. A. Mulder, POTENCI: prediction of temperature, neighbor and pH-corrected chemical shifts for intrinsically disordered proteins, J. Biomol. NMR, 2018, 70(3), 141–165 CrossRef CAS PubMed.
- O. W. Howarth and M. J. Lilley, Carbon-13-NMR of peptides and proteins, Prog. Nucl. Magn. Reson. Spectrosc., 1978, 12(1), 1–40 CrossRef CAS.
- R. Richarz and K. Wüthrich, C-13 NMR chemical-shifts of common amino-acid residues measured in aqueous-solutions of linear tetrapeptides H-Gly-Gly-X-L-Ala-OH, Biopolymers, 1978, 17(9), 2133–2141 CrossRef CAS.
- P. Granger, M. Bourdonneau, O. Assemat and M. Piotto, NMR chemical shift measurements revisited: High precision measurements, Concepts Magn. Reson., Part A, 2007, 30(4), 184–193 CrossRef.
- L. Y. Wang and J. L. Markley, Empirical correlation between protein backbone N-15 and C-13 secondary chemical shifts and its application to nitrogen chemical shift re-referencing, J. Biomol. NMR, 2009, 44(2), 95–99 CrossRef CAS PubMed.
- S. P. Mielke and V. V. Krishnan, Protein structural class identification directly from NMR spectra using averaged chemical shifts, Bioinformatics, 2003, 19(16), 2054–2064 CrossRef CAS PubMed.
- S. P. Mielke and V. V. Krishnan, Characterization of protein secondary structure from NMR chemical shifts, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 54(3–4), 141–165 CrossRef CAS PubMed.
- M. Kjaergaard and F. M. Poulsen, Disordered proteins studied by chemical shifts, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 60, 42–51 CrossRef CAS PubMed.
- J. Kragelj, V. Ozenne, M. Blackledge and M. R. Jensen, Conformational Propensities of Intrinsically Disordered Proteins from NMR Chemical Shifts, ChemPhysChem, 2013, 14(13), 3034–3045 CrossRef CAS PubMed.
- W. M. Borcherds and G. W. Daughdrill, Using NMR Chemical Shifts to Determine Residue-Specific Secondary Structure Populations for Intrinsically Disordered Proteins, in Intrinsically Disordered Proteins. Methods in Enzymology, ed. E. Rhoades, 2018, vol. 611, pp. 101–136 Search PubMed.
- M. Kjaergaard, S. Brander and F. M. Poulsen, Random coil chemical shift for intrinsically disordered proteins: effects of temperature and pH, J. Biomol. NMR, 2011, 49(2), 139–149 CrossRef CAS PubMed.
- N. R. Luman, M. P. King and J. D. Augspurger, Predicting N-15 amide chemical shifts in proteins. I. An additive model for the backbone contribution, J. Comput. Chem., 2001, 22(3), 366–372 CrossRef CAS.
- J. A. Vila, D. R. Ripoll, H. A. Baldoni and H. A. Scheraga, Unblocked statistical-coil tetrapeptides and pentapeptides in aqueous solution: A theoretical study, J. Biomol. NMR, 2002, 24(3), 245–262 CrossRef CAS PubMed.
- J. A. Vila, H. A. Baldoni, D. R. Ripoll and H. A. Scheraga, Unblocked statistical-coil tetrapeptides in aqueous solution: Quantum-chemical computation of the carbon-13 NMR chemical shifts, J. Biomol. NMR, 2003, 26(2), 113–130 CrossRef CAS PubMed.
- D. A. Case, Chemical shifts in biomolecules, Curr. Opin. Struct. Biol., 2013, 23(2), 172–176 CrossRef CAS PubMed.
- X. He, T. Zhu, X. W. Wang, J. F. Liu and J. Z. H. Zhang, Fragment Quantum Mechanical Calculation of Proteins and Its Applications, Acc. Chem. Res., 2014, 47(9), 2748–2757 CrossRef CAS PubMed.
- T. M. O'Connell, L. Wang, A. Tropsha and J. Hermans, The “random-coil” state of proteins: Comparison of database statistics and molecular simulations, Proteins: Struct., Funct., Genet., 1999, 36(4), 407–418 CrossRef.
- A. Bundi and K. Wüthrich, Use of amide H-1-NMR titration shifts for studies of polypeptide conformation, Biopolymers, 1979, 18(2), 299–311 CrossRef CAS.
- S. Meier, M. Blackledge and S. Grzesiek, Conformational distributions of unfolded polypeptides from novel NMR techniques, J. Chem. Phys., 2008, 128(5), 052204 CrossRef PubMed.
- P. Kukic, D. Farrell, C. R. Sondergaard, U. Bjarnadottir, J. Bradley and G. Pollastri, et al., Improving the analysis of NMR spectra tracking pH-induced conformational changes: Removing artefacts of the electric field on the NMR chemical shift, Proteins: Struct., Funct., Bioinf., 2010, 78(4), 971–984 CrossRef CAS PubMed.
- A. I. de Opakua, N. Merino, M. Villate, T. N. Cordeiro, G. Ormaza and M. Sanchez-Carbayo, et al., The metastasis suppressor KISS1 is an intrinsically disordered protein slightly more extended than a random coil, PLoS One, 2017, 12(2), e0172507 CrossRef PubMed.
- W. Peti, L. J. Smith, C. Redfield and H. Schwalbe, Chemical shifts in denatured proteins: Resonance assignments for denatured ubiquitin and comparisons with other denatured proteins, J. Biomol. NMR, 2001, 19(2), 153–165 CrossRef CAS PubMed.
- T. Kakeshpour, V. Ramanujam, C. A. Barnes, Y. Shen, J. F. Ying and A. Bax, A lowly populated, transient beta-sheet structure in monomeric A beta(1-42) identified by multinuclear NMR of chemical denaturation, Biophys. Chem., 2021, 270, 106531 CrossRef CAS PubMed.
- D. K. Klimov and D. Thirumalai, Stiffness of the distal loop restricts the structural heterogeneity of the transition state ensemble in SH3 domains, J. Mol. Biol., 2002, 317(5), 721–737 CrossRef CAS PubMed.
- J. R. Costa and S. N. Yaliraki, Role of rigidity on the activity of proteinase inhibitors and their peptide mimics, J. Phys. Chem. B, 2006, 110(38), 18981–18988 CrossRef CAS PubMed.
- X. Y. Bai, G. Meng, M. Luo and X. F. Zheng, Rigidity of Wedge Loop in PACSIN 3 Protein Is a Key Factor in Dictating Diameters of Tubules, J. Biol. Chem., 2012, 287(26), 22387–22396 CrossRef CAS PubMed.
- Z. Shahbazi and A. Demirtas, Rigidity Analysis of Protein Molecules, J. Comput. Inf. Sci. Eng., 2015, 15(3), 031009 CrossRef.
- Y. Gu, D. W. Li and R. Bruschweiler, Statistical database analysis of the role of loop dynamics for protein-protein complex formation and allostery, Bioinformatics, 2017, 33(12), 1814–1819 CrossRef CAS PubMed.
- M. S. Choy, Y. Li, L. Machado, M. B. A. Kunze, C. R. Connors and X. Y. Wei, et al., Conformational Rigidity and Protein Dynamics at Distinct Timescales Regulate PTP1B Activity and Allostery, Mol. Cell, 2017, 65(4), 644–+ CrossRef CAS PubMed.
- C. J. Holland, B. J. MacLachlan, V. Bianchi, S. J. Hesketh, R. Morgan and O. Vickery, et al., In Silico and Structural Analyses Demonstrate That Intrinsic Protein Motions Guide T cell Receptor Complementarity Determining Region Loop Flexibility, Front. Immunol., 2018, 9, 674 CrossRef PubMed.
- M. A. Majorina, V. A. Balobanov, V. N. Uversky and B. S. Melnik, Loops linking secondary structure elements affect the stability of the molten globule intermediate state of apomyoglobin, FEBS Lett., 2020, 594(20), 3293–3304 CrossRef CAS PubMed.
- K. I. Oh, Y. S. Jung, G. S. Hwang and M. Cho, Conformational distributions of denatured and unstructured proteins are similar to those of 20 × 20 blocked dipeptides, J. Biomol. NMR, 2012, 53(1), 25–41 CrossRef CAS PubMed.
- D. Curco, C. Michaux, G. Roussel, E. Tinti, E. A. Perpete and C. Aleman, Stochastic simulation of structural properties of natively unfolded and denatured proteins, J. Mol. Model., 2012, 18(9), 4503–4516 CrossRef CAS PubMed.
- F. Avbelj, S. G. Grdadolnik, J. Grdadolnik and R. L. Baldwin, Intrinsic backbone preferences are fully present in blocked amino acids, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(5), 1272–1277 CrossRef CAS PubMed.
- B. Shan, S. Bhattacharya, D. Eliezer and D. P. Raleigh, The low-pH unfolded state of the C-terminal domain of the ribosomal protein L9 contains significant secondary structure in the absence of denaturant but is no more compact than the low-pH urea unfolded state, Biochemistry, 2008, 47(36), 9565–9573 CrossRef CAS PubMed.
- D. A. C. Beck, D. O. V. Alonso, D. Inoyama and V. Daggett, The intrinsic conformational propensities of the 20 naturally occurring amino acids and reflection of these propensities in proteins, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(34), 12259–12264 CrossRef CAS PubMed.
- C. L. Towse, J. Vymetal, J. Vondrasek and V. Daggett, Insights into Unfolded Proteins from the Intrinsic phi/psi Propensities of the AAXAA Host-Guest Series, Biophys. J., 2016, 110(2), 348–361 CrossRef CAS PubMed.
- M. B. Erlach, J. Koehler, E. Crusca, W. Kremer, C. E. Munte and H. R. Kalbitzer, Pressure dependence of backbone chemical shifts in the model peptides Ac-Gly-Gly-Xxx-Ala-NH2, J. Biomol. NMR, 2016, 65(2), 65–77 CrossRef CAS PubMed.
- M. B. Erlach, J. Koehler, E. Crusca, C. E. Munte, M. Kainosho and W. Kremer, et al., Pressure dependence of side chain C-13 chemical shifts in model peptides Ac-Gly-Gly-Xxx-Ala-NH2, J. Biomol. NMR, 2017, 69(2), 53–67 CrossRef PubMed.
- M. B. Erlach, J. Koehler, C. E. Munte, W. Kremer, E. Crusca and M. Kainosho, et al., Pressure dependence of side chain H-1 and N-15-chemical shifts in the model peptides Ac-Gly-Gly-Xxx-Ala-NH2, J. Biomol. NMR, 2020, 74(8–9), 381–399 CrossRef PubMed.
- J. Koehler, M. B. Erlach, E. Crusca, W. Kremer, C. E. Munte and H. R. Kalbitzer, Pressure Dependence of N-15 Chemical Shifts in Model Peptides Ac-Gly-Gly-X-Ala-NH2, Materials, 2012, 5(10), 1774–1786 CrossRef CAS.
- M. R. Arnold, W. Kremer, H. D. Lüdemann and H. R. Kalbitzer, 1H-NMR parameters of common amino acid residues measured in aqueous solutions of the linear tetrapeptides Gly-Gly-X-Ala at pressures between 0.1 and 200 MPa, Biophys. Chem., 2002, 96(2–3), 129–140 CrossRef CAS PubMed.
- E. A. Bienkiewicz and K. J. Lumb, Random-coil chemical shifts of phosphorylated amino acids, J. Biomol. NMR, 1999, 15(3), 203–206 CrossRef CAS PubMed.
- A. C. Conibear, K. J. Rosengren, C. F. W. Becker and H. Kaehlig, Random coil shifts of posttranslationally modified amino acids, J. Biomol. NMR, 2019, 73(10–11), 587–599 CrossRef CAS PubMed.
- V. Thanabal, D. O. Omecinsky, M. D. Reily and W. L. Cody, The 13C chemical shifts of amino acids in aqueous solution containing organic solvents: application to the secondary structure characterization of peptides in aqueous trifluoroethanol solution, J. Biomol. NMR, 1994, 4(1), 47–59 CrossRef CAS PubMed.
- M. L. Tremblay, A. W. Banks and J. K. Rainey, The predictive accuracy of secondary chemical shifts is more affected by protein secondary structure than solvent environment, J. Biomol. NMR, 2010, 46(4), 257–270 CrossRef CAS PubMed.
- R. Schweitzer-Stenner, Exploring Nearest Neighbor Interactions and Their Influence on the Gibbs Energy Landscape of Unfolded Proteins and Peptides, Int. J. Mol. Sci., 2022, 23(10), 5643 CrossRef CAS PubMed.
- K. Tamiola, https://github.com/ktamiola/ncIDP/tree/master/private/original-data-csv.
- E. A. Carlisle, J. L. Holder, A. M. Maranda, A. R. de Alwis, E. L. Selkie and S. L. McKay, Effect of pH, urea, peptide length, and neighboring amino acids on alanine alpha-proton random coil chemical shifts, Biopolymers, 2007, 85(1), 72–80 CrossRef CAS PubMed.
- A. S. Maltsev, J. F. Ying and A. Bax, Impact of N-Terminal Acetylation of alpha-Synuclein on Its Random Coil and Lipid Binding Properties, Biochemistry, 2012, 51(25), 5004–5013 CrossRef CAS PubMed.
- L. Willard, A. Ranjan, H. Y. Zhang, H. Monzavi, R. F. Boyko, B. D. Sykes and D. S. Wishart, VADAR: a web server for quantitative evaluation of protein structure quality, Nucleic Acids Res., 2003, 31(13), 3316–3319 CrossRef CAS PubMed.
- W. Kabsch and C. Sander, Dictionary of protein secondary structure - pattern-recognition of hydrogen-bonded and geometrical features, Biopolymers, 1983, 22(12), 2577–2637 CrossRef CAS PubMed.
- M. Vendruscolo, https://www-cohsoftware.ch.cam.ac.uk/index.php/camcoil.
- F. Poulsen https://spin.niddk.nih.gov/bax/nmrserver/Poulsen_rc_CS/.
- M. Sanz-Hernández and A. De Simone, http://desimone.bio.ic.ac.uk/prosecco/.
- A. G. Georgiev, Interpretable Numerical Descriptors of Amino Acid Space, J. Comput. Biol., 2009, 16(5), 703–723 CrossRef CAS.
- D. Farrell, E. S. Miranda, H. Webb, N. Georgi, P. B. Crowley and L. P. McIntosh, et al., Titration_DB: Storage and analysis of NMR-monitored protein pH titration curves, Proteins: Struct., Funct., Bioinf., 2010, 78(4), 843–857 CrossRef CAS PubMed.
- G. Platzer, M. Okon and L. P. McIntosh, pH-dependent random coil H-1, C-13, and N-15 chemical shifts of the ionizable amino acids: a guide for protein pK (a) measurements, J. Biomol. NMR, 2014, 60(2–3), 109–129 CrossRef CAS PubMed.
- R. L. Croke, S. M. Patil, J. Quevreaux, D. A. Kendall and A. T. Alexandrescu, NMR determination of pK(a) values in alpha-synuclein, Protein Sci., 2011, 20(2), 256–269 CrossRef CAS PubMed.
- C. Cozza, J. L. Neira, F. J. Florencio, M. I. Muro-Pastor and B. Rizzuti, Intrinsically disordered inhibitor of glutamine synthetase is a functional protein with random-coil-like pK(a) values, Protein Sci., 2017, 26(6), 1105–1115 CrossRef CAS PubMed.
- K. Tamiola, R. M. Scheek, P. van der Meulen and F. A. A. Mulder, pepKalc: scalable and comprehensive calculation of electrostatic interactions in random coil polypeptides, Bioinformatics, 2018, 34(12), 2053–2060 CrossRef CAS PubMed.
- N. J. Baxter and M. P. Williamson, Temperature dependence of H-1 chemical shifts in proteins, J. Biomol. NMR, 1997, 9(4), 359–369 CrossRef CAS PubMed.
- P. Rovó, P. Stráner, A. Láng, I. Bartha, K. Huszár, L. Nyitray and A. Perczel, Structural Insights into the Trp-Cage Folding Intermediate Formation, Chem.–Eur. J., 2013, 19(8), 2628–2640 CrossRef PubMed.
- A. Fizil, Z. Gáspári, T. Barna, F. Marx and G. Batta, “Invisible” Conformers of an Antifungal Disulfide Protein Revealed by Constrained Cold and Heat Unfolding, CEST-NMR Experiments, and Molecular Dynamics Calculations, Chem.–Eur. J., 2015, 21(13), 5136–5144 CrossRef CAS PubMed.
- K. Trainor, J. A. Palumbo, D. W. S. MacKenzie and E. M. Meiering, Temperature dependence of NMR chemical shifts: Tracking and statistical analysis, Protein Sci., 2020, 29(1), 306–314 CrossRef CAS PubMed.
- E. F. Dudás, G. Pálfy, D. K. Menyhárd, F. Sebák, P. Ecsédi, L. Nyitray and A. Bodor, Tumor-Suppressor p53TAD(1-60)Forms a Fuzzy Complex with Metastasis-Associated S100A4: Structural Insights and Dynamics by an NMR/MD Approach, Chembiochem, 2020, 21(21), 3087–3095 CrossRef PubMed.
- F. Sebák, P. Ecsédi, W. Bermel, B. Luy, L. Nyitray and A. Bodor, Selective H-1(alpha) NMR Methods Reveal Functionally Relevant Proline cis/trans Isomers in Intrinsically Disordered Proteins: Characterization of Minor Forms, Effects of Phosphorylation, and Occurrence in Proteome, Angew. Chem., Int. Ed., 2022, 61(1), e202108361 CrossRef PubMed.
- M. Iwadate, T. Asakura and M. P. Williamson, C-alpha and C-beta carbon-13 chemical shifts in proteins from an empirical database, J. Biomol. NMR, 1999, 13(3), 199–211 CrossRef CAS PubMed.
- D. S. Weinstock, C. Narayanan, J. Baum and R. M. Levy, Correlation between C-13 alpha chemical shifts and helix content of peptide ensembles, Protein Sci., 2008, 17(5), 950–954 CrossRef CAS PubMed.
- G. P. F. Wood and U. Rothlisberger, Secondary Structure Assignment of Amyloid-beta Peptide Using Chemical Shifts, J. Chem. Theory Comput., 2011, 7(5), 1552–1563 CrossRef CAS PubMed.
- A. B. Mantsyzov, A. S. Maltsev, J. F. Ying, Y. Shen, G. Hummer and A. Bax, A maximum entropy approach to the study of residue-specific backbone angle distributions in alpha-synuclein, an intrinsically disordered protein, Protein Sci., 2014, 23(9), 1275–1290 CrossRef CAS PubMed.
- A. B. Mantsyzov, Y. Shen, J. H. Lee, G. Hummer and A. Bax, MERA: a webserver for evaluating backbone torsion angle distributions in dynamic and disordered proteins from NMR data, J. Biomol. NMR, 2015, 63(1), 85–95 CrossRef CAS PubMed.
- J. Roche, Y. Shen, J. H. Lee, J. F. Ying and A. Bax, Monomeric A beta(1-40) and A beta(1-42) Peptides in Solution Adopt Very Similar Ramachandran Map Distributions That Closely Resemble Random Coil, Biochemistry, 2016, 55(5), 762–775 CrossRef CAS PubMed.
- J. L. Morgan, M. R. Jensen, V. Ozenne, M. Blackledge and E. Barbar, The LC8 Recognition Motif Preferentially Samples Polyproline II Structure in Its Free State, Biochemistry, 2017, 56(35), 4656–4666 CrossRef CAS PubMed.
- J. R. Xie, K. X. Zhang and A. T. Frank, PyShifts: A PyMOL Plugin for Chemical Shift-Based Analysis of Biomolecular Ensembles, J. Chem. Inf. Model., 2020, 60(3), 1073–1078 CrossRef CAS PubMed.
- K. Héberger, Sum of ranking differences compares methods or models fairly, TrAC, Trends Anal. Chem., 2010, 29(1), 101–109 CrossRef.
- K. Héberger and K. Kollár-Hunek, Sum of ranking differences for method discrimination and its validation: comparison of ranks with random numbers, J. Chemom., 2011, 25(4), 151–158 CrossRef.
- D. Bajusz, A. Rácz and K. Héberger, Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations?, J. Cheminf., 2015, 7, 20 Search PubMed.
- A. Gere, K. Héberger and S. Kovács, How to predict choice using eye-movements data?, Food Res. Int., 2021, 143, 110309 CrossRef PubMed.
- T. S. Ulmer and A. Bax, Comparison of structure and dynamics of micelle-bound human alpha-synuclein and Parkinson disease variants, J. Biol. Chem., 2005, 280(52), 43179–43187 CrossRef CAS PubMed.
- T. S. Ulmer, A. Bax, N. B. Cole and R. L. Nussbaum, Structure and dynamics of micelle-bound human alpha-synuclein, J. Biol. Chem., 2005, 280(10), 9595–9603 CrossRef CAS PubMed.
- F. Longhena, G. Faustini and A. Bellucci, Study of alpha-synuclein fibrillation: state of the art and expectations, Neural Regener. Res., 2020, 15(1), 59–60 CrossRef CAS PubMed.
- J. M. Krieger, G. Fusco, M. Lewitzky, P. C. Simister, J. Marchant and C. Camilloni, et al., Conformational Recognition of an Intrinsically Disordered Protein, Biophys. J., 2014, 106(8), 1771–1779 CrossRef CAS PubMed.
- http://aki.ttk.hu/srd/.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00977g |
| This journal is © The Royal Society of Chemistry 2023 |