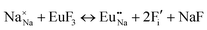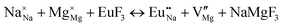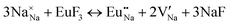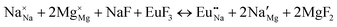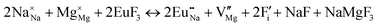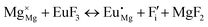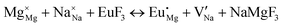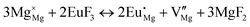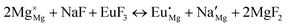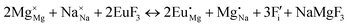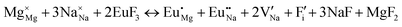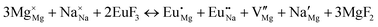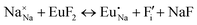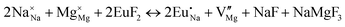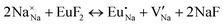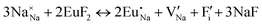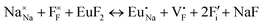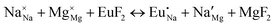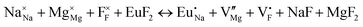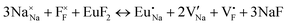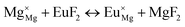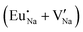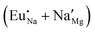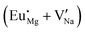Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Defect clustering in an Eu-doped NaMgF3 compound and its influence on luminescent properties†
Afranio
Sousa
 a,
Adelmo
Souza
a,
Adelmo
Souza
 b and
Heveson
Lima
b and
Heveson
Lima
 *c
*c
aDepartamento de Física, Universidade Federal de Sergipe, 49100-000, São Cristóvão, SE, Brazil
bCentro Multidisciplinar do Campus de Bom Jesus da Lapa, Universidade Federal do Oeste da Bahia, 47600-000, Bom Jesus da Lapa, BA, Brazil
cCentro Multidisciplinar do Campus de Luís Eduardo Magalhães, Universidade Federal do Oeste da Bahia, 47850-000, Luís Eduardo Magalhães, BA, Brazil. E-mail: heveson.matos@ufob.edu.br
First published on 26th January 2021
Abstract
Luminescent properties of compounds based on lanthanide ions are strongly influenced by defect clustering, and unfortunately, these defects are not fully understood in lanthanide-doped fluoroperovskite materials. In this context, we studied the structural properties and effects upon incorporation of divalent and trivalent Europium dopant ions in the orthorhombic phase of NaMgF3, combining classic atomistic simulations and crystal field models. We developed a new set of interatomic potentials that reproduce the structural properties, as well as lattice parameters, interatomic distances and volumes, and elastic properties, with good accordance with experimental results. Analysis of the solution energy revealed that Eu3+ is most energetically favourable in the Mg site, while Eu2+ is most favourable in the Na site. The mechanism of charge compensation was investigated in both cases. We also analysed the local symmetry, charge transfer in Eu–F chemical bonding, crystal field parameters, and 7F1 energy sub-levels of the Eu3+ ion in the host matrix based on crystal field and electronegativity models. In addition, we discussed the photoionization cross-section and optically stimulated luminescence (OSL) decay pattern for Eu2+-doped NaMgF3. Thus, this work provides direction for new material design and opens up a framework to analyse structural and defect changes of fluroperovskite compounds upon lanthanide ion insertion.
1 Introduction
Perovskite compounds are a class of special materials that have attracted wide attention in recent years for interesting applications, such as magnetoelectrics,1,2 photovoltaics devices,3–6 light-emitting diodes,7,8 lasers,9,10 photocatalysis,11 memristors,12 and ionizing radiation detectors.13–15 Fluoroperovskite materials, ABF3 (where A and B stand for alkali and alkaline earth metals, respectively), are a sub-class of perovskite compounds. In particular, NaMgF3 is a material inserted in this family, with interesting properties related to optics and ionizing radiation dosimetry.16,17 Rare earth-doped NaMgF3 compounds have been considered promising materials for personal dosimetry because of the effective atomic number, similar to human tissue, and high sensitivity at low dosages.18,19 Unlike the other materials of this class, such as AMgF3 (A = Rb, K, and Cs), NaMgF3 presents an orthorhombic perovskite structure with space group Pbnm at room temperature and standard pressure.20Luminescent properties of NaMgF3 nanoparticles doped with lanthanide ions and Mn, synthesized using a reverse micro-emulsion method, have been reported.21,22 Furthermore, lanthanide ions doped into NaMgF3 polycrystalline samples have also been prepared by the conventional solid-state reaction method.23,24 In fact, lanthanide incorporation in compounds has been largely used to enhance luminescent properties. In particular, Eu3+-doped materials are a well-known red emitting phosphors, widely used as spectroscopic probes because of their unique emission characteristics.25–27 Valuable characterization information, such as local symmetry of the optically active ion, occupancy number, and Stark levels, can be obtained from emission characteristics of the Eu3+ ion. However, in many cases, the Eu ion is incorporated in a host matrix and aliovalent substitution occurs. The difference between the ionic radii of both ions (doped and host) is an important factor in evaluating the influence of aliovalent substitution, giving rise to material defects. Identifying these defects is crucial to accurately describing the spectroscopic properties and understanding specific mechanisms relevant to their application in optics and ionizing radiation detectors. Mechanisms of charge compensation are not yet established for Eu3+- and Eu2+-doped NaMgF3. Some reports have suggested different types of charge compensation in materials of the same family (KMgF328–30 and RbMgF331) doped with different lanthanide ions. However, these discussions are based on ion sizes (doped and host), ignoring discussions about lattice solution energy. In addition, the symmetry site and coordination number of the optically active ion are not clear, as well as the substitution site in the host matrix. The optically stimulated luminescence (OSL) decay pattern and high sensibility of the NaMgF3:Eu2+ compound for low dose levels are not fully established. Therefore, a systematic study is necessary to make predictions about the incorporation of defects in the NaMgF3 structure.
Classical atomistic simulation is a reliable tool for modelling a range of ionic materials and to help understand theoretical and experimental results. In this methodology, interactions between atoms are determined by interatomic potentials that are essential to studying physical properties of the simulated systems. Several studies have been widely used to examine structural, mechanical, elastic, and dielectric properties in solid-state materials.32–36 Furthermore, atomistic simulation is able to perform studies on defect properties with low computational cost, compared with other methodologies, and has been successfully employed to study defects.37–40 In addition, atomistic simulation procedures, combined with crystal field theory, is an practical method for describing spectroscopic properties of lanthanide ion-doped compounds and their dopant-related effects. Recently, Otsuka et al.41 performed a study from a spectroscopic point of view, combining atomistic simulation, the simple overlap model (SOM),42 and the method of nearest neighbours43 (theoretical models of crystal field). The combination of both methodologies successfully described local symmetry and coordination number of the optically active ion, crystal field parameters, crystal field strength, 7F1 stark sub-levels, and splitting.
Thus, in this work, we used a combination of classic atomistic simulation-based ionic models and crystal field models to study the orthorhombic phase of NaMgF3. Firstly, atomistic simulation was used to describe structural properties and the defect formation process with the incorporation of Eu3+ and Eu2+ ions into NaMgF3. For this, we developed a new set of interatomic potentials to describe the interactions between ions for the compound in the orthorhombic phase and performed a study of the structural and elastic properties. We carried out a defect study to obtain the most favourable charge compensation mechanism. Secondly, crystal field models were used to study spectroscopic properties of Eu2+ and Eu3+ ion-doped NaMgF3. Detailed local geometry of the optically active ion in this host matrix was obtained. In addition, photoionization cross-section calculations, associated with the first-order kinetic model, gave us information about the OSL decay pattern and high sensibility of the Eu2+-doped NaMgF3 compound.
2 Methodologies
2.1 Computational simulation
The atomistic simulation technique was used to study the perfect structure and defective lattice of orthorhombic NaMgF3, performed by GULP code.44 Relaxation of the lattice parameters and atomic positions was completed to find the lowest energy. A description of the structural properties of the system depends on a set of potential parameters, adopted for a reliable description of fundamental interactions between the ions. Long-range interactions were calculated by Coulomb potential and short-range interactions by Buckingham potential. Eqn (1) shows the representation of repulsive (or Pauli repulsion) and attractive (or van der Waals interaction) terms of the Buckingham potential: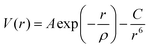 | (1) |
In addition, a model for efficient treatment of ionic polarization effects is necessary, and a simple model, known as the shell model,45 was used. Ions in this model are represented by a core (massive, includes the nucleus plus core electrons) and shell (massless, includes valence electrons) connected by a harmonic constant. The formal charge of the ion is obtained by the sum of the core and shell charges.
The defect calculation was performed using a two-region strategy.46 This method is very useful for calculating defects in atomistic simulations and has been used successfully.47–51 The crystal lattice is divided into two spherical regions (I and II), where the defect (or defect cluster) is placed in the centre of these regions. The inner region I is the portion of the crystal located around the defect, allowing explicit relaxation of all the ion positions under the action of a force field. Region II is more distant from the defect and can be treated using an approximate continuous method, since ions in this region exhibit an interatomic displacement smaller than the ions in region I. To obtain reliable results, a convergence test, with an appropriate radius for these regions, is necessary. In this work, we used 12 and 18 Å for regions I and II, respectively. This corresponds to approximately 1000 ions in the region I and 2400 ions in region II. The total energy (ET) can be calculated by the expression ET = E1(x) + E12(x,u) + E2(u), where E1(x) is the energy of region I, E2(u) is the energy of region II, and E12(x,u) is the energy of the interaction region between them.
2.2 Crystal field parameters and Stark levels of the 7F1 multiplet
Interaction between the lanthanide ion and its nearest neighbours (NNs) has been a discussion theme in research groups that work with lanthanide spectroscopy, for a long time. The point charge electrostatic model (PCEM)52 was the first non-parametric model to discuss crystal field parameters from a theoretical point of view. The PCEM considers that the bond between the lanthanide ion and its chemical surrounding is purely ionic, where the charge factor is equal to ligand valence and is located at the NN's position. Although some considerations of the PCEM have led to unsatisfactory results from a quantitative point of view, it has been the base model for the development of other theoretical models.The simple overlap model42 used in our predictions is a theoretical model based on the PCEM, which has been largely used in lanthanide spectroscopy with satisfactory predictions.53,54 The SOM introduces a small covalent character to describe Ln–NN chemical bonding. In this assumption, the effective interaction charge is defined as −ρjgje and is located around the Ln–NN middle distance (Rj/2β). gj is the charge factor devoted to Ln–NN chemical bonding, Rj is j-th NN distance from the Ln ion, e is the elementary charge, and βj = 1/(1 ± ρj) is a factor that determines the position of the effective charge in the middle distance. The minus sign is applied when the charge is closer to the Ln ion, and the plus sign is applied when the charge is closer to the ligand. ρj = ρ0(R0/Rj)3.5 describes the overlap of interacting wavefunctions, where R0 is the smaller Ln–NN distance, and ρ0 = 0.05 is the maximum overlap between the 4f and 2s (or 2p) orbitals.55
Through these considerations, the crystal field parameters (Bkq) of the SOM can be related to PCEM, as show eqn (2):
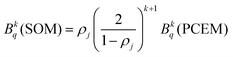 | (2) |
The 7F1 energy sublevels of Eu3+ can be obtained through diagonalization of the crystal field matrix within the 7F1 manifold.56 Thus,
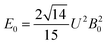 | (3) |
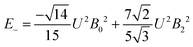 | (4) |
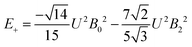 | (5) |
2.3 Photoionization cross-section of trap levels
The photoionization cross-section (σ) is an essential quantity to understand the interaction processes of electromagnetic radiation with matter. Recently, Lima–Batista–Couto57 proposed a model to obtain σ of localized traps in the band gap with activation energy Ei with respect to the conduction band, based on time-dependent perturbation theory. The model describes the trap level by a three-dimensional isotropic harmonic oscillator wavefunction with angular frequency ω0, and the electron in the conduction band is described by the plane wavefunction. Following the same steps reported previously57 and using the Fermi's golden rule, we obtain: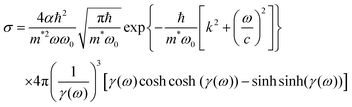 | (6) |
3 Results and discussion
3.1 Interatomic potentials of NaMgF3
To analyse the structural properties and influence of defect clustering on the luminescent properties of the compound, describing the interactions between ions of the materials through a reliable set of interatomic potentials is necessary. We developed a new set of interatomic potentials for the orthorhombic phase of NaMgF3 from an empirical fitting procedure, carried out with GULP code.44 The empirical fitting was used to obtain Buckingham potential parameters for the Na–F interaction. The potential parameters used for Mg–F and F–F interactions were taken from a previous study33 and have already been tested and validated for compounds of the same family, AMgF3 (A = K, Cs, and Rb). Table 1 shows the interatomic potentials and shell model parameters used in all calculations of this work. A short range potential cutoff of 12 Å was used.This set of interatomic potentials was validated, and the calculated lattice parameters of the NaMgF3 compound are in excellent agreement with X-ray diffraction values, as well as mechanical properties. Elastic and dielectric constants are close to experimental values (see next section). The fluoride precursors NaF and MgF2 are commonly used to synthesize NaMgF3. In addition, the same set of potentials is also capable of modelling precursor fluorides (NaF and MgF2). Even though the focus of this work was to analyse the orthorhombic NaMgF3 phase, we were able to show that this set of interatomic potentials is transferable to the cubic phase of NaMgF3, as well. Calculations of the various precursor fluoride properties and cubic NaMgF3 are shown in the supporting information (see Tables S1–S7, ESI†). These facts are important validation characteristics for successfully calculating defect properties.
3.2 Structural properties of the orthorhombic NaMgF3
Table 2 presents a comparison between calculated and experimental data from lattice parameters and cell volumes for orthorhombic NaMgF3. A relative error of less than 0.82% was calculated for all lattice parameters and cell volumes with respect to X-ray diffraction data.59Table 3 shows the most relevant interatomic distances for orthorhombic NaMgF3 calculated in this work compared to experimental data.59 The distances presented a relative error below 3% in all cases. These results show that our atomistic simulation has good acceptance in the reproduction of NaMgF3 structural properties. In addition, a similar relative error was observed for all properties studied for cubic NaMgF3 using the same set of interatomic potentials, as shown in the supporting information.| Lattice parameters | Ref. 59 | This work | % |
|---|---|---|---|
| a (Å) | 5.360 | 5.404 | 0.82 |
| b (Å) | 5.488 | 5.473 | −0.27 |
| c (Å) | 7.666 | 7.689 | 0.30 |
| V (Å3) | 225.53 | 227.40 | 0.83 |
| Distance | Ref. 59 | This work | % |
|---|---|---|---|
| Na–F1(x1) | 2.322 | 2.322 | 0.00 |
| Na–F2(x2) | 2.303 | 2.337 | 1.48 |
| Na–F1(x1) | 2.416 | 2.474 | 2.40 |
| Na–F2(x2) | 2.563 | 2.640 | 3.00 |
| Na–F2(x2) | 2.710 | 2.710 | 0.00 |
| Na–F1(x1) | 3.097 | 3.079 | −0.58 |
| Na–F1(x1) | 3.185 | 3.118 | −2.09 |
| Mg–F2(x2) | 1.981 | 1.974 | −0.35 |
| Mg–F1(x2) | 1.979 | 1.976 | −0.15 |
| Mg–F2(x2) | 1.989 | 1.977 | −0.60 |
Fig. 1 presents the orthorhombic NaMgF3 phase with space group Pbnm calculated for this work. The structure contains four non-equivalent (Na, Mg, F1, and F2) atoms. Mg2+ ions are coordinated by six F atoms, organized into three pairs of Mg–F bonds with approximately the same distances (two pairs of Mg–F2 bonds are equatorials and one pair of Mg–F1 bonds is apical). The Na atom is coordinated by eight F atoms, with only two Na–F1 bonds, and almost all bond distances are between Na–F2. This compound presents a different structural behaviour at room temperature and pressure compared to other materials of the same family (AMgF3, A = Cs, Rb, and K).33
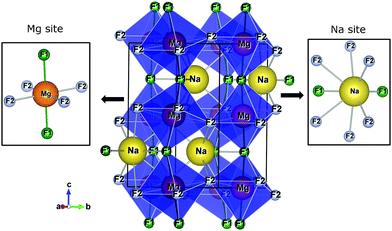 | ||
| Fig. 1 The crystalline structure of NaMgF3 in an orthorhombic lattice with space group Pbnm. Na and Mg sites are shown in detail. | ||
The elastic constants (C11, C22, C12, C13, C23, C33, C44, C55, and C66) of NaMgF3 in the orthorhombic phase are shown in Table 4, and the values calculated in this work are compared with experimental data.60 The elastic constants satisfy Born's criteria and prove its mechanical stability. The reproducibility of these properties validates the potentials and transferability, which is crucial for modelling physical properties under conditions different from the initial fitting procedure. The bulk modulus, shear modulus, static dielectric constant (ε0), and high-frequency dielectric constant (ε∞) for orthorhombic NaMgF3 are also shown in Table 4. In addition, our results show excellent transferability of these potentials for cubic NaMgF3 (see ESI†). Having successfully completed this first step, we next analysed defect properties and their influence on spectroscopic properties of NaMgF3.
| Elastic constants (GPa) | Ref. 60 | This work | % |
|---|---|---|---|
| C11 | 125.7 | 132.9 | 5.7 |
| C22 | 147.3 | 134.9 | −8.4 |
| C12 | 49.5 | 50.2 | 1.4 |
| C13 | 45.1 | 46.2 | 2.4 |
| C23 | 43.1 | 47.8 | 10.9 |
| C33 | 142.5 | 135.1 | −5.2 |
| C44 | 46.7 | 45.3 | −3.0 |
| C55 | 44.8 | 43.4 | −3.1 |
| C66 | 50.4 | 43.8 | −13.1 |
| Dielectric constants | |||
| ε 0 | — | 7.75 | — |
| ε ∞ | — | 2.20 | — |
| Bulk modulus (GPa) | — | 76.82 | — |
| Shear modulus (GPa) | — | 43.72 | — |
3.3 Defect calculations
The process of incorporating Eu3+ and Eu2+ ions into the NaMgF3 compound requires a charge compensation mechanism to stabilize the local structure and accommodate extra charge in the relaxed structure. Interatomic potential used to describe Eu–F interactions was taken from a previous study for modelling natural apatite crystals,61 and have already been tested and validated for Rare-Earth fluorides. The incorporation of defects into the crystalline structure, obtained by our atomistic simulation, can estimate the preferred doping site and mechanism of charge compensation most favourably. Firstly, we consider the various possible schemes of charge compensation for the incorporation of Eu3+ and Eu2+ in the NaMgF3 compound. Tables 5 and 6 show the proposed chemical reaction schemes, expressed in Kröger–Vink notation,62 for the incorporation of Eu3+ and Eu2+ ions, respectively. After that, the next stage is the calculation of solution energy (Esol) for each reaction, performed to predict the most energetically favourable scheme. The solution energy was obtained by a combination of defect energies, lattice energy of the fluoride precursor, and lattice energy of the dopant ion. In this work, the solution energies are calculated considering defects as isolated species (or unbound defects) and simulated in a cluster of defects (or bound defects). The motivation for calculating a cluster of defects is to account for the binding energy for different arrangements that frequently present the lowest energy. An example of how to calculate the solution energy for unbound (Eunboundsol) or bound defects (Eboundsol) is shown in eqn (7a) and (7b) for the first reaction (Scheme I) in Table 5. For the other reactions, a similar procedure is employed.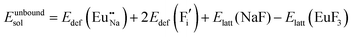 | (7a) |
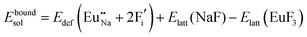 | (7b) |
Tables S8–S12 in the ESI† show defect and lattice energies required to perform the solution energy calculations.
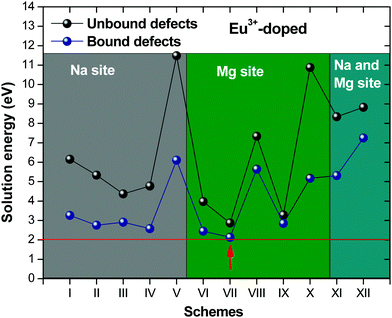
Fig. 2 presents a solution energy diagram for bound and unbound defects for each reaction of Eu3+-doped NaMgF3, represented by schemes shown in Table 5. Notably, Eu3+ prefers to be incorporated into the Mg2+ site (Eboundsol = 2.129 eV), compensated by a sodium vacancy (Scheme VII). Other reactions proposed here lead to values close to the red line. Reactions IV (entering into a Na+ site) and VI (entering into a Mg2+ site), for instance, have approximate differences of 0.5 and 0.3 eV, respectively, with respect to the lowest point. Our predictions show that mechanisms involving two substitutional defects in Na+, Mg2+, or both sites are practically unlikely in this configuration. In all cases, the calculations carried out in clusters lead to a decreased solution energy because of interactions between defects. Some reactions show considerable binding energy, leading to lower solution energy in comparison with unbound defect calculations.
In fact, the valence of ions is a determining factor for Eu3+ entering into the Mg2+ site instead of the Na+ site. The ionic radius varies with coordination number, charge states, and other parameters.63 Even though Eu3+ (0.947 Å for a coordination number of six) has a larger ionic radius than Mg2+ (0.72 Å for a coordination number of six) and is smaller than Na+ (1.18 Å for a coordination number of eight), Eu3+ is preferable for replacing Mg2+ in the host matrix. In this case, the difference between the ionic radii of Eu3+ and Mg2+ ions are practically the same as Eu3+ and Na+ ions. Thus, according to our calculations, the difference in valence between the Eu and Na ions leads to less favourable charge compensations for the system, even though the Eu3+ ion could be better accommodated by replacing the Na site instead of the Mg site.
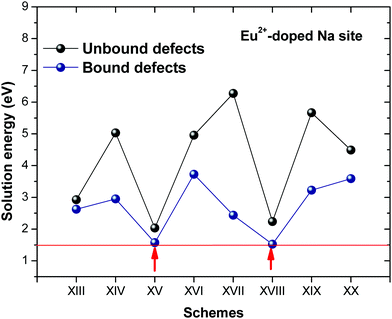
Fig. 3 shows solution energy versus proposed charge compensation schemes (see Table 6) for incorporation of Eu2+ into the Na site of NaMgF3. The most favourable mechanism of charge compensation is through the sodium vacancy (scheme XV) and anti-site (scheme XVIII), both with energy solutions of approximately 1.5 eV (see red arrow). Analyses of scheme XXI show (see Table 6, but not shown in Fig. 3), evidently, that the Eu2+-doped Mg site requires no compensation mechanism because these ions have the same valence. The solution energy calculated for this scheme is approximately 2 eV. In other words, the calculations show that the Na site is energetically most favourable for the incorporation of the Eu2+ ion, rather than at the Mg site. In addition, our predictions show that the solution energy of bound defects is lower than unbound defects in all proposed schemes. These results show the importance of defect clustering in this system.
The most probable mechanism of Eu3+ and Eu2+ ion incorporation into NaMgF3, charge compensation is illustrated in Fig. 4. Analysing the proposed chemical reactions and calculation of solution energies, we see that when calculations are carried out considering defects and the respective mechanism of charge compensation, as a defect cluster, the solution energy is less than when calculated as isolated defects. The configuration of the local site is modified in terms of distances and distortions. Understanding these changes is of great importance for a better understanding of luminescent properties of optically active ions in the host matrix.
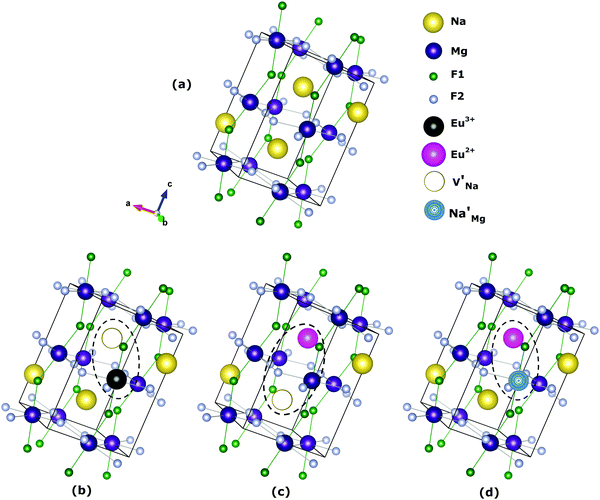 | ||
Fig. 4 Illustration of Eu3+ and Eu2+ incorporation into NaMgF3 with the most favourable charge compensation mechanism: (a) pure NaMgF3, (b) 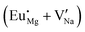 cluster, (c) cluster, (c) 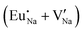 cluster, and (d) cluster, and (d) 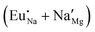 cluster. cluster. | ||
Table 7 shows the interatomic distances (d) from the atomistic simulation after doping Eu3+ and Eu2+ ions into NaMgF3 for the most favourable schemes found in this work. The percentage difference between Eu–F and Na–F (or Mg–F) interatomic distances is represented by Δ (%). The Na–F and Mg–F distances are taken from the pure NaMgF3 phase (see Table 3) for comparison. We note that some distances are reduced, while others are increased for both cases (schemes) involving Eu2+. For the cluster 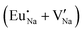 , the atoms drastically approach Eu2+ with distances of less than 3 Å. For Eu3+, in contrast with Eu2+, all distances increase after doping. In this case, Δ (%) is around 10% for all interactions.
, the atoms drastically approach Eu2+ with distances of less than 3 Å. For Eu3+, in contrast with Eu2+, all distances increase after doping. In this case, Δ (%) is around 10% for all interactions.
| Eu2+ into Na site, | Eu2+ into Na site, | Eu3+ into Mg site, | ||||||
|---|---|---|---|---|---|---|---|---|
| Eu–F | d (Å) | Δ (%) | Eu–F | d (Å) | Δ (%) | Eu–F | d (Å) | Δ (%) |
| Eu–F2 | 2.436 | 4.2 | Eu–F2 | 2.467 | 5.6 | Eu–F2 | 2.163 | 9.4 |
| Eu–F2 | 2.436 | 4.2 | Eu–F2 | 2.479 | 6.1 | Eu–F2 | 2.197 | 11.1 |
| Eu–F1 | 2.458 | 5.9 | Eu–F1 | 2.463 | 6.1 | Eu–F1 | 2.205 | 11.6 |
| Eu–F1 | 2.592 | 4.8 | Eu–F1 | 2.486 | 0.5 | Eu–F1 | 2.161 | 9.4 |
| Eu–F2 | 2.672 | −1.4 | Eu–F2 | 2.532 | −6.6 | Eu–F2 | 2.201 | 11.5 |
| Eu–F2 | 2.672 | −1.4 | Eu–F2 | 2.727 | 0.6 | Eu–F2 | 2.168 | 9.8 |
| Eu–F2 | 2.633 | −0.3 | Eu–F2 | 2.533 | −4.1 | |||
| Eu–F2 | 2.633 | −0.3 | Eu–F2 | 2.632 | −0.3 | |||
| Eu–F1 | 2.715 | −11.8 | Eu–F1 | 2.911 | −5.5 | |||
| Eu–F1 | 2.936 | −5.8 | Eu–F1 | 3.121 | 0.1 | |||
Experimental results based on photoluminescence spectra indicate that both Eu2+ and Eu3+ ions can co-exist in NaMgF3, even although the emission spectrum from Eu3+ is quite different from the Eu2+ ion. In this case, when the NaMgF3 is excited at 256 nm the emission from Eu2+ is observed at 366 nm, and when excited at 396 nm emission from Eu3+ at 590 nm is observed.22 Although the Eu2+/Eu3+ ratio depends on the chemical composition of the host,64 the synthesis method65 and exposure to ionizing radiation,66,67 our calculations suggest that, from the perspective of solution energy, the Eu ion prefers to be incorporated into NaMgF3 in its divalent state (see Fig. 2 and 3). Unlike Eu in the Na site, our calculations reveal that on the Mg2+ site, both Eu2+ and Eu3+ trivalent Europium are energetically favourable, once the energy difference is about 0.133 eV. Thus, Eu2+ emission can arise from Eu localized in the Na and Mg sites. In fact, experimental results show that Eu2+ is dominant at lower concentrations, but Eu3+ becomes important when concentration increases. This behaviour is similar to that reported for Eu3+ and Eu2+ in CaF2:Eu crystals.68
3.4 Spectroscopic properties of Eu ions in NaMgF3
Spherical coordinates of the Eu3+ ion, obtained by atomistic simulations of defect clustering, are shown in Table 8. In dealing with a distorted structure, all Eu–F distances are slightly different and, consequently, symmetry discussions here are approximate.
| Spherical coordinatesa | ||||||
|---|---|---|---|---|---|---|
| NN | Distorted S6 | Ideal S6 | ||||
| R | θ | ϕ | R | θ | ϕ | |
| a The ideal S6 point symmetry corresponds to one site of Eu3+ in C-rare earth sesquioxides, taken from ref. 69, for comparison. The radial coordinates are given in angstroms, and the angular coordinates are given in degrees. The centroid (F1, F2, F3) coming out of the x′–y′ plane is taken as the z′-axis. | ||||||
| F1 | 2.168 | 63.36 | 0 | 2.345 | 62.81 | 0 |
| F2 | 2.161 | 60.77 | 240.83 | 2.345 | 62.81 | 240 |
| F3 | 2.163 | 62.61 | 121.50 | 2.345 | 62.81 | 120 |
| F4 | 2.197 | 128.30 | 302.49 | 2.345 | 117.19 | 300 |
| F5 | 2.201 | 127.65 | 180.74 | 2.345 | 117.19 | 180 |
| F6 | 2.205 | 130.11 | 61.56 | 2.345 | 117.19 | 60 |
We chose the principal axis of symmetry (z′-axis) by diagonalizing the tensor of the quadrupolar field, which is experienced by the optically active ion. In this case, the eigenvector takes the highest eigenvalues. The centroid (coming out the x′–y′ plane) between the F1, F2, and F3 atoms is taken as the z′-axis to measure the spherical coordinates.
F1, F2, and F3 have slightly different distances, as well as F4, F5, and F6 atoms. The C3 symmetry operation about the z′-axis takes, approximately, F2 to F1 and F1 to F3. Similarly, the atoms in the lower plane bounce off each other. Then, F1, F2, and F3 are approximately equivalent to each other. Likewise, F4, F5, and F6 may be considered approximately equivalent. This procedure reduces the degree of freedom in crystal field calculations by employing the same charge factor to equivalent atoms. Thus, we have used the charge factor g1 to yellow atoms and g2 to orange atoms.
Atomistic simulation was used to better understand the true nature of the defects in NaMgF3, giving us information about spatial coordinates of the Eu3+ ion, which is not easily obtained by X-ray diffraction because of the low concentration of the Eu ion in the host matrix. Notably, a C3 symmetry operation (Fig. 5) following a σh operation (reflection plane that contains the x′–y′ plane) takes the same structural pattern, approximately. The bond distances illustrated in Fig. 5 can be found in Table 8. A combination of C3 and σh operations is termed S6 symmetry in group theory.56 In this case, a distorted S6 point symmetry occurs because all distances are slightly different, and the angles differ from that of ideal S6 symmetry. Once in S6 point symmetry, the electric dipole 4f–4f transitions are forbidden, and the distorted S6 symmetry explains the weak electric dipole 4f–4f transitions of Eu3+ observed in NaMgF3.
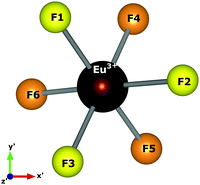 | ||
| Fig. 5 Local symmetry of the optically active ion, and the axis adopted to obtain spherical coordinates. The centroid coming out the x′–y′ plane is taken as the z′-axis. | ||
Spectroscopic properties of Eu3+ in the Na sites must be quite different from Eu3+ substituting Mg2+, due to low symmetry of the Na site. In addition, our simulation shows that there is also distortion when Eu2+ substitutes Na. This suggests that Eu2+ must be in a site with very low symmetry, which induces a high intensity 4f–4f transition. In fact, 4f–4f emission from Eu2+ in NaMgF3 has intensity comparable with broad 4f65d1–4f7 emission, which is an allowed transition and occurs with a high transition probability. On the other hand, experimental results show that Eu3+ in low symmetry sites are less unlikely, and this has also been predicted in our simulations, showing that Eu3+ in a Na site is less probable.
| B k q | β − | β + |
|---|---|---|
| a β − and β+ define the charge factor position around the middle distance of Eu–F. The minus signal means that g is closer to Eu3+, and the plus sign indicates that g is closer to the ligands. A rotation (30.5°) about the principal axis was carried out to eliminate the imaginary part of B22. | ||
| B 20 | −299.6 | −299.53 |
| B 21 | −8.144 − 27.578i | −7.555 − 26.408i |
| B 22 | 22.523 | 22.225 |
| B 40 | −269.799 | −211.583 |
| B 41 | −0.98 − 8.615i | −1.118 − 6.937i |
| B 42 | −20.045 − 8.944i | −16.209 − 6.732i |
| B 43 | −50.207 + 522.044i | −28.773 + 416.689i |
| B 44 | 2.264 + 1.095i | 1.657 + 1.034i |
| B 60 | 413.269 | 272.774 |
| B 61 | 8.86 + 34.918i | 6.044 + 22.983i |
| B 62 | 5.69i | 0.049 + 3.418i |
| B 63 | 11.311–134.588i | 5.575 − 93.281i |
| B 64 | 35.648–4.526i | 22.963 − 3.444i |
| B 65 | 0.292 + 22.377i | 0.333 + 14.947i |
| B 66 | −282.947 − 53.841i | −187.929 − 25.489i |
| g 1 | 0.435 | 0.58 |
| g 2 | 0.034 | 0.031 |
This leads us to conclude that Eu3+ occupies is a distorted S6 point symmetry. Furthermore, we have calculated Bkq using β− and β+, which define the charge factor positions around the middle distance of Eu–F.42 The minus signal means that g is closer to the Eu3+ ion, and the plus signal means that g is closer to the ligands. This parameter is a way (according to the SOM) to include covalence effects on the chemical bond because the charge is localized in a middle distance (R/2β) instead of being located at the position of the ligand, as proposed by the PCEM. In this case, the use of β+ leads to a lower contribution from Bkq that does not belong to ideal S6 symmetry. In addition, the phenomenological charge factors, adjusted to reproduce the 7F1 state energy sublevels, are higher.
We also use the model proposed by Lima et al.70 to calculate charge transferred to the Eu–F chemical bond. This model is valid for high symmetry systems, in which only one charge factor is needed to describe the system. With ideal S6 point symmetry, the model would be well applied, but for the sake of comparison, we have calculated one of the charges through this model using the following expression:
| g = Δχ(D)/REu−F | (8) |
The B20 sign defines the position of the 7F1 state ground sublevel from the barycentre. We see in Table 8 that it is correctly predicted using β− and β+ because B20 is negative, and the 7F1 state ground sublevel is non-degenerate. We will discuss this point in more detail in the next section.
| E (cm−1) | E exp | E(β−) | E(β+) |
|---|---|---|---|
| E 0 | −65.344 (315.689) | −58.674 | −58.660 |
| E −1 | 32.672 (413.705) | 19.230 | 19.357 |
| E +1 | 32.672 (413.705) | 39.444 | 39.303 |
| ΔE | 98.016 | 98.118 | 97.963 |
The photoluminescence emission spectra of NaMgF3 nanoparticles containing Eu, excited at 396 nm, for 1% Eu show 5D0 → 7FJ transitions from Eu3+. The emission spectrum reported by Gaedtke and William22 at room temperature presents one peak corresponding to the 5D0–7F0 transition, two peaks from 5D0–7F1, two peaks from 5D0–7F2, and four peaks from 5D0–7F4. 5D0–7F1 is a magnetic dipole transition, which is not influenced by the crystalline environment. The number of lines and intensities in relation to the 5D0–7F2 transition indicates if the system is lower or higher in symmetry. The other transitions are electric dipole moment transitions which are strongly influenced by the crystalline environment.
The second peak of the 5D0–7F1 transition is doubly degenerate, and the 7F1 splitting is less than 100 cm−1. The emission spectrum reported by Gaedtke and William22 shows that the 5D0–7F1 transition is approximately 50% more intense than the 5D0–7F2 transition. This suggests that the Eu3+ ion occupies point symmetry with a distorted inversion centre, although the emission spectrum shows peaks corresponding to the 5D0–7F0 and 5D0–7F2 transitions.
Schuyt and William,24 based on the Tanner diagram,72 suggested that the Eu3+ occupies sites with Cs, Cnv or Cn symmetry because the 5D0–7F0 transition is presented in the emission spectrum. Cs is part of low symmetry groups, which is not the case here because the 7F1 splitting is less than 350 cm−1 (ref. 73). Analysing the number of lines for each transition in the emission spectrum and comparing it with the Tanner diagram72 indicates C3v or C4v symmetry. Previous work carried out with Eu3+-doped KMgF3 suggested the same symmetry.28–30 However, C3v, C4v, and Cn are symmetry groups without inversion centres. The crystal field parameters related to the odd part of the crystal field potential is different from zero for this symmetry set (C3v, C4v, and Cn). In this case, the 5D0–7F2 transition, allowed by electric dipole and strongly influenced by the environment, would be more intense than the transition 5D0–7F1. This is not observed in the NaMgF3:Eu emission spectrum. Thus, the most probable symmetry is distorted S6 point symmetry. Due to distortion in the luminescent site, other transitions, beyond 5D0–7F1, are apparent in the emission spectrum beyond transition.
E −1 and E+1 are slightly different because B22 is nonzero. The distortion in S6 point symmetry leads to a small contribution of this parameter in relation to B20. This behaviour is not observed in the emission spectrum obtained experimentally. However, Seo et al.28 showed a slight splitting of the second line around 0.7 nm in KMgF3:Eu using site-selective laser-excitation spectroscopy. This agrees very well with our predictions because E−1 and E+1 are separated by approximately 20 cm−1. In fact, the spectrometer used has a lower resolution, and a splitting of 0.7 nm cannot be identified in the emission spectrum.
Another point that deserves to be highlighted is the substitutional defect and charge compensation created by inserting Eu3+ into the host matrix. Reports for materials from the same family (Eu3+-doped KMgF328–30 and RbMgF331) have diverged in relation to substitutional defects and charge compensation. The reports for Eu-doped KMgF3 have suggested a Na substitutional defect,28–30 while one report for Eu-doped RbMgF3 suggested an Mg substitutional defect.31
Our results for the Eu3+ ion in NaMgF3 show a Mg substitutional defect compensated by a Na vacancy in the calculations with defect clustering (see Fig. 2, scheme VII). The energy difference of the most favourable mechanism for Eu3+ incorporation in Na and Mg sites is around 0.5 eV. Reaction (IV) in the Na site is less favourable; the local geometry of the optically active ion has a lower symmetry (with eight NNs) and higher distortion compared with the most favourable reaction. We tested this geometry in crystal field parameter calculations, but the predictions do not reproduce the emission spectrum characteristics through a set of positive charge factors. Moreover, values of Bkq do not lead to any conclusion about the local symmetry of the Eu3+ ion (doped in the Na site). Thus, our conclusions are based on atomistic simulation, group theory, crystal field calculations, and emission spectrum characteristics of NaMgF3:Eu. These results lead us to strongly believe that the Eu3+ ion is incorporated in the Mg site.
3.5 Photoionization cross-section and OSL decay pattern of NaMgF3:Eu2+
Polycrystalline NaMgF3:Eu2+ has been shown to be a suitable material for application in personal dosimetry. The material has high sensitivity and is able to monitor small doses, having a linear dose–response behaviour between μGy dose levels up to approximately 100 Gy.18 However, this behaviour and the mechanism of electron de-trapping are not completely explained in the literature.In this section, we discuss this point based on the photoionization cross-section (σ) of the trap level and associated it with the substitutional defect to understand the origin of the OSL signal from NaMgF3:Eu2+. We employed the model developed by Lima–Batista–Couto57 to predict σ, and ref. 57 can be consulted for more details on the method.
Fig. 6 shows the photoionization cross-section as a function of the electromagnetic radiation energy for NaMgF3:Eu2+. The curve has a broad excitation interval that leads to electron de-trapping processes of localized traps in the band gap. OSL emission reported by Dotzler et al.,18 excited at 450 nm, shows a broad interval of the emission spectra from samples pre-irradiated with X-rays. This agrees with our predictions. We also observe that the maximum peak occurs for light stimulus at approximately 2.2 eV, which corresponds to the maximum probability of electrons to be de-trapped from this localized trap.
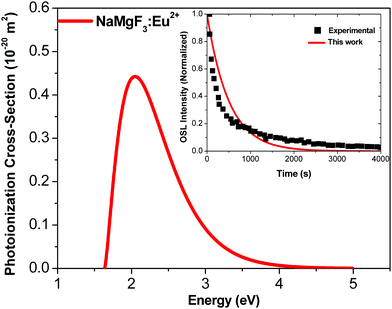 | ||
| Fig. 6 Photoionization cross-section versus electromagnetic radiation energy for NaMgF3:Eu2+. Inset shows experimental data from ref. 77 and theoretical OSL decay patterns for NaMgF3:Eu2+. The experimental decay curve was obtained after irradiation with an X-ray dose of 219 mGy.77 | ||
We calculate the magnitude of σ to the specific wavelength, λ = 470 nm, which was the same wavelength used in the most OSL measurements. The phonon frequency used here is 325 cm−1, obtained from ref. 74 CaF2:Yb2+. The electron effective mass used is 0.74me, reported for fluoroperovskites in ref. 75. The activation energy used is 1.2 eV.72 By using these values in eqn (6), we obtain σ = 0.244 × 10−20 m2 for the NaMgF3:Eu2+ compound. This value is close to that obtained by Daniel et al.76 for NaMgF3:Eu2+, Ce3+ using the fitting method of the linearly modulated (LM)-OSL experimental curve. There, the fitting curve was carried out with four components, and one value of σ was obtained for each component. The dominant term presents a magnitude of 0.112 × 10−20 m2.
Using the value of σ calculated here, we estimate the OSL decay pattern of NaMgF3:Eu3+ based on the first-order kinetic approximation (no re-trapping), which assumes the OSL signal decay with stimulation time is due to de-trapping of captured electrons and subsequent radiative recombination. Fig. 6 (inset) shows the experimental and theoretical OSL decay patterns. The experimental OSL decay curve was obtained after irradiation with an X-ray dose of 219 mGy.77 The decay time is slower than that exhibited in the commercial material, Al2O3:C.58 We note that the theoretical curve deviates slightly from the experimental curve because the model used here is the first-order kinetic model.
The rate at which electrons captured in the trap are optically excited to the conduction band is proportional to σ, and the OSL decay pattern is governed by σ. Our predictions show that σ of NaMgF3 is on the same order of magnitude (10−20 m2) as the calculated value for Al2O3:C.58 This explains the high sensibility when stimulated with blue light.
4 Conclusion
In summary, we combined classical atomistic simulation and crystal field models to describe the origin of defects and their influence on luminescent properties of Eu-doped NaMgF3 in the orthorhombic phase. We proposed a new set of interatomic potentials that reproduce the main properties of the orthorhombic phase. Defect calculations based on these interatomic potentials provide information regarding the energetic balance of dopant incorporation in this fluoroperovskite compound. In addition, using crystal field calculations, we explored, in detail, the type of defect and spectroscopic properties of the optically active ion. The main findings of this work are summarized below.– The new set of interatomic potentials reproduced structural and elastic properties in the orthorhombic phase and precursor fluorides. In addition, the interatomic potential is transferable to the cubic phase, consistent with the literature.
– Defect calculations show that incorporation of Eu3+ ions into the Mg site, compensated by the Na vacancy, is the most energetically favourable. Further, the Eu2+ ion prefers to incorporate into the Na site, compensated by a Na vacancy or anti-site, in the host matrix. In addition, the solution energy with Eu2+ is lower than with Eu3+.
– We predict the local symmetry and 7F1 energy sub-levels of the Eu3+ ion by using the simple overlap model and the local geometry obtained in defect calculations.
– The weak intensity of the 5D0–7F2 transition, as well as the small splitting of the second peak of the 5D0–7F1 transition (observed in emission spectrum as doubly degenerate), occurs due to the distortion in S6 local symmetry occupied by Eu3+ ions.
– Our predictions of the photoionization cross-section and OSL decay pattern show that NaMgF3:Eu2+ presents a high sensibility for stimulus over a large range of wavelengths.
The new insights presented in this work show the importance of defect calculations, combined with crystal field and photoionization cross-section models, to successfully describe the luminescent properties of lanthanide-doped compounds.
Author contribution
Afranio Sousa: data curation, formal analysis, investigation, methodology, validation, writing – original draft, writing – review and editing. Adelmo Souza: visualization, investigation, data curation, writing – original draft. Heveson Lima: conceptualization, formal analysis, data curation, investigation, project administration, supervision, validation, visualization, writing – original draft, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the CNPq (No. 441451/2019-5), CAPES and FAPESB/BA, Brazilian funding agencies for financial support.References
- M. Yang, A. Kc, A. C. Garcia-Castro, P. Borisov, E. Bousquet, D. Lederman, A. H. Romero and C. Cen, Sci. Rep., 2017, 7, 7182 CrossRef.
- K. Miyata and X.-Y. Zhu, Nat. Mater., 2018, 17, 379–381 CrossRef CAS.
- M. Petrović, V. Chellappan and S. Ramakrishna, Sol. Energy, 2015, 122, 678–699 CrossRef.
- H. Liu, Z. Huang, S. Wei, L. Zheng, L. Xiao and Q. Gong, Nanoscale, 2016, 8, 6209–6221 RSC.
- H. J. Snaith, Nat. Mater., 2018, 17, 372–376 CrossRef CAS.
- W. Ke and M. G. Kanatzidis, Nat. Commun., 2019, 10, 965 CrossRef.
- P. Meredith and A. Armin, Nature, 2018, 562, 197–198 CrossRef CAS.
- Y. Wang, G. Ding, J.-Y. Mao, Y. Zhou and S.-T. Han, Sci. Technol. Adv. Mater., 2020, 21, 278–302 CrossRef CAS.
- A. Fu and P. Yang, Nat. Mater., 2015, 14, 557–558 CrossRef CAS.
- Z. Song, J. Zhao and Q. Liu, Inorg. Chem. Front., 2019, 6, 2969–3011 RSC.
- K. Nie, H. Yang, Z. Gao and J. Wu, Mater. Sci. Semicond. Process., 2018, 83, 12–17 CrossRef CAS.
- X. Xiao, J. Hu, S. Tang, K. Yan, B. Gao, H. Chen and D. Zou, Adv. Mater. Technol., 2020, 5, 1900914 CrossRef CAS.
- D. J. Daniel, A. Raja, U. Madhusoodanan, O. Annalakshmi and P. Ramasamy, Opt. Mater., 2016, 58, 497–503 CrossRef CAS.
- H. Wei and J. Huang, Nat. Commun., 2019, 10, 1066 CrossRef.
- A. Raja, R. Nagaraj, K. Ramachandran, V. Sivasubramani, G. Annadurai, D. Joseph Daniel and P. Ramasamy, Mater. Sci. Eng., B, 2020, 255, 114531 CrossRef CAS.
- Y.-P. Du, Y.-W. Zhang, Z.-G. Yan, L.-D. Sun, S. Gao and C.-H. Yan, Chem. – Asian J., 2007, 2, 965–974 CrossRef CAS.
- J. J. Schuyt and G. V. M. Williams, Radiat. Meas., 2020, 134, 106326 CrossRef CAS.
- C. Dotzler, G. V. M. Williams, U. Rieser and A. Edgar, Appl. Phys. Lett., 2007, 91, 121910 CrossRef.
- J. J. Schuyt, J. Donaldson, G. V. M. Williams and S. V. Chong, J. Phys.: Condens. Matter, 2020, 32, 025703 CrossRef CAS.
- B. Lütgert and D. Babel, Z. Anorg. Allg. Chem., 1992, 616, 133–140 CrossRef.
- G. V. M. Williams, S. Janssens, C. Gaedtke, S. G. Raymond and D. Clarke, J. Lumin., 2013, 143, 219–225 CrossRef CAS.
- C. Gaedtke and G. V. M. Williams, Radiat. Meas., 2014, 71, 258–261 CrossRef CAS.
- J. J. Schuyt and G. V. M. Williams, Mater. Res. Bull., 2018, 106, 455–458 CrossRef CAS.
- J. J. Schuyt and G. V. M. Williams, J. Lumin., 2019, 211, 413–417 CrossRef CAS.
- R. Pazik, J.-M. Nedelec and R. J. Wiglusz, CrystEngComm, 2014, 16, 5308–5318 RSC.
- K. Binnemans, Coord. Chem. Rev., 2015, 295, 1–45 CrossRef CAS.
- R. V. Perrella, C. S. N. Júnior, M. S. Góes, E. Pecoraro, M. A. Schiavon, C. O. Paiva-Santos, H. Lima, M. A. Couto dos Santos, S. J. L. Ribeiro and J. L. Ferrari, Opt. Mater., 2016, 57, 45–55 CrossRef CAS.
- H. J. Seo, T. Tsuboi and K. Jang, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205113 CrossRef.
- V. S. Singh, C. P. Joshi, T. K. Gundu Rao and S. V. Moharil, J. Alloys Compd., 2016, 657, 848–854 CrossRef CAS.
- N. Pathak, S. Mukherjee, D. Das, D. Dutta, S. Dash and R. M. Kadam, J. Mater. Chem. C, 2020, 8, 7149–7161 RSC.
- A. Raja, G. Annadurai, D. J. Daniel and P. Ramasamy, J. Alloys Compd., 2017, 727, 215–223 CrossRef CAS.
- A. M. Sousa, A. F. Lima and M. V. dos S. Rezende, J. Solid State Chem., 2019, 269, 312–319 CrossRef CAS.
- A. Sousa and H. Lima, J. Comput. Chem., 2020, 41, 646–652 CrossRef CAS.
- N. J. Henson, A. K. Cheetham and J. D. Gale, Chem. Mater., 1996, 8, 664–670 CrossRef CAS.
- A. Walsh, C. R. A. Catlow, A. A. Sokol and S. M. Woodley, Chem. Mater., 2009, 21, 4962–4969 CrossRef CAS.
- K. T. Butler, J. Mater. Chem. C, 2018, 6, 12045–12051 RSC.
- A. M. Sousa, A. F. Lima and M. V. dos S. Rezende, J. Alloys Compd., 2016, 689, 977–982 CrossRef CAS.
- N. Kuganathan, S. Ganeshalingam and A. Chroneos, Materials, 2019, 12, 2851 CrossRef CAS.
- E. Gonzalo, A. Kuhn, F. García-Alvarado and M. S. Islam, J. Mater. Chem. A, 2013, 1, 6588 RSC.
- Q. Hou, J. Buckeridge, T. Lazauskas, D. Mora-Fonz, A. A. Sokol, S. M. Woodley and C. R. A. Catlow, J. Mater. Chem. C, 2018, 6, 12386–12395 RSC.
- A. M. Otsuka, D. O. Junot, H. Lima, M. V. dos, S. Rezende and M. A. C. dos Santos, J. Lumin., 2020, 226, 117503 CrossRef CAS.
- O. L. Malta, Chem. Phys. Lett., 1982, 88, 353–356 CrossRef CAS.
- Y. A. R. Oliveira, H. Lima, A. S. Souza and M. A. Couto dos Santos, Opt. Mater., 2014, 36, 655–657 CrossRef CAS.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC.
- G. Busker, A. Chroneos, R. W. Grimes and I.-W. Chen, J. Am. Ceram. Soc., 2004, 82, 1553–1559 CrossRef.
- A. Corgne, N. L. Allan and B. J. Wood, Phys. Earth Planet. Inter., 2003, 139, 113–127 CrossRef CAS.
- J. A. Dawson, C. L. Freeman, J. H. Harding and D. C. Sinclair, J. Solid State Chem., 2013, 200, 310–316 CrossRef CAS.
- C. A. J. Fisher, V. M. Hart Prieto and M. S. Islam, Chem. Mater., 2008, 20, 5907–5915 CrossRef CAS.
- M. S. Islam, D. J. Driscoll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085–5092 CrossRef CAS.
- M. R. Kibler, Int. J. Quantum Chem., 1975, 9, 403–420 CrossRef CAS.
- P. Porcher, M. Couto Dos Santos and O. Malta, Phys. Chem. Chem. Phys., 1999, 1, 397–405 RSC.
- H. Lima, H. C. C. de Oliveira, X. Bidault, T. S. dos Santos, S. Chaussedent and M. A. Couto dos Santos, J. Non-Cryst. Solids, 2016, 448, 62–67 CrossRef CAS.
- J. D. Axe and G. Burns, Phys. Rev., 1966, 152, 331–340 CrossRef CAS.
- C. Görller-Walrand and K. Binnemans, in Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 1996, vol. 23, pp. 121–283 Search PubMed.
- H. Lima, J. V. Batista and M. A. Couto dos Santos, EPL, 2016, 115, 33002 CrossRef.
- B. Novais, E. Ferraz, A. S. Souza, P. L. Antonio, L. V. E. Caldas, J. Batista and H. Lima, Opt. Mater., 2020, 102, 109792 CrossRef CAS.
- Y. Zhao, J. B. Parise, Y. Wang, K. Kusaba, M. T. Vaughan, D. J. Weidner, T. Kikegawa, J. Chen and O. Shimomura, Am. Mineral., 1994, 79, 615–621 CAS.
- Y. Zhao and D. J. Weidner, Phys. Chem. Miner., 1993, 20, 419–424 CrossRef CAS.
- J. A. L. Rabone and N. H. De Leeuw, J. Comput. Chem., 2006, 27, 253–266 CrossRef CAS.
- F. A. Kröger and H. J. Vink, Solid State Physics, Elsevier, 1956, vol. 3, pp. 307–435 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767 CrossRef.
- H. Terraschke and C. Wickleder, Chem. Rev., 2015, 115, 11352–11378 CrossRef CAS.
- K. Biswas, A. D. Sontakke, R. Sen and K. Annapurna, J. Fluoresc., 2012, 22, 745–752 CrossRef CAS.
- V. N. Bapat, J. Phys. C: Solid State Phys., 1977, 10, L465–L467 CrossRef CAS.
- P. W. Levy, Nucl. Tracks Radiat. Meas., 1985, 10, 547–556 CAS.
- H. Yu, B. Zhang, X. Chen, X. Qian, D. Jiang, Q. Wu, J. Wang, J. Xu and L. Su, Opt. Express, 2019, 27, 523 CrossRef CAS.
- H. Kohlmann, C. Hein, R. Kautenburger, T. C. Hansen, C. Ritter and S. Doyle, Z. Kristallogr. Cryst. Mater., 2016, 231, 517–523 CAS.
- H. Lima and M. A. Couto dos Santos, J. Phys. Chem. Solids, 2016, 96–97, 38–41 CrossRef CAS.
- H. Lima, D. Ferreira, A. S. Souza and M. A. C. dos Santos, J. Braz. Chem. Soc., 2021, 32, 405–412 Search PubMed.
- P. A. Tanner, in Lanthanide Luminescence, ed. P. Hänninen and H. Härmä, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 7, pp. 183–233 Search PubMed.
- K. Binnemans and C. Görller-Walrand, Chem. Phys. Lett., 1995, 245, 75–78 CrossRef CAS.
- M. F. Reid, P. S. Senanayake, J.-P. R. Wells, G. Berden, A. Meijerink, A. J. Salkeld, C.-K. Duan and R. J. Reeves, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 113110 CrossRef.
- H. Benmhidi, H. Rached, D. Rached and M. Benkabou, J. Electron. Mater., 2017, 46, 2205–2210 CrossRef CAS.
- D. J. Daniel, O. Annalakshmi, U. Madhusoodanan and P. Ramasamy, J. Rare Earths, 2014, 32, 496–500 CrossRef CAS.
- J. J. Schuyt and G. V. M. Williams, Radiat. Meas., 2019, 121, 99–102 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00953a |
| This journal is © The Royal Society of Chemistry 2021 |