Cobalt adipate, Co(C6H8O4): antiferromagnetic structure, unusual thermal expansion and magnetoelastic coupling†
Paul J.
Saines
*a,
Phillip T.
Barton
b,
Marek
Jura
c,
Kevin S.
Knight
c and
Anthony K.
Cheetham
d
aDepartment of Chemistry, University of Oxford, Inorganic Chemistry Laboratory, South Parks Road, Oxford, OX1 3QR, UK
bMaterials Research Laboratory and Materials Department, University of California Santa Barbara, Santa Barabara, California 93106, USA
cISIS Facility, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, OX11 0QX, UK
dDepartment of Materials Science and Metallurgy, University of Cambridge, Charles Babbage Road, Cambridge, CB3 0FS, UK
First published on 24th January 2014
Abstract
Co adipate, Co(C6H8O4), has been found to order near 10 K into a magnetic structure featuring sheets of tetrahedral Co cations coupled antiferromagnetically in two dimensions through carboxylate groups. The emergence of this order is accompanied by magnetoelastic coupling, which drives anisotropic negative thermal expansion along the a-axis below 50 K, the first time such behaviour has been observed in a metal-organic framework. The monoclinic angle, β, has also been found to decrease on cooling, passing through a metrically orthorhombic phase without a phase transition; this unusual behaviour has been rationalised in terms of the thermal expansion along the principal axes.
Introduction
For more than a decade porous metal–organic frameworks (MOFs) have been extensively studied due to their fascinating range of structures and useful properties.1 More recently denser frameworks have attracted significant attention for exhibiting low dimensional and meta-magnetic behaviour, multiferroicity and strong magnetocaloric effects.2–6 In particular the transition metal dicarboxylate frameworks have shown a wide range of low dimensional and field dependent magnetic behaviour.2–4,6,7 Compounds in this family exhibit two dimensional magnetic order in structures that can readily be made into nanosheets,3,8 while related materials transform from antiferromagnetic to ferromagnetic phases or feature spin flop transitions with applied magnetic fields.4,6The magnetic properties of frameworks depend on their precise magnetic interactions and a deeper understanding of these is required to underpin their future development. This is particularly true for compounds having unique phenomena and strong coupling between their lattice and magnetic order. Neutron diffraction has proved to be a powerful probe for such studies of magnetic materials, but its application to hybrid frameworks is still limited to a handful of cases.9 This is due to significant challenges in solving the structure of these dilute yet complex magnetic compounds.
As part of our recent studies of dicarboxylate frameworks we have synthesised a new monoclinic Co adipate, Co(C6H8O4).6 Its pseudo-orthorhombic structure is very similar to the glutarate10 and pimelate11 analogues, which are reported as forming monoclinic antiferromagnetic and orthorhombic weak ferromagnetic phases, respectively. The subtle difference in the reported structures and magnetic properties of these compounds inspired us to more closely examine the magnetic and structural behaviour of Co(C6H8O4). We have solved its magnetic structure using neutron diffraction and found that it exhibits negative thermal expansion driven by magnetoelastic coupling at low temperatures. In combination with X-ray diffraction we have also shown that the monoclinic angle, β, of this phase decreases on cooling, passing through a metrically orthorhombic structure without any apparent phase transition. We have rationalised this unusual behaviour in terms of thermal expansion along its principal axis.
Experimental
Co adipate, Co(C6H8O4), was made using the method previously reported,6 resulting in the formation of purple platelet crystals. For the deuterated sample, used for powder diffraction measurements, the reaction was carried out with perdeuterated adipic acid and D2O.Single crystal X-ray diffraction measurements were performed at 10 K using an Oxford Diffraction Gemini diffractometer, utilising MoKα radiation. It was equipped with a Sapphire CCD detector and a Helijet cryocooler. Data were integrated using CrysAlis Pro,12 the structure solved using direct methods in SIR2011,13 and refinements carried out using SHELX-97 (ref. 14) via the Olex2 interface15 (see ESI† for further details).‡
Phase purity was initially assessed using patterns collected on a Bruker D8 Advance powder diffractometer utilising a linear position detector and CuKα radiation. These patterns indicated that both the hydrogenous and perdeuterated materials contained a small amount of another known adipate, Co2(C6H8O4)2(H2O)6·4H2O.16
Synchrotron X-ray diffraction patterns were obtained using beamline I11 at the Diamond Light Source UK.17 The sample was held in a rotating glass capillary, whose temperature was varied from 90 K to 500 K by a nitrogen cryostream, and data were collected using 0.82612 Å X-rays and a Mythen position sensitive detector. The patterns were fitted using the LeBail method utilising the program Rietica18 and revealed traces of a second, unknown, impurity.
Time-of-flight powder neutron diffraction patterns were recorded using the high-resolution powder diffractometer (HRPD) at the ISIS neutron facility, Rutherford Appleton Laboratories, UK.19 Data were collected between 4 K and 300 K, using an AS Scientific Orange cryostat, utilising all three detector banks, thereby covering d-spacings from 0.7 Å to 10 Å. The patterns were fitted using the Rietveld method as implemented in the program GSAS,20 using the EXPGUI interface (see ESI† for further details).21 Magnetic structure solutions were directed by the magnetic distortion modes allowed by the symmetry of the crystal structure, as determined by the ISODISTORT software suite.22
Temperature and field dependent dc magnetisation data were measured with a Quantum Design MPMS 5XL SQUID magnetometer. Powder samples were contained in gel caps and held in a straw with a uniform diamagnetic background.
Results and discussion
Single crystal X-ray structure determination
Single crystal X-ray diffraction measurements at 10 K indicated that Co(C6H8O4) retains a P2/c monoclinic structure to low temperatures. While the data indexed well to a metrically orthorhombic cell, integration assuming orthorhombic symmetry yielded an unacceptably high Rint, around 18%. The data could, however, be integrated assuming monoclinic symmetry with an excellent Rint, of 3.1%, and successfully solved in the same structure adopted at 295 K.6 As previously reported, the material can be viewed as having planes of tetrahedral Co cations, connected via carboxylate groups, with neighbouring layers connected by the backbone of the adipate ligands (see Fig. 1). The bond distances and angles of the CoO4 tetrahedra and adipate ligands are very similar to those found at 295 K.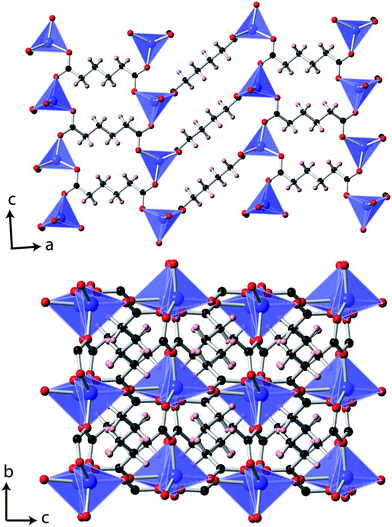 | ||
| Fig. 1 The structure of Co(C6H8O4) determined at 10 K. The Co, C, O and H atoms are represented in blue, black, red and pink, respectively. | ||
Magnetic properties
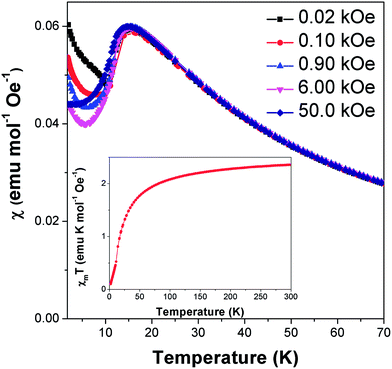
Field cooled magnetic susceptibility measurements of Co(C6H8O4) featured a maximum centred around 15 K, consistent with the onset of antiferromagnetic order at this temperature (see Fig. 2). A further increase in the susceptibility was noted below 10 K. The latter feature is similar to those found in the analogous glutarate10 and pimelate11 frameworks, which were ascribed to the onset of canted antiferromagnetic order or a paramagnetic impurity, respectively. We find that this feature in Co(C6H8O4) is suppressed on application of higher magnetic fields. This is consistent with it being caused by a paramagnetic impurity, probably from the small amount of Co2(C6H8O4)2(H2O)6·4H2O16 found in the sample. χmT (χm is molar susceptibility and T is the temperature in Kelvin) versus temperature continues to decrease on cooling below 10 K, as expected for an antiferromagnet (see Fig. 2 insert). Isothermal magnetisation measurements at 12 K do not show any hysteresis and do not saturate, with a maximum magnetisation of 0.51 μB detected in a field of 50 kOe, consistent with antiferromagnetic order (see Fig. S1†).Above the ordering temperature Co(C6H8O4) behaves as a simple Curie–Weiss paramagnet with fits to the 100 Oe data indicating a Curie–Weiss temperature of −22.2 K and an effective magnetic moment of 4.50 μB. A plot of C/(χm|Θ|)−1 as a function of T/|Θ| (where C is the Curie constant and Θ is the Curie–Weiss temperature) reveals a positive deviation from Curie–Weiss behaviour near Θ, consistent with purely antiferromagnetic behaviour (see Fig. S2†).23 The effective magnetic moment is very similar to that reported for the glutarate10 and pimelate11 phases and is higher than the spin only moment of 3.87 μB. This is consistent with a significant spin-orbital contribution to the magnetic behaviour of this compound, as expected for Co2+. Its Θ is intermediate between those of the analogous glutarate, −25.8 K,10 and pimelate, −21.3 K;11 this highlights the weakening of the antiferromagnetic interactions as the ligand gets longer and the cations are more separated along the a-axis.
Analysis of thermal expansion
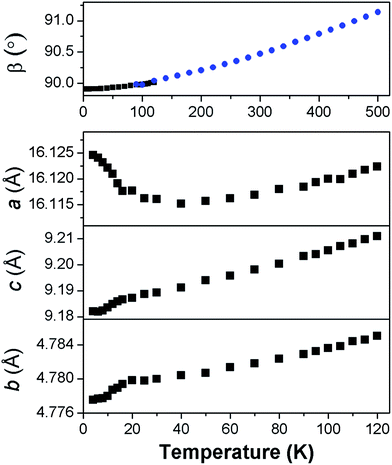
Fits to the synchrotron X-ray and neutron diffraction data showed that deuterated Co adipate, Co(C6D8O4) is, as expected, isostructural with the non-deuterated material (see Fig. S3†). The patterns were found to exhibit significant preferred orientation, which we believe reduces the accuracy of the atomic positions refined from fits to the powder neutron diffraction data compared to those obtained from single crystal refinements. The analysis of the powder diffraction data will therefore focus on the thermal expansion and magnetic structure of this material, which could be determined unambiguously. It should be noted, however, that the fits to the powder neutron diffraction data were consistent with full deuteration of the sample.For most of the temperature range examined the unit cell lengths and volume of Co(C6D8O4) decrease on cooling, as expected (see Fig. S4†). This is also true, more unusually, for the monoclinic angle, β (see Fig. 3). Co(C6D8O4) passes through a metrically orthorhombic structure around 110 K and continues to decrease slowly to a minimum value of 89.908(5)° at 4 K. The structure passes through a metrically orthorhombic structure, while maintaining monoclinic symmetry, regardless of the crystallographic setting used. While very small, the impressive resolution of the patterns obtained allows some peak asymmetry to be resolved consistent with the retention of monoclinic symmetry at low temperatures, as indicated by the single crystal X-ray measurements. Since the atomic positions determined from the single crystal X-ray diffraction measurements at 10 K and 295 K were within three standard deviations of each other, any structural changes in this material can be analysed by examining the thermal expansion coefficients, which requires precise lattice parameters. This highlights the benefits of joint single crystal and powder diffraction studies of complex frameworks in that, while the former provided more accurate refinements of atomic positions, fits to high-resolution powder diffraction patterns provide precise lattice parameters and are sensitive to the small monoclinic distortion.
In order to understand the thermal expansion behaviour, coefficients were obtained along the principal axes using infinitesimal Lagrangian strains in the program PASCal.24 Between 50 K and 500 K the principal axes were determined to be (0.572a + 0.821c), (b), and (−0.424a + 0.906c), which had coefficients of thermal expansions of 5.35(14) mK−1, 17.6(4) mK−1 and 52.6(1.2) mK−1. These values are all within the typical range exhibited by ceramic and polymeric materials, but provide insight into the cause of the unusual behaviour of the monoclinic angle.25 We have interpreted these values treating ligands as flexible linkers, which can change the relative position of their carboxylate groups. There are two distinct ligands in the structure, which run approximately perpendicular to the a- and b-axis, respectively. The second of these is almost parallel to the principal axis with the smallest coefficient of thermal expansion, suggesting it exhibits relatively rigid behaviour with changes in temperature. In contrast, the principal axis with the largest thermal expansion is close to the direction the other ligand runs along when viewed in the ac plane. This suggests this ligand straightens somewhat in this direction with increasing temperature since the bonding distances do not change. The orientation of the principal axis with the largest thermal expansion also drives the increase in the monoclinic angle, β on heating. This highlights the importance of analysing the thermal expansion of low symmetry structures along principal rather than crystallographic axes.
Magnetic structure and magnetoelastic coupling
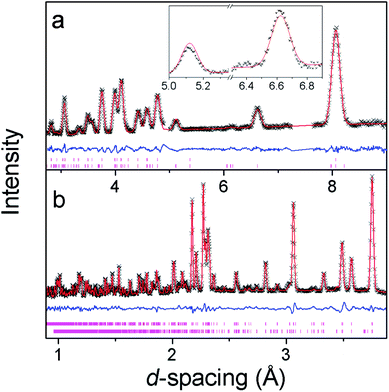
Additional reflections appear in the neutron diffraction patterns at 10 K, which can be indexed with a cell in which the b-axis is doubled (see Fig. 4). These additional reflections are considered to be magnetic in nature since they emerge close to the Néel temperature. Since there are no discontinuities in the lattice parameters this transition is presumed to be second order in nature, which is consistent with four possible magnetic structures. These are in the magnetic space groups Pb2/c or Pb21/c with either the same origin as the crystal structure or a shift to (0,0.5,0). Rietveld refinements appropriate for each of these possibilities were carried out, but only those with the origin shifted to (0,0.5,0) fitted the intensities of the magnetic reflections. Of these the solution in Pb21/c gave a significantly better fit (cf. Rp and Rwp of 2.9% and 3.8% compared to 3.2% and 4.6%, respectively, in the Pb2/c model). In the refinements carried out in Pb21/c the magnetic moment lies along the a-axis, with any moment along the b- and c-axis not significantly improving the fit. The total magnetic moment refines to 3.22(2) μB at 4 K, only slightly more than the moment of 2.90(3) μB observed at the onset of magnetic order. Careful examination did not reveal any increase in the intensity of the reflections indexed by the non-magnetic cell and, even if a small component of the moment is along the b- or c-axis, the chosen magnetic structure must be strictly antiferromagnetic.The magnetic structure of Co(C6D8O4) shows antiferromagnetic coupling between nearest neighbour Co cations along both the b- and c-axes (see Fig. 5). This presumably arises from super-exchange across the carboxylate groups, along an approximately 6.5 Å path. Co atoms appear to be ferromagnetically coupled to those directly above and below them in neighbouring layers. The long adipate ligands bridging these layers (a super-exchange path would be at least 14 Å) and their connection to an antiferromagnetically coupled pair of Co atoms on each end suggests the interlayer coupling occurs via dipole–dipole interactions. Since tetrahedral Co2+ does not have any significant single ion-anisotropy the alignment of the magnetic spins along the a-axis is likely driven by dipole–dipole interactions, which favours the spins lying in the directions in which this coupling occurs. This is akin to the magnetic structures of MnO and NiO where the dominate magnetic anisotropy term arises from the relatively weak dipole–dipole interactions due to a lack of first order-orbital contributions.26
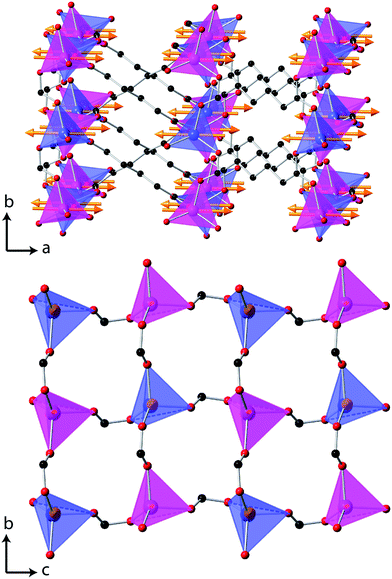 | ||
| Fig. 5 The magnetic structure of Co(C6D8O4), in which the arrows indicate the orientation of the magnetic spins and the two colours for the Co, blue and magenta, indicate the up and down spin directions. The D atoms are omitted for clarity, all other colours are the same as for Fig. 1 and in the lower figure only one layer of Co tetrahedra are shown. | ||
Below 40 K the a-axis begins to expand and the rate at which this occurs increases closer to the magnetic ordering temperature (see Fig. 3). This is accompanied by the b- and c-axis decreasing at a greater rate, hence the rate of change of the unit cell volume remains similar. Below 50 K the principal axes effectively correspond to the crystallographic axis and the rate of negative thermal expansion along the a-axis increases to −30(3) mK−1 below 20 K. We interpret this effect as arising from magnetoelastic coupling, which is known to cause anisotropic negative thermal expansion in a number of magnetic materials.27 Magnetoelastic coupling has been recently found in other metal–organic frameworks; however, to the best of our knowledge this is the first case where it has been established to cause negative thermal expansion.28 The contraction in the b- and c-axis near the Néel temperature is likely driven by antiferromagnetic exchange-striction within the sheets drawing the Co cations closer together. The weaker dipole–dipole coupling along the a-axis facilitates the relief of the resulting strain by allowing the structure to expand along this axis, thereby moving Co cations apart.
Conclusions
We have examined the structure and magnetic interactions of Co adipate, Co(C6H8O4), solving its magnetic structure and interpreting its unusual thermal expansion behaviour. Co(C6H8O4) is found to retain its monoclinic structure at low temperatures despite a continual decrease in its monoclinic angle, β, which passes through a metrically orthorhombic phase. This behaviour has been rationalised by examining the thermal expansion of the framework in terms of its principal axes. The compound has been found to exhibit antiferromagnetic order near 10 K, adopting a structure in which layers of tetrahedral Co are antiferromagnetically coupled through carboxylate groups. Nearest neighbour Co cations in adjacent planes interact ferromagnetically and the magnetic moments are aligned along the a-axis. The framework is also found to exhibit negative thermal expansion of the a-axis below 50 K. This is due to magnetoelastic coupling related to the emergence of the antiferromagnetic state and likely arises from relieving the strain caused by exchange-striction between Co cations within the bc plane.Acknowledgements
The authors would like to thank Chiu Tang and Stephen Thompson for their assistance with collecting data on I11 at Diamond. The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Grant 88538. PJS would like to thank the Glasstone Bequest for financial support through the provision of a Glasstone Fellowship. Experiments at the ISIS Pulsed Neutron Source were supported by a beamtime allocation from the Science and Technology Facilities Council and we acknowledge Diamond Light Source for time on Beamline I11. PTB is supported by the National Science Foundation Graduate Research Fellowship Program.Notes and references
- (a) A. J. Fletcher, K. M. Thomas and M. J. Rosseinsky, J. Solid State Chem., 2005, 178, 2491–2510 CrossRef CAS PubMed; (b) G. Férey, Chem. Soc. Rev., 2008, 37, 191–214 RSC.
- M. Kurmoo, Chem. Soc. Rev., 2009, 38, 1353–1379 RSC.
- P. J. Saines, J.-C. Tan, H. H.-M. Yeung, P. T. Barton and A. K. Cheetham, Dalton Trans., 2012, 41, 8585–8593 RSC.
- P. J. Saines, M. Steinmann, J.-C. Tan, W. Li, P. T. Barton and A. K. Cheetham, Inorg. Chem., 2012, 51, 11198–11209 CrossRef CAS PubMed.
- (a) G. Rogez, N. Viart and M. Drillon, Angew. Chem., Int. Ed., 2010, 49, 1921–1923 CrossRef CAS PubMed; (b) Y.-Z. Zheng, G.-J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014 10.1039/C3CS60337G.
- P. J. Saines, P. T. Barton, P. Jain and A. K. Cheetham, CrystEngComm, 2012, 14, 2711–2720 RSC.
- (a) H.-P. Jia, W. Li, Z.-F. Ju and J. Zhang, Eur. J. Inorg. Chem., 2006, 4264–4270 CrossRef CAS; (b) Y.-G. Huang, D.-Q. Yuan, L. Pan, F.-L. Jiang, M.-Y. Wu, X.-D. Zhang, W. Wei, Q. Gao, J. Y. Lee, J. Li and M.-C. Hong, Inorg. Chem., 2007, 46, 9609–9615 CrossRef CAS PubMed.
- J.-C. Tan, P. J. Saines, E. G. Bithell and A. K. Cheetham, ACS Nano, 2011, 6, 615–621 CrossRef PubMed.
- (a) O. Fabelo, L. Cañadillas-Delgado, I. S. Puente Orench, J. A. Rodríguez-Velamazán, J. Campo and J. Rodríguez-Carvajal, Inorg. Chem., 2011, 50, 7129–7135 CrossRef CAS PubMed; (b) P. J. Saines, J. R. Hester and A. K. Cheetham, Phys. Rev. B: Condens. Matter, 2010, 82, 144435 CrossRef; (c) P. J. Saines, H. H. M. Yeung, J. R. Hester, A. R. Lennie and A. K. Cheetham, Dalton Trans., 2011, 40, 6401–6410 RSC; (d) R. A. Mole, M. A. Nadeem, J. A. Stride, V. K. Peterson and P. T. Wood, Inorg. Chem., 2013, 52, 13462–13468 CrossRef CAS PubMed.
- E. Lee, Y. Kim and D.-Y. Jung, Inorg. Chem., 2002, 41, 501–506 CrossRef CAS PubMed.
- C. Livage, C. Egger, M. Nogues and G. Férey, C. R. Acad. Sci., Ser. IIc: Chim., 2001, 4, 221–226 CrossRef CAS.
- CrysAlis PRO version 171.36.28, Agilent Technologies, Yarnton, Oxfordshire, England, 2013 Search PubMed.
- M. C. Burla, R. Caliandro, M. Camalli, B. Carrozzini, G. L. Cascarano, C. Giacovazzo, M. Mallamo, A. Mazzone, G. Polidori and R. Spagna, J. Appl. Crystallogr., 2012, 45, 357–361 CrossRef CAS.
- G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- Y.-Q. Zheng, J.-L. Lin and A.-Y. Pan, Z. Anorg. Allg. Chem., 2000, 626, 1718–1720 CrossRef CAS.
- S. P. Thompson, J. E. Parker, J. Potter, T. P. Hill, A. Birt, T. M. Cobb, F. Yuan and C. C. Tang, Rev. Sci. Instrum., 2009, 80, 075107 CrossRef CAS PubMed.
- B. A. Hunter and C. J. Howard, A Computer Program for Rietveld Analysis of X-Ray and Neutron Powder Diffraction Patterns, Lucas Heights Laboratories, 1998 Search PubMed.
- R. M. Ibberson, W. I. F. David and K. S. Knight, The High Resolution Neutron Powder Diffractometer (HRPD) at ISIS - A User Guide, RAL Report 92–031, Rutherford Appleton Laboratory, Didcot, 1992 Search PubMed.
- A. C. Larson and R. B. Von Dreele, General Strucuture Analysis System (GSAS), Los Alamos National Laboratory Report LAUR 86-748, Los Alamos National Laboratory, Los Alamos, 1994 Search PubMed.
- B. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614 CrossRef CAS.
- B. C. Melot, J. E. Drewes, R. Seshadri, E. M. Stoudenmire and A. P. Ramirez, J. Phys.: Condens. Matter, 2009, 21, 216007 CrossRef PubMed.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- R. S. Krishnan, R. Srinivasan and S. Devanarayanan, Thermal Expansion of Crystals, Pergamon Press, Oxford, United Kingdom, 1979 Search PubMed.
- (a) W. L. Roth, Phys. Rev., 1958, 110, 1333–1341 CrossRef CAS; (b) A. K. Cheetham and D. A. O. Hope, Phys. Rev. B: Condens. Matter, 1983, 27, 6964–6967 CrossRef CAS.
- (a) C. dela Cruz, F. Yen, B. Lorenz, Y. Q. Wang, Y. Y. Sun, M. M. Gospodinov and C. W. Chu, Phys. Rev. B: Condens. Matter, 2005, 71, 060407 CrossRef; (b) J. Hemberger, H. A. K. von Nidda, V. Tsurkan and A. Loidl, Phys. Rev. Lett., 2007, 98, 147203 CrossRef CAS.
- (a) R. I. Thomson, P. Jain, A. K. Cheetham and M. A. Carpenter, Phys. Rev. B: Condens. Matter, 2012, 86, 214304 CrossRef; (b) Z. Wang, P. Jain, K.-Y. Choi, J. van Tol, A. K. Cheetham, H. W. Kroto, H.-J. Koo, H. Zhou, J. Hwang, E. S. Choi, M.-H. Whangbo and N. S. Dalal, Phys. Rev. B: Condens. Matter, 2013, 87, 224406 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: A crystallographic information file of the structure of Co(C6H8O4) obtained at 10 K and further plots of lattice parameters and magnetic susceptibility. CCDC 980786. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4mh00009a |
| ‡ Crystal data for 1: CoC6H8O4, M = 203.05 g mol−1, T = 10(2) K, monoclinic, space group P2/c, a = 16.1473(8) Å, b = 4.7928(2) Å, c = 9.2488(5) Å, α = 90°, β = 90.212(5)°, γ = 90°, V = 715.77(6) Å3, Z = 4, ρcalc = 1.884 g cm−3, μ = 2.355 cm−1, reflections measured/unique = 2444/1605(1345 I > 2σ(I)) [Rint = 0.0311]. Final results (for 100 parameters) were R1(all) = 0.0847, R1 (obs) = 0.0725, wR2(all) = 0.1986 and wR2(obs) = 0.1898 and χ2 = 1.178. |
| This journal is © The Royal Society of Chemistry 2014 |