First-principles studies on facet-dependent photocatalytic properties of bismuth oxyhalides (BiOXs)

Abstract

The photocatalytic properties were compared for the {001}, {110} and {010} facets of bismuth oxyhalides (BiOXs) through density functional theory (DFT) computations. X-terminated bulk-like {001} facets with clear boundary of [Bi₂O₂] and halogen slabs result in high thermodynamic stability and efficient separation of photo-induced e⁻-h⁺ pairs. Moreover, surface O vacancies, which act as e⁻-h⁺ recombination centers, are energetically unfavorable within {001} facets. BiX-terminated {110} and other facets with surface O vacancies introduce deep defect levels to the band gap, which are detrimental to the separation of e⁻-h⁺ pairs. These findings can better understand the origin of facet-dependent photocatalytic activities in BiOXs, and provide guidance for the design of high-efficiency photocatalysts.

---

1. Introduction

During the past decade, bismuth oxyhalides, BiOXs (X = F, Cl, Br, I),^1–15 have attracted much attention due to their remarkable photocatalytic activities under ultraviolet (UV) or visible-light illumination. The promising photocatalytic activities of BiOXs may result from their unique crystal structure and the corresponding electronic and optical properties. The BiOX compounds have a tetragonal PbFCl-type structure (space group P4/nmm; No. 129) and crystallize into unique layered structures consisting of [X–Bi–O–Bi–X] sheets stacked together by the nonbonding interaction through the X atoms along the c-axis. In other words, the structure comprises of a layer of [Bi₂O₂]²⁺ slabs interleaved by double slabs of halogen atoms. The internal static electric fields between [Bi₂O₂]²⁺ and the anionic halogen layers are believed to induce the efficient separation of photogenerated electron-hole pairs, which favors the photocatalytic properties of the catalysts. However, the crystal structure of the photocatalysts is not the only predominant factor on the photocatalysis efficiency.

For the purpose of enhancing the photocatalytic activities, the band engineering and morphology control of semiconductors have been intensively investigated. The band configuration of semiconductors plays a significant role in the absorption of light and in the determination of redox potentials. Also, band engineering represents an effective approach for the exploration and development of visible-light-sensitive photocatalysts with advanced performance.^16–20 Meanwhile, the emergence of nanostructured semiconductor photocatalysts has given rise to diverse and flexible ways of promoting photocatalytic efficiency.^21,22 Reducing particle size is generally beneficial for surface-dependent photocatalysis because it leads to quadratic growth of the specific surface area and hence the number of active sites.

Since photocatalytic reactions occur on the surfaces of semiconductors, the exposed crystal facets play a critical role in determining the photocatalytic reactivity and efficiency. Accordingly, the synthesis of single crystals with exposed highly reactive facets has attracted much interest, which represents a promising and efficient method for the further improvement of photocatalytic performance.^23,24 It is known that the {001} facets are the reactive facets for anatase TiO₂, and {110} facets for rutile TiO₂.^25,26 Recently, Ye et al. have synthesized BiOX (X = Cl, I) single-crystal nanosheets and disclosed their {001} facet-dependent photoactivity.^27–29 By comparing the photocatalytic degradation efficiency of Rhodamine B on different percentages of the {001} facets of BiOCl, they found that the {001} facets are photo-reactive in BiOX crystals. However, the origin of this facet-dependent photocatalytic activity remains unclear. In this work, we investigated the structural and electronic properties of the {001} and {110} surfaces of BiOXs (X = F, Cl, Br, I) by employing a slab model through periodic density functional theory (DFT) computations. By examining the effective mass of electrons and the difference in electron/hole mobilities which have implications in photocatalytic activities, we tried to disclose the origin of facet-dependent photocatalytic activity of BiOXs.

2. Computational details

Periodic DFT computations were performed by using a plane-wave method implemented in the Vienna ab initio simulation package (VASP)³⁰ code and the generalized gradient approximation (GGA) with the PW91 functional.³¹ The ion–electron interaction is described by the projector-augmented plane wave (PAW) approach^32,33 and a 480 eV cutoff for the plane-wave basis set was adopted in all computations. The tolerance for energy convergence was set to be 10⁻⁴ eV, while the ionic relaxation is converged when the force on the atoms is smaller than 10⁻³ eV Å⁻¹. The Brillouin zone was integrated by using Monkhorst–Pack generated sets of k-points. The 4 × 4 × 4 k-point mesh and 2 × 2 × 1 supercell were benchmarked to be sufficient to reach the convergence for bulk computations. Band structures of bulk BiOXs were computed along the special lines connecting the following high-symmetry points: G (0, 0, 0), X (0, 0.5, 0), Z (0, 0, 0.5), M (0.5, 0.5, 0), R (0, 0.5, 0.5), and A (0.5, 0.5, 0.5) in k-space.

The surface computations were performed by using the slab model, in which a finite number of crystal layers in a three-dimensional periodic cell were used to generate two surfaces via the introduction of a vacuum gap perpendicular to the surface. The structure of BiOXs belongs to the tetragonal space group P4/nmm (No. 129). In this work, the experimental values of lattice parameters were adopted as the starting points. Both the atomic positions and lattice constants were optimized for bulk BiOXs. For the cleaved slab models, only the atomic positions are allowed to relax. In this work, six terminations, two stoichiometric ({001}–1X and {010}), and four nonstoichiometric ({001}–2X, {001}–BiO, {110}–O, and {110}–BiX) surfaces were considered, as depicted in Fig. 1. The vacuum gap must be large enough that interactions between the periodic images perpendicular to the surface are negligible. The slab must also be of sufficient thickness that the structure in the middle of the slab is almost bulk-like. The cleavage energies calculated in this work are converged to 10⁻⁴ J m⁻² with respect to both the number of layers in the slab and the vacuum thickness, where a 15 Å vacuum gap was used throughout. Slabs with seven, five and ten BiOX trilayers were utilized to simulate the {110}, {001} and {010} surfaces, respectively. For the surface relaxation a 3 × 3 × 1 k-point grid was used, with the third vector perpendicular to the surface, and the energy cut-off was the same as the converged bulk calculation (480 eV). On the basis of fully relaxed slabs, band structures were computed along the special lines connecting the following high-symmetry points: G (0, 0, 0), M (0.5, 0.5, 0), and X (0, 0.5, 0) in k-space.

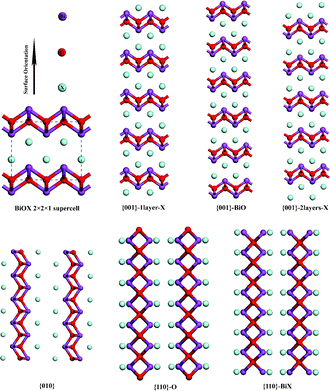Fig. 1 Slab models for {010}, {110} and {001} surfaces of BiOX.

3. Results and discussion

3.1 Geometry and structural stability

After full relaxation of the atomic positions, there is little inward or outward motion of the surface atoms, as a result of surface reconstruction. Accordingly, the bond lengths are different between the surface Bi–O bond (Bi–X bond) and central Bi–O bond (Bi–X bond), as listed in Table S1 (Electronic Supplementary Information (ESI)).† As expected, all the central Bi–O and Bi–X bond lengths of the slab model BiOXs are approximately equal to those of the bulk BiOXs, which indicates that the layers of slab models are thick enough to ensure that the central BiOX trilayers are bulk-like. Significantly, the difference between the surface and central Bi–O (Bi-X) bond lengths in the {001}–1X facet is slight. As a result, the physical and chemical properties of {001}–1X facet BiOXs are similar to the bulk BiOXs, due to its low surface reconstruction.

Thermodynamic stability is an essential factor for the photocatalytic performance of photocatalysts. The cleavage energy is a measure of the energy required to split a crystal into two parts with complementary terminations. To estimate the overall stability of the split crystal along the [001], [110], and [010] orientations, the cleavage energy (E^rel_cl) of a relaxed surface can be considered as:

E^rel_cl = [E^rel_slab (A) + E^rel_slab (B) − nE^bulk_BiOX]/4S (1)

where E^rel_slab and E^bulk_BiOX are the total energies of the relaxed slab and bulk crystal, respectively, n is the total number of BiOXs in the bulk crystal which is cleaved into two faceted models with complementary terminations, and S represents the surface area per unit cell.³⁴ A and B denote the complementary terminations with 2-layers of X on one side and BiO on the other for {001} facets (O on one side and BiX on the other for {110} facets). The remaining {010} facets and 1-layer of X terminated {001} facets are considered as self-complementary.

The cleavage energy, as summarized in Table 1, reflects the overall stability of a split crystal, without considering the specific chemical conditions. Regarding the same BiOX (X = F, Cl, Br, I), we can conclude that {001}–1X possesses the lowest cleavage energy, followed by {010}, {110}–O and {110}–BiX, and then {001}–2X and {001}–BiO. Except for {010}, all the cleavage energies of BiOX facets decrease with increasing the halogen atomic number. Therefore, {001}–1X facets are energetically the most favorable, resulting from their low surface reconstruction mentioned above. Meanwhile, as a result of the weakest electronegativity and activity of the I atom, both {001} and {110} facets with any terminations for BiOI are more stable than other BiOX facets. On the contrary, the {010} facets of BiOI have the highest cleavage energy, due to the incompact geometry of the {010} surface and the weakest electronegativity of I atom.

Table 1 Cleavage energies, E^rel_cl (in J m⁻²), for different BiOX facets

Terminations	BiOF	BiOCl	BiOBr	BiOI
{001}–1X	0.203	0.026	0.006	−0.094
{001}–2X	2.639	2.349	1.944	1.259
{001}–BiO	2.639	2.349	1.944	1.259
{110}–O	1.895	1.426	1.237	0.860
{110}–BiX	1.895	1.426	1.237	0.860
{010}	0.346	0.532	0.584	0.614

---

3.2 Band structures for {001}, {110} and {010} facets

Besides the thermodynamic stability, the electronic structure of photocatalysts is another key factor for their photocatalytic performances. Therefore, we also computed the band structures of bulk BiOXs and all investigated BiOX facets. For simplicity, only the band structures of BiOF are presented in Fig. 2. For BiOF, the {001}–1F and {010} facets have band gaps of 2.95 eV and 2.97 eV, respectively, which are approximately equal to that of bulk BiOF (3.01 eV). The band gap of the {110}–O facet (3.09 eV) is larger than that of the bulk structure, and all the other nonstoichiometric terminations have smaller band gaps than the corresponding bulk. Moreover, the other three BiOXs have features similar to this tendency, as presented in Fig. 3. This variation of band gap with the facet termination may be a result of the competition between the size and surface effects. The band gaps of facets with O terminations and the other three nonstoichiometric terminations are predominantly determined by the size and surface effects, respectively. Accordingly, there is a congruous red shift of the absorption spectrum for the BiOX {001} surface with nonstoichiometric terminations, which is beneficial to the photocatalytic performance. But for {110} facets, the absorption spectrum will be red- and blue-shifted for facets with BiX and O terminations, respectively. Another noteworthy characteristic of facets with nonstoichiometric terminations is that the facets with metal terminations ({001}–BiO and {110}–BiX) and nonmetal terminations ({001}–2X and {110}–O) are n- and p-type semiconductors, respectively, which is due to the surface state.

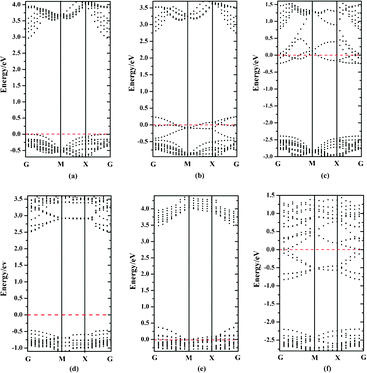Fig. 2 (a–c) Band structures of 1-layer F, 2-layer F and BiO terminated {001} facets for BiOF, respectively. (e) and (f) are band structures of O and BiF terminated {110} BiOF facets, respectively. (d) represents the band structure of the BiOF with {010} facet. Red dashed lines represent the Fermi level at 0 eV.

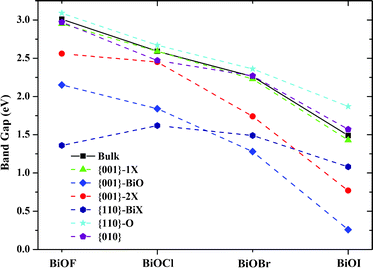Fig. 3 Variation of band gaps with the facet terminations for BiOX (X = F, Cl, Br, I). Solid and dashed lines are guides for eyes.

For an analysis of the recombination rate of e⁻-h⁺ pairs within different BiOX facets, which is also a crucial factor for their photocatalytic properties, we computed the curvature of the parabolic portions of the bands near the conduction band minimum (CBM) and the valence band maximum (VBM). The relationship between the curvature of the bands and the effective mass of the excitons can be functioned as follows:^35,36

m^* = ħ/2a (2)

where m* is the effective mass of charge carrier and a is the coefficient of the second-order term in a quadratic fit of E(k). Here, a larger coefficient of the second-order term corresponds to a lower effective mass of the charge carrier, indicating a higher mobility of the charge carrier. As summarized in Table 2, all the six terminated facets of BiOXs have a_CB's (a_VB's) smaller than those of the corresponding bulk structure. Therefore, the facet-structured BiOXs have activated electrons (holes) with lower mobility than in bulk BiOXs, especially the {010} facets, which is a result of the two-dimensional (2D) confinement of electrons (holes).

Table 2 Coefficients of the second-order term in a quadratic fit of CBM/VBM (a_CB/a_VB) for bulk and faceted BiOXs

Terminations	BiOF	BiOCl	BiOBr	BiOI
Bulk	74.98/−26.9	83.13/−33.9	88.09/−35.2	71.32/−19.2
{001}–1X	13.28/−2.02	19.24/−5.79	17.20/−5.71	12.34/−2.98
{001}–2X	15.34/−3.16	13.39/−0.61	17.12/−4.58	12.22/−7.56
{001}–BiO	3.97/−1.56	14.54/−8.44	13.86/−4.79	12.44/−2.96
{110}–O	2.02/−2.35	4.64/−1.78	5.56/−1.47	3.36/−1.14
{110}–BiX	1.63/−1.13	1.65/−1.69	2.03/−2.41	1.28/−1.28
{010}	0.01/−0.004	0.02/−0.009	0.02/−0.008	0.02/−0.01

---

To further analyze the recombination rate of excitons within different BiOXs, we adopt a definition for the relative ratio of effective mass, D, in eqn (3) and depict the variation of D with structures in Fig. 4.

D = m^*_h/m^*_e = |a_CB/a_VB| (3)

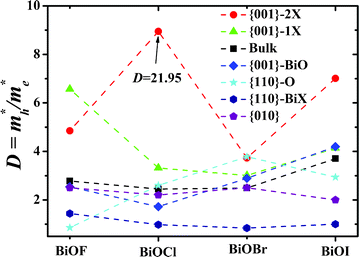Fig. 4 Variation of D with BiOX structures. For clarity and harmony, the relative ratio D of the 2-layer Cl terminated BiOCl {001} facet, which has a numerical value of 21.95, is shown as 9 in this figure. Dashed lines are guides for eyes.

As for the results in our previous work,³⁶ a higher D indicates a greater difference of electron-hole mobility and, thus, a lower recombination rate of e⁻-h⁺ pairs. As shown in Fig. 4, all the BiOX {001}–1X and {001}–2X facets have the highest D values, due to clear separation of the [Bi₂O₂] and halogen slabs at the BiOX surface. Therefore, the BiOX {001} facets with 1- and 2-layer X terminations have much lower electron-hole recombination rates than other facets and bulk structures. Especially, the BiOCl {001}–2Cl facet has a D value as high as 21.95, which may be due to the appropriate electronegativity of the Cl element and the special geometry of this facet. However, there was no experimental report up to now. Meanwhile, the {110}–BiX facets have D values around 1, which implies comparable mobility of activated electrons and holes, and accordingly a much higher recombination rate of e⁻-h⁺ pairs. The BiO terminated {001} and O terminated {110} facets do not have uniformly higher or lower D values than bulk BiOX. Considering the factor of carrier mobility, {001}–1X and {001}–2X facets have significantly higher photocatalytic efficiencies than other faceted and bulk BiOXs. In particular, the {110}–BiX facets with D values around 1 are ill-suited as BiOX photocatalysts.

3.3 Surface states in band gaps

As aforementioned, the electronic properties of {001} and {110} surfaces with nonstoichiometric terminations are highly affected by the surface states. We also computed density of states (DOS) and partial DOS (PDOS) to deeply verify the surface states and compare the depth of defect levels. For simplicity, Fig. 5 only shows the PDOS of BiOF facets. The stoichiometric {001}–1F and {010} facets do not have surface states, while the other four facets with nonstoichiometric terminations do. The surface atoms have different geometric and electronic conditions, and then result in surface defects, which can be generalized to all the other BiOXs. During the process of photocatalysis, the deep defect level in the band gap may be the recombination center for photo induced e⁻ and h⁺.³⁷ Unfortunately, the {110}–BiXs have deep defect levels at around −0.80 ± 0.05 eV, relative to the Fermi level. Taking BiOF with {110}–BiF facets for an example, we show in Fig. 2f and Fig. 5e that the deepest defect level is −0.84 eV at the G point, relative to Fermi level. Consequently, in view of the deep defect level as the recombination center, BiOXs with {110}–BiX facets are not preferable photocatalysts.

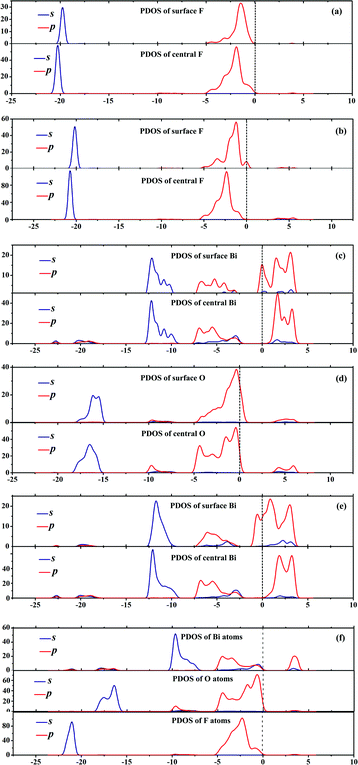Fig. 5 Partial density of states (PDOS) for surface and central (a) F atoms within {001}–1F, (b) F atoms within {001}–2F, (c) Bi atoms within {001}–BiO, (d) O atoms within {110}–O, and (e) Bi atoms within {110}–BiF. (f) is the PDOS of the BiOF with {010} surface. Dashed lines represent the Fermi level at 0 eV.

3.4 Surface O vacancies

As one kind of point defects, oxygen vacancies play a very important role in the photocatalytic reaction.²⁷ The separation efficiency of the excitons is affected by this defect.^28,38 We have found that the O vacancy, within the BiOX bulk, could act as a capture trap for photon-induced electrons and, thus, promote the separation of the e⁻-h⁺ pairs.³⁶ Consequently, it is interesting and significant to investigate how the surface O vacancies affect the electronic structure and photocatalytic properties of BiOXs with different facets. In this work, we computed the DOS and PDOS of these facets with surface O vacancies and, for simplicity, presented the PDOS and DOS of BiOCl facets with surface O vacancies in Fig. 6. However, surface O vacancies within all facets, except the {110}–O facet, result in deep defect levels in the band gap which act as recombination centers for photo induced e⁻-h⁺ pairs, which is obviously different from the O vacancies in the bulk BiOXs.

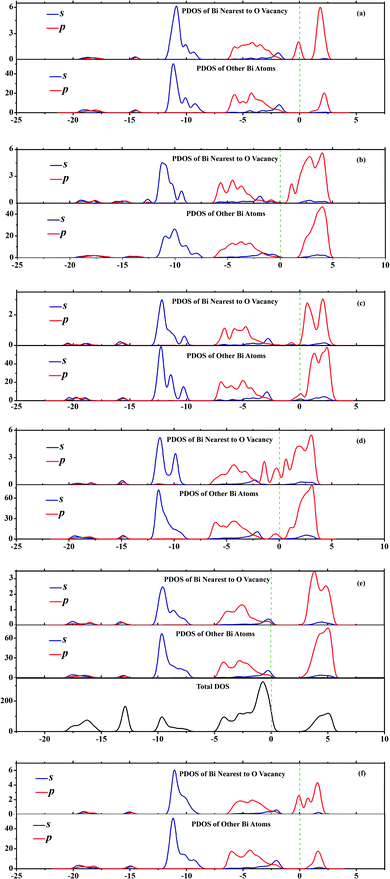Fig. 6 PDOS and TDOS of (a) {001}–1Cl, (b) {001}–2Cl, (c) {001}–BiO, (d) {110}–BiCl, (e) {110}–O and (f) {010} terminated BiOCl facets with O vacancies. Green dashed lines represent the Fermi level at 0 eV.

For a further insight, the formation energies (E_f) of all BiOX facets with surface O vacancies were calculated, as presented in Fig. 7. The formation energy of an O vacancy can be defined as:

E_f = E_vacancy − E_perfect + μ_O (4)

where E_vacancy and E_perfect are the total energy of the BiOX facets with and without an O vacancy, respectively. μ_O is the chemical potential of O atoms, which is half of the calculated energy of O₂ (9.18 eV).³⁹ Such formation energy is defined under O-rich conditions. We can see from Fig. 7 that the surface O vacancies within {001}–1X facets have E_f's close to those of O vacancies within bulk BiOX, due to their low surface reconstruction and bulk-like geometry. All the surface O vacancies within other facets of BiOXs have formation energies smaller than those of {001}–1X facets, especially the {110}–O with a high density of surface O atoms, have negative formation energies. Consequently, the surface O vacancy, which will induce a deep defect level as a e⁻-h⁺ recombination center, is energetically unfavorable within {001}–1X facets and favorable within {110}–O facets.

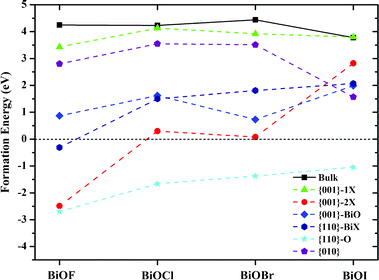Fig. 7 Formation energies of O vacancies within BiOX bulk and facets. Solid and dashed lines are guide for eyes.

Many reports suggest that the nanocrystallization of photocatalysts is a commendable strategy for enhancing the photocatalytic efficiency, because the nanocrystals with extremely large surface areas have abundant active sites.^2,4–6 BiOXs with {001} facets are more stable and photo-induced e⁻-h⁺ pairs within these facets can be efficiently separated. Otherwise, the surface O vacancies, which should be the recombination centers of e⁻-h⁺ pairs, are energetically unfavorable within {001} facets. All in all, the whole results propose {001} facet-dependent high photoactivity of BiOXs, which agrees well with experimental studies.^27–29

4. Conclusion

To summarize, we have investigated the photocatalytic properties of {001}, {110} and {010} facets within BiOXs by employing DFT computations. The clear boundary of [Bi₂O₂] and halogen slabs at the BiOXs' X-terminated {001} surface results in efficient separation of photo-activated e⁻-h⁺ pairs within these facets. The {001} facets with 1 layer of X termination have ignorable cleavage energies, and accordingly, an extremely high thermodynamic stability. For this reason, the surface O vacancy within these facets, which will induce a deep defect level as an e⁻-h⁺ recombination center, is energetically unfavorable within {001}–1X facets, but favorable within other facets. Meanwhile, the BiX-terminated {110} facets and other facets with surface O vacancies have deep defect levels in the band gap, which are detrimental to the separation of e⁻-h⁺ pairs.

Considering all factors in photocatalysis, the {001}–1X facets with extremely high thermodynamic stability, proper sunlight absorption, and low e⁻-h⁺ recombination rate are superior for BiOX photocatalysts, whereas the {110}–BiX and other facets with easily-introduced deep defect levels as e⁻-h⁺ recombination centers and low thermodynamic stability should be avoided in future photocatalyst design.

Acknowledgements

This work was supported by Tianjin Municipal Science and Technology Commission (11JCZDJC24800 & 12JCZDJC28100), MOE Innovation Team (IRT0927), Fundamental Research Funds for the Central Universities, and China-US Center for Environmental Remediation and Sustainable Development. The computations were performed on Magic Cube at Shanghai Supercomputer Center.

References

1. H. L. Peng, C. K. Chan, S. Meister, X. F. Zhang and Y. Cui, Chem. Mater., 2009, 21, 247.
2. L. L. Zhu, Y. Xie, X. W. Zheng, X. Yin and X. B. Tian, Inorg. Chem., 2002, 41, 4560.
3. Y. F. Fang, Y. P. Huang, J. Yang, P. Wang and G. W. Cheng, Environ. Sci. Technol., 2011, 45, 1593.
4. J. Zhang, F. J. Shi, J. Lin, D. F. Chen, J. M. Gao, Z. X. Huang, X. X. Ding and C. C. Tang, Chem. Mater., 2008, 20, 2937.
5. Z. H. Ai, W. Ho, S. Lee and L. Z. Zhang, Environ. Sci. Technol., 2009, 43, 4143.
6. Y. Y. Li, J. S. Wang, H. C. Yao, L. Y. Dang and Z. J. Li, J. Mol. Catal. A: Chem., 2011, 334, 116.
7. L. Q. Ye, C. Q. Gong, J. Y. Liu, L. H. Tian, T. Y. Peng, K. J. Deng and L. Zan, J. Mater. Chem., 2012, 22, 8354.
8. S. M. Sun, W. Z. Wang, L. Zhang, L. Zhou, W. Z. Yin and M. Shang, Environ. Sci. Technol., 2009, 43, 2005.
9. C. L. Yu, J. C. Yu, C. F. Fan, H. R. Wen and S. J. Hu, Mater. Sci. Eng., B, 2010, 166, 213.
10. Z. T. Deng, D. Chen, B. Peng and F. Q. Tang, Cryst. Growth Des., 2008, 8, 2995.
11. J. Henle, P. Simon, A. Frenzel, S. Scholz and S. Kaskel, Chem. Mater., 2007, 19, 366.
12. X. Zhang, Z. H. Ai, F. L. Jia and L. Z. Zhang, J. Phys. Chem. C, 2008, 112, 747.
13. X. F. Chang, J. Huang, C. Cheng, Q. Sui, W. Sha, G. B. Ji, S. B. Deng and G. Yu, Catal. Commun., 2010, 11, 460.
14. J. Y. Xiong, G. Cheng, G. F. Li, F. Qin and R. Chen, RSC Adv., 2011, 1, 1542.
15. H. F. Cheng, B. B. Huang, X. Y. Qin, X. Y. Zhang and Y. Dai, Chem. Commun., 2012, 48, 97.
16. E. Borgarello, J. Kiwi, M. Graetzel, E. Pelizzetti and M. Visca, J. Am. Chem. Soc., 1982, 104, 2996.
17. Z. G. Zou, J. H. Ye, K. Sayama and H. Arakawa, Nature, 2001, 414, 625.
18. J. W. Tang, Z. G. Zou and J. H. Ye, Chem. Mater., 2004, 16, 1644.
19. S. X. Ouyang and J. H. Ye, J. Am. Chem. Soc., 2011, 133, 7757.
20. G. L. Li and Z. Yin, Phys. Chem. Chem. Phys., 2011, 13, 2824.
21. N. Q. Wu, J. Wang, D. Tafen, H. Wang, J. G. Zheng, J. P. Lewis, X. G. Liu, S. S. Leonard and A. Manivannan, J. Am. Chem. Soc., 2010, 132, 6679.
22. Q. Liu, Y. Zhou, J. H. Kou, X. Y. Chen, Z. P. Tian, J. Gao, S. C. Yan and Z. G. Zou, J. Am. Chem. Soc., 2010, 132, 14385.
23. A. Selloni, Nat. Mater., 2008, 7, 613.
24. H. G. Yang, C. H. Sun, S. Z. Qiao, J. Zou, G. Liu, S. C. Smith, H. M. Cheng and G. Q. Lu, Nature, 2008, 453, 638.
25. X. Q. Gong and A. Selloni, J. Phys. Chem. B, 2005, 109, 19560.
26. J. Abad, O. Bohme and E. Roman, Langmuir, 2007, 23, 7583.
27. L. Q. Ye, L. Zan, L. H. Tian, T. Y. Peng and J. J. Zhang, Chem. Commun., 2011, 47, 6951.
28. L. Q. Ye, L. H. Tian, T. Y. Peng and L. Zan, J. Mater. Chem., 2011, 21, 12479.
29. J. Jiang, K. Zhao, X. Y. Xiao and L. Z. Zhang, J. Am. Chem. Soc., 2012, 134, 4473.
30. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1994, 49, 14251.
31. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1992, 45, 13244.
32. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 1795.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
34. G. X. Zhang, Y. Xie, H. T. Yu and H. G. Fu, J. Comput. Chem., 2009, 30, 1785.
35. L. Thulin and J. Guerra, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195112.
36. H. J. Zhang, L. Liu and Z. Zhou, Phys. Chem. Chem. Phys., 2012, 14, 1286.
37. X. G. Ma, B. Lu, D. Li, R. Shi, C. S. Pan and Y. F. Zhu, J. Phys. Chem. C, 2011, 115, 4680.
38. J. Geng, W. H. Hou, Y. N. Lv, J. J. Zhu and H. Y. Chen, Inorg. Chem., 2005, 44, 8503.
39. G. L. Chai, C. S. Lin, J. Y. Wang, M. Y. Zhang, J. Wei and W. D. Cheng, J. Phys. Chem. C, 2011, 115, 2907.

---

Footnote

† Electronic Supplementary Information (ESI) available: Bi–O and Bi–X bond lengths within different BiOX structures. See DOI: 10.1039/c2ra20881d/

---