Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correlations between helicity and optical losses within general electromagnetic scattering theory
Jon
Lasa-Alonso
 *ab,
Jorge
Olmos-Trigo
b,
Aitzol
García-Etxarri
*bc and
Gabriel
Molina-Terriza
*abc
*ab,
Jorge
Olmos-Trigo
b,
Aitzol
García-Etxarri
*bc and
Gabriel
Molina-Terriza
*abc
aCentro de Física de Materiales, Paseo Manuel de Lardizabal 5, 20018 Donostia, Spain. E-mail: jonqnanolab@gmail.com; gabriel.molina.terriza@gmail.com
bDonostia International Physics Center, Paseo Manuel de Lardizabal 4, 20018 Donostia, Spain
cIKERBASQUE, Basque Foundation for Science, María Díaz de Haro 3, 48013 Bilbao, Spain
First published on 8th March 2022
Abstract
Helicity preserving nanostructures and metasurfaces have been recently proposed as suitable candidates to enhance spectroscopic features of chiral molecules. With this in mind, we highlight that losses in the constituent nonmagnetic materials dramatically affect the possibility of constructing structures which conserve helicity. We first present a general procedure that permits the evaluation of the normalized helicity expectation value, 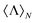 , i.e. the observable that allows for the identification of helicity preserving scatterers. We then apply this procedure to the case of a chiral sphere, which in an orientation averaged picture can capture the optical response of chiral inorganic nanostructures, obtaining a widely applicable analytical expression of
, i.e. the observable that allows for the identification of helicity preserving scatterers. We then apply this procedure to the case of a chiral sphere, which in an orientation averaged picture can capture the optical response of chiral inorganic nanostructures, obtaining a widely applicable analytical expression of 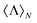 . Finally, we numerically show that optical losses impose an upper bound to the helicity expectation value on nonmagnetic core–shells and chiral spheres.
. Finally, we numerically show that optical losses impose an upper bound to the helicity expectation value on nonmagnetic core–shells and chiral spheres.
The study of chirality in its various forms is a cornerstone of modern sciences. In particular, most of the biomolecules which are essential for the biological processes are chiral, i.e. they do come in two different enantiomers, which are atomically identical, but can only match to each other after applying rotations and at least a mirror reflection transformation. One way of distinguishing these two enantiomers is by their ability to absorb or delay differently the left and right circular polarizations of light. Thus, the techniques related to optical chiral sensing and circular dichroism spectroscopy, are extremely important to several branches of the chemical and biological sciences.1–4 Unfortunately, the molecular optical rotatory power and the circular dichroism are typically small. In order to increase the light matter interaction, one can resort to highly focused beams or to the use of techniques in near field optics. In both cases, the description of the polarization of the electromagnetic field gets rather convoluted and light cannot be described anymore as a simple circularly polarized field. The helicity of light provides a solution to this problem. Optical helicity can be considered as the nonparaxial generalization of the notion of polarization.5 It is a magnitude that has gained attention in the last few years within the field of nanophotonics.6,7 In particular, this quantity is intimately related to the electromagnetic duality symmetry, i.e. that free-space Maxwell's equations are invariant under the exchange of the electric and magnetic fields.8 Also, this symmetry can be restored in macroscopic Maxwell's equations for materials fulfilling ε = μ, where ε is the electric permittivity, and μ is the magnetic permeability of the sample. The symmetry between the electric and magnetic fields is also at the core of the theoretical descriptions of circular dichroism.9 On a different basis, Cohen and Tang, between others,10–12 gave an alternative theoretical measure of the circular dichroism of chiral matter under very general illumination conditions through the local density of electromagnetic chirality. Soon after, this quantity proved to be intimately connected with the helicity of light.7 In fact, it has been proposed that dual particles, i.e. those in which duality symmetry is restored, are the adequate building blocks to enhance circular dichroism.
Light scattering on dual particles has some interesting properties. For example, on cylindrically symmetric scatterers, the restoration of the duality symmetry implies the absence of backscattered light.13 This, provides a fundamental theoretical description of the so-called first Kerker condition.14 Helicity conservation, in principle, requires the existence of magnetic materials (μ ≠ 1). However, natural magnetic materials at optical frequencies do not exist, and hence, both helicity conservation and the absence of backscattered light in principle should not be observable in this spectral regime. Nevertheless, this situation changed with the advent of high refractive index (HRI) nanostructured materials that present an electric and magnetic dipolar response in the visible.15 When both dipolar modes oscillate in-phase and with equal amplitudes, the first Kerker condition is satisfied16 and, hence, helicity preserving nanoparticles can be built from nonmagnetic constituent materials with μ = 1. As a result, the zero optical backscattering condition could be experimentally measured in the visible spectral regime for HRI Si nanospheres.17 Since then, the conservation of helicity in nonmagnetic particles has been widely employed by different branches of optics, ranging from enhanced errors in optical localization18 or isotropic polarization of speckle patterns,19 to light transport phenomena.20
In the recent past, the applications of these materials to enhance chiral sensing and circular dichroism spectroscopy have spawned. First, surface enhanced molecular circular dichroism was predicted on isolated dual particles.12 Soon after, dual metasurfaces, namely, planar arrays of Kerker-like particles designed to control the properties of light at both the far- and the near-field, proved to be more efficient in revealing and enhancing spectroscopic signals of chiral molecules.21–24 Unfortunately, the spectroscopic features of many industrially relevant molecules appear in the ultraviolet, where most of the HRI materials that constitute the building blocks of the aforementioned metasurfaces present losses.25 In this regime, the study of helicity preserving dual structures is scarce. For example, it has been recently shown that losses inhibit the emergence of the first Kerker condition for homogeneous nonmagnetic spheres.26 Consequently, the conservation of helicity is precluded for metasurfaces made of lossy spherical resonators, limiting their possible application in chiral spectroscopy. This is the current state-of-the-art of the intertwining between helicity, chirality, and energy conservation.
In this work, we demonstrate that the presence of losses not only precludes the emergence of the first Kerker condition in nonmagnetic spheres. We show that these correlations are more general, affecting also other systems such as core–shells or chiral inorganic spheres. To do so, we first settle an homogenized framework for the simultaneous study of energy and helicity measurements within general electromagnetic scattering theory. We detail a generally applicable procedure to calculate the normalized helicity expectation value, 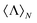 , which is the observable that, in practice, permits the identification of helicity preserving scatterers. Then, we apply this method to the case of a chiral inorganic sphere illuminated by a circularly polarized planewave and explicitly obtain a particular expression for
, which is the observable that, in practice, permits the identification of helicity preserving scatterers. Then, we apply this method to the case of a chiral inorganic sphere illuminated by a circularly polarized planewave and explicitly obtain a particular expression for 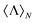 . The formula obtained is a generalization of a previously reported one,26 which allowed for the evaluation of the helicity expectation value in conventional spheres and core–shell particles. Making use of this expression, we finally show that the presence of losses in core–shells and chiral inorganic spheres sets an upper bound to the helicity expectation value.
. The formula obtained is a generalization of a previously reported one,26 which allowed for the evaluation of the helicity expectation value in conventional spheres and core–shell particles. Making use of this expression, we finally show that the presence of losses in core–shells and chiral inorganic spheres sets an upper bound to the helicity expectation value.
The paper is organized as follows: in Section 1, we set the general stage for the calculation of the helicity expectation value; Section 2 is devoted to the derivation of the helicity expectation value for chiral spheres; in Section 3 we show that losses impede helicity conservation in core–shells and chiral inorganic spheres; finally, in Section 4 we resume the main conclusions of our work. The interested reader in scattering theory and the general discussion on the helicity expectation value is advised to follow the whole derivation. On the other hand, the reader only interested in the results for helicity preserving structures can go directly to Section 2.
1 Helicity expectation value for a generic linear electromagnetic scatterer
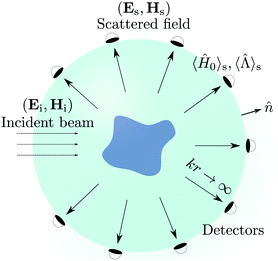
First and foremost, let us briefly put forward how measurements are considered within general linear scattering theory. A scheme of a typical scattering measurement setup is given in Fig. 1. A set of detectors are used to measure the energy and polarization densities. Mathematically, this can be expressed with measurements in the operators 〈H0〉 (Hamiltonian) and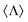 (helicity), respectively. Moreover, detectors are usually placed in the far-field region where energy can only exist in the form of electromagnetic waves. In this limit, the total scattered energy per unit time is usually calculated from the flux of the scattered Poynting vector, Ss, across a spherical surface with normal vector
(helicity), respectively. Moreover, detectors are usually placed in the far-field region where energy can only exist in the form of electromagnetic waves. In this limit, the total scattered energy per unit time is usually calculated from the flux of the scattered Poynting vector, Ss, across a spherical surface with normal vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) which is centered in the sample. However, one can check that in the radiation zone Ss·
which is centered in the sample. However, one can check that in the radiation zone Ss·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) = c〈H0〉,27 where c is the speed of light in vacuum and the usual notation 〈O〉 is employed to express the expected value of an operator O. Consequently, the flux is proportional to the local energy density in the far-field. In terms of experimentally quantifiable magnitudes, such as Stokes parameters, measuring 〈H0〉 would be associated with evaluating the parameter s0, whereas determining
= c〈H0〉,27 where c is the speed of light in vacuum and the usual notation 〈O〉 is employed to express the expected value of an operator O. Consequently, the flux is proportional to the local energy density in the far-field. In terms of experimentally quantifiable magnitudes, such as Stokes parameters, measuring 〈H0〉 would be associated with evaluating the parameter s0, whereas determining 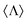 with the parameter s3.28,29 Finally, we consider that measurements are carried in a spherical surface around the sample which covers all the possible scattering angles.
with the parameter s3.28,29 Finally, we consider that measurements are carried in a spherical surface around the sample which covers all the possible scattering angles.
To deal with scattering problems in the most general way it is convenient to introduce the expansions of the scattered electromagnetic field in terms of vector spherical harmonics, as given in several books of reference in the field.27,30 The expansion of a monochromatic electric field can be written as (see, for instance, eqn (9.122) in ref. 27):
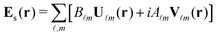 | (1) |
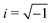 , A
, A![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m and B
m and B![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m are the electric and magnetic frequency-dependent scattering coefficients, which most generally depend on the incident illumination; U
m are the electric and magnetic frequency-dependent scattering coefficients, which most generally depend on the incident illumination; U![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m(r) = h
m(r) = h![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (kr)X
(kr)X![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m(θ,φ) and
m(θ,φ) and 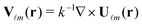 are Hansen's multipoles, with h
are Hansen's multipoles, with h![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (kr) the spherical Hankel function of the first kind and X
(kr) the spherical Hankel function of the first kind and X![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m(θ,φ) the vector spherical harmonics;27 finally, k is the wavenumber of light in vacuum, and a time-harmonic dependence exp
m(θ,φ) the vector spherical harmonics;27 finally, k is the wavenumber of light in vacuum, and a time-harmonic dependence exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−iωt) is implicitly considered through the text, with ω the angular frequency of light. Analytical expressions for the electric and magnetic complex scattering coefficients are available only for certain specific problems. In general, A
(−iωt) is implicitly considered through the text, with ω the angular frequency of light. Analytical expressions for the electric and magnetic complex scattering coefficients are available only for certain specific problems. In general, A![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m and B
m and B![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m coefficients can be computed numerically if the current distribution in the interior part of the sample is known.31 The possibility of computing the scattering coefficients from an arbitrary distribution of currents makes the expression in eqn (1) completely general and applicable to any solvable electromagnetic scattering problem. On the other hand, for our aim it is necessary to impose certain constraints on the multipolar expansion of the incident beam. In particular, we require the incident beam to have a well-defined helicity, σ = ±1. This is an imperative condition if we want to obtain an observable,
m coefficients can be computed numerically if the current distribution in the interior part of the sample is known.31 The possibility of computing the scattering coefficients from an arbitrary distribution of currents makes the expression in eqn (1) completely general and applicable to any solvable electromagnetic scattering problem. On the other hand, for our aim it is necessary to impose certain constraints on the multipolar expansion of the incident beam. In particular, we require the incident beam to have a well-defined helicity, σ = ±1. This is an imperative condition if we want to obtain an observable, 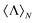 , that helps us in the identification of helicity preserving structures. This type of illumination can be generally written as:
, that helps us in the identification of helicity preserving structures. This type of illumination can be generally written as: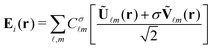 | (2) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m are the expansion coefficients which determine the spatial form of the incident beam. Ũ
m are the expansion coefficients which determine the spatial form of the incident beam. Ũ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m(r) = j
m(r) = j![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (kr) X
(kr) X![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m(θ,φ) and
m(θ,φ) and 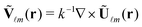 , where j
, where j![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (kr) is the spherical Bessel function of the first kind.
(kr) is the spherical Bessel function of the first kind.
Even if the expression in eqn (1) fully determines the fields generated from an arbitrary harmonic scatterer, it is more convenient for our aim to switch to the Riemann–Silberstein (RS) representation of the electromagnetic field. The RS vectors are constructed by taking the following superpositions of the complex electric and magnetic fields: 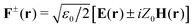 , where ε0 is the permittivity of vacuum and Z0 is the impedance of vacuum. The column vector
, where ε0 is the permittivity of vacuum and Z0 is the impedance of vacuum. The column vector 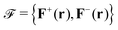 has been elsewhere regarded as the object from which the expectation values associated to fundamental electromagnetic observables can be obtained.32 Indeed, the time-averaged local density of electromagnetic energy can be derived as
has been elsewhere regarded as the object from which the expectation values associated to fundamental electromagnetic observables can be obtained.32 Indeed, the time-averaged local density of electromagnetic energy can be derived as 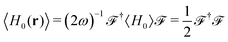 , where the “†” symbol means transpose conjugate and 〈H0〉 = i∂t. The time-averaged local density of electromagnetic helicity can also be computed in this notation as
, where the “†” symbol means transpose conjugate and 〈H0〉 = i∂t. The time-averaged local density of electromagnetic helicity can also be computed in this notation as 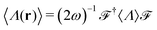 , bearing in mind that the RS vectors are eigenstates of the helicity operator,
, bearing in mind that the RS vectors are eigenstates of the helicity operator, 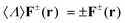 , with
, with 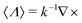 . Moreover, let us define the ratio between the scattering electric/magnetic multipolar coefficients and the incident electric/magnetic coefficients as:
. Moreover, let us define the ratio between the scattering electric/magnetic multipolar coefficients and the incident electric/magnetic coefficients as: 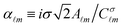 and
and 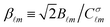 . As a result, in the RS representation, the field scattered by an arbitrary sample which has been illuminated by an incident beam with well-defined helicity σ can be compactly written as:
. As a result, in the RS representation, the field scattered by an arbitrary sample which has been illuminated by an incident beam with well-defined helicity σ can be compactly written as:
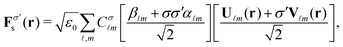 | (3) |
Determining the optical scattering of an object implies measuring the total radiation over the full solid angle of 4π at large distances from the sample under study. Experimentally, this is usually achieved with the aid of an integrating sphere. Mathematically, in order to calculate the total scattered energy one needs to integrate the observable 〈H0(r)〉 over the full solid angle. Similarly, the computation of the total scattered helicity requires to integrate the observable 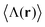 over all possible scattering directions. In addition, one can split the scattered fields into its helicity conserved (σ′ = + σ) and helicity flipped (σ′ = − σ) components. Making use of this notation, one can evaluate the energy and helicity densities for the whole solid angle:
over all possible scattering directions. In addition, one can split the scattered fields into its helicity conserved (σ′ = + σ) and helicity flipped (σ′ = − σ) components. Making use of this notation, one can evaluate the energy and helicity densities for the whole solid angle:
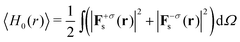 | (4) |
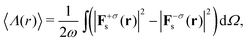 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθdφ, the integration limits being θ ∈ [0,π] and φ ∈ [0,2π]. Employing the orthogonality properties of the vector spherical harmonics U
θdθdφ, the integration limits being θ ∈ [0,π] and φ ∈ [0,2π]. Employing the orthogonality properties of the vector spherical harmonics U![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m and V
m and V![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m,33,34 one can explicitly calculate the energy and helicity densities as a function of the radial coordinate, r. However, as previously stated, in scattering theory measurements are typically carried out in the radiation zone. This implies that the total scattered energy and helicity observables are obtained by integrating only the far-field terms. Analytically, this means that the total scattered energy and helicity are obtained as:
m,33,34 one can explicitly calculate the energy and helicity densities as a function of the radial coordinate, r. However, as previously stated, in scattering theory measurements are typically carried out in the radiation zone. This implies that the total scattered energy and helicity observables are obtained by integrating only the far-field terms. Analytically, this means that the total scattered energy and helicity are obtained as: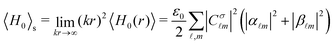 | (6) |
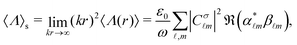 | (7) |
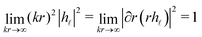 . From eqn (6) and (7) we can derive a completely general expression for the normalized (and unit-less) helicity expectation value:
. From eqn (6) and (7) we can derive a completely general expression for the normalized (and unit-less) helicity expectation value: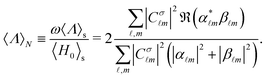 | (8) |
This is a physical magnitude which can also be determined in terms of the experimentally quantifiable Stokes parameters: 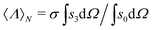 . It is a bounded observable,
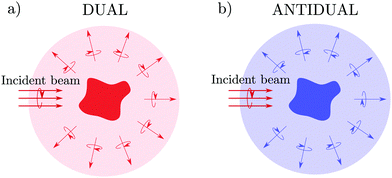
. It is a bounded observable, 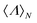 ∈ [−1,1], and its extreme values correspond to a dual,
∈ [−1,1], and its extreme values correspond to a dual, 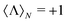 , or an antidual,
, or an antidual, 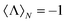 , scatterer. Dual scatterers are those which preserve the helicity of the incident beam (Fig. 2a), whereas antidual samples are those which flip it (Fig. 2b). Given an incident electromagnetic beam with well-defined helicity σ, a dual scatterer only emits in the same helicity channel (F−σs = 0). On the contrary, an antidual sample only scatters in the opposite helicity component (F+σs = 0). As it can be checked from the expression in eqn (3), dual scatterers are generally found whenever α
, scatterer. Dual scatterers are those which preserve the helicity of the incident beam (Fig. 2a), whereas antidual samples are those which flip it (Fig. 2b). Given an incident electromagnetic beam with well-defined helicity σ, a dual scatterer only emits in the same helicity channel (F−σs = 0). On the contrary, an antidual sample only scatters in the opposite helicity component (F+σs = 0). As it can be checked from the expression in eqn (3), dual scatterers are generally found whenever α![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m = β
m = β![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m, whereas antidual scatterers are obtained whenever α
m, whereas antidual scatterers are obtained whenever α![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m = −β
m = −β![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) m. Note that the s3 Stokes parameter has recently been related to the far-field measurement of the optical chirality flux.35 Importantly, we would like to highlight once again that the expression given in eqn (8) helps in the identification of dual or antidual scatterers if and only if the incident beam has a well-defined helicity σ. In the case of the incident beam being a superposition of helicity states (for instance, a linearly polarized planewave) the scattered field is generally described by both RS vector components and, consequently,
m. Note that the s3 Stokes parameter has recently been related to the far-field measurement of the optical chirality flux.35 Importantly, we would like to highlight once again that the expression given in eqn (8) helps in the identification of dual or antidual scatterers if and only if the incident beam has a well-defined helicity σ. In the case of the incident beam being a superposition of helicity states (for instance, a linearly polarized planewave) the scattered field is generally described by both RS vector components and, consequently, 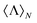 loses its usefulness in the identification of helicity preserving scatterers.
loses its usefulness in the identification of helicity preserving scatterers.
Finally, to finish with the discussion of the general expression for 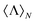 given in eqn (8), we would like to note that the multipolar basis chosen in eqn (1) is not the only one that can be employed for the derivation. Any other complete multipolar basis set (Stratton, Rose…) may be adopted if one knows the solid angle integral orthogonality expressions and the limits in the far-field.36,37 Moreover, we would also like to note that the normalized helicity expectation value can also be computed numerically from the first equality in eqn (8): given a point by point solution of the scattered electromagnetic field, one can always compute the integrals in eqn (4) and (5) in the radiation zone as discrete sums. This makes our approach to calculate
given in eqn (8), we would like to note that the multipolar basis chosen in eqn (1) is not the only one that can be employed for the derivation. Any other complete multipolar basis set (Stratton, Rose…) may be adopted if one knows the solid angle integral orthogonality expressions and the limits in the far-field.36,37 Moreover, we would also like to note that the normalized helicity expectation value can also be computed numerically from the first equality in eqn (8): given a point by point solution of the scattered electromagnetic field, one can always compute the integrals in eqn (4) and (5) in the radiation zone as discrete sums. This makes our approach to calculate 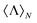 completely general and applicable to any electromagnetic scattering problem for which the solution of the scattered fields is known.
completely general and applicable to any electromagnetic scattering problem for which the solution of the scattered fields is known.
2 Helicity expectation value for a chiral inorganic sphere
As a practical implementation of all the previously discussed ideas, we have calculated the normalized helicity expectation value for an optically active (or chiral) inorganic spherical sample. Note that such spheres can capture the optical response of artificial chiral systems in an effective medium—orientation averaged—approximation.38–40 The light scattering by a chiral sphere under planewave illumination has a closed analytical solution (see Section 8.3 in ref. 41). The multipolar expansion of such scattered fields is actually a generalization of the well-known Mie theory for conventional spherical particles and can be expressed as: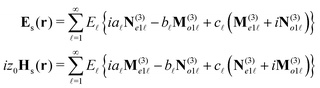 | (9) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = E0i
= E0i![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (2
(2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) + 1)/
+ 1)/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) + 1) and E0 is the amplitude of the incident electric field. {Me|m|
+ 1) and E0 is the amplitude of the incident electric field. {Me|m|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,Mo|m|
,Mo|m|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,Ne|m|
,Ne|m|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,No|m|
,No|m|![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) } are the vector spherical harmonics used by Stratton (see Section 7.11 in ref. 36) and Bohren, which can also be related to the set employed by Jackson.42 Finally, a
} are the vector spherical harmonics used by Stratton (see Section 7.11 in ref. 36) and Bohren, which can also be related to the set employed by Jackson.42 Finally, a![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , b
, b![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and c
and c![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) are the Mie coefficients which can be computed either for an optically active sphere (see page 188 in ref. 41), a conventional sphere (see eqn (4.56) and (4.57) in ref. 41) or a core–shell system (see eqn (8.2) in ref. 41) requiring, in these last two cases, that c
are the Mie coefficients which can be computed either for an optically active sphere (see page 188 in ref. 41), a conventional sphere (see eqn (4.56) and (4.57) in ref. 41) or a core–shell system (see eqn (8.2) in ref. 41) requiring, in these last two cases, that c![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 0.
= 0.
It is of utmost importance to note that the incident field employed to compute the scattered fields in eqn (9) is a linearly polarized planewave propagating along the OZ direction (see eqn (4.21) and (4.37) in ref. 41). Thus, to obtain a meaningful expression of the normalized helicity expectation value, we should consider only one circular polarization component for the incident field and, consequently, take into account only the scattered fields associated to such a component. We have done this by switching from Bohren's vector spherical harmonics notation in eqn (9) to Jackson's notation and identifying the different total angular momentum contributions, m = ±1, to the expansion of the incident planewave. As a planewave contains no orbital angular momentum, m is fully associated to the z-component of the spin angular momentum and, therefore, to the two possible circular polarizations (or helicities). Moreover, as m is the eigenvalue associated to the z-component of the total angular momentum operator, it is a conserved quantity in scattering problems with cylindrically symmetric samples along the OZ axis. Thus, to identify the fields scattered due to a single helicity component of the incident field, we must separately consider the terms in the expansion given by eqn (9) with a total angular momentum m = 1 and m = − 1.
By doing so and following, step by step, the previously discussed general procedure, one obtains a closed analytical multipolar expression of the normalized helicity expectation value for a chiral sphere:
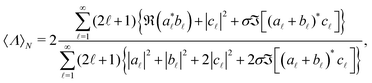 | (10) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 0, one recovers the well-known expression of the normalized helicity expectation value for such systems.26,43 However, considering the c
= 0, one recovers the well-known expression of the normalized helicity expectation value for such systems.26,43 However, considering the c![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) coefficients makes the expression in eqn (10) also applicable to optically active spheres. It can be checked that, in opposition to the case of a conventional sphere and core–shell, this more general expression for
coefficients makes the expression in eqn (10) also applicable to optically active spheres. It can be checked that, in opposition to the case of a conventional sphere and core–shell, this more general expression for 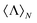 critically depends on the helicity of the incident field, σ. This is so because, by definition, chiral scatterers are those whose response depends on the polarization of the incident beam, i.e. their refractive index is a function of the input helicity state. Let us also remark that the expression in eqn (10) is the theoretical prediction for the ratio of the experimentally measurable solid angle integrals of s3 and s0 Stokes parameters for a chiral inorganic sphere. Expressions similar to eqn (10) can be calculated for other systems for which an analytical solution is known, for instance, an optically active spherical shell.44
critically depends on the helicity of the incident field, σ. This is so because, by definition, chiral scatterers are those whose response depends on the polarization of the incident beam, i.e. their refractive index is a function of the input helicity state. Let us also remark that the expression in eqn (10) is the theoretical prediction for the ratio of the experimentally measurable solid angle integrals of s3 and s0 Stokes parameters for a chiral inorganic sphere. Expressions similar to eqn (10) can be calculated for other systems for which an analytical solution is known, for instance, an optically active spherical shell.44
In what follows, we employ the expression for the helicity expectation value in eqn (10) to show that the correlations between energy and helicity reported in ref. 26 are also present in core–shells and optically active spheres. Therein it was analytically demonstrated that helicity preservation in nonmagnetic conventional spheres, the so-called first Kerker condition, can only be achieved for scatterers built up from lossless materials. Moreover, it is also known that the helicity conservation condition can only be achieved in pure multipolar regimes, i.e. in spectral areas where only one multipolar order ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) dominates.43 In practice, dual particles are usually constructed within the dipolar regime (
dominates.43 In practice, dual particles are usually constructed within the dipolar regime (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 1) or, in other words, in the limit where the particle is small compared to the illuminating wavelength. Consequently, the reported results imply that dipolar helicity preserving spheres can only be constructed with materials and at wavelengths in which the refractive index,
= 1) or, in other words, in the limit where the particle is small compared to the illuminating wavelength. Consequently, the reported results imply that dipolar helicity preserving spheres can only be constructed with materials and at wavelengths in which the refractive index, 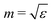 , is a real number. This was shown by using analytical properties of the Bessel functions that define the electric and magnetic Mie coefficients, which indicates that the correlations might be also present in other nonmagnetic scatterers. With the aid of eqn (10), we show that these correlations are indeed more general.
, is a real number. This was shown by using analytical properties of the Bessel functions that define the electric and magnetic Mie coefficients, which indicates that the correlations might be also present in other nonmagnetic scatterers. With the aid of eqn (10), we show that these correlations are indeed more general.
3 Helicity conservation in lossy core–shells and chiral inorganic spheres
To show that the correlations mentioned above between energy and helicity are not limited to the dipolar regime, we have first addressed the case of a multipolar core–shell, i.e. a core–shell that cannot be described only by the first Mie coefficients a1 and b1. For core–shell systems under planewave illumination, the expression for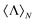 is exactly the same as the one found for spheres, i.e. imposing c
is exactly the same as the one found for spheres, i.e. imposing c![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 0 in eqn (10) and substituting the appropriate analytical expressions for the scattering coefficients a
= 0 in eqn (10) and substituting the appropriate analytical expressions for the scattering coefficients a![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and b
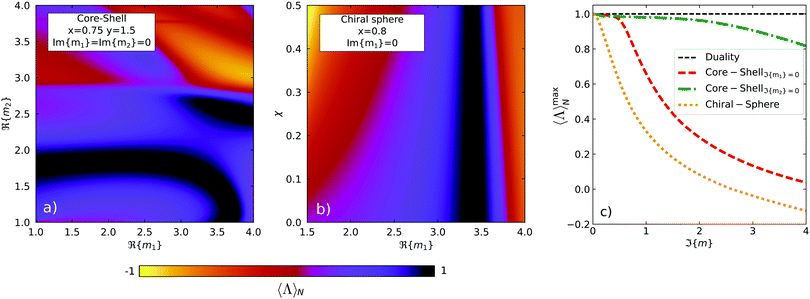
and b![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . In Fig. 3a we show the computed normalized helicity expectation value for a wide range of real refractive indices associated both to the core, m1, and to the shell, m2. The size parameters of the core, x, and the shell, y, have been chosen such that the response of the system is determined both by the dipolar (a1, b1) and quadrupolar (a2, b2) Mie coefficients. As it can be checked from Fig. 3a, when setting the imaginary parts of the refractive indices to zero, there are several combinations of ℜ(m1) and ℜ(m2) which enable the construction of helicity preserving scatterers, i.e. the points at which
. In Fig. 3a we show the computed normalized helicity expectation value for a wide range of real refractive indices associated both to the core, m1, and to the shell, m2. The size parameters of the core, x, and the shell, y, have been chosen such that the response of the system is determined both by the dipolar (a1, b1) and quadrupolar (a2, b2) Mie coefficients. As it can be checked from Fig. 3a, when setting the imaginary parts of the refractive indices to zero, there are several combinations of ℜ(m1) and ℜ(m2) which enable the construction of helicity preserving scatterers, i.e. the points at which 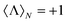 (black areas).
(black areas).
On the other hand, we have also computed the normalized helicity expectation value for a system in which the constituent relations consider cross electric–magnetic terms, i.e. media in which electric fields generate magnetization currents and magnetic fields generate polarization currents. In Fig. 3b we show the helicity expectation value for a system characterized by a chiral constant χ, which determines the refractive indices of a chiral medium both for a left (σ = +1) or right (σ = − 1) polarized incident planewave. More explicitly, the refractive indices are computed as nσ = m1 − σχ. As it can be noted from the figure, for a dipolar particle (x = 0.8), helicity preserving samples can be constructed for several values of χ and with an approximately constant value of ℜ(m1). For an optically active dipolar sphere, the chiral nature of the media induces a symmetric change in the electric, a1, and magnetic, b1, dipolar scattering coefficients. Given an incident circularly polarized planewave, the electric scattering coefficient is effectively changed into ach1 = a1 − iσc1 and, similarly, the magnetic scattering coefficient into bch1 = b1 − iσc1. Thus, starting at the first Kerker condition for a nonchiral spherical particle (χ = 0), the equality of the electric and magnetic dipolar scattering coefficients, a1 = b1, is seen to hold well also for points at which χ ≠ 0.
In Fig. 3c, we analyze the behaviour of core–shells and chiral particles when losses are considered. To do so, we have progressively modified the imaginary part of the refractive indices, ℑ(m), recalculating the maps equivalent to the ones shown in Fig. 3a and b. For each value of the imaginary part of the refractive index, we take the maximum value of the whole colormap, 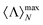 , and then we plot it against ℑ(m) in Fig. 3c. As it can be checked, all the maximum values of the computed helicity expectation values are sensitive to the presence of absorption in the system. For the case of the core–shell, introducing losses in the outer volume leads to a much faster decay of
, and then we plot it against ℑ(m) in Fig. 3c. As it can be checked, all the maximum values of the computed helicity expectation values are sensitive to the presence of absorption in the system. For the case of the core–shell, introducing losses in the outer volume leads to a much faster decay of 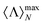 (red line). However, the system appears to be more robust to the presence of losses in the inner volume, even if still
(red line). However, the system appears to be more robust to the presence of losses in the inner volume, even if still 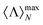 < 1 for any value of ℑ(m) > 0 (green line). This result is in agreement with previous results reported for core–shells in ref. 45. For core–shells with small core radii, the presence of losses in the inner volume does not significantly increase the absorption cross-section of the system as a whole. Thus, as it was shown therein, unidirectionality of the scattered field, which implies helicity conservation for cylindrically symmetric structures, can still be approximately reached in this case.
< 1 for any value of ℑ(m) > 0 (green line). This result is in agreement with previous results reported for core–shells in ref. 45. For core–shells with small core radii, the presence of losses in the inner volume does not significantly increase the absorption cross-section of the system as a whole. Thus, as it was shown therein, unidirectionality of the scattered field, which implies helicity conservation for cylindrically symmetric structures, can still be approximately reached in this case.
4 Conclusions
In conclusion, we have set the general stage for the study of helicity conservation from an observational point of view in arbitrary electromagnetic scattering problems. We have given an expression for the normalized helicity expectation value, i.e.eqn (8), which permits the identification of helicity preserving structures in the most possible general way. Then, we have applied the general procedure to a case of practical interest, i.e. the fields scattered by a chiral inorganic sphere, obtaining a closed analytical expression for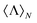 in eqn (10). Finally, we have employed this expression to show that correlations between helicity and energy preservation are also present in chiral inorganic spheres and core–shells. On the one hand, we have shown that losses in chiral spheres and in the outer volume of core–shells completely preclude the first Kerker condition. On the other hand, losses in the interior part of core–shell systems seem to be less critical for the preservation of helicity, but still determinant. These results indicate that lossy nonmagnetic materials are not ideal candidates to construct helicity preserving metasurfaces and, thus, to build suitable systems to enhance CD spectroscopy of surrounding chiral molecules.
in eqn (10). Finally, we have employed this expression to show that correlations between helicity and energy preservation are also present in chiral inorganic spheres and core–shells. On the one hand, we have shown that losses in chiral spheres and in the outer volume of core–shells completely preclude the first Kerker condition. On the other hand, losses in the interior part of core–shell systems seem to be less critical for the preservation of helicity, but still determinant. These results indicate that lossy nonmagnetic materials are not ideal candidates to construct helicity preserving metasurfaces and, thus, to build suitable systems to enhance CD spectroscopy of surrounding chiral molecules.
Author contributions
J. L. A., J. O. T., A. G. E., and G. M. T. initiated the project. J. L. A. and J. O. T. developed the theory and performed the simulations. All the authors discussed the results and wrote the manuscript. A. G. E. and G. M. T. coordinated the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. L. A., J. O. T. and A. G. E. acknowledge support from the Spanish Ministerio de Ciencia e Innovación (PID2019-109905GA-C2) and from Eusko Jaurlaritza (IT1164-19 and KK-2021/00082). A. G. E. acknowledges funding from Programa Red Guipuzcoana de Ciencia, Tecnología e Innovación 2021 (Grant Nr. 2021-CIEN-000070-01. Gipuzkoa Next). A. G. E. and G. M. T. acknowledge funding from the Basque Government's IKUR initiative on Quantum technologies (Department of Education). The authors would like to acknowledge insightful discussions with Dr Nuno de Sousa. J. L. A. would also like to thank Carlos Maciel Escudero for valuable discussions on the Riemann–Silberstein vectors and Álvaro Nodar for his indications regarding the choice of vector spherical harmonics.Notes and references
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, 2nd edn, 2004 Search PubMed.
- A. Rodger, Encyclopedia of Analytical Chemistry, John Wiley and Sons, 2006 Search PubMed.
- P. L. Polavarapu and C. Zhao, Fresenius’ J. Anal. Chem., 2000, 366, 727–734 CrossRef CAS PubMed.
- C. D. Aiello, M. Abbas, J. M. Abendroth, A. Afanasev, S. Agarwal, A. S. Banerjee, D. N. Beratan, J. N. Belling, B. Berche, A. Botana, J. R. Caram, G. L. Celardo, G. Cuniberti, A. Garcia-Etxarri, A. Dianat, I. Diez-Perez, Y. Guo, R. Gutierrez, C. Herrmann, J. Hihath, S. Kale, P. Kurian, Y.-C. Lai, A. Lopez, E. Medina, V. Mujica, R. Naaman, M. Noormandipour, J. L. Palma, Y. Paltiel, W. T. Petuskey, J. C. Ribeiro-Silva, J. J. Saenz, E. J. G. Santos, M. Solyanik, V. J. Sorger, D. M. Stemer, J. M. Ugalde, A. Valdes-Curiel, S. Varela, D. H. Waldeck, P. S. Weiss, H. Zacharias and Q. H. Wang, 2021, arXiv: 2009.00136.
- M. G. Calkin, Am. J. Phys., 1965, 33, 958 CrossRef.
- N. Tischler, I. Fernandez-Corbaton, X. Zambrana-Puyalto, A. Minovich, X. Vidal, M. L. Juan and G. Molina-Terriza, Light: Sci. Appl., 2014, 3, e183 CrossRef CAS.
- L. V. Poulikakos, J. A. Dionne and A. García-Etxarri, Symmetry, 2019, 11, 1113 CrossRef CAS.
- I. Fernandez-Corbaton, X. Zambrana-Puyalto, N. Tischler, X. Vidal, M. L. Juan and G. Molina-Terriza, Phys. Rev. Lett., 2013, 111, 060401 CrossRef PubMed.
- E. U. Condon, Rev. Mod. Phys., 1937, 9, 432–457 CrossRef CAS.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 CrossRef PubMed.
- Y. Tang and A. E. Cohen, Science, 2011, 332, 333–336 CrossRef CAS PubMed.
- A. García-Etxarri and J. A. Dionne, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235409 CrossRef.
- X. Zambrana-Puyalto, I. Fernandez-Corbaton, M. L. Juan, X. Vidal and G. Molina-Terriza, Opt. Lett., 2013, 38, 1857–1859 CrossRef CAS PubMed.
- M. Kerker, D.-S. Wang and C. L. Giles, J. Opt. Soc. Am., 1983, 73, 765–767 CrossRef.
- A. García-Etxarri, R. Gómez-Medina, L. S. Froufe-Pérez, C. López, L. Chantada, F. Scheffold, J. Aizpurua, M. Nieto-Vesperinas and J. J. Sáenz, Opt. Express, 2011, 19, 4815–4826 CrossRef PubMed.
- M. Nieto-Vesperinas, R. Gomez-Medina and J. J. Saenz, J. Opt. Soc. Am. A, 2011, 28, 54–60 CrossRef CAS PubMed.
- Y. H. Fu, A. I. Kuznetsov, A. E. Miroshnichenko, Y. F. Yu and B. Lukyanchuk, Nat. Commun., 2013, 4, 1527 CrossRef PubMed.
- J. Olmos-Trigo, C. Sanz-Fernández, A. García-Etxarri, G. Molina-Terriza, F. S. Bergeret and J. J. Sáenz, Phys. Rev. A, 2019, 99, 013852 CrossRef CAS.
- M. K. Schmidt, J. Aizpurua, X. Zambrana-Puyalto, X. Vidal, G. Molina-Terriza and J. J. Sáenz, Phys. Rev. Lett., 2015, 114, 113902 CrossRef PubMed.
- J. Olmos-Trigo, C. Sanz-Fernández, F. S. Bergeret and J. J. Sáenz, Opt. Lett., 2019, 44, 1762–1765 CrossRef CAS PubMed.
- C.-S. Ho, A. García-Etxarri and J. A. Dionne, ACS Photonics, 2017, 4, 197–203 CrossRef CAS.
- M. L. Solomon, J. Hu, M. Lawrence, A. García-Etxarri and J. A. Dionne, ACS Photonics, 2019, 6, 43–49 CrossRef CAS.
- J. Lasa-Alonso, D. R. Abujetas, A. Nodar, J. A. Dionne, J. J. Sáenz, G. Molina-Terriza, J. Aizpurua and A. García-Etxarri, ACS Photonics, 2020, 7, 2978–2986 CrossRef CAS.
- J. Feis, D. Beutel, J. Köpfler, X. Garcia-Santiago, C. Rockstuhl, M. Wegener and I. Fernandez-Corbaton, Phys. Rev. Lett., 2020, 124, 033201 CrossRef CAS PubMed.
- J. Hu, M. Lawrence and J. A. Dionne, ACS Photonics, 2020, 7, 36–42 CrossRef CAS.
- J. Olmos-Trigo, C. Sanz-Fernández, D. R. Abujetas, J. Lasa-Alonso, N. de Sousa, A. García-Etxarri, J. A. Sánchez-Gil, G. Molina-Terriza and J. J. Sáenz, Phys. Rev. Lett., 2020, 125, 073205 CrossRef CAS PubMed.
- J. D. Jackson, Classical Electrodynamics, John Wiley and Sons, Inc., 1999 Search PubMed.
- J. H. Crichton and P. L. Marston, Electron. J. Differ. Equ., 2000, 4, 37–50 Search PubMed.
- I. Bialynicki-Birula, J. Opt., 2019, 21, 094002 CrossRef CAS.
- A. Zangwill, Modern Electrodynamics, Cambridge University Press, 2012 Search PubMed.
- R. Alaee, C. Rockstuhl and I. Fernandez-Corbaton, Opt. Commun., 2018, 407, 17–21 CrossRef CAS.
- I. Bialynicki-Birula, in Progress in Optics, ed. E. Wolf, Elsevier, 1996, ch. 5, vol. 36, pp. 245–294 Search PubMed.
- R. G. Barrera, G. A. Estevez and J. Giraldo, Eur. J. Phys., 1985, 6, 287–294 CrossRef.
- B. Carrascal, G. A. Estevez, P. Lee and V. Lorenzo, Eur. J. Phys., 1991, 12, 184–191 CrossRef.
- L. V. Poulikakos, P. Gutsche, K. M. McPeak, S. Burger, J. Niegemann, C. Hafner and D. J. Norris, ACS Photonics, 2016, 3, 1619–1625 CrossRef CAS.
- J. A. Stratton, Electromagnetic Theory, McGraw-Hill Book Company, Inc., 1941 Search PubMed.
- M. E. Rose, Elementary Theory of Angular Momentum, John Wiley and Sons, Inc., 1957 Search PubMed.
- M. Schäferling, D. Dregely, M. Hentschel and H. Giessen, Phys. Rev. X, 2012, 2, 031010 Search PubMed.
- X. Yin, M. Schäferling, B. Metzger and H. Giessen, Nano Lett., 2013, 13, 6238–6243 CrossRef CAS PubMed.
- A. Fazel-Najafabadi, S. Schuster and B. Auguié, Phys. Rev. B, 2021, 103, 115405 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley and Sons, Inc., 1998 Search PubMed.
- N. Tischler, X. Zambrana-Puyalto and G. Molina-Terriza, Eur. J. Phys., 2012, 33, 1099–1109 CrossRef.
- J. Olmos-Trigo, D. R. Abujetas, C. Sanz-Fernández, X. Zambrana-Puyalto, N. de Sousa, J. A. Sánchez-Gil and J. J. Sáenz, Phys. Rev. Res., 2020, 2, 043021 CrossRef CAS.
- C. F. Bohren, J. Chem. Phys., 1975, 62, 1566–1571 CrossRef CAS.
- W. Liu, E. Miroshnichenko, D. N. Neshev and Y. S. Kivshar, ACS Nano, 2012, 6, 5489–5497 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |