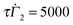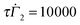DOI:
10.1039/C6SM01199C
(Paper)
Soft Matter, 2016,
12, 7688-7697
Coupled dynamics of flow, microstructure, and conductivity in sheared suspensions
Received
24th May 2016
, Accepted 3rd August 2016
First published on 3rd August 2016
Abstract
We propose a model for the evolution of the conductivity tensor for a flowing suspension of electrically conductive particles. We use discrete particle numerical simulations together with a continuum physical framework to construct an evolution law for the suspension microstructure during flow. This model is then coupled with a relationship between the microstructure and the electrical conductivity tensor. Certain parameters of the joint model are fit experimentally using rheo-electrical conductivity measurements of carbon black suspensions under flow over a range of shear rates. The model is applied to the case of steady shearing as well as time-varying conductivity of unsteady flow experiments. We find that the model prediction agrees closely with the measured experimental data in all cases.
Introduction
Microstructural anisotropy has been an active area of research for decades. It plays a critical role in biomechanics,5,7 plasticity,9 granular materials,3,6,26,32,37,41,45 liquid crystals,44 and more. Some materials, such as elastic composites, have fixed anisotropy that does not evolve over time. However, other materials may develop anisotropy due to deformation, e.g. kinematic hardening of solids,9 or due to an externally-applied field, such as an electric field, as is typical of liquid crystals.44
Of particular interest in this study is the flow-induced anisotropy of colloidal suspensions.11,12,22,28,31,34–36,40,46,47 Suspensions of carbon black, an electrically-conductive form of carbon, have recently found application in a class of semi-solid batteries called “flow batteries”.8,50 At concentrations above the percolation threshold, the carbon black creates an electrically conductive network inside the flowing electrolytes of the battery, allowing for higher reaction rates and overall system efficiency. However, it has been experimentally demonstrated that the networks in these carbon suspensions are highly sensitive to shearing.1,2,4,42 In these studies, the conductivity of the carbon network drops precipitously with shear and recovers dynamically when brought to rest. This has serious implications for battery performance if the evolution of network structure and conductivity are not properly considered during design. Recent studies43 on optimizing the efficiency of a flow battery have neglected the effect of a shear-induced drop in suspension conductivity. In addition to the drop in conductivity, it has been observed that the suspension microstructure becomes anisotropic during shearing flow, which can lead to anisotropic conductivity.18,29,49 In this study, we use discrete-particle simulations and continuum physical arguments to derive a general constitutive law for the flow-induced evolution of a tensor-valued measure of suspension network anisotropy. We couple this with a nonlinear structure–conductivity relation and show that the calibrated joint model makes quantitative predictions of conductivity evolution in many different experimental flows of carbon black.
We use a fabric tensor to describe the structure of the particle network in suspension. This concept was originally devised to describe the contact network in granular materials.26,32,41 The fabric tensor can be defined at the particle level with the relation
| |  | (1) |
where ⊗ denotes the dyadic product and
n(i) the contact unit normals. The fabric tensor is a local (particle-level) 2nd-order tensor measure of the number and orientations of contacts with neighboring particles. The contact vectors in
(1) are illustrated in
Fig. 1.
 |
| | Fig. 1 Schematic of particles in contact showing unit contact normal vectors ni for computation of the fabric tensor. | |
It is often illustrative to examine the average fabric of a group of particles rather than the particle-level information, i.e.A = 〈AP〉P. This definition yields a number of useful properties. The trace of AP is equal to the coordination number of contacts on a particle. Consequently, trA represents the average coordination number, Z, of a group of particles. Second, this definition results in a symmetric, positive semi-definite tensor. This is appealing because these tensorial properties are shared by the conductivity tensor K.
In a previous numerical study,33 we modeled the conductivity tensor of a general particle network as a function of the average fabric tensor A, by assuming the electrical properties of the network could be represented by a regular lattice of identical particles arranged to achieve with the same average fabric tensor as the given network. The fabric–lattice relationship can be inverted to obtain a model for conductivity as shown below in 3D:
| | 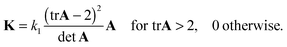 | (2) |
The model was derived assuming that the suspending medium is a perfect insulator, the particles are perfect conductors, and that electrical resistance arises at the contacts between particles. Although the model neglects conductivity below the tr
A = 2 threshold—which occurs in particle assemblies with many disconnected islands and a small number of percolating chains—the model's predictions for both the isotropic and anisotropic components of conductivity are demonstrably stronger, over a wide range of coordination numbers, compared to the existing upper-bound models for particle-network conductivity,
19 which ultimately relate to the Hashin–Shtrickman bounds.
Eqn (2) was validated for computer-generated random sphere networks, but was never tested experimentally; a byproduct of its usage in the current study is a de facto experimental test and a check on its robustness for non-spherical particles.
General evolution law
We set out to develop a continuum model to accurately characterize the evolution of flowing particle networks indicated by the aforementioned experiments. Although the fundamental quantity—the particle network—is composed of discrete units, we make a continuum approximation such that quantities at a point represent local spatial averages, e.g. velocity or fabric. This is a valid approximation since typical applications of these particle networks are several orders of magnitude larger than the constituents of the networks.
We define the velocity gradient  , the strain-rate tensor D = ½(L + LT), and the spin tensor W = ½(L − LT). We postulate a fabric evolution law of the form
, the strain-rate tensor D = ½(L + LT), and the spin tensor W = ½(L − LT). We postulate a fabric evolution law of the form 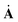 = Ψ(A, L), where
= Ψ(A, L), where  denotes the material time derivative of A. In order for an evolution law such as this to be indifferent under a change in an observer's frame of reference, the evolution law must be expressible as
denotes the material time derivative of A. In order for an evolution law such as this to be indifferent under a change in an observer's frame of reference, the evolution law must be expressible as  = WA − AW +
= WA − AW +  (A, D), where
(A, D), where  is an isotropic function of the fabric tensor and the strain-rate tensor.14 A representation theorem for isotropic functions of 3 × 3 symmetric tensors38 can be applied, allowing us to write
is an isotropic function of the fabric tensor and the strain-rate tensor.14 A representation theorem for isotropic functions of 3 × 3 symmetric tensors38 can be applied, allowing us to write
| |  | (3) |
In the above expression,
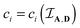
, where the full set of simultaneous invariants of
A and
D is
| |  | (4) |
The left-hand side of
(3) is the co-rotational time derivative of
A, or Jaumann rate, given the symbol
Å. In general, the left-hand side can be any objective time derivative of the tensor field, all of which are specializations of the Lie derivative.
24 Without loss of generality, we chose to use the co-rotational rate of
A for ease of modeling; other objective rates, such as the contravariant or covariant time derivatives, do not equal

in a spin-free flow.
13
The general evolution law in (3) has a large number of scalar functions that must be specified. For simplicity, we neglect higher-order tensorial terms by setting  for i ≥ 4. This leaves the quasi-linear form
for i ≥ 4. This leaves the quasi-linear form
The task of modeling, therefore, is reduced to choosing physically meaningful functions for
c1,
c2, and
c3.
By examining the effect of each term on the evolution of the fabric, some physical constraints must be satisfied by the choice of the ci. First, the fabric will be positive, isotropic, and unchanging after a long period of no flow; anisotropy induced by shearing flow must relax away over time once flow is stopped. This implies
| |  | (6) |
If either of these constraints are violated, then the fabric would either decay away to a non-positive isotropic state or diverge.
Second, contacts are formed on the compressive axis of shearing flow and broken on the extension axis (as experimentally confirmed in Hoekstra et al.18). This gives us the condition
| |  | (7) |
Third, while the electrical conductivity decreases with increasing shear rate, the conductivity never reaches zero despite the fluid being a strong insulator.
2 Based on the conductivity model assumption in
(2), this implies that tr
A remains above 2 at all times. This condition implies
| |  | (8) |
Finally, as the fabric is necessarily positive semi-definite, the evolution law must guarantee this property is preserved. A sufficient condition for this, as derived in the Appendix, is
| |  | (9) |
Numerical experiments
To gain insight on the relaxation behavior of the fabric, as characterized through the functions c1 and c2, we created a discrete particle aggregation code. In our simulation, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles are seeded into a periodic box at a 3.5% volume fraction and allowed to diffuse. The volume fraction was chosen to match approximately the volume fraction in physical experiments that will be described in subsequent sections. Particles and clusters are assigned velocities such that the distance that a cluster moves in a single time step is drawn from a Gaussian distribution with variance DΔt, where D is the diffusion coefficient, and Δt is the simulation time step length. As hit-and-stick behavior is typical in diffusion-limited aggregation,21 all clusters in contact after a step are deemed to stick, creating a larger cluster. As clusters grow, the diffusion coefficient is adjusted according to D = D0/N, where D0 is the diffusion coefficient for a single particle, and N is the number of particles in a cluster. Because clusters typically have a snake-like shape, dominated by long strands of particles, this relation was chosen for its similarity to the asymptotic solution for the diffusion coefficient of a string of N particles.15 We neglect hydrodynamic forces between clusters and rotational diffusion. These assumptions result in a code similar to the off-lattice Monte Carlo aggregation method described in Rottereau et al. 2004.39 The effect of shear thickening was not considered, since the method represents particles in a quiescent medium subjected to Brownian forces.
000 particles are seeded into a periodic box at a 3.5% volume fraction and allowed to diffuse. The volume fraction was chosen to match approximately the volume fraction in physical experiments that will be described in subsequent sections. Particles and clusters are assigned velocities such that the distance that a cluster moves in a single time step is drawn from a Gaussian distribution with variance DΔt, where D is the diffusion coefficient, and Δt is the simulation time step length. As hit-and-stick behavior is typical in diffusion-limited aggregation,21 all clusters in contact after a step are deemed to stick, creating a larger cluster. As clusters grow, the diffusion coefficient is adjusted according to D = D0/N, where D0 is the diffusion coefficient for a single particle, and N is the number of particles in a cluster. Because clusters typically have a snake-like shape, dominated by long strands of particles, this relation was chosen for its similarity to the asymptotic solution for the diffusion coefficient of a string of N particles.15 We neglect hydrodynamic forces between clusters and rotational diffusion. These assumptions result in a code similar to the off-lattice Monte Carlo aggregation method described in Rottereau et al. 2004.39 The effect of shear thickening was not considered, since the method represents particles in a quiescent medium subjected to Brownian forces.
The simulation results are shown in Fig. 2, where Ass is the steady-state fabric. After a brief startup period, the deviation of the average coordination number from steady state (trAss − trA) is related to time through a power law
| | | (trAss − trA) ∼ (t/Δt)−0.745 | (10) |
Although many studies, both experimental
23 and numerical,
39 have examined the evolution of various cluster properties, such as radius of gyration and mass, very few have examined the average coordination of particles. We have not found any prior studies that track the average coordination number through time, though it seems plausible that this power law exponent could be deduced through a random walk analysis.
 |
| | Fig. 2 Log–log plot of trAss − trAvs. time shows power-law evolution of trA to steady state in the absence of external shearing. Inset images (for illustration purposes only) from a highly dilute simulation demonstrate the aggregation of particles into clusters in the simplified discrete model. Clusters in the simulation used to generate the curve span the domain after a short period of aggregation, forming conductive networks. | |
Form of evolution coefficients
Motivated by the power-law decay of trA to steady state that we have just determined, we choose the following functional forms for the ci coefficients:| |  | (11) |
| |  | (12) |
where Z0 = trAss (in the absence of flow), Z∞ = trAss as |D| → ∞, τ is the time scale of thermal fabric relaxation, β reflects the network creation or disruption due to non-affine flow perturbations, α is the initial rate of anisotropy formation when started from an isotropic state, and n characterizes the power-law relaxation to the no-flow steady state (see Fig. 2). The particular forms of the functions were chosen in order to satisfy all of the constraints (6–9) and to reproduce the power-law relaxation of the coordination number observed in Fig. 2. The above constraints imply the following inequalities on these parameters:| | 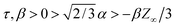 | (15) |
The value of n can be predicted from the discrete simulation data by taking the trace of eqn (5), setting L to 0, integrating to find trA as a function of time, and relating the answer back to the power-law in eqn (10). Using this, we find n = 1.34.
In previous studies on attractive colloids, both experiments20 and numerical simulations25 indicate that the average coordination number at rest is slightly above the isostatic condition of frictionless, hard spheres (Z = 6) for certain degrees of attraction. In our experiments, the carbon black of interest has an attractive interaction potential of 12kBT,48 which is similar to the materials studied in the aforementioned studies. Thus, for consistency, we expect Z0 to be ≈7 for our material.
Experimental methods
The system studied is a carbon black suspension prepared in the absence of any dispersant by mixing carbon black powder (Cabot Vulcan XC72R of specific gravity 1.8) in a light mineral oil (Sigma-Aldrich, specific gravity 0.838, viscosity 20 mPa s) as described in ref. 12 at a weight concentration of 8% w/w (approximately 3.5% volume fraction). The suspension is sonicated for one hour and mixed vigorously prior to each test to minimize the effects of sedimentation.
Simultaneous rheo-electric measurements were performed using a custom setup on an ARG2 torsional stress-controlled rheometer with a parallel plate geometry. This setup uses liquid metal (EGaIn) to create a low-friction continuous electrical connection to the rotating shaft,16 allowing a prescribed voltage to be applied across the shearing suspension layer. DC potentiostatic tests with ϕ = 100 mV were performed using a Solartron SI1287 potentiostat. The plates (diameter d = 40 mm, average surface roughness Ra = 0.10 μm), acting as a two-electrode system, are coated with gold to reduce contact resistance. All rheo-electric tests were performed at gap h = 0.75 mm and T = 26 ± 0.3 °C. A schematic of the device used to perform the rheo-electric measurements is shown in Fig. 3.
 |
| | Fig. 3 (top) Photo of device used to perform simultaneous rheo-electric measurements. (bottom) Circuit diagram of experimental setup. | |
Two sets of experiments were performed using the setup described above. The first was a set of steady-state current measurements taken at nominal shear rates in the range  . At each shear rate, both the current and stress were allowed to equilibrate before the measurement was recorded to ensure that it had relaxed to its steady value. The shear rates were swept in descending order to mitigate complications such as shear-induced phase separation that arise at low shear rates, below
. At each shear rate, both the current and stress were allowed to equilibrate before the measurement was recorded to ensure that it had relaxed to its steady value. The shear rates were swept in descending order to mitigate complications such as shear-induced phase separation that arise at low shear rates, below  .16
.16
The second dataset was a collection of transient ramp tests wherein current data was collected continuously for the duration of the test. The ramp tests consisted of 5 minutes of nominal shear rate  , ramping linearly to
, ramping linearly to  over duration tR, holding for 5 minutes, and abruptly setting
over duration tR, holding for 5 minutes, and abruptly setting  , collecting data for 15 additional minutes. Pre-shear at
, collecting data for 15 additional minutes. Pre-shear at  was applied for 5 minutes before each test to ensure consistent initial conditions.
was applied for 5 minutes before each test to ensure consistent initial conditions.
The parameters Z∞, β, and α were fitted to the steady-state current measurements using the 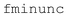 Matlab optimization routine, minimizing the squared difference between predicted and measured electrical currents. The τ parameter, which is primarily responsible for controlling the fabric's relaxation time, was chosen from the experimental dynamics of the ramp tests. Lastly, the k1 parameter can be chosen to match the steady-state current observed at
Matlab optimization routine, minimizing the squared difference between predicted and measured electrical currents. The τ parameter, which is primarily responsible for controlling the fabric's relaxation time, was chosen from the experimental dynamics of the ramp tests. Lastly, the k1 parameter can be chosen to match the steady-state current observed at  .
.
The predicted current is calculated by evaluating the integral
| | 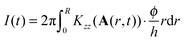 | (16) |
where
Kzz is the component of conductivity perpendicular to the plate,
ϕ is the applied potential difference across the plates,
h is the plate separation, and
R is the plate radius. Note that the fabric tensor is a function of radial position; each point along a radius is subjected to a different shear rate due to the applied torsional motion, and thus evolves differently. The form of
(16) can be modified slightly in order to solve for the current at steady-state for a given nominal shear rate

, by substituting
A(
r,
t) with

where
Ass(
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
) is the steady-state fabric tensor, whose components are obtained algebraically from
eqn (5) by defining
D and
W to correspond to simple shearing at
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
and setting
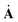
= 0. A detailed outline of the fitting procedure can be found in the Appendix.
To simulate the electrical current for a transient test, the evolution law must be directly integrated at each point across the disk where the conductivity will be evaluated. To do this, one must input the time-dependent nominal shear-rate 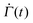 from the experimental protocol. The evolution law was numerically integrated to obtain the fabric tensor at all time points. After the fabric is known, (16) can be approximated directly using a Riemann sum to give the predicted current as a function of time.
from the experimental protocol. The evolution law was numerically integrated to obtain the fabric tensor at all time points. After the fabric is known, (16) can be approximated directly using a Riemann sum to give the predicted current as a function of time.
Results
The power law index n was determined a priori using the discrete simulation, and all other model parameters were found using the fitting procedure described above. The parameters used to generate all of the following plots, which satisfy all necessary constraints, are Z0 = 7, Z∞ = 2.41, τ = 50 s, β = 0.009, α = −0.0089, n = 1.34, and k1 = 0.0282 S m−1.
Steady-state experiments
Fig. 4 shows the steady-state current predicted by the model compared to experimental data measured at various nominal shear rates, represented in the form of a scaled current as a function of a dimensionless shear rate, or Deborah number. The results indicate the model does an excellent job predicting the steady-state current measurements over the entire tested range of  .
.
 |
| | Fig. 4 Model fit of steady-state current measurements at different nominal shear rates. Values are normalized by the static current measurement I0. | |
Transient ramp experiments
The results in Fig. 5 show the temporal evolution of the current under imposed shearing normalized by the static current measurement. The close agreement indicates that the model is capable of making accurate, quantitative predictions for the transient behavior of the normalized current. The close agreement at the steady plateaus of  and
and  were expected due to the close fit of steady-state data in Fig. 4. The most critical test in the ramp experiments was the relaxation of the conductivity when flow was abruptly stopped. The model does an excellent job predicting this non-trivial behavior, especially given that each point along the radius of the plate begins decaying from a different initial steady-state condition.
were expected due to the close fit of steady-state data in Fig. 4. The most critical test in the ramp experiments was the relaxation of the conductivity when flow was abruptly stopped. The model does an excellent job predicting this non-trivial behavior, especially given that each point along the radius of the plate begins decaying from a different initial steady-state condition.
 |
| | Fig. 5 Transient ramp experiments from (top)  to to 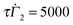 , and (bottom) , and (bottom)  to to 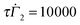 with ramp times tR/τ of 0.6, 1.2, and 6 (top to bottom). A vertical offset of 0.2 has been added between successive curves for clarity, with the y-axis correct as displayed for the bottom curve. Current values are normalized by the static current measurement I0. with ramp times tR/τ of 0.6, 1.2, and 6 (top to bottom). A vertical offset of 0.2 has been added between successive curves for clarity, with the y-axis correct as displayed for the bottom curve. Current values are normalized by the static current measurement I0. | |
Asymptotic model predictions
With the model, we were able to examine analytical solutions for the evolution of the coordination number Z in the limiting cases of diffusion-dominated and shear-dominated evolution. The evolution of Z is governed by the differential equation that results from taking the trace of (5) under the assumption of incompressible flow, substituting (11) and (12) into the resulting expression, and collecting terms:| |  | (17) |
The case of diffusion-dominated evolution corresponds to the condition |D| → 0. Applying this to (17) results in an ODE that, together with an appropriate initial condition, may be analytically solved for Z(t). The solution of this ODE predicts a power-law approach of Z to Z0 given by |Z − Z0| ∼ t−1/n. Shear-dominated evolution is given by the condition |D| ≫ 1/(βτ). Under these conditions, the first term in (17) is much smaller than the second, and the resulting ODE predicts exponential decay of Z to Z∞, given by Z − Z∞ ∼ e−β|D|t. These two analytical results highlight the important transition from power-law to exponential evolution as |D| increases. The power-law behavior at low shear is consistent with our numerical simulations of particle aggregation and the |D| = 0 dynamics in our experiments, shown in Fig. 5. The exponential decay is consistent with previously published simulations of attractive fluid–particle systems in shear-dominated flow.25
These analytical results are plotted in Fig. 6 together with numerically integrated solutions of (17). In all cases, the initial condition was set to Z|t=0 = (Z0 + Z∞)/2. Each panel shows the same numerically-integrated data (solid lines), with the only difference between the top and bottom being the axes definitions. On the top and bottom, respectively, the thick dashed line is the analytical solution at |D| = 0 and the analytical solution for shear-dominated flow, both defined above.
 |
| | Fig. 6 Evolution of Z = trA in pure shearing under different shear rates, as predicted by the model. (top) βτ|D| ≪ 1 yields power-law approach of Z to steady state; |Z − Z0| ∼ t−1/n as |D| → 0, dotted line. (bottom) βτ|D| ≫ 1 yields exponential approach to steady state; log(Z − Z∞) ∼ −|D|t as |D| → ∞, dotted line. | |
Discussion
We have demonstrated a model for the conductivity of sheared suspensions by linking conductivity and flow to a common microstructural description. Although the model parameters were obtained using conductivity measurements, it is interesting to note the following points, which emphasize that the structure indeed plays the assumed role: (i) the best-fit parameters obtained from the experiments obey constraints expected of a particle structure (eqn (6)–(9)), (ii) parameters taken from existing particle-level simulation data—n and Z0—yield quantitatively accurate results (Fig. 4 and 5) when used in the evolution law, and (iii) the structural evolution model, on which the experimental agreement hinges, gives the same asymptotic behaviors as those observed in suspension simulations. Conversely, our approach highlights the possibility of using conductivity measurements to infer discrete microstructural properties of systems, a notion also suggested in ref. 51. It should be noted that a simpler constitutive specialization of the ci functions using n = 0 does not capture the measured evolution of conductivity well. A model using n = 0 predicts exponential, rather than power-law, relaxation of fabric upon cessation of flow. The resulting conductivity evolution cannot predict the observed behavior shown in Fig. 5. For comparison, we show the predictions of such a model (using n = 0) in the Appendix.
There are strong analogies to be drawn between this proposed microstructural evolution model coupled to conductivity, and the thixotropic family of rheological models. In thixotropy models, fluid viscosity is often modeled as a function of an implicit material field that is intended to represent the underlying fluid microstructure. This field is prescribed to evolve according to a differential equation, properly stated as a transport equation that encompasses both the advective conservation and the non-conservative creation and destruction of the field.27,30 It should be unsurprising that our conductivity model strongly resembles these thixotropy models, as the fluid microstructure is believed to give rise to the flow-history-dependent behavior of both the conductivity and viscosity in these types of complex fluids. See the Appendix for a demonstration of some conductivity modeling results that mirror those often associated with thixotropy.
The new model (eqn (2), (5) and (11–13)) can be applied as a quantitative tool for designing systems of flowing, electrically-active particulate suspensions, for example in a semi-solid flow battery architecture.8,17,43 Because the shear-induced conductivity loss can be strong even under moderate shear rates, the ability to predict this component of the performance envelope through a quantitative continuum model should enable subsequent geometric and flow protocol optimization.
Appendix
Constraint derivations
This section lays out in more detail the derivation of constraints on the fabric tensor evolution law below:
Trace condition.
To find the physical conditions on the coefficients in the evolution law, we take the trace of (A1) and solve for the steady-state trace of the fabric, trAss. The flow is assumed to be incompressible, so trD = 0. We observe experimentally that electrical conductivity never entirely shuts off, regardless of the imposed strain rate |D|. According to (2) in the main text, this implies that trA > 2. This restriction yields a constraint between c1 and c2.| |  | (A3) |
Positive semidefinite constraint.
The fabric tensor is by definition a symmetric, positive semi-definite tensor. Thus, we must ensure that under no circumstances will the evolution law violate this condition. We can write the fabric tensor aswhere Q is the eigenvector matrix and Λ is a diagonal matrix of eigenvalues. The time derivative of this quantity, then, is| |  | (A5) |
This can be rewritten as| | 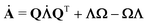 | (A6) |
where Ω = ![[Q with combining dot above]](https://www.rsc.org/images/entities/b_char_0051_0307.gif) QT, the spin of the eigenvectors, is a skew-symmetric matrix.
QT, the spin of the eigenvectors, is a skew-symmetric matrix.
Suppose that during flow one of the eigenvalues approaches zero. The condition that A always be positive semi-definite requires that the rate of change of that eigenvalue be greater than or equal to zero. Without loss of generality, we choose Λ11 = λ1, to be zero. Suppose also that our global basis was chosen such that, at the moment when λ1 = 0, the eigenvectors were aligned with the global basis, so Q = 1. The evolution for the λ1 eigenvalue is
| | ![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) 1 = c1 + c3D11 ≥ 0 1 = c1 + c3D11 ≥ 0 | (A7) |
Now, due to our constraint from
(7) in the main text, we know that
c3 is a negative-valued function, so we rewrite it as
| | ![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) 1 = c1 − ĉ3D11 ≥ 0 1 = c1 − ĉ3D11 ≥ 0 | (A8) |
where
ĉ3 = −
c3 is a positive-valued function.
It can be shown that for incompressible flow,  . Therefore it is sufficient to find a relationship between c1 and ĉ3 that satisfies
. Therefore it is sufficient to find a relationship between c1 and ĉ3 that satisfies
| | 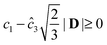 | (A9) |
Solving, and substituting
c3 back in, we obtain the final form of the constraint.
| |  | (A10) |
Linearized evolution law
In the main text, we assert that the evolution law with the power-law index n set to 0 cannot capture the power-law relaxation behavior observed at low shear rates. The fabric relaxes at an exponential rate when n = 0, rather than at the power-law rate observed in our simulations. If we force fit n = 0 and refit the experimental data using the fitting procedure, we obtain the parameters Z0 = 8.8, Z∞ = 3.2, τ = 1/50 s−1, β = 0.002, α = −0.0026, n = 0, and k1 = 0.0241 S m−1. The model is able to adequately reproduce the steady-state current measurements, but it fails to capture the relaxation upon cessation of flow. The results are shown in Fig. 7. Compare results to Fig. 5 in the main text.
 |
| | Fig. 7 Transient ramp experiments reproduced with the evolution law with n = 0. The model fails to adequately capture the relaxation behavior that occurs upon cessation of flow. | |
Thixotropy
As discussed at the end of the main text, the evolution law coupled with the fabric–conductivity relationship (2) is analogous to the family of thixotropic rheological models. The defining feature of these models is that there is an observed variable, usually viscosity, described as a function of an internal variable that evolves in accord with some evolution rule. In these models, the internal variable typically represents some aspect of the fluid microstructure. A more comprehensive definition and review of thixotropy models can be found in Mewis and Wagner.27 In our study, the observed variable is the electrical conductivity and the implicit structural variable is the fabric tensor which evolves due to shearing flow and particle Brownian motion. As a result, the observed conductivity is dependent on the full history of flow; there is not a one-to-one relationship between conductivity and shear rate. The non-unique behavior can be inferred from Fig. 5, but can be seen clearly by re-plotting one of the ramp experiments as normalized current against the normalized nominal shear rate  , shown in Fig. 8. It can be seen, for example, that the conductivity takes multiple values at
, shown in Fig. 8. It can be seen, for example, that the conductivity takes multiple values at  .
.
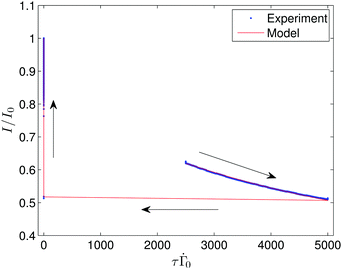 |
| | Fig. 8 Ramp experiment replotted from Fig. 5 show non-unique relationship between measured current and imposed shear rate. Arrows show progression of time. | |
A common characteristic of thixotropic material response is the formation of stable loops in the observed variable when subjected to cyclic input (e.g.: up/down ramps in shear rate). To demonstrate this phenomenon, we simulated a set of experiments where a simple shear rate is ramped linearly from  to
to  and back down again over the cycle period T. The maximum shear rate was chosen to be in the intermediate range of diffusion-dominated and shear-dominated rates. See the “Asymptotic Model Predictions” part of the Results section for more details. The input was cycled until the conductivity had reached a visually-stable trajectory. Six different cycle periods were chosen in order to probe the range of short cycle times (T/τ = 0.05) to long cycle times (T/τ = 500). The results of the simulation are shown in Fig. 9. For very short cycle times, we observe that the driving force changes much faster than the conductivity can evolve, resulting in small oscillations around a single value of conductivity. For very long cycle times, we observe that the conductivity is able to essentially maintain its long-term steady-state value at all times, with small deviations occurring only at very low shear rates. Intermediate cycle times show the transition between the short and long cycle states. In these cases, the comparable time scales of the fabric evolution and the driving shear rate lead to the formation of large hysteresis loops in the conductivity trajectories.
and back down again over the cycle period T. The maximum shear rate was chosen to be in the intermediate range of diffusion-dominated and shear-dominated rates. See the “Asymptotic Model Predictions” part of the Results section for more details. The input was cycled until the conductivity had reached a visually-stable trajectory. Six different cycle periods were chosen in order to probe the range of short cycle times (T/τ = 0.05) to long cycle times (T/τ = 500). The results of the simulation are shown in Fig. 9. For very short cycle times, we observe that the driving force changes much faster than the conductivity can evolve, resulting in small oscillations around a single value of conductivity. For very long cycle times, we observe that the conductivity is able to essentially maintain its long-term steady-state value at all times, with small deviations occurring only at very low shear rates. Intermediate cycle times show the transition between the short and long cycle states. In these cases, the comparable time scales of the fabric evolution and the driving shear rate lead to the formation of large hysteresis loops in the conductivity trajectories.
 |
| | Fig. 9 Plot of normalized stable conductivity loops that are formed during cyclic shear rate simulations for six different cycle periods. Arrows indicate the progression of time along each side of the cycle. | |
A striking feature of the figure is the non-monotonic conductivity in the increasing shear rate portion of the stable loops. At low, increasing shear rates, the rate of fabric formation due to the random motion of particles is still greater than the rate of fabric destruction due to shearing up to some finite  , where the rates are balanced and we observe a local maximum in conductivity. This non-monotonic effect is again observed at the high, decreasing range of shear rates, although the effect is less pronounced. This is evidenced by the local minimum in the observed conductivity that does not correspond exactly with the maximum shear rate. Similar non-monotonic behavior in conductivity has been seen experimentally by Genz et al.10
, where the rates are balanced and we observe a local maximum in conductivity. This non-monotonic effect is again observed at the high, decreasing range of shear rates, although the effect is less pronounced. This is evidenced by the local minimum in the observed conductivity that does not correspond exactly with the maximum shear rate. Similar non-monotonic behavior in conductivity has been seen experimentally by Genz et al.10
Data-fitting algorithm
Algorithm 1 Computation of Ass for given simple-shear flow with strain-rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) |
Input: Simple-shear strain-rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . . |
|
Output: Steady-state fabric Ass |
Construct L = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ⊗ ŷ. ⊗ ŷ. |
| Define D = ½(L + LT), W = ½(L − LT). |
| Solve nonlinear equation for trAss. |
| Compute c1 and c2 from trAss and |D| |
Use algebraic solution of (A1) with  = 0 to find Ass. = 0 to find Ass. |
|
Algorithm 2 Objective function for evolution law optimization routine |
|
Input: Z0, Z∞, τ, β, α, n, k1 |
|
Output: Squared error = Score |
| Score ← 0 |
for all do do |
Compute  using (13) from main text using (13) from main text |
| and Algorithm 1 |
| Compute error between model and experiment: |
 . . |
| Score ← Score + err |
| end for |
| returnScore |
The following algorithm outlines the high-level procedure for fitting the evolution law to a set of experimental data. It relies heavily on the preceding procedures laid out in Algorithm 1 and Algorithm 2.
|
Algorithm 3 Experimental fitting procedure |
Input: List of  pairs from steady-state experiments pairs from steady-state experiments |
|
Output: Evolution law coefficients {Z0,Z∞,τ,β,α,n,} |
| Estimate b1 from relaxation time of transient ramp tests. |
| Choose n to match discrete particle simulations |
| Call fminunc with objective function given by Algorithm 2. |
| {Z0,Z∞,τ,β,α,n,} ← Output from fminunc. |
| Verify that all constraints are satisfied |
Adjust b1 estimate and repeat until ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = 0 transient is well-matched. 0 = 0 transient is well-matched. |
Acknowledgements
The authors acknowledge support from the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Science (BES). The authors declare that there are no conflicts of interest.
References
- I. Alig, T. Skipa, M. Engel, D. Lellinger, S. Pegel and P. Pötschke, Electrical conductivity recovery in carbon nanotube–polymer composites after transient shear, Phys. Status Solidi B, 2007, 244(11), 4223–4226 Search PubMed.
- T. Amari and K. Watanabe, Flow properties and electrical conductivity of carbon black-linseed oil suspension, J. Rheol., 1990, 34(2), 207 Search PubMed.
- E. Azéma, N. Estrada and F. Radjai, Nonlinear effects of particle shape angularity in sheared granular media, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86(4), 041301 Search PubMed.
- W. Bauhofer, S. C. Schulz, A. E. Eken, T. Skipa, D. Lellinger, I. Alig, E. J. Tozzi and D. J. Klingenberg, Shear-controlled electrical conductivity of carbon nanotubes networks suspended in low and high molecular weight liquids, Polymer, 2010, 51(22), 5024–5027 Search PubMed.
- J. E. Bischoff, E. M. Arruda and K. Grosh, A Microstructurally Based Orthotropic Hyperelastic Constitutive Law, J. Appl. Mech., 2002, 69(5), 570 CrossRef CAS.
- F. da Cruz, S. Emam, M. Prochnow, J.-N. Roux and F. Chevoir, Rheophysics of dense granular materials: discrete simulation of plane shear flows, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72(2), 021309 CrossRef PubMed.
- J. M. Deneweth, S. G. McLean and E. M. Arruda, Evaluation of hyperelastic models for the non-linear and non-uniform high strain-rate mechanics of tibial cartilage, J. Biomech., 2013, 46(10), 1604–1610 CrossRef PubMed.
- M. Duduta, B. Ho, V. C. Wood, P. Limthongkul, V. E. Brunini, W. Craig Carter and Y.-M. Chiang, Semi-Solid Lithium Rechargeable Flow Battery, Adv. Energy Mater., 2011, 1(4), 511–516 CrossRef CAS.
- C. O. Frederick and P. J. Armstrong, A mathematical representation of the multiaxial Bauschinger effect, Mater. High Temp., 2007, 24(1), 1–26 CrossRef.
- U. Genz, J. A. Helsen and J. Mewis, Dielectric spectroscopy of reversibly flocculated dispersions during flow, J. Colloid Interface Sci., 1994, 165(1), 212–220 CrossRef CAS.
- V. Grenard, N. Taberlet and S. Manneville, Shear-induced structuration of confined carbon black gels: steady-state features of vorticity-aligned flocs, Soft Matter, 2011, 7(8), 3920–3928 RSC.
- V. Grenard, T. Divoux, N. Taberlet and S. Manneville, Timescales in creep and yielding of attractive gels, Soft Matter, 2014, 10, 1555–1571 RSC.
-
M. E. Gurtin, E. Fried and L. Anand, The Mechanics and Thermodynamics of Continua, Cambridge University Press, 2010 Search PubMed.
- G. L. Hand, A theory of anisotropic fluids, J. Fluid Mech., 1962, 13(1), 33 CrossRef.
-
J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Springer Science & Business Media, 2012, vol. 1 Search PubMed.
-
A. Helal, T. Divoux and G. H. McKinley, Simultaneous rheo-electric measurements of strongly conductive complex fluids, 2016, arXiv preprint arXiv:1604.00336.
-
A. Helal, K. Smith, F. Fan, X. Wei Chen, J. Miguel Nobrega, Y.-M. Chiang and G. H. McKinley, Study of the rheology and wall slip of carbon black suspensions for semi-solid flow batteries, The Society of Rheology 86th Annual Meeting, 2014.
- H. Hoekstra, J. Vermant, J. Mewis and G. G. Fuller, Flow-induced anisotropy and reversible aggregation in two-dimensional suspensions, Langmuir, 2003, 9134–9141 CrossRef CAS.
- A. Jagota and C. Y. Hui, The Effective Thermal Conductivity of a Packing of Spheres, J. Appl. Mech., 1990, 789–791 CrossRef.
- I. Jorjadze, L.-L. Pontani, K. A. Newhall and J. Brujić, Attractive emulsion droplets probe the phase diagram of jammed granular
matter, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(11), 4286–4291 CrossRef CAS PubMed.
- T. A. Witten Jr and L. M. Sander, Diffusion-limited aggregation, a kinetic critical phenomenon, Phys. Rev. Lett., 1981, 47(19), 1400–1402 CrossRef.
- N. Koumakis, M. Laurati, S. U. Egelhaaf, J. F. Brady and G. Petekidis, Yielding of Hard-Sphere Glasses during Start-Up Shear, Phys. Rev. Lett., 2012, 108(9), 098303 CrossRef CAS PubMed.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. C. B. R. Klein, R. C. Ball and P. Meakin, Universal diffusion-limited colloid aggregation, J. Phys.: Condens. Matter, 1990, 2(13), 3093 CrossRef.
-
J. E. Marsden and T. J. R. Hughes, Mathematical foundations of elasticity, Courier Corporation, 1994 Search PubMed.
- N. S. Martys, D. Lootens, W. George and P. Hébraud, Contact and stress anisotropies in start-up flow of colloidal suspensions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80(3), 031401 CrossRef PubMed.
- M. M. Mehrabadi, S. Nemat-Nasser and M. Oda, On statistical description of stress and fabric in granular materials, Int. J. Numer. Anal. Methods Geomech., 1982, 6(1), 95–108 CrossRef.
- J. Mewis and N. J. Wagner, Thixotropy, Adv. Colloid Interface Sci., 2009, 147, 214–227 CrossRef PubMed.
- A. Mohraz and M. J. Solomon, Orientation and rupture of fractal colloidal gels during start-up of steady shear flow, J. Rheol., 2005, 49(3), 657–681 CrossRef CAS.
- J. F. Morris and B. Katyal, Microstructure from simulated Brownian suspension flows at large shear rate, Phys. Fluids, 2002, 14(6), 1920 CrossRef CAS.
- A. Mujumdar, A. N. Beris and A. B. Metzner, Transient phenomena in thixotropic systems, J. Non-Newtonian Fluid Mech., 2002, 102(2), 157–178 CrossRef CAS.
- A. Singh Negi and C. O. Osuji, New insights on fumed colloidal rheology—shear thickening and vorticity-aligned structures in flocculating dispersions, Rheol. Acta, 2009, 48(8), 871–881 CrossRef.
- M. Oda, S. Nemat-Nasser and M. M. Mehrabadi, A statistical study of fabric in a random assembly of spherical granules, Int. J. Numer. Anal. Methods Geomech., 1982, 6, 77–94 CrossRef.
- T. Olsen and K. Kamrin, Modeling tensorial conductivity of particle suspension networks, Soft Matter, 2015, 11(19), 3875–3883 RSC.
- C. O. Osuji, C. Kim and D. A. Weitz, Shear thickening and scaling of the elastic modulus in a fractal colloidal system with attractive interactions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77(6), 8–11 CrossRef PubMed.
- C. O. Osuji and D. A. Weitz, Highly anisotropic vorticity aligned structures in a shear thickening attractive colloidal system, Soft Matter, 2008, 4(7), 1388–1392 RSC.
- J. D. Park and K. H. Ahn, Structural evolution of colloidal gels at intermediate volume fraction under start-up of shear flow, Soft Matter, 2013, 9(48), 11650–11662 RSC.
- F. Radjai, J.-Y. Delenne, E. Azéma and S. Roux, Fabric evolution and accessible geometrical states in granular materials, Granular Matter, 2012, 14(2), 259–264 CrossRef.
- R. S. Rivlin, Further remarks on the stress–deformation relations for isotropic materials, Journal of Rational Mechanics and Analysis, 1955, 4(5), 681–702 Search PubMed.
- M. Rottereau, J. Christophe Gimel, T. Nicolai and D. Durand, Monte Carlo simulation of particle aggregation and gelation: I. growth, structure and size distribution of the clusters, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 15(2), 133–140 CrossRef CAS PubMed.
- P. H. S. Santos, O. H. Campanella and M. A. Carignano, Effective attractive range and viscoelasticity of colloidal gels, Soft Matter, 2013, 9(3), 709 RSC.
-
M. Satake, Constitution of mechanics of granular materials through the graph theory, Continuum Mechanical and Statistical Approaches in the Mechanics of Granular Materials, 1978, pp. 47–62 Search PubMed.
- S. C. Schulz and W. Bauhofer, Shear influenced network dynamics and electrical conductivity recovery in carbon nanotube/epoxy suspensions, Polymer, 2010, 51(23), 5500–5505 CrossRef CAS.
- K. C. Smith, Y.-M. Chiang and W. C. Carter, Maximizing Energetic Efficiency in Flow Batteries Utilizing Non-Newtonian Fluids, J. Electrochem. Soc., 2014, 161(4), A486–A496 CrossRef CAS.
- M. J. Stephen and J. P. Straley, Physics of liquid crystals, Rev. Mod. Phys., 1974, 46(4), 617 CrossRef CAS.
- J. Sun and S. Sundaresan, A constitutive model with microstructure evolution for flow of rate-independent granular materials, J. Fluid Mech., 2011, 682, 590–616 CrossRef.
- V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Jamming phase diagram for attractive particles, Nature, 2001, 411(6839), 772–775 CrossRef CAS PubMed.
- V. Trappe and D. A. Weitz, Scaling of the viscoelasticity of weakly attractive particles, Phys. Rev. Lett., 2000, 85(2), 449–452 CrossRef CAS PubMed.
- V. Trappe, E. Pitard, L. Ramos, A. Robert, H. Bissig and L. Cipelletti, Investigation of q-dependent dynamical heterogeneity in a colloidal gel by X-ray photon correlation spectroscopy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76(5), 051404 CrossRef CAS PubMed.
- J. Vermant and M. J. Solomon, Flow-induced structure in colloidal suspensions, J. Phys.: Condens. Matter, 2005, 17(4), R187–R216 CrossRef CAS.
- M. Youssry, L. Madec, P. Soudan, M. Cerbelaud, D. Guyomard and B. Lestriez, Non-aqueous carbon black suspensions for lithium-based redox flow batteries: rheology and simultaneous rheo-electrical behavior, Phys. Chem. Chem. Phys., 2013, 15(34), 14476–14486 RSC.
- X. Zhuang, A. K. Didwania and J. D. Goddard, Simulation of the quasi-static mechanics and scalar transport properties of ideal granular assemblages, J. Comput. Phys., 1995, 121(2), 331–346 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

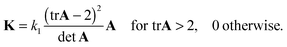
 , the strain-rate tensor D = ½(L + LT), and the spin tensor W = ½(L − LT). We postulate a fabric evolution law of the form
, the strain-rate tensor D = ½(L + LT), and the spin tensor W = ½(L − LT). We postulate a fabric evolution law of the form 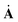 = Ψ(A, L), where
= Ψ(A, L), where  denotes the material time derivative of A. In order for an evolution law such as this to be indifferent under a change in an observer's frame of reference, the evolution law must be expressible as
denotes the material time derivative of A. In order for an evolution law such as this to be indifferent under a change in an observer's frame of reference, the evolution law must be expressible as  = WA − AW +
= WA − AW +  (A, D), where
(A, D), where  is an isotropic function of the fabric tensor and the strain-rate tensor.14 A representation theorem for isotropic functions of 3 × 3 symmetric tensors38 can be applied, allowing us to write
is an isotropic function of the fabric tensor and the strain-rate tensor.14 A representation theorem for isotropic functions of 3 × 3 symmetric tensors38 can be applied, allowing us to write
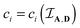 , where the full set of simultaneous invariants of A and D is
, where the full set of simultaneous invariants of A and D is
 in a spin-free flow.13
in a spin-free flow.13
 for i ≥ 4. This leaves the quasi-linear form
for i ≥ 4. This leaves the quasi-linear form



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles are seeded into a periodic box at a 3.5% volume fraction and allowed to diffuse. The volume fraction was chosen to match approximately the volume fraction in physical experiments that will be described in subsequent sections. Particles and clusters are assigned velocities such that the distance that a cluster moves in a single time step is drawn from a Gaussian distribution with variance DΔt, where D is the diffusion coefficient, and Δt is the simulation time step length. As hit-and-stick behavior is typical in diffusion-limited aggregation,21 all clusters in contact after a step are deemed to stick, creating a larger cluster. As clusters grow, the diffusion coefficient is adjusted according to D = D0/N, where D0 is the diffusion coefficient for a single particle, and N is the number of particles in a cluster. Because clusters typically have a snake-like shape, dominated by long strands of particles, this relation was chosen for its similarity to the asymptotic solution for the diffusion coefficient of a string of N particles.15 We neglect hydrodynamic forces between clusters and rotational diffusion. These assumptions result in a code similar to the off-lattice Monte Carlo aggregation method described in Rottereau et al. 2004.39 The effect of shear thickening was not considered, since the method represents particles in a quiescent medium subjected to Brownian forces.
000 particles are seeded into a periodic box at a 3.5% volume fraction and allowed to diffuse. The volume fraction was chosen to match approximately the volume fraction in physical experiments that will be described in subsequent sections. Particles and clusters are assigned velocities such that the distance that a cluster moves in a single time step is drawn from a Gaussian distribution with variance DΔt, where D is the diffusion coefficient, and Δt is the simulation time step length. As hit-and-stick behavior is typical in diffusion-limited aggregation,21 all clusters in contact after a step are deemed to stick, creating a larger cluster. As clusters grow, the diffusion coefficient is adjusted according to D = D0/N, where D0 is the diffusion coefficient for a single particle, and N is the number of particles in a cluster. Because clusters typically have a snake-like shape, dominated by long strands of particles, this relation was chosen for its similarity to the asymptotic solution for the diffusion coefficient of a string of N particles.15 We neglect hydrodynamic forces between clusters and rotational diffusion. These assumptions result in a code similar to the off-lattice Monte Carlo aggregation method described in Rottereau et al. 2004.39 The effect of shear thickening was not considered, since the method represents particles in a quiescent medium subjected to Brownian forces.


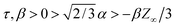

 . At each shear rate, both the current and stress were allowed to equilibrate before the measurement was recorded to ensure that it had relaxed to its steady value. The shear rates were swept in descending order to mitigate complications such as shear-induced phase separation that arise at low shear rates, below
. At each shear rate, both the current and stress were allowed to equilibrate before the measurement was recorded to ensure that it had relaxed to its steady value. The shear rates were swept in descending order to mitigate complications such as shear-induced phase separation that arise at low shear rates, below  .16
.16 , ramping linearly to
, ramping linearly to  over duration tR, holding for 5 minutes, and abruptly setting
over duration tR, holding for 5 minutes, and abruptly setting  , collecting data for 15 additional minutes. Pre-shear at
, collecting data for 15 additional minutes. Pre-shear at  was applied for 5 minutes before each test to ensure consistent initial conditions.
was applied for 5 minutes before each test to ensure consistent initial conditions.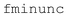 Matlab optimization routine, minimizing the squared difference between predicted and measured electrical currents. The τ parameter, which is primarily responsible for controlling the fabric's relaxation time, was chosen from the experimental dynamics of the ramp tests. Lastly, the k1 parameter can be chosen to match the steady-state current observed at
Matlab optimization routine, minimizing the squared difference between predicted and measured electrical currents. The τ parameter, which is primarily responsible for controlling the fabric's relaxation time, was chosen from the experimental dynamics of the ramp tests. Lastly, the k1 parameter can be chosen to match the steady-state current observed at  .
.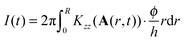
 , by substituting A(r,t) with
, by substituting A(r,t) with  where Ass(
where Ass(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is the steady-state fabric tensor, whose components are obtained algebraically from eqn (5) by defining D and W to correspond to simple shearing at
) is the steady-state fabric tensor, whose components are obtained algebraically from eqn (5) by defining D and W to correspond to simple shearing at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and setting
and setting  = 0. A detailed outline of the fitting procedure can be found in the Appendix.
= 0. A detailed outline of the fitting procedure can be found in the Appendix.
 from the experimental protocol. The evolution law was numerically integrated to obtain the fabric tensor at all time points. After the fabric is known, (16) can be approximated directly using a Riemann sum to give the predicted current as a function of time.
from the experimental protocol. The evolution law was numerically integrated to obtain the fabric tensor at all time points. After the fabric is known, (16) can be approximated directly using a Riemann sum to give the predicted current as a function of time. .
.

 and
and  were expected due to the close fit of steady-state data in Fig. 4. The most critical test in the ramp experiments was the relaxation of the conductivity when flow was abruptly stopped. The model does an excellent job predicting this non-trivial behavior, especially given that each point along the radius of the plate begins decaying from a different initial steady-state condition.
were expected due to the close fit of steady-state data in Fig. 4. The most critical test in the ramp experiments was the relaxation of the conductivity when flow was abruptly stopped. The model does an excellent job predicting this non-trivial behavior, especially given that each point along the radius of the plate begins decaying from a different initial steady-state condition.



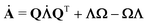
![[Q with combining dot above]](https://www.rsc.org/images/entities/b_char_0051_0307.gif) QT, the spin of the eigenvectors, is a skew-symmetric matrix.
QT, the spin of the eigenvectors, is a skew-symmetric matrix.
![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) 1 = c1 + c3D11 ≥ 0
1 = c1 + c3D11 ≥ 0![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) 1 = c1 − ĉ3D11 ≥ 0
1 = c1 − ĉ3D11 ≥ 0 . Therefore it is sufficient to find a relationship between c1 and ĉ3 that satisfies
. Therefore it is sufficient to find a relationship between c1 and ĉ3 that satisfies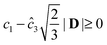


 , shown in Fig. 8. It can be seen, for example, that the conductivity takes multiple values at
, shown in Fig. 8. It can be seen, for example, that the conductivity takes multiple values at  .
.

 to
to  and back down again over the cycle period T. The maximum shear rate was chosen to be in the intermediate range of diffusion-dominated and shear-dominated rates. See the “Asymptotic Model Predictions” part of the Results section for more details. The input was cycled until the conductivity had reached a visually-stable trajectory. Six different cycle periods were chosen in order to probe the range of short cycle times (T/τ = 0.05) to long cycle times (T/τ = 500). The results of the simulation are shown in Fig. 9. For very short cycle times, we observe that the driving force changes much faster than the conductivity can evolve, resulting in small oscillations around a single value of conductivity. For very long cycle times, we observe that the conductivity is able to essentially maintain its long-term steady-state value at all times, with small deviations occurring only at very low shear rates. Intermediate cycle times show the transition between the short and long cycle states. In these cases, the comparable time scales of the fabric evolution and the driving shear rate lead to the formation of large hysteresis loops in the conductivity trajectories.
and back down again over the cycle period T. The maximum shear rate was chosen to be in the intermediate range of diffusion-dominated and shear-dominated rates. See the “Asymptotic Model Predictions” part of the Results section for more details. The input was cycled until the conductivity had reached a visually-stable trajectory. Six different cycle periods were chosen in order to probe the range of short cycle times (T/τ = 0.05) to long cycle times (T/τ = 500). The results of the simulation are shown in Fig. 9. For very short cycle times, we observe that the driving force changes much faster than the conductivity can evolve, resulting in small oscillations around a single value of conductivity. For very long cycle times, we observe that the conductivity is able to essentially maintain its long-term steady-state value at all times, with small deviations occurring only at very low shear rates. Intermediate cycle times show the transition between the short and long cycle states. In these cases, the comparable time scales of the fabric evolution and the driving shear rate lead to the formation of large hysteresis loops in the conductivity trajectories. , where the rates are balanced and we observe a local maximum in conductivity. This non-monotonic effect is again observed at the high, decreasing range of shear rates, although the effect is less pronounced. This is evidenced by the local minimum in the observed conductivity that does not correspond exactly with the maximum shear rate. Similar non-monotonic behavior in conductivity has been seen experimentally by Genz et al.10
, where the rates are balanced and we observe a local maximum in conductivity. This non-monotonic effect is again observed at the high, decreasing range of shear rates, although the effect is less pronounced. This is evidenced by the local minimum in the observed conductivity that does not correspond exactly with the maximum shear rate. Similar non-monotonic behavior in conductivity has been seen experimentally by Genz et al.10![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ⊗ ŷ.
⊗ ŷ. = 0 to find Ass.
= 0 to find Ass. do
do using (13) from main text
using (13) from main text .
.