Open Access Article
Open Access ArticlePhotoinduced energy and electron transfer at graphene quantum dot/azobenzene interfaces†
Magdalena
Kaźmierczak
 a,
Samuele
Giannini‡
a,
Samuele
Giannini‡
 b and
Silvio
Osella
b and
Silvio
Osella
 *a
*a
aChemical and Biological Systems Simulation Lab, Centre of New Technologies, University of Warsaw, Banacha 2C, 02-097 Warsaw, Poland. E-mail: s.osella@cent.uw.edu.pl
bLaboratory for Chemistry of Novel Materials, University of Mons, 7000 Mons, Belgium
First published on 20th November 2023
Abstract
To respond to the constant miniaturization of modern devices, it is imperative to develop novel classes of hybrid materials with outstanding functionalities. One of the most promising developments in this regard is photoswitchable nanoelectronics, which offer non-invasive structural changes via irradiation. Azobenzenes, in particular, represent a widely investigated group of compounds due to their reversible photoisomerization and flexibility to introduce modifications by functionalizing the aryl ring. Here, an interface consisting of graphene quantum dots (GQDs) and a pyrene functionalized azobenzene (AZO) is built and investigated to unravel the energy and charge transfer dynamics at play. The influence of the conformation, isomerization and thermal effects on the photophysics is described using a multiscale computational approach coupled to electronic structure calculations. By computing the photoinduced energy and charge transfer rates we found that the small exciton reorganization energy and favorable alignment of the energy levels at the interface favor excitation energy transfer. A significant increase of photoinduced hole transfer from AZO to GQDs is observed when thermal effects are considered. Moreover, these photoinduced processes for the azobenzene molecules in their trans configuration are always faster than those related to the cis isomer. This is due to a favorable overlap and a stronger interaction of the trans isomer, considered the active state, with the GQDs. On the other hand, the cis configuration, featuring slower photoinduced energy and charge transfer processes, can be considered as the inactive species. Nevertheless, its contribution to the overall photophysics remains non-negligible.
Introduction
Graphene quantum dots (GQDs) are unique, zero-dimensional materials derived from graphene with properties depending on the size of the particles.1 Unlike graphene, GQDs are semiconductors and exhibit a tunable non-zero band gap due to their constricted size2,3 as well as their edge geometry4 and functionalization.5,6 Quantum confinement and edge effects are also responsible for improving GQDs’ optical properties compared to other carbon allotropes, not only by opening their band gap but also by enhancing their dispersibility. The highly adjustable optical properties such as photoluminescence, electrochemiluminescence and photostability, together with the simplicity of functionalization, make GQDs highly versatile materials.7 The main drawback – low photoluminescence quantum yield – can be significantly improved by further changes in their surface composition or doping.8,9 The formation of an interface between GQDs and small organic molecules can lead to functional materials, whose optoelectronic properties can be easily tuned by incorporating changes within the molecules.10–13 GQDs are applied to a number of applications such as solar cells,14–17 light-emitting diodes18–21 and supercapacitors.22–24 Moreover, their low toxicity and biocompatibility enable the use of these materials in medical bioimaging25 and drug delivery applications.26The ability to control a device based on a GQD–small molecule interface with an external stimulus, for example through irradiation, is a further step towards enhancing the complexity of the device. Azobenzene can be considered as an archetype in this field since full control over geometrical changes is enabled by photoisomerization via absorption of a photon. Since cis/trans isomerization is a fully reversible process,27 the different sets of optoelectronic properties of two isomers can be accessed and swapped.28,29 Additionally, the photoswitching performance at different excitation wavelengths and/or intensities, which is a result of those fundamental properties, can be readily modified by adding electron donating or withdrawing groups in the para position of the benzene ring forming an azobenzene molecule. As a consequence, tunable on/off states in which one isomer facilitates charge or energy transfer whereas the other inhibits this process, allow using these materials as switches in biosensors,30 energy storage devices31–33 and molecular machines.34
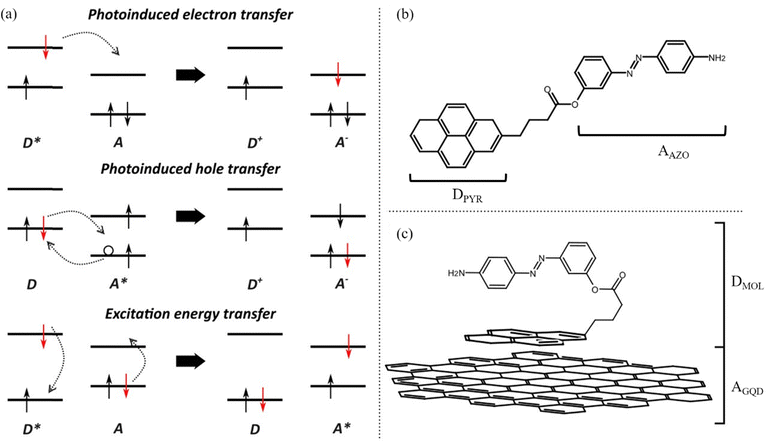
Upon excitation of a photoactivated interface three distinct processes can occur: photoinduced electron transfer (PET), photoinduced hole transfer (PHT) and excitation energy transfer (EET). When considering PET and PHT, an excitation of a generic donor/acceptor interface leads to excitation of an electron from the ground state to the excited state of either the donor or acceptor, respectively. The excitation process is followed by the transfer of an excited electron from the donor to the acceptor in PET, while a hole is transferred from the acceptor to the donor in the PHT process. On the other hand, EET involves a simultaneous transition of electrons from an excited state to the ground state for the donor and vice versa for the acceptor (Fig. 1(a)).
In this study, the optoelectronic properties of a push–pull 4-[(4-aminophenyl)diazenyl]phenyl 4-pyrenebutanoate (hereafter labelled as AZO, Fig. 1(b)) molecule physisorbed on GQDs are investigated through multiscale simulations combining molecular dynamics and electronic structure. The AZO molecule considered in this study has already been synthesized and reported in the literature.35 Webb and coworkers reported the synthesis and absorption properties of a series of AZO–pyrene molecules connected with an ester linker, in which substituents (either NH2 or OH) were added in the para position of the azobenzene moiety. This allowed the modulation of the absorption spectra, and for the amine substitution the authors observed that the strong electron-donating effect was responsible for a red shift in the spectrum with respect to pyrene. In this work, we focus on the ammine-substituted system and compute the UV-Vis spectra. Along with the examination of the optical properties of the AZO–pyrene molecules, we examine here the excited state characters and describe possible charge or energy transfer processes in the single molecule and at the interface of the AZO–pyrene and the GQDs.
Specifically, by calculating the interaction between different states (i.e., electronic couplings), the reorganization energies of the various photoinduced processes, driving force and finally the Marcus rates between electron donor and acceptor sites, we aim to describe the photophysics of the GQD–AZO interfaces. We first consider the isolated AZO molecule to assess the possibility of such a system undergoing intramolecular excited state processes upon irradiation (Fig. 1(b)). Marcus rates were computed to rationalize various competitive pathways. Next, we discuss how the formation of an interface between the AZO molecule and a GQD (Fig. 1(c)) alters the optical and electronic properties and the photophysics at the interface. Finally, we take into account thermal effects in molecular dynamics simulations to assess the effects of structural disorder and temperature on the transfer rates.
Methodology
Azobenzenes can be converted from the trans to the cis isomer at a specific wavelength of UV light, which relates to the π → π* excitation, whereas the opposite isomerization appears at longer wavelengths (in the visible range) and corresponds to the n → π* transition. The characteristic trait of the investigated AZO molecule is that upon irradiation it undergoes photoisomerization as the parent azobenzene.35 In order to systematically evaluate the optoelectronic properties’ changes occurring when AZO molecules are interacting with a GQD, isolated AZO molecules in different conformations as well as GQD–AZO interfaces are optimized and analyzed.First, isolated AZO molecules as well as GQD–AZO interfaces are optimized at the DFT level using the CAM-B3LYP functional36 together with GD3 van der Waals dispersion37 with the 6-31G(d) basis set38 as implemented in the Gaussian 16 software.39 The PET, PHT and EET processes at the interface are evaluated by combining TD-DFT calculations performed with the same functional and basis set used for the geometry optimization and evaluation of the transfer rates (as explained below).
The GDQ–AZO interface is built by considering 42 AZO molecules (either trans or cis) physisorbed on graphene and then performing molecular dynamics (MD) simulations to assess the stability and magnitude of the interactions taking place at the interface. The simulations are performed using the GROMACS package40–45 with the CHARMM36 force field.46 To correctly describe the AZO trans and cis isomers, two different sets of parameters for the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, angles and dihedrals are taken from the literature.27 Dihedral angles for the ester bond are reparametrized at the MP2 level of theory using Gaussian 16 software, whereas the ESP charges for the AZO are taken from the optimized structure at the DFT level. Both interfaces are solvated with water molecules using the TIP3P description for the solvent. The calculations are performed at room temperature using the NVT ensemble and the Nose–Hoover thermostat (300 K and 0.5 ps). Periodic boundary conditions are considered while building the cell, which has dimensions equal to a = 8.08 nm, b = 8.11 nm and c = 5.0 nm to prevent spurious interaction with repeating images along the c direction. 60 ns MD simulations with a time step of 2 fs are run to equilibrate and minimize the energy of the system (the estimated error of total energy and Lennard-Jones (LJ) interactions between the GQDs and AZO fell below 20 kJ mol−1, which is less than 0.01% for average total energy and less than 0.5% for LJ interactions). A 30 ns production simulation is sampled, and from it, 50 frames, consisting of AZO and GQDs (114 carbon atoms in a hexagonal shape with all armchair edges), are extracted along the trajectory. The selected frames are subsequently considered as input structures for TD-DFT calculations, to assess the thermal effects on the optical properties (such as the absorption spectrum) and electronic properties (such as electronic couplings and reorganization energies).
N bond, angles and dihedrals are taken from the literature.27 Dihedral angles for the ester bond are reparametrized at the MP2 level of theory using Gaussian 16 software, whereas the ESP charges for the AZO are taken from the optimized structure at the DFT level. Both interfaces are solvated with water molecules using the TIP3P description for the solvent. The calculations are performed at room temperature using the NVT ensemble and the Nose–Hoover thermostat (300 K and 0.5 ps). Periodic boundary conditions are considered while building the cell, which has dimensions equal to a = 8.08 nm, b = 8.11 nm and c = 5.0 nm to prevent spurious interaction with repeating images along the c direction. 60 ns MD simulations with a time step of 2 fs are run to equilibrate and minimize the energy of the system (the estimated error of total energy and Lennard-Jones (LJ) interactions between the GQDs and AZO fell below 20 kJ mol−1, which is less than 0.01% for average total energy and less than 0.5% for LJ interactions). A 30 ns production simulation is sampled, and from it, 50 frames, consisting of AZO and GQDs (114 carbon atoms in a hexagonal shape with all armchair edges), are extracted along the trajectory. The selected frames are subsequently considered as input structures for TD-DFT calculations, to assess the thermal effects on the optical properties (such as the absorption spectrum) and electronic properties (such as electronic couplings and reorganization energies).
To characterize the photophysics of the systems and the characteristic rates of the different EET, PET and PHT processes, we adopt here the well-established Marcus rate equation. In the weak coupling and the high-temperature classical limits, the rate constant (kif) for nonadiabatic transfer between two diabatic states (referred to as the initial and final states, |i and |f) can be written as:
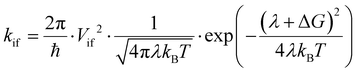 | (1) |
The internal reorganization energy (λi) instead is the energy cost to bring the nuclear configuration of the initial state into that of the final state while keeping the electronic configuration fixed at the initial state and was computed via the so-called four-point scheme:51
| λPET = E−(QN) − E−(Q−) + EN(Q−) − EN(QN) | (2) |
| λPHT = E+(QN) − E+(Q+) + EN(Q+) −EN(QN) | (3) |
When considering the interface consisting of donor and acceptor fragments, one can separately calculate the internal reorganization energy as an average of the backward (λBw) and forward transitions (λFw, see the ESI† for more details).47,52,53 Finally in eqn (1), ΔG is the free energy difference between the initial and final states, and is approximated in this work as the energy difference between the states that are coupled.
The electronic couplings are computed considering both the intramolecular couplings between the electron donor pyrene (DPYR) and electron acceptor azobenzene (AAZO) moieties in the isolated AZO molecules, and intermolecular coupling between the trans/cis pyrene-azo molecule (DMOL) and the electron acceptor GQDs (AGQD) in the interfaces considered (see Fig. 1(b) and (c)). As mentioned above, to quantify these interactions, we used a multi-state diabatization procedure (MS-FED-FCD).47–49 This method involves the partition of a given donor–acceptor pair into two fragments and by using appropriate additional operators, the adiabatic Hamiltonian of the dimer (formed by two or more adiabatic states of the system) is transformed into a fragment-related diabatic basis, to subsequently extract the couplings between states of different characters from the Hamiltonian matrix written in such a localized basis. In practice, first, the adiabatic excited states of the donor–acceptor pair are calculated followed by diabatization to localized, (maximally) diabatic excitonic states. Then, the couplings can be found as the off-diagonal elements of this matrix. Importantly, MS-FED-FCD allows us to include several adiabatic excited states of the donor–acceptor system in the diabatization procedure (in this work, we used up to 40 excited states) to ensure a complete de-mixing between excitations of different nature and an optimal reconstruction of localized excitonic and charge transfer states. This is particularly useful for the investigated system where there is a high density of states and a given adiabatic state is the combination of many diabatic states of both D and A moieties. We refer to ref. 47–49 for a more detailed description of the method. When degenerated states are present in the system, the procedure is modified to consider the effective coupling (Veff) computed as the square root of the sum of the squared couplings related to the number of degenerate states found in the calculation. For example, for two degenerate initial states i1, i2 and two degenerate final states f1, f2, the effective coupling will be:
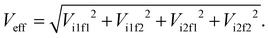 | (4) |
Results and discussion
Isolated AZO molecules
Before considering the optoelectronic properties of the interfaces, we assess the properties of the isolated AZO molecule for both its trans (tAZO) and cis (cAZO) isomers, and the possible intramolecular photoinduced processes which can occur from the different isomerization. As reported in the literature,35 two different conformations can be present, in which the AZO part of the molecule is either perpendicular to the pyrene moiety (labelled as ‘open’) or parallel to it (labelled as ‘fold’) (see Fig. S1, S2, ESI† and Fig. 2).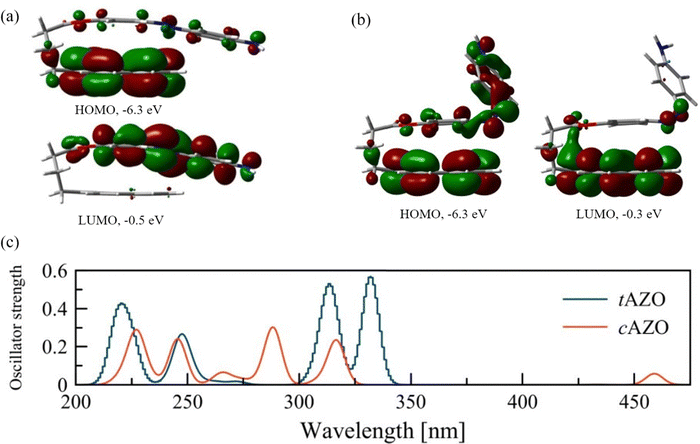 | ||
| Fig. 2 Frontier orbitals of the isolated AZO molecules: (a) trans isomer, (b) cis isomer. (c) Computed UV-Vis spectra for the isolated AZO molecules in trans (tAZO) and cis (cAZO) configurations. | ||
As the tAZO fold conformation is more stable than the open one by 0.4 eV (in agreement with the 0.3 eV energy difference reported in the literature),35 we will consider only the fold conformers for further analyses (details of the open conformers can be found in the ESI†). As expected, and in agreement with the parent molecule, tAZO is found to be the more stable state compared to cAZO, with a stabilization energy of 0.7 eV. The modifications of the AZO structure compared to the parent molecule are also responsible for the dipole moment of 1.26 Debye for tAZO and 6.4 Debye for cAZO, due to the presence of both the amino group and the pyrene moieties. Moreover, for both isomers, the HOMO energies have similar values of −6.3 eV, while the LUMO has an energy of −0.5 eV for tAZO and it is slightly lower for the cAZO molecule (−0.3 eV). This leads to a similar wide energy gap of about 6.0 eV for both isomers. When considering the localization of the frontier molecular orbitals (FMO), we observe that for the trans isomer, the HOMO is localized on pyrene, whereas the LUMO is localized on the AZO moiety, suggesting the formation of an intramolecular charge transfer state upon excitation (Fig. 2(a)). On the other hand, for cAZO, the HOMO is delocalized over the whole molecule, while the LUMO is localized over the pyrene moiety, suggesting a different behavior in intramolecular charge transfer ability for this isomer (Fig. 2(b)).
The absorption spectra of the two isomers are reported in Fig. 2(c). Four main peaks can be found for tAZO in the absorption spectrum, with the fold conformation bathochromically shifted by approximately 5 nm with respect to the open one (details for the open conformation are reported in the ESI†). The first excited state is a forbidden n → π* transition (HOMO–3 to LUMO, see Table S1 (ESI†) for a detailed description of all transitions). The first bright peak at 332 nm relates to the second excited state (S2) and corresponds to the HOMO–1 to LUMO transition (π →π*). The next peak at 314 nm corresponds to the HOMO to LUMO+1 transition. For the cAZO isomer, similar absorption peaks are obtained compared to tAZO, albeit blue-shifted by 20 nm. In addition, the first excited state is now allowed, and it shows a weak peak at 459 nm, which corresponds to the n → π* (HOMO–1 to LUMO+1) transition. This observation confirms that AZO undergoes photoisomerization because a similar transition is responsible for this process in the unsubstituted cis-azobenzene.54 The next peak at 317 nm corresponds to the π →π* HOMO to LUMO transition. Interestingly, our results well agree with the reported absorption in the literature,35 although some expected discrepancies are present due to the absence of solvent contributions in our calculations.
To gain deeper insight into the charge and energy transfer rates of the AZO isomers, we compute the natural transition orbitals (NTOs) and intramolecular coupling for the investigated AZO isomers. This analysis suggests that the electron donor site is the pyrene moiety (DPYR), whereas AZO acts as the acceptor (AAZO) (see Fig. S3, ESI†). The energy transfer process taking place due to pyrene local excitation at 314 nm to AZO local excitation at 332 nm features a coupling value of 46.4 meV. A nearly identical coupling value is found for the PET process of the same isomer, which occurs from the excited 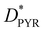 at 314 nm, transferring an electron to the AZO moiety. A considerably higher coupling value of 64.3 meV is found for PHT, which involves AZO excitation at 332 nm and AZO to pyrene charge transfer state. Similar trends can be observed for cAZO for which both EET and PET couplings have rather low values of 9.0 meV and 8.9 meV, respectively, compared to 105.5 meV for the PHT coupling, which occurs between the AZO local excitation at 288 nm and the AZO to pyrene charge transfer state at 246 nm (see Table 1). On the whole, we can conclude that the better overlapping states of the trans configuration tend to favor greater interactions with respect to the cis form.
at 314 nm, transferring an electron to the AZO moiety. A considerably higher coupling value of 64.3 meV is found for PHT, which involves AZO excitation at 332 nm and AZO to pyrene charge transfer state. Similar trends can be observed for cAZO for which both EET and PET couplings have rather low values of 9.0 meV and 8.9 meV, respectively, compared to 105.5 meV for the PHT coupling, which occurs between the AZO local excitation at 288 nm and the AZO to pyrene charge transfer state at 246 nm (see Table 1). On the whole, we can conclude that the better overlapping states of the trans configuration tend to favor greater interactions with respect to the cis form.
| Process | λ [eV] | Coupling [eV] | ΔG [eV] | k [s−1] | |
|---|---|---|---|---|---|
| tAZO | EET | 0.19 | 0.046 | −0.220 | 8.0 × 1013 |
| PET | 0.80 | 0.045 | −0.048 | 3.9 × 1010 | |
| PHT | 1.28 | 0.064 | 0.172 | 6.9 × 106 | |
| cAZO | EET | 0.21 | 0.009 | 0.335 | 3.2 × 106 |
| PET | 1.38 | 0.009 | 1.083 | 2.9 × 10−7 | |
| PHT | 1.14 | 0.106 | 0.748 | 1.0 × 101 |
To quantify the transfer rates, we calculate next the reorganization energies for the different processes considering the four point model (eqn (2) and (3)) described in the Method section. For the PET process (Fig. 1(a)), we compute a λPET of 0.80 eV for tAZO, and a nearly double value for cAZO of 1.38 eV (a similar situation holds true for the open conformers, see the ESI† for more details). The difference in reorganization energies for holes between the two isomers for the PHT process is much less pronounced compared to the PET process, with values of 1.28 eV and 1.14 eV for tAZO and cAZO, respectively. As a result, the geometrical changes related to cAZO require less energy for the hole transfer, whereas tAZO should favor the PET process. The high reorganization energy values are due to the strong geometrical distortions arising from the presence of an additional electron/hole in the structure. For PHT, we observe planarization of the NH2 group and changes in the CNNC dihedral angle for both isomers; for PET, there is a bending of the tAZO structure towards the pyrene moiety, while for cAZO, we observe an opening of the CNNC dihedral angle from 9 to 42 degrees (see Fig. S4, ESI†). Much lower values of 0.19 and 0.21 eV have been obtained for the EET process for tAZO and cAZO, respectively, suggesting that this process might be favored from a geometrical point of view due to much less severe molecular distortions (Fig. S4, ESI†). These results are confirmed by the analysis of the driving force, for which low values for EET are observed for both tAZO and cAZO isomers (Table 1).
With all the computed parameters, we can calculate the Marcus rates for the three processes, reported in Table 1. First of all, we can observe that the rates for the three processes – EET, PHT, PET – are always higher for tAZO compared to cAZO, suggesting that the former can be considered as an active state for intramolecular photoinduced charge/energy transfer. Going into the details of the specific mechanism, we observe that for tAZO, the EET is favored, with a kEET of 8 × 1013 s−1, compared to the photoinduced charge transfer processes, following the kEET > kPET > kPHT trend. Although the coupling value for PHT is the highest among the three different processes, its reorganization energy and driving force also have the highest values, resulting in a lower rate for hole transport. On the other hand, for cAZO, the kEET > kPHT ≫ kPET trend is found. EET is once more the favored process, with a kEET of 3.2 × 106 s−1, while PET is now completely inhibited (due to very low coupling and high values of both reorganization energy and driving force). PHT shows very slow rates, despite the high coupling value, because of the strong geometrical deformation translating into a high reorganization energy value of 1.14 eV. As a result, the intramolecular EET is the main process occurring upon irradiation, with a higher rate for the trans isomer compared to the cis isomer, making tAZO the active state for this photophysical process. As the parent azobenzene molecule, the system investigated here can be used not only as an optical probe (due to the cis–trans isomerization) but also as an efficient on/off switch in which the trans isomer is the active state.
GQD–AZO interface
Next, we built an interface between the AZO molecule and a GQD to study its intermolecular photophysical properties. For this system, we consider the GQDs as an electron donor and the whole pyrene–AZO molecule as a single accepting unit (see Fig. 1(c)). For the sake of brevity, we indicate in the following the whole pyrene–AZO molecule as AZO. The GQD–AZO interfaces are optimized and analyzed only for the fold conformation, since it is more stable than the open one (Fig. 3). For both interfaces, the distance between graphene and pyrene nearly ideally corresponds to a π–π stacking distance of 0.33 nm. The formation of the interface significantly changes the dipole moments, increasing its absolute value from 0.89 Debye for tAZO to −4.03 Debye for GQD–tAZO, and from −0.8 Debye to 1.7 Debye for cAZO alone and at the interface, respectively. For both isomers, the occupied (HOMO–1 and HOMO) and virtual (LUMO and LUMO+1) frontier orbitals are degenerated in energy, lying at −5.5 eV and −1.7 eV for the trans isomer and −5.5 eV and −1.6 eV for the cis isomer, respectively. Therefore, the presence of the GQDs is responsible for the decrease of the energy gap from about 6 eV to 3.8 eV, making the interface a semiconductor (see Fig. S5–S7, ESI†). The localization of the frontier orbitals over the GQDs indicates no contribution arising from the AZO molecules, with the nearest orbital taking part in PET and PHT processes being HOMO–2 (delocalized over graphene and pyrene for both isomers).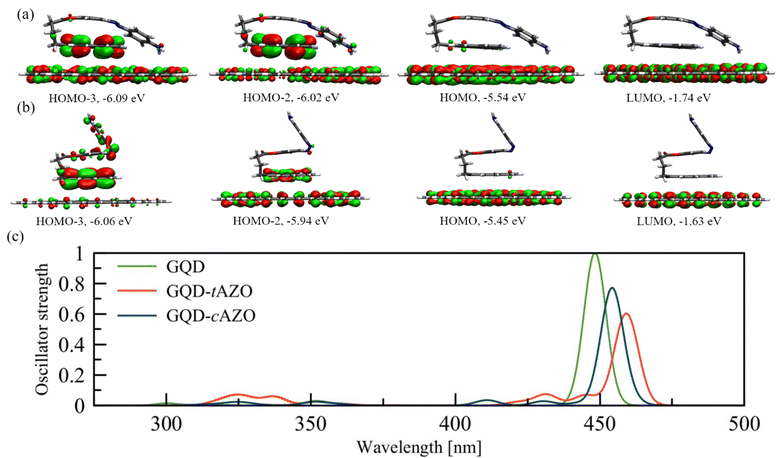 | ||
| Fig. 3 Frontier orbitals of (a) GQD–tAZO and (b) GQD–cAZO. (c) UV-Vis spectra of GQD–AZO interfaces (red and blue lines) and GQDs (green line). | ||
The absorption spectrum of the GQD–tAZO interface is red shifted with respect to the spectra of tAZO in the fold conformation by 100 nm, due to the presence of GQDs. Degenerate electronic transitions are observed. The first two excited states are dark and correspond to the π(GQD) → π*(GQD) transitions, and the first bright peak consists of two strongly allowed transitions at 461 and 458 nm, delocalized over the AZO moiety and GQDs, respectively (Fig. S8, ESI†). The peak at 445 nm corresponds to the π → π* transition localized over the GQD fragment. The same shift towards longer wavelengths and degerate electronic transitions are observed for the GQD–cAZO interface. Once again, the first two transitions are dark and localized over the GQD fragment, while the first bright peak at 454 nm consists of two strong transitions, involving both AZO and GQD fragments. As for the GQD–tAZO interface, the peak at 443 nm corresponds to the two localized transitions on the GQDs. The presence of the AZO molecule at the interface is also responsible for the redshift of the absorption spectra compared to the bare GQDs, of 10 and 15 nm for cAZO and tAZO, respectively, also decreasing the shift in absorption between the two isomers compared to the isolated case. In fact, now the GQD–tAZO interface exhibits a redshift of 10 nm compared to the GQD–cAZO interface, while for the isolated molecule, the cAZO isomer exhibits a redshift of more than 100 nm compared to the trans one. In addition, the presence of the graphene dots at the GQD–cAZO interface is responsible for the suppression of the weak, long wavelength peaks related to the S1 n → π* transition observed for the isolated molecule.
The NTO analysis of the orbitals involved in the photophysics of the two configurations indicates that for these interfaces, AZO acts as the donor (DMOL), whereas the GQDs is the acceptor (AGQD). It is important to notice that since both interfaces exhibit degerate orbitals, an effective coupling has been calculated as discussed in the Method section. Depending on the number of degenerate states involved in the transition, we considered a combination of multiple coupling values (as in eqn (4)). For GQD–tAZO, the EET process is facilitated by a local AZO excitation at 436 nm, which is followed by an energy transfer to two degenerated GQD local excitations at 461 and 458 nm, respectively. Although the EET takes place between two GQDs’ transitions with high oscillator strengths, the unfavorable overlap between the transition densities of these localized states causes a relatively low coupling value of 5.3 meV. For GQD–cAZO, the states involved in the EET are local AZO excitation at 462 nm, from which energy is transferred to the two GQDs’ local excitations at 455 and 453 nm, leading to a coupling value of 10.4 meV. On the other hand, the PET process is hindered for both interfaces, with the local excitation of the AZO at 436 (462) nm for the trans (cis) isomer for the electron transfer from AZO to GQDs (visible as two almost degenerated final states at 423/420 nm and 411/409 nm for trans and cis, respectively), leading to a very weak coupling with a value lower than 4 meV (Table 2). This is a consequence of the weaker overlap between the diabatic wavefunctions of the initial and final states, which in the PET case are, in a first approximation, the LUMOs of AZO and GQD moieties. As one can already see in Fig. 3, where the frontier orbitals of the whole donor:acceptor system are represented for both interfaces, the LUMO is localized only on the GQDs. Ultimately, the dominant process for both interfaces is the PHT, with the local excitations of the GQDs (two degenerated  at 433/430 nm), allowing a transfer of a hole from the GQDs to AZO (visible as two almost degenerated final states at 423/422 nm and 411/409 nm for trans and cis, respectively), leading to holes’ coupling values up to 51.2 and 70.4 meV, for the trans and cis isomers, respectively. The higher value of PHT coupling compared to PET coupling is a consequence of the larger delocalization of the HOMO orbitals involved in the former process compared to the LUMOs (as visible in Fig. 3). Moreover, the different delocalization and overlap between the wavefunctions of the initial and final states are slightly more favorable for GQD–cAZO compared to the trans isomer, although the difference is too small to be visually appreciated.
at 433/430 nm), allowing a transfer of a hole from the GQDs to AZO (visible as two almost degenerated final states at 423/422 nm and 411/409 nm for trans and cis, respectively), leading to holes’ coupling values up to 51.2 and 70.4 meV, for the trans and cis isomers, respectively. The higher value of PHT coupling compared to PET coupling is a consequence of the larger delocalization of the HOMO orbitals involved in the former process compared to the LUMOs (as visible in Fig. 3). Moreover, the different delocalization and overlap between the wavefunctions of the initial and final states are slightly more favorable for GQD–cAZO compared to the trans isomer, although the difference is too small to be visually appreciated.
| Process | λ [eV] | Coupling [eV] | ΔG [eV] | k [s−1] | |
|---|---|---|---|---|---|
| GQD–tAZO | EET | 0.19 | 0.005 | −0.146 | 1.0 × 1012 |
| PET | 0.33 | 0.001 | 0.095 | 3.6 × 107 | |
| PHT | 0.71 | 0.051 | 0.068 | 1.3 × 1010 | |
| GQD–cAZO | EET | 0.20 | 0.010 | 0.043 | 2.3 × 1011 |
| PET | 0.11 | 0.004 | 0.337 | 2.8 × 104 | |
| PHT | 0.64 | 0.070 | 0.142 | 9.4 × 109 |
The PHT reorganization energy for GQD–tAZO computed using the forward and backward reorganization energy scheme (eqn (S1)–(S3), ESI†), where the AZO molecule is considered as a donor and GQDs as an acceptor, has values of 0.71 and 0.64 eV, respectively (Table 2). For the EET process, the values are similar: 0.19 eV and 0.20 eV for tAZO and cAZO isomers, respectively. A different scenario is observed for the PET process, for which the presence of the GQDs decreased the λ to 0.33 eV for GQD–tAZO and to 0.11 eV for GQD–cAZO. Overall, the presence of GQDs has a strong influence on the reorganization energies in the GQD–AZO interfaces, significantly decreasing their magnitude to similar values. This can be explained considering the nature of the GQDs, since they can easily accommodate one additional electron/hole, with little or negligible distortions in the interfacial structure. Thus, since it is not obvious which photoinduced process will dominate due to the lack of a clear trend in the different components (reorganization energy, electronic coupling and driving force), it is crucial to compute the Marcus rates, to quantify and disentangle the different contributions.
From the analysis of the Marcus rates, we observe that the trend characterizing the rates for the different processes follows: kEET > kPHT > kPET for the GQD–tAZO interface, in which the fastest process after photoexcitation is EET, with a kEET value of 1 × 1012 s−1. PHT might also take place, although with a smaller rate of 1.3 × 1010 s−1. On the other hand, PET is rather slow (Table 2). Opposite to GQD–tAZO, the GQD–cAZO interface presents an overall lower rate for all the three processes, following the kEET > kPHT ≫ kPET trend. PHT could become favorable also for the GQD–cAZO interface, as its rate of 9.4 × 109 s−1 is high, albeit smaller compared to the EET rate (2.3 × 1011 s−1). It is also worth noting the effect of the isomer on the rate values. In fact, as already discussed for the intramolecular processes for the isolated molecules, also when intermolecular photoinduced transfer at the interface is considered, the rates for the trans isomer are always higher in magnitude compared to the cis isomer. At first glance, this can appear counterintuitive, because the couplings are smaller for GQD–tAZO compared to GQD–cAZO, and the reorganization energies have rather similar values. We can thus infer that this effect is mainly due to the driving force, which presents large variations for the different processes for both isomers. This confirms that tAZO is the active state for the interface, presenting higher rates for all the processes, while cAZO is the inactive state.
GQD–AZO – MD simulations
In order to assess the effects of structural disorder and temperature on the transfer rates, we consider here the analysis of an assembly of AZO molecules, in which we explicitly consider the thermal effects using MD simulations.The first observation from MD simulations is that the majority of the AZO molecules prefer the fold conformation (88% for trans and 83% for cis) over the open one and they tend to aggregate in one place of the surface (Fig. S9–S11, ESI†). The presence of thermal energy results in the distortion of the AZO molecule geometry, which in turn tends to decrease the degeneracy of the occupied and virtual frontier molecular orbitals. The GQD–tAZO interface shows a double distribution for all four frontier orbitals, leading to an energy gap of 3.8 eV (Fig. S12 and S13, ESI†).
The convoluted absorption spectra for all the extracted frames from the MD simulations are reported in Fig. 4. The first absorption peak for the GQD–tAZO interface is slightly blue shifted by 8 nm compared to the optimized interface. This peak at 459 nm corresponds to the π(GQD) → π*(GQD) transition. It is worth noting that the first four excited states are now dark. The shoulder at 427 nm consists of series of three π(GQD + AZO) → π*(GQD) transitions. Opposite to trans, the absorption spectrum for the GQD–cAZO interface is not shifted compared to the model interface, however two additional weakly allowed peaks at 515 and 494 nm appear due to the molecular distortion induced by the thermal energy. The peak at longer wavelength corresponds to the first excited state and the second relates to the second excited state and both have a π(GQD) → π*(GQD) character. The high-intensity peak at 454 nm is related to a transition localized over the GQD fragment of the interface. A mixture of contributions from different excited states (S8 (25%), S9 (37%), S10 (16%) and S11 (22%)) is found for the peak at 430 nm and correspond to π(GQD + AZO) → π*(GQD) transitions. Overall, the distortion of the molecular geometry of the interface due to thermal energy marginally affects the GQD–tAZO interface while it has a much stronger effect on the GQD–cAZO interface, resulting in two weakly allowed transitions at longer wavelengths, which might result in an enhanced the photoinduced transfer rate.
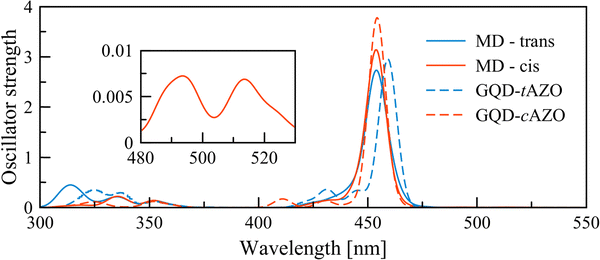 | ||
| Fig. 4 Convoluted UV-Vis spectrum recorded using 50 frames extracted from the MD simulations and the absorption spectra of the optimized interfaces (replotted from Fig. 3). The inset shows a magnification of the long wavelength peaks for the cAZO interface. | ||
To quantify and assess how the thermal effects affect EET, PET and PHT processes at the GQD–AZO interfaces, the couplings are evaluated for all the frames extracted from the MD simulations. Once again the GQD is found to be an acceptor (AGQD) and AZO acts as a donor site (DMOL). For all the transfer processes, we observed that the same states already found in the optimized interfaces take part in the transitions. Surprisingly, the EET coupling between the first allowed degenerated GQD (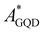 ) local excitations and AZO (
) local excitations and AZO ( ) local excitation for the GQD–tAZO interface increases four times in value compared to the optimized interface, with a final value of 18 meV. Similarly, the EET coupling between
) local excitation for the GQD–tAZO interface increases four times in value compared to the optimized interface, with a final value of 18 meV. Similarly, the EET coupling between 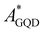 and
and  for the GQD–cAZO interface exhibits a value of 57 meV, which corresponds to an almost six time increase in value compared to the optimized interface (Table S3, ESI†). We believe that this is due to the fact that thermal effects and related structural fluctuations increase the conformational motion allowing for a broader sampling of the potential energy surface for the selected process, resulting in the discovery of different local minima which can enhance the electronic coupling. A similar effect has been reported in the literature for biosystems,55 as well as for other types of couplings in organic crystals and semiconducting polymers depending on the transport regime.56,57 On the other hand, for the PET process, the coupling values have not changed compared to the optimized interfaces (Table 3). A strong decrease in coupling is observed for the PHT process, with 35% lower value for the GQD–tAZO interface compared to the optimized interface, leading to a final hole coupling value of 38 meV, and of 75% decrease for the GQD–cAZO interface, with the final value of 24 meV. The fact that we observe different degrees of geometrical distortions induced by the presence of thermal energy on the two interfaces helps us in rationalizing the coupling values for PHT. For the GQD–tAZO interface, we observe that almost all the molecules are in the fold conformation, with some minor amount in the open one (12% of the total). On the other hand, a higher percentage of molecules are found in their open conformation for the GQD–cAZO interface (17%) with a non-negligible number of molecules with geometries that lie somewhere in between open and fold conformations (Fig. S8 and S9 in the ESI†). Since we determined that the couplings for open conformations are generally lower compared to the fold ones (see Table S2, ESI†), we can rationalize the large drop in coupling observed for GQD–cAZO and the relatively small decrease in the value for GQD–tAZO compared to the model interfaces.
for the GQD–cAZO interface exhibits a value of 57 meV, which corresponds to an almost six time increase in value compared to the optimized interface (Table S3, ESI†). We believe that this is due to the fact that thermal effects and related structural fluctuations increase the conformational motion allowing for a broader sampling of the potential energy surface for the selected process, resulting in the discovery of different local minima which can enhance the electronic coupling. A similar effect has been reported in the literature for biosystems,55 as well as for other types of couplings in organic crystals and semiconducting polymers depending on the transport regime.56,57 On the other hand, for the PET process, the coupling values have not changed compared to the optimized interfaces (Table 3). A strong decrease in coupling is observed for the PHT process, with 35% lower value for the GQD–tAZO interface compared to the optimized interface, leading to a final hole coupling value of 38 meV, and of 75% decrease for the GQD–cAZO interface, with the final value of 24 meV. The fact that we observe different degrees of geometrical distortions induced by the presence of thermal energy on the two interfaces helps us in rationalizing the coupling values for PHT. For the GQD–tAZO interface, we observe that almost all the molecules are in the fold conformation, with some minor amount in the open one (12% of the total). On the other hand, a higher percentage of molecules are found in their open conformation for the GQD–cAZO interface (17%) with a non-negligible number of molecules with geometries that lie somewhere in between open and fold conformations (Fig. S8 and S9 in the ESI†). Since we determined that the couplings for open conformations are generally lower compared to the fold ones (see Table S2, ESI†), we can rationalize the large drop in coupling observed for GQD–cAZO and the relatively small decrease in the value for GQD–tAZO compared to the model interfaces.
| Process | λ [eV] | Coupling [eV] | ΔG [eV] | k [s−1] | |
|---|---|---|---|---|---|
| GQD–tAZO | EET | 0.05 (0.01) | 0.018 (0.02) | −0.152 (0.06) | 2.8 × 1012 |
| PET | 0.08 (0.03) | 0.002 (0.002) | 0.119 (0.02) | 1.3 × 109 | |
| PHT | 0.19 (0.79) | 0.038 (0.03) | 0.070 (0.03) | 1.7 × 1012 | |
| GQD–cAZO | EET | 0.06 (0.03) | 0.057 (0.03) | 0.297 (0.12) | 1.4 × 105 |
| PET | 0.10 (0.04) | 0.004 (0.003) | 0.480 (0.12) | 5.6 × 10−3 | |
| PHT | 0.23 (0.94) | 0.024 (0.01) | 0.055 (0.02) | 6.5 × 1011 |
The reorganization energy obtained using eqn (1) and (2) calculated over 35 frames for the PET process has values of 0.08 eV and 0.10 eV for GQD–tAZO and GQD–cAZO, respectively. Considerably higher values of 0.19 eV and 0.23 eV are found for PHT, suggesting that a higher barrier must be crossed between the initial and final states to facilitate PHT than PET. Finally, a similar value of 0.05 eV has been computed for EET for both interfaces (Table 3). The driving force analysis shows a different trend for the two interfaces compared to the reorganization energy, with EET favored for the GQD–tAZO interface and PHT favored for the GQD–cAZO interface, suggesting that additional electronic factors rather than the pure geometrical distortions are responsible for the different computed Marcus rates.
The inclusion of thermal effects has interesting repercussions on the Marcus rates of the two interfaces. While this effect at the GQD–tAZO interface is negligible for the EET process, accounting for structural disorder induced by thermal fluctuations strongly enhances the PHT rate up to 1.7 × 1012 s−1, resulting in a strong competition between PHT and EET to dominate the photophysics of the system. Moreover, the PET rate is also enhanced, making the overall trend (kEET ∼ kPHT > kPET) different from the case at 0 K. If we compare the optimized GQD–tAZO interface and the current one in which thermal effects are considered, we observe that especially for PHT (and to a lesser extent also PET), the reorganization energy is strongly decreased, while driving force and coupling remain similar. This suggests that the reorganization of the tAZO molecules on the surface allows for a beneficial relaxation of this conformer, resulting in an increased PHT rate. Structural disorder induced by thermal energy has a strong impact also at the GQD–cAZO interface, for all processes. In fact, now the rates follow the kPHT ≫ kEET ≫ kPET trend, with a value of 6.5 × 1011 s−1 for PHT, much higher than that for EET (1.4 × 105 s−1). Although the coupling for EET is strongly enhanced compared to the optimized interface and the PHT is decreased, the driving force for PHT is strongly decreased, while it is almost 7 times higher for EET. In addition, a stronger decrease in reorganization energy of 36% for PHT compared to a 30% decrease for EET ensures that the dominant process for the GQD–cAZO interface is PHT. Despite these large variations in values, all processes are faster at the GQD–tAZO interface compared to those at the GQD–cAZO interface. This confirms that tAZO is an active isomer for photoinduced processes, while cAZO can be considered to be less active.
Conclusions
A comprehensive study of photoinduced charge and energy transfer in azobenzene derivatives as well as their interfaces with graphene quantum dots is reported. By means of DFT calculations as well as MD simulations, the effects of conformational changes for the two isomers on the magnitude of PET, PHT and EET processes are investigated through the calculation of reorganization energies, intra- and inter-molecular couplings, driving force and eventually Marcus transfer rates. For isolated AZO, the fold conformations are more stable compared to the open one and these are predominately present when performing MD simulations for the GQD–AZO interfaces as well. The comparison between the UV-Vis spectra of cis and trans isomers revealed that the azobenzene derivatives presented in this study are capable of undergoing photoisomerization, thereby presenting a unique opportunity to create an on/off switch by connecting them with GQDs.We found that EET dominates the intramolecular process for both isomers of the isolated molecules, as well as the intermolecular process at the GQD–AZO interfaces, although for the latter system, PHT can be a competitive pathway. This effect is mainly due to the presence of the GQDs, which strongly decrease the reorganization energy at the interfaces of both isomers and enhance their hole coupling values. On the other hand, PET is strongly suppressed, due to a negligible electronic coupling (lower than 0.005 eV) between the moieties of the interfaces, as well as the sizable activation barrier characterizing the electron transfer in this case.
A striking decrease of reorganization energies when thermal effects are included in the model causes the enhancement of PET and PHT for both interfaces. This is a direct consequence of the presence of the GQDs that can accommodate an additional electron or hole without significant deformation of the interfacial geometrical structure. On the other hand, thermal effects strongly decrease the EET rates at the GQD–cAZO interface, favouring PHT instead, which becomes the fastest process (occurring on a ps time-scale). Crucially, the formation of the interface with the trans isomer of the AZO molecule ensures higher rates for all the processes compared to the cis isomer. Thus, tAZO can be considered as the active form of interest for photoinduced applications in comparison with the corresponding cAZO isomer. We would like to remark here that the presented results might depend on the specific system. Different functionalization of the AZO molecule might lead to different morphological and photophysical properties (such as energy level alignment) which need to be studied for each case. Moreover, this study highlights the importance of considering thermal fluctuations and structural dynamics as they play an important role in the determination of the kinetics of the different processes. Considering only the position of the energy levels as descriptors for the photophysical process taking place at interfaces might present an incomplete picture. This study paves the way to assess the photoisomerization transfer mechanism of low-dimensional material interfaces by means of a material design approach for selected applications in which one of the three processes is desired.
Author contributions
The manuscript was written through the contributions of all authors. All of the authors discussed the results and participated in writing the final version of the manuscript and have given approval to the final version of the manuscript. S. O. proposed the research direction, supervised the project conceptually and experimentally and helped with the interpretation of the results. M. K. participated in the design of the research and performed the calculations, including all data collection and further analysis and interpretation. S. O. and S. G. supervised the preparation of the manuscript, including the interpretation of the results and participated in finalizing the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. O. thanks the National Science Centre, Poland (grant no. UMO/2020/39/I/ST4/01446) and the “Excellence Initiative – Research University” (IDUB) Program, Action I.3.3 – “Establishment of the Institute for Advanced Studies (IAS)” for funding (grant no. UW/IDUB/2020/25). The computation was carried out with the support of the Interdisciplinary Center for Mathematical and Computational Modeling at the University of Warsaw (ICM UW) under grants no. G83-28 and GB80-24. The authors acknowledge David Beljonne for fruitful discussions.References
- A. Ghaffarkhah,
et al., Synthesis, Applications, and Prospects of Graphene Quantum Dots: A Comprehensive Review, Small, 2022, 18, 2102683 CrossRef CAS
.
- L. A. Ponomarenko,
et al., Chaotic Dirac billiard in graphene quantum dots, Science, 2008, 320, 356–358 CrossRef CAS
.
- Z. Ji, E. Dervishi, S. K. Doorn and M. Sykora, Size-Dependent Electronic Properties of Uniform Ensembles of Strongly Confined Graphene Quantum Dots, J. Phys. Chem. Lett., 2019, 10, 953–959 CrossRef CAS PubMed
.
- Y. Li, H. Shu, S. Wang and J. Wang, Electronic and optical properties of graphene quantum dots: The role of many-body effects, J. Phys. Chem. C, 2015, 119, 4983–4989 CrossRef CAS
.
- J. Qian,
et al., Tailoring the Electronic Properties of Graphene Quantum Dots by P Doping and Their Enhanced Performance in Metal-Free Composite Photocatalyst, J. Phys. Chem. C, 2018, 122, 349–358 CrossRef CAS
.
- J. Feng,
et al., Theoretical insights into tunable optical and electronic properties of graphene quantum dots through phosphorization, Carbon, 2019, 155, 491–498 CrossRef CAS
.
- P. Elvati, E. Baumeister and A. Violi, Graphene quantum dots: effect of size, composition and curvature on their assembly, RSC Adv., 2017, 7, 17704–17710 RSC
.
- M. T. Hasan,
et al., Photo-and Electroluminescence from Nitrogen-Doped and Nitrogen–Sulfur Codoped Graphene Quantum Dots, Adv. Funct. Mater., 2018, 28, 1804337 CrossRef
.
- D. Qu,
et al., Highly luminescent S, N co-doped graphene quantum dots with broad visible absorption bands for visible light photocatalysts, Nanoscale, 2013, 5, 12272–12277 RSC
.
- Y. Kim,
et al., Graphene quantum dot (GQD)-induced photovoltaic and photoelectric memory elements in a pentacene/GQD field effect transistor as a probe of functional interface, J. Phys. D: Appl. Phys., 2017, 50, 365303 CrossRef
.
- G. Konstantatos,
et al., Hybrid graphene-quantum dot phototransistors with ultrahigh gain, Nat. Nanotechnol., 2012, 7, 363–368 CrossRef CAS
.
- H. Tetsuka, A. Nagoya, T. Fukusumi and T. Matsui, Molecularly Designed, Nitrogen-Functionalized Graphene Quantum Dots for Optoelectronic Devices, Adv. Mater., 2016, 28, 4632–4638 CrossRef CAS
.
- S. Osella and S. Knippenberg, Environmental effects on the charge transfer properties of Graphene quantum dot based interfaces, Int. J. Quantum. Chem., 2019, 119, e25882 CrossRef
.
- H. Bian,
et al., Nitrogen-doped graphene quantum dots for 80% photoluminescence quantum yield for inorganic γ-CsPbI3 perovskite solar cells with efficiency beyond 16%, J. Mater. Chem. A, 2019, 7, 5740–5747 RSC
.
- W. Wu, H. Wu, M. Zhong and S. Guo, Dual Role of Graphene Quantum Dots in Active Layer of Inverted Bulk Heterojunction Organic Photovoltaic Devices, ACS Omega, 2019, 4, 16159–16165 CrossRef CAS PubMed
.
- M. Li,
et al., Graphene quantum dots as the hole transport layer material for high-performance organic solar cells, Phys. Chem. Chem. Phys., 2013, 15, 18973–18978 RSC
.
- Z. Ding, Z. Miao, Z. Xie and J. Liu, Functionalized graphene quantum dots as a novel cathode interlayer of polymer solar cells, J. Mater. Chem. A, 2016, 4, 2413–2418 RSC
.
-
P. Minsu, Y. Hyewon and J. Seokwoo, Graphene-based quantum dot emitters for light-emitting diodes, Graphene for Flexible Lighting and Displays, Elsevier, 2019, pp.117–150 DOI:10.1016/B978-0-08-102482-9.00007-1
.
- H. Yoon,
et al., Blue Graphene Quantum Dots with High Color Purity by Controlling Subdomain Formation for Light-Emitting Devices, ACS Appl. Nano. Mater., 2020, 3, 6469–6477 CrossRef CAS
.
- L. Yin, J. Zhou, W. Li, J. Zhang and L. Wang, Yellow fluorescent graphene quantum dots as a phosphor for white tunable light-emitting diodes, RSC Adv., 2019, 9, 9301–9307 RSC
.
- L. Yin,
et al., White light emitting diodes based on green graphene quantum dots and red graphene quantum dots, Mol. Cryst. Liq. Cryst., 2022, 733, 46–51 CrossRef CAS
.
- S. Mondal, U. Rana and S. Malik, Graphene quantum dot-doped polyaniline nanofiber as high performance supercapacitor electrode materials, Chem. Commun., 2015, 51, 12365–12368 RSC
.
- S. Zhang,
et al., Graphene quantum dots as the electrolyte for solid state supercapacitors, Sci. Rep., 2016, 6, 19292 CrossRef CAS
.
- S. Zhang,
et al., High-Performance Supercapacitor of Graphene Quantum Dots with Uniform Sizes, ACS Appl. Mater. Interfaces, 2018, 10, 12983–12991 CrossRef CAS
.
- G. Wang,
et al., Green preparation of lattice phosphorus doped graphene quantum dots with tunable emission wavelength for bio-imaging, Mater. Lett., 2019, 242, 156–159 CrossRef CAS
.
- Z. Xue,
et al., Graphene quantum dot assisted translocation of drugs into a cell membrane, Nanoscale, 2019, 11, 4503–4514 RSC
.
- O. Klaja, J. A. Frank, D. Trauner and A. N. Bondar, Potential energy function for a photo-switchable lipid molecule, J. Comput. Chem., 2020, 41, 2336–2351 CrossRef CAS PubMed
.
- E. Margapoti,
et al., Emergence of photoswitchable states in a graphene-azobenzene-au platform, Nano. Lett., 2014, 14, 6823–6827 CrossRef CAS PubMed
.
- M. Min, S. Seo, S. M. Lee and H. Lee, Voltage-controlled nonvolatile molecular memory of an azobenzene monolayer through solution-processed reduced graphene oxide contacts, Adv. Mater., 2013, 25, 7045–7050 CrossRef CAS
.
- P. Dietrich,
et al., An anchoring strategy for photoswitchable biosensor technology: Azobenzene-modified SAMs on Si(111), Appl. Phys. A: Mater. Sci. Process., 2008, 93, 285–292 CrossRef CAS
.
- W. Luo,
et al., High-energy, stable and recycled molecular solar thermal storage materials using AZO/graphene hybrids by optimizing hydrogen bonds, Nanoscale, 2015, 7, 16214–16221 RSC
.
- G. v Dubacheva, C.-K. Liang and D. M. Bassani, Functional monolayers from carbon nanostructures – fullerenes, carbon nanotubes, and graphene – as novel materials for solar energy conversion, Coord. Chem. Rev., 2012, 256, 2628–2639 CrossRef CAS
.
- Y. Feng,
et al., Covalent functionalization of graphene by azobenzene with molecular hydrogen bonds for long-term solar thermal storage, Sci. Rep., 2013, 3, 3260 CrossRef PubMed
.
- Y. Norikane and N. Tamaoki, Light-driven molecular hinge: A new molecular machine showing a light-intensity-dependent photoresponse that utilizes the trans-cis isomerization of azobenzene, Org. Lett., 2004, 6, 2595–2598 CrossRef CAS PubMed
.
- O. Nachtigall,
et al., Pyrene–Azobenzene Dyads and Their Photochemistry, Eur. J. Org. Chem., 2014, 966–972 CrossRef CAS
.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef
.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules, J. Chem. Phys., 1971, 54, 720–723 CrossRef
.
-
M. J. Frisch, et al., Gaussian 16, Revision C01., 2016 Search PubMed
.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: A message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS
.
- E. Lindahl, B. Hess and D. van der Spoel, GROMACS 3.0: A package for molecular simulation and trajectory analysis, J. Mol. Model., 2001, 7, 306–317 CrossRef CAS
.
- D. van der Spoel,
et al., GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed
.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GRGMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS
.
- M. J. Abraham,
et al., Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- S. Páll,
et al., Heterogeneous parallelization and acceleration of molecular dynamics simulations in GROMACS, J. Chem. Phys., 2020, 153, 134110 CrossRef
.
- E. Lindahl, P. Bjelkmar, P. Larsson, M. A. Cuendet and B. Hess, Implementation of the charmm force field in GROMACS: Analysis of protein stability effects from correction maps, virtual interaction sites, and water models, J. Chem. Theory Comput., 2010, 6, 459–466 CrossRef PubMed
.
- L. Cupellini, S. Giannini and B. Mennucci, Electron and excitation energy transfers in covalently linked donor–acceptor dyads: mechanisms and dynamics revealed using quantum chemistry, Phys. Chem. Chem. Phys., 2018, 20, 395–403 RSC
.
- M. Nottoli,
et al., The role of charge-transfer states in the spectral tuning of antenna complexes of purple bacteria, Photosynth. Res., 2018, 137, 215–226 CrossRef CAS
.
- J. Tölle, L. Cupellini, B. Mennucci and J. Neugebauer, Electronic couplings for photo-induced processes from subsystem time-dependent density-functional theory: the role of the diabatization, J. Chem. Phys., 2020, 153, 184113 CrossRef
.
- N. Gildemeister, G. Ricci, L. Böhner, J. M. Neudörfl, D. Hertel, F. Würthner, F. Negri, K. Meerholz and D. Fazzi, Understanding the structural and charge transport property relationships for a variety of merocyanine single-crystals: a bottom up computational investigation, J. Mater. Chem. C, 2021, 9, 10851 RSC
.
- J. Blumberger, Recent Advances in the Theory and Molecular Simulation of Biological Electron Transfer Reactions, Chem. Rev., 2015, 115, 11191–11238 CrossRef CAS
.
- S.-J. Lee, H.-C. Chen, Z.-Q. You, K.-L. Liu, T. J. Chow, I.-C. Chen and C.-P. Hsu, Theoretical characterization of photoinduced electron transfer in rigidly linked donor–acceptor molecules: the fragment charge difference and the generalized Mulliken–Hush schemes, Mol. Phys., 2010, 108, 2775–2789 CrossRef CAS
.
- G. Pourtois, D. Beljonne, J. Cornil, M. A. Ratner and J. L. Bredas, Photoinduced Electron-Transfer Processes along Molecular Wires Based on Phenylenevinylene Oligomers:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Quantum-Chemical Insight, J. Am. Chem. Soc., 2002, 124, 4436–4447 CrossRef CAS PubMed
A Quantum-Chemical Insight, J. Am. Chem. Soc., 2002, 124, 4436–4447 CrossRef CAS PubMed .
- H. M. D. Bandara and S. C. Burdette, Photoisomerization in different classes of azobenzene, Chem. Soc. Rev., 2012, 41, 1809–1825 RSC
.
- L. Cupellini, S. Jurinovich, I. G. Prandi, S. Caprasecca and B. Mennucci, Photoprotection and triplet energy transfer in higher plants: the role of electronic and nuclear fluctuations, Phys. Chem. Chem. Phys., 2016, 18, 11288–11296 RSC
.
- S. Giannini and J. Blumberger, Charge Transport in Organic Semiconductors: The Perspective from Nonadiabatic Molecular Dynamics, Acc. Chem. Res., 2022, 55, 819–830 CrossRef CAS PubMed
.
- S. Prodhan, S. Giannini, L. Wang and D. Beljonne, Long-Range Interactions Boost Singlet Exciton Diffusion in Nanofibers of π-Extended Polymer Chains, J. Phys. Chem. Lett., 2021, 12, 8188–8193 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Complete excited state analysis of the isolated molecules, description of the properties of the open conformation for both isomers, (partial) density of states, energy levels, natural transition orbitals (NTOs) and molecular dynamics analyses. See DOI: https://doi.org/10.1039/d3tc03667g |
| ‡ Present address: Institute of Chemistry of OrganoMetallic Compounds, National Research Council (ICCOM-CNR), I-56124 Pisa, Italy. |
| This journal is © The Royal Society of Chemistry 2024 |