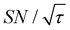Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Background signal suppression by opposite polarity subtraction for targeted DNP NMR spectroscopy on mixture samples†
Zhongliang
Zhang
a,
Ken
Kato
a,
Hajime
Tamaki
a and
Yoh
Matsuki
 *ab
*ab
aInstitute for Protein Research, Osaka University, Suita, Osaka 565-0871, Japan. E-mail: yoh@protein.osaka-u.ac.jp
bCenter for Quantum Information and Quantum Biology, Osaka University, Toyonaka, Osaka 560-0043, Japan
First published on 30th January 2024
Abstract
A novel method for background signal suppression is introduced to improve the selectivity of dynamic nuclear polarization (DNP) NMR spectroscopy in the study of target molecules within complex mixtures. The method uses subtraction between positively and negatively enhanced DNP spectra, leading to an improved contrast factor, which is the ratio between the target and background signal intensities. The proposed approach was experimentally validated using a reverse-micelle system that confines the target molecules together with the polarizing agent, OX063 trityl. A substantial increase in the contrast factor was observed, and the contrast factor was optimized through careful selection of the DNP build-up time. A simulation study based on the experimental results provides insights into a strategy for choosing the appropriate DNP build-up time and the corresponding selectivity of the method. Further analysis revealed a broad applicability of the technique, encompassing studies from large biomolecules to surface-modified polymers, depending on the nuclear spin diffusion rate with a range of gyromagnetic ratios.
Introduction
Nuclear magnetic resonance (NMR) spectroscopy is unique in its ability to characterize the structural and functional properties of target molecules at atomic resolution in a mixture with other molecules not of interest or background.1,2 This feature of NMR provides a powerful means to study, for example, the surface functionalization of polymers as-is,3 electric cells in operando,4 and biomacromolecules in situ,5,6 without isolating or purifying the target moiety or molecules. For the latter case, an idea is that the structure and dynamics of proteins in a highly crowded intracellular environment can be distinct from those in purified and dilute buffer solutions,7–9 which have historically been used for the analysis of proteins. Also, the polymorph of protein aggregates or fibrils is strongly affected not only by the primary sequence but also by the intracellular environment.10,11 These facts make in situ protein analysis a long-standing challenge in structural biology.Although solution-state NMR can be used to study small proteins undergoing free Brownian tumbling in the cytoplasm,12 magic-angle-spinning (MAS) solid-state NMR, which does not have a molecular-weight limitation, is a powerful tool for examining larger non-Brownian assemblies such as membrane proteins and amyloid fibrils.10,13 However, its lower sensitivity due to the difficulty in 1H signal detection and the generally smaller active sample volume in an MAS rotor are the primary drawbacks compared with its solution-state counterparts. Moreover, in the aforementioned as-is measurements, the target moieties or molecules are, by nature, strongly diluted by a large amount of background molecules, making the sensitivity issue even more critical.
The high-field dynamic nuclear polarization (DNP) technique has become popular over the past two decades because it can enhance the sensitivity of MAS NMR typically by two orders of magnitude. This involves applying microwaves (MWs) to transfer high electron-spin polarization in a polarizing agent (PA) to adjacent nuclear spins. Subsequent spin diffusion spreads the polarization to nearby nuclear spins, thereby enhancing the NMR signals within the spin diffusion range.14–16 The site-specific delivery of the PA to target molecules therefore provides a method to preferentially enhance the signals of the targets.17–20 In such a targeted DNP-NMR study in a mixture sample, a primary challenge is suppressing the relaxation-induced background signals from regions outside the diffusion range, which can interfere with or, depending on the size of the background, overwhelm the target signals. Although selective isotopic labeling of the target molecules and/or deuteration of the background can be employed, this approach is often difficult, expensive, and/or labor-intensive for “as-is” material or cellular samples and is not always applicable. In particular, preparing two samples with different spin labels or PA distributions for data subtraction is not generally straightforward in practice for complex samples. Alternatively, data acquired without DNP (MW-off data) can be subtracted from the DNP-enhanced data (MW-on data) to remove the background. However, this method is inefficient because the MW-off data require the same averaging time as the MW-on data to preserve the signal-to-noise (S/N) ratio after the subtraction; in addition, the subtraction will partially remove the target signals. Thus, an alternative method is needed to fully exploit the potential of DNP-NMR for targeted measurements in a mixture sample.
In this research, we propose an alternative approach to suppress not-of-interest background signals by taking the difference between the spectra of positively and negatively enhanced DNP (referred to as positive and negative DNP) data. With many DNP mechanisms, including the solid effect (SE) and the cross effect (CE), the DNP can be selectively excited in opposite polarities by simply choosing an appropriate excitation MW frequency. This selective excitation is most practically achieved using the frequency tunability of the MW source (in our case, a gyrotron). We refer to this approach as “opposite polarity subtraction” (Oops), and it enables the selection of NMR signals from a “target region” responding to the polarity switch of the DNP while suppressing NMR signals from the “background region” outside the diffusion range, which arises purely from the spin relaxation. Compared with the MW-off data subtraction, the Oops treatment can up to double the S/N ratio for the target signals in the same total experimental time. In addition, this approach enables the application of both positive and negative DNP on a single sample, thereby avoiding the challenges associated with preparing multiple samples. To validate this idea, we used a reverse-micelle system that enables the target region to be defined relative to the background space in the sample. We experimentally demonstrate the efficacy of the method and analyze the data using a classical spin diffusion model. This approach enables us to evaluate the performance under different conditions expected in practical applications.
Experimental section
Sample preparation
The conventional water/sodium bis(2-ethylhexyl) sulfosuccinate (Aerosol OT, AOT)/isooctane reverse-micelle system21,22 was modified to ensure the transition of the sample into a glassy state at cryogenic temperatures, thereby preventing the aggregation of the PA and preserving the structure of the reverse micelles. To this end, we used isooctane/2-butanol (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, v/v) as the nonpolar solvent and glycerol/water (6
3, v/v) as the nonpolar solvent and glycerol/water (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
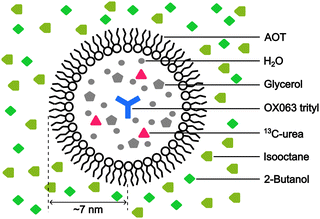
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, v/v)23 as the polar solvent. To prepare the reverse-micelle sample, AOT was lyophilized. Then, 1.5 μL of a 250 mM OX063 trityl water solution was mixed with 80 μL of a 0.25 M AOT isooctane/2-butanol solution. After the resultant mixture was vortexed and centrifuged, solid OX063 trityl was found to be precipitated out. A 1.3 M 13C-urea glycerol/water solution (0.5 μL) was then added repeatedly, with vortexing and centrifugation after each addition. A cumulative 21.5 μL of the 13C-urea glycerol/water solution was added until a homogeneous reverse-micelle sample was obtained without any precipitation. The final composition of the sample included 80 μL of nonpolar solvent, 23 μL of polar solvent, 0.194 M AOT in the whole sample, and 16.3 mM OX063 trityl and 1.22 M 13C-urea in the polar solvent. Fig. 1 shows the molecular structures of the chemicals used in this preparation.
4, v/v)23 as the polar solvent. To prepare the reverse-micelle sample, AOT was lyophilized. Then, 1.5 μL of a 250 mM OX063 trityl water solution was mixed with 80 μL of a 0.25 M AOT isooctane/2-butanol solution. After the resultant mixture was vortexed and centrifuged, solid OX063 trityl was found to be precipitated out. A 1.3 M 13C-urea glycerol/water solution (0.5 μL) was then added repeatedly, with vortexing and centrifugation after each addition. A cumulative 21.5 μL of the 13C-urea glycerol/water solution was added until a homogeneous reverse-micelle sample was obtained without any precipitation. The final composition of the sample included 80 μL of nonpolar solvent, 23 μL of polar solvent, 0.194 M AOT in the whole sample, and 16.3 mM OX063 trityl and 1.22 M 13C-urea in the polar solvent. Fig. 1 shows the molecular structures of the chemicals used in this preparation.
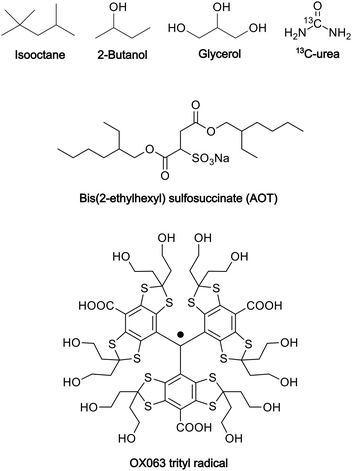 | ||
| Fig. 1 Molecular structures of the chemicals used in the preparation of the reverse-micelle samples. | ||
To determine the size of the reverse micelles, we used dynamic light scattering (DLS, Wyatt Technology DynaPro NanoStar). To avoid interference in the measurements as a result of the color of OX063 trityl, the sample for DLS was prepared without OX063 trityl while keeping all other conditions unchanged.
DNP-NMR and ESR experiments
To assess the potential leakage of OX063 trityl, we conducted electron-spin resonance (ESR) experiments on an X-band ESR spectrometer (BRUKER ELEXSYS-II E500 CW-EPR) with a field sweep set at 20 G.
13C DNP-NMR experiments were conducted on a 16.4 T MAS NMR spectrometer (JEOL ECA-700II) equipped with a homemade 460 GHz gyrotron and a closed-cycle He MAS system.24,25 The output power of the gyrotron was ∼10 W. For these experiments, samples were placed inside a 3.2 mm MAS rotor, which was rotated at 7 kHz. The DNP-NMR experiments were conducted at 37 K, whereas the DNP-off NMR experiments were conducted at 28 K. The frequency for the continuous-wave MWs was set to 459.80 GHz for the positive DNP and 460.19 GHz for the negative DNP. Prior to each scan, to initialize the magnetization for both the target and background, 13C and 1H spins were pre-saturated with a train of ∼160° pulses, each lasting 10 μs, with a 10 ms interval between pulses. A series of DNP build-up times τ ranging from 0 to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s were used in the experiments. For acquisition, a 90° pulse with a duration of 7.63 μs was used; the 1H spins were decoupled using a SPINAL64 decoupling sequence.26 Two transients were added for each spectrum. The basic NMR data processing was performed using JEOL Delta. The exponential window function (10 Hz) was applied prior to zero-filling (to 1024 complex points) and Fourier transformation. Oops spectral editing and other analyses were performed using MATLAB (version R2023b, MathWorks, Natick, Massachusetts).
000 s were used in the experiments. For acquisition, a 90° pulse with a duration of 7.63 μs was used; the 1H spins were decoupled using a SPINAL64 decoupling sequence.26 Two transients were added for each spectrum. The basic NMR data processing was performed using JEOL Delta. The exponential window function (10 Hz) was applied prior to zero-filling (to 1024 complex points) and Fourier transformation. Oops spectral editing and other analyses were performed using MATLAB (version R2023b, MathWorks, Natick, Massachusetts).
Results
Principle of background suppression
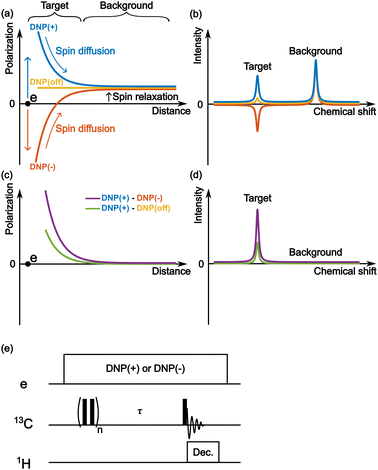
Fig. 2a schematically depicts the spatial distribution of polarization around a PA molecule at a certain polarization build-up time. The electron spin at the origin produces positive (blue) or negative (red) DNP enhancement, and spin diffusion propagates this enhancement to the nearby nuclear spins. Outside the diffusion range, the nuclear spins always relax toward a small positive value (i.e., the thermal equilibrium state) irrespective of the polarity of the hyperpolarization in the diffusion range (Fig. 2a and b). Therefore, when the difference between the two (i.e., DNP(+)–DNP(−) (the Oops procedure)) is taken, polarization accumulates in the target space while being canceled in the background space (Fig. 2c and d). Using this method, we can selectively enhance the NMR signals of the target molecules and suppress the NMR signals of the molecules in the background. Subtracting the MW-off data gives similar background signal suppression but only one-half of the target signal intensity (Fig. 2d, green).One of the simplest methods to experimentally demonstrate the efficacy of this method is to separately acquire the spectra from positive and negative DNP experiments and then calculate the difference between them. For this approach, we used the pulse sequence shown in Fig. 2e. The MW source was continuously on, and its frequency was set to excite the positive or negative DNP. After the initial saturation pulses, the polarization build-up/spin diffusion time (τ) was set before the data acquisition, which determines the range of the target space together with the spin diffusion rate D. For proof of principle, we experimentally demonstrated background suppression and its range of selection based on the direct 13C-excitation DNP with 13C–13C spin diffusion and evaluated the results using simulations.
Reverse micelle as a model
To emulate the case where the PA is delivered near the target molecule, we employed the water–AOT–isooctane reverse-micelle system (Fig. 3; Experimental section). The micelles contain the water-soluble PA OX063 trityl, along with 13C-labeled urea as the target molecule, and are suspended in the naturally abundant isooctane, which serves as background molecules present in large amounts. Glycerol (60 vol%) and 2-butanol (30 vol%) were added to water and isooctane, respectively, to ensure glass formation under the low-temperature DNP conditions. The radius of the micelles was estimated to be ∼7 nm from DLS measurements (Fig. S1, ESI†). On the basis of the expected micelle concentration, the separation between the micelles was ∼28 nm on average (supposing that the surface area of each AOT is 0.25 nm2).27 The trityl radical was used because of its insolubility in nonpolar solvents, which helps prevent its leakage from the micelles. The ESR experiments confirmed that trityl did not leak into the nonpolar solvent (Fig. S2, ESI†).Background signal suppression
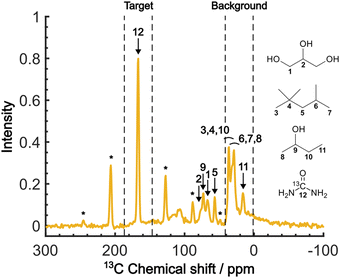
Fig. 4 shows the direct-excitation 13C NMR spectrum of the micelle sample collected at τ = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s (≳3T1 for both target and background) without MW irradiation (MW-off data). The assignment for each peak is shown in the spectrum.28,29 The sample is suitable for validating our method because the peaks of the target (13C-urea) and the background (isooctane/2-butanol) exhibit distinctive chemical shifts (Fig. 4; regions indicated by dashed lines). To evaluate the efficacy of the background signal suppression, we defined a contrast factor as C = IT/IB, where IT is the integral spectral intensity of the target (peak 12; integral from 146.7 to 186.7 ppm) and IB is that of the background (peaks 3, 4, 6–8, 10, 11; integral from 1.6 to 41.6 ppm). The observed integral spectral intensities were [IT, IB, IN] = [13.9, 24.9, 1.0] when normalized to the thermal noise intensity IN (integral from 1.6 to 41.6 ppm at τ = 0). Thus, the contrast factor was very low, C = 0.56. This shows that, with no bias toward the target, the background signals can seriously interfere with the target signal even if they are not isotopically labeled. Our aim is to attain a higher contrast factor by selectively enhancing the target signal by DNP while suppressing the background signals.
000 s (≳3T1 for both target and background) without MW irradiation (MW-off data). The assignment for each peak is shown in the spectrum.28,29 The sample is suitable for validating our method because the peaks of the target (13C-urea) and the background (isooctane/2-butanol) exhibit distinctive chemical shifts (Fig. 4; regions indicated by dashed lines). To evaluate the efficacy of the background signal suppression, we defined a contrast factor as C = IT/IB, where IT is the integral spectral intensity of the target (peak 12; integral from 146.7 to 186.7 ppm) and IB is that of the background (peaks 3, 4, 6–8, 10, 11; integral from 1.6 to 41.6 ppm). The observed integral spectral intensities were [IT, IB, IN] = [13.9, 24.9, 1.0] when normalized to the thermal noise intensity IN (integral from 1.6 to 41.6 ppm at τ = 0). Thus, the contrast factor was very low, C = 0.56. This shows that, with no bias toward the target, the background signals can seriously interfere with the target signal even if they are not isotopically labeled. Our aim is to attain a higher contrast factor by selectively enhancing the target signal by DNP while suppressing the background signals.
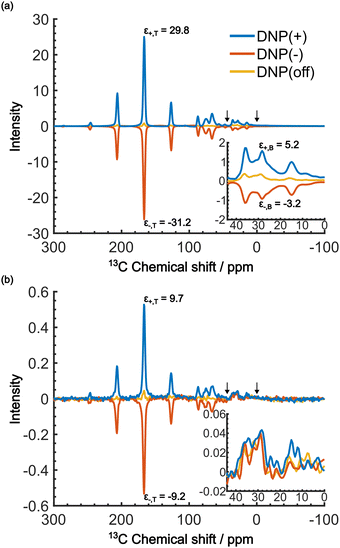
When the PA is located in the micelles with the target molecules, applying DNP should increase the contrast factor. Fig. 5a shows the DNP-enhanced 13C NMR spectra at τ = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s. The DNP-NMR spectra were acquired using our gyrotron to irradiate the maximum positive or negative DNP enhancement, and their MW frequencies were determined on the basis of the DNP frequency profile (Fig. S3, ESI†). In the profile, the separation of the enhancement maxima matched twice the 13C Zeeman frequency at B0 = 16.4 T (∼360 MHz). Thus, we concluded that the 13C-SE DNP is operative for this sample, similar to a recent report at 14.1 T and 100 K.30 A clear DNP enhancement was observed. The observed spectral intensities in the DNP conditions were [IT, IB, IN] = [436.7, 135.4, 1.0] (for DNP+) and [394, 72.6, 1.0] (for DNP−) with the DNP enhancement of εT = 29.8 (for DNP+), −30 (for DNP−) and εB = 5.2 (for DNP+), −3.2 (for DNP−). When the trityl radical was confined to the reverse micelles, a much higher DNP enhancement was obtained for the target than for the background, which increased the contrast factor to C = 3.22, although IB was still much higher than IN.
000 s. The DNP-NMR spectra were acquired using our gyrotron to irradiate the maximum positive or negative DNP enhancement, and their MW frequencies were determined on the basis of the DNP frequency profile (Fig. S3, ESI†). In the profile, the separation of the enhancement maxima matched twice the 13C Zeeman frequency at B0 = 16.4 T (∼360 MHz). Thus, we concluded that the 13C-SE DNP is operative for this sample, similar to a recent report at 14.1 T and 100 K.30 A clear DNP enhancement was observed. The observed spectral intensities in the DNP conditions were [IT, IB, IN] = [436.7, 135.4, 1.0] (for DNP+) and [394, 72.6, 1.0] (for DNP−) with the DNP enhancement of εT = 29.8 (for DNP+), −30 (for DNP−) and εB = 5.2 (for DNP+), −3.2 (for DNP−). When the trityl radical was confined to the reverse micelles, a much higher DNP enhancement was obtained for the target than for the background, which increased the contrast factor to C = 3.22, although IB was still much higher than IN.
We now consider how to improve the contrast factor further. Noting that the spins in the background experience finite negative DNP enhancement, it is evident that, at τ = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, spin diffusion propagates the DNP enhancement to the space outside the reverse micelles. To reduce this leakage of hyperpolarization, the DNP build-up time could be reduced, thereby reducing the polarization propagating through spin diffusion. Assuming that the 13C spin-diffusion rate is on the order of 0.01 nm2 s−1, as estimated from the literature values31–33 scaled by
000 s, spin diffusion propagates the DNP enhancement to the space outside the reverse micelles. To reduce this leakage of hyperpolarization, the DNP build-up time could be reduced, thereby reducing the polarization propagating through spin diffusion. Assuming that the 13C spin-diffusion rate is on the order of 0.01 nm2 s−1, as estimated from the literature values31–33 scaled by 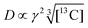 ,34 the build-up time needs to be within ∼100 s to confine the hyperpolarization to a few nanometers from the PA (i.e., within the micelles). Fig. 5b shows the MW-on spectra acquired at τ = 60 s. Rather unexpectedly, however, the background peaks are still clearly visible, and the contrast factor C = 3.84 in this case did not substantially increase compared to the case where τ = 20
,34 the build-up time needs to be within ∼100 s to confine the hyperpolarization to a few nanometers from the PA (i.e., within the micelles). Fig. 5b shows the MW-on spectra acquired at τ = 60 s. Rather unexpectedly, however, the background peaks are still clearly visible, and the contrast factor C = 3.84 in this case did not substantially increase compared to the case where τ = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s (C = 3.22). This result is understandable given the sheer volume of the background that has a build-up rate similar to that of the target. Therefore, simply shortening the diffusion time τ is often ineffective for suppressing the background signal and it just adversely affects the S/N ratio of the target signal.
000 s (C = 3.22). This result is understandable given the sheer volume of the background that has a build-up rate similar to that of the target. Therefore, simply shortening the diffusion time τ is often ineffective for suppressing the background signal and it just adversely affects the S/N ratio of the target signal.
Even in this situation, the Oops procedure enables clean background signal suppression because, at τ = 60 s, the background signal shows a similar positive intensity under both positive and negative DNP conditions (Fig. 5b, inset), which will cancel each other. Fig. 6c shows the results of the Oops treatment. The peaks representing the background signal are successfully suppressed to the noise level ([IT, IB, IN] = [18.4, 1.43, 1.0]), increasing the contrast factor to C = 12.9. Compared with the MW-off data subtraction approach (Fig. 6(b); [IT, IB, IN] = [11.2, 1.62, 1.0], C = 6.91), our method achieves an 87% higher contrast factor in the same total experimental time. These results validate the efficacy of our method relative to the conventional approaches for background signal suppression.
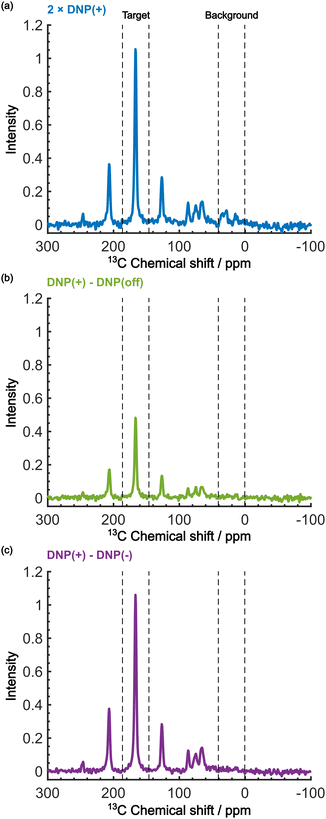 | ||
| Fig. 6 Demonstration of background signal suppression at τ = 60 s. The DNP-enhanced spectra with (a) the positive DNP, (b) the MW-off data subtraction, and (c) the Oops treatment are shown. The data in (a) are the same as in Fig. 5b (blue, an average of two scans), but were vertically scaled by a factor of 2 for direct comparability in the same total experimental time. | ||
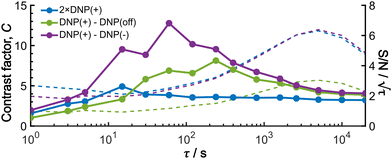
To provide an overview of the background signal suppression efficiency, we plotted in Fig. 7 the contrast factors against the build-up time. Each curve corresponds to the three distinct conditions described above: (i) conventional positive DNP, (ii) the MW-off data subtraction, and (iii) the Oops treatment. All the cases are displayed for the same total experimental time. Consistent with our observations described above, simply reducing the build-up time in the conventional positive DNP condition barely improves the contrast factor (blue data). In contrast, the Oops procedure improves the contrast factor at short τ (purple data), with C always being higher than that for MW-off subtraction (green). Both cases (ii) and (iii) show contrast factors that first increase with τ, and then decrease toward that for case (i), with a maximum at τ ≈ 100 s. These results are qualitatively explained by the hyperpolarization that does not propagate to the background space before reaching the maximum, whereas the target signal increases with increasing τ. After reaching the maximum, hyperpolarization propagates to the background space, which reduces the contrast. For the Oops treatment, the maximum contrast was C = 12.9, which is much higher than C = 6.91 for MW-off subtraction and C = 3.84 for the conventional DNP.
Shortening τ controls the target range, and the Oops procedure maximizes the contrast factor; however, this approach inevitably reduces the S/N ratio for the target signal if τ is shorter than the polarization build-up time constant. To investigate this point, we also plotted the unit-time S/N 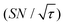 (dashed lines in Fig. 7). The nearly identical
(dashed lines in Fig. 7). The nearly identical 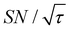 traces for cases (i) and (iii) show that the decrease in
traces for cases (i) and (iii) show that the decrease in 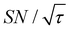 is not due to the Oops procedure per se. At τ = 60 s, where C is maximal, the
is not due to the Oops procedure per se. At τ = 60 s, where C is maximal, the 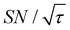 for the target (∼2.2) was approximately one-third of its maximum value (∼6.4) at τ = 5000 s. This result indicates that the background signal is suppressed at the expense of two-thirds of the unit-time sensitivity for the investigated micelle sample (purple) (other cases are examined in the Discussion). By contrast, with conventional DNP, shortening the diffusion time results in no significant contrast but simply loses the sensitivity for the target (blue).
for the target (∼2.2) was approximately one-third of its maximum value (∼6.4) at τ = 5000 s. This result indicates that the background signal is suppressed at the expense of two-thirds of the unit-time sensitivity for the investigated micelle sample (purple) (other cases are examined in the Discussion). By contrast, with conventional DNP, shortening the diffusion time results in no significant contrast but simply loses the sensitivity for the target (blue).
Analysis of the DNP build-up process
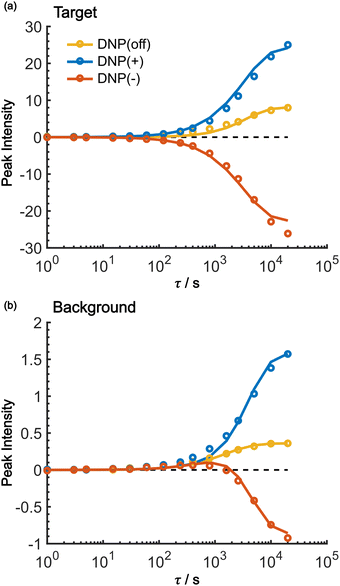
As shown in Fig. 7, the propagation of hyperpolarization into the not-of-interest/background region causes a decrease of the contrast factor. Therefore, the diffusion size should be carefully controlled to match the target to be selected. The size of the target region depends on the spin diffusion rate, diffusion time, and longitudinal spin relaxation rate. To understand more quantitatively how the polarization spreads in time and space, we built a classical one-dimensional spin diffusion model to fit the experimental polarization build-up curves (details of the model and its optimization are described in the ESI;† Fig. S4). Briefly, we consider in the model a thin polarization source region (x = (0, xS)) directly hyperpolarized by the PA (located at x = 0), which is followed by the target region (x = [xS, xT)) and then the background region (x = [xT, xB)); each region has distinct diffusion and relaxation rates. In the above experiments, xT corresponds to the micelle radius and xB corresponds to the midpoint between the micelles. The parameters in the model were optimized to fit the following six experimental build-up curves globally: build-up of the height of the target (peak 12) and background (peaks 6/7/8), each taken under the DNP-off, DNP(+), and DNP(−) conditions. As shown in Fig. 8, the fitting result closely matches the observed build-up dynamics. For example, for the background build-up in the DNP(−) condition (Fig. 8b, red), the intensity initially showed a small positive growth and then changed to a large negative growth. This subtle feature was also reproduced in the model. This feature is attributed to the initial relaxation-induced background polarization, which is subsequently overwhelmed by the negative hyperpolarization relayed from the micelles. The parameters obtained in the optimization are summarized and compared with the measured/estimated values in Table 1. All the values are close to the corresponding measured/estimated values, supporting the adequacy of the model.| Parameter | From fitting | Measured/estimated | Comment |
|---|---|---|---|
| a The larger relaxation rate for 13C spins outside the micelles is attributable to the large number of methyl groups in isooctane and butanol. | |||
| x S/nm | 1.84 | ∼3 | Estimated from the e-13C PRE distance |
| x T/nm | 6.43 | ∼7 | Micelle radius measured by DLS |
| x B/nm | 23.2 | ∼14 | Estimated from the micelle concentration |
| R 1,S/s−1 (RDNP) | 1.1 × 10−5 (9.1 × 104 s) | ND | — |
| R 1,T/s−1 | 1.3 × 10−4 (7.7 × 103 s) | 5 × 103 s | Measured from the MW-off build-up |
| R 1,B/s−1 | 6.5 × 10−4 (1.5 × 103 s) | 1.4 × 103 sa | Measured from the MW-off build-up |
| D T/nm2 s−1 | 0.011 | 0.01 | Estimated from literature values |
| M 0,S | 2650 | 2640 | Estimated from the gamma ratio γe/γC |
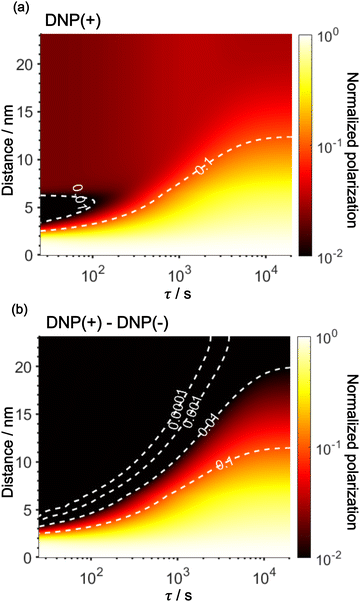
Using the parameters obtained in the model study described above, we reproduced the space-time dependence of the effective polarization around the PA (Fig. 9). In the plot, the polarization values were normalized by those at x = 0 for all τ to focus on the polarization spatial distribution. Fig. 9a and b shows the results for the standard positive DNP and after the Oops procedure, respectively. In both cases, the effective distribution of the hyperpolarization around the PA remains largely unaltered, whereas in the case of the Oops procedure (Fig. 9b), the relaxation-induced polarization outside the diffusion range is cleanly suppressed regardless of the τ chosen. Thus, the target region is now simply determined by the diffusion time τ. Consistent with the aforementioned experiments, at τ ≲ 100 s, the size of the target region is indeed restricted to within ∼3 nm from the PA, i.e., within the average radius of the micelle (with a ∼1% drop-off criterion from the polarization at x = 0; refer to the dashed line labeled “0.01”). In the other extreme, at τ > 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, a target region as large as 18 nm can be selected (Fig. 9b). With the ultra-low temperature used in the present work (37 K), the 13C longitudinal relaxation time typically exceeds ∼1000 s even for the isooctane/butanol matrix with a high density of methyl groups and supports this long-range selection.
000 s, a target region as large as 18 nm can be selected (Fig. 9b). With the ultra-low temperature used in the present work (37 K), the 13C longitudinal relaxation time typically exceeds ∼1000 s even for the isooctane/butanol matrix with a high density of methyl groups and supports this long-range selection.
Discussion
The effective space-time distribution of hyperpolarization obtained from the analysis of the micelle data (Fig. 9b) is not far from the result of an order-of-magnitude estimation based only on the typical 13C diffusion rate (from D = 0.01 nm2 s−1 and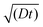 ): the hyperpolarization spreads to ∼1 nm at 100 s and ∼14 nm at 20
): the hyperpolarization spreads to ∼1 nm at 100 s and ∼14 nm at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s from the PA. Such a simple estimate can be useful in practical applications when choosing the diffusion time for target selection. When the sample's spectrum displays at least one distinguishable peak identifiable as the background signal, such as peaks of lipids or sugars separated from the target protein signals, τ can be empirically optimized in reference to the observability of these peaks. In addition, varying τ while monitoring the identity of the background signal would offer valuable information on the distance range for the background molecules from the PA. Note that it is impossible to obtain such information without the Oops treatment because, conventionally, relaxation-induced signals that have no distance dependence from the PA contaminate the observed spectrum.
000 s from the PA. Such a simple estimate can be useful in practical applications when choosing the diffusion time for target selection. When the sample's spectrum displays at least one distinguishable peak identifiable as the background signal, such as peaks of lipids or sugars separated from the target protein signals, τ can be empirically optimized in reference to the observability of these peaks. In addition, varying τ while monitoring the identity of the background signal would offer valuable information on the distance range for the background molecules from the PA. Note that it is impossible to obtain such information without the Oops treatment because, conventionally, relaxation-induced signals that have no distance dependence from the PA contaminate the observed spectrum.
Target selection by reducing the diffusion time comes at the expense of the S/N ratio for the target signal. In general, the smaller the target range, the greater the decrease in the S/N ratio. In our reverse-micelle case, where the selection of only a few nanometers from the PA was necessary, approximately two-thirds of 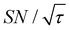 was lost compared with that when the target signal was fully built. However, the signal enhancement was on the order of 10 for the urea target in the reverse-micelle sample (Fig. 5b), and the cost might be acceptable, especially when selectivity is critical. We also note that the signals from the MAS rotor materials (e.g., 27Al in a sapphire rotor, 17O in a ZrO2 rotor, or 29Si in a Si3N4 rotor) can always be removed with the Oops treatment without adversely affecting the S/N ratio.
was lost compared with that when the target signal was fully built. However, the signal enhancement was on the order of 10 for the urea target in the reverse-micelle sample (Fig. 5b), and the cost might be acceptable, especially when selectivity is critical. We also note that the signals from the MAS rotor materials (e.g., 27Al in a sapphire rotor, 17O in a ZrO2 rotor, or 29Si in a Si3N4 rotor) can always be removed with the Oops treatment without adversely affecting the S/N ratio.
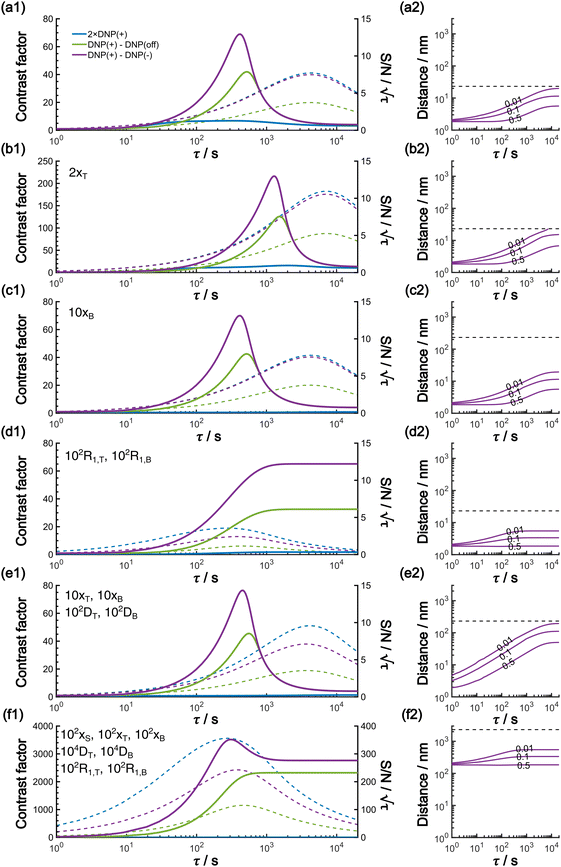
In this work, based on 13C spin diffusion, the method can potentially target molecules or moieties that are within ∼2 nm to ∼15 nm of the PA. This target range might enable individual molecular entities such as a protein fibril, a membrane protein assembly, or a thin functional layer on polymers/films to be targeted. To compare the performance of the Oops treatment in various other potential applications, we simulated the space–time dependence of the contrast factor (details are given in the ESI†) by altering some of the parameters used in the model we established above (Fig. 10a1–f1). The corresponding space–time distribution of the effective polarization is also shown in Fig. 10a2–f2; they are similar to Fig. 9, but only show the contour lines for simplicity. Fig. 10a shows the simulated dependence with the parameters optimized for the micelle sample with 13C diffusion, where the set of relevant parameters is 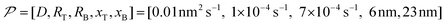 (Table 1). The space–time dependence qualitatively reproduced the experimental result in Fig. 7 despite a right-shifted maximum and generally overestimated C. This discrepancy most likely arises from the size distribution of the micelles because modeling the size distribution in the simulation improved the correspondence between Fig. 7 and 10a (see ESI;† Fig. S5). Given that we are interested in the effects of parameter changes, we will continue with this level of accuracy to examine other related cases in the following text.
(Table 1). The space–time dependence qualitatively reproduced the experimental result in Fig. 7 despite a right-shifted maximum and generally overestimated C. This discrepancy most likely arises from the size distribution of the micelles because modeling the size distribution in the simulation improved the correspondence between Fig. 7 and 10a (see ESI;† Fig. S5). Given that we are interested in the effects of parameter changes, we will continue with this level of accuracy to examine other related cases in the following text.
As previously mentioned, selecting a larger target is easier. Fig. 10b shows the case for 2xT (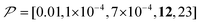 , the varied parameter is shown in bold). This corresponds, e.g., to a twice-larger target micelle or twice-thicker polymer coating. As expected, the maximum C occurs at a longer diffusion time because of the larger target. Also, the best contrast factor (C ≈ 220) and the corresponding unit-time sensitivity (
, the varied parameter is shown in bold). This corresponds, e.g., to a twice-larger target micelle or twice-thicker polymer coating. As expected, the maximum C occurs at a longer diffusion time because of the larger target. Also, the best contrast factor (C ≈ 220) and the corresponding unit-time sensitivity (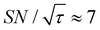 ) were approximately three and two times higher, respectively, than those shown in Fig. 10a (C ≈ 70 and
) were approximately three and two times higher, respectively, than those shown in Fig. 10a (C ≈ 70 and 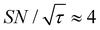 ). Only a ∼30% loss of the
). Only a ∼30% loss of the 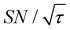 relative to the fully built target was required to maximize C.
relative to the fully built target was required to maximize C.
Fig. 10c shows a plot of the result for a larger background, 10xB (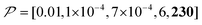 ). This scenario occurs, e.g., when the target proteins are diluted in a larger cell or a given surface coating is deposited onto a thicker base film. In this case, only the conventional positive DNP (blue) exhibited a substantially lower contrast factor; by contrast, the result was not affected by off-data subtraction (green) or the Oops treatment (purple). These results demonstrate that Oops background suppression maintains the best efficacy, which is, in principle, impervious to the size of the background. This result is reasonable because the effective space–time dependence of the hyperpolarization around the PA is nearly unaffected by the definition of the background size (Fig. 10a2–c2).
). This scenario occurs, e.g., when the target proteins are diluted in a larger cell or a given surface coating is deposited onto a thicker base film. In this case, only the conventional positive DNP (blue) exhibited a substantially lower contrast factor; by contrast, the result was not affected by off-data subtraction (green) or the Oops treatment (purple). These results demonstrate that Oops background suppression maintains the best efficacy, which is, in principle, impervious to the size of the background. This result is reasonable because the effective space–time dependence of the hyperpolarization around the PA is nearly unaffected by the definition of the background size (Fig. 10a2–c2).
The spin relaxation rate is a strong function of the type of nuclear species, molecular structure, temperature, and magnetic field strength, and is a major factor that changes the space–time dependence of the contrast factor. Fig. 10d shows results simulated for 100RT/B (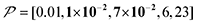 ). Because of the strong sinking effect of hyperpolarization, the S/N ratio of the target was reduced substantially. Interestingly, however, the contrast factor remained high, similar to the case in Fig. 10a, and reached a constant value at τ > 1000 s. This result is attributable to the rapid relaxation curtailing of the polarization propagation, thereby alleviating the leakage of polarization beyond xT = 6 nm. Indeed, the effective spatial distribution of polarization also remains constant at τ > 1000 s (Fig. 10d2), which is a manifestation of the intrinsic targeting set by the balance between the diffusion and relaxation rates. When the size of the target matches the intrinsic range, the longer-than-optimal diffusion time τ is not a concern; only a slow loss of
). Because of the strong sinking effect of hyperpolarization, the S/N ratio of the target was reduced substantially. Interestingly, however, the contrast factor remained high, similar to the case in Fig. 10a, and reached a constant value at τ > 1000 s. This result is attributable to the rapid relaxation curtailing of the polarization propagation, thereby alleviating the leakage of polarization beyond xT = 6 nm. Indeed, the effective spatial distribution of polarization also remains constant at τ > 1000 s (Fig. 10d2), which is a manifestation of the intrinsic targeting set by the balance between the diffusion and relaxation rates. When the size of the target matches the intrinsic range, the longer-than-optimal diffusion time τ is not a concern; only a slow loss of 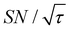 needs to be considered.
needs to be considered.
The spin diffusion rate also strongly varies depending on the nuclear spin species (gyromagnetic ratio) and its concentration. Slow spin diffusion among various low-γ nuclei (e.g., 31P, 6/7Li, 29Si, 113Cd, and 119Sn) has been used to show that the hyperpolarization can relay from the surface to the bulk supported by their long longitudinal relaxation time.35,36 In such cases, the spin diffusion rate was often on the order of D ≈ 1.0 nm2 s−1 or more under MAS, being at least ∼100-fold higher than our micelle sample (D ≈ 0.01 nm2 s−1), and the characteristic diffusion length was ∼100 nm.35,36Fig. 10e1 shows the results for 100D and 10xT/B (the size of the source region xS was fixed such that [1.0, 1e−4, 7e−4, 60, 230]). The behavior of the contrast factor is similar to that observed in Fig. 10a, which is understandable given that it should be invariant with a 10-fold scaling of the distance parameters xS, xT, xB (nm) together with a 100-fold scaling of the spin diffusion rate DT, DB (nm2 s−1). However, the plot in Fig. 10e2 reveals that the target range is substantially enlarged, reaching a maximum of ∼200 nm, which is consistent with the diffusion length observed for the impregnated solid particles.35,36 An advantage of the Oops technique is that it allows selective observation of the surface signals even when they overlap with those of the bulk matrix; in addition, the size of the observable target from the surface can be controlled between 5 and 200 nm in this example by varying the diffusion time. Furthermore, the observed surface signals are at least partly enhanced by DNP, in contrast to the previously reported “surface-only spectroscopy,” which relies on the observation of the two-spin order for the spatial selectivity, not on direct observation of the DNP-enhanced NMR signals.37
When the size of the target substantially exceeds ∼100 nm, the Oops technique combined with 1H spin diffusion might become useful either through direct 1H or 13C NMR through {1H}–13C cross-polarization (CP). Diffusion among high-γ spins (such as 1H and 19F) is generally characterized by a high diffusion rate as well as a high relaxation rate. For example, the typical 1H spin-diffusion rate in organic substances is approximately four to five orders of magnitude greater than that for 13C, and the relaxation time T1H is on the order of 10 s at 30 K. Fig. 10f shows the results for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000D, 100RT/B, and 100xS/T/B (
000D, 100RT/B, and 100xS/T/B (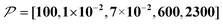 ). The behavior resembles that in Fig. 10d, where the contrast factor reaches a constant value at long diffusion times although the targeted space is ∼100-fold larger, becoming on the order of several hundred nanometers to 1 μm. This target range might be useful for selecting, e.g., whole-aggregation foci (∼0.5 μm) or nucleoli (∼1 μm) in eukaryotic cells (∼10 μm).
). The behavior resembles that in Fig. 10d, where the contrast factor reaches a constant value at long diffusion times although the targeted space is ∼100-fold larger, becoming on the order of several hundred nanometers to 1 μm. This target range might be useful for selecting, e.g., whole-aggregation foci (∼0.5 μm) or nucleoli (∼1 μm) in eukaryotic cells (∼10 μm).
The Oops background suppression can, in principle, be incorporated into multi-dimensional NMR experiments when the required τ is reasonably short relative to the total acquisition time. However, given the finite instrumental stability (such as the temperature, MAS rate, and MW output power), the interval between positive and negative DNP excitations should be as short as possible for the exact cancellation of the background signals. If the measurement is based on the 1H spin diffusion, this interval is of less concern; however, for the long low-γ spin diffusion, separately recorded two 2D datasets under DNP(+) and DNP(−) conditions for the subtraction would not be recommended. To address this issue, we propose a modified method that incorporates the Oops treatment directly in the polarization build-up time period (Fig. 11a). The positive and negative DNP are excited sequentially in a pulsed manner (with a duration τ0) with a 180° pulse on the nuclear spin placed in-between. In the target space next to the PA, hyperpolarization with opposite polarities is accumulated because of the polarization-inversion 180° pulse. By contrast, in the background space, the polarization arising from the spin relaxation is consistently saturated by a series of 180° pulses. The size of the target region is still determined by the total DNP build-up time τ. Fig. 11b and c show an example simulated using the parameters in Table 1 and with n = 7 and 20. As expected, the target intensity steadily increases with the polarization inversions, whereas the background intensity is gradually saturated (to less than ∼1% of the target). The efficacy of background suppression slightly improves with the number of repetitions n = τ/(2τ0) but does not show a large change (i.e., not sensitive to the choice of n). Implementing this polarization inversion in experiments, however, requires a frequency-agile microwave source. Our double-gyrotron setup is one possibility.38 We are also currently constructing a DNP spectrometer based on an amplifier–multiplier chain, whose frequency agility would be useful. This application will be a new and unique use of the frequency agility of a MW source; the results will be reported in forthcoming papers.
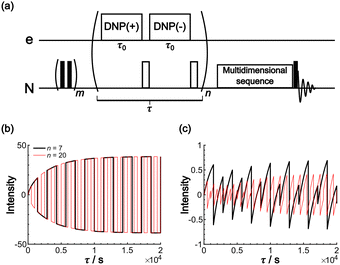 | ||
| Fig. 11 (a) Pulse sequence proposed for incorporating Oops background suppression in the polarization build-up time period. Each DNP block is carried out for τ0. The DNP(+), 180° and DNP(−), 180° pulses are repeated n times for a total time τ. The simulated build-up of the (b) target and (c) background signal intensity are shown. The signal intensity is simulated with the parameters in Table 1 and with n = 7 (black) and 20 (red). The target signal intensity is represented as the value at x = 0, and the background signal intensity is represented as the value at x = xB. | ||
Conclusion
We proposed a new method for background signal suppression, which takes the difference between positively and negatively DNP-enhanced NMR spectra to selectively enhance the target signals in the presence of substantial background signals. We refer to this method as the opposite polarity subtraction (Oops) DNP. This approach requires a method to deliver the PA in the vicinity of the target molecules. Methods using bio-orthogonal chemical reactions39 and signal peptides have been previously reported.20 To validate the efficacy of the method, we used a reverse-micelle sample that enabled the PA (OX063 trityl) and the target (urea) to be confined within the reverse micelles and the external isooctane matrix to be used as the background. The efficacy of background suppression was evaluated using a contrast factor, defined as the ratio of the absolute value of the integral of the target and background peaks.Three cases were compared in this study: (i) conventional positive DNP, (ii) the MW-off data subtraction, and (iii) the Oops procedure. A comparison of the results consisting of the time dependence of the contrast factors for these cases emphasizes that selecting an appropriate build-up time along with the Oops treatment is crucial for efficiently suppressing the background signal. In our demonstrative sample with an optimal build-up time of 60 s, our method achieved a contrast factor C = 12.9, which is much higher than C = 3.22 achieved with the conventional DNP and 0.56 with the MW-off data (i.e., regular MAS NMR). The maximum achievable contrast factor was also approximately twice as high as that of MW-off data subtraction (C = 6.91) because it can up to double the target signal intensity within the same total experiment time.
Simulations were conducted to gain deeper insight into the background signal suppression method and its possible applications. Using a classical diffusion model, the parameters were optimized to globally fit the simulated build-up for the experimental build-ups of the target and background signals recorded under MW-off, DNP(+), and DNP(−) conditions. The resultant parameters were in good agreement with theoretical predictions and other experimental measurements. The simulation of the effective spatial polarization distribution highlighted the spatial selectivity of our method with a certain DNP build-up time. Alterations of the parameters demonstrated the performance of the background signal suppression method under various scenarios. For instance, variations in the sizes of the background did not substantially affect the method's efficiency. A faster nuclear spin relaxation rate can suppress the reach of hyperpolarization in space, thereby facilitating the selection of an optimal build-up time to achieve the maximum contrast factor. Spin diffusion mediated by other types of nuclei, such as 1H, is much faster than that mediated by the 13C used in our sample. Faster spin diffusion would enable the targeted measurements to be applied to much larger molecular entities. To fully exploit the uniqueness of DNP-enhanced MAS NMR as a valid method for analyzing a complex mixture sample with high sensitivity, proper treatment of background signals from the not-of-interest region is a critical problem. The simple methods described here would provide a valid option for expanding the applicability of DNP MAS NMR for intracellular structural biology and other unexplored applications by reducing annoyance from backgrounds.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the JST Adaptable and Seamless Technology Transfer Program through Target-Driven R&D (A-STEP, JPMJTR204D) (K. K., H. T., Y. M.). This work was also partially supported by JST Program on Open Innovation Platform with Enterprises, Research Institute and Academia (OPERA) JPMJOP1861 and JEOL YOKOGUSHI Research Alliance Laboratories of Osaka University.References
- R. Novoa-Carballal, E. Fernandez-Megia, C. Jimenez and R. Riguera, Nat. Prod. Rep., 2011, 28, 78–98 RSC.
- R. R. Forseth and F. C. Schroeder, Curr. Opin. Chem. Biol., 2011, 15, 38–47 CrossRef CAS PubMed.
- Y. B. Patil, U. S. Toti, A. Khdair, L. Ma and J. Panyam, Biomaterials, 2009, 30, 859–866 CrossRef CAS PubMed.
- F. Blanc, M. Leskes and C. P. Grey, Acc. Chem. Res., 2013, 46, 1952–1963 CrossRef CAS PubMed.
- S. Chordia, S. Narasimhan, A. Lucini Paioni, M. Baldus and G. Roelfes, Angew. Chem., Int. Ed., 2021, 60, 5913–5920 CrossRef CAS PubMed.
- S. L. Speer, W. Zheng, X. Jiang, I.-T. Chu, A. J. Guseman, M. Liu, G. J. Pielak and C. Li, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2019918118 CrossRef CAS PubMed.
- D. Sakakibara, A. Sasaki, T. Ikeya, J. Hamatsu, T. Hanashima, M. Mishima, M. Yoshimasu, N. Hayashi, T. Mikawa, M. Wälchli, B. O. Smith, M. Shirakawa, P. Güntert and Y. Ito, Nature, 2009, 458, 102–105 CrossRef CAS PubMed.
- K. Inomata, A. Ohno, H. Tochio, S. Isogai, T. Tenno, I. Nakase, T. Takeuchi, S. Futaki, Y. Ito, H. Hiroaki and M. Shirakawa, Nature, 2009, 458, 106–109 CrossRef CAS PubMed.
- C. M. DeMott, S. Majumder, D. S. Burz, S. Reverdatto and A. Shekhtman, Biochemistry, 2017, 56, 4117–4126 CrossRef CAS PubMed.
- J.-X. Lu, W. Qiang, W.-M. Yau, C. D. Schwieters, S. C. Meredith and R. Tycko, Cell, 2013, 154, 1257–1268 CrossRef CAS PubMed.
- U. Dettmer, D. Selkoe and T. Bartels, Curr. Opin. Neurobiol., 2016, 36, 15–22 CrossRef CAS PubMed.
- J. A. Gerez, N. C. Prymaczok, H. Kadavath, D. Ghosh, M. Bütikofer, Y. Fleischmann, P. Güntert and R. Riek, Commun. Biol., 2022, 5, 1322 CrossRef CAS PubMed.
- Y. Zhang, Y. Gan, W. Zhao, X. Zhang, Y. Zhao, H. Xie and J. Yang, JACS Au, 2023, 3, 3412–3423 CrossRef CAS PubMed.
- A. S. Lilly Thankamony, J. J. Wittmann, M. Kaushik and B. Corzilius, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 102–103, 120–195 CrossRef CAS PubMed.
- A. C. Pinon, J. Schlagnitweit, P. Berruyer, A. J. Rossini, M. Lelli, E. Socie, M. Tang, T. Pham, A. Lesage, S. Schantz and L. Emsley, J. Phys. Chem. C, 2017, 121, 15993–16005 CrossRef CAS.
- J. Eills, D. Budker, S. Cavagnero, E. Y. Chekmenev, S. J. Elliott, S. Jannin, A. Lesage, J. Matysik, T. Meersmann, T. Prisner, J. A. Reimer, H. Yang and I. V. Koptyug, Chem. Rev., 2023, 123, 1417–1551 CrossRef CAS PubMed.
- T. Viennet, A. Viegas, A. Kuepper, S. Arens, V. Gelev, O. Petrov, T. N. Grossmann, H. Heise and M. Etzkorn, Angew. Chem., Int. Ed., 2016, 55, 10746–10750 CrossRef CAS PubMed.
- I. Marin-Montesinos, D. Goyard, E. Gillon, O. Renaudet, A. Imberty, S. Hediger and G. De Paëpe, Chem. Sci., 2019, 10, 3366–3374 RSC.
- D. Gauto, O. Dakhlaoui, I. Marin-Montesinos, S. Hediger and G. De Paëpe, Chem. Sci., 2021, 12, 6223–6237 RSC.
- B. J. Albert, C. Gao, E. L. Sesti, E. P. Saliba, N. Alaniva, F. J. Scott, S. T. Sigurdsson and A. B. Barnes, Biochemistry, 2018, 57, 4741–4746 CrossRef CAS PubMed.
- B. Tamamushi and N. Watanabe, Colloid Polym. Sci., 1980, 258, 174–178 CrossRef CAS.
- A. Suzuki and H. Yui, J. Colloid Interface Sci., 2015, 443, 188–196 CrossRef CAS PubMed.
- A. Leavesley, C. B. Wilson, M. Sherwin and S. Han, Phys. Chem. Chem. Phys., 2018, 20, 9897–9903 RSC.
- Y. Matsuki, S. Nakamura, S. Fukui, H. Suematsu and T. Fujiwara, J. Magn. Reson., 2015, 259, 76–81 CrossRef CAS PubMed.
- Y. Matsuki and T. Fujiwara, eMagRes, 2018, 7, 9–24 CAS.
- B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97–101 CrossRef CAS PubMed.
- M. Kotlarchyk, J. S. Huang and S. H. Chen, J. Phys. Chem., 1985, 89, 4382–4386 CrossRef CAS.
- L. P. Lindeman and J. Q. Adama, Anal. Chem., 1971, 43, 1245–1252 CrossRef CAS.
- A. Ejchart, Org. Magn. Reson., 1981, 15, 22–24 CrossRef CAS.
- X. Wang, B. G. Caulkins, G. Riviere, L. J. Mueller, F. Mentink-Vigier and J. R. Long, Solid State Nucl. Magn. Reson., 2019, 100, 85–91 CrossRef CAS PubMed.
- J. Clauss, K. Schmidt-Rohr and H. W. Spiess, Acta Polym., 1993, 44, 1–17 CrossRef CAS.
- Q. Chen and K. Schmidt-Rohr, Solid State Nucl. Magn. Reson., 2006, 29, 142–152 CrossRef CAS PubMed.
- M. Kaushik, T. Bahrenberg, T. V. Can, M. A. Caporini, R. Silvers, J. Heiliger, A. A. Smith, H. Schwalbe, R. G. Griffin and B. Corzilius, Phys. Chem. Chem. Phys., 2016, 18, 27205–27218 RSC.
- G. R. Khutsishvili, Phys.-Usp., 1965, 87, 211–254 CAS.
- S. Björgvinsdóttir, B. J. Walder, A. C. Pinon and L. Emsley, J. Am. Chem. Soc., 2018, 140, 7946–7951 CrossRef PubMed.
- S. Björgvinsdóttir, P. Moutzouri, P. Berruyer, M. A. Hope and L. Emsley, J. Phys. Chem. C, 2020, 124, 16524–16528 CrossRef.
- Y. Matsuki, T. Sugishita and T. Fujiwara, J. Phys. Chem. C, 2020, 124, 18609–18614 CrossRef CAS.
- Y. Matsuki, T. Idehara, J. Fukazawa and T. Fujiwara, J. Magn. Reson., 2016, 264, 107–115 CrossRef CAS PubMed.
- B. J. Lim, B. E. Ackermann and G. T. Debelouchina, ChemBioChem, 2020, 21, 1315–1319 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06280e |
| This journal is © the Owner Societies 2024 |