Open Access Article
Open Access ArticleDynamical effects on the O(3P) + D2 reaction and its impact on the Λ-doublet population
A.
Veselinova
 a,
M.
Menéndez
a,
M.
Menéndez
 b,
L.
González-Sánchez
b,
L.
González-Sánchez
 a,
A.
Zanchet
a,
A.
Zanchet
 c,
F. J.
Aoiz
c,
F. J.
Aoiz
 b and
P. G.
Jambrina
b and
P. G.
Jambrina
 *a
*a
aDepartamento de Química-Física, Universidad de Salamanca, Salamanca, 37008, Spain. E-mail: pjambrina@usal.es
bDepartamento de Química-Física, Universidad Complutense de Madrid, Madrid, 28040, Spain
cInstituto de Física Fundamental (CSIC), 28006, Madrid, Spain
First published on 18th January 2024
Abstract
The O(3P) + D2 → OD(2Π) + D reaction presents the peculiarity of taking place on two different potential energy surfaces (PESs) of different symmetry, 3A′ and 3A′′, which become degenerate for collinear configurations where the saddle-point of the reaction is located. The degeneracy is broken for non-collinear approaches with the energy on the 3A′ PES rising more abruptly with the bending angle, making the frequency of this mode higher on the 3A′ state. Consequently, the 3A′ PES should be less reactive than the 3A′′ one. Nevertheless, quantum scattering calculations show that the cross section is higher on the 3A′ PES for energies close to the classical reaction threshold and rotationless reactant. It is found that the differences between the reactivity on the two PESs are greater for low values of total angular momentum, where the centrifugal barrier is lower and contribute to the higher population of the Π(A′) Λ-doublet states of OD at low collision energies. At high collision energies, the Π(A′) Λ-doublet state is also preferentially populated. Analysis of the differential cross sections reveals that the preponderance for the Π(A′) Λ-doublet at low energies comes from backward scattering, originating from the reaction on the 3A′ PES, while at high energies, it proceeds from a different mechanism that leads to sideways scattering on the 3A′′ PES and that populates the Π(A′) manifold.
1 Introduction
The dynamics of the gas-phase reaction between atomic oxygen and molecular hydrogen has been widely studied experimentally1–4 and computationally5–18 due to its importance in combustion processes, the chemistry of the upper atmosphere, and the chemistry of the OH radical in the interstellar space. In combustion, it is important for chain branching and propagation during the combustion of hydrogen and hydrocarbons.19,20 In spite of being associated with a high activation barrier (∼0.6 eV),7,17 it is also one of the most important sources of OH in the mesosphere, where collisions between atomic oxygen and vibrationally excited H2 account for 4–19% of the OH produced.21 This reaction is also one of the major sources of OH in several astronomical environments,22–28 in particular in the photon-dominated regions and protoplanetary disks where H2 can be efficiently pumped to excited vibrational states. It is also one of the benchmark systems for kinetics, and their thermal rate coefficients have been measured using different techniques in a wide range of temperatures (see ref. 29 for a compilation). For the particular case of the reaction between O(3P) and D2, experimental rate coefficients have been obtained in ref. 30–34.The mechanism of the O(3P) + H2 → OH(2Π) + H reaction can be described as the simultaneous homolytic cleavage of the H–H bond and formation of a new O–H bond. The oxygen atom has four electrons distributed in three p orbitals (p4), such that in its electronic ground state it has two single and one double occupied valence p orbitals. At the reactant asymptote, before O and H2 begin to interact, there are three degenerate potential energy surfaces (PESs), one PES of 3A′ symmetry (where the two p single occupied orbitals of the oxygen atom lie on the three-atom plane), and two PESs of 3A′′ symmetry (in which one of the two singly occupied p orbitals is perpendicular to the three-atom plane). The formation of the O–H bond is only possible if one of the oxygen's singly occupied p orbitals points towards H2,35 which occurs on the 3A′ and one of the 3A′′ PESs, which are degenerate for collinear approaches, resulting from the Π character of the linear arrangement. The second 3A′′ PES represents the situation in which the doubly occupied p orbital points towards H2 and is therefore repulsive and cannot give rise to the reaction. At the product asymptote, the open-shell OH(2Π) molecule is formed, for which the rotational levels split into two spin–orbit states, and each of them splits into a pair of Λ-doublet levels. Λ-doublet states can be labelled as Π(A′) or Π(A′′) where the symmetry index indicates the location of the singly occupied orbital of OH with respect to the diatom rotation plane. The Λ-doublet pair of states is almost degenerate, but can be spectroscopically resolved due to different selection rules.
Ab initio calculations consistently predicted a collinear transition state7,17 and a barrier height that increases as the reactants’ approach moves away from collinear geometries. This effect is more pronounced on the 3A′ PES, resulting in a steeper bending potential and consequently a narrower cone of acceptance. The steeper bending potential on the 3A′ PES results in a higher vibrationally adiabatic potential (which includes the zero point energy) even though the electronic energy barrier is the same on the 3A′ and 3A′′ PESs. At high collision energies, Ecoll, the small difference in the adiabatic potentials is not relevant, but the narrower cone of acceptance leads to a lower reactivity on the 3A′ PES. All the characteristics of the PESs allow us to conclude that the reactivity should always be lower on the 3A′ PES than on the 3A′′ PES.
Although the symmetry of the Λ-doublet states is referred to the diatom rotation plane of the products, and the symmetry of the PESs refers to the three-atom plane, the analysis of the Λ-doublet relative populations provides information about the reactivity on the two PESs, which otherwise could not be extracted. By explicitly considering the reaction stereodynamics, we developed a method to calculate Λ-doublet populations from adiabatic Quantum Mechanics (QM) and quasiclassical trajectory (QCT) scattering calculations.16,36 This method was applied to the simulation and interpretation of the experiments by Minton, McKendrick and coworkers,3,4 who determined the OD(2Π) state-to-state Λ-double population ratio for O(3P) + D2 collisions using crossed molecular beams with hyperthermal atomic oxygen and detection by laser-induced fluorescence. They found a significantly higher population for the Π(A′) Λ-doublet state compared to Π(A′′) regardless of Ecoll, and final vibrational state. Our theoretical treatment showed that at hyperthermal energies, the propensity towards Π(A′) was caused by an additional mechanism on the 3A′′ PES which leads to a significant 3A′′ → Π(A′) population transfer.
Recently, we studied the O(3P) + H2 reaction in a wide range of collision energies from 0.2 eV (well below the electronic energy barrier) to 1.7 eV. QM and QCT calculations were performed on the PESs of ref. 17, which accurately reproduce the degeneracy of the collinear saddle point. Surprisingly, our results showed that although the 3A′′ PES is generally more reactive than the 3A′ PES, this is not the case for energies around the vibrationally adiabatic barrier, for which the 3A′ PES is slightly more reactive (up to a 10%) when H2 was in its ground rotational state. The prevalence of the 3A′ PES was found to have been caused by a reorientation effect, which diverts some of the incoming flux towards collinear approaches where the reactivity is higher. This effect is absent on the 3A′′ PES. At Ecoll below or near the barrier, this effect competes with tunnelling, which is favoured on the 3A′′ PES due to its narrower vibrationally adiabatic barrier. However, in a range of energies close to the barrier, the reorientation effect on the 3A′ PES overcomes tunnelling on the 3A′′ PES, and the cross section on the 3A′ PES is higher than on the 3A′′ PES. In this article, we study the reaction of O(3P) + D2. Our results show that the reorientation effect is magnified, which we attribute to a smaller contribution of tunnelling due to the higher reduced mass of D2 compared to H2. We predict that the preference for the 3A′ PES is more important for vibrationally excited D2 and this is even reflected as a sharp peak on the Π(A′) Λ-doublet populations.
The article is laid out as follows: in Section 2, QM and the QCT scattering calculations are briefly described, with particular emphasis on the calculation of Λ-doublet cross sections and quantum deflection functions; in Section 3, the results are presented and discussed. The last section contains the summary of this work and the conclusions.
2 Methodology
2.1 QM scattering calculations
Time-independent QM scattering calculations were carried out using the ABC code37 on the 3A′ and 3A′′ PESs, described in ref. 17. For the O(3P) + D2 reaction, calculations were carried out between 0.37 eV and 2.0 eV total energy, including all partial waves to convergence. The propagation was carried out in 300 log-derivative steps up to a maximum hyperradius, ρmax = 15a0. The maximum value of helicity was Ωmax = 30. Additional calculations were carried out to describe the behavior of O(3P) + D2 (v = 1) at low collision energies, below the adiabatic barrier. In these additional calculations, Ωmax = 15, and ρmax was set to 60a0 (in 2500 log-derivative steps). For the O(3P) + H2 (v = 1, j = 0) reaction, QM calculations were also carried out in the 0.01–1.71 eV collision energy range, using propagation in 300 log-derivative steps up to a ρmax = 15a0. The maximum value of helicity was Ωmax = 26. At the lowest collision energies, ρmax = 20a0 and Ωmax = 15.In this work, we will assume that the two states 3A′ and 3A′′, which are adiabatically correlated with the reactants and products, are uncoupled. Our calculations do not include the intersystem crossing (ISC) to the singlet 1A′ PES. In previous studies using QCT and surface hoping, it was found that for the O + H2 system, the singlet state crosses the two triplet states after the barrier on the products side. So even if some collisions sample the singlet PES, spin–orbit coupling has a relatively minor effect on the dynamics of the system at Ecoll above 0.4 eV while at energies near the threshold, the effect is negligible.8,38 Similar conclusions have been drawn in a QM non-adiabatic study.13 As for the Renner-Teller coupling between the 3A′ and 3A′′ PESs, neither is considered. It is expected that its effect would be more pronounced at high orbital angular momentum (impact parameters) values. Be that as it may, the fact that there is a very good agreement between experimental results and QM calculations seems to indicate that a description of the reaction in terms of the two separate triplet PESs can account for detailed aspects of this reaction.1,11
2.2 Quasiclassical trajectories
QCT trajectories were run using the procedure described in ref. 39 and 40. The excitation function was calculated by running batches of 107 trajectories for each D2 rovibrational state considered in this work. For each initial state, Ecoll was chosen randomly and uniformly between 0.45 (0.3 for v = 1) and 1.75 eV.39 The trajectories were started at an atom–diatom distance of 10 Å using an integration step of 3 × 10−17 s, which guarantees a total energy conservation better than one part in 105. For each collision energy, the maximum impact parameter, bmax(Ecoll), was previously determined by running a reduced number of trajectories at several energies. The absolute maximum value of the impact parameter in the whole range of collision energies was found to be 1.6 Å. The rovibrational energies of the OD diatom were calculated by semiclassical quantisation of action using the diatomic potential (which is the same on the two PESs), with their values fitted to Dunham expansions. The real v′ and j′ values were rounded to their nearest integer value. The procedure to assign the Λ-doublet state is detailed in Section 2.3.To describe the behavior near the classical energy threshold, we also calculated trajectories at fixed collision energies. Additional batches of 2 × 105–5 × 105 trajectories were run at 7 collision energies between Ecoll = 0.5 and 0.65 eV (0.3–0.45 eV for v = 1) on each of the two 3A′ and 3A′′ PESs.
2.3 Calculation of Λ-doublet cross sections
The calculation of the Λ-doublet cross sections from adiabatic QM or QCT calculations is carried out using the procedure described in ref. 16 and 36. It assumes that the reaction takes places independently on each of the PES, so that the state-to-state Λ-doublet integral cross sections are given by: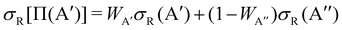 | (1) |
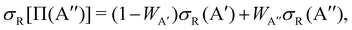 | (2) |
In ref. 16, it was demonstrated that WA′/A′′ can be calculated from the distribution of helicities, Ω′, and the projection of j′ on the products’ recoil direction, k′, can be determined using the expression:
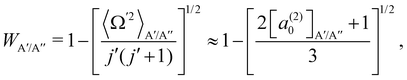 | (3) |
According to eqn (3), reactive flux from the 3A′ PES populates Π(A′) states (3A′ → Π(A′)), and reactive flux from the 3A′′ PES populates Π(A′′) states (3A′′ → Π(A′′)) if j′ is aligned perpendicular to k′. Similarly, 3A′ → Π(A′′) (3A′′ → Π(A′)) when k′ and j′ are parallel to each other. Neglecting the interference between the respective wave functions on the two PESs, it is also possible to define the Λ-doublet differential cross section (DCS), which is related to the DCS calculated on each of the PESs as:
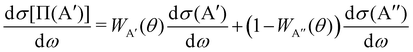 | (4) |
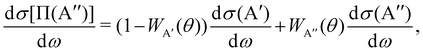 | (5) |
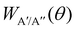 depend on the scattering angle, and can be calculated from the product Polarization-Dependent Differential Cross Sections (PDDCS) S(2)0(θ) as:
depend on the scattering angle, and can be calculated from the product Polarization-Dependent Differential Cross Sections (PDDCS) S(2)0(θ) as: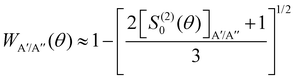 | (6) |
2.4 Generalized quantum deflection functions
To shed light into the concurrent reaction mechanisms, it is useful to calculate the Generalized Quantum Deflection Functions (GDFs or Qr(θ, J)), which are defined as the joint quasi-probability density function of J and θ. Analysis of the GDFs makes possible to plot a J−θ map in which the mechanisms (and their interference) can be seen in different regions of the map. The GDF is defined as:44,45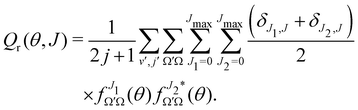 | (7) |
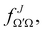 the J-dependent scattering amplitude, is defined as:
the J-dependent scattering amplitude, is defined as: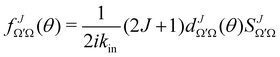 | (8) |
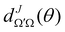 is the Wigner reduced rotation matrix element, kin is the reactant's relative wavenumber, and
is the Wigner reduced rotation matrix element, kin is the reactant's relative wavenumber, and 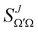 is an element of the scattering matrix, in which the indices related to the initial and final rovibrational states are omitted for the sake of simplicity. Please note that the GDF defined in eqn (7) includes the sum over the final states of the products and it is not multiplied by sin
is an element of the scattering matrix, in which the indices related to the initial and final rovibrational states are omitted for the sake of simplicity. Please note that the GDF defined in eqn (7) includes the sum over the final states of the products and it is not multiplied by sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ to better appreciate scattering at 0° and 180°.
θ to better appreciate scattering at 0° and 180°.
Unlike the DCS, the GDFs can take positive or negative values (which indicate destructive interference). The latter, however, are expected to be important only if state-to-state GDFs are calculated, as they will be probably washed out by the incoherent sum over final rovibrational states.
By analogy, it is possible to calculate the Λ-doublet resolved GDF, as:
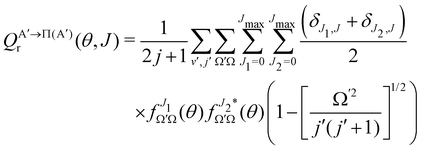 | (9) |
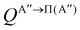 if the J-dependent scattering amplitudes were obtained from calculations on the 3A′′ PES. Analogously,
if the J-dependent scattering amplitudes were obtained from calculations on the 3A′′ PES. Analogously,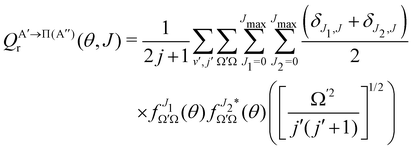 | (10) |
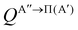 ) if they are obtained from calculations on the 3A′′ PES.
) if they are obtained from calculations on the 3A′′ PES.
3 Results and discussion
Panel (a) of Fig. 1 shows the QM excitation function, σR(Ecoll), representing the reactive cross section as a function of Ecoll, for the O(3P) + D2 (v = 0, j = 0) reaction calculated on the two PESs. The respective excitation functions calculated using QCT (not shown here) are in good agreement except near the threshold as classical trajectories cannot reproduce tunnelling. The σR(Ecoll) rises monotonically with increasing Ecoll, as it is expected for a direct reaction featuring an electronic barrier. This behavior was also observed for the O(3P) + H2 reaction.10,11,17,18 In the inset, it could be seen how the present calculations include the deep-tunneling region, with cross sections as low as 10−12 Å2. At these low energies, the 3A′′ PES is more reactive, as expected due to its lower and slightly narrower vibrational adiabatic barrier. The 3A′′ PES is also significantly more reactive for Ecoll > 0.9 eV, a consequence of the broader cone-of-acceptance. The cross-sections resolved in the two Λ-doublet manifolds are shown in panel (b). As it was observed experimentally,3,4 the Π(A′) manifold is more populated, in contrast to what could be expected if 3A′′ → Π(A′′). The relative σR(Ecoll) values calculated as σR(A′)/σR(A′′) are shown in panel (c). As it was observed in the inset of panel (a), the 3A′′ PES is more reactive than the 3A′ PES in the tunneling region, especially at the lowest energies where differences in the adiabatic barrier have a stronger effect on the dynamics. However, in the 0.5–0.8 eV Ecoll range, around the classical barrier, the 3A′ PES is up to 32% more reactive than the 3A′′ PES. For Ecoll > 0.8 eV, the 3A′′ PES is again more reactive, reaching the σR(A′)/σR(A′′) ratio a value of 0.75. | ||
| Fig. 1 (a) QM excitation function summed over final states for the O(3P) + D2 (v = 0, j = 0) reaction on the 3A′ (red) and 3A′′ PES (blue). The inset represents the excitation function for low Ecoll in the logarithm scale. (b) QM excitation function resolved in the two Λ-doublet manifolds: Π(A′) (dark green) and Π(A′′) (purple). (c) Ratio between the QM cross sections on the 3A′ and 3A′′ PES as a function of Ecoll. QCT results are shown as the dashed grey lines. (d) Ratio between the QM cross sections resolved in the two Λ-doublet manifolds. Results for Ecoll = 0.41 eV, 0.6 eV, 1.0 eV, and 1.6 eV, for which P(J) and DCS are shown in Fig. 2 and/or Fig. 3 and 4 are highlighted. | ||
Based only on the shape of the PESs, it is not obvious why 3A′ should be more reactive than 3A′′ in a particular range of Ecoll. Moreover, the QCT results also predict that close to the classical threshold, the 3A′ PES is significantly more reactive, ruling out the hypothesis that the higher 3A′ reactivity is a consequence of a quantum effect such as a resonance. A similar effect was observed for the O(3P) + H2 reaction, although in this case, σR(A′) was never more than 15% higher than σR(A′′).18 Through the analysis of QCT trajectories for the O(3P) + H2 reaction, we found that the higher reactivity on the 3A′ PES is a consequence of non-collinear trajectories, hitting the strong repulsive walls of the 3A′ potential and being reoriented towards collinearity, for which the barrier is smaller and could lead to the reaction. Below the vibrationally adiabatic barrier, this effect competes with tunnelling, which is more important for the 3A′′ PES, so that the 3A′ PES is only more reactive in the vicinity of the classical barrier, where the non-tunneling reaction is also possible. There is no tunneling in the QCT calculations, so for energies just above the classical barrier, the reorientation pathway is the only possible option, explaining the higher reactivity on the 3A′ PES. With increasing Ecoll, the effect of the wider cone of acceptance of the 3A′′ PES dominates over the reorientation effect and the 3A′′ PES becomes more reactive again. The present results for O(3P) + D2 (v = 0, j = 0) confirm this hypothesis. For O(3P) + D2, the tunneling contribution, which favours the reactivity on the 3A′′ PES, is less important for D2 due to its larger reduced mass and to the broader adiabatic barrier. As a consequence, the reorientation effect will be more important for D2 than for H2, leading to a higher relative reactivity of the 3A′ state compared to the 3A′′ state, which can exceed 30% (compared to 15% in the case of H2). As we will see later, this effect has strong implications on the prevalence of Π(A′) states for this isotopic variant. As shown in panel (d) of Fig. 1, the Π(A′) manifold is more populated than the Π(A′′) states for Ecoll ≥ 0.3 eV.
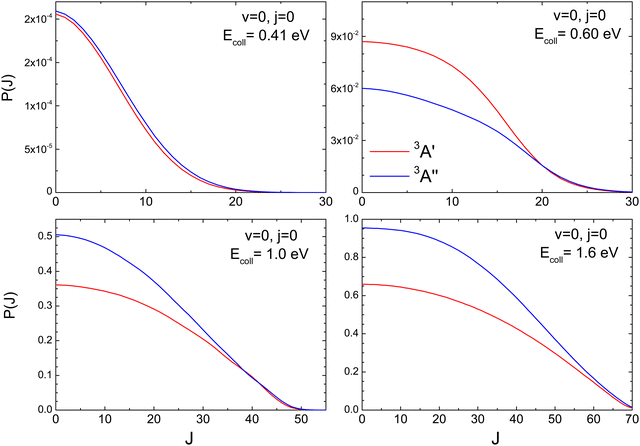
To better understand the existence of an energy range in which the 3A′ PES is more reactive, we show in Fig. 2 the QM total reaction probability as a function of the total angular momentum, P(J), calculated at four Ecoll; namely, at 0.41 eV, well below the classical barrier and where the reactivity is mediated by tunnelling; at 0.6 eV, where 3A′ is more reactive; and at 1.0 eV and 1.6 eV, where 3A′′ is again more reactive. For Ecoll = 0.41 eV, P(J) shows the typical shape of a direct reaction: it peaks at J = 0 and decreases slowly with increasing J due to the effect of the centrifugal barrier. The reaction probability for the two PESs is very similar, with the 3A′′ being more reactive for all but the largest Js, where the value of the P(J) is negligible.
At Ecoll = 0.6 eV, the shape of the P(J) is similar, showing a plateau for the lowest J and decreasing with increasing J. However, we observe a clear preference for the 3A′ PES at low Js, while at high J, both P(J) converge. In fact, while the 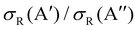 ratio reaches a maximum value of 1.32, the ratio of
ratio reaches a maximum value of 1.32, the ratio of 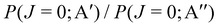 reaches a maximum value of 1.62. With increasing Ecoll (to 1.0 and 1.6 eV), the shape of the P(J) does not change, and differences between 3A′ and 3A′′ PESs are also more important at low J, although in this case the 3A′′ PES is more reactive. Regardless of the energy, we observe that the difference in reactivity between the two PESs cannot be attributed to the effect of the centrifugal barrier, which becomes more important at the highest J.
reaches a maximum value of 1.62. With increasing Ecoll (to 1.0 and 1.6 eV), the shape of the P(J) does not change, and differences between 3A′ and 3A′′ PESs are also more important at low J, although in this case the 3A′′ PES is more reactive. Regardless of the energy, we observe that the difference in reactivity between the two PESs cannot be attributed to the effect of the centrifugal barrier, which becomes more important at the highest J.
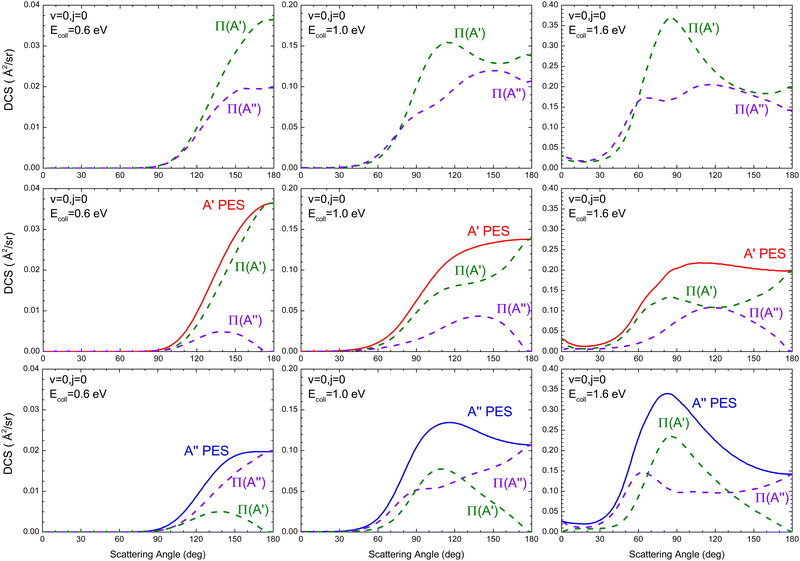
The DCSs resolved in the Π(A′) and Π(A′′) Λ-doublet manifolds at Ecoll = 0.6 eV, 1.0 eV, and 1.6 eV are shown in Fig. 3, where we also show the DCS obtained only on the 3A′ PES (middle panels) and on the 3A′′ PES (lower panels). Results for Ecoll = 0.41 eV are not shown because of their small value of the cross sections.
At 0.6 eV, the shape of the Π(A′) and Π(A′′) DCS is similar, both showing a clear preference for backward scattering. This behaviour at low energies suggests the existence of a direct abstraction mechanism, similar to the so-called the spiral mechanism in ref. 46, where there is a correlation between low J and extreme backward angles.44 At Ecoll = 0.6 eV, it is found that σR(Π(A′)) is larger than σR(Π(A′′)), and the DCS shows that this preponderance is due to the flux scattered at backward angles, θ = 130–180°, where the Π(A′) Λ-doublet state is preferentially produced. In order to understand the origin of this preponderance, we have analyzed the flux leading to Π(A′) and Π(A′′) on the two PESs. We found that Π(A′) OD states are preferentially populated on the 3A′ PES, while a higher population is observed for the Π(A′′) states on the 3A′′ PES. Furthermore, the conversion 3A′ → Π(A′′) (the amount of flux from 3A′ leading to Π(A′′) OD states) is similar to 3A′′ → Π(A′). Thus the overall preference for the Π(A′) is due to the higher reactivity on the 3A′ PES, which is due to the reorientation effect.
At Ecoll = 1.0 eV, the Π(A′) DCS is larger for θ > 80°, the region which accounts for most of the reactive flux. The analysis of the fluxes leading to Π(A′) and Π(A′′) on the two PESs shows that in this case, it is a consequence of a higher 3A′′ → Π(A′) contribution, which is mainly responsible for scattering at sideways angles (≈100°). One might wonder whether the sideways bump in the DCS on the 3A′′ PES could be caused by a higher contribution from higher Js. However, P(J) at high J is similar on both PESs, ruling out this possibility. With increasing energy, Ecoll = 1.6 eV, the shape of the Π(A′) and Π(A′′) is very different, with the former featuring a relatively sharp sideways peak, due to the 3A′′ → Π(A′) contribution. This peak has the same origin as the bump observed at 1.0 eV, and it is not observed on the 3A′ PES, not even at 1.6 eV. Outside the sideways region, the reactivity leading to Π(A′) and Π(A′′) Λ-doublet states is similar. In ref. 16, we attributed the preference for Π(A′) states at high Ecoll to the existence of one additional mechanism on the 3A′′ PES that produces Π(A′) states. The DCS calculated here confirms this hypothesis. It is another mechanism that ultimately causes that Π(A′) to be more populated at high energies, as has been observed experimentally.
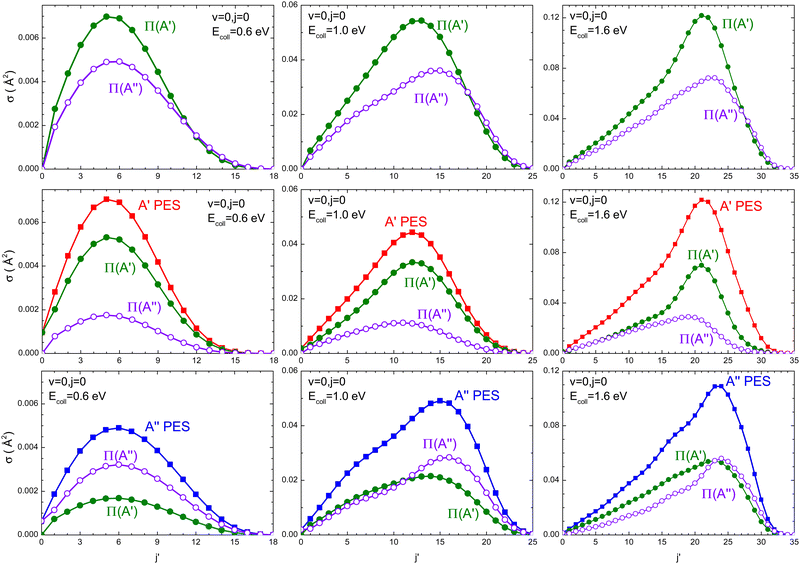
Regardless of the Ecoll and the PES considered, most of the OD is originated in its vibrational ground state (v′ = 0). To gain more insight into the mechanisms, Fig. 4 shows the rotational distribution (cross section as a function of j′) for v′ = 0 resolved in the Λ-doublet at the three energies for which the DCSs were also calculated. Independent of Ecoll, the overall preference for Π(A′) states is higher for medium to high values of j′, especially at Ecoll = 1.6 eV. When we analyzed the population of the Λ-doublet states obtained from the 3A′ PES, we found that the population of Π(A′) states is always higher, especially for high j′ values. Mechanistically, this means that j′ is preferentially aligned perpendicular to k′. On the 3A′′ PES, in turn, at Ecoll = 0.6 eV, the population on the Π(A′′) is larger, but with increasing Ecoll, Π(A′) dominates, especially for low j′. Mechanistically, this means that at low Ecoll, j′ is preferentially aligned perpendicular to k′ (as on the 3A′ PES), but with increasing Ecoll, j′ is preferentially aligned along k′, suggesting the existence of an additional mechanism on the 3A′′ PES at high Ecoll.
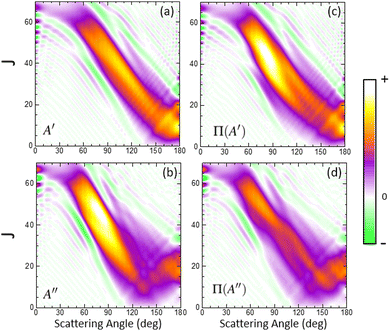
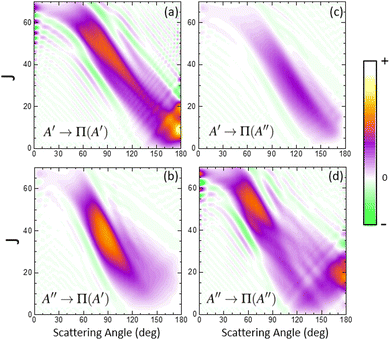
In order to characterize this reaction mechanism, we have calculated the GDFs at 1.6 eV on the 3A′ and 3A′′ PES, which are depicted in panels (a) and (b) of Fig. 5. On the 3A′ PES, we observe a broad band diagonally across the θ−J map with a negative slope, which is similar to the mechanism in which low Js correlate with extreme backward angles (spiral).46 The GDF on the 3A′′ PES shows two main bands: a broad one with a negative slope (as on the 3A′ PES), which has a maximum at J = 45 and θ = 70° and results in the sideways maximum observed on the DCS (Fig. 3), and a narrower band with a positive slope running from θ = 120° to 180° and J = 0–20. Fig. 5 also shows the GDF corresponding to the reaction leading to the Π(A′) (panel (c)) and Π(A′′) (panel (d)) Λ-doublet states. The shapes are similar to those on the 3A′ and 3A′′ PES, although that of Π(A′) is more intense in the sideways region at the expense of the Π(A′′) GDF.
When the contribution from 3A′ to Π(A′) is singled out (see Fig. 6(a)), two regions where the GDF reaches a maximum value can be observed. The first, at θ ≈ 180°, is identical to that found on the 3A′ PES, and the other at θ ≈ 70°, J = 35 ± 10. The GDF showing the 3A′′ → Π(A′′) contribution (panel (c)) is rather faint, appearing as a background signal to the GDF observed on the 3A′ PES. The GDF for the 3A′′ → Π(A′) contribution shows a single maximum at (θ = 80°, J = 20–55), which includes most of the signal observed on the 3A′′ PES in this region. The 3A′′ → Π(A′′) contribution to the GDF presents two maxima that are connected through a region with small values of the GDF. Mechanistically, 3A′′ → Π(A′′) and 3A′ → Π(A′) correspond to flux in which j′ is preferentially aligned perpendicular to k′, while 3A′′ → Π(A′) and 3A′ → Π(A′′) mean that j′ is preferentially aligned along k′. From our results, we conclude that the latter are responsible for the Π(A′) preponderance, in particular the strong maximum for 3A′′ → Π(A′).
Overall, our results conclude that at high Ecoll, the preference from Π(A′) states comes from an additional mechanism on the 3A′′ PES, which occurs for moderate to high values of J (J ∼ 35 at Ecoll = 1.6 eV), where OD nascent molecules are scattered in the sideways region with their rotational angular momentum aligned perpendicular to the recoil direction.
In our previous calculations for O(3P) + H2, we observed that the H2 rotational excitation suppresses the reorientation effect, so that the 3A′ PES is no more reactive than the 3A′′ PES, and the 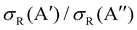 ratio did not show a maximum near the classical barrier.
ratio did not show a maximum near the classical barrier. 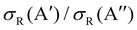 ratio calculations for O(3P) + D2 (v = 0, j = 2) (Fig. 7) show that while the ratio in QM calculations never exceeds one, a maximum can be observed at energies around the classical barrier, where the values of cross-sections on the 3A′ and 3A′′ PES are very similar. Therefore, the suppression of the reorientation effect is not complete and, in fact, for the QCT calculation, the 3A′ PES is slightly more reactive at energies just above the energy treshold. These differences are reflected in the propensity for Π(A′) states, a phenomenon only observed for Ecoll > 0.55 eV. Outside the classical barrier region, the results are very similar to those for D2 (j = 0), and 3A′′ is more reactive due to the broadening of the cone of acceptance.
ratio calculations for O(3P) + D2 (v = 0, j = 2) (Fig. 7) show that while the ratio in QM calculations never exceeds one, a maximum can be observed at energies around the classical barrier, where the values of cross-sections on the 3A′ and 3A′′ PES are very similar. Therefore, the suppression of the reorientation effect is not complete and, in fact, for the QCT calculation, the 3A′ PES is slightly more reactive at energies just above the energy treshold. These differences are reflected in the propensity for Π(A′) states, a phenomenon only observed for Ecoll > 0.55 eV. Outside the classical barrier region, the results are very similar to those for D2 (j = 0), and 3A′′ is more reactive due to the broadening of the cone of acceptance.
 | ||
| Fig. 7 Same as Fig. 1 but for the O(3P) + D2 (v = 0, j = 2) reaction. | ||
As it was mentioned in the introduction, collisions between O(3P) and vibrationally excited H2 play an important role in the formation of OH in the upper atmosphere or in the photon-dominated region of the interstellar space.21,27 Accordingly, we have also studied the reaction of O(3P) + D2 (v = 1, j = 0). The results shown in Fig. 8 are similar to those obtained for D2 (v = 0, j = 0), although all the features appear at lower Ecoll, as a consequence of lowering of the adiabatic barriers with the vibrational excitation of the reactants. For v = 1, the maximum of the 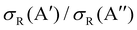 ratio is slightly higher than for v = 0, and our calculations show that this is also due to the higher reactivity on the 3A′ PES at low J (results not shown). In fact, when only the J = 0 partial wave is considered, the maximum value of the ratio is slightly above 1.8. The sharp maximum in the
ratio is slightly higher than for v = 0, and our calculations show that this is also due to the higher reactivity on the 3A′ PES at low J (results not shown). In fact, when only the J = 0 partial wave is considered, the maximum value of the ratio is slightly above 1.8. The sharp maximum in the 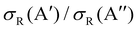 ratio is reflected in the
ratio is reflected in the 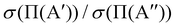 ratio, which also shows a peak at energies around the classical barrier.
ratio, which also shows a peak at energies around the classical barrier.
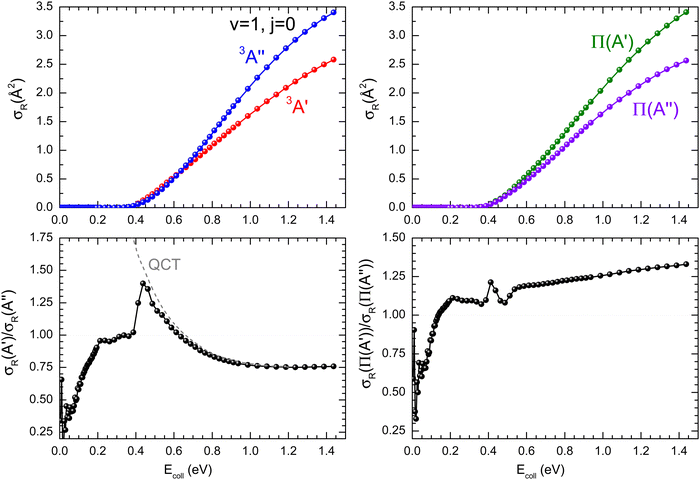 | ||
| Fig. 8 Same as Fig. 1 but for the O(3P) + D2 (v = 1, j = 0) reaction. | ||
Differences in the 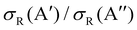 ratios for the different rovibrational states as well as for the two isotopic variants are shown in Fig. 9. While at high Ecoll, the ratios converge to the same value (≈0.75), and the differences between the O(3P) + H2/D2 reactions are important close to their classical barrier. First, the energy range in which 3A′ is more reactive is broader for the reaction with D2, which also shows a more positive
ratios for the different rovibrational states as well as for the two isotopic variants are shown in Fig. 9. While at high Ecoll, the ratios converge to the same value (≈0.75), and the differences between the O(3P) + H2/D2 reactions are important close to their classical barrier. First, the energy range in which 3A′ is more reactive is broader for the reaction with D2, which also shows a more positive 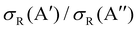 ratio. This is a consequence of more efficient tunnelling in the collision with H2, which partly compensates for the reorientation effect. Since for D2, this contribution is smaller, the reorientation effect will be more pronounced. Second, while the rotational excitation suppresses the aforementioned maximum for collisions with H2, this maximum is not completely washed out for D2 (j = 2) although it is not sufficient to make the 3A′ PES more reactive.
ratio. This is a consequence of more efficient tunnelling in the collision with H2, which partly compensates for the reorientation effect. Since for D2, this contribution is smaller, the reorientation effect will be more pronounced. Second, while the rotational excitation suppresses the aforementioned maximum for collisions with H2, this maximum is not completely washed out for D2 (j = 2) although it is not sufficient to make the 3A′ PES more reactive.
 | ||
| Fig. 9 Comparison of the ratios of the QM cross sections on the 3A′ and 3A′′ PES as a function of Ecoll for the O(3P) + D2(v,j) (left panel) and O(3P) + H2(v,j) reactions (right panel). | ||
4 Conclusions
We have studied the dynamics of the O(3P) + D2 reaction using time-independent QM scattering calculations over a wide range of collision energies, ranging from the deep tunnelling region, where the reactivity is very low, due to the high electronic barrier, to relatively high collision energies, where the collision energy is significantly higher than the electronic barrier and the cone of acceptance becomes wider. The reaction can take place on two potential energy surfaces (PESs) of symmetries 3A′ and 3A′′, both of which are degenerate at the saddle point. The former exhibits a higher and wider vibrationally adiabatic barrier due to the higher bending frequency at the transition state. Based on the shape of the PESs, one would expect that the 3A′′ PES, with a less stiff bending potential, should be more reactive at all energies. However, this is not the case at energies close to the classical barrier, where the 3A′ PES becomes significantly more reactive (up to a 32%). We attribute the higher reactivity on the 3A′ PES to a reorientation effect, which diverts incoming flux towards collinear approaches where the barrier is lower and hence the reactivity is higher. This effect competes with tunnelling across the vibrationally adiabatic barrier. Since tunnelling below the barrier is much lower for the O(3P) + D2 reaction than for the O(3P) + H2 reaction, the importance of the reorientation effect is higher for the former reaction. With increasing collision energy, both tunnelling and reorientation become less important, and the reactivity on the 3A′′ PES, with a wider cone of acceptance, is significantly higher than on the 3A′ PES.Our calculations show that for collision energies above the deep tunneling region, the OD(2Π) produced by the reaction preferentially populates the Π(A′) manifold. This is a consequence of two effects: (i) at energies around the classical barrier, most of the reactivity on the 3A′ (3A′′) PES produces Π(A′) (Π(A′′)) OD, so the higher reactivity on the 3A′ PES leads to the higher Π(A′) population; (ii) with the increasing collision energy, the 3A′′ PES becomes more reactive, but the presence of an additional mechanism on the 3A′′ PES leads to the higher population on the Π(A′) states. Analysis of the generalized deflection function showed that this mechanism is associated with relatively high partial waves giving rise to sideways scattering. The rotational excitation of D2 partially suppresses the reorientation effect, ultimately leading to a preference for Π(A′′) states at energies around the classical barrier. From relatively high collision energies, the QCT calculations of the ratio of the cross sections calculated on the 3A′ and 3A′′ PESs are in good agreement with the results from QM calculations, suggesting that the new mechanism on the 3A′′ PES has a classical origin. At low collision energies, the QCT method fails to reproduce the QM ratio of the cross sections calculated on the 3A′ and 3A′′ PESs and predicts higher reactivity on the 3A′ PES. This is due to the absence of tunneling in classical trajectories, so that at very low collision energies, only the reorientation effect is important in QCT trajectories.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge grant PID2020-113147GA-I00, PID2021-122839NB-I00, PID2019-107115GB-C21 and PID2021-122549NB-C21 funded by Spanish Ministry of Science and Innovation (MCIN/AEI/10.13039/MCIN/AEI/10.13039/501100011033).Notes and references
- D. J. Garton, T. K. Minton, B. Maiti, D. Troya and G. C. Schatz, J. Chem. Phys., 2003, 118, 1585–1588 CrossRef CAS
.
- D. J. Garton, A. L. Brunsvold, T. K. Minton, D. Troya, B. Maiti and G. C. Schatz, J. Phys. Chem. A, 2006, 110, 1327–1341 CrossRef CAS PubMed
.
- S. A. Lahankar, J. Zhang, K. G. McKendrick and T. K. Minton, Nat. Chem., 2013, 5, 315 CrossRef CAS
.
- S. A. Lahankar, J. Zhang, T. K. Minton and K. G. McKendrick, J. Am. Chem. Soc., 2014, 136, 12371–12384 CrossRef CAS PubMed
.
- J. M. Bowman, Chem. Phys. Lett., 1987, 141, 545 CrossRef CAS
.
- D. C. Chatfield, R. S. Friedman, G. C. Lynch, D. G. Truhlar and D. W. Schwenke, J. Chem. Phys., 1993, 98, 342 CrossRef CAS
.
- D. Rogers, A. Kuppermann and S. Walsh, J. Phys. Chem. A, 2000, 104, 2308 CrossRef
.
- M. R. Hoffmann and G. C. Schatz, J. Chem. Phys., 2000, 113, 9456 CrossRef CAS
.
- J. Han, X. Chen and B. R. Weiner, Chem. Phys. Lett., 2000, 332, 243 CrossRef CAS
.
- N. Balakrishnan, J. Chem. Phys., 2003, 119, 195–199 CrossRef CAS
.
- N. Balakrishnan, J. Chem. Phys., 2004, 121, 6346–6352 CrossRef CAS PubMed
.
- P. F. Weck, N. Balakrishnan, J. Brandao, C. Rosa and W. Wang, J. Chem. Phys., 2006, 124, 074308 CrossRef CAS PubMed
.
- J. Zhao, J. Chem. Phys., 2013, 138, 134309 CrossRef PubMed
.
- J. Brandao, W. Wang and C. M. A. Rio, Univ. J. Chem., 2015, 3, 80 Search PubMed
.
- P.-Y. Zhang and S.-J. Lv, Commun. Comput. Chem., 2013, 1, 63 CrossRef
.
- P. G. Jambrina, A. Zanchet, J. Aldegunde, M. Brouard and F. J. Aoiz, Nat. Commun., 2016, 7, 13439 CrossRef CAS PubMed
.
- A. Zanchet, M. Menéndez, P. G. Jambrina and F. J. Aoiz, J. Chem. Phys., 2019, 151, 094307(1-10) CrossRef PubMed
.
- P. G. Jambrina, A. Zanchet, M. Menéndez, V. J. Herrero and F. J. Aoiz, Phys. Chem. Chem. Phys., 2019, 21, 25389–25396 RSC
.
- W. Tsang and R. F. Hampson, J. Phys. Chem. Ref. Data, 1986, 15, 1087 CrossRef CAS
.
-
I. Glassman and R. A. Yetter, Combustion, Academic Press, 2008 Search PubMed
.
- L. M. Reynard and D. J. Donaldson, Geophys. Res. Lett., 2001, 28, 2157 CrossRef CAS
.
- M. M. Graff and A. Dalgarno, Astrophys. J., 1987, 317, 432 CrossRef CAS
.
- M. Agundez, J. Cernicharo and J. Goicoechea, Astron. Astrophys., 2008, 483, 831 CrossRef CAS
.
- D. Fedele, S. Bruderer, E. F. van Dishoeck, J. Carr, G. J. Herczeg, C. Salyk, N. J. Evans, J. Bouwman, G. Meeus, T. Henning, J. Green, J. R. Najita and M. Güdel, A & A, 2013, 559, A77 Search PubMed
.
- B. Godard, E. Falgarone and G. Pineau des Forêts, A & A, 2014, 570, A27 Search PubMed
.
- J. R. Goicoechea, L. Chavarra, J. Cernicharo, D. A. Neufeld, R. Vavrek, E. A. Bergin, S. Cuadrado, P. Encrenaz, M. Etxaluze, G. J. Melnick and E. Polehampton, ApJ, 2015, 799, 102 CrossRef
.
- A. Veselinova, M. Agúndez, J. R. Goicoechea, M. Menéndez, Z. Zanchet, E. Verdasco, P. G. Jambrina and F. J. Aoiz, A & A, 2021, 648, A76 Search PubMed
.
- M. Zannese, B. Tabone, E. Habart, J. R. Goicoechea, A. Zanchet, E. F. van Dishoeck, M. C. van Hemert, J. H. Black, A. G. G. M. Tielens, A. Veselinova, P. G. Jambrina, M. Menendez, E. Verdasco, F. J. Aoiz, L. Gonzalez-Sanchez, B. Trahin, E. Dartois, O. Berne, E. Peeters, J. He, A. Sidhu, R. Chown, I. Schroetter, D. V. D. Putte, A. Canin, F. Alarcon, A. Abergel, E. A. Bergin, J. Bernard-Salas, C. Boersma, E. Bron, J. Cami, D. Dicken, M. Elyajouri, A. Fuente, K. D. Gordon, L. Issa, C. Joblin, O. Kannavou, B. Khan, O. Lacinbala, D. Languignon, R. L. Gal, A. Maragkoudakis, R. Meshaka, Y. Okada, T. Onaka, S. Pasquini, M. W. Pound, M. Robberto, M. Rollig, B. Schefter, T. Schirmer, S. Vicente and M. G. Wolfire, Nat. Astron., 2024 DOI:10.1038/s41550-024-02203-0
.
- T. L. Nguyen and J. F. Stanton, J. Phys. Chem. A, 2014, 118, 4918–4928 CrossRef CAS PubMed
.
- A. A. Westenberg and N. de Haas, J. Chem. Phys., 1967, 47, 4241–4246 CrossRef
.
- P. Marshall and A. Fontijn, J. Chem. Phys., 1987, 87, 6988–6994 CrossRef CAS
.
- J. V. Michael, J. Chem. Phys., 1989, 90, 189–198 CrossRef CAS
.
- Y. F. Zhu, S. Arepalli and R. J. Gordon, J. Chem. Phys., 1989, 90, 183–188 CrossRef CAS
.
- K. S. G. W. C. J. Yang and H. X. Shin, Chem. Phys. Lett., 1993, 207, 69–74 CrossRef
.
- M. H. Alexander, Nat. Chem., 2013, 5, 253–255 CrossRef PubMed
.
- P. G. Jambrina, M. Menéndez, A. Zanchet, E. García and F. J. Aoiz, J. Phys. Chem. A, 2018, 122, 2739–2750 CrossRef CAS PubMed
.
- D. Skouteris, J. F. Castillo and D. E. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128–135 CrossRef CAS
.
- B. Maiti and G. C. Schatz, J. Chem. Phys., 2003, 119, 12360 CrossRef CAS
.
- F. J. Aoiz, L. Bañares and V. J. Herrero, J. Chem. Soc., Faraday Trans., 1998, 94, 2483–2500 RSC
.
- F. J. Aoiz, V. J. Herrero and V. Sáez-Rábanos, J. Chem. Phys., 1992, 97, 7423–7436 CrossRef CAS
.
- T. R. Sharples, J. G. Leng, T. F. M. Luxford, K. G. McKendrick, P. G. Jambrina, F. J. Aoiz, D. W. Chandler and M. L. Costen, Nat. Chem., 2018, 10, 1148 CrossRef CAS PubMed
.
- C. G. Heid, V. Walpole, M. Brouard, P. G. Jambrina and F. J. Aoiz, Nat. Chem., 2019, 11, 662–668 CrossRef CAS PubMed
.
- J. Aldegunde, M. P. de Miranda, J. M. Haigh, B. K. Kendrick, V. Sáez-Rábanos and F. J. Aoiz, J. Phys. Chem. A, 2005, 109, 6200–6217 CrossRef CAS PubMed
.
- P. G. Jambrina, M. Menéndez and F. J. Aoiz, Chem. Sci., 2018, 9, 4837 RSC
.
- P. G. Jambrina, M. Menéndez, A. Zanchet, E. García and F. J. Aoiz, Phys. Chem. Chem. Phys., 2019, 21, 14012–14022 RSC
.
- S. J. Greaves, D. Murdock and E. Wrede, J. Chem. Phys., 2008, 128, 164307 CrossRef PubMed
.
| This journal is © the Owner Societies 2024 |