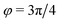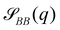Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reaction-driven assembly: controlling changes in membrane topology by reaction cycles†
Gregor
Häfner
 ab and
Marcus
Müller
ab and
Marcus
Müller
 *a
*a
aInstitute for Theoretical Physics, Georg-August University, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany. E-mail: mmueller@theorie.physik.uni-goettingen.de
bMax Planck School Matter to Life, Jahnstraße 29, 69120 Heidelberg, Germany
First published on 7th August 2023
Abstract
Chemical reaction cycles are prototypical examples how to drive systems out of equilibrium and introduce novel, life-like properties into soft-matter systems. We report simulations of amphiphilic molecules in aqueous solution. The molecule's head group is permanently hydrophilic, whereas the reaction cycle switches the molecule's tail from hydrophilic (precursor) to hydrophobic (amphiphile) and vice versa. The reaction cycle leads to an arrest in coalescence and results in uniform vesicle sizes that can be controlled by the reaction rate. Using a continuum description and particle-based simulation, we study the scaling of the vesicle size with the reaction rate. The chemically active vesicles are inflated by precursor, imparting tension onto the membrane and, for specific parameters, stabilize pores.
1 Introduction
Amphiphilic molecules are commonly used to artificially produce compartmentalized nanostructures through their ability to form bilayers and vesicles in aqueous solution, may it be lipids,1,2 diblock copolymers3–6 or even short peptides.7,8 Such assemblies have promising applications in therapeutics9–11 and as models for synthetic cells.12–18 In living systems, the size of compartments is tightly controlled and compartments undergo topological changes in the course of transport processes, e.g., in membrane vesicle trafficking.In order to mimic life-like properties, such as e.g., spontaneous adaptation, one can employ beyond-equilibrium dynamics by incorporating mechanisms that allow the system to dissipate energy.19 One way to do so is to exploit reaction cycles, where a high-energy molecule, a fuel, enables a forward reaction to a product that is (partly) immiscible with the reactant but, after some time, deactivates back into the reactant state.20,21 Already the simplest of such systems, an immiscible reactant-product system exhibits a variety of effects that differ from immiscible binary mixtures such as an arrest of droplet coalescence22–24 or a shape instability for emerging droplets, leading to fission.25–27
It has remained a challenge to reproduce these predicted effects experimentally for which high reaction rates are necessary.
For instance, Heckel and coworkers observed the arrest in coarsening in the course of spinodal decomposition of reacting polymers.28 Tena-Solsona et al., however, observed an accelerated coalescence of a chemically fueled mixture compared to its equilibrium counterpart.29 More complex reaction cycles have shown to produce exciting new features in recent years, such as the transient assembly of fibers,30,31 colloids and gels32–38 or polymeric micelles that were used as nano-reactors.39,40 The transient assembly of vesicles was achieved by the use of an ATP-hydrolizing reaction cycle,41 peptides that are switched to their cyclic anhydride at the expense of a carbodiimide42 or by polymerization induced self-assembly with a pH or light-responsive deactivation.43,44
In this work, we elucidate which effects may occur for a class of molecular architectures, where the product is amphiphilic. Specifically, we present simulations of macromolecules in aqueous solution that are involved in a reaction cycle, switching between a hydrophilic and an amphiphilic state. In the latter state, the amphiphiles self-assemble into bilayer membranes or vesicles. We explore the effects of this reaction-driven assembly (RDA) by employing two complementary simulation schemes, a continuum model and a particle-based description. We study the stationary states for varying reaction rates, both analytically and by simulations, and describe the kinetic pathways that are taken to form vesicles. Furthermore, we show how compartments formed by RDA become inflated with precursor, which, in turn, stabilizes the formation of pores in their membrane.
2 Methodology
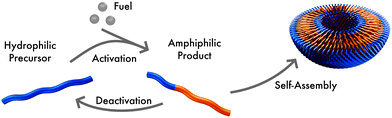
We consider a system that is comprised of an aqueous solvent, S, small fuel molecules, F and amphiphiles, modeled as asymmetric diblock copolymers. The diblock copolymers can, in principle, also represent different molecules, such as short peptides, to which we expect our results also qualitatively apply. The two blocks of the copolymer are denoted A and B. The minority block A is always hydrophilic. In the presence of fuel, the majority block B may react to become hydrophobic, forming an amphiphilic product P that self-assembles to micelles or vesicles. The reaction cycle is completed by a spontaneous reversion of the tail B from hydrophobic to hydrophilic. In this state we denote the effective homopolymer as R (reactant). Hence, there are two types of chemical reactions: (i) a binary forward reaction in which the precursor molecule reacts with the fuel to form the amphiphile, P, and (ii) the spontaneous deactivation of product. Within both models the average fuel concentration is fixed which corresponds to a situation where fuel is refilled continuously and diffusing quickly. A sketch of this reaction cycle is depicted in Fig. 1.Note that the reaction simultaneously switches the hydrophilicity of the entire tail block. Such a reaction is feasible experimentally, for instance, with a small molecule where a single reaction at the tail end can change the physical properties of the complete molecule.
2.1 Particle-based simulations
The particle-based simulations employ a soft, coarse-grained model that represents several monomer repeat units by a single particle. Within the soft, coarse-grained model the Hamiltonian is split into strong bonded (b) and weak non-bonded (nb) interactions,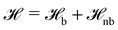 . The strong bonded interactions are taken to be harmonic springs
. The strong bonded interactions are taken to be harmonic springs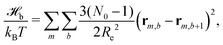 | (1) |
The weak non-bonded interactions are expressed in terms of the normalized densities ϕc(r) of component c at position r, i.e.,
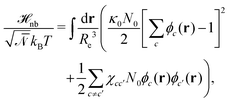 | (2) |
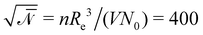 denotes the invariant degree of polymerization and sets the strength of thermal fluctuations. n denotes the total number of beads in the cubic simulation cell of volume, V, with periodic boundary conditions. The system sizes are in the range 15 ≤ L/Re ≤ 20. The densities are calculated on a cubic collocation grid with linear spacing Δx = Re/8.
denotes the invariant degree of polymerization and sets the strength of thermal fluctuations. n denotes the total number of beads in the cubic simulation cell of volume, V, with periodic boundary conditions. The system sizes are in the range 15 ≤ L/Re ≤ 20. The densities are calculated on a cubic collocation grid with linear spacing Δx = Re/8.
We employ the single-chain-in-mean-field (SCMF) algorithm46,47 that temporarily replaces the weak, non-bonded interactions by external fields and thereby exploits the different strengths of strong bonded and weak but computationally costly non-bonded interactions. Particle positions are updated by the smart-Monte-Carlo algorithm, using the strong bonded forces to bias the trial displacement. The time it takes a copolymer to diffuse its own mean end-to-end distance, Re, in a disordered system is τ0 = 2616 MCS and serves as time unit. We use the highly parallel and graphics processing unit (GPU)-accelerated software SOft coarse-grained Monte carlo Acceleration (SOMA).47
New in this work is the use of polymer-type conversions that model macromolecular reactions. We attempt the forward reaction, R → P, of every hydrophilic precursor molecule to an amphiphilic product not after every MCS but with a period τconv. Typically we use 10 ≤ τconv/MCS ≤ 50. The attempted conversion is accepted with probability 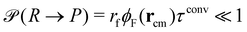 where rcm denotes the center-of-mass of the polymer. Likewise the deactivation of the product to the reactant is accepted with the concentration-independent probability,
where rcm denotes the center-of-mass of the polymer. Likewise the deactivation of the product to the reactant is accepted with the concentration-independent probability, 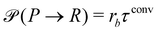 . After this sequence of conversion attempts the density fields and external fields are recomputed.
. After this sequence of conversion attempts the density fields and external fields are recomputed.
2.2 Continuum model
As a second, complementary tool, we employ a continuum model for micro- and macrophase separation in block copolymer solutions, introduced by Uneyama and Doi.45 It operates on the same set of parameters, allowing for a direct comparison. Within the Uneyama–Doi model (UDM) local concentrations, ϕpi(r), for each polymer architecture p and its respective blocks i at position r are order-parameter fields, and the free energy is given as a functional of the former. Chain conformations are not treated explicitly at the advantage of significantly shorter simulation times and the possibility of analytical predictions. Conceptually, the UDM is an extension of Ginzburg–Landau theories for multicomponent systems and remains valid even beyond the weak-segregation limit (WSL) by accurately approximating the long-range interactions.The molecules are comprised of Np segments and the block fractions are denoted by fpi. NS = NF = 1. The ratios NP/NS = NP/NF = 10 coincide with the particle-based model. Given the local concentrations, the free-energy functional 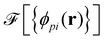 takes the form45,48
takes the form45,48
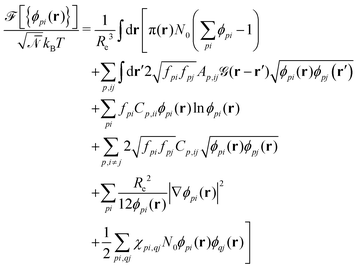 | (3) |
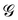 is a long-range kernel, which fulfills the modified Poisson equation,
is a long-range kernel, which fulfills the modified Poisson equation, 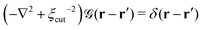 , with cutoff length ξcut = 2Re,48 and π(r) is a Lagrange field that enforces local incompressibility.48 In the free-energy functional the second term describes a long-range interaction due to the covalent bonding of the two blocks of the copolymer. For solvents and homopolymers, we have fp = 1 and the coefficients are given by Ap = 0, Cp = N0/Np. For the diblock copolymer with blocks A and B, these take the form
, with cutoff length ξcut = 2Re,48 and π(r) is a Lagrange field that enforces local incompressibility.48 In the free-energy functional the second term describes a long-range interaction due to the covalent bonding of the two blocks of the copolymer. For solvents and homopolymers, we have fp = 1 and the coefficients are given by Ap = 0, Cp = N0/Np. For the diblock copolymer with blocks A and B, these take the form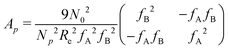 | (4) |
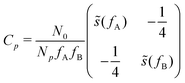 | (5) |
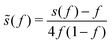 | (6) |
The third and fourth terms in eqn (3) describe the entropic contributions. For a homopolymer blend, the second term reduces to the Flory–Huggins entropy of mixing,52,53 and the third term is chosen to match the order–disorder transition for diblock copolymers. The fifth term represents a square-gradient penalty to match the structure factor at large wavevectors. The sixth term accounts for the local, binary repulsions between two distinct block types. χAS = 0.5, χBS = 4, and χAB = 2.
Given the free-energy functional, we obtain the chemical potentials as the functional derivative of the free energy with respect to the concentrations, 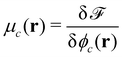 , with the joint index c = (p,i). We give their explicit form in section Chemical potentials and time evolution in the UDM of the ESI.† The spatio-temporal evolution of the concentrations follows model-B dynamics54 that locally conserves the concentrations. Gradients in the chemical potentials give rise to fluxes,
, with the joint index c = (p,i). We give their explicit form in section Chemical potentials and time evolution in the UDM of the ESI.† The spatio-temporal evolution of the concentrations follows model-B dynamics54 that locally conserves the concentrations. Gradients in the chemical potentials give rise to fluxes, 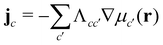 , with Λcc′(r) being Onsager coefficients that describe the concentration-dependent mobility of the components. Ignoring nonlocality in space or time,55,56 assuming that the molecular mobilities do not depend on local concentrations, and enforcing incompressibility via a Lagrange field, we use a diagonal Onsager matrix,
, with Λcc′(r) being Onsager coefficients that describe the concentration-dependent mobility of the components. Ignoring nonlocality in space or time,55,56 assuming that the molecular mobilities do not depend on local concentrations, and enforcing incompressibility via a Lagrange field, we use a diagonal Onsager matrix, 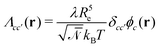 . The parameter λ is related to the diffusion coefficient by λRe2 and dictates a time scale, λ−1 = τ0, which is the diffusion time of the reference polymer in the particle-based model and will be taken as the reference.
. The parameter λ is related to the diffusion coefficient by λRe2 and dictates a time scale, λ−1 = τ0, which is the diffusion time of the reference polymer in the particle-based model and will be taken as the reference.
The time evolution of the locally conserved concentrations is given by a continuity equation,
| ∂tϕc(r,t) = −∇·jc(r,t) + ξc(r,t) | (7) |
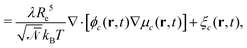 | (8) |
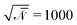 . ξc(r,t) is thermal noise, which we take to be Gaussian with its moments dictated by the fluctuation-dissipation relation48
. ξc(r,t) is thermal noise, which we take to be Gaussian with its moments dictated by the fluctuation-dissipation relation48| 〈ξc(r,t)〉 = 0 | (9) |
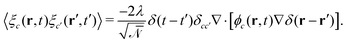 | (10) |
This concludes the contributions to the time evolution of the system without reactions, which are valid close to equilibrium and with which the system will relax into the equilibrium configuration.
A second contribution to the time evolution of the concentration fields stems from the chemical reactions. Within an infinitesimal time interval, dt, the reaction probability for the precursor is given by 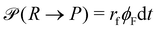 . The spontaneous deactivation to the precursor state occurs at probability,
. The spontaneous deactivation to the precursor state occurs at probability, 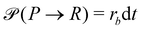 . Reactions do not conserve the order parameters and extend the model-B dynamics, eqn (10), by the additional reaction-induced concentration change
. Reactions do not conserve the order parameters and extend the model-B dynamics, eqn (10), by the additional reaction-induced concentration change
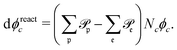 | (11) |
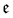 runs over all reactions with component c as a reactant, and
runs over all reactions with component c as a reactant, and 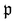 runs over all reactions with component c as product and
runs over all reactions with component c as product and 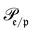 are the corresponding probabilities. This yields the final kinetic equation
are the corresponding probabilities. This yields the final kinetic equation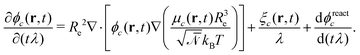 | (12) |
In both models we apply homogeneous initial conditions, with mean concentrations 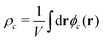 for the different species c in the system volume V. Unless noted otherwise, we use ρR + ρP = 0.25, ρF = 0.1, and ρS + ρR + ρP + ρF = 1. Eqn (12) is integrated with the time step of Δtλ = 4 × 10−5 in a cubic volume (12.8Re) covered by a grid with spacing Δx = Re/10. Further details of the numerical implementation are described in section Numerical implementation of the ESI.†
for the different species c in the system volume V. Unless noted otherwise, we use ρR + ρP = 0.25, ρF = 0.1, and ρS + ρR + ρP + ρF = 1. Eqn (12) is integrated with the time step of Δtλ = 4 × 10−5 in a cubic volume (12.8Re) covered by a grid with spacing Δx = Re/10. Further details of the numerical implementation are described in section Numerical implementation of the ESI.†
3 Results and discussion
3.1 Analytical predictions
We start with analytical considerations for the initial structure formation and the stationary state, based on the continuum model, to show that emerging aggregates will arrange on a lattice and take on uniform size. Afterwards, we compare this to the simulation results.To make progress, we introduce two simplifications: (i) we assume the fuel be homogeneously distributed throughout the system. Hence, the forward reaction of precursor (reactant) to product occurs with rate rfρF and effectively becomes a first-order reaction. In the long-time limit, the mean concentrations become independent of the morphology and are given by  and ρP + ρR = const., as determined by the initial conditions. (ii) Moreover, we assume the hydrophilic reactant, R, be distributed like the solvent, S, and lump the two components into one, hydrophilic species H, with ϕH = ϕR + ϕS and ϕR = ρRϕH/ρH. By virtue of incompressibility, 1 − ϕH(r) = ϕA(r) + ϕB(r), i.e., the system locally has only two degrees of freedom, ϕA and ϕB.
and ρP + ρR = const., as determined by the initial conditions. (ii) Moreover, we assume the hydrophilic reactant, R, be distributed like the solvent, S, and lump the two components into one, hydrophilic species H, with ϕH = ϕR + ϕS and ϕR = ρRϕH/ρH. By virtue of incompressibility, 1 − ϕH(r) = ϕA(r) + ϕB(r), i.e., the system locally has only two degrees of freedom, ϕA and ϕB.
For the short-time structure formation, we perform a linear stability analysis of eqn (12) around the spatially homogeneous, initial state in terms of the deviations, δϕA(r) = ϕA(r) − ρA and δϕB. Details are provided in section Growth rates of phase-separation processes of the ESI.† The linearized time evolution takes the form
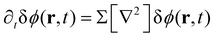 | (13) |
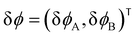 and the linearized evolution operator Σ[∇2]. This is readily solved in Fourier space by the superposition of two exponentially growing modes,
and the linearized evolution operator Σ[∇2]. This is readily solved in Fourier space by the superposition of two exponentially growing modes,| δϕ(q,t) = c+(q)δϕ+(q)eσ+(q)t + c−(q)δϕ−(q)eσ−(q)t | (14) |
The two local degrees of freedom give rise to two distinct demixing characteristics: (i) phase separation between amphiphile and solvent (termed “PH”, 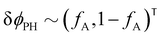 ) and (ii) (micro)phase separation of the two blocks of the amphiphile (denoted “AB”,
) and (ii) (micro)phase separation of the two blocks of the amphiphile (denoted “AB”, 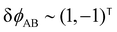 ). In general, however, these demixing characteristics are not eigenmodes of the evolution operator but linear combinations thereof. The character of an eigenmode can be quantified by the wavevector-dependent angle φ±(q). Here, the angle
). In general, however, these demixing characteristics are not eigenmodes of the evolution operator but linear combinations thereof. The character of an eigenmode can be quantified by the wavevector-dependent angle φ±(q). Here, the angle 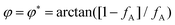 corresponds to the process PH, whereas
corresponds to the process PH, whereas 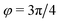 signals the microphase-separation process AB. To distinguish which demixing characteristics dominates, we obtain their initial growth rates,
signals the microphase-separation process AB. To distinguish which demixing characteristics dominates, we obtain their initial growth rates, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) AB/PH, by projecting onto the eigenmodes.
AB/PH, by projecting onto the eigenmodes.
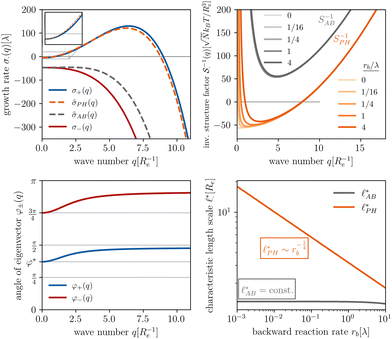
The results of this analysis are presented on the left of Fig. 2 for the typical parameters of this simulation study. It becomes clear that the initial growth of density fluctuations is dominated by the demixing of amphiphilic molecule from hydrophilic solution at length scale ∼Re because the exponentially growing eigenmode σ+(q) has an angle close to φ+ ≈ φ* and a maximum at wave number q*Re ≈ 2π. In turn, microphase separation between the blocks of the amphiphile will only commence after the amphiphilic product has separated from the solvent, in regions of higher amphiphile concentration. Such kinetics have also been observed in experimental systems of amphiphilic block copolymers in solution.57
Without reactions, the evolution operator in the linear spinodal regime and the static structure factor, 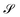 are related by
are related by 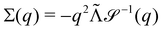 for proper choice of a non-diagonal Onsager matrix
for proper choice of a non-diagonal Onsager matrix 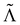 as detailed in section Effective free-energy functional of the ESI.† We use this relation to define an effective structure factor of block–block concentration fluctuations,
as detailed in section Effective free-energy functional of the ESI.† We use this relation to define an effective structure factor of block–block concentration fluctuations, 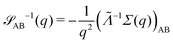 , and likewise for
, and likewise for 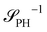 . In the ESI,† we confirm that this identification is compatible with an effective free-energy functional of the reactive system, that can be mapped onto the Ohta–Kawasaki model,49 describing a diblock copolymer melt without reactions.
. In the ESI,† we confirm that this identification is compatible with an effective free-energy functional of the reactive system, that can be mapped onto the Ohta–Kawasaki model,49 describing a diblock copolymer melt without reactions.
The inverse of these effective static structure factors, 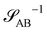 and
and 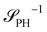 , are presented in the top right panel of Fig. 2 for various reaction rates, rb. As expected, the inverse block–block structure factor,
, are presented in the top right panel of Fig. 2 for various reaction rates, rb. As expected, the inverse block–block structure factor, 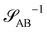 , exhibits a minimum at a finite wavevector,
, exhibits a minimum at a finite wavevector, 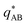 , that indicates the characteristic inverse length scale of microphase separation between the two blocks of the amphiphile in the WSL.51 Moreover,
, that indicates the characteristic inverse length scale of microphase separation between the two blocks of the amphiphile in the WSL.51 Moreover, 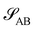 is rather insensitive to the reaction rate, rb.
is rather insensitive to the reaction rate, rb.
Intriguingly, the effective static structure factors, 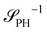 also exhibits a minimum at a finite wavevector,
also exhibits a minimum at a finite wavevector, 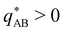 ; qualitatively similar to the equilibrium structure factor of a copolymer melt in the WSL.51 This indicates that the phase separation between product molecules and solvent does not occur macroscopically but, instead, is characterized by a finite, microscopic length scale,
; qualitatively similar to the equilibrium structure factor of a copolymer melt in the WSL.51 This indicates that the phase separation between product molecules and solvent does not occur macroscopically but, instead, is characterized by a finite, microscopic length scale, 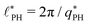 . This results from the interplay between diffusion time of precursor molecules through the solution and their lifetime, dictated by the reactions. Thus, the effect of reactions can be conceived as introducing a connectivity between product molecules and solvent that prevents macroscopic phase separation and induces stationary amphiphile-rich domains of a characteristic size. In analogy to the equilibrium behavior of asymmetric copolymers without reaction,51 the nonequilibrium stationary state of the reactive system at small product concentration will result in amphiphile-rich droplets that densely pack into a body centered cubic (BCC) lattice.
. This results from the interplay between diffusion time of precursor molecules through the solution and their lifetime, dictated by the reactions. Thus, the effect of reactions can be conceived as introducing a connectivity between product molecules and solvent that prevents macroscopic phase separation and induces stationary amphiphile-rich domains of a characteristic size. In analogy to the equilibrium behavior of asymmetric copolymers without reaction,51 the nonequilibrium stationary state of the reactive system at small product concentration will result in amphiphile-rich droplets that densely pack into a body centered cubic (BCC) lattice.
The top right panel of Fig. 2 demonstrates that the location of the minimum, 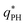 , shifts to large wavevectors and becomes less deep upon increase of the reaction rate, rb, i.e., larger rb results in smaller amphiphile-rich droplets and decrease the effective incompatibility between amphiphiles and solvent.
, shifts to large wavevectors and becomes less deep upon increase of the reaction rate, rb, i.e., larger rb results in smaller amphiphile-rich droplets and decrease the effective incompatibility between amphiphiles and solvent.
In the ESI,† we explicitly map our reactive system onto the Ohta–Kawasaki model,49 describing the equilibrium of a diblock copolymer melt. Using the results for the domain spacing of equilibrium diblock copolymers in the WSL, the characteristic distance between the domains scales like58,59
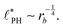 | (15) |
In the strong segregation limit (SSL), i.e., at smaller reaction rates, rb > 0, the domain spacing is larger and the analogy to the Ohta–Kawasaki model yields49,58–60
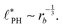 | (16) |
The above analysis yields a prediction for the dense packing of building blocks, arbitrarily shaped product aggregates, assuming that the two phase separation processes evolve separately, as observed for amphiphiles in solution.57 In the following, the mean product density, ρP, is small such that the aggregates form droplets that ideally arrange on a cubic lattice. At large values of rb, compact micelles form inside these droplets whose radius, R, scales like the lattice spacing, 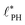 , of the amphiphile-rich droplet lattice. For smaller reaction rates, however, the lattice spacing becomes larger, and so does the number of amphiphilic molecules in a unit cell,
, of the amphiphile-rich droplet lattice. For smaller reaction rates, however, the lattice spacing becomes larger, and so does the number of amphiphilic molecules in a unit cell, 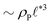 . In this case, the amphiphiles form bilayers that close into unilamellar vesicles. We assume that the bilayer thickness, D, is much smaller than the vesicle radius, D/R ≪ 1, i.e., the number of molecules in a vesicle of size R scales like DR2. In this case, the scaling of the radius, R, of densely packed vesicles with reaction rate takes the form
. In this case, the amphiphiles form bilayers that close into unilamellar vesicles. We assume that the bilayer thickness, D, is much smaller than the vesicle radius, D/R ≪ 1, i.e., the number of molecules in a vesicle of size R scales like DR2. In this case, the scaling of the radius, R, of densely packed vesicles with reaction rate takes the form
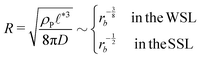 | (17) |
When the reaction rate is decreased further, or the average product concentration is increased, the unilamellar vesicle becomes too large to fit into the unit cell, i.e., 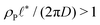 . In this case, a dense arrangement of multilamellar vesicles will form or in more extreme cases, stacked planar membranes.
. In this case, a dense arrangement of multilamellar vesicles will form or in more extreme cases, stacked planar membranes.
3.2 Kinetics of structure formation
To test the above predictions for the emergence of dense packings of vesicles, we start our simulations from a spatially homogeneous distribution of components. We treat the fuel only implicitly, fixing the forward reaction rate of the precursor rfρF to be constant without explicitly considering the fuel. We will later assess the quality of this approximation for a hydrophilic fuel.For the initial formation of vesicles from a homogeneous solution, two pathways have been proposed: one describes the emergence of vesicles via a disc-like micelle that spontaneously bends to minimize the line tension along its edge and finally closes,48,61–63 as shown schematically in the inset of Fig. 3(a). We refer to this kinetic mechanism as ‘pathway I’. Alternatively, a vesicle may emerge directly from a spherical micelle via a semi-vesicle, i.e., a micelle in which hydrophilic head groups are enriched in the center, by flip-flopping of amphiphiles to the inside. This way, the vesicle's bilayer emerges gradually,64,65 see the inset of Fig. 3(b). We refer to this process as ‘pathway II’. Which of these paths is taken, depends on the nature of the amphiphiles. In nonreactive systems, pathway I is favored for a stronger repulsion between head group and tail. Because of this, pathway I appears to be the generic process in experiments.66–69 Pathway II, in turn, is only rarely evidenced in experiments.70,71
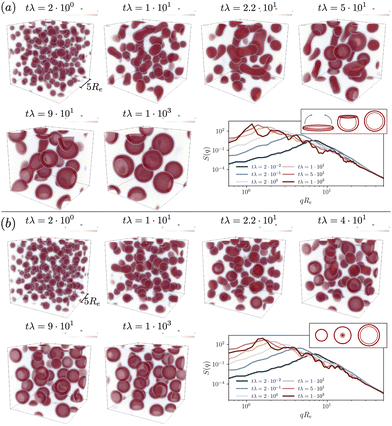
To illustrate the time-evolution of the reaction-directed assembly, we take two different reaction rates and show morphological snapshots and the corresponding structure factor of B-density fluctuations in Fig. 3. Additionally, we provide the Videos udm-impl-fuel-rb1e-2.mp4 and udm-impl-fuel-rb4e-2.mp4 in the ESI.†
The time evolution for an exemplary reaction rate is illustrated in Fig. 3(a). Starting from a homogeneous distribution at tλ = 0, small micelles quickly nucleate. Initially, their size is on the order of ∼Re, as visible in the structure factor at tλ = 2 × 10−2, and subsequently they quickly coalesce. Rather than forming larger spherical micelles, the structures elongate to form cylindrical micelles, tλ = 2.2 × 101, and eventually disk-like micelles, tλ = 5 × 101. The latter are unstable. They bend to minimize the line tension along their edge and finally close the remaining pore to form a vesicle. Hence, vesicle formation proceeds via pathway I.
Smaller vesicles continue to coalesce, tλ = 9 × 101. In the late stage, coarsening arrests and the vesicles adopt a rather uniform, finite size. Since product molecules are continuously deactivated and precursor molecules are continuously activated within the aqueous solution, the vesicles constantly exchange material, via diffusion of the hydrophilic precursor molecules through the solution. This is in marked contrast to micelles and vesicle in systems without reactions, where exchange of amphiphiles across the solution is extremely slow. This exchange allows for an efficient size matching because all vesicles are equally capable to compete for product as well as to adjust their positioning in the lattice structure. In the stationary state one obtains a structure factor that reflects the lattice periodicity at low wave numbers and is reminiscent of existing predictions for vesicle form factors at high wavenumbers.72–74
The material exchange and size matching can be quantitatively investigated by using a Hoshen-Koppelman cluster analysis (HKCA)75,76 to obtain the radii, R, of individual micelles and vesicles. A description is outlined in section Measurement of micelle and vesicle radii in the ESI.† The individual and mean radii as a function of time are presented in Fig. 4. As observed qualitatively in Fig. 3(a), the radius distribution of the vesicles becomes narrow and all vesicles approach a common mean radius by the redistribution of material.
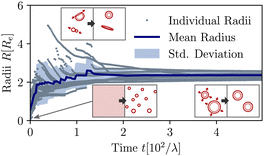 | ||
| Fig. 4 Temporal evolution of individual and mean aggregate sizes, as well as its variance in the UDM for the system of Fig. 3(a). 0 ≤ tλ < 2 × 101: initial coarsening, 2 × 101 ≤ tλ < 1.2 × 102: sporadic fusion of micelles and vesicles. Ultimately, the efficient exchange between aggregates via diffusion of hydrophilic precursor through the solution, results in a well-define and narrowly distributed aggregate size. The different processes are depicted by the pictograms in the insets. | ||
For a second, larger reaction rate, rb, presented in Fig. 3(b), the behavior of the structure factor, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) BB, is qualitatively similar but we observe two differences: (i) the fast reaction rate, specifically the quicker deactivation rate of product molecules inside the aggregates, leads to an increased densities of precursor material on the inside. For a growing micelle, this facilitates the formation of a semi-vesicle, i.e., a large micelle with a hydrophilic core, made up of precursor molecules and head-groups, such as structures observed at tλ = 2.2 × 101–4 × 101. By flip-flopping of amphiphiles to the inside, a small vesicle can form immediately, following pathway II. This effect is qualitatively similar to the formation of complex, multiphase condensates formed by RDA.77 (ii) Additionally, as predicted by the analytical consideration, coarsening arrests at smaller vesicle sizes.
BB, is qualitatively similar but we observe two differences: (i) the fast reaction rate, specifically the quicker deactivation rate of product molecules inside the aggregates, leads to an increased densities of precursor material on the inside. For a growing micelle, this facilitates the formation of a semi-vesicle, i.e., a large micelle with a hydrophilic core, made up of precursor molecules and head-groups, such as structures observed at tλ = 2.2 × 101–4 × 101. By flip-flopping of amphiphiles to the inside, a small vesicle can form immediately, following pathway II. This effect is qualitatively similar to the formation of complex, multiphase condensates formed by RDA.77 (ii) Additionally, as predicted by the analytical consideration, coarsening arrests at smaller vesicle sizes.
The corresponding results in the particle-based model are given in section Kinetics of structure formation in particle-based simulations in the ESI.†
3.3 Scaling with reaction rates
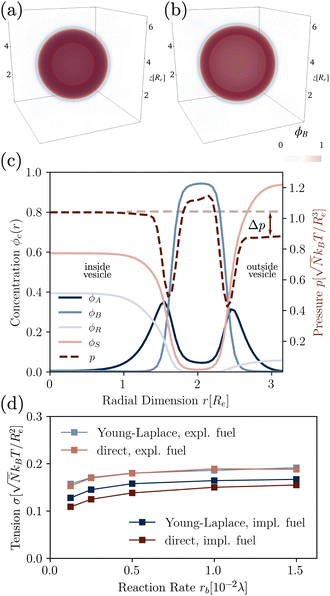
To quantify the dependence of the size scale on the reaction rates, we measure the vesicle radii for a range of reaction rates. We start with the implicit fuel.This size dependence is depicted in Fig. 5 for both the UDM (a) and two different sizes of the simulation box for the particle-based simulations (b). As expected, larger vesicles are observed for smaller reaction rates, while for high reaction rates, the distance, 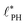 , between aggregates is small and they have smaller size, R. Note that the error bars for the mean radii only show the standard deviations of individual radii, ignoring that different realizations of the structure formation may result in different number of aggregates and thus slightly different mean radii at finite simulation times. Small variations in the numbers of vesicles in the simulation cell are expected because fusion events become rare as the system approaches the stationary state as well as due to finite-size effects. To estimate the spread among realizations, we repeated the simulations for reaction rates rb = 1 × 10−2λ and rb = 4 × 10−2λ in the UDM simulations twice, yielding a deviation of the mean radii within the standard deviation of each distribution, as visible in Fig. 5(a).
, between aggregates is small and they have smaller size, R. Note that the error bars for the mean radii only show the standard deviations of individual radii, ignoring that different realizations of the structure formation may result in different number of aggregates and thus slightly different mean radii at finite simulation times. Small variations in the numbers of vesicles in the simulation cell are expected because fusion events become rare as the system approaches the stationary state as well as due to finite-size effects. To estimate the spread among realizations, we repeated the simulations for reaction rates rb = 1 × 10−2λ and rb = 4 × 10−2λ in the UDM simulations twice, yielding a deviation of the mean radii within the standard deviation of each distribution, as visible in Fig. 5(a).
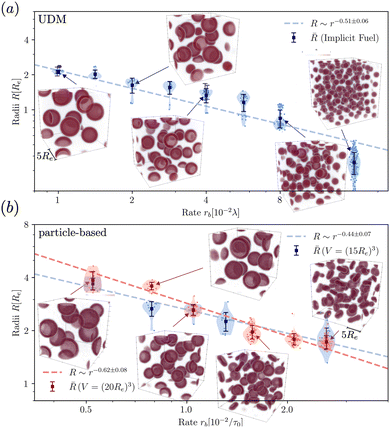 | ||
| Fig. 5 Dependence of stationary micelle and vesicle radii on the reaction rates in (a) for the UDM after time tλ = 103 and in (b) for the particle-based simulations after t = 3.4 × 103τ0. The stationary morphologies for a subset of reaction rates are shown as the insets. We calculated the vesicle and micelle radii by a HKCA,75,76 assuming a spherical aggregate shape. Radii of individual aggregates are given as semi-transparent dots, whereas the mean and standard deviation are depicted in solid colors. In (a) two additional simulations were performed for rb = 1 × 10−2λ and rb = 4 × 10−2λ, only indicated by the mean radii. In (b) two different sizes of the simulation box are probed, depicted in shades of red and blue, as indicated in the legends. For all three scenarios a power-law fit was performed with mean radii as fit values and standard deviations as weights. | ||
For all three scenarios we fit a power-law R ∼ rν and obtain the exponent ν = −0.51 ± 0.06 for the UDM, and ν = −0.44 ± 0.07 for the particle-based simulations with the small simulation box and ν = −0.62 ± 0.08 for the larger one. Thus, within the statistical uncertainty we confirm the scaling of the vesicle size, 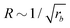 , predicted by eqn (17) in the SSL.
, predicted by eqn (17) in the SSL.
3.4 Inflation of chemically fueled vesicles
Compartments formed by RDA tend to accumulate precursor on the inside. To analyze the origin of this effect, we set up a single vesicle within the particle-based model and track the evolution of individual molecules. A detailed analysis is given in Sec. Precursor enrichment in RDA vesicles of the ESI.† When amphiphilic product molecules in the inner leaflet of a vesicle deactivate to become hydrophilic precursors, they majorly diffuse to the inside of the vesicle, and vice versa. The diffusive transport of hydrophilic precursor across the vesicle membrane is protracted because the hydrophilic precursor needs to pass the hydrophobic membrane core. Thus, the number of precursors trapped inside the vesicle, Vin, is proportional to the number of molecules in the inner leaflet, and the same holds for the number of precursor molecules in the volume, Vout, between the vesicles.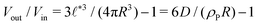 according to eqn (17). For the parameters studied, Vout/Vin > 1.
according to eqn (17). For the parameters studied, Vout/Vin > 1.
Hence, vesicles formed by RDA sort precursor molecules, enriching them inside the vesicles. The higher concentration of the precursor inside the vesicle increases the osmotic pressure, Δp > 0, of the inside compared to the outside and thereby inflates the vesicle. The concomitant stretching of the vesicle membrane imparts a tension, σ, onto the membrane.78 This membrane tension and the pressure difference between the vesicle's inside and outside are related by the Young-Laplace equation
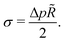 | (18) |
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) denotes the vesicle radius to the center of the bilayer.
denotes the vesicle radius to the center of the bilayer.
We use the UDM to accurately measure the pressure difference, Δp, and the resulting membrane tension, σ. We doubled the grid resolution for precision but left all other parameters unchanged. The morphology of an isolated, RDA vesicle in a periodic cell of size, 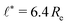 is presented in Fig. 6(b). Panel (a) depicts an equilibrium vesicle without reactions but with the same ρP as in panel (b). The inflation expresses itself in a visible decrease of membrane thickness, D, compared to the chemically inactive counterpart.
is presented in Fig. 6(b). Panel (a) depicts an equilibrium vesicle without reactions but with the same ρP as in panel (b). The inflation expresses itself in a visible decrease of membrane thickness, D, compared to the chemically inactive counterpart.
The corresponding radial profiles of the RDA vesicle are presented in Fig. 6(c). The reactant (precursor) profile, ϕR(r), clearly demonstrates the precursor enrichment inside the spherical vesicle. The pressure (or negative grandcanonical free-energy density, g) can be obtained from the Helmholtz free-energy density f of the UDM via Legendre transformation
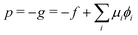 | (19) |
From the pressure difference and the Young-Laplace eqn (18) we can estimate the membrane tension, σ. Alternatively, we can approximate the membrane tension by that of a planar membrane of the same thickness, equilibrated without reactions. Noting that the membrane tension is the excess grandcanonical free energy, ΔG, per unit area, we estimate σ from 1D pressure profiles
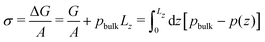 | (20) |
Fig. 6(d) demonstrates the consistency of the two tension estimates according to eqn (18) and (20) for various reaction rates, both with implicit and explicit fuel. This validates that the precursor enrichment inside the vesicle results in the inflation of the vesicle. In the case of explicit fuel, the fuel concentration is inhomogeneous, decreased inside the vesicle, similar to the solvent concentration in Fig. 6(b). We observe that (i) the inflation increases with increasing reaction rates and (ii) for explicit fuel the tension is higher. (i) is explained by the fact that pressure can be released by diffusion of precursor through the membrane and more of it escapes within its lifetime for smaller reaction rates. (ii) Since less fuel is present inside of the RDA vesicle, less precursor reacts on the inside, raising its concentration and thus the membrane tension.
3.5 Metastable pore anomaly
When exploring RDA of vesicles from homogeneous solution with explicit fuel i.e., we allow for inhomogeneous fuel concentration, we observe an interesting anomaly where vesicles that emerge via pathway I, retain a metastable pore, which causes accelerated coarsening, see Fig. 7. This is related to the fact that inflation and hence increase in membrane tension is accelerated compared to homogeneously treated fuel. A pore arising during the vesicle formation process results from an interplay between two timescales: the reaction-dependent inflation time and the architecture-dictated time it takes for a planar bilayer to bend and close. This will be demonstrated in the following.The dependence of the characteristic size on the reaction rates with explicit fuel is depicted in Fig. 7(a). Similar to the previous, implicit-fuel case, the scaling roughly agrees with eqn (17), R ∼ rb−1/2 with a measured exponent ν = −0.57 ± 0.06.
The vesicles originate exclusively via pathway II for large forward reaction rates, rb ≥4 × 10−2λ. For smaller rates, when vesicles emerge via pathway I, however, the vesicle radii deviate from the expectation, eqn (17). In this case, disk-like micelles bend and form a vesicle with a pore, see Fig. 7. Remarkably, panel b illustrates that such a pore persists until the vesicle merges with a neighbor.‡
Vesicles formed by RDA are inflated by precursor, and the membrane is under tension. With a pore present, the pressure difference, Δp, can be reduced by exchanging precursor between the vesicle's inside and outside. If the pore is large, this exchange is effective. Thus, the pressure difference, Δp, decreases. This, in turn, reduces the membrane tension, σ, and the balance between the pore's line tension, Λ, and the membrane tension shifts towards shrinking the pore diameter, Dpore = 2σ/Λ.80 If, on the contrary, the pore is small, the precursor exchange is limited, the pressure difference is increased and so is the membrane tension. This, in turn, tends to expand the pore size. As small pores expand and large pores shrink, a finite pore size is stabilized.
Additionally, small RDA vesicles with an open pore exhibit a directed movement opposite to the pore. This effect is depicted in Fig. 7(b) and can also be appreciated in the Movie udm-expl-fuel-tumbling-vesicle.mp4 of the ESI.† In the dense fluid of vesicles, the highlighted vesicle initially moves in the direction opposite to its pore. When the vesicle-free space (void) behind it becomes large, the movement slows down and stalls. Since RDA vesicles ideally pack on a dense, regular lattice, vesicle–vesicle interactions give rise to a force that pulls the vesicle back towards the center of the void. The vesicle tumbles and the direction of motion spontaneously changes. At tλ ≈ 4.7 × 102, the highlighted vesicle collides with a neighboring vesicle and both fuse. Such collision-fusion processes greatly enhance the coarsening dynamics and explain the observed increase in vesicle size as a function of reaction rate in Fig. 7(a) at a finite time.
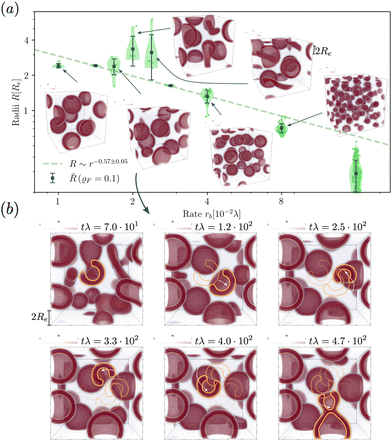
In Fig. 8 we study the properties of a vesicle with a metastable pore, using the UDM and particle-based simulations. The simulation cell contains a single vesicle and we study different reaction rates. rb. We monitor their average pore diameter and velocity, when the pore is present. Pores remain stable for high reaction rates because of the larger pressure difference and membrane tension. Pores shrink and become unstable as we decrease rb. For rb = 10−2λ the realization is shown in the Movie udm-metastable-pore-analysis.mp4 of the ESI.†
Additionally, Fig. 8 presents the velocity of RDA vesicles with an open pore, as observed in the UDM and the particle-based simulations. The velocity is opposite to the direction from the center of the vesicle to the pore. In the absence of a pore, i.e., at small rf, the vesicles diffuse and the velocity is vanishingly small.
The presence of a pore in the vesicle allows for an osmotic-pressure-driven flux of the precursor along the direction from the vesicle center to the pore, reducing the precursor enrichment inside the vesicle. Incompressibility, in return, enforces that this outward flux is compensated by an inward flux of solvent, fuel, and amphiphile in the opposite direction. The latter slightly deforms the vesicle around the pore and induces the movement of the vesicle in the opposite direction of the pore.
Note, that vesicle inflation and pore stabilization are dynamic effects. In the above analysis, vesicles were initialized in the inflated state, allowing for a precise measurement of pore stability. In the dynamic system, a pore only becomes stable if sufficient inflation occurs on the time scales, on which the bilayer bends, forming a vesicle with a pore. This is why the effect is not visible in the simulations with homogeneously distributed fuel, with slower inflation, as well as in the dynamic, particle-based simulations. Alternatively, a pore could potentially form spontaneously in a closed vesicle under tension by thermal fluctuations.
4 Conclusion
Investigating the behavior of compartmentalizing amphiphiles in aqueous solution driven out of equilibrium by a coupling to a reaction cycle, we observe a variety of reaction-driven assembly (RDA) phenomena. The reaction cycle converts a hydrophilic precursor molecule (reactant, R) into a amphiphile (product, P) in the presence of a fuel (F). The amphiphilic product, P, assembles into micelles or vesicle but spontaneously converts back to the hydrophilic reactant, R. We focus on the regime, where a dense arrangement of micelles or vesicles is formed.Using analytical considerations and simulations of the Uneyama–Doi model (UDM) and a particle-based model, we show that the structure initially forms by microphase separation between the hydrophilic components (solvent S and precursor R) and the amphiphilic product, P. This behavior can be described by an effective free-energy functional, analog to the Ohta–Kawaski model that describes microphase separation in the absence reactions.
Vesicles form in an initial, homogeneous solution by converting spherical micelles to disk-like micelles that bend and close to a vesicle (pathway I) at small reaction rates or via the direct flip-flopping of amphiphiles to the center of the micelle (pathway II) at high reaction rates. Along the former pathway I, we observed the formation of (meta)stable pores in the bilayer that result in the directed motion of vesicles due to the exchange of precursor between the vesicle's inside and its surrounding through the pore.
There are multiple characteristics that distinguish the RDA of vesicles from the formation of vesicles by amphiphilic molecules in equilibrium:
• The size distribution of the vesicles is narrow, and the average vesicle radius scales like 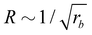 with the reaction rate, i.e., it is responsive to thermodynamic parameters that influence the reaction rate.
with the reaction rate, i.e., it is responsive to thermodynamic parameters that influence the reaction rate.
• There is a fast, efficient transfer of building blocks between micelles that is based on the diffusion of molecules in its hydrophilic precursor state and allows for a rapid adjustment of vesicle sizes. This is in marked contrast to the protracted exchange of amphiphiles between aggregates (micelles or vesicles) in equilibrium self-assembly.
• In contrast to self-assembled vesicles in equilibrium, RDA results in inflated vesicles, characterized by a finite membrane tension. This membrane tension depends on the reaction rate, as well as on the density of aggregates. Vesicle tension, in turn, facilitates topological changes such as pore formation or the fusion of vesicles with membranes that are implicated in various transport processes in cells or subcellular compartments or could be exploited for targeted, tunable release of drugs.
These characteristics allow to control the vesicle assembly by external stimuli without changing the chemistry of the constituents.
Taking a reported diffusion coefficient of 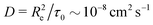 81 for an amphiphilic diblock copolymer with Re∼102 nm yields a common self-diffusion time of τ0 ∼ 10−2 s and hence the presented simulations cover times of t ∼ 30 s. The corresponding deactivation times in our case would be on the order of
81 for an amphiphilic diblock copolymer with Re∼102 nm yields a common self-diffusion time of τ0 ∼ 10−2 s and hence the presented simulations cover times of t ∼ 30 s. The corresponding deactivation times in our case would be on the order of 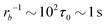 for the slowest reaction rates. Commonly reported values of
for the slowest reaction rates. Commonly reported values of 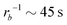 82 are higher, implying the lattice spacing would increase by a factor of
82 are higher, implying the lattice spacing would increase by a factor of 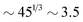 . Notice, that lower molecular weights will require higher reaction rates.
. Notice, that lower molecular weights will require higher reaction rates.
Further topics of interest may include the study of fuel that is consumed by the reaction (instead of being a catalyst) and thus needs to be re-supplied. This may give rise to additional spatial inhomogeneities. Additionally, detailed reaction schemes that do not rapidly switch an entire block but allow for segment-wise reactions could be considered. We expect, however, that the qualitative differences between RDA of vesicles will remain unaltered.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was conducted within the Max Planck School Matter to Life supported by the German Federal Ministry of Education and Research (BMBF) in collaboration with the Max Planck Society. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (http://www.gauss-centre.eu) for providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC), as well as the North-German Supercomputing Alliance (HLRN).References
- E. Rideau, R. Dimova, P. Schwille, F. R. Wurm and K. Landfester, Chem. Soc. Rev., 2018, 47, 8572–8610 RSC.
- R. Dimova, P. Stano, C. M. Marques and P. Walde, in The Giant Vesicle Book, ed. R. Dimova and C. M. Marques, CRC Press, Taylor & Francis Group, 2020 Search PubMed.
- B. M. Discher, Y.-Y. Won, D. S. Ege, J. C.-M. Lee, F. S. Bates, D. E. Discher and D. A. Hammer, Science, 1999, 284, 1143–1146 CrossRef CAS PubMed.
- K. Kita-Tokarczyk, J. Grumelard, T. Haefele and W. Meier, Polymer, 2005, 46, 3540–3563 CrossRef CAS.
- D. E. Discher, V. Ortiz, G. Srinivas, M. L. Klein, Y. Kim, D. Christian, S. Cai, P. Photos and F. Ahmed, Prog. Polym. Sci., 2007, 32, 838–857 CrossRef CAS PubMed.
- G. Srinivas, J. C. Shelley, S. O. Nielsen, D. E. Discher and M. L. Klein, J. Phys. Chem. B, 2004, 108, 8153–8160 CrossRef CAS.
- A. J. van Hell, C. I. C. A. Costa, F. M. Flesch, M. Sutter, W. Jiskoot, D. J. A. Crommelin, W. E. Hennink and E. Mastrobattista, Biomacromolecules, 2007, 8, 2753–2761 CrossRef CAS PubMed.
- V. Haridas, A. Rao Sapala and J. P. Jasinski, Chem. Commun., 2015, 51, 6905–6908 RSC.
- F. Meng, Z. Zhong and J. Feijen, Biomacromolecules, 2009, 10, 197–209 CrossRef CAS PubMed.
- O. Onaca, R. Enea, D. W. Hughes and W. Meier, Macromol. Biosci., 2009, 9, 129–139 CrossRef CAS PubMed.
- F. Meng and Z. Zhong, J. Phys. Chem. Lett., 2011, 2, 1533–1539 CrossRef CAS.
- K. Göpfrich, I. Platzman and J. P. Spatz, Trends Biotechnol., 2018, 36, 938–951 CrossRef PubMed.
- W. K. Spoelstra, S. Deshpande and C. Dekker, Curr. Opin. Biotechnol, 2018, 51, 47–56 CrossRef CAS PubMed.
- R. Bleul, R. Thiermann and M. Maskos, Macromolecules, 2015, 48, 7396–7409 CrossRef CAS.
- A. F. Mason and P. Thordarson, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 3817–3825 CrossRef CAS.
- P. Schwille, J. Spatz, K. Landfester, E. Bodenschatz, S. Herminghaus, V. Sourjik, T. J. Erb, P. Bastiaens, R. Lipowsky, A. Hyman, P. Dabrock, J.-C. Baret, T. Vidakovic-Koch, P. Bieling, R. Dimova, H. Mutschler, T. Robinson, T.-Y. D. Tang, S. Wegner and K. Sundmacher, Angew. Chem., Int. Ed., 2018, 57, 13382–13392 CrossRef CAS PubMed.
- T. Robinson, Adv. Biosyst., 2019, 3, 1800318 CrossRef PubMed.
- M. Weiss, J. P. Frohnmayer, L. T. Benk, B. Haller, J.-W. Janiesch, T. Heitkamp, M. Börsch, R. B. Lira, R. Dimova, R. Lipowsky, E. Bodenschatz, J.-C. Baret, T. Vidakovic-Koch, K. Sundmacher, I. Platzman and J. P. Spatz, Nat. Mater., 2018, 17, 89–96 CrossRef CAS PubMed.
- A. Walther, Adv. Mater., 2020, 32, 1905111 CrossRef CAS PubMed.
- B. Rieß, R. K. Grötsch and J. Boekhoven, Chem, 2020, 6, 552–578 Search PubMed.
- S. Amano, S. Borsley, D. A. Leigh and Z. Sun, Nat. Nanotechnol., 2021, 16, 1057–1067 CrossRef CAS PubMed.
- D. Zwicker, A. A. Hyman and F. Jülicher, Phys. Rev. E, 2015, 92, 012317 CrossRef PubMed.
- K. A. Rosowski, E. Vidal-Henriquez, D. Zwicker, R. W. Style and E. R. Dufresne, Soft Matter, 2020, 16, 5892–5897 RSC.
- D. Zwicker, Curr. Opin. Colloid Interface Sci., 2022, 61, 101606 CrossRef CAS.
- D. Zwicker, R. Seyboldt, C. A. Weber, A. A. Hyman and F. Jülicher, Nat. Phys., 2017, 13, 408–413 Search PubMed.
- C. A. Weber, D. Zwicker, F. Jülicher and C. F. Lee, Rep. Prog. Phys., 2019, 82, 064601 CrossRef CAS PubMed.
- J. Bauermann, C. A. Weber and F. Jülicher, Ann. Phys., 2022, 534, 2200132 CrossRef.
- J. Heckel, F. Batti, R. T. Mathers and A. Walther, Soft Matter, 2021, 17, 5401–5409 RSC.
- M. Tena-Solsona, J. Janssen, C. Wanzke, F. Schnitter, H. Park, B. Rieß, J. M. Gibbs, C. A. Weber and J. Boekhoven, ChemSystemsChem, 2021, 3, e2000034 CrossRef CAS.
- J. Boekhoven, A. M. Brizard, K. N. K. Kowlgi, G. J. M. Koper, R. Eelkema and J. H. van Esch, Angew. Chem., Int. Ed., 2010, 49, 4825–4828 CrossRef CAS PubMed.
- J. Boekhoven, J. M. Poolman, C. Maity, F. Li, L. van der Mee, C. B. Minkenberg, E. Mendes, J. H. van Esch and R. Eelkema, Nat. Chem., 2013, 5, 433–437 CrossRef CAS PubMed.
- J. Heckel, S. Loescher, R. T. Mathers and A. Walther, Angew. Chem., Int. Ed., 2021, 60, 7117–7125 CrossRef CAS PubMed.
- B. Klemm, R. W. Lewis, I. Piergentili and R. Eelkema, Nat. Commun., 2022, 13, 6242 CrossRef CAS PubMed.
- C. Donau, F. Späth, M. Sosson, B. A. K. Kriebisch, F. Schnitter, M. Tena-Solsona, H.-S. Kang, E. Salibi, M. Sattler, H. Mutschler and J. Boekhoven, Nat. Commun., 2020, 11, 5167 CrossRef CAS PubMed.
- B. G. P. van Ravensteijn, I. K. Voets, W. K. Kegel and R. Eelkema, Langmuir, 2020, 36, 10639–10656 CrossRef CAS PubMed.
- R. W. Lewis, B. Klemm, M. Macchione and R. Eelkema, Chem. Sci., 2022, 13, 4533–4544 RSC.
- K. Dai, M. Tena-Solsona, J. R. Fores, A. M. Bergmann and J. Boekhoven, Nanoscale, 2021, 13, 19864–19869 RSC.
- C. Sharma and A. Walther, Angew. Chem., Int. Ed., 2022, 61, e202201573 CrossRef CAS PubMed.
- X. Lang, U. Thumu, L. Yuan, C. Zheng, H. Zhang, L. He, H. Zhao and C. Zhao, Chem. Commun., 2021, 57, 5786–5789 RSC.
- M. A. Würbser, P. S. Schwarz, J. Heckel, A. M. Bergmann, A. Walther and J. Boekhoven, ChemSystemsChem, 2021, 3, e2100015 CrossRef.
- S. Maiti, I. Fortunati, C. Ferrante, P. Scrimin and L. J. Prins, Nat. Chem., 2016, 8, 725–731 CrossRef CAS PubMed.
- C. Wanzke, A. Jussupow, F. Kohler, H. Dietz, V. R. I. Kaila and J. Boekhoven, ChemSystemsChem, 2020, 2, e1900044 CrossRef CAS.
- E. Poros-Tarcali and J. Perez-Mercader, Soft Matter, 2021, 17, 4011–4018 RSC.
- G. Cheng and J. Perez-Mercader, Chem, 2020, 6, 1160–1171 CAS.
- T. Uneyama and M. Doi, Macromolecules, 2005, 38, 196–205 CrossRef CAS.
- K. C. Daoulas and M. Müller, J. Chem. Phys., 2006, 125, 184904 CrossRef PubMed.
- L. Schneider and M. Müller, Comput. Phys. Commun., 2019, 235, 463–476 CrossRef CAS.
- T. Uneyama, J. Chem. Phys., 2007, 126, 114902 CrossRef PubMed.
- T. Ohta and K. Kawasaki, Macromolecules, 1986, 19, 2621–2632 CrossRef CAS.
- O. Dreyer, G. Ibbeken, L. Schneider, N. Blagojevic, M. Radjabian, V. Abetz and M. Müller, Macromolecules, 2022, 55, 7564–7582 CrossRef CAS.
- L. Leibler, Macromolecules, 1980, 13, 1602–1617 CrossRef CAS.
- M. L. Huggins, J. Chem. Phys., 1941, 9, 440 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435–479 CrossRef CAS.
- G. Wang, Y. Ren and M. Müller, Macromolecules, 2019, 52, 7704–7720 CrossRef CAS.
- J. Rottler and M. Müller, ACS Nano, 2020, 14, 13986–13994 CrossRef CAS PubMed.
- A. Ianiro, H. Wu, M. M. J. van Rijt, M. P. Vena, A. D. A. Keizer, A. C. C. Esteves, R. Tuinier, H. Friedrich, N. A. J. M. Sommerdijk and J. P. Patterson, Nat. Chem., 2019, 11, 320–328 CrossRef CAS PubMed.
- J. J. Christensen, K. Elder and H. C. Fogedby, Phys. Rev. E, 1996, 54, R2212–R2215 CrossRef CAS PubMed.
- M. Müller and J. C. O. Rey, Mol. Syst. Des. Eng., 2018, 3, 295–313 RSC.
- S. C. Glotzer, E. A. Di Marzio and M. Muthukumar, Phys. Rev. Lett., 1995, 74, 2034–2037 CrossRef CAS PubMed.
- X. He and F. Schmid, Phys. Rev. Lett., 2008, 100, 137802 CrossRef PubMed.
- J. C. Shillcock, Langmuir, 2012, 28, 541–547 CrossRef CAS PubMed.
- J. Li, H. Zhang, F. Qiu and A.-C. Shi, Phys. Rev. E, 2013, 88, 012719 CrossRef PubMed.
- T. Uneyama and M. Doi, Macromolecules, 2005, 38, 5817–5825 CrossRef CAS.
- X. He and F. Schmid, Macromolecules, 2006, 39, 2654–2662 CrossRef CAS.
- J. Leng, S. U. Egelhaaf and M. E. Cates, Europhys. Lett., 2002, 59, 311 CrossRef CAS.
- J. Leng, S. U. Egelhaaf and M. E. Cates, Biophys. J., 2003, 85, 1624–1646 CrossRef CAS PubMed.
- T. M. Weiss, T. Narayanan, C. Wolf, M. Gradzielski, P. Panine, S. Finet and W. I. Helsby, Phys. Rev. Lett., 2005, 94, 038303 CrossRef CAS PubMed.
- R. Takahashi, T. Narayanan, S.-I. Yusa and T. Sato, Macromolecules, 2022, 55, 684–695 CrossRef CAS.
- J. Du and Y. Chen, Macromolecules, 2004, 37, 5710–5716 CrossRef CAS.
- E. V. Korchagina, X.-P. Qiu and F. M. Winnik, Macromolecules, 2013, 46, 2341–2351 CrossRef CAS.
- J. Gummel, M. Sztucki, T. Narayanan and M. Gradzielski, Soft Matter, 2011, 7, 5731–5738 RSC.
- Z. Ye, Z. Wu and A. Jayaraman, JACS Au, 2021, 1, 1925–1936 CrossRef CAS PubMed.
- V. Chappa, Y. Smirnova, K. Komorowski, M. Müller and T. Salditt, J. Appl. Crystallogr., 2021, 54, 557–568 CrossRef CAS PubMed.
- J. Hoshen and R. Kopelman, Phys. Rev. B, 1976, 14, 3438–3445 CrossRef CAS.
- J. Hoshen, M. W. Berry and K. S. Minser, Phys. Rev. E, 1997, 56, 1455–1460 CrossRef.
- C. Donau, F. Späth, M. Stasi, A. M. Bergmann and J. Boekhoven, Angew. Chem., Int. Ed., 2022, 61, e202211905 CrossRef CAS PubMed.
- R. Lipowsky, Adv. Biol., 2022, 6, 2101020 CrossRef PubMed.
- C. L. Ting and M. Müller, J. Chem. Phys., 2017, 146, 104901 CrossRef PubMed.
- T. V. Tolpekina, W. K. den Otter and W. J. Briels, J. Chem. Phys., 2004, 121, 8014–8020 CrossRef CAS PubMed.
- J. C.-M. Lee, M. Santore, F. S. Bates and D. E. Discher, Macromolecules, 2002, 35, 323–326 CrossRef CAS.
- C. Donau and J. Boekhoven, Trends Chem., 2022, 5, 45–60 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00876b |
| ‡ In rare occasions the pore closes by itself. Furthermore, for reaction rates rb = 2.0 × 10−2λ and rb = 2.8 × 10−2λ a cylindrical micelle with cup-shaped ends persists for long times, up to tλ = 2.5 × 103, where a pure cylindrical micelle remains. Videos of these kinetics are prepared for two exemplary reaction rates in the ESI,† udm-expl-fuel-rb1.67e-2.mp4 and udm-expl-fuel-rb2.00e-2.mp4. |
| This journal is © The Royal Society of Chemistry 2023 |