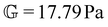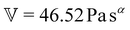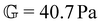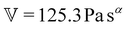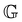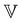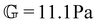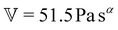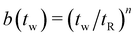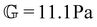Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Elastoviscoplasticity, hyperaging, and time–age-time–temperature superposition in aqueous dispersions of bentonite clay†
Joshua David John
Rathinaraj‡
 a,
Kyle R.
Lennon‡
a,
Kyle R.
Lennon‡
 b,
Miguel
Gonzalez
b,
Miguel
Gonzalez
 c,
Ashok
Santra
c,
James W.
Swan§
b and
Gareth H.
McKinley
c,
Ashok
Santra
c,
James W.
Swan§
b and
Gareth H.
McKinley
 *a
*a
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA. E-mail: gareth@mit.edu
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA
cAramco Services Company: Aramco Research Center, Houston, TX, USA
First published on 9th August 2023
Abstract
Clay slurries are both ubiquitous and essential in the oil exploration industry, and are most commonly employed as drilling fluids. Due to its natural abundance, bentonite clay is often the de facto choice for these materials. Understanding and predicting the mechanical response of these fluids is critical for safe and efficient drilling operations. However, rheological modeling of bentonite clay suspensions is complicated by the fact that thermally-driven microscopic arrangements of particle aggregates lead to a continual evolution of the viscoelastic properties and the yield stress of the suspension with time. Ergodic relations fundamental to linear viscoelastic theory, such as the Boltzmann superposition principle, do not hold in this scenario of ‘rheological aging’. We present an approach for modeling the linear viscoelastic response of aging bentonite suspensions across a range of temperatures that is based on the transformation from laboratory time to an effective ‘material time’ domain in which time-translation invariance holds, and the typical relations of non-aging linear viscoelastic theory apply. In particular, we model the constitutive relationship between stress and strain-rate in the bentonite suspensions as fractional Maxwell gels with constant relaxation dynamics in the material time domain, in parallel with a non-aging Newtonian viscous contribution to the total stress. This approach is supported by experimental measurements of the stress relaxation and rapid time-resolved measurements of the linear viscoelastic properties performed using optimized exponential chirps. This data is then reduced to master curves in the material domain using time–age-time superposition to obtain best fits of the model parameters over a range of operating temperatures.
1 Introduction
Aqueous dispersions of discotic clay platelets exhibit a number of mechanical properties that are of great interest to certain commercial applications, perhaps most notably to drilling operations in the oil and gas industry1–8 where these dispersions are pumped into boreholes and serve a number of purposes including the removal of rock cuttings produced in the drilling process.7,9 The essential thermo-rheo-mechanical properties of the dispersion in such applications include the rapid development of a yield stress – which allows the dispersion to suspend rock cuttings for subsequent transport – as well as a low plastic viscosity – which minimizes the energy required to pump the fluid downhole at high shear rates.8 A proper understanding of the rheology of these clay dispersions and how it evolves with time and the local temperature of the downhole environment is therefore critical for safe and effective drilling operations.One inorganic clay commonly used in these dispersions is bentonite; a naturally abundant clay comprised of microscopic charged platelets of approximate lateral size ∼300 nm. When dispersed in water or brine at appropriate concentrations, the charged bentonite platelets rapidly disperse and produce a viscoelastic yield stress fluid that exhibits a high degree of shear thinning in steady shearing flows, thus simultaneously achieving two essential properties for a drilling fluid.2–5 However, accurate rheological characterization of bentonite dispersions is complicated by the fact that the yield stress and viscosity (along with other mechanical properties of the fluid) are not constant in time. Rather, they evolve continuously with time as the small and highly mobile clay platelets self associate in the suspending matrix fluid, a phenomenon known as rheological aging.10 The additional complexity of incorporating the age of the dispersions as a parameter on which mechanical properties can depend substantially broadens the space of rheological behavior that must be studied, and renders many conventional rheometric tests ineffective.
As an example of the practical effects of this complication, consider the startup of drilling operations after a shutdown. Shutdowns may occur for a number of reasons, including regular maintenance or unforeseen accidents, and their duration is variable. An important requirement for drilling fluids is to rapidly and reversibly develop a yield stress or ‘gel strength’ to suspend drill cuttings and prevent sedimentation. However, during a shutdown period the rheological properties of a drilling mud or fracturing fluid will continue to evolve with time. For non-aging complex fluids, the operational conditions required to ‘break’ the gel and restart steady flow in the drill string do not depend on the duration of the shutdown (assuming the shutdown is longer than the longest relaxation time of the fluid). However, for an aging material, key process conditions, such as the applied pressure required to restart flow in the drill strings, do vary with the shutdown duration, possibly dramatically. Anticipating this change is critical to avoid undesirable affects associated with large required pressures for recirculation.11
In this work, we investigate in detail the age-dependent rheological behavior of bentonite dispersions, with the goals of understanding the microstructural origins of aging in these fluids, quantitatively describing this aging process using an appropriate constitutive equation, and examining the effects of aging on the linear and nonlinear rheological properties of the dispersions. We begin with a physical description of bentonite clay and bentonite dispersions in Section 2, which outlines the physical origins of their yield stress and rheological aging, and then describe techniques used to study these features in Section 3. In Section 4, we investigate the age-dependent steady, transient, and dynamic rheological properties of bentonite dispersions using multiple conventional and modern rheometric techniques. Finally, in Section 5 we develop a constitutive model for the age-dependent linear viscoelastic properties of bentonite dispersions, which quantitatively captures the non-ergodic parametric dependence of the linear relaxation modulus and the frequency-dependent complex modulus with both age-time and temperature. Understanding how these aging materials evolve with elapsed time and with temperature renders the model useful for predicting the mechanical response of bentonite-based drilling fluids in many industrially relevant conditions. Moreover, the model for the linear rheology connects the macroscopic physical properties of bentonite dispersions to their microscopic structure, thereby providing experimental evidence for the physical origins of aging in these attractive colloidal dispersions.
Before embarking on a study of the time-dependent mechanical properties of bentonite clay dispersions, it is instructive to clarify the particular terminology used to describe this ‘time dependence’. Many terms are employed in the rheology literature to describe the dependence of mechanical properties with time. One common term, which is often used to describe the evolution of the plastic viscosity and yield stress of drilling fluids,13 is ‘thixotropy’. The precise definition of thixotropy can vary; some authors adopt a definition which classifies fluids that exhibit a continuous decrease in viscosity during flow (and a subsequent continuous increase in viscosity after cessation of flow) as thixotropic,14 focusing exclusively on the evolution of inelastic properties with time during or after flow, a response sometimes distinguished as ‘ideal thixotropy’.15 Some adopt a much broader definition by also considering time-evolving changes in viscoelastic properties (such as the relaxation modulus or the storage modulus) that are not associated with the viscoelastic relaxation timescale.16 Adopting the latter definition, we may view rheological aging as a subset of the broad spectrum of thixotropic effects, in which the evolution of material properties after cessation of flow is perpetual.
Moreover, the phenomenon of rheological aging is often measured through measurements of material properties other than the viscosity (e.g. the complex modulus G*(ω)), and is driven by evolution in the entire relaxation spectrum (and is therefore not purely inelastic).15 Rheological aging can also be observed during periods of quiescence, rather than only during or after flow.17 These are all features of the time-evolution of the mechanical properties of bentonite dispersions, as will become evident through this study. Thus, we adopt the more precise nomenclature of ‘rheological aging’ for this work.
Although the terms ‘thixotropy’ and ‘rheological aging’ are often employed in studies of drilling fluids in the scientific literature, other descriptive terms are perhaps more commonplace in industrial settings. Simple on-site measurements of drilling fluids involve measuring the shear viscosity and ‘gel strength’ at specified times after the cessation of a short and strong shear flow (e.g. 10 seconds, 10 minutes, and 30 minutes after flow cessation).18 If the gel strength, which is an approximate measure of the static yield stress, is observed to increase substantially between measurements at subsequent times, the gel is referred to as a ‘progressive gel’.18 Rheological aging gives rise to this type of behavior, as the yield stress and the elastic modulus both increase continuously with time. Progressive gels are often not ideal for drilling applications, as they may require large pumping pressures to restart flow along the drill string, which can lead to undesirable effects such as unwanted hydraulic fracturing. Conversely, a gel whose strength does not increase substantially between two measurements is called ‘mild’ or ‘flat’.18 Flat gels may still exhibit time-dependent properties on shorter time-scales; however, this time-dependence either arrests entirely or slows substantially, leading to more predictable, and typically lower, required pressures for recirculation.
2 Physical origins of rheological aging in bentonite
Rheological aging is one of the distinct features of clay suspensions, and can be understood directly from physical considerations of the nano-crystalline structure of bentonite platelets. Sodium bentonite is a montmorillonite clay (see Fig. S1 for the XRD analysis of the sample ESI†), composed of discotic crystals with the chemical formula: Na0.33 [(Al1.67Mg0.33)(O(OH))2(SiO2)4].19 These discotic crystals are three-layered, composed of tetrahedral structures with silicon and aluminum ions in the center, and octahedral structures with aluminum and magnesium ions in the center. The corners of both the tetrahedral and octahedral structures are either oxygen atoms or hydroxyl groups,12,20 with the octahedral structure packed between two tetrahedral layers as shown in Fig. 1(d). Due to the net negative charge of the three-layer crystalline structure, the top and bottom faces of the disc-like crystals carry a negatively charged double-layer, and are therefore associated with free Na+ cations in solution. The exposed edges of the crystals, on the other hand, reveal the internal metal cations, and therefore generate a positively charged double-layer.21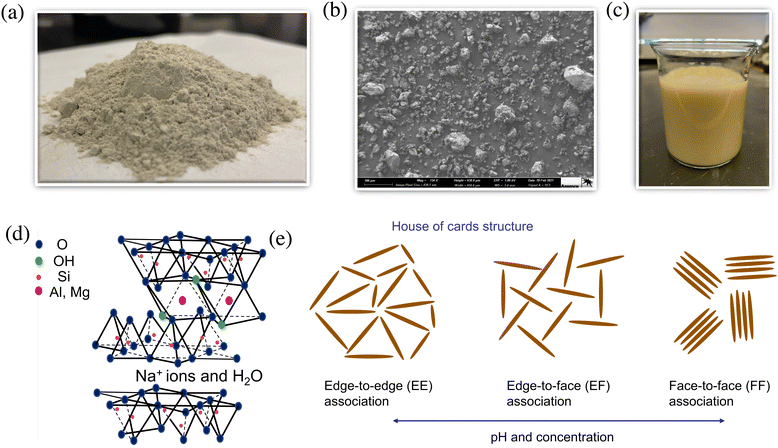 | ||
| Fig. 1 (a) Photograph of anhydrous Wyoming bentonite clay powder (as received). (b) SEM image of anhydrous bentonite particles. (c) Aqueous dispersion of 5 wt% bentonite. (d) The crystalline structure of Na+-montmorillonite platelets, depicting the three-layer structure consisting of outer tetrahedral layers and an inner octahedral layer. Image reproduced from ref. 12. (e) The different modes of association for a dispersion of bentonite platelets. | ||
Individual crystals are separated by exchangeable cations and a hydration layer with a typical separation of 10–20 Å.19 When not dispersed in water, bentonite clay particles are typically 6–200 μm in size7 (please see Fig. S2 for the particle size distribution of the anhydrous bentonite particles, ESI†). A representative photograph of dry Wyoming bentonite clay is shown in Fig. 1(a), and a scanning electron microscope (SEM) image of these clay particles is shown in Fig. 1(b). When dispersed in water (Fig. 1(c)), these clay particles hydrate and exfoliate into disc-shaped platelets. The major axis of the individual platelets is approximately 300–500 nm in length, while the minor axis of the platelets is typically in the range of 200–300 nm. These platelets are very thin with thicknesses typically on the order of 1 nm.22
The process of rheological aging and the development of a viscoelastic gel structure that results in the appearance of a macroscopic yield stress can be rationalized by the different ways in which these platelets associate, and how these associations evolve with time.23 For bentonite platelets, there are three types of possible associations between two platelets: face-to-face association (FF), edge-to-face association (EF), and edge-to-edge association (EE).21 These different platelet configurations are depicted schematically in Fig. 1(e). The relative prevalence of these different modes of association depends on the pH and salt concentration of the aqueous dispersion. For solutions at high pH and high salt concentrations, the double layers on the surface and edges of the crystals are screened; thus the FF mode of interaction dominates. For low pH solutions, when the edges possess a positive charge, the EE and EF associations are more prevalent.19,24–27 The coagulation of a bentonite dispersion can be influenced by the addition of inorganic salts. At a neutral pH, the coagulation process is primarily governed by face–face configurations.28 The structural configurations and clusters of bentonite platelets can be influenced and manipulated by the surface chemistry of the material as well. For example, the adsorption of pyrophosphate anions to the edges and polyetheramines to the faces of montmorillonite platelets has been shown to have a controlling effect on these configurations and thus also influences the rheological properties.29
The inter-particle arrangements and relative prevalence of each mode of association influence the strength of the elastoplastic gel network, including the elastic modulus measured at small strains and the apparent yield stress at large deformations. The average particle anisotropy in a bentonite dispersion can significantly influence the sol-to-gel transition. The concentration required to form a gel increases as the average particle anisotropy increases.30
In a fully dispersed state – when the platelets do not form any large-scale structure, and are instead randomly oriented and distributed throughout the medium (e.g. as a result of large applied shearing deformations in the recent past) – the elastic modulus of the material is the lowest because of the absence of a sample-spanning microstructure able to distribute an applied load. Aggregation due to FF association can similarly decrease the gel strength or elastic modulus by decreasing the number of effective particles in solution.31Flocculation, on the other hand, arises from progressive increases in EF or EE association,19 and is responsible for the appearance and continuous evolution of a gel-like structure. This microstructure is often called a ‘house of cards’ structure.32
The small size of the disc-shaped Brownian particles that constitute this ‘house of cards’ structure in bentonite dispersions mean they are in continuous motion due to thermal fluctuations, causing a slow but steady structural evolution to form progressively more stable microstructures through the development of ever more EF and EE associations. This self-association underpins the process of rheological aging, and these out-of-thermodynamic-equilibrium materials (which show a progressive slowing of their relaxation dynamics with elapsed time) are often known as soft glassy materials.33–35 In the process of rheological aging, the characteristic elastic modulus and relaxation time of these materials both increase progressively with time (i.e., the elastic, solid-like character of a soft glassy material increases with time).19,34,36–41 Thus, in this soft glassy state, the linear storage modulus is generally significantly greater than the loss modulus (i.e., 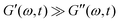 , usually by one order of magnitude), with the storage modulus typically exhibiting a weak power-law dependence on frequency and logarithmic variation in elapsed time.42 Finally, we note that by subjecting these materials to large deformations, one can rejuvenate, or ‘shear melt’, soft glassy materials by breaking up the developed microstructure, thereby reversing some of the effects of rheological aging.43
, usually by one order of magnitude), with the storage modulus typically exhibiting a weak power-law dependence on frequency and logarithmic variation in elapsed time.42 Finally, we note that by subjecting these materials to large deformations, one can rejuvenate, or ‘shear melt’, soft glassy materials by breaking up the developed microstructure, thereby reversing some of the effects of rheological aging.43
3 Materials and methods
The rheological behavior of bentonite is fascinating but at the same time challenging to characterize, because the dispersions exhibit the complex non-ergodic dynamics of rheological aging on top of the rich phenomenology of a viscoelastic yield stress fluid. They may thus be succinctly referred to as thixotropic elasto-viscoplastic (or TEVP) materials.44 In Section 4, we undertake a detailed rheological characterization of these two distinct aspects of the complex thermomechanical response of bentonite. Section 4.1 focuses predominantly on the mechanics of yielding in bentonite dispersions in static, transient, and dynamic contexts. This investigation includes steady shear flow tests, creep tests, and large-amplitude oscillatory shear tests, all of which are commonly employed to characterize soft glassy materials.In Section 4.2, we study in greater detail the dynamics of aging in bentonite dispersions. In particular, we investigate through stress relaxation experiments and mechanical spectroscopy how the linear viscoelastic response of a bentonite suspension evolves as the material ages. Although the rapid and repetitive nature of step stress relaxation experiments generalize well to aging materials, conventional spectral characterization methods such as small-amplitude oscillatory frequency sweeps do not, because of the sample's continuous mutation or change in physical properties during the time required to complete a single frequency sweep. Therefore, the present study makes use of a more rapid characterization approach by imposing trains of optimally windowed chirps to distinguish frequency-dependent and age-dependent effects. The data obtained in this latter approach will inform the rheological modeling presented in Section 5 and enable us to systematically unravel how the viscoelastic properties of these aging soft glasses evolve with both time and temperature. Similar stress relaxation tests and conventional frequency sweep experiments have previously been conducted on discotic clays at longer wait times.38,40,41 Here, we focus on the less studied challenge of extracting data at short wait times whilst still obtaining valuable mechanistic insights into material thixotropy through incorporation of a novel constitutive framework for modeling rheological measurements of aging materials that are not time-translation invariant.
3.1 Material preparation
The 5 wt% aqueous bentonite dispersion was prepared using dry Wyoming bentonite. First, the bentonite powder was added to water and mixed at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 30 minutes using a high shear mixer (Ultra-Turrax T 50 basic mixer, IKA). The dispersion was then placed in a rolling mill for one day to ensure homogeneity and enable the entrained air to separate from the dispersion.
000 rpm for 30 minutes using a high shear mixer (Ultra-Turrax T 50 basic mixer, IKA). The dispersion was then placed in a rolling mill for one day to ensure homogeneity and enable the entrained air to separate from the dispersion.
3.2 Rheometry
Rheometric measurements were performed using a controlled stress rheometer (DHR-3 Discovery Hybrid Rheometer, TA Instruments), with a bottom Peltier plate used to set the system temperature, and an upper 60 mm, 2° aluminum cone textured to prevent slip by attaching self adhesive abrasive sandpaper (Trizact A10, 3 M). The cone-and-plate fixture was encapsulated within a solvent trap sealed with water to mitigate solvent evaporation from the sample. Before every experiment, an aliquot of the bentonite suspension was presheared at 500 s−1 for 30 s to standardize the initial state and reset the material clock. The ‘wait time’ tw (or age time) is considered to be the elapsed time between the cessation of the preshear and the start of an experiment, and the expetimental time t is taken to be the total time elapsed after the end of preshear. The test protocols and data acquisition were performed using the rheometer software (TRIOS v5.0.0). In the case of steady shear flow experiments, results from the DHR were also compared to results obtained in an industry-standard FANN 35 A rotational viscometer.4 Experimental results
4.1 Yielding in bentonite dispersions
In the FANN 35 A viscometer, fluid is contained in the gap between concentric cylinders. The outer cylinder is rotated at a controlled angular speed f (measured in rotations-per-minute, or rpm), and the ensuing motion of the fluid generates a torque on the inner spring-loaded cylinder due to viscous drag, resulting in a small deflection. One degree of deflection corresponds to 0.511 Pa and conversion between rpm in the FANN 35A and the steady shear rate within the fluid is: ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.71f.45 There are six speed settings available in the FANN 35 A viscometer: 3, 6, 100, 200, 300, and 600 rpm.
= 1.71f.45 There are six speed settings available in the FANN 35 A viscometer: 3, 6, 100, 200, 300, and 600 rpm.
Fig. 2 depicts the measured steady shear stress and the corresponding steady shear viscosity η = σ/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for a 5 wt% bentonite dispersion at room temperature (25 °C), measured with the FANN viscometer (blue circles) and with the DHR at shear rates
for a 5 wt% bentonite dispersion at room temperature (25 °C), measured with the FANN viscometer (blue circles) and with the DHR at shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∈[1,1000] s−1 with five points per decade (red circles). The stress and viscosity values measured for the six different shear rates from the FANN are in good agreement with the flow curve measured by the DHR for the 5 wt% bentonite dispersion. The shear thinning property of the bentonite dispersion observed in Fig. 2 is one feature that makes this formulation highly desirable for drilling applications, as the bentonite mud can effectively suspend drill cuttings due to its high viscosity at low shear rates while reducing the required pumping power due to its low viscosity at high shear rates.46–48
∈[1,1000] s−1 with five points per decade (red circles). The stress and viscosity values measured for the six different shear rates from the FANN are in good agreement with the flow curve measured by the DHR for the 5 wt% bentonite dispersion. The shear thinning property of the bentonite dispersion observed in Fig. 2 is one feature that makes this formulation highly desirable for drilling applications, as the bentonite mud can effectively suspend drill cuttings due to its high viscosity at low shear rates while reducing the required pumping power due to its low viscosity at high shear rates.46–48
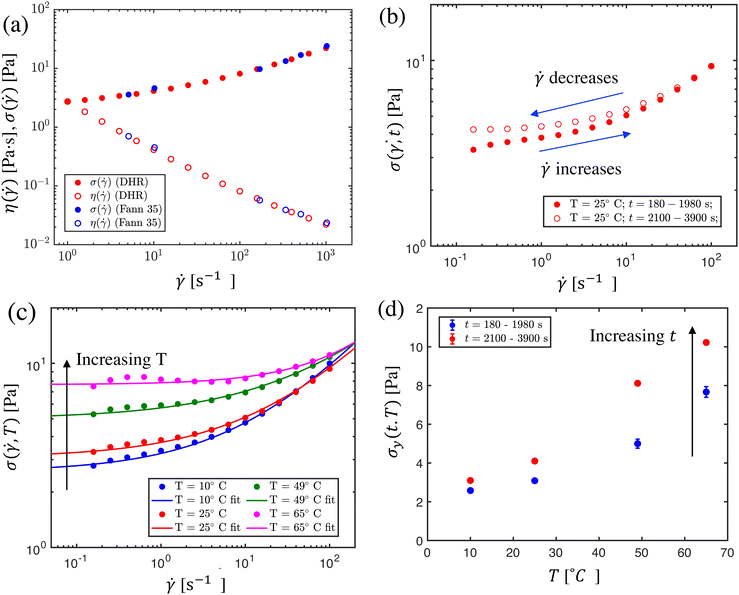 | ||
Fig. 2 The steady flow curve for bentonite dispersions at different temperatures and age times. (a) Comparison of the steady shear stress (filled circles) and viscosity (unfilled circles) measured by the FANN 35A viscometer (blue) and DHR-3 rheometer (red) for a 5 wt% aqueous bentonite dispersion at room temperature (25 °C). (b) The flow curve measured at room temperature by an increasing-rate sweep and decreasing-rate sweep, showing hysteresis due to rheological aging. (c) Flow curves measured at different temperatures via increasing-rate sweeps. The Herschel Bulkley (HB) model, σ = σy + k![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n, is fit to the data to calculate the apparent dynamic yield stress. The parameters of the HB fits for different temperatures T = 10 °C, 25 °C, 49 °C and 65 °C are: σy = 2.5 Pa, 3 Pa, 5 Pa, and 7.6 Pa; k = 0.66 Pa sn, 0.64 Pa sn, 0.73 Pa sn and 0.17 Pa sn; and n = 0.52, 0.49, 0.44 and 0.64, respectively. (d) The apparent dynamic yield stress at each measured temperature for increasing- and decreasing-rate sweeps. Please see Fig. S3 (ESI†) for the decreasing-rate sweeps and their corresponding Herschel Bulkley fits. n, is fit to the data to calculate the apparent dynamic yield stress. The parameters of the HB fits for different temperatures T = 10 °C, 25 °C, 49 °C and 65 °C are: σy = 2.5 Pa, 3 Pa, 5 Pa, and 7.6 Pa; k = 0.66 Pa sn, 0.64 Pa sn, 0.73 Pa sn and 0.17 Pa sn; and n = 0.52, 0.49, 0.44 and 0.64, respectively. (d) The apparent dynamic yield stress at each measured temperature for increasing- and decreasing-rate sweeps. Please see Fig. S3 (ESI†) for the decreasing-rate sweeps and their corresponding Herschel Bulkley fits. | ||
Having validated the accuracy of the FANN viscometer against the flow curve measured by the DHR rheometer, we next characterized the flow curve of the bentonite dispersion at four different temperatures: 10 °C, 25 °C, 49 °C, and 65 °C, using the controlled stress rheometer. To better resolve the yield stress plateau, we studied a lower range of shear rates, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∈[0.1,100] s−1, with five points per decade. At each temperature, the shear rate is first progressively increased from 0.1 s−1 to 100 s−1, beginning after a wait time of tw = 180 s, and then progressively decreased from 100 s−1 to 0.1 s−1, beginning at tw = 2100 s. In each direction, the duration of the entire flow sweep was 1800 s. Measurements of the resulting steady shear stress are shown in Fig. 2.
∈[0.1,100] s−1, with five points per decade. At each temperature, the shear rate is first progressively increased from 0.1 s−1 to 100 s−1, beginning after a wait time of tw = 180 s, and then progressively decreased from 100 s−1 to 0.1 s−1, beginning at tw = 2100 s. In each direction, the duration of the entire flow sweep was 1800 s. Measurements of the resulting steady shear stress are shown in Fig. 2.
The flow curves depicted in Fig. 2 illustrate two notable features of the steady flow behavior of bentonite. Firstly, rheological hysteresis is evident in the upwards and downwards sweeps in Fig. 2(b), as the steady shear stress measured during the decreasing shear rate sweep is higher than that measured by the earlier increasing shear rate sweep, particularly at low shear rates. For clarity, only room temperature (25 °C) data is shown in the plot; however, flow curves at other test temperatures display similar qualitative features, and are presented in the ESI.† The observed hysteresis is due to the gradual build-up of the gel-like microstructure49,50 as the shear rate is progressively decreased, leading to a stronger gel developing in the decreasing-rate sweeps especially at low rates, (corresponding to longer sample age times) whereas the same development of structure of the bentonite platelets cannot occur in the shorter elapsed time between the initial preshear and the first low-rate measurements in the increasing-rate sweeps. Ultimately, the flow curves for the increasing- and decreasing-rate sweeps converge at high shear rates above 50 s−1, as the gel-like structure is broken down faster than it can be rebuilt, and viscous dissipation dominates the observed rate-dependent response.
The second important characteristic of these flow curves is that they exhibit the expected shape for a yield–stress fluid with shear-thinning characteristics. Flow curves of this form are well-described by the simple viscoplastic Herschel–Bulkley model:
σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = σy + k ) = σy + k![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n n | (1) |
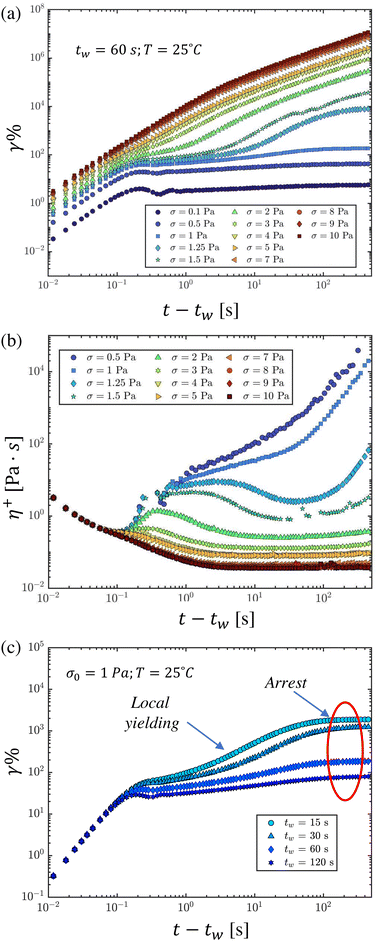
We first conducted creep tests for a range of applied stresses σ0∈ [0.1,10] Pa at T = 25 °C, and for a wait time of tw = 60 s after preshear. The evolution of the accumulated strain, as shown in Fig. 3(a), depends sensitively on the applied stress. It has been proposed that these strain trajectories can be classified into three distinct regimes, based on the applied stress.10 In the solid-like regime, the applied stress is less than a value called the first critical stress, σc1. In this regime, the applied stress does not generate enough shear to break down the gel microstructure faster than it is rebuilt due to thermal motion. This results in a progressive decrease in the rate of shearing, and eventual cessation of flow. Another regime is characterized by applied stresses greater than the second critical stress, σc2. In this regime, the applied stress imposes sufficient shear strain in the sample to break down the microstructure faster than it can be rebuilt, leading to a net breakdown of structure and increase in the rate of shearing to an eventual steady rate, which is set either by the balance between structural break down and build up, or by viscous dissipation in the dispersion at very high rates. Fluids in this regime may be described as exhibiting viscoplastic liquid-like behavior, and the second critical stress is typically considered to be the static yield stress of the material.10 More complex effects such as transient shear banding may also develop in the material.23
In the intermediate regime between σc1 and σc2, more complicated elastoviscoplastic (EVP) transients are observed, representing the complex interplay between structural break down due to both the accumulated strain, the stress-activated rate of microstructural breakdown and the structural build-up with time. Initially, the young sample is at its most disordered, and therefore continues to build up internal structure. This build-up eclipses the initial rate of break down, causing a decrease in the instantaneous rate of shearing. However, as the rate of aging slows in the soft glassy material, the shear has not decreased to complete cessation, and eventually structural break down overtakes microstructure formation, resulting in a delayed yielding and transition to a steady flow. This slow flow is not steady in time, however, and fluctuations in the local microstructure eventually may lead to cessation of flow.10
This complex phenomenon is generically known as viscosity bifurcation,56 and can be seen in the evolution of the apparent viscosity ηapp(t,σ0) = σ0/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (tage) evolution with time of creep as illustrated in Fig. 3(b), where flow curves measured at high applied stress stabilize at low values of the steady-shear viscosity, while a bifurcation is observed at a critical stress corresponding to σc2, after which (i.e., σ < σc2)the curves tend towards infinite viscosities at long times.
(tage) evolution with time of creep as illustrated in Fig. 3(b), where flow curves measured at high applied stress stabilize at low values of the steady-shear viscosity, while a bifurcation is observed at a critical stress corresponding to σc2, after which (i.e., σ < σc2)the curves tend towards infinite viscosities at long times.
These three classes of yielding transients, and the corresponding viscosity bifurcation, are evident in both Fig. 3(a), which depicts the accumulated strain after loading, and Fig. 3(b), which depicts the evolution in the apparent viscosity defined as ηapp(t,σ0) = σ0/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t). In all cases there is an initial inertial response of the instrument (corresponding to the quadratic increase in strain at early times57). For the 5 wt% bentonite dispersion there is a monotonic decrease in the rate of shearing
(t). In all cases there is an initial inertial response of the instrument (corresponding to the quadratic increase in strain at early times57). For the 5 wt% bentonite dispersion there is a monotonic decrease in the rate of shearing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) – or equivalently a monotonic increase in the apparent viscosity for applied stresses below σc1 = 1 Pa. A more complex intermediate, transient elastoviscoplastic creep response is observed for curves between this first critical stress and the second critical stress of approximately σc2 = 2 Pa. Beyond σc2, the transient motion always evolves to a steady shearing deformation (with the shear strain increasing as γ ∼
(t) – or equivalently a monotonic increase in the apparent viscosity for applied stresses below σc1 = 1 Pa. A more complex intermediate, transient elastoviscoplastic creep response is observed for curves between this first critical stress and the second critical stress of approximately σc2 = 2 Pa. Beyond σc2, the transient motion always evolves to a steady shearing deformation (with the shear strain increasing as γ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t) and the viscoplastic material ‘flows’.
t) and the viscoplastic material ‘flows’.
It is clear from these results and accompanying discussion that the transient creep dynamics of bentonite below the second critical stress, σc2, are sensitive to the rate of physical aging, which itself depends on the rheological age of the dispersion and also on the wait time tw since the initial preshear. We investigate this sensitivity by holding the applied stress constant at σ0 = 1 Pa, and instead varying the wait time tw before the load is applied. The resulting creep trajectories are depicted in Fig. 3(c). For small wait times, we observe an elastoviscoplastic response characteristic of the intermediate regime, σc1 ≤ σ0 ≤ σc2. However beyond a waiting time of tw = 60 s the material has sufficiently aged that it responds (at this level of applied stress) as a viscoelastic solid.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ω(t − tw)) is applied beginning at the end of the wait time tw, and the output strain or strain rate measured. One convenient tool for visualising LAOS data is the Lissajous curve, which parameterically represents the shear stress σ(t) on one axis and the shear strain γ(t) (or strain rate
sin(ω(t − tw)) is applied beginning at the end of the wait time tw, and the output strain or strain rate measured. One convenient tool for visualising LAOS data is the Lissajous curve, which parameterically represents the shear stress σ(t) on one axis and the shear strain γ(t) (or strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t)) on the other. The shape of these Lissajous curves indicate important features about the material response at the time scale dictated by ω and the deformation scale dictated by σ0, such as whether the experiment is in the linear or nonlinear deformation regime, and whether energy storage (elastic effects) or energy dissipation (viscous effects) is dominant.
(t)) on the other. The shape of these Lissajous curves indicate important features about the material response at the time scale dictated by ω and the deformation scale dictated by σ0, such as whether the experiment is in the linear or nonlinear deformation regime, and whether energy storage (elastic effects) or energy dissipation (viscous effects) is dominant.
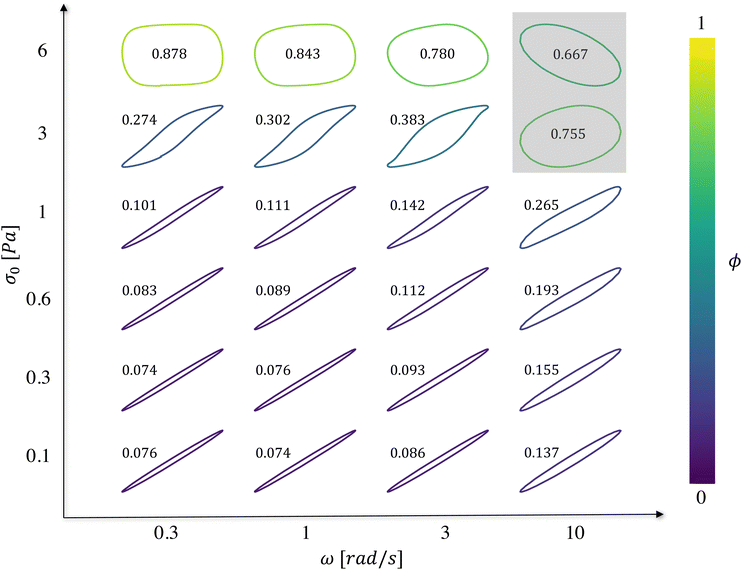
In Fig. 4, we depict Lissajous curves taken at T = 25 °C for four frequencies ω∈[0.3,10] rad s−1 and six stress amplitudes σ0∈[0.1,6], with a wait time of tw = 300 s. Before we interpret these curves in the context of dynamic yielding, we note that it is important in stress-controlled dynamical tests such as LAOS to assess sources of instrumental bias – in this case, inertia from the cone-and-plate fixture at high frequencies and high amplitudes. To quantify such effects, we apply the dimensionless ‘inertia number’ In, defined by Dimitrou et al. as the ratio of inertial torque Ti and sample torque Ts.60 For a cone-and-plate fixture with radius R and angle θ0, the inertial torque Ti ≈ Iω2θ0γ0 and the sample torque is given by 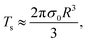 thus the inertia number is:
thus the inertia number is:
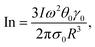 | (2) |
With inertial corrections in place, the Lissajous curves may be used to extract information about dynamic yielding in bentonite dispersions. One useful heuristic for characterizing the extent of dynamic yielding from these curves is the normalized area fraction,60 defined as:
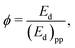 | (3) |
| Ed = σdγ, | (4) |
| (Ed)pp = (σmax − σmin)(γmax − γmin). | (5) |
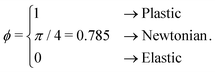 | (6) |
This area fraction ϕ is also reported for every Lissajous curve in Fig. 4. For low stress amplitudes, the Lissajous curves are elliptic, meaning the material response is approximately linear viscoelastic in character. Moreover, ϕ is nearly zero for these low-amplitude measurements across the frequency range, indicating a predominantly elastic, solid-like response. With increasing stress amplitude, the Lissajous curves widen, indicating a more dissipative viscoelastic response. At intermediate stress amplitudes the material response is clearly nonlinear and fully elastoviscoplastic models60–62 are required to describe the stress-dependent and frequency-dependent yielding dynamics. At the highest stress amplitude of σ0 = 6 Pa, ϕ exceeds the value for a Newtonian fluid. For these largest stress amplitude experiments, therefore, the dispersion appears to dynamically yield and flow. For these high amplitude, viscoplastic-like responses, we observe that ϕ decreases with increasing frequency, indicating that the extent to which the dispersion yields has decreased. Thus, dynamical yielding in bentonite dispersions appears to be frequency-dependent, with an apparent yield stress that increases with increasing frequency, or decreasing deformation time-scale.
From the flow curve experiments at various temperatures discussed in Section 4.1.1, it is observed that the yield stress increases with temperature. Therefore, we expect the plastic flow regimes observed in LAOS tests to occur at higher imposed stress amplitudes as the temperature increases. However, it is important to note that despite these changes, we can still anticipate qualitatively similar Lissajous curves characterized by a transition from a predominantly linear elastic response at small strains to a non-linear viscoelastic response, and eventually to a plastic (yielding) response, as the imposed oscillatory stress increases. The principal difference would be that each of these material state transitions will occur at higher stress amplitudes with increasing temperature.
4.2 Rheological aging in bentonite dispersions
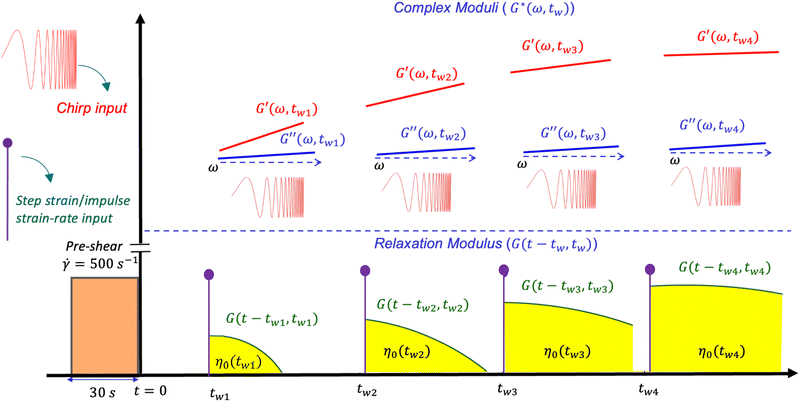
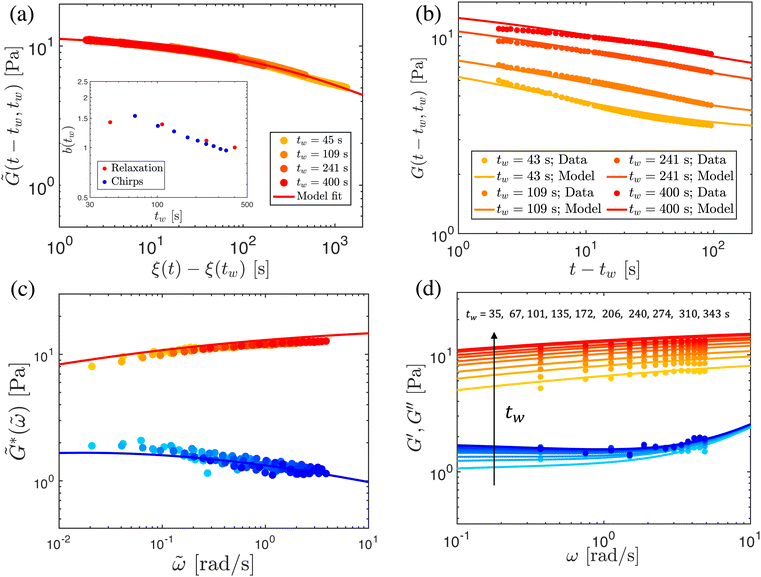
The previous sections detailed three nonlinear rheological tests, which revealed a rich phenomenology of wait-time, temperature, and deformation time-scale-dependent yielding in bentonite dispersions. In some instances, we investigated the dependence of these effects on rheological aging; however, the high-dimensional state and response spaces of nonlinear rheological tests make a detailed quantification and constitutive modeling of rheological aging in this soft glassy material difficult. To simplify this modeling challenge, we turn instead to linear rheological studies. In linear time invariant (LTI), non-aging systems, the linear stress relaxation modulus depends only on the elapsed time since the imposition of the deformation, G(t − tw). One common description of rheological aging for non-LTI systems is that the linear relaxation modulus is parametric in the wait time since initial sample preparation or resetting of the material clock by preshear, G(t − tw,tw).17 Similarly, treating tw parametrically and assuming the material response is pseudo-steady in tw, we may define a linear complex modulus, G*(ω,tw).A natural way to characterize the wait time-dependent relaxation modulus is through stress relaxation tests, performed at different wait times. This is sufficient for a non-LTI system, because in defining G(t − tw,tw) we have only assumed that the step strain is applied instantaneously at tw. However, in defining the complex modulus G*(ω,tw), we have assumed that the material response is pseudo-steady in tw, meaning that the material does not substantially age during the time required to perform an experimental measurement at frequency ω. For traditional small amplitude frequency sweeps, which take minutes to complete, this criterion is clearly not satisfied. Therefore, we must turn to modern techniques with higher time resolution to characterize G*(ω,tw) within the pseudo-steady approximation. Here, we employ exponential chirps, which take only ∼10 seconds to characterize G*(ω,tw) over one order of magnitude in frequency. As with the stress relaxation experiments, we may apply these chirps at successive wait times, to characterize the linear viscoelasticity of the suspensions as a function of both time-scale and material age. A schematic diagram of the data collected by applying optimally windowed, exponential chirps, along with stress relaxation experiments, to bentonite dispersion is presented in Fig. 5.
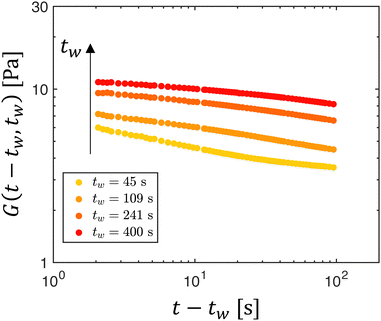
The stress relaxation experiments at fixed temperature reveal two important features of rheological aging, both of which are in agreement with our physical description of aging in bentonite dispersions in Section 2 and with the previous experimental results. Firstly, the relaxation modulus increases with tw at each temperature. This increase is simply a result of the stronger, more developed microstructure in dispersions that have undergone more aging, compared to the relatively weak character of the young dispersions. Secondly, the relaxation modulus decays faster for small wait times, corresponding to a progressive slowing of relaxation dynamics with rheological aging as the system gradually settles into a more energetically stable microstructural state. In some of the shortest wait time experiments (e.g., the wait time of 45 s in Fig. 6), we also observe a long-time plateau in the relaxation modulus i.e., the system mechanically ‘arrests’. This is another notable feature of rheological aging systems, but its origins from physical considerations are less obvious. In the Appendix, we instead explore the origins of this feature from a modeling perspective, which incorporates phenomenological theories of rheological aging. Moreover, in Fig. 5, we note that the area under the stress relaxation curves is equivalent to the zero-shear viscosity η0(tw); thus, the data in Fig. 6 indicate graphically that the system's viscosity increases as the suspension ages.
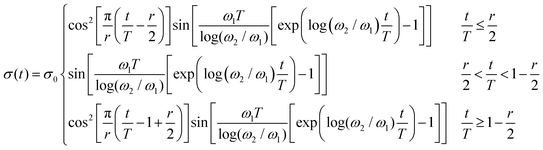 | (7) |
In our experiments the period of the chirp is T = 14 s, the cutoff frequencies are ω1 = 0.3 rad s−1 and ω2 = 5 rad s−1. Since we are working with a shorter chirp signal (time-bandwidth TB = T(ω2 − ω1)/(2π) = 10.62 < 100), windowing the exponential chirp signal is essential to reduce spectral leakage and restore general periodicity in the output signal. This enables a reduction in oscillatory errors in the moduli measurements.64 In the present study, we utilize a Tukey window with a tapering parameter of r = 0.1 combined with our exponential chirp, as it has been shown to be the optimal window for obtaining rheological measurements.64 The imposed stress amplitude is σ0 = 0.1 Pa and is far below the yield stress of the dispersion even at short age times. Because we have confirmed using stress relaxation experiments that stress signals of this amplitude do not alter the microstructure of bentonite, we may interpret each successive chirp as an independent measurement of the frequency spectrum of the aging dispersion, as though the material had remained undisturbed until the time tw at which the chirp signal begins. We treat each chirp as an “instantaneous” measurement, which is of course a coarse approximation at early times. However, it is important to note that as the wait time increases in an aging material the mutation number monotonically decreases. This decrease occurs due to the progressive slowing down in the rate of aging with time, resulting in progressively improved accuracy in the localization and computation of the complex moduli as the wait time increases and the chirp duration becomes much smaller than the sample age.50
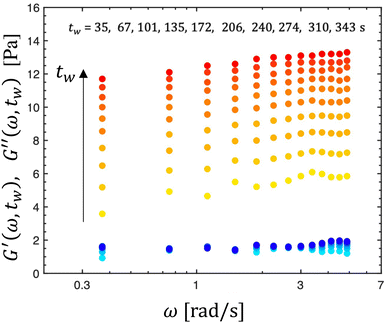
The storage and loss moduli measured by a series of ten chirps at T = 10 °C are presented in Fig. 7. The storage modulus measured by each chirp increases with the age time of the dispersion and displays a weak power-law dependence with frequency, consistent with previous observations and theoretical predictions for soft glassy materials.17,33 The loss modulus, on the other hand, remains relatively insensitive to both the imposed frequency and to the age of the suspension. Although these qualitative observations are consistent with the physical description of rheological aging in bentonite suspensions, obtaining deeper quantitative insight into the data requires the development of an appropriate viscoelastic constitutive model, which is the focus of the next section.
5 Modeling linear viscoelasticity and rheological aging in bentonite suspensions
We now seek to develop a constitutive model, based on the data obtained from the chirp experiments and stress relaxation experiments reported in the previous section, to enable prediction of the linear rheological properties of aging bentonite dispersions over a range of time scales and temperatures. To describe the time-, age-, and temperature-dependent linear viscoelastic behavior of the bentonite dispersions, we will proceed in three steps. First, we supply the hypothesis that the microstructure within the dispersion responds to imposed deformations or loading on a time scale proportional to its characteristic relaxation time, while this relaxation time itself increases as the material ages. Thus, we may rescale the ‘laboratory’ (or real) time coordinate by this relaxation time to obtain an effective ‘material time’, in which the microstructural response appears constant. This process of ‘time–age-time superposition’ (TATS) generates a master curve of the relaxation and complex modulus in the material time and frequency domain for each temperature. With this transformation complete, the next step in modeling is to select a constitutive equation to describe the linear viscoelastic response in material time. Here, we employ the Fractional Maxwell Gel (FMG) model for this purpose. Finally, we may use the parameters of the FMG model fits at each temperature to shift the individual TATS master curves obtained at each temperature onto a single superposed ‘grand master curve’, representing ‘time–age-time–temperature superposition’ (TATTS) of the data. The resulting constitutive model accounts both for the temperature-dependent dynamics and aging of the linear response. It can then be used to predict the TATS master curves over a range of temperatures, and remapping the time coordinate of each master curves to the laboratory time produces predictions for the evolution in the relaxation modulus G(t − tw,tw,T) and complex modulus G*(ω,tw,T) at any intermediate time or temperature.5.1 Transformation to material time
As a result of aging, the Boltzmann superposition principle does not hold for the linear rheology of the bentonite dispersion.34,66 For systems in which the relaxation modulus is age-time dependent, the stress must be written in the form:17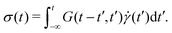 | (8) |
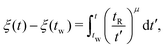 | (9) |
Now, considering the elapsed time in the material time domain, the output stress can be written in terms of the Boltzmann superposition integral with the effective relaxation modulus ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) defined in the material time domain:34,36,42
defined in the material time domain:34,36,42
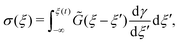 | (10) |
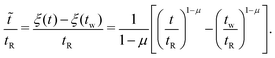 | (11) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) in the material time domain by multiplying with a vertical shift factor b(tw), which accounts for the age-dependent modulus scale:
in the material time domain by multiplying with a vertical shift factor b(tw), which accounts for the age-dependent modulus scale:![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ( (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) = b(tw)G( ) = b(tw)G(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ,tw) ,tw) | (12) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = ξ(t) − ξ(tw) axis. To obtain the effective complex modulus
= ξ(t) − ξ(tw) axis. To obtain the effective complex modulus ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) * in the effective frequency domain
* in the effective frequency domain ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) , we apply a Fourier transform with respect to the material domain variables
, we apply a Fourier transform with respect to the material domain variables ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) and
and ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif)
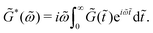 | (13) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) *( *(![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) = b(tw)[G*(ω(tw/tR)μ,tw) − iη0ω], ) = b(tw)[G*(ω(tw/tR)μ,tw) − iη0ω], | (14) |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) in the material domain in terms of the actual imposed laboratory frequency ω:
in the material domain in terms of the actual imposed laboratory frequency ω: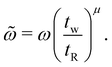 | (15) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) and complex modulus
) and complex modulus ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) *(
*(![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ) in the material time domain.
) in the material time domain.
5.2 The fractional Maxwell gel model in material time
One phenomenological viscoelastic model that is capable of describing many of the qualitative features of the linear rheology of bentonite is the fractional Maxwell gel (FMG) model.69,70 In what follows, we model the linear rheology of bentonite by applying the FMG model to describe the component of the rheological response that ages, and adding a non-aging viscous element in parallel to describe background solvent effects. The proposed micromechanical model is shown in Fig. 8.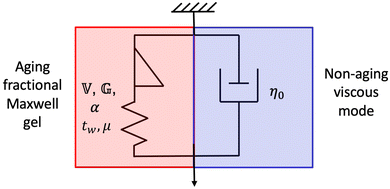 | ||
| Fig. 8 Proposed mechanical model for the aging linear viscoelastic response of the 5 wt% bentonite dispersion, which is composed of an aging FMG model in parallel with a non-aging viscous mode. | ||
The constitutive equation for the aging FMG69,70 in the material time domain is:
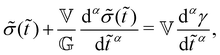 | (16) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) is the stress in the material time domain and
is the stress in the material time domain and 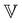 ,
, 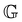 and α are the parameters of the FMG model. Dimensional considerations show that
and α are the parameters of the FMG model. Dimensional considerations show that 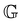 is a modulus with SI units of [Pa] and
is a modulus with SI units of [Pa] and 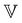 is a quasistatic property with units [Pa sα].69 The contribution to the total stress for the non-aging viscous mode, σv, in laboratory time is given by:
is a quasistatic property with units [Pa sα].69 The contribution to the total stress for the non-aging viscous mode, σv, in laboratory time is given by:σv(t) = η0![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t). (t). | (17) |
σ(t − tw,tw) = ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ( (![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) )/b(tw) + σv(t − tw), )/b(tw) + σv(t − tw), | (18) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) given by eqn (11).
given by eqn (11).
In order to fit the viscoelastic response of the bentonite dispersion in the material time domain using the FMG model, the non-aging viscous mode should first be subtracted from the total real-time response. The relaxation modulus for the model sketched in Fig. 8 in the real time domain is given by the expression:
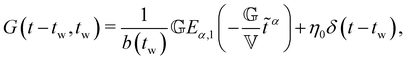 | (19) |
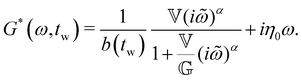 | (20) |
 parameterize the aging FMG model with the characteristic material time scale:
parameterize the aging FMG model with the characteristic material time scale: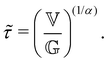 | (21) |
5.3 Fitting the model to experimental data
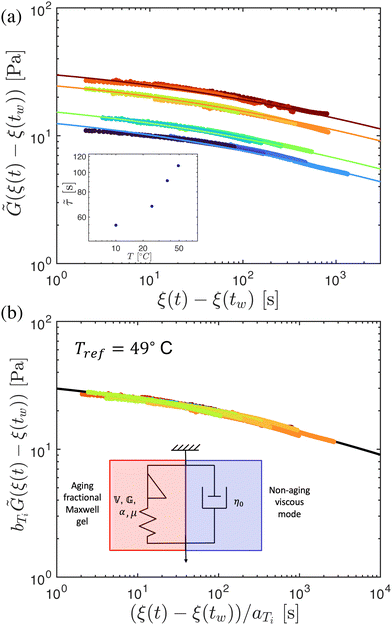
To fit the exponentially-measured chirp and stress relaxation data at a fixed temperature to the proposed constitutive model, we first determine the values of η0, μ, and the set of {b(t(i)w)} for each t(i)w within the data set, which optimally superpose the data onto separate master curves for the relaxation modulus and complex modulus (using eqn (11), (12) and (14) with a reference time of tR = 400 s). This fitting is done by visual inspection. For the T = 10 °C data, the optimal values for η0 and μ were found to be η0 = 0.15 Pa s and μ = 1.6, which were validated using a automated technique for data superposition we have recently developed.72 For determining the vertical shift factors ({b(t(i)w)}) from measurements of the evolving complex moduli in the post-gelled bentonite dispersion, it is convenient to use the age-dependent storage modulus data (G′(ω,tw)) data because it is not influenced by the non-aging solvent contribution to the oscillatory stress (which affects measurements of the viscous loss modulus). However, at early times, when the dispersion is in a pre-gel case, and the dominant contribution to the stress is the aging viscous response, more robust determination of the vertical shift factors can be obtained from the loss moduli data (G′′(ω,tw)).73 Once these master curves were constructed, they were fit to the FMG model (eqn (19) and (20)) simultaneously using nonlinear least-squares regression, giving parameter values of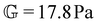 ,
, 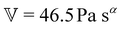 , α = 0.24 and
, α = 0.24 and ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) = 54.7 s for the T = 10 °C data. The resulting master curves and model fit for this temperature, both in the material time and the laboratory time, are shown in Fig. 9.
= 54.7 s for the T = 10 °C data. The resulting master curves and model fit for this temperature, both in the material time and the laboratory time, are shown in Fig. 9.
This time–age-time superposition (TATS) process, and the subsequent regression of the master curve to the FMG model, was repeated for the experimental data at each temperature. The fits to the relaxation modulus in material time and laboratory time for temperatures T = 25 °C, T = 37 °C, and T = 49 °C are shown in the Fig. S5 (ESI†). Master curves for the relaxation modulus at each temperature are presented in Fig. 10(a). In the fits of these master curves to the FMG model, we have constrained η0 = 0.15 Pa s and α = 0.24 at every temperature. The latter of these assumptions is necessary such that the model itself is parametrically self-similar in temperature. That is, in order to superpose these TATS master curves onto a time–age-time–temperature (TATTS) grand master curve at a reference temperature (Tref), we must have that the FMG model predictions at temperatures Tref and T are related by horizontal and vertical shift factors aT and bT, respectively (note that bT here is a shift factor with respect to temperature, distinct from the b(tw) shift factors used for TATS):
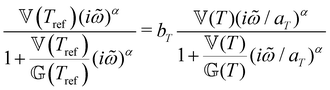 | (22) |
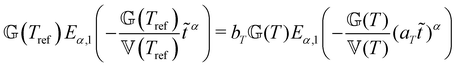 | (23) |
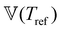 ,
, 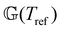 ) and (
) and (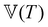 ,
, 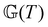 ) are the FMG model parameters determined at the selected reference temperature (Tref) and an individual test temperatures (T), respectively. For eqn (22) and (23) to hold requires that the horizontal and vertical shift factors aT and bT are given by:
) are the FMG model parameters determined at the selected reference temperature (Tref) and an individual test temperatures (T), respectively. For eqn (22) and (23) to hold requires that the horizontal and vertical shift factors aT and bT are given by: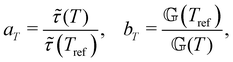 | (24) |
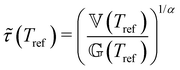 and
and 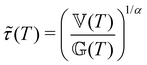 .
.
Thus, by fitting the FMG model to the data sets obtained at each temperature with α held constant, we may construct the grand master curve directly from the regressed model parameters. The constraint that α = 0.24 for all temperatures does not affect the quality of the fits, as evidenced by Fig. 10(a), supporting the hypothesis of parametric self-similarity in temperature. The grand master curve of the stress relaxation data constructed via this procedure (with Tref = 49 °C) is shown in Fig. 10(b), and the values of the model parameters for each temperature are tabulated in Table 1.
One observation of note from the grand master curve is that the horizontal shift factors aT increase monotonically with temperature, corresponding to an increase in the characteristic relaxation time, while the vertical shift factor bT decreases with temperature, corresponding to an increase in the modulus scale. This increase in the modulus is likely attributable to the increased rate of microstructural rearrangement due to enhanced thermal motion, which leads to the faster development of a stronger microstructure. We may also attribute the increase in the characteristic relaxation time with temperature to these stronger microstructures, though this effect may be confounded with other effects, such as faster energy dissipation due to enhanced thermal fluctuations, which would tend to decrease the relaxation time.
6 Discussion
Although the aging FMG model is valuable on its own as a predictive tool for describing the rheology of bentonite dispersions at different temperatures, certain aspects of the model may be interpreted in a physical context as well, and may therefore provide a connection between the microscopic structure of bentonite dispersions and their mechanical properties. In particular, it has been previously reported that the aging exponent μ(T) is a linear function of 1/T.40 We find that this functional form describes our data well, as illustrated in Fig. 11(a). The best fit for μ with 1/T is determined by least-squares regression to be: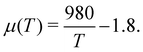 | (25) |
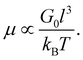 | (26) |
In motivating this study of bentonite dispersions, we noted that it is critical to anticipate the physical properties of suspensions in industrial applications, such as drilling operations. In those circumstances, however, nonlinear properties such as the yield stress of the suspension are also important. It is difficult to model these nonlinear properties for an aging dispersion; thus, we have focused in the previous section on modeling the linear thermorheological properties of the suspension. In our discussion of the physical origins of aging in Section 2, we noted that the elastic strength of the suspension in the linear regime and the yield stress both relate to the same physical feature: the continuously aging gel microstructure. Thus, our model for aging in the linear response may provide useful predictions for nonlinear properties as well, such as the yield stress.
To examine the correlation between the linear model and nonlinear properties, we cross plot the yield stress and the linear viscoelastic modulus determined from the FMG model in Fig. 11(c). The measurements of the yield stress corresponds to increasing shear-rate sweeps (flow curve) beginning at tw = 180 s, whereas the FMG modulus corresponds to a reference wait time of tw = 400 s. Thus, we first correct for aging in the yield stress by interpolating the vertical shift factors b(tw) determined for the stress relaxation data using eqn (19). With this correction in place, we see that a log–log plot of σyvs.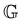 reveals a near linear relationship with a slope near unity, corresponding to linear proportionality between
reveals a near linear relationship with a slope near unity, corresponding to linear proportionality between 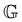 and σy. Thus, in practice, our model for the linear response of bentonite suspensions, which accounts for both temperature- and age-related effects, may be used to predict the gel modulus
and σy. Thus, in practice, our model for the linear response of bentonite suspensions, which accounts for both temperature- and age-related effects, may be used to predict the gel modulus 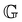 at a particular wait time and temperature, and this prediction can subsequently be correlated to the anticipated static yield stress. This procedure may be of direct utility in industrial drilling applications, where the evolution of the yield stress of the drilling fluid after a period of shutdown is a critically important property.
at a particular wait time and temperature, and this prediction can subsequently be correlated to the anticipated static yield stress. This procedure may be of direct utility in industrial drilling applications, where the evolution of the yield stress of the drilling fluid after a period of shutdown is a critically important property.
7 Conclusions
As evidenced by the richness of the data sets presented throughout this work, the thermomechanical behavior of bentonite dispersions in shear is quite complex. In steady shear, creep, and LAOS tests, we have observed the rich phenomenology of an aging yield–stress fluid, with a temperature-dependent yield stress plateau, multi-step transient yielding, and an apparent dynamic yielding transition that depends on the deformation time-scale. The yield stress, as well as the transient signatures in the creep compliance observed below this stress, depend on the age of the material as well as its temperature, with older dispersions appearing stronger due to the development of a more stable microstructure. In drilling applications, the temperature- and age-dependence of this yielding transition highlights the importance of understanding the fluid's rheology for safe and efficient operations. During shut-downs the time at which drilling fluids remain at rest, along with the downstream temperature, can be used to anticipate the additional pumping power required to restart flow.The inherent complexities introduced by plasticity and aging in the nonlinear rheology of bentonite dispersions renders modeling difficult in that regime. However, the signatures of aging are still evident in the linear response, and therefore we have developed a quantitative model to describe the observations from small-amplitude oscillatory chirp and linear stress relaxation data. This model captures the power-law aging in the mechanical properties of bentonite and the linear viscoelastic response in the reduced ‘material time’ domain is well-described by a fractional Maxwell gel (FMG) model. Moreover, the response is self-similar in temperature, and therefore measurements at different temperatures may be collapsed onto a ‘grand master curve’ to allow for rapid predictions of the evolving linear rheological properties of the aging gel at different temperatures and wait times. Not only does this time–age-time–temperature (TATTS) framework provide a predictive tool for describing the linear viscoelastic properties of the bentonite dispersions, but the aging dynamics observed at different temperatures are consistent with certain microscopic physical properties of the material, such as an intrinsic modulus and the size of platelets. Recognizing these connections, it may be possible to directly apply the same modeling framework outlined in this work to other discotic clay dispersions with varying particle sizes. We have also documented a linear correlation between the elastic strength of the material in the linear regime and the yield stress at the same age time allowing the model we have developed to describe both aging and temperature effects in the linear viscoelastic response of the dispersion to also provide quantitative predictions of the evolution in the sample yield stress, which is relevant to industrial operations with such aging materials.
In developing an appropriate model for the linear viscoelasticity of this bentonite dispersion, we required data that spanned a two-dimensional domain: capturing variations in both the deformation time-scale (t − tw), and the material age (tw). Many commonplace techniques for characterizing the linear response of soft materials, in particular small-amplitude frequency sweeps combined with Fourier transform analysis, cannot provide adequate resolution in age time (due to the elapsed time required to sweep over a range of frequencies), and this convolves the effects of stress relaxation and rheological aging. Thus, the study of rapidly aging soft materials represents a particularly suitable application of modern rheometric techniques, such as the optimally windowed exponential chirps employed in this work. Rheological aging also highlights the need for particular care in developing and employing rheometric techniques that provide high data-density to enable systematic transformation to the material time domain and construction of time–age-time–temperature (TATTS) master curves. Such experiments are crucial for resolving the additional complexities of rheologically aging viscoelastic materials.
Conflicts of interest
There are no conflicts to declare.Appendix
Appendix: Signatures of hyperaging (μ > 1)
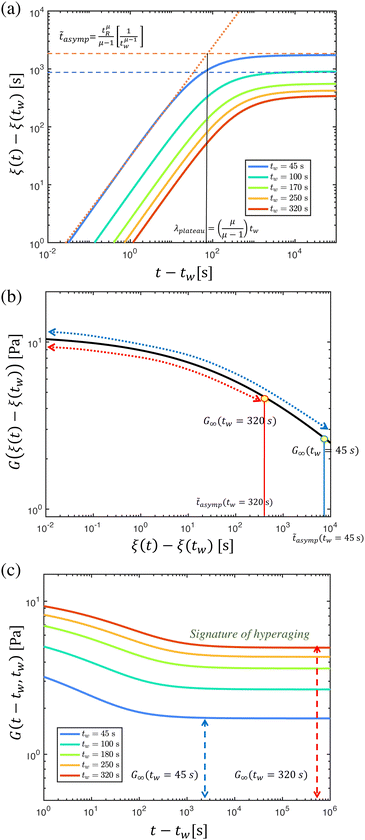
Hyperaging (μ > 1) soft glassy materials exhibit unique signatures in their linear dynamics, which can be visually identified in experimental data. Here, we explore characteristic signatures of hyperaging materials in stress relaxation experiments. For μ > 1, it is perhaps more instructive to write eqn (11) as follows: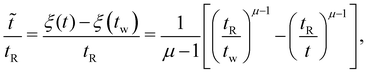 | (27) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) is nonnegative and increases (nonlinearly) with laboratory time scale t.
is nonnegative and increases (nonlinearly) with laboratory time scale t.
The dependence of the material time interval ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) on the elapsed laboratory time t − tw since the beginning of an experiment at time t = tw is illustrated in Fig. 12, which plots eqn (27) for a set of distinct age times tw. Each of these curves is observed to approach an asymptote as the wall clock time t → ∞. The asymptotic value can be derived by direct inspection of eqn (27) in that limit:
on the elapsed laboratory time t − tw since the beginning of an experiment at time t = tw is illustrated in Fig. 12, which plots eqn (27) for a set of distinct age times tw. Each of these curves is observed to approach an asymptote as the wall clock time t → ∞. The asymptotic value can be derived by direct inspection of eqn (27) in that limit:
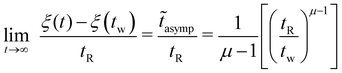 | (28) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) increases in time without bound.
increases in time without bound.
The presence of an asymptote in the material time interval is a consequence of the superlinear evolution of the sample's relaxation time with the laboratory time t for μ > 1. The superlinear dependence of the relaxation timescale τ on the age time of the material leads to a divergence in the amount of time needed for a fixed absolute magnitude of stress in the material to decay. As a result, the material approaches a structurally arrested state, beyond which it is unable to further relax. The inverse dependence of the asymptotic material time interval ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) on tw predicted by eqn (28) is due to the acceleration in aging that occurs between preshear and tw. The dependence of
on tw predicted by eqn (28) is due to the acceleration in aging that occurs between preshear and tw. The dependence of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) on tR is simply due to the arbitrary scale of the material time coordinate set by the reference time. When the reference time of choice (tR) is kept the same for all experimental observations it has no bearing on the actual predictions of the model.
on tR is simply due to the arbitrary scale of the material time coordinate set by the reference time. When the reference time of choice (tR) is kept the same for all experimental observations it has no bearing on the actual predictions of the model.
Although mathematically the asymptotic value of the material time interval, ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) asymp, is formally reached only at infinite laboratory time, we may make an estimate of the finite laboratory time at which the plateau in the material time is practically reached in experiment. At short laboratory time scale
asymp, is formally reached only at infinite laboratory time, we may make an estimate of the finite laboratory time at which the plateau in the material time is practically reached in experiment. At short laboratory time scale 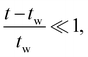 the evolving material time
the evolving material time ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) is linearly dependent on the laboratory time (or wall clock) t:
is linearly dependent on the laboratory time (or wall clock) t:
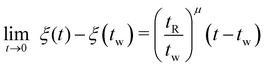 | (29) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) with t given by this equation is evident in Fig. 12(a) and can be used to evaluate an approximate laboratory time (t) at which the asymptotic value of
with t given by this equation is evident in Fig. 12(a) and can be used to evaluate an approximate laboratory time (t) at which the asymptotic value of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) is obtained which we denote by λplateau:
is obtained which we denote by λplateau: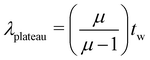 | (30) |
This relationship is shown graphically in Fig. 12(a) and suggests that the characteristic laboratory time at which structural arrest occurs increases linearly with the wait time. Moreover, we see from any eqn (30) that this relationship is indeed independent of the arbitrarily set reference time tR.
Therefore, for hyperaging materials subjected to a step deformation after a wait time tw, the material is only able to access its material-domain relaxation modulus ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ) in the interval between 0 ≤
) in the interval between 0 ≤ ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) ≤
≤ ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) asymp(tw). This effect is depicted in Fig. 12(b) for two different wait times, tw = 45 s and tw = 320 s. For laboratory times (wall clock) greater than t ≈ λplateau, the material time approaches its plateau value of
asymp(tw). This effect is depicted in Fig. 12(b) for two different wait times, tw = 45 s and tw = 320 s. For laboratory times (wall clock) greater than t ≈ λplateau, the material time approaches its plateau value of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) =
= ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) asymp(tw), with the associated value of the material-domain relaxation modulus
asymp(tw), with the associated value of the material-domain relaxation modulus ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) asymp(tw)). Therefore, the true relaxation modulus G(t) measured in the laboratory time domain reaches a plateau for times greater than t ≈ λplateau as shown in Fig. 12(c). The value of this plateau can be computed directly from the relaxation modulus in the material domain at
asymp(tw)). Therefore, the true relaxation modulus G(t) measured in the laboratory time domain reaches a plateau for times greater than t ≈ λplateau as shown in Fig. 12(c). The value of this plateau can be computed directly from the relaxation modulus in the material domain at ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) asymp using eqn (12): G∞(tw) =
asymp using eqn (12): G∞(tw) = ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) asymp(tw))/b(tw).
asymp(tw))/b(tw).
Fig. 12(c) depicts the resulting plateau in the relaxation modulus for step deformations at different wait times tw, with the plateau modulus values G∞(tw) = ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (
(![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) asymp(tw))/b(tw), using the empirical form
asymp(tw))/b(tw), using the empirical form 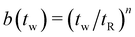 for the vertical shift factor where tR = 400 s and n = −0.36.
for the vertical shift factor where tR = 400 s and n = −0.36.
As a consequence of the structural arrest in the material time coordinate, two signatures can be observed in stress relaxation experiments performed to identify the hyperaging behavior of colloidal gels and glasses:
1. the increase of the asymptotic plateau in the relaxation modulus with wait time tw, and
2. the linear increase in the laboratory time λplateau taken to reach this plateau in the relaxation modulus.
Eqn (30) also presents an alternative method for finding the aging exponent μ in hyperaging systems. The traditional method for determining the aging exponent μ in aging systems is by identifying the value of μ that gives the best superposition of relaxation modulus data measured at different values of the waiting time tw (when accompanied by judicious user-selected choices of the vertical shift factors b(tw)). Instead, one can use eqn (30) to identify the aging exponent μ by experimentally evaluating the laboratory time λplateau, it takes for the relaxation modulus to reach a plateau as a function of the wait time tw. Linear regression may then used to obtain the slope of this relationship, which is equal to μ/(μ − 1) according to eqn (30). This method is particularly convenient because it decouples the process of finding the aging exponent μ from the problem of identifying the vertical shift factors b(tw) that superpose stress relaxation data at different wait times tw. However it does require the modulus of the soft glassy material be large enough to be measured at long times (t − tw) following a small step strain deformation.
Acknowledgements
JDJR was supported by Aramco Americas for his studies into the complex rheology of drilling fluids. K. R. L. was supported by the U.S. Department of Energy Computational Science Graduate Fellowship program under Grant No. DE-SC0020347.Notes and references
- Advances in Inhibitive Water-Based Drilling Fluids-Can They Replace Oil-Based Muds? 2007 DOI:10.2118/106476-MS.
- A. A. Anthony, O. C. Esther, D. O. Chris and B. A. Oni, J. Pet. Explor. Prod. Technol., 2020, 10, 2815–2828 CrossRef CAS.
- M. I. Abdou, A. M. Al-sabagh and M. M. Dardir, Egypt. J. Pet., 2013, 22, 53–59 CrossRef.
- W. Huang, Y.-K. Leong, T. Chen, P.-I. Au, X. Liu and Z. Qiu, J. Pet. Sci. Eng., 2016, 146, 561–569 CrossRef CAS.
- B. Erdoǧan and S. Demirci, Appl. Clay Sci., 1996, 10, 401–410 CrossRef.
- S. Morariu, M. Teodorescu and M. Bercea, J. Pet. Sci. Eng., 2022, 210, 110015 CrossRef CAS.
- Z. Vryzas, V. C. Kelessidis, L. Nalbantian, V. Zaspalis, D. I. Gerogiorgis and Y. Wubulikasimu, Appl. Clay Sci., 2017, 136, 26–36 CrossRef CAS.
- S. Bridges and L. Robinson, A Practical Handbook for Drilling Fluids Processing, Gulf Professional Publishing, 2020 Search PubMed.
- A. Olatunde, M. Usman, O. Olafadehan, T. Adeosun and O. Ufot, Pet. Coal, 2012, 54, 65–75 CAS.
- P. Coussot, H. Tabuteau, X. Chateau, L. Tocquer and G. Ovarlez, J. Rheology, 2006, 50, 975–994 CrossRef CAS.
- S. K. Howard, Formate Brines for Drilling and Completion: State of the Art, Paper presented at the SPE Annual Technical Conference and Exhibition, Dallas, Texas, October 1995, DOI:10.2118/30498-MS.
- I. Mukasa-Tebandeke, P. Ssebuwufu, S. Nyanzi, A. Schumann, G. Nyakairu, M. Ntale and F. Lugolobi, Adv. Mater. Phys. Chem., 2015, 05, 67–86 CrossRef.
- H. J. Skadsem, A. Leulseged and E. Cayeux, Appl. Rheol., 2019, 29, 1–11 CrossRef CAS.
- J. Mewis and N. J. Wagner, Adv. Colloid Interface Sci., 2009, 147–148, 214–227 CrossRef CAS.
- R. G. Larson and Y. Wei, J. Rheol., 2019, 63, 477–501 CrossRef CAS.
- M. Agarwal, S. Sharma, V. Shankar and Y. M. Joshi, J. Rheol., 2021, 65, 663–680 CrossRef CAS.
- S. M. Fielding, P. Sollich and M. E. Cates, J. Rheol., 2000, 44, 323–369 CrossRef CAS.
- R. Monicard, Drilling Mud and Cement Slurry Rheology Manual, Springer Science + Business Media, 1982 Search PubMed.
- P. F. Luckham and S. Rossi, Adv. Colloid Interface Sci., 1999, 82, 43–92 CrossRef CAS.
- R. E. Grim, Applied Clay Mineralogy, McGraw-Hill, 1962 Search PubMed.
- H. van Olphen, J. Colloid Sci., 1964, 19, 313–322 CrossRef CAS.
- V. C. Kelessidis, Rheology: Open Access, 2017, 1, 1000101 Search PubMed.
- T. Bhattacharyya, A. R. Jacob, G. Petekidis and Y. M. Joshi, J. Rheol., 2023, 67, 461–477 CrossRef CAS.
- R. W. Mooney, A. G. Keenan and L. A. Wood, J. Am. Chem. Soc., 1952, 74, 1367–1371 CrossRef CAS.
- R. Keren, I. Shainberg and E. Klein, Soil Sci. Soc. Am. J., 1988, 52, 76–80 CrossRef CAS.
- P. Becher, J. Dispersion Sci. Technol., 1988, 9, 425–426 Search PubMed.
- D. M. Marum, M. D. Afonso and B. B. Ochoa, Appl. Rheol., 2020, 30, 107–118 CrossRef CAS.
- L. J. Michot, I. Bihannic, F. Thomas, B. S. Lartiges, Y. Waldvogel, C. Caillet, J. Thieme, S. S. Funari and P. Levitz, Langmuir, 2013, 29, 3500–3510 CrossRef CAS PubMed.
- W. J. Ganley and J. S. Van Duijneveldt, Langmuir, 2015, 31, 4377–4385 CrossRef CAS PubMed.
- L. J. Michot, I. Bihannic, K. Porsch, S. Maddi, C. Baravian, J. Mougel and P. Levitz, Langmuir, 2004, 20, 10829–10837 CrossRef CAS PubMed.
- R. Greene-Kelly, Clay Minerals Bulletin, 1952, 1, 221–227 CrossRef CAS.
- H. van Olphen, An Introduction to Clay Colloid Chemistry, John Wiley & Sons, Ltd, 1963 Search PubMed.
- Y. M. Joshi and G. R. K. Reddy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 021501 CrossRef PubMed.
- Y. Joshi, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 181–202 CrossRef CAS PubMed.
- Y. M. Joshi, G. K. Reddy, A. L. Kulkarni, N. Kumar and R. P. Chhabra, Proc. R. Soc. London, Ser. A, 2008, 464, 469–489 CAS.
- A. Shahin and Y. M. Joshi, Langmuir, 2010, 26, 4219–4225 CrossRef CAS.
- A. Shahin and Y. M. Joshi, Phys. Rev. Lett., 2011, 106, 038302 CrossRef CAS PubMed.
- A. Shukla, S. Shanbhag and Y. M. Joshi, J. Rheol., 2020, 64, 1197–1207 CrossRef CAS.
- B. Baldewa and Y. M. Joshi, Polym. Eng. Sci., 2011, 51, 2085–2092 CrossRef CAS.
- R. Gupta, B. Baldewa and Y. M. Joshi, Soft Matter, 2012, 8, 4171–4176 RSC.
- M. Kaushal and Y. M. Joshi, Soft Matter, 2014, 10, 1891–1894 RSC.
- V. Awasthi and Y. M. Joshi, Soft Matter, 2009, 5, 4991–4996 RSC.
- S. Jatav and Y. M. Joshi, J. Rheol., 2014, 58, 1535–1554 CrossRef CAS.
- R. H. Ewoldt and G. H. McKinley, Rheol. Acta, 2017, 56, 195–210 CrossRef CAS.
- R. R. Fernandes, G. Turezo, D. E. V. Andrade, A. T. Franco and C. O. R. Negrão, J. Pet. Sci. Eng., 2019, 177, 872–879 CrossRef CAS.
- M.-C. Li, Q. Wu, K. Song, Y. Qing and Y. Wu, ACS Appl. Mater. Interfaces, 2015, 7, 5006–5016 CrossRef CAS PubMed.
- M.-C. Li, Q. Wu, T. Lei, C. Mei, X. Xu, S. Lee and J. Gwon, Energy Fuels, 2020, 34, 8206–8215 CrossRef CAS.
- G. Roberts, H. Barnes and P. Carew, Chem. Eng. Sci., 2001, 56, 5617–5623 CrossRef CAS.
- R. Ran, S. Pradeep, S. Kosgodagan Acharige, B. C. Blackwell, C. Kammer, D. J. Jerolmack and P. E. Arratia, J. Rheol., 2023, 67, 241–252 CrossRef CAS.
- J. D. John Rathinaraj and G. H. McKinley, J. Rheol., 2023, 67, 479–497 CrossRef CAS.
- J. D. Martin and Y. T. Hu, Soft Matter, 2012, 8, 6940–6949 RSC.
- T. Divoux, D. Tamarii, C. Barentin and S. Manneville, Phys. Rev. Lett., 2010, 104, 208301 CrossRef PubMed.
- P. Coussot and G. Ovarlez, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 183–188 CrossRef CAS PubMed.
- S. Sharma, Y. M. Joshi and V. Shankar, arXiv, 2023, preprint, arXiv:2302.06129, DOI:10.48550/arXiv.2302.06129.
- Y. Lin, L. K.-J. Cheah, N. Phan-Thien and B. C. Khoo, Colloids Surf., A, 2016, 506, 1–5 CrossRef CAS.
- P. Coussot, Q. D. Nguyen, H. T. Huynh and D. Bonn, J. Rheol., 2002, 46, 573–589 CrossRef CAS.
- R. H. Ewoldt, C. Clasen, A. E. Hosoi and G. H. McKinley, Soft Matter, 2007, 3, 634–643 RSC.
- R. H. Ewoldt, A. E. Hosoi and G. H. McKinley, J. Rheol., 2008, 52, 1427–1458 CrossRef CAS.
- R. H. Ewoldt, A. E. Hosoi and G. H. McKinley, Integr. Comp. Biol., 2009, 49, 40–50 CrossRef PubMed.
- C. J. Dimitriou, R. H. Ewoldt and G. H. McKinley, J. Rheol., 2013, 57, 27–70 CrossRef CAS.
- S. Varchanis, G. Makrigiorgos, P. Moschopoulos, Y. Dimakopoulos and J. Tsamopoulos, J. Rheol., 2019, 63, 609–639 CrossRef CAS.
- K. Kamani, G. J. Donley and S. A. Rogers, Phys. Rev. Lett., 2021, 126, 218002 CrossRef CAS PubMed.
- J. D. J. Rathinaraj, J. Hendricks, G. H. McKinley and C. Clasen, J. Non-Newtonian Fluid Mech., 2022, 301, 104744 CrossRef CAS.
- M. Geri, B. Keshavarz, T. Divoux, C. Clasen, D. J. Curtis and G. H. McKinley, Phys. Rev. X, 2018, 8, 041042 CAS.
- E. Ghiringhelli, D. Roux, D. Bleses, H. Galliard and F. Caton, Rheol. Acta, 2012, 51, 413–420 CrossRef CAS.
- L. C. E. Struik, Physical Aging in Amorphous Polymers and Other Materials, Elsevier Science Publishing Company, 1977 Search PubMed.
- A. Shahin and Y. M. Joshi, Langmuir, 2012, 28, 5826–5833 CrossRef CAS PubMed.
- A. Shahin and Y. M. Joshi, Langmuir, 2012, 28, 15674–15686 CrossRef CAS PubMed.
- J. D. J. Rathinaraj, G. H. McKinley and B. Keshavarz, Fract. Fract., 2021, 5, 174 CrossRef.
- B. Keshavarz, D. G. Rodrigues, J.-B. Champenois, M. G. Frith, J. Ilavsky, M. Geri, T. Divoux, G. H. McKinley and A. Poulesquen, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2022339118 CrossRef CAS PubMed.
- J. D. J. Rathinaraj, B. Keshavarz and G. H. McKinley, Phys. Fluids, 2022, 34, 033106 CrossRef CAS.
- K. Lennon, G. McKinley and J. Swan, Data-Centric Engineering, 2023, 4, E13 Search PubMed.
- K. Lennon, J. D. J. Rathinaraj, M. Gonzalez, A. Santra, J. W. Swan and G. H. McKinley, Rheol. Acta, 2023 DOI:10.1007/s00397-023-01407-x.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00492a |
| ‡ These authors contributed equally to this work. |
| § Deceased. |
| This journal is © The Royal Society of Chemistry 2023 |