Untangling product selectivity on clean low index rutile TiO₂ surfaces using first-principles calculations

Abstract

Computational modeling of metal oxide surfaces provides an important tool to help untangle complex spectroscopy and measured catalytic reactivity. There are many material properties that make rational catalytic design challenging, and computational methods provide a way to evaluate possible structural factors, like surface structure, individually. The mechanism of water oxidation or oxygen evolution is well studied on some anatase surfaces and the rutile TiO₂ (110) surface but has not yet been mapped on other low-index Miller rutile surfaces that are present in most experimental nano-titania catalysts. Here first principles calculations provide new insights into water oxidation mechanisms and reactivity of the most common low-index Miller facets of rutile TiO₂. The reactivity of three surfaces, (101), (010), and (001), are explored for the first time and the product selectivity of multistep electron transfer on each surface is compared to the well-studied (110) surface. Density functional theory shows that a peroxo, O^(p), intermediate is more favorable for water oxidation on all facets. The ˙OH radical formation is favored on the (001) facet resulting in a high overpotential for oxygen evolution reaction (OER). The (101) and (110) facets have low overpotentials, ∼0.3 V, and favor two-electron proton-coupled electron transfer to produce H₂O₂. The only facet that prefers direct OER is (001), leading to O₂ evolution in a four-electron process with an overpotential of 0.53 V. A volcano plot predicts the selectivity and activity of low-index Miller facets of rutile TiO₂, revealing the high activity of the peroxo OER mechanism on the (010) facet.

---

1. Introduction

Photocatalytic water splitting via solid-state materials might provide an inexpensive way to generate energy from renewable resources.^1–3 Early active photocatalysts were developed using sacrificial reagents for either H₂ or O₂ evolution.⁴ However, discovering the ideal material capable of spontaneously achieving the two reactions remains a major challenge. In particular, semiconductor-based photocatalysts with multiple facets allow important properties to be tuned, like light absorption, mobility of charge carriers, and their driving force to the water solution.^5–8 An ideal material will have a large enough band gap to absorb a large amount of sunlight,^9,10 while the valence band maximum (VBM) and conduction band minimum (CBM) must lie energetically below O₂/H₂O and above H⁺/H₂ potentials to drive holes for water oxidation and electrons for reducing H⁺, respectively.¹¹

Titanium dioxide (TiO₂) is one of the most used materials in heterogeneous photocatalysis because of its strong stability under different conditions.^12,13 Rutile TiO₂'s wide band gap of 3.0 eV, makes it a UV light-responsive material, and the number of different stable facets allow for a range of activity for different reactants.^14,15 The overpotential of multiple water oxidation mechanisms has been investigated on the rutile TiO₂ (110) surface, which is considered to be the most stable facet.^16–18 Specifically, the amount of energy required to drive each step beyond the equilibrium potential, known as overpotential,^19–22 provides a good metric of surface reactivity. The photo-oxidation of water on defect-free rutile (110) surfaces has been broadly explored,^{19,21,23–31} as well as, direct prediction of OER on rutile (110) with subsurface oxygen vacancies,^32–42 multiple surface coverages,^19,29,43,44 and metal nanoclusters^45–50 adsorbed on the surface provides a detailed picture of its reactivity.

In contrast, other terminations of rutile TiO₂ that are experimentally accessible and have received much less attention. In particular, understanding the photocatalytic activity, especially the effect on yields, rates, or selectivity, of the lower index surfaces has been largely overlooked.⁵¹ Initially, these surfaces were not explored by computational scientists because surface energy calculations show that they are less stable than the (110) surfaces, with stability decreasing (100)^52–54 > (101)^55–58 > (001),^58–61 which is correlated to the density of undercoordinated surface sites.¹⁸ A recent article that calculated the electronic structures of hydroxylated low-index surfaces of rutile and anatase titanium dioxide, suggested that hydroxyl-bridged surfaces have a lot of potential for photo-electrocatalysis but did not directly assess the catalytic performance of these low-index facets.⁶² In the absence of studies identifying the role of each crystal facet in photocatalytic redox reactions, the understanding of photo-oxidation of water by nano-titania is incomplete as only 64% of particle surfaces are (110).^63–65 Thus, computational studies that can separately calculate the properties of each surface are critical to understanding the reactivity of experimental nanostructures.

An important consideration whenever generating models of catalytic surfaces is the stability of those surfaces, especially under catalytic conditions. It is well known that some low-index facets of anatase TiO₂, in particular (101),⁶⁶ reconstruct significantly. In general, very little surface reconstruction is seen when rutile surfaces are optimized using DFT.¹⁸ However, while rutile is a more stable phase in general, there is experimental evidence for the reconstruction of atomically flat rutile (001) above 750 °C.⁶⁷ This is not surprising as stochiometric (001) has a surface step edge. This edge in the 〈001〉 can either be a row of in-plane Ti atoms⁶⁸ or in-plane oxygen atoms.⁶⁹ Scanning tunneling microscopy has shown that the (001) rutile surfaces synthesized have bright rows on the surface⁷⁰ that can be assigned to the surface oxygen rows. When (001) rutile surfaces terminated with in-plane oxygens rather than raised bridging oxygens have been optimized no reconstruction is observed.²³

A second structural consideration in modeling metal oxide catalysis is atomic vacancies observed in experimental materials.^{54–56,71–74} Due to the minimal surface disorder seen in rutile crystals and DFT, most studies of rutile,^75–77 both (110) and other surfaces, focus on oxygen vacancies and surface coverages.^78,79 When adsorbed species are more stable than bare surfaces, this type of surface coverage can be thought of as a surface reconstruction. Typically, the dissociation of species on surfaces in a water environment are adsorbed oxygen species like hydroxyl-bridges.⁶² Before computational effort is invested in fully exploring the reactivity of other low-index surfaces of rutile TiO₂, a detailed understanding of the complex oxidation of water on each stoichiometric surface is required.

Of the two half-reactions of water splitting, the oxidation step is the most challenging due to the coupling of 4 electron and proton transfers and the creation of an oxygen–oxygen (O₂) bond.⁸⁰ One major issue contributing to catalytic inefficiency is side reactions leading to unproductive products or products that directly block active sites. In particular, water oxidation could lead to ˙OH radicals, H₂O₂, or O₂ evolution electrochemically or photoelectrochemically.²⁰ These three half-cell reactions that lead to the above-mentioned products depend on the number of electrons transferred, 1, 2, or 4 electrons. The formation energy of ˙OH in the aqueous phase from H₂O (eqn (1)) at pH = 0 is 2.4 V.⁸¹ When ΔG_OH* > 2.4 eV, water oxidation occurs via the one-electron process resulting in the formation of unproductive ˙OH. In a two-electron process, the amount of energy required for the production of H₂O₂ in the aqueous phase (eqn (2)) is 1.76 V.⁸² When ΔG_OH* < 2.4 eV and ΔG_O* > 3.5 eV at pH = 0, H₂O₂ is formed. If ΔG_OH* < 2.4 eV and ΔG_O* < 3.5 eV at pH = 0, water oxidation would undergo the four-electron process to the desired O₂ evolution. The required energy for the production of O₂ in the aqueous phase from H₂O is 1.23 V.⁸²

H₂O → ˙OH + (H⁺ + e⁻) (1)

2H₂O → H₂O₂ + 2 (H⁺ + e⁻) (2)

2H₂O → O₂ + 4 (H⁺ + e⁻) (3)

This work uses computational catalytic tools to predict solar-to-chemical energy conversion on the four low-index Miller surfaces of rutile TiO₂, (110), (101), (010), and (001) (Fig. S1, ESI†). First-principle calculations can predict the redox potentials of multielectron proton-coupled electron transfer mechanisms on each facet. Unlike experimental reactivity, density functional theory (DFT) allows the mechanism through two distinct reactive intermediates, i.e., dangling O* and surface-bound peroxo O* denoted as (O^(d)) and (O^(p)), to be examined separately. The structure of each surface and the intermediates and thermodynamic analysis of the free energy for the three possible products, i.e., ˙OH/H₂O₂/O₂, provide insights into the selectivity of these understudied surfaces. This work provides experimentalists with design guidelines for faceted TiO₂ crystalline nanomaterials that should enhance photocatalytic water oxidation by identifying the most suitable facets for OER and criteria for product selectivity.

2. Computational methodology

Spin-polarized density functional theory (DFT) characterized the intermediates for OER activity of the rutile TiO₂ (001), (101), (110), and (010) surfaces. For the structure determination, the Perdew–Burke–Ernzer (PBE) parameterizations of the exchange and correlation potential in the generalized gradient approximation (GGA)⁸³ as applied in the Vienna Ab Initio Simulation Package (VASP) code was adopted.^84,85 To expand the electronic wave function, and valence configurations of the atoms: 3s²3p⁶4s²3d² for Ti's (12 valence electrons), 2s²2p⁴ for O's (6 valence electrons), and 1s for H (1 valence electron) with PAW potentials to account for the core electrons a plane-wave energy cutoff of 400 eV was applied. The self-consistent DFT energies convergence criterion was 10⁻⁴ eV with a force on each atom of 0.01 eV Å⁻¹. The bulk rutile with tetragonal symmetry of TiO₂ was cleaved along the (001), (101), (110), and (010) surfaces to form stoichiometric and symmetric slabs. A 2 × 2 × 1 supercell was used for calculations. The slabs thickness were set to four Ti layers, and the vacuum length was 15 Å. The bottom Ti layer was fixed while the other three Ti layers were allowed to relax. The optimized lattice parameters are a = 18.41 Å, b = 9.20 Å, c = 20.16 Å and α = β = 90.00°, γ = 90.32° for (001), a = 21.85 Å, b = 9.18 Å, c = 23.97 Å, and α = β = γ = 90.00° for (101), a = 11.80 Å, b = 12.99 Å, c = 24.45 Å, and α = β = γ = 90.00° for (110), and a = 11.76 Å, b = 9.51 Å, c = 31.12 Å and α = β = γ = 90.00° for (010). After complete optimization of slabs, we chose the Ti metal atom as an active site on the surface and the OER intermediates (OH*, O^(d), O^(p), and OOH*) were adsorbed at a Ti–O bond length of 2.00 Å and again allowed to relax. For sampling the Brillouin zone, a Γ-centered 3 × 2 × 1 k-point mesh was used based on the Monkhorst–Pack scheme.⁸⁶ All reported energetics and electronic density of states were calculated using HSE06.⁸⁷ Photoexcitation is accounted for as an initial potential provided by the photoexcited electron in the first reaction step as explained in the scheme for free energy profile calculations for OER given in the ESI.†

3. Results and discussion

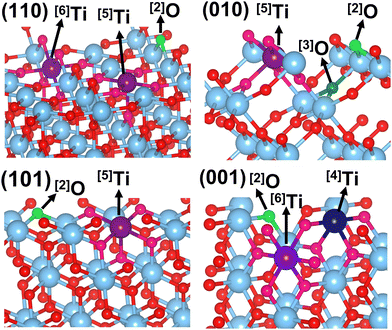
The rutile polymorph of titania is composed of TiO₆ octahedra, which are arranged to form edge-sharing chains along the [001] direction and are corner-sharing in the (001) plane. The surface orientations determine how these octahedra are cut at each of the four low-index Miller surfaces (110), (101), (010), and (001) (Fig. 1) resulting in a variation of local geometry and coordination number for the stoichiometric surface atoms. On the lowest energy rutile surface, (110) (Fig. 1), half of the Ti atoms are five-coordinated (^[5]Ti, where ^[n]A is a n-coordinated atom of A) and the other half are ^[6]Ti along the [001] surface rows, these ^[6]Ti have additional bridging surface oxygen atoms (^[2]O) joining them, completing their octahedral coordination. In contrast, the rutile (010) surface has only ^[5]Ti atoms, with surface ^[2]O atoms bridging them (Fig. 1). On the (110) surface the bridging Ti–O bonds are perpendicular to the surface plane while on the (010) surface the bridging oxygens are inclined at an angle to the surface (61° in the relaxed stoichiometric structure). The (101) surface also has only ^[5]Ti with bridging ^[2]O. However, while on both the (010) and (101) surfaces the ^[5]Ti lie at the center of the base TiO₅ square pyramids that are slanted from the surface normal. On the (101) surface the (–O–Ti–O–Ti–) chains are zigzagged along the [101̄] direction, giving the TiO₅ square pyramids alternating tilts (Fig. 1). When truncated to the (101) surface, the bulk TiO₆ octahedra form rows where long and short Ti–O bonds have been removed, forming chains of alternating enantiomeric Ti surface sites. The (001) surface exhibits alternating O and Ti rows in the [110] direction, with alternating ^[6]Ti and ^[4]Ti (Fig. 1). The ^[6]Ti surface metal sites occupy the center of TiO₆ octahedra, whereas the elimination of two oxygen atoms leads to the relaxation of the octahedron to a distorted tetrahedral ^[4]Ti. Each (001) surface O atom is bonded to one ^[4]Ti and one ^[6]Ti. The diverse coordination of Ti and O is known to result in a range of surface energies; (110) < (010) < (101) < (001),^17,38 matching well with the formation energies per atom of each unit cell (Table S8, ESI†). The density of states (DoS, Fig. S6, ESI†) of each surface show that their valence bands are all composed of O (2p) orbitals and their conduction bands are mostly comprised of Ti (3d) orbitals. In addition, all of the plots showed a shift in the Fermi energy (E_f) toward the valence band edge with a typical rutile band gap of ∼3 eV.

Fig. 1 Rutile (110), (010), (101), and (001) surfaces and surface atom coordination (dark blue ^[4]Ti, dark purple ^[5]Ti, light purple ^[6]Ti, and bright green ^[2]O, dark green ^[3]O) on each. Red atoms are O and light blue are Ti.

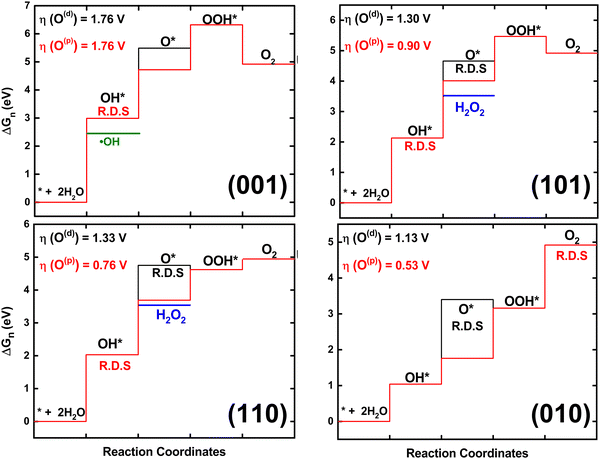
Here we directly measure the effect of surface chemistry on water-splitting catalytic properties. The multistep proton-coupled electron transfer (PCET) processes for one-, two-, and four-electron transfer reactions (eqn (1)–(3)) are considered for each surface. The (110) surface has been well explored^{19,21,23–31} and is included here for direct comparison, but all the results are consistent with previous DFT studies on the bare surface. The detailed PCET mechanism is shown in Section 1 of the SI. For both the peroxo and dangling oxygen mechanisms the free energies of OH* and O* were calculated (Table 1). It is striking that the lowest possible energy mechanism on all the facets goes through the surface-bound peroxo O* (Table 1), denoted as O^(p). This is important as this mechanism is often overlooked in favor of the similar but less plausible dangling O* intermediate, signified as O^(d) (Fig. 2). The formation energy of each intermediate adsorbed on the surfaces is within DFT error of the surface formation energy and about 2 × s (∼−4.5 eV) more favorable than the dissociation energy of water (5.15 eV).

Table 1 Free energies relative to the resting state ‘*+2H₂O’ for (ΔG_*), ‘OH*’ (ΔG_OH*), O^(d) (ΔG_O^(d)), O^(p) (ΔG_O^(p)), OOH* (ΔG_OOH*), and O₂ (ΔG_O2) and overpotentials ‘η’ through four-, two- and one-electron (O₂/H₂O₂/˙OH evolution) processes for all surfaces and mechanisms, labeled surface^{(intermediate)}. The rate-limiting step for each mechanism is bolded

Mechanism	ΔGOH*	ΔGO^(d)	ΔGO^(p)	ΔGOOH*	ΔGO2	Product	R.D.S	η (V) 1e^−	η (V) 2e^−	η (V) 4e^−
001^(d)	2.99	5.19	—	6.02	4.92	˙OH	OH*	1.76	—	—
001^(p)	2.99	—	4.72	6.02	4.92	˙OH	OH*	1.76	—	—
101^(d)	2.13	4.66	—	5.47	4.92	H2O2	O*	—	0.77	1.30
101^(p)	2.13	—	4.01	5.47	4.92	H2O2	OH*	—	0.37	0.90
110^(d)	1.99	4.55	—	4.48	4.92	H2O2	O*	—	0.80	1.33
110^(p)	1.99	—	3.64	4.48	4.92	H2O2	OH*	—	0.23	0.76
010^(d)	1.04	3.40	—	3.16	4.92	O2	O*	—	—	1.13
010^(p)	1.04	—	1.76	3.16	4.92	O2	O2	—	—	0.53

---

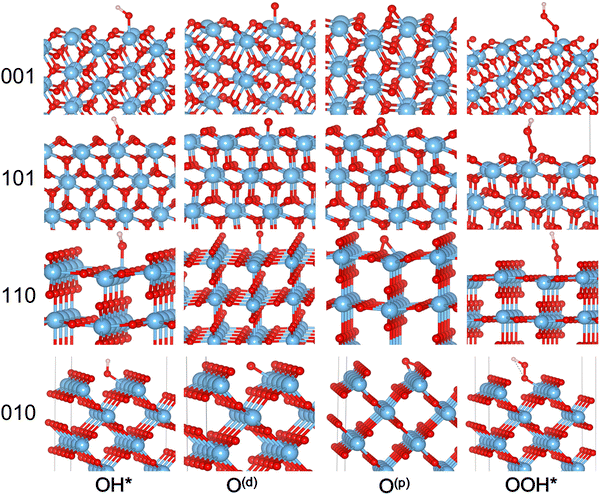Fig. 2 Optimized structures of Rutile (110), (010), (101), and (001) their four possible OER intermediates.

For O₂ evolution, the rate-determining step is *OH for the (001), (101), and (110) surfaces, whereas, the rate on (010) is determined through the last O₂ evolution. The surface adsorption of OH* is the first step in OER, and its energy and charge transfer (as determined by a ∼0.41 to 0.48 e⁻ Bader charge, Table S6, ESI†) remains the same for all mechanisms. This step is lowest in energy on the (010) surface at 1.04 eV (Fig. 3). Loss of the proton to generate O* is the branching point for the O^(d)vs. O^(p) mechanisms (each mechanism is labeled as surface^{(intermediate)}). Each mechanism only has one newly adsorbed surface oxygen, however in the peroxo mechanism the O* forms a bond with an existing surface oxygen. O^(p) formation is more favorable for all facets and is significantly lower in energy on (010) (∼1 eV) than all the other surfaces. This is probably due to the charge transfer to the dangling O^(d) intermediates as compared to the newly adsorbed oxygen in the peroxo O^(p) intermediates, thus lowering the binding energies of the peroxo mechanism. Interestingly, some of the peroxo O* charge seems to be shared with its bonded surface oxygen (Table S6, ESI†) proving that peroxo specie is preferable on defect-free TiO₂ surface which is in good agreement with previous studies.^23,24

Fig. 3 Free energy profiles and overpotential of OER on stoichiometric (001), (101), (110), and (010) rutile through dangling O^(d) (black) and peroxo O^(p) (red) intermediates under no external potential. The rate-determining step (R.D.S.) is marked and H₂O₂ formation (blue) and ˙OH formation (green) are shown for relevant surfaces.

Adsorption of a second OH leading to an OOH* depends on the energy and mechanism of the O* step. The observed charge transfer is ∼0.94 to 1.49 to the OOH* on all surfaces. Interestingly, the dangling mechanism on the (010) and (110) surfaces has a downhill OOH* step. This however isn’t enough to make the dangling mechanism more favorable overall. While the step energies for the two mechanisms are very different (Table S3, ESI†), according to Sabatier's principle⁸⁸ of reactivity, catalytic activity is actually a balance between strong and weak interactions between the substrate and the catalyst.

For the ˙OH formation 1-electron process, all of the surfaces have the same overpotential. For the H₂O₂ formation 2-electron process, 110^(p) has the lowest overpotential of 0.23 V, followed by 101^(p) at 0.37 V with OH* as the rate-limiting step, for both. Four-electron O₂ evolution through the 010^(p) has the least overpotential of 0.53 V. Interestingly, among all surfaces (010) showed highest charge transfer from surface to intermediates supporting high photocatalytic activity of this surface.

The product selectivity map^20,21 (Fig. 4) compares the relative free energies of OH* and O* to the reaction equilibrium potentials for H₂O₂, O₂, and ˙OH formation. None of the surfaces predict a different product for the two mechanisms. Instead, ˙OH formation is favored on (001), H₂O₂ formation for (110) and (101), while only O₂ evolution is preferred for (001). Interestingly, rutile 110^(p) is adjoining the O₂ evolution boundary, indicating that with very little added energy (110) could evolve O₂. Importantly, under irradiation, the redox potential of photogenerated holes in the valence band is almost equal to the band gap (over ∼3 eV) making all three mechanisms (1e⁻, 2e⁻, and 4e⁻) realistic on all these surfaces. Water oxidation gates most easily on (110) and (101) through the formation of H₂O₂. On the (001) surface however ˙OH formation likely makes the surface unproductive for O₂ evolution.

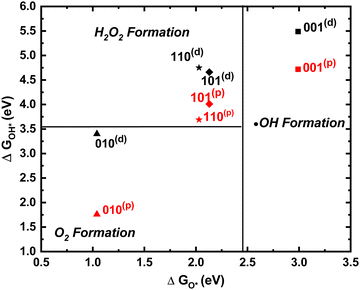Fig. 4 Phase diagram for product selectivity for rutile (001), (101), (110), and (010) surfaces. Black and red show dangling and peroxo mechanisms, respectively.

Because these reactions occur in the presence of water and involve protons moving at many steps, pH plays a role in the reactivity. In particular, the energy of every step is modulated by pH. By using a pH-dependent reference electrode, the calculated overpotential can directly account for the effect of pH on surface reactivity.^{17,21,89–91} While a pH of 14 (pH = 0 in Table 1) alters the binding energies of the reaction intermediates (Table S3, ESI†) and affects the threshold values for the 1e⁻, 2e⁻, and 4e⁻ processes, it does not affect the selectivity and overpotential of OER on each surface.

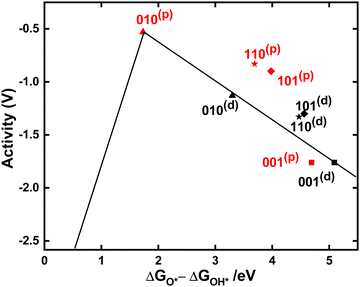
Volcano plots have been extensively used for the analysis of OER activity of different oxide systems.^92–94 ΔG_O* − ΔG_OH* provides a computational metric of OER activity⁹⁵ that can predict the activity of various catalysts. Plotting the negative value of calculated overpotential (−η, activity) as a function of this metric for each of the facets considered here leads to a volcanic relationship (Fig. 5). The top of the volcano shows the best OER activity with the lowest overpotential for 010^(p). It is clear in the volcano plot that the overpotential depends strongly on the mechanism for each surface, i.e. O^(d) or O^(p). Among all the facets (001) results in the highest overpotential indicating that this facet is least active for water oxidation. This is in good agreement with previous studies that show (001) is unstable, with high surface energy and experimental reconstruction.^96–98 However, these results show clearly that other low-indexed facets, beyond the well-studied (110), should be considered for water oxidation. In particular, 010^(p) is more reactive and 101^(p) is almost as reactive as than 110^(p).

Fig. 5 Volcano plot (−η vs. ΔG_O* − ΔG_OH*) for the oxygen evolution reaction on low-indexed TiO₂ surfaces explored in this study. The data points are grouped with black color for dangling O^(d) and red color for peroxo O^(p).

4. Conclusions

This work provides the first direct calculations of water oxidation on low-index rutile TiO₂ facets, (001), (101), and (101), using DFT. This work provides new insights into water oxidation mechanisms and reactivity of various low-index Miller facets of rutile TiO₂. In particular, water oxidation proceeds through the peroxo intermediate on all of these stoichiometric facets. The (001) facet resulted in high overpotential for OER leading to ˙OH radical formation. A two-electron process to produce H₂O₂ is favored on the (101) and (110) facets with fairly low overpotentials, ∼0.3 V, for OER. The only facet that prefers direct OER is (010), with an overpotential of 0.53 V. These results are supported via a volcano plot which predicts the high activity of a peroxo mechanism of OER on the (010) facet. Critically, these results show that facets beyond the well-studied (110) may play a role in measured reactivity and should be explored further to better understand the effect of surface coverage and oxygen vacancies.

Conflicts of interest

The authors declare that they have no competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

Portions of this research were conducted with research computing resources provided by the TG-CHE190011 allocation from Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562 and the NSF CC* Compute program (OAC-2019035) for funding to increase computing resources at Lehigh University. Financial support for this research also comes from Lehigh University.

References

1. K. Maeda and K. Domen, New non-oxide photocatalysts designed for overall water splitting under visible light, J. Phys. Chem. C, 2007, 111, 7851–7861.
2. A. Kudo and Y. Miseki, Heterogeneous photocatalyst materials for water splitting, Chem. Soc. Rev., 2009, 38, 253–278.
3. K. Maeda and K. Domen, Photocatalytic water splitting: recent progress and future challenges, J. Phys. Chem. Lett., 2010, 1, 2655–2661.
4. J. Schneider and D. W. Bahnemann, Undesired Role of Sacrificial Reagents in Photocatalysis, J. Phys. Chem. Lett., 2013, 4, 3479–3483.
5. S. Wang, G. Liu and L. Wang, Crystal facet engineering of photoelectrodes for photoelectrochemical water splitting, Chem. Rev., 2019, 119, 5192–5247.
6. W. Li, K. R. Yang, X. Yao, Y. He, Q. Dong, G. W. Brudvig, V. S. Batista and D. Wang, Facet-dependent kinetics and energetics of hematite for solar water oxidation reactions, ACS Appl. Mater. Interfaces, 2018, 11, 5616–5622.
7. R. Li, F. Zhang, D. Wang, J. Yang, M. Li, J. Zhu, X. Zhou, H. Han and C. Li, Spatial separation of photogenerated electrons and holes among {010} and {110} crystal facets of BiVO4, Nat. Commun., 2013, 4, 1–7.
8. C. Li, C. Koenigsmann, W. Ding, B. Rudshteyn, K. R. Yang, K. P. Regan, S. J. Konezny, V. S. Batista, G. W. Brudvig and C. A. Schmuttenmaer, Facet-dependent photoelectrochemical performance of TiO₂ nanostructures: an experimental and computational study, J. Am. Chem. Soc., 2015, 137, 1520–1529.
9. I. Vurgaftman and J. R. Meyer, Band parameters for III-V compound semiconductors and their alloys, J. Appl. Phys., 2001, 89, 5815.
10. O. Madelung, Semiconductors: data handbook, Springer Science & Business Media, 2004.
11. A. L. Linsebigler, G. Lu and J. T. Yates Jr., Photocatalysis on TiO₂ surfaces: principles, mechanisms, and selected results, Chem. Rev., 1995, 95, 735–758.
12. M. A. Henderson and I. Lyubinetsky, Molecular-level insights into photocatalysis from scanning probe microscopy studies on TiO₂(110), Chem. Rev., 2013, 113, 4428–4455.
13. T. L. Thompson and J. T. Yates, Surface science studies of the photoactivation of TiO₂ new photochemical processes, Chem. Rev., 2006, 106, 4428–4453.
14. D. C. Cronemeyer, Infrared Absorption of Reduced Rutile TiO₂ Single Crystals, Phys. Rev., 1959, 113, 1222–1226.
15. N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. L. Wang, Synthesis of tetrahexahedral platinum nanocrystals with high-index facets and high electro-oxidation activity, Science, 2007, 316, 732–735.
16. C. Xu, F. Xu, X. Chen, Z. Li, Z. Luan, X. Wang, Q. Guo and X. Yang, Wavelength-Dependent Water Oxidation on Rutile TiO₂ (110), J. Phys. Chem. Lett., 2021, 12, 1066–1072.
17. A. Imanishi, T. Okamura, N. Ohashi, R. Nakamura and Y. Nakato, Mechanism of Water Photooxidation Reaction at Atomically Flat TiO₂ (Rutile) (110) and (100) Surfaces: Dependence on Solution pH, J. Am. Chem. Soc., 2007, 129, 11569–11578.
18. H. Perron, C. Domain, J. Roques, R. Drot, E. Simoni and H. Catalette, Optimisation of accurate rutile TiO₂ (110),(100),(101) and (001) surface models from periodic DFT calculations, Theor. Chem. Acc., 2007, 117, 565–574.
19. Á. Valdés, Z.-W. Qu, G.-J. Kroes, J. Rossmeisl and J. K. Nørskov, Oxidation and Photo-Oxidation of Water on TiO₂ Surface, The, J. Phys. Chem. C, 2008, 112, 9872–9879.
20. S. Siahrostami, G.-L. Li, V. Viswanathan and J. K. Nørskov, One- or Two-Electron Water Oxidation, Hydroxyl Radical, or H₂O₂ Evolution, J. Phys. Chem. Lett., 2017, 8, 1157–1160.
21. A. S. Malik, T. Liu, M. Dupuis, R. Li and C. Li, Water Oxidation on TiO₂: A Comparative DFT Study of 1e⁻, 2e⁻, and 4e⁻ Processes on Rutile, Anatase, and Brookite, J. Phys. Chem. C, 2020, 124, 8094–8100.
22. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, Electrolysis of water on oxide surfaces, J. Electroanal. Chem., 2007, 607, 83–89.
23. U. Diebold, The surface science of titanium dioxide, Surf. Sci. Rep., 2003, 48, 53–229.
24. C. L. Pang, R. Lindsay and G. Thornton, Chemical reactions on rutile TiO₂ (110), Chem. Soc. Rev., 2008, 37, 2328–2353.
25. X. Yin, M. Calatayud, H. Qiu, Y. Wang, A. Birkner, C. Minot and C. Wöll, Diffusion versus desorption: complex behavior of H Atoms on an oxide surface, ChemPhysChem, 2008, 9, 253–256.
26. P. M. Kowalski, B. Meyer and D. Marx, Composition, structure, and stability of the rutile TiO₂ (110) surface: Oxygen depletion, hydroxylation, hydrogen migration, and water adsorption, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115410.
27. A. Sasahara, T. Murakami and M. Tomitori, XPS and STM study of TiO₂ (110)-(1× 1) surfaces immersed in simulated body fluid, Surf. Sci., 2018, 668, 61–67.
28. X. Yu, Z. Zhang, C. Yang, F. Bebensee, S. Heissler, A. Nefedov, M. Tang, Q. Ge, L. Chen and B. D. Kay, Interaction of formaldehyde with the Rutile TiO₂ (110) Surface: A combined experimental and theoretical study, The, J. Phys. Chem. C, 2016, 120, 12626–12636.
29. D. Zhang, M. Yang and S. Dong, Hydroxylation of the rutile TiO₂ (110) surface enhancing its reducing power for photocatalysis, The, J. Phys. Chem. C, 2015, 119, 1451–1456.
30. A. Imanishi, E. Tsuji and Y. Nakato, Dependence of the work function of TiO₂ (Rutile) on crystal faces, studied by a scanning auger microprobe, The, J. Phys. Chem. C, 2007, 111, 2128–2132.
31. D. Wang, T. Sheng, J. Chen, H.-F. Wang and P. Hu, Identifying the key obstacle in photocatalytic oxygen evolution on rutile TiO₂, Nat. Catal., 2018, 1, 291–299.
32. T. V. Perevalov and V. A. Gritsenko, Electronic structure of TiO₂ rutile with oxygen vacancies: Ab initio simulations and comparison with the experiment, J. Exp. Theor. Phys., 2011, 112, 310–316.
33. B. J. Morgan and G. W. Watson, A DFT+U description of oxygen vacancies at the TiO₂ rutile (1 1 0) surface, Surf. Sci., 2007, 601, 5034–5041.
34. S. Wendt, R. Schaub, J. Matthiesen, E. K. Vestergaard, E. Wahlström, M. D. Rasmussen, P. Thostrup, L. M. Molina, E. Lægsgaard and I. Stensgaard, Oxygen vacancies on TiO₂ (1 1 0) and their interaction with H₂O and O₂: A combined high-resolution STM and DFT study, Surf. Sci., 2005, 598, 226–245.
35. G. Mattioli, F. Filippone, P. Alippi and A. A. Bonapasta, Ab initio study of the electronic states induced by oxygen vacancies in rutile and anatase TiO₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 241201.
36. M. Elahifard, M. R. Sadrian, A. Mirzanejad, R. Behjatmanesh-Ardakani and S. Ahmadvand, Dispersion of defects in TiO₂ semiconductor: Oxygen vacancies in the bulk and surface of rutile and anatase, Catalysts, 2020, 10, 397.
37. N. G. Petrik and G. A. Kimmel, Reaction kinetics of water molecules with oxygen vacancies on rutile TiO₂ (110), The, J. Phys. Chem. C, 2015, 119, 23059–23067.
38. B. J. Morgan and G. W. Watson, A density functional theory+ U study of oxygen vacancy formation at the (110),(100),(101), and (001) surfaces of rutile TiO₂, J. Phys. Chem. C, 2009, 113, 7322–7328.
39. A. Tilocca and A. Selloni, O₂ and vacancy diffusion on rutile (110): pathways and electronic properties, ChemPhysChem, 2005, 6, 1911–1916.
40. R. Schaub, P. Thostrup, N. Lopez, E. Lægsgaard, I. Stensgaard, J. K. Nørskov and F. Besenbacher, Oxygen vacancies as active sites for water dissociation on rutile TiO₂ (110), Phys. Rev. Lett., 2001, 87, 266104.
41. Y. Yamamoto, S. Kasamatsu and O. Sugino, Scaling relation of oxygen reduction reaction intermediates at defective TiO₂ surfaces, The, J. Phys. Chem. C, 2019, 123, 19486–19492.
42. M.-C. Tsai, T.-T. Nguyen, N. G. Akalework, C.-J. Pan, J. Rick, Y.-F. Liao, W.-N. Su and B.-J. Hwang, Interplay between molybdenum dopant and oxygen vacancies in a TiO₂ support enhances the oxygen reduction reaction, ACS Catal., 2016, 6, 6551–6559.
43. L. Mino, C. Negri, R. Santalucia, G. Cerrato, G. Spoto and G. Martra, Morphology, Surface Structure and Water Adsorption Properties of TiO₂ Nanoparticles: A Comparison of Different Commercial Samples, Molecules, 2020, 25, 4605.
44. S. Siahrostami and A. Vojvodic, Influence of Adsorbed Water on the Oxygen Evolution Reaction on Oxides, The, J. Phys. Chem. C, 2015, 119, 1032–1037.
45. Y. Adachi, Y. Sugawara and Y. J. Li, Atomic Scale Three-Dimensional Au Nanocluster on a Rutile TiO₂ (110) Surface Resolved by Atomic Force Microscopy, J. Phys. Chem. Lett., 2020, 11, 7153–7158.
46. R. S. Haider, S. Wang, Y. Gao, A. S. Malik, N. Ta, H. Li, B. Zeng, M. Dupuis, F. Fan and C. Li, Boosting photocatalytic water oxidation by surface plasmon resonance of AgxAu1−x alloy nanoparticles, Nano Energy, 2021, 87, 106189.
47. A. S. Malik, T. Liu, M. Rittiruam, T. Saelee, J. L. F. da Silva, S. Praserthdam and P. Praserthdam, On a high photocatalytic activity of high-noble alloys Au–Ag/TiO₂ catalysts during oxygen evolution reaction of water oxidation, Sci. Rep., 2022, 12, 2604.
48. M. Nolan, Alkaline earth metal oxide nanocluster modification of rutile TiO₂ (110) promotes water activation and CO₂ chemisorption, J. Mater. Chem. A, 2018, 6, 9451–9466.
49. B. J. Hwang, W.-N. Su, B.-J. Shieh and M.-C. Tsai, in ECS Meeting Abstracts, IOP Publishing, 2017, p. 1585.
50. M. García-Mota, A. Vojvodic, H. Metiu, I. C. Man, H. Su, J. Rossmeisl and J. K. Nørskov, Tailoring the Activity for Oxygen Evolution Electrocatalysis on Rutile TiO₂ (110) by Transition-Metal Substitution, ChemCatChem, 2011, 3, 1607–1611.
51. T. Ohno, K. Sarukawa and M. Matsumura, Crystal faces of rutile and anatase TiO₂ particles and their roles in photocatalytic reactions, New J. Chem., 2002, 26, 1167–1170.
52. F. Lindberg, J. Heinrichs, F. Ericson, P. Thomsen and H. Engqvist, Hydroxylapatite growth on single-crystal rutile substrates, Biomaterials, 2008, 29, 3317–3323.
53. O. Warschkow, Y. Wang, A. Subramanian, M. Asta and L. D. Marks, Structure and local-equilibrium thermodynamics of the c (2 × 2) reconstruction of rutile TiO₂ (100), Phys. Rev. Lett., 2008, 100, 086102.
54. Y. Lu, B. Jaeckel and B. A. Parkinson, Preparation and characterization of terraced surfaces of low-index faces of anatase, rutile, and brookite, Langmuir, 2006, 22, 4472–4475.
55. X. Zhou, Z. Wang, X. Xia, G. Shao, K. Homewood and Y. Gao, Synergistic cooperation of rutile TiO₂ {002},{101}, and {110} facets for hydrogen sensing, ACS Appl. Mater. Interfaces, 2018, 10, 28199–28209.
56. X. Yang, C. Jin, C. Liang, D. Chen, M. Wu and C. Y. Jimmy, Nanoflower arrays of rutile TiO₂, Chem. Commun., 2011, 47, 1184–1186.
57. Y. Yamamoto, Y. Matsumoto and H. Koinuma, Homo-epitaxial growth of rutile TiO₂ film on step and terrace structured substrate, Appl. Surf. Sci., 2004, 238, 189–192.
58. B. D. Sosnowchik, H. C. Chiamori, Y. Ding, J.-Y. Ha, Z. L. Wang and L. Lin, Titanium dioxide nanoswords with highly reactive, photocatalytic facets, Nanotechnology, 2010, 21, 485601.
59. G. E. Poirier, B. K. Hance and J. M. White, Identification of the facet planes of phase I TiO₂ (001) rutile by scanning tunneling microscopy and low energy electron diffraction, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 1992, 10, 6–15.
60. H. Nörenberg, F. Dinelli and G. A. D. Briggs, Network-like (72 × 2) R45° surface reconstruction on rutile TiO₂ (001) by non-equilibrium self-organization, Surf. Sci., 1999, 436, L635–L640.
61. J. Muscat and N. M. Harrison, The physical and electronic structure of the rutile (001) surface, Surf. Sci., 2000, 446, 119–127.
62. L. Wu, J. Lin, L. Ren, Q. Li, X. Chi, L. Luo, Y. Zhang and M.-H. Zeng, Electronic structures of hydroxylated low index surfaces of rutile and anatase-type titanium dioxide, Phys. Chem. Chem. Phys., 2022, 24, 15091–15102.
63. U. Terranova and D. R. Bowler, Adsorption of Catechol on TiO₂ Rutile (100): A Density Functional Theory Investigation, J. Phys. Chem. C, 2010, 114, 6491–6495.
64. E. German, R. Faccio and Á. W. Mombrú, Theoretical study of new potential semiconductor surfaces performance for dye sensitized solar cell usage: TiO₂-B (001), (100) and H₂Ti₃O₇ (100), Appl. Surf. Sci., 2017, 426, 1182–1189.
65. P. Jones and J. A. Hockey, Infra-red studies of rutile surfaces. Part 2.—hydroxylation, hydration and structure of rutile surfaces, Trans. Faraday Soc., 1971, 67, 2679–2685.
66. M. Xu, S. Shao, B. Gao, J. Lv, Q. Li, Y. Wang, H. Wang, L. Zhang and Y. Ma, Anatase (101)-like structural model revealed for metastable rutile TiO₂ (011) surface, ACS Appl. Mater. Interfaces, 2017, 9, 7891–7896.
67. Y. Wang, S. Lee, P. Vilmercati, H. N. Lee, H. H. Weitering and P. C. Snijders, Atomically flat reconstructed rutile TiO₂ (001) surfaces for oxide film growth, Appl. Phys. Lett., 2016, 108, 091604.
68. U. Diebold, J. Lehman, T. Mahmoud, M. Kuhn, G. Leonardelli, W. Hebenstreit, M. Schmid and P. Varga, Intrinsic defects on a TiO₂ (110)(1 × 1) surface and their reaction with oxygen: a scanning tunneling microscopy study, Surf. Sci., 1998, 411, 137–153.
69. S. Fischer, A. W. Munz, K.-D. Schierbaum and W. Göpel, The geometric structure of intrinsic defects at TiO₂ (110) surfaces: an STM study, Surf. Sci., 1995, 337, 17–30.
70. C. Xu, X. Lai, G. W. Zajac and D. W. Goodman, Scanning tunneling microscopy studies of the TiO₂ (110) surface: structure and the nucleation growth of Pd, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 13464.
71. K. P. Maenetja and P. E. Ngoepe, Unravelling the Catalytic Activity of MnO₂, TiO₂, and VO₂ (110) Surfaces by Oxygen Coadsorption on Sodium-Adsorbed MO₂ {M = Mn, Ti, V}, ACS Omega, 2022, 7, 25991–25998.
72. Y.-F. Li, U. Aschauer, J. Chen, A. Selloni, J. F. Montoya, D. W. Bahnemann, P. Salvador, J. Peral, M. Setvin, U. Aschauer, J. Hulva, T. Simschitz, B. Daniel, M. Schmid, A. Selloni, U. Diebold, I. Sokolović, M. Reticcioli, M. Čalkovský, M. Wagner, M. Schmid, C. Franchini, U. Diebold and M. Setvín, Catalytic role of bridging oxygens in TiO₂ liquid phase photocatalytic reactions: analysis of H₂O₁₆ photooxidation on labeled Ti₁₈O₂, Catal. Sci. Technol., 2017, 138, 9565–9571.
73. L. Hou, M. Zhang, Z. Guan, Q. Li and J. Yang, Effect of annealing ambience on the formation of surface/bulk oxygen vacancies in TiO₂ for photocatalytic hydrogen evolution, Appl. Surf. Sci., 2018, 428, 640–647.
74. C. Xiao, B.-A. Lu, P. Xue, N. Tian, Z.-Y. Zhou, X. Lin, W.-F. Lin and S.-G. Sun, High-Index-Facet- and High-Surface-Energy Nanocrystals of Metals and Metal Oxides as Highly Efficient Catalysts, Joule, 2020, 4, 2562–2598.
75. A. Valdes and G.-J. Kroes, First principles study of the photo-oxidation of water on tungsten trioxide (WO3), J. Chem. Phys., 2009, 130, 114701.
76. R. Kishore, X. Cao, X. Zhang and A. Bieberle-Hütter, Electrochemical water oxidation on WO3 surfaces: A density functional theory study, Catal. Today, 2019, 321, 94–99.
77. C. Shao, A. S. Malik, J. Han, D. Li, M. Dupuis, X. Zong and C. Li, Oxygen vacancy engineering with flame heating approach towards enhanced photoelectrochemical water oxidation on WO3 photoanode, Nano Energy, 2020, 77, 105190.
78. E. Jossou, L. Malakkal, N. Y. Dzade, A. Claisse, B. Szpunar and J. Szpunar, DFT+U Study of the Adsorption and Dissociation of Water on Clean, Defective, and Oxygen-Covered U₃Si₂{001}, {110}, and {111} Surfaces, J. Phys. Chem. C, 2019, 123, 19453–19467.
79. H. Ouhbi and U. Aschauer, Water oxidation catalysis on reconstructed NaTaO3 (001) surfaces, J. Mater. Chem. A, 2019, 7, 16770–16776.
80. S. Hammes-Schiffer and A. A. Stuchebrukhov, Theory of Coupled Electron and Proton Transfer Reactions, Chem. Rev., 2010, 110, 6939–6960.
81. A. Bard, Standard potentials in aqueous solution, Routledge, 2017.
82. D. A. Armstrong, R. E. Huie, S. Lymar, W. H. Koppenol, G. Merényi, P. Neta, D. M. Stanbury, S. Steenken and P. Wardman, Standard electrode potentials involving radicals in aqueous solution: inorganic radicals, BioInorg. React. Mech., 2013, 9, 59–61.
83. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
84. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
85. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
86. J. I. Rodríguez, P. W. Ayers, A. W. Götz and F. de L Castillo-Alvarados, Virial theorem in the Kohn–Sham density-functional theory formalism: Accurate calculation of the atomic quantum theory of atoms in molecules energies, J. Chem. Phys., 2009, 131, 021101.
87. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215.
88. H. Ooka, J. Huang and K. S. Exner, The sabatier principle in electrocatalysis: Basics, limitations, and extensions, Front. Energy Res., 2021, 9, 654460.
89. L. Giordano, B. Han, M. Risch, W. T. Hong, R. R. Rao, K. A. Stoerzinger and Y. Shao-Horn, pH dependence of OER activity of oxides: Current and future perspectives, Catal. Today, 2016, 262, 2–10.
90. G. He, M. Zhang and G. Pan, Influence of pH on Initial Concentration Effect of Arsenate Adsorption on TiO₂ Surfaces: Thermodynamic, DFT, and EXAFS Interpretations, The, J. Phys. Chem. C, 2009, 113, 21679–21686.
91. S. Bendjabeur, R. Zouaghi, B. Zouchoune and T. Sehili, DFT and TD-DFT insights, photolysis and photocatalysis investigation of three dyes with similar structure under UV irradiation with and without TiO₂ as a catalyst: Effect of adsorption, pH and light intensity, Spectrochim. Acta, Part A, 2018, 190, 494–505.
92. K. S. Exner, Overpotential-Dependent Volcano Plots to Assess Activity Trends in the Competing Chlorine and Oxygen Evolution Reactions, ChemElectroChem, 2020, 7, 1448–1455.
93. X. Li, S. Duan, E. Sharman, Y. Zhao, L. Yang, Z. Zhuo, P. Cui, J. Jiang and Y. Luo, Exceeding the volcano relationship in oxygen reduction/evolution reactions using single-atom-based catalysts with dual-active-sites, J. Mater. Chem. A, 2020, 8, 10193–10198.
94. M. Craig, G. Coulter, E. Dolan, J. Soriano-López, E. Mates-Torres, W. Schmitt and M. García Melchor, Universal scaling relations for the rational design of molecular water oxidation catalysts with near-zero overpotential, Nat. Commun., 2019, 10, 4993.
95. I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165.
96. A. Gomer and T. Bredow, Effect of Doping on Rutile TiO₂ Surface Stability and Crystal Shapes, ChemistryOpen, 2022, 11, e202200077.
97. L. Museur, G. D. Tsibidis, A. Manousaki, D. Anglos and A. Kanaev, Surface structuring of rutile TiO₂ (100) and (001) single crystals with femtosecond pulsed laser irradiation, J. Opt. Soc. Am. B, 2018, 35, 2600–2607.
98. B. Wei, F. Tielens and M. Calatayud, Understanding the role of rutile TiO₂ surface orientation on molecular hydrogen activation, Nanomaterials, 2019, 9, 1199.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04939b

---