The role of the intermediate triplet state in iron-catalyzed multi-state C–H activation

Abstract

Efficient activation and functionalization of the C–H bond under mild conditions are of a great interest in chemical synthesis. We investigate the previously proposed spin-accelerated activation of the C(sp²)–H bond by a Fe(II)-based catalyst to clarify the role of the intermediate triplet state in the reaction mechanism. High-level electronic structure calculations on a small model of a catalytic system utilizing the coupled cluster with the single, double, and perturbative triple excitations [CCSD(T)] are used to select the density functional for the full-size model. Our analysis indicates that the previously proposed two-state quintet–singlet reaction pathway is unlikely to be efficient due to a very weak spin–orbit coupling between these two spin states. We propose a more favorable multi-state quintet–triplet–singlet reaction pathway and discuss the importance of the intermediate triplet state. This triplet state facilitates a spin-accelerated reaction mechanism by strongly coupling to both quintet and singlet states. Our calculations show that the C–H bond activation through the proposed quintet–triplet–singlet reaction pathway is more thermodynamically favorable than the single-state quintet and two-state singlet–quintet mechanisms.

---

1. Introduction

Catalytic C–H bond activation and functionalization are important for efficient synthesis of organic molecules with applications in materials science, biochemistry, and the petroleum and pharmaceutical industries.^1,2 The development of new catalysts capable of activating C–H bonds using earth-abundant and non-toxic first-row transition metals, instead of the traditionally used precious metals, is critical for economy and sustainability.^1,2 Norinder et al. reported efficient iron-catalyzed C(sp²)–H bond activation and arylation at temperatures as low as 0 °C.³ While it was demonstrated that the C–H bond activation is the rate limiting step in the arylation reaction,¹ the overall reaction mechanism remained a mystery (Fig. 1). Understanding the mechanisms of this and similar catalytic reactions proceeding under very mild conditions is critical for the development of novel catalysts based on non-toxic and earth-abundant transition metals.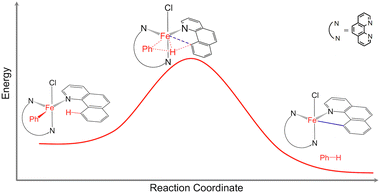

Fig. 1 Schematic representation of the C(sp²)–H bond activation in the Fe(bqn)(phen)(Ph)Cl complex (bqn – α-benzoquinoline, phen – 1,10-phenanthroline, Ph – phenyl).

To explain the thermodynamic efficiency of the C–H bond activation by first-row transition metals, Sun et al. carried out an extensive computational study of the catalytic cycles.⁴ This study showed that the reaction mechanisms involving transitions between two electronic states with different spin multiplicities often have lower reaction barriers than the mechanisms limited to a single spin state. For the iron-catalyzed C–H bond activation, based on the density functional theory (DFT) and small model coupled cluster calculations, they proposed a two-state mechanism involving the quintet and singlet state of Fe(II).⁴ This two-state mechanism can accelerate a chemical transformation by following a reaction path that involves transition between electronic states with different spin multiplicities and have a lower activation energy compared to the traditional single-state mechanism. The two-state, formally spin-forbidden, reaction mechanism requires a non-zero coupling between the participating electronic states with different spins. The spin–orbit coupling (SOC) is often the main contributor to this interstate coupling. In recent years, the two-state reaction mechanisms^5–7 received significant attention due to their important roles in C–H bond activation,^8–11 hydrogen atom transfer and oxidation reactions,^12–15 catalyzed hydroxylation,^16–18 isomerization,¹⁹ catalytic and electron-transfer properties of metalloproteins,^20–22 excited-state relaxation,²³ and interstellar chemistry.²⁴

To explain the efficient low-temperature iron-catalyzed C–H bond activation,³ Sun et al. proposed a two-state mechanism involving a transition between the singlet and quintet spin states of Fe(II).⁴ The proposed two-state C–H bond activation mechanism has a lower energy barrier than the single-state mechanism involving only the quintet state. However, the direct transition between the quintet and singlet states is expected to be very inefficient because the SOC between the states with the spin multiplicities different by more than one unit is small (zero according to the fist-order perturbation theory). In this work, we demonstrate the importance of the intermediate-spin triplet state that is strongly coupled to both the quintet and singlet states, facilitating the indirect quintet–singlet coupling. Based on these findings we propose a new multi-state reaction mechanism for iron-catalyzed C–H bond activation.

2. Computational details

The critical points on the potential energy surfaces (PESs) of the lowest-energy singlet, triplet, and quintet states were obtained by fully optimizing the geometries of reactants, transition states (TS), and products. The harmonic vibrational analysis was performed at each critical point to characterize it as a minimum (no imaginary frequency) or TS (one imaginary frequency). All geometries were optimized with the unrestricted density functional theory (DFT) using the B3LYP functional^25–27 with the def2-SVP basis set.²⁸ The single point energy calculations for the optimized geometries were performed using the B3LYP with Grimme's dispersion correction and Becke–Johnson damping [D3(BJ)],^29,30 MN15-L,³¹ and ωB97X-V³² functionals combined with the larger def2-TZVP basis set.^28,33 The solvent effect was accounted for with the conductor-like screening model (COSMO).³⁴ High-level electronic structure calculations on a small model of the complex were performed using the restricted coupled cluster with singles, doubles and perturbative triples [CCSD(T)] method,³⁵ as well as the domain local pair natural orbital (DLPNO) approximation [DLPNO-CCSD(T)],^36–38 combined with the def2-TZVP basis set. The initial screening of the enantiomers of the Fe complex, TS search, and harmonic vibrational analysis were performed using the GAMESS software package.^39,40 The following geometry optimization for the lowest energy enantiomer was carried out in the Molpro package.⁴¹ For the calculations with the MN15-L and ωB97X-V density functionals, the Q-Chem package⁴² was used. All CCSD(T) calculations were carried out with Molpro, while the DLPNO-CCSD(T) calculations and minimum energy crossing point (MECP) searches were performed using the ORCA package.⁴³ To compare the Hartree–Fock and DFT wave functions, Hirshfeld atomic charge analysis⁴⁴ was performed with Multiwfn software.⁴⁵ The SOC values between the spin states were calculated with the first-order perturbation theory using the state-averaged complete active space self-consistent field (SA-CASSCF) wave functions and the two-electron Breit–Pauli Hamiltonian.⁴⁶ The CASSCF active space comprised of six electrons and five d-orbitals of Fe(II), and the state-averaging was done over the two spin states of interest (quintet and triplet, or triplet and singlet). At the first-order perturbation theory, the SOC between the quintet and singlet states is zero. All SOC calculations were performed using the GAMESS package. The localized orbitals were obtained with the JANPA package using the chemist's localized property-optimized orbital procedure,^47,48 and visualized using Jmol.⁴⁹

3. Results and discussion

3.1. Selection of stereoisomers and density functionals

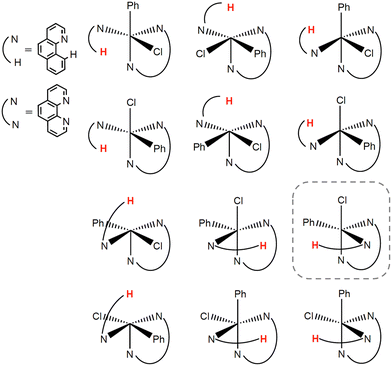
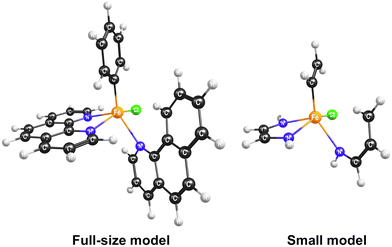
To find the most stable stereoisomer of the [Fe^II(bqn)(phen)(Ph)Cl]⁰ complex (bqn – α-benzoquinoline, phen – 1,10-phenanthroline, Ph – phenyl) proposed by Sun and co-workers,⁴ we optimized the geometries of all twelve possible stereoisomers with the B3LYP-D3(BJ)/def2-SVP level of theory (Fig. 2). We assumed that α-benzoquinoline cannot rotate around the N–Fe bond and no isomerization occurs before the C–H bond activation step. The geometries were optimized for the lowest-energy singlet, triplet, and quintet states. The order of the spin state in each stereoisomer was found to be E_quintet < E_triplet < E_singlet. The quintet state of the stereoisomer in the dashed box in Fig. 2 was found to have the lowest energy and used in all following calculations.

Fig. 2 Stereoisomers of the Fe(bqn)(phen)(Ph)Cl complex (bqn – α-benzoquinoline, phen – 1,10-phenanthroline, Ph – phenyl). The hydrogen atom of the activated C(sp²)–H bond is shown in red. The lowest energy stereoisomer is in the dashed box.

To select the best DFT functional to study the catalytic C–H activation involving multiple spin states, we preformed the CCSD(T) calculations on a small model of the complex and compared the relative energies of the spin states with those obtained with different density functionals. The small model was constructed from the full-size model of the selected stereoisomer by replacing the atoms of the iron's second coordination sphere with hydrogens (Fig. 3). The positions of these hydrogen atoms were optimized, while the coordinates of all other atoms were kept fixed. In addition to the B3LYP functional that has been shown to reproduce spin-dependent properties of iron complexes,^50–53 we tested the MN15-L and ωB97X-V functionals, which are known to work well for transition metal compounds.^33,54,55

Fig. 3 Full-size and small models of the [Fe^II(bqn)(phen)(Ph)Cl]⁰ complex.

All three density functionals predict the same order of the spin states for the reactant geometries (E_quintet < E_triplet < E_singlet) and the TS geometries (E_singlet < E_quintet < E_triplet), with the exception of the isoenergetic singlet and triplet states at the reactant geometry predicted by ωB97X-V and the different state order at the TS geometries predicted by MN15-L (Table 1). For the TS geometries, this order of the spin states is also consistent with the CCSD(T) results. For the reactant geometry, CCSD(T) predicts the singlet state to be 5.4 kcal mol⁻¹ below the triplet state.

Table 1 Relative energies (kcal mol⁻¹) of the spin states for the small model obtained with the def2-TZVP basis set

Spin state	B3LYP-D3(BJ)		MN15-L		ωB97X-V		CCSD(T)
	Reactant	Transition State	Reactant	Transition State	Reactant	Transition State	Reactant	Transition State
Singlet	14.7	31.7	33.1	48.4	9.6	24.0	5.8	23.8
Triplet	10.2	47.3	14.2	56.4	9.6	45.2	11.2	52.9
Quintet	0.0	41.3	0.0	40.2	0.0	37.8	0.0	37.2

---

The three density functionals and CCSD(T) predict similar relative energies for the quintet and triplet states at the reactant and TS geometries. The MN15-L singlet state energies are significantly overestimated compared to those of CCSD(T) and the other two density functionals. However, all three density functionals and CCSD(T) predict similar TS barriers (the energy differences between the reactant and TS structures) for the singlet, triplet and quintet states. For each spin state, the highest occupied molecular orbital (HOMO), singly occupied molecular orbitals (SOMOs) and the Hirshfeld atomic charges obtained with different density functionals are similar (Fig. S2–S13, ESI†), indicating convergence to the same self-consistent field solutions. The quantitative differences in the relative energies of the spin states predicted by three DFT functionals are likely related to the different treatment of the exchange interaction.^56,57 The energy gaps between different spin states predicted by hybrid functionals are sensitive to the amount of the Hartree-Fock (HF) exchange.^57,58 For example, the B3LYP containing 20% of HF exchange is known to over stabilize high-spin states.^59,60 This can be seen in Table 1 by comparing the singlet–triplet energy gaps at the reactant and TS geometries. For example, for reactants, these gaps are 18.9 kcal mol⁻¹ for MN15-L (0% HF exchange), 4.5 kcal mol⁻¹ for B3LYP-D3(BJ) (20% HF exchange) and 0.0 kcal mol⁻¹ for range-separated ωB97X-V (16.7% HF exchange for short-range and 100% for long-range). These values can be compared with −5.4 kcal mol⁻¹ predicted by CCSD(T). A similar trend is observed for the singlet-quintet energy gap.

The efficiency of the C–H bond activation, which is known to proceed at temperatures as low as 0 °C, depends on the lowest TS barrier. The CCSD(T) predicts the singlet TS to be significantly lower than triplet and quintet TSs. The CCSD(T) singlet TS energy (23.8 kcal mol⁻¹) is in very good agreement with the ωB97X-V value (24.0 kcal mol⁻¹). Therefore, based on the agreement between the CCSD(T) and ωB97X-V values for the interstate energy gaps and the lowest TS energy, all energy calculations on the full-size model were performed with the ωB97X-V functional.

To ensure the applicability of the single reference methods, the CCSD(T) T₁ diagnostic and the unrestricted DFT spin contamination were calculated. In all CCSD(T) calculations, the T₁ diagnostic for the triplet and quintet states was always below the critical value of 0.05,^61,62 while for the singlet reactant and TS the corresponding values were 0.059 and 0.053. For the ωB97X-V functional, the spin contamination calculated as a difference between the expectation value of Ŝ² operator and the exact value of S(S + 1) was below 0.2.

3.2. Effects of model size, molecular geometry, basis set and solvent on the spin state energies

According to the ωB97X-V calculations on the small model, the singlet and triplet reactants were predicted to be isoenergetic (Table 1). In the full-size model, the triplet reactant energy is predicted to be 1.9 kcal mol⁻¹ lower than the singlet, as seen in Fig. S14 (ESI†). The order of the spin states at the TS geometries for small and full-size models are the same; however, the TS energies of the quintet and triplet states are noticeably lower in the full-size model. Therefore, the CCSD(T) energies calculated for the small model, while providing useful insight into the relative stability of the spin state, are not necessarily more accurate than the full-size model values obtained with ωB97X-V.

To estimate the effect of the B3LYP-D3(BJ) geometry optimization on the spin state energies, the selected geometries were also optimized with ωB97X-V, using the same def2-SVP basis set. The single point energies were recalculated with the ωB97X-V/def2-TZVP level of theory. As illustrated in Fig. 4, the largest difference between the relative energies obtained for the ωB97X-V and B3LYP geometries is 4.2 kcal mol⁻¹ for the triplet TS. Thus, the relative energies of the spin states are not very sensitive to the functional used for the geometry optimization.

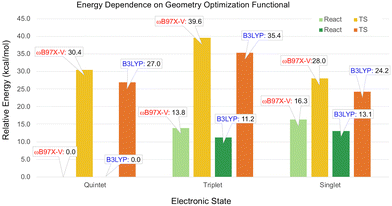Fig. 4 Relative energies of the spin states calculated with the ωB97X-V/def2-TZVP level of theory for the geometries optimized using the B3LYP and ωB97X-V functionals with the def2-SVP basis set.

In Table 2, we compare the relative energies of the spin states calculated using the def2-SVP and the larger def2-TZVP basis sets. There are two sets of the energies reported, one in the gas phase and another in the tetrahydrofuran (THF) solvent using the dielectric constant value of 7.58. The largest difference between the relative energies obtained with the two basis sets is 6.7 kcal mol⁻¹ for the triplet reactant in THF. This indicates that the def2-TZVP energies are likely converged within the chemical accuracy with respect to the basis set limit, which is expected for the DFT energies calculated with the triple-zeta basis set.^28,33 The implicit solvent effect described by the COSMO model slightly stabilizes the singlet and triplet states with respect to the quintet, with the largest stabilization of 3.6 kcal mol⁻¹ observed for the triplet reactant. While the TS of the quintet state in THF is destabilized by 1.5 kcal mol⁻¹ with respect to the gas phase. These small energy changes are not expected to influence the overall reaction mechanism. To estimate the explicit solvent effect, a single THF molecule was placed next to the TS structure of the quintet state (Fig. S15, ESI†). The geometry optimization indicates that this THF molecule does not bind to the complex and, therefore, should not affect the overall C–H bond activation reaction.

Table 2 Relative energies (kcal mol⁻¹) of the spin states for the full-size model obtained with the ωB97X-V functional. The molecular geometries optimized at the B3LYP-D3(BJ)/def2-SVP level of theory in the gas phase

	Gas phase				THF solvent
	def2-SVP		def2-TZVP		def2-SVP		def2-TZVP
	Reactant	Transition State	Reactant	Transition State	Reactant	Transition State	Reactant	Transition State
Singlet	16.5	26.1	13.1	24.2	15.7	26.6	11.5	24.1
Triplet	16.1	36.0	11.2	35.4	14.3	36.0	7.6	35.1
Quintet	0.0	28.0	0.0	27.0	0.0	29.3	0.0	28.5

---

3.3. Spin-accelerated reaction mechanism

The C–H bond activation by transition metal complexes, including spin-accelerated mechanisms,^63,64 requires the presence of an unoccupied 3d-orbital.⁶⁵ The donation of the sigma-bond electrons to the d-orbitals of iron facilitates the C–H bond activation. There are no unoccupied 3d-orbitals in the quintet state (the ground state of the reactant); hence, the lowest-energy TS is likely to correspond to the singlet or a triplet spin state. The chemist's localized property-optimized orbitals shown in Fig. 5 clearly demonstrate the contribution of the d_z² orbital of iron and the C–H sigma bond to the same molecular orbitals. As a result of this orbital mixing, even at the reactant geometries, the C–H bond goes out of the plane of the α-benzoquinoline ligand. This effect is present in all three spin states but especially prominent in the singlet state (Fig. S16, ESI†).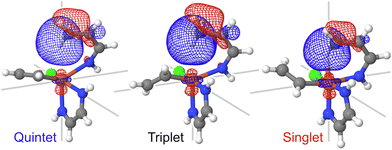

Fig. 5 The C–H bond localized molecular orbital for three different spin states. The plots demonstrate the contribution of the d_z² orbital of iron to this molecular orbital at the reactant geometries. Similar plots for the TS geometries are shown in Fig. S17 (ESI†).

Fig. 6 depicts the crystal-field diagrams of the distorted octahedral reactant geometries for the three spin states, showing the electron distribution over d-orbitals. The weak interaction between the hydrogen atom on the z-axis and the iron center leads to the d_z² orbital to be less destabilized than the d_x²−y² orbital, which strongly interacts with the ligands on the x- and y-axis. According to these crystal field diagrams, the d_z² orbital is unoccupied only in the singlet state. For the C–H bond to be activated, this d_z² orbital must accept electron density from the C–H sigma bond. For the quintet and triplet states, this electron transfer will result in an energy penalty due to the repulsion with the single electron already present on the d_z² orbital. Therefore, the C–H bond activation must be more efficient in the singlet state with the empty d_z² orbital.

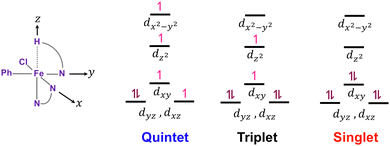Fig. 6 Cartesian coordinates defined for the octahedral reactant geometries and the crystal-field diagrams for the three spin states.

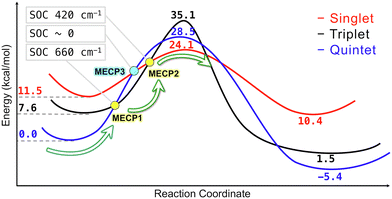
The more efficient C–H bond activation in the singlet state predicted by the simple crystal-field diagrams is supported by the reaction pathways obtained from the electronic structure calculations (Table 2 and Fig. 7). The singlet reaction pathway has the lowest activation barrier compared to the triplet and quintet pathways. Based on this picture, we propose the following mechanism for the iron-catalyzed C–H bond activation. The reaction starts on the lowest-energy high-spin quintet state and proceeds to the crossing point between the quintet and triplet states. After crossing to the triplet state, the second crossing from the triplet to singlet takes place, allowing the C–H bond activation to proceed through the lowest energy barrier. The existence of the interstate crossings was confirmed by locating the MECPs between quintet–triplet and triplet–singlet states (Fig. S18, ESI†). The proposed multi-state mechanism is thermodynamically more favorable than the single-state reaction mechanism involving only the quintet state with a higher energy barrier. Also, this multi-state mechanism proceeding through the intermediate triplet state is expected to be more efficient than the two-state mechanism with the direct quintet–singlet transition proposed earlier.⁴ The rates of transitions between the electronic states with different spin multiplicities strongly depend on the magnitude of SOC between these states. The SOC values calculated with the perturbation theory at the MECP geometries are 660 and 420 cm⁻¹ for the quintet-triplet and singlet–triplet crossings, indicating significant transition probabilities between these states. In contrast, for the two-state reaction mechanism, the coupling between the quintet and singlet states is expected to be very small (zero within the first-order perturbation theory). Therefore, we expect the spin-accelerated C–H bond activation to proceed via a multi-state mechanism involving all three electronic states, as shown in Fig. 7.

Fig. 7 Multi-state reaction mechanism for the iron-catalyzed C(sp²)–H bond activation involving three different spin states. The energies are obtained with the ωB97X-V/def2-TZVP//B3LYP-D3(BJ)/def2-SVP level of theory. The bold blue, black and red numbers are relative energies in kcal mol⁻¹ with respect to the quintet reactant energy. The values of spin–orbit coupling between the spin states at MECPs are shown in gray boxes.

4. Conclusion

We presented a detailed study of the Fe(II)-catalyzed C(sp²)–H bond activation mechanisms involving multiple electronic states with different spin multiplicities. In an earlier study, based on the calculated relative energies of the different spin states, a two-state mechanism with the direct transition from the quintet to the singlet state was proposed.⁴ In this work, we investigated the importance of the intermediate triplet state in this catalytic C–H bond activation reaction. The CCSD(T) calculations on the small model of the reaction complex was used to select the density functional capable of accurately predicting the relative energies of the spin states. The energies of the reactants, TSs and MECPs of the full-size model were calculated at the ωB97X-V/def2-TZVP level of theory. The spin–orbit coupling between the states at the MECP geometries were obtained with the state-averaged CASSCF method and the Breit–Pauli Hamiltonian. The large SOC values between the quintet–triplet and triplet–singlet states indicate the high interstate transition probabilities and rates, while the very small coupling between the quintet and singlet corresponds to a very low transition rate between these states. Therefore, we proposed a multi-state quintet–triplet–singlet reaction mechanism for the iron-catalyzed C(sp²)–H bond activation, which is more favorable than the direct two-state quintet–singlet mechanism. We believe that this multi-state reaction mechanism could open a new direction in the development of the next-generation of efficient catalysts based on the earth-abundant and inexpensive first-row transition metals.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr. Aleksandr Lykhin for his contribution to the earlier stages of this work. The authors acknowledge the American Chemical Society Petroleum Research Fund (ACS PRF) for supporting this work through grant number PRF# 60481-ND6.

References

1. R. Shang, L. Ilies and E. Nakamura, Chem. Rev., 2017, 117, 9086–9139.
2. P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, Chem. Rev., 2019, 119, 2192–2452.
3. J. Norinder, A. Matsumoto, N. Yoshikai and E. Nakamura, J. Am. Chem. Soc., 2008, 2, 5858–5859.
4. Y. Sun, H. Tang, K. Chen, L. Hu, J. Yao, S. Shaik and H. Chen, J. Am. Chem. Soc., 2016, 138, 715–3730.
5. D. Schröder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145.
6. A. O. Lykhin, D. S. Kaliakin, G. E. dePolo, A. A. Kuzubov and S. A. Varganov, Int. J. Quantum Chem., 2016, 116, 750–761.
7. J. N. Harvey, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 1–14.
8. D. Mandal and S. Shaik, J. Am. Chem. Soc., 2016, 138, 2094–2097.
9. Y. Yu, G. Luo, J. Yang and Y. Luo, Catal. Sci. Technol., 2019, 9, 1879–1890.
10. A. K. Hickey, S. A. Lutz, C.-H. Chen and J. M. Smith, Chem. Commun., 2017, 53, 1245–1248.
11. B. E. Haines, J.-Q. Yu and D. G. Musaev, Chem. Sci., 2018, 9, 1144–1154.
12. Y. H. Kwon, B. K. Mai, Y. M. Lee, S. N. Dhuri, D. Mandal, K. Bin Cho, Y. Kim, S. Shaik and W. Nam, J. Phys. Chem. Lett., 2015, 6, 1472–1476.
13. S. Shaik, S. P. de Visser, F. Ogliaro, H. Schwarz and D. Schröder, Curr. Opin. Chem. Biol., 2002, 6, 556–567.
14. Z. Zhang, J.-X. Zhang, F. K. Sheong and Z. Lin, ACS Catal., 2020, 10, 12454–12465.
15. X.-F. Su, W. Guan, L.-K. Yan, Z.-L. Lang and Z.-M. Su, J. Catal., 2019, 376, 146–149.
16. H. Hirao, D. Kumar, L. Que and S. Shaik, J. Am. Chem. Soc., 2006, 128, 8590–8606.
17. J. C. Schöneboom, S. Cohen, H. Lin, S. Shaik and W. Thiel, J. Am. Chem. Soc., 2004, 126, 4017–4034.
18. D. Ricciarelli, Q. M. Phung, L. Belpassi, J. N. Harvey and P. Belanzoni, Inorg. Chem., 2019, 58, 7345–7356.
19. S. A. Lutz, A. K. Hickey, Y. Gao, C.-H. Chen and J. M. Smith, J. Am. Chem. Soc., 2020, 142, 15527–15535.
20. D. S. Kaliakin, R. R. Zaari and S. A. Varganov, J. Phys. Chem. A, 2015, 119, 1066–1073.
21. G. E. Depolo, D. S. Kaliakin and S. A. Varganov, J. Phys. Chem. A, 2016, 120, 8691–8698.
22. D. S. Kaliakin, D. G. Fedorov, Y. Alexeev and S. A. Varganov, J. Chem. Theory Comput., 2019, 15, 6074–6084.
23. A. O. Lykhin and S. A. Varganov, Phys. Chem. Chem. Phys., 2020, 22, 5500–5508.
24. S. Ahmadvand, R. R. Zaari and S. A. Varganov, Astrophys. J., 2014, 795, 173.
25. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
26. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
30. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
31. H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293.
32. N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924.
33. D. Zhang and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 4416–4428.
34. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
35. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
36. F. Neese, A. Hansen and D. G. Liakos, J. Chem. Phys., 2009, 131, 64103.
37. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 34106.
38. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
39. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347–1363.
40. M. S. Gordon and M. W. Schmidt, in Advances in Electronic Structure Theory: GAMESS a Decade Later, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189.
41. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
42. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 84801.
43. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
44. T. Lu and F. Chen, J. Theor. Comput. Chem., 2012, 11, 163–183.
45. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
46. D. G. Fedorov and M. S. Gordon, J. Chem. Phys., 2000, 112, 5611–5623.
47. T. Y. Nikolaienko, L. A. Bulavin and D. M. Hovorun, Comput. Theor. Chem., 2014, 1050, 15–22.
48. T. Y. Nikolaienko and L. A. Bulavin, Int. J. Quantum Chem., 2019, 119, e25798.
49. Jmol: An Open-Source Java Viewer for Chemical Structures in 3D, https://www.jmol.org/.
50. S. Ossinger, H. Naggert, E. Bill, C. Näther and F. Tuczek, Inorg. Chem., 2019, 58, 12873–12887.
51. S. Ossinger, C. Näther, A. Buchholz, M. Schmidtmann, S. Mangelsen, R. Beckhaus, W. Plass and F. Tuczek, Inorg. Chem., 2020, 59, 7966–7979.
52. S. Schönfeld, K. Dankhoff, D. Baabe, M.-K. Zaretzke, M. Bröring, K. Schötz, A. Köhler, G. Hörner and B. Weber, Inorg. Chem., 2020, 59, 8320–8333.
53. F. Vlahovic, M. Gruden, S. Stepanovic and M. Swart, Int. J. Quantum Chem., 2020, 120, e26121.
54. B. Chan, P. M. W. Gill and M. Kimura, J. Chem. Theory Comput., 2019, 15, 3610–3622.
55. I. Efremenko and J. M. L. Martin, J. Phys. Chem. A, 2021, 125, 8987–8999.
56. J. N. Harvey, in DFT Computation of Relative Spin-State Energies of Transitions Metal Compounds, ed. N. Kaltsoyannis and J. E. McGrady, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, pp. 151–184.
57. M. Radoń, Phys. Chem. Chem. Phys., 2014, 16, 14479–14488.
58. A. Droghetti, D. Alfè and S. Sanvito, J. Chem. Phys., 2012, 137, 124303.
59. M. Reiher, Inorg. Chem., 2002, 41, 6928–6935.
60. D. N. Bowman and E. Jakubikova, Inorg. Chem., 2012, 51, 6011–6019.
61. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199–207.
62. W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460–468.
63. S. M. Bellows, T. R. Cundari and P. L. Holland, Organometallics, 2013, 32, 4741–4751.
64. P. L. Holland, Acc. Chem. Res., 2015, 48, 1696–1702.
65. D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823.

---

Footnote

† Electronic supplementary information (ESI) available: Bond distances between the iron center and the coordinated atoms in the reactant and TS geometries (Fig. S1), Hirshfeld atomic dipole moment corrected charges, and highest doubly and singly occupied molecular orbitals for the small model (Fig. S2–S13), energies of the spin states in the full-size model and the small model (Fig. S14), initial and final optimized structures of the complex with a THF solvent molecule (Fig. S15), dihedral angle of the out-of-plane C–H bond in α-benzoquinoline for different spin states (Fig. S16), C–H bond localized molecular orbital for the TS geometries of the small model (Fig. S17), structures of the quintet–triplet and triplet–singlet MECPs (Fig. S18), relative energies of the spin states for the small model obtained with DLPNO-CCSD(T₁) (Table S1), CASSCF active space orbitals (Fig. S19), relative energies of the quintet–triplet and triplet–singlet MECPs (Table S2), and Cartesian coordinates of the optimized reactant, MECP, TS, and product geometries for different spin states (Tables S3–S14). See DOI: https://doi.org/10.1039/d2cp02733j

---