Investigation of nonadiabatic dynamics in the photolysis of methyl nitrate (CH₃ONO₂) by on-the-fly surface hopping simulation

Abstract

The photolysis mechanism of methyl nitrate (CH₃ONO₂) was studied using the on-the-fly surface hopping dynamics at the XMS-CASPT2 level. Several critical geometries, including electronic state minima and conical intersections, were obtained, which play essential roles in the nonadiabatic dynamics of CH₃ONO₂. The ultrafast nonadiabatic decay dynamics to the ground state were simulated, which gives a proper explanation on the broad and structureless absorption spectra of CH₃ONO₂. The photodissociation channels, including CH₃O + NO₂, CH₃O + NO + O, and others, as well as their branching ratios, were identified. When the dynamics starts from the lowest two electronic states (S₁ and S₂), the CH₃O + NO₂ channel is the dominant photolysis pathway, although we observed the minor contributions of other channels. In contrast, when the trajectories start from the third excited state S₃, both CH₃O + NO₂ and CH₃O + NO + O channels become important. Here the CH₃O–NO₂ bond dissociation takes place first, and then for some trajectories, the N–O bond of the NO₂ part breaks successively. The quasi-degeneracy of electronic states may exist in the dissociation limits of both CH₃O + NO₂ and CH₃O + NO + O channels. The current work provides valuable information in the understanding of experimental findings of the wavelength-dependent photolysis mechanism of CH₃ONO₂.

---

1. Introduction

Alkyl nitrates (RONO₂, R = CH₃, C₂H₅, etc) have received considerable research attention because they play an essential role in the NO_x-involved chemical reactions in the atmosphere.^1–11 The oxidation and photoinduced reactions of reactive nitrogen oxides cause significant impacts on our atmospheric environments, such as affecting air quality, changing climates, and modifying nutrient cycles.^1–4,7–13 A group of stable organic nitrates involved in the atmospheric NO_x reactions are RONO₂. On one side, this series of compounds are generated by the photo-oxidation of hydrocarbons in the presence of NO_x or reactions of NO₃ with alkenes.^{1,2,6,11–16} Due to the thermal stability of RONO₂, they may survive in the atmosphere for a sufficiently long time and may be transferred to regions far from where they are produced. Therefore, several studies tried to explore their potential roles as NO_x reservoirs in the troposphere.² On the other side, RONO₂ experience photolysis and give NO₂ again after UV radiation.^1,2,17–35 Therefore, the study of RONO₂ photoreaction at the atomic level is certainly important.

As the simplest alkyl nitrate, methyl nitrate (CH₃ONO₂) was found in marine boundary layer of the South Pacific, which was related to 20–80% of the reactive nitrogen (NO_x).¹⁶ The UV absorption spectra of CH₃ONO₂^{6,19,24,27,28,33,35–37} display an intense band around 190–220 nm, along with a much weaker diffusion band extending to around 330 nm. In fact, both are rather broad and structureless, namely, lack of vibronic progression. The broadness of the absorption band strongly indicates that the lifetime of the excited states should be extremely short.^38,39 Therefore, after UV absorption, the wavepacket should quickly move out of the Franck–Condon (FC) region on the excited-state surfaces, and even decay via conical intersections (CIs). This implies that ultrafast excited-state dynamics in principle should take place.

Several experimental studies focused on the photolysis dynamics of CH₃ONO₂ and other alkyl nitrates.^{6,20,22–24,27,28,31,32,35,40} In particular, these works demonstrated that different photolysis products may be formed with laser excitation at different wavelengths. Yang et al.²⁰ found that the photolysis of CH₃ONO₂ at 248 and 193 nm results in different dissociation products. The photolysis at 248 nm mainly gives CH₃O + NO₂ with a rather high quantum yield. At 193 nm two different channels were observed after the CH₃O–NO₂ bond breaking, in which the low-energy channel gives CH₃O + NO₂ products and the high-energy channel induces a further dissociation of the N–O bond in NO₂, giving the CH₃O + NO + O reaction. An additional channel CH₃ONO + O was also identified. The UV photolysis of CH₃ONO₂ was examined by Talukdar et al.,³⁵ who suggested that the CH₃ONO₂ photodissociation at long wavelengths, namely 248 nm and 308 nm, is dominated by the CH₃O + NO₂ channel. At a much shorter wavelength of 193 nm, a visible quantum yield of the O atom was observed, which may come from the further dissociation of the NO₂ fragment. The photolysis of CH₃ONO₂ at a long wavelength (>300 nm) closing to the low-energy absorption tail always results in the CH₃O + NO₂ photoproducts. Derro et al.²⁴ examined the photolysis dynamics of CH₃ONO₂ at 193 nm. They suggested that the excitation of CH₃ONO₂ at 193 nm causes the local excitation of the −NO₂ moiety, and most available energy is thus partitioned to the NO₂ fragment during dissociation. As a consequence, after the CH₃O + NO₂ photoproducts are generated by the laser excitation at 193 nm, the highly excited NO₂ fragment may experience the further N–O bond dissociation, resulting in the CH₃O + NO + O channel. Other alkyl nitrates and derivatives were also studied experimentally,^{6,17,21–24,27,28,31,32,35,40} which indicates a similar tendency.

Several theoretical efforts were made to examine the reactions of alkyl nitrates and similar compounds.^{5,18,25,26,41–49} The ground-state reactivity and the dissociation dynamics of CH₃ONO₂ were examined by electronic structure calculations and Born–Oppenheimer dynamics simulations.²⁵ One of the early theoretical studies on the excited states of alkyl nitrates was performed by Harris^18,49 at the semi-empirical level, who provided the excitation energies and oscillator strengths of the low-lying excited states for the initial assignment of the absorption spectra of these species. Recently, Soto, Arenas and coworkers performed systematic studies on the photoreactions of CH₃ONO₂ and derivatives.^{26,41,43,48,50–52} At the multi-state complete active space second order perturbation theory (MS-CASPT2) level, they built the highly accurate potential energy surfaces (PESs) of several excited states along the CH₃O–NO₂ dissociative coordinate.²⁶ The pathways towards different products were constructed. Several key geometries including the minimum-energy geometries and CIs were located. We noticed that the quasi-degeneracy of the low-lying electronic states exists in the dissociation limit due to the symmetry property of the photoproducts. This provides an important starting point to address the photolysis mechanism of CH₃ONO₂.

From the theoretical point of view, the direct simulation of the excited-state dynamics of CH₃ONO₂ should provide valuable information for the understanding of the CH₃ONO₂ photolysis mechanism. Therefore, we tried to employ the on-the-fly trajectory surface hopping (TSH) dynamics with the extended multi-state complete active space second order perturbation theory (XMS-CASPT2)^53–55 to study the excited-state nonadiabatic dynamics of CH₃ONO₂. Several key geometries, including the minima of electronic states and CIs, were located. The nonadiabatic dynamics including low-lying excited states was simulated. The results showed that the ultrafast nonadiabatic dynamics takes place after photoexcitation, followed by the successive dissociation dynamics. Different photoproducts were identified when dynamics starts from different excited states. The simulated results were in qualitative agreement with available experimental studies. This work deepens our understanding of the photochemistry of alkyl nitrates. In addition, we clearly demonstrate that both nonadiabatic internal conversion and photodissociation dynamics of CH₃ONO₂ take place within the ultrafast time scale. This indicates that such a system may become an interesting candidate in future experimental studies of ultrafast spectroscopy. At the same time, the theoretical treatment of photodynamics of volatile organic compounds (VOCs) becomes more and more attractive in recent years.^1,2,56–60 We believe that the on-the-fly nonadiabatic dynamics^56,58–67 may provide an indispensable simulation tool in the explanation of the photochemistry of VOCs.^{56,58–60,68,69}

2. Computational details

Scheme 1 shows the molecular structure of CH₃ONO₂ and atomic labels. The critical internal coordinates are listed in Table 1, in which the O–N, O–O_a, and O–O_b distances are described by r_a, r_b, and r_c, respectively. The distances of N–O_a and N–O_b are shown as r_d and r_e, respectively. The angle O_a–N–O_b (θ_a) describes the bending motion of the NO₂ fragment. The dihedral angle O–O_a–O_b–N (τ_a) describes the pyramidalization at the N atom.

Scheme 1 Molecular structure of CH₃ONO₂.

Table 1 Labels of important internal coordinates of CH₃ONO₂

Label	Internal coordinate
r a	Distance O–N
r b	Distance O–Oa
r c	Distance O–Ob
r d	Distance N–Oa
r e	Distance N–Ob
θ a	Angle Oa–N–Ob
τ a	Dihedral angle O–Oa–Ob–N

---

The geometry optimization of the ground-state minimum (S₀-min) and the vibrational analysis of methyl nitrate were performed at the B3LYP/6-311+G* level with the Gaussian 16 package.⁷⁰ The optimized S₀-min geometry was used to calculate excited states using the XMS-CASPT2 with the def2-SVPD basis set. The XMS-CASPT2 calculations employed the active space of 12 electrons in 9 orbitals and four states were averaged, namely, XMS(4)-CASPT2(12,9). The active space contains three π, one σ and one n orbital, as well as one antibonding π* orbital, two antibonding σ* orbitals, one n/σ mixed orbital. The orbitals in the active space are given in Fig. S1 in ESI.† The optimization of the S₁ minimum (S₁-min) was also performed by the XMS(4)-CASPT2/def2-SVPD method with the same active space.

The ultrafast nonadiabatic decay dynamics simulations of CH₃ONO₂ were studied by the on-the-fly TSH method with Tully's fewest-switches algorithm⁷¹ at the XMS(4)-CASPT2(12,9)/def2-SVPD level. The initial geometries and velocities were sampled from the Wigner distribution function⁷² of the lowest vibrational state at the S₀-min. After the generation of many geometries by the Wigner sampling, their vertical excitation energies and oscillator strengths were calculated at the XMS(4)-CASPT2(12,9)/def2-SVPD level. The absorption spectrum was calculated by the nuclear ensemble approach (NEA),⁷³ in which 500 snapshots were taken, and the stick spectra were broadened by the Gaussian line shape with the phenomenological broadening parameter as 0.10 eV.

In the on-the-fly nonadiabatic dynamics simulation, the nuclear motion was propagated with a time step of 0.5 fs with the velocity-Verlet algorithm, and 100 steps of electronic motion were integrated within each step of nuclear motion. The decoherence correction approach proposed by Granucci et al.⁷⁴ was taken, and the parameter was set to 0.1 hartree.⁷⁵ Finally, 100, 99, and 98 trajectories were performed for the dynamics initialized from S₁, S₂, and S₃, respectively. All dynamics calculations were performed with the JADE-NAMD package.^67,76,77 We developed the Python interface between the TSH dynamics in the JADE-NAMD package and the XMS-CASPT2 calculations in the BAGEL package.^78,79 In the dynamics propagation process, the PESs, nuclear gradients, and nonadiabatic coupling vectors were calculated directly at the XMS-CASPT2 level using the BAGEL package.

The S₁–S₀ (CI₁₀), S₂–S₁ (CI₂₁), and S₃–S₂ (CI₃₂) minimum-energy CIs (MECIs) were optimized at the state-averaged complete active space self-consistent field,^80,81 SA(4)-CASSCF(12,9)/cc-pVDZ using the OpenMolcas package,⁸² in which the initial geometries were taken from hopping geometries in nonadiabatic dynamics. The single-point calculations were performed at those optimized CIs using the XMS(4)-CASPT2(12,9)/def2-SVPD level with the same setup as other XMS-CASPT2 calculations. We constructed the excited-state potential energy curves by the linear interpolation in internal coordinates (LIIC) approach from S₀-min to S₁–S₀ MECIs at the XMS(4)-CASPT2(12,9)/def2-SVPD level.

Furthermore, the S₁–S₀ CI seams (CI₁₀-seams) along the O–N distance (r_a) were also built at the SA(2)-CASSCF(12,9)/def2-SVPD level by the constrained optimization using the MOLPRO package.^83–85 For convergence, only two-state averaged calculations were employed in the CI₁₀-seam construction. Although this only provided a preliminary view, the obtained CI-seam structure information is reasonable enough for our analysis purpose because we mainly focused on the CI₁₀ here.

3. Results

3.1. S₀-min and S₁-min

The molecular structures at the S₀ and S₁ minima of CH₃ONO₂ are shown in Fig. 1. The important geometrical parameters and excited-state energies at S₀-min and S₁-min are displayed in Tables S1 and S2 in ESI.† The geometrical structure of S₀-min shows C_s symmetry, where C, O, N, O_a, and O_b atoms are located in the same plane (τ_a = 0°). The distances of N–O_a (r_d) and N–O_b (r_e) are 1.21 Å and 1.20 Å, respectively. This geometry is similar to previous work.⁸⁶ At S₀-min, the XMS(4)-CASPT2(12,9)/def2-SVPD calculations show that the vertical energies of S₁ and S₂ are 4.84 and 5.76 eV, respectively. S₁ and S₂ correspond to the n (HOMO−1) → π* (LUMO) and n/σ (HOMO) → π* (LUMO) transition, respectively. Here the electronic character of the HOMO displays the mixture of n and σ, see Fig. S1 in ESI.† The orbitals involved in the electronic transition of S₁ are shown in Fig. S2(a) in ESI.† Both S₁ and S₂ show very weak oscillator strengths, while S₃ is a bright state. The vertical excitation energy of S₃ is 6.54 eV, which is dominated by the π (HOMO−2) → π* (LUMO) transition. The excitation energies of these states are similar to those of previous theoretical studies.^26,28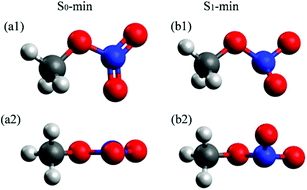

Fig. 1 Optimized S₀-min (B3LYP/6-311+G*) and S₁-min [XMS(4)-CASPT2(12,9)/def2-SVPD] geometries of CH₃ONO₂. The top and side views are shown up and down, respectively.

We calculated the absolute crossing section of the theoretical absorption spectra, including all individual contributions to different excited states using the NEA.⁷³ The absorption spectra in the broad energy range (from 180 nm to 320 nm) and in the long-wavelength domain (from 240 nm to 320 nm) are given in Fig. 2(a) and (b), respectively, along with the experimental ones.^6,27 Please notice that all available experimental works only gave the absorption spectra above 190 nm.⁸⁷

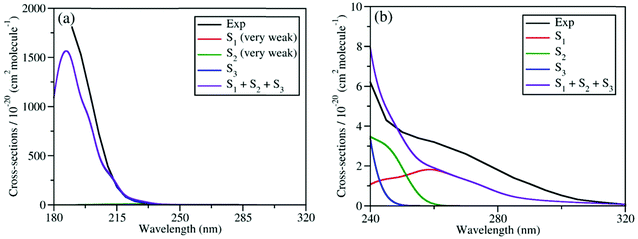Fig. 2 Comparison of experimental and simulated UV absorption spectra of CH₃ONO₂: (a) from 180 nm to 320 nm; (b) from 240 nm to 320 nm. The theoretical spectra were simulated at XMS(4)-CASPT2(12,9)/def2-SVPD level. The experimental spectra in (a) and (b) were taken from previous works.^6,27 The intensities of absorption bands shown in (a) and (b) differ by several magnitudes.

As shown in Fig. 2(a), the theoretical and experimental absorption spectra agree well in the whole energy domain. The short-wavelength absorption band is dominant by the S₃ transition with very high oscillator strength. The profiles of theoretical and experimental bands near 190 nm are highly consistent, except that the theoretical peak intensity is a little lower. The electronic transitions to both S₁ and S₂ are much weaker, and their absorption intensities are several magnitudes lower than the transition to S₃. Thus, the contribution of the former two components cannot be seen directly in Fig. 2(a). If we examine the long-wavelength region (from 240 nm to 320 nm) in Fig. 2(b), the very weak long tail of the whole absorption band is attributed to the summation of the transitions to both S₁ and S₂. Their overall contribution basically agrees well with the experimental data, except that the theoretical band is slightly weaker.

Overall, the simulated spectra agree well with the experimental one in the broad energy domain, including peak position, intensity, and profile. In particular, the transition amplitudes to different excited states differ by several magnitudes, while the absolute crossing sections in theoretical spectra agree well with available experimental data in all relevant energy domains. This confirms that the XMS-CASPT2 gives a reliable description of these low-lying excited states of the current system in the FC region. In addition, this also indicates that the initial sampling of nuclear conditions used in the further TSH dynamics are reasonable.

In contrast to the S₀-min geometry, the S₁-min geometry displays a significant pyramidalization at the N atom (τ_a = 26.8°). With the pyramidal movement of the N atom, we observed the elongation of the N–O_a (r_d = 1.27 Å) bond and the N–O_b (r_e = 1.32 Å) bond, as well as the bending motion of the O_a–N–O_b (θ_a = 109.0°) angle. This geometry deformation implies that the hybridization status of the N atom changes from sp² to sp³ when the geometry changes from S₀-min to S₁-min. At S₁-min, the relative energies of S₀, S₁, S₂, and S₃ with respect to the S₀ energy of S₀-min are 2.06, 3.74, 5.54, and 7.27 eV, respectively. The transition of the S₁ state is n (HOMO) → π* (LUMO), and the orbitals are shown in Fig. S2(b) in ESI.† We noticed that HOMO−1 at S₀-min becomes HOMO at S₁-min, and the same occupied orbital is always involved in the electronic transitions of S₁, indicating that its electronic character remains unchanged from S₀-min to S₁-min.

3.2. Conical intersections

Fig. 3 shows all optimized MECIs, and Table S2 (ESI†) gives their corresponding energies. Normally, it is better to perform the dynamics simulation and the CI optimation at the same level of theories. However, several test CI optimization tasks at the XMS-CASPT2 level did not give us the converged results. To give a comprehensive picture of all involved MECIs and CI-seams, we took the CASSCF method to perform the CI optimization, since it is easier to obtain the converged results. To make sure that all obtained MECIs are reasonable, the single-point calculations at the XMS-CASPT2 level were conducted again. The results in Table S2 (ESI†) show that these MECIs optimized at the CASSCF level are reasonable because the energy gaps of electronic states involved in the state degeneracy are very small at the XMS-CASPT2 level.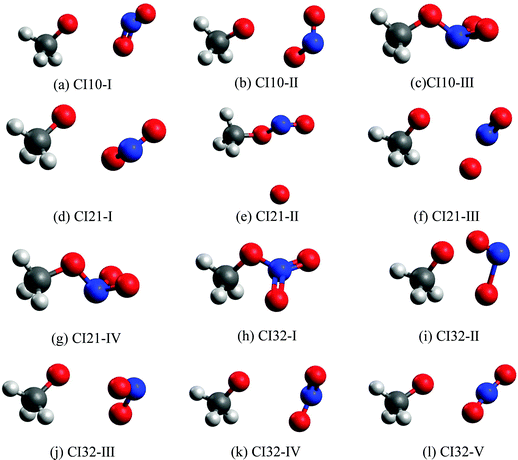

Fig. 3 The MECIs optimized at the SA(4)-CASSCF(12,9)/cc-pVDZ level: (a)–(c): S₁–S₀ CIs; (d)–(g): S₂–S₁ CIs; (h)–(l): S₃–S₂ CIs.

The first minimum-energy CI₁₀ is CI₁₀-I (1.91 eV) characterized by the significant CH₃O–NO₂ stretching motion (r_a = 3.11 Å) with respect to the S₀-min geometry. The O_a–N–O_b bond angle (θ_a = 133.5°) at this CI is very close to that (130.0°) at the S₀-min geometry. At CI₁₀-I, the system is roughly viewed as two radical fragments, CH₃O and NO₂. The important frontier orbitals are composed of the p orbital located at the O atom of the CH₃O radical and the π orbital at the NO₂ side. Here the later π orbital is a delocalized one, which is the linear combination of p orbitals at O_a and O_b atoms in the NO₂ part, as shown in Fig. 4(a).

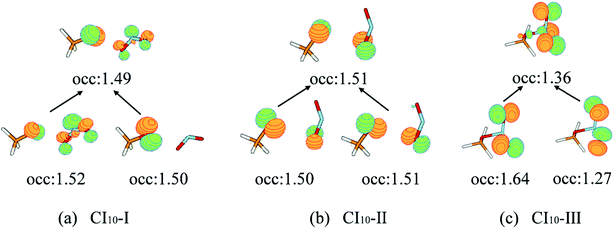Fig. 4 The natural transition orbitals along with their fractional occupation numbers at the S₁–S₀ MECIs optimized at the SA(4)-CASSCF(12,9)/cc-pVDZ level.

The second minimum-energy CI₁₀ (CI₁₀-II) lies at a higher energy domain (3.92 eV). At CI₁₀-II, both the large CH₃O–NO₂ stretching and the O_b–N–O_a bond angle bending motion were observed, which are characterized by 3.19 Å and 110.3°, respectively. Here the frontier orbitals are still composed of the p orbital located at the O atom of the CH₃O radical and the p orbital at the O_b atom of the NO₂ side. Different from the CI₁₀-I, the frontier orbitals of the NO₂ side become fully localized at the O_b atom, shown in Fig. 4(b). The underlying reason is easy to understand; the distances of N–O_a and N–O_b are very similar at CI₁₀-I. Two localized p orbitals associated with the O_a and O_b atoms show similar energies; thus, their electronic coupling results in the delocalized molecular orbitals, see Fig. 4(a). In contrast, the bond r_d and r_e of the NO₂ radical are quite different at CI₁₀-II. Therefore, the frontier orbitals become localized at the O_b atom, see Fig. 4(b).

At the third minimum-energy CI₁₀, labeled as CI₁₀-III, the O–N bond is in a bonded status and the strong pyramidalization at the N atom exists (τ_a = 34.8°). Different from CI₁₀-I and CI₁₀-II, as shown in Fig. 4(c), the frontier orbitals are localized in the NO₂ fragment.

We noticed that a previous study once localized a CI₁₀ that is close to the CI₁₀-II here.²⁶ Another study showed that a similar system CH₃NO₂ has a CI that displays the bonded O–N bond and the pyramidalization at the N atom.⁵² This is similar to the CI₁₀-III in the current work.

We also located the MECIs between different excited states, namely CI₂₁ and CI₃₂, and all obtained CI geometries are given in Fig. 3. The CI₂₁-IV and CI₃₂-I display the obvious pyramidalization at the N atom, and no bond breaking is observed at these two CIs, while the bond cleavage is observed at other CI₂₁ and CI₃₂. More information about other CIs is listed in Tables S2 and S3 (ESI†).

3.3. Nonadiabatic dynamics

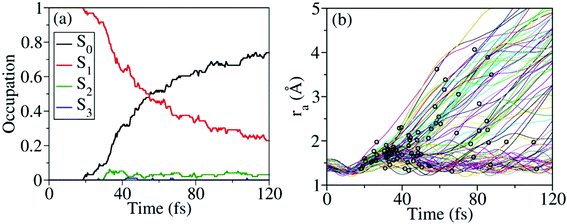
Nonadiabatic excited-state dynamics of CH₃ONO₂ were simulated using the on-the-fly TSH dynamics at the XMS-CASPT2 level. We first considered the dynamics starting from S₁. After excitation to S₁, the ultrafast S₁ → S₀ population decay was observed, see Fig. 5(a). Within the first 18 fs, almost all trajectories were propagating on S₁, and no decay was observed. After 53 fs, 50% of the trajectories jumped back to S₀. At 120 fs, the S₁ population decayed to 23%. In the whole decay dynamics, both S₂ and S₃ did not play important roles here.

Fig. 5 Time-dependent (a) average fractional occupation and (b) r_a value of several trajectories simulated in the nonadiabatic dynamics starting from S₁ at the XMS(4)-CASPT2(12,9)/def2-SVPD level. Black circles mark the S₁ to S₀ hops. After 120 fs, the electronic structure calculations of several trajectories may not be converged at random steps. Thus the overall population dynamics is only shown up to 120 fs.

The current population dynamics indicates that most trajectories go back to the ground state and only a few trajectories stay on the excited state. Thus it is necessary to identify which molecular motion is essential to drive the S₁ → S₀ decay dynamics. From the trajectory propagation from the FC region to the S₁ → S₀ hops, the obvious elongation of the CH₃O–NO₂ (r_a = 1.31–4.24 Å) bond and the significant pyramidalization at the N atom (τ_a = 7.2–170.1°) were noticed. After the S₁ → S₀ internal conversion, most trajectories continue moving towards the dissociation limit, which results in the CH₃O–NO₂ bond cleavage, as shown in Fig. 5(b).

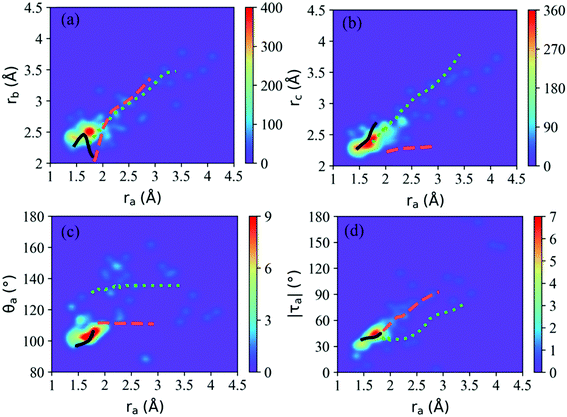
According to Fig. 5(b), most hops take place at geometries with a long CH₃O–NO₂ distance, while the system is still not fully broken. Thus the CH₃O–NO₂ bond strengthening motion should be one of the key degrees of freedom in the nonadiabatic dynamics. The S₁–S₀ CI seams along the CH₃O–NO₂ bond length were built with the constrained optimization by freezing the CH₃O–NO₂ distance, as shown in Fig. 6. The energies of three CI₁₀-seams as a function of r_a are shown in Fig. S3 (ESI†).

Fig. 6 Distribution of the important geometric parameters at the first S₁ to S₀ hops within 120 fs. In all panels, the green dotted line, orange dashed line, and black solid line mark the CI₁₀-seam-I, CI₁₀-seam-II, and CI₁₀-seam-III, respectively.

Both the CI₁₀-seam-I and CI₁₀-seam-II exist extensively in both short CH₃O–NO₂ distance and long CH₃O–NO₂ distance regions. We only obtained a small part of the CI₁₀-seam-III, and the other optimization jobs did not give the converged results. From the geometrical distribution at hops within 120 fs, many hops are governed by the CI₁₀-seam-III (∼72% of hops). Therefore, these hopping geometries do not show the full cleavage of the CH₃O–NO₂ bond. Instead, the strong pyramidalization at the N atom is observed. The other two CI₁₀ seams result in the hop geometries displaying the longer CH₃O–NO₂ distances, and the ratio of hops around CI₁₀-seam-I and CI₁₀-seam-II is about 13% and 11% of all hops, respectively, assigned by the O_a–N–O_b bond angles of these hops.

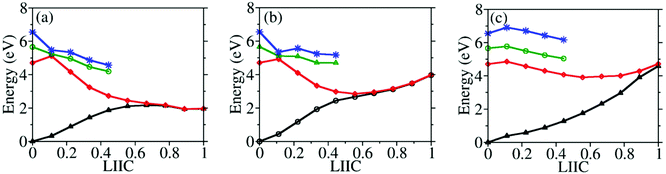
To understand why CI₁₀-III is the leading channel in the S₁ to S₀ nonadiabatic decay dynamics, the linear-interpolated PESs from S₀-min to S₁–S₀ CIs were constructed, as shown in Fig. 7. At the SA(4)-CASSCF(12,9) optimized MECI geometries, the single point calculations at the XMS-CASPT2 level also indicated that the lowest two states remain nearly degenerated. Thus the SA(4)-CASSCF(12,9) optimized CI geometries are reasonable. Although the energy of CI₁₀-III is higher, the reaction pathway from S₀–min to it shows a minor barrier on the S₁ PES. Although CI₁₀-I and CI₁₀-II lie in the low-energy region, the pathways towards them display obvious barriers that may be caused by the existence of the CIs between different excited-states. In addition, the CI₁₀-III geometry is close to the FC region; this also means that the system may easily access the CI₁₀-III without undergoing drastic structural deformation.

Fig. 7 Linear-interpolated PESs between S₀-min and S₁–S₀ MECIs in the FC region at the XMS-CASPT2 levels: (a) S₀-min to CI₁₀-I; (b) S₀-min to CI₁₀-II; (c) S₀-min to CI₁₀-III. In all panels, the black line, the red line, the green line, and the blue line represent the S₀, S₁, S₂, and S₃ states, respectively.

After the analysis of the first S₁ → S₀ hops, the next task is to examine the final photoreaction products. In fact, most trajectories follow the CH₃O + NO₂ dissociation pathway, no matter via which CI. Only for a few of the trajectories passing CI₁₀-III, the CH₃O + NO + O channel was found, as shown in Table 2.

Table 2 Final photoproducts and reaction ratios

Initial state	Final products	Ratio (%)
S1	CH3O + NO2	83
	CH3O + NO + O	5
	CH3ONO2 (no breaking)	12
S2	CH3O + NO2	87
	CH3O + NO + O	3
	CH3ONO + O	3
	CH3ONO2 (no breaking)	7
S3	CH3O + NO2	53
	CH3O + NO + O	42
	CH3ONO + O	5

---

The typical trajectories towards different dissociation channels are given in Fig. S4–S7(a) (ESI†), along with the state degeneracy in the dissociation limit. These trajectories start from S₁, experience the S₁–S₀ hop via CI₁₀-I (Fig. S4, ESI†), CI₁₀-II (Fig. S5, ESI†), and CI₁₀-III (Fig. S6, ESI†), and move to the CH₃O + NO₂ channel at the end. No matter which CI is passed, the CH₃O + NO₂ dissociation limit always displays the quasi-degeneracy of two lowest states S₀ and S₁. Although the trajectory starting from S₁ may generate the CH₃O + NO + O channel, this channel becomes important in the dynamics initialized from the S₃ state. Thus the typical trajectory towards this channel in Fig. S7 (ESI†) starts from S₃, in which all four lowest electronic states included in the state-averaged calculations become nearly degenerated in the CH₃O + NO + O dissociation limit. The underlying reasons for the state degeneracy are relevant to the symmetries of molecular geometries and the degeneracy of frontier orbitals, and more details are given in the below section.

In a short summary, the ultrafast decay dynamics (the lifetime ∼53 fs) was observed for CH₃ONO₂ when the trajectories start from S₁, which is governed by three S₁–S₀ CIs (CI₁₀-I, CI₁₀-II, and CI₁₀-III). Among them, CI₁₀-III plays a crucial role in the S₁ to S₀ hops. Most trajectories passing CI₁₀-III finally move towards two dissociation channels, in which the major channel is CH₃O + NO₂, and the minor channel is CH₃O + NO + O. The trajectories decaying via the other S₁–S₀ CIs (CI₁₀-I and CI₁₀-II) give dissociation products CH₃O + NO₂. Overall, the primary photolysis channel is CH₃O + NO₂ and the ratio towards this channel is 83%. The minor channel gives the CH₃O + NO + O products with a ratio ∼5%.

Please notice that the above ratio is only a rough estimation of the probabilities of photolysis product channels. The reason is as follows. When trajectories jump back to the ground state, the high kinetic energy results in distorted geometries. At some of these geometries, the electronic structure calculations become unstable, giving either the non-convergence results or the sudden flip of state energies. Therefore, we only considered the trajectory propagation before these questionable events. However, the geometries at these events may not be easily assigned as the dissociative or bonded status. For instance, the N–O bond in the NO₂ fragment may become quite long while it is still not fully dissociated. In this case, our assignment of the photolysis channels according to the N–O bond distance was highly approximated. In this sense, the current estimation of the photolysis products ratio is rather qualitative, while such information should still be quite useful to understand the CH₃ONO₂ photodynamics.

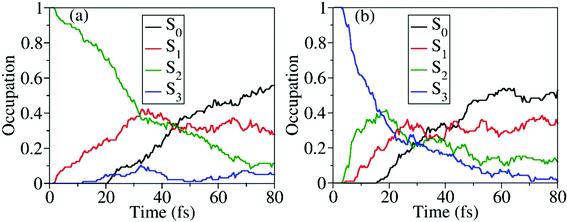
When the dynamics starts from S₂ and S₃, the time-dependent occupations of electronic states are shown in Fig. 8(a) and (b). No matter whether the trajectory starts from S₂ or S₃, the ultrafast nonadiabatic dynamics was observed, as shown in Fig. 8(a) and (b). Even in the early time of dynamics, the excited-state population decays were observed, and the S₀ population started to increase quickly. As expected, when the higher excited states are prepared, the S₀ population rises more quickly.

Fig. 8 Time-dependent average fractional occupations of adiabatic electronic states in nonadiabatic dynamics: (a) initiated from S₂; (b) initiated from S₃. After 80 fs, the electronic structure calculations of several trajectories may not be converged at random steps. Thus the overall population dynamics is only shown up to 80 fs.

Starting from the S₂, all three S₁–S₀ CIs play essential roles in the nonadiabatic decay to the ground state, as shown in Fig. S8 (ESI†). It is hard to distinguish their precise contributions here because more distorted hopping geometries appear. More than 93% trajectories move to the dissociation limit, giving three different reaction channels, CH₃O + NO₂ (∼87%), CH₃O + NO + O (∼3%), and CH₃ONO + O (∼3%). When the dynamics starts from S₃, the final photoproducts are CH₃O + NO₂ (∼53%), CH₃O + NO + O (∼42%), and CH₃ONO + O (∼5%), as shown in Table 2.

4. Discussion

The theoretical study of the nonadiabatic dynamics of CH₃ONO₂ represents a great challenging task due to its rather complicated electronic configurations in the photolysis dynamics. First, the different types of complicated multi-state quasi-degeneracy may appear from time to time along the CH₃O–NO₂ dissociation pathway, which brings difficulty in electronic treatments. Second, the photochemistry of CH₃ONO₂ involves high-lying excited states, while their theoretical description by currently available electronic structure approaches may not be accurate enough. Third, after the internal conversion, the excessive energy could lead to highly distorted geometries at which the electronic structure calculations become non-converged or state energies may change suddenly. Because we can only trust the trajectory propagation before these improper events, the estimation of the branching ratio of the final photoproducts is rather qualitative. One question is whether it is possible to use some tricks to improve the numerical stability in the trajectory propagation after hops, for instance using some more robust theories, such as the algebraic diagrammatic construction method to the second order [ADC(2)] or density functional theory (DFT), to restart our propagation after S₁–S₀ hops. However, we do not prefer this approach because the quasi-degeneracy of the two-lowest electronic states (S₁ and S₀), even the multi-state degeneracy, exists in the dissociation limit. At the same time, the shorter time step may also not solve the numerical instability problem. In the current system, many orbitals may show very similar energies and start to highly mix due to orbital symmetry in the dissociation limit. In this case, the orbitals inside and outside of the active space are easily mixed, and this brings the discontinuities of the electronic wavefunctions. When the strong geometry distortion exists, this orbital mixture becomes even more pronounced. Therefore, the employment of the smaller-time step does not alleviate this problem.

However, considering the computational facilities and available theoretical approaches currently, the current treatment represents a state-of-the-art approach that in principle provides valuable information to address the major reaction channels and relevant key molecular motion of the excited-state dynamics of CH₃ONO₂. Previous computational work demonstrated the existence of visible barriers along the direct CH₃O–NO₂ bond-breaking pathway when no additional nuclear motions are involved.²⁶ In the current work, we demonstrated that the pyramidalization at the N atom along with the CH₃O–NO₂ bond stretching can drive the system accessing an S₁–S₀ CI (CI₁₀-III) and induce the ultrafast internal conversion dynamics. Even when the inclusion of other relevant degrees of freedom modifies the barrier height for the direct excited-state CH₃O–NO₂ dissociation channel (Fig. 7), the pathways towards the CI₁₀-I and CI₁₀-II still display visible barriers. Thus these two CIs only act as the secondary channels in the internal conversion dynamics of CH₃ONO₂ starting from S₁. When the trajectories start from high-lying excited states (S₂ and S₃), the barriers towards CI₁₀-I and CI₁₀-II may be overcome more easily, and thus they start to play more important roles here.

No matter which CI is passed, most trajectories finally move to dissociation limits. One major dissociation channel gives the products CH₃O + NO₂. At this dissociation limit, the ground state CH₃O radical geometry is very close to the C_3v symmetry and the two lowest electronic states of the CH₃O radical become almost degenerated. This explains the existence of the state degeneracy in the dissociation limit of this channel. In fact, such state degeneracy was also noticed by previous work.²⁶ In principle, the existence of the 3-fold rotational axis of the CH₃O may give the high symmetry structure,^88,89 and this is the origin of the state degeneracy.^38,39 Such a symmetric geometry is easily destroyed by the Jahn–Teller effects.^38,39 For CH₃O, previous theoretical discussions clearly demonstrated that such Jahn–Teller distortion is very weak.^88,89 As a consequence, the energy gap between the two lowest electronic states remains extremely small after considering the geometry distortion due to the symmetry breaking. Therefore, when the trajectories following the CH₃O + NO₂ channel move to the dissociation limit, we observed the state degeneracy.

In fact, the state degeneracy may also exist for the NO₂ part.^90–92 As shown in previous studies, the two lowest electronic states of the NO₂ part may become close to each other when the O–N–O bond angle approaches ∼106° or ∼180°.^90,92 In our calculations, we seldom saw that the O_a–N–O_b bond angle accesses these values in the CH₃O + NO₂ dissociation limit when the trajectory starts from S₁. When the higher excited electronic state is excited initially, the excessive energy may drive the strong bending motion to nearly 106° during the dynamics and push the system close to such degeneracy. If so, many states become nearly degenerated, and one of such typical trajectories is shown in Fig. S9 (ESI†).

Some trajectories give the CH₃O + NO + O photolysis channel. The resulting O atom has three p orbitals with the same energies. When two lowest quasi-degenerated states of the CH₃O radical were taken into account, a much higher state degeneracy situation should exist. In this situation, electronic characters become extremely complicated in the dissociation limit. Our current calculation setup cannot provide the perfect description of this highly degenerated situation involving many electronic states. However, the current calculations still roughly captured the existence of this channel. Here we also showed that the ratio of this channel increases when the high-lying electronic state is excited. This feature shows a qualitative agreement with experimental works.^20,24,27,35

Although the current calculations face many limitations, we still can get a valuable explanation of available experimental works. First, we provided a clear interpretation of the absorption spectra of CH₃ONO₂. The ultrafast nonadiabatic decay dynamics in the current simulation indicated that the excited-state lifetime is extremely short. This gives an excellent explanation of why the low-lying bands in the absorption spectra of CH₃ONO₂ are quite broad and diffusive.^6,27 Considering the existence of ultrafast nonadiabatic dynamics, the further ultrafast-spectroscopy experimental studies of such dynamics of CH₃ONO₂ and derivatives should be highly interesting. Second, the current simulation gives some valuable data to explain the photolysis dynamics. In experimental works,^20,27,35,37 the photolysis dynamics at the long wavelength, ∼250 nm or > 300 nm, always gives the CH₃O + NO₂ channel. In our calculations, the dynamics starting from both S₁ and S₂ show that this channel is always dominant. Although we obtained other channels possibly due to the limitation of current calculations, their branching ratios of the minor channels are rather low. We also observed that some trajectories starting from S₁ do not show dissociation, and this may explain why the quantum yield of the CH₃O + NO₂ photolysis channel is not unity in low-pressure long-wavelength (>300 nm) experimental work. Only when the trajectories started from S₃, did we observe that both CH₃O + NO₂ and CH₃O + NO + O channels become important. The system first breaks into CH₃O + NO₂, and then the N–O bond of NO₂ breaks. These features are consistent with experimental works.^20,24,30 In the end, the CH₃ONO + O is observed when the trajectories start from S₃. This channel was confirmed by previous experimental studies with short-wavelength laser excitation.^20,24,35

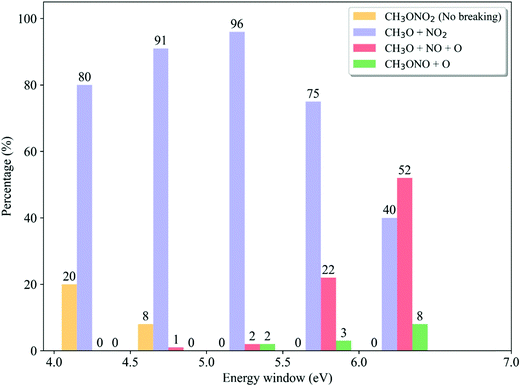
We analyzed the dependence of the ratios of dissociation channels on the excitation energy. In each energy window, the reaction probability of each channel is determined by the destination of trajectory propagation starting from such a window and the transition probability of each initial sample.⁵⁸ As shown in Fig. 9, only in the low-energy domain (4.0–4.5 eV and 4.5–5.0 eV), the non-dissociative channel appears while it vanishes quickly with the increase of photolysis excitation energy. At the same time, the CH₃O + NO₂ channel is always dominant when the low excitation energy is taken. Above 5.0–5.5 eV, the ratio of the CH₃O + NO₂ channel decreases monotonically with the higher photolysis excitation energy, 75% at 5.5–6.0 eV and 40% at 6.0–7.0 eV. As contrast, the CH₃O + NO + O channel does not appear at all in the very low-energy domain (4.0–4.5 eV) and is basically neglectable (≤2% at 4.5–5.0 eV). This channel starts to be important with the increase of the photolysis excitation energy, giving 22% at 5.5–6.0 eV and even more than half in the high-energy domain (52% at 6.0–7.0 eV). The CH₃ONO + O channel only appears in the high-energy domain. This observation is even more consistent with the experimental results,^6,24,27,28 compared to the data obtained by considering the photolysis from different excited states only. All experimental observations indicated that the CH₃O + NO₂ channel is dominant in the low-energy excitation, while both CH₃O + NO₂ and CH₃O + NO + O channels may become equally important in the high-energy photolysis excitation situations.

Fig. 9 The dissociation channel ratios of different initial energy windows.

As discussed in ref. 93 and 94, the excitations of sunlight, short-pulse laser fields, and continuum-wave laser fields in principle should give rather different initial conditions for photoreactions. Using more advanced theoretical approaches suggested by these works, the proper initial conditions can be defined in the nonadiabatic dynamics simulation. In principle, these theoretical treatments should be important because the dynamics simulation results may be dependent on the selection of initial conditions. In the current work, we still keep the original ways of the initial sampling in nonadiabatic dynamics simulations. As discussed in our manuscript several times, this work represents our initial efforts to treat the photolysis dynamics of alkyl nitrate systems. In the current stage, we only wish to provide some initial understanding of the photolysis dynamics of these compounds qualitatively, instead of the accurate description at the quantitative level. In particular, the nonadiabatic dynamics simulation of these systems is still rare. Our calculations of both PES and nonadiabatic dynamics indicate that the photolysis reaction of CH₃ONO₂ is extremely fast. We also get the branching ratios of photolysis channels vs. the excitation wavelengths, which agrees well with the experimental observations. Therefore, the main purpose of the current research is basically achieved. For the precise lifetime, we still do not have any available experimental data for comparison. As our current simulation gives the primary results on the ultrafast excited-state lifetime, this result certainly should be verified by further experimental and theoretical works. The new time-resolved ultrafast pump–probe experiments may be helpful to address the ultrafast photolysis dynamics. At the same time, additional efforts should be made to give a better representation of the initial conditions in the nonadiabatic dynamics simulation of similar systems, in order to give better descriptions of the experimental setups and even sunlight. We believe that such a challenging study should be an important research topic in the future. On one side, this provides the direct bridge to link the experimental observations and theoretical simulations. On another side, this helps us to get a deep understanding of the realistic photochemistry of these alkyl nitrates in the atmosphere, which are environmentally significant.

It is well known that the nitro- and nitrate- compounds may undergo intersystem crossing, as shown by several previous works.^95–97 In the current system, the intersystem crossing dynamics may not play an essential role here. The current photolysis dynamics takes place extremely fast, less than 60 fs. Within such a short time scale, the contribution of the intersystem crossing dynamics should not be significant, because in principle the weak spin-orbital coupling should exist in such molecules due to the missing heavy atom. On the other hand, the investigation of the possible role of the intersystem crossing dynamics should be an interesting topic in the future.

In the simulation of excited-state dynamics, the selection of suitable electronic state methods and dynamics approaches is not a trivial task. In the electronic-structure treatments, it is well known that all excited-state electronic-structure approaches have their own advantages and shortcomings. Among them, the CASPT2 approaches display reasonable accuracy in many benchmark calculations.^58,98,99 In this sense, this approach can more or less be viewed as the “accurate approach” in the excited-state electronic-structure calculations, while its shortcoming is also well known.¹⁰⁰ In the current work, the XMS-CASPT2 method is an extended MS-CASPT2 approach, while it essentially provides a similar computational accuracy with higher efficiency.^54,55 On the other hand, some other high-level approaches, such as multireference configuration interaction (MRCI),¹⁰¹ may also be the possible choice. In recent years, we noticed that there is a huge development in other advanced excited-state calculation approaches, such as multireference coupled cluster (MRCC),¹⁰² and full configuration-interaction quantum Monte Carlo (FCI-QMC) methods.¹⁰³ If these methods can be used to simulate the excited state dynamics, we expect that more fruitful insights can be generated. However, there is still a long way to employ them in the excite-state dynamics.

In the choice of the dynamics approaches, a similar situation is held. The on-the-fly TSH is a practical choice that gives a reasonable description of the excited-state nonadiabatic dynamics with the balance of computational accuracy and efficiency. However, its shortcoming is also widely known, for instance, its overcoherence problems.^74,104,105 Other more advanced approaches, such as ab initio multiple spawning,⁶² multi-configurational Ehrenfest,¹⁰⁶ variational multiconfiguration Gaussian (vMCG),^107,108 different on-the-fly semiclassical dynamics based on the mapping Hamiltonian,^77,109 and coupled-trajectory surface-hopping dynamics based on exact factorization,^110–112 may become possible choices in the future. If we find a suitable electronic structure method that shows enough accuracy in the treatment of the excited state, it would be highly interesting to take it and try to benchmark the performance of different on-the-fly mixed-quantum-classical and semiclassical dynamics approaches. This should provide important evidence to help us select the proper dynamics approaches in the treatment of realistic polyatomic systems with full dimensionality.

5. Conclusion

In this work, we studied the excited-state nonadiabatic dynamics of CH₃ONO₂ using the on-the-fly TSH simulation at the XMS(4)-CASPT2(12,9)/def2-SVPD level. We mainly paid close attention to the nonadiabatic decay dynamics and the successive photolysis channels.

Three S₁–S₀ MECIs were located at the SA(4)-CASSCF(12,9)/cc-pVDZ level. Both CI₁₀-I and CI₁₀-II display significant CH₃O–NO₂ elongation, while the O_a–N–O_b bond angle bending motion is observed at CI₁₀-II. The CI₁₀-III shows strong pyramidalization at the N atom, as well as a much shorter CH₃O–NO₂ distance with respect to CI₁₀-I and CI₁₀-II.

The ultrafast decay processes from different initial excited states were simulated using the on-the-fly TSH simulations. A majority of trajectories starting from S₁ jump back to S₀via the CI₁₀-III geometries with the weakness of the CH₃O–NO₂ bond and the pyramidalization at the N atom. When the trajectories start from high-lying excited states (S₂ and S₃), the internal conversion dynamics becomes faster as expected, and all three CI₁₀ become essential in the nonadiabatic decay.

Starting from both S₁ and S₂, most trajectories show the photodissociation and follow the CH₃O + NO₂ photolysis channel. In the dissociation limit, the state degeneracy exists between S₁ and S₀ due to the 3-fold rotational symmetric geometry of CH₃O. The other channels only play a minor role here. When the trajectories start from S₃, we still observed that the CH₃O + NO₂ channel is the major one, while the secondary channel CH₃O + NO + O also becomes important. For the latter one, the CH₃O–NO₂ bond first breaks and the cleavage of the N–O bond in the NO₂ fragment then occurs. A third photolysis channel CH₃ONO + O also appears. The dependence of the photoproduct channels on the UV excitation wavelength is qualitatively in agreement with available experimental studies.

The current work presents a primary study of our understanding of organic nitrate photochemistry. It should be highly interesting to simulate these processes with highly accurate electronic structure methods, treat the highly-excited state dynamics with more proper dynamics approaches, simulate the experimental signals and study the chemical substitution effects on the photolysis. At the same time, in recent years we witness that great experimental efforts were made to study the ultrafast nonadiabatic dissociation dynamics of VOC systems.^113–118 On the basis of the current theoretical work, the CH₃ONO₂ and derivatives may be a group of interesting prototype VOC systems in experimental ultrafast spectroscopy studies. These works will help us understand more thoroughly the photochemistry of VOCs and this represents a great challenging task in future studies.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by NSFC projects (No. 21933011 and 21873112). The authors thank the Supercomputing Center, Computer Network Information Center, Chinese Academy of Sciences; National Supercomputing Center in Shenzhen for providing computational resources.

References

1. R. Atkinson and J. Arey, Atmospheric degradation of volatile organic compounds, Chem. Rev., 2003, 103(12), 4605–4638.
2. A. E. Perring, S. E. Pusede and R. C. Cohen, An observational perspective on the atmospheric impacts of alkyl and multifunctional nitrates on ozone and secondary organic aerosol, Chem. Rev., 2013, 113(8), 5848–5870.
3. A. L. Chuck, S. M. Turner and P. S. Liss, Direct evidence for a marine source of C₁ and C₂ alkyl nitrates, Science, 2002, 297(5584), 1151–1154.
4. Y. Miller, B. J. Finlayson-Pitts and R. B. Gerber, Ionization of N₂O₄ in contact with water: mechanism, time scales and atmospheric implications, J. Am. Chem. Soc., 2009, 131(34), 12180–12185.
5. H. Xiao, S. Maeda and K. Morokuma, Excited-state roaming dynamics in photolysis of a nitrate radical. J. Phys, Chem. Lett., 2011, 2(9), 934–938.
6. M. P. Turberg, D. M. Giolando, C. Tilt, T. Soper, S. Mason, M. Davies, P. Klingensmith and G. A. Takacs, Atmospheric photochemistry of alkyl nitrates, J. Photochem. Photobiol., 1990, 51(3), 281–292.
7. J. E. Williams, G. Le Bras, A. Kukui, H. Ziereis and C. A. M. Brenninkmeijer, The impact of the chemical production of methyl nitrate from the NO + CH₃O₂ reaction on the global distributions of alkyl nitrates, nitrogen oxides and tropospheric ozone: a global modelling study, Atmos. Chem. Phys., 2014, 14(5), 2363–2382.
8. C. Reed, M. J. Evans, P. Di Carlo, J. D. Lee and L. J. Carpenter, Interferences in photolytic NO₂ measurements: explanation for an apparent missing oxidant?, Atmos. Chem. Phys., 2016, 16(7), 4707–4724.
9. F. Keshavarz, J. A. Thornton, H. Vehkamäki and T. Kurtén, Reaction mechanisms underlying unfunctionalized alkyl nitrate hydrolysis in aqueous aerosols, ACS Earth Space Chem., 2021, 5(2), 210–225.
10. J. M. Roberts, The atmospheric chemistry of organic nitrates, Atmos. Environ., Part A, 1990, 24(2), 243–287.
11. S. M. Aschmann, J. Arey and R. Atkinson, Products of the OH radical-initiated reactions of 2- and 3-hexyl nitrate, Atmos. Environ., 2012, 46, 264–270.
12. R. Atkinson, S. M. Aschmann, W. P. L. Carter, A. M. Winer and J. N. Pitts, Alkyl nitrate formation from the NO_x-air photooxidations of C₂-C₈ n-alkanes, J. Phys. Chem., 1982, 86(23), 4563–4569.
13. S. He, Z. Chen and X. Zhang, Photochemical reactions of methyl and ethyl nitrate: a dual role for alkyl nitrates in the nitrogen cycle, Environ. Chem., 2011, 8(6), 529–542.
14. A. Lesar, M. Hodošček, E. Drougas and A. M. Kosmas, Quantum mechanical investigation of the atmospheric reaction CH₃O₂ + NO, J. Phys. Chem. A, 2006, 110(25), 7898–7903.
15. J. R. Barker, L. L. Lohr, R. M. Shroll and S. Reading, Modeling the organic nitrate yields in the reaction of alkyl peroxy radicals with nitric oxide. 2. reaction simulations, J. Phys. Chem. A, 2003, 107(38), 7434–7444.
16. R. M. Moore and N. V. Blough, A marine source of methyl nitrate, Geophys. Res. Lett., 2002, 29(15), 27-1–27-4.
17. R. E. Rebbert, Primary processes in the photolysis of ethyl nitrate, J. Phys. Chem., 1963, 67(9), 1923–1925.
18. L. E. Harris, The lower electronic states of nitrite and nitrate ion, nitromethane, nitramide, nitric acid, and nitrate esters, J. Chem. Phys., 1973, 58(12), 5615–5626.
19. W. D. Taylor, T. D. Allston, M. J. Moscato, G. B. Fazekas, R. Kozlowski and G. A. Takacs, Atmospheric photodissociation lifetimes for nitromethane, methyl nitrite, and methyl nitrate, Int. J. Chem. Kinet., 1980, 12(4), 231–240.
20. X. Yang, P. Felder and J. R. Huber, Photodissociation of methyl nitrate in a molecular beam, J. Phys. Chem., 1993, 97(42), 10903–10910.
21. K. C. Clemitshaw, J. Williams, O. V. Rattigan, D. E. Shallcross and K. S. Law, Anthony Cox, R., Gas-phase ultraviolet absorption cross-sections and atmospheric lifetimes of several C₂-C₅ alkyl nitrates, J. Photochem. Photobiol., 1997, 102(2), 117–126.
22. L. Zhu and C.-F. Ding, Temperature dependence of the near UV absorption spectra and photolysis products of ethyl nitrate, Chem. Phys. Lett., 1997, 265(1), 177–184.
23. L. Zhu and D. Kellis, Temperature dependence of the UV absorption cross sections and photodissociation products of C₃-C₅ nitrates, Chem. Phys. Lett., 1997, 278(1), 41–48.
24. E. L. Derro, C. Murray, M. I. Lester and M. D. Marshall, Photodissociation dynamics of methyl nitrate at 193 nm: energy disposal in methoxy and nitrogen dioxide products, Phys. Chem. Chem. Phys., 2007, 9(2), 262–271.
25. I. V. Schweigert and B. I. Dunlap, Electronic structure and molecular dynamics of breaking the RO–NO₂ bond, J. Chem. Phys., 2009, 130(24), 244110.
26. J. Soto, D. Peláez, J. C. Otero, F. J. Avila and J. F. Arenas, Photodissociation mechanism of methyl nitrate. A study with the multistate second-order multiconfigurational perturbation theory, Phys. Chem. Chem. Phys., 2009, 11(15), 2631–2639.
27. P. G. Carbajo and A. J. Orr-Ewing, NO₂ quantum yields from ultraviolet photodissociation of methyl and isopropyl nitrate, Phys. Chem. Chem. Phys., 2010, 12(23), 6084–6091.
28. C. M. Higgins, L. A. Evans, G. C. Lloyd-Jones, D. E. Shallcross, D. P. Tew and A. J. Orr-Ewing, Quantum yields for photochemical production of NO₂ from organic nitrates at tropospherically relevant wavelengths, J. Phys. Chem. A, 2014, 118(15), 2756–2764.
29. J. A. Gray and D. W. G. Style, The photolysis of ethyl nitrate, Trans. Faraday Soc., 1953, 49, 52–57.
30. P. Gray and G. T. Rogers, The explosion and decomposition of methyl nitrate in the gas phase, Trans. Faraday Soc., 1954, 50(0), 28–36.
31. W. T. Luke and R. R. Dickerson, Direct measurements of the photolysis rate coefficient of ethyl nitrate, Geophys. Res. Lett., 1988, 15(11), 1181–1184.
32. W. T. Luke, R. R. Dickerson and L. J. Nunnermacker, Direct measurements of the photolysis rate coefficients and Henry's law constants of several alkyl nitrates, J. Geophys. Res.: Atmos., 1989, 94(D12), 14905–14921.
33. I. Barnes, K. H. Becker and T. Zhu, Near UV absorption spectra and photolysis products of difunctional organic nitrates: Possible importance as NO_x reservoirs, J. Atmos. Chem., 1993, 17(4), 353–373.
34. R. K. Talukdar, S. C. Herndon, J. B. Burkholder, J. M. Roberts and A. R. Ravishankara, Atmospheric fate of several alkyl nitrates Part 1 Rate coefficients of the reactions of alkyl nitrates with isotopically labelled hydroxyl radicals, J. Chem. Soc., Faraday Trans., 1997, 93(16), 2787–2796.
35. R. K. Talukdar, J. B. Burkholder, M. Hunter, M. K. Gilles, J. M. Roberts and A. R. Ravishankara, Atmospheric fate of several alkyl nitrates Part 2 UV absorption cross-sectionsand photodissociation quantum yields, J. Chem. Soc., Faraday Trans., 1997, 93, 2797–2805.
36. J. M. Roberts and R. W. Fajer, UV absorption cross sections of organic nitrates of potential atmospheric importance and estimation of atmospheric lifetimes, Environ. Sci. Technol., 1989, 23(8), 945–951.
37. O. Rattigan, E. Lutman, R. L. Jones, R. A. Cox, K. Clemitshaw and J. Williams, Temperature-dependent absorption cross-sections of gaseous nitric acid and methyl nitrate. J, Photochem. Photobiol., 1992, 66(3), 313–326.
38. Conical Intersections I: Electronic Structure, Dynamics and Spectroscopy, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientic, Singapore, 2004.
39. Conical Intersections II: Theory, Computation and Experiment, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientific, Singapore, 2011.
40. R. Atkinson, W. P. L. Carter and A. M. Winer, Effects of temperature and pressure on alkyl nitrate yields in the NO_x photooxidations of n-pentane and n-heptane, J. Phys. Chem., 1983, 87(11), 2012–2018.
41. J. F. Arenas, F. J. Avila, J. C. Otero, D. Peláez and J. Soto, Approach to the atmospheric chemistry of methyl nitrate and methylperoxy nitrite. Chemical mechanisms of their formation and decomposition reactions in the gas phase, J. Phys. Chem. A, 2008, 112(2), 249–255.
42. Z. Homayoon and J. M. Bowman, Quasiclassical trajectory study of CH₃NO₂ decomposition via roaming mediated isomerization using a global potential energy surface, J. Phys. Chem. A, 2013, 117(46), 11665–11672.
43. J. F. Arenas, J. C. Otero, D. Peláez and J. Soto, The ground and excited state potential energy surfaces of nitromethane related to its dissociation dynamics after excitation at 193 nm, J. Chem. Phys., 2003, 119(15), 7814–7823.
44. J. Zhang, T. Dransfield and N. M. Donahue, On the mechanism for nitrate formation via the peroxy radical + NO reaction, J. Phys. Chem. A, 2004, 108(42), 9082–9095.
45. A. G. Sage, T. A. Oliver, D. Murdock, M. B. Crow, G. A. Ritchie, J. N. Harvey and M. N. Ashfold, nσ* and πσ* excited states in aryl halide photochemistry: a comprehensive study of the UV photodissociation dynamics of iodobenzene, Phys. Chem. Chem. Phys., 2011, 13(18), 8075–8093.
46. M. Isegawa, F. Liu, S. Maeda and K. Morokuma, Ab initio reaction pathways for photodissociation and isomerization of nitromethane on four singlet potential energy surfaces with three roaming paths, J. Chem. Phys., 2014, 140(24), 244310.
47. D. Aranda, F. J. Avila, I. López-Tocón, J. F. Arenas, J. C. Otero and J. Soto, An MS-CASPT2 study of the photodecomposition of 4-methoxyphenyl azide: role of internal conversion and intersystem crossing, Phys. Chem. Chem. Phys., 2018, 20(11), 7764–7771.
48. J. Soto, D. Peláez and J. C. Otero, A SA-CASSCF and MS-CASPT2 study on the electronic structure of nitrosobenzene and its relation to its dissociation dynamics, J. Chem. Phys., 2021, 154(4), 044307.
49. L. E. Harris, Lower electronic states of nitric acid and esters, Nature, 1973, 243(128), 103–104.
50. J. Soto, J. F. Arenas, J. C. Otero and D. Peláez, Effect of an S₁/S₀ conical intersection on the chemistry of nitramide in its ground state. A comparative CASPT2 study of the nitro-nitrite isomerization reactions in nitramide and nitromethane, J. Phys. Chem. A, 2006, 110(26), 8221–8226.
51. J. Soto, F. J. Avila, J. C. Otero, D. Peláez and J. F. Arenas, A molecular mechanism for direct generation of nitric oxide, peroxynitrite and superoxide in the reaction of nitroglycerin with a cysteil-cysteine derivative, Theor. Chem. Acc., 2010, 128(4-6), 593–599.
52. J. F. Arenas, J. C. Otero, D. Peláez and J. Soto, Role of surface crossings in the photochemistry of nitromethane, J. Chem. Phys., 2005, 122(8), 084324.
53. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299.
54. A. A. Granovsky, Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory, J. Chem. Phys., 2011, 134(21), 214113.
55. T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, Communication: extended multi-state complete active space second-order perturbation theory: energy and nuclear gradients, J. Chem. Phys., 2011, 135(8), 081106.
56. P. Cattaneo, G. Granucci and M. Persico, Simulations of condensed phase photochemistry:  cage effect and internal conversion in azoalkanes and nitrosamines, J. Phys. Chem. A, 1999, 103(18), 3364–3371.
57. H. Lignell, S. A. Epstein, M. R. Marvin, D. Shemesh, B. Gerber and S. Nizkorodov, Experimental and Theoretical Study of Aqueous cis-Pinonic Acid Photolysis, J. Phys. Chem. A, 2013, 117(48), 12930–12945.
58. A. Prlj, L. M. Ibele, E. Marsili and B. F. E. Curchod, On the theoretical determination of photolysis properties for atmospheric volatile organic compounds. J. Phys, Chem. Lett., 2020, 11(14), 5418–5425.
59. D. Shemesh, S. A. Nizkorodov and R. B. Gerber, Photochemical Reactions of Cyclohexanone: Mechanisms and Dynamics, J. Phys. Chem. A, 2016, 120(36), 7112–7120.
60. D. Shemesh, Z. Lan and R. B. Gerber, Dynamics of Triplet-State Photochemistry of Pentanal: Mechanisms of Norrish I, Norrish II, and H Abstraction Reactions, J. Phys. Chem. A, 2013, 117(46), 11711–11724.
61. M. Persico and G. Granucci, An overview of nonadiabatic dynamics simulations methods, with focus on the direct approach versus the fitting of potential energy surfaces, Theor. Chem. Acc., 2014, 133(9), 1526.
62. B. F. E. Curchod and T. J. Martínez, Ab initio nonadiabatic quantum molecular dynamics, Chem. Rev., 2018, 118(7), 3305–3336.
63. M. Persico and G. Granucci, Photochemistry: A Modern Theoretical Perspective, Berlin, Springer, 2018.
64. M. Ben-Nun and T. J. Martínez, Ab initio quantum molecular dynamics, Adv. Chem. Phys., 2002, 121, 439–512.
65. S.-H. Xia, G. Cui, W.-H. Fang and W. Thiel, How photoisomerization drives peptide folding and unfolding: insights from QM/MM and MM dynamics simulations, Angew. Chem., Int. Ed., 2016, 55(6), 2067–2072.
66. G. Cui, Z. Lan and W. Thiel, Intramolecular Hydrogen Bonding Plays a Crucial Role in the Photophysics and Photochemistry of the GFP Chromophore, J. Am. Chem. Soc., 2012, 134(3), 1662–1672.
67. L. Du and Z. Lan, An on-the-fly surface-hopping program JADE for nonadiabatic molecular dynamics of polyatomic systems: implementation and applications, J. Chem. Theory Comput., 2015, 11(9), 4522–4523.
68. C. Xu, F. L. Gu and C. Zhu, Ultrafast intersystem crossing for nitrophenols: ab initio nonadiabatic molecular dynamics simulation, Phys. Chem. Chem. Phys., 2018, 20(8), 5606–5616.
69. K. Lin, D. Hu, J. Peng, C. Xu, F. L. Gu and Z. Lan, Prediction of the excited-state reaction channels in photo-induced processes of nitrofurantoin using first-principle calculations and dynamics simulations, Chemosphere, 2021, 281, 130831.
70. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
71. J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93(2), 1061–1071.
72. E. Wigner, On the quantum correction for thermodynamic equilibrium, Phys. Rev., 1932, 40(5), 749–759.
73. R. Crespo-Otero and M. Barbatti, Spectrum simulation and decomposition with nuclear ensemble: formal derivation and application to benzene, furan and 2-phenylfuran, Theor. Chem. Acc., 2012, 131(6), 1237.
74. G. Granucci and M. Persico, Critical appraisal of the fewest switches algorithm for surface hopping, J. Chem. Phys., 2007, 126(13), 134114.
75. C. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, Coherent switching with decay of mixing: An improved treatment of electronic coherence for non-Born–Oppenheimer trajectories, J. Chem. Phys., 2004, 121(16), 7658–7670.
76. D. Hu, Y. F. Liu, A. L. Sobolewski and Z. Lan, Nonadiabatic dynamics simulation of keto isocytosine: a comparison of dynamical performance of different electronic-structure methods, Phys. Chem. Chem. Phys., 2017, 19(29), 19168–19177.
77. D. Hu, Y. Xie, J. Peng and Z. Lan, On-the-fly symmetrical quasi-classical dynamics with Meyer–Miller mapping Hamiltonian for the treatment of nonadiabatic dynamics at conical intersections, J. Chem. Theory Comput., 2021, 17(6), 3267–3279.
78. BAGEL, Brilliantly Advanced General Electronic-structure Library, (http://www.nubakery.org).
79. T. Shiozaki, BAGEL: Brilliantly Advanced General Electronic-structure Library, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1331.
80. P. J. Knowles and N. C. Handy, A determinant based full configuration interaction program, Cornp. Phys. Commun., 1989, 54(1), 75–83.
81. H.-J. Werner and P. J. Knowles, A second order multiconfiguration SCF procedure with optimum convergence, J. Chem. Phys., 1985, 82(11), 5053–5063.
82. I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From Source Code to Insight, J. Chem. Theory Comput., 2019, 15(11), 5925–5964.
83. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(2), 242–253.
84. Q. Ma and H.-J. Werner, Explicitly correlated local coupled-cluster methods using pair natural orbitals, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(6), e1371.
85. H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, The Molpro quantum chemistry package, J. Chem. Phys., 2020, 152(14), 144107.
86. A. M. Launder, J. Agarwal and H. F. Schaefer III, Exploring mechanisms of a tropospheric archetype: CH₃O₂ + NO, J. Chem. Phys., 2015, 143(23), 234302.
87. http://satellite.mpic.de/spectral_atlas/cross_sections .
88. T. A. Barckholtz and T. A. Miller, The Calculation of spectroscopic Jahn–Teller parameters by ab initio methods, J. Phys. Chem. A, 1999, 103(14), 2321–2336.
89. C. F. Jackels, A theoretical potential energy surface study of several states of the methoxy radical, J. Chem. Phys., 1982, 76(1), 505–515.
90. G. D. Gillispie, A. U. Khan, A. C. Wahl, R. P. Hosteny and M. Krauss, The electronic structure of nitrogen dioxide. I. Multiconfiguration self-consistent-field calculation of the low-lying electronic states, J. Chem. Phys., 1975, 63(8), 3425–3444.
91. V. Kurkal, P. Fleurat-Lessard and R. Schinke, NO₂: Global potential energy surfaces of the ground (1²A₁) and the first excited (1²B₂) electronic states, J. Chem. Phys., 2003, 119(3), 1489–1501.
92. C. F. Jackels and E. R. Davidson, An ab initio potential-energy surface study of several electronic states of NO₂, J. Chem. Phys., 1976, 65(8), 2941–2957.
93. J. Suchan, D. Hollas, B. F. E. Curchod and P. Slavíček, On the importance of initial conditions for excited-state dynamics, Faraday Discuss., 2018, 212(0), 307–330.
94. M. Barbatti, Simulation of excitation by sunlight in mixed quantum-classical dynamics, J. Chem. Theory Comput., 2020, 16(8), 4849–4856.
95. M. Richter, S. Mai, P. Marquetand and L. González, Ultrafast intersystem crossing dynamics in uracil unravelled by ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2014, 16(44), 24423–24436.
96. S. Bai and M. Barbatti, Why Replacing Different Oxygens of Thymine with Sulfur Causes Distinct Absorption and Intersystem Crossing, J. Phys. Chem. A, 2016, 120(32), 6342–6350.
97. B. F. Curchod, C. Rauer, P. Marquetand, L. González and T. J. Martínez, Communication: GAIMS—Generalized Ab Initio Multiple Spawning for both internal conversion and intersystem crossing processes, J. Chem. Phys., 2016, 144(10), 101102.
98. M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, Benchmarks for electronically excited states: CASPT2, CC2, CCSD, and CC3, J. Chem. Phys., 2008, 128(13), 134110.
99. J. W. Park, R. Al-Saadon, M. K. MacLeod, T. Shiozaki and B. Vlaisavljevich, Multireference Electron Correlation Methods: Journeys along Potential Energy Surfaces, Chem. Rev., 2020, 120(13), 5878–5909.
100. N. Forsberg and P.-Å. Malmqvist, Multiconfiguration perturbation theory with imaginary level shift, Chem. Phys. Lett., 1997, 274(1-3), 196–204.
101. H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Multireference Approaches for Excited States of Molecules, Chem. Rev., 2018, 118(15), 7293–7361.
102. D. I. Lyakh, M. Musiał, V. F. Lotrich and R. J. Bartlett, Multireference Nature of Chemistry: The Coupled-Cluster View, Chem. Rev., 2012, 112(1), 182–243.
103. G. H. Booth, A. J. W. Thom and A. Alavi, Fermion Monte Carlo without fixed nodes: A game of life, death, and annihilation in Slater determinant space, J. Chem. Phys., 2009, 131(5), 054106.
104. J. E. Subotnik, A. Jain, B. Landry, A. Petit, W. Ouyang and N. Bellonzi, Understanding the Surface Hopping View of Electronic Transitions and Decoherence, Annu. Rev. Phys. Chem., 2016, 67(1), 387–417.
105. L. Wang, A. Akimov and O. V. Prezhdo, Recent Progress in Surface Hopping: 2011–2015. J. Phys, Chem. Lett., 2016, 7(11), 2100–2112.
106. S. Fernandez-Alberti, D. V. Makhov, S. Tretiak and D. V. Shalashilin, Non-adiabatic excited state molecular dynamics of phenylene ethynylene dendrimer using a multiconfigurational Ehrenfest approach, Phys. Chem. Chem. Phys., 2016, 18(15), 10028–10040.
107. I. Burghardt, H.-D. Meyer and L. S. Cederbaum, Approaches to the approximate treatment of complex molecular systems by the multiconfiguration time-dependent Hartree method, J. Chem. Phys., 1999, 111(7), 2927–2939.
108. G. A. Worth and I. Burghardt, Full quantum mechanical molecular dynamics using Gaussian wavepackets, Chem. Phys. Lett., 2003, 368(3), 502–508.
109. W. Zhou, A. Mandal and P. Huo, Quasi-Diabatic Scheme for Nonadiabatic On-the-Fly Simulations. J. Phys, Chem. Lett., 2019, 10(22), 7062–7070.
110. A. Abedi, N. T. Maitra and E. K. U. Gross, Exact Factorization of the Time-Dependent Electron-Nuclear Wave Function, Phys. Rev. Lett., 2010, 105(12), 123002.
111. J.-K. Ha, I. S. Lee and S. K. Min, Surface Hopping Dynamics beyond Nonadiabatic Couplings for Quantum Coherence, J. Phys. Chem. Lett., 2018, 9(5), 1097–1104.
112. B. F. E. Curchod, F. Agostini and E. K. U. Gross, An exact factorization perspective on quantum interferences in nonadiabatic dynamics, J. Chem. Phys., 2016, 145(3), 034103.
113. V. G. Stavros, A bright future for sunscreens, Nat. Chem., 2014, 6(11), 955–956.
114. G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, Direct observation of hydrogen tunneling dynamics in photoexcited phenol. J. Phys, Chem. Lett., 2012, 3(3), 348–352.
115. K. I. Hilsabeck, J. L. Meiser, M. Sneha, J. A. Harrison and R. N. Zare, Nonresonant photons catalyze photodissociation of phenol, J. Am. Chem. Soc., 2019, 141(2), 1067–1073.
116. L. A. Baker, M. D. Horbury, S. E. Greenough, P. M. Coulter, T. N. V. Karsili, G. M. Roberts, A. J. Orr-Ewing, M. N. R. Ashfold and V. G. Stavros, Probing the ultrafast energy dissipation mechanism of the sunscreen oxybenzone after UVA irradiation, J. Phys. Chem. Lett., 2015, 6(8), 1363–1368.
117. L. A. Baker, B. Marchetti, T. N. Karsili, V. G. Stavros and M. N. Ashfold, Photoprotection: extending lessons learned from studying natural sunscreens to the design of artificial sunscreen constituents, Chem. Soc. Rev., 2017, 46(12), 3770–3791.
118. M. N. Ashfold, D. Murdock and T. A. Oliver, Molecular photofragmentation dynamics in the gas and condensed phases, Annu. Rev. Phys. Chem., 2017, 68, 63–82.

---

Footnote

† Electronic supplementary information (ESI) available: I: Relevant information: the active space and transition orbitals, the geometrical parameters and state energies at S₀-min, S₁-min, and all CIs mentioned in this work, CI₁₀–seams, typical trajectories via different decay channels, and distribution of geometric parameters at S₁ to S₀ hops. II: The Cartesian coordinates of all critical geometries. See DOI: 10.1039/d1cp03226g

---