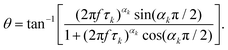Open Access Article
Open Access ArticleStudy of ferro- and anti-ferroelectric polar order in mesophases exhibited by bent-core mesogens†
Susanta
Chakraborty
 a,
Malay
Kumar Das
a,
Malay
Kumar Das
 *a,
Christina
Keith
b and
Carsten
Tschierske
*a,
Christina
Keith
b and
Carsten
Tschierske
 b
b
aDepartment of Physics, University of North Bengal, Siliguri-734 013, India. E-mail: mkdnbu@yahoo.com
bMartin-Luther-Universität Halle-Wittenberg, Institut für Chemie, Physikalische Chemie, Halle, Germany
First published on 3rd November 2020
Abstract
The polar nature of three pure homologous bent-core compounds derived from 4-cyanoresorcinol bisbenzoates as a central core unit were studied based on dielectric spectroscopy measurements and electro-optical investigation. All these compounds exhibited a highly correlated nematic phase (NCybC) followed by a phase (CybC) comprising elongated but not completely fused strings of cybotactic clusters. Additionally, the higher homologous compounds exhibited one or more tilted smectic phases (SmC(I), SmC(II)). Based on all the investigated results, the NCybC phase was found to be quite different from the usual nematics, consisting of tiny polar clusters, which in effect revealed a ferroelectric polarization within the medium. Moreover, the lower temperature SmC phases (SmC(I) and SmC(II)) characterized an anti-ferroelectric type of molecular dipolar ordering in adjacent layers. The intermediate CybC phase accomplished the transition from the ferroelectric-type NCybC phase to the anti-ferroelectric type of the SmC(I) phase, where the cybotactic clusters were elongated. The SmC(II) phase was a SmC phase with an enhanced packing density in comparison to the SmC(I) phase, which seems like a more solid-like state or glassy state. The field reversal polarization technique and the simultaneous observation of the optical textures corroborated the polar nature of the mesophases. These outcomes were explained by considering the structural changes of the molecules by increasing the chain length and the combined effect of their association in the dielectric parameters of the respective mesophases. Finally, it was concluded that the SmC(I) phase should be designated as SmCsPA phase (Cs stands for a synclinic-type of molecular organization and PA corresponds to an anti-ferroelectric ordering of the polar orientation in neighboring layers), where the SmC(II) phase was characterized by a quite solid-like state or close-packed SmC phase with a similar type of synclinic anti-ferroelectric ordering (SmC′sPA phase).
1. Introduction
Investigations of the structural property correlation in liquid crystals (LC) have achieved a new platform subsequent to the discovery of bent-core (BC) mesogens. Encompassing the unique conformational features compared to the usual calamitic molecules, BC mesogens are enriched with exotic mesomorphic behaviors, such as giant flexo-electricity,1,2 unique rheological properties,3,4 a considerable Kerr effect,5 an unpredictable behavior of the electro-convection patterns,6–8 a polar switching behavior, and structural layer chirality.9–12 Owing to all these unique properties, BC compounds are quite interesting from both the application point of view and understanding the structural property correlation.13–19 Additionally, the signature of a fascinating polar behavior in the banana or B phases as well as experimental evidence of significant ferro- and anti-ferroelectric ordering are other intriguing aspects of these BC materials. Moreover, in BC compounds, different mesophases exhibit unusual and quite rare characteristics depending on the magnitude and position of the bend-angle, the size of the molecules as well as the influence of the terminal chain, linking groups, number of aromatic rings, transverse molecular polarity, etc.20–22 Therefore, significant attention has been paid by researchers over the last few decades to the design, synthesis, and characterization of new BC materials with striking features. Extensive efforts have also been employed toward the understanding or overview of the effective mesomorphic properties linked with the molecular conformers and the remarkable improvements of the physical properties.In contrast to a variety of smectic-like phases (banana or B phases), the divulgence of a stable nematic phase in these BC compounds is quite challenging and unveils a fascinating new domain in the branch of thermotropic LCs. Smectic-like strong short-range local ordering in the nematic phase (namely the cybotactic nematic mesophase, NCybC) has been reported23–33 in a number of cases. Later investigation of a bent-core compound based on 1,2,4-oxadiazole as a central unit demonstrated a ferroelectric-like response in the nematic phase due to the existence of smectic-like polar cybotactic clusters.32 Keith et al. reported a homologous series of bent-core compounds having a broad range of cybotactic nematic phases along with higher ordered smectic phases and put forward an idea about the molecular orientations within these mesophases.33 Chirality in layers was also observed for BC mesogens34 due to the combined effect of a molecular tilt and the polar vector of the molecules in adjacent layers, though they are achiral in nature.35 In a majority of BC mesogens, the chirality is an often encountered phenomenon, such as in NCybC* (chiral cybotactic nematic)36 and the recently discovered Ntb (twist-bent nematic) phase (chirality emerges as an induced feature).37,38 Apart from the conventional calamitic compounds, such exciting characteristics observed in BC compounds arise due to the steric hindrance induced by the bent geometry, which distorts the symmetry of these molecules.
Based on determining the frequency-dependent complex permittivity, the study of dielectric spectroscopy has emerged as an attractive technique for investigating the dielectric and molecular properties of BC liquid crystals (LCs). Over the past few decades, enormous efforts have been devoted to characterizing the relaxation modes in different LC systems, comprising calamitic,39–41 discotic,42 T-shaped,43 and chiral44–46 molecules, and also some LC systems doped with nanoparticles and porous media.47–50 Usually, the calamitic nematogens are found to exhibit three dielectric relaxation modes in the high-frequency range,40 while a number of relaxation modes at the lower frequency region have been explored in some BC systems compared to calamitics.51,52 Till now, different experimental verifications have confirmed that the presence of smectic C (SmC)-type polar nanoclusters is responsible for the occurrence of such unusual behavior53 and ferroelectric-like switching has been observed in these nematic phases.53,54 Therefore, the presence of these types of unusual mesophases and a proper understanding of the appearance of the polar nature in these BC compounds is quite motivating to perform this dielectric spectroscopy study in a broad sense.
In this paper, we focus on the dielectric spectroscopy and the electro-optical investigation of three pure achiral bent-core compounds of a homologous series derived from 4-cyanoresorcinol bisbenzoates. The manifestation of the relaxation modes throughout the entire mesomorphic regions has been discussed in light of the associative molecular behavior both in planar and homeotropic alignments. A simultaneous comparison of the relaxation modes was also performed for all the homologs in accordance with the variation of temperature and chain length as well as the strength of the dipoles in respective mesophases. The obtained outcomes are interpreted herein in terms of the molecular structure, a correlation of the dipoles, and simultaneous observation of the response of the relaxation modes when applying external DC bias voltage. Additionally, we measured the field reversal switching behavior to validate the polar nature of the mesophases, which implied that the nematic phase was a ferroelectric type while both the lower temperature SmC phases (SmC(I) and SmC(II)) were anti-ferroelectric type.
2. Experimental
2.1 Materials
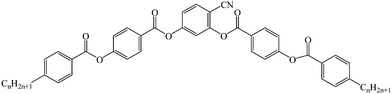
The investigated three homologous bent-core compounds were symmetric in shape and they were derived from a 4-cyanoresorcinol bisbenzoates-based central unit having terminally substituted alkyl chains.33,55The structural formula and phase-transition scheme of these homologs (1/7, 1/9, and 1/10) are shown below and their synthesis has been reported elsewhere.33 All these compounds exhibited a highly correlated nematic phase (NCybC) over a wide temperature range followed by a LC phase (CybC) comprising elongated but not completely fused strings of cybotactic clusters. In addition, the higher homologs (1/9 and 1/10) exhibited one or more tilted smectic phases (SmC(I), SmC(II)). Both compounds 1/9 and 1/10 exhibited a negative value of dielectric anisotropy, while compound 1/7 revealed an inversion from positive to negative dielectric anisotropy in the NCybC phase.55
Phase sequences for the compounds during the cooling cycle (the transition temperatures are from the POM and optical transmission measurement study55):
Compound 1/7 (n = 7): CybC 313.3 K NCybC 383 K I
Compound 1/9 (n = 9): SmC(I) 325.4 K CybC 333.5 K NCybC 378.6 K I
Compound 1/10 (n = 10): SmC(II) 330.1 K SmC(I) 341.6 K CybC 351.6 K NCybC 377.6 K I
2.2 Dielectric spectroscopy study
Different dielectric parameters were explored for the investigated compounds using an impedance analyzer Agilent 4294A in the frequency range of 40 Hz–15 MHz with a maximum AC voltage of 0.5 V (RMS) to avoid nonlinear responses. Samples were filled into ITO-coated LC cells (procured from AWAT PPW, Warsaw, Poland) with a thickness of ∼9 μm having both planar (HG) and homeotropic (HT) configurations. The LC cells were placed inside a hot/cool stage (INSTEC HCS 302), which was controlled by INSTEC mK1000 programmable temperature controller having a maximum temperature resolution of 0.001 °C. During cooling from the isotropic phase, the real (ε′) and the imaginary (ε′′) parts of the complex dielectric permittivity were measured at each temperature (kept stabilized for 5 min at each temperature) throughout the entire mesomorphic range at an interval of 1 K. The temperature-dependent complex dielectric permittivity, ε*(f), can be well described by the Havriliak–Negami (H–N) equation with an additional term standing for the low-frequency conductivity contribution as follows:56,57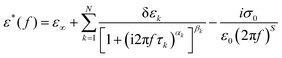 | (1) |
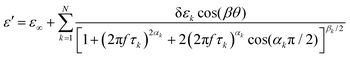 | (2) |
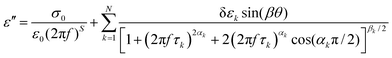 | (3) |
2.3 Electro-optical investigation
Electro-optical investigations for the three investigated bent-core compounds were carried out in combination with the field reversal polarization technique59 by applying a triangular wave AC input voltage (amplified by 20 times) and by observation of the optical texture (by using the square wave of low frequency) under a crossed polarizing optical microscope (POM) BANBROS BPL400 B attached with a CCD camera Moticam 580 (5.0 MP). An absolute voltage of 180 Vpp, 20 Hz was applied with a proper resistive circuit to the sample filled ITO-coated commercial cells, both in planar and homeotropic orientations. Hence, an effective voltage of about ±20 V acted per μm on the cell, which drove a current through the material. The output switching current was acquired by using an Agilent DSOX2000A oscilloscope at a temperature interval of 1 K.3. Results and discussion
3.1 Dielectric spectroscopy study
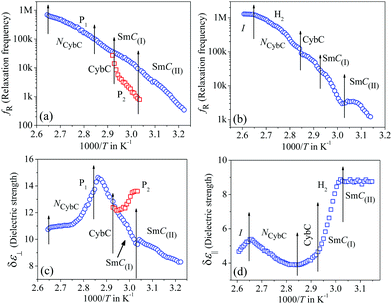
The frequency-dependent real (ε′) and imaginary (ε′′) parts of the complex permittivity for compound 1/7 (at a particular temperature of 348 K) are presented in Fig. 1(a) and (b) for the planar (HG) and homeotropic (HT) alignments, respectively. The corresponding temperature dependence of the relaxation frequency (fR) for the different relaxation modes is illustrated in Fig. 2(a and b) for both cell configurations, while the associated dielectric strengths (δε) are shown in Fig. 2(c and d).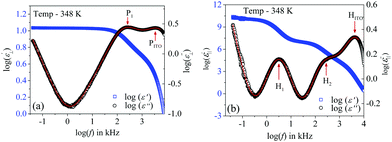 | ||
| Fig. 1 Frequency dependence of the real (ε′) and imaginary (ε′′) parts of the permittivity for compound 1/7: in (a) HG or planar and (b) HT or homeotropic sample configurations. Red solid curves represent the fit to the data points with eqn (3). | ||
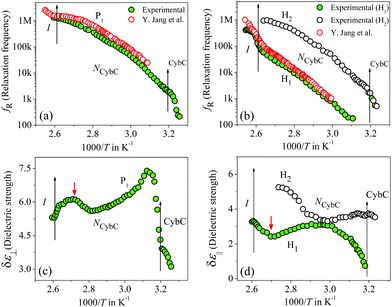
The obtained dielectric spectra in Fig. 1(a) for the HG cell clearly indicated two relaxation peaks, one marked as P1 that appeared in a few kHz ranges and a high-frequency peak marked as PITO that was independent of temperature and arose due to the influence of ITO resistance in series with the cell capacitance. Conversely, in the case of the HT cell, the corresponding relaxation modes are presented in Fig. 1(b), indicating a high-frequency peak HITO along with two temperature-dependent peaks (H1, H2) appearing at the lower frequency side of HITO. Noticeably, the P1 mode in the HG cell had a smaller value of dielectric strength (δε) throughout the whole cybotactic nematic (NCybC) phase. On the other hand, the H1 mode in the HT cell appeared at a lower frequency range with a smaller value of δε and was weakly sensitive to the externally applied bias field. The reason behind the appearance of the P1 and H1 modes might be regarded as the rotation of the molecules around their long and short axes, respectively.60 In the case of the transverse component (HG cell), the effect of the molecular rotation around the long axis led to a high-frequency relaxation peak, while in the longitudinal component (HT cell), the same occurred about the short axis subjected to a low-frequency relaxation peak. Similar observations were reported by Jang et al.60 both in planar and homeotropic orientations. The extracted experimental values of the relaxation frequency (fR) for the present compound agreed quite well with the reported value60 in both orientations, as represented in Fig. 2(a and b). However, in addition to the H1 relaxation mode in the HT cell, the present investigation showed a second mode (H2) in the higher frequency region. Upon lowering the temperature, the value of the relaxation frequency (fR) for this mode progressively decreased toward the lower frequency region throughout the NCybC phase. Moreover, the values of fR were found to be nearly equal to those for the P1 mode in the planar configuration and also revealed a weak dependence on the applied biasing field. Hence, it can be assumed that the superposition of different independent rotations of polar molecules around their long axis or around the principle director implements this relaxation mode. Earlier investigations by Tadapatri et al. for a similar type of molecule with alkoxy terminal chain also support the present outcomes.61,62 This type of high-frequency relaxation mode in longitudinal components appears in the GHz range for the usual calamitics but a downshift of this mode in the bent-core compound may be attributed to the molecular size and very high viscosity of the sample. A quite analogous identification of three relaxation peaks (H1, H2 in HT cell, and P1 in HG cell) has also been observed in some bent-core nematic as well as in mixtures with calamitics.63–65 Interestingly, in the present investigation, the dielectric strength (δε) for the modes P1 and H1 was found to demonstrate an anomalous behavior at a region below ∼15 K from the isotropic–nematic (I–NCybC) phase transition, as shown in Fig. 2(c and d). The δε value initially increased in the HG cell, while it was reduced in the HT cell followed by the I–NCybC phase transition. Surprisingly, near the temperature 365 K (marked with the red arrow), the δε value in both cases revealed a kink and followed the opposite pattern thereafter. Previous investigation of this compound also revealed an inversion of positive to negative dielectric anisotropy at ∼18 K below the I–NCybC phase-transition temperature.55 Due to the presence of SmC-type polar nanoclusters in the nematic phase, the mutual alignment of these clusters leads to such a behavior. However, this inversion of dielectric anisotropy is also dependent on the frequency and the nature of the corresponding crossover frequency is a highly non-Arrhenius type at lower temperature.60,66 Recently, Jang et al. explained that inversion by assuming the values of the anisotropic Kirkwood correlation factors (g‖ and g⊥) were not equal to 1, rather g‖ decreased and g⊥ increased from unity, i.e., g‖ < 1 and g⊥ > 1.66
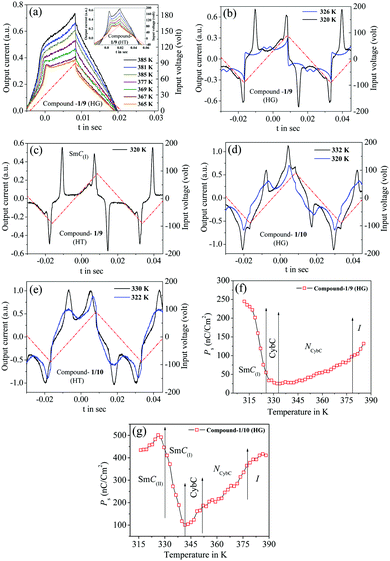
The frequency-dependent imaginary (ε′′) part of the complex permittivity for the second homologous compound 1/9 is shown in Fig. S3 in the ESI.† The corresponding temperature-dependent relaxation frequencies (fR) and the dielectric strengths (δε) are plotted in Fig. 3(a–d) for the HG and HT orientations, respectively.
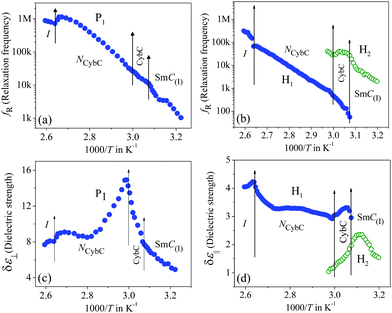
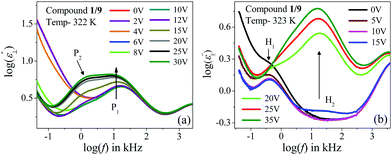
In this case, the planar-oriented compound 1/9 was characterized by a single relaxation peak (P1). On the other hand, in the HT cell, the dielectric modes were portrayed by two relaxation peaks: H1 and H2. The H1 mode appeared at a frequency of about 100 kHz and was found to decrease throughout the NCybC phase with lowering the temperature; while the other mode (H2) arose near the NCybC–CybC phase transition but at a relatively higher frequency region than the H1 mode. A closer look at the temperature variation of fR for the P1 mode suggested the almost same variation as observed in the planar-aligned compound 1/7. The dielectric strength (δε) of this peak was strongly dependent on the temperature, i.e., it gradually increased its magnitude in the nematic phase with the decreasing temperature. Further lowering the temperature, the value of δε decreased sharply in the SmC(I) phase via the CybC phase. A similar type of observation for the dielectric strength was reported by Eremin et al. for the transition to a para-electric to anti-ferroelectric SmC phase transition for a bent-core compound.67 Since, the NCybC phase comprised a number of small-sized cybotactic clusters with the SmC-type layer structure, this corresponded to a strong short-range correlation among the molecules and the cluster size was elongated by lowering the temperature.33 Thus, the appearance of this mode could be assigned as due to the rotation of molecules within the clusters around the long axis of the director in the nematic phase. However, the presence of a transverse dipole moment of the molecules essentially affected this mode in the SmC(I) phase and this process was related to a collective relaxation of the dipoles. It can thus be considered that the short-range polar correlation now became anti-parallel in the SmC(I) phase. The CybC phase is a phase comprising elongated but not completely fused strings of cybotactic clusters and therefore, the anti-parallel dipolar alignments were observed to be initiated from the NCybC–CybC phase transition. Although, compound 1/9 possessed a larger molecular size and dimensions of the cluster in comparison to that of compound 1/7, the temperature-dependent variation of the cluster size as well as the molecular tilt played significant roles in the entire NCybC mesophase. The tilt angle of these molecules was enhanced from 15° in the NCybC phase to 32° in the perfectly aligned SmC(I) phase through the intermediate CybC phase in which the molecular tilt angle was 28°.33 Therefore, the assembly of molecular dipole moments associated with SmC-type polar clusters in the NCybC phase formed a short-range ferroelectric type ordering, which thereby increased the strength of the relaxation modes by decreasing the temperature followed by the elongation of the cluster size. Consequently, the value of δε was enhances gradually in the NCybC phase. With further decreasing the temperature, clusters were fused into elongated ribbon-like aggregates in the CybC phase and the dipole moments were oriented in such a way that an anti-ferroelectric type of ordering of the dipoles developed in adjacent layers. The strong dipole−dipole interaction favored aligning the molecular dipole moments in adjacent layers with an anti-parallel ordering. This anti-ferroelectric type of orientation continued by itself throughout the SmC(I) phase, which caused an effective decrease in the δε value in the CybC and SmC(I) phases. An almost identical type of behavior was observed by Guo et al. for a bent-core compound at the transition from the SmAPR phase to anti-ferroelectric SmAPA phase.68 Additionally, this mode is sensitive to the external bias field. From Fig. 4(a), clear evidence of the strengthening of the P1 mode was found by increasing the bias field without any measurable change in fR. This indicated that this mode (P1) developed due to the molecular rotation about the long axis and additionally was influenced by the local anti-ferroelectric ordering of the molecular dipoles in adjacent layers of the SmC(I) phase. A complete realization of this issue has been drawn from the field-induced polarization technique as described later. With a further increase in the field strength, the trivial appearance of an additional peak (P2) was seen in the SmC(I) phase at a lower frequency side compared to that of the P1 mode. This implies that there also existed an additional motion of the molecules around the short axis or bow axis, and also that it has an influence on the local polar ordering and therefore, apparently could be recognized due to the application of external voltage. Nevertheless, in the case of the HT configuration, both the H1 and H2 peaks had a relatively smaller dielectric strength than the P1 mode and a weak temperature dependency. However, a noticeable change in δε was found in the CybC and SmC(I) phases. The relaxation frequency for the H1 mode was quite similar to that of compound 1/7 in the NCybC phase. This mode could also be assigned to the molecular relaxation, which appears due to the end-over-end rotation of molecules around their short axis or bow axis.62 The signature of the H2 mode was found from the CybC mesophase at a relatively higher frequency region than for H1 and it extended to the entire SmC(I) phase. Interestingly, the strength of this mode was highly sensitive to the external bias field, i.e., the value of δε increased with increasing the bias voltage, while it was very small in the absence of the field, as observed in Fig. 4(b). This mode could be attributed to a relaxation in which anti-ferroelectric domains of the polar molecules in the SmC(I) phase are transformed to ferroelectric domains by the application of an external DC field, thereby effectively increasing the strength. Fig. 4 implies that the electric field response of the relaxation modes was much stronger in the HT configuration than that in the HG. This demonstrated that the contribution of the effective molecular dipole moment along the field direction in HT alignment was strong compared to in the HG configuration subsequent to the application of bias voltage. Therefore, due to the anti-parallel alignment of the molecular dipoles, the effective dielectric strength initially showed a much smaller value in the absence of the field. With increasing the external field, the dipolar groups tended to reorient progressively in parallel to the field direction, while the long molecular axes remained randomly distributed around the field direction. This resulted in an enhancement of the dielectric strength along the field direction with increasing the field strength. However, in the case of the HG cell, the component of the dipole moment along the field direction was too weak compared to that in HT cell and therefore, it was not so sensitive to the external bias field.
 | ||
| Fig. 4 Variation of the frequency-dependent imaginary (ε′′) part of the permittivity with the bias voltage for compound 1/9: in (a) planar and (b) homeotropic alignment of cells. | ||
The frequency-dependent imaginary (ε′′) part of the complex permittivity for the higher homolog 1/10 is shown in Fig. S5 in the ESI,† for both cell configurations. The corresponding temperature-dependent relaxation frequencies (fR) and the dielectric strengths (δε) are plotted in Fig. 5(a–d), respectively.
Compound 1/10 in a planar configuration revealed a high-frequency peak (P1) in a frequency range identical to the lower homologous compounds, with a relatively large value of δε. During cooling from the isotropic phase, the value of δε gradually increased in the NCybC phase and was found to decrease in the following CybC and SmC(I) phases. This observation was quite similar to the planar-aligned compound 1/9. Moreover, in the SmC(I) phase, an additional relaxation mode (P2) with a very close value of fR was detected. Upon applying an external bias field, these two modes could be clearly resolved (see Fig. 6(a)). During further reduction of the temperature, the P1 mode persisted over the lower temperature SmC(II) phase. Therefore, similar to compound 1/9, the P1 mode in compound 1/10 could be ascribed to the molecular mode in the NCybC phase, while in the tilted SmC(I) phase, the orientation of the molecules were in an anti-parallel fashion with a greater tilt angle, describing a kind of collective process of relaxation. Conversely, in the homeotropic-oriented sample, a single relaxation mode (H2) was observed throughout the whole mesomorphic regime rather than the two relaxation modes (H1 and H2) present in lower homologous compounds (1/7 and 1/9). The strength of this mode was comparatively lower than that of the HG configuration. Although, during cooling, the value of δε slightly decreased in the NCybC phase, it was further enhanced in the following the CybC and SmC(I) phases. Furthermore, the δε value remained almost constant throughout the SmC(II) phase, in which the molecules were considered to be organized in a quite close-packed structure. Interestingly, the strength of this mode in the SmC(I) phase sharply increased with the applied biasing field, as shown in Fig. 6(b). Noticeably, upon applying the bias voltage, the first longitudinal mode (H1) was minutely observed at a lower frequency region than H2, which appeared predominantly in the lower homologous compounds without any bias voltage. This can be explained as due to the enhancement of the molecular length in compound 1/10, whereby the terminal chains easily escaped into the surface boundary and produced aliphatic excrescences around the cluster.33 Moreover, the combination of steric interaction and dipole–dipole interaction favored orienting the terminal chains parallel to the layer boundary, which allowed interdigitation of the terminal chains.69 As a result, the rotation of the molecules about its short axis was hindered in the HT configuration, but imparted a significant influence in the case of the planar-oriented sample. In addition to this, an emergence of the P2 mode was observed in the case of the planar orientation without any bias field. By applying an external field, for both compounds 1/9 and 1/10, the relaxation peak (P2) in the planar anchoring SmC(I) phase could be clearly resolved, as seen from Fig. 4(a) and 6(a). This mode basically refers to a molecular mode that arises due to a rotation of the molecules around their short axis; again, this mode had an effect on the anti-ferroelectric organization of molecular dipoles. Thus, it can be summarized that mode P2, which was definitively absent in compound 1/7, appeared in compound 1/9 after the application of the external field and predominantly found in compound 1/10 without any bias field. This implied that by increasing the chain length, the molecular rotation about the short axis in the HG-configured sample was facilitated gradually. It can be predicted that a further increase in the chain length should exhibit a noticeable appearance of this mode with a greater value of dielectric strength.68,70 However, in the case of the HT configuration, the direction of the effective dipole moment diverged from the field direction with increasing the chain length. Additionally, the molecular rotation about the short axis inhibited the enhancement of the chain length. A prominent emergence of the H1 mode in the lower homologs led to an insignificant peak in compound 1/10 that was visible in the spectrum subsequent to the application of bias voltage (Fig. 6(b)). Therefore, the relaxation process exhibited a collective phenomenon in the SmC(I) phase, i.e., the relaxation process can be assumed due to the cooperative fluctuation of the dipoles. The associative arrangement of the molecules resulted in an anti-ferroelectric ordering in adjacent layers as reported with other bent-core molecules.70,71 However, the SmC(II) phase was like a glassy state or solid-like state, which did not respond to the external bias field. For a deeper understanding of the polar ordering for these smectic phases, the field-induced switching behavior was also studied, as described below.
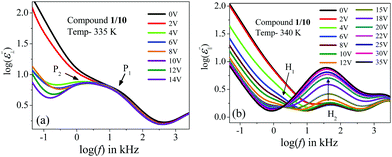 | ||
| Fig. 6 Variation of the frequency-dependent imaginary part (ε′′) of the complex permittivity with the bias voltage for compound 1/10: in (a) planar and (b) homeotropic alignments. | ||
3.2 Electro-optical investigation
Out of these three investigated compounds, the lower homolog 1/7 had NCybC and CybC phases where no prominent polarization peak was detected throughout the whole mesomorphic range. On the other hand, the higher homologous compounds (1/9 and 1/10) exhibited two significant polarization peaks in the lower temperature smectic phases and a single polarization peak in the NCybC phase, with some extending into the isotropic phase. The obtained current response curves along with the applied AC triangular wave voltage for compounds 1/9 and 1/10 are depicted in Fig. 7(a–e) for both the cell alignments, while the corresponding temperature dependence of the spontaneous polarization (Ps) is illustrated in Fig. 7(f and g). Simultaneous observations of optical textures in response to the applied field are also represented in Fig. 8 and Fig. S7 (ESI†).The switching current response for the planar-aligned compound 1/9 exhibited a broad asymmetrical current peak in the NCybC phase, even also in the isotropic phase as represented in Fig. 7(a) at different temperature above and below the I–NCybC phase transition. However, the appearance of a sharp current peak was observed in the HT configuration, which is shown in the inset of Fig. 7(a). A similar observation was also noticed in the case of compound 1/10 in the NCybC phase for both cell configurations. The area covered by the peak for both the compounds was sufficiently large near the isotropic phase and then slowly diminished in the NCybC phase upon lowering the temperature. Thus, the corresponding value of polarization (Ps) was found to be about 140 nC cm−2 at the isotropic phase for compound 1/9 (see Fig. 7(f)), while compound 1/10 revealed a much higher value (∼320 nC cm−2), as represented in Fig. 7(g). With further lowering the temperature, the value of Ps gradually decreased throughout the entire NCybC phase. It may be concluded that the existence of small clusters consisting of SmC-type polar molecules in the NCybC phase and even in the isotropic phase induced such a polarization peak. A quite similar type of observation has been reported in four-ring bent-core samples72 and in the SmA phase of three-ring bent-core compounds.73 Therefore, the single peak observed in the switching current indicated that the fluctuation of the polarization vector of these polar cybotactic clusters was induced by the application of the external field, resulting in a ferroelectric-like polar switching72,74,75 in the NCybC phase. That the peak was due to polar clusters and not to conductivity was supported by the growing dielectric strength at the I–NCybC transition. However, the average size of the polar clusters was very small near the isotropic phase, which makes the reorientation of the dipolar axes easier and hence it demonstrated a high value of polarization.27 Moreover, as the temperature decreased, the polar clusters increased in size, resulting in an effective increase in viscosity which also restricted the reorientation of the clusters within the NCybC phase and hence the polarization value decreased with lowering the temperature. Noticeably, the planar-aligned birefringent texture followed a sharp change upon the application of an electric field (180 VPP, 5 Hz) in the NCybC phase for both compounds, as shown in Fig. 8(a). When the field was removed, the texture switched back into the initial state within a few milliseconds. A similar observation was also found in the HT cell as well, as seen from Fig. 8(c). Such a ferroelectric nature in the nematic phase revealed a good consistency with several experimental reports27,72,76 and often a quite higher value of polarization has also been reported in bent-core nematic phases.77 Moreover, an irregular streak texture arose in the CybC phase as a result of the applied field for the HG cell, as depicted in Fig. S7 in the ESI.† However, compound 1/10 in the HT cell resembled a broken-fan-shaped texture. Additionally, an appearance of two insignificant peaks in the switching current was found in this phase (blue curve in Fig. 7(b)). With further decreasing the temperature, these two peaks became well distinct and sharp in the SmC(I) phase, as shown in Fig. 7(b and c), for both cell configurations. This is the signature of weak anti-ferroelectric ordering of the dipoles in adjacent layers. Nevertheless, the optical texture also showed a considerable change in the field-on state in the SmC(I) phase, as represented in Fig. 8(b) for the HG cell and Fig. 8(d) for the HT cell. Although the texture patterns were almost identical in the CybC (compound 1/9 in HG cell) and SmC(I) phases (compound 1/10 in HT cell), a considerable change in the birefringence was observed between these two phases. However, as the anti-parallel organization of the molecules in the neighboring layers initiated from the CybC phase, the dual insignificant polarization peaks were found to appear from the CybC phase. With lowering the temperature, the obtained polarization value sharply increased to 250 nC cm−2 for the HG configuration in the SmC(I) phase, as shown in Fig. 7(f). This enhancement of the polarization value has also been reported in some bent-core anti-ferroelectric smectic phases.63,67,78–82 Possibly, the steric interaction between the molecules reorients the terminal chains parallel to the layer boundary. Moreover, the strong dipole–dipole interaction also favored the alignment of the molecular dipole moments in adjacent layers in an anti-parallel fashion. The combination of both interactions stabilized the anti-ferroelectric phase.83 In addition, two well-distinct sharp peaks of compound 1/10 became initially distorted in the SmC(II) phase and finally disappeared at a lower temperature, as represented in Fig. 7(d and e) for the HG and HT cell configurations, respectively. Moreover, the field-on optical texture in the SmC(II) phase eventually did not return to its initial state when the bias field was switched off, as shown in Fig. 8(f and h) for the HG and HT cells, respectively. This was essentially due to the effect of a more viscous medium with a closely packed nature of the molecules in this phase. Thus the SmC(II) phase corresponded to a more solid-like SmC phase or a glassy state. The obtained value of Ps increased with the decrease in the temperature, having a maximum value up to 520 nC cm−2 for the HG configuration in the SmC(I) phase, while it decreased in the SmC(II) phase (see Fig. 7(g)). Surprisingly, the value of polarization for compound 1/10 was found to be greater in the lower temperature smectic phases compared to the second homologous compound 1/9. This unusual behavior can be explained by considering the deviation of the resultant dipolar contribution with the variation of the chain length. The magnitudes of dipole moment for both compounds were nearly equal, but owing to the elongation of the chain length, a strong component of the effective dipole moment was oriented toward the direction of the field. Recently, similar types of bent-core molecules (n = 6, 8, 12, 14, 16, 18) were synthesized from a 4-cyanoresorcinol aromatic core80,84–88 with the reversal of the ester linking groups, in which the higher homologous compounds (n = 16, 18) possessed a non-tilted and non-polar uniaxial SmA phase in addition to two uniform tilted SmC phases (SmCSPF and SmCSPA). These compounds also exhibited a similar type of bulk polarization behavior, with polarization randomized in the polar domain phases (SmCPR phases), showing ferroelectric-like switching domains (replacing the NCybC phase) and heliconical SmCsPF phases (replacing the CybC phases), followed by anti-ferroelectric SmCsPA phases.87,88 The field-induced polarization study of the present compounds (1/9 and 1/10) indicated that both lower temperature SmC phases were polar in nature with anti-ferroelectric ordering of the dipoles and had a sufficiently high value of polarization (Ps). All these observations were found to be supportive with the conclusions made from the dielectric spectroscopy measurements. Finally, it appeared that the SmC(I) phase should be designated as SmCsPA phase (Cs stands for a synclinic-type of molecular organization and PA corresponds to anti-ferroelectric ordering of the polar orientation in neighboring layers), while the SmC(II) phase was nothing but a quite solid-like state or close-packed SmC phase having another version of synclinic-anti-ferroelectric ordering (SmC′sPA phase).
4. Conclusions
Three homologous bent-core compounds (1/7, 1/9, and 1/10) derived from 4-cyanoresorcinol bisbenzoates with terminally substituted varying alkyl chains (n = 7, 9, 10) were investigated through precise dielectric spectroscopy and electro-optical measurements. Observations from the dielectric spectroscopy study for the planar and homeotropically aligned compounds revealed that the dielectric modes originated from molecular motion and in some cases it was associated with the local polar ordering of the molecules. Interestingly, the dielectric modes in the SmC(I) phase of higher homologs were quite sensitive to the externally applied bias field, indicating an influence of the effective dipole moment of the molecules on these modes, while there was no response in the NCybC phase. The field reversal switching polarization study also confirmed the polar contribution of these mesophases. Overall, the measurements clearly explained that the NCybC phase of these compounds mostly differed from the usual nematics and exhibited a switchable macroscopic bulk polarization in the direction of the applied electric field, which defines a ferroelectric type of polar ordering. Additionally, the lower temperature SmC phases (SmC(I) and SmC(II)) possessed an anti-ferroelectric type of polar ordering in adjacent layers, and the intermediate CybC phase endorsed this ferroelectric to anti-ferroelectric type of transition. Considering all the experimental findings, it was concluded that the SmC(I) phase could be designated as SmCsPA (synclinic-anti-ferroelectric ordering), while the SmC(II) phase was a quite solid-like state or close-packed SmC phase with a similar type of synclinic-anti-ferroelectric ordering. This type of transition character from a rare ferroelectric NCybC phase to an anti-ferroelectric SmC phase is quite interesting among bent-core molecules. All the obtained outcomes can open up a new direction in LC research and supramolecular chemistry by providing a deeper understanding of the structural–property relationship of achiral bent-core molecules. However, these achiral bent-core compounds may be used in electro-optic device technology and could be useful for designing binary or multicomponent mixtures for improving material parameters like induced biaxiality, effective dipole moment, switching time, etc. for practical applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support from Department of Science and Technology, New Delhi [Project No: EEQ/2017/000829].References
- J. Harden, B. Mbanga, N. Eber, K. Fodor-Csorba, S. Sprunt, J. T. Gleeson and A. Jakli, Phys. Rev. Lett., 2006, 97, 157802 CrossRef CAS.
- J. Harden, R. Teeling, J. T. Gleeson, S. Sprunt and A. Jakli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031702 CrossRef CAS.
- C. Bailey, K. Fodor-Csorba, J. T. Gleeson, S. N. Sprunt and A. Jakli, Soft Matter, 2009, 5, 3618 RSC.
- E. Dorjgotov, K. Fodor-Csorba, J. T. Gleeson, S. Sprunt and A. Jakli, Liq. Cryst., 2008, 35, 149 CrossRef CAS.
- S. Dhara, F. Araoka, M. Lee, K. V. Le, L. Guo, B. K. Sadashiva, K. Song, K. Ishikawa and H. Takezoe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 050701 CrossRef.
- D. Wiant, J. T. Gleeson, N. Eber, K. Fodor-Csorba, A. Jakli and T. Toth-Katona, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 041712 CrossRef CAS.
- S. Tanaka, S. Dhara, B. K. Sadashiva, Y. Shimbo, Y. Takanishi, F. Araoka, K. Ishikawa and H. Takezoe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041708 CrossRef.
- S. Tanaka, H. Takezoe, N. Eber, K. Fodor-Csorba, A. Vajda and A. Buka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 021702 CrossRef.
- M. Kohout, M. Chambers, A. Vajda, G. Galli, A. Domjan, J. Svoboda, A. Bubnov, A. Jakli and K. Fodor-Csorba, Liq. Cryst., 2010, 37, 537 CrossRef CAS.
- M. Alaasar, M. Prehm, S. Poppe and C. Tschierske, Chem. – Eur. J., 2017, 23, 5541 CrossRef CAS.
- N. Sebastian, S. Belau, A. Eremin, M. Alaasar, M. Prehm and C. Tschierske, Phys. Chem. Chem. Phys., 2017, 19, 5895 RSC.
- D. Guzeller, H. Ocak, B. B. Eran, M. Prehm and C. Tschierske, J. Mater. Chem. C, 2015, 3, 4269 RSC.
- G. Pelzl, S. Diele and W. Weissflog, Adv. Mater., 1999, 11, 707 CrossRef CAS.
- C. Tschierske and G. Dantlgraber, Pramana, 2003, 61, 455 CrossRef CAS.
- M. B. Ros, J. L. Serrano, M. R. De la Fuente and C. L. Folcia, J. Mater. Chem., 2005, 15, 5093 RSC.
- R. Amaranta Reddy and C. Tschierske, J. Mater. Chem., 2006, 16, 907 RSC.
- H. Takezoe and Y. Takanishi, Jpn. J. Appl. Phys., 2006, 45, 597 CrossRef CAS.
- M. Castillo-Vallés, A. Martínez-Bueno, R. Giménez, T. Sierra and M. B. Ros, J. Mater. Chem. C, 2019, 7, 14454–14470 RSC.
- A. Bobrovsky, K. Mochalov, V. Oleinikov, D. Solovyeva, V. Shibaev, Y. Bogdanova, V. Hamplová, M. Kašpar and A. Bubnov, J. Phys. Chem. B, 2016, 120, 5073 CrossRef CAS.
- S. Patranabish, G. Mohiuddin, N. Begum, A. R. Laskar, S. K. Pal, N. V. S. Rao and A. Sinha, J. Mol. Liq., 2018, 257, 144 CrossRef CAS.
- S. K. Lee, S. Heo, J. G. Lee, K.-T. Kang, K. Kumazawa, K. Nishida, Y. Shimbo, Y. Takanishi, J. Watanabe, T. Doi, T. Takahashi and H. Takezoe, J. Am. Chem. Soc., 2005, 127, 11085 CrossRef CAS.
- S. Kumar and A. N. Gowda, Liq. Cryst. Rev., 2015, 3, 99 CrossRef CAS.
- O. Francescangeli, V. Stanic, S. I. Torgova, A. Strigazzi, N. Scaramuzza, C. Ferrero, I. P. Dolbnya, T. M. Weiss, R. Berardi, L. Muccioli, S. Orlandi and C. Zannoni, Adv. Funct. Mater., 2009, 19, 2592 CrossRef CAS.
- S. Patranabish, Y. Wang, A. Sinha and A. Majumdar, Phys. Rev. E, 2019, 99, 012703 CrossRef CAS.
- S. Stojadinovic, A. Adorjan, S. Sprunt, H. Sawade and A. Jákli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 060701 CrossRef CAS.
- D. Wiant, S. Stojadinovic, K. Neupane, S. Sharma, K. Fodor-Csorba, A. Jakli, J. T. Gleeson and S. Sprunt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 030703 CrossRef CAS.
- O. Francescangeli, V. Stanic, S. Torgova, A. Strigazzi, N. Scaramuzza, C. Ferrero, I. P. Dolbnya, T. M. Weiss, R. Berardi, L. Muccioli, S. Orlandi and C. Zannoni, Adv. Funct. Mater., 2009, 19, 2592 CrossRef CAS.
- O. Francescangeli and E. T. Samulski, Soft Matter, 2010, 6, 2413 RSC.
- O. Francescangeli, F. Vita, C. Ferrero, T. Dingemans and E. T. Samulski, Soft Matter, 2011, 7, 895 RSC.
- S. Chakraborty, J. T. Gleeson, A. Jákli and S. Sprunt, Soft Matter, 2013, 9, 1817 RSC.
- C. Zhang, M. Gao, N. Diorio, W. Weissflog, U. Baumeister, S. Sprunt, J. T. Gleeson and A. Jákli, Phys. Rev. Lett., 2012, 109, 107802 CrossRef CAS.
- S. Torgova, S. P. Sreenilayam, Y. P. Panarin, O. Francescangeli, F. Vita, J. K. Vij, E. Pozhidaev, M. Minchenko, C. Ferrero and A. Strigazzi, Phys. Chem. Chem. Phys., 2017, 19, 22946 RSC.
- C. Keith, A. Lehmann, U. Baumeister, M. Prehm and C. Tschierske, Soft Matter, 2010, 6, 1704 RSC.
- D. R. Link, G. Natale, R. Shao, J. E. Maclennan, N. A. Clark, E. Körblova and D. M. Walba, Science, 1997, 278, 1924 CrossRef CAS.
- G. Pelzl, S. Diele and W. Weissflog, Adv. Mater., 1999, 11, 707 CrossRef CAS.
- V. Punjani, G. Mohiuddin, S. Kaur, R. K. Khan, S. Ghosh and S. K. Pal, Chem. Commun., 2018, 54, 3452 RSC.
- M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. De La Fuente, D. J. B. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704 CrossRef CAS.
- V. Borshch, Y. K. Kim, J. Xiang, M. Gao, A. Jákli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635 CrossRef CAS.
- A. H. Price and Á. Buka, Advances in Liquid Crystal Research and Applications, ed. L. Bata, Pergamon Press, New York, Budapest, 1980 Search PubMed.
- H. Kresse, Physical Properties of Liquid Crystals: Nematics, ed. D. A. Dunmur, A. Fukuda and G. R. Luckhurst, Inspec, London, 2001 Search PubMed.
- W. T. Coffey and Y. P. Kalmykov, Adv. Chem. Phys., 2000, 113, 487 CAS.
- C. Krause, H. Yin, C. Cerclier, D. Morineau, A. Wurm, C. Schick, F. Emmerling and A. Schonhals, Soft Matter, 2012, 8, 11115 RSC.
- M. Marik, A. Mukherjee, D. Jana, A. Yoshizawa and B. K. Chaudhuri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012502 CrossRef.
- K. Kurp, M. Czerwiński, M. Tykarska, P. Salamon and A. Bubnov, J. Mol. Liq., 2019, 290, 111329 CrossRef CAS.
- H. Takezoe and Y. Takanishi, Smectic Liquid Crystals: antiferroelectric and ferrielectric phases, ed. H. S. Kitzerow and C. Bahr, Springer-Verlag, Berlin, 2001 Search PubMed.
- M. K. Das, B. Barman, B. Das, V. Hamplová and A. Bubnov, Crystals, 2019, 9, 473 CrossRef CAS.
- M. Rajnak, P. Kopcansky, V. Gdovinova, V. Zavisova, I. Antal, J. Kurimsky, B. Dolnik, J. Jadzyn, N. Tomasovicova, M. Koneracka and M. Timko, Mol. Cryst. Liq. Cryst., 2015, 611, 40 CrossRef CAS.
- A. Bubnov, A. Bobrovsky, I. Rychetský, L. Fekete and V. Hamplová, Nanomaterials, 2020, 10, 1498 CrossRef CAS.
- G. P. Sinha and F. M. Aliev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 58, 2001 CrossRef CAS.
- R. K. Shukla, A. Chaudhary, A. Bubnov and K. K. Raina, Liq. Cryst., 2018, 45, 1672 CrossRef CAS.
- Á. Buka, N. Éber, K. Fodor-Csorba, A. Jákli and P. Salamon, Phase Transitions, 2012, 85, 872 CrossRef.
- P. Salamon, N. Éber, Á. Buka, J. T. Gleeson, S. Sprunt and A. Jákli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031711 CrossRef.
- G. Shanker, M. Prehm, M. Nagaraj, J. K. Vij, M. Weyland, A. Eremin and C. Tschierske, ChemPhysChem, 2014, 15, 1323 CrossRef CAS.
- G. Shanker, M. Nagaraj, A. Kocot, J. K. Vij, M. Prehm and C. Tschierske, Adv. Funct. Mater., 2012, 22, 1671 CrossRef CAS.
- A. Chakraborty, M. K. Das, B. Das, A. Lehmann and C. Tschierske, Soft Matter, 2013, 9, 4273 RSC.
- S. Havriliak and S. Negami, J. Polym. Sci., 1966, 14, 99 Search PubMed.
- S. Chakraborty, M. K. Das, A. Bubnov, W. Weissflog, D. Weglowska and R. Dabrowski, J. Mater. Chem. C, 2019, 7, 10530 RSC.
- S. Ghosh, P. Nayek, S. K. Roy, T. P. Majumder and R. Dabrowski, Liq. Cryst., 2010, 37, 369 CrossRef CAS.
- A. Pramanik, M. K. Das, B. Das, M. Żurowska and R. Dabrowski, Liq. Cryst., 2015, 42, 412 CrossRef CAS.
- Y. Jang, V. P. Panov, C. Keith, C. Tschierske and J. K. Vij, Appl. Phys. Lett., 2010, 97, 152903 CrossRef.
- P. Tadapatri, U. M. Hiremath, C. V. Yelamaggad and K. S. Krishnamurthy, J. Phys. Chem. B, 2010, 114, 1745 CrossRef CAS.
- P. Tadapatri, K. S. Krishnamurthy and W. Weissflog, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031706 CrossRef.
- L. Kovalenko, M. W. Schröder, R. A. Reddy, S. Diele, G. Pelzl and W. Weissflog, Liq. Cryst., 2005, 32, 857 CrossRef CAS.
- P. Salamon, N. Eber, A. Buka, J. T. Gleeson, S. Sprunt and A. Jákli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031711 CrossRef.
- R. Balachandran, V. P. Panov, J. K. Vij, G. Shankar, C. Tschierske, K. Merkel and A. Kocot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032506 CrossRef CAS.
- Y. Jang, V. P. Panov, A. Kocot, A. Lehmann, C. Tschierske and J. K. Vij, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 060701 CrossRef.
- A. Eremin, H. Nádasi, G. Pelzl, S. Diele, H. Kresse, W. Weissflog and S. Grande, PhysChemPhys, 2004, 6, 1290 CAS.
- L. Guo, K. Gomola, E. Grecka, D. Pociecha, S. Dhara, F. Araoka, K. Ishikawa and H. Takezoe, Soft Matter, 2011, 7, 2895 RSC.
- R. A. Reddy and C. Tschierske, J. Mater. Chem., 2006, 16, 907 RSC.
- Y. P. Panarin, S. P. Sreenilayam, J. K. Vij, A. Lehmann and C. Tschierske, Beilstein J. Nanotechnol., 2018, 9, 1288 CrossRef CAS.
- H. Schlacken, P. Schiller and H. Kresse, Liq. Cryst., 2001, 28, 1235 CrossRef CAS.
- S. Ghosh, N. Begum, S. Turlapati, S. K. Roy, A. K. Das and N. V. S. Rao, J. Mater. Chem. C, 2014, 2, 425 RSC.
- W. Weissflog, U. Baumeister, M.-G. Tamba, G. Pelzl, H. Kresse, R. Friedmann, G. Hempel, R. Kurz, M. Roos, K. Merzweiler, A. Jakli, C. Zhang, N. Diorio, R. Stannarius, A. Eremin and U. Kornek, Soft Matter, 2012, 8, 2671 RSC.
- G. Shanker, M. Prehm, M. Nagaraj, J. K. Vij, M. Weyland, A. Eremin and C. Tschierske, ChemPhysChem, 2014, 15, 1323 CrossRef CAS.
- G. Shanker, M. Nagaraj, A. Kocot, J. K. Vij, M. Prehm and C. Tschierske, Adv. Funct. Mater., 2012, 22, 1671 CrossRef CAS.
- S. Turlapati, R. K. Khan, S. Ghosh, P. Tadapatri, R. Pratibha and N. V. S. Rao, J. Appl. Phys., 2016, 120, 174101 CrossRef.
- O. Francescangeli, F. Vita and E. T. Samulski, Soft Matter, 2014, 10, 7685 RSC.
- N. Sebastian, S. Belau, A. Eremin, M. Alasar, M. Prehm and C. Tschierske, Phys. Chem. Chem. Phys., 2017, 19, 5895 RSC.
- S. Sreenilayam, M. Nagaraj, Y. P. Panarin, J. K. Vij, A. Lehmann and C. Tschierske, Mol. Cryst. Liq. Cryst., 2012, 553, 140 CrossRef CAS.
- C. Keith, M. Prehm, Y. P. Panarin, J. K. Vij and C. Tschierske, Chem. Commun., 2010, 46, 3702 RSC.
- M. Alaasar, M. Prehm, S. Poppe and C. Tschierske, Chem. – Eur. J., 2017, 23, 5541 CrossRef CAS.
- S. P. Sreenilayam, Y. P. Panarin, J. K. Vij, A. Lehmann, M. Poppe and C. Tschierske, Phys. Rev. Mater., 2017, 1, 035604 CrossRef.
- K. Nishida, M. Čepič, W. J. Kim, S. K. Lee, S. Heo, J. G. Lee, Y. Takanishi, K. Ishikawa, K.-T. Kang, J. Watanabe and H. Takezoe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021704 CrossRef.
- M. Nagaraj, Y. P. Panarin, J. K. Vij, C. Keith and C. Tschierske, Appl. Phys. Lett., 2010, 97, 213505 CrossRef.
- S. Sreenilayam, Y. P. Panarin, J. K. Vij, M. Osipov, A. Lehmann and C. Tschierske, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012504 CrossRef CAS.
- Y. P. Panarin, M. Nagaraj, J. K. Vij, C. Keith and C. Tschierske, Europhys. Lett., 2010, 92, 26002 CrossRef.
- S. P. Sreenilayam, Y. P. Panarin, J. K. Vij, P. Panov, A. Lehmann, M. Poppe, M. Prehm and C. Tschierske, Nat. Commun., 2016, 7, 11369 CrossRef CAS.
- A. Lehmann, M. Alaasar, M. Poppe, S. Poppe, M. Prehm, M. Nagaraj, S. P. Sreenilayam, Y. P. Panarin, J. K. Vij and C. Tschierske, Chem. – Eur. J., 2020, 26, 4714 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00678e |
| This journal is © The Royal Society of Chemistry 2020 |