Easy approach to synthesize N/P/K co-doped porous carbon microfibers from cane molasses as a high performance supercapacitor electrode material†
Alfin Kurniawana,
L. K. Onga,
Fredi Kurniawana,
C. X. Linb,
Felycia E. Soetaredjoa,
X. S. Zhao*c and
Suryadi Ismadji*a
aDepartment of Chemical Engineering, Widya Mandala Surabaya Catholic University, Kalijudan 37, Surabaya 60114, Indonesia. E-mail: suryadiismadji@yahoo.com; Fax: +62 31 389 1267; Tel: +62 31 389 1264
bAustralian Institute for Bioengineering and Nanotechnology, The University of Queensland, Brisbane, QLD 4072, Australia
cSchool of Chemical Engineering, The University of Queensland, Brisbane, QLD 4072, Australia. E-mail: george.zhao@uq.edu.au; Fax: +61 7 3365 4199; Tel: +61 7 3346 9997
First published on 5th August 2014
Abstract
In this study, we demonstrate a simple and low cost method to synthesize N/P/K co-doped porous carbon microfibers (CMFs) from a sugar-rich byproduct (cane molasses) as the precursor material. A two-step method for the synthesis of N/P/K co-doped porous CMFs involving electrospinning of precursor material followed by simple carbonization at various temperatures (773.15–1173.15 K) was successfully applied. The N/P/K co-doped porous CMFs exhibited high specific surface area (∼580 m2 g−1) and hierarchical porous structure. The potential application of N/P/K co-doped porous CMFs as supercapacitor electrodes was investigated in a two-electrode configuration employing aqueous K2SO4 solution and ionic liquids/acetonitrile (ILs/ACN) mixtures as the electrolytes. A series of electrochemical measurements include cyclic voltammetry, galvanostatic charge–discharge and cycling durability all confirmed that the CMF-1073.15 supercapacitor exhibited good electrochemical performance with a specific capacitance of 171.8 F g−1 at a current load of 1 A g−1 measured in 1.5 M tetraethylammonium tetrafluoroborate (TEABF4)/ACN electrolyte, which can be charged and discharged up to a cell potential of 3.0 V. The specific energy density and power density of 53.7 W h kg−1 and 0.84 kW kg−1 were achieved. Furthermore, the CMF-1073.15 supercapacitor showed excellent cycling performance with capacitance retention of nearly 91% after 2500 charge–discharge cycles, characterizing its electrochemical robustness and stable capacitive performance.
1. Introduction
Li-ion batteries and supercapacitors have gained increasing attention over the past decade and are currently considered to be promising energy storage devices for creating sustainable and high efficiency energy systems. These energy storage devices have a key role to play in energy storage and harvesting where high energy or high power delivery are required. The charge storage mechanisms in supercapacitors are based on the two following mechanisms:1 (1) electrostatic storage at the electrolyte–electrode interface through reversible adsorption of ions on the surface of active electrode material when a potential difference is applied or (2) faradaic electrochemical storage with electron charge-transfer on the electrode originated from reversible redox reactions, intercalation or electrosorption. Given this, supercapacitors can be charged and discharged quickly and their energy storage capability can last for thousands to millions of charging–discharging cycles. However, the main shortcoming of supercapacitors is their low energy density particularly when compared to batteries. Additionally, the cost of electrode materials such as graphene, carbon nanotubes (CNTs), carbon aerogels and transition metal oxides to construct high electrocapacitive performance and flexible supercapacitors often exceeds the cost of battery materials. Recent technological challenges and research frontiers in supercapacitors have been directed toward the development of new and less expensive electrode materials to bridge the energy density gap for designing next-generation supercapacitors.Porous carbons are the most common electrode materials used today in supercapacitors; owing to their attracting features include high specific surface area, accommodates surface chemical attributes that can promote the double-layer capacitive performance, thermally and chemically stable and tunable porous structure to ease the transport of electrolyte ions for rapid double-layer charging–discharging.2,3 The morphology of carbon materials is heavily reliant on the synthesis methods and nanostructured carbons exhibiting powder, rod, tube, spherical and sheet shapes have been synthesized via template growth,4 thermal reduction catalysis,5 hydrothermal,6 solvothermal,7 direct pyrolysis carbonization,8 chemical vapor deposition9 and self-assembly methods.10 has become a facile and efficient pathway to produce self-standing, continuous, ultrafine fibers with controllable diameter, porous structure and surface chemistry. Thanks to large surface-to-volume ratio, excellent mechanical strength, low electrical resistivity and binder-free electrodes, the as-electrospun carbonized micro/nanofibers are a potential candidate for supercapacitors. Various kinds of polymer solutions or moltens have been investigated as precursor materials such as phenol–formaldehyde resins,11 polyacrylonitrile (PAN),12 polyvinylpyrrolidone (PVP),13 polyimide (PI),14 polyaniline (PANI),15 poly(acrylonitrile-co-vinylimidazole) (poly(AN-co-VIM)),16 poly(ethylene glycol) (PEG)17 and poly(vinylidene fluoride) (PVDF).18 In spite their commercial availability, good electronic conductivity and high tensile strength, the obtained carbonized fibers from these synthetic polymers often pose limitations such as low specific surface area (caused by packing of polymer chains during thermal treatment) and carbon yield.19,20 Also, a common requirement for toxic or corrosive organic solvents to prepare electrospinning solution does not meet “green engineering” conceptual for next-generation energy storage devices.
Natural materials have become today's spotlight for building one-dimensional hierarchical porous carbon micro/nanofibers. Silk cocoon, an electrospun fiber-like natural biopolymer, has been utilized by Liang et al.21 to prepare one-dimensional carbon microfibers with an average diameter of 6 µm and a unique hierarchical porous structure. In the present study, cane molasses is highlighted as a new, cheap, easily available precursor material to prepare N/P/K co-doped carbon microfibers featuring high specific surface area, well-developed pore network and good electrocapacitive properties. Cane molasses is a highly viscous and dark brown liquid byproduct of the sugarcane extraction, which to date has not been recovered by an economically viable approach. This syrupy liquid contains considerable amounts of sucrose as well as reducing sugars (glucose and fructose), oligo- or polysaccharides at lower concentrations. It also contains water and non-sugar components include minerals (e.g., Na, K, Ca, Mg and Si), non-protein nitrogenous (NPN) compounds, free and bound amino acids, gummy substances and suspended solids.22 Phosphate salts are also present in cane molasses, together with chlorides, sulfates and silicates accounted for about 20% of the crude ash. Approximately three to seven tons of cane molasses can be generated from 100 tons of fresh cane processing, offering a renewed opportunity to utilize this less-valued natural resource for energy storage applications. The present strategy to prepare N/P/K co-doped porous carbon microfibers is via a one-step electrospinning process of cane molasses, followed by carbonization at various temperatures. The doping of foreign elements such as alkali metals (e.g., potassium), boron, oxygen, phosphorus, sulfur or nitrogen into the graphitic framework can intrinsically and effectively modify the electronic properties of host materials and is consequently expected to improve electrochemical performance through additional pseudocapacitance faradaic reactions.23–25 In addition, low-cost nanostructured transition metal oxides such as Co3O4, Fe2O3, V2O5, SnO2, In2O3, MoO2 and MnO2 can be employed to construct asymmetric supercapacitors with improved device performance in terms of specific capacitance and power density.26–28 The preparation of self-doped N/P/K porous carbon microfibers demonstrated in this study is considered to be a simpler and greener approach rather than the incorporation of external harmful dopants that are commonly described in earlier studies. The electrochemical testing of porous carbon microfibers supercapacitor electrodes is performed by cyclic voltammetry (CV), galvanostatic charge–discharge and cycling durability techniques in neutral aqueous and ionic liquids/acetonitrile electrolytes. Comparison study of capacitance performance between porous carbon microfibers and commercial activated carbon (Maxsorb®) as electrode materials for supercapacitors is also taken. Lastly, the present study has the potential to open up a new avenue to design functionalized porous carbon microfibers from renewable resources that facilitate fast ion transport while achieving high ion adsorption capacity in the same time for next-generation supercapacitor applications.
2. Experimental
2.1. Materials
Cane molasses (Grade C) was collected as the end byproduct from a cane sugar mill located at Klaten district, Central Java and stored at −4 °C until use. The Grade C molasses, also known as “blackstrap” molasses is generally found as a commercial feed ingredient in the liquid form and its chemical composition is presented in Table 1. All chemicals include anhydrous grade 2-propanol and acetonitrile, potassium sulfate, poly(tetrafluoroethylene), tetraethylammonium tetrafluoroborate ([TEA]+[BF4]−), 1-ethyl-3-methylimidazolium tetrafluoroborate ([EMI]+[BF4]−) and 1-ethyl-3-methylimidazolium dicyanamide ([EMI]+[DCA]−) ILs were of analytically pure from Sigma-Aldrich Co., Singapore and used as-received. The molecular structures and some relevant properties of TEABF4, EMIBF4 and EMIDCA ILs are given in the ESI Table S1.† Acetylene black (99.9%) was purchased from Soltex Chemical Corp. and used without further purification. Commercial high surface area KOH-activated carbon (Maxsorb®) was obtained from Kansai Coke and Chemicals Co. Ltd., Japan. Nickel foil substrate (99.9%, 0.03 mm thick) was employed as a current collector for supercapacitor electrodes. Double distilled water was used in all experiments.2.2. Electrospinning process
The schematic setup of electrospinning unit is shown in the ESI Fig. S1.† The electrospinning system consists of a high voltage power supply device, a 2-channel syringe pump (10 ml individual syringe), single nozzle spinnerets with an i.d. of 0.7 mm, a grounded rotating drum collector wrapped with aluminium foil and a digital panel controller. Prior to electrospinning, the cane molasses was vacuum-filtered to remove coarse particles and centrifuged at 5000 rpm for 10 min to remove fine solid particles. The cane molasses was then loaded into a syringe and the feeding rate was set constant at 0.5 ml h−1 using a syringe pump. A steady voltage of 20 kV was applied between the tip of metal spinneret and grounded Al-foil located at a 10 cm distance away. The microfiber webs collected after 10 h of electrospinning were peeled from Al-foil on a drum collector and vacuum-dried at room temperature for 24 h.The synthesis of carbon microfibers was performed by a two-step thermal treatment in a Thermolyne® horizontal tubular furnace (Model 21100). First, the as-electrospun microfiber webs were stabilized at 523.15 K in air for 2 h and they were allowed to self-cool down to room temperature. The stabilized microfiber webs were further subjected to carbonization with programmed temperature rise at 20 K min−1 from ambient to final temperatures of 773.15, 873.15, 973.15, 1073.15 and 1173.15 K in a high-purity flowing N2 of 100 ml min−1. The carbonization process was held for 2 h. Then, the system was allowed to self-cool down to room temperature. Finally, the carbonized microfiber webs were stored in the desiccators for further experiments. Here, the samples were designated as M-EMFs and CMFs-T for molasses electrospun microfibers and carbonized microfibers, respectively. The notation ‘T’ in CMFs-T indicates the carbonization temperature and correspondingly five samples are denoted as CMF-773.15, CMF-873.15, CMF-973.15, CMF-1073.15 and CMF-1173.15.
2.3. Characterizations of M-EMFs and CMFs
The field-emission scanning electron microscopy (FE-SEM, JEOL JSM-6390F) was applied for morphological characterization at an accelerating voltage of 15 kV. All specimens were sputter-coated with gold. Thermogravimetric-derivative thermogravimetry (TG-DTG) curves were obtained using a Mettler-Toledo TGA/DTA 1 thermal analyzer apparatus in dynamic N2 atmosphere with a flow rate of 100 ml min−1. The samples were tested from 303.15 K to 1173.15 K in a platinum pan with a heating rate of 20 K min−1. X-ray diffraction (XRD) was performed on a Philips PANalytical X'Pert powder X-ray diffractometer at 40 kV and 30 mA in a 2θ scan mode with Ni-filtered Cu Kα1 line as the radiation source (λ = 0.15406 nm). Nitrogen adsorption–desorption isotherms were measured at 77.15 K using an automated Micromeritics 2010 accelerated surface area and porosimetry analyzer. Before measurement, the samples were outgassed on a vacuum line at 423.15 K for at least 6 h. The BET specific surface area (SBET) was determined by employing a standard Brunauer–Emmett–Teller (BET) method applied to adsorption data over relative pressures (P/P°) of 0.05–0.30. Total pore volume (VT) was estimated from the amount of adsorbed gas at a relative pressure of 0.99. The pore size distribution (PSD) was derived from the adsorption branches of the isotherms based on Barrett–Joyner–Halenda (BJH) model. X-ray photoelectron spectroscopy (XPS) was carried out in vacuum with a Kratos Axis Ultra X-ray photoelectron spectrometer using an excitation source of monochromatic Al Kα radiation (hν = 1486.6 eV) at 15 kV and 150 W. The Raman spectra were collected on a Renishaw RA100 micro-Raman spectrometer excited by 514.5 nm radiation from an argon ion laser at 10 mW.2.4. Electrochemical measurements
Electrochemical measurements were carried out in a CR2032 two-electrode coin-type cell without a reference electrode. The binder-free working electrodes were directly obtained from the microfiber webs (M-EMFs or CMFs) by punching out a circular area of 10 mm. The typical mass load of the active materials on each electrode disk was about 3.0 mg cm−2. For the electrical double-layer capacitance (EDLC) tests, the simple coin-type supercapacitor device was assembled by sandwiching two electrode disks containing equal mass of active material with a separator (porous polypropylene membrane, Celgard® 2400) between them. Then, two Ni-foil substrates were attached onto the edge of the electrodes in order to connect the electrochemical cell. The assembly of the electrochemical cells was conducted in an argon-filled glove box with less than 1 ppm of water and oxygen content. Four kinds of electrolytes namely 0.5 M K2SO4 solution, 1.5 M [TEA]+[BF4]−, [EMI]+[BF4]− or [EMI]+[DCA]− ILs in acetonitrile (TEABF4/ACN, EMIBF4/ACN and EMIDCA/ACN) were tested. The CV curves were obtained using a CHI660D electrochemical workstation at various scan rates (5–100 mV s−1) within applied potential of 0–1 V for aqueous K2SO4 solution and 0–3 V for ILs/ACN mixtures. The charge–discharge tests were performed galvanostatically on a Neware battery testing system with current density from 0.5 to 20 A g−1 over applied potential range. For comparison purposes, a working electrode with Maxsorb carbon as the active material was constructed by the same procedure. The carbon paste was prepared by mixing 90 wt% active material, 5 wt% acetylene black and 5 wt% poly(tetrafluoroethylene) binder dispersed in 2-propanol. Prior to capacitance measurements, the coin cells were conditioned by immersing them in the electrolyte-containing small seal bags inside an argon-filled glove box. All electrochemical measurements were carried out at room temperature.2.5. Calculations
The specific capacitance, Cs, of the two-electrode cell was calculated from charge–discharge curve by the following equation:
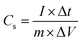 | (1) |
| Cm = 4Cs | (2) |
Here, the multiplier factor 4 is used to obtain the gravimetric capacitance of a single cell since the device is considered as two capacitors in series. The specific energy density (Ed) and power density (Pd) of supercapacitor cell can be determined using the equation:29
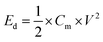 | (3) |
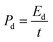 | (4) |
3. Results and discussion
The representative SEM images of M-EMFs and CMF-973.15 are depicted in Fig. 1. As shown by the low-magnification SEM image in Fig. 1(a), the as-electrospun M-EMFs has regular, randomly oriented and bead-free fibrous morphology with an average diameter of 1.23 ± 0.21 µm and length reaching several hundreds of micron. From the high-magnification SEM image in Fig. 1(b), it can be shown that M-EMFs is essentially non-porous, judging from smooth surface and low BET specific surface area of 15.7 m2 g−1. After carbonization process, the woven microfibrous structure of M-EMFs is well-preserved (Fig. 1(c)). The surface morphology of the carbonized fibers becomes somewhat of rough with obvious pits being observed, characterizing porous structure (Fig. 1(d)). The diameter of CMF-973.15 was measured to be about 0.5–0.8 µm by means of ImageJ 1.41 software. In comparison to the diameter of M-EMFs ranging from 1.0 to 1.8 µm, smaller diameter of CMF-973.15 might be due to shrinkage phenomenon during carbonization process that resulted from weight loss (burn-off) of non-carbon elements and carbon-containing compounds. Fig. 1(e) and (f) show the distribution curves of fiber diameter sizes of M-EMFs and CMF-973.15, with an average diameter size of 1.23 ± 0.21 and 0.68 ± 0.13 µm, respectively. | ||
| Fig. 1 SEM images of M-EMFs (a and b) and CMF-973.15 (c and d) at different magnifications; the distribution curves of fiber diameter sizes of M-EMFs (e) and CMF-973.15 (f). | ||
The porous properties of CMFs obtained from N2 adsorption measurements are given in Table 2. It can be seen that the BET specific surface areas of CMFs are considerably larger compared to M-EMFs. This suggested that activating M-EMFs at high temperatures would lead to the creation of porosity within the interior and on the surface of microfibers. With increasing carbonization temperatures from 773.15 to 1173.15 K, the BET specific surface area increases from 252.8 to 578.3 m2 g−1 and the average diameter size of fibers becomes obviously smaller. Higher BET specific surface area is an indication of CMFs materials that are high in microporosity. Similar trend applies to total pore volume in which total pore volume increases from 0.15 to 0.27 cm3 g−1 at higher carbonization temperatures. The microporous surface area (Smic) and external surface area (Sext) derived from a t-plot method is presented in Table 2 and these surface properties increase with increase in carbonizing temperature. The pore size distribution (PSD) curves in Fig. 2 show that CMF-1173.15 possesses a hierarchical porous structure consisting of plentiful micropores and large-sized pores. Several notable PSD peaks of CMF-1173.15 can be elucidated as follows: micropores peaked at ∼1.5 nm, mesopores peaked at ∼10.2 nm and macropores peaked at ∼69.0 nm. Interestingly, it was observed that carbonization temperature played an important role in controlling porous structures of CMFs and consequently the transport of ions inside the nanopores to form an electric double-layer structure. As shown in Fig. 2, the intensities of PSD peaks correspond to micropores and mesopores declined as carbonization takes place at lower temperatures. At low carbonization temperatures, the evolution of micropores was rather insignificant due to incomplete opening of inaccessible pores and lesser extent of creation of new pores from thermal decomposition of organic compounds. The existence of macropores was apparently not observed in samples CMF-773.15 and CMF-873.15. The formation of mesoporous and macroporous networks may arise from the pore widening phenomena at high carbon burn-off, at the expense of micropores and also possible from the compact and loose aggregation of carbon nanoparticles which are interconnected in different directions.21,30
| Samples | Porous properties | Average ∅ (µm) | |||
|---|---|---|---|---|---|
| SBET/m2 g−1 | Smic/m2 g−1 | Sext/m2 g−1 | VT/cm3 g−1 | ||
| CMF-773.15 | 252.8 | 164.6 | 88.2 | 0.15 | 0.79 ± 0.15 |
| CMF-873.15 | 338.2 | 231.7 | 106.5 | 0.18 | 0.74 ± 0.08 |
| CMF-973.15 | 447.4 | 322.7 | 124.7 | 0.22 | 0.68 ± 0.13 |
| CMF-1073.15 | 512.8 | 390.5 | 122.3 | 0.25 | 0.63 ± 0.11 |
| CMF-1173.15 | 578.3 | 437.4 | 140.9 | 0.27 | 0.57 ± 0.08 |
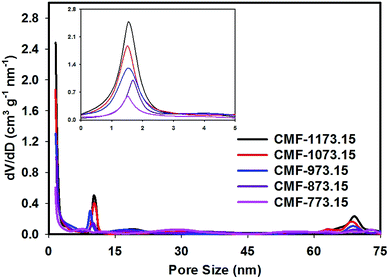 | ||
| Fig. 2 The BJH pore size distribution curves of CMFs series obtained at various carbonization temperatures (the inset shows magnified 0–5 nm pore size region). | ||
The wide-angle XRD patterns of CMFs carbonized at various temperatures are depicted in Fig. 3(a). From this figure, two broad diffraction peaks at 2θ of ∼25° and ∼43° are clearly observed and they can be indexed to (002) and (100)/(101) lattice planes of hexagonal graphitic carbon according to standard database JCPDS no. 75-1621. The (002) and (10) reflections are related with the stacking height of parallel graphene sheets (Lc) and the size of a graphene sheet (La), respectively. It is well-known that the relative intensity of the peak in the XRD pattern is associated with the degree of crystallinity. The relative intensity of the (002) peak to that of pure graphite powder (Sigma-Aldrich, 45 µm, 99.9%) increases in the sequence of CMF-773.15 < CMF-873.15 < CMF-973.15 < CMF-1073.15 < CMF-1173.15. This implies that CMF-1173.15 was more crystalline than other samples carbonized at lower temperatures. The interlayer distance between the graphene sheets, d002, was determined to be between 0.353 and 0.347 nm using the Bragg equation. Other crystallite parameters (La, Lc and Lc/d002) estimated using the Scherrer formula are given in the ESI Table S2.† In this table, it can be shown that La, Lc and Lc/d002 (the number of graphene sheets) all increase as carbonization temperature becomes higher. On the other hand, the d002 values decrease with increase of carbonization temperature, also macroscopically considered as a contraction in volume of graphite. This suggests that graphitizing process to form more ordered graphitic domains becomes more pronounced at higher temperatures. Also, one can seek information about the degree of structural ordering of carbon materials. According to Pimenta et al. work,31 the turbostratic and crystalline graphite possesses the interlayer distance of >0.342 and 0.335 nm, respectively. Thus, it can be implied that CMFs samples exhibited turbostratic disorder of graphite layered structures. In addition, CMFs consisting of graphitic structure would show an impressive electrocapacitive performance at high current density because graphitic carbon preserves good electronic conductivity.32,33
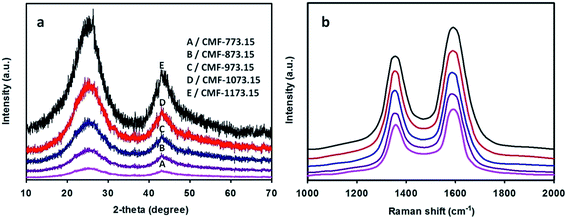 | ||
| Fig. 3 Wide-angle XRD patterns (a) and Raman spectra (b) of CMFs series obtained at various carbonization temperatures. | ||
The Raman spectra of CMFs are given in Fig. 3(b). In this figure, two broad peaks are clearly observed at around 1580 and 1350 cm−1, featuring ordered crystalline graphitic carbon (G-peak) and in-plane disordered/defective graphitic structures (D-peak), respectively. The G-peak is attributed to the bond stretching of all pairs of sp2 atoms in ring and chain structures34 and also well-correlated to the (002) basal reflection in the XRD pattern. The integrated intensity ratio of D-peak to G-peak (ID/IG) provides a useful index to assess the degree of graphitization of carbon materials. As shown in Fig. 3(b), the G-peak becomes narrower and of more prominent intensity with increase of carbonization temperatures and accordingly lower ID/IG ratios of 1.02, 0.98, 0.93, 0.87 and 0.83 was obtained for CMF-773.15, CMF-873.15, CMF-973.15, CMF-1073.15 and CMF-1173.15, respectively. This implies that fewer defects and more ordered graphitic crystallites are present at higher carbonization temperatures. High temperature carbonization also leads to the restoration of the π-conjugation network within the graphene plane as a consequence of deoxygenation phenomena.29 The co-existence of D-peak and G-peak suggests that CMFs materials are partially graphitic, which is beneficial to achieve excellent electrochemical performance.
The weight loss curves of M-EMFs and CMFs under inert high temperature environment are shown in Fig. 4. From the TG curve, it was revealed that M-EMFs exhibited multi-step weight losses due to decomposition of different species, in sharp contrast to TG curve of CMFs series. From room temperature to about 110 °C, the minor weight loss (∼3.8%) was due to release of moisture. The steep loss step within temperature range of 220–350 °C (∼63.9%) could be attributed to thermal decomposition (pyrolysis) of sugar and non-sugar organic constituents accompanying the breakdown of polysaccharide macromolecules. The gaseous byproducts from this pyrolytic decomposition are primarily H2O and CO according to Burket et al. study.35 The weight loss between 500 and 700 °C was insignificant and the TG curve eventually became a straight line at temperatures close to 900 °C, giving a residual weight of 30.6%. This could be ascribed to complete carbonization process and the formation of polyaromatic carbon structures was initiated in this temperature regime. In this point, the change of fiber color is noticeable from dark brown into black. These multiple weight loss steps were also evidenced in the DTG curve with peaks at temperatures of 108 °C, 232 °C, 272 °C and 314 °C. On the other hand, the TG curves of CMFs series reflect a different weight loss behavior compared to that of M-EMFs. All samples experienced a weight loss (10–12%) at temperatures between 50 and 110 °C. A single peak in the TG derivative thermograms was detected at temperature about 102 °C. The weight loss might be resulted from the evaporation of water adsorbed in the carbon material (i.e., capillary condensation), which suggested the existence of porous structure in CMFs. At higher temperatures, the weight of samples slightly decreased with increasing temperature and the residual weights of 84–88% were obtained at 900 °C. In addition, the degree of weight loss was found to depend on the final carbonization temperature of CMFs. Higher degree of weight loss was observed for CMF-773.15 (16.1%) compared to CMF-873.15 (15.1%) and then remained almost constant for samples CMF-973.15 (12.6%), CMF-1073.15 (12.0%) and CMF-1173.15 (12.8%). The reasonable explanation is that at carbonization temperatures of 773.15 and 873.15 K, the pyrolytic decomposition may still take place and further increase in temperature beyond 973.15 K resulted in the formation of more polyaromatic domains.
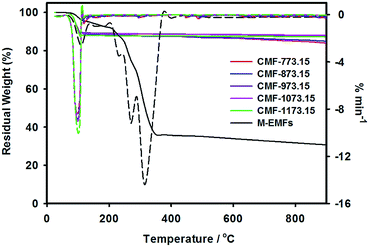 | ||
| Fig. 4 TG-DTG curves at a heating rate of 20 K min−1 for M-EMFs and CMFs series (the dashed lines represent the TG derivative thermograms). | ||
The degree of heteroatoms doping and types of functional groups can be controlled by varying carbonization temperature. In this light, the surface compositions of nitrogen and oxygen species in the graphitic framework of CMFs series as examined by XPS analysis are listed in Table 3. Total atomic contents of N, P, O and K on the surface (mol%) in M-EMFs obtained from XPS survey spectrum are calculated to be 4.2, 0.8, 21.8 and 6.2, respectively. The weighted surface concentrations of nitrogen and oxygen species are calculated by fitting the N 1s and O 1s electron core level signals of XPS spectra. The data calculations were conducted by multiplying the relative surface concentrations in atomic% by total atomic contents of the relevant atoms. The nitrogen-containing groups are determined by the deconvolution of high resolution N 1s region spectrum and fitted with a Gaussian function into three peaks, which are attributed to three types of functional nitrogen namely aliphatic amino N (N-1, 399.3 eV, 38.3 at%), amidic N (N-1, 400.2 eV, 27.5 at%) and protonated quaternary N (4°-N+, carboxybetaine ammonium N, 402.6 eV, 33.6 at%). After carbonization process, several nitrogen functional groups, all being aromatic moieties are generated. The pyridinic N (N-6, 398.5 eV), pyrrolic/pyridone N (N-5, 400.1 eV), graphitic/quaternary N (N-Q, 400.8 eV) and pyridinic-N-oxides (N-X, 403.2 eV) are the four Gaussian peaks present in CMFs. The deconvoluted N 1s peaks at 398.5 and 400.8 eV can be assigned to P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and P–N bonds, respectively.36 It is expected that carbonization under conditions of increasing severity would change the distribution of surface nitrogen groups. As shown in Table 3, two major surface nitrogen groups in CMF-773.15 and CMF-873.15 are pyridine and pyrrole/pyridone-type groups, which generated from the conversion of aliphatic amino N and amidic N groups upon carbonization at temperatures above 673.15 K. For CMF-973.15, CMF-1073.15 and CMF-1173.15 samples, the relative surface concentrations of pyridinic N and graphitic/quaternary N were higher compared to those in CMF-773.15 and CMF-873.15, which might be ascribed to the generation of these surface groups at the expense of pyrrolic/pyridone N. The complete rupture of pyrrolic rings occurred at temperatures above 873.15 K (ref. 37 and 38) since N-5 group was absent in CMF-973.15, CMF-1073.15 and CMF-1173.15. The peak of pyridinic-N-oxides was observed in CMF-1073.15 and CMF-1173.15, possibly due to the oxidation of carbon upon exposure to the ambient. Similar observations were obtained by Chen et al.37 and Shrestha and Mustain39 that worked on the synthesis of polypyrrole-coated carbonized nanofibers and N-functionalized ordered mesoporous carbon, respectively. The ratio of N-Q to N-6 was essentially unaffected by carbonization temperature since N-Q/N-6 ratio was slightly changed from 1.42 at 973.15 K to 1.43 at 1173.15 K. According to the results obtained, it can be concluded that the surface nitrogen content decreased or changed in the composition upon severe carbonization (3.6 mol% at 773.15 K to 2.5 mol% at 1173.15 K), either due to certain surface groups are released to the gas phase or they undergo thermal transformations from one functional form into another form (mainly pyridinic and quaternary nitrogen). The availability of nitrogen containing groups, particularly in the speciation of N-6 and N-Q distributed in the pores that are accessible to ions would provide chemically-active sites to improve the power density of supercapacitors through additional pseudocapacitance. Furthermore, the positively charged nitrogen atom in N-X group can take part in the pseudocapacitive Faradaic reactions.
N and P–N bonds, respectively.36 It is expected that carbonization under conditions of increasing severity would change the distribution of surface nitrogen groups. As shown in Table 3, two major surface nitrogen groups in CMF-773.15 and CMF-873.15 are pyridine and pyrrole/pyridone-type groups, which generated from the conversion of aliphatic amino N and amidic N groups upon carbonization at temperatures above 673.15 K. For CMF-973.15, CMF-1073.15 and CMF-1173.15 samples, the relative surface concentrations of pyridinic N and graphitic/quaternary N were higher compared to those in CMF-773.15 and CMF-873.15, which might be ascribed to the generation of these surface groups at the expense of pyrrolic/pyridone N. The complete rupture of pyrrolic rings occurred at temperatures above 873.15 K (ref. 37 and 38) since N-5 group was absent in CMF-973.15, CMF-1073.15 and CMF-1173.15. The peak of pyridinic-N-oxides was observed in CMF-1073.15 and CMF-1173.15, possibly due to the oxidation of carbon upon exposure to the ambient. Similar observations were obtained by Chen et al.37 and Shrestha and Mustain39 that worked on the synthesis of polypyrrole-coated carbonized nanofibers and N-functionalized ordered mesoporous carbon, respectively. The ratio of N-Q to N-6 was essentially unaffected by carbonization temperature since N-Q/N-6 ratio was slightly changed from 1.42 at 973.15 K to 1.43 at 1173.15 K. According to the results obtained, it can be concluded that the surface nitrogen content decreased or changed in the composition upon severe carbonization (3.6 mol% at 773.15 K to 2.5 mol% at 1173.15 K), either due to certain surface groups are released to the gas phase or they undergo thermal transformations from one functional form into another form (mainly pyridinic and quaternary nitrogen). The availability of nitrogen containing groups, particularly in the speciation of N-6 and N-Q distributed in the pores that are accessible to ions would provide chemically-active sites to improve the power density of supercapacitors through additional pseudocapacitance. Furthermore, the positively charged nitrogen atom in N-X group can take part in the pseudocapacitive Faradaic reactions.
| Samples | Relative surface concentrations % | Weighted surface concentrations mol% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N-6 | N-5 | N-Q | N-X | O-I | O-II | O-III | N-6 | N-5 | N-Q | N-X | O-I | O-II | O-III | |
| CMF-773.15 | 44.8 | 37.0 | 18.2 | — | 54.8 | 39.7 | 5.5 | 1.61 | 1.34 | 0.65 | — | 4.55 | 3.30 | 0.47 |
| CMF-873.15 | 53.1 | 25.2 | 21.7 | — | 52.5 | 42.4 | 5.1 | 1.75 | 0.83 | 0.72 | — | 3.94 | 3.18 | 0.38 |
| CMF-973.15 | 58.7 | — | 41.3 | — | 48.9 | 45.8 | 5.3 | 1.82 | — | 1.28 | — | 3.47 | 3.25 | 0.38 |
| CMF-1073.15 | 54.1 | — | 38.0 | 7.9 | 42.7 | 52.5 | 4.8 | 1.52 | — | 1.06 | 0.22 | 3.07 | 3.78 | 0.35 |
| CMF-1173.15 | 54.1 | — | 37.8 | 8.1 | 45.2 | 50.6 | 4.2 | 1.35 | — | 0.95 | 0.20 | 3.03 | 3.39 | 0.28 |
The deconvolution of P 2p region spectrum for CMFs carbonized at 773.15–1073.15 K results in the single peak at 133.2 eV, which can be assigned to phosphate-like structures bound to carbon lattices via C–O–P bonding. The binding energy around 133.0 eV also covers the contribution from non-bridging (P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and bridging oxygen bonded to phosphorus (C–O–P) as well as phosphonate structures (C–PO3, C2–PO2 or C3–P).36,40 Another surface phosphorus group at the binding energy of 136.1 eV was observed for CMF-1173.15, which can be attributed to phosphorus oxide (P2O5).40 Total phosphorus content on the surface shows an increase up to 1073.15 K and then decreases with further increase in the carbonization temperature. Puziy et al.40 and Wang et al.41 have reported similar trend in their work. Hulicova-Jurcakova et al.36 have shown that P-doping could increase the voltage window tolerated by the electrode material at positive potentials due to the blockage of active oxidation sites by phosphate groups. The K 2p spectrum comprises two asymmetric peaks at the binding energy of 293.4 (K 2p3/2) and 296.1 eV (K 2p1/2), which represents the spin–orbit-split doublet of K oxides and cations,42 respectively. The contribution of metallic K is also revealed in the K 2p3/2 and K 2p1/2 small peaks at 294.5 and 297.2 eV. The broad O 1s peaks can be deconvoluted into three surface groups namely O-I (530.8 eV), O-II (532.6 eV) and O-III (535.2 eV), which represents oxygen double bonded to carbon (C
O) and bridging oxygen bonded to phosphorus (C–O–P) as well as phosphonate structures (C–PO3, C2–PO2 or C3–P).36,40 Another surface phosphorus group at the binding energy of 136.1 eV was observed for CMF-1173.15, which can be attributed to phosphorus oxide (P2O5).40 Total phosphorus content on the surface shows an increase up to 1073.15 K and then decreases with further increase in the carbonization temperature. Puziy et al.40 and Wang et al.41 have reported similar trend in their work. Hulicova-Jurcakova et al.36 have shown that P-doping could increase the voltage window tolerated by the electrode material at positive potentials due to the blockage of active oxidation sites by phosphate groups. The K 2p spectrum comprises two asymmetric peaks at the binding energy of 293.4 (K 2p3/2) and 296.1 eV (K 2p1/2), which represents the spin–orbit-split doublet of K oxides and cations,42 respectively. The contribution of metallic K is also revealed in the K 2p3/2 and K 2p1/2 small peaks at 294.5 and 297.2 eV. The broad O 1s peaks can be deconvoluted into three surface groups namely O-I (530.8 eV), O-II (532.6 eV) and O-III (535.2 eV), which represents oxygen double bonded to carbon (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) or non-bridging oxygen bonded to phosphorus (P
O) or non-bridging oxygen bonded to phosphorus (P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), singly bonded oxygen (–O–) in alcohol (C–OH) or ether (C–O–C), also includes bridging oxygen in the phosphate group (C–O–P) and chemisorbed oxygen (carboxylic groups) and water,36,40 respectively. The surface oxygen content gradually decreased with carbonization temperature increasing from 773.15 to 1173.15 K due to deoxygenation phenomena and further aromatization of the graphitic framework.29 This has also been corroborated by Raman spectroscopy that the portion of graphitic structure is higher for CMFs carbonized at higher temperatures. The XPS data of C 1s is useful to evaluate the degree of graphitization of carbon materials. The C 1s core level spectrum from 280 to 290 eV is composed of a strong peak at 284.7 eV, which is assigned to C–C and C–H bonding in the sp2-hybridized graphitic carbon. Other small peaks of the carbon species in alcohol or ether (C–O), carbonyl/quinone carbons (C
O), singly bonded oxygen (–O–) in alcohol (C–OH) or ether (C–O–C), also includes bridging oxygen in the phosphate group (C–O–P) and chemisorbed oxygen (carboxylic groups) and water,36,40 respectively. The surface oxygen content gradually decreased with carbonization temperature increasing from 773.15 to 1173.15 K due to deoxygenation phenomena and further aromatization of the graphitic framework.29 This has also been corroborated by Raman spectroscopy that the portion of graphitic structure is higher for CMFs carbonized at higher temperatures. The XPS data of C 1s is useful to evaluate the degree of graphitization of carbon materials. The C 1s core level spectrum from 280 to 290 eV is composed of a strong peak at 284.7 eV, which is assigned to C–C and C–H bonding in the sp2-hybridized graphitic carbon. Other small peaks of the carbon species in alcohol or ether (C–O), carbonyl/quinone carbons (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and carboxylic/ester carbons (O
O) and carboxylic/ester carbons (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C) with corresponding binding energy of 285.4, 286.8 and 288.7 eV are observed.25,40 With the increase of carbonization temperature, the surface contents of oxygenated carbons (peaks at 285.4, 286.8 and 288.7 eV) decreased while the surface content of graphitic carbon increases, indicating that higher carbonization temperatures can facilitate the arrangement of more ordered carbon structure. The XRD and Raman spectroscopy analyses are in good agreement with XPS-related results.
C–C) with corresponding binding energy of 285.4, 286.8 and 288.7 eV are observed.25,40 With the increase of carbonization temperature, the surface contents of oxygenated carbons (peaks at 285.4, 286.8 and 288.7 eV) decreased while the surface content of graphitic carbon increases, indicating that higher carbonization temperatures can facilitate the arrangement of more ordered carbon structure. The XRD and Raman spectroscopy analyses are in good agreement with XPS-related results.
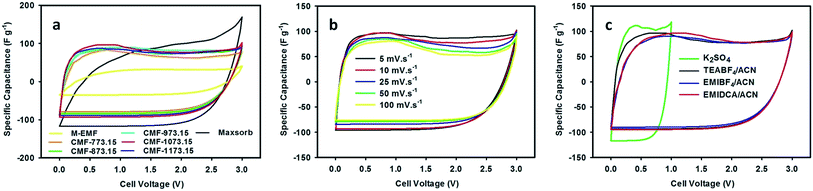
Over the past decade, ILs have attracted a great deal of attention for use as an interesting choice of non-aqueous electrolyte in the electrochemical applications, owing to their greenness (non-flammable and very low volatility) and fascinating properties include thermally stable over a wide range of temperatures, high ionic conductivity and broad window of electrochemical stability at room temperature. The advent of ILs allows volatile and harmful traditional organic electrolytes to be eliminated and also improves safety, operational stability and energy density of supercapacitors. In this regard, M-EMFs and CMFs series were tested as the active electrode materials in a two-electrode configuration. The electrocapacitive properties of M-EMFs and CMFs series were first evaluated by CV measurements at scan rates from 5 to 100 mV s−1 in different electrolytes. The shape of the CV curve has been widely used to gain information on the capacitive behavior involved in the charging and discharging of electrical double-layer, in relation to the interaction between electrolyte ions and the surface of the carbon pores. The voltage window was fixed at 0–1 V for aqueous K2SO4 solution and 0–3 V for ILs/ACN mixtures. From the CV curves in Fig. 5(a), the remarkable difference in the electrochemical surface activity between M-EMFs and CMFs series at a scan rate of 10 mV s−1 can be easily recognized. In detail, the M-EMFs supercapacitor exhibits a small curve area corresponding to poor capacitive energy storage, attributable to low specific surface area of the electrode material. On the contrary, the CMFs supercapacitors represent the capacitive behavior with the appearance of roughly box-like shape. The voltammetry charges covered under the CV curves are much larger than that of M-EMFs, showing an improvement in capacitance. Another characteristic is the CV curve slightly deviated from a rectangular shape, which indicates that the mechanism of charge storage is not purely due to electrostatic adsorption of ions in pores of carbon electrodes. Compared with Maxsorb supercapacitor, a high asymmetry of the CV curve with a slower current response can be observed even at a low voltage sweep rate of 10 mV s−1, which may be attributed to large intrinsic resistance in the electrode material arising from disordered pore structure and narrow pore size that limits the migration of ions into the carbon pores. The typical CV curve for CMF-1073.15 supercapacitor still retained without obvious distortion even at high scan rates (Fig. 5(b)). Such an excellent rate performance indicates small equivalent series resistance (ESR) and a quick diffusion rate of electrolyte ions, which are important features for high charge storage and high power supercapacitors when ionic liquids are used as the electrolyte with a wide working voltage. The existence of nitrogen containing surface groups N-Q and N-X contributes positively on the electron transfer through the carbon electrodes and hence improves the electrochemical performance at fast charge–discharge rates.36 There is an apparent redox hump in the CV curves of CMFs supercapacitors in the voltage range of 0–1.5 V, confirming the occurrence of pseudocapacitance associated with plentiful nitrogen and oxygen containing surface groups which are stable and electrochemically active such as N-6, N-Q, N-X and O-II groups. Also, one can show that the electrochemical performance in TEABF4/ACN electrolyte is superior to those in EMIDCA/ACN and EMIBF4/ACN electrolytes (Fig. 5(c)). Regardless of the types of ILs/ACN electrolytes, an improved ionic conductivity and decreased viscosity of ILs after blending with acetonitrile (see ESI Table S1†) can facilitate the movement of ions into the electrochemically active surface of electrode materials. The cathodic and anodic limiting potentials of neat TEABF4, EMIBF4 and EMIDCA ILs are found to be −1.3/+1.0 V, −2.0/+2.4 V and −2.0/+1.5 V, respectively.43–45 Thus, the capacitive energy storage in ILs/ACN mixtures should be higher and supercapacitors could be charged and discharged to higher operating cell potential (up to anodic limiting potential of 3.0 V) in comparison to aqueous K2SO4 solution with anodic limiting potential of 1.0 V without sacrificing the rate performance. Similar observation was reported by Lei and colleagues.29 To study the contribution of anion species of ILs on the capacitive behavior, the capacitive energy storage of CMF-1073.15 supercapacitor in EMIBF4/ACN and EMIDCA/ACN electrolytes was compared. The solvated ion size was estimated by molecular dynamics simulation using HyperChem 8.0.10 software following Lin et al. study.46 The results show that the capacitive energy storage was higher in EMIDCA/ACN electrolyte as compared in EMIBF4/ACN electrolyte due to smaller ion size of solvated DCA− anion (1.09 nm) than solvated BF4− anion (1.17 nm). The effect of cation species of ILs between EMI+ and TEA+ on the capacitive behavior was also evaluated and it was found that the latter cation was preferentially adsorbed in the pores of electrode materials. Computer simulation shows that the ion size of bare EMI+ cation was 0.77 nm (1.79 nm with a solvation shell) while bare TEA+ cation was 0.69 nm (1.31 nm with a solvation shell). Smaller size also means an increase in the population of ionic species adsorbed on both electrodes, leading to higher capacitance. It is expected that ILs-based ions carrying solvation shells are partially desolvated when they enter sub-nanometer pores under applied potential because of larger size of solvated ions than pore size of the carbon.46 Since the average size of micropores in CMFs are about 1.5 nm, both solvated DCA− and BF4− anions can access the micropores of the carbon with the former species can be accommodated in more amounts. In the case of EMI+ and TEA+ cations, it can be shown that only TEA+ cations are adsorbed into the micropores without any restriction while the bigger EMI+ cations are blocked or at least there is partially desolvation of the ions.
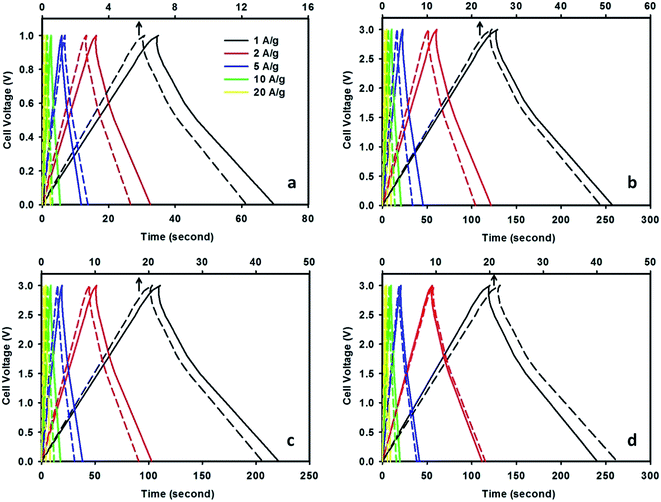
The galvanostatic charge–discharge curves measured at various current densities in a two-electrode system are depicted in Fig. 6. It can be seen that CMF-1073.15 supercapacitor exhibits longer discharging time compared with that of M-EMFs supercapacitor both at low and high current densities. The E–t response of the charge process shows almost the mirror image of their corresponding discharge counterparts with no obvious Ohmic drop. This suggests that CMF-1073.15 supercapacitor possesses a small ESR and its capacitance is not kinetically limited, which agreed well with the CV results. Obviously, the charge–discharge curves are shaped like an arc line, which is the representation of pseudocapacitance of CMFs materials (see ESI Fig. S2†). The occurrence of pseudocapacitance might be generated from the faradaic surface or near surface redox reactions and is associated with rich heteroatom surface groups. Table 4 lists the specific capacitance, energy density and power density of CMF-1073.15 supercapacitor with varying current densities. The specific capacitance of CMF-1073.15 supercapacitor calculated from charge–discharge at a current density of 1 A g−1 in TEABF4/ACN electrolyte is 171.8 F g−1, which is five times higher than that of M-EMFs supercapacitor (32.6 F g−1). Also, TEABF4/ACN electrolyte provides the highest specific capacitance among the electrolytes studied at the same current density. An increase in the current density leads to a larger voltage drop, causing a decrease in specific capacitance. It can be seen that the specific capacitance is preserved fairly well even at high current density, indicating good capacitance retention capability. The specific capacitance in TEABF4/ACN electrolyte reaches 130.6 F g−1 at 20 A g−1, which is 76% of the specific capacitance at 1 A g−1. Furthermore, supercapacitors with ILs/ACN mixtures as the electrolyte delivered energy density considerably higher (34–54 W h kg−1) compared to that measured in aqueous K2SO4 solution (3–5 W h kg−1). This clearly confirms that the cell voltage window plays a crucial role in boosting the energy density of supercapacitor. The power density of CMF-1073.15 supercapacitor in TEABF4/ACN electrolyte ranged between 0.84 and 15.8 kW kg−1. It is noteworthy to mention that at high current densities of 10 and 20 A g−1, the power densities of supercapacitor are 7.81 and 15.8 kW kg−1. These values are higher compared to those of commercial carbon supercapacitors (normally in the range of 7–8 kW kg−1).37 The power density and energy density of CMF-1073.15 supercapacitor are comparable to carbon nanofibers derived from microporous rigid polymer PIM-1 in 1,3-ethylmethylimidazolium bis(trifluoromethanesulfonyl)imide IL (Ed = 60 W h kg−1, Pd = 1.72 kW kg−1)20 and higher than that of N/P co-doped nonporous carbon nanofibers from PAN and phosphoric acid precursor solutions in 1 M H2SO4 (Ed = 7.81 W h kg−1, Pd = 0.03 kW kg−1),47 N/P co-doped glucose derived porous carbons in 6 M KOH (Ed = 4.08 W h kg−1)41 and N-doped carbon microfibers from silk cocoon in 6 M KOH (Ed = 7.47 W h kg−1).21 The specific capacitance of Maxsorb supercapacitor is 132.3 F g−1 at 1 A g−1 in 1.5 M TEABF4/ACN electrolyte. The lesser capacitance of Maxsorb supercapacitor compared to CMF-1073.15 supercapacitor might be due to steric effect in the adsorption of ions into narrow micropores. The obtained specific capacitance in this study is higher than that previously reported by Ruiz et al.,48 which is ∼120 F g−1 in 1 M TEABF4/ACN electrolyte. The energy density and power density of Maxsorb supercapacitor at 1 A g−1 are 42.3 W h kg−1 and 0.77 kW kg−1, respectively.
| Electrolytes | Specific capacitance (F g−1) | Specific energy density (W h kg−1) | Power density (kW kg−1) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 A g−1 | 2 A g−1 | 5 A g−1 | 10 A g−1 | 20 A g−1 | 1 A g−1 | 2 A g−1 | 5 A g−1 | 10 A g−1 | 20 A g−1 | ||||||
| K2SO4 | 139.6 | 130.3 | 117.8 | 108.4 | 99.2 | 4.8 | 4.5 | 4.1 | 3.8 | 3.4 | 0.25 | 0.50 | 1.25 | 2.52 | 4.94 |
| TEABF4/ACN | 171.8 | 162.3 | 151.7 | 139.2 | 130.6 | 53.7 | 50.7 | 47.4 | 43.5 | 40.8 | 0.84 | 1.78 | 3.92 | 7.81 | 15.8 |
| EMIBF4/ACN | 147.6 | 137.2 | 127.9 | 118.3 | 109.4 | 46.1 | 42.9 | 40.0 | 37.0 | 34.2 | 0.73 | 1.54 | 3.78 | 7.59 | 13.6 |
| EMIDCA/ACN | 160.4 | 148.7 | 138.3 | 131.2 | 120.5 | 50.1 | 46.5 | 43.2 | 41.0 | 37.7 | 0.78 | 1.65 | 3.84 | 7.67 | 14.3 |
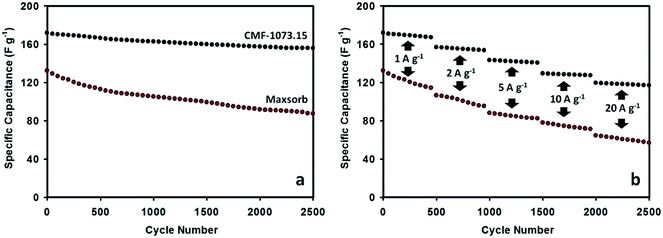
The long cycle life stability is one of desirable properties of supercapacitors for practical applications. The durability of Maxsorb and CMF-1073.15 supercapacitors was examined by consecutive galvanostatic charging–discharging. The variation of specific capacitance as a function of cycle number is given in Fig. 7. The cycling process was performed at current densities ranging from 1 to 20 A g−1. The CMF-1073.15 supercapacitor shows excellent cycling performance with no more than 10% loss in capacitance at the end of 2500 cycles. This demonstrates excellent rate capability which is a beneficial feature for supercapacitors exhibiting high energy density and power output. After continuously charging–discharging for 500 cycles at a current load of 1 A g−1, the specific capacitance stabilized at ∼167 F g−1. Furthermore, the specific capacitance was preserved high levels of ∼153, ∼140, ∼127 and ∼117 F g−1 during further cycling at current densities of 2, 5, 10 and 20 A g−1, respectively. The excellent cycling and electrochemical stability of CMF-1073.15 supercapacitor can be ascribed to the following aspects: (i) proper pore structure of the active electrode material which enhances the kinetics of ionic transport and storage and (ii) appreciable doping amounts of surface heteroatom groups which improve the electronic conductivity and wettability of electrode material in the electrolyte and thus increase the efficiency of ion transfer. The long-term stability may also be ascribed from phosphorus doping, which is able to suppress the generation of unstable and electrochemically active surface oxygen groups associated with capacitance decay during cycling such as quinone, hydroxyl or O-III species.37,47 Compared with Maxsorb supercapacitor, the long cycle life performance of CMF-1073.15 supercapacitor is robust and more electrochemically stable. In Fig. 7(b), it can be shown that after an initial discharge capacitance of 132.3 F g−1 at a current load of 1 A g−1, the Maxsorb supercapacitor experienced an important capacitance fading during cycling and the capacitance retention of 66% is attained after 2500 cycles. Although Maxsorb carbon has a very developed surface area (∼3000 m2 g−1) which is desirable to generate an ultrahigh specific capacitance, this carbon provides a large internal resistance for ion transport and storage due to disordered pore structure and very small micropore size, leading to a poorer cycling performance.
4. Conclusions
We demonstrated herein the synthesis of N/P/K co-doped porous CMFs from a low-cost and renewable precursor (cane molasses) by combining electrospinning with carbonization processes. The carbonization temperature was found to play a part in controlling porous structure of the carbon as well as the degree of heteroatoms doping and types of surface groups. The obtained CMFs materials exhibited hierarchical porous structure consisting of micropores (∼1.5 nm) and large-sized pores (∼10.2 nm in mesopores and ∼69.0 nm in macropores). The electrochemical performance of CMFs supercapacitors were tested by cyclic voltammetry, galvanostatic charge–discharge and cycling durability in 0.5 M K2SO4 and 1.5 M ILs/ACN electrolytes. The ILs/ACN mixtures were shown to be excellent electrolyte for CMFs supercapacitors, which could operate over a wide range of cell voltage window (0–3 V). This contributed to high specific energy density of 34.2–53.7 W h kg−1 at power density of 0.73–15.8 kW kg−1, which greatly surpassed those measured in 0.5 M K2SO4 aqueous electrolyte. In particular, CMF-1073.15 supercapacitor in 1.5 M TEABF4/ACN electrolyte gave the highest specific capacitance of 171.8 F g−1 at a current load of 1 A g−1, excellent rate performance and desirable cycling stability. Furthermore, the combination of electrospinning and carbonization techniques may present a new possibility to synthesis heteroatoms-doped porous carbon micro/nanofibers from renewable resources for energy storage applications.References
- G. Z. Chen, Prog. Nat. Sci., 2013, 23, 245–255 CrossRef PubMed.
- E. Frackowiak and F. Beguin, Carbon, 2001, 39, 937–950 CrossRef CAS.
- L. L. Zhang and X. S. Zhao, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- H. Yu, Q. Zhang, J. B. Joo, N. Li, G. D. Moon, S. Tao, L. Wang and Y. Yin, J. Mater. Chem. A, 2013, 1, 12198–12205 CAS.
- X. Wang, J. Lu, Y. Xie, G. Du, Q. Guo and S. Zhang, J. Phys. Chem. B, 2002, 106, 933–937 CrossRef CAS.
- N. Brun, C. A. Garcia-Gonzalez, I. Smirnova and M. M. Titirici, RSC Adv., 2013, 3, 17088–17096 RSC.
- Y. C. Zhao, L. Zhao, L. J. Mao and B. H. Han, J. Mater. Chem. A, 2013, 1, 9456–9461 CAS.
- J. Ding, H. Wang, Z. Li, A. Kohandehghan, K. Cui, Z. Xu, B. Zahiri, X. Tan, E. M. Lotfabad, B. C. Olsen and D. Mitlin, ACS Nano, 2013, 7, 11004–11015 CrossRef CAS PubMed.
- H. Guo and Q. Gao, Rare Met., 2011, 30, 35–37 CrossRef CAS.
- S. Zhang, L. Chen, S. Zhou, D. Zhao and L. Wu, Chem. Mater., 2010, 22, 3433–3440 CrossRef CAS.
- M. Teng, J. Qiao, F. Li and P. K. Bera, Carbon, 2012, 50, 2877–2886 CrossRef CAS PubMed.
- G. Wang, C. Pan, L. Wang, Q. Dong, C. Yu, Z. Zhao and J. Qiu, Electrochim. Acta, 2012, 69, 65–70 CrossRef CAS PubMed.
- P. Wang, D. Zhang, F. Ma, Y. Ou, Q. N. Chen, S. Xie and J. Li, Nanoscale, 2012, 4, 7199–7204 RSC.
- N. T. Xuyen, E. J. Ra, H. Z. Geng, K. K. Kim, K. H. An and Y. H. Lee, J. Phys. Chem. B, 2007, 111, 11350–11353 CrossRef CAS PubMed.
- H. Mi, X. Zhang, S. Yang, X. Ye and J. Luo, Mater. Chem. Phys., 2008, 112, 127–131 CrossRef CAS PubMed.
- K. H. Jung, W. Deng, D. W. Smith Jr and J. P. Ferraris, Electrochem. Commun., 2012, 23, 149–152 CrossRef CAS PubMed.
- C. W. Huang, Y. T. Wu, C. C. Hu and Y. Y. Li, J. Power Sources, 2007, 172, 460–467 CrossRef CAS PubMed.
- Y. Yang, A. Centrone, L. Chen, F. Simeon, T. A. Hatton and G. C. Rutledge, Carbon, 2011, 49, 3395–3403 CrossRef CAS PubMed.
- C. Ma, Y. Song, J. Shi, D. Zhang, X. Zhai, M. Zhong, Q. Guo and L. Liu, Carbon, 2013, 51, 290–300 CrossRef CAS PubMed.
- J. S. Bonso, G. D. Kalaw and J. P. Ferraris, J. Mater. Chem. A, 2014, 2, 418–424 CAS.
- Y. Liang, D. Wu and R. Fu, Sci. Rep., 2013, 3, 1119 Search PubMed.
- H. Olbrich, Institut fur Zuckerindustrie, Biotechnologie-Kempe GmbH, Berlin, 2006 Search PubMed.
- D. W. Wang, F. Li, Z. G. Chen, G. Q. Lu and H. M. Cheng, Chem. Mater., 2008, 20, 7195–7200 CrossRef CAS.
- D. Hulicova-Jurcakova, M. Kodama, S. Shiraishi, H. Hatori, Z. H. Zhu and G. Q. Lu, Adv. Funct. Mater., 2009, 19, 1800–1809 CrossRef CAS PubMed.
- X. R. Li, F. Y. Kong, J. Liu, T. M. Liang, J. J. Xu and H. Y. Chen, Adv. Funct. Mater., 2012, 22, 1981–1988 CrossRef CAS PubMed.
- Y. Xiao, S. Liu, F. Li, A. Zhang, J. Zhao, S. Fang and D. Jia, Adv. Funct. Mater., 2012, 22, 4052–4059 CrossRef CAS PubMed.
- P. C. Chen, G. Shen, Y. Shi, H. Chen and C. Zhou, ACS Nano, 2010, 4, 4403–4411 CrossRef CAS PubMed.
- Y. Xiao, A. Zhang, S. Liu, J. Zhao, S. Fang, D. Jia and F. Li, J. Power Sources, 2012, 219, 140–146 CrossRef CAS PubMed.
- Z. Lei, Z. Liu, H. Wang, X. Sun, L. Lu and X. S. Zhao, J. Mater. Chem. A, 2013, 1, 2313–2321 CAS.
- F. Xu, R. Cai, Q. Zeng, C. Zou, D. Wu, F. Li, X. Lu, Y. Liang and R. Fu, J. Mater. Chem., 2011, 21, 1970–1976 RSC.
- M. A. Pimenta, G. Dresselhaus, M. S. Dresselhaus, L. G. Cancado, A. Jorio and R. Saito, Phys. Chem. Chem. Phys., 2007, 9, 1276–1290 RSC.
- A. B. Fuertes and T. A. Centeno, J. Mater. Chem., 2005, 15, 1079–1083 RSC.
- S. Mitani, S. I. Lee, K. Saito, Y. Korai and I. Mochida, Electrochim. Acta, 2006, 51, 5487–5493 CrossRef CAS PubMed.
- P. K. Chu and L. Li, Mater. Chem. Phys., 2006, 96, 253–277 CrossRef CAS PubMed.
- C. L. Burket, R. Rajagopalan, A. P. Marencic, K. Dronvajjala and H. C. Foley, Carbon, 2006, 44, 2957–2963 CrossRef CAS PubMed.
- D. Hulicova-Jurcakova, M. Seredych, G. Q. Lu, N. K. A. C. Kodiweera, P. E. Stallworth, S. Greenbaum and T. J. Bandosz, Carbon, 2009, 47, 1576–1584 CrossRef CAS PubMed.
- L. F. Chen, X. D. Zhang, H. W. Liang, M. Kong, Q. F. Guan, P. Chen, Z. Y. Wu and S. H. Yu, ACS Nano, 2012, 6, 7092–7102 CrossRef CAS PubMed.
- J. R. Pels, F. Kapteijn, J. A. Moulijn, Q. Zhu and K. M. Thomas, Carbon, 1995, 33, 1641–1653 CrossRef CAS.
- S. Shrestha and W. E. Mustain, J. Electrochem. Soc., 2010, 157, B1665–B1672 CrossRef CAS PubMed.
- A. M. Puziy, O. I. Poddubnaya, R. P. Socha, J. Gurgul and M. Wisniewski, Carbon, 2008, 46, 2113–2123 CrossRef CAS PubMed.
- C. Wang, Y. Zhou, L. Sun, P. Wan, X. Zhang and J. Qiu, J. Power Sources, 2013, 239, 81–88 CrossRef CAS PubMed.
- J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, in Handbook of X-ray Photoelectron Spectroscopy, ed. J. Chastain, Perkin-Elmer Corp., Minnesota, 3 edn, 1992, pp. 66–67 Search PubMed.
- R. Lin, P. L. Taberna, J. Chmiola, D. Guay, Y. Gogotsi and P. Simon, J. Electrochem. Soc., 2009, 156, A7–A12 CrossRef CAS PubMed.
- T. Nishida, Y. Tashiro and M. Yamamoto, J. Fluorine Chem., 2003, 120, 135–141 CrossRef CAS.
- D. R. MacFarlane, J. Golding, S. Forsyth, M. Forsyth and G. B. Deacon, Chem. Commun., 2001, 1430–1431 Search PubMed.
- R. Lin, P. Huang, J. Segalini, C. Largeot, P. L. Taberna, J. Chmiola, Y. Gogotsi and P. Simon, Electrochim. Acta, 2009, 54, 7025–7032 CrossRef CAS PubMed.
- X. Yan, Y. Liu, X. Fan, X. Jia, Y. Yu and X. Yang, J. Power Sources, 2014, 248, 745–751 CrossRef CAS PubMed.
- V. Ruiz, T. Huynh, S. R. Sivakkumar and A. G. Pandolfo, RSC Adv., 2012, 2, 5591–5598 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra05243a |
| This journal is © The Royal Society of Chemistry 2014 |