Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Playing catch and release with single molecules: mechanistic insights into plasmon-controlled nanogaps†
Katrin F.
Domke
*ab and
Albert C.
Aragonès
 *cd
*cd
aUniversity of Duisburg-Essen, Faculty of Chemistry, Universitätsstr. 5, 45141 Essen, Germany
bMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: katrin.domke@uni-due.de
cDepartament de Ciència de Materials i Química Física, Universitat de Barcelona, Marti i Franquès 1, 08028, Barcelona, Spain
dInstitut de Química Teòrica i Computacional (IQTC), Universitat de Barcelona, Diagonal 645, 08028, Barcelona, Spain. E-mail: acortijos@ub.edu
First published on 16th November 2022
Abstract
Single-molecule (SM) detection is essential for investigating processes at the molecular level. Nanogap-based detection approaches have proven to be highly accurate SM capture and detection platforms in the last decade. Unfortunately, these approaches face several inherent drawbacks, such as short detection times and the effects of Brownian motion, that can hinder molecular capture. Nanogap-based SM detection approaches have been successfully coupled to optical-based setups to exploit nearfield-assisted trapping to overcome these drawbacks and thus improve SM capture and detection. Here we present the first mechanistic study of nearfield effects on SM capture and release in nanogaps, using unsupervised machine learning methods based on hidden Markov models. We show that the nearfield strength can manipulate the kinetics of the SM capture and release processes. With increasing field strength, the rate constant of the capture kinetics increase while the release kinetics decrease, favouring the former over the latter. As a result, the SM capture state is more likely and more stable than the release state above a specific threshold nearfild strength. We have also estimated the decrease in the capture free-energy profile and the increase in the release profiles to be around 5 kJ mol−1 for the laser powers employed, ranging from laser-OFF conditions to 11 mW μm−2. We envisage that our findings can be combined with the electrocatalytic capabilities of the (nearfield) nanogap to develop next-generation molecular nanoreactors. This approach will open the door to highly efficient SM catalysis with precise extended monitoring timescales facilitated through the longer residence times of the reactant trapped inside the nanogap.
Introduction
Single-molecule (SM) detection is fundamental for investigating individual molecules as well as physical, chemical and biological processes at the molecular level and is therefore one of the most sought-after research objectives in molecular analysis.1 Besides, SM detection is extremely appropriate for studying systems where analyte species are found in small sample volumes and/or at extremely low concentrations.2 Nanogaps are undoubtably the most suitable analytical dimensions for SM detection since they are tiny geometric spaces equivalent to the size of the analyte molecule to be studied.2,3 They can provide SM sensitivity with a minimised ensemble effect common in micro and macroscopic measurements.2,4 Efficient SM detection is based on the precise control of the trapping and release of target species in the nanogap, which is, however, a challenging task because of the prevailing lack of a full understanding of the mechanistic details of SM trapping.2Reliable SM tools based on nanogaps have been developed during the last two decades5 for high-precision SM trapping and detection to characterise individual molecules, enabling molecular recognition6 and sensing.7 Among them, electrically based detection tools8 are most appealing ones. Electrical current readouts render these approaches label-free, since they rely on molecular electrical capture and release between the individual molecule and the nanogap.9–14 One of the most versatile electrical approaches to trap and study individual molecules is the one based on fixed and motionless interelectrode nanogaps of precise sub-nanometric dimensions.10,11,13–15
Electrical SM detection approaches are facing different inherent problems,8 because working at room temperature (RT) and under ambient conditions make the localisation of the individual molecules in the reduced geometric space an entropically unfavoured process. On the one hand, the SM release to the nanogap is a thermally activated stochastic processes16 with significantly reduced lifetimes at RT conditions, commonly ranging between tens and hundreds of milliseconds and thus resulting in very limited time resolution in current readouts. On the other hand, the Brownian motion of the target molecules when they are dissolved in a liquid environment is of remarkable relevance since this motion governs the diffusion pathway of an analyte molecule into the interelectrode nanogap region to be detected. Consequently, the detection rate is mainly governed by Brownian motion unless a potential energy larger than the thermal energy is provided to the system.17,18 Different platforms have been employed to overcome the above-mentioned inherent problems to the SM detection approaches, such as electrokinetic19,20 and optical traps.18,21
Nearfield traps22 are plasmon-supported platforms that can secure individual objects of a size much smaller than the interacting wavelength (Rayleigh regime), such as molecules, inside a nanogap by way of optical trapping. Nanogaps based on metallic nanostructures provide excited localised surface plasmons when irradiated with laser photons of a resonant wavelength23 and behave as nano-antennas. The resulting electromagnetic field is confined to a nanometre-sized region (hotspot), resulting in a (near)field strength increase of up to three orders of magnitude compared to the laser excitation (far)field.23,23,24 As such, the nearfield gradient exerts amplified attractive forces inside the nanogap and directs molecules into the hotspot.17,24,25 Electrical SM detection platforms are based on interelectrode metallic nanogaps and have proven to be excellently suited26 for adopting nearfield trapping to improve the capture and detection of individual molecules.18,21,27 Various aspects have been revealed, such as a drastic increase in capturing lifetimes,21,27 the improvement of detection probability18,21,27,28 and the modulation of the ratio of molecules that are trapped and released in solution by overcoming Brownian motion.18
Here, we present the first mechanistic study of the use of plasmon-assisted nearfield trapping to manipulate a complete SM trapping process including molecular capture and release in a controlled nanogap. The presented study is based on an unsupervised machine learning methodology to extract lifetimes of both, SM capture and release states from the I(t) readouts. The incorporation of SM release current signatures in the analysis procedure represents a novelty in the field of electrical SM detection. It enables unbiased data processing and explores the complete junction formation and release mechanism beyond the conventional focus on SM capture current signatures only.29–32
We have found that the nearfield optomechanical effects alter the kinetics of both, the SM capture and release process as well as the free-energy capture and release profiles. On the one hand, the presence of the nearfield increases the rate constant of the capture while it decreases the one of the release process exponentially with the nearfield strength. In other words, the nearfield can be employed to govern the kinetics of both processes, turning the capture kinetics more favourable than the release kinetics, i.e. making the SM capture state more likely, and hence more stable, than the release state, above a threshold nearfield strength. On the other hand, we have quantified the decrease of the capture free-energy profile and increase of the release profile. The profiles display a difference of ca. 5 kJ mol−1 between the laser-OFF and the maximum employed laser power of 11 mW μm−2 conditions. The modulation of the free-energy profiles combined with the studied kinetics variation well explains the observed I(t) behaviour as defined by SM capture states dominating the electric current readouts at the employed medium to high laser powers.
Results and discussion
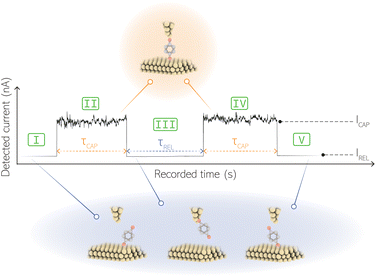
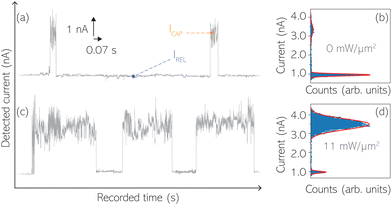
For the presented research we have employed the plasmon-supported break-junction (PBJ) technique (see details in ESI S1.1†).21 This technique allows SM detection through electric current measurements in the presence of a nearfield gradient that can be tuned by the applied laser power density. Since PBJ is an I(t) monitoring method, it allows a time-dependent electrical characterisation with high temporal resolution. PBJ is a particular variant of the break-junction (BJ) technique based on scanning tunnelling microscopy (STM),9 and it is based on an I(t) approach called blinking (see details in ESI S1.2†).13,33 PBJ takes advantage of the subnanometer-precise, controllable interelectrode distance of the STM that can be adapted to the molecular size. The capture and release states of individual molecules are detected in the I(t) captures as a telegraphic signal that oscillate between two levels.6,13,14,29,30,32,34 One level is related to the low-current regime (Fig. 1, scenarios I, III and V) when the molecule releases from one or both electrodes (tip and substrate) and hence only background (tunnelling) current is detected (IREL). The other level is related to the high-current regime (Fig. 1, panels II and IV) when the molecule is captured between both electrodes (ICAP). The (stochastic) capture of the molecule causes the sudden increase in the detected current (Fig. 1, scenario I to II) from IREL to ICAP. Upon release, i.e. the stochastic release, of the molecule, the current returns from ICAP to IREL level (Fig. 1, panels II to III and IV to V). The duration of a SM capture stage has a characteristic lifetime or dwell-time (τCAP). The duration of the release stage, i.e. the time between two consecutive SM capture current signatures, is defined by the release dwell-time (τREL). We have employed 1,4-benzenedithiol (BDT) as target molecule (see sample preparation details in ESI S1.3†). Current detection focused on the BDT characteristic conductance of 1 × 10−2 G0, related to a bridge contact geometry,35,36 that for our setup and experimental conditions equals to a current signature of 2.3 nA. The detected current signature of the BDT is not affected by the laser illumination. This is because there is a mismatch between the energy distribution of the Au hot carriers (holes),37 created due to the presence of the nearfield,38 and the HOMO level of the BDT. This mismatch prevents a hot-carrier contribution to the detectable current.37,39 The mismatch is significant, with the HOMO level being approximately 1.2 eV away from the Fermi level of the Au electrodes,37,40 while the applied (small) bias voltage is only 3 mV.Time-dependent electrical characterisation was performed with a sampling rate of 10 kHz to monitor the SM capture and release current signatures of individual BDT molecules in the nanogap. Representative I(t) readouts are presented in Fig. 2a and c. They show how the SM capture and release states are clearly affected by the presence of the nearfield. Their characteristic τCAP and τREL dwell-times are modified by the laser illumination conditions, namely enlarged and shortened, respectively with increasing laser power. The τCAP enlargement dependence on the nearfield strength is in agreement with our recently reported works,21,27 where the SM release is stabilised by increasing nearfield gradients, which leads to an increase of the SM detection timescale. We have built 1D histograms for the entire I(t) datapoint readouts under laser-OFF and under laser illumination conditions of 11 mW μm−2 (see power laser density calculations from (far)field laser power in ESI S2†) that are shown in Fig. 2b and d, respectively. Under laser-OFF conditions, the prominent peak corresponds to the τREL population, and contrarily, in the presence of the nearfield (laser-ON conditions), the peak corresponding to the τCAP population is the prominent one. The integrated peak area ratio (τCAP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τREL) for laser-OFF conditions is 1
τREL) for laser-OFF conditions is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17, and under illumination conditions of 11 mW μm−2 is 4
17, and under illumination conditions of 11 mW μm−2 is 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It attests a clear population inversion between τCAP and τREL peaks for the two laser conditions.
1. It attests a clear population inversion between τCAP and τREL peaks for the two laser conditions.
Clustering and statistics of capture and release states
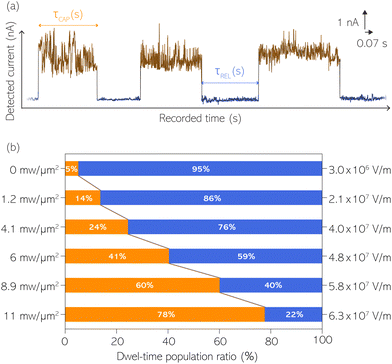
With the aim to perform a quantitative analysis of the τCAP and τREL dependence on the nearfield gradients, we have monitored I(t) readouts at four different laser power densities of 1.2, 4.1, 6.0 and 8.9 mW μm−2, in addition to the maximum power of 11 mW μm−2 and laser-OFF conditions. To perform a complete analysis of a whole cycle of SM junction formation and disruption (i.e. SM capture and release pair), it was necessary to include also the τrmREL extracted from the SM release current signatures besides the τCAP extracted from the SM capture signatures. This analysis procedure goes beyond the common practise in molecular electronics and SM detection studies in which the focus lies solely on the capture current signatures of the molecule in the nanogap (τCAP).13,15,29,30,32,34 To carry out the analysis of the telegraphic signal in an unbiased way and hence exclude any (biased) manual data inspection, we have developed an automatised states finder based on the hidden Markov model (HMM) formalism.41 Our tool is an unsupervised machine learning framework for time-series analysis based on a continuous-time algorithm that maximizes the likelihood of a sequence of intervals.42 Accordingly, this framework identifies and clusters (classifies)43 the different current levels detected in the I(t) readout (see ESI S3.1† for a detailed description). Our states finder tool is based on two HMM states attributed to the SM capture and release discrete states in time, to identify and cluster the ICAP and IREL levels (see Fig. 3a and ESI S3.2†). This approach results in an efficient clustering (see ESI S3.3†). Facilitated by the HMM clustering, the total τCAP and τREL can be extracted by classifying all datapoints of the I(t) readout datasets for each investigated laser power density. In this way, we explore the ratios between the populations of the two states (Fig. 3b) and assess potential correlations of the respective populations with the nearfield strength.From Fig. 3b we can easily note that with increasing laser power density, the τCAP relative population increases and the τREL population decreases (field gradient strength equivalences in Fig. 3b and details in ESI S2†). τCAP rises from an initial mean dwell-time population of 5% under laser-OFF conditions to 78% for the maximum power conditions of 11 mW μm−2. On the other hand, the τREL population shows a negative correlation with the nearfield strength and drops from an initial relative value of 95% down to 22% as the laser power grows. These opposite trends of the dwell-time populations with respect to the laser power are in line with the observations denoted in Fig. 2. Thanks to this complete population-based analysis, we can now define the transition laser-condition from the least likely to the most likely state and vice versa. For our experimental conditions, the transition point lies in the range between 6.0 and 8.9 mW μm−2 where τCAP (τREL) reaches values above (below) 50% of the total population. Below these laser power densities, the release state dominates the I(t) readout of the nanogap while at stronger nearfield strengths, the capture state is the more probable one.
Studying the dwell times and modelling the SM kinetics under nearfield conditions
SM capture and release processes in nanogaps can be understood as chemical reactions of different types involving bond formation and bond breaking (commonly desorption), respectively,31,44,45 each with their own kinetics.31 As we have seen, the nearfield clearly affects the populations of both SM capture and release states, which implies variations in their kinetics as a function of nearfield strength.46,47 From the distribution of τCAP and τREL values, clustered from the SM capture and release states in the I(t) readouts, the hidden kinetic properties of both states can be revealed.47–49Exponential probability distribution functions,50 characteristic for Markovian processes,51 have been vastly employed in SM kinetic studies of molecular stochastic detection6,52,53 and they have been well described for I(t) approaches.48,49 For the research presented here, we have considered single-exponential distributions since we presume a single rate-limiting process for the SM capture and release processes because of two complementary reasons: on the one hand, the molecule|electrode contact interface is equivalent for both contact points (molecule–tip electrode and molecule–substrate electrode) since both electrodes are made of the same material and the molecule is symmetric. On the other hand, all the accumulated current signatures correspond to a bridge contact geometry,35,36 thus themolecule|electrode interfaces of all studied junctions are equivalent. A well-established methodology for analysing the distribution of dwell-times is based on a semilog representation.50,54 In it, the probability of occurrence or frequency (Y-axis) of each discrete state (here 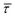 , X-axis) is plotted by adding to its own frequency the sum of the corresponding frequencies of all previous states and normalised by the total accumulated frequency.55 Using the semilog cumulative frequency distribution (Fig. 4a and b), we extract a mean dwell-time value
, X-axis) is plotted by adding to its own frequency the sum of the corresponding frequencies of all previous states and normalised by the total accumulated frequency.55 Using the semilog cumulative frequency distribution (Fig. 4a and b), we extract a mean dwell-time value 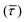 for each SM capture
for each SM capture 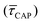 and release
and release 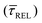 state by fitting a single-exponential distribution as a function of τ,49 in the form of a sigmoidal, according to
state by fitting a single-exponential distribution as a function of τ,49 in the form of a sigmoidal, according to
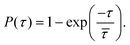 | (1) |
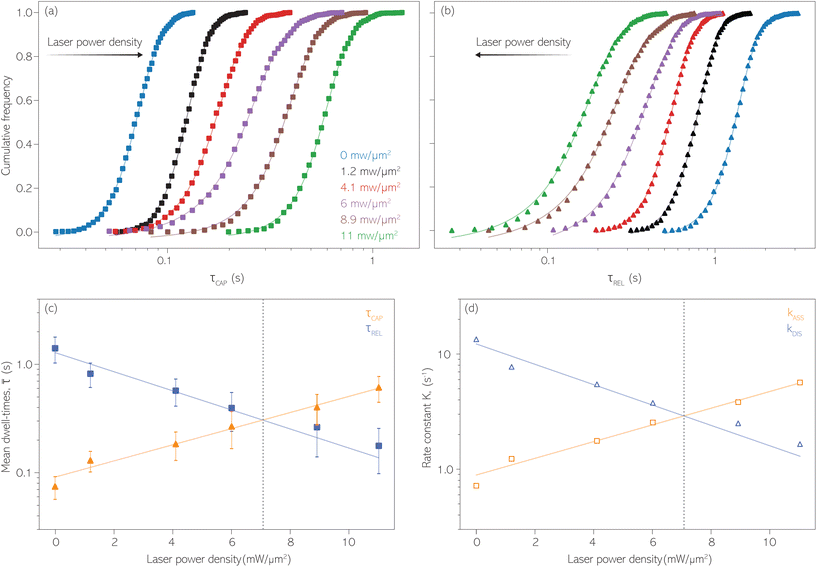 | ||
Fig. 4 1D semilog cumulative distribution plots for SM capture “τCAP” (squares) and release “τREL” (triangles) state dwell-times (a and b, respectively) for each laser power density (indicated in figure). Solid lines are the fits based on eqn (1). (c)  (triangle) and (triangle) and  (squares) values as a function of employed laser power density. (d) Quantitative kinetic description of KDIS (empty triangles) and KASS (empty squares) values as a function of laser power density. Solid lines in c and d are fits with the exponential function y = a (squares) values as a function of employed laser power density. (d) Quantitative kinetic description of KDIS (empty triangles) and KASS (empty squares) values as a function of laser power density. Solid lines in c and d are fits with the exponential function y = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−c·x). Error bars in (c) indicate the standard deviation of the dataset for each laser power density. Vertical dashed lines in (c) and (d) indicate the transitions where exp(−c·x). Error bars in (c) indicate the standard deviation of the dataset for each laser power density. Vertical dashed lines in (c) and (d) indicate the transitions where  becomes larger than becomes larger than 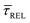 and KASS larger than KDIS, respectively. and KASS larger than KDIS, respectively. | ||
The cumulative frequency distribution is an intuitive form of representation as the shift between sigmoidal fits is a visual analogy to the trend for the extracted 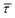 values.
values.
Fig. 4 shows the 1D semilog cumulative distribution plots for τCAP (Fig. 4a) and τREL (Fig. 4b) for each investigated laser power density. The fits of 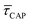 and
and 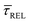 show opposite trends. The
show opposite trends. The 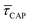 variation is correlated with the increasing laser power density (from left to right) while, contrarily,
variation is correlated with the increasing laser power density (from left to right) while, contrarily, 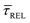 is anticorrelated (from right to left). The extracted values of
is anticorrelated (from right to left). The extracted values of 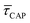 range from 7.5 × 10−2 ± 1.8 × 10−2 s to 6.1 × 10−1 ± 1.6 × 10−1 s. The ones for
range from 7.5 × 10−2 ± 1.8 × 10−2 s to 6.1 × 10−1 ± 1.6 × 10−1 s. The ones for 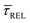 range from 1.4 ± 3.8 × 10−1 s to 1.8 × 10−1 ± 7.9 × 10−2 s. Over the range of employed laser power densities, the values thus increase by a factor 8.2
range from 1.4 ± 3.8 × 10−1 s to 1.8 × 10−1 ± 7.9 × 10−2 s. Over the range of employed laser power densities, the values thus increase by a factor 8.2 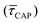 and decrease by a factor of 7.9
and decrease by a factor of 7.9 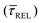 between 11 mW μm−2 and laser-OFF conditions. The
between 11 mW μm−2 and laser-OFF conditions. The 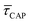 and
and 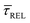 values plotted against the laser power density (Fig. 4c) show a positive exponential dependence for
values plotted against the laser power density (Fig. 4c) show a positive exponential dependence for 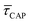 and a negative one for
and a negative one for 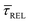 . The plot reveals that the nearfield effects shorten the release states, besides promoting the capture states. The mechanics of SM trapping by means of a plasmonic nearfield thus turns out to be more complex than revealed by previous studies concentrating on the elongation of the SM trapping lifetimes (τCAP).21,27
. The plot reveals that the nearfield effects shorten the release states, besides promoting the capture states. The mechanics of SM trapping by means of a plasmonic nearfield thus turns out to be more complex than revealed by previous studies concentrating on the elongation of the SM trapping lifetimes (τCAP).21,27
Since the rate constant (K) equals the reciprocal of 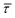 ,56 we can deduce the SM dissociation and association kinetics to the nanogap (
,56 we can deduce the SM dissociation and association kinetics to the nanogap (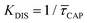 and
and 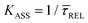 , respectively47,49,56) at the temperature at which the experiment was performed (RT). Despite the use of low and medium power (far-field) intensities, the photothermal effects (optical heating)57–59 of exposure of the BDT molecule to laser illumination and the possible repercussions over its capture/release kinetics should be discussed here. As a very recent study revealed,59 the expected local temperature increase is estimated to be below 3 K for the nearfield in a nanogap of Au-tip|Au-surface configurations in aqueous media using a tip radius of 25 nm, and under the same laser power densities here employed, even considering a field magnification of the order of 50, almost twice that of ours. This temperature increase is insufficient to promote Au–S desorption,60 Au–Au fracture,61or thiol–Au bond instabilities that have been estimated to be significant from a temperature increase of 30 K.62 Accordingly, the expected small (local) thermal increase will not affect the stability of the junction.21,27,63 Decomposition of BDT molecules, as attested by previous tip-enhanced Raman spectroscopy experiments,21 is also not feasible assuming the aforementioned temperature increase under the exerted nearfield under our conditions. Considering this and the fact that unstabilising effects should lead to a decrease τCAP of and an increase of τREL – contrary to the effect observed here under increasing laser power densities – we can rule out any thermal effect on the studied kinetics.
, respectively47,49,56) at the temperature at which the experiment was performed (RT). Despite the use of low and medium power (far-field) intensities, the photothermal effects (optical heating)57–59 of exposure of the BDT molecule to laser illumination and the possible repercussions over its capture/release kinetics should be discussed here. As a very recent study revealed,59 the expected local temperature increase is estimated to be below 3 K for the nearfield in a nanogap of Au-tip|Au-surface configurations in aqueous media using a tip radius of 25 nm, and under the same laser power densities here employed, even considering a field magnification of the order of 50, almost twice that of ours. This temperature increase is insufficient to promote Au–S desorption,60 Au–Au fracture,61or thiol–Au bond instabilities that have been estimated to be significant from a temperature increase of 30 K.62 Accordingly, the expected small (local) thermal increase will not affect the stability of the junction.21,27,63 Decomposition of BDT molecules, as attested by previous tip-enhanced Raman spectroscopy experiments,21 is also not feasible assuming the aforementioned temperature increase under the exerted nearfield under our conditions. Considering this and the fact that unstabilising effects should lead to a decrease τCAP of and an increase of τREL – contrary to the effect observed here under increasing laser power densities – we can rule out any thermal effect on the studied kinetics.
In Fig. 4d, we have plotted the deduced KASS and KDIS values as a function of laser power density. The KASS and KDIS values under laser-OFF conditions can be considered as the intrinsic kinetics governed by the SM in absence of an additional nearfield trapping force (K0). KASS increases exponentially with increasing nearfield gradient (i.e., shorter τREL values) from 0.71 s−1 under laser-OFF conditions to 5.6 s−1 under the maximum laser power density condition of 11 mW μm−2. In contrast, KDIS undergoes an exponential decrease (i.e., longer τCAP values), ranging from 13 s−1 under laser-OFF conditions to 1.6 s−1 under the maximum laser power density condition. These findings confirm that the nearfield governs both, the SM capture and the release kinetics. As explained above, nearfield effects on τCAP and τREL are noticeable in the I(t) readouts from laser power densities larger than 8.9 mW μm−2. In the range between 6.0 and 8.9 mW μm−2, the τCAP state becomes the majority population. From Fig. 4c and d, we can extract the transition point to a laser power density of ca. 7.1 mW μm−2, as indicated by the vertical dashed line, where 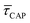 becomes larger than
becomes larger than 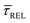 because the SM capture kinetics become more favourable than the release kinetics (KASS > KDIS). Given the opposite exponential behaviour of SM capture and release kinetics with increasing laser power densities, and the known reciprocity between
because the SM capture kinetics become more favourable than the release kinetics (KASS > KDIS). Given the opposite exponential behaviour of SM capture and release kinetics with increasing laser power densities, and the known reciprocity between 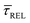 and
and 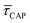 ,45,64,65 we conjecture that the two processes should not be independent of each other, and that an increase in one implies the decrease in the other – we will return to this point later–.
,45,64,65 we conjecture that the two processes should not be independent of each other, and that an increase in one implies the decrease in the other – we will return to this point later–.
We attribute a first-order reaction rate to the deduced SM capture (KASS) and release kinetics (KDIS) because of the exponential dependence between SM capture and release states (N) with τ (ref. 31) as attested by the single-exponential distribution displayed in Fig. 4a and b. Thus, the corresponding rate equation is N ∝ exp(−Kt), where t is time. Interestingly, this expression can be associated with changes in N due to the nearfield gradient, because the latter alters K as we observed. The association between N and the nearfield gradient tuned by the laser power density has already been noted in previous works.18,21
Modelling the SM thermodynamics under nearfield conditions
To date, two complementary effects have been associated with the presence of nearfields as an enhancement for SM capture and detection. On the one hand, there is the nearfield gradient attractive force that induces translational mass transport toward the center of the hotspot.17,24,25,66 This phenomenon has been attested by the observation of an increased probability of SM capture.18,28On the other hand, the nearfield gradient acts on the molecule trapped inside the nanogap and causes an angular motion of the molecule.66–68 Due to the exerted torque on the molecular dipoles,68 in a way that the molecular orientation is aligned along the field vector perpendicular to the nanogap axis, thus stabilising the SM junction optomechanically. In an earlier work, it was shown that there is an increase in the molecule–nanogap dissociation barrier “EB” (molecule–electrode binding energy in the thermodynamic model) as a consequence of this nearfield stabilisation that results in the prolongation of the SM capture timescales.21
To figure out the main effect that governs our observables, we validate both effects independently. The mass transport promoted by nearfield gradient attraction may be understood as an increase of the local molecule concentration in the vicinity of the nanogap. In order to assess this affect in more detail, we take previous works also based on stochastic SM detection47,56,69 and optical trapping70 as a reference, where changes in capture and release kinetics have been studied as a function of the target molecule concentration. In these works, the authors found a positive linear correlation of KASS with the target molecule concentration, and, interestingly, a lack of correlation for KDIS and the molecule concentration. Given the mismatch between the previously described kinetic vs. concentration response and our findings, here we can discard a nearfield-induced mass transport as the main parameter determining KASS and KDIS. This result is somewhat expected because of the absence of Brownian motion of the target BDT molecules since they are ex situ attached (see ESI S1.3†) rather than free objects in solution. As such, it is sensible to assume that the EB variation is the main parameter that modulates the kinetics of the SM capture and release processes.
According to the reasoned above, we can describe the exponential increase of 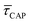 –
– 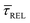 case is reasoned below – with help of the effects of EB according to the bond-breaking thermodynamic theory,
case is reasoned below – with help of the effects of EB according to the bond-breaking thermodynamic theory,
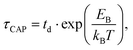 | (2) |
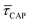 for each laser power density (Fig. 4c, orange traces). Given the aforementioned reciprocity between
for each laser power density (Fig. 4c, orange traces). Given the aforementioned reciprocity between 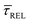 and
and 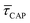 , it is plausible to consider that
, it is plausible to consider that 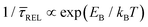 .45 In this way, the opposite behaviour of
.45 In this way, the opposite behaviour of 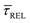 with respect to
with respect to 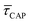 that shows an anticorrelation to the nearfield gradient (Fig. 4c, blue traces) is explained. From the laser power densities employed here, the energy gain provided by the nearfield gradient to EB can be calculated as previously described (details in ESI S2†).21,27 The increase in EB in the employed laser power range ranges from 0.80kBT nm−1 for the minimum laser power (1.1 mW μm−2) to 2.2kBT nm−1 for the maximum laser power (11 mW μm−2). Thus, according to eqn (2), an exponential increase of τCAP between a factor of 2 and 8 can be estimated between the minimum and maximum laser power density, respectively, compared to the 0 mW μm−2 case (laser-OFF conditions). Analogously, and following the mentioned reciprocity, the exponential decrease of τREL can be estimated to lie between a factor 1/2 and 1/8. Despite the approximations in the field enhancement, the estimated exponential increase (τCAP) and decrease (τREL) factors agree very well with those observed experimentally, as discussed above.
that shows an anticorrelation to the nearfield gradient (Fig. 4c, blue traces) is explained. From the laser power densities employed here, the energy gain provided by the nearfield gradient to EB can be calculated as previously described (details in ESI S2†).21,27 The increase in EB in the employed laser power range ranges from 0.80kBT nm−1 for the minimum laser power (1.1 mW μm−2) to 2.2kBT nm−1 for the maximum laser power (11 mW μm−2). Thus, according to eqn (2), an exponential increase of τCAP between a factor of 2 and 8 can be estimated between the minimum and maximum laser power density, respectively, compared to the 0 mW μm−2 case (laser-OFF conditions). Analogously, and following the mentioned reciprocity, the exponential decrease of τREL can be estimated to lie between a factor 1/2 and 1/8. Despite the approximations in the field enhancement, the estimated exponential increase (τCAP) and decrease (τREL) factors agree very well with those observed experimentally, as discussed above.
The optomechanical stabilisation effects of the nearfield gradient through an increase in EB have been validated to be the main parameter affecting 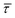 and the associated kinetics. Given the relation between EB of the molecule–nanogap bond and the capture and release processes of the molecule,45,72 it seems fair to assume that the respective associated release free-energy (ΔGREL) and capture free-energy (ΔGrmCAP) barriers are also affected by the nearfield gradient.
and the associated kinetics. Given the relation between EB of the molecule–nanogap bond and the capture and release processes of the molecule,45,72 it seems fair to assume that the respective associated release free-energy (ΔGREL) and capture free-energy (ΔGrmCAP) barriers are also affected by the nearfield gradient.
Interestingly, previous SM studies have demonstrated experimentally65,73 that the presence of strong electric fields facilitates SM trapping in nanogaps, reporting a ΔGCAP exponential decrease and a ΔGREL increase correlated with the electric field strength. As theory predicts,74 electric fields are capable of modifying the ΔG profiles of a trapping nanogap. Here, making use of the Eyring–Polanyi equation,75
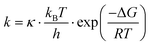 | (3) |
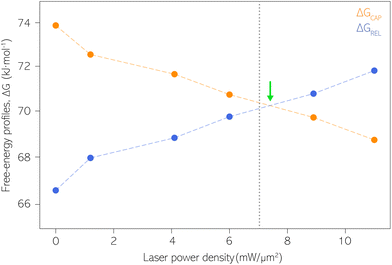 | ||
| Fig. 5 Capture and release barriers, ΔGREL and ΔGCAP, respectively, as a function of the laser power density. The dashed lines are a guide to the eye. Vertical dashed line at 7.1 mW μm−2 indicates the transition where KASS becomes larger than KDIS according to Fig. 4. Green arrow indicates the intersection point between ΔGREL and ΔGCAP trends. | ||
Our estimates of ΔGCAP and ΔGREL have been extracted from the kinetic parameters KASS and KDIS. Both ΔG parameters could be influenced by different factors present at the molecule|electrode interface, beyond the one molecule–nanogap bond. Multiple surface effects due to optical irradiation have been reported that could influence the ΔG profile. They are the thermal atomic expansion of the electrode,80 that can result in a size variation of the nanogap on the sub-Å scale,81 and the creation of picocavities at RT.82 The effects of the nearfield over the Au electrodes’ surface on our experiment is essentially avoided since the laser irradiation is activated prior to definition and stabilization of the interelectrode nanogap. The laser power density condition is then maintained throughout the respective experiment (see details about PBJ methodology in ESI S1.1†). Thus, if at all, thermal nanogap shrinkage would occur before the SM detection experiment and be counterbalanced by the STM I(t) feedback. Furthermore, using MilliQ water as working medium displays excellent heat dissipation, which contributes to the minimization of thermal electrode expansion. Note that, by employing PBJ, the atomic rearrangement or any other surface dynamics of the Au atoms would be detectable as fluctuations in the I(t) readouts12 and should be particularly evident in the longer τCAP states. Since we do not observe any significant dependence of the magnitude of the fluctuations on the laser power density, we can again exclude motion-related effects.
As we previously stated, SM capture and release processes must be coupled since they are mutually dependent, which is in line with the assumption that they can be considered parts of a single metastable state.64 Interestingly, the same metastable treatment is given to the bond-formation and -breaking processes, which govern the SM capture and release respectively, in the bond-breaking thermodynamic theory for SM junctions,45 where both processes are understood as counterparts of a dynamical state. Accordingly, we speculate that the nearfield gradient (correlated with the laser power density) alters the equilibrium of the dynamic “KASS ⇄ KDIS” state by displacing it toward SM capture. As the laser power density increases (higher EB), the formation of the molecule–electrode bond is promoted, ΔGCAP decreases and the molecule has a higher probability of being captured (KASS increases) while in the counterpart of the equilibrium displacement, ΔGREL increases and the probability of molecule release diminishes (KDIS decreases). This idea justifies the mismatch between the observed changes of KASS and KDIS under increasing laser power densities in our work and those due to increasing concentrations in earlier studies.47,56,69,70 In these studies, as explained before, the release process is independent of the concentration change and shows no correlation with the trapping process. We, on the other hand, have observed a negative correlation between KASS and KDIS with increasing laser power densities. We can relate this fact to the displacement between the capture and release equilibrium. The anticorrelation between KASS and KDIS under growing laser power densities, and their followed behaviour different from the reported by changing the captured molecule's concentration, lead us to think that the kinetic parameters deduced from the I(t) readouts encompass primarily the SM capture and release processes, and disregard the involvement of surface and/or molecular transport,18,28,60,82 processes out of the equilibrium.
Conclusions
In summary, thanks to the PBJ technique we have studied mechanistically, for the first time, the manipulation effects of the over the SM capture and release processes in plasmonic nanogaps. The nearfield gradient's optomechanical stabilisation complementary to the extending SM capture lifetimes, also shortens the release times of the trapped individual molecule with the interelectrode nanogap. The induced changes in the timescales for SM capture and release processes are close to an order of magnitude for the employed laser mid-power range. The stabilisation effect is due to the fact that the nearfield alters the capture and release mechanism by changing its kinetics, increasing the capture rate from a KASS of 7.1 × 10−1 s−1 to 5.6 s−1, and decreasing the release rate from a KDIS of 13 s−1 down up to a 1.6 s−1 in the employed laser range, i.e., the capture kinetics becomes more favourable than the release kinetics. Under laser-OFF conditions and low laser power densities, the release state is the most likely, but above the transition point, found at a power laser density of ca. 7.1 mW μm−2, the capture state dominates over the release. We associate the described kinetics variation with the increase of EB, which is dependent on the growth of the nearfield gradient. We have also estimated how the ΔG profiles of the capture and release mechanisms vary, decreasing the former and increasing the latter by about 5 kJ mol−1 for both, thus facilitating the SM capture inside the nanogap. The mechanisms of the SM capture and release processes are clearly tuned by the nearfield gradient. Likewise, they also prove to be coupled and dependent to each other, as their changes in kinetics and thermodynamics show a clear anti-correlation between them, since they can be considered counterparts of the metastable state of the molecule in the junction.As we have reported in previous works, electrocatalysis at SM level is possible in interelectrode nanogaps under exerted strong electric fields applied via accessible voltages by an STM.13,33 By combining the nanogap's electrocatalytic capability with the nearfield capacity to affect the molecule's capture and release mechanism, different applications can be envisaged. On the one hand, the enhanced capture process will improve the efficiency of the SM catalysis, by stabilising the reactant molecules inside the nanogap for extended residence timescales. On the other hand, the enlarged monitoring timescales (i.e. higher temporal resolution), yield by the promoted longer capture lifetimes, will allow obtaining hidden insights into catalysed SM reactions. This fact is especially relevant for slow kinetic SM processes that have longer timescales than the common (non-plasmonic) electrical SM detection times.
Author contributions
K. F. D. acquired funding, contributed to conceptualisation, and performed writing, reviewing and editing. A. C. A. acquired funding, performed writing of the original draft, contributed to conceptualisation, developed the software and data analyses, and performed reviewing and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
All authors would like to thank Prof. Dr Elke Scheer for fruitful discussions about thermal expansion due to laser focusing and enhanced fields in metallic nanogaps. K. F. D. is grateful for generous funding through the Plus 3 program of the Boehringer Ingelheim Foundation. A. C. A. thanks to the support of a fellowship (code LCF/BQ/PI22/11910017) from “la Caixa” Foundation (ID 100010434) and from the Max Planck Society. Open Access funding provided by the Max Planck Society.References
- Y. Li, C. Yang and X. Guo, Acc. Chem. Res., 2020, 53, 159–169 CrossRef CAS.
- J. J. Gooding and K. Gaus, Angew. Chem., Int. Ed., 2016, 55, 11354–11366 CrossRef CAS.
- L. Xue, H. Yamazaki, R. Ren, M. Wanunu, A. P. Ivanov and J. B. Edel, Nat. Rev. Mater., 2020, 5, 931–951 CrossRef CAS.
- M. J. Levene, J. Korlach, S. W. Turner, M. Foquet, H. G. Craighead and W. W. Webb, Science, 2003, 299, 682–686 CrossRef CAS.
- B. N. Balzer and T. Hugel, Single-molecule detection and manipulation, In Reference Module in Materials Science and Materials Engineering, Elsevier, 2016 Search PubMed.
- S. Huang, J. He, S. Chang, P. Zhang, F. Liang, S. Li, M. Tuchband, A. Fuhrmann, R. Ros and S. Lindsay, Nat. Nanotechnol., 2010, 5, 868–873 CrossRef CAS PubMed.
- X. Guo, Adv. Mater., 2013, 25, 3397–3408 CrossRef CAS PubMed.
- K. F. Domke and A. C. Aragonès, Current Opinion in Electrochemistry, 2022, 35, 101032 CrossRef CAS.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- W. Haiss, R. J. Nichols, H. van Zalinge, S. J. Higgins, D. Bethell and D. J. Schiffrin, Phys. Chem. Chem. Phys., 2004, 6, 4330–4337 RSC.
- E. A. Osorio, M. Ruben, J. S. Seldenthuis, J. M. Lehn and H. S. J. van der Zant, Small, 2010, 6, 174–178 CrossRef CAS PubMed.
- D. Xiang, T. Lee, Y. Kim, T. Mei and Q. Wang, Nanoscale, 2014, 6, 13396–13401 RSC.
- A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef.
- H. Jeong, H. B. Li, L. Domulevicz and J. Hihath, Adv. Funct. Mater., 2020, 30, 2000615 CrossRef CAS.
- C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D.-H. Qu, H. Tian, M. A. Ratner, H. Q. Xu, A. Nitzan and X. Guo, Science, 2016, 352, 1443–1445 CrossRef CAS PubMed.
- S.-M. Lu, Y.-Y. Peng, Y.-L. Ying and Y.-T. Long, Anal. Chem., 2020, 92, 5621–5644 CrossRef CAS.
- L. Novotny, R. X. Bian and X. S. Xie, Phys. Rev. Lett., 1997, 79, 645–648 CrossRef CAS.
- C. Zhan, G. Wang, J. Yi, J.-Y. Wei, Z.-H. Li, Z.-B. Chen, J. Shi, Y. Yang, W. Hong and Z.-Q. Tian, Matter, 2020, 3, 1350–1360 CrossRef.
- R. Hölzel, N. Calander, Z. Chiragwandi, M. Willander and F. F. Bier, Phys. Rev. Lett., 2005, 95, 128102 CrossRef.
- L. Tang, B. P. Nadappuram, P. Cadinu, Z. Zhao, L. Xue, L. Yi, R. Ren, J. Wang, A. P. Ivanov and J. B. Edel, Nat. Commun., 2021, 12, 913 CrossRef CAS.
- A. C. Aragonès and K. F. Domke, Cell Rep. Phys. Sci., 2021, 2, 100389 CrossRef.
- M. L. Juan, M. Righini and R. Quidant, Nat. Photonics, 2011, 5, 349–356 CrossRef CAS.
- T. D. Bouloumis and S. Nic Chormaic, Appl. Sci., 2020, 10, 1375 CrossRef.
- L. Novotny, Near-Field Optics and Surface Plasmon Polaritons, 2007 Search PubMed.
- L. Long, J. Chen, H. Yu and Z.-Y. Li, Photonics Res., 2020, 8, 1573 CrossRef CAS.
- M. Wang, T. Wang, O. S. Ojambati, T. J. Duffin, K. Kang, T. Lee, E. Scheer, D. Xiang and C. A. Nijhuis, Nat. Rev. Chem., 2022, 1–24 Search PubMed.
- A. C. Aragonès and K. F. Domke, J. Mater. Chem. C, 2021, 9, 11698–11706 RSC.
- N. Oyamada, H. Minamimoto and K. Murakoshi, J. Am. Chem. Soc., 2022, 144, 2755–2764 CrossRef CAS PubMed.
- A. C. Aragonès, N. Darwish, S. Ciampi, F. Sanz, J. J. Gooding and I. Díez-Pérez, Nat. Commun., 2017, 8, 15056 CrossRef.
- T. Harashima, Y. Hasegawa, S. Kaneko, M. Kiguchi, T. Ono and T. Nishino, Angew. Chem., Int. Ed., 2019, 58, 9109–9113 CrossRef CAS PubMed.
- Y. Hasegawa, T. Harashima, Y. Jono, T. Seki, M. Kiguchi and T. Nishino, Chem. Commun., 2019, 56, 309–312 RSC.
- X. Yao, X. Sun, F. Lafolet and J.-C. Lacroix, Nano Lett., 2020, 20, 6899–6907 CrossRef CAS.
- C. S. Quintans, D. Andrienko, K. F. Domke, D. Aravena, S. Koo, I. Díez-Pérez and A. C. Aragonès, Appl. Sci., 2021, 11, 3317 CrossRef CAS.
- A. Vezzoli, R. J. Brooke, S. J. Higgins, W. Schwarzacher and R. J. Nichols, Nano Lett., 2017, 17, 6702–6707 CrossRef CAS PubMed.
- S. Kaneko, D. Murai, S. Marqués-González, H. Nakamura, Y. Komoto, S. Fujii, T. Nishino, K. Ikeda, K. Tsukagoshi and M. Kiguchi, J. Am. Chem. Soc., 2016, 138, 1294–1300 CrossRef CAS.
- S. Kaneko, E. Montes, S. Suzuki, S. Fujii, T. Nishino, K. Tsukagoshi, K. Ikeda, H. Kano, H. Nakamura, H. Vázquez and M. Kiguchi, Chem. Sci., 2019, 10, 6261–6269 RSC.
- Y. Dubi, I.-W. Un and Y. Sivan, Nano Lett., 2022, 22, 2127–2133 CrossRef.
- J. M. Ziman, Principles of the Theory of Solids, Cambridge University Press, Cambridge, 2nd edn, 1972 Search PubMed.
- H. Reddy, K. Wang, Z. Kudyshev, L. Zhu, S. Yan, A. Vezzoli, S. J. Higgins, V. Gavini, A. Boltasseva, P. Reddy, V. M. Shalaev and E. Meyhofer, Science, 2020, 369, 423–426 CrossRef CAS PubMed.
- P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568–1571 CrossRef CAS.
- L. E. Baum, T. Petrie, G. Soules and N. Weiss, Ann. Math. Stat., 1970, 41, 164–171 CrossRef.
- J. Bilmes, A Gentle Tutorial of the EM algorithm and its application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models, ICSI Technical Report TR-97–021, 1997.
- E. Coviello, A. B. Chan and G. R. G. Lanckriet, J. Mach. Learn. Res., 2014, 15, 697–747 Search PubMed.
- M. S. Inkpen, Z.-F. Liu, H. Li, L. M. Campos, J. B. Neaton and L. Venkataraman, Nat. Chem., 2019, 11, 351–358 CrossRef CAS PubMed.
- E. Evans, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 CrossRef CAS.
- J.-C. Liao, J. A. Spudich, D. Parker and S. L. Delp, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 3171–3176 CrossRef CAS.
- A. Asandei, A. Apetrei, Y. Park, K.-S. Hahm and T. Luchian, Langmuir, 2011, 27, 19–24 CrossRef CAS.
- L. S. Milescu, G. Akk and F. Sachs, Biophys. J., 2005, 88, 2494–2515 CrossRef CAS PubMed.
- R. Wei, V. Gatterdam, R. Wieneke, R. Tampé and U. Rant, Nat. Nanotechnol., 2012, 7, 257–263 CrossRef CAS.
- F. J. Sigworth and S. M. Sine, Biophys. J., 1987, 52, 1047–1054 CrossRef CAS.
- H. L. Breunig, J. Pharm. Sci., 1973, 62, 177–178 CrossRef.
- J. Mathé, H. Visram, V. Viasnoff, Y. Rabin and A. Meller, Biophys. J., 2004, 87, 3205–3212 CrossRef.
- R. Szoszkiewicz, S. R. K. Ainavarapu, A. P. Wiita, R. Perez-Jimenez, J. M. Sanchez-Ruiz and J. M. Fernandez, Langmuir, 2008, 24, 1356–1364 CrossRef CAS.
- B. S. Erwin Neher, Single-Channel Recording, Springer New York, NY, 1995 Search PubMed.
- G. C. R. George and C. Runger, Applied Statistics and Probability for Engineers, 7th Edition, John Wiley & Sons, Inc, 2008 Search PubMed.
- S.-H. Shin, T. Luchian, S. Cheley, O. Braha and H. Bayley, Angew. Chem., Int. Ed., 2002, 41, 3707–3709 CrossRef CAS PubMed.
- A. Downes, D. Salter and A. Elfick, Opt. Express, 2006, 14, 5216 CrossRef.
- W. Zhang, T. Schmid, B.-S. Yeo and R. Zenobi, J. Phys. Chem. C, 2008, 112, 2104–2108 CrossRef CAS.
- J. Rigor, D. Kurouski and N. Large, J. Phys. Chem. C, 2022, 126, 13986–13993 CrossRef CAS.
- T. Bürgi, Nanoscale, 2015, 7, 15553–15567 RSC.
- T. N. Todorov, J. Hoekstra and A. P. Sutton, Physical Review Letters, 2001, 86, 3606–3609 CrossRef CAS PubMed.
- Z. Huang, B. Xu, Y. Chen, M. Di Ventra and N. Tao, Nano Lett., 2006, 6, 1240–1244 CrossRef CAS PubMed.
- M. P. Ruiz, A. C. Aragonès, N. Camarero, J. G. Vilhena, M. Ortega, L. A. Zotti, R. Pérez, J. C. Cuevas, P. Gorostiza and I. Díez-Pérez, J. Am. Chem. Soc., 2017, 139, 15337–15346 CrossRef CAS.
- A. Asandei, A. E. Rossini, M. Chinappi, Y. Park and T. Luchian, Langmuir, 2017, 33, 14451–14459 CrossRef CAS PubMed.
- A. Asandei, M. Chinappi, J.-k. Lee, C. Ho Seo, L. Mereuta, Y. Park and T. Luchian, Sci. Rep., 2015, 5, 10419 CrossRef CAS PubMed.
- M. Artamonov and T. Seideman, Nano Lett., 2010, 10, 4908–4912 CrossRef CAS PubMed.
- J. Kohoutek, D. Dey, A. Bonakdar, R. Gelfand, A. Sklar, O. G. Memis and H. Mohseni, Nano Lett., 2011, 11, 3378–3382 CrossRef CAS PubMed.
- K. Ikeda, N. Fujimoto and K. Uosaki, J. Phys. Chem. C, 2014, 118, 21550–21557 CrossRef CAS.
- L.-Q. Gu and H. Bayley, Biophys. J., 2000, 79, 1967–1975 CrossRef CAS PubMed.
- M. Rief, R. S. Rock, A. D. Mehta, M. S. Mooseker, R. E. Cheney and J. A. Spudich, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 9482–9486 CrossRef CAS PubMed.
- Z. Huang, F. Chen, P. A. Bennett and N. Tao, J. Am. Chem. Soc., 2007, 129, 13225–13231 CrossRef CAS PubMed.
- E. Evans and K. Ritchie, Biophys. J., 1997, 72, 1541–1555 CrossRef CAS PubMed.
- A. Asandei, M. Chinappi, H.-K. Kang, C. H. Seo, L. Mereuta, Y. Park and T. Luchian, ACS Appl. Mater. Interfaces, 2015, 7, 16706–16714 CrossRef CAS PubMed.
- M. Chinappi, T. Luchian and F. Cecconi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032714 CrossRef PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- T. Ohmichi, H. Nakamuta, K. Yasuda and N. Sugimoto, J. Am. Chem. Soc., 2000, 122, 11286–11294 CrossRef CAS.
- S. Howorka, L. Movileanu, O. Braha and H. Bayley, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 12996–13001 CrossRef CAS PubMed.
- S. Vernick, S. M. Trocchia, S. B. Warren, E. F. Young, D. Bouilly, R. L. Gonzalez, C. Nuckolls and K. L. Shepard, Nat. Commun., 2017, 8, 15450 CrossRef CAS PubMed.
- C. Zhan, G. Wang, X.-G. Zhang, Z.-H. Li, J.-Y. Wei, Y. Si, Y. Yang, W. Hong and Z.-Q. Tian, Angew. Chem., Int. Ed., 2019, 58, 14534–14538 CrossRef CAS PubMed.
- D. Guhr, D. Rettinger, J. Boneberg, A. Erbe, P. Leiderer and E. Scheer, J. Microsc., 2008, 229, 407–414 CrossRef CAS PubMed.
- S. Zhang, C. Guo, L. Ni, K. M. Hans, W. Zhang, S. Peng, Z. Zhao, D. C. Guhr, Z. Qi, H. Liu, M. Song, Q. Wang, J. Boneberg, X. Guo, T. Lee, E. Scheer and D. Xiang, Nano Today, 2021, 39, 101226 CrossRef CAS.
- C. Carnegie, J. Griffiths, B. De Nijs, C. Readman, R. Chikkaraddy, W. M. Deacon, Y. Zhang, I. Szabó, E. Rosta, J. Aizpurua and J. J. Baumberg, J. Phys. Chem. Lett., 2018, 24(9), 7146–7151 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr05448e |
| This journal is © The Royal Society of Chemistry 2023 |