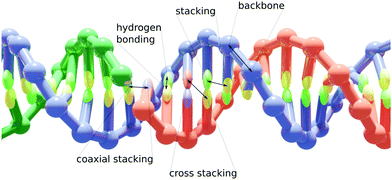
Coarse-grained nucleic acid–protein model for hybrid nanotechnology†
Jonah
Procyk
 ,
Erik
Poppleton
,
Erik
Poppleton
 and
Petr
Šulc
and
Petr
Šulc
 *
*
School of Molecular Sciences and Center for Molecular Design and Biomimetics, The Biodesign Institute, Arizona State University, 1001 South McAllister Avenue, Tempe, Arizona 85281, USA. E-mail: psulc@asu.edu
First published on 16th December 2020
Abstract
The emerging field of hybrid DNA–protein nanotechnology brings with it the potential for many novel materials which combine the addressability of DNA nanotechnology with the versatility of protein interactions. However, the design and computational study of these hybrid structures is difficult due to the system sizes involved. To aid in the design and in silico analysis process, we introduce here a coarse-grained DNA/RNA–protein model that extends the oxDNA/oxRNA models of DNA/RNA with a coarse-grained model of proteins based on an anisotropic network model representation. Fully equipped with analysis scripts and visualization, our model aims to facilitate hybrid nanomaterial design towards eventual experimental realization, as well as enabling study of biological complexes. We further demonstrate its usage by simulating DNA–protein nanocage, DNA wrapped around histones, and a nascent RNA in polymerase.
Introduction
Molecular nanotechnology designs biomolecular interactions to assemble nanoscale devices and structures. DNA nanotechnology, in particular, has attracted lots of attention and experienced rapid growth over the past three decades. While originally envisioned as a method of developing a DNA lattice for crystallizing proteins for structure determination,1 DNA nanotechnology is seeing promising applications in e.g. biomaterial assembly,2 biocatalysis,3 therapeutics,4 and diagnostics.5 The programmability of DNA allows for the rapid design and experimental realization of complex shapes, yielding an unprecedented level of control and functionality at the nanoscale. As DNA nanotechnology has developed, so have parallel technologies with other familiar biomolecules such as RNA,6 and, to some extent, proteins.7,8 While DNA nanostructures and devices have been unequivocally successful in realizing more complex and larger constructs, they are inherently limited in function by their available chemistry; with one possible solution being the use of functionalized DNA nanostructures.9 Of particular interest is hybrid DNA–protein nanotechnology, which can combine the already well developed design strategies of DNA nanotechnology and cross-link them with functional proteins. The combination of the two molecules in nanotechnology will open new applications, such as diganostics, therapeutics, molecular “factories” and new biomimetic materials.10 Examples of successfully realized hybrid nanostructures include DNA–protein cages,11 a DNA nanorobot with nucleolin aptamer for cancer therapy4 and peptide-directed assembly of large nanostructures.12At the same time, computational tools for the study and design of DNA and RNA nanostructures have become increasingly relevant as size and complexity of nanostructures grow. Design tools such as Adenita13 MagicDNA,14 CaDNAno,15 and Tiamat16 are essential for the structural design of DNA origamis. New coarse-grained models have been introduced to study DNA nanostructures, as the sizes (thousands or more) as well as rare events (formation or breaking of large sections of base pairs) involved in the study of these systems make atomistic-resolution modeling impractical. Several coarse-grained models have been developed to match thermodynamic and energetic properties of nucleic acids.17–20 Among the available tools, the oxDNA and oxRNA models21–24 have been quite popular over the past few years, being used by dozens of research groups in over one hundred articles to study various aspects of DNA and RNA nanosystems including the biophysical properties of DNA and RNA.25–30 Each nucleotide is represented as a rigid body in the simulation, with interactions between different sites parameterized to reproduce mechanical, structural and thermodynamic properties of single-stranded and double-stranded DNA and RNA respectively.
However, the oxDNA/oxRNA models only allow for representation of nucleic acids alone, limiting their scope of usability. While there have been coarse-grained simulation models developed for protein–DNA interactions,31–37 none are able to be directly used with the oxDNA model. The development of an efficient tool compatible with oxDNA would allow for efficient study of arbitrary protein–DNA complexes.
Here, we introduce such a coarse-grained model that uses an Anisotropic Network Model (ANM) to represent proteins alongside the oxDNA or oxRNA model. The ANM is a form of elastic network model used to probe the dynamics of biomolecules fluctuating around their native state. Originally formulated by Atilgan et al.,38 the ANM has become fundamental tool in probing protein dynamics, often closely matching residue–residue fluctuations and normal modes of fully atomistic simulations.39–41 Here we use the ANM to approximately capture native state protein dynamics. The ANM representation of proteins interact with just an excluded volume interaction with the oxDNA/oxRNA representation, but specific attractive or repulsive interactions can be added as well. The mass of each residue is set as equal to that of a nucleotide. The less than one order of magnitude difference between the average masses of nucleotides and amino acids makes the equal mass approximation acceptable within the high level of coarse-graining employed by ANM and oxDNA/oxRNA models. We further provide parameterization of common linkers that are used to conjugate proteins to DNA in typical hybrid nanotechnology applications.
The ANM-oxDNA/oxRNA hybrid models are intended to help design and probe function of large nucleic-acid protein hybrid nanostructures, but also aim to study biological complexes and processes which can be captured within the approximations employed by the models. As an example of the model's use, we show simulations of DNA–protein hybrid nanocage, DNA wrapped around a histone, and a nascent RNA strand inside a polymerase exit channel.
Model description
Implemented in the oxDNA simulation package,42 our model allows for a coarse-grained simulation of large hybrid nanostructures. It consists of two coarse-grained particle representations, the already existing oxDNA2 or oxRNA model for their respective nucleic acids and an Anisotropic Network Model (ANM) for proteins.43 The detailed descriptions of the oxDNA2/oxRNA models are available in ref. 22 and 23. A DNA duplex with a nicked strand is schematically illustrated in Fig. 1. The ANM allows us to represent a protein with a known structure as beads connected by springs. We chose to use the ANM to represent proteins for its efficiency and relative simplicity, while still providing reasonably accurate representations of proteins crosslinked to DNA nanostructures. Furthermore, it can be implemented using only pairwise interaction potentials, the same as oxDNA/oxRNA models.Protein model
In the ANM representation, each protein residue is represented solely by its α-carbon position. All residues within a specified cutoff distance rmax from one another are considered ‘bonded’. Please see ref. 38 for a more detailed introduction. Each bond between residues i and j in the ANM is represented as a harmonic potential that fluctuates around the equilibrium length rij0: | (1) |
The total bonded interaction potential Vbonded–anm is the sum of terms eqn (1) for all pairs i,j of aminoacids at a distance smaller than rmax in the resolved protein structure, as schematically illustrated in Fig. 2. We set rij0 to the distance between α-carbons of the residues i and j in the PDB file. Free parameter γ is set uniformly on each bond in the ANM and is chosen to best fit the Debye–Waller factors of the original PDB structure. Debye–Waller factors (or B-factors when applied specifically to proteins) describe the thermal motions of each resolved atom in a protein given by their respective X-ray scattering assay. As previously done,38 we use the B-factor of the α-carbon to approximately capture the fluctuations of the protein backbone. Since an ANM is typically an analytical technique, it has no excluded volume effects. Hence we here extend the model to use a repulsive part Lennard-Jones potential between both bonded and non-bonded particles (eqn (2)) to model the excluded volume at a per particle excluded volume diameter of 2.5 Å.
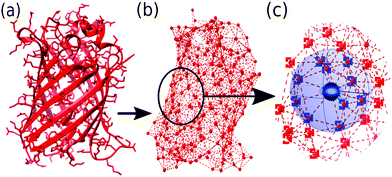 | ||
| Fig. 2 Illustration of ANM using GFP protein (PDB code: 1W7S) from (a) starting PDB structure to (b) ANM representation at rmax of 8 Å, (c) bonding criteria per residue: all particles within distance rmax (bounds depicted by blue sphere) of center particle (black circle) are considered ‘bonded’ (blue squares) while those further (outside of sphere) are considered ‘nonbonded’ (red squares). | ||
For any two particles (either protein/protein or protein–DNA/RNA) that are at distance r, we define the excluded volume interaction in eqn (2):
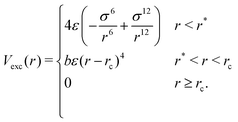 | (2) |
The excluded volume diameter rc between protein particles was set by simulating both large and small proteins at various values to tune to a value allowing excluded volume interactions between nearest neighbors with little deviation between simulated and analytical B-factors. protein–DNA/RNA rc values were set as the sum of the excluded volume radii of both particle types. Parameters b and r* were calculated so that Vexc is a differentiable function. The constant ε sets the strength of the potential and we use ε = 82 pN nm−1.
Parameterization
In parameterizing our model for simulation, the goal is to mimic the dynamics of the protein in the native state. Though not without their drawbacks,44,45 we selected B-factors for their widespread availability in PDB structures and history of being used to fit elastic network models of proteins.44 Our model contains two free parameters, the cutoff distance rmax and the spring constant γ. The rmax value alone determines which connections will be present in the ANM network. As noted in the original formulation of the ANM,38 the best choice of rmax should reproduce the distribution found for globular proteins' densities of vibrational states.46,47 A value of 13 Å was found to approximately capture the shape of the target distribution for a large set of proteins with rmax values much lower (7 Å) or higher (20 Å) tending to shift the eigenfrequencies towards lower and higher frequencies respectively. In practice, the best rmax varies from protein to protein but can usually be varied in a narrow range (12–18 Å) with little effect on the distribution of normal mode frequencies.For each protein (consisting of N aminoacids) represented by ANM, we linearly fit the analytically computed B-factors to their experimental counterpart with γ as a free parameter. To solve for the B-factors analytically, we first calculate the 3N × 3N Hessian matrix of the spring potential Vspring, a task made simple by the harmonic potential energy function.38 After constructing the Hessian H for the system at a specified cutoff rmax, the mean squared deviation from the mean position for each residue i can be calculated from the ensemble average:
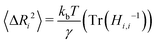 | (3) |
The B-factor B of the residue i can be directly computed from our previous result as:38
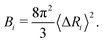 | (4) |
The experimental B-factors are provided along with resolved crystal structures of proteins, and we can hence use eqn (3) and (4) to obtain N equations. We then fit γ parameter to minimize
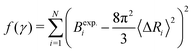 | (5) |
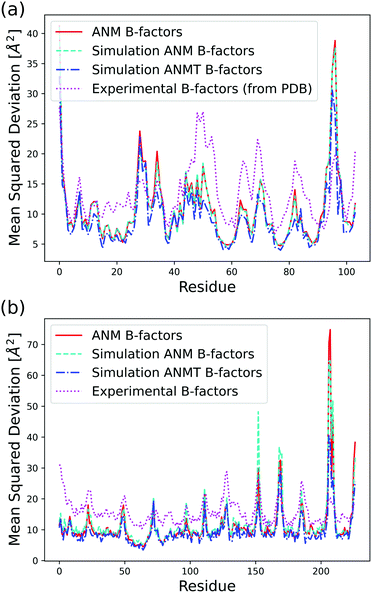 | ||
| Fig. 3 Analytical, classic ANM simulation, ANMT simulation, and experimentally determined B-factors calculated in Å2 per residue for (a) ribonuclease T1 (PDB code 1BU4) at 25 °C (rmax = 15, ks = 42.2 pN Å−1, kb = kt = 171.3 pN Å−1) and (b) green fluorescent protein (PDB code 1W7S) at 25 °C (rmax = 13, ks = 33.2 pN Å−1, kb = kt = 171.3 pN Å−1). | ||
Expansion of the ANM model
In addition to the classic ANM model, our model can also optionally use unique γij for each bonded pair of residues, which allows for implementation of other analytical models, such as the heterogeneous ANM (HANM)48 and multiscale ANM (mANM)49 that can generate better fits to experimental B-factors using the γij values. The HANM iteratively fits a normal ANM network to given experimental B-factors with variable realistic force parameters γij. While unquestionably useful, the inaccuracy of B-factor data particularly in large or low resolution structures limits its application. In the mANM model, our conversion from the PDB structure to ANM representation also allows the fitting of multiple networks with varying γij values tuned by scale parameters49 (similar to rmax). A linear combination of the networks is then solved to minimize the difference between the ANM network's predicted and experimental B-factors. The original formulation of the mANM49 is limited in computational application as it has no cutoff value (rmax); a protein of size N residues would have N(N − 1)/2 connections, significantly more than the average ANM. For the proteins studied in this work, neither HANM nor mANM provided a significant advantage, so we decide to use the simple ANM with fixed rmax and the same γ for all spring interactions. A Cα coarse-grained HANM and a mANM with an additional cutoff value parameter are, however, implemented in our conversion scripts and can be optionally used to represent proteins in our model.One major obstacle in using an ANM is known as the tip effect.50 The result is an extremely large spike in the B-factors due to a residue being under-constrained. Often this can be solved by raising the cutoff value in ANM construction; however, doing so raises the computational requirements of simulations. Furthermore, we found the ANM model did not accurately represent short peptides, as the spring network does not provide enough constraints to reproduce their end-to-end distance as seen when simulated with more detailed models like AWSEM-MD.51
To overcome this obstacle, we implemented harmonic pairwise bending and torsional modulation forces into the existing simulation model. These new constraints allow for reduced rmax values, and also can more accurately represent shorter peptides, which are often used in DNA–hybrid nanostructures. We introduce these optional modulation forces below.
Bending and torsional modulation
We introduce the torsional and bending potential as optional interaction potentials in our protein representation on top of the ANM model with bonded and excluded volume potentials. Each protein residue corresponds to a spherical particle, with associated orientation given by its orthonormal axes î1, î2, î3 (Fig. 4a). Harmonic terms control the angle between the normalized interparticle distance vector![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij and the normal vector of each particle î1, ĵ1 to control bond bending. The angles between two sets of orientation vectors, î1, ĵ1 and î3, ĵ3, are controlled as well allowing for modulation of the torsion based on the particles relative orientations. The full pairwise potential is given by eqn (6):
ij and the normal vector of each particle î1, ĵ1 to control bond bending. The angles between two sets of orientation vectors, î1, ĵ1 and î3, ĵ3, are controlled as well allowing for modulation of the torsion based on the particles relative orientations. The full pairwise potential is given by eqn (6): | (6) |
The function VB&Tij is defined for all pairs of residues that are neighbors along the protein backbone. We set the energy minimum values aij0, bij0, cij0, dij0 to correspond to the cosines of respective angles between residues in the PDB file for the protein structure. The terms kb and kt are two new global parameters that control the strength of the bending and torsion potential respectively. Currently, we set their values empirically, though pair specific terms could lead to further agreement with experimental data. Fig. 3 shows the effect of the torsional and bonding modulation on the same set of proteins used prior. As intended, a noticeable decrease in high peak B-factors is observed using a modest kb and kt value. Fig. 4 illustrates the potential in a two particle system. Hereafter, we will refer to the ANM model with torsional and bending modulation as the ANMT model.
Protein–nucleic acid interactions
In our current implementation of the model, protein residues and nucleotides have no interaction except for excluded volume and optional explicitly specified spring potentials between user-designated protein residues and nucleotides: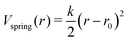 | (7) |
The excluded volume interaction potential between protein and DNA/RNA residues has the same form as defined in eqn (2), with the respective interaction parameters given in Table 1. In the oxDNA/oxRNA models, each nucleotide has two distinct interaction sites (backbone and base), each of which is interacting with the protein residue using separate excluded volume parameters. Future expansion of the model will include an approximate treatment of electrostatic interaction between protein and nucleic acids based on Debye–Hückel theory as implemented in oxDNA,22 as well as coarse-grained protein model AWSEM.51 Many non-specific DNA–protein interactions make use of the electrostatic interactions between the DNA backbone and positively charged portions of the protein.52 Sensitive to salt concentration, these electrostatic contributions have been previously modeled using Debye–Hückel theory53 to investigate the role of protein frustration in regulating DNA binding kinetics. Similarly an extension of our model with an appropriate Debye–Hückel potential can capture and enable study of non-specific DNA-binding protein systems.
| Parameter | (a) | (b) | (c) |
|---|---|---|---|
| σ | 0.350 | 0.360 | 0.570 |
| r c | 0.353 | 0.363 | 0.573 |
| r* | 0.349 | 0.359 | 0.569 |
| b | 30.7 × 107 | 29.6 × 107 | 17.9 × 107 |
Since we are interested in exploring conjugated hybrid systems, it is necessary to have an approximation for the covalent linkers bridging the nucleic acid base and protein residue. We model the two bioconjugate linkers, LC-SPDP and DBCO–triazole, (Fig. 5), that are typically used in protein–DNA hybrid nanotechnology54,55 using a spring potential as defined in eqn (7) with parameters k and r0 parameterized to mimic the end-to-end average distance and standard deviation of each linker at temperature 300 K. LC-SPDP links the thiol group of a modified cysteine residue to an amine-modified nucleotide. DBCO–trizaole is the product of a copper-free click reaction involving a DBCO-modified residue to link to an azide-modified nucleotide. Each of the linkers (Fig. 5) was first drawn in MolView and then converted into OPLS-AA 1.14*CM1A forcefield format via LibParGen.56–58 In GROMACS,59 each linker was first equilibrated and then simulated in both SPCE and TIP3P water molecules at 300 K for three trials of 10 nanoseconds each. The obtained averaged end-to-end distance and standard deviation for each trial are shown in Table 2.
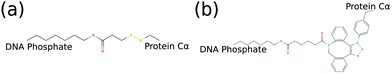 | ||
| Fig. 5 2D molecular structures of common bioconjugate linkers dubbed (a) LC-SPDP and (b) DBCO–triazole; both can be used to conjugate proteins to DNA phosphate groups. | ||
| SPCE solvent | 〈r〉 (Å) | 〈r2〉 (Å2) | k (pN Å−1) |
|---|---|---|---|
| LC-SPDP | 9.18 | 2.68 | 5.75 × 10−2 |
| DBCO–triazole | 10.97 | 3.43 | 3.51 × 10−2 |
| TIP3P solvent | 〈r〉 (Å) | 〈r2〉 (Å2) | k (pN Å−1) |
|---|---|---|---|
| LC-SPDP | 9.05 | 2.8 | 5.28 × 10−2 |
| DBCO–triazole | 10.95 | 3.56 | 3.25 × 10−2 |
Examples
Visualization of our model is supported by the latest version of the visualization tool oxView60 for both the design of hybrid nanomaterials as well as the viewing of simulation trajectories. The one caveat is that protein topologies are non-editable. Instead each protein starts from their PDB crystal structure and is converted into oxDNA format while the ANM spring constant is set to best match the experimental B-factors via our provided scripts. The output files can then be loaded into oxView as well as used for simulation in our model.The model is theoretically able to represent any protein or protein complex that the ANM model can represent. Not beyond the scope of our model, biologically relevant multi-chain proteins such as nucleosomes, RNA polymerases, and viral assemblies can be also simulated, allowing for the nucleic acid behavior present in each of these systems to be modeled, studied, and compared to experimental data. While the detailed study of these systems is beyond the scope of this article, we show examples of both biological and designed nanosystems as represented by our ANM-oxDNA or ANM-oxRNA model.
Biological constructs
Two prominent cases of nucleic acid–protein interactions, RNA polymerases and nucleosomes, were constructed and simulated using the ANMT model for future study. As many PDB files are missing residues, we first reconstruct each individual chain using the best scoring of ten models generated by the Modeller tool.61 The reconstructed RNA polymerase was converted into oxDNA format from its PDB entry (6ASX) using an rmax of 15 Å. A fragment of the RNA was reinserted into the exit channel and the subsequent MD simulation was allowed to sample the RNA's escape from the exit channel. The reconstructed nucleosome was converted into oxDNA simulation format from its PDB entry (3LEL) using an rmax of 12 Å. Spring potentials were added to observed contacts between the DNA and protein residues present in the PDB structure. A snapshot of the RNA polymerase system and fluctuation analysis of the nucleosome are shown in Fig. 6a and b.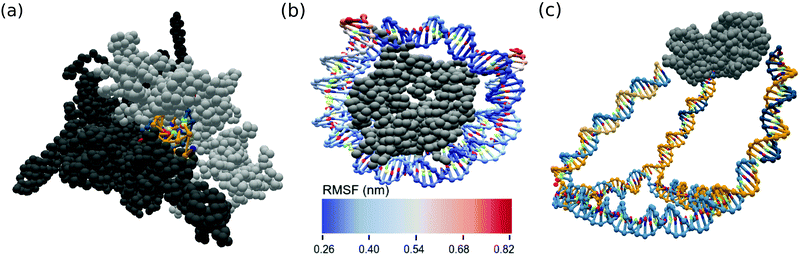 | ||
| Fig. 6 OxView visualization of simulated biological assemblies (a) RNA in exit channel of paused RNA polymerase (PDB code: 6ASX) and (b) root mean squared fluctuation (nm) of human nucleosome made up of histone octamer and DNA (PDB code: 3LEL), (c) mean structure from MD simulation of KDPG aldolase (PDB code: 1WA3) conjugated to a DNA cage. | ||
While no process was explicitly modeled, our new model can be used to explore behavior of large scale systems of nucleosomes, as at the latest version of GPU cards, the oxDNA model has been shown to be able to equilibrate systems consisting of over 1 million nucleotides.
More pertinent to our goal of aiding in the design of hybrid nanostructures, our model supports conversion of CadNano, Tiamat, and other popular DNA origami design tools into the oxDNA format27 where they can easily be edited in oxView to include linked proteins of interest. Since an ANM is a highly simplified model of protein dynamics, the predictive power of our model lies not in prediction of protein structure but rather the collection of statistical data of the protein's effect on the nucleic acid component of the system. Available and compatible with this model is also the suite of oxDNA analysis scripts60 allowing for a detailed exploration of system-specific effects.
Peptides
Synthetic peptides are used in many chemistry applications. Since these peptides are often very small and lack long-distance contacts that enforce specific 3D conformations, we wanted to explore how our models perform on these small structures. We compared the end-to-end distance of 3 hemagglutinin binding peptides62 simulated in our ANM model, the ANMT model, and another popular coarse-grained protein model, AWSEM-MD.37 For AWSEM-MD simulations, initial structure predictions were generated from sequence using I-TASSER.63 A secondary structure weight (ssweight) file was generated using jpred,64 and the structure and weight files were converted to the appropriate formats for AWSEM-MD simulation in LAMMPS65 using tools provided with AWSEM-MD. Simulations were run for 109 steps with end-to-end distance sampled every 105 steps.Using the classic ANM, each peptide was built using strong backbone connections and significantly weaker long-range connections to empirically match the AWSEM mean and standard deviation of the end-to-end distance. The resulting simulation of each peptide; however, produced a trajectory showing many stretched, nonphysical conformations. The subsequent inclusion of the bending and torsion modulation using the ANMT model allowed for the same level of accuracy using only strong short-range connections. The ANMT model showed much higher rigidity with no stretched conformations when compared to the ANM model alone. Final end-to-end distances and standard deviation are shown in Table 3.
| Model | AWSEM | ANM | ANMT |
|---|---|---|---|
| Peptide 125 – CSGHNIYAQYGYPYDHMYEG, Peptide 149 – CSGKSQEIGDPDDIWNQMKW, Peptide 227 – CSGSGNQEYFPYPMIDYLKK. | |||
| Peptide 125 | |||
| 〈r〉 (Å) | 12.02 | 12.9 | 12.09 |
| 〈r2〉 (Å2) | 4.9 | 4.51 | 4.34 |
| Peptide 149 | |||
| 〈r〉 (Å) | 12.9 | 12.9 | 12.9 |
| 〈r2〉 (Å2) | 6.6 | 4.6 | 4.6 |
| Peptide 227 | |||
| 〈r〉 (Å) | 14.5 | 16.2 | 14.7 |
| 〈r2〉 (Å2) | 7.4 | 5.4 | 5.1 |
KDPG aldolase–DNA cage
Hybrid DNA–protein nanostructure constructs such as those developed by the Stepahanopoulos Lab are of particular interest. The Stephanopoulos group has experimentally realized their size-tunable DNA cage attached to homotrimeric protein KDPG aldolase making use of a LC-SPDP linker (Fig. 5) to join the DNA and protein components.11 The DNA cage was converted from Tiamat format into oxDNA format and the protein was converted from its PDB structure. The linker between the components was modeled as a spring potential (eqn (7)) using the parameters from Table 2. We conducted a short MD simulation of the full system corresponding to time of about 30 ns. The mean structure from simulation of the experimental cage was calculated using our analysis scripts60 and is displayed in Fig. 6c.Conclusions
We present a coarse-grained protein model, based on elastic network representation of proteins, for use in conjunction with existing coarse-grained nucleic acid models capable of simulating large hybrid nanostructures. Implemented on GPU as well as CPU, our model allows for simulations of large systems based on nanotechnology designs as well as large biological complexes.Looking forward, we plan to study the paused RNA polymerase and nucleosome systems using this model. In addition, experimental systems such as the hybrid cage in Fig. 6 can be simulated and directly compared to available experimental data. While widely available, B-factors are severely limited particularly in terms of accuracy. However, our model can be parameterized to approximate any available fluctuation data including but not limited to fully atomistic simulation and solution NMR data. In addition to the model, we also extended a nanotechnology design and simulation analysis tool, oxView, to include a protein representation to aid computer design of DNA/RNA–protein hybrid nanostructures. The subsequent analysis of the designs can be used to optimize nanostructure parameters, such as placement of the linkers and lengths of duplex segments in order to achieve desired geometry.
The simulation code is freely available on github.com/sulcgroup/anm-oxdna and will also be incorporated in the future release of the oxDNA simulation package. The visualization of protein–hybrid systems has been incorporated into our previously developed oxView tool.60 The aforementioned analysis scripts and visualizer are available in git repositories github.com/sulcgroup/oxdna_analysis_tools and github.com/sulcgroup/oxdna-viewer respectively. We also provide the description of the file formats used to setup the simulation in the ESI.†
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank all members of the Šulc group for their support and helpful discussions, in particular to H. Liu and M. Matthies. We thank Dr Stephanopoulos for helpful comments and feedback about simulation study of his DNA–protein hybrid system. We acknowledge support from the NSF grant no. 1931487.Notes and references
- N. C. Seeman, J. Theor. Biol., 1982, 99(2), 237–247 CrossRef CAS.
- W. Liu, M. Tagawa, H. L. Xin, T. Wang, H. Emamy, H. Li, K. G. Yager, F. W. Starr, A. V. Tkachenko and O. Gang, Science, 2016, 351(6273), 582–586 CrossRef CAS.
- C. Geng and P. J. Paukstelis, J. Am. Chem. Soc., 2014, 136(22), 7817–7820 CrossRef CAS.
- S. Li, Q. Jiang, S. Liu, Y. Zhang, Y. Tian, C. Song, J. Wang, Y. Zou, G. J. Anderson, J. Y. Han, Y. Chang, Y. Liu, C. Zhang, L. Chen, G. Zhou, G. Nie, H. Yan, B. Ding and Y. Zhao, Nat. Biotechnol., 2018, 36(3), 258–264, DOI:10.1038/nbt.4071.
- F. Zhang, J. Nangreave, Y. Liu and H. Yan, J. Am. Chem. Soc., 2014, 136(32), 11198–11211 CrossRef CAS.
- P. Guo, Nat. Nanotechnol., 2010, 5(12), 833–842 CrossRef CAS.
- R. V. Ulijn and R. Jerala, Chem. Soc. Rev., 2018, 47(10), 3391–3394 RSC.
- N. P. King, J. B. Bale, W. Sheffler, D. E. McNamara, S. Gonen, T. Gonen, T. O. Yeates and D. Baker, Nature, 2014, 510(7503), 103–108 CrossRef CAS.
- M. Madsen and K. V. Gothelf, Chem. Rev., 2019, 119(10), 6384–6458 CAS.
- N. Stephanopoulos, Chem, 2020, 6(2), 364–405 CAS.
- Y. Xu, S. Jiang, C. R. Simmons, R. P. Narayanan, F. Zhang, A. M. Aziz, H. Yan and N. Stephanopoulos, ACS Nano, 2019, 13(3), 3545–3554 CrossRef CAS.
- J. Jin, E. G. Baker, C. W. Wood, J. Bath, D. N. Woolfson and A. J. Turberfield, ACS Nano, 2019, 13, 9927–9935 CrossRef CAS.
- E. De Llano, H. Miao, Y. Ahmadi, A. J. Wilson, M. Beeby, I. Viola and I. Barisic, Nucleic Acids Res., 2020, 48(15), 8269–8275 CrossRef.
- C. M. Huang, A. Kucinic, J. A. Johnson, H. Su and C. E. Castro, bioRxiv, 2020 DOI:10.1101/2020.05.28.119701.
- S. M. Douglas, A. H. Marblestone, S. Teerapittayanon, A. Vazquez, G. M. Church and W. M. Shih, Nucleic Acids Res., 2009, 37, 5001–5006 CrossRef CAS.
- S. Williams, K. Lund, C. Lin, P. Wonka, S. Lindsay and H. Yan, International Workshop on DNA-Based Computers, 2008, pp. 90–101 Search PubMed.
- D. M. Hinckley, G. S. Freeman, J. K. Whitmer and J. J. De Pablo, J. Chem. Phys., 2013, 139, 144903 CrossRef.
- D. Chakraborty, N. Hori and D. Thirumalai, J. Chem. Theory Comput., 2018, 14, 3763–3779 CrossRef CAS.
- N. A. Denesyuk and D. Thirumalai, J. Phys. Chem. B, 2013, 117, 4901–4911 CrossRef CAS.
- S. Pasquali and P. Derreumaux, J. Phys. Chem. B, 2010, 114, 11957–11966 CrossRef CAS.
- T. E. Ouldridge, A. A. Louis and J. P. Doye, J. Chem. Phys., 2011, 134, 02B627 CrossRef.
- B. E. Snodin, F. Randisi, M. Mosayebi, P. Šulc, J. S. Schreck, F. Romano, T. E. Ouldridge, R. Tsukanov, E. Nir and A. A. Louis, et al. , J. Chem. Phys., 2015, 142, 06B613_1 CrossRef.
- P. Šulc, F. Romano, T. E. Ouldridge, J. P. Doye and A. A. Louis, J. Chem. Phys., 2014, 140, 235102 CrossRef.
- P. Šulc, F. Romano, T. E. Ouldridge, L. Rovigatti, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2012, 137, 5101 CrossRef.
- R. Sharma, J. S. Schreck, F. Romano, A. A. Louis and J. P. Doye, ACS Nano, 2017, 11, 12426–12435 CrossRef CAS.
- M. C. Engel, D. M. Smith, M. A. Jobst, M. Sajfutdinow, T. Liedl, F. Romano, L. Rovigatti, A. A. Louis and J. P. Doye, ACS Nano, 2018, 12, 6734–6747 CrossRef CAS.
- A. Suma, E. Poppleton, M. Matthies, P. Šulc, F. Romano, A. A. Louis, J. P. Doye, C. Micheletti and L. Rovigatti, J. Comput. Chem., 2019, 40, 2586–2595 CrossRef CAS.
- F. Hong, S. Jiang, X. Lan, R. P. Narayanan, P. Šulc, F. Zhang, Y. Liu and H. Yan, J. Am. Chem. Soc., 2018, 140, 14670–14676 CrossRef CAS.
- J. P. Doye, T. E. Ouldridge, A. A. Louis, F. Romano, P. Šulc, C. Matek, B. E. Snodin, L. Rovigatti, J. S. Schreck, R. M. Harrison and W. P. Smith, Phys. Chem. Chem. Phys., 2013, 15, 20395–20414 RSC.
- M. Matthies, N. P. Agarwal, E. Poppleton, F. M. Joshi, P. Šulc and T. L. Schmidt, ACS Nano, 2019, 13, 1839–1848 CAS.
- A. K. Sieradzan, A. Giełdoń, Y. Yin, Y. He, H. A. Scheraga and A. Liwo, J. Comput. Chem., 2018, 39, 2360–2370 CrossRef CAS.
- G. Mishra and Y. Levy, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5033–5038 CrossRef CAS.
- C. Tan, T. Terakawa and S. Takada, J. Am. Chem. Soc., 2016, 138, 8512–8522 CrossRef CAS.
- C. Tan and S. Takada, J. Chem. Theory Comput., 2018, 14, 3877–3889 CrossRef CAS.
- B. Zhang, W. Zheng, G. A. Papoian and P. G. Wolynes, J. Am. Chem. Soc., 2016, 138, 8126–8133 CrossRef CAS.
- R. V. Honorato, J. Roel-Touris and A. M. Bonvin, Front. Mol. Biosci., 2019, 6, 102 CrossRef CAS.
- A. Davtyan, N. P. Schafer, W. Zheng, C. Clementi, P. G. Wolynes and G. A. Papoian, J. Phys. Chem. B, 2012, 116, 8494–8503 CrossRef CAS.
- A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin and I. Bahar, Biophys. J., 2001, 80, 505–515 CrossRef CAS.
- S. K. Mishra and R. L. Jernigan, PLoS One, 2018, 13(6), e0199225 CrossRef.
- M. Gur, E. Zomot and I. Bahar, J. Chem. Phys., 2013, 139, 121912 CrossRef CAS.
- L. Yang, G. Song, A. Carriquiry and R. L. Jernigan, Structure, 2008, 16, 321–330 CrossRef CAS.
- L. Rovigatti, P. Šulc, I. Z. Reguly and F. Romano, J. Comput. Chem., 2015, 36, 1–8 CrossRef CAS.
- A. R. Atilgan, S. Durell, R. L. Jernigan, M. Demirel, O. Keskin and I. Bahar, Biophys. J., 2001, 80, 505–515 CrossRef CAS.
- Z. Sun, Q. Liu, G. Qu, Y. Feng and M. T. Reetz, Chem. Rev., 2019, 119, 1626–1665 CrossRef CAS.
- E. Fuglebakk, N. Reuter and K. Hinsen, J. Chem. Theory Comput., 2013, 9, 5618–5628 CrossRef CAS.
- R. Elber and M. Karplus, Phys. Rev. Lett., 1986, 56, 394–397 CrossRef CAS.
- T. Haliloglu, I. Bahar and B. Erman, Phys. Rev. Lett., 1997, 79, 3090–3093 CrossRef CAS.
- F. Xia, D. Tong and L. Lu, J. Chem. Theory Comput., 2013, 9, 3704–3714 CrossRef CAS.
- K. Xia, Phys. Chem. Chem. Phys., 2017, 20, 658–669 RSC.
- M. Lu, B. Poon and J. Ma, J. Chem. Theory Comput., 2006, 2, 464–471 CrossRef CAS.
- M. Y. Tsai, W. Zheng, D. Balamurugan, N. P. Schafer, B. L. Kim, M. S. Cheung and P. G. Wolynes, Protein Sci., 2016, 25, 255–269 CrossRef CAS.
- V. K. Misra, J. L. Hecht, A. S. Yang and B. Honig, Biophys. J., 1998, 75(5), 2262–2273 CrossRef CAS.
- A. Marcovitz and Y. Levy, J. Phys. Chem. B, 2013, 117, 13005–13014 CrossRef CAS.
- A. Buchberger, C. R. Simmons, N. E. Fahmi, R. Freeman and N. Stephanopoulos, J. Am. Chem. Soc., 2019, 142, 1406–1416 CrossRef.
- Y. Xu, S. Jiang, C. R. Simmons, R. P. Narayanan, F. Zhang, A.-M. Aziz, H. Yan and N. Stephanopoulos, ACS Nano, 2019, 13(3), 3545–3554 CrossRef CAS.
- L. S. Dodda, I. C. De Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS.
- L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS.
- H. J. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: a message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91(1–3), 43–56 CrossRef CAS.
- E. Poppleton, J. Bohlin, M. Matthies, S. Sharma, F. Zhang and P. Šulc, Nucleic Acids Res., 2020, 48, e72 CrossRef CAS.
- A. Šali and T. L. Blundell, J. Mol. Biol., 1993, 234(3), 779–815 CrossRef.
- S. A. Johnston, V. Domenyuk, N. Gupta, M. T. Batista, J. C. Lainson, Z.-G. Zhao, J. F. Lusk, A. Loskutov, Z. Cichacz and P. Stafford, et al. , Sci. Rep., 2017, 7, 1–11 CrossRef CAS.
- J. Yang and Y. Zhang, Nucleic Acids Res., 2015, 43, W174–W181 CrossRef CAS.
- A. Drozdetskiy, C. Cole, J. Procter and G. J. Barton, Nucleic Acids Res., 2015, 43, W389–W394 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01639j |
| This journal is © The Royal Society of Chemistry 2021 |