View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C5RA25052H (Paper) RSC Adv., 2016, 6, 30353-30361

A modified random forest approach to improve multi-class classification performance of tobacco leaf grades coupled with NIR spectroscopy

Jun Bina, Fang-Fang Aib, Wei Fan*a, Ji-Heng Zhou*a, Yong-Huan Yunc and Yi-Zeng Liangc
aCollege of Bioscience and Biotechnology, Hunan Agricultural University, Changsha, China. E-mail: wei_fan@foxmail.com; jihengzhou211@163.com; Tel: +86-731-84635356 Tel: +86-731-84785708
bShanghai Tobacco Group Co., Ltd., Shanghai, China
cCollege of Chemistry and Chemical Engineering, Central South University, Changsha, China

Received 25th November 2015 , Accepted 16th March 2016

First published on 17th March 2016

Abstract

To select informative variables for improving the ensemble performance in random forests (RF), a modified RF method, named random forest combined with Monte Carlo and uninformative variable elimination (MC-UVE-RF), is proposed for multi-class classification analysis of near-infrared (NIR) spectroscopy in this work. The MC method is used to increase the diversity of classification trees in RF and the UVE method is applied to gradually eliminate the less important variables based on variable reliability obtained by aggregation of each sub-model. The above two steps can be regarded as a variable selection process. As comparisons to MC-UVE-RF, the conventional RF, model population analysis combined with RF (MPA-RF) and support vector machine (SVM) for discrimination of tobacco grades by NIR spectroscopy have also been investigated. MC-UVE-RF has a marked superiority for discriminating tobacco samples into high-quality, medium-quality and low-quality groups of dataset I and II with external validation accuracy 100% and 96.83%, respectively (coarse classification). Furthermore, a good external validation accuracy in the subdivision of high-quality, medium-quality and low-quality groups of dataset I is 88.46%, 97.22% and 96%, and that of the subdivision of dataset II's three groups is 100%, 97.14% and 100%, respectively, which are better than or equal to those by other methods (refined classification). Therefore, MC-UVE-RF is a powerful alternative to multiple classification problems. Moreover, it could be a fast and powerful method for discrimination of tobacco leaf grades coupled with NIR technology instead of artificial judgment.

1. Introduction

Multiple classifiers are important in pattern recognition. In recent studies, various classification algorithms have been proposed or employed to classification problems. These methods include Bayesian methods, ensemble learning methods, neural networks, and kernel learning methods.1–4 Especially, the ensemble learning methods, constructed by a combination of several classifiers, have become one of the most efficient approaches to complex multi-class classification problems.5–7 Over the years, it has been demonstrated that, both empirically and theoretically, an ensemble classifier is often more accurate than a single one.8,9 Random forests (RF) classification algorithm, as a powerful ensemble method, consisting of many classification trees is intensively studied in recent years and shows premium performance in multi-class classification problems.10–12 During tree construction, “out of bag” (OOB) data which consists of one-third of the training samples at each iteration is used to evaluate the performance of each tree. Compared to other machine learning methods, RF can natively estimate an OOB error in the process of constructing the forest. At each node of each tree, RF randomly selects a certain amount of variables from all variables and chooses the best split from those selected variables. However, when the data is populated by too many unimportant variables, in individual tree models, the use of such variables likely generates noise and makes the probability that each splitting node selects the informative variables remarkably decline, ultimately leading to the decrease of the ensemble performance. As a newly developed method, RF coupled with model population analysis (MPA-RF),13 has been applied to solve the problem by replacing total variables with the variables whose mean decrease in accuracy (MDA) index is greater than zero. Nevertheless, there is no evidence showing that the cutoff threshold value ‘zero’ is the most reasonable. More importantly, the threshold value may be meaningless when MDA indexes of almost all variables are bigger than zero. Thus, to determine the number of retained variables which decides the accuracy of the model, RF has been modified by gradually eliminating the number of variables based on mean and standard deviation of variable importance value obtained by aggregation of each sub-model.

Near-infrared (NIR) spectroscopy, as a rapid, simple and non-destructive technique, has become an increasingly popular analytical method in classification problems.14–17 Especially, a realizing of portable NIR spectrometer instrument provides a favorable condition for real-time measurement and makes it more popular in classification problems of practical production recently. The conventional method in the discrimination of tobacco leaf grade is artificial judgment according to the appearance of the leaves and sensory taste.18,19 The main influence factor for the discrimination results of tobacco leaf grade is the different level of classification operators. Therefore, establishing a standard and reliable method to classify the quality grade of tobacco leaf samples is valuable and essential. Many published studies20,21 have successfully utilized NIR spectra coupled with chemometrics to predict the content of some chemical components which are important indicators of tobacco leaf quality.22,23 As a consequence, in this paper, a speediness and efficient method in distinguishing different tobacco leaf qualities by NIR spectroscopy would be presented and discussed.

The purposes of this study are the following: (i) modify RF with gradually eliminating the number of variables according to the order of variable reliability which obtained by aggregation of each sub-model; and (ii) compare the novel approach, namely MC-UVE-RF, with RF, MPA-RF and support vector machine (SVM) by discriminating different grades of tobacco leaf samples.

2. Materials and methods

2.1. Samples

Baoshan Oriental Tobacco Limited Liability Company provided all samples: dataset I and dataset II. These samples were inspected by artificial judgment in accordance with Flue-cured Tobacco GB 2635-1992 of China by two national tobacco grading technicians. A group and grade is determined on the basis of maturity, texture, oil content, color, and length, as well as hurts.

Dataset I which was collected in the year of 2014 contains 3 groups, including high-quality group (I), medium-quality group (I) and low-quality group (I), of 428 NIR spectra of samples. The high-quality group (I) is consisted of 9 grades of 128 samples. The medium-quality group (I) contains 14 grades of 179 samples and the low-quality group (I) contains 9 grades of 121 samples.

Dataset II which was collected in the year of 2015 also contains 3 groups, including high-quality group (II), medium-quality group (II) and low-quality group (II), of 317 NIR spectra of samples. The high-quality group (II) is consisted of 5 grades of 59 samples. The medium-quality group (II) contains 13 grades of 171 samples and the low-quality group (II) contains 8 grades of 87 samples. Detailed information about samples is shown in Tables 1 and 2.

Table 1 Statistical information of tobacco leaf samples
  Groups Grade labels Number of samples   Groups Grade labels Number of samples
Dataset I High-quality group (I) B1F 11 Dataset II High-quality group (II) B1F Null
B1L 16 B1L 11
B2F 10 B2F Null
C1F 16 C1F 9
C1L 9 C1L 15
C2F 27 C2F Null
C2L 14 C2L 12
C3F 11 C3F Null
X1F 14 X1F 12
Medium-quality group (I) B2L 15 Medium-quality group (II) B2L 12
B2V 12 B2V 9
B3F 15 B3F 14
B3L 15 B3L 13
B3V 7 B3V 12
B4F 11 B4F 13
C3L 15 C3L Null
C3V 9 C3V 15
C4L 5 C4L 14
X1L 15 X1L 15
X2F 15 X2F 14
X2L 17 X2L 15
X2V 15 X2V 15
X3F 13 X3F 10
Low-quality group (I) B1K 11 Low-quality group (II) B1K 13
B2K 16 B2K 6
B4L 16 B4L Null
CX1K 12 CX1K 12
CX2K 16 CX2K 12
GY1 7 GY1 13
X3L 13 X3L 14
X4F 15 X4F 7
X4L 16 X4L 10

Table 2 Statistical information of samples division
Datasets Classes Total Training set Testing set
Dataset I 3 428 341 87
High-quality group (I) 9 128 102 26
Medium-quality group (I) 14 179 143 36
Low-quality group (I) 9 121 96 25
Dataset II 3 317 254 63
High-quality group (II) 5 59 47 12
Medium-quality group (II) 13 171 136 35
Low-quality group (II) 8 87 69 18

2.2. Near-infrared spectral measurement

Diffuse reflectance spectra were obtained by means of a BWTEK i-Spec NIR spectrometer System (B&W Tek, Newark, DE, USA) which is equipped with a standard probe, a diffuse whiteboard and an optical fiber designed for nondestructive analysis. Spectrum was acquired by using the standard probe to scan tobacco leaf vertically, and integration time was set to 10 ms. The spectrum of each sample (results of 32 scans; spectral resolution 1.6 nm) was acquired in sextuplicate over the wavelength range 900–1700 nm with software package BWSpec 4.0 (B&W Tek, Newark, DE, USA), and the mean of six measurements was used for further analysis. Each spectrum, containing 494 wavelengths, was recorded in reflectance mode. Spectrometer warmed up 30 min before scanning. All operations under environment temperature was controlled at 25 ± 1 °C with an air conditioner.

2.3. Spectral data preprocessing and division

Spectral data preprocessing is a precondition for constructing a high-quality model. Firstly, in order to eliminate the undesired scatter effects as much as possible, such as baseline shift and non-linearity, which will influence the recorded NIR spectra, the commonly used Savitzky–Golay (SG)24 smoothing technique, multiplicative scatter correction (MSC)25 method and second derivative (2nd derivative)26 approach were applied to pre-process the NIR spectra. Then, all datasets were separated into training set (80%) and testing set (20%) by sample set partitioning based on joint x–y distances (SPXY),27 respectively.

2.4. Chemometrics methods

2.4.1. Random forest. Random forests, proposed by Breiman in 2001,28 probably is one of the frequently employed methods for multi-class classification. It grows a collection of decision trees, called a forest, and uses these for classifying an object into one of the classes. In these trees, leaves represent class labels and branches represent conjunctions of features that lead to those class labels. The random forests algorithm for classification can be implemented as follows:

(1) Draw ntree bootstrap samples from the original training dataset. In the bootstrap set, about two-thirds of the original training samples are used to grow a classification tree. Other one-third of the samples are left which are called OOB samples. Here, OOB samples can be used to obtain estimate of classification accuracy of internal validation.

(2) For each bootstrap sample, grow an unpruned classification tree, and modify with the following procedure: at each node, randomly select mtry variables and choose the best split from among those variables. That is, each tree is constructed using the bootstrap samples of the training data and random feature selection.

(3) Predict new data by aggregating the predictions of the ntree trees with the majority vote of all analogous trees in the forest.

The frequently used type of RF to measure variable importance is the MDA index based on permutation. For each tree, the classification accuracy of the OOB samples is determined both with and without random permutation of the values to each variable, one by one. The MDA of the classification was used to measure variable importance. The importance of each variable j can be calculated as following:

Importance (j) = accuracy (j)normal − accuracy (j)permuted

2.4.2. MC-UVE-RF method. In the RF algorithm, the diversity is obtained by randomly choosing training samples on which to train each tree and by randomly choosing parts of variables at each node of each tree. The performance of individual trees is guaranteed by using unpruned tree classifiers with maximal splitting depth. However, some uninformative or interfering variables might affect the performance of the RF models. Therefore, a new method, called MC-UVE-RF, is proposed for the reliable selection of more informative variables to improve the performance of RF. MC coupled with RF is similar to MPA-RF.13 The main idea of MPA-RF is to extract interesting information from a “population” of sub-models, which are built on different sub-datasets sampled from the original dataset using Monte Carlo (MC) sampling technique. The variables whose MDA indexes are greater than zero are selected. However, the cutoff threshold “zero” is not so reasonable because it does not represent that the selected variables are the optimum. Therefore, we combine the idea of UVE29 to eliminate uninformative variables. Furthermore, reliability value of MDA index is more reasonable for evaluation of each variable importance than mean value of that index obtained by model population analysis. The detailed procedures of MC-UVE-RF can be intrinsically described as follows:

(1) By the MC sampling technique, a certain ratio of samples is randomly selected from the training set as the training subset and the procedure would be repeated for thousands of times.

(2) After setting up the training subset, thousands of classification sub-models would be established utilizing RF.

(3) For each sub-models, the variable importance order would be obtained by RF. Subsequently, the reliability of each variable j would be calculated by aggregation of the variable importance results of all sub-models, which can be quantitatively measured by the reliability defined as:

r(j) = mean (importance (j))/std (importance (j))
where mean (importance (j)) and std (importance (j)) are the mean and standard deviation of the variable importance of variable j, separately. The larger the reliability, the more important the corresponding variable is. Finally, rank the reliability for each variable.

(4) Select the optimum variable combination by running the RF with gradually eliminating the number of variables based on the order of variable reliability according to the OOB error of each established model with different number of variables.

(5) Build the RF model with the newly selected variables and predict new data by aggregating the predictions of the ntree trees with the majority vote of all analogous trees in the forest.

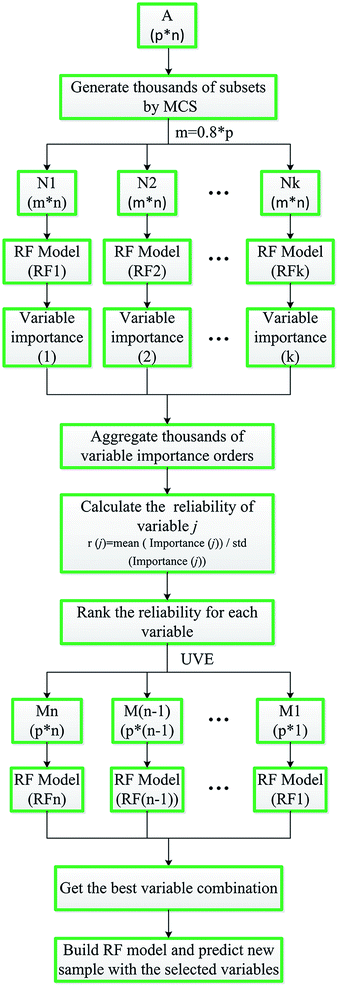
In order to better understand this approach, a simple graphic flowchart of MC-UVE-RF is briefly shown in Fig. 1.


image file: c5ra25052h-f1.tif
Fig. 1 A simple flowchart of MC-UVE-RF method.

2.5. Statistics and software

For actual implementation, the partial least squares linear discriminant analysis (PLS–LDA)30 based on the plsgenomics package. Random Forest package was applied to RF, MPA-RF and MC-UVE-RF. All the data analysis scripts were coded in R language with R2.15.2 except SVM. LIBSVM (version 3.20) package was used to performed SVM computations in Matlab 2015a (Mathworks, Natick, USA).

3. Results and discussion

3.1. Classification by PLS–LDA

In this study, one of the most important purposes is to classify all the samples into three groups, including high-quality, medium-quality and low-quality group (coarse classification). Moreover, subdivision of those three groups into different grades, respectively (refined classification), is also the goal of this article. In the following discussion involving figures, the division of dataset I into high-quality, medium-quality and low-quality groups is regarded as an example.

PLS–LDA method, combination of PLS and LDA, employs class information to maximize the separation between classes. It is better than PLS, because it can be validated by a set of independent data. In this part, dataset I was analyzed by PLS–LDA to construct a linear discrimination model and to explore the distribution trends of the samples. The PLS–LDA score plot for dataset I is shown in Fig. 2. One can clearly see that classified result of PLS–LDA is not satisfactory. The best principal components of 7, 4, 6 and 5 in dataset I and its three sub-classes were chosen to build discrimination models, respectively. The best principal components of 2, 3, 4 and 5 in dataset II and its three sub-classes were selected to build discrimination models, respectively. The classification accuracy of training set and testing set of dataset I is only 50% and 44.19%, respectively. The rest of PLS–LDA predicted results of dataset I and dataset II are shown in Tables 3 and 4. As these classification results are inacceptable, it is necessary to looking for more powerful classification algorithm to solve this problem.


image file: c5ra25052h-f2.tif
Fig. 2 Score plot of dataset I by PLS–LDA.
Table 3 The comparison results of prediction accuracy (%) between MC-UVE-RF and other three methods for grades classification of dataset I and its three sub-classes
Datasets Samples PLS–LDA SVM RF MPA-RF MC-UVE-RF
a A/B represents the right predicted samples/all used predicted samples.
Dataset I Training set 50(171/342)a 98.24(336/342) 100(342/342) 100(342/342) 100(342/342)
Testing set 44.19(38/86) 97.67(84/86) 98.84(85/86) 98.84(85/86) 100(86/86)
High-quality group (I) Training set 67.65(69/102) 100(102/102) 100(102/102) 100(102/102) 100(102/102)
Testing set 53.85(14/26) 84.62(22/26) 88.46(23/26) 88.46(23/26) 88.46(23/26)
Medium-quality group (I) Training set 81.82(117/143) 97.90(140/143) 100(143/143) 100(143/143) 100(143/143)
Testing set 88.89(32/36) 91.67(33/36) 94.44(34/36) 94.44(34/36) 97.22(35/36)
Low-quality group (I) Training set 77.08(74/96) 97.92(94/96) 100(96/96) 100(96/96) 100(96/96)
Testing set 56(14/25) 80(20/25) 88(22/25) 92(23/25) 96(24/25)

Table 4 The comparison results of prediction accuracy (%) between MC-UVE-RF and other three methods for grades classification of dataset II and its three sub-classes
Datasets Samples PLS–LDA SVM RF MPA-RF MC-UVE-RF
Dataset II Training set 60.24(153/254) 97.24(247/254) 100(254/254) 100(254/254) 100(254/254)
Testing set 61.90(39/63) 96.83(61/63) 93.65(59/63) 93.65(59/63) 96.83(61/63)
High-quality group (II) Training set 85.11(40/47) 93.62(44/47) 100(47/47) 100(47/47) 100(47/47)
Testing set 75(9/12) 91.67(11/12) 91.67(11/12) 91.67(11/12) 100(12/12)
Medium-quality group (II) Training set 73.53(100/136) 99.26(135/136) 100(136/136) 100(136/136) 100(136/136)
Testing set 68.57(24/35) 94.28(33/35) 97.14(34/35) 97.14(34/35) 97.14(34/35)
Low-quality group (II) Training set 79.71(55/69) 97.10(67/69) 100(69/69) 100(69/69) 100(69/69)
Testing set 61.11(11/18) 100(18/18) 100(18/18) 100(18/18) 100(18/18)

3.2. MC-UVE-RF analysis

The RF classifier needs to optimize two parameters in the training process: the number of classification trees (ntree) and the number of split variables (mtry). Therefore, the influence of the two parameters is investigated as following. The OOB classification errors are plotted against the number of trees grown. As it can be seen from Fig. 3, the OOB errors for dataset I and its three sub-datasets neither decrease nor increase greatly when ntree varies from 500 to 2000, or the models would not be overfitted as the errors reach a certain value, no matter how many trees are built. Then, mtry is optimized by running the RF 100 times, and the starting value of mtry is the default value (the square root of total number of variables31), and the step factor at each iteration is 2. Fig. 4 shows that there are also no big differences between OOB errors with different mtry for dataset I and its three sub-datasets. Among them, the errors are the lowest or equally to other points when mtry are set to the default value (mtry = 22). Therefore, the default values of these two parameters were adopted (ntree = 500, mtry = sqrt (number of total variables)).
image file: c5ra25052h-f3.tif
Fig. 3 Effects of number of trees (ntree) on OOB errors for classifying training samples of dataset I and its three sub-classes by RF.

image file: c5ra25052h-f4.tif
Fig. 4 Effects of random split variables (mtry) on OOB errors for classifying training samples of dataset I and its three sub-classes by RF.

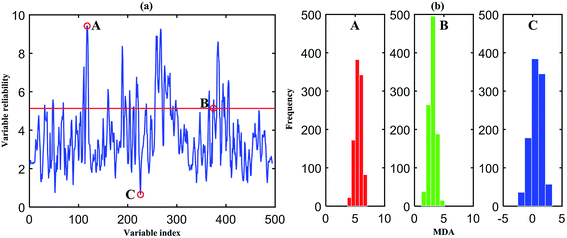
In the following, only the classification process of overall samples of dataset I is described in detail. In the process of each sub-model building, variable importance is calculated. The MDA index in classification based on permutation is used to evaluate the importance of each variable. The prediction accuracy of after permutation is subtracted from the prediction accuracy before permutation and averaged over all trees in the forest to give the permutation importance value. Since the MDA shows a large value when these variables are permutated, it may be thought that these variables are very important. However, as is illustrated by Huang et al.13 different variable importance orders could be obtained by RF model using the same dataset in different times. That is because the trees in the forest are different between each other, which will cause different results. Therefore, in order to select the informative and reliable variables, 1000 RF sub-models are established combining with MC sampling method and 80% samples are selected in each sub-model. Each variable is given a MDA index in each sub-model. Gather 1000 MDA values, and the reliability of each variable is calculated by mean/std of MDA value. The reliability of each variable is shown in Fig. 5(a). Then, sort the reliability and select the optimum variable by running the RF with gradually eliminating the number of variables. As shown in Fig. 6, the lowest OOB error is obtained when the variable number is 80. Accordingly, these 80 variables are presented above the red line in Fig. 5(a). Three representative variables are selected to show the MDA distribution in Fig. 5(b). Among them, the reliability of variable A, B and C rank 1, 80 and 494, respectively. A and B are the selected variables, and C is the eliminated one. Obviously, the mean of MDA index from high to low is A, B and C. The distribution range from big to small is C, B and A. It can be concluded that the selected variables are important and relatively stable.


image file: c5ra25052h-f5.tif
Fig. 5 (a) The variable reliability measurement given by MC-UVE-RF method. The red line is the critical line. A and B are the selected variables, and C is the eliminated variable; (b) the distribution range of MDA index of variable A, B and C.

image file: c5ra25052h-f6.tif
Fig. 6 The selection of the important variable number by MC-UVE-RF.

Therefore, those 80 reliable variables are selected as the combination variables in the following RF running. The cutoff value of variable reliability is 5.1318. Other datasets are operated with the same process as described above. The cutoff values of variable reliability of all datasets are given in Table 5. From Tables 3 and 4, it can be seen that the external validation accuracies by MC-UVE-RF are decent. It demonstrates that MC-UVE-RF is expert in classifying the tobacco leaf samples into high-quality, medium-quality and low-quality groups. Meanwhile, it has performed well in all subdivisions. In RF, multidimensional scaling (MDS) can be used to visualize the similarities of samples to some extent. By using this approach, most of the similarity information can be displayed in a 2-dimensional or 3-dimensional space. It can be seen from Fig. 7 that a much better classification result is obtained for the three grades when compared to that of PLS–LDA. Because of perspective, it seems that samples in Fig. 7 are not separated very well. But, they actually are kept apart completely in multiple-dimensional space.

Table 5 The cutoff values of variable reliability of all datasets
Datasets Cutoff values
Dataset I 5.1318
High-quality group (I) 2.7907
Medium-quality group (I) 4.6030
Low-quality group (I) 2.9372
Dataset II 4.5035
High-quality group (II) 1.0605
Medium-quality group (II) 2.8718
Low-quality group (II) 3.5328


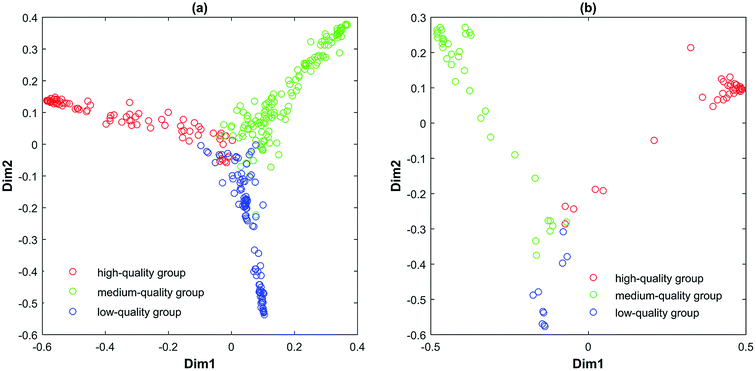image file: c5ra25052h-f7.tif
Fig. 7 Classification by MC-UVE-RF: (a) denotes training set of dataset I and (b) denotes testing set of dataset I.

The stability of discriminant methods relying on a random component is an important issue. High stability across different runs is considered to be an asset. Thus, MC-UVE-RF, as a cluster ensemble algorithm based on random strategy, its stability should be paid close attention to. An experimental study was carried out to examine whether MC-UVE-RF can give stable results. The MC-UVE-RF algorithm had run 100 times for each sub-dataset. The external validation accuracy with the highest frequency of all datasets has been shown in Table 6. The frequency of its external validation accuracy of each dataset exceeding 70% has demonstrated the preferable stability of MC-UVE-RF method, except that of dataset II.

Table 6 The external validation accuracy with the highest frequency of MC-UVE-RF
Datasets External validation accuracy (%) Highest frequency (%)
Dataset I 100 71
High-quality group (I) 88.46 71
Medium-quality group (I) 97.22 72
Low-quality group (I) 96 74
Dataset II 96.83 47
High-quality group (II) 100 100
Medium-quality group (II) 97.14 94
Low-quality group (II) 100 100

3.3. Comparison with RF, MPA-RF and SVM

In order to check the performance of the proposed method, the external validation accuracy results of other three methods were compared, including RF, MPA-RF and SVM. In the process of RF, MPA-RF and MC-UVE-RF analysis, there are all existed tree model establishments. One of the differences between them is that there is just one model for RF, while for MPA-RF and MC-UVE-RF, there are thousands of sub-models. As illustrated in the section of MC-UVE-RF analysis, the parameter mtry almost has no impact on the model performance and ntree also has no obvious influence when the value is varied from 500 to 2000. Therefore, for RF and MPA-RF, default values (ntree = 500, mtry = sqrt (number of total variables)) of these two parameters were also adopted. One can clearly see from Tables 3 and 4 that there is almost no difference between RF and MPA-RF classification results except a small difference between them for the subdivision of low-quality group of dataset I. That is because the MDA of variable importance of all variables are bigger than zero except that of only one variable in low-quality group of dataset I is lower than zero by MPA-RF. Therefore, MPA-RF utilizes 494, 494, 494 and 493 variables for RF running with the four sets in dataset I, respectively. That is to say, the data of this manuscript suggest that MPA-RF does not improve the performance. It is clearly that MC-UVE-RF achieves better or equal classification results compared to that of RF and MPA-RF. Combining with MC sampling method could enhance the tree diversity, because different samples of the training sets are used to grow trees in each sub-model. By this method, the calculation of the reliability of each variable in the following is reasonable. A reliable and informative variable subset is used for growing trees in RF could also lower the classification error rate by utilizing the idea of UVE.

SVM,32 proposed by Cortes and Vapnik in 1995, is a linear machine working in the high dimensional feature space formed by the non-linear mapping of the n-dimensional input vector x into a K-dimensional feature space (K > n) with a function. In order to get best results, the PCA dimension reduction method and normalization are applied before running SVM. For SVM, there are some parameters needed to be optimized, including core function, penalty parameter C and kernel parameter gamma (γ). A grid search method with exponentially growing sequences of C and γ were applied. The parameters which could generate best cross-validation accuracy were used. Finally, radial basis function (RBF) was chosen as the core function for the two datasets. From Tables 3 and 4, it can be seen that the external validation accuracy by the proposed method are better or equal to that of SVM.

As many method-comparison studies suffer from equivocalness or from comparisons not being quite fair, a method comparison method known as sum of ranking differences (SRD)33–35 had been employed to evaluate the classification ability of MC-UVE-RF and other methods. SRD is a simple objective procedure to ensemble multiple method merits for ranking methods allowing automatic selection of a set of methods. The smaller the SRD value is, the better the method is. In many applications, row average is used as the benchmark. In this case, such a benchmark would correspond to a hypothetical average column. Other data integration possibilities also exist, such as row minimum for error rates, residuals, row maximum for the best classification rates, etc. Since we were to solve classification problems in this paper, the row maximum value should be selected as the benchmark. It can be seen from Table 7, when row maximum was chosen as the benchmark, MC-UVE-RF which has the smallest SRD values turned to be the best method.

Table 7 The SRD and ranking on the basis of SRD of MC-UVE-RF and other methods
Datasets References PLS–LDA SVM RF MPA-RF MC-UVE-RF
Dataset I Row maximum 18 12 4 2 0
Rank 5 4 3 2 1
Dataset II Row maximum 18 16 8 8 0
Rank 5 4 3 2 1

The comparison of MC-UVE-RF with other three classification methods in chemometrics and method-comparison methodology showed that MC-UVE-RF can acquire nice prediction results and superior to other classical algorithms in tobacco leaf grade spectral data.

4. Conclusion

In this study, a modified RF approach, named as MC-UVE-RF, was proposed and applied to classify different grades of tobacco NIR spectral datasets. In contract to commonly RF, MC which can increase the diversity of decision trees in RF runs for providing a reliable and stable variable importance order is combined in this approach. Moreover, UVE is employed to perform the extraction of a reliable and informative variable subset for growing trees in RF according to the order of variable reliability. By applications of MC and UVE to variable selection, it was demonstrated that the proposed method was effective and competitive. NIR technology could provide a fast and nondestructive alternative to reference methods, as it dramatically reduces analysis time without damage to samples. The established method of MC-UVE-RF coupled with NIR showed a good performance for discriminating tobacco leaf quality grades. The external validation accuracy in coarse classification of dataset I and dataset II is 100% and 96.83%, respectively. And the external validation accuracy in refined classification of dataset I's three groups is 88.46%, 97.22% and 96%, and that of the subdivision of dataset II's three groups is 100%, 97.14% and 100%, respectively. Compared with three recent and frequently-used classification methods, including RF, MPA-RF, and SVM, MC-UVE-RF had a marked superiority in classification accuracy.

Therefore, the proposed method is a promising tool for the solution of tobacco leaf grade classification problems. Also, applicability is by no means limited to the text mentioned, and wide applications of this method to multi-class classification systems can be foreseen.

Acknowledgements

This work is financially supported by the National Nature Foundation Committee of PR China (Grant No. 21275164), Youth Foundation of Hunan Agricultural University (Grant No. 15QN17) and Hunan Provincial Innovation Foundation for Postgraduate (Grant No. CX2015B237).

References

  1. R. Soyer, Technometrics, 2004, 2, 251–252 CrossRef .
  2. S. Oh, S. L. Min and B. T. Zhang, IEEE/ACM Trans. Comput. Biol. Bioinf., 2010, 8, 316–325 Search PubMed .
  3. G. B. Ou and L. M. Yi, Pattern Recogn., 2007, 40, 4–18 CrossRef .
  4. T. Sun, L. Jiao, F. Liu, S. Wang and J. Feng, Pattern Recogn., 2013, 46, 3081–3090 CrossRef .
  5. J. W. Chan and D. Paelinckx, Rem. Sens. Environ., 2008, 112, 2999–3011 CrossRef .
  6. A. C. Tan, D. Gilbert and Y. Deville, Genome Inf. Ser., 2003, 14, 206–217 CAS .
  7. Y. Peng, Comput. Biol. Med., 2006, 36, 553–573 CrossRef CAS PubMed .
  8. R. Maclin and D. Opitz, J. Artif. Intell. Res., 2011, 11, 169–198 Search PubMed .
  9. A. Boublenza, M. A. Chikh and S. Bouchikhi, Journal of Medical Imaging and Health Informatics, 2015, 5, 513–519 CrossRef .
  10. F. F. Ai, J. Bin, Z. M. Zhang, J. H. Huang, J. B. Wang, Y. Z. Liang, L. Yu and Z. Y. Yang, Food Chem., 2014, 143, 472–478 CrossRef CAS PubMed .
  11. L. Dai, C. M. V. Gonçalves, Z. Lin, J. H. Huang, H. M. Lu, L. Z. Yi, Y. Z. Liang, D. Wang and D. An, Talanta, 2015, 135, 108–114 CrossRef CAS PubMed .
  12. J. H. Huang, R. H. He, L. Z. Yi, H. L. Xie, D. S. Cao and Y. Z. Liang, Talanta, 2013, 110, 1–7 CrossRef CAS PubMed .
  13. J. H. Huang, J. Yan, Q. H. Wu, M. D. Ferro, L. Z. Yi, H. M. Lu, Q. S. Xu and Y. Z. Liang, Talanta, 2013, 117, 549–555 CrossRef CAS PubMed .
  14. H. P. Xie, J. H. Jiang, Z. Q. Chen, G. L. Shen and R. Q. Yu, Anal. Sci., 2006, 22, 1111–1116 CrossRef CAS PubMed .
  15. X. G. Shao and Y. Zhuang, Anal. Sci., 2004, 20, 451–454 CrossRef CAS PubMed .
  16. R. Jukka, W. M. HaKan, T. Rebecca and L. S. Taylor, Anal. Chem., 2005, 77, 556–563 CrossRef PubMed .
  17. M. Casale, M. J. S. Abajo, J. M. G. Sáiz, C. Pizarro and M. Forina, Anal. Chim. Acta, 2006, 557, 360–366 CrossRef CAS .
  18. M. Liang, J. Y. Cai, K. Yang, R. X. Shu, L. L. Zhao, L. D. Zhang and J. H. Li, Chin. J. Anal. Chem., 2014, 42, 1687–1691 CAS .
  19. P. Y. Xia, X. Q. Ding and N. Yang, 10th ACIS International Conference on Software Engineering, Artificial Intelligences, Networking and Parallel/Distributed Computing, 2009, pp. 144–148 Search PubMed .
  20. C. Tan, M. Li and X. Qin, Anal. Sci., 2008, 24, 647–653 CrossRef CAS PubMed .
  21. Z. Yong, C. Qian, Y. Xie, J. X. Yang and Z. Bing, Spectrochim. Acta, Part A, 2008, 71, 1408–1413 CrossRef PubMed .
  22. J. Sádecká and J. Polonský, J. Chromatogr. A, 2003, 988, 161–165 CrossRef .
  23. G. Jm, S. Garrigues, I. G. M. De and A. Perez-Ponce, Anal. Chim. Acta, 1998, 373, 63–71 CrossRef .
  24. A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef CAS .
  25. T. Isaksson and T. Næs, Appl. Spectrosc., 1988, 42, 1273–1284 CrossRef CAS .
  26. A. Rinnan, F. V. D. Berg and S. B. Engelsen, TrAC, Trends Anal. Chem., 2009, 28, 1201–1222 CrossRef CAS .
  27. R. K. H. GalvãO, M. C. U. Araujo, J. Gledson Emídio, M. J. C. Pontes, S. Edvan Cirino and T. C. B. Saldanha, Talanta, 2005, 67, 736–740 CrossRef PubMed .
  28. L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef .
  29. W. Cai, Y. Li and X. Shao, Chemom. Intell. Lab. Syst., 2008, 90, 188–194 CrossRef CAS .
  30. L. Z. Yi, J. He, Y. Z. Liang, D. L. Yuan and F. T. Chau, FEBS Lett., 2006, 580, 6837–6845 CrossRef CAS PubMed .
  31. A. Liaw and M. Wiener, R News, 2002, 2/3, 18–22 Search PubMed .
  32. C. Cortes and V. Vapnik, Mach. Learn., 1995, 2, 1–28 Search PubMed .
  33. K. Héberger, TrAC, Trends Anal. Chem., 2010, 29, 101–109 CrossRef .
  34. K. Kollár-Hunek and K. Héberger, Chemom. Intell. Lab. Syst., 2013, 127, 139–146 CrossRef .
  35. C. West, M. A. Khalikova, E. Lesellier and K. Heberger, J. Chromatogr. A, 2015, 1409, 241–250 CrossRef CAS PubMed .
This journal is © The Royal Society of Chemistry 2016
Click here to see how this site uses Cookies. View our privacy policy here.