Interaction mechanism of doxorubicin and SWCNT: protonation and diameter effects on drug loading and releasing

Abstract

In the present work the adsorption of doxorubicin (DOX) on the surface of single-walled carbon nanotubes (SWCNTs) as well as its encapsulation in SWCNTs, and their dependence on the protonation of the NH₂ group of DOX, solvent, and the diameter of armchair (n, n) SWCNTs were systematically investigated using theoretical methods such as PM6-DH2 and M06-2X in the scheme of OMIOM. It was found that the two loadings, adsorption on the sidewall of CNTs and encapsulation in CNTs, have distinct solvent, protonation and diameter dependences. The encapsulation is much stronger than the adsorption of DOX on the sidewall of CNTs, and the former also has significantly higher solvent and protonation effects than the latter. The adsorption primarily occurs through π–π stacking and just becomes slightly stronger as the diameter of the CNTs increases, while besides the π–π stacking the additional C–H/N–H/O–H⋯π and C=O⋯π also contribute to the encapsulation of DOX in CNTs. It seems that (8, 8) CNT with a diameter of ∼ 11 Å is energetically an onset for the encapsulation, since the encapsulation turns from endothermic to exothermic when the diameter is larger than approximately 11 Å, and the optimal diameter for the encapsulation is 14 Å corresponding to (10, 10) CNT. Thus for the thick CNT the encapsulation may also play an important role in the loading and releasing for the CNT-based drug delivery system of the DOX.

---

Introduction

As one of the most promising applications of carbon nanotubes (CNTs), tumor-targeted drug delivery systems on the basis of CNTs have received much effort from both experimentalists and theoreticians.^1–18 The potential drug delivery systems are superior to free drugs in a few aspects, such as longer circulation time, higher drug uptake and selectivity, lower dosage, and better therapeutic efficacy. Doxorubicin (DOX, Adriamycin, C₂₇H₂₉NO₁₁) is commonly used in chemotherapy, for example for the treatment of Kaposi's sarcoma, ovarian carcinoma, and lung and breast cancer.¹⁹ DOX shows chemotherapeutic activity through intercalating between adjacent DNA bases pairs and preventing replication by causing conformational changes in the DNA molecule. However, DOX is also highly toxic, especially to hearts and kidneys, limiting its therapeutic applications. Novel drug-delivery strategies for DOX are thus essential for its more effective and wide application.

For this purpose Dai et al. suggested a single-walled CNT (SWCNT)-based drug delivery system for DOX,^4,6,20–22 consisting of SWCNTs, phospholipid (PL)-poly (ethylene glycol) (PEG) chains, and a cyclic tripeptide (arginine–glycine–aspartic acid, RGD). The PL-PEG functionalizes the SWCNTs through noncovalent interaction between the PL chain and SWCNTs, and the PEG group pulls the SWCNT to aqueous solutions, while DOX can be ultra-highly loaded to the SWCNT system through its adsorption on the sidewall of SWCNTs due to the high degree of π-stacking. It was estimated that the surface area of the SWCNTs is covered by the PL-PEG (two hydrocarbon chains of PL) and DOX in percentages of 10% and 75%, respectively. In this conjugate system (DOX–SWCNT–PL-PEG–RGD), the RGD imparts a recognition ligand for the receptors (integrin α_vβ₃ up-regulated in a wide range of solid tumors). The targeting moiety plays very important roles in enhancing the cellular uptake of DOX, and accordingly the toxicity of DOX could be reduced to normal cells as compared with free DOX.

It is very amazing that the above DDS conjugates have a strong pH dependence (enhanced at high pH and reduced at low pH).^4,6 DOX remains bound to the SWCNTs at pH > 7, yet is readily released in acidic solution. This was mainly attributed to the protonation of the NH₂ group of DOX at low pH values, which enhances the hydrophilicity and solubility of DOX. This feature has a very important implication to regulate drug loading and releasing from the SWCNT-based DDS since the physiological environment is weakly basic (pH = 7.4) while intracellular lysosomes are acidic, enabling high extracellular loading of DOX and its ready release intracellular of tumors. The spontaneous encapsulation of biomolecules such as single strand DNA,^23–26 protein,^27–29 and anticancer drug molecules³⁰ has been well established. Although SWCNTs have a great potential to encapsulate DOX into their cavities, the relevant experimental studies^4,6 attributed the loading to the adsorption on the surface of SWCNTs through π–π stacking. The encapsulation may be achieved through cooperative π–π stacking and X–H⋯π (X = N and C), and may be even stronger than the surface adsorption, implying that DOX releases slowly which may actually be important for the DDS, since slow release is critically significant in drug delivery for minimizing the amount of drug lost before reaching targets and increasing the circulation time.

In the present work, the adsorption on the outer surface of SWCNTs (the adsorption on the sidewall of CNTs hereafter referred to as DOX–CNT) as well as the encapsulation of DOX in CNTs (DOX@CNT), and their dependences on the protonation of the NH₂ group in DOX and the diameter of armchair (n, n) SWCNTs were systematically investigated with a series of theoretical methods such as PM6-DH2 and M06-2X in the scheme of OMIOM. It was found that the two loadings, on the sidewall and encapsulation, have distinct solvent, protonation and diameter effects. (8, 8) CNT may be an onset for the encapsulation since the encapsulation changes from endothermic to exothermic when the diameter is larger than approximately 11 Å, and the optimal diameter for the encapsulation is 14 Å corresponding to (10, 10) CNT. The encapsulation may play an important role in the loading and releasing for the CNT-based drug delivery system of DOX.

Model and theoretical methods

It is well known that, in spite of great improvement over LDA, typical GGA types of density functional theory (DFT) like the PW91 and PBE methods still greatly underestimate the binding for systems mainly arising from weak noncovalent interaction. Hybrid meta-GGA functionals, M05-2X and M06-2x, developed by Truhlar et al.³¹ have been well applied to the small typical π⋯π stacking systems, e.g., benzene and adenine dimers,³² and the π⋯π stacking systems of DNA bases and carbon nanomaterials.^33–36 Recently DFT-D methods were widely used to deal with the weak systems by directly supplementing the DFT methods with van der Waals terms.^37,38 However, the M06-2X as well as other dispersion corrected DFTs (DFT-D) are hard to directly apply to the entire system for the SWCNTs–DOX because of huge computational demand.

It was reported that the dispersion and hydrogen bonds corrected PM6 (referred to as PM6-DH2)^39,40 is able to yield the most accurate results for non-covalent interactions of all the semiempirical quantum mechanical methods.⁴¹ The PM6-DH2 predicted binding energies for the non-covalent interaction between DNA bases and C₆₀/Li@C₆₀ agree well within 0.5 kcal mol⁻¹ with those from the DFT-D method.^35,36,42 Because of significant low computational demand, PM6-DH2 may be applied to macromolecular systems for describing H-bond and non-covalent interactions; however, it needs to be carefully validated before extensive applications. Thus, in the present work, the PM6-DH2 implemented in the MOPAC2009 package⁴³ was firstly validated for the adsorptions of the DOX on a few SWCNTs by comparing with higher level methods such as the M06-2X and DFT-D in the scheme of ONIOM.⁴⁴ To include the solvent effect in the PM6-DH2 method, a conductor-like screening model (COSMO) approach is applied.⁴⁵

To validate the PM6-DH2 method for the present systems, in the present work the two layer ONIOM (M06-2X/6-31G*:UFF) was performed for the binding of the DOX on the sidewall of three CNTs (7, 7), (10, 10), and (13, 13). In the ONIOM scheme the higher level model includes DOX/DOXH⁺ and twenty six-member rings of the CNT just below the DOX, and the rest was treated with the lower level model. To get the preliminary interaction configurations between DOX and the CNTs, the docking with the PATCHDOCK program⁴⁶ was employed through calculating the non-bonded terms of the molecular mechanic (MM) force field. However, for the investigated CNTs the procedure only resulted in those for the adsorption of DOX on the sidewall of the CNTs. Thus, the initial configurations for the encapsulation were generated by manually inserting DOX into the cavity of the CNTs with GaussView 5, followed by using the clean tool in Gaussview to roughly adjust the distance between DOX and the CNTs.

Results and discussion

A conspicuous feature of doxorubicin is that it has three aromatic hydroxyanthraquinonic rings, and a grand π orbital thus delocalizes over the planar aromatic rings. A few intramolecular hydrogen bonds through O⋯H–O stabilize its conformation. The tetrahydropyran ring takes a chair configuration, where the hydroxyl and NH₂ groups are in staggered positions. Fig. 1 displays the frontier molecular orbitals of DOX and DOXH⁺ (protonated doxorubicin). The highest occupied molecular orbital (HOMO) of DOX delocalizes with prominent contributions from the three aromatic rings as well as the NH₂ group, while for the HOMO of DOXH⁺ the contribution mainly comes from the three aromatic rings and the protonated NH₂ group does not have a clear contribution. However, the LUMOs of the DOX and DOXH⁺ are rather similar, mainly centering over the aromatic rings.

Fig. 1 Structures, HOMO (2nd row), and LUMO (3rd row) of doxorubicin (DOX), the protonated DOX (DOXH⁺), and (10, 10) CNT at the M06-2X/6-31G* level (the isosurface = 0.01 au).

The armchair SWCNTs (n, n) (n = 7–14) with a length of 24.45 Å and a diameter in the range of 9–20 Å were used in this investigation. Both ends of the CNTs are saturated with hydrogen atoms to avoid the suspending carbon bonds. Because of the sp²-hybridized carbon atoms constituting the CNTs, a grand delocalized π frontier molecular orbital spreads over the inside and outside wall surfaces of the CNTs. Compared with the frontier orbitals of the DOX, the HOMO of the CNTs matches well with the LUMO of DOX when the plane of the three aromatic rings of DOX approaches the surface of the CNT in parallel along with the central axis of the CNT, while the HOMO of DOX does not match the LUMO of the CNTs. The former gap (2.50 eV) for DOX-(10, 10) CNTs is also significantly smaller than the latter one (3.95 eV). This implies that they may weakly interact with each other through the HOMO of the CNTs and the LUMO of DOX when both planes approach mutually. Table 1 lists the energy levels of the frontier molecular orbitals of DOX, DOXH⁺, CNTs (n, n) (n = 7, 9, 10, and 12), and the complexes for DOX and DOXH⁺ with (10, 10) CNTs.

Table 1 The HOMO (au), LUMO (au) and gap (eV) for DOX, DOXH⁺ and CNTs at the M06-2X/6-31G(d) level^a

	HOMO	LUMO	Gap
a * adsorption on the surface; ** encapsulation.
DOX	−0.2658	−0.0794	5.07
DOXH^+	−0.3749	−0.1896	5.04
(7, 7)	−0.1772	−0.1124	1.76
(9, 9)	−0.1740	−0.1176	1.54
(10, 10)	−0.1716	−0.1205	1.39
(12, 12)	−0.1695	−0.1230	1.26
(13, 13)	−0.1687	−0.1240	1.22
DOX-(10, 10)*	−0.1721	−0.1208	1.39
DOX @(10, 10)**	−0.1716	−0.1200	1.40
DOXH^+-(10, 10)*	−0.2074	−0.1565	1.38

---

Fig. 2 displays the orbital energy changes of both LUMOs and HOMOs with respect to the diameters of (n, n) (n = 7–14) CNTs at the M06-02X/6-31G* level. It can be seen that the energies of the HOMOs of the CNTs are in the range of −4.82 to −4.59 eV and those of the LUMOs of CNTs are in the range of −3.06 to −3.38 eV. The former goes up slightly with an increase in the diameter and the latter gently goes down. In spite of the lower variation the HOMO and LUMO from PM6-DH2 for the CNTs support this trend.

Fig. 2 LUMOs and HOMOs of doxorubicin (DOX), protonated DOX (DOXH⁺), and carbon nanotubes (CNTs) at the M06-2X/6-31G* level.

Two types of DOX loading to CNTs, adsorption on the outer sidewall and encapsulation in the CNT, were thoroughly located. To ensure the minimized structures for the current large systems, a few configurations were explored by translating the doxorubicin along the axis of the CNTs from left to right for the encapsulation, and wrapping the doxorubicin in a few places for the adsorption on the surface of the CNTs. The binding energy was calculated for the most stable structure for the given configuration. According to Fig. 3 in spite of a rather low isosurface (0.01 au) both the HOMO and the LUMO for the complexes through the adsorption on the sidewall dominantly come from the CNTs. Their energy levels in Table 1 are only slightly different than those of the CNTs. Although it is hard to reflect the interaction between the DOX and the CNTs using the HOMO and LUMO, the π–π stacking can be obviously visualized via the isosurface of sign (λ₂) × ρ defined by Yang et al.,⁴⁷ which will be discussed below. Similar to the other complexes via π–π stacking, in the complex of Fig. 3 the three conjugated six-member rings are parallel to the CNTs, and they sit above the CNT 6-member ring in a displaced configuration in a vertical distance of approximately 3.3 Å.

Fig. 3 The HOMO (left, isosurface = 0.01 au) and LUMO (right) for the adsorption between DOX and (10, 10) CNTs at the M06-2X/6-31G* level.

Fig. 4 shows the binding energy of DOX loaded on the sidewall of the CNTs at the PM6-DH2 level for the most stable loading of the given CNT. In the gas phase, with the diameter increasing from CNT (7, 7) to CNT (14, 14) the binding energy changes from −33.2 kcal mol⁻¹ to −40.0 kcal mol⁻¹, which qualitatively agrees with the trend of π-stacking between aromatic bio-molecules and SWCNTs.^33,34 The weaker adsorption on the thinner CNT may be mainly attributed to the bigger curvature of the nanotube, which leads to less contact of the outer surface of the CNTs with the three aromatic rings of DOX. With the diameter increasing, a higher degree of contact between the CNTs and DOX strengthens the adsorption. A similar trend also appears on the adsorption in aqueous solution. In the aqueous solution the adsorption energies change from −27.9 to −32.6 kcal mol⁻¹ with an increase in the diameter of the CNTs. Due to the solvation of DOX, the binding strength of DOX on the CNTs is weakened by 5.3–7.4 kcal mol⁻¹ as compared with that in the gas phase. However, it can be found that the protonation effect on the binding is predicted to be much less than the solvent effect. In Fig. 4, in the aqueous solution the bindings of DOXH⁺ on the CNTs are only slightly weaker, by approximately 1.0 kcal mol⁻¹, than those of DOX on the CNTs until (10, 10), and the bindings of the DOX and DOXH⁺ on the larger diameter CNTs are then rather close. The result implies that it is hard to attribute the strong pH dependence for the releasing of DOX from the CNTs to the loading on the surface of the CNTs.

Fig. 4 Binding energies of DOX-loaded on the outer surface of the CNTs with respect to the CNT diameter with the PM6-DH2 method.

The binding energy of the DOX with the sidewall of three CNTs (7, 7), (10, 10), and (13, 13) predicted with the ONIOM (M06-2X/6-31G*:UFF) method was plotted in Fig. 5. In the ONIOM scheme the higher level model includes DOX/DOXH⁺ and twenty six-member rings of the CNTs. Fig. 5 also shows that the binding decreases with an increase in the diameter. This is the same trend as predicted with the PM6-DH2 level although the absolute binding energies for the DOX in the gas and the aqueous solution are approximately 8 and 4 kcal mol⁻¹, respectively, less than the corresponding values at the PM6-DH2 level. At the M06-2X/6-31G* level the binding energies of the DOXH⁺ on CNTs (7, 7), (10, 10) and (13, 13) in the aqueous solution are predicted to be −20.4, −24.8, and −25.6 kcal mol⁻¹, respectively, which reasonably agrees with those predicted by the PM6-DH2, and is slightly weaker than those of the DOX–CNTs in aqueous solutions by 3.3, 1.5, and 3.0 kcal mol⁻¹, respectively, implying that the protonation of DOX can somewhat enhance the release of DOX from the adsorption situation. The PM6-DH2 method somewhat underestimates the inductive action of –NH₃⁺ on the three aromatic rings. However, because of the binding trend consistency predicted by the two theoretic methods, the semi-empirical PM6-DH2 may provide reasonable geometry and binding energy, especially for such a large system as DOX–CNTs after the dispersion force was explicitly introduced.

Fig. 5 Binding energies of DOX-loaded on outer surface of the CNTs with respect to CNT diameters, calculated at the ONIOM (M06-2X/6-31G*:UFF) level.

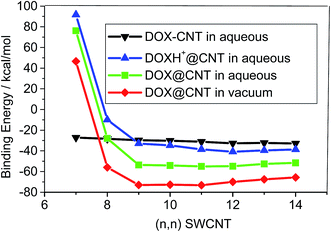
Fig. 6 shows the encapsulation of the DOX in the (n, n) SWCNTs (n = 7, 8, 9 and 11). The encapsulation of DOX in (7, 7) leads to a significant deformation of the CNTs (Fig. 6a), accompanied by a rather high deformation energy of approximately 120 kcal mol⁻¹ (Fig. 7) and positive binding energies (46.5 and 76.2 kcal mol⁻¹ in the respective gas phase and aqueous solution) for the DOX@(7, 7) CNTs. The encapsulation of DOX in (7, 7) CNTs is endothermic because of the approximate volume of DOX (14.9 × 10.8 × 6.4 ų), in which the width of 10.8 Å is even larger than the diameter of 9.5 Å of (7, 7) CNTs. This spatial effect is weakened rapidly with an increase of the CNT diameter. For the (8, 8) CNTs its binding becomes exothermic due to a considerable decrease of the deformation energy upon the encapsulation, as shown below in Fig. 8. It is apparent that the spatial effect disappears for the (9, 9) CNT (diameter, 12.4 Å) and thicker CNTs, with only a few kcal mol⁻¹ of the deformation energy that has mainly resulted from the noncovalent interaction between the DOX and the thicker CNT. Thus, the (8, 8) CNT with a diameter of 10.9 Å can be considered as an onset for the encapsulation loading of the DOX with respect to the exothermic binding.

Fig. 6 The encapsulation of DOX@(n, n) CNT (n = 7, 8, 9 and 11) predicted by PM6-DH2.

Fig. 7 Deformation energy of DOX–CNT and DOX@CNT complexes with respect to the diameters predicted with PH6-DH2. The deformation energy is the difference of the heat of formation between DOX/CNT of DOX@CNT and the individually optimized DOX/CNT = ΔH_f (DOX in the complex, DOX–CNT or DOX@CNT) + ΔH_f (CNT in the complex) − ΔH_f(DOX) − ΔH_f(CNT).

Fig. 8 Binding energies of DOX loaded on the inner surface of the CNTs (encapsulation, DOX@CNT and DOXH⁺@CNT) with respect to the CNT diameters with PM6-DH2.

The deformation energies of the SWCNTs were shown in Fig. 7 for both DOX–CNT and DOXH⁺–CNT in aqueous solutions. It can be seen that for the sidewall adsorption the deformation energies of both DOX–CNT and DOXH⁺–CNT are only approximately 3 kcal mol⁻¹. The sidewall adsorption only slightly changes the geometric conformation because of the absence of spatial limitation. However, for the encapsulation there are quite high deformation energies for both DOX and DOXH⁺ loaded on the cavity of CNTs (7, 7) and (8, 8) due to the considerable spatial limitation. In the cases of encapsulation, not only is DOX deformed considerably (deformation energy: 87 and 26 kcal mol⁻¹ for DOX@(7, 7) and DOX@(8, 8)) but also the CNT (30 and 7.2 kcal mol⁻¹) is changed seriously from a circle into an ellipse. However, with an increase in the diameter of the CNTs the deformation of the CNTs decreases gradually and the deformation energies for DOX and DOXH⁺@CNT (12, 12) are 3.8 and 4.5 kcal mol⁻¹, respectively, which are slightly greater than that of the corresponding adsorption.

Fig. 8 displays the binding energy of DOX loaded in the cavity of the CNT, i.e., encapsulation at the PM6-DH2 level. For the smaller diameter CNTs than the (8, 8) CNT, the drug loading dominantly occurs through the sidewall adsorption because of their endothermic encapsulation. It is plausible that encapsulation of the DOX occurs in the (9, 9) and thicker CNTs. From Fig. 8 the binding energies for the DOX encapsulation in (n, n) CNTs (n = 9–14) are −65.8 to −73.0 kcal mol⁻¹ in the vacuum phase, and drop to −51.6 to −53.7 kcal mol⁻¹ in aqueous solution. The solvent effects (∼15–20 kcal mol⁻¹) for DOX@CNT are higher than those of DOX–CNT, where the solvent effects are only a few kcal mol⁻¹ as shown in Fig. 4. For (8, 8) CNT, the binding strengths of the encapsulation and sidewall adsorption in the aqueous solution are rather close, −28 kcal mol⁻¹, while for the thicker CNTs the former becomes much stronger than the latter by approximately 20 kcal mol⁻¹. The encapsulation with the strong binding to the CNT may prolong the circulation time of the drug, which is actually desired for designing a novel drug delivery system. In addition, the encapsulation of the DOX varies differently with the diameter of the CNT than the adsorption on the sidewall of the CNT. The encapsulation becomes stronger until (10, 10) CNT in the vacuum and then tends to be slightly weaker for the thicker CNTs. This is due to the further contact of the DOX with the CNTs and the van der Waals forces consequently becomes less for the thicker CNTs, which will be discussed in detail below. The results indicate that the encapsulation of DOX in CNTs becomes exothermic when the diameter is larger than approximately 11 Å, and the optimal diameter for the encapsulation is 14 Å.

According to Fig. 8, the binding energies for the encapsulations of the protonated DOX (DOXH⁺) in (n, n) CNTs (n = 9–14) in aqueous solutions (the blue line) are predicted to be in a range of −32.9 to −38.7 kcal mol⁻¹, 13–20 kcal mol⁻¹ weaker than those of the DOX (the green line). This distinct binding between the DOX and DOXH⁺ has a very important implication to the cancer-targeted drug delivery system, suggesting that the DOX loading in the CNT conjugates may have a strong pH dependence, enhanced at a high pH and reduced at a low pH. The DOX remains strongly bound to the SWCNTs at pH > 7, yet the protonated DOXH⁺ readily releases in acidic solution. This was mainly attributed to the protonation of the NH₂ group of DOX at low pH values, which enhances the hydrophilicity and therefore solubility of the DOX. Due to a more significant decrease of the binding energy, the protonated-DOX–CNT complex is more ready to dissociate in acidic circumstances. This feature has a very important implication to regulate drug loading and releasing from the SWCNT-based DDS since the physiological environment is weakly basic (pH = 7.4) while intracellular lysosomes are acidic, enabling a high extracellular loading of DOX and its ready release intracellular of tumors.

Compared with the adsorption on the sidewall of the CNT, the encapsulation of the DOX is much more sensitive to the protonation that decreases its binding with the CNTs by 13–20 kcal mol⁻¹. However, for the former the protonation only slightly weakens its binding with the CNT as shown in Fig. 4. Thus, the encapsulation of the DOX may also play an important role in the loading and releasing of the DDS. Even for the strong encapsulation, the frontier molecular orbitals (HOMO and LUMO, not shown) still dominantly come from the CNTs.

To understand the binding difference for the adsorption and the encapsulation, the noncovalent interactions for the encapsulation in and the adsorption on the surface of (9, 9) CNT were visualized via the isosurface of sign (λ₂) × ρ defined by Yang et al.⁴⁷ According to the color code that green/yellow shows van der Waals (vdw) interaction and red shows a strong nonbonded overlap, vdw interactions for the encapsulation are very obvious via cooperative π⋯π, N–H⋯π as well as C–H⋯π, while for the adsorption on sidewall the vdw comes mainly from the π⋯π stacking. Inside the CNTs the NH₂ and a few CH₂ groups are approximately 3.0–3.5 Å from the inner wall carbons of the CNTs, and the vdw between the NH₂/CH₂/C=O groups and the SWCNTs enhances their binding with N–H⋯π, C–H⋯π, O–H⋯π and C=O⋯π in a few areas (Fig. 9).

Fig. 9 Reduced density gradient isosurface (0.5 au) for the adsorption of the DOX on (10, 10) CNT (right) and its encapsulation DOX@CNT (left). Green and yellow indicate van der Waals interaction and red indicates a strong nonbonded overlap.

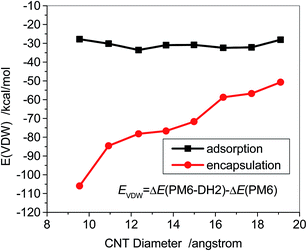
The vdw contribution (E_VDW) was also quantitatively estimated for the DOX–CNT complexes in the gas phase through the binding energy difference, E_VDW = ΔE(PM6-DH2) − ΔE(PM6), which was shown in Fig. 10. For the adsorption of DOX on the sidewall of the CNTs the van der Waals contribution (E_VDW) is basically in a short range of −27.8 to −33.6 kcal mol⁻¹; while for the encapsulation E_VDW becomes rather high, −106 kcal mol⁻¹ for the small diameter (7, 7) and −50 kcal mol⁻¹ for the large diameter (14, 14), showing that the small inner space of the CNTs has the higher van der Waals interaction between DOX and the CNTs because of the closer contact. The van der Waals contribution approximately accounts for 80% of the total binding energy for the adsorptions, which can be primarily attributed to the π–π stacking between DOX and the CNTs. The high E_VDW (−106 kcal mol⁻¹) for the encapsulations in (7, 7) SWCNTs is not able to compensate for the large deformation due to the encapsulation. The E_VDW (−85 kcal mol⁻¹) is dominantly responsible for the encapsulations in (8, 8) SWCNTs, and leads to an exothermic binding energy of −56 kcal mol⁻¹. The E_VDW for the encapsulation tends to be weaker with an increase in the diameter of the CNTs, and it is dominantly resulting from the π–π stacking, CH–π, and NH–π, as well as C=O–π interactions.

Fig. 10 Van der Waals contribution to the binding energy for DOX–CNT and DOX@CNT complexes with respect to CNT diameters. The E_VDW is the binding energy difference predicted by the PM6-DH2 and PM6.

Table 2 lists the amounts of charges carried by the DOX/DOXH⁺ upon their binding with the CNTs. For the adsorptions, the charge slightly decreases with an increase in the diameter of the CNTs, and the transferred charge from the CNTs to DOX is similar to that from CNT to DOXH⁺. Opposite to the sidewall adsorption, for the encapsulation only a little amount of approximately 0.01e charge is transferred from the CNT to DOX and DOXH⁺, and again the charges carried by the DOX and DOXH⁺ are very similar. The very little amount of transferred electrons also highlights the non-covalent interaction between DOX and the CNTs in both adsorption and encapsulation.

Table 2 Amounts of charges (e) carried by the DOX and DOXH⁺ in adsorption complexes at PM6-DH2

CNT (n, n)	Encapsulation		Sidewall adsorption
	DOX	DOXH^+	DOX	DOXH^+
(7, 7)	−0.0066	−0.0067	−0.1332	−0.1601
(8, 8)	−0.0070	−0.0072	−0.0597	−0.0730
(9, 9)	−0.0084	−0.0099	−0.0386	−0.0512
(10, 10)	−0.0100	−0.0104	−0.0275	−0.0366
(11, 11)	−0.0109	−0.0091	−0.0252	−0.0316
(12, 12)	−0.0108	−0.0102	−0.0246	−0.0278
(13, 13)	−0.0096	−0.0086	−0.0235	−0.0273
(14, 14)	−0.0094	−0.0101	−0.0224	−0.0251

---

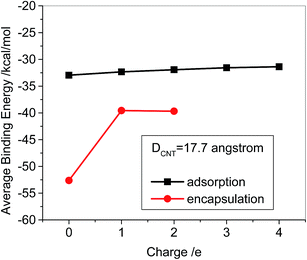
Because of ultrahigh surface areas up to ∼2600 m² g⁻¹, Dai et al. estimated that for the laser-ablation-grown SWCNTs (mean diameter ∼ 1.9 nm) ∼50 DOX molecules can bind to 10 nm long SWCNTs.⁴ Due to the specificity of the frontier orbitals of the SWCNTs as discussed above, the adsorbates could somewhat influence each other on the adsorption strength. Thus, we took into account the DOXH⁺–CNT (13, 13) (diameter ∼ 1.7 nm) system in the aqueous solution as an example to illustrate the effect. Fig. 11 shows that for the multi-adsorption of DOXH⁺ on the sidewall of the SWCNT the average binding energy becomes slightly less with an increase in the number of the DOXH⁺. The positive slope is approximately 0.4 kcal per mol per DOXH⁺, suggesting that one more adsorbed DOXH⁺ can approximately decrease the average adsorption energy by 0.4 kcal mol⁻¹. Assuming that it would be applied to multi adsorbates of 40 DOXH⁺, the average binding energy would change to ∼−16 kcal mol⁻¹, which approaches the experimentally estimated −14.1 kcal mol⁻¹ for the DOX on the laser-ablation SWCNTs.⁴ As for the encapsulation, Fig. 11 displays the binding energy comparison of DOX, DOXH⁺, and two DOXH⁺ because the inner of the CNTs can accommodate only a few of DOXs in the confined space. It can be seen that the average binding energies for the two DOXH⁺ and one DOXH⁺ are almost the same (−39.7 ∼ −39.6 kcal mol⁻¹) although there is a significant binding decrease in comparison with the DOX@CNT complex (∼−39.7 vs. −52.7 kcal mol⁻¹).

Fig. 11 Average binding energy of DOX, (DOXH⁺) – (13, 13) CNT complex with respect to charge with PH6-DH2.

In addition, the mutual influence of the adsorption and encapsulation of DOX–CNT (13, 13) was investigated (Fig. 12). As the two DOX molecules are rather far from each other as in case a, for a few located configurations the total binding energies are slightly lower than the sum of the individual DOX (−83.6 vs. −85.5 kcal mol⁻¹). However, if the encapsulation is just beneath the surface adsorption as in case b the total binding energy is generally stronger than the sum of the individual DOX binding energies (−86.6 vs. −85.5 kcal mol⁻¹), suggesting a weak π⋯π stacking cooperativity.⁴⁸

Fig. 12 Mutual influence of adsorption and encapsulation of DOXH⁺–CNT (13, 13) in the case of rather separated molecules (a), and in the case of neighbor molecules (b).

Conclusion

The dispersion and hydrogen bonding corrected semi-empirical quantum method, PM6-DH2 and the meta-hybrid density functional theory M06-2X in the scheme of OMIOM were employed to systematically investigate the loading of doxorubicin (DOX) on the single-walled carbon nanotube (SWCNT), including the adsorption on the sidewall of the SWCNT, encapsulation in the CNT, and their dependences on the protonation of the NH₂ group of DOX and the diameter of the armchair (n, n) SWCNT. The adsorption primarily occurs through π–π stacking and just becomes slightly stronger as the diameter of the CNT is increased. The encapsulation is much stronger than the adsorption because of the C–H/N/O–H⋯π and C=O⋯π interaction, besides the π–π stacking as in the adsorption. (8, 8) CNT (diameter ∼ 11 Å) is an energetic onset for the encapsulation since the encapsulation turns from endothermic to exothermic when the diameter is larger than approximately 11 Å, and the optimal diameter for the encapsulation is 14 Å corresponding to (10, 10) CNT. Thus for the thick CNT the encapsulation may also play an important role in the loading and releasing of the CNT-based drug delivery system of the DOX.

Acknowledgements

This work was supported by the National Institute of General Medical Science of the National Institute of Health (SC3GM105576 and SC3GM082324).

References

1. R. Singh, D. Pantarotto, D. McCarthy, O. Chaloin, J. Hoebeke, C. D. Partidos, J. P. Briand, M. Prato, A. Bianco and K. Kostarelos, J. Am. Chem. Soc., 2005, 127, 4388–4396.
2. N. W. S. Kam and H. J. Dai, J. Am. Chem. Soc., 2005, 127, 6021–6026.
3. N. W. S. Kam, M. O'Connell, J. A. Wisdom and H. J. Dai, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11600–11605.
4. Z. Liu, X. Sun, N. Nakayama-Ratchford and H. Dai, ACS Nano, 2007, 1, 50–56.
5. Z. Liu, S. Tabakman, K. Welsher and H. Dai, Nano Res., 2009, 2, 85–120.
6. Z. Liu, A. C. Fan, K. Rakhra, S. Sherlock, A. Goodwin, X. Chen, Q. Yang, D. W. Felsher and H. Dai, Angew. Chem., Int. Ed., 2009, 48, 7668–7672.
7. G. Prencipe, S. M. Tabakman, K. Welsher, Z. Liu, A. P. Goodwin, L. Zhang, J. Henry and H. Dai, J. Am. Chem. Soc., 2009, 131, 4783–4787.
8. F. Lu, L. Gu, M. J. Meziani, X. Wang, P. G. Luo, L. M. Veca, L. Cao and Y.-P. Sun, Adv. Mater., 2009, 21, 139–152.
9. Z. Liu, J. T. Robinson, S. M. Tabakman, K. Yang and H. Dai, Mater. Today, 2011, 14, 316–323.
10. C. Fabbro, H. Ali-Boucetta, T. Da Ros, K. Kostarelos, A. Bianco and M. Prato, Chem. Commun., 2012, 48, 3911–3926.
11. E. Heister, V. Neves, C. Lamprecht, S. R. P. Silva, H. M. Coley and J. McFadden, Carbon, 2012, 50, 622–632.
12. C. L. Lay, J. Liu and Y. Liu, Expert Rev. Med. Devices, 2011, 8, 561–566.
13. Y.-J. Gu, J. Cheng, J. Jin, S. H. Cheng and W.-T. Wong, Int. J. Nanomed., 2011, 6, 2889–2898.
14. L. Meng, X. Zhang, Q. Lu, Z. Fei and P. J. Dyson, Biomater., 2012, 33, 1689–1698.
15. N. Saikia and R. C. Deka, Comput. Theor. Chem., 2011, 964, 257–261.
16. C. Wang, P. Lv, W. Wei, S. Tao, T. Hu, J. Yang and C. Meng, Nanotech., 2011, 22, 415101–415108.
17. P. Sornmee, T. Rungrotmongkol, O. Saengsawang, U. Arsawang, T. Remsungnen and S. Hannongbua, Comp. Theor. Nanosci., 2011, 8, 1385–1391.
18. T. Kavitha, S. I. Haider Abdi and S.-Y. Park, Phys. Chem. Chem. Phys., 2013, 15, 5176–5185.
19. Y. Collins and S. Lele, J. Natl. Med. Assoc., 2005, 97, 1414–1416.
20. N. M. Dinan, F. Atyabi, M.-R. Rouini, M. Amini, A.-A. Golabchifar and R. Dinarvand, Mater. Sci. Eng., C, 2014, 39, 47–55.
21. S. Lv, Z. Tang, M. Li, J. Lin, W. Song, H. Liu, Y. Huang, Y. Zhang and X. Chen, Biomater., 2014, 35, 6118–6129.
22. H. Xu, M. Fan, A. M. Elhissi, Z. Zhang, K.-W. Wan, W. Ahmed, D. A. Phoenix and X. Sun, Nanomed., 2015, 10, 1247–1262.
23. K. Kamiya and S. Okada, Phys. Rev. B, 2011, 83, 155444.
24. Y.-F. Xing, C.-L. Yang, Y.-F. Mo, M.-S. Wang and X.-G. Ma, J. Phys. Soc. Jpn., 2014, 83, 024801–024807.
25. M. H. Alshehri, B. J. Cox and J. M. Hill, Micro Nano Lett., 2014, 9, 113–118.
26. F. J. A. L. Cruz, J. J. de Pablo and J. P. B. Mota, RSC Adv., 2014, 4, 1310–1321.
27. Y. Kang, Q. Wang, Y.-C. Liu, J.-W. Shen and T. Wu, J. Phys. Chem. B, 2010, 114, 2869–2875.
28. Q. Chen, Q. Wang, Y.-C. Liu, T. Wu, Y. Kang, J. D. Moore and K. E. Gubbins, J. Chem. Phys., 2009, 131, 015101–015106.
29. Y. Kang, Y.-C. Liu, Q. Wang, J.-W. Shen, T. Wu and W.-J. Guan, Biomater., 2009, 30, 2807–2815.
30. A. Mejri, D. Vardanega, B. Tangour, T. Gharbi and F. Picaud, J. Phys. Chem. B, 2015, 119, 604–611.
31. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
32. C. A. Morgado, P. Jurecka, D. Svozil, P. Hobza and J. Sponer, Phys. Chem. Chem. Phys., 2010, 12, 3522.
33. Y. Wang, J. Phys. Chem. C, 2008, 112, 14297–14305.
34. Y. Wang and Y. Bu, J. Phys. Chem. B, 2007, 111, 6520–6526.
35. W. Sun, Y. Bu and Y. Wang, J. Phys. Chem. C, 2011, 115, 3220–3228.
36. W. Sun, Y. Bu and Y. Wang, J. Comput. Chem., 2012, 33, 490–501.
37. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
38. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397.
39. J. Rĕzáč, J. I. Fanfrlík, D. Salahub and P. Hobza, J. Chem. Theory Comput., 2009, 5, 1749–1760.
40. M. Korth, M. Pitoňák, J. Rĕzáč and P. Hobza, J. Chem. Theory Comput., 2009, 6, 344–352.
41. K. E. Riley, M. Pitoňák, P. Jurečka and P. Hobza, Chem. Rev., 2010, 110, 5023–5063.
42. Z. Xu, B. R. Meher, D. Eustache and Y. Wang, J. Mol. Graphics Modell., 2014, 47, 8–17.
43. J. J. P. Stewart, James J. P. Stewart, MOPAC2009, Stewart Computational Chemistry, Version 11.052W, web: http://OpenMOPAC.net.
44. S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct., 1999, 462, 1–21.
45. A. Klamt and G. Schüümann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
46. D. Schneidman-Duhovny, Y. Inbar, R. Nussinov and H. J. Wolfson, Nucleic Acids Res., 2005, 33, W363–W367.
47. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
48. C. Kulkarni, S. K. Reddy, S. J. George and S. Balasubramanian, Chem. Phys. Lett., 2011, 515, 226–230.

---