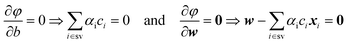Support Vector Machines for classification and regression

Abstract

The increasing interest in Support Vector Machines (SVMs) over the past 15 years is described. Methods are illustrated using simulated case studies, and 4 experimental case studies, namely mass spectrometry for studying pollution, near infrared analysis of food, thermal analysis of polymers and UV/visible spectroscopy of polyaromatic hydrocarbons. The basis of SVMs as two-class classifiers is shown with extensive visualisation, including learning machines, kernels and penalty functions. The influence of the penalty error and radial basis function radius on the model is illustrated. Multiclass implementations including one vs. all, one vs. one, fuzzy rules and Directed Acyclic Graph (DAG) trees are described. One-class Support Vector Domain Description (SVDD) is described and contrasted to conventional two- or multi-class classifiers. The use of Support Vector Regression (SVR) is illustrated including its application to multivariate calibration, and why it is useful when there are outliers and non-linearities.

---

Centre for Chemometrics, University of Bristol

Richard Brereton obtained his BA, MA and PhD at the University of Cambridge, and subsequently moved to the University of Bristol where he is Professor of Chemometrics. He has published 322 scientific articles, including 7 books and 143 refereed papers. He has given 147 invited lectures in 23 countries worldwide, and there have been 118 members of his group from 17 countries. His interests are in chemometrics, with especial current emphasis on pattern recognition as applied to a variety of areas including metabolomics, pharmaceuticals, forensics, environmental, materials and cultural heritage studies.

Gavin Lloyd obtained his BSc from the University of Bristol. After a short spell working for Mass Spec Analytical (in forensic data analysis) he studied for a PhD in the Centre for Chemometrics which he is currently completing. He has so far published 6 papers with a further 4 submitted. He has developed a graphical user interface for use in forensic mass spectrometry and also the majority of Matlab code for the book Chemometrics for Pattern Recognition. His interests are in pattern recognition and signal deconvolution and development of software.

---

1 Introduction

SVMs (Support Vector Machines) were originally proposed by Cortes and Vapnik¹ and have become increasingly popular after their introduction in the late 1990s, particularly within the Machine Learning community.^2–6 After their introduction, SVM applications have been successfully developed in several areas, including bioinformatics,⁷ which is probably the most rapidly growing discipline in terms of new methodologies due to the recent explosion of data volumes, econometrics⁸ and biometrics.⁹ More recently, SVMs have been proposed for the analysis of chemical data¹⁰ and have attracted the attention of the chemometrics community, both as a classification technique, and also because their use has been successfully extended to solve calibration problems. There is an increasing number of articles focussing on the comparison of SVMs with more traditional chemometrics approaches.^11–18 Most applications of SVMs are applied to datasets with relatively small numbers of variables to those typically obtained in analytical chemistry; however, there is no inherent reason why they cannot be extended to highly multivariable datasets, often, however, requiring a prior variable reduction step such as PCA (Principal Component Analysis) first.

The tremendous expansion of interest in SVM methods can be shown by citations to Cortes and Vapnik¹ and Cristianini and Shawe-Taylor⁴ totalling around 2000 and 3000 citations as recorded by ISI since first cited in 1995 and 2000 respectively. This compares with a total of around 7000 articles citing papers from J. Chemom. since 1990 when first entered in the ISI database and 15 000 from Chemom. Intell. Lab. Syst. since 1986, the two main chemometrics journals at time of writing. This rapid acceptance of Support Vector methods is illustrated in Fig. 1, where the citations of both articles and journals are plotted against year after they received their first recorded citation over a 12 year period (or 9 for Cristianini and Shawe-Taylor) at time of writing (15 July 2009). This shows a remarkable interest in such approaches. Whether this momentum will be maintained remains to be seen, but certainly at the moment SVMs and related kernel methods are very widespread.

Fig. 1 Citations of refs 1 and 4 since first cited compared to the two chemometrics journals.

Within applications to analytical chemistry, the growth of SVM approaches has been much slower. One of the issues is the lack of graphically user-oriented packaged software that is suitable for laboratory based chemists, unlike older and more established methods such as PLS (Partial Least Squares),^19–21 so whereas there is big potential in SVMs many hands-on laboratory chemists are reluctant to use the method. In areas such as biology or economics there is a much better established tradition of separate data analysis sections with dedicated staff who would be comfortable using scripts, e.g. in Matlab. Hence SV approaches, whilst of significant interest and the subject of numerous papers, have been slow to take off in mainstream analytical chemistry. Yet one issue is that many problems encountered by the modern analytical chemist are non-linear, and approaches such as PLS find it hard to cope. Take an example in metabolomic profiling where we use compound concentrations to determine whether a patient has a disease or not. A model might be formed between disease state and compound concentration: we do not expect this model to be linearly related to concentrations of compounds and so traditional linear methods are not necessary appropriate. This contrasts to traditional applications in analytical chemistry, e.g. calibration in atomic spectroscopy or ultraviolet/visible spectroscopy in order to determine accurately the concentration of analytes in a mixture: providing that the experiment has been done well and spectra are within the Beer–Lambert limits we expect a linear relationship between concentration and signal and, as such, methods such as PLS that are founded on linearity perform very well.

We will illustrate the methods described in this paper using a variety of case studies as discussed below.

2 Case studies

2.1 Simulations L1 to L4: classification using two variables

The simulations are used to illustrate methods for classification. They consist of two classes or groups of samples characterised by two variables. Each class, A and B, consists of 20 samples, so the datasets can be arranged in a 40 × 2 matrix and are illustrated in Fig. 2.

Fig. 2 Simulated case studies L1 to L4.

• Case study L1 represents two linearly separable classes.

• Case studies L2 and L3 represent two classes that are not linearly separable, based on case study L1, but moving class B closer to class A.

• Case study L4 represents the situation where class B surrounds class A, so although it is visually obvious which class is which, a curved boundary is necessary that encloses class A.

2.2 Simulations C1 and C2: calibration

Simulation C1 involves 21 points that are approximately linearly related and characterised by 2 variables, x and c, as illustrated in Fig. 3.

Fig. 3 Simulated case study C1 for calibration.

Usually in calibration we try to predict c from x, e.g. a concentration from a spectroscopic or chromatographic measurement. In this paper we use the x/c notation²² rather than the tradition x/y notation because x and y tend to get swapped around: for univariate calibration x is usually the property (e.g. concentration – represented by the horizontal axis) and y the measured variable (e.g. a chromatographic peak-height), but in multivariate chemometrics these are changed with X representing a spectral matrix and y a concentration vector, for example.

Simulation C2 involves 63 points characterised by one measured variable (x) and an underlying property we wish to predict (c). In dataset C2, there is a curvilinear relationship between x and c, the aim being to predict ĉ = f(x) where the ^ means predicted. There is one point that is a clear outlier that may have an influence on the model under certain circumstances. This dataset is illustrated in Fig. 4.

Fig. 4 Simulated case study C2 for calibration.

2.3 Experimental case studies R1 to R3 for classification

For the experimental case studies although we have several variables we project onto the first 2 or 3 Principal Components (PCs)^22–25 prior to performing classification, which is done in the space of the scores of the most significant PCs. Of course, classification could be performed in the space of the original variables, but the aim of this article is to illustrate the methods visually. We do not necessarily advocate that PCA has to be performed prior to classification. Only brief essential details of preprocessing are discussed below. More details are in the references cited below and in a recent text on Pattern Recognition.²⁶ PC plots of the scores of the first 2 and 3 PCs are presented in Fig. 5.

Fig. 5 Scores of the first 2 and 3 PCs for case studies R1 to R3.

2.3.1 Case study R1: environmental pollution studied by headspace mass spectrometry. This dataset consisted of 213 samples of soil and sand analysed by headspace mass spectrometry (HS-MS), with an aim to determine whether the samples are polluted or not. More details are presented elsewhere.¹⁷ Of these, 179 were spiked with oil in the laboratory at different levels, representing polluted samples, and 34 were clean, representing unpolluted samples. For the purpose of this paper we are primarily concerned with determining whether a sample comes from the polluted group (class A) or the unpolluted group (class B), rather than the extent of pollution. We are trying to ask whether it is possible to distinguish polluted from unpolluted samples using MS and pattern recognition and then to determine how well we can classify samples into one of these two groups. Mass spectra are recorded from m/z 49 to 160. Data preprocessing has to take this into account and the following steps are performed The MS intensities are first square rooted. Each square rooted MS is then row scaled to a total of 1. Finally the columns (each variable) are standardized to allow each m/z value to have equal influence on the resultant pattern recognition.

For this particular dataset quite a variety of preprocessing options could be employed, most giving comparable answers (in other cases a correct choice of preprocessing is essential), but for this paper we stick to one protocol as the aim is primarily to illustrate how Support Vector methods work in classification studies.

From the PC scores plots (Fig. 5) we can see that the two groups are mainly separable although not linearly in the space of PCs 1 and 2; however, there is a small subgroup of samples from class A buried within class B.

2.3.2 Case study R2: near infrared analysis of food. This study involves trying to assign samples of vegetable oils into one of four classes, using NIR (Near Infrared) spectroscopy, a traditional technique for the application of chemometrics. The dataset has been kindly supplied by Camo AS and is described further in their training manual.²⁷

The data consist of 72 spectra from:

(1) 18 samples of Corn Oils (class A),

(2) 30 samples of Olive Oils (class B),

(3) 16 samples of Safflower Oils (class C),

(4) 8 samples of Corn Margarines (class D).

Note that the number of Corn Margarine samples is quite low and there can be problems in modelling groups with few samples.

In this dataset the following steps are used to prepare the data. The NIR data are baseline corrected using an approach called MSC (Multiplicative Scatter Correction). A region of the spectrum between 600 and 1500 nm wavelength is used for pattern recognition. The data are mean-centred because some regions are more intense than others, but the variability at each wavelength is very similar.

The MSC corrected spectra are illustrated in Fig. 6. It can be seen that there are some small differences between spectra of the groups, for example, at around 700 nm the safflower oils appear to exhibit more intense absorbance followed by the corn oil; however, these differences are quite small and there is a little bit of spread within each group (as expected), so it would be quite hard to identify an unknown oil, by eye, using a single NIR spectrum, and pattern recognition techniques can be employed to determine whether the groups can be distinguished, which spectral features are best for discrimination and how well an unknown can be assigned to a specific group.

Fig. 6 MSC corrected NIR spectra of the four groups of oils.

This particular application is very much one of classical chemometrics and is a classification problem, but unlike that of case study R1, there are 4 rather than 2 classes, in addition these are particular issues about dealing with data when there are more than two groups in the data. Furthermore, in addition to having a multiclass structure, there also is a problem in that the number of corn margarines is very small. However, all groups are very well separated as can be seen in the scores plot (Fig. 5), but this is an example of a multiclass problem.

2.3.3 Case studies R3a and R3b: thermal analysis of polymers. Most commercial plastics are polymers. The aim of this study is to be able to determine the group a plastic belongs to using its thermal properties. Commercial plastics have different properties, as their structure changes when heated, and each type of plastic has a different use so will have different characteristics. The changes involve going from a solid to a glass to a liquid state. By applying an oscillating force and measuring the resulting displacement, the stiffness of the sample can be determined, which will change as the polymer is heated, using the technique of Dynamic Mechanical Analysis (DMA). Several parameters can be measured, but in this study we use the Loss Modulus (E″), which is related to the proportion of the energy dissipated or non-recoverable per cycle, as a force is applied.

The temperature range studied is from −51 °C until the minimum stiffness is reached, after which no further meaningful data can be collected. Measurements are made approximately every 1.5 °C. Each raw trace curve consists of between 99 and 215 data points dependent on the highest recordable data point of the polymer. After the highest recordable temperature, in order to ensure a similar temperature range for each sample, values (which were not recorded) are replaced by the value of E″ obtained at the highest measurable temperature. Because the measurements for different samples are not performed at the same equally spaced temperatures the data are linearly interpolated to 215 equally spaced data points corresponding to an interpolated E″ value for each of the temperatures between −51 °C and 270 °C in increments of 1.5 °C.

293 samples are used to give a data matrix X of dimensions 293 × 215, which is first centred. An interest in this dataset is that there are two ways in which the polymers can be classified, either into type by their main physical properties (amorphous or semi-crystalline) to two main classes, or into nine groups according to polymeric material as listed in Table 1. Note in the class lettering system we will use, that class A (polymer type) is different from class A (polymer group). The classification is hierarchical in nature, as a particular polymeric group is all of one type. This dataset can be viewed either as a two-class problem (as in case study R1) which we will denote as R3a or a multiclass problem (as in case study R2) which we will denote as R3b. The aim is to determine the origins of a polymer using DMA. There are many potential reasons for this: one possible area is waste recycling of industrial plastics, where plastics have to be treated in different ways for environmentally safe disposal. More details are available in several papers.^28–32

Table 1 Samples for case study R3

Type			Group
Amorphous	A	92	Polystyrene (PS)	A	35
			Acrylonitrile- Butadiene-Styrene (ABS)	B	47
			Polycarbonate (PCarb)	C	10
Semi-crystalline	B	201	Low Density Polyethylene (LDPE)	D	56
			Polypropylene (PP)	E	45
			High Density Polyethylene (HDPE)	F	30
			Polyamide6 (PA6)	G	20
			Polybutylene Terephthalate (PBT)	H	10
			Polyethylene Terephthalate (PET)	I	40

---

From the scores plots (Fig. 5) we can see that the two main types are almost separable in the space of the first 2 PCs, with just a little overlap, but there is quite a lot of overlap between the groups. Some of the nine groups are separated into subclasses as they consist of several grades. This dataset is an example of both a two-class and a nine-class problem.

2.4 Experimental case study S1 for calibration: UV/vis spectra of polyaromatic hydrocarbons

The experimental case study for this application is of the UV/vis (ultraviolet visible) spectra of a series of mixtures of 10 polyaromatic hydrocarbons (PAHs) which has been described previously.^20,22Table 2 is of the concentrations of these PAHs in 25 spectra; for the purpose of this paper we take the spectral intensities over wavelengths between 220 and 350 nm at 5 nm intervals, forming a matrix that has 25 rows (individual spectra) and 27 columns (individual wavelengths). The aim is to determine the concentration of individual PAHs in the mixture spectra. Because there are 27 variables it is not possible to represent the spectra in the 27 dimensional dataspace formed by these variables graphically.

Table 2 Concentrations of polyarenes in dataset A for case study S1

Spectrum	PAH^a concentration/mg L^−1
	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
a Py = Pyrene; Ace = Acenaphthene; Anth = Anthracene; Acy = Acenaphthylene; Chry = Chrysene; Benz = Benzanthracene; Fluora = Fluoranthene; Fluore = Fluorene; Nap = Naphthalene; Phen = Phenanthracene.
1	0.456	0.120	0.168	0.120	0.336	1.620	0.120	0.600	0.120	0.564
2	0.456	0.040	0.280	0.200	0.448	2.700	0.120	0.400	0.160	0.752
3	0.152	0.200	0.280	0.160	0.560	1.620	0.080	0.800	0.160	0.118
4	0.760	0.200	0.224	0.200	0.336	1.080	0.160	0.800	0.040	0.752
5	0.760	0.160	0.280	0.120	0.224	2.160	0.160	0.200	0.160	0.564
6	0.608	0.200	0.168	0.080	0.448	2.160	0.040	0.800	0.120	0.940
7	0.760	0.120	0.112	0.160	0.448	0.540	0.160	0.600	0.200	0.118
8	0.456	0.080	0.224	0.160	0.112	2.160	0.120	1.000	0.040	0.118
9	0.304	0.160	0.224	0.040	0.448	1.620	0.200	0.200	0.040	0.376
10	0.608	0.160	0.056	0.160	0.336	2.700	0.040	0.200	0.080	0.118
11	0.608	0.040	0.224	0.120	0.560	0.540	0.040	0.400	0.040	0.564
12	0.152	0.160	0.168	0.200	0.112	0.540	0.080	0.200	0.120	0.752
13	0.608	0.120	0.280	0.040	0.112	1.080	0.040	0.600	0.160	0.376
14	0.456	0.200	0.056	0.040	0.224	0.540	0.120	0.800	0.080	0.376
15	0.760	0.040	0.056	0.080	0.112	1.620	0.160	0.400	0.080	0.940
16	0.152	0.040	0.112	0.040	0.336	2.160	0.080	0.400	0.200	0.376
17	0.152	0.080	0.056	0.120	0.448	1.080	0.080	1.000	0.080	0.564
18	0.304	0.040	0.168	0.160	0.224	1.080	0.200	0.400	0.120	0.118
19	0.152	0.120	0.224	0.080	0.224	2.700	0.080	0.600	0.040	0.940
20	0.456	0.160	0.112	0.080	0.560	1.080	0.120	0.200	0.200	0.940
21	0.608	0.080	0.112	0.200	0.224	1.620	0.040	1.000	0.200	0.752
22	0.304	0.080	0.280	0.080	0.336	0.540	0.200	1.000	0.160	0.940
23	0.304	0.200	0.112	0.120	0.112	2.700	0.200	0.800	0.200	0.564
24	0.760	0.080	0.168	0.040	0.560	2.700	0.160	1.000	0.120	0.376
25	0.304	0.120	0.056	0.200	0.560	2.160	0.200	0.600	0.080	0.752

---

We will illustrate the method for SVR primarily for the determination of the benzanthracene concentration. The use of PLS as an alternative has been discussed in previous publications as referenced above.

3 Support vector machines as two-class classifiers

We will assume that we are trying to find a model in a series of samples that form a training set. Note that much of the terminology of Support Vector Machines was developed by the machine learning community, where autopredictive models, that is models formed on an entire dataset, are usual, whereas in the chemometrics and analytical chemistry literature it is more common to divide data into a training set, on which the model is formed, and a separate test set which is used to determine how well the model performs.²⁶ The descriptions in this section will be based on training set or autopredictive models.

SVMs are usually introduced as a solution to a two-class problem – how can we differentiate between samples that are members of two groups? The description of the SVM algorithm below is in three parts. First, the basic definitions for linearly separable classes; second, the extension to the non-linearly separable case with the use of kernel functions; and third, the generalised solution with the incorporation of the trade-off pernalty parameter to control complexity. Two-class classifiers attempt to form a boundary between two groups. This boundary may be of varying types, and two possible classifiers are illustrated in Fig. 7. Note that almost all classifiers can be expressed in the form of boundaries, and although SVMs are normally defined in terms of boundary problems and some other approaches not, in fact most two-class classifiers (sometimes called hard models) can be visualised in terms of boundaries

Fig. 7 Illustration of two-class classifiers, applied to two separable groups: (top) a linear classifier, and (bottom) a curvilinear classifier.

3.1 Linear learning machines

The simplest type of classifier is a linear classifier. However, SVMs treat linear classification problems somewhat differently to the other common methods such as Linear Discriminant Analysis (LDA)^33–35 and Partial Least Squares Discriminant Analysis (PLS-DA).^36–38 Whereas for two linearly separable classes the method is probably overkill, if first understood this is an initial conceptual building block for understanding SVMs and the extension to more complex problems.

Consider a binary classification problem where samples, each of whose experimentally measured variables are represented by a row vector x, have been obtained that have membership of two classes g (= A or B) with labels c = +1 for class A and −1 for class B and are perfectly linearly separable. These samples can be used to determine a decision function to separate two classes, which in its simplest form can be expressed by a linear boundary

where w and b are often called weight and bias parameters that are determined from the training set. In this paper we will denote x for an individual sample to be a row vector rather than a column vector, but otherwise adopt notation that is common in the SVM literature. It is important to understand the relationship between different common approaches, and that the SVM when expressed in its simplest linear form has analogies to PLS-DA which also is related to LDA, but advocates of SVM would argue that SVM is a more generalised and universal approach, although one which carries risks of overfitting and unnecessary complexity if one is not careful, and which forms a boundary using a different criterion to LDA or PLS-DA. However, this simple classification function corresponds to representing the border between two classes as a hyperplane, or a line if x is characterised by two variables. The sign of g determines which class a sample is assigned to: if positive class A and if negative class B. Any generic hyperplane (w, b) can be defined by coordinates x satisfying the condition wx′ + b = 0 which divides the dataspace into two regions opposite in sign. In Fig. 8 we illustrate a variety of different hyperplanes (in this case lines as there are only two variables) for case study L1, based on different values of w and b. It can be seen that any line can be defined this way, some of which perfectly separate the data and some do not.

Fig. 8 Illustration of the line given by wx′ + b for case study L1: (a) b = 0, changing w, and (b) b = −1 and +1, changing w. Lines that separate the two classes perfectly are indicated in black.

If the two classes are separable we can define a ‘margin’ between the two classes, such that

since no samples will be precisely on the boundary. The value ±1 can be obtained by scaling w and b appropriately, for example, a hyperplane (or line) in two dimensions with w = [1 3] and b = −1 is identical to one with w = [2 6] and b = −2, so it is always possible to scale the margins so they are of a distance of ±1 from the central line. The boundary (or hyperplane) should be equidistant from the two extreme samples in each class. The boundary separates the classes with no error if every sample x_i is projected in the region of the dataspace with sign equal to the respective class membership c_i or at least on the boundary, i.e. the hyperplane must satisfy the condition

c_i(wx_i′ + b) ≥ 1

for all the samples providing that they are perfectly linearly separable. However, there are an infinite number of possible hyperplanes (w, b) satisfying this so there needs to be a further rule to determine which of these hyperplanes is best.

The optimal separating hyperplane, as chosen using SVM, defined by the parameters w and b is one for which the margin between the most similar samples in each group is largest. It can be shown that this hyperplane is the one that minimises ½(ww′), subject to the constraint c_i(wx_i′ + b) ≥ 1 for all samples. This optimal separating line (or boundary) for case study L1 is illustrated in Fig. 9. The samples on the margins are called support vectors (SVs) as illustrated in the figure. Note that for such a linear boundary the number of SVs is limited and will be between 2 and 4. In addition to the boundary we can visualise the margins. Note that this boundary now depends only on the SVs, and other samples have no influence over the boundary. In Fig. 10 we represent four possible boundaries, each of which are formed from 2 samples from one class and 1 from another class (in fact, these are the only solutions for case study L1 that can be obtained using 3 samples), and it can be seen that the solution of Fig. 9 has the widest margin and so is chosen as the optimal solution. Note that there will only be a finite number of boundaries that can be defined by using samples on both margins, and most of the possible boundaries cannot be defined this way.

Fig. 9 Optimal boundary that maximises the margins for separating classes A and B in case study L1. SV = support vectors, with w = [1.184 −0.027] and b = −0.768.

Fig. 10 Four possible boundaries for case study L1, consisting of 3 samples on the margins. The solution with the widest boundary is chosen as illustrated in Fig. 9.

For readers interested in the algebra, this optimisation task can be expressed by the structure error function:

where N_sv is the number of samples for which both c_i(wx_i′ + b) ≥ 1 and in addition α_i > 0, which are a subset of the original samples called the Support Vectors (SVs). The samples that have α_i > 0 are those that are closest to the boundary. Hence the SV solution depends only on samples close to the boundary between two (or more) classes. In this way, SVM models differ from most other common approaches to classification within analytical chemistry which use all the samples in the dataset to determine the boundaries between classes.

The parameter α is called a Lagrange multiplier and is common in calculus and is used to optimise a function subject to one or more constraints. A simple example involves finding the minimum or maximum of f(x,y) = x + y subject to the constraint g(x,y) = x² + y² = 1 (in fact a unit circle). The Lagrange multipliers are defined by the value of α that is obtained from the following equation, subject to the constraint

∇f = α∇g

where ∇ is the partial derivative over each of the variables. Since there are two variables, we have three equations we need to solve, the latter representing the constraint:
We can solve these equations to give (x,y) = (±1/√2, ±1/√2) and hence α = ±1/√2 also. The two solutions give values of f(x,y) = x + y = ±√2 or for a maximum (−) or minimum (−1) solution.

In the context of SVMs, the value of φ has to be minimised with respect to w and b and maximised with respect to the Lagrange multipliers α_i. The minimum of φ with respect to w and b is given by

where the samples i are formally support vectors (sv).

Hence,

The optimisation task is that of minimising φ(α) with respect to α, a vector consisting of Lagrange multipliers, satisfying the constraints
Finally, the optimal α = (α₁, α₂,…, α_Nsv) allows determination of the weight vector w of the optimal separating hyperplane
while the offset b can be calculated from any pair of samples of opposite classes satisfying the conditions that their values of α are greater than 0. In technical terns, the optimisation of φ is a quadratic programming problem, which can be generally written in the form:
where H has elements h_i,l = c_i(x_i′x_l)c_l (for samples i and l) and z is a row vector of −1s. This a well known type of optimisation problem that is straightforward to solve because it has only one global minimum, thus making the learning procedure reproducible. We will not discuss the details of this optimisation method in this paper which can be found in many general references on numerical programming. The expression for φ contains a scalar product of vectors and explains why the approach is particularly fast and suitable when dealing with samples having many variables. Last but not least, this opens the way to treat some of the more complicated non-linearly separable cases using kernels as discussed in Section 3.2.

The classifier can be directly expressed as a decision function in terms of the support vectors s_i (those samples whose value of α > 0) as follows

where if positive the samples are assigned to class A, otherwise to class B. Returning to Fig. 9, there are 3 SVs namely
and the value of b = 0.7684. (Note that since c₁ = c₂ = +1 and c₃ = −1 for the three SVs listed above.) In more familiar matrix terms we could define g(x_l) = sgn(x_iS′c + b) for each sample where S′ is a J × N_sv (or in our case 2 × 3) matrix containing the support vectors, and c is an N_sv × 1 vector whose elements equal the product of α and c for each support vector, which can be extended to a matrix form when all samples in a dataset are included. This calculation is illustrated in Fig. 11 for case study L1. It can be seen that all samples are correctly classified, in this particular case.

Fig. 11 Illustration of SVM calculation for the data of case study L1 and Fig. 9.

SVs are often visualised as being on the margins of each class, with the hyperplane representing the decision boundary. Which side of the hyperplane a sample lies on relates to its class membership, whilst the SVs and margins are the extremes of each class. In an ideal situation there will be an empty space between the margins, providing that classes are completely separable.

3.2 Kernels

Determining a class boundary in the form of a separating hyperplane is adequate for simpler cases where the classes are nearly or completely linearly separable. However, this is a situation where arguably many other methods would return satisfactory results and SVMs would not appeal very much due to their relatively complex formulation, and so are most useful where classes are not linearly separable.

SVMs handle this by adding an extra step to the procedure described above. Instead of forming a boundary in the original variable space, where the two classes are not separable, a new higher dimensional (feature) space, where the samples are projected by means of a feature function Φ(x), is defined. The back-projection of the optimal separating boundary (in the form of a hyperplane) from this new feature space to the original variable space will then result in a non-linear boundary of given complexity that better suits the distribution in the original variable space, providing that the feature space is correctly defined, as illustrated in Fig. 12. The new dataspace is often of high dimensionality with one dimension per SV. Their mappings by means of Φ(x) allows the determination of a hyperplane that separates them. A feature function is found that makes separation easier in higher dimensions. Finally the back-projection of this plane into the original dataspace generates a non-linear boundary which can theoretically be of any complexity. For the separable case study L1 we can also obtain a kernel space (which will no longer result in linear boundaries) and visualise this transformation, for a Radial Basis Function (RBF) model (see below) defined by 3 SVs, as each SV defines an axis in this space (Fig. 13). However, if the number of SVs increases beyond 3, as happens in most situations, it is not possible to visualise this space directly. As an example of a more complex problem we will illustrate below how to produce a boundary between the two classes represented in case study L4 (Fig. 2), which are not linearly separable.

Fig. 12 Creation of the boundary for a non-separable case. (a) Two linearly inseparable classes in two dimensions. (b) Projection onto a higher dimensional space where it is possible to separate the classes using a plane, with three support vectors indicated. (c) Projection back into two dimensions.

Fig. 13 Illustration of kernel space for an RBF model for case study L1. The three axes, K(1) to K(3), correspond to each of the three SVs, marked with a cross, the green surface being the projection of the samples onto this kernel space.

In many situations if the two boundaries between the two classes are very complex, the set of functions Φ(x) that is used to map the data is of very high dimensionality, which means that many more dimensions are generally required to find a separating hyperplane, but it is consequently possible to find boundaries to suit a variety of complex distributions. Mathematically, this is done by reformulating the optimisation task by replacing the scalar product of input vectors (x_ix_l′) with the scalar product of the respective feature functions defined by 〈Φ(x_i),Φ(x_l)〉 as follows:

so it is mainly necessary to find these functions to develop an SVM model using kernels.

An important concept in SVMs is that there exist kernel functions K in the original variable space that corresponds to the dot product of functions in the new feature space:

K(x_i,x_l) = 〈Φ(x_i),Φ(x_l)〉

The optimisation task can therefore be re-written:
The optimisation task still involves a quadratic convex programming problem, hence being particularly easy to handle, but most importantly, by means of K(x_i,x_l) rather than Φ(x), it is possible to proceed with the transformation, omitting the intermediate step of creating the feature space and working only in the original dataspace where K(x_i,x_l) is defined (which can be added as an extra dimension). This powerful attribute is known as the ‘kernel trick’ and it is what makes SVMs effective in addressing complex tasks. The classification decision function can be re-written as
and is still explicitly expressed in a dependence on the SVs.

Only certain kernels can be employed (as they also must satisfy some additional conditions). Some of the most common are as follows.

(1) Radial basis function (RBF), defined as K(x_i,x_j) = exp(−γ‖x_i − x_j‖²) or

(2) Polynomial function (PF), K(x_i,x_j) = (ax_i^Tx_j + b)^c

(3) Sigmoidal function (SF), K(x_i,x_j) = tanh(ax_i^Tx_j + b)

These kernel functions can be visualised as creating an extra dimension, involving a sum of functions centred on each sample that is assigned as an SV. The creation of this kernel function (in this example a RBF) is exemplified in Fig. 14, in which a third dimension, representing the decision function which is given by the kernel function multiplied by the class membership label of each sample and its Lagrange multiplier (), is added: note that this function is only used to obtain a surface defined by samples that are SVs – for all other samples this function is used to project them onto this new surface or mesh. The mesh relates to the value of the distance of each sample from the centre in the RBF higher dimensional space that cannot be visualised (the additional vertical axis should not be confused with the additional higher dimensional feature space which has as many axes as there are SVs, and is called the decision function).

Fig. 14 Creating a decision function for separating two classes of case study L4. The vertical axis relates to the kernel function multiplied by the class label and used employed with σ = 0.2sd of the overall dataset.

The procedure of forming boundaries and back-propagation are represented Fig. 15 for case study L4. The value of b represents a decision place that separates the surface into two parts, those above the plane (assigned to class A) and those below (class B). We can see that when projected back into two dimensions samples from class A are enclosed within an irregular shaped boundary. In Fig. 16, we illustrate how the model depends on SVs. Each of the samples that are identified as SVs are the centre of a Gaussian RBF, the sign being positive for members of class A (c_i = 1) and negative for members of class B (c_i = −1). For the RBF chosen the vast majority of samples are in fact SVs although this is not always the case. Non-SVs are projected onto the surface, but are not used to form this surface. We can rotate the surface onto the original data plane to see the distribution of the SVs, or at right angles to this to see where these are distributed and so the empty margin between the SVs for each class.

Fig. 15 Developing an SVM model for case study L4, using the parameters of Fig. 14. The vertical axis represents a decision function. The decision plane represents the value of b that divides the classes.

Fig. 16 Support Vectors – marked with a cross.

Each kernel is characterised by a set of parameters that must be optimised for a particular problem. The RBF is particularly popular because it requires only one parameter to be optimised (the value of γ or σ). This has many advantages in optimisation as SVMs are computationally intensive procedures, so optimising several parameters using procedures such as cross-validation (Section 3.4) can be time-consuming, if there are several parameters to optimise, and if incorrectly performed can lead to risks such as overfitting which involves forming boundaries that are very complex but not justified by the data. In this paper we will restrict the illustration to RBFs, which should cover the vast majority of situations encountered. The interested reader may want to look at source literature if it is felt that this type of function is inadequate. There is usually a limit to the level of complexity that can reasonably be modelled, especially when datasets are limited in size and contain experimental error, and RBFs result in some quite complex boundaries so are probably at the upper limit of what an analytical chemist might encounter; biologists mining large databases (e.g. in genetics) may have problems that justify going farther. We will discuss the influence of different RBF parameters on SVM boundaries in Section 3.4.

3.3 Controlling complexity and soft margin SVMs

Intuitively, because the kernel trick allows SVMs to define complex boundaries, the risk of overfitting is particularly high; that is, it is possible to define almost any boundary around training set samples even if there is no particular significance to these complex boundaries, so as complexity increases there is also a risk that the overcomplicated boundaries have no real predictive power. If we increase boundaries no end we can end up with perfect classification of samples from a training set (or a series of samples whose origins we know about) but when test set or unknown samples are included the classification results are very poor. In traditional analytical chemistry where most models are linear, often samples could be cleanly classified using linear models, but with the interface of analytical chemistry to other disciplines such as biology and medicine and cultural studies, for example, we do not expect nice linear behaviour and anticipate that the boundaries may become quite complex – a question is how complicated is it justified?

To this end a concept called Structural Risk Minimisation has been developed. SVMs are equipped with an additional parameter that allows a control on complexity. To introduce this parameter it is easiest to recall the example of the simplest case where the optimal separating boundary is determined in the original dataspace, without projecting the samples into a higher dimensional feature space. If these cannot be perfectly separated by a hyperplane, one may also allow deviations defined by ξ_i > 0 for individual samples x_i. Those samples for which ξ_i = 0 are on the margin of its correct class, those with ξ_i = 1 on the separating plane, and those with ξ_i > 1 the wrong side of the dividing line, or misclassified samples. This is illustrated in Fig. 17, for which there are five SVs: three are exactly on the margins, and two between the margins in what would be empty space if the classes were perfectly separable. Of the two between the margins, one is misclassified and so has ξ_i > 1. This now allows a number of samples to be misclassified, and also for samples to be between the margins. This allows simpler boundaries to be obtained but which have the disadvantage that there are now some misclassified samples. In Fig. 18 we illustrate this principle for case studies L2 and L3, neither of which are linearly separable, but using a linear model rather than an RBF. We note that all misclassified samples are between the margins and are SVs which have an influence on the model. We also note that the margins have to be wider for the less linearly separable data and therefore include more samples the wrong side of the boundary and more Support Vectors. Note that this approach is complementary to changing σ although we will see in Section 3.4 that considering both approaches together is the usual approach for optimising and using SVMs.

Fig. 17 Illustration of slack variables. The support vectors for two classes are illustrated with filled symbols. Samples with ξ = 0 are on the margins; with ξ > 0 between the margins and with ξ > 1 are misclassified. The five SVs are indicated with borders around the symbols.

Fig. 18 Finding boundaries using slack variables for the non-linearly separable case studies L2 and L3. SVs are marked with crosses.

Mathematically, the optimisation task of Section 3.1 requires simultaneously maximising the margin ½(ww′) and minimising the empirical error, given by the sum of the allowed deviations , hence becoming

subject to the constraint c_i(wx_i′ + b) ≥ 1 − ξ. C is called the penalty error; the higher it is the more significant misclassifications are but the more complex the boundary (see below). It should be noted that the margin errors ξ_i become training errors only when ξ_i > 1. The SVs are now no longer all exactly on the margins but are somewhere between the two extreme margins. Every sample on or between the margins is an SV. When p = 1 the SVM is called a Level 1 Support Vector Machine, and when p = 2 a Level 2 Support Vector Machine. In this paper we illustrate SVMs using Level 1 methods, for simplicity, but when using packages or comparing results be sure to check whether the method is Level 1 or Level 2.

SVMs can be divided into two categories, hard- and soft-margin SVMs. Hard margin SVMs require finding a space or using a kernel for which two classes are perfectly separable, and aim to find the optimal boundary that exactly separates the classes, with the maximum possible margin between the two classes, and in practice involve setting an infinite value of C: this was employed for the example of Fig. 14, meaning that misclassifications are never tolerated. However, it is always possible to find a feature space in which the two classes are perfectly separable when using a kernel function such as an RBF, and forcing the algorithm to search for this feature space may lead to overfitting. To avoid this, most people use soft margin SVMs which tolerate a degree of misclassification, and are designed to balance the classification error against the complexity of the model; in this paper we will illustrate our examples using soft margin SVMs which are the most common available.

The parameter C is set to determine the level of tolerance the model has, with larger C values reflected in lower tolerance of misclassification and more complex boundaries. Mathematically, C is included as an upper bound on the Lagrange multipliers, so that:

0 ≤ α_i ≤ C

This additional parameter determines which one of the two criteria is emphasised most during the optimisation (either ½(ww′) or ). Lower penalty error values emphasise the first term, allowing higher deviations from the margin ξ_i, hence the emphasis will be on margin maximisation rather than minimising the distance of misclassified samples from the boundary. In contrast, higher penalty error values will emphasise the second term, hence allowing smaller deviations across the boundary ξ_i and minimising the training error. C offers the opportunity to pursue a trade-off between complexity of the boundary and the importance attached to misclassified samples or samples near the boundary. Note that a very high value of C tends towards a hard margin SVM, as this occurs when there is a very large penalty error for misclassification, i.e. one tries to construct boundaries that perfectly model the training set.

As an example we examine linear models for case study L2. We can see that the two classes are not linearly separable and a member of class A (blue) happens to fall within the region of class B (red). We see the effect of changing C for a linear model in Fig. 19. When C is reduced, more samples become SVs and the margins are broader, as more samples are allowed to influence the model. One important and often neglected issue is that most SVM software allows the user to enter any value of C. This means that it is possible to obtain solutions that have no meaning. As an example see Fig. 20 for case study L3. This dataset is not linearly separable and so an infinite value of C (hard model) will be impossible to obtain if we use a linear boundary; therefore there will be an upper limit to the value of C that provides an analytically correct answer. When exceeding this, it is usual for most software still to try to produce an answer: this is because of computational issues, for example when optimising the maximum allowed number of iterations is obtained without final convergence or because in practice computers cannot handle infinite numbers so the maximum (or minimum) number within computational precision is obtained. When exceeded, often nonsensical or unpredictable results are obtained, for example in Fig. 20 we see that using the value of C of 1 no longer encloses the SVs within the boundaries and results in some misclassification. This is because the algorithm tries to find an impossibly narrow boundary, as it is impossible to obtain a perfect (hard boundary) model using a linear function for two classes that are not linearly separable. When close to the upper limit of C that is acceptable for any specific dataset and SVM model, the results can be a little unpredictable and depend a bit on the algorithm used, but it is usually unwise to work in this region.

Fig. 19 Effect of changing C for linear models and case study L2. SVs are marked with crosses.

Fig. 20 Apparent effect of changing C for linear models and case study L3. Note that C = 1 is algebraically an impossible solution. SVs are marked with crosses.

In such situations we need to include a kernel function, and the results for case study L3 and an RBF are presented in Fig. 21 for varying values of C. Note that all samples within the boundaries and all misclassified samples are also Support Vectors. As the value of C increases the boundaries are tighter, there are less Support Vectors and the boundaries are more complex. Note that although the number of misclassified samples tends to decrease with C this is only an approximate rule; what certainly happens is that the number of SVs decrease but some are due to samples being within the margins and some as SVs. The appearance of the boundaries at the two highest values of C are identical, this is because the SVs are the same in both cases, having reached a very tight solution; for an identical value of σ for an RBF, the appearance of the boundaries depends only on which samples are chosen as SVs. Note also that for this RBF (σ = standard deviation of the data), there is a solution for high values of C which can perfectly classify all samples (equivalent to a hard margin) unlike in the linear case. Whether such a solution is achievable depends on the value of σ.

Fig. 21 Effect of changing C for RBF models and case study L3, using σ = 1 × the standard deviation of the data. SVs are marked with crosses.

3.4 Choice and influence of SVM parameters

It is important to understand the influence of C and σ (for an RBF) on the SVM solution. We will illustrate this with case studies R3a (polymers – two groups) and R1 (environmental). Samples that are the wrong side of the boundary are misclassified. In all cases σ will be cited in units of the overall standard deviation of the dataset.

In Fig. 22 we illustrate both the changing boundaries and the decision function for case study R3a. For each chosen C value, in the left-hand column both the boundary (or decision function) and margins are presented, but in the right-hand column we illustrate only the decision function rather than the margins for clarity.

Fig. 22 Illustration of the influence of C and σ on the boundaries for case study R3a (polymers).

For low σ (0.1) the decision function is very spiky as anticipated, each point that is an SV represented by a sharp spike. Because class A (blue) samples tend to be clustered in compact groups the spikes add together to produce small regions surrounded by a boundary. Class B (red) samples are more disperse and so the neighbouring spikes do not add together and as such there are very narrow margins around most samples; however, the decision function encloses class A samples, and all the rest of the dataspace would represent class B, but be within the margins. This of course is probably an unrealistic model as it would class most unknowns that are in fact part of none of the known clusters as being members of class B and so is probably overfitted. As σ increases the small regions merge, for example when σ = 0.5 and C = 1 there is one contiguous and large region representing class A. This is because the RBF is broader and so the neighbouring Gaussians overlap more to give a flatter surface. This principle is illustrated diagrammatically in Fig. 23: for σ = 5 and C = 1, the boundary is nearly linear, but with a wide margin. This is because the Gaussians are very broad and so give a surface that is nearly flat. Quite a lot of samples between the margins are tolerated.

Fig. 23 Summation of five Gaussians of increasing width, representing, in two dimensions, an RBF function of increasing width.

The main conceptual difference between the model for C = 1 and C = 100, is that in the latter the margins are narrower and the number of SVs are less. The consequence of this is that the shape of the surface can be more complex. In Fig. 24 we show the effect of including only three out of the five Gaussians in Fig. 23 to construct the surface and we can see that it appears much less smooth for similar widths. Using σ = 5 we see that the surface represents more a quadratic than a linear model using C = 100 and that there are often more regions since the shape of the surface is less smooth, due to there being less support vectors, compare for example σ = 0.5.

Fig. 24 Similar to Fig. 23 but only three of the Gaussians are used for the summation, Gaussians represented by black dashed lines not being part of the summation.

For case study R3a, the main difference when changing parameters involves the smoothness or complexity of boundaries and in most cases samples are correctly classified, although the number within the margins changes. However, for case study R1 (environment) there is a particular challenge in that there are three samples in an outlying group of class B (clean or unpolluted), that appear within the samples of class A (polluted) (Fig. 25). We can see that for σ = 0.1 these are clearly identified as a small region for both values of C, and there is no real difference in the models as almost all samples are selected as SVs. However, for C = 1, once σ reaches 0.5, this small group is classified as part of class A, but within the margin, but as σ = 1 this small group is outside the margin. A different behaviour is observed for C = 100 with the samples being correctly classified (within their own region of PC space) up to σ = 1. Of course it is probably up to the chemist to decide which model is appropriate; is there a reason why this small group is really part of class B or is it that these samples could have been mislabelled or even mis-sampled (sometimes a sample that is thought to be unpolluted actually does contain pollutants)? If we wanted to hedge our bets and say that samples between the margins are ambiguous, using C = 1 and σ = 0.75 finds relatively few samples between the margins but puts this small group of ambiguous samples within this region. Using a higher value of C forces them to be correctly classified in most cases, but is this overinterpreting the evidence?

Fig. 25 Illustration of the influence of C and σ on the boundaries for case study R1 (environment).

Unlike methods such as PLS, or PCA, there has been less emphasis on formal optimisation of SVM parameters, and this is not the main aim of this paper, the area of which is still one for active research. However, general principles are to divide data into training sets (for which the model is developed) and separate test sets. The test set is a portion of data that is left out to be predicted by the mathematical model.^26,39 There are many ways of forming a test set. These include Leave One Out Cross Validation,⁴⁰ where a single sample is left out each time as a test set until each sample has been removed once; the bootstrap, where the training set involves sampling the overall dataset with repetition and the test set is those samples never chosen;⁴¹ and repeated dividing into test and training sets.³⁶ Whereas there is no universal guidance, a simple strategy may be to test a range of values of C and for an RBF σ, for example using 5 levels for each parameter (so there will be 25 combinations of parameters). A method such as the bootstrap or cross-validation is then used to determine how well the test set samples are predicted – usually an indicator of success is required such as %CC (percentage correctly classified) or %PA (average percent predictive ability);^18,26 these relate to how well the samples are classified by a given model. The higher this is (for the test set samples), the better. Usually the training set is predicted well, but this approach protects against overfitting – whereby the SVM model too closely fits the training set but then cannot model well the test set, as the boundaries are too complicated. There are, however, several problems here unique in the case of SVMs. First, not all samples will influence the boundary. Therefore approaches such as cross-validation may not always be good methods of choice, as leaving out one sample that is not on the boundary will not influence the model: in traditional approaches such as PCA all samples contribute to the model. Methods that involve leaving out groups of samples are preferable. The second is that some indicators such as %CC can result in very flat solutions, for example if there are 50 samples to be assessed, there may be several solutions that give an identical %CC, e.g. 47 out of 50 samples correctly classified, and so it is not possible to choose – in which case alternatives such as %PA which provides a fine structure to %CC may be preferable but this is computationally very much more intensive. The third is that these methods are very intensive and can take several hours or even days even on parallel processors, e.g. quadcores. The fourth is that models may be identical over a range of values of C: this is because the effect of this parameter is to change the number and nature of the SVs but there is not a smooth transition so, for example, a model with C = 1 may be identical to that with C = 5 under certain circumstances. Finally it is necessary to establish a range of tunable parameters in advance that is sensible for the problem in hand.

There is no universal panacea for overcoming these problems, and unlike PLS or PCA models we often cannot pinpoint an exact optimum that everyone would agree to. The main issue though is to avoid overfitting and to ensure that the optimisation and validation are done correctly. Because optima are likely to be relatively flat, it is often impossible to define the precise value of the tunable parameters that are ‘best’, but so long as the model is safe, that is it does not overfit the data, the model is probably adequate. Often it is up to the person that sets up the SVM model to make decisions about what he or she thinks is sensible, for example how important it is to reject outliers (and which samples are outliers) or whether the underlying differentiation between groups of samples is likely to be linear. Sometimes it is impossible to generalise and this depends on knowledge of the underlying problem. Most traditional statistical tests are based on underlying assumptions of normality and so the majority of tests for outliers, for example, depend on this type of assumption. In many cases, e.g. metabolomics and proteomics, we do not necessarily expect samples to be normally distributed, so can take advantage of the flexibility of Support Vector based models.

4 Multiclass support vector machine models

Multiclass models involve deciding which group a sample belongs to when there are more than two classes in a dataset.²⁶ Support Vector Machines were not originally formulated as a multiclass method, but there are extensions that are available when there are more than two groups in the data, e.g. case study R2 (NIR of food) where there are four classes and case study R3b (polymers where there are nine classes). In this and later sections we will define the group that is being modelled as the ‘in group’ and all other samples (which may arise from several classes) as the ‘out group’.

4.1 One vs. all

One vs. all⁴² is the earliest method reported for extending two-class SVMs to solve the multiclass problem and involves determining how well a sample is modelled by each class individually and choosing the class it is modelled by best. Given G classes under consideration, G binary SVM models can be constructed, samples either being considered as part of the class or outside it, so that each model consists of two groups, the first being class g and the second all other classes. The gth (g = 1,…,G) SVM model is trained with all of the samples in the gth class being labelled by +1 and all other samples being labelled by −1 (note that the alternative approach of one-class SVDD is discussed in Section 5). Hence G SVM decision functions can be obtained, for each model. Instead of using a sign function to determine the class membership, the numerical outputs of the decision functions for each SVM model are compared, as described below. The membership g(x) of an unknown sample x is determined by finding the class for which the corresponding decision function is a maximum
where
is the decision function for class model g.

A way of illustrating this method is to present the decision function for each class. For R2 (NIR of food), all four decision functions can be superimposed. In Fig. 26 we illustrate this principle, for four values of σ and C = 1 using a 2 PC projection of the data. For σ = 0.05 we find that all the samples are correctly classified, but that the four decision functions are primarily of the form of planes with sharp spikes where the samples are. The planes are at different levels. For very small values of σ, all samples become SVs, and all are on the margin and of equal height, because the Gaussians are in effect in the form of a series of sharp spikes centred on each sample and do not overlap. Since , if all samples are SVs, we have

where I_in is the number of samples in the ‘in group’ (being modelled) and I_out the number in the ‘out group’ (the remainder of samples in the training set), but because the decision margins are scaled to width 2 (so that there is a maximum distance of 1 for each sample to the decision boundary – see Section 3.1), then α_in + α_out = 2 so that α_in = 2I_out/I and α_out = 2I_in/I. If there are equal numbers of samples in each group the values of α become 1; the more unequal the number of samples, the more these differ from 1. The bias term which is simply half the difference between the values of α is therefore given by (α_in − α_out)/2 = (I_out − I_in)/2; if there are equal numbers of samples in each group, this becomes 0. The principle of how the bias term is influenced by the number of samples is illustrated in Fig. 27. In our case for class A the bias term is 0.5, class B is 0.1667, class C is 0.5556 and class D 0.7778, which relates directly to the number of samples in each class. Class B has by far the largest number of samples (= 30), and so the lowest bias term and therefore is the highest plane, meaning that samples outside the four closely defined clusters are assigned to class B (olive oils), suggesting that the model overfits samples in the region between the clusters. Note that the positive spikes are support vectors from ‘in groups’ and negative spikes are samples from the out classes; because the number of samples in the ‘out group’ is always more than the ‘in group’ the height of the negative spikes appears less than that of the positive spikes.

Fig. 26 Illustration of one vs. all SVMs, using the first 2 PCs of case study R2 (NIR of food) and a value of C = 1 and different values of σ relative to the overall standard deviation of the data.

Fig. 27 Illustration of bias term and Lagrange multipliers for the case where all samples are infinitely sharp support vectors, but there are unequal numbers in each class. In this case the blue group (‘in group’) contains more samples than the red group (‘out group’).

As σ increases to 0.25, the region assigned to each group increases, as the RBF is broader. Class C (safflower oil) whereas consisting of fewer samples than class B (olive oil) is more dispersed, and because the Gaussians are broader they do not reach 0 between samples of each ‘in group’ and as such the class with the greater dispersion wins out, so the background appears to be from class C. However, still this value of σ suggests that the data are overfitted. A value of σ = 0.5 begins to sort out these problems, with each group having its own defined region of dataspace. Since there are no samples in the bottom left-hand corner of the PC plot, the predictions of origins of samples that fall into this unknown area are not certain. However, multiclass SVMs are a supervised method for pattern recognition and as such they try to force samples into one of several predefined groups, so every region of the PC plot has to be assigned to a specific group, even if there are no training set samples, in order to obtain an unambiguous answer. Once σ = 1 well defined regions of the PC scores plot are found. If the property that all regions of dataspace are uniquely assigned to one class is undesirable, it is necessary to use other approaches such as one-class classifiers (Section 5).

4.2 One vs. one

Given G classes, the one vs. one approach constructs G(G − 1)/2 two-class SVM classifiers, each classifier only separating two of the G classes. For example, we can form a model between classes A and B and ask which class each sample is assigned to, even if the origin of the samples is from outside these groups. If there are four classes we can test A vs. B, A vs. C, A vs. D, B vs. C, B vs. D and C vs. D. We then combine the results of these tests. The simplest approach involves using ‘majority vote’, that is assigning a sample (or a region in dataspace) to the class it is most frequently classified into. Where there is a tie, the sample (or region in space) is considered ambiguous.

For case study R3b (polymers) we illustrate the result of one vs. one decision making using C = 1 and four values of σ in Fig. 28. Note that there are a small number of areas (shaded in white) for which there is no unambiguous answer, where the one vs. one method is tied. Note that as σ is increased the regions occupied by each group become more similar in size.

Fig. 28 Result of one vs. one decision making for case study R3b (polymers) using various values of σ.

One anticipated problem is that there are several areas in Fig. 28 where the answer is ambiguous, that is there is a tie as samples are equally assigned to one class or the other. There is no universal agreement as to how to cope under such situations but one common approach involves fuzzy rules,⁶ as follows:

• For each point in dataspace, perform all comparisons 1 vs. 2, 1 vs. 3 to 1 vs.G and predict c for each model.

• If the predicted value of c is greater than 1 for any comparison, set it to 1.

• Keep the minimum value of c for this set of comparisons, call it m₁.

• Perform the full set of comparisons for all classes G, giving m_g for each class g.

• Assign the sample or region of dataspace to the class for which m_g is a maximum.

The result of using fuzzy rules is presented in Fig. 29. It can be seen that the classes are now quite well represented apart from classes D and I which overlap with other groups and cannot be easily modelled using two PCs. An advantage of fuzzy rules is that there is always an answer as to which class is most appropriate, but the disadvantage is that this could be prone to overfitting, and having an answer that is ambiguous sometimes provides an alert that the new sample is an outlier. In much classical machine learning there is almost always an underlying answer that is certain (for example, if we are testing whether a person is male or female there will be an answer and every sample must fall into one of the known groups), but in areas of chemometrics we may have an outlier or a sample that is not a member of any modelled groups (e.g. a type of polymer that has yet to be analysed).

Fig. 29 As Fig. 28 but using fuzzy rules.

4.3 DAG trees

When there are large number of classes, using one vs. one methods of Section 4.2, the number of comparisons can be quite substantial (in the case of R3b there are 36 possible one vs. one comparisons), especially if there are also test and training set comparisons, so computationally more efficient methods are often desirable. A DAG (Directed Acyclic Graph) tree is an alternative and more computationally efficient approach, although it starts on the same basis of forming all possible one against one models on the training set. But when predicting the origins of a sample, it uses a rooted binary DAG tree with G(G − 1)/2 internal nodes (or decisions) and G leaves (or outcomes or classification results). Each node involves a binary one against one model. A test sample starts from the root node, and the binary decision function is evaluated depending on the output value of the decision function. Examples of DAG trees for 3- and 4-class problems are shown in Fig. 30. The computational time for a DAG tree is shorter than one vs. one because it is not necessary to go through every binary classifier to test an unknown sample; only G comparisons are necessary, so this could shorten the time considerably for predictive models, for example, if there are 9 classes, instead of forming 36 models and taking the majority vote, only 9 comparisons are required. There is no universal guidance as to which two classes are tested in each node, but for most problems the result only changes slightly according to the arrangement of the nodes. A possible strategy, for example, would be to choose the two most different classes for the first decision in the tree and so on. The improvement in computational efficiency will be significant when predicting unknowns, especially if algorithms are quite slow. As an illustration of the use of DAG we present the results of three possible solutions in Fig. 31. There are slight differences according to which decision tree is employed. However, when there are a large number of classes, this can speed up the model building substantially, and although there is some variability between solutions, this is unlikely to be no more than that introduced by other factors such as sampling error, instrumental noise, data preprocessing or choice of decision function.

Fig. 30 Examples of possible DAG trees for 3- and 4-class problems.

Fig. 31 Results of DAG tree for dataset R3b (polymers) using a one vs. one SVM, fuzzy rules, C = 1 and σ = 1.

5 One-class support vector domain description

5.1 One-class classifiers

In Sections 3 and 4 we introduce classifiers that aim to divide dataspace into two or more regions, each of which corresponds to one class of samples. The classification of a sample is given by which region of the dataspace it falls into. These classifiers are often sometimes called hard models, in that they divide space up into sections using one, or a series of, boundaries, the principle of which is the basis of the most widespread classification methods. However, when there are several classes it is sometimes hard to re-express these classifiers in a multiclass form, and the boundaries become quite complicated as discussed in Section 4, and indeed SVM methods cannot naturally be formulated as multiclass approaches, unlike methods such as QDA (Quadratic Discriminant Analysis) or LDA where the decision rules are easy to extend. Furthermore, hard models find it difficult to deal with outliers, that is samples that belong to none of the predefined groups – the inherent assumption of such classifiers is that all samples must belong to one group – and cannot deal well with samples that are genuinely ambiguous. A final weakness of hard models is that they have to be reformed if new groups are introduced, unless these groups are subsets of the existing groups.

In order to overcome these limitations a set of modelling techniques which are called one-class classifiers⁴³ have been developed. The approaches are often sometimes called soft models, and in the area of chemometrics, Soft Independent Modelling by Class Analogy (SIMCA) is the best known, although by no means unique. A one-class classifier models each group independently. There is no limit to the number of groups that can be modelled, and a decision is made whether a sample is a member of a predefined group or not. The difference between one-class and two-class classifiers is illustrated in Fig. 32. For the two-class classifiers a line (or more complex boundary) is drawn between the two classes and a sample is assigned according to which side of the boundary it falls. For the data illustrated, there are two possible one-class classifiers, and these can be represented by boundaries that in the case of the data illustrated are ellipsoidal. Samples outside these boundaries would be assigned as outliers belonging to neither known class. Fig. 33 extends this theme. In this case there are three groups; although class A and B are separate, class C overlaps with both of them; in addition there is an outlier that belongs to none of the three classes. A one-class classifier establishes a model for each class separately and is able to conclude that samples belong to no class, or to more than one class, simultaneously.

Fig. 32 Difference between (a) a single two-class classifier or (b) 2 one-class classifiers.

Fig. 33 Example of three classes with some overlap and an outlier.

5.2 Support vector domain description

Although SVMs are usually introduced as a form of binary classifiers, one-class modifications are available. Rather than being used to separate two or more classes, one-class SVMs are built on a single class. There are two main one-class SVM algorithms: one is called ‘Support Vector Domain Description’ (SVDD)⁴⁴ and another is called ‘ν-Support Vector Classifier’ (ν-SVC).⁴⁵ We will restrict discussion to the SVDD method in this paper, whilst reminding readers that there are, as always, several alternatives available. We will assume that we are using an RBF kernel.

Whereas SVMs find lines or hyperplanes either in the original dataspace or more usually in kernel space to separate classes, SVDD tries to find a circle (or hypersphere in kernel space) that encloses a class. One problem is that we can always find such a hypersphere if the radius is large enough to enclose a class, so there usually need to be other rules. Fig. 34 illustrates some of the key principles of SVDD. Only one class is modelled and each sample is characterised by two variables. Instead of a line dividing different regions of dataspace a circle is found that encloses the data. This circle has radius R. Samples on the boundary or circumference of the circle are defined as unbounded support vectors. Samples outside the boundary or misclassified are defined as bounded support vectors. Of the unbounded SVs these can be divided into essential (required to define the boundary) or non-essential (not required to define the boundary). The latter are very rare and we will neglect, and would only occur if samples happen (by accident) to be exactly on an existing boundary. Note that for one-class SVDD, there is only one boundary and no margins.

Fig. 34 Some definitions for SVDD.

Whereas a circle of large radius can always be found that encloses any dataset exactly, this may result in overfitting the data, especially if one or two samples are outliers. Hence a value analogous to C is used to determine what proportion of samples of the ‘in group’ are to be enclosed by the circle. In this paper we define a parameter D. A value of D = 0 means that all samples are within the boundary, and D = 1 that no samples are within the boundary. As D increases the region enclosed by the boundary decreases. The principle is illustrated with reference to case study L4 in Fig. 35. The value of D relates approximately to the proportion of samples that are outside the boundary. Hence if D = 0.75 we would expect around 5 out of 20 samples in each class to be outside the boundary (bound SVs). This is an approximation (for example, it is not possible to have exactly 25% of 10 samples), but usually holds up well when there is no kernel. The samples would by definition be misclassified but this is analogous to a confidence limit; if we have D = 0.25, we are finding the 75% confidence limit, i.e. the bound in which approximately 75% of the training set are enclosed. The samples on the boundaries normally equal 2 or 3, and are correctly classified but called the unbounded SVs. For D = 0 in most cases the unbounded SVs are the samples farthest apart in the dataset, but if drawing a circle containing these samples on the circumference does not enclose the training set then a third sample is necessary to redefine the circle. The circle is the smallest possible one that encloses all samples. Two different scenarios are illustrated in Fig. 36. Note that very occasionally the boundary appears to be defined just by one SV: in fact there is more than one sample very close to the boundary and this is a result of numerical approximation and slow convergence of algorithms since it is not always possible to converge to a precise analytical solution; however, in Fig. 35 this only happens for the case of D = 0.75 and class A when in practice the border is so narrow that one would not use this in practice as a model. Note that although the SVDD boundary is in the form of a circle in the dataspace if there is no kernel, as D changes we do not get concentric circles, as illustrated in Fig. 37, and as such SVDD differs from methods such as QDA (using the Mahalanobis distance) where circles (or ellipsoids) are all centred on the mean of the dataset as the confidence level changes. The value of the radius of the circle, however, is related to D as illustrated in Fig. 38 for class A of case studies L1 to L4.

Fig. 35 Appearance of one-class SVDD boundaries for case study L1 and different values of D. Misclassified samples from each ‘in group’ are indicated by filled symbols, and can be called bounded SVs. Unbounded SVs are indicated in filled light colour on the boundary.

Fig. 36 Illustration for the example of Fig. 35 and D = 0 how boundaries can be obtained using either two or three SVs dependent on data structure.

Fig. 37 Illustration of SVDD boundaries for D = 0 (largest circle) to D = 0.9 (smallest circle) by steps of 0.1 for class A of case study L2.

Fig. 38 Illustration of how the radius R for the SVDD solution for class A of case studies L1 to L4 changes with D.

Mathematically, in analogy to SVM, it is possible to define a structure error function for a SVDD model as

with µ being the centre of the data enclosed within the model space, R the radius, ξ_i is the slack variable modelling the training error and the tolerance of the training error is controlled by the term C which controls the size of ξ and therefore controls the fraction of samples lying outside the boundary. SVs are either on the boundary (ξ_i = 0) or outside the boundary (ξ_i > 0) as discussed above. The more rigid the boundary the greater the value of R. The mathematics is rather complicated but the RBF in kernel space is the same as for two-class SVMs except that the SVs all come from one class, and therefore the decision function is always positive, so that the position of the separating hyperplane (or decision boundary) must be changed, and is given by 0.5(b − R²) where b is defined slightly differently (and is negative in value) to b for two-class SVMs. Using this formalisation, one-class SV models can be obtained in a similar manner to two-class SVM models, using Lagrange multipliers to find the Support Vectors, but we will not go through the mathematics in detail which is described elsewhere.^43,44

It is important to realise that R changes the appearance of the boundary but is controlled by C. The more rigid the boundary the larger the value of R. Although C is often called the penalty error it is not strictly analogous to that used in two-class SVMs; however, the higher it is the more the samples that are included within the model space. Because there is only one class to be modelled, the boundary can either be set to include all samples or to misclassify a certain proportion of samples. The larger the number samples misclassified, the smaller the region in dataspace. However, unlike two-class SVMs, one-class models do not use information about the ‘out group’ and as such are not trying to avoid samples of different classes. C can be related to D which has been defined above by

where I_g is the number of samples in the training set, to emphasise that C no longer has a similar meaning to that in two-class SVM, and so that D is directly comparable to a confidence limit. Hence a value of D = 0 corresponds to an infinite penalty error (that is there can be no misclassified samples), and a D of 0.1 for a class size of 20 corresponds to a value of C of 0.5. A D of 0.5 would correspond to a C of 0.1 for that class size.

5.3 Kernels

Just as for SVMs, kernels can be introduced to the model. It is now no longer necessary that the boundaries are circular. If we use an RBF, as usual the sharper the radius, the more complex the boundary. However, because, unlike SVMs, we are only modelling one class, the boundaries tend to be smoother. In this section we will calculate σ in terms of the standard deviation for each class separately, rather the entire dataset as a whole.

In Fig. 39 we illustrate the change in boundary with change in σ for case study L2 and D = 0.2. In this case we have to visualise separate decision functions for each class, although the boundaries can be superimposed in flat projection. Note that now there can be samples that are within more than one region. We see that for small values each sample has an RBF so sharp that it is in practice an SV in its own rights, but once σ increases the boundaries become smoother, first encompassing small groups of samples, and ultimately nearly resembling the boundary when there is no kernel (Fig. 35), for an infinite value of σ, the decision function will be completely flat and so exactly resemble the models of Section 5.2. As the value of σ increases, the boundaries get smoother and resemble circles more. For D = 0.2 we expect around 8 out of 40 samples to be misclassified, and but the actual number is slightly less than expected. However, there are, in fact, 4 SVs for class A and 5 for class B, so if we count the number of SVs this is close the number anticipated from D. The approximation only holds well when σ is large.

Fig. 39 SVDD boundaries and decision functions for both cases and case study L2, using D = 0.2 and various values of σ in units of multiples of the standard deviation of each class SVs indicated by symbols with crosses.

The mathematics is rather complicated but the RBF in kernel space is the same as for two-class SVMs except that SVs come from only one class, so the kernel function is always positive.

5.4 Influence of SVDD parameters

We can now visualise the effect of adjusting both D and σ together. For case study L2, we show the influence of D when σ = 0.5 in Fig. 40. As D decreases, the boundaries become wider and more complicated, as they have to incorporate all the samples. Note interestingly that for this value of σ there is no difference between the boundaries for D = 0 and 0.25. In fact the value of D approximates the proportion of samples misclassified best when σ is large – resembling a model without a kernel. When σ is very small the RBF decision function is very sharp and almost all samples become SVs. This is illustrated in Fig. 41 for class A of case studies L1 to L4. The number of bounded SVs equals the number of misclassified samples – that is, samples outside the boundary. For D = 0 no samples are misclassified and as such there are no bounded SVs; however, the number of unbounded SVs reduces with σ until it reaches a number that equals the number of SVs needed to define a boundary in the model without a kernel (Fig. 35) which is equal to 2 in this case (or 0.1 of the samples) since only 2 samples are required to define a circle; for low values of σ the high proportion of samples that are SVs reflects the fact that most samples are SVs so the boundaries become very complex. A similar trend can be noticed for the case where D = 0.25, except that the number of unbounded SVs approximates to 0.2 rather than 0.25 (4 samples), since the relationship between D and the number of misclassified samples is approximate. Some of the sudden ‘dips’ or discontinuities occur because when σ is changed there are sudden changes in which samples are defined as SVs, the solution being stable for a range of values and it changes as different samples define the boundary. As we can see in Fig. 37, this may involve quite different samples, and sometimes different numbers of samples. An expansion of the graph for D = 0.25, for σ between 0 and 2, is illustrated in Fig. 42. It can be seen that for σ = 0.5 there are no bounded SVs; that is, all SVs fall on the margins. Four bounded SVs (corresponding to unclassified samples) are obtained once σ exceeds 1.2.

Fig. 40 Appearance of boundaries and decision functions for case study L2, σ = 0.5 the standard deviation of the each class and different values of D. SVs are indicated by symbols with crosses.

Fig. 41 Number of bounded and unbounded SVs for class A of case studies L1 to L4 for different values of σ.

Fig. 42 Expansion of the graph of Fig. 41 for values of σ between 0 and 2 and D = 0.25.

We illustrate the changing boundaries for case study R1 (pollution) as both D and σ are varied, in Fig. 43. For very small values of σ, SVDD attempts to form boundaries around all or most samples, individually. An interesting feature of this dataset is that there are 3 outlying samples from class B (clean) that appear to be present within class A (polluted). For low values of σ these are characterised by their own small clusters, but as σ increases, the appearance is of large overlapping clusters. When D = 0 these outlying samples have a large influence on the class B model as the boundary is required to include them, and when σ is very high this results in two highly overlapping circular regions. When D = 0.25, the model can afford to ignore these samples, as approximately 25% of the samples will be outside the boundary and so misclassified from each class. Note that these samples are very far from the boundaries, whereas the other misclassified samples are quite close, suggesting that the distance from the boundary could also be used to determine how badly a sample is misclassified.

Fig. 43 Illustration of SVDD boundaries for different values of D and σ (relative to the standard deviation of each class) for case study R1 (pollution) using the scores of the first two PCs.

It can be seen that when D and σ are low there is a risk of overfitting. For case study R1 this could have a considerable influence on the model. In other situations, the values of these parameters may have little influence on the model. We return to case study R2 (the four types of oil). Fig. 44 illustrates the boundaries when D = 0 and σ = 1. These are identical for σ = 0.5 and 2, as the same samples are chosen as SVs and the classes are very well defined. Note a very significant advantage of one-class SVs for this case study: compared to Fig. 26, since the groups are very well defined, it is only necessary to select the region of dataspace occupied by the samples for the model, and samples that are outside the predefined classes are no longer forced into a specific group.

Fig. 44 SVDD boundaries for case study R2 for D = 0 and σ = 1 times the standard deviation of each class using the scores of the first two PCs.

One major dilemma is how to optimise the SVDD parameters. In SVMs if there are two classes and as such it is possible to determine classification errors, since if a sample from class A is assigned to class B, this contributes to the training set error. In SVDD there is only one group and, of course, the model that performs best encompasses all samples. A circle (or hypersphere in kernel space) that is large enough can always be found that encloses all training set samples from the ‘in group’ but this is not necessarily a suitable solution. If we were to include an ‘out group’ in the assessment, then of course, as the size of the circle increases, ‘out group’ samples will be enclosed in the circle, resulting in classification errors, so there will be a limit to the optimum radius of the circle. However, for one-class SVDD we should not take into account information about any other group. Therefore, traditional approaches for optimisation are not likely to be successful.

We will discuss one possible approach to the optimisation of σ. To overcome the problem associated with the lack of ‘out group’ samples, a possible approach for optimisation of σ is proposed using the bootstrap⁴¹ involving the repeated formation of bootstrap training and test sets, the data being split into two, one the bootstrap training set that is used to develop the SVDD model and the other bootstrap test set that is used to show how well it performs. This involves finding a compromise solution that attempts to minimise the proportion of bootstrap test set samples rejected as belonging to the ‘in group’ (defined by f_rej) whilst also minimising the radius R_h that surrounds the bootstrap training set in kernel space, since the lower R_h the tighter the fit to the ‘in group’ samples. In order that the radius R_h is comparable in magnitude to f_rej, the boundary radius can be scaled from 0 to 1 by:

where d_min is the minimum pairwise distance between samples in a bootstrap training set and d_max is the maximum pairwise distance between these samples. Therefore, we can define the optimum σ by the value that results in the minimum of k + f_rej, since f_rej is calculated using a bootstrap test set, and this will be dependent in part on which samples are selected in the bootstrap test set. Hence this procedure is repeated a number of times (typically 100–200) with different samples being selected each time for the bootstrap test and training sets. The average value of k over all iterations can be calculated for a range of σ between the values of d_min and d_max for all the ‘in group’ samples (which is usually wider than for the bootstrap training set) and the minimum chosen as the optimum. During this procedure, the sample rejection rate D is fixed ideally at 0 to include all samples in the bootstrap training set model. After optimising σ it is possible to then change D if required for any specific confidence limit.

6 Support vector regression

6.1 Principles

SVR (Support Vector Regression)^46–48 is an extension of SVM to cope with regression, which is a common application especially in analytical chemistry. For simple linear calibration, where there is only one variable measured, we aim to form a model between x (horizontal axis) and c (vertical axis) of the form ĉ = b + wx, where ĉ is predicted (e.g. a concentration) from x (e.g. a spectral intensity). Note that the notation in this paper is consistent with various previous articles^22,20 and is used because in multivariate calibration, usually the property to be measured is denoted by ‘y’ and the spectral or chromatographic intensity by ‘x’, whereas in traditional analytical chemistry this terminology is reversed. Hence we do not use ‘y’ which can be confusing as there is a direct incompatibility between the two conventions, and employ ‘c’ which can be used to denote calibrant or concentration, and, in two dimensions, is represented by the vertical axis. This is often called inverse calibration. The discussion below could be extended to other types of calibration, but we restrict to one way of expressing the equations for brevity.

In order to illustrate the principle, we will consider case study C1 and try to develop a linear model between x and c. For illustration we refer to Fig. 45. To understand the method, we need to introduce a new parameter, ε. The linear model between the two variables is analogous to the boundary between two groups in SVM. However, ε defines the width of the margin, and an aim of calibration is to enclose all samples within the margin. We can see that as the line becomes flatter, the width of the margin increases. In order to enclose all samples between the margins there will be a maximum value of ε (which equals the largest difference in value of c between the samples and is a completely flat line), and a corresponding minimum value, which depends on the distribution of the samples around a linear model. For a range of values of ε we can draw lines of the form ĉ = b + wx, defined by the SVs or samples exactly on the margins.

Fig. 45 Case study C1. Illustration of different best fit straight lines, together with the SVs (indicated by filled symbols) and corresponding values of ε.

Usually it is necessary to specify ε, which is the error tolerance, in advance of training a model. If there are outliers, for example, the choice is not necessarily straightforward, but this value could be regarded as the maximum sensible error expected in the data. However, for a given value of ε there will usually be several different possible straight lines. If we restrict these lines to those for which at least two samples are on the margins, the number of possible lines is limited. However, unlike SVM, samples do not have to be on both of the margins, and an alternative solution to that of Fig. 45 for ε = 0.152 is illustrated in Fig. 46, in which case two samples are on the upper margin.

Fig. 46 An alternative straight line for ε = 0.152 and case study C1.

A key feature of SVs as linear learning machines is that they try to minimise ½(ww′). In the case of the SVR model of case study C1, x is one-dimensional, so we are trying to minimise ½w² or find the flattest line for a given value of ε. Since w = 0.326 for the case illustrated in Fig. 46 and 0.3 for the case illustrated in Fig. 45 (when ε = 0.152) we choose the solution of Fig. 45 as our preferred out of the two solutions (there are a few other possible solutions also but they can easily be ranked according to the value of w). This is the preferred SVR solution (using a hard model) for the chosen value of ε of 0.152.

6.2 Penalty errors and kernels

In the example above we try to form models that include all samples between two margins, of a given width. Providing that ε is chosen correctly a linear model can always be formed with these properties and there is always a way of deciding which model is the most appropriate.

However, in many practical cases it may be inappropriate to force all samples to be within the margins, and we allow samples to fall outside these margins. We need to extend the SVR models, and the main principles are illustrated in Fig. 47. Samples on the margin are SVs that define the margin, and those outside are analogous to bounded SVs (see Section 5.2). The slack variable ξ defines the distance a sample is from the margin. Samples between the margins are not SVs. Many of the principles are now similar to those described above. The task is now to minimise

where ξ_i is the slack variable for sample i: in this paper we will assume that this is always positive whether the sample is below or above the margin. We can see that there is now a penalty error C that determines how important it is to ensure that all variables are within the margins. Fig. 48 illustrates a variety of solutions for case study C1 where ε and C are varied. Note that in this case C makes very little difference as the two variables are related approximately in a linear fashion, although for very narrow ε there is a small difference when C is changed (for the other variables there is no difference over a wide range). There will, of course, be some combinations of these two parameters for which there is no solution, e.g. a very narrow margin with a high penalty error.

Fig. 47 Main definitions of parameters for SVR.

Fig. 48 SVR solutions for case study S1 for a variety of values of ε and C: (left) best SVR lines; (right) predicted (vertical) versus observed (horizontal). SVs on the margins are indicated with circles (all samples outside the margins are also SVs), and on the right the bars represent 2ε.

When the relationship is no longer linear, as in case study C2, it is necessary to introduce a kernel. We will restrict this paper to an RBF, and similar principles apply as to how to include an RBF as for other implementations of SVs, so are not repeated for brevity. This case study is characterised both by a curvilinear relationship between the variables and by a strong outlier, which is coloured in red. We illustrate the solutions using a fixed value of ε (= 0.2) but with varying σ and C in Fig. 49. We can see that under such circumstances both parameters now have a major role in defining the SVR solution. When σ is small, the solution is much less smooth as expected, but as C increases, the outlier becomes more influential, and for C = 5, lies on the boundary. For low values of C the solution is quite flat. Increasing σ to 1 × the overall standard deviation of the data results in a far smoother solution and one which is less influenced by the outlier. As σ increases the solution will approach a linear model, but some combinations of ε, C and σ are impossible. For example, if we were to have a narrow value of ε and a fairly flat model with a large value of σ it is not possible to increase C to a very high value for this case study since such a model cannot encompass the outlier on the margin.

Fig. 49 SVR solutions for case study C2 using ε = 0.2, and different values of C and σ (in units of the standard deviation of the data) for an RBF. SVs on the margins are indicated with circles (all samples outside the margins are also SVs), and on the right the bars represent 2ε.

6.3 Multivariate calibration

SVR can be employed for multivariate calibration. We will illustrate this using case study S1, which consists of 25 UV/vis spectra each consisting of mixtures of 10 PAHs. The experiments are designed so that the concentrations of each analyte are orthogonal and are at 5 levels.⁴⁹ In Fig. 50 we illustrate the effect of differing values of ε, C and σ on the calibration predictions for benzanthracene. For each chosen ε value, in the left-hand column the model is autopredictive, whilst for the right-hand column we remove 10 of the samples (1, 2, 4, 6, 7, 9, 10, 12, 16, 18) as a test set which are indicated in red, and the remainder are used to determine the model and a training set (see Table 2).

Fig. 50 Results of SVR on case study S1. For each ε: (left) autopredictive model, and (right) training set model (blue crosses) plus test set prediction (red crosses). SVs on the margins are marked with circles. The margins are indicated in green. The concentration of benzanthracene is predicted.

We can immediately see that for low values of ε on the whole the predicted concentrations using autopredictive models are forced closer to the best fit straight line but this does not necessarily mean that the test set is well predicted, e.g. compare σ = 0.5 and C = 1 for ε = 0.05 and 0.2: there is very little difference in the test set predictions. Note that low σ can cause overfitting. Compare ε = 0.05, C = 10 and both σ = 0.5 and 1: we see that for the lower value of σ that autopredictive models appear slightly better but the test set models are considerably worse. Note that in some cases when C is changed, the models are identical because the SVs are unchanged.

Looking at Fig. 50 it appears that the most suitable models are for a low value of ε and high values of σ and C. This is primarily because the data are related in a linear fashion, so having high σ makes the model close to a linear one, whereas low ε reduces the error tolerance, and high C forces the points into or between the margins. There will be a limit to these combinations of parameters outside which there are no solutions; however, the best SV solution does reduce the experimental error substantially. For case study S1 there is only limited advantage of SVR models over more conventional PLS approaches, but there are advantages (a) if there are outliers and (b) if there are any non-linearities. If one wants to force a linear model this can be done without a kernel. We do not illustrate this for brevity, but because the data are already quite linear for case study C1 there is very little difference to those illustrated in this paper.

In many cases in analytical chemistry, experiments are designed to ensure that models are linear and so SVR does not offer much above traditional methods and is overly complicated, with several parameters that must be adjusted. However, the advantage is flexibility; for example, if we suspect that there are outliers the models can be produced using different values of C to see how far they differ, or indeed to include different levels of opinion as to how significant it felt is to include information on the outliers in the model. It is important to realise that least squares methods are often unduly influenced by outliers and as such it is usually necessary to remove such samples prior to modelling, or else use alternatives such as median methods or fuzzy calibration, whereas this is unnecessary for SVR which can be considered much more flexible. In areas such as Quantitative Structure–Activity Relationship (QSAR) where the relationship between the response and the experimental factors is unlikely to be linear, support vector based approaches have a great deal of potential.

It is possible to optimise SVR parameters using similar principles to other methods in multivariate calibration,²⁰e.g.via cross-validation or use of test sets, finding the combination of ε, C and σ that gives the lowest prediction error. However, because several parameters may need optimising, it is usually a good idea to look at the performance graphically first and possibly fix one of these according to what seems sensible for any specific dataset, usually ε which represents the error tolerance, rather than to try to change all three simultaneously: some combinations will be impossible and other combinations will result in identical answers because identical SVs are chosen. If the model is likely to be linear, fixing a value of ε that is quite low by visual inspection and then setting C and σ to be as high as is sensible to give a solution is probably the best approach. There are no hard and fast rules unlike in PLS where there is a strong literature on optimisation (or finding the most appropriate number of PLS components) because varying the values of SVR parameters involves introducing additional assumptions about non-linearity and outliers that can always result in a slightly better fit to the data and so depend on what is expected from the data.

The somewhat limited applicability to calibration problems contrasts to the wide applicability to pattern recognition applications as we do not necessarily expect groups of samples to be linearly separable, e.g. coming from biological, medical or environmental studies and as such flexible non-linear solutions are often necessary.

7 Conclusion

Most articles on Support Vector methods are based around the original description in the machine learning literature, for which the presentation has been largely unaltered over more than a decade. This paper has tried to describe these approaches in a more visual way whilst still retaining the basic algebraic description and references to the key source papers. As these approaches become more widespread there is a need to express the methods in a form that applied scientists can appreciate, especially to understand the influence of the main parameters on the model.

The original applications were less concerned with multivariate data, and less concerned with model validation, as the types of problems often encountered, for example, in engineering have different features: non-linearity though is probably more important outside analytical chemistry and as such SVMs are particularly flexible in dealing with such situations. Many experts would say that SVMs can encompass almost any model, ranging from the linear to the highly complex, and therefore could be regarded as a universal method for classification and calibration. Whereas this is certainly potentially true, for simple situations they are probably unnecessarily complex with the risk of overfitting and dependence of the model on several adjustable parameters that most users do not understand well. However, when mining, for example large databases in genomics, trends may be highly non-linear with outliers and Support Vector approaches offer significant opportunities. We hope, however, that in this paper we offer a graphical insight that allows users of SVM based methods to understand better the consequences of adjusting these parameters (C, σ, and ε where appropriate), so that the methods can be employed safely. In addition, as the analytical chemist gets access to large and more sophisticated datasets, for example from biology, medicine, environmental and cultural studies, traditional linear approaches such as PLS, SIMCA and PCA may in some cases be inadequate and not able to cope with this additional complexity. It is important to remember though that traditional approaches are adequate if the structure of the data is quite simple, and are easier to validate and optimise, so a careful choice must be made. For calibration there is often less need for Support Vector based methods unless there are outliers and non-linearities: some analytical chemists would say that if so the dataset is not a good one, but in some practical situations this may happen and it can be expensive in time and money to acquire perfect calibration sets. In areas such as QSAR there are likely to be non-linearities and outliers in most datasets so SV based methods have a potentially strong role. Direct comparisons between Support Vector based methods and others are often a bit difficult and depend very much on the data structure.

However, it is always necessary to use these approaches with caution to avoid overfitting. This is especially key in most modern chemometrics as there are often far more variables than samples, a situation not usually encountered in most other areas of science. Support Vector methods though are likely to become an important plank of scientific data analysis for many years to come, and there is an urgent need for understanding of the basis of such approaches.

Acknowledgements

We are very grateful to Kanet Wongravee, Sila Kittiwachana and Agnieszka Lemanska for help with the diagrams and for valuable discussions.

References

1. C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–295.
2. V. N. Vapnik, The Nature of Statistical Learning Theory, Springer, New York, 2nd edn, 2000.
3. C. J. C. Burges, Data Min. Knowl. Discovery, 1998, 2, 121–167.
4. N. Cristianini and J. Shawe-Taylor, An Introduction to Support Vector Machines and Other Kernel-based Learning Methods, Cambridge University Press, Cambridge, 2000.
5. B. Schölkopf and A. J. Smola, Learning with Kernels, MIT Press, Cambridge, MA, 2002.
6. S. Abe, Support Vector Machines for Pattern Classification, Springer, London, 2005.
7. T. S. Furey, N. Cristianini, N. Duffy, D. W. Bednarski, M. Schummer and D. Haussler, Bioinformatics, 2000, 16, 906–914.
8. F. E. H. Tay and L. J. Cao, Neurocomputing, 2002, 48, 847–861.
9. G. Guo, S. Z. Li and K. L. Chan, Image Vision Comput., 2001, 19, 631–638.
10. A. I. Belousov, S. A. Verzakov and J. Von Frese, Chemom. Intell. Lab. Syst., 2002, 64, 15–25.
11. Y. Xu, S. Zomer and R. G. Brereton, Crit. Rev. Anal. Chem., 2006, 36, 177–188.
12. U. Thissen, B. Üstün, W. J. Melssen and L. M. C. Buydens, Anal. Chem., 2004, 76, 3099–3105.
13. S. R. Amendolia, G. Cossu, M. L. Ganadu, B. Golisio, G. L. Masala and G. M. Mura, Chemom. Intell. Lab. Syst., 2003, 69, 13–20.
14. U. Thissen, M. Pepers, B. Ustun, W. J. Melssen and L. M. C. Buydens, Chemom. Intell. Lab. Syst., 2004, 73, 169–179.
15. T. Czekaj, W. Wu and B. Walczak, J. Chemom., 2005, 19, 341–354.
16. S. Zomer, C. Guillo, R. G. Brereton and M. Hanna-Brown, Anal. Bioanal. Chem., 2004, 378, 2008–2020.
17. S. Zomer, M. Sánchez, R. G. Brereton and J. L. Pérez Pavón, J. Chemom., 2004, 18, 294–305.
18. S. J. Dixon and R. G. Brereton, Chemom. Intell. Lab. Syst., 2009, 95, 1–17.
19. P. Geladi and B. R. Kowalski, Anal. Chim. Acta, 1986, 185, 1–17.
20. R. G. Brereton, Analyst, 2000, 125, 2125–2154.
21. H. Martens and T. Næs, Multivariate Calibration, Wiley, Chichester, 1989.
22. R. G. Brereton, Chemometrics: Data Analysis for the Laboratory and Chemical Plant, Wiley, Chichester, 2003.
23. S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37.
24. I. T. Jolliffe, Principal Components Analysis, Springer, Berlin, 2nd edn, 2002.
25. K. V. Mardia, J. T. Kent and J. Bibby, Multivariate Analysis, Academic Press, London, 1979.
26. R. G. Brereton, Chemometrics for Pattern Recognition, Wiley, Chichester, 2009.
27. CAMO training exercise MVA II, http://www.camo.com.
28. B. M. Lukasiak, S. Zomer, R. G. Brereton, R. Faria and J. C. Duncan, Chemom. Intell. Lab. Syst., 2007, 87, 18–25.
29. B. M. Lukasiak, S. Zomer, R. G. Brereton, R. Faria and J. C. Duncan, Analyst, 2006, 131, 73–80.
30. R. Faria, J. C. Duncan and R. G. Brereton, Polym. Test., 2007, 26, 402–412.
31. G. R. Lloyd, R. Faria, R. G. Brereton and J. C. Duncan, J. Chem. Inf. Model., 2007, 47, 1553–1563.
32. G. R. Lloyd, R. G. Brereton and J. C. Duncan, Analyst, 2008, 133, 1046–1059.
33. R. A. Johnson and D. W. Wishern, Applied Multivariate Statistical Analysis, Prentice Hall, London, 1988.
34. R. A. Fisher, Ann. Eugenics, 1936, 7, 179–188.
35. I. E. Frank and J. H. Friedman, J. Chemom., 1989, 3, 463–475.
36. S. J. Dixon, Y. Xu, R. G. Brereton, A. Soini, M. V. Novotny, E. Oberzaucher, K. Grammer and D. J. Penn, Chemom. Intell. Lab. Syst., 2007, 87, 161–172.
37. L. Ståhle and S. Wold, J. Chemom., 1987, 1, 185–196.
38. M. Baker and W. Rayens, J. Chemom., 2003, 17, 166–173.
39. R. G. Brereton, TrAC, Trends Anal. Chem., 2006, 25, 1103–1111.
40. S. Wold, Technometrics, 1978, 20, 397–405.
41. B. Efron and R. J. Tibshirani, An Introduction to the Bootstrap, Chapman and Hall, New York, 1993.
42. L. Bottou, C. Cortes, J. Denker, H. Drucker, I. Guyon, L. Jackel, Y. LeCun, U. Muller, E. Sackinger, P. Simard and V. Vapnik, in International Conference on Pattern Recognition, IEEE Computer Society Press, 1994, vol. 2, pp. 77–82.
43. D. M. J. Tax, One-class classification, Concept-learning in the absence of counter-examples, PhD thesis, University of Delft, 2001, http://www-ict.et.tudelft.nl/%7Edavidt/papers/thesis.pdf, accessed 3 Sep 2009.
44. D. M. J. Tax and R. P. W. Duin, Mach. Learn., 2004, 54, 45–56.
45. B. Schölkopf, A. J. Smola, R. C. Williamson and P. L. Bartlett, Neural Comput., 2000, 12, 1207–1245.
46. A. J. Smola and B. Schölkopf, Stat. Comput., 2004, 14, 199–222.
47. B. Üstün, W. J. Melssen and L. M. C. Buydens, Anal. Chim. Acta, 2007, 595, 299–309.
48. F. Parrella, Online Support Vector Regression, Thesis in Information Science, University of Genoa, Italy, 2007, http://onlinesvr.altervista.org/, accessed 24 Aug 2009.
49. R. G. Brereton, Analyst, 1997, 122, 1521–1529.

---