Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Topological data analysis enhanced prediction of hydrogen storage in metal–organic frameworks (MOFs)†
Shivanshu
Shekhar
a and
Chandra
Chowdhury
 *b
*b
aDepartment of Electrical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
bInstitute of Catalysis Research and Technology (IKFT), Karlsruhe Institute of Technology (KIT), 76344 Eggenstein-Leopoldshafen, Germany. E-mail: pc.chandra12@gmail.com
First published on 13th December 2023
Abstract
Metal–organic frameworks (MOFs) have the capacity to serve as gas capturing, sensing, and storing systems. It is usual practice to select the MOF from a vast database with the best adsorption property in order to do an adsorption calculation. The costs of computing thermodynamic values are sometimes a limiting factor in high-throughput computational research, inhibiting the development of MOFs for separations and storage applications. In recent years, machine learning has emerged as a promising substitute for traditional methods like experiments and simulations when trying to foretell material properties. The most difficult part of this process is choosing characteristics that produce interpretable representations of materials that may be used for a variety of prediction tasks. We investigate a feature-based representation of materials using tools from topological data analysis. In order to describe the geometry of MOFs with greater accuracy, we use persistent homology. We show our method by forecasting the hydrogen storage capacity of MOFs during a temperature and pressure swing from 100 bar/77 K to 5 bar/160 K, using the synthetically compiled CoRE MOF-2019 database of 4029 MOFs. Our topological descriptor is used in conjunction with more conventional structural features, and their usefulness to prediction tasks is explored. In addition to demonstrating significant progress over the baseline, our findings draw attention to the fact that topological features capture information that is supplementary to the structural features.
1 Introduction
The push to create new fuel sources was sparked by the depleting supply of fossil fuels and climate change brought on by carbon dioxide emissions. When looking to phase out carbon-based energy sources, hydrogen (H2) is among the most attractive alternatives. H2 is widely considered to be the clean, sustainable fuel of the future because of its potential to replace fossil fuels in the energy sector and its many advantages over traditional energy sources, including its abundance, low environmental impact during combustion, and high specific energy.1–3 H2 gas's extremely low volumetric energy density due to its volatility to ambient conditions is a major roadblock to its broad usage as a primary fuel source, especially for on-board mobile transportation.4,5 As a result, there is still a lot of focus on making sure H2 is stored in a way that is safe, efficient, and technically and economically viable.6,7 Adsorption as a method for enhancing H2 storage density has been presented and has garnered a lot of interest.8–10 However, the technique will only be successful if new materials are developed that can store a substantial quantity of H2 under mild conditions, while also being compact, lightweight, having fast kinetics for charging and delivering H2, and being highly reversible.Since metal–organic frameworks (MOFs) are synthesised modularly from metal centres and organic ligands, they are a novel class of functional porous crystalline solids with a wide range of controllable properties and a wide variety of chemical and structural forms.11,12 Theoretically, MOF materials can be designed in an almost infinite number of ways, with the modification of metal ions/clusters and organic ligands enabling for the tailoring of their porosity and pore chemistry for an extensive range of conceivable uses.13,14 For a variety of adsorbent applications, MOFs have shown promise.15,16 The BET surface area and porosity of MOFs are relatively large in contrast to other materials that may store hydrogen molecules, such as CNT, hydrides, zeolites, and clathrates. Opportunities in gas separation, catalysis, energy storage, and conversion have recently piqued interest in MOF-based materials. Predicting the adsorption and diffusion behaviour of guest species in nanoporous materials like MOF has benefited greatly from molecular simulations.17,18 They've made it possible to calculate things like Henry's coefficients, adsorption loads, and diffusion coefficients under different circumstances. However, this strategy is often restricted to tens of thousands of structures due to the high computational costs incurred by molecular simulations.
The field of machine learning (ML) is an exciting area to study for solving this problem. The screening of huge MOF databases and the prediction of their properties using ML algorithms are faster than using molecular simulations. The creation of an appropriate descriptor is crucial to the achievement of ML.19,20 Descriptors need to be able to instantly categorise nanoporous materials based on structural characteristics, as well as recognise their performance properties, like their adsorption properties for gas storage and separation. How to systematically characterise similarity of pore architectures is a critical topic in constructing a descriptor for nanoporous materials. Some common ways of describing nanoporous materials are by their pore volume, density, surface area, maximum included sphere, etc.21,22 Unfortunately, these descriptors are still not sufficient to identify the best materials, despite being easily calculable and having the potential to correlate with a material's performance. Because these descriptors are based on a collection of coefficients about pore topology, it is possible that they do not encode enough information to characterise pore structure because each coefficient only contains a portion of the pore's information and there is no established rule for how to combine them as a descriptor.
A novel descriptor for nanoporous materials has been presented recently, and it uses topological principles to assess the degree of similarity between pore patterns.23,24 High-dimensional data sets, beyond the capabilities of most traditional data-mining methods, are required to describe the full pore architecture of a material. Thus, topological data analysis (TDA) was used to examine the multi-dimensional pore structure data.
TDA is applicable to high-dimensional and noisy datasets because it analyses the data's “shape,” or its overall structure, rather than its individual features. To some extent, missing information can impact TDA's output, although the method is still useful for discriminating between data sets of varying shapes. Topology is the subfield of mathematics that studies the geometry of the structures. TDA analyses the “shape” of large and high-dimensional data to find meaningful structure and valuable subgroups within the data. TDA has been effectively implemented in a number of medical applications, such as the identification of a previously unknown sub-type of breast cancer by analysing patient gene expression data.25 In addition, TDA's scope of use has recently been expanded to include identification and characterisation in the field of materials research.26,27 Very recently some studies show the effective applications of TDA on the adsorption property of nanoporous materials.28–31 It has been shown that topological features as well as structural features enhanced the predicting power for some adsorption applications in nanoporous materials.
Inspired by the above studies, we have designed the deep learning (DL) framework for the prediction of H2 storage capacity in MOFs using topological as well as conventional features. With the advent of DL algorithms, it is expected that ML will help propel the material revolution to a paradigm of full autonomy within the next 5–10 years.32,33 One groundbreaking example is the ability to recreate a phase transition with only a few layers of convolutional neural networks (CNNs).34 DL algorithms were first designed for image identification. Examples include the ability of computer vision algorithms to swiftly and accurately analyse large numbers of images and extract relevant data.35 Since TDA involves visual data, using deep learning-based computer vision algorithms to examine the outcomes seems like a natural fit. This line of thinking led us to consider implementing a cutting-edge CNN-based architecture called residual network (ResNet), which was initially developed by a team of Microsoft researchers and has since shown significant gains in a number of different settings.36 In particular, inspired by the several successful implementations of the ResNet model in image detection, we conceived of employing ResNet in our TDA investigation to successfully extract crucial features from persistence images.37–40 To the best of our knowledge, this level of sophisticated DL models has never been used in such scenarios before. In our model first, we have predicted the hydrogen deliverable capacity using only conventional feature vectors. Then we incorporate the topological features along with conventional features and have shown a great improvement for predicting the target property. Our model is showing reasonable performances compared to other models exist in literature, albeit it should be emphasised that the datasets employed by the various studies are distinct.41,42 The manuscript is organised as follows: next section we will describe the computational setup and methodology which includes description of data, detailed description of creation of topological feature vectors, description about ResNet model used here followed by results and discussion in another section and in the last section we will describe about the conclusions drawn from this work.
2 Computational setup and methodology
2.1 Dataset
The hydrogen materials advanced research consortium (HyMARC) database serves as the source of the MOF data published by Ahmed et al.18 Grand Canonical Monte Carlo simulations (GCMC) were used to determine the usable hydrogen storage capacity of 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 MOFs for the temperature and pressure fluctuation between 100 bar/77 K and 5 bar/160 K. For the comparison purpose we have also considered the other condition like with a fixed temperature of 77 K with pressure swing between 100 bar and 5 bar. We have taken into account the CoRE MOFs structures from this database and continued our study. For our analysis, we have used 4029 experimentally synthesized CoRE MOFs from this database. The pore limiting diameter (PLD), largest cavity diameter (LCD), pore volume (PV), volumetric surface area (VSA), crystal density (d), gravimetric surface area (GSA), void fraction (VF) of all MOFs were all calculated using the Zeo++ code as discussed in the paper. We refer to these identifiers as structural descriptors, and we use them as a benchmark against which to evaluate topological descriptors.
695 MOFs for the temperature and pressure fluctuation between 100 bar/77 K and 5 bar/160 K. For the comparison purpose we have also considered the other condition like with a fixed temperature of 77 K with pressure swing between 100 bar and 5 bar. We have taken into account the CoRE MOFs structures from this database and continued our study. For our analysis, we have used 4029 experimentally synthesized CoRE MOFs from this database. The pore limiting diameter (PLD), largest cavity diameter (LCD), pore volume (PV), volumetric surface area (VSA), crystal density (d), gravimetric surface area (GSA), void fraction (VF) of all MOFs were all calculated using the Zeo++ code as discussed in the paper. We refer to these identifiers as structural descriptors, and we use them as a benchmark against which to evaluate topological descriptors.
2.2 Persistent homology
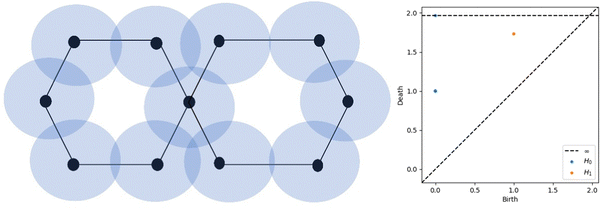
Algebraic topology is the theoretical foundation for TDA, a statistical method. The key claim of TDA is that a mathematical “signature” may be used to decode the data's structure and disclose insights like the relationships between individual data points. Persistent homology, a cutting-edge topological method, is one of the most well-known TDA techniques. By establishing a scale parameter pertinent to topological events, persistent homology is able to characterise the geometric features that exhibit persistent topological invariants. Persistent homology has the capability of continually capturing topological structures across several spatial scales by filtering and persisting data. By embedding geometric information to topological invariants, persistent homology allows for the monitoring of the “birth” and “death” of isolated components, circles, rings, loops, pockets, voids, and cavities across all geometric scales, in contrast to the results of commonly used computational homology, that lead in truly metric free or coordinate free representations. Analysing the ensuing sequence of geometric structures, one for each time/growth of radii, yields the temporal dependency of the three output features, known as homology in dimensions 0, 1, and 2. A persistent homology analysis yields these primary results. Any two atoms, no matter how far apart they are, will be connected through a sequence of edges when the balls have grown to a large enough size, as the feature of dimension 0 is connected components, meaning that the centres of the atoms are connected to each other when an edge is inserted (i.e., when the balls intersect). Features in dimension 1 consist of loops and rings. Features in dimension 2 are voids, or triangles forming a shape devoid of border loops and so including a void. The form can be spherical, toroidal, or something more intricate.A persistence diagram (PD) is a set of points in two dimensions, where each point represents a different value for the birth and death parameters of the homology groups in a given dimension. Dimension 0, 1, and 2 persistence diagrams for the distance function provide quantitative measures of the system's connectedness, as well as its gaps and empty spaces. But the persistence diagram isn't immediately useful in ML systems. The fundamental issue is that machine learning algorithms require fixed-dimensional vectors as input, but converting a PD to a vector using the coordinates of the points would result in a vector with dimensions double the number of points. Additionally, the PDs of various atomic configurations contain varying numbers of points, preventing them from being seen as identical vectors. Fig. 1 represents the schematic diagram for the creation of PD. Here, a point set of balls with increasing radius is presented by the hexagon figure and the two hexagons are connected through one point assuming the edge lengths of hexagons are one unit. Initially, each was separate point set and at 1 unit radius this becomes one connected component. So, there is one point in the PD which corresponds to 0D. Similarly, with a radius of around 1.75 unit, this becomes fully circularly connected and one point comes near this point which corresponds to 1D PD. The literature is plenty with suggestions for how to express the PD in a way that can be used by ML techniques. To the best of our knowledge, there is no method that is demonstrably superior to the rest; yet, one of the most widely used approaches is the persistence image (PI). For a more mathematical description of the persistence image, see ref. 43.
After transforming a PD's coordinate from birth time vs. death time to birth time vs. lifetime (i.e., death minus birth), the PI can be calculated. The longevity of an attribute is sometimes called its “lifetime.” The diagram's ensuing cloud of points is then transformed into a persistence surface, a kind of continuous surface map. This can be achieved, for instance, by augmenting each topological feature in the modified PD with a distribution function (for instance, a Gaussian) and summing to get a fully continuous surface. To further ensure that more persistent features are given more prominence in the final persistence image, a weighting function is often employed. At last, an integration over points in a predetermined grid pixelizes the representation of the persistence surface. Each pixel's location and value together give a representation of the PD that is amenable to machine learning methods since it is stable and insensitive to variations in the original PD (such as the number of loops).
2.3 MOFs structure morphology
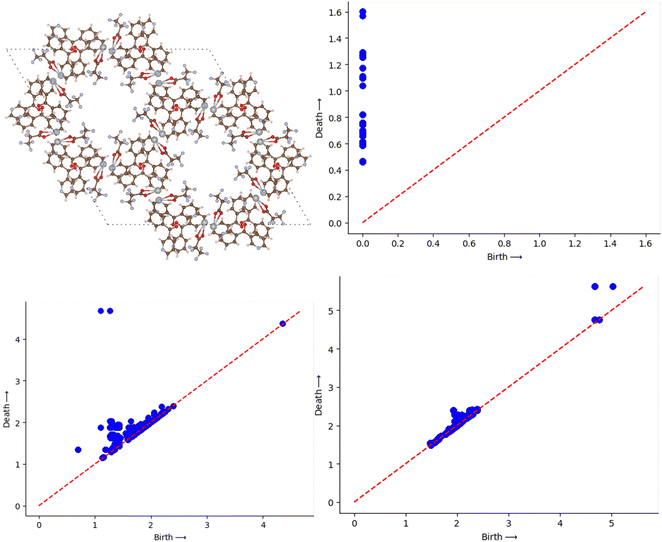
MOFs are the crystalline porous structures and it is common practice to express them using atomic positions relative to the periodic cell, which can be implicitly repeated over an arbitrary volume. The cells themselves come in a wide range of sizes. We standardise the calculation by setting up a supercell of each material with dimensions of 64 Å × 64 Å × 64 Å. This is selected to be at least a factor of two-to-three times larger than the largest base cell. This is well accepted method as discussed in the earlier studies.28,30 To symbolise a MOF, we join together rigid spheres with their centres at the atoms. Viewing the atoms in a supercell as individual points, we built Voronoi cells, Vi, and concentric spheres, Bi(α), for each atom i, where α is the squared radius of the concentric sphere. As their radii grow, we record the topological shifts brought about by their union which basically comes from the change in the alpha shape of the atoms. The DioDe Python binding (https://github.com/mrzv/diode, viewed on July 2, 2021) was used to compute the alpha shapes; it is based on the features available in the computational geometry algorithms library (CGAL) version 4.13. As discussed earlier the PD is a set of birth-death pairs of radii that come from a change in topological feature, such as the appearance or disappearance of a loop or emptiness. Here we are interested mainly in two types of PD namely, 1D PD which tracks the birth and death of loops that interpret as tunnels in MOF. The other one is 2D PD which tracks the voids that can be thought as a pocket in a MOF. The software used to create the persistence diagrams is called Dionysus (https://github.com/mrzv/dionysus). To compute persistence images, we employ a modified version of the PersIm package (https://persim.scikit-tda.org). By integrating the resulting mixture of Gaussians in the cells of the grid, the birth vs. persistence points are discretized onto a grid of fixed size. We do this with a 50 × 50 pixel grid and a Gaussian blur of σ = 0.15 to accomplish the desired effect as discussed in the previous papers.30,31Fig. 2 represents an example MOF structure and then the corresponding PD and PI are shown in Fig. 2 and 3.2.4 ResNet model
Residual networks (or ResNet for short) was coined by He et al. in 2015.36 The ResNet architecture was designed to overcome the problem of vanishing gradients in deep neural networks. This problem occurs when the gradients become too small during backpropagation, which can lead to slower convergence or even complete saturation of the network. ResNet uses skip connections, also known as residual connections, to address this issue. These connections allow the network to skip one or more layers and pass the input directly to a later layer, which helps to preserve the gradient and prevent it from becoming too small.The 72-layer architecture used in ResNet-18 is 18 layers deep. This network was built with the intention of efficiently supporting many convolutional layers with varying filter sizes and numbers of filters, followed by a global average pooling layer and a fully connected layer for classification. Layers such as convolution, maxpool, fully linked, and softmax are present in the network. It has been used for a wide range of computer vision tasks, including image classification, object detection, and semantic segmentation. ResNet-18 is a relatively shallow architecture compared to some of the larger ResNet variants like ResNet-50 or ResNet-101. However, it still achieves state-of-the-art performance on many computer vision benchmarks.44–46Fig. 4 represents the layered approach of ResNet-18 model.
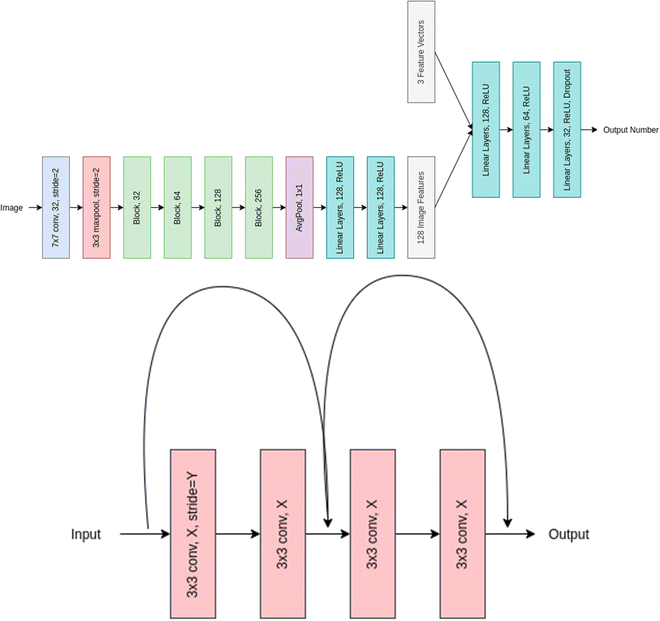 | ||
| Fig. 4 Overall representation of ResNet-18 model (upper panel) and Block XY of the model where X and Y represent the filter number and stride used respectively. | ||
In our method we used the ResNet-18 architecture to extract meaningful feature representation from the images, we use half the number of features used at each layer in the vanilla implementation and after Average pooling, we concatenate the image feature vector with our feature vector, and then pass this through multiple linear layers to get our final out. The XY in Block XY in the architecture diagram represents filter numbers and stride used respectively. We use a stride of one for the first block layer and 2 for the rest.
We finally apply the Average pool operation to the output to get a 256-dimensional feature map which is passed through two linear layers with ReLU activation to get 128 feature maps which is further concatenated with the feature vectors and downsized via the linear layers to finally output a single number. Table 1 details the obtainable number of trainable parameters and the corresponding convolutional layers.
| Parameter | Value |
|---|---|
| Initial learning rate | 1 × 10−3 |
| Dropout ratio | 0.2 |
| Bias | True |
| Batch size | 32 |
| Number of epochs | 200 |
| Activation | ReLU |
| Number of layers | 21 |
| Random state | 10 |
| Batch normalization | True |
| Trainable parameters | 3.222017 |
The ResNet-18 architecture first includes a convolutional layer of filter size 7 × 7 with a stride of 2 and padding of 3 this layer applies 32 such filters and these outputs are then passed to a batch normalization layer, whose output is again passed through a ReLU activation function followed by a Maxpool layer of kernel size of 3 and stride of 3 with padding of 1. The output obtained after doing the above is then passed through a series of Blocks which have 4 convolutional layers each of different filter numbers. Every block's first convolutional layer will have a stride of 2 other than the first block which has a stride of 1, the filter size for each of the blocks is 3 × 3 with stride and padding set to 1.
In any deep learning model, the hyperparameters play a crucial role in deciding how well the model performs. It is possible to fine-tune the model to achieve optimal performance by adjusting the hyperparameters, which include the training accuracy, training loss, validation accuracy, validation accuracy, batch size, learning rate, and the number of training epochs. In our model, we have used optimised hyperparameters.
Another important thing is, the model's effectiveness relies heavily on its learning rate. This slow training procedure means that the corresponding network weights won't be modified very quickly once they've been learned. The results of a higher learning rate, on the other hand, are likely to deviate from expectations. The learning rate is determined by optimising and minimising the loss function of the neural network. In the current experimental setup, we assume an initial learning rate of 0.001 and conclude that the models and learning rate have reached saturation after 200 training iterations.
We leverage the ResNet-18 architecture to incorporate the feature vectors along with the images, we first pass the images alone to the ResNet model and extract final features which have been passed through linear layers to restructure it to the required dimension, this image feature vector is then concatenated with the original feature vectors without any preprocessing to give us our final feature vector with is subsequently passed through a neural network that finally predicts one value. We used mean squared error (MSE) as our loss metric and which is determined by the equation given eqn (1) where yi, 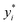 and m denote the true values, predicted values and the number of samples in the dataset, respectively. The model is trained end to end using images and feature vectors.
and m denote the true values, predicted values and the number of samples in the dataset, respectively. The model is trained end to end using images and feature vectors.
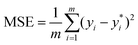 | (1) |
3 Results and discussion
3.1 Effect of the training set on ML predictions
For accurate ML-based property prediction, a high-quality training set, consisting of a subset of the data, is necessary. The availability of sufficient data about the complete set is an important feature of a successful training set. In this article, we examine the differences between randomly selecting a training set and selecting it based on diversity with the help of a min-max algorithm. Training sets of 1000 structures are used in both methods. As discussed previously, we chose ResNet-18 technique for our ML model. We used the ResNet-18 model to predict H2 deliverable capacity, and we did so using two distinct methods for selecting a training set: one that only used structural feature vectors (Structural Descriptor or SD) and another that only used image vectors (Image Descriptor or ID). The accuracy of the predictions for both scenarios is comparable. For the remainder study, we adopt a random selection technique due to the computational expense of creating a training set using a diversity selection algorithm.3.2 Ability of model to distinguish among different images
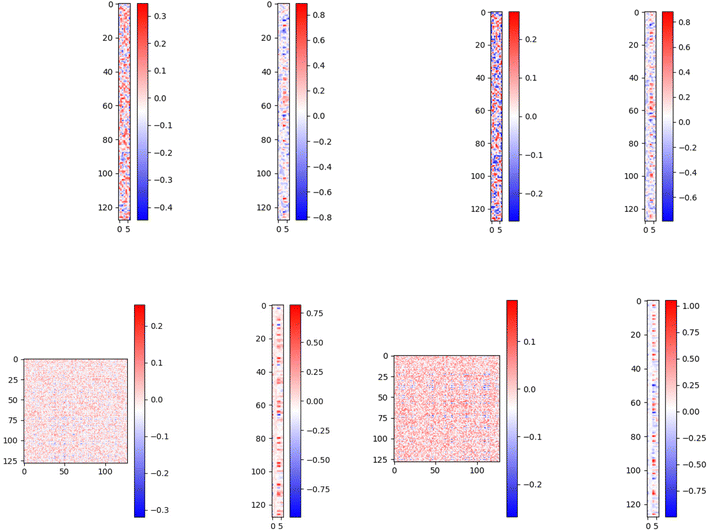
We need to know if our model can tell the difference between a persistence image and a random image in order to ensure its accuracy in predicting H2 deliverable capacity, which is the primary goal of this paper. The comparison between regular vectors and regular vectors with images is the most crucial part, so it's vital to make this distinction. Below we plot the matrix which is acting on the concatenated feature vector:We used 7 image features, we see that the matrix has relatively high values for only a few parts of the image features and input vector features which signifies that the neural network is focusing only on the important part of the image and feature vector and ignoring the rest. This does not represent overfitting as the weights are not too large. This signifies that the model is not totally ignoring the other features; rather, it is giving them a significantly lower weight. The top left side of the right panel image, which corresponds to the dog image feature vectors, appears very dense in comparison to the original persistence image feature vectors (top left side of the left panel image) when we pass random images like dog images instead of the actual persistence images. This means that the model is giving every image feature almost equal weight, i.e. it is not able to extract meaningful features, it is using all the features possible to bring the loss lower. To make up for the picture feature's increased importance, the model is assigning less weight to the normal feature vectors (top right side of the right panel), resulting in a sparser representation. We also get a higher loss for the dog images than the actual feature image. In order to better highlight the effect, we repeated the trials with 128 image features, and the results are displayed in the bottom panel of Fig. 5.
3.3 Comparison of prediction performances
After being confirmed about the validation of our model, we then proceed for further study. First we train our neural network model to predict the hydrogen deliverable capacity of MOFs in the unit namely, UG at TPS (usable gravimetric hydrogen capacity for the temperature + pressure swing between 100 bar/77 K and 5 bar/160 K in units of weight percent) using only the conventional feature vectors. In order to train the neural network, a five-fold cross-validation method is used. Our model exhibits consistent behaviour throughout all five folds. Initially we have chosen 7 feature vectors of the MOFs as discussed in the earlier section. We have seen a validation loss of around 0.069 using these 7 feature vectors. Then we can see that pore volume (PV), void fraction (VF), and density (d) are the most relevant features by applying the feature importance values supplied to the individual features by our model. The importance of these features can be rationalized by two factors. First, based on the empirical Chahine rule, the pore volume of a MOF correlates with its excess uptake. Second, pore volume and void fraction are related (since PV = VF × d−1) – MOFs with larger PV have larger VF, and vice versa. Nevertheless, VF, PV and d remain the three most important single features for both UV and UG conditions, in that order.From Fig. 6, it is seen that the 3 features contribute mostly to the target property predictions. The testing loss while utilising 3 feature vectors is 0.059 respectively as shown in Table 2. Now, while using the persistence images as image feature vectors taking into consideration of all 0D, 1D and 2D topological features along with the traditional structural feature vectors, it is seen that test loss decreases to 0.043 value which shows the complementarity of image features along with conventional features. This is shown in Fig. 6. To confirm more about our prediction, we have used same dataset for different condition and the prediction here is the usable hydrogen storage capacity of MOFs at 77 K for the pressure swing between 100 and 5 bar (PS condition). Interestingly here also, using persistence images along with feature vectors we are getting a good accuracy than that of only using feature vectors. Table 2 summarizes the performances of feature vectors with that of persistence images. The more improvement using persistence images in PS condition than that of TPS condition is due to the fact that the functional relationships between output capacities (UG/UV) and input features under PS and TPS conditions are likely different, as was observed in previously reported structure(feature)–property(capacity) relationships.18
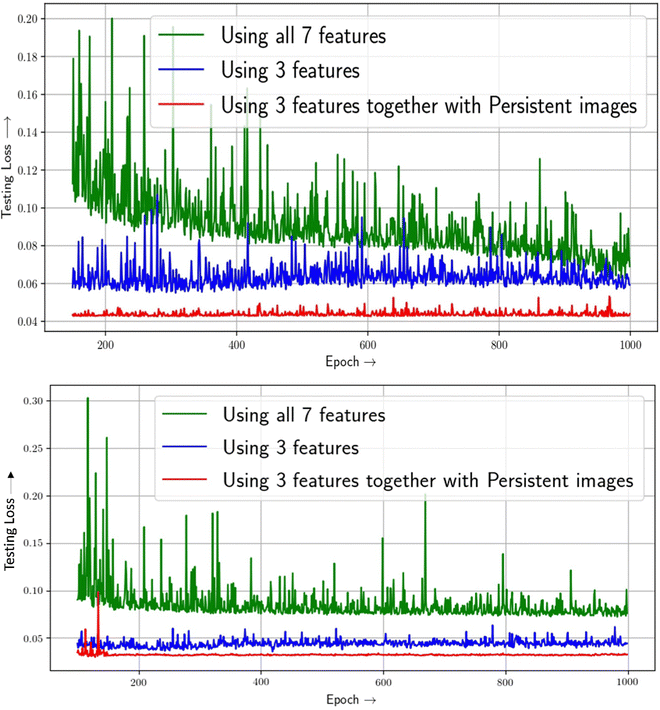 | ||
| Fig. 6 Multivariate feature importance on predicting H2 deliverable capacity of MOFs at TPS condition (upper panel) and PS (lower panel) conditions. | ||
| Condition | Method | Test loss |
|---|---|---|
| TPS | 7-features | 0.069 |
| 3-features | 0.059 | |
| 3-features+ PI | 0.043 | |
| PS | 7-features | 0.076 |
| 3-features | 0.044 | |
| 3-features+ PI | 0.033 |
Predicting H2 storage in MOFs is a well-known challenge, and various prior literatures have attempted to do so using an ML model in an effort to reduce both computational and experimental costs.41,42,47 Among these, Ahmed et al.41 conducted an in-depth analysis drawing from several existing literatures to forecast under TPS and PS situations, and they concluded that the extensively randomised tree (ERT) model is effective. They calculated RMSE values of 0.18 and 0.23 (capacity unit) for UG under TPS and PS circumstances. By building an ML model on top of a TDA, we can forecast H2 storage with a reasonable accuracy. The prediction of H2 storage capacity in MOFs is an area of critical research, and in this work we are able, for the first time, to integrate topological information with the state-of-the-art ResNet model, which is a proclaimed advanced successful model in computer vision technologies.
4 Detailed analysis of best five MOFs
Table 3 represents the best five MOFs found through our study with their corresponding features. It is found that MOFs with lower density show higher storage capacity. It is due to the fact that the porosity provides more surface area within the material, which is crucial for hydrogen adsorption.| MOF | Density | GSA | VSA | VF | PV | LCD | PLD | UG at TPS | UV at TPS |
|---|---|---|---|---|---|---|---|---|---|
| XAHQAA | 0.17 | 6250.1 | 1065.2 | 0.95 | 5.44 | 23.04 | 21.61 | 19.33 | 15.72 |
| XAHPUT | 0.18 | 6301.4 | 1125.9 | 0.94 | 5.15 | 21.83 | 20.59 | 18.46 | 14.93 |
| NIBJAK | 0.22 | 5417.2 | 1210.4 | 0.94 | 4.09 | 32.0 | 17.55 | 16.51 | 13.2 |
| RAVXOD | 0.18 | 3299.1 | 590.9 | 0.88 | 5.02 | 71.64 | 71.5 | 15.45 | 12.66 |
| RUTNOK | 0.24 | 6199.7 | 1493.0 | 0.9 | 3.73 | 24.61 | 14.65 | 14.89 | 12.05 |
Other than density, high gravimetric surface area in MOFs is crucial for hydrogen storage, particularly for mobile applications such as vehicles, where minimizing weight is essential for operational efficiency and range. This metric indicates more surface area per unit weight, providing more adsorption sites for hydrogen molecules and thus higher storage capacity. While volumetric surface area, which measures surface area per unit volume, is also important, it's secondary to gravimetric considerations in scenarios where weight has a greater impact on performance than the space occupied by the storage system. Consequently, materials with a high gravimetric surface area are favored for their ability to store a significant amount of hydrogen without adding substantial weight to the energy storage system. This is also confirmed from our study as evident from the values of GSA and VSA where both of which have higher values for all the best five MOFs. In addition to that it is seen that the best MOFs have high VF which can be explained from chemical intuition. MOFs with a high void fraction are particularly effective for hydrogen storage because the vast empty space translates to a higher surface area for the adsorption of hydrogen molecules. This structural characteristic ensures that there are ample sites for the physical adsorption of hydrogen, optimizing the storage capacity. Additionally, a high void fraction allows for more efficient diffusion of hydrogen molecules throughout the MOF, promoting uniform distribution and accessibility to adsorption sites. The delicate balance of having pores just slightly larger than the hydrogen molecules maximizes the van der Waals forces necessary for adsorption without overly restricting or loosening the hydrogen molecules. Consequently, MOFs with large void fractions are typically superior for hydrogen storage, providing both high capacity and fast kinetics, which are essential for real-world energy applications. MOFs with higher PV show higher hydrogen storage property and this is due to the due to the increased space available for hydrogen adsorption. From crucial inspection of Table 3, it is seen that MOFs with low LCD and high PLD show high hydrogen adsorption capacity. The LCD refers to the size of the largest void space within the MOF structure. A lower LCD indicates smaller, more compact cavities, which can be beneficial for maximizing surface area and adsorption sites within a given volume. Meanwhile, a high PLD, which represents the smallest diameter through which a molecule can pass to access a cavity, ensures that hydrogen molecules can easily enter and fill these cavities. This combination of a compact cavity structure with accessible pores allows for efficient storage of hydrogen. The small cavities increase the surface interaction with hydrogen molecules, boosting adsorption capacity, while the larger pore entrances facilitate easy diffusion of hydrogen into the MOF. To get an insight about the structure of the MOFs, we have included the structures of two MOFs, namely, XAHQAA and RUTNOK in Fig. 7.
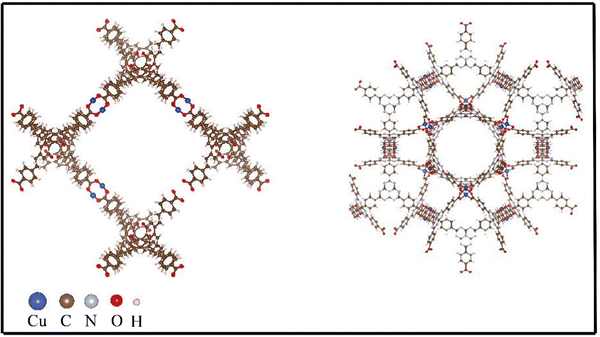 | ||
| Fig. 7 Structure of two best MOFs in terms of high hydrogen storage capacity. Left panel shows the structure of XAHQAA MOF and right panel corresponds to structure of RUTNOK MOF. | ||
5 Conclusion
In this paper, we offer a deep learning-based method for accurately predicting the structural characteristics and performance of MOFs in the context of hydrogen storage applications by using persistent homology. As a topological representation, we use a vectorized persistence diagram built from the normalized supercell representation of a material's atomic coordinates. It can be implemented in any algorithm for automatic learning. We have implemented and evaluated this strategy by training residual network regressors working on our representations of 4000 MOF structures and their hydrogen storage capacity obtained using grand canonical Monte Carlo simulations. The results of these trials demonstrate a considerable performance boost compared to those of conventional structural descriptors. Due to their superiority over more generic structural descriptors, topological descriptors can be easily implemented to improve the efficiency of any machine learning technique. Our findings demonstrate that topological descriptors are useful for predicting adsorption in porous materials and get us one step closer to developing a universal predictor.Author contributions
C. C. conceptualized the project. S. S. and C. C. both performed the research. C. C. wrote the manuscript.Data availability
Data used in this study is available online. Code developed is available from this github link: https://github.com/ChandraChennai/TDA.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. C. gratefully acknowledges her sincere gratitude to Prof. Dr Felix Studt of the Karlsruhe Institute of Technology (KIT) for the generous support.References
- M. Kayfeci and A. Keçebas. Hydrogen Storage, Solar Hydrogen Production, Elsevier, 2019, pp. 85–110 Search PubMed.
- S. Satyapal, J. Petrovic, C. Read, G. Thomas and G. Ordaz, The US Department of Energy's National Hydrogen Storage Project: Progress Towards Meeting Hydrogen-Powered Vehicle Requirements, Catal. Today, 2007, 120(3–4), 246–256 CrossRef CAS.
- D. L. Greene and G. Duleep, Worldwide Status of Hydrogen Fuel Cell Vehicle Technology and Prospects for Commercialization, US Department of Energy, 2013 Search PubMed.
- M. D. Allendorf, Z. Hulvey, T. Gennett, A. Ahmed, T. Autrey, J. Camp, E. Seon Cho, H. Furukawa, M. Haranczyk and M. Head-Gordon, et al., An Assessment of Strategies for the Development of Solid-State Adsorbents for Vehicular Hydrogen Storage, Energy Environ. Sci., 2018, 11(10), 2784–2812 RSC.
- A. W. Thornton, C. M. Simon, J. Kim, O. Kwon, K. S. Deeg, K. Konstas, S. J. Pas, M. R. Hill, D. A. Winkler and M. Haranczyk, et al., Materials Genome in Action: Identifying the Performance Limits of Physical Hydrogen Storage, Chem. Mater., 2017, 29(7), 2844–2854 CrossRef CAS PubMed.
- US Department of Energy, DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles, 2017 Search PubMed.
- T. Riis, G. Sandrock, O. Ulleberg and P. J. S. Vie, Hydrogen Storage R&D: Priorities and Gaps, Hydrogen Production and Storage: R&D Priorities and Gaps (International Energy Agency), 2006, pp. 19–33 Search PubMed.
- J. Yang, A. Sudik, C. Wolverton and D. J. Siegel, High Capacity Hydrogen Storage Materials: Attributes for Automotive Applications and Techniques for Materials Discovery, Chem. Soc. Rev., 2010, 39(2), 656–675 RSC.
- Y. Xia, G. S. Walker, D. M. Grant and R. Mokaya, Hydrogen Storage in High Surface Area Carbons: Experimental Demonstration of the Effects of Nitrogen Doping, J. Am. Chem. Soc., 2009, 131(45), 16493–16499 CrossRef CAS PubMed.
- P. Jena, Materials for Hydrogen Storage: Past, Present, and Future, J. Phys. Chem. Lett., 2011, 2(3), 206–211 CrossRef CAS.
- L. Öhrström, Let's Talk about MOF—Topology and Terminology of Metal-Organic Frameworks and Why We Need Them, Crystals, 2015, 5(1), 154–162 CrossRef.
- S. R. Batten, N. R. Champness, X.-M. Chen, J. G. Martinez, S. Kitagawa, L. Öhrström, M. O'Keeffe, M. P. Suh and J. Reedijk., Coordination Polymers, Metal-Organic Frameworks and the Need for Terminology Guidelines, CrystEngComm, 2012, 14(9), 3001–3004 RSC.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Systematic Design of Pore Size and Functionality in Isoreticular MOFs and Their Application in Methane Storage, Science, 2002, 295(5554), 469–472 CrossRef CAS PubMed.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling and J. S. Camp, et al., Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019, J. Chem. Eng. Data, 2019, 64(12), 5985–5998 CrossRef CAS.
- O. K. Farha, A. M. Shultz, A. A. Sarjeant, S. T. Nguyen and J. T. Hupp, Active-Site-Accessible, Porphyrinic Metal- Organic Framework Materials, J. Am. Chem. Soc., 2011, 133(15), 5652–5655 CrossRef CAS PubMed.
- J. Sculley, D. Yuan and H.-C. Zhou, The Current Status of Hydrogen Storage in Metal-Organic Frameworks—Updated, Energy Environ. Sci., 2011, 4(8), 2721–2735 RSC.
- L.-C. Lin, A. H. Berger, R. L. Martin, J. Kim, J. A. Swisher, K. Jariwala, C. H. Rycroft, A. S. Bhown, M. W. Deem and M. Haranczyk, et al., In Silico Screening of Carbon-Capture Materials, Nat. Mater., 2012, 11(7), 633–641 CrossRef CAS PubMed.
- A. Ahmed, S. Seth, J. Purewal, A. G. Wong-Foy, M. Veenstra, A. J. Matzger and D. J. Siegel, Exceptional Hydrogen Storage Achieved by Screening Nearly Half a Million Metal-Organic Frameworks, Nat. Commun., 2019, 10(1), 1568 CrossRef PubMed.
- J. Behler, Perspective: Machine Learning Potentials for Atomistic Simulations, J. Chem. Phys., 2016, 145(17), 170901 CrossRef PubMed.
- A. Deshwal, C. M. Simon and J. R. Doppa, Bayesian Optimization of Nanoporous Materials, Mol. Syst. Des. Eng., 2021, 6(12), 1066–1086 RSC.
- R. L. Martin, B. Smit and M. Haranczyk, Addressing Challenges of Identifying Geometrically Diverse Sets of Crystalline Porous Materials, J. Chem. Inf. Model., 2012, 52(2), 308–318 CrossRef CAS PubMed.
- R. L. Martin, T. F. Willems, L.-C. Lin, J. Kim, J. A. Swisher, B. Smit and M. Haranczyk, Similarity-Driven Discovery of Zeolite Materials for Adsorption-Based Separations, ChemPhysChem, 2012, 13(16), 3595–3597 CrossRef CAS PubMed.
- Y. Lee, S. D. Barthel, P. Dłotko, S. M. Moosavi, K. Hess and B. Smit, Quantifying Similarity of Pore-Geometry in Nanoporous Materials, Nat. Commun., 2017, 8(1), 1–8 CrossRef CAS.
- P. Y. Lum, G. Singh, A. Lehman, T. Ishkanov, M. Vejdemo-Johansson, M. Alagappan, J. Carlsson and G. Carlsson, Extracting Insights from the Shape of Complex Data Using Topology, Sci. Rep., 2013, 3(1), 1–8 Search PubMed.
- M. Nicolau, A. J. Levine and G. Carlsson, Topology Based Data Analysis Identifies a Subgroup of Breast Cancers with a Unique Mutational Profile and Excellent Survival, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(17), 7265–7270 CrossRef CAS PubMed.
- Y. Schiff, V. Chenthamarakshan, S. C. Hoffman, K. N. Ramamurthy and P. Das, Augmenting Molecular Deep Generative Models with Topological Data Analysis Representations, ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, 2022, pp. 3783–3787.
- M. Kramár, A. Goullet, L. Kondic and K. Mischaikow, Persistence of Force Networks in Compressed Granular Media, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87(4), 042207 CrossRef PubMed.
- Y. Lee, S. D. Barthel, P. Dłotko, S. M. Moosavi, K. Hess and B. Smit, High-Throughput Screening Approach for Nanoporous Materials Genome Using Topological Data Analysis: Application to Zeolites, J. Chem. Theory Comput., 2018, 14(8), 4427–4437 CrossRef CAS PubMed.
- X. Zhang, J. Cui, K. Zhang, J. Wu and Y. Lee, Machine Learning Prediction on Properties of Nanoporous Materials Utilizing Pore Geometry Barcodes, J. Chem. Inf. Model., 2019, 59(11), 4636–4644 CrossRef CAS PubMed.
- A. S. Krishnapriyan, M. Haranczyk and D. Morozov, Topological Descriptors Help Predict Guest Adsorption in Nanoporous Materials, J. Phys. Chem. C, 2020, 124(17), 9360–9368 CrossRef CAS.
- A. S. Krishnapriyan, J. Montoya, M. Haranczyk, J. Hummelshøj and D. Morozov, Machine Learning with Persistent Homology and Chemical Word Embeddings Improves Prediction Accuracy and Interpretability in Metal-Organic Frameworks, Sci. Rep., 2021, 11(1), 8888 CrossRef CAS PubMed.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz and H. Tribukait, et al., Accelerating the Discovery of Materials for Clean Energy in the Era of Smart Automation, Nat. Rev. Mater., 2018, 3(5), 5–20 CrossRef CAS.
- A. Agrawal and A. Choudhary, Perspective: Materials Informatics and Big Data: Realization of the “Fourth Paradigm” of Science in Materials Science, APL Mater., 2016, 4(5), 053208 CrossRef.
- J. Carrasquilla and R. G. Melko, Machine learning phases of matter, Nat. Phys., 2017, 13(5), 431–434 Search PubMed.
- F. Ramezani, S. Parvez, J. P. Fix, A. Battaglin, S. Whyte, N. J. Borys and B. M. Whitaker, Automatic Detection of Multilayer Hexagonal Boron Nitride in Optical Images Using Deep Learning-Based Computer Vision, Sci. Rep., 2023, 13(1), 1595 Search PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, Deep Residual Learning for Image Recognition, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
- M. Shafiq and Z. Gu, Deep residual learning for image recognition: A survey, Appl. Sci., 2022, 12(18), 8972 Search PubMed.
- J. Liang, Image classification based on resnet, Journal of Physics: Conference Series, IOP Publishing, 2020, vol. 1634, p. 012110 Search PubMed.
- Z. Hu, J. Tang, Z. Wang, K. Zhang, L. Zhang and Q. Sun, Deep learning for image-based cancer detection and diagnosis- a survey, Pattern Recognit., 2018, 83, 134–149 CrossRef.
- G. Guo and N. Zhang, A survey on deep learning based face recognition, Comput. Vision Image Understanding, 2019, 189, 102805 CrossRef.
- A. Ahmed and D. J. Siegel, Predicting Hydrogen Storage in MOFs via Machine Learning, Patterns, 2021, 2(7), 100291 CrossRef CAS PubMed.
- K. Salehi, M. Rahmani and S. Atashrouz, Machine Learning Assisted Predictions for Hydrogen Storage in Metal–Organic Frameworks, Int. J. Hydrogen Energy, 2023, 48, 33260–33275 CrossRef CAS.
- H. Adams, T. Emerson, M. Kirby, R. Neville, C. Peterson, P. Shipman, S. Chepushtanova, E. Hanson, F. Motta and L. Ziegelmeier, Persistence Images: A Stable Vector Representation of Persistent Homology, J. Mach. Learn. Res., 2017, 18, 1–35 Search PubMed.
- K. M. Black, H. Law, A. Aldoukhi, J. Deng and K. R. Ghani, Deep Learning Computer Vision Algorithm for Detecting Kidney Stone Composition, BJU Int., 2020, 125(6), 920–924 CrossRef CAS PubMed.
- S. Bianco, R. Cadene, L. Celona and P. Napoletano, Benchmark Analysis of Representative Deep Neural Network Architectures, IEEE Access, 2018, 6, 64270–64277 Search PubMed.
- A. Z. D. Costa, H. E. H. Figueroa and J. A. Fracarolli, Computer vision based detection of external defects on tomatoes using deep learning, Biosyst. Eng., 2020, 190, 131–144 CrossRef.
- B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Energy-Based Descriptors to Rapidly Predict Hydrogen Storage in Metal-Organic Frameworks, Mol. Syst. Des. Eng., 2019, 4(1), 162–174 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Figure showing the effect of training set size. See DOI: https://doi.org/10.1039/d3ma00591g |
| This journal is © The Royal Society of Chemistry 2024 |