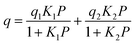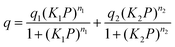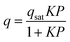Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unusual adsorption-induced phase transitions in a pillared-layered copper ethylenediphosphonate with ultrasmall channels†
Margherita
Cavallo
 a,
Matteo
Signorile
a,
Matteo
Signorile
 a,
Roberto
Köferstein
a,
Roberto
Köferstein
 b,
Valentina
Crocellà
b,
Valentina
Crocellà
 *a and
Marco
Taddei
*a and
Marco
Taddei
 *cd
*cd
aDipartimento di Chimica, Centro di riferimento NIS e INSTM, Università di Torino, Via G. Quarello 15, I-10135 and Via P. Giuria 7, I-10125 Torino, Italy. E-mail: valentina.crocella@unito.it
bInstitute of Chemistry, Inorganic Chemistry, Martin Luther University Halle-Wittenberg, Kurt-Mothes-Strasse 2, 06120 Halle, Germany
cDipartimento di Chimica e Chimica Industriale, Unità di Ricerca INSTM, Università di Pisa, Via Giuseppe Moruzzi 13, 56124 Pisa, Italy. E-mail: marco.taddei@unipi.it
dEnergy Safety Research Institute, Swansea University, Fabian Way, Swansea, SA1 8EN, UK
First published on 28th November 2023
Abstract
In this work, we thoroughly assess the CO2 adsorption behaviour of a recently reported, pillared-layered CuII ethylenediphosphonate of formula Cu2(H2O)1.7(O3P–C2H4–PO3)·1.5H2O (Cu-EtP), that features narrow channel-like pores (diameter < 5 Å). Once the metal coordinated H2O molecules are removed, Cu-EtP features a very high density of open metal sites (0.0188 sites Å−3) and can adsorb a significant amount of CO2 at saturation (2.9 mmol g−1, 6.9 mmol cm−3). Most interesting, it displays a step-shaped CO2 isotherm, whereby a preliminary adsorption event takes place, followed by a step occurring at higher pressure, during which adsorption kinetics become very slow. Hysteresis in desorption suggests that structural rearrangements could be responsible for the unusual isotherm shape. Cu-EtP does not adsorb N2, probably due to its very narrow pores, thus it displays virtually infinite CO2/N2 selectivity. The isosteric heat of adsorption extracted using the Clausius–Clapeyron equation is in the range of 35–40 kJ mol−1, suggesting a strong physisorptive character. This is further confirmed by CO2 adsorption microcalorimetry. In situ synchrotron powder X-ray diffraction analysis, carried out during evacuation and CO2 adsorption, proves that the MOF undergoes phase transitions during both stages, with shrinking of the interlayer spacing upon removal of water and partial reopening of the structure once CO2 is adsorbed. The phase transitions are slow, in agreement with the slow adsorption kinetics observed. In situ infrared spectroscopy suggests that CO2 interacts with the open metal sites generated after removal of strongly adsorbed water and that CO2 cannot displace H2O if this is not fully removed from the surface. NO was also used as a probe molecule to further demonstrate the existence of open metal sites, finding that it is not able to diffuse within the framework when pure, but that it can displace coordinated water. Optical spectroscopy suggests that changes in the coordination sphere of Cu take place during evacuation and CO2 adsorption. Finally, periodic density functional theory calculations were carried out to unravel the structural evolution of Cu-EtP and the energetics of interaction with H2O and CO2, finding that the change in coordination environment of Cu is mainly responsible for the observed phase transitions.
Introduction
Structural flexibility is a distinctive feature of metal–organic frameworks (MOFs), which makes them stand out in the realm of porous materials.1–3 Flexibility in MOFs can be induced by various external stimuli, such as guest insertion, temperature, pressure, electrical fields, etc. Adsorption-driven flexibility in MOFs is widely documented in the literature and occurs in a wide range of forms: framework expansion,4 swelling,5–7 framework contraction,8–10 breathing,11,12 subnetwork displacement,13–15 and linker rotation.16,17 Flexible MOFs usually display step-shaped isotherms, associated with the adsorption of large amounts of gas in a narrow range of pressures, once a threshold pressure is reached that triggers a well-defined structural response. Such peculiar behaviour is interesting both from a fundamental standpoint, as some forms of adsorption-driven flexibility, e.g., breathing (“open” to “close” to “open” phase transition as the partial pressure of gas increases)11,12 or framework contraction (“open” to “close” phase transition leading to negative gas adsorption),8–10 are unique to MOFs, and from a practical standpoint, because it can lead to improved gas separation/storage performance.18,19Phosphonate-based MOFs are a small subclass of MOFs, notable for their superior stability.20–24 Pillared-layered structures, consisting of two-dimensional inorganic building units (IBUs) composed of metal ions linked by phosphonate groups and connected via organic linkers in the third dimension, are ubiquitous in metal phosphonate chemistry.25–27 These structures are usually non-porous, because of the high density of organic moieties in the interlayer space that leaves little or no room for small molecules to diffuse and adsorb. This structural arrangement is considerably different from other carboxylate-based MOFs, also commonly termed “pillared-layered”, which are typically based on zero-dimensional paddlewheel type secondary building units of general formula M2(COO)4 (where M is a divalent metal, most often Cu, Zn or Ni), connected in two dimensions by dicarboxylic linkers, e.g., terephthalic acid, to form layers with square lattice topology that are pillared in the third dimension by aza-heterocyclic linkers, e.g., 1,4-diazabicyclo[2.2.2]octane (DABCO).28,29 These frameworks usually display high porosity and, in some instances, flexible behaviour.30–32
Nonetheless, a few examples of porous pillared-layered metal phosphonates have appeared in the literature.26,33,34 One of the most notable is a ZrIV-based compound containing both a sterically demanding diphenyldiphosphonate linker and a phosphite ligand, which displays ordered microporosity.35 “Unconventional” MOFs based on disordered pillared-layered metal phosphonates with broad pore size distribution in the mesoporous regime have also been reported.21 The “accordion effect” in response to solvent adsorption observed in pillared-layered ZrIV-phosphonates, obtained by partial topotactic exchange of the dihydrogen phosphate groups of γ-ZrIV phosphate with diphosphonic acids with either aliphatic or polyethylenoxide chains, is a prototypical example of flexible behaviour in organic–inorganic hybrid materials, being described already in 1998.36,37
The family of metal phosphonates does feature a few interesting examples of flexible open frameworks, such as AlIII-, LaIII-, CeIII-, NdIII- and ZrIV-based derivatives of the linker N,N′-bis-(phosphonomethyl)-piperazine,38–41 a ZrIV-based derivative of the linker N,N,N′,N′-tetrakis-(phosphonomethyl)-1,4-diaminocyclohexane,42,43 a LaIII-based derivative of the linker N,N′-bis-(phosphonomethyl)-bipiperidine,44 and isoreticular mixed linker CuII-based derivatives of the linker N,N,N′,N′-tetrakis-(phosphonomethyl)-1,6-diaminohexane with either 4,4′-bipyridine or 1,2-bis(pyridyl)ethane as ancillary ligands.45 Notably, all these materials display three-dimensional crystal structures based on one-dimensional IBUs and linkers with aliphatic nature, whose combination allows enough degrees of freedom to enable flexible behaviour.
We report here on the recently discovered pillared-layered CuII ethylenediphosphonate of formula Cu2(H2O)1.7(O3P–C2H4–PO3)·1.5H2O (hereafter Cu-EtP),46 which features both porosity to H2O and CO2, and a rather unusual structural behaviour induced by adsorption and desorption of these species, as evidenced by gas sorption analysis, adsorption microcalorimetry, in situ synchrotron powder X-ray diffraction (PXRD), in situ infrared (IR) spectroscopy, optical spectroscopy and density functional theory (DFT) calculations.
Results and discussion
Crystal structure of Cu-EtP
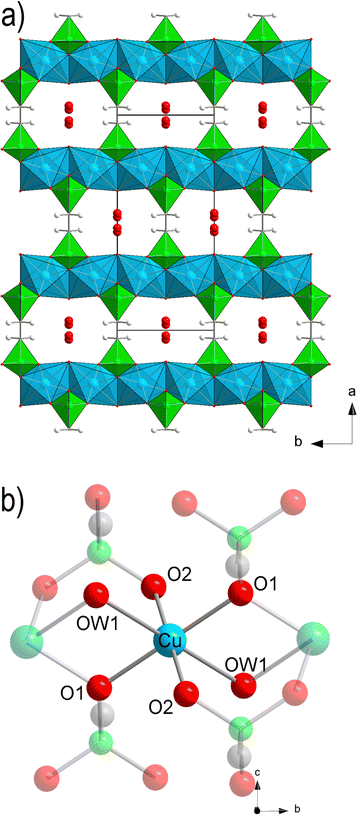
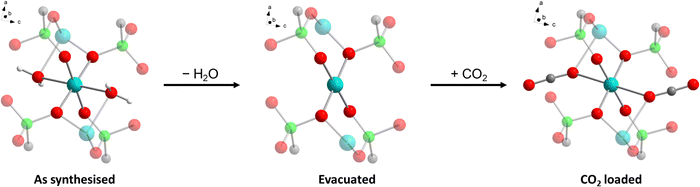
The crystal structure of Cu-EtP (Cambridge Structural Database refcode UXUPEK)46 is constituted of layers built from the connection of CuII ions and phosphonate groups, pillared by the aliphatic chain of the linker (Fig. 1a and Fig. S1, ESI†). The interlayer distance (as indicated by the 200 reflection) is 7.42 Å. Cu is coordinated by four phosphonate oxygens and two water molecules in distorted octahedral geometry (Fig. 1b). Each phosphonate group connects four Cu atoms via two crystallographically equivalent monodentate oxygens O1 and one bidentate oxygen O2 (Cu–O1 = 1.932 Å, Cu–O2 = 2.024 Å). The coordinated water molecule OW1 is bridging between two Cu atoms (Cu–OW1 = 2.453 Å). OW1 has an occupancy of 0.85. Additional water molecules (OW2 with occupancy of 0.41, OW3 with occupancy of 0.34) are physisorbed within the narrow channels running along the c axis. Thus, as-synthesised Cu-EtP can be formulated as Cu2(H2O)1.7(O3P–C2H4–PO3)·1.5H2O.The removal of all the coordinated water molecules should, in principle, generate two open metal sites (OMSs) per Cu atom, affording a square planar geometry (Fig. S2–S4, ESI†). Indeed, after removal of the coordinated water molecules the colour changes from turquoise to blue (as reported in Fig. S5, ESI†), suggesting that changes are taking place in the Cu coordination sphere. The distance, measured from the atomic centres, between two H atoms belonging to neighbouring linkers along the b axis is 5.044 Å. If the van der Waals radii of the two H atoms (1.1 Å)47 are subtracted, the distance decreases to 2.844 Å, in the sub-ultramicroporous regime.48,49 Assuming that the unit cell was to keep the same volume (432.0 Å3), this ideal, fully dehydrated MOF of formula Cu2(O3P–C2H4–PO3) would have a formula weight of 313.1 g mol−1 and a density of 2.41 g mL−1. This corresponds to a density of 0.0094 Cu atoms Å−3, that is, 0.0188 OMSs Å−3. Such a density of OMSs is much higher than most MOFs known in the literature, such as MOF-74 (0.0045 OMSs Å−3),50 HKUST-1 (0.0026 OMSs Å−3),51 MAF-35 (0.0104 OMSs Å−3)52 and F4_MIL-140A(Ce) (0.0034 OMSs Å−3)17 (Table S1, ESI†).
Gas sorption properties
The evacuation of as-synthesised Cu-EtP was initially assessed by thermogravimetric analysis (TGA). In the original report,46 the TG curve (recorded in air at a rate of 10 K min−1) displayed two distinct weight losses ending at 313 K and 413 K, associated with the release of physisorbed and coordinated water, respectively (Fig. S6, ESI†). The total weight loss amounted to 14.8%, in good agreement with the expected 15.5%. Here, we kept Cu-EtP at 413 K under an Ar stream (100 mL min−1), observing a gradual weight loss taking place over eight hours, after which the curve had plateaued at a residual mass of about 86.3% (Fig. S7, ESI†). At this point, the temperature was decreased to 313 K and, as soon as it was equilibrated, the gas stream was switched to a 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 CO2/Ar mixture (100 mL min−1). The solid immediately started gaining weight, clearly indicating adsorption of CO2, but equilibrium was not achieved over three hours of exposure to the CO2-rich mixture. The mass gain after three hours was 4.6%, corresponding to about 1.0 mmol g−1. This experiment provided two important pieces of information: the first is that Cu-EtP must be held at 413 K for six hours under an Ar stream to fully remove the coordinated water, the second is that the evacuated solid can adsorb an appreciable amount of CO2, even though with apparently slow kinetics.
10 CO2/Ar mixture (100 mL min−1). The solid immediately started gaining weight, clearly indicating adsorption of CO2, but equilibrium was not achieved over three hours of exposure to the CO2-rich mixture. The mass gain after three hours was 4.6%, corresponding to about 1.0 mmol g−1. This experiment provided two important pieces of information: the first is that Cu-EtP must be held at 413 K for six hours under an Ar stream to fully remove the coordinated water, the second is that the evacuated solid can adsorb an appreciable amount of CO2, even though with apparently slow kinetics.
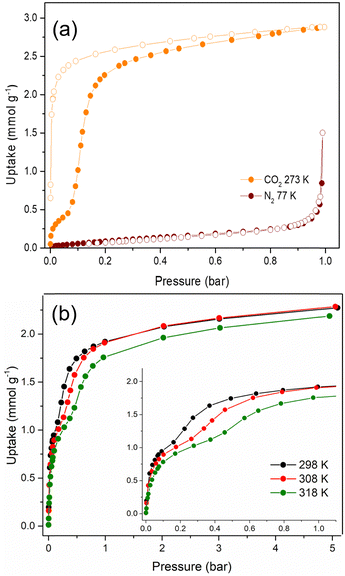
The textural properties of Cu-EtP, upon an overnight activation at 393 K under dynamic vacuum, were first investigated by performing adsorption/desorption isotherms with N2 at 77 K and CO2 at 273 K (Fig. 2a and b). The isotherm collected with N2 at 77 K can be classified as a type III (following IUPAC classification),53 suggesting the non-porous nature of Cu-EtP or, alternatively, an extremely low affinity towards this molecular probe. Additionally, the use of N2 at 77 K as probe for ultra- or sub-ultra-microporous materials has different drawbacks, due to the uncertainty in the evaluation of its cross-sectional area, the micropore filling shifted at very low relative pressures (P/P0 ∼ 10−7) and the diffusion limitations imposed by the cryogenic temperature.54 In contrast, the material adsorbs CO2 at 273 K, displaying a peculiar step-shaped adsorption isotherm with a hysteresis loop in desorption and a considerable maximum CO2 uptake of 2.9 mmol g−1 (6.9 mmol cm−3, if a density of 2.41 g mL−1 is assumed) at 1 bar, corresponding to about 67 cm3 (STP) g−1. This value is equivalent to 12.8 wt% of CO2 adsorbed, which translates to about 0.9 molecules of CO2 per formula unit, as opposed to the 3.2 molecules of water (1.7 coordinated to Cu plus 1.5 physisorbed within the channels) per formula unit present in the as synthesised Cu-EtP. The considerable adsorption of CO2 at 273 K suggests that its smaller kinetic diameter (3.3 Å), together with a higher adsorption temperature with respect to 77 K employed for N2 isotherm, help the diffusion of this molecule inside the sub-ultramicroporous structure of Cu-EtP. However, the peculiar hysteretic step-shaped isotherm implies that Cu-EtP might undergo a phase transition upon adsorption of CO2, which is only reversible in desorption at low pressure. This behaviour is usually associated with an adsorption-induced transition from a “narrow pore” to a “large pore” phase.11,12,30 By using CO2 at 273 K, the highest achievable relative pressure is ∼0.03, therefore it is able to probe the textural properties of materials with a pore size lower than 10 Å.55 By applying the Brunauer–Emmett–Teller (BET) equation to the desorption branch of the CO2 adsorption isotherm, we extracted a value of specific surface area of 295 m2 g−1 for the new phase that appears to persist over a large range of pressures (Fig. S8, S9 and Tables S2, S3, ESI†). It is worth noting that, due to the structural rearrangement induced by CO2 adsorption, the value of the surface area extracted from the desorption branch of the isotherm by means of the BET equation is related to the material no more in the fully evacuated form, therefore it should be considered as a mere estimation of the CO2 accessible surface in Cu-EtP. Indeed, the application of the BET model to the adsorption isotherm is prevented by its peculiar step-shaped behaviour. The peculiar shape of the adsorption isotherm is also preventing the study of pore size distribution and pore volume by means of conventional non local DFT method. A valid alternative to estimate the micropore volume is the application of t-plot to the desorption branch of the isotherm which results in a micropore volume of 0.093 cm3 g−1. The CO2 adsorption of Cu-EtP was further investigated by collecting adsorption/desorption isotherms up to 5 bar pressure at three temperatures, namely, 298, 308 and 318 K. Fig. 2b shows a comparison of the adsorption branches, whereas the full isotherms and respective fittings are available in the ESI† (Fig. S10–S15 and Tables S4, S5). The adsorption isotherms display a steep increase at pressures below 0.2 bar, when the loading is in the range of 1 mmol g−1. After this first adsorption event, a step appears, leading to the adsorption of additional CO2, followed by saturation at about 2 mmol g−1 at pressures exceeding 1 bar. The step shifts to higher pressures as the temperature increases, as observed for other adsorbents displaying analogous behaviour.4,14,17,56
An interesting insight comes from inspection of the kinetic curves recorded during collection of the isotherms in Fig. 2b, which display a significant slowdown of the adsorption rate at pressures associated with the step (Fig. S16–S18, ESI†). This behaviour suggests that there could be either a slow structural rearrangement associated with the adsorption of CO2 or a kinetics effect due to the small size of the channels of Cu-EtP, which is comparable to the kinetic diameter of CO2 (3.3 Å), or a combination of the two. Since the kinetics may have an impact on the adsorption of CO2 in the sample, another CO2 adsorption isotherm was collected at 273 K with the low-pressure apparatus, using twice the equilibration time compared to the one employed for the isotherms reported above (Fig. S19, ESI†). By comparing the two isotherms collected using 60 and 120 s equilibration time, it is possible to observe a change in the shape of the adsorption branch, which displays a step shifted towards lower pressures at a shorter equilibration time (Fig. S19, ESI†). These observations suggest that the shape of the adsorption isotherm depends on how equilibrium conditions (i.e., equilibration time and pressure tolerance) are defined and how sensitive the instrument is in terms of pressure resolution. The root of such variability is most likely the sluggish kinetics observed during CO2 adsorption. It is worth noting that the equilibration time does not affect the desorption branch of the isotherms. For this reason, the desorption isotherms can be reasonably employed to estimate the CO2 accessible surface. Indeed, by applying the BET equation to the desorption branch of the CO2 isotherm measured with an equilibration time of 120 s, a value of 278 m2 g−1 was computed. This result is in line with the value obtained at 60 s of equilibration time (Fig. S20 and Tables S6, S7, ESI†). Additionally, the micropore volume, estimated by applying the t-plot method to the desorption isotherm, is 0.094 cm3 g−1, fully in agreement with what obtained from the 60 s isotherm.
N2 adsorption was also assessed by collecting an isotherm at 298 K up to 5 bar pressure (Fig. S21, S22, ESI†). The isotherm displays an almost linear shape and the uptake of N2 at 5 bar reaches only 0.2 mmol g−1. The ideal adsorbed solution theory (IAST) selectivity was calculated from this isotherm and the CO2 isotherm collected at the same temperature, assuming a 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 CO2/N2 mixture, representative of post-combustion capture from a coal-fired power plant (Fig. S23, ESI†). The IAST selectivity increases with increasing total pressure, displaying values that vary between 2300 and 11
85 CO2/N2 mixture, representative of post-combustion capture from a coal-fired power plant (Fig. S23, ESI†). The IAST selectivity increases with increasing total pressure, displaying values that vary between 2300 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in the 0.1–2 bar pressure range. Such ultrahigh values indicate that Cu-EtP might be able to separate CO2 from N2via a molecular sieving mechanism, taking advantage of the larger kinetic diameter of N2 (3.6 Å), which considerably restricts its diffusion in the sub-ultramicropores of Cu-EtP.
000 in the 0.1–2 bar pressure range. Such ultrahigh values indicate that Cu-EtP might be able to separate CO2 from N2via a molecular sieving mechanism, taking advantage of the larger kinetic diameter of N2 (3.6 Å), which considerably restricts its diffusion in the sub-ultramicropores of Cu-EtP.
The isosteric heat of CO2 adsorption (Qst) was extracted from the three high-pressure isotherms using the Clausius–Clapeyron equation (Fig. S24, ESI†). The isotherms were fitted using both the dual site Langmuir and the dual site Langmuir–Freundlich models, obtaining a better result with the latter, even though the shape of the isotherms was not fully reproduced by the model (Fig. S13–S15 and Tables S4, S5, ESI†). Given the difficulty in fitting the curves, the Qst values at low loading and near saturation suffer from a certain degree of error, but the plot suggests that there are two events associated with a Qst in the range of 40 kJ mol−1, before the step in the isotherm, and a Qst in the range of 30 kJ mol−1, in correspondence of the step. Additionally, since the shape of the adsorption isotherm step is affected by the equilibration time (see Fig. S19, ESI†), also the Qst values could slightly change by modifying this parameter and, therefore, they should be considered as estimated isosteric heats of CO2 adsorption. Anyhow, these values are consistent with a strong physisorptive character, which might involve the interaction of CO2 with the abundant OMSs present in the evacuated MOF.
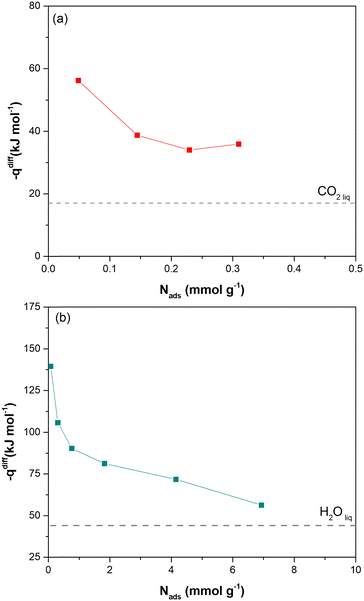
Direct evidence of the heat of adsorption is provided by adsorption microcalorimetry. The differential molar adsorption heat of CO2 at 308 K and H2O at 303 K was measured on dehydrated Cu-EtP samples (Fig. 3 and Fig. S25, ESI†). The CO2 differential molar adsorption heat curve (Fig. 3a) shows an initial differential heat of 56 kJ mol−1 and then a rapid decrease to 38 kJ mol−1 at 0.15 mmol g−1. This value remains almost constant up to 0.3 mmol g−1, in agreement with the isosteric heat of adsorption derived from Clausius–Clapeyron equation. Notably, the adsorption isotherm obtained with the volumetric line coupled with the microcalorimeter does not perfectly correspond with the low-pressure volumetric CO2 isotherm performed at 308 K (Fig. S26, ESI†). This behaviour is consistent with what previously observed for the volumetric isotherms and provides further proof of the dependence of the shape of the isotherm to the definition of the equilibrium conditions. Indeed, in adsorption microcalorimetry, equilibrium is not defined as a pressure variation over a set time, but by the achievement of thermal equilibrium. This can lead to small deviations in the final shape of the adsorption isotherm. Additionally, it is worth mentioning that the CO2 differential molar adsorption heat curve is limited to 0.3 mmol g−1, corresponding to 0.1 bar of absolute pressure (Fig. S24a, ESI†). Unfortunately, higher CO2 pressures coincide with a reduction of the overall adsorbed amount (the slope of the adsorption isotherm decreases reaching a sort of plateau before the step at 0.6 bar) and with the slowdown of the adsorption rate according to the kinetic curves (Fig. S17, ESI†). Both these issues prevent a correct measurement of the adsorption heat at higher coverage.
In agreement with the very steep H2O adsorption isotherm at low pressure (Fig. S25b, ESI†), the differential molar adsorption heat of H2O exhibits a very high initial value (about 140 kJ mol−1 at 0.08 mmol g−1). The differential heat rapidly decreases to 90 kJ mol−1 at 0.77 mmol g−1 and then it slowly lowers until 70 kJ mol−1 at a coverage of 4 mmol g−1. After that, the differential heat curve again changes slope, gradually approaching the heat of liquefaction of H2O (44 kJ mol−1). The high differential heats at low H2O coverage (higher than 90 kJ mol−1), suggest the presence of strong defective interaction sites in Cu-EtP sample. The second family of sites, associated with a weaker interaction (between around 85–75 kJ mol−1) at higher H2O coverages (1–4 mmol g−1), could be compatible with the adsorption of coordinated water molecules on the OMSs of the MOF.
In situ powder X-ray diffraction
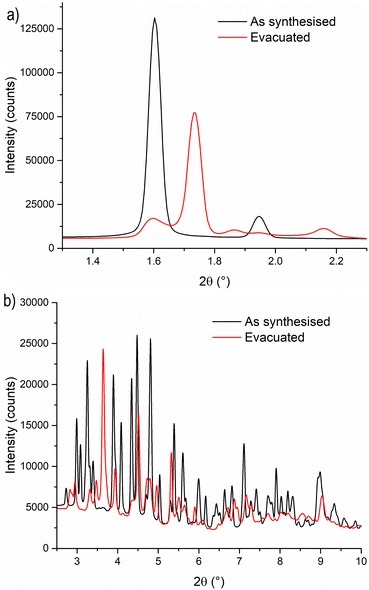
To gain a deeper understanding of the structural origin of the step in the CO2 adsorption isotherm of Cu-EtP, we performed an in situ PXRD study. First, we followed the evacuation process of as synthesised Cu-EtP. The sample was held in a capillary and heated with a hot air blower under vacuum (pressure in the range of 10−5–10−6 bar). The sample was equilibrated for 10 min at 303, 353, 373, 393 and 413 K, observing no significant changes in the PXRD pattern (Fig. S27, S28, ESI†). Heating to 433 K induces rearrangements in the pattern, visible already after 10 min. The sample was held at 433 K for 300 min, collecting one pattern every 10 min, showing that the structural evolution continued for at least 120 min (Fig. S29 and S30, ESI†). Fig. 4 shows a comparison of the PXRD patterns of the as synthesised and evacuated Cu-EtP. The first observation to be made is that the evacuated Cu-EtP is characterised by a basal peak located at higher 2θ angles than the as synthesised Cu-EtP. This suggests that the structure is rearranging to a slightly more compact conformation upon removal of water. In the as synthesised MOF, the interlayer distance (as deduced from the position of the 200 reflection, located at 1.60°2θ) is 7.42 Å, while in the evacuated MOF it is reduced to 6.86 Å (as deduced from the position of the most intense Bragg reflection located at 1.73°2θ), corresponding to a 7.5% contraction. The second observation is that the phase transition appears not to be complete, as evidenced by the residual peak at 1.60°2θ and by the IR spectra discussed herein. Unfortunately, due to the simultaneous presence of two crystalline phases and to the loss of long-range order upon evacuation, all our attempts to index the unit cell for the new phase failed, preventing us from gaining further structural information.Next, we introduced increasing pressures of CO2 in the capillary at the temperature of 308 K. No changes were observed at pressure as high as 0.490 bar, while new reflections appeared when the pressure was 1.064 bar and kept growing in intensity over 70 min at the expense of the characteristic reflections of the evacuated form (Fig. S31 and S32, ESI†). Apparently, the residual as synthesised phase was not involved in the process, as demonstrated by the constant intensity of the reflection at 1.60°2θ. Further increasing the pressure to 1.271 bar did not cause any other change in the pattern. Notably, the pressure of 0.490 bar is located at the end of the step in the isotherm collected at the same temperature (Fig. S33, ESI†), where one would expect a possible phase transition to be well underway, yet no changes are observed in the PXRD pattern. This could be due to the slow kinetics of phase transition, already anticipated by the adsorption kinetics previously discussed. To gain further insight into this aspect, the sample was evacuated again and subsequently exposed to a fixed CO2 pressure of 1.410 bar at 308 K for 65 min (Fig. S34 and S35, ESI†). The reflection at 1.65°2θ, associated with a new crystalline phase, appeared as soon as CO2 was introduced in the capillary and kept increasing in intensity during the whole experiment, confirming the slow kinetics of phase transition. The CO2 loaded Cu-EtP displays a PXRD pattern (Fig. 5 and Fig. S36, S37, ESI†) that retains features of the evacuated Cu-EtP, plus a new crystalline phase characterised by an interlayer distance of 7.19 Å (as deduced from the position of the Bragg reflection located at 1.65°2θ). The coexistence of three crystalline phases in this sample made any further structural analysis impossible.
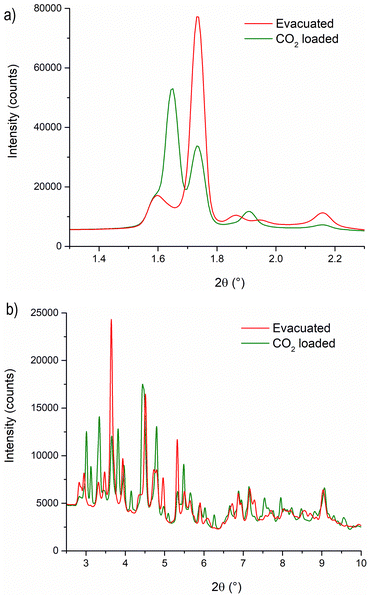 | ||
| Fig. 5 Comparison of the low angle (a) and high angle (b) regions of the PXRD patterns of evacuated (red line) and CO2 loaded (green line) Cu-EtP. | ||
In situ infrared spectroscopy
We used in situ IR spectroscopy to further investigate both the structure and the role of Cu sites in the adsorption of small molecules. As in the PXRD experiment, the evacuation of Cu-EtP was evaluated first (Fig. 6a). The sample was outgassed under low vacuum conditions (∼7 × 10−3 mbar) and then heated from 313 K to 393 K at a 1.5 K min−1 rate. The as synthesised Cu-EtP sample (see the black dot spectrum in Fig. 6a and Fig. S38, ESI†) is characterised, in the 3600–1450 cm−1 spectral region, by the broad intense bands of the OH stretching vibrations (3600–3000 cm−1) and of the HOH bending vibrations (1680–1530 cm−1) and by two sharper bands at ∼2940–2820 cm−1 associated to CH stretching modes.57 In the lower frequency region (1450–550 cm−1), the spectrum displays vibrational modes ascribed to the Cu-EtP framework, among which: (i) a sharp component at 1413 cm−1 characteristic of the bending vibrations of the methylene −CH2 groups bonded to P atoms, (ii) an out of scale intense band in the 1200–800 cm−1 frequency range, associated to both C–C and P–O stretchings of the phosphonate groups and (iii) a wide number of signals between 800 and 550 cm−1 due to the overlapping of several framework vibrations.57,58 The outgassing of the sample at beam temperature causes the desorption of physisorbed water, as proved by the erosion of the molecular water signals (OH stretching and HOH bending). A slight downward shift of the 1413 cm−1 band to 1410 cm−1 is observed accordingly. Upon heating, a new band at 1424 cm−1 grows at the expense of the 1410 cm−1 component, which progressively decreases in intensity, as also testified by the isosbestic point located at 1419 cm−1. However, even after a prolonged heating at 393 K (around 12 h) the 1410 cm−1 band does not totally disappear and the two signals stay unchanged upon cooling down the sample in vacuum (Fig. S39, ESI†). The spectral modifications occurring in the 1440–1405 cm−1 spectral range, related to the deformations of the CH2 groups bonded to P atoms, suggest a partial rearrangement in the Cu-EtP structure during the removal of molecularly adsorbed H2O. It is worth noting that those spectral modifications are fully in agreement with PXRD data (Fig. 4) that prove the formation of a new dehydrated phase which coexists with the original hydrated one. In the whole mid-IR spectral region (Fig. S38, ESI†), the spectrum of the totally evacuated Cu-EtP sample displays the erosion of the broad band of interacting OH species at ∼3600–3200 cm−1 and the simultaneous growth of a sharp signal at ∼3660 cm−1, probably associated with the formation of isolated P–OH groups.39,59 It may be noted that, during evacuation, the HOH bending region (see inset of Fig. 6a) is deeply modified, progressively revealing a more complex band evolution: a new component appears at 1680 cm−1 close to the main 1654 cm−1 band that decreases in intensity upon heating, while another signal at lower wavenumber (1580 cm−1) gradually appears, persisting also at higher temperature. The different stability of these bands suggests that the former ones, which rapidly decrease with the temperature, should be associated to the physisorbed water, while the latter one, which can be detected even at temperature higher than 378 K, is probably ascribable to the water strongly coordinated to CuII sites.60 Eventually, the bands in the low spectral region (800–550 cm−1), assigned to the superposition of many framework vibrations, are strongly perturbed during the material evacuation (as displayed in Fig. S40, where the ATR-IR spectra are reported to better highlight the spectral modifications observed in the low frequency region, ESI†), in accordance with the proposed structural rearrangement.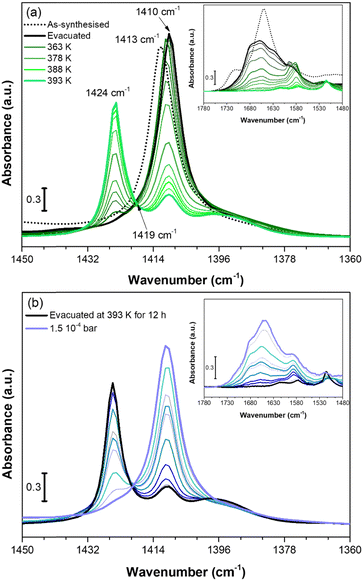 | ||
| Fig. 6 IR spectra of Cu-EtP collected in the 313–393 K temperature range (a) and dosing 0.35–1.5 10−4 bar of H2O (b), reported in the 1450–1360 cm−1 spectral region. Dashed black curves represents the as synthesised Cu-EtP, black curves the evacuated sample at RT (a) and 393 K (b), green bold curves represent Cu-EtP spectra at increasing temperatures and blue bold curves the incremental pressure doses of H2O employed during the IR experiment and specified in Fig. S41 (ESI†). The insets report the corresponding 1780–1480 cm−1 spectral region. | ||
After studying the spectral evolution upon dehydration, Cu-EtP, previously evacuated at 393 K for 12 h under vacuum, was exposed to increasing pressures of H2O (from 0.35 × 10−4 to 1.5 × 10−4 bar) (Fig. 6b and Fig. S41, S42, ESI†). The changes observed during the hydration of the material reflect what previously noted upon H2O desorption. In particular, the 1424 cm−1 band present in the evacuated material progressively decreases upon increasing the H2O pressures, while the band at 1410 cm−1 is totally restored. In the same way, in the HOH bending region, the water is first adsorbed on the most energetic CuII sites, originating the 1580 cm−1 (coordinated water) band and only at higher H2O coverage, the 1680–1654 cm−1 bands associated to physisorbed water appear. The band evolution suggests a total rehydration of the material, since the final spectrum of Fig. 6b perfectly matches with the IR spectrum of the as synthesised material. It is worth noting that the total rehydration of the sample occurs at very low relative pressure of water (between 0.3–2.2 × 10−3), suggesting that Cu-EtP has a strong affinity for water, in agreement with the calorimetric isotherm (Fig. S25, ESI†). The spectral evolution observed during Cu-EtP dehydration/hydration proves the occurrence of a reversible structural rearrangement upon H2O adsorption/desorption.
We also investigated the vibrational behaviour of a fully dehydrated Cu-EtP sample when exposed at beam temperature (i.e. around 313 K) to an increasing CO2 pressure (in the range between 0.005 and 0.55 bar). The time between the different CO2 incremental doses was gradually increased when approaching the pressures corresponding to the second isotherm step (0.2–0.8 bar), due to the slow kinetics observed for this adsorption event (Fig. S43 and S44, ESI†). The incremental CO2 doses are responsible for significant changes in both the CO2 asymmetric stretching region between 2400 and 2220 cm−1 (Fig. 7a) and in the 1450–1360 cm−1 spectral range (Fig. 7b).
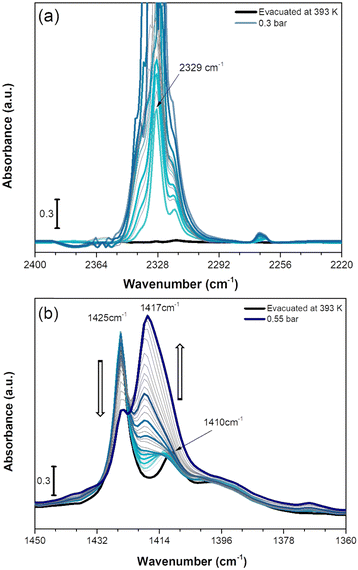 | ||
| Fig. 7 IR spectra of CO2 adsorption on Cu-EtP evacuated at 393 K reported in the 2400–2200 cm−1 (a) and 1450–1360 cm−1 (b) spectral ranges. The incremental pressure doses of CO2 employed during the IR experiment are reported with thicker coloured curves and specified in Fig. S43 (ESI†). The 2400–2200 cm−1 spectral region is corrected by subtracting the rotovibrational profile of gaseous CO2, the original spectrum is reported in Fig. S44a (ESI†). | ||
As reported in Fig. 7a, upon CO2 dosing, the ν3 OCO asymmetric stretching vibrations in the 2400–2220 cm−1 are quickly going out of scale due to the large extinction coefficient of this spectral mode. Already after the first incremental doses of CO2, an intense band at 2329 cm−1 with a low frequency shoulder at 2318 cm−1 appears, exhibiting a rapid increase of intensity. At lower wavenumber, a much weaker signal at 2264 cm−1 forms at low CO2 coverage exhibiting a slight upward shift to 2268 cm−1 by increasing the coverage. The component at 2329 cm−1 could be assigned to CO2 interaction with CuII sites present in the Cu-EtP sample after H2O removal. However, the 2329 cm−1 signal is significantly downward shifted compared to the asymmetric signals of CO2 in gas phase (2349 cm−1) while, usually, the linear interactions of CO2 over acid sites results in an upward shift of the ν3 band, whose extent should be correlated with the acid strength of the site.61 However, a similar behaviour has been previously observed by Bordiga et al. on HKUST-1, in which a band at 2333 cm−1 was assigned to the interaction of CO2 with the full Cu2(CO2)4 unit.62 Similarly, the 2329 cm−1 band could be due to a more complex CO2 interaction with Cu-EtP sample involving not only the bare adsorption on CuII cations. Even if this attribution cannot be carried out with absolute certainty, a clue in favour of this assignment comes from the analysis of the desorption CO2 spectra (Fig. S44b, ESI†). In the 2400–2220 cm−1 spectral region, the CO2 asymmetric vibrations quickly decrease in intensity, except for the 2329 cm−1 band that persists even after prolonged outgassing under dynamic vacuum. The high stability of this band further suggests the presence of a strong interaction between CO2 and the OMSs of Cu-EtP. The same interaction involving 13CO2 is responsible for the appearance of the weak 2264 cm−1 band, while the 2268 cm−1 is probably due to 13CO2 in the gas phase, which has been subtracted in the spectra for the most abundant 12CO2 isotopic form.
In the P–CH2 vibrations spectral range (1450–1360 cm−1), the fully evacuated sample shows both the 1425 cm−1 band (indicative of the dehydrated phase) together with a partial persistence of the 1410 cm−1 (deriving from the residual hydrated phase of Cu-EtP), as previously described in Fig. 6a. By increasing the CO2 pressure, a new vibrational mode of P–CH2 moieties appears at ∼1417 cm−1, suggesting the formation of a new phase, in accordance with the PXRD data. Interestingly, at low CO2 coverage (until 0.2 bar) the bands at 1425 and 1410 cm−1 are not perturbed, while the new band at 1417 is gradually growing. Upon increasing the CO2 pressure (0.2–0.4 bar), the bands at 1425 cm−1 and 1410 cm−1 slightly decrease, while the 1417 cm−1 band increases. Finally, at higher CO2 pressures (0.4–0.5 bar), the 1425 cm−1 band suddenly decreases while the 1417 cm−1 band rapidly increases, generating an isosbestic point at 1422 cm−1. However, the 1417 cm−1 band exhibits a shoulder at lower wavenumbers. By performing the computer-assisted deconvolution of the 1450–1360 cm−1 bands (Fig. S45, ESI†), the increase of the 1410 cm−1 band becomes evident at higher CO2 coverages. It is worth noting that the increase of the 1410 cm−1 band and the simultaneous decrease of the 1425 cm−1 signal was previously observed during the hydration of the material. To keep up with the slow kinetics of the CO2 adsorption, after contact with the highest CO2 doses, the sample was left for a long time in the cell under static conditions, leading to some (uncontrollable) H2O contamination, as also proved by the increase of both the OH stretching and HOH bending bands (Fig. S46, ESI†). In a CO2 saturated atmosphere, the co-presence of a slight fraction of H2O seems to facilitate the entrance (and consecutive adsorption) of CO2 and the transition of Cu-EtP to a new, partially opened structure.
Finally, increasing CO2 pressures were dosed directly on a sample outgassed at 298 K, where only physisorbed (and not coordinated) water was removed, to observe the CO2 interaction on Cu-EtP in the open phase (Fig. S47, ESI†). In this case, the CO2 asymmetric stretching region (2400–2220 cm−1) shows only the signals typical of CO2 in the gas phase, while the 1750–1450 cm−1 and the 1450–1360 cm−1 spectral regions totally coincide with those of as synthesised sample, suggesting that CuII OMSs, saturated by coordinated H2O, are totally inaccessible to CO2.
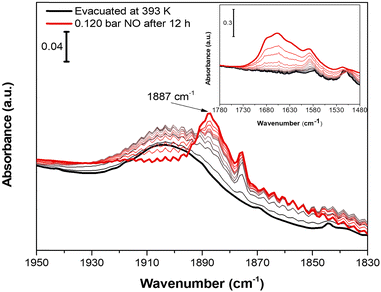
Nitrogen oxide (NO) was chosen as molecular probe to further investigate the accessibility of CuII OMSs, not only for the affinity displayed toward CuII sites by this molecule, but also for its small kinetic diameter (3.17 Å).63 Indeed, the sub-ultramicroporous nature of Cu-EtP avoids the entrance of the mostly used basic molecular probes, such as CO, whose kinetic diameter is 3.76 Å.63 0.12 bar of NO was dosed on a sample evacuated at 393 K overnight. Initially, NO does not interact with Cu-EtP and only its rotovibrational profile was observed in the IR spectrum. Only after 12 h, a band at 1887 cm−1, ascribable to the interaction of NO with CuII sites, appears together with the 1875 cm−1 signal of NO in the gas-phase (Fig. 8). However, as previously observed for the CO2 interaction, the prolonged contact time is responsible for some H2O contamination (see the appearance of HOH bending modes at 1654 cm−1 in the inset of Fig. 8). The presence of a small fraction of H2O favours the transition to the partially opened structure and the consecutive NO adsorption at CuII OMSs, as testified, in the 1450–1350 cm−1 region, by the simultaneous decrease of the 1425 cm−1 band in favour of the 1410 cm−1 one (see Fig. S48, ESI†). Also for NO, an experiment was performed on a sample outgassed at 298 K, in order to observe the possible NO interaction on Cu-EtP in the open phase (Fig. S49, ESI†). In this case, the signal at 1887 cm−1 (generated by the interaction of NO with CuII sites) appears after just 2 h. No major changes can be detected in the P–CH2 vibrational region, except for some intensity variation of the 1410 cm−1 signal. This behaviour is in accordance with the existence of an already opened structure, which does not display any significant change upon adsorption of NO. It is worth noting that, unlike CO2, NO seems unable to create a new crystalline phase upon adsorption but is still able to interact with CuII sites even in the presence of a partially hydrated structure, replacing part of the H2O molecules (see the inset of Fig. S49a (ESI†) showing an intensity decrease of the HOH bending modes after NO dosing). However, also CO2 may display some interactions with partially hydrated Cu-EtP after a prolonged contact time but, unfortunately, as previously pointed out, a slight H2O contamination occurs upon an overnight exposure to CO2 under static conditions, preventing a complete understanding of the CO2 adsorption process.
Optical spectroscopy
In situ PXRD and IR spectroscopy clearly demonstrated that Cu-EtP experiences a structural rearrangement upon evacuation and, subsequently, CO2 adsorption. Nevertheless, none of these techniques provided a direct information on the rearrangement of the local coordination sphere around the CuII cations. Electronic spectroscopies represent the election tool for this type of investigation, as the electronic transition associated to the metal centre directly correlate with the energies of involved orbitals that, in turn, depend on the ligand field around the metal itself. Accordingly, we collected diffuse reflectance optical spectra for Cu-EtP in its as synthesised form, after evacuation at 393 K and upon contacting the evacuated material with CO2, specifically focussing on the analysis of the spectral region typical of d–d transitions, as shown in Fig. 9.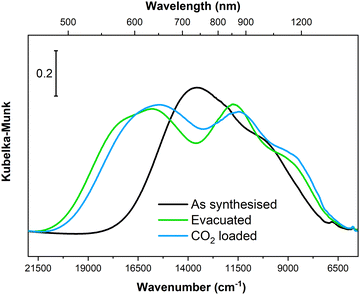 | ||
| Fig. 9 Diffuse reflectance optical spectra of Cu-EtP collected on the as synthesised material, upon evacuation at 393 K and after contacting the evacuated material with CO2 (ca. 0.5 bar). | ||
In the as synthesised material, a doublet of bands with maxima at ca. 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 and 10
500 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are observed, in agreement with previous report.46 According to crystal field theory, and as already detailed in ref. 46 in the as-synthesised sample, three distinct d–d transitions are expected given the distorted octahedral geometry of ligands around CuII (four almost equivalent O atoms from phosphonate groups on the equatorial xy plane + two O atoms from apical water molecules at longer distance along the z axis). Upon evacuation at 393 K, the d–d transitions of Cu-EtP significantly change, with a blue-shift of the absorption maxima to ca. 15
000 cm−1 are observed, in agreement with previous report.46 According to crystal field theory, and as already detailed in ref. 46 in the as-synthesised sample, three distinct d–d transitions are expected given the distorted octahedral geometry of ligands around CuII (four almost equivalent O atoms from phosphonate groups on the equatorial xy plane + two O atoms from apical water molecules at longer distance along the z axis). Upon evacuation at 393 K, the d–d transitions of Cu-EtP significantly change, with a blue-shift of the absorption maxima to ca. 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 and 11
500 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. A third component is instead red-shifted to ca. 8500 cm−1. Such shifts are compatible with a change in the coordination sphere of CuII causing a variation in the gap between the non-degenerate d orbitals of the cation, most probably toward a square planar coordination geometry (see Fig. S50, ESI†). By loading CO2 (at a pressure compatible with the second step in the adsorption isotherm) on the evacuated sample, a small red-shift of the absorption features is observed, though in overall the shape of the d–d transitions remains very similar to those of evacuated Cu-EtP, suggesting the CO2 only weakly interacts with the CuII site by likely giving a new distorted octahedral coordination sphere. It is worth mentioning that PXRD showed that the formation of the CO2 loaded phase at the expense of the evacuated one is only partial, further supporting the fact that associated optical spectra look similar to each other.
500 cm−1. A third component is instead red-shifted to ca. 8500 cm−1. Such shifts are compatible with a change in the coordination sphere of CuII causing a variation in the gap between the non-degenerate d orbitals of the cation, most probably toward a square planar coordination geometry (see Fig. S50, ESI†). By loading CO2 (at a pressure compatible with the second step in the adsorption isotherm) on the evacuated sample, a small red-shift of the absorption features is observed, though in overall the shape of the d–d transitions remains very similar to those of evacuated Cu-EtP, suggesting the CO2 only weakly interacts with the CuII site by likely giving a new distorted octahedral coordination sphere. It is worth mentioning that PXRD showed that the formation of the CO2 loaded phase at the expense of the evacuated one is only partial, further supporting the fact that associated optical spectra look similar to each other.
Computational simulations
The foregoing experimental evidence collectively point towards structural rearrangements occurring in Cu-EtP in response to evacuation and adsorption of CO2, respectively. Given the impossibility to gather insight into the atomic structure of the different crystalline phases of Cu-EtP using PXRD, we resorted to periodic DFT calculations to gain insight into said structural rearrangements. First, a triclinic subcell (space group P1) was identified for the as synthesised MOF, whose volume is half that of the original monoclinic unit cell (space group C2/m). This choice allows to work with 16 independent atoms in the unit cell to describe the framework, plus those needed to describe H2O and CO2, when the as synthesised and the CO2 loaded forms are respectively considered. Three models were built for the as synthesised, evacuated and CO2 loaded forms of Cu-EtP (Fig. S51–S56 and Table S8, ESI†). In these models, the inorganic layers lie on the (110) plane. The DFT optimised structures suggest that the main structural rearrangements occurring during evacuation and CO2 adsorption involve the inorganic part of the framework, as outlined in Table 1 and Fig. 10.In the as synthesised material, the local Cu coordination is distorted octahedral, with pairs of inequivalent Cu–O distances in the equatorial plane and axial ligands (i.e., H2O) positioned at a significantly longer distance. Upon desolvation, the coordination environment around Cu rearranges to a square planar geometry with a reduced inequivalence in the equatorial Cu–O distances. The introduction of CO2 leads to a situation that is midway between those discussed above, with an apparently octahedral coordination characterised by an even higher distortion of the ligand field, as suggested by the very long Cu–O axial distances. All the PO–Cu bond lengths shrink when water is removed from the coordination sphere of Cu and increase again once CO2 is adsorbed. The change of the coordination geometry of Cu also confirms the modification in the optical properties of Cu-EtP upon desolvation and consequent CO2 loading.
The coordination rearrangements lead to changes in the interlayer spacing in line with those experimentally observed by PXRD: the Cu–Cu distance along the [110] direction varies from 7.621 Å to 7.404 Å to 7.436 Å in the as synthesised, evacuated and CO2 loaded Cu-EtP, respectively. While these values appear to be systematically overestimated, compared to those experimentally observed, they suggest that DFT provides a reliable description of the structural evolution. The organic part of the framework appears to be relatively unaffected during evacuation, with the P–P distance inside the linker changing from 4.443 Å (as synthesised) to 4.449 Å (evacuated), while CO2 adsorption causes an increase to 4.539 Å.
The interaction energy per H2O/CO2 molecule adsorbed was computed considering the adsorption of two molecules per formula unit from gas phase onto the evacuated structure. In the same way, adsorption enthalpy and Gibbs free energy were calculated (at 298 K and 1.013 bar). The results are summarised in Table 1. H2O binds with a high interaction energy, compatible with a strong physisorption as inferred by microcalorimetry. In detail, the computed adsorption enthalpy of −83.8 kJ mol−1 nicely reproduces the heat experimentally evolved at intermediate coverages. This suggests that H2O adsorption over OMSs takes place at intermediate coverages, whereas the higher adsorption heat evolved at low coverages may be reasonably associated with coordination of water on defective sites. The adsorption of water is significantly favoured, as demonstrated by the largely negative Gibbs free energy associated to the process, in line with the strong competitive adsorption H2O exhibits toward other adsorbates. A similar good agreement with experimental heat values for CO2 adsorption is observed as well. Interestingly, CO2 adsorption is a slightly endergonic process, featuring a positive (though small in magnitude) Gibbs free energy. This feature could explain the only partial conversion of the evacuated phase of Cu-EtP into the CO2 loaded one, as inferred by PXRD.
DFT simulation also allowed investigating in closer details the peculiar evolution of spectroscopic features observed during in situ IR experiments. The simulated spectra in the region typical of CH2 bending modes are shown in Fig. S57 (ESI†). In absolute terms, the computed frequencies for the three considered structures are overestimated with respect to the experimental results, with an upshift of approximately 40 cm−1 for the as synthesised model. Nonetheless, the dataset can be effectively considered in a relative way, i.e., accounting for the shift of the δ(CH2) mode as a consequence of the presence/absence of the different adsorbates. Through this method, the computed shift of the CH2 bending mode upon interaction with H2O and CO2 compared to the evacuated model experiences a shift of −15 cm−1 and −5 cm−1, respectively. These values are in good agreement with the experimental shift of −14 cm−1 and −8 cm−1, as derived at the maximum coverage experimentally considered, further confirming the supposed structure of the adsorbed molecules within Cu-EtP.
Additionally, to validate the unconventional experimental quantification of the BET area and micropore volume using the desorption isotherm, we performed an estimation of the surface area for the evacuated model. This verification was carried out using the Zeo++ software.64 In this simulation, we systematically adjusted the probe diameter, gradually reducing it from the kinetic diameter of N2 (3.60 Å) to the maximum value that yielded a non-zero surface area in the simulation (see Table S9, ESI†). It is important to note that a reduced probe radius (compared to the experimental one), as required to observe a non-zero surface area within the theoretical framework employed by the Zeo++ software, has been previously documented in the literature.65 By employing this approach, we identified an optimal probe diameter of 2.8 Å, which resulted in a simulated surface area of 262 m2 g−1. This simulated value closely matches the experimental surface area we obtained, proving the validity of our non-conventional BET area quantification. To further validate our findings, we repeated the same procedure for the as synthesised model. However, in this case, the results consistently indicated a negligible surface area, regardless of the selected probe diameter. Additionally, we carried out a simulation of the pore size distribution (Fig. S58, ESI†), which revealed a single family of pores with a diameter of 3.5 Å and a total accessible pore volume of 0.099 cm3 g−1. It is worth noting that the pore volume is fully consistent with the value extrapolated from the t-plot. This simulated pore size distribution provides further confirmation of the ultramicroporous nature of Cu-EtP and highlights the need for specific characterisation strategies to comprehensively evaluate its textural properties.
Conclusions
By combining gas sorption analysis, adsorption microcalorimetry, in situ PXRD, in situ IR, optical spectroscopy and DFT calculations, we have investigated in depth the CO2 adsorption properties of Cu-EtP and the associated structural transitions. The phase transitions occurring in Cu-EtP in response to adsorption/desorption of H2O and CO2 are rather unexpected, since its structure is based on rigid, two-dimensional IBUs, and the connectivity along the third dimension is ensured by a very short aliphatic chain with a limited number of degrees of freedom. We find that the rearrangement of the coordination sphere of Cu, which switches between distorted octahedral and square planar, is mainly responsible for the observed behaviour. The structural response of Cu-EtP to the adsorption/desorption of water and CO2, involving partially complete phase transitions, is distinct from common stimuli responsive MOFs, such as MIL-53, ELM-11 and ZIF-7, where clear cut transitions take place, driven by cooperative phenomena that imply a flexible behaviour of the framework but no changes in the coordination geometry of the metal. Thanks to the strong interaction with CO2 and its ultrasmall channels, Cu-EtP can separate CO2 from N2 by molecular sieving, which makes it a potentially interesting solid sorbent for post-combustion carbon capture. However, given the slow CO2 adsorption kinetics associated with the phase transition, the hysteretic CO2 desorption isotherm, and the high affinity for H2O, further investigation is needed to fully assess its real separation potential. Analogues of Cu-EtP based on organic linkers with longer aliphatic chains have been reported in the literature,66,67 but their adsorption properties were never assessed to the level of depth reached here, and it is reasonable to expect that these compounds might as well display peculiar structural behaviour, by virtue of the potentially higher flexibility of the organic part of the framework.Experimental procedures
Materials
1,2-Ethylenediphosphonic acid (97%) was purchased from Alfa Aesar, Cu(NO)2·3H2O (ACS grade) was purchased from Riedel-de Haën and urea (puriss.) from VEB Laborchemie Apolda. All reagents were used as received, with no further purification.Synthesis of Cu-EtP
Cu-EtP was synthesised by slightly modifying a literature procedure: 1 g urea was added to 5 mL of a 0.1 M aqueous solution of 1,2-ethylenediphosphonic acid in a round bottom flask, which was kept at 80 °C in a drying oven. After 17 h, 5 mL of a 0.2 M Cu(NO3)2-solution was added, whereupon a light blue precipitate appeared. The whole solution was further kept at 80 °C for 4 h. The formed turquoise fine crystalline precipitate was washed with distilled water several times.Thermogravimetric analysis
Thermogravimetric analysis was performed either using a Netzsch STA 449 instrument heating at 10 K min−1 up to 1273 K under an air flow, or with a TA Instruments SDT-Q600 instrument heating at 10 K min−1 up to 413 K under an Ar flow for 8 h, followed by cooling to 313 K and switching to a 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 CO2/Ar flow for 3 h.
10 CO2/Ar flow for 3 h.
Gas adsorption volumetry
N2 and CO2 isothermal physisorption measurements were performed on a Micromeritics 3Flex at 77 K and 273 K (using 60 and 120 s as equilibration time) respectively (Fig. 2a). For CO2 adsorption the temperature was kept constant thanks to a home-made patented glass coating cell in which a coolant or heating fluid, connected to a thermostatic bath (JULABO F25), is recirculating.68 Prior to the measurement, the sample was heated overnight at 393 K under vacuum. Specific surface areas were determined, by using the Brunauer–Emmett–Teller (BET) equation, from the desorption branch of the CO2 isotherm measured at 273 K using both 60 and 120 seconds of equilibration time and 5% tolerance (Tables S2, S3 and Fig. S8, ESI†). The micropore volume was extrapolated from the t-plot curve derived from the desorption branch of CO2 isotherms at 273 K using 60 and 120 s of equilibration time, considering the statistical thickness range 6 < t < 17 Å.High pressure adsorption–desorption isotherms were measured with a Quantachrome iSorb High Pressure Gas Analyser. CO2 isotherms were collected up to 5 bar at 298, 308 and 318 K using 60 s equilibration time and 0.5 mbar tolerance. N2 isotherm was collected up to 5 bar at 298 K. About 450 mg of sample was used for the adsorption studies. The sample was degassed at 413 K under dynamic vacuum for 6 h prior to analysis and at 413 K for 1 h in between subsequent measurements.
The adsorption branches of the high pressure CO2 isotherms were fitted using either the dual site Langmuir equation:
where q is the gas loading at pressure P, q1 and q2 are the saturation loadings for each site, K1 and K2 are the affinity constants for each site, n1 and n2 are the indices of heterogeneity for each site. We note that the physical meaning of the models might not be representative of the actual CO2 adsorption phenomenon occurring in Cu-EtP, but they provide a reasonable fit of the experimental data nonetheless (see Fig. S13–S15 and Tables S4, S5, ESI†). Using the isotherms fitted with the dual site Langmuir–Freundlich model, the isosteric heat of adsorption was extracted using the linear version of the Clausius–Clapeyron equation in the loading range 0.1–2.0 mmol g−1.
The high pressure N2 adsorption isotherm was fitted using the single site Langmuir equation:
The IAST CO2/N2 selectivity for a 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 mixture in the total pressure range 0.1–2 bar was calculated using the software IAST++.69
85 mixture in the total pressure range 0.1–2 bar was calculated using the software IAST++.69
Adsorption microcalorimetry
The differential molar heat of adsorption was evaluated on Cu-EtP by means of a heat flow microcalorimeter (Calvet C80 by Setaram) connected to a high-vacuum (≈10−4 mbar) glass line equipped with a Varian Ceramicell 0–100 mbar gauge and a Leybold Ceramicell 0–1000 mbar gauge. Prior to the measurement, the sample was activated in vacuum at 120 °C for 12 h and subsequently placed overnight in the calorimeter under isothermal conditions for the equilibration. The measurement in CO2 was performed at 308 K (35 °C), intermediate temperature previously selected for one of the high-pressure isotherms (Fig. 3a and Fig. S24a, ESI†). For H2O the selected temperature was 303 K (30 °C) (Fig. 3b and Fig. S24b, ESI†). The measurement was performed for both CO2 and H2O following a well-established step-by-step procedure described elsewhere.70 By means of adsorption microcalorimetric it is possible to determine, for small increments of the adsorptive pressure, both the integral heats evolved (−Qint) and the adsorbed amounts (Nads). The heats of adsorption obtained for each small dose of gas (−qdiff) are reported as a function of coverage, in order to obtain the (differential) enthalpy changes. The differential heat plot was obtained by taking the middle point of the partial molar heat (ΔQint/ΔNads, kJ mol−1) vs. Nads histogram relative to the individual incremental dose. A volumetric isotherm of CO2 at 303 K was also collected by means of a Micromeritics ASAP 2020 instrument, in order to compare the isotherm obtained with the microcalorimetric apparatus (Fig. S25, ESI†).In situ PXRD
The in situ PXRD study here described took place at Beamline P02.1 (PETRA III, DESY, Hamburg).71 PXRD patterns were collected using 60.0 keV (0.207124 Å) radiation. The sample was held in a 0.5 mm internal diameter glass capillary, which was mounted on a custom-built spinner device that allows for rotating a gas-filled capillary mounted on a commercial Huber goniometer head by 360° forth and back. The temperature of the sample was controlled between 298 and 413 °C with an Oxford Hot-Air Blower. The beamline was equipped with a PerkinElmer XRD1621 CN3 – EHS detector (200 × 200 μm2 pixel size, 2048 × 2048 pixel area). The detector was positioned at 1000 mm from the sample stage. Each PXRD pattern was collected in the 0.0071–16.3041°2θ range, with a 0.0067°2θ step size and a total acquisition time of 30 s. The resulting 2D images were azimuthally integrated to 1D diffraction patterns using the software Fit2D.72In situ IR spectroscopy
IR spectra were performed on a Bruker Invenio equipped with a MCT (mercury cadmium telluride) cryo-detector. All the spectra were recorded in a spectral range of 4500–250 cm−1 with a resolution of 2 cm−1 and an average of 32 scans. Before the analysis self-supported pellets were prepared starting from the Cu-EtP powder.Firstly, the evolution of IR spectra at increasing temperatures was studied. The sample pellet, inserted in a AABISPEC cell, was heated from 313 K to 393 K with 1.5 K min−1 temperature ramp, under mild vacuum conditions (∼7 × 10−3 mbar). IR spectra were automatically recorded every 60 seconds and plotted after a baseline correction (Fig. 6a in the main text and Fig. S37, ESI†). After reaching 393 K, the sample was left under isothermal conditions for 1 h, without detecting significant changes (spectra not reported in the manuscript for the sake of brevity). Finally, the sample was cooled down to 313 K and compared to the sample heated at 393 K (Fig. S38, ESI†).
A further comparison of the spectral evolution of Cu-EtP under activation condition was carried out by performing ATR-IR spectra of the as-synthesised sample, of the sample evacuated for 12 h at RT and of the sample evacuated for 12 h at 393 K (Fig. S39, ESI†). The spectra were collected using a Bruker Alpha II spectrophotometer located inside the glovebox. The spectra were recorded under controlled atmosphere with a DTGS detector by accumulating 32 scans (64 for the background spectrum), with a resolution of 2 cm−1.
The study of the interaction of Cu-EtP with H2O was carried out sending incremental doses of H2O (0.35–1.5 10−4 bar) on the activated sample (see Fig. 6b for the 1450–1360 cm−1 spectral region, Fig. S41 (ESI†) for the full spectral region and Fig. S40 (ESI†) for the schematic representation of the incremental pressures of H2O dosed in time during the IR experiment).
Next, the vibrational behaviour of Cu-EtP previously evacuated at 393 K overnight was investigated upon exposure to increasing CO2 pressures in the range between 0.005 and 0.550 bar, at beam temperature (i.e., around 313 K). The time between consecutive CO2 doses was gradually increased by approaching the isotherm step, due to the slow kinetics of the CO2 adsorption process (Fig. S42, ESI†). The same experiment was repeated on Cu-EtP not fully activated (i.e., evacuated at RT for just 1 h) to follow the CO2 adsorption process in presence of (coordinated) water (Fig. S46, ESI†).
Lastly, NO interaction with the sample were studied by dosing a proper amount of gas (∼0.12 bar) into the cell at beam temperature. Also in this case, the experiment was performed on both fully activated sample (overnight evacuated at 393 K) and evacuated one (evacuated at RT for 1 h) (Fig. 8 in the main text and Fig. S48, ESI†). The spectra reported for both the experiments were collected in outgassing through subsequent expansions, until complete degas was achieved.
Optical spectroscopy
Optical spectra were recorded in reflectance mode on a Varian Cary 5000 spectrophotometer, equipped with an integration sphere. Polytetrafluoroethylene powder was measured as the 100% reflectance reference before measuring Cu-EtP. The sample, loaded in a sealable Suprasil quartz cuvette, was evacuated and subsequently loaded with >0.5 bar of CO2 following the same thermo-chemical protocol as for IR. In between the different experimental steps, all sample manipulations were performed in a N2-filled glovebox, in order to avoid its re-exposure to moist air.Periodic DFT simulations
Periodic DFT simulations were performed with the CRYSTAL17 code.73,74 The B3LYP functional75,76 was adopted in conjunction with the POB-TZVP-rev2 basis set.77 Since CuII is an open-shell ion (d9 electron configuration), the unrestricted Kohn–Sham formalism was adopted: an antiferromagnetic spin state was imposed in agreement with experimental evidence.46 Dispersive interactions were empirically included in the Hamiltonian according to the Becke–Johnson dumped version of the Grimme's D3 scheme.78,79 Calculations were performed on a reduced triclinic unit cell having half the volume of the original C-centred monoclinic cell and containing a single unit formula of the compound, without imposing any symmetry constraint during geometry optimization. Initially, a model derived by removing water molecules featuring the OW2 and OW3 atoms from the experimental one was optimized, aiming at reproducing the as synthesised structure. The evacuated structure was modeled by relaxing a structure were the water molecule represented by the OW1 atoms were further removed. Finally, a CO2 loaded structure was modelled by introducing two CO2 molecules per unit cell, with one of their oxygen atoms placed at the same coordinates as for OW1. Adsorption interaction energies were computed and corrected for the basis set superposition method through the counterpoise method.80 For each of the models above, harmonic frequencies were computed, confirming all the relaxed structures are minima (no imaginary frequencies). Furthermore, IR intensities and thermodynamic functions (enthalpy and Gibbs free energy) were computed.Author contributions
R. K. carried out the synthesis. M. C., V. C. and M. T. carried out the gas sorption experiments and data analysis. M. C. and V. C. carried out the IR and adsorption microcalorimetry experiments and data analysis. M. S. performed the optical spectroscopy experiments and the DFT calculations and data analysis. M. T. carried out the PXRD experiments and data analysis. M. C., M. S., V. C. and M. T. drafted the manuscript. V. C. and M. T. coordinated the work. M. T. conceived the study.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The in situ PXRD experiments were carried out at P02.1/PETRAIII at DESY, a member of the Helmholtz Association (HGF) (Proposal I-20190224 EC). The research leading to this result has been supported by the project CALIPSOplus under the Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON2020. The authors acknowledge the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no 663830 (M. T.). The authors acknowledge the University of Pisa for funding through the Progetti di Ricerca di Ateneo scheme (PRA2020_39) (M. T.). The authors (M. C., M. S., V. C.) acknowledge support from the Project CH4.0 under the MUR program “Dipartimenti di Eccellenza 2023–2027” (CUP: D13C22003520001). M. S. acknowledges the C3S consortium for granting computational resources on the OCCAM cluster, funded by the Compagnia di San Paolo. The authors acknowledge Dr Alexander Schökel and Dr Sergej Wenz (Beamline P02.1 at PETRAIII, DESY) for technical assistance during the beamtime. The authors acknowledge Prof. Ferdinando Costantino (University of Perugia) and Dr Athanasios Koutsianos (TU Dortmund) for support during the beamtime. The authors acknowledge Dr Stephen J. I. Shearan and Dr Matthew J. McPherson (Swansea University) for help with gas sorption analysis during the early stages of the work.References
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096 RSC.
- G. Férey, New J. Chem., 2016, 40, 3950–3967 RSC.
- S. Krause, N. Hosono and S. Kitagawa, Angew. Chem., Int. Ed., 2020, 59, 15325–15341 CrossRef.
- J. A. Mason, J. Oktawiec, M. K. Taylor, M. R. Hudson, J. Rodriguez, J. E. Bachman, M. I. Gonzalez, A. Cervellino, A. Guagliardi, C. M. Brown, P. L. Llewellyn, N. Masciocchi and J. R. Long, Nature, 2015, 527, 357–361 CrossRef PubMed.
- C. Serre, F. Millange, S. Surblé and G. Férey, Angew. Chem., Int. Ed., 2004, 43, 6285–6289 CrossRef PubMed.
- C. Mellot-Draznieks, C. Serre, S. Surblé, N. Audebrand and G. Férey, J. Am. Chem. Soc., 2005, 127, 16273–16278 CrossRef PubMed.
- C. Serre, C. Mellot-Draznieks, S. Surblé, N. Audebrand, Y. Filinchuk and G. Férey, Science, 2007, 315, 1828–1831 CrossRef PubMed.
- U. Stoeck, S. Krause, V. Bon, I. Senkovska and S. Kaskel, Chem. Commun., 2012, 48, 10841–10843 RSC.
- S. Krause, V. Bon, I. Senkovska, U. Stoeck, D. Wallacher, D. M. Többens, S. Zander, R. S. Pillai, G. Maurin, F.-X. Coudert and S. Kaskel, Nature, 2016, 532, 348–352 CrossRef.
- J. D. Evans, L. Bocquet and F.-X. Coudert, Chem, 2016, 1, 873–886 Search PubMed.
- C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526 CrossRef PubMed.
- T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem. – Eur. J., 2004, 10, 1373–1382 CrossRef PubMed.
- D. Li and K. Kaneko, Chem. Phys. Lett., 2001, 335, 50–56 CrossRef.
- H. Kajiro, A. Kondo, K. Kaneko and H. Kanoh, Int. J. Mol. Sci., 2010, 11, 3803–3845 CrossRef PubMed.
- R. M. P. Colodrero, A. Cabeza, P. Olivera-Pastor, A. Infantes-Molina, E. Barouda, K. D. Demadis and M. A. G. Aranda, Chem. – Eur. J., 2009, 15, 6612–6618 CrossRef CAS PubMed.
- D. Fairen-Jimenez, S. A. Moggach, M. T. Wharmby, P. A. Wright, S. Parsons and T. Düren, J. Am. Chem. Soc., 2011, 133, 8900–8902 CrossRef CAS PubMed.
- M. Cavallo, C. Atzori, M. Signorile, F. Costantino, D. M. Venturi, A. Koutsianos, K. A. Lomachenko, L. Calucci, F. Martini, A. Giovanelli, M. Geppi, V. Crocellà and M. Taddei, J. Mater. Chem. A, 2023, 11, 5568–5583 RSC.
- M. Taddei and C. Petit, Mol. Syst. Des. Eng., 2021, 6, 841–875 RSC.
- T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocellà, F. Giordanino, S. O. Odoh, W. S. Drisdell, B. Vlaisavljevich, A. L. Dzubak, R. Poloni, S. K. Schnell, N. Planas, K. Lee, T. Pascal, L. F. Wan, D. Prendergast, J. B. Neaton, B. Smit, J. B. Kortright, L. Gagliardi, S. Bordiga, J. A. Reimer and J. R. Long, Nature, 2015, 519, 303–308 CrossRef CAS PubMed.
- G. K. H. Shimizu, R. Vaidhyanathan and J. M. Taylor, Chem. Soc. Rev., 2009, 38, 1430–1449 RSC.
- K. J. Gagnon, H. P. Perry and A. Clearfield, Chem. Rev., 2012, 112, 1034–1054 CrossRef CAS PubMed.
- S. R. Miller and P. A. Wright, Encyclopedia of Inorganic and Bioinorganic Chemistry, 2011 Search PubMed.
- G. Yücesan, Y. Zorlu, M. Stricker and J. Beckmann, Coord. Chem. Rev., 2018, 369, 105–122 CrossRef.
- S. J. I. Shearan, N. Stock, F. Emmerling, J. Demel, P. A. Wright, K. D. Demadis, M. Vassaki, F. Costantino, R. Vivani, S. Sallard, I. Ruiz Salcedo, A. Cabeza and M. Taddei, Crystals, 2019, 9, 270 CrossRef CAS.
- G. Alberti, M. Casciola, U. Costantino and R. Vivani, Adv. Mater., 1996, 8, 291–303 CrossRef CAS.
- A. Clearfield and Z. Wang, J. Chem. Soc., Dalton Trans., 2002, 2937–2947 RSC.
- A. Clearfield and K. D. Demadis, Metal Phosphonate Chemistry: From Synthesis to Applications, Royal Society of Chemistry, 2011 Search PubMed.
- D. N. Dybtsev, H. Chun and K. Kim, Angew. Chem., Int. Ed., 2004, 43, 5033–5036 CrossRef CAS.
- F. ZareKarizi, M. Joharian and A. Morsali, J. Mater. Chem. A, 2018, 6, 19288–19329 RSC.
- S. Henke, A. Schneemann, A. Wütscher and R. A. Fischer, J. Am. Chem. Soc., 2012, 134, 9464–9474 CrossRef CAS.
- S. Henke, A. Schneemann and R. A. Fischer, Adv. Funct. Mater., 2013, 23, 5990–5996 CrossRef CAS.
- G. F. Turner, S. C. McKellar, D. R. Allan, A. K. Cheetham, S. Henke and S. A. Moggach, Chem. Sci., 2021, 12, 13793–13801 RSC.
- G. Alberti, R. Vivani, F. Marmottini and P. Zappelli, J. Porous Mater., 1998, 5, 205–220 CrossRef CAS.
- R. M. P. Colodrero, P. Olivera-Pastor, E. R. Losilla, D. Hernández-Alonso, M. A. G. Aranda, L. Leon-Reina, J. Rius, K. D. Demadis, B. Moreau, D. Villemin, M. Palomino, F. Rey and A. Cabeza, Inorg. Chem., 2012, 51, 7689–7698 CrossRef CAS.
- G. Alberti, U. Costantino, F. Marmottini, R. Vivani and P. Zappelli, Angew. Chem., Int. Ed. Engl., 1993, 32, 1357–1359 CrossRef.
- G. Alberti, S. Murcia-Mascarós and R. Vivani, J. Am. Chem. Soc., 1998, 120, 9291–9295 CrossRef CAS.
- G. Alberti, E. Brunet, C. Dionigi, O. Juanes, M. J. de la Mata, J. C. Rodríguez-Ubis and R. Vivani, Angew. Chem., Int. Ed., 1999, 38, 3351–3353 CrossRef CAS.
- C. Serre, J. A. Groves, P. Lightfoot, A. M. Z. Slawin, P. A. Wright, N. Stock, T. Bein, M. Haouas, F. Taulelle and G. Férey, Chem. Mater., 2006, 18, 1451–1457 CrossRef CAS.
- P. L. Llewellyn, M. Garcia-Rates, L. Gaberová, S. R. Miller, T. Devic, J.-C. Lavalley, S. Bourrelly, E. Bloch, Y. Filinchuk, P. A. Wright, C. Serre, A. Vimont and G. Maurin, J. Phys. Chem. C, 2015, 119, 4208–4216 CrossRef CAS.
- M. Taddei, F. Costantino and R. Vivani, Inorg. Chem., 2010, 49, 9664–9670 CrossRef CAS.
- J. P. S. Mowat, J. A. Groves, M. T. Wharmby, S. R. Miller, Y. Li, P. Lightfoot and P. A. Wright, J. Solid State Chem., 2009, 182, 2769–2778 CrossRef CAS.
- R. Vivani, F. Costantino, U. Costantino and M. Nocchetti, Inorg. Chem., 2006, 45, 2388–2390 CrossRef CAS.
- F. Costantino, A. Donnadio and M. Casciola, Inorg. Chem., 2012, 51, 6992–7000 CrossRef CAS PubMed.
- D. A. Levenson, J. Zhang, P. M. J. Szell, D. L. Bryce, B. S. Gelfand, R. P. S. Huynh, N. D. Fylstra and G. K. H. Shimizu, Chem. Mater., 2020, 32, 679–687 CrossRef CAS.
- M. Taddei, F. Costantino, A. Ienco, A. Comotti, P. V. Dau and S. M. Cohen, Chem. Commun., 2013, 49, 1315–1317 RSC.
- R. Köferstein, M. Arnold and C. Robl, Z. Anorg. Chem., 2016, 642, 1126–1132 CrossRef.
- R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391 CrossRef CAS.
- B. Zdravkov, J. Čermák, M. Šefara and J. Janků, Open Chem., 2007, 5, 385–395 CrossRef CAS.
- D. H. Everett, Pure Appl. Chem., 1972, 31, 577–638 CrossRef.
- W. L. Queen, M. R. Hudson, E. D. Bloch, J. A. Mason, M. I. Gonzalez, J. S. Lee, D. Gygi, J. D. Howe, K. Lee, T. A. Darwish, M. James, V. K. Peterson, S. J. Teat, B. Smit, J. B. Neaton, J. R. Long and C. M. Brown, Chem. Sci., 2014, 5, 4569–4581 RSC.
- S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- D.-D. Zhou, C.-T. He, P.-Q. Liao, W. Xue, W.-X. Zhang, H.-L. Zhou, J.-P. Zhang and X.-M. Chen, Chem. Commun., 2013, 49, 11728–11730 RSC.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CrossRef CAS.
- K. A. Cychosz, R. Guillet-Nicolas, J. García-Martínez and M. Thommes, Chem. Soc. Rev., 2017, 46, 389–414 RSC.
- T. Islamoglu, K. B. Idrees, F. A. Son, Z. Chen, S.-J. Lee, P. Li and O. K. Farha, J. Mater. Chem. A, 2022, 10, 157–173 RSC.
- A. Boutin, F.-X. Coudert, M.-A. Springuel-Huet, A. V. Neimark, G. Férey and A. H. Fuchs, J. Phys. Chem. C, 2010, 114, 22237–22244 CrossRef CAS.
- N. B. Colthup, L. H. Daly and S. E. Wiberley, Introduction to Infrared and Raman Spectroscopy, Academic Press, 3rd edn, 1990 Search PubMed.
- S. R. Miller, G. M. Pearce, P. A. Wright, F. Bonino, S. Chavan, S. Bordiga, I. Margiolaki, N. Guillou, G. Férey, S. Bourrelly and P. L. Llewellyn, J. Am. Chem. Soc., 2008, 130, 15967–15981 CrossRef CAS.
- A. Airi, A. Damin, J. Xie, U. Olsbye and S. Bordiga, Catal. Sci. Technol., 2022, 12, 2775–2792 RSC.
- J. B. DeCoste, G. W. Peterson, B. J. Schindler, K. L. Killops, M. A. Browe and J. J. Mahle, J. Mater. Chem. A, 2013, 1, 11922–11932 RSC.
- M. Signorile, J. G. Vitillo, M. D’Amore, V. Crocellà, G. Ricchiardi and S. Bordiga, J. Phys. Chem. C, 2019, 123, 17214–17224 CrossRef CAS.
- S. Bordiga, L. Regli, F. Bonino, E. Groppo, C. Lamberti, B. Xiao, P. S. Wheatley, R. E. Morris and A. Zecchina, Phys. Chem. Chem. Phys., 2007, 9, 2676–2685 RSC.
- K. I. Hadjiivanov, D. A. Panayotov, M. Y. Mihaylov, E. Z. Ivanova, K. K. Chakarova, S. M. Andonova and N. L. Drenchev, Chem. Rev., 2021, 121, 1286–1424 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- R. D’Amato, A. Donnadio, M. Carta, C. Sangregorio, D. Tiana, R. Vivani, M. Taddei and F. Costantino, ACS Sustainable Chem. Eng., 2019, 7, 394–402 CrossRef.
- D. M. Poojary, B. Zhang and A. Clearfield, J. Am. Chem. Soc., 1997, 119, 12550–12559 CrossRef CAS.
- D. I. Arnold, X. Ouyang and A. Clearfield, Chem. Mater., 2002, 14, 2020–2027 CrossRef CAS.
- V. Crocellà, C. Atzori, G. Latini and M. Signorile “Kit for volumetric measurements of gas adsorption”, no. 102020000005014 filed on 9/3/2020 and granted on 29/3/2022.
- S. Lee, J. H. Lee and J. Kim, Korean J. Chem. Eng., 2018, 35, 214–221 CrossRef CAS.
- C. Atzori, N. G. Porcaro, V. Crocellà, F. Bonino, M. Signorile, P. Antico, C. Daniel, V. Venditto, C. A. Grande and S. Bordiga, Microporous Mesoporous Mater., 2022, 341, 112106 CrossRef CAS.
- A.-C. Dippel, H.-P. Liermann, J. T. Delitz, P. Walter, H. Schulte-Schrepping, O. H. Seeck and H. Franz, J. Synchrotron Radiat., 2015, 22, 675–687 CrossRef CAS PubMed.
- A. P. Hammersley, J. Appl. Crystallogr., 2016, 49, 646–652 CrossRef CAS.
- A. Erba, J. Baima, I. Bush, R. Orlando and R. Dovesi, J. Chem. Theory Comput., 2017, 13, 5019–5027 CrossRef CAS PubMed.
- https://www.crystal.unito.it/Manuals/crystal17.pdf .
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- D. Vilela Oliveira, J. Laun, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2019, 40, 2364–2376 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- P. Valiron, Á. Vibók and I. Mayer, J. Comput. Chem., 1993, 14, 401–409 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00356f |
| This journal is © The Royal Society of Chemistry 2024 |