Open Access Article
Open Access ArticleInsight into the K channel's selectivity from binding of K+, Na+ and water to N-methylacetamide†
Mark J.
Stevens
 * and
Susan L. B.
Rempe
* and
Susan L. B.
Rempe
 *
*
Center for Integrated Nanotechnologies, Sandia National Laboratories, Albuquerque, NM 87185, USA. E-mail: msteve@sandia.gov; slrempe@sandia.gov
First published on 21st July 2023
Abstract
In potassium channels that conduct K+ selectively over Na+, which sites are occupied by K+ or water and the mechanism of selectivity are unresolved questions. The combination of the energetics and the constraints imposed by the protein structure yield the selective permeation and occupancy. To gain insight into the combination of structure and energetics, we performed density functional theory (DFT) calculations of multiple N-methyl acetamide (NMA) ligands binding to K+ and Na+, relative to hydrated K+ and Na+. NMA is an analogue of the amino acid backbone and provides the carbonyl binding to the ions that occurs in most binding sites of the K+ channel. Unconstrained optimal structures are obtained through geometry optimization calculations of the NMA ligand binding. The complexes formed by 8 NMA binding to the cations have the O atoms positioned in nearly identical locations as the O atoms in the selectivity filter. The transfer free energies between bulk water and K+ or Na+ bound to 8 NMA are almost identical, implying there is no selectivity by a single site. For water optimized with 8 NMA, binding is weak and O atoms are not positioned as in the K+ channel selectivity filter, suggesting that the ions are much more favored than water. Optimal structures of 8 NMA binding with two cations (K+ or Na+) are stable and have lower binding free energy than the optimal structures with just one cation. However, in the Na+ case, the optimal structure deforms and does not match the K+ channel; that is, two bound Na+ are destabilizing. In contrast, the two K+ structure is stabilized and the selectivity free energy favors K+. Overall, this study shows that binding site occupancy and the mechanism for K+ selectivity involves multiple K+ binding in multiple neighboring layers or sites of the K+ channel selectivity filter.
1 Introduction
Potassium (K+) channels are an important family of membrane proteins that regulate cellular processes.1 A key aspect of potassium channels is the rapid and selective conduction of K+ while excluding the smaller Na+. Because of their significance to health and their exceptional properties, many studies of K+ channel selectivity and conduction mechanisms have been performed.1–15 The crystal structure of a model potassium channel, KcsA,16 provides the basis for understanding the mechanisms and shows electron density in the four continuous ion binding sites of the selectivity filter (SF), which is highly conserved among structurally diverse K+ channels. Furthermore, experiments on mutant ion channels demonstrated that all four binding sites of the SF are necessary for selecting K+ over Na+.17Despite their extensive study, mechanistic questions about K+ channels still remain.18 In particular, the occupancy of each binding site is unclear since distinguishing between K+, Na+, and water in crystallographic structures is challenging. One hypothesis for the occupancy is that K+ only binds at two non-adjacent sites at a time to avoid strong electrostatic repulsion between ions.16,19 In this two-ion hypothesis, a “soft knock-on” mechanism results in two alternating configurations, K+–water–K+–water and water–K+–water–K+, that produce the four peaks in the electron density.16,19 In support of that mechanism, a two-dimensional infrared (2D-IR) spectroscopy study found that only the alternating ion–water configurations are compatible with the spectra from the selectivity filter20 although a later study challenged that interpretation.21 A second hypothesis of ion occupancy has been presented that has neighboring sites occupied by K+.22 Data that support this “direct knock-on” mechanism include (i) a reanalysis of crystallography data showing the total occupancy is close to four,22 and (ii) anomalous X-ray diffraction on a mutant K+ channel that shows full occupancy of the SF by K+.23
Similar to the experimental studies, molecular dynamics (MD) simulations also give inconsistent results on ion occupancy. Some studies support the soft knock-on mechanism of conduction involving alternating occupancy by ions and water in the SF, while other MD studies instead support ion conduction without water.21,22 However, MD simulations are not expected to resolve this question as the results are sensitive to force field parameters.24–27 Furthermore, the importance of polarization, to allow the protein and water to respond to changes in the electric field generated by the presence of ions, has been well-recognized.14,18,28–32 Despite these findings, previous MD simulations of KcsA predominantly used fixed-charge (nonpolarizable) force fields.2 Recently, and for the first time, a polarizable force field was developed from quantum chemistry studies on small molecular systems, and applied in MD simulations to investigate ion occupancy in KcsA.15 That study reported support for a single vacancy mechanism of ion conduction, which resembles the direct knock-on mechanism in terms of favoring the occupation of neighboring ion binding sites.15 Free energy calculations carried out by Jing et al. also offered the first computational support for full ion occupancy,15 as reported in recent anomalous X-ray diffraction studies.23 While the occupancy of a single ion in a single binding site has been studied extensively with density functional theory (DFT), a quantum chemistry study of ion occupancy in the full selectivity filter is still missing.7,8,12,14,28,31,33–38
Given that selectivity requires all four sites in K+ channel selectivity filters,17 the mechanism by which the multiple sites combine to achieve selectivity is an essential part of understanding the K+ channel. Most quantum chemistry studies of the K+ channel selectivity have addressed the difference between K+ and Na+ in only a single site of the channel, as mentioned above. Selectivity for K+ in a single site must be weak to be consistent with the experimental data. While features like ion coordination and binding site flexibility for the individual site are clearly relevant to selective binding, they cannot play a dominant role for selective transport or only one site would be needed in the selectivity filter. In the context of understanding the transport selectivity due to multiple sites, the occupancy of these sites plays an important role because the interactions between the sites is a contributing factor to the overall free energy.
The binding of cations, particularly K+ and Na+, to carbonyls is a key part of the K+ channel selectivity filter (Fig. 1). Fig. 1 shows the selectivity filter for the 1K4C crystal structure, with labels for the residues and the K+ binding sites. To carry-out quantum chemistry calculations, surrogate carbonyl-containing ligands have been studied.7,8,12,14,28,31,33–36,39–41 In particular, a number of works have simulated systems with N-methyl acetamide (NMA) because the K+ channel amino acid backbone corresponds to NMA.40–42 Experiments have also probed the interactions between NMA and ions.43,44 Here, using contemporary computing capability, we present results of density functional theory calculations for NMA. We are able to treat multiple ligands, corresponding to a single layer and two layers in the selectivity filter. Moreover, we go beyond systems with a single cation and address two cations, which provides distinguishing results between K+ and Na+ and addresses occupancy issues in the selectivity filter with a quantum chemistry approach.
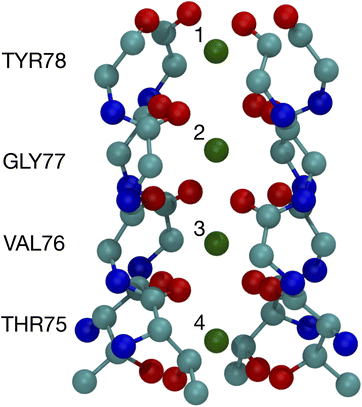 | ||
| Fig. 1 Image of the selectivity filter in the 1K4C crystal structure of the K+ channel. The backbones of residues 75 to 78 are shown along with the K+ binding sites, which are numbered according to the site index. All of residue 75 is shown since the hydroxyl oxygens (THR75:OG) bind as well as the backbone carbonyls. The atom colors are: O red, C cyan, N blue, and K+ green. | ||
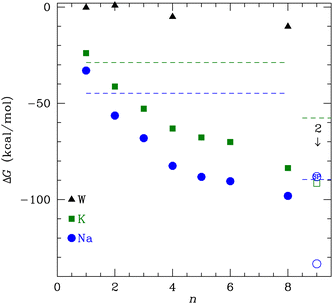
In this study, we calculate the optimal structures and binding free energies for a varying number of NMA binding separately to K+ or Na+. We perform these calculations using a basis set and functional well matched for the strong electrostatic interactions and that treats van der Waals interactions, which are important for systems with many ligands.29 The 8-NMA structure binding to a single K+ or Na+ corresponds well to layers of the carbonyls in the K+ channel selectivity filter. The binding free energies are lowest for Na+, but the free energy of transfer from bulk water, which determines the ligand site occupancy, is small (<1.5 kcal mol−1) and switches to favoring K+ at 8 NMA. Furthermore, calculations with multiple (two) neighboring cations are stable, with lower binding free energies, and suggest a preference for K+.
2 Methods
The local clustering of N-methyl acetamide ligands about an ion corresponds to the following reaction,| X + nNMA ⇄ X(NMA)n, | (1) |
We calculated the free energy change (ΔG) for the reactions in eqn (1) using the Gaussian 16 quantum chemistry package.49 The geometry optimizations were carried out in the gas phase using the density functional theory (DFT) approach with the hybrid ωB97X-D approximation to the exchange–correlation energy.50 This choice is based on previous work on DFT of ionic systems29,51–53 and treats the van der Waals interactions, which are important for the large clusters studied here. For the basis sets, we used Dunning's correlation-consistent polarized double-zeta basis sets augmented with diffuse functions (aug-cc-pvDz).54,55 The double zeta basis represents a good compromise between accuracy and calculation speed.53 The correlation-consistent basis sets were developed to describe core–core and core–valence electron correlation effects in molecules, and previously have been shown to be accurate for a single carboxylate.56
To obtain free energies, we performed a normal mode frequency analysis57 using the same level of theory as for optimization. Stable structures for which the forces are zero and frequencies positive confirmed true minima on the potential energy surfaces. The thermodynamic analysis yielded zero point energies and thermal corrections to the electronic energy due to translational, electronic, and vibrational motions calculated at a temperature of 298 K and pressure of 1 atm.
To calculate the free energy change for the reactions in eqn (1), we calculated the difference in free energy between the product (p) and the sum of the reactants (r) in stoichiometric proportions (nr):
| ΔG = Gp − ΣnrGr. | (2) |
The structures resulting from these calculations will be compared to the binding sites of the selectivity filter in the KcsA K+ channel with PDB ID 1K4C.16 We use the labeling of this PDB entry for the residues and atoms in discussing the K+ channel structure.
3 Results
The binding free energy in Fig. 2 monotonically decreases with increasing number of NMA ligands, n, for both K+ and Na+ to n = 8. This behavior contrasts to the binding of water to these cations, where a minimum occurs at 4 tetrahedral waters.58 A major difference between water and NMA ligands is the binding among the NMA molecules themselves, as will be shown below in the discussion of the structures. For n ≥ 4, the NMA molecules H-bond to each other in the optimized structures, and the H-bonding makes a significant contribution to the binding free energy. Other structures with fewer H-bonds have free energies that are higher (less favorable) by several kcal mol−1. The figure (Fig. 2) shows that ΔG is lower for Na+ than for K+ (see Table 1). When water replaces the cations, the ΔG magnitude is much smaller than for the cations. In fact, for n = 1 and 2, ΔG is within 1 kcal mol−1 of zero. The electrostatic binding of the cations is much stronger than the hydrogen bonding of water and can be shared among many more O atoms, yielding distinctly different structures, as will be shown below.| n | ΔG (K+) | ΔG (Na+) | ΔG (W) |
|---|---|---|---|
| 1 | −23.9 | −33.0 | −0.3 |
| 2 | −41.3 | −56.4 | 0.8 |
| 3 | −52.8 | −68.1 | |
| 4 | −63.1 | −82.5 | −5.1 |
| 5 | −67.8 | −88.3 | |
| 6 | −70.1 | −90.5 | |
| 8 | −83.6 | −98.1 | −10.1 |
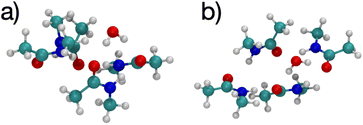
The K+ channel comprises layers of 4 amide carbonyls in a square configuration that forms part of the selectivity filter. The optimal structures for K+ and Na+ binding to 4 NMA both have the carbonyl O atoms forming a square in a single plane (see Fig. 3), and each of the carbonyl O atoms bind to the respective cation. Hydrogen bonds among the NMA help stabilize the square carbonyl O configuration. The amines in each NMA form a hydrogen bond to a carbonyl in the neighboring NMA. The H-bond connection among all the NMA stabilizes the planar structure.
 | ||
| Fig. 3 Images61,62 of K+ (a, b) and Na+ (c, d) complexes binding to 4 NMA ligands showing top view (a, c) and side view (b, d). The atom colors are: O red, C cyan, N blue, H white, K green and Na purple. | ||
While water forms a tetrahedral coordination with either cation, a tetrahedral coordination by 4 NMA would not allow hydrogen bonding among the NMA. As noted above, n = 4 structures at metastable minima with tetrahedral coordination have fewer total H-bonds and, thus, ΔG is higher (less favorable) by several kcal mol−1. The cyclic hydrogen bonding provides a large contribution to the free energy that more than compensates for the non-tetrahedral coordinations of the cations.
This planar n = 4 structure forms the basis for the n = 8 structure that, as we will show, has the O atoms positioned in nearly identical locations as the O atoms in the layers of the K+ channel selectivity filter. This positioning occurs in the NMA cluster, in part, due to the hydrogen bonding among the NMA; in the protein channel, the folded structure yields the O atom positioning.
Fig. 3 shows a key difference between the K+ and Na+ optimal structures: the K+ is offset above the plane of the O atoms by 0.94 Å. The NMA molecules in the K+ structure are slightly tilted with respect to the plane formed by the O atoms. In contrast, all the heavy atoms lie in the same plane in the Na+ structure. In general, K+ will have a larger separation when bonded to O than Na+, similar to the structural differences between the ions in liquid water (2.4 Å vs. 2.7 Å).14,58–60 For n = 4 (Fig. 3), the carbonyl O–K+ separation is 2.66 Å, and the carbonyl O–Na+ separation is 2.33 Å. The O–O separations along the square sides for K+ are 3.50 Å and for Na+ are 3.29 Å. The larger O–K+ separation is achieved by a slightly larger square of O and the displacement of the K+ atom above the plane of the O atoms.
Fig. 4 shows images of a single water molecule binding to 4 NMA, which differs significantly compared with the cation structures. In the water complex, the NMA molecules are not in a plane although the NMA O atoms are planar (see Fig. 4(a)). Some amines form hydrogen bonds to the NMA O atoms, but none bond to water. Overall, there is no geometry for which all possible hydrogen bond pairs occur. Some hydrogen bondable atoms in the water complex do not have a partner. Consequently, the water complex structure differs from the cation complex structure. The charge of the cations results in equal binding to all 4 of the NMA O, but the water can only hydrogen bond equally to 2 NMA. Thus, the cation configurations have the O atoms in a square with all O atoms equivalent, but the water configuration has the O atoms in a quadrilateral because the binding among the O atoms are not equivalent. In the cation configurations, the amine H (positively charged) need to be as far as possible from the cation, but still allow the amine–O to hydrogen bond. This constraint forces the NMA molecules to be mostly planar. In contrast, the water configuration does not have this constraint, and the NMA molecules have more rotational freedom.
The lowest free energy configuration is for n = 8, and the positioning of the carbonyl O atoms corresponds well with carbonyls in the K+ channel selectivity filter (Fig. 1). For K+, the optimal 8-NMA structure is found by starting with the n = 4 structure and copying the 4 NMAs, doing a mirror image flip, translating to a position above the K+ by the same distance, and rotating such that the O atoms in one layer lie under/over the amine H atom of the layer above/under, respectively. Basically the same procedure was done for the Na+ system, but the spacing between the two layers had to be estimated since Na+ resides in the plane at n = 4.
The optimized structures for the n = 8 systems (Fig. 5) are similar in layout, with the main difference being that the separation distances for K+ are larger than for Na+. The positioning of the O atoms is close to two of the layers in the selectivity filter of the K+ channel. Fig. 6 shows the backbone atoms for residues VAL76 and GLY77 of KcsA that contain site 2 for K+.16 Squares of carbonyl O atoms are in a plane for each residue and the combination forms an octagon, when viewed from the top, that appears similar to the n = 8 structures in Fig. 5.
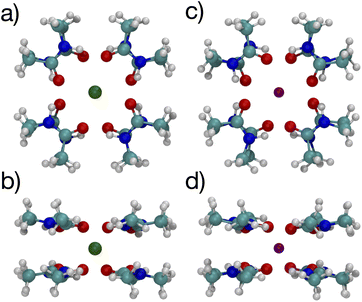 | ||
| Fig. 5 Images of K+ (left) and Na+ (right) complexes binding to 8 NMA ligands showing two viewpoints. | ||
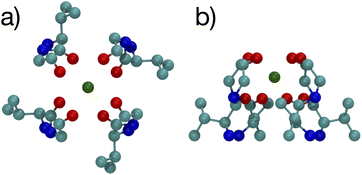 | ||
| Fig. 6 Images of the backbones of Val76 and Gly77 residues bound to K+ in the 1K4C crystal structure of the K+ channel viewed from (a) down the channel, and (b) the side.16 | ||
The separations for binding sites 1, 2 and 3 in the K+ channel crystal structure 1K4C match well with the cation–O distances for both K+ and Na+ in the 8-NMA optimized structures. In Table 2, the distances between atom pairs for the K+ and Na+ binding to 8 NMA are given, respectively. The average K+–O separation is 2.833 Å and the average Na+–O separation is 2.680 Å. In the 1K4C crystal structure, the THR75:OG separation from K+ is 2.883 Å, and the VAL76:O separation is 2.857 Å; both of these match the K+:O distance in the 8 NMA structure. However, the THR75:O is 2.710 Å and GLY77:O is 2.722 Å from K+, which better match the Na+:O distance in the 8-NMA structure. For the n = 8 K+ structure, the root mean squared deviation (rmsd) between the 8 NMA O atoms and the O atom in the binding sites 1, 2 and 3 of the selectivity filter are 0.24, 0.45 and 0.21, respectively. For the Na+ and 8-NMA case, the rmsd are 0.45, 0.20, and 0.47, respectively. Thus, these layers in the selectivity filter have O positioning that closely resembles the 8-NMA structures.
| Atom 1 | Atom 2 | K+ | Na+ |
|---|---|---|---|
| X | O | 2.833 | 2.681 |
| X | O | 2.832 | 2.679 |
| O | O | 3.487 | 3.295 |
| O | O | 3.488 | 3.295 |
The position of the O atoms about site 4 differs in geometry from the other layers. The O atoms stack above each other such that the view along the axis of the channel is a square of O atoms, not the octagon of the other layers (see Fig. S3†). This site is not matched by the NMA structures.
The spacings between the K+ sites in the crystal are 3.40, 3.21 and 3.34 Å. For the 8-NMA structure, the spacing between the planes, determined from the N–C separation, is 3.20 Å for K+ and 3.14 Å for Na+ occupancy. The larger spacing for K+ better matches the K+ channel, but the spacing between layers of NMA could change in calculations of 3 or 4 layers, which are outside the capability of the present calculations.
The optimized structure for n = 8 NMA and water does not form a layered structure for the NMA carbonyls, as shown in Fig. 7. Water can only H-bond to two carbonyl O atoms and cannot order the 8 NMA carbonyls the way the cations can. Two other H-bonds are made to the water by amines, which removes them from forming H-bonds with other NMA and further pushes the structure away from a layered geometry. The free energy of binding for water is much weaker than the cations, at only −10.1 kcal mol−1 (see Table 1). This result suggests that the likelihood of water in such a binding site will be low relative to either K+ or Na+. With respect to the K+ channel, the binding energy for water in sites 1, 2 or 3 of the selectivity filter will be small and much lower than for K+ or Na+. Thus, in the K+ channel, water will also have a low likelihood of binding.
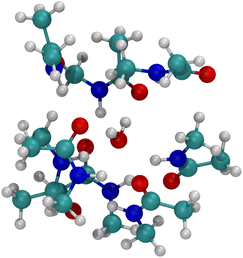 | ||
| Fig. 7 Image of H2O binding to 8 NMA ligands. H-bonds form between water and NMA. No layered structure exists in the optimized geometry. | ||
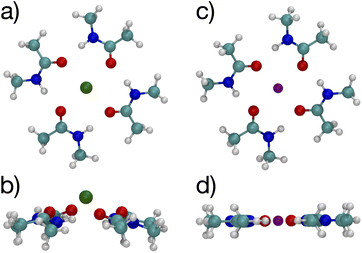
Since multiple cations occupying neighboring binding sites in the selectivity filter is one hypothesized scenario, we performed geometry optimization and free energy binding calculations for two (2) cations. The binding free energies for 8 NMA and 2 cations are shown in Fig. 2 as open data points at n = 9 to distinguish them from the single cation data. For either cation, these simulations started from the structures in Fig. 5, with an additional cation placed inline with the already present cation and above the top layer of 4 NMA. For K+ binding, the free energy of the optimized structure is below the free energy for 8 NMA and a single cation, implying that the two-cation structure is more stable. The K+ case preserves the layered structure, with the cation in a central channel (Fig. 8a and b). Thus, in the idealized environment of the gas phase, the repulsion between two cations does not destabilize the K+ structure, but instead stabilizes the structure. This stabilization implies that the presence of multiple K+ in the K+ channel is actually stabilizing.
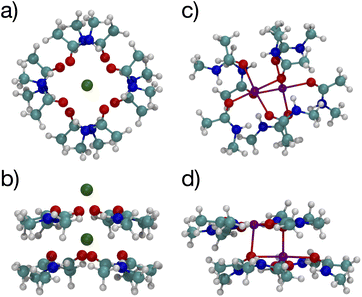 | ||
| Fig. 8 Images of two K+ (a, b) or Na+ (c, d) binding to 8 NMA ligands showing top view (a, c) and side view (b, d). | ||
In contrast, the structure in the Na+ case changes significantly (Fig. 8c and d). The Na+ become 5-fold coordinated by a lateral shifting of the NMA layers relative to each other, and each Na+ atom moves to the central location within the NMA plane, similar to the 4-NMA structure. This Na+ complex structure does not match the K+ and O positioning of the K+ channel. This structural shift is consistent with the unconstrained, preferred local binding of O atoms by Na+ preferring a smaller coordination compared with K+ when in a crowded binding site surrounded by a low dielectric environment.7,8,12,14,33,35 In the addition of a second Na+ to the 8 NMA complex, the H-bond constraints that yield the layers of 4 NMA remain, but now the positioning of the Na+ and the relative positioning of the layers can and do adjust to satisfy better the Na+ preferred binding geometry (Fig. 8c and d). The binding free energy in this distorted structure, relative to the crystal structure, is much more favorable than the other binding sites (−133.4 kcal mol−1).
To determine the free energy of Na+ in an NMA complex that matches the K+ channel structure, we carry out a single point calculation of a two-Na+ structure that fixes the positions of the layered structure to one that has low rmsd with respect to the K+ channel (see ESI†). Specifically, we use the single Na+ structure (Fig. 5c and d) and place the second Na+ 3.4 Å above the first one, as in the K+ channel crystal structure. Since this is a single point calculation, we have to estimate the free energy, which we do by adding the enthalpy from the calculation to the entropy term from the fully optimized structure. For this structure, the binding free energy is −88.1 kcal mol−1 (see Fig. 2), which is slightly above the optimized two-K+ structure (ΔG = −91.6 kcal mol−1) and well above the optimized two-Na+ structure in the 8 NMA complex (−133.4 kcal mol−1). This result suggests that multiple cations might destabilize neighboring Na+ in binding sites with the KcsA architecture.
The change in free energy to transfer an ion between the bulk solution and the ligand binding site is the quantity that determines the preference for binding between K+ and Na+. We can use the ΔG(X+:NMA) for X+ = K+ and Na+ in Fig. 2 to calculate the free energy of transfer, ΔΔG. Earlier, we calculated the free energy change for both cations binding to water using the same functional and basis set as used here.63 The free energy of transfer is then
| ΔΔG = ΔG(X+:nNMA) − ΔG(X+:4H2O) | (3) |
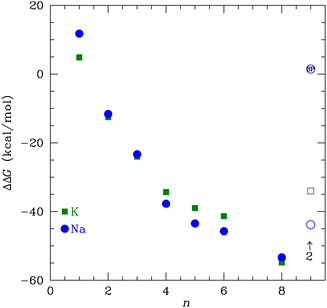 | ||
| Fig. 9 The transfer free energy ΔΔG from eqn (3) as a function of the number of NMA ligands, n, for K+ (green squares) and Na+ (blue circles). The solid points are for single cations and the open points are for 2 cations, as indicated. The Na+ point with SP inside is the single point calculation within the channel structure. See text and ESI for details.† | ||
If we consider multiple layers of NMA that have m cations corresponding to occupying m sites in the K+ channel, then the transfer free energy is
| ΔΔG = ΔG(Xm+:nNMA) − mΔG(X+:4H2O) | (4) |
4 Conclusions
We used DFT to calculate the geometry-optimized structures for K+, Na+, and water binding to multiple N-methyl acetamide molecules. In the fully relaxed 4-fold NMA structures, the carbonyl O atoms form a square binding geometry to the cation in the middle. The optimized 8-fold NMA ligand structure has the cations in-between two layers of the 4-fold structure. In these 8-fold NMA ligand structures with a single cation, the NMA carbonyl O atoms take nearly identical positions to the carbonyl O atom in the K+ channel selectivity filter.The 8-NMA structures have the lowest free energy as a function of the number of NMA, with Na+ being lower than K+. A water molecule in the 8 NMA structure has a small binding free energy, implying that either K+ or Na+ binding is much more favored over water. Calculations of the transfer free energy between bulk water and the ligand binding site find K+ preferred over Na+ in the maximally crowded n = 8 binding site, although the difference is small. These results imply that a single site in the K+ channel is insufficient to yield high selectivity of K+ over Na+, which is consistent with experiments that demonstrated that fewer than four binding sites do not distinguish between K+ and Na+.
Calculations for 8 NMA and 2 cations suggest that multiple layers of carbonyl O atoms and adjacent occupancy of K+ yields clear selectivity of K+ over Na+. The optimal structure for 2 K+ and 8 NMA has a lower free energy than with just one K+, implying that neighboring K+ in the K+ channel selectivity filter are not only possible, but stabilizing and favored. In contrast, the optimal structure for 2 Na+ results in a rearrangement of the NMA layers relative to the single Na+ structure that yields O positions substantially different from the K+ channel. This result implies that two Na+ are destabilizing. Single point calculations for 2 Na+, in a geometry corresponding to the K+ channel structure, have a slightly larger free energy than the optimized K+ value. As a consequence, the transfer free energy between water and the binding site has a strong preference for K+ over Na+. Altogether, these results suggest that the multi-ion, multi-layer structure of the selectivity filter is important for selectivity of K+ over Na+.17 The selectivity comes from the sum of the free energies over all the sites, yielding a sufficiently more favorable total free energy for neighboring K+ than for Na+. Future work in this area that can treat multiple ions and multiple layers of the full selectivity filter using quantum chemistry approaches is clearly warranted, once it becomes computationally feasible.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. DOE's National Nuclear Security Administration under contract DE-NA-0003525. We gratefully thank Sandia's Laboratory-Directed Research and Development program for funding. The views expressed in the article do not necessarily represent the views of the U.S. DOE or the United States Government.Notes and references
- M. LeMasurier, L. Heginbotham and C. Miller, J. Gen. Physiol., 2001, 118, 303–314 CrossRef CAS PubMed.
- E. Flood, C. Boiteux, B. Lev, I. Vorobyov and T. W. Allen, Chem. Rev., 2019, 119, 7737–7832 CrossRef CAS.
- L. Guidoni, V. Torre and P. Carloni, Biochemistry, 1999, 38, 8599–8604 CrossRef CAS.
- L. Guidoni and P. Carloni, Biochim. Biophys. Acta, Biomembr., 2002, 1563, 1–6 CrossRef CAS PubMed.
- I. H. Shrivastava, D. P. Tieleman, P. C. Biggin and M. Sansom, Biophys. J., 2002, 83, 633–645 CrossRef CAS.
- F. I. Valiyaveetil, M. Leonetti, T. M. Muir and R. MacKinnon, Science, 2006, 314, 1004–1007 CrossRef CAS PubMed.
- S. Varma and S. B. Rempe, Biophys. J., 2007, 93, 1093–1099 CrossRef CAS.
- S. Varma, D. Sabo and S. B. Rempe, J. Mol. Biol., 2008, 376, 13–22 CrossRef CAS.
- G. Miloshevsky and P. Jordan, Biophys. J., 2008, 95, 3239–3251 CrossRef CAS PubMed.
- P. Fowler, K. Tai and M. Sansom, Biophys. J., 2008, 95, 5062–5072 CrossRef CAS PubMed.
- B. Roux, S. Bernèche, B. Egwolf, B. Lev, S. Y. Noskov, C. N. Rowley and H. Yu, J. Gen. Physiol., 2011, 137, 415–426 CrossRef CAS.
- S. Varma, D. M. Rogers, L. R. Pratt and S. B. Rempe, J. Gen. Physiol., 2011, 137, 479–488 CrossRef CAS.
- S. W. Lockless, J. Gen. Physiol., 2015, 146, 3–13 CrossRef CAS.
- M. I. Chaudhari, J. M. Vanegas, L. Pratt, A. Muralidharan and S. B. Rempe, Annu. Rev. Phys. Chem., 2020, 71, 461–484 CrossRef CAS.
- Z. Jing, J. A. Rackers, L. R. Pratt, C. Liu, S. B. Rempe and P. Ren, Chem. Sci., 2021, 12, 8920–8930 RSC.
- Y. Zhou, J. Morais-Cabral, A. Kaufman and R. MacKinnon, Nature, 2001, 414, 43–48 CrossRef CAS.
- M. G. Derebe, D. B. Sauer, W. Zeng, A. Alam, N. Shi and Y. Jiang, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 598–602 CrossRef CAS.
- A. Mironenko, U. Zachariae, B. L. de Groot and W. Kopec, J. Mol. Biol., 2021, 433, 167002 CrossRef CAS PubMed.
- J. Morais-Cabral, Y. Zhou and R. MacKinnon, Nature, 2001, 414, 37–42 CrossRef CAS.
- H. T. Kratochvil, J. K. Carr, K. Matulef, A. W. Annen, H. Li, M. Maj, J. Ostmeyer, A. L. Serrano, H. Raghuraman, S. D. Moran, J. L. Skinner, E. Perozo, B. Roux, F. I. Valiyaveetil and M. T. Zanni, Science, 2016, 353, 1040–1044 CrossRef CAS PubMed.
- W. Kopec, D. A. Köpfer, O. Vickery, A. Bondarenko, T. Jansen, B. L. de Groot and U. Zachariae, Nat. Chem., 2018, 10, 813–820 CrossRef CAS PubMed.
- D. A. Köpfer, C. Song, T. Gruene, G. M. Sheldrick, U. Zachariae and B. L. de Groot, Science, 2014, 346, 352–355 CrossRef.
- P. Langan, V. Vandavasi and K. Weiss, Nat. Commun., 2018, 9, 4540 CrossRef PubMed.
- F. T. Heer, D. J. Posson, W. Wojtas-Niziurski, C. M. Nimigean and S. Berneche, eLife, 2017, 6, e25844 CrossRef.
- S. Furini and C. Domene, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16074–16077 CrossRef CAS.
- V. Oakes, S. Furini and C. Domene, J. Chem. Theory Comput., 2020, 16, 794–799 CrossRef CAS PubMed.
- C. K. Lam and B. L. de Groot, J. Chem. Theory Comput., 2023, 19, 2574–2589 CrossRef CAS PubMed.
- S. Varma and S. B. Rempe, Biophys. J., 2010, 99, 3394–3401 CrossRef CAS.
- M. Soniat, D. M. Rogers and S. B. Rempe, J. Chem. Theory Comput., 2015, 11, 2958–2967 CrossRef CAS.
- X. Peng, Y. Zhang, H. Chu, Y. Li, D. Zhang, L. Cao and G. Li, J. Chem. Theory Comput., 2016, 12, 2973–2982 CrossRef CAS.
- M. I. Chaudhari and S. B. Rempe, J. Chem. Phys., 2018, 148, 222831 CrossRef PubMed.
- V. Ngo, H. Li, A. D. J. MacKerell, T. W. Allen, B. Roux and S. Noskov, J. Chem. Theory Comput., 2021, 17, 1726–1741 CrossRef CAS PubMed.
- S. Varma and S. B. Rempe, J. Am. Chem. Soc., 2008, 130, 15405–15419 CrossRef CAS.
- D. M. Rogers and S. B. Rempe, J. Phys. Chem. B, 2011, 115, 9116–9129 CrossRef CAS PubMed.
- D. M. Rogers, D. Jiao, L. Pratt and S. Rempe, Annu. Rep. Comput. Chem., 2012, 8, 71 CAS.
- M. Rossi, A. Tkatchenko, S. B. Rempe and S. Varma, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12978–12983 CrossRef CAS.
- M. J. Stevens and S. L. B. Rempe, J. Phys. Chem. B, 2016, 120, 12519–12530 CrossRef CAS PubMed.
- D. Gomez, L. R. Pratt, D. N. Asthagiri and S. B. Rempe, Acc. Chem. Res., 2022, 55, 2201–2212 CrossRef CAS PubMed.
- T. Dudev and C. Lim, J. Am. Chem. Soc., 2009, 131, 8092–8101 CrossRef CAS.
- H. Yu, C. L. Mazzanti, T. W. Whitfield, R. E. Koeppe, O. S. Andersen and B. Roux, J. Am. Chem. Soc., 2010, 132, 10847–10856 CrossRef CAS.
- J. Heyda, J. Vincent, D. Tobias, J. Dzubiella and P. Jungwirth, J. Phys. Chem. B, 2010, 114, 1213–1220 CrossRef CAS PubMed.
- S. Y. Noskov, S. Bernèche and B. Roux, Nature, 2004, 431, 830–834 CrossRef CAS.
- D. J. Miller and J. M. Lisy, J. Phys. Chem. A, 2007, 111, 12409–12416 CrossRef CAS.
- J. P. Beck, M.-P. Gaigeot and J. M. Lisy, Phys. Chem. Chem. Phys., 2013, 15, 16736–16745 RSC.
- L. R. Pratt and S. B. Rempe, in Quasi-Chemical Theory and Solvent Models for Simulations, ed. G. Hummer and L. R. Pratt, AIP Conference Proceedings, 1999, vol. 492, pp. 172–201 Search PubMed.
- D. Asthagiri, L. R. Pratt, M. E. Paulaitis and S. B. Rempe, J. Am. Chem. Soc., 2004, 126, 1285–1289 CrossRef CAS.
- D. Asthagiri, P. D. Dixit, S. Merchant, M. E. Paulaitis, L. R. Pratt, S. B. Rempe and S. Varma, Chem. Phys. Lett., 2010, 485, 1–7 CrossRef CAS PubMed.
- M. I. Chaudhari, L. R. Pratt and S. B. Rempe, Mol. Simul., 2018, 44, 110–116 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc, Wallingford CT, 2016 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. I. Chaudhari, M. Soniat and S. B. Rempe, J. Phys. Chem. B, 2015, 119, 8746–8753 CrossRef CAS.
- D. Sabo, D. Jiao, S. Varma, L. R. Pratt and S. B. Rempe, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2013, 109, 266–278 RSC.
- Z. L. Seeger and E. I. Izgorodina, J. Chem. Theory Comput., 2020, 16, 6735–6753 CrossRef CAS PubMed.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548 CrossRef CAS.
- J. G. Hill and K. A. Peterson, J. Chem. Phys., 2017, 147, 244106 CrossRef.
- M. Tafipolsky and R. Schmid, J. Chem. Theory Comput., 2009, 5, 2822–2834 CrossRef CAS.
- S. B. Rempe and H. Jónsson, Chem. Educ., 1998, 3, 1–17 CrossRef.
- S. B. Rempe and L. R. Pratt, Fluid Phase Equilib., 2001, 183–184, 121–132 CrossRef CAS.
- S. B. Rempe, D. Asthagiri and L. R. Pratt, Phys. Chem. Chem. Phys., 2004, 6, 1966 RSC.
- S. Varma and S. B. Rempe, Biophys. Chem., 2006, 124, 192–199 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Stone, MSc thesis, Computer Science Department, University of Missouri-Rolla, 1998.
- M. J. Stevens and S. L. B. Rempe, Phys. Chem. Chem. Phys, 2023 Search PubMed , in review.
- M. J. Stevens and S. L. B. Rempe, Phys. Chem. Chem. Phys., 2022, 24, 22198–22205 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Tables listing the distances between atom pairs in the K+ channel, decomposition of free energies, and figures for all optimized structures and individual layers of the KcsA selectivity filter. The positions of the structures are available as separate data files. These files are named Kn_NMAm.xyz and Nan_NMAm.xyz, where n gives the number of K or Na atoms in systems and m gives the NMA molecules. In addition, there is the file Na2_NMA8_SP.xyz that has the positions for the single point (SP) calculations of 2 Na+ and 8 NMA. See DOI: https://doi.org/10.1039/d3fd00110e |
| This journal is © The Royal Society of Chemistry 2024 |