Photoelectrochemical behaviour of photoanodes under high photon fluxes†
Isaac
Holmes-Gentle‡
 ,
Franky E.
Bedoya-Lora‡
,
Franky E.
Bedoya-Lora‡
 ,
Lorenzo
Aimone
and
Sophia
Haussener
,
Lorenzo
Aimone
and
Sophia
Haussener
 *
*
Laboratory of Renewable Energy Science and Engineering, École Polytechnique Fédérale de Lausanne, 1015 Lausanne, Switzerland. E-mail: sophia.haussener@epfl.ch
First published on 23rd October 2023
Abstract
The experimental behaviour of photoelectrochemical materials illuminated under high irradiance conditions >100 kW m−2 has not been studied despite being potentially advantageous for improving the photoelectrochemical performance and the system-level design through the miniaturisation of PEC cells, and for providing conditions that can mimic accelerated ageing or long term operation. This study presents the design of a high flux photoelectrochemical (HFPEC) test cell, which ensured adequate cooling through forced convention, and experimental setup in a high flux solar simulator for the study of light-dependent behaviour of two reference materials, Sn-doped Fe2O3 and BiVO4, under high irradiances (up to 358 kW m−2). Current densities of up to 1500 and 300 A m−2 were achieved for FTO|Fe2O3 and FTO|BiVO4, respectively. To qualitatively deconvolve the different phenomena and their effects, temperature dependence studies under approx. 1 sun (1 sun = 1 kW m−2) illumination were performed. It was found that the sublinear light-dependent behaviour was not explained by the temperature increase under illumination and, based on multiphysics modelling, likely primarily arises from bubble-induced losses. Furthermore, whilst the overall degradation rate increases for FTO|BiVO4 samples under increasing irradiance, a fitted phenomenological model indicates that the degradation kinetics are light-dependent, where increased irradiance diminishes the fraction of charge consumed by photocorrosion reactions. This study highlights the potential of HFPEC experiments to contribute to the scientific analysis of semiconductor–electrolyte behaviour at high photon flux conditions and to identify and resolve the practical challenges of engineering HFPEC devices.
1 Introduction
Photoelectrochemical (PEC) water splitting is seen as a potential sustainable pathway to solar-derived fuels.1 PEC devices typically consist of at least one semiconductor and an electrolyte, with a direct semiconductor–electrolyte junction. There have been only a few experimental reports of PEC water splitting devices, that include a semiconductor–electrolyte junction, under high solar irradiance. Whilst this experimental space remains understudied, it is of significant interest from both a scientific perspective and an engineering one. Firstly, although the behaviour of solid-state photo-voltaic junctions are well-studied in the established field of concentrated photovoltaics (CPV), there is a knowledge gap in the equivalent field of concentrated photoelectrochemistry. Secondly, solar concentration could be a promising route to increase the current density and miniaturise the device, which could conceivably improve the economic feasibility.1–3 Furthermore, high solar concentration could permit the thermal absorbed energy to be extracted at high temperatures and thereby utilised.The earliest PEC cell under any appreciable solar concentration was reported in 1998 where Khaselev and Turner achieved a 12.4% solar-to-hydrogen efficiency using a p-GaInP2 photocathode integrated with a GaAs p–n junction in a monolith at 12 suns (1 sun = 1 kW m−2).4 Ten years later, Wang et al. achieved unassisted water splitting by coupling a Fe2O3 or WO3 photoanode and a p-GaInP2 photocathode under 10 suns, although with very small currents (below 20 μA cm−2 at 10 suns).5 Wang et al. also investigated the effect of light intensity on photoelectrochemical properties and that the short-circuit photocurrent dependence on light intensity was nonlinear and was affected by photoanode illumination orientation. More recently, there has been a renewed interest in irradiance-dependence studies, but still limited to relatively low solar concentrations (<30 suns). Segev et al.6 and Gupta et al.7 performed comprehensive analysis of the performance of various doped Fe2O3 films up to 25 suns and LaFeO3 up to 18 suns, respectively. Both studies reported three-electrode experiments, which isolates the individual behaviour of the photoelectrode, and found that the photocurrent at maximum power point (where the photocurrent and photovoltage was defined as the difference between light and dark for current and applied potential, respectively)8 was found to increase linearly with flux concentration, whereas the photovoltage at maximum power point was found to increase logarithmically. Shaner et al.9 showed improved performance at 12 suns of core–shell type Si|WO3 micro-wires based photoelectrode originating from the improved photovoltage, resulting in improved current-matching. In the present work, the term photovoltage will be used to refer to the separation of quasi-Fermi levels under illumination,10,11 rather than the voltage difference between light and dark at a given current.
There has been a number of photoelectrochemical reactor designs which consider solar concentration. Ong et al.12 designed and modelled a PEC reactor design with a sample area of ca. 6 cm2 and tested up to 3.5 suns using a Fresnel lens and solar simulator. Vilanova et al.13 achieved unassisted water splitting by coupling a photovoltaic module (Si) to a photoelectrochemical junction (Fe2O3) in a flow reactor designed for low solar concentrations (<17 kW m−2). This design was then scaled to an active area of 200 cm2 and demonstrated continuous operation under concentrated natural sunlight (∼12.8 kW m−2) over 4 days (ca. 23 operational hours).14 Logarithmic saturation behaviour of the photocurrent with increasing solar concentration was observed, which was attributed to bulk recombination losses and substrate ohmic losses, an effect that has also been found in BiVO4 photoelectrodes.15 The real-world operating considerations of the PEC-PV reactor design from Vilanova et al.13,14 were theoretically studied for various solar tracking optical designs, and it was shown that a limited maximum device tilt angle (which is potentially required for efficient bubble removal) could lead to a reduced daily system performance.16 Along with our previous modelling work on high flux PEC cells,17 this demonstrates that bubble removal and gas separation must be considered in the early stages of reactor design and when interpreting the experimental results.
In comparison, more studies have been done on integrated PV-EC devices, sometimes referred to as photo-electrochemical devices based on their high degree of integration, under high photon flux. This solar-fuel device architecture has arguable demonstrated higher efficiencies18–20 and pilot-scale systems21–23 under significant solar concentrations (>400 kW m−2).20,21 Notably, in a number of these devices the water has dual functionality: acting as a coolant for the PV and reactant for the EC.20,22,24–26 Similarly, all high flux PEC cells that continuously operate with a flowing electrolyte could inherently take advantage of this cooling effect of the photoabsorber.
One of the main challenges of performing water splitting under high irradiances is the increased temperature at the photoelectrode surface resulting from the increased photon flux density and correspondingly larger thermal losses. In order to understand and decouple the effects of high irradiances and high temperatures, it is important to study the behaviour of photoelectrodes at different temperatures under 1 sun illumination. Experimentally, this can be achieved by using a PEC test cell immersed in a temperature-controlled water bath or using a flow cell with external electrolyte heating (or cooling). Regarding hematite photoelectrodes, only a few reports have discussed the temperature-dependence behaviour, with the consensus being that high temperatures (up to 65 °C) promote higher saturation currents, while onset potentials shifts towards positive values,27 causing the current–potential (JV) curves to have a steeper S-shape. A recent systematic study associates the increased saturated current with band gap shrinkage and increased carrier concentration, allowing more photons to be effectively converted to charge carriers.28 The delayed onset potential for the photocurrent has been linked to increased flat band potentials for non-doped hematite photoanodes.28 Although an opposite effect has been found for Si-doped hematite, where the onset potential was found to shift towards lower values.29 Similarly, a few studies have reported the performance of BiVO4 at increased temperatures (between 10 and 85 °C). For this case, saturated currents were also found to increase with temperature,30–32 possibly due to suppressed recombination rates in the bulk of the semiconductor due to increased carrier mobility.30 Analogous temperature-dependence studies have been published for other metal oxide photoelectrodes, including CuWO4,33 TiO2 and SrTiO3,34 reporting similar findings. Nevertheless, there is still a lack of consensus on the origin of temperature-dependent behaviour of photoelectrode materials; even studies on similar materials have reached contradicting findings. These disparities might be due to the diverse routes of synthesis, doping, layer architecture, morphology of the photoelectrode materials, and also experimental setup.
As summarised in Fig. S1 in the ESI,† there is a fundamental lack of experimental reports on the behaviour of photoelectrochemical materials at high light intensities. We seek to address this deficit in this work in order to further our physical understanding of these materials under high irradiance. Building upon our previous simulation work,17 we describe the design of a high flux photoelectrochemical (HFPEC) test cell and the experimental setup in a High Flux Solar Simulator (HFSS) for the study of photoelectrochemical phenomena. In this work, we present the light-dependent behaviour of Sn-doped Fe2O3 and BiVO4 photoelectrodes in the range of 40 to 360 kW m−2; and as a complement, we also performed temperature dependence studies between room temperature and 55 °C under 1 sun illumination with the aim of decoupling the effect of high irradiance and temperature.
2 Design of high flux photoelectrochemical cell and experimental setup
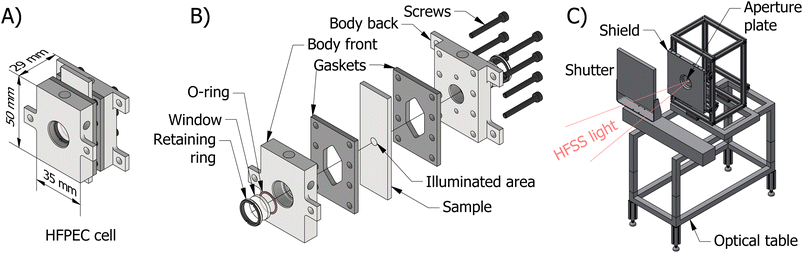
There are multiple design challenges for the PEC test cell that are imposed by high irradiances. Firstly, solar concentration leads to higher current densities at the surface of the photoelectrodes. This can lead to increased losses induced by bubble formation through increased light scattering, blockage of electrochemical surface by adherent bubbles (i.e. reactant mass transport limitations) and a reduction in the effective electrolyte resistance. This issue has been noted in previous work,4,6 where Khaselev and Turner go as far as to hypothesis that PEC systems may be limited in practical solar concentration to 10 to 20 suns due the aforementioned issue with bubble formation.4 High photon fluxes can also exacerbate current density maldistribution which leads to parts of the electrochemically active area to be underutilised. Furthermore, increased currents will lead to larger ohmic losses in the electrolyte and current collector (e.g. substrate).Consequently, operation at high irradiances (>100 kW m−2) above the historically investigated range (<30 kW m−2) will require a novel cell design and experimental setup. As discussed in our previous simulation work,17 the challenges associated with an increased rate of bubble formation can be partially mitigated through removal by high fluid velocities. Similarly, adequate heat transfer from photoelectrode to electrolyte will be achieved by using high fluid velocities over both the front and back surfaces of the photoelectrode. This heat removal through forced convection will also help minimise the effects of temperature on the photoelectrochemical behaviour. The ohmic resistance will be reduced by minimising the distance between electrodes and the use of high-conductivity substrates along with a reference electrode coupled to a Luggin capillary, which should be placed close (within a few millimetres) to the illuminated photoactive area. In this work, two photoelectrode substrates were used, namely, fluorine-doped tin oxide (FTO) glass slides and pure titanium, which enabled the effect of different substrate ohmic losses to be investigated. Furthermore, the sample area was minimised to reduce issues with current density distributions and other scaling effects, as previously observed by Ahmet et al.35 Finally, due to the high temperature limitations of the fluoropolymers commonly used for the construction of PEC cells, the cell was machined from stainless steel (316 grade). Whilst our previous simulations17 show no dangerous hotspots within the reactor, it was prudent to use a material robust enough to ensure that no issues would occur due to light misalignment.
The final reactor design for the HFPEC cell is presented in Fig. 1(A) and (B), and was validated in silico using a multiphysics modelling described elsewhere.17 The reactor is composed of two end plates with accompanying gaskets that sandwich the sample creating two cavities in which electrolyte can flow on the front and back sides of the sample. Fluidic routing ensures that bubbles are removed by both bubble buoyancy and forced convection (i.e. flow direction against gravity on the front and back sides). The HFPEC cell is then assembled within the experimental setup shown in Fig. 1(C) which comprises of an adjustable position optical table for alignment of the HFPEC cell relative to the lamp (and therefore changing irradiances), a water-cooled aperture which defines the illuminated sample area, and a water-cooled shield for absorbing stray illumination which protects the nonilluminated components of the experimental setup.
3 Methodology
3.1 Photoelectrode synthesis and preparation
Three types of photoelectrodes were fabricated via spray pyrolysis for testing under high irradiances: (1) Sn-doped Fe2O3 deposited on FTO substrate (FTO|Fe2O3), (2) Sn-doped Fe2O3 on titanium foil substrate (Ti|Fe2O3), and (3) BiVO4 on FTO|SnO2 substrate (FTO|SnO2|BiVO4). These well-known photoabsorbers were selected as model materials as they have been well-studied under AM1.5G spectrum36–38 and have contrasting stability characteristics which allow comparison of the results produced within this study and with previously published literature. Fe2O3 and BiVO4 are known for their relatively high and poor stability respectively, where unmodified Fe2O3 (without catalytic layer) is known to perform for over 1000 h without any significant changes in their performance.39 Conversely, unmodified BiVO4 suffers from instabilities that render the photoelectrode inoperative after only a few hours, although protective and catalytic layers can improved considerably its stability up to 1000 h.40 State-of-the-art Fe2O3 and BiVO4 photoelectrodes will employ catalysts (e.g., NiFeOx,38 Ru–P,36 Pt37etc.) to enhance the charge transfer efficiency at the semiconductor–electrolyte interface but, in this work, a catalyst deposition step was omitted in order to simplify the photoelectrode synthesis methodology and simplify the discussion regarding the mechanism of possible degradation pathways. Spray pyrolysis was used to deposit both films by spraying the precursor solutions onto a heated substrate. For hematite a precursor comprised of 0.1 M FeCl3·6H2O (>99%, Acros Organics) and 0.6 mM SnCl4 (anhydrous, 99%, Thermo Fisher Scientific) in ethanol (99.8% Fisher Chemical) solution was sprayed (20 passes) onto FTO substrates (Solaronix TC22-15, 2 mm) and annealed for 1 h in air at 400 °C.41 For Ti substrates (99.7% Sigma Aldrich, 0.126 mm), 40 passes were performed with the precursor. For bismuth vanadate photoanodes, 0.1 M SnCl4 in ethyl acetate was first spray pyrolysed onto FTO substrates to form a thin layer of SnO2 to improve charge transfer between the substrate and BiVO4; then 8 mM Bi(NO3)2 + 8 mM VO(AcAc)2 in a solution of acetic acid/ethanol was sprayed and annealed at 450 °C in air for 2 h.42 Further details related to the photoelectrode fabrication methods can be found in the ESI in Sections S2.2 and S2.3.† Finally, cyanoacrylate-based glue was painted on the non-illuminated areas of the sample to minimise the dark current contribution.3.2 Photoelectrochemical testing under high flux light
The photoelectrodes were tested under high irradiances generated from a single lamp at the EPFL high flux solar simulator (HFSS), detailed further in Levêque et al.43 The irradiance was characterised by flux distribution mapping of images of a Lambertian target taken by a calibrated IR camera, and a water-cooled calorimeter placed behind the light aperture.43,44 Irradiances in the range of 40 and 360 kW m−2 where achieved by placing the optical table at different distances from the focal point of the lamp (up to ∼22 cm). As the light beam is not collimated, beam divergence between the 5 mm diameter aperture and the sample must be taken into consideration. Consequently, the true illuminated area was estimated from the degradation pattern of the BiVO4 samples. A detailed description of the calibration procedure and results can be found in Section S2.4 of the ESI.† Finally, the spectrum of HFSS light was measured far out of focal point with a UV-vis spectrometer (Ocean Optics) as shown in Fig. S8 of the ESI.†The HFPEC cell, which was introduced in the previous section, is composed of two stainless steel end plates, two 3 mm thick silicone gaskets, and the photoelectrode. Each end plate has a 2 mm thick quartz window, sealed with an EPDM o-ring and an aluminium retainer ring. Fluidic tubing (PTFE) is connected to the cell via PEEK flangeless fittings. Electrolyte (1 M NaOH or 1 M KPi buffer solution, pH 6.6) is circulated using a diaphragm pump with an integrated pulsation dampener (KNF, FP70 KPDCB-4B) at a volumetric flowrate of 3.5 cm3 s−1. A potentiostat (Autolab PGSTAT302n) was connected to the HFPEC cell, where the photoelectrode sample was connected as the working electrode, the front reactor stainless steel plate was used as the counter electrode and an external reference electrode (RHE, HydroFlex/Gaskatel) connected to the cell via a PTFE/Nafion tube Luggin capillary to ensure that the reference potential was sensed ca. 2 mm away from the illuminated surface of the working electrode. Cyclic voltammetry and chronoamperometry measurements were conducted, and the resulting data were postprocessed to perform ohmic drop compensation (where the uncompensated resistance is determined from EIS measurements at open circuit potential). Further details on ohmic drop compensation can be found in the ESI Section 2.5.† Finally, temperature sensors were placed in the electrolyte reservoir and at the inlet and outlet of the HFPEC. In order to study the thermal performance of the HFPEC further, and with the aim of estimating the temperature at which the photoelectrode operates, a Ti|Fe2O3 sample was probed with multiple thin-wire thermocouples attached on the back side of the photoelectrode.
3.3 Photoelectrochemical testing at different temperatures
The photoelectrodes were also tested at different temperatures between 24 and 55 °C under 1 sun (AM1.5G) illumination (Trisol Solar Simulator, AOI). The light source spectrum can be found in the ESI in Fig. S8.† A three-electrode flow cell with an exposed/illuminated area of 8 mm in diameter was used to measure the performance of the photoelectrodes. A RHE electrode (RHE, HydroFlex/Gaskatel) and a Pt wire were used as reference and counterelectrode, respectively. A flow rate of 3.5 cm3 s−1 was used to ensure conditions similar to those under high irradiances. The electrolyte temperature was controlled by placing a reservoir in a water bath, which was set to different temperatures. Due to heat losses through the pipes, the temperatures were recorded by a thermocouple inside the flow cell a few millimetres away from the exposed area of the photoelectrode.The PEC properties at different temperatures were measured by voltammetry and chronoamperometry following protocols reported elsewhere.45–47 For the photoelectrochemical characterisation of Fe2O3 photoelectrodes, voltammograms at 10 mV s−1 were performed under dark and illuminated conditions. With the aim of measuring charge transfer efficiencies at the surface, chronoamperometries were performed for 10 seconds in dark and 10 seconds under illumination with a time resolution of 1 μs at different electrode potentials. 1 M NaOH was used as electrolyte for these tests.
In the case of BiVO4 photoelectrodes, chronoamperometries were performed at 1.23 V vs. RHE in 1 M KPi buffer (pH 6.6) for 7 hours under 1 sun illumination at different temperatures. Due to the poor stability of the BiVO4 samples, a full photoelectrochemical characterisation, similarly to the one performed for Fe2O3 samples, was not possible. Instead, the use of this material presents with the possibility of assessing the transient degradation and photocurrent decay observed during the chronoamperometries. Electrochemical impedance spectroscopy was used to measure the ohmic resistance, which was then used to perform chronoamperometries with iR compensation.
3.4 Optical and morphological characterisation
The absorbance spectra of the samples (Fe2O3 and BiVO4) can be found in Fig. S14 and S15 in the ESI,† and were measured using a UV-vis spectrometer (UV-2600 Shimadzu) with an integrating sphere (ISR-2600PLUS Shimadzu). The direct band gaps were 2.19, 2.16 and 2.58 eV for Fe2O3 (20 passes), Fe2O3 (40 passes), and BiVO4, respectively, in agreement with previous reports for both materials.41,48 SEM images were performed for pristine Fe2O3 and BiVO4, as shown in Fig. S10 and S11 in the ESI.† Postmortem images were also taken for BiVO4 photoelectrodes after experiments under high irradiances, images are shown in Fig. S12.† EDX analysis (Gemini II, Zeiss) was performed on BiVO4 photoelectrodes before and after experiments, detailed results are shown in Fig. S13.†4 Results and discussion
4.1 Thermal performance of the HFPEC cell
In order to study the thermal behaviour of the HFPEC test cell, multiple thermocouples were attached to the back of a sample with a titanium foil substrate and three resistance temperature sensors measured the electrolyte temperature at the inlet and outlet of both sides of the cell. The electrolyte volumetric flow was kept constant for all experiments (3.5 cm3 s−1). Shown in Fig. 2(A), the recorded temperature of the sample understandably increased under increasing irradiation, where the thermocouple placed directly in the centre of the illuminated area reached ca. 54 °C at 358.5 kW m−2. The experimental results showed close agreement with simulations (model outlined in ref. 17), and it is hypothesised that the under-prediction of the model at higher light powers could be attributed to the method of thermocouple attachment inherently leading to increased thermal insulation of the backside of the thermocouple to the fluid flow in the rear chamber of the HFPEC. Regardless, this demonstrates the validity of the cooling strategy and that the HFPEC design is successful in limiting the temperatures to safe levels. Furthermore, as the electrolyte is recirculated, the electrolyte reservoir temperature was monitored during all experiments and was typically raised from ca. 18 to 22 °C during all of the experiments outlined in this work, as can be observed in Fig. S17.† The thermal validation presented above serves as confirmation that the model can be used to estimate the surface temperature of the photoelectrodes. Direct temperature measurements on the surface were not possible due to the thermocouples obstructing the incident light. Therefore, the surface temperatures of the photoelectrodes deposited on Ti and FTO were predicted by the thermal model, and can be found in Fig. 2(B). The average predicted surface temperature ranges between 20 and 45 °C depending on the irradiance and the type of substrate used.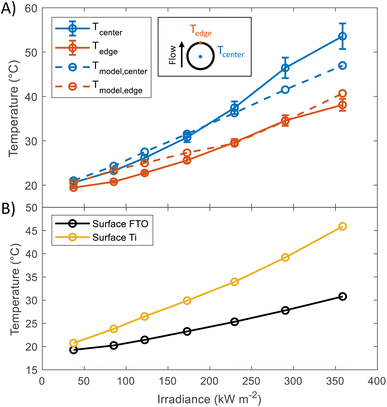 | ||
| Fig. 2 (A) Temperature at the back of Ti substrate at different irradiances. Values were taken in steady state condition (after 10 minutes of illumination). Dashed lines show the predicted temperatures, the model used for these predictions has been described in a previous publication.17 (B) Predictions of the average surface temperature as a function of irradiance obtained using the same model. | ||
4.2 Photoelectrochemistry of hematite under high flux
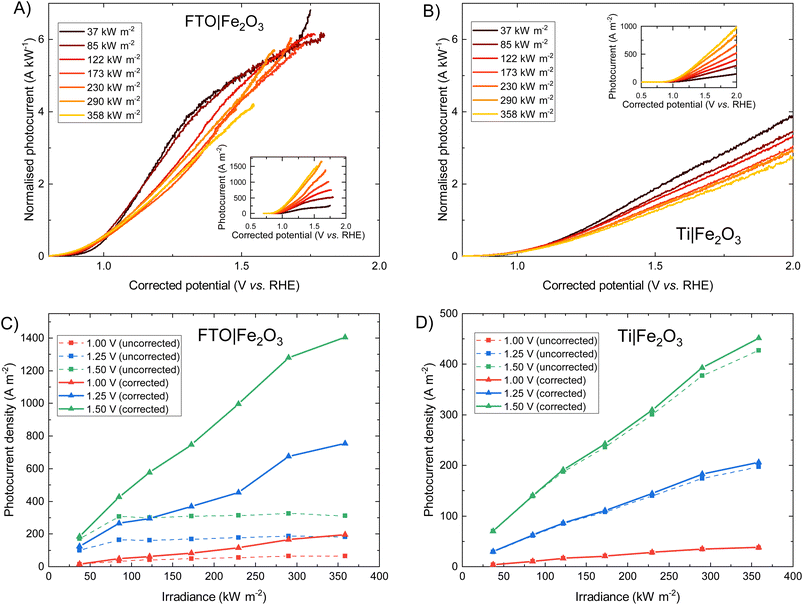
The photoelectrochemical behaviour of FTO|Fe2O3 and Ti|Fe2O3 samples under high irradiances was measured and the results shown in Fig. 3. The FTO|Fe2O3 dataset at 358 kW m−2 was affected by considerable experimental noise and a large ohmic drop compensation. Therefore, the results above ca. 1.5 V vs. RHE were removed for clarity; the original data is shown in Fig. S18.† At the highest solar irradiance tested (358 kW m−2), the recorded photocurrent densities for both substrates at 1.25 V vs. RHE were between 100 and 200 A m−2vs. without ohmic compensation. Conversely, after ohmic drop compensation (also known as iR compensation and described in detail in the ESI, Section S2.5†), FTO|Fe2O3 significantly outperformed the Ti|Fe2O3 sample, registering photocurrent densities of ∼750 A m−2vs. at 1.25 V vs. RHE. Given that this is the highest irradiance used for PEC experiments, it is unsurprising that the recorded photocurrent densities demonstrated in this work are significantly larger than previous demonstrations.6,13,14As it can be seen in Fig. 3(D), the performance of the Ti|Fe2O3 sample was relatively unaffected by compensating for the series resistance which indicates that the uncompensated resistance in the FTO|Fe2O3 sample is primarily from the substrate resistance. Whilst this finding was previously reported in Segev et al.6 for <30 kW m−2 and Vilanova et al.14 for <13 kW m−2, the unique high irradiance experimental conditions in this work mean that the full asymptotic behaviour is seen (cf.Fig. 3(C) dotted lines), which demonstrate the severe unsuitability of unmodified FTO for such photoelectrodes at high solar concentrations (>100 kW m−2). Nevertheless, the conductivity of FTO substrates could improved though the deposition of conductive metal busbars,35,49 potentially permitting the use of FTO under high flux conditions.
For both photoelectrochemical and photovoltaic junctions, the current generated from absorbed photons is hypothetically linearly proportional to irradiance50,51 and from a number of first-principles derivations,52–54 it is possible to derive an analytical equation for the charge transfer of minority carriers (holes) in photoanodes. For an ideal photoanode under high enough reverse bias, the measured current will primarily be the photogenerated current and any recombination in the space-charge region will be minimised, and therefore a simplified Gärtner–Butler equation can be used (eqn (1)). Assuming that the term j0 = eDpp0/Lp is small relative to the 2nd term in eqn (1) (which is a good approximation under 1 sun illumination for hematite55), the ideal total current density jtotal should be proportional to the light intensity I0, assuming that the absorption coefficient α, the thickness of space charge region WSCR and the diffusion length of holes Lp are independent of I0. However, it is very important to highlight that this proportionality relation is only valid under relatively low injection conditions for an ideal photoelectrode and will not necessarily hold under high injection conditions found at high irradiances studied in this work. Nevertheless, the experimental results will be compared with this ideal linear dependence.
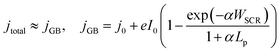 | (1) |
Fig. 3 show that when iR compensation is taken into consideration, the photocurrent density scales sub-linearly with irradiance. For example, for FTO|Fe2O3 at 1.23 V vs. RHE, the measured normalised photocurrent at 122 kW m−2 and 358 kW m−2 is 28% and 36% respectively less that expected from the results at 37.3 kW m−2. Equivalently for Ti|Fe2O3, this is 27% and 36% respectively. Notably, this sub-linear behaviour is maximal at intermediate potentials for FTO|Fe2O3 (1.0–1.6 V vs. RHE in Fig. 3(A)) but maximal at highest potentials for Ti|Fe2O3 (Fig. 3(B)).
For Fe2O3, this approximately linear behaviour of photocurrent densities at relatively low irradiances (i.e. <30 kW m−2) has been previously observed by a number of authors.6,41,56 Vilanova et al.14 observed a non-linear increase in uncompensated photocurrent with increasing solar concentration which can likely be attributed to substrate conductivity, and is broadly similar to the behaviour shown in Fig. 3(C). Notably, a number of researchers used varying monochromatic light under low irradiance (<0.4 kW m−2) as a strategy to study the mechanism of charge transfer56,57 and observed a non-linear relationship between the surface hole charge and irradiance. Whilst the exact mechanism is disputed (i.e. attributed to both a change in reaction mechanism,56,58 light dependence of the water oxidation rate constant,59 and band edge unpinning effects60), these results demonstrate the complexity in building a detailed model from first principles which unequivocally explains the photoelectrochemical behaviour experimentally observed. Therefore, given the challenges in performing the typical diagnostic experiments required to elucidate mechanism (e.g. EIS, transient photocurrent, IMPS, TAS etc.) under the high simulated solar flux conditions achieved in this work, we seek to give a more qualitative discussion on the observed photoelectrochemical behaviour under high flux.
As discussed in our previous modelling work,17 there are a number of photoelectrochemical engineering phenomena that may conceal the fundamental behaviour of the semiconductor–electrolyte interface such as ohmic losses caused by the substrate, electrolyte and bubbles, light scattering by bubbles, and bubble coverage of the electrochemically active area. Furthermore, the temperature of the junction increases with increasing irradiance which will impact various photoelectrochemical properties (e.g. recombination rate, kinetics of transfer to the electrolyte etc.). In the results presented in Fig. 3, ohmic compensation applied removes the ohmic drop associated with substrate/electrolyte under no illumination, but the bubble ohmic losses will remain (where previous modelling suggests a photocurrent loss of up to 10% (ref. 17)).
In order to qualitatively deconvolve the differing phenomena and their effects, the temperature-dependent photoelectrochemical behaviour of Fe2O3 under 1 sun illumination was studied, as an increase in sample temperature was observed with increasing high flux. Shown in Fig. 4, the photocurrent density for both samples initially decreases with increasing temperature at low potentials, and then increases at higher potentials (where the switch in temperature dependent behaviour is observed at ca. 1.3 and 1.2 V vs. RHE for FTO and Ti substrates). However, the magnitude of this change in the two regions is contrasting, where FTO|Fe2O3 shows a larger decrease compared to Ti|Fe2O3 for low potentials. Furthermore, at high potentials, FTO|Fe2O3 exhibits only a minor improvement (ca. 2% at 1.4 V vs. RHE) in the saturated photocurrent whereas it is significantly improved for Ti|Fe2O3 (ca. 70% at 1.4 V vs. RHE). Similar behaviour can be observed in the charge transfer efficiency data (Fig. S21 and S22†) calculated using chronoamperometry.46
 | ||
| Fig. 4 Temperature dependence of voltammograms for (A) FTO|Fe2O3 and (B) Ti|Fe2O3. Further details are found in the ESI in Fig. S21 and S22.† | ||
The difference between FTO|Fe2O3 and Ti|Fe2O3 samples observed in Fig. 4 can be associated to undesired formation of a TiO2 layer during the spray pyrolysis (450 °C) on Ti, and posterior thermal treatment (400 °C). Prior the spray, when the substrates were reaching the deposition temperature, a change in colour from grey to blue was observed on the Ti substrates, which is consistent with the formation of TiO2. This layer might act as a barrier for electron transfer between the hematite film and the Ti substrate,41 which can introduce a temperature dependence. Unintentional Ti-doping could also contribute to this behaviour, which has been found to have a temperature-dependent behaviour for hematite photoanodes.27
Whilst the temperature dependence of photoelectrodes will be specific to sample composition and preparation, a number of studies have shown similar behaviour,27,29,34 albeit with a more significant increase in the saturated photocurrent at high potentials for FTO|Fe2O3 samples. By comparison of these results with the experiments under high irradiances, the general decrease in the normalised photocurrent cannot be wholly explained by the effects of temperature. This is most apparent for Ti|Fe2O3 where opposite trends were observed: a decrease in photocurrent with irradiance vs. an increase in photocurrent with temperature for >1.2 V vs. RHE. Therefore, based on our previous numerical simulation which extrapolated photoanode behaviour from 1 sun experiments,17 it is expected that a significant proportion of the observed decrease is caused by bubble losses. However, it remains likely that there is fundamental irradiance-dependent phenomena of the semiconductor–electrolyte junction (e.g. bandgap, reaction kinetics, space charge layer thickness etc.) which cannot be easily deconvoluted from the engineering phenomena, without further challenging diagnostic experiments (e.g. EIS, IMPS etc.).
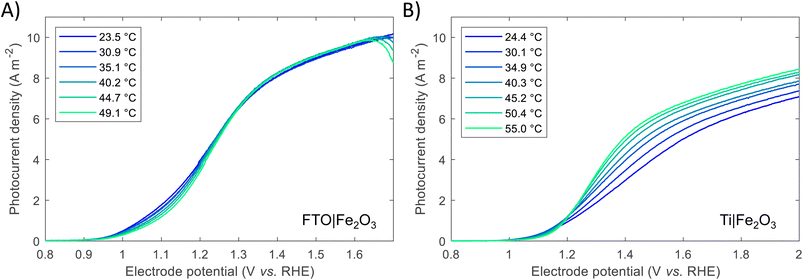
Previous studies have indicated that photovoltage improves with increasing solar concentration for various PEC systems.6,7,9 The onset potential, as defined in Section S2.6 in the ESI,† is plotted in Fig. 5 and displays a similar trend. The calculated gradient of −150 mV per decade for FTO|Fe2O3 and −192 mV per decade for Ti|Fe2O3 is comparable to that measured previously,6 and, as highlighted by Segev et al., is significantly higher than the open-circuit voltage of state-of-the-art CPV cells.6 This further highlights the potential benefit of solar concentration for PEC photoanode materials. This logarithmic dependence on irradiance is observed over the entire range (38–358 kW m−2) for FTO|Fe2O3 but only up to 173 kW m−2 for Ti|Fe2O3 where it is asymptotic towards ∼0.79 V vs. RHE. The mechanism responsible for this dissimilar behaviour is likely non-trivial and requires further study to account for the temperature effect. One diagnostic technique that could be used to probe PEC samples is photoelectrochemical impedance spectroscopy (PEIS) and this was attempted under high irradiances, but resulted in noisy spectra due to the significant rate of bubble formation. However, these time-consuming experiments did demonstrate the temporal-stability of Fe2O3 samples through the similarity of photoelectrochemical behaviour before and after multiple experiments (shown in Fig. S20†).
 | ||
| Fig. 5 Onset potential vs. irradiance for FTO|Fe2O3 and Ti|Fe2O3 and the linear fit. For Ti|Fe2O3, only the range 38–173 kW m−2 are fitted. | ||
A number of mitigation strategies could be employed to reduce the bubble losses further,61 and we suggest that the bubble concentration could be further decreased through the optimisation of our HFPEC flow reactor design to further maximise electrolyte velocity across the photoelectrochemically active area. Alternative methods include the use of surfactants, magnetic and acoustic fields,62 although their suitability for high flux PEC systems remains to be tested. Furthermore, to study the fundamental behaviour of the semiconductor–electrolyte junction under high irradiances, a potentially instructive research direction would be into developing and performing the challenging diagnostic experiments, such as PEIS, transient photocurrent and intensity-modulated photocurrent spectroscopy (IMPS), under >100 kW m−2 illumination from a high flux solar simulator.
4.3 Photoelectrochemistry of bismuth vanadate under high flux
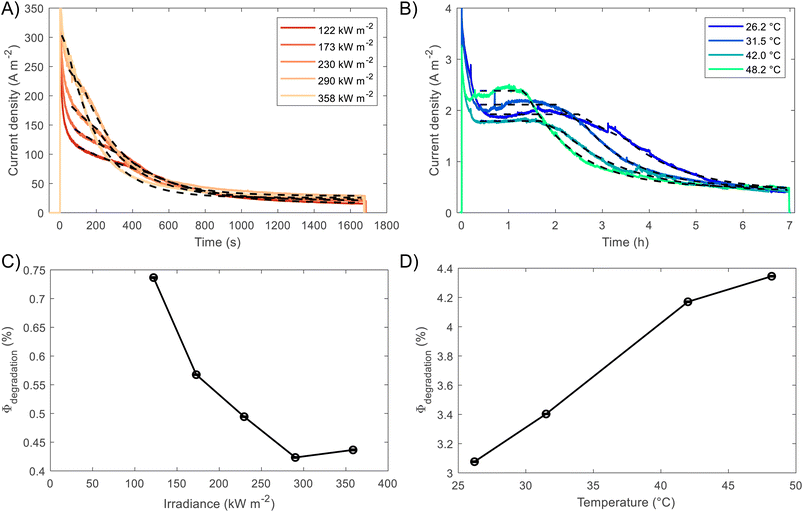
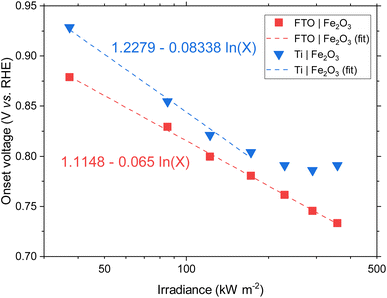
BiVO4 films of 170 nm thickness were spray pyrolysed on FTO substrates previously coated with a film of SnO2 of ca. 200 nm, as shown in the SEM images in the ESI, Fig. S10 and S11.† The SnO2 layer was necessary to improve the hole transfer by acting as a hole barrier and preventing recombination at the FTO|BiVO4 interface,15 additionally it improved the homogeneity of the films during the spray deposition. With the aim of studying the degradation processes occurring at high photon fluxes, FTO|BiVO4 samples were exposed at different irradiances and currents were measured at an applied potential of 1.23 V vs. RHE (after iR compensation) in 1 M KP, pH = 6.6. Chronoamperometries in Fig. 6(A) show the transient current densities at different irradiances; as expected, higher current densities were observed at higher irradiances, although with faster current decay. Fig. 6(B) shows the same set of data with current densities normalised by irradiance. It is evident that during the initial stages (<20 seconds) higher irradiance-normalised currents are obtained at ca. 120 kW m−2 (see inset of Fig. 6(B)). For example, after 20 seconds of illumination at 85 kW m−2 a normalised current density of 1.02 A kW−1 was achieved, while at 122 kW m−2 it was 1.33 A kW−1, meaning a 30% increase in normalised-irradiance current. This is an indication of possible optimal conditions for water splitting at high irradiances when opposing effects influence the photocurrent densities. Similarly to the behaviour observed for Fe2O3 samples, among these effects we can consider the favourable improved kinetics and decreased thermodynamic requirements due to increased surface temperature, enhanced electron conductivity in the bulk of BiVO4,32 and thermally activated minority carrier transport,30 but also unfavourable light scattering, increased ohmic drop and surface coverage due to bubble evolution,17 and increased recombination rates in the bulk due to saturation of band edges with charge carriers at high photon fluxes.15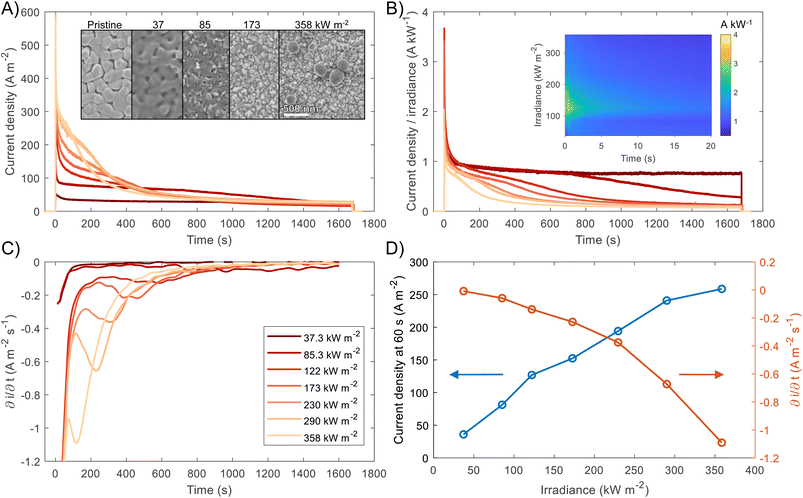 | ||
| Fig. 6 (A) Chronoamperometry of FTO|BiVO4 at 1.23 V vs. RHE and different irradiances, inset shows the SEM images for the pristine sample and postmortem for selected irradiances, the full set of SEM images can be found in the ESI in Fig. S12.† (B) Current densities normalised by irradiance, inset shows the first 60 s after illumination. (C) Derivative of current density vs. time. (D) Current density at 60 s, and maximum derivative of current density vs. time as a function of irradiance. For the calculation of the maximum derivative, the first 20 s after illumination were not considered because the fast decay during this 20 s-period is associated to fast processes not related to photocorrosion. | ||
The increase in photocurrent density decay expressed as ∂j/∂t, shown in Fig. 6(C), is evidence of increased degradation rates with increased irradiances. Fig. 6(D) shows the current density at 60 seconds and the maximum current density decay for each irradiance (after the initial 20-second peaks). The influence of the aforementioned competing effects are evidenced by the non-linearity of both curves in Fig. 6(D). Although, the chronoamperometries were performed with ohmic drop compensation, the effect of bubbles at higher current densities was not corrected for, and it is estimated to be a contributor for the decrease of photocurrent densities at higher irradiances, in a similar manner as found for Fe2O3 samples in the previous section.
The loss of the BiVO4 film was monitored by postmortem SEM imaging after irradiation for 28 minutes. As shown in Fig. 6(B), the samples irradiated up to 85.3 kW m−2 still exhibited significant photoactivity after 28 minutes, this was confirmed by the presence of BiVO4 film on the substrate. For irradiances >173 kW m−2, no film was observed on the substrates, as seen in the inset of Fig. 6(A). Remarkably, for exposures higher than 290 kW m−2, spherical deposits of ca. 200 nm in diameter were observed after high irradiance exposure. EDX analysis (Fig. S13 in the ESI†) showed that these deposits are rich in Bi and P, possibly related to the re-deposition of dissolved Bi present in the phosphate electrolyte or the formation of a more stable Bi-rich phase. This suggests that the mechanism of BiVO4 at lower irradiances follows the dissolution process proposed by Toma et al.63 with dissolution of both metal ions, Bi and V, and without formation of a thermodynamically stable Bi oxide layer. However, at higher irradiances, the formation of Bi-rich phases could occur due to increased surface temperatures, allowing structural rearrangement of V-deficient phases to form, for example, Bi oxides.63 Additionally, a white residue was observed on the samples subjected to irradiances >290 kW m−2, which can be attributed to the Bi-rich spherical particles observed in the SEM images. Moreover, the Bi-rich particles were absent on the edges of the exposed area, this suggests the effect of current density distributions (i.e. heterogeneity in current density). Higher current densities have been predicted for the edges of the electroactive area relative to the centre of the sample,17 promoting a decrease in local pH and thermodynamically hindering the formation of Bi oxide, as suggested by the E–pH diagram for the Bi–V system in aqueous solution.63
It should be mentioned that the stable photocurrent densities observed for lower irradiances (<37.3 kW m−2) are not an indication of film stability. Chronoamperometries shown in Fig. 6(A) are in agreement with the measurements by Zhang et al.,64 who also found that dissolution occurs even during the early stages of ‘stable’ photocurrent densities. This is because the instant film thickness is still thicker than the hole diffusion length at the early stages of degradation.
In the case of completely dissolved films (for irradiances >173 kW m−2), small and stable photocurrent densities (ca. 10% of the initial photocurrent) were still observed after ca. 1000 seconds, as seen in Fig. 6(B). These small photocurrents could be attributed to remnant BiVO4 protrusions still present on the substrate after dissolution of the film. These sparse protrusions were observed in pristine samples and samples subjected to 10 h of continuous water splitting under 1 sun at 1.23 V vs. RHE, SEM images of these defects can be found in Fig. S23.†
The present consensus for the BiVO4 degradation process is a dissolution mechanism as reported by Toma et al.63 and Siyuan Zhang et al.64 Liming Zhang et al. reported the effect of temperature on the performance of nanostructured BiVO4 and how the size of the particles impact the photocurrent densities regarding the relation between their size, the depletion layer and the minority diffuse region thickness.30 This dissolution mechanism was confirmed by the SEM/EDX analysis observed for our BiVO4 samples (Fig. S12 and S13†). Using these reports as a basis, a phenomenological model is proposed below for the transient dissolution of BiVO4 under high irradiances. The assumptions for the model and a more detail description can be found in the ESI in Section S3.7.† Due to the film thickness decreasing with time, the Gärtner–Butler relationship was defined as a piecewise-defined function depending on the relationships between the instantaneous film thickness (Lfilm), the diffusion length of holes (Lp) and the space charge region thickness (WSCR), expressed as follows:
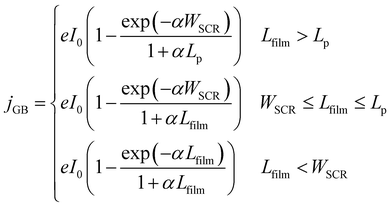 | (2) |
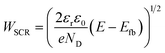 | (3) |
Assuming two-electron transfer for the dissolution of BiVO4 and that the formation of a passivating film is kinetically hindered,63 the instantaneous corrosion rate can be estimated as:
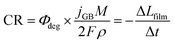 | (4) |
The contribution to the photocurrent due to BiVO4 protrusions and other defects on the film, which dissolved at considerably slower rates, was assumed constant and equivalent to the current density measured at the end of the experiment. Therefore, the total current density can be estimated as jtotal = jstable + jGB, where jstable was experimentally measured as the average photocurrent density in the last 10 seconds of illumination. The contribution of dark current densities was negligible, as was confirmed experimentally. The predicted film thickness history of the BiVO4 films and instantaneous dissolution rates (CR) at different irradiances and temperatures (under 1 sun illumination) are shown in the ESI in Fig. S26(C) and (D).†
The piecewise function described above allows for the prediction of the photocurrent at the different stages of degradation. In the case of transient experiments under high irradiances, four regions were observed as shown in Fig. S24:† (1) capacitive region and other fast transfer phenomena (recombination kinetics), (2) dissolution for the case WSCR ≤ Lfilm ≤ Lp, (3) dissolution when Lfilm < WSCR, and (4) stable photocurrent due to residual BiVO4. The fitting of this model to chronoamperometries obtained at low irradiances (37.3 and 85.3 kW m−2) was not possible due to absence of the last two regions in the experimental data. In order to extract useful information from the chronoamperometries, three parameters were fitted to the transient photocurrent densities for regions (2) and (3): the dissolution fraction (Φdeg), the space charge region width (WSCR) and the diffusion length (Lp).
In the case of the experiments performed under 1 sun at different temperatures, 5 regions were observed as shown in Fig. S25:† (1) capacitive region and other fast phenomena, (2) dissolution for the case Lfilm > Lp, (3) dissolution for WSCR ≤ Lfilm ≤ Lp, (4) dissolution when Lfilm < WSCR, and (5) stable photocurrent due to residual BiVO4. For this case, four parameters were fitted to the transient photocurrent densities for regions (2), (3) and (4): the dissolution fraction (Φdeg), the space charge region width (WSCR), the diffusion length (Lp) and the absorptivity (α).
The fittings to the model for the two cases, high irradiances and high temperatures, can be seen in Fig. 7(A) and (B), respectively. The confidence interval (95%) for the fitted parameters is very narrow, ca. 2% of the values, as shown by the error bars in Fig. 7(C) and (D), as well for the rest of fitted parameters as shown in Fig. S26.† For high irradiances (>122 kW m−2), the region at which Lfilm > Lp seems to occur too fast to be observable on the chronoamperometries, this could be explained by the fast dissolution of BiVO4 in the first stages when the current density is the highest. The fitted space charge region width (WSCR) was found to increase with irradiance (Fig. S26(A)†). As this parameter is a function of different materials parameters that are temperature dependent, see eqn (3), the interpretation of this trend is difficult elucidate. For example, the relative permittivity,65,66 donor density and flatband potential28 are known to increase with temperature for semiconducting materials. Hence, the de-convolution of these parameters is challenging given their relation to the space charge region width. On the other hand, the dissolution fraction was found to decrease with irradiance as seen in Fig. 7(C); at first, this might seem contradictory, as faster degradation rates were observed for higher irradiances. To confirm this effect, the photocurrent density was normalised by irradiance, and the time of measurement was divided by the time at which the current density decay was fastest. Hence, effectively normalising the chronoamperometry curves in the current and time domain. It was found that at higher irradiances the normalised current density decays at a slower rate (see Fig. S28(A)†). This confirms that at higher irradiances the dissolution fraction decreases, although the net degradation rate increases due to increased photocurrent densities. Fitted hole diffusion lengths (Lp) showed a decreases with irradiance between 93 and 65 nm, as observed in Fig. S26(A).† For BiVO4 it has been reported that Lp is in the order of 100 nm,67 and it is proportional to the square of the lifetime and mobility of the charge carrier (holes). The decrease of this parameter with irradiance can be explained by the increased recombination caused by hole-saturated valence band and exacerbated by the poor kinetics for oxygen evolution at the surface.
To decouple the effects of temperature from irradiance on the degradation rates, the fitting was also performed on BiVO4 samples at different temperatures but illuminated under 1 sun (1 kW m−2). Fig. 7(B) shows that degradation rates increased with temperature under the same irradiance, which is confirmed by the dissolution fraction as shown in Fig. 7(D). This suggests that the decrease in the dissolution fraction at higher irradiances is not directly related to the higher temperatures at the surface of the photoanode. Instead, it might be due to the high photon fluxes being absorbed by the film. Hence, we expect that operating at high irradiances while keeping the photoelectrode at room or lower temperatures (e.g. with active cooling), it could further decreased the dissolution fraction. This assertion was tested by running the fitting while accounting for temperature changes in WSCR and Ld, and recalculating Φdeg. As expected the dissolution factor was lower when temperature was kept constant, the results can be seen in Fig. S27.†
Abdi and van de Krol performed studies at different irradiances (<10 kW m−2) for bare BiVO4 and BiVO4|CoPi samples, and found that the absorbed photon to current efficiency (APCE) decreased with irradiance for both cases.15 In the case of bare samples, they associated this behaviour to slow kinetics for oxygen evolution, while high irradiances increased the conductivity of the material (photodoping) caused by accumulation of electrons in the conduction band. This issue could be alleviated by adding a catalyst on the surface, e.g. CoPi, although the charge transfer would still be limited by poor electron conductivity at higher irradiances. This behaviour could also be linked to the non-linearity found between irradiance and current density in Fig. 6(D) and the slower rate of dissolution as shown in Fig. 7(C). In contrast, it has been found that for electrodeposited Mo-doped BiVO4, the onset potential shifts in the positive direction, while saturated current densities increased with temperature following an Arrhenius-type behaviour.30 Similarly, it has been found that at high temperatures (≈40 °C), the charge carrier recombination in the bulk was suppressed for non-doped BiVO4 produced via PLD, achieving higher photocurrents at those temperatures.32 Although, a recent study found that for spin-coated non-doped BiVO4 photoelectrodes, the temperature does not impact its performance, while V-doped samples exhibited an increased saturation current, higher incident to photon current efficiencies (IPCE) at 85 °C and shifted onset potentials in the cathodic direction.31 The disparity among these reports are possibly due to the different types of doping, morphology and architectures used for the fabrication of the photoelectrodes.
Regarding the other three fitted parameters for the temperature-dependence study: WSCR, Lp and α, the results are shown in Fig. S26(B).†WSCR was found to increase with temperature, however, in a similar manner to the irradiance-dependence study, it is difficult to establish the origin of this trend due to the convoluted effects associated to this parameter. In the case of Lp, it increased slightly from 80 to 90 nm with temperature from 26 to 48 °C. This effect might be related to increased diffusion coefficients and mobilities of holes with temperature. For α, an overall decrease was observed with temperature but with a weak correlation, this might be due to the weak dependence of absorbance with temperature. To date, no study on the temperature dependence of absorbance, or absorptivity, with temperature has been reported for BiVO4.
As presented above, only a few studies have studied the joint effect of temperature and irradiance on the performance of BiVO4 photoelectrodes. To elucidate further these inconsistencies, it is critical to study photoelectrode performances under different conditions to effectively de-convolute the effects occurring at high irradiances. For this, it is necessary to characterise the behaviour of photoelectrodes (i) at different temperatures (at constant irradiance), (ii) at higher irradiances with known surface temperature, (iii) and under different conditions to isolate different recombination processes, e.g. by using appropriate catalysts or sacrificial reagents. Here, we present the results of the first two approaches for high photon fluxes (>100 kW m−2), which have not been reported previously for BiVO4 photoanodes. In summary, although bulk recombination aggravates with irradiance for BiVO4, but it is suppressed at high temperatures, the increased surface temperature at higher irradiances could also preferentially enhance the kinetics for oxygen evolution over the dissolution kinetics, specially when the conduction and valence band are saturated with electrons and holes, respectively. This could lead to relative improved stability as shown by the decrease in the dissolution factor and improved performances as observed in the optimal normalised photocurrent achieved at ca. 120 kW m−2.
High irradiance measurements could potentially be used as accelerated tests for degradation of stable BiVO4. The results presented in this study seem to indicate that at very high irradiances the temperature at the surface and the charge-saturated band edges might change the degradation mechanism and alter the kinetic rates of dissolution and recombination. Hence, these effects must be taken into account when such accelerated degradation tests are formulated and if this approach is used to assess the performance and stability of photoelectrodes.
5 Conclusions
This work reports the study of photoelectrode materials (Fe2O3 and BiVO4) under high irradiances (up to 358 kW m−2). For this, a unique PEC test cell for high flux applications was designed and successfully used to conduct photoelectrochemical experiments with thermal management to keep the photoelectrode samples at suitable temperatures. Current densities of up to 1500 and 300 A m−2 were achieved for FTO|Fe2O3 and FTO|BiVO4 respectively at 358 kW m−2. The sublinear behaviour observed for the current densities as a function of irradiance has been attributed to macroscale effects such as excessive bubble formation at the surface, ohmic drop due to poorly conductive substrates, and current density maldistribution.17 However, it is also possible that competing effects in the semiconducting properties of the material could arise from the increased temperature at the surface. For this, temperature-dependent studies were also performed under low irradiance (AM1.5G, 1 kW m−2). It was found that for FTO|Fe2O3 samples the effect of temperature is minimal compared to the current density losses at high irradiances. In the case of Ti|Fe2O3, it was found that the photocurrent at high bias increases with temperature, which is in contrast with the decrease in performance observed at high irradiances. Whilst the effect of temperature has qualitatively been eliminated as the explanation for the sub-linear irradiance dependence, these losses could be caused by bubbles, as predicted from multiphysics modelling, but also due to changes to the semiconductor properties that are challenging to deconvolve without further study. For FTO|BiVO4, it was found that at high temperatures the dissolution fraction increases, although an opposite effect was found at high irradiances. Future studies involving in situ measurements, e.g. IMPS, PEIS, IPCE and ICP-MS, are needed to fully decouple the contribution of temperature and high photon fluxes on the mechanism of photocurrent generation and degradation of photoelectrode materials, this would require the development and modification of the aforementioned techniques to operate under these challenging experimental conditions.The experimental methodology proposed here would facilitate the study of other semiconducting materials, such as WO3, LaFeO3, or Cu2O under high fluxes, for example with the promise of finding optimal conditions for the irradiance and temperature at which photoelectrode materials could operate for efficient solar-driven water splitting. These optimal conditions are caused by intertwined competing effects: favourable enhanced kinetics and thermodynamic requirements for oxygen evolution, thermally activated mobility carrier transport and electron conductivity; and, unfavourable effects due to excessive bubble evolution, and increased recombination rates in the bulk of the semiconductor under charge carrier saturation of band edges. The results from this study open the possibility of using high photon fluxes as means of accelerated testing for assessing the stability of photoelectrodes. Although care must be taken to confirm that the degradation mechanism has not been altered at high irradiances. Furthermore, this study allows to study fundamental transport phenomena in the materials and provides insight into the engineering design of high flux PEC systems, which would allow the miniaturisation of these devices and the possibility of advantageous thermal integration.
Author contributions
Isaac Holmes-Gentle: conceptualisation, methodology, investigation, visualization, writing – original draft. Franky E. Bedoya-Lora: conceptualisation, methodology, investigation, visualization, writing – original draft. Lorenzo Aimone: investigation, writing – original draft. Sophia Haussener: conceptualisation, supervision, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work performed with the financial support of the Swiss National Science Foundation Sinergia grant #CRSII5_202225 and Backup scheme Starting Grant “Strategic Computation and Optimization of Unified Templates for Solar Fuels” #155876. The authors thank Philip Suter (EPFL) for the design of the shield and the aperture, Clemens Suter (EPFL) on advice regarding HFSS operation, Roberto Valenza (EPFL) for the design of the cell for characterisation at low intensities, and Fatwa Abdi (HZB) for his advice on the fabrication of BiVO4 photoelectrodes via spray pyrolysis.References
- Q. Wang, C. Pornrungroj, S. Linley and E. Reisner, Nat. Energy, 2021, 13–24 CrossRef CAS.
- M. Dumortier, S. Tembhurne and S. Haussener, Energy Environ. Sci., 2015, 8, 3614–3628 RSC.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 RSC.
- O. Khaselev and J. A. Turner, Science, 1998, 280, 425–427 CrossRef CAS PubMed.
- H. Wang, T. Deutsch and J. A. A. Turner, ECS Trans., 2008, 6, 37–44 CrossRef CAS.
- G. Segev, H. Dotan, K. D. Malviya, A. Kay, M. T. Mayer, M. Grätzel and A. Rothschild, Adv. Energy Mater., 2016, 6, 1500817 CrossRef.
- M. V. N. S. Gupta, H. Baig, K. S. Reddy, T. K. Mallick, B. Pesala and A. A. Tahir, ACS Appl. Energy Mater., 2020, 3, 9002–9009 CrossRef CAS.
- H. Dotan, N. Mathews, T. Hisatomi, M. Grätzel and A. Rothschild, J. Phys. Chem. Lett., 2014, 5, 3330–3334 CrossRef CAS PubMed.
- M. R. Shaner, K. T. Fountaine, S. Ardo, R. H. Coridan, H. A. Atwater and N. S. Lewis, Energy Environ. Sci., 2014, 7, 779–790 RSC.
- L. Peter, Curr. Opin. Green Sustainable Chem., 2021, 31, 100505 CrossRef CAS.
- Z. Chen, H. N. Dinh and E. Miller, Photoelectrochemical Water Splitting: Standards, Experimental Methods, and Protocols, Springer New York, New York, NY, 2013 Search PubMed.
- C. K. Ong, S. Dennison, K. Hellgardt and G. Kelsall, ECS Trans., 2011, 35, 11–19 CrossRef CAS.
- A. Vilanova, T. Lopes, C. Spenke, M. Wullenkord and A. Mendes, Energy Storage Mater., 2018, 13, 175–188 CrossRef.
- A. Vilanova, P. Dias, J. Azevedo, M. Wullenkord, C. Spenke, T. Lopes and A. Mendes, J. Power Sources, 2020, 454, 227890 CrossRef CAS.
- F. F. Abdi and R. van de Krol, J. Phys. Chem. C, 2012, 116, 9398–9404 CrossRef CAS.
- S. Caron, M. Röger and M. Wullenkord, Energies, 2020, 13, 5196 CrossRef CAS.
- F. E. Bedoya-Lora, I. Holmes-Gentle and S. Haussener, Electrochim. Acta, 2023, 462, 142703 CrossRef CAS.
- S. A. Bonke, M. Wiechen, D. R. MacFarlane and L. Spiccia, Energy Environ. Sci., 2015, 8, 2791–2796 RSC.
- J. Jia, L. C. Seitz, J. D. Benck, Y. Huo, Y. Chen, J. W. D. Ng, T. Bilir, J. S. Harris and T. F. Jaramillo, Nat. Commun., 2016, 7, 13237 CrossRef CAS PubMed.
- S. Tembhurne, F. Nandjou and S. Haussener, Nat. Energy, 2019, 4, 399–407 CrossRef CAS.
- I. Holmes-Gentle, S. Tembhurne, C. Suter and S. Haussener, Nat. Energy, 2023, 586–596 CrossRef CAS.
- A. Fallisch, L. Schellhase, J. Fresko, M. Zedda, J. Ohlmann, M. Steiner, A. Bösch, L. Zielke, S. Thiele, F. Dimroth and T. Smolinka, Int. J. Hydrogen Energy, 2017, 42, 26804–26815 CrossRef CAS.
- N. Kelly, T. Gibson and D. Ouwerkerk, Int. J. Hydrogen Energy, 2008, 33, 2747–2764 CrossRef CAS.
- M. A. Khan, I. Al-Shankiti, A. Ziani, N. Wehbe and H. Idriss, Angew. Chem., 2020, 132, 14912–14918 CrossRef.
- G. Peharz, F. Dimroth and U. Wittstadt, Int. J. Hydrogen Energy, 2007, 32, 3248–3252 CrossRef CAS.
- S. Rau, S. Vierrath, J. Ohlmann, A. Fallisch, D. Lackner, F. Dimroth and T. Smolinka, Energy Technol., 2014, 2, 43–53 CrossRef CAS.
- X. Ye, J. Yang, M. Boloor, N. A. Melosh and W. C. Chueh, J. Mater. Chem. A, 2015, 3, 10801–10810 RSC.
- H. Huang, J. Wang, M. Zhao, N. Zhang, Y. Hu, J. Feng, Z. Li and Z. Zou, ACS Mater. Lett., 2022, 4, 1798–1806 CrossRef CAS.
- P. Dias, T. Lopes, L. Andrade and A. Mendes, J. Power Sources, 2014, 272, 567–580 CrossRef CAS.
- L. Zhang, X. Ye, M. Boloor, A. Poletayev, N. A. Melosh and W. C. Chueh, Energy Environ. Sci., 2016, 9, 2044–2052 RSC.
- W. Jiang, Y. An, Z. Wang, M. Wang, X. Bao, L. Zheng, H. Cheng, P. Wang, Y. Liu, Z. Zheng, Y. Dai and B. Huang, Appl. Catal., B, 2022, 304, 121012 CrossRef CAS.
- C. Zhou, L. Zhang, X. Tong and M. Liu, ACS Appl. Mater. Interfaces, 2021, 13, 61227–61236 CrossRef CAS PubMed.
- Y. Liu, L. Chen, X. Zhu, H. Qiu, K. Wang, W. Li, S. Cao, T. Zhang, Y. Cai, Q. Wu and J. Li, J. Electroanal. Chem., 2022, 924, 116859 CrossRef CAS.
- F. Alhersh, PhD thesis, Imperial College London, London, 2019.
- I. Y. Ahmet, Y. Ma, J.-W. Jang, T. Henschel, B. Stannowski, T. Lopes, A. Vilanova, A. Mendes, F. F. Abdi and R. van de Krol, Sustainable Energy Fuels, 2019, 3, 2366–2379 RSC.
- R.-T. Gao, L. Liu, Y. Li, Y. Yang, J. He, X. Liu, X. Zhang, L. Wang and L. Wu, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2300493120 CrossRef CAS PubMed.
- R.-T. Gao, J. Zhang, T. Nakajima, J. He, X. Liu, X. Zhang, L. Wang and L. Wu, Nat. Commun., 2023, 14, 2640 CrossRef CAS PubMed.
- H. Wu, L. Zhang, A. Du, R. Irani, R. van de Krol, F. F. Abdi and Y. H. Ng, Nat. Commun., 2022, 13, 6231 CrossRef CAS PubMed.
- P. Dias, A. Vilanova, T. Lopes, L. Andrade and A. Mendes, Nano Energy, 2016, 23, 70–79 CrossRef CAS.
- Y. Kuang, Q. Jia, G. Ma, T. Hisatomi, T. Minegishi, H. Nishiyama, M. Nakabayashi, N. Shibata, T. Yamada, A. Kudo and K. Domen, Nat. Energy, 2016, 2, 1–9 Search PubMed.
- F. Bedoya-Lora, A. Hankin, I. Holmes-Gentle, A. Regoutz, M. Nania, D. Payne, J. Cabral and G. Kelsall, Electrochim. Acta, 2017, 251, 1–11 CrossRef CAS.
- F. F. Abdi, T. J. Savenije, M. M. May, B. Dam and R. van de Krol, J. Phys. Chem. Lett., 2013, 4, 2752–2757 CrossRef CAS.
- G. Levêque, R. Bader, W. Lipiński and S. Haussener, Opt. Express, 2016, 24, A1360 CrossRef PubMed.
- R. Gill, E. Bush, P. Haueter and P. Loutzenhiser, Rev. Sci. Instrum., 2015, 86, 125107 CrossRef PubMed.
- F. E. Bedoya-Lora, I. Holmes-Gentle and A. Hankin, Curr. Opin. Green Sustainable Chem., 2021, 29, 100463 CrossRef CAS.
- F. E. Bedoya-Lora, M. E. Valencia-García, A. Hankin, D. Klotz and J. A. Calderón, Electrochim. Acta, 2022, 402, 139559 CrossRef CAS.
- A. Hankin, F. E. Bedoya-Lora, J. C. Alexander, A. Regoutz and G. H. Kelsall, J. Mater. Chem. A, 2019, 7, 26162–26176 RSC.
- H. Luo, A. H. Mueller, T. M. McCleskey, A. K. Burrell, E. Bauer and Q. X. Jia, J. Phys. Chem. C, 2008, 112, 6099–6102 CrossRef CAS.
- I. Holmes-Gentle, H. Agarwal, F. Alhersh and K. Hellgardt, Phys. Chem. Chem. Phys., 2018, 20, 12422–12429 RSC.
- R. Memming, Semiconductor Electrochemistry, John Wiley & Sons, Ltd, 2015, pp. 1–22 Search PubMed.
- P. Würfel, Physics of Solar Cells: from Principles to New Concepts|Wiley, John Wiley & Sons, Ltd, 2008 Search PubMed.
- W. W. Gärtner, Phys. Rev., 1959, 116, 84–87 CrossRef.
- M. A. Butler, J. Appl. Phys., 1977, 48, 1914–1920 CrossRef CAS.
- J. Reichman, Appl. Phys. Lett., 1980, 36, 574 CrossRef CAS.
- F. E. Bedoya Lora, A. Hankin and G. H. Kelsall, J. Mater. Chem. A, 2017, 5, 22683–22696 RSC.
- F. Le Formal, E. Pastor, S. D. Tilley, C. A. Mesa, S. R. Pendlebury, M. Grätzel and J. R. Durrant, J. Am. Chem. Soc., 2015, 137, 6629–6637 CrossRef CAS PubMed.
- K. Upul Wijayantha, S. Saremi-Yarahmadi and L. M. Peter, Phys. Chem. Chem. Phys., 2011, 13, 5264 RSC.
- C. A. Mesa, L. Francàs, K. R. Yang, P. Garrido-Barros, E. Pastor, Y. Ma, A. Kafizas, T. E. Rosser, M. T. Mayer, E. Reisner, M. Grätzel, V. S. Batista and J. R. Durrant, Nat. Chem., 2020, 12, 82–89 CrossRef CAS PubMed.
- S. Zhang and W. Leng, Nat. Chem., 2020, 12, 1097–1098 CrossRef CAS PubMed.
- L. M. Peter, A. B. Walker, T. Bein, A. G. Hufnagel and I. Kondofersky, J. Electroanal. Chem., 2020, 872, 114234 CrossRef CAS.
- I. Holmes-Gentle, F. Bedoya-Lora, F. Alhersh and K. Hellgardt, J. Phys. Chem. C, 2019, 123, 17–28 CrossRef CAS.
- A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. Fernández Rivas, Joule, 2020, 4, 555–579 CrossRef CAS.
- F. M. Toma, J. K. Cooper, V. Kunzelmann, M. T. McDowell, J. Yu, D. M. Larson, N. J. Borys, C. Abelyan, J. W. Beeman, K. M. Yu, J. Yang, L. Chen, M. R. Shaner, J. Spurgeon, F. A. Houle, K. A. Persson and I. D. Sharp, Nat. Commun., 2016, 7, 12012 CrossRef PubMed.
- S. Zhang, I. Ahmet, S.-H. Kim, O. Kasian, A. M. Mingers, P. Schnell, M. Kölbach, J. Lim, A. Fischer, K. J. J. Mayrhofer, S. Cherevko, B. Gault, R. van de Krol and C. Scheu, ACS Appl. Energy Mater., 2020, 3, 9523–9527 CrossRef CAS PubMed.
- R. Ertuğrul and A. Tataroğlu, Chin. Phys. Lett., 2012, 29, 077304 CrossRef.
- I. Strzalkowski, S. Joshi and C. R. Crowell, Appl. Phys. Lett., 2008, 28, 350–352 CrossRef.
- K. T. Butler, B. J. Dringoli, L. Zhou, P. M. Rao, A. Walsh and L. V. Titova, J. Mater. Chem. A, 2016, 4, 18516–18523 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta05257e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |