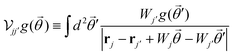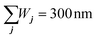DOI:
10.1039/D2NR06286K
(Paper)
Nanoscale, 2023,
15, 3150-3158
Nonlocal and cascaded effects in nonlinear graphene nanoplasmonics†
Received
9th November 2022
, Accepted 24th December 2022
First published on 17th January 2023
Abstract
The ability of plasmons to focus light on nanometer length scales opens a wide range of enticing applications in optics and photonics, among which the enhancement of nonlinear light–matter interactions for all-optical modulation and spectral diversification emerges as a prominent theme. However, the subwavelength plasmonic near-field enhancement in good plasmonic materials such as noble metals is hindered by large ohmic losses, while conventional phase-matching of fields in bulk nonlinear crystals is not suitable for realizing nonlinear optical phenomena on the nanoscale. In contrast, anharmonic electron motion of free charge carriers in highly-doped graphene, which supports long-lived, highly-confined, and actively-tunable plasmons, renders the carbon monolayer an excellent platform for both plasmonics and nonlinear optics. Here we theoretically explore the enhancement in nonlinear response that can be achieved by interfacing multiple graphene nanostructures in close proximity to trigger nonlocal effects associated with large gradients in the electromagnetic near field. Focusing on second- and third-harmonic generation, we introduce a semianalytical formalism to describe interacting graphene nanoribbons with independent width, location, and electrical doping, so as to realize configurations in which plasmonic resonances may simultaneously enhance both the fundamental optical excitation frequency and harmonic intermediary and/or output frequencies. Our findings reveal the importance of both passive and active tuning in the design of atomically-thin nanostructures for nonlinear optical applications, and in particular emphasize the role played by nonlocal effects in generating an even-ordered nonlinear response that may contribute to other nonlinear optical processes through a cascaded interaction. We anticipate that our findings can aid in the design of actively-tunable nonlinear plasmonic resonators and metasurfaces.
1 Introduction
Current research in nonlinear plasmonics seeks to intensify nonlinear optical phenomena on the nanoscale by exploiting the extreme light-focusing ability of plasmons—the collective oscillations of free charge carriers.1–4 The manipulation of light on nanometer length scales enabled by plasmonics,5,6 in tandem with spectral and temporal control of light by light through nonlinear optics,7 paves way for full spatio-temporal control over electromagnetic fields, with appealing prospects to develop all-optical integrated devices.8–10 However, in practice, the subwavelength optical excitations supported by noble metals—the traditional material platform for plasmonics—are impeded by high ohmic losses that limit the achievable near-field enhancement sought in nonlinear optics applications.11,12 Furthermore, being defined by the intrinsic electronic properties of the host media and its geometry, plasmon resonances at near-infrared and visible frequencies in noble metals offer limited opportunities to achieve active tunability.13,14
Graphene—the atomically-thin carbon monolayer—is now recognized as a platform for nano-optics at terahertz (THz) and infrared (IR) frequencies that supports high-quality plasmon resonances when doped with additional charge carriers.15,16 The emergence of highly-doped graphene in plasmonics has been further catalyzed by the electrical tunability of its plasmons, which exhibit stronger optical confinement than their noble metal counterparts, thus stimulating explorations across all areas of nanophotonics that capitalize on long-lived, strongly confined, and actively tunable optical resonances spanning the THz and near-IR spectral regimes.17–20 Within nonlinear plasmonics, graphene is rendered a particularly attractive material platform by its linear electronic dispersion relation at low energies that results in electron motion deviating significantly from the harmonic oscillation of an external electromagnetic field.21,22 The electron dispersion of graphene is thus deemed anharmonic, and gives rise to a strong intrinsic optical nonlinearity associated with harmonic generation that can be further amplified by graphene plasmons.23,24
The nonlinear optical properties of extended graphene have been widely studied in experiment,25–29 where in some cases plasmon-assisted nonlinear optical phenomena have been observed.30–33 In parallel, theoretical proposals to develop nonlinear metasurfaces comprised of arrays of graphene nanostructures predict dramatic enhancements in the nonlinear yield due to localized plasmon resonances.34–36 Typically, such nonlinear metasurfaces are comprised of identical units arranged periodically on length scales comparable to the impinging light wavelength, so that the morphology and intrinsic optical properties of each isolated graphene nanostructure determine the optical response. However, two-dimensional (2D) materials such as graphene offer intriguing possibilities to develop heterostructures that combine nanoscale elements with complementary optical properties to interact on truly nanometer (i.e., ≃1 nm) length scales,37 leading to functionalities exceeding the sum of their individual components.38,39 In the case of graphene, such heterostructures offer additional promise due to the possibility of independently and electrically tuning the optical properties of different components,40 which has yet to be explored in the context of nonlinear plasmonics.
Here, we theoretically investigate the plasmon-driven nonlinear optical response associated with second- and third-harmonic generation in actively-tunable graphene nanoribbon heterostructures. Our explorations emphasize the effect of spatial inhomogeneity on the plasmonic near fields produced by closely-spaced graphene nanoribbons, which can trigger even-ordered nonlinear optical processes in otherwise inversion-symmetric nanostructures.29,41,42 We base our work on a theoretical formalism that we introduce to facilitate a broad parametric sweep of the geometrical and intrinsic electrical properties of graphene nanoribbon ensembles to reveal the enhancement in harmonic generation that can be achieved by independent active and/or passive tuning of individual structures. We furthermore elucidate the role of cascaded nonlinear optical effects in graphene heterostructures, whereby third-harmonic generation is influenced by the second-order mixing of the fundamental field and its second harmonic. We anticipate that our findings can aid in the design of polariton-driven nonlinear optical processes in two-dimensional heterostructures.
2 Theory
We investigate graphene nanoribbon ensembles driven by monochromatic plane wave illumination, where parallel ribbons of varying size and doping can be arranged to tailor the plasmon-enhanced near fields that trigger a nonlinear optical response, which we quantify by the net induced dipole moment of the ensemble that radiates into the far field. In what follows, we first outline the theoretical methods employed to describe both the linear and nonlinear optical response of arbitrary interacting 2D nanostructures in the quasistatic approximation, which is applied here to one-dimensional nanoribbons but can be straightforwardly adapted to treat other 2D geometries. We then provide expressions governing the intrinsic nonlocal nonlinear optical response of free electrons in graphene.
2.1 Optical response of two-dimensional nanostructure ensembles
We theoretically explore the interaction of N distinct 2D nanostructures with light characterized by a uniform electric field Eexte−iωt + c.c., where the amplitude Eext is assumed to be real and linearly polarized. When the nanostructures are all contained within a region of size well-below the wavelength of light that excites them, the optical response can be described in the quasistatic approximation by the scalar potential| | 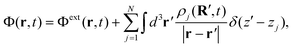 | (1) |
where Φext denotes the external potential associated with Eext and ρj is the induced 2D charge density in structure j that lies on the plane r = (R, zj) spanning coordinates R = (x, y). It is convenient to decompose the total potential in a perturbation series with the external field amplitude as a perturbation parameter according to| | 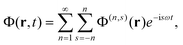 | (2) |
where n indicates the perturbation order in Eext and s the harmonic index, such that |s| ≤ n with n ≥ 1. Now, at order n and harmonic s, the induced charge in structure j satisfies the continuity equation ρ(n,s)j = −(i/sω)∇R· j(n,s)j for the associated (surface) current density| | | j(n,s)j(R) = fj(R)σ(1,s)jE(n,s)j(R) + j(n,s)j,NL(R), | (3) |
where the first term accounts for the linear response to the field E(n,s)j(R) = −∇RΦ(n,s)(R, zj) within the 2D structure, mediated by a filling function fj(R) that captures the spatial dependence of the intrinsic linear conductivity σ(1,s)j (i.e., fj = 1 for points in the structure and 0 otherwise), and the second term describes contributions from the intrinsic (i.e., bulk) nonlinear response of graphene.
To linear order, we take n = s = 1 in eqn (3) and recover Ohm's law j(1,1)j = fj![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ(1,1)jE(1,1)j, from which the charge density can be expressed in terms of the potential as
σ(1,1)jE(1,1)j, from which the charge density can be expressed in terms of the potential as
| | 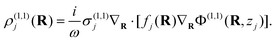 | (4) |
We then introduce a normalized coordinate 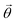 that parametrizes a 2D structure, such that
that parametrizes a 2D structure, such that 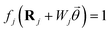 within structure j and vanishes elsewhere, effectively defining its geometry in terms of a characteristic size Wj (here taken as the ribbon width) and location rj = (Rj, zj) (e.g., the center of mass). Combining eqn (1) and (4), the potential in structure j is found to satisfy the self-consistent relation
within structure j and vanishes elsewhere, effectively defining its geometry in terms of a characteristic size Wj (here taken as the ribbon width) and location rj = (Rj, zj) (e.g., the center of mass). Combining eqn (1) and (4), the potential in structure j is found to satisfy the self-consistent relation
| | 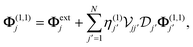 | (5) |
where, adopting the formalism of ref.
43, we have introduced the integrals
and the differential operator
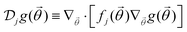
, while the dimensionless parameter
η(s)j = i
σ(1,s)j/
sωWj contains all the frequency and material dependence entering the intrinsic conductivity. In effect, the Coulomb integral
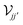
yields the potential produced at
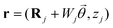
in ribbon
j by the charge at
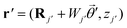
in ribbon
j′. The system of
eqn (5) can then be solved by constructing a block matrix spanning discretized real space elements: indeed, defining the potential in each structure as
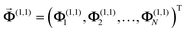
(similarly for
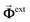
), the self-consistent solution for the combined system is
| | 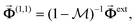 | (6) |
where
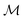
is a square block matrix comprised of matrices
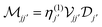
, here defined by representing the operators
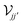
and
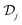
on a real space grid, while 1 denotes the identity matrix. In the ESI
† we provide details on the spatial representation of the operators
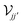
and
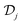
leading to the block matrix equation of
eqn (6) for nanoribbons.
The nonlinear response is conveniently described in terms of the induced charge density by using the continuity equation to recast eqn (3) as
| | 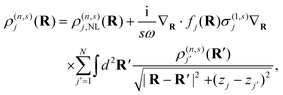 | (7) |
where
ρ(n,s)j,NL = −(i/
sω)∇
R·
j(n,s)j,NL acts as a nonlinear source term analogous to Φ
ext in
eqn (1). Then, adopting the formalism leading to
eqn (5) and (6), the integro-differential equation above can be expressed as
| | 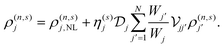 | (8) |
Defining vectors 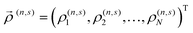 , the solution of eqn (8) can also be expressed in block-matrix form as
, the solution of eqn (8) can also be expressed in block-matrix form as
| | 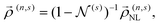 | (9) |
where the elements
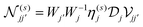
may be constructed by representing the operators
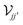
and
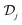
as matrices spanning discrete real-space elements in the 2D structures
j and
j′. In the ESI
† we provide further details on the derivation of
eqn (9) for the specific case of ribbons with translational symmetry in one dimension, which leads to a dependence of
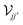
and
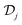
on the harmonic index
s. In analogy to
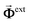
in
eqn (6), the vector
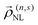
in
eqn (9) acts as the external source of nonlinear response in the system, and depends on the specific definition of the nonlinear current
j(n,s)NL.
2.2 Nonlinear response of graphene
In graphene doped to a Fermi energy EF, the dominant contribution to the optical response at frequencies ħω ≲ EF stems from intraband charge carrier motion, which can be described in the Boltzmann transport equation formalism by adopting the linearized electronic dispersion ħεk = ±ħvF|k| for electron (upper sign) and hole (lower sign) doping, where vF ≈ c/300 is the Fermi velocity in graphene. Following the prescription and methods of ref. 44, we express the current associated with the optical response at perturbation order n and harmonic index s in extended graphene as| | | j(n,s) = σ(1,s)E(n,s) + j(n,s)NL, | (10) |
where the first term accounts for the response of graphene to the induced field E(n,s) mediated by the linear conductivity σ(1,s) = (ie2EF/πħ2)Dsω, where Dsω ≡ (sω + iγ)−1 is a complex frequency factor that includes inelastic scattering processes in the phenomenological rate γ introduced in the relaxation-time approximation, while the second term in eqn (10) accounts for nonlinear optical processes. In obtaining specific expressions for j(n,s)NL, nonlocal effects in the optical response are incorporated by retaining terms up to linear order in the gradient of the electric field. For second-harmonic generation (SHG), we recover the result of ref. 44,| | 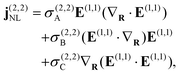 | (11) |
where| | | σ(2,2)A = ∓S(2)D2ωDω(3Dω + 4D2ω), | (12a) |
| | 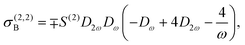 | (12b) |
| | 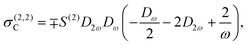 | (12c) |
with the prefactor S(2) ≡ ie3vF2/4πħ2. The current obtained in eqn (11) reflects the centrosymmetry of the honeycomb lattice in graphene, so that an even-ordered nonlinear response emerges only from gradients in the local electric field.29,45,46 Retaining electric field gradients in the third-order optical response, we obtain the third-harmonic generation (THG) current| | | j(3,3)NL = σ(3,3)E(1,1)(E(1,1)·E(1,1)) + j(2,{1,2})NL, | (13) |
where σ(3,3) = (3ie4vF2/4πħ2EF)D3ωD2ωDω is the local third-order THG conductivity and the term j(2,\{1,2\})NL describes the cascaded contribution to the nonlinear optical response that arises from the second-order mixing of the linear field with the nonlinear field generated by the current of eqn (11) at the second harmonic.47 As we show in the ESI,† the cascaded contribution to THG is tantamount to sum/difference frequency generation described by the nonlinear current| | 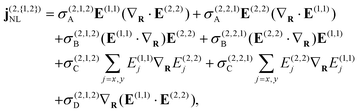 | (14) |
where| | 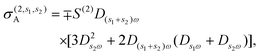 | (15a) |
| | 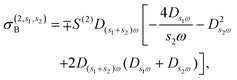 | (15b) |
| | 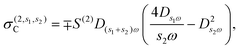 | (15c) |
| | 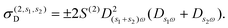 | (15d) |
The cascaded contribution to THG thus involves electric field gradients of both the fundamental and SHG fields produced in graphene. The nonlinear conductivities of graphene derived above incorporate nonlocal effects by including terms up to linear order in the electric field gradient, for which even-ordered nonlinear optical phenomena emerge in a centrosymmetric material. While this approximation is valid for optical wave vectors ≲1 nm−1, higher-order corrections may become relevant for extremely-confined fields that vary dramatically on sub-nanometer length scales.37,39 In general, the perturbative formalism described here is compatible with optical pulses of moderate intensity employed in nonlinear optical experiments,27,28 while pulses of fluence ≳1 J m−2 are expected to produce transient effects associated with the induced out-of-equilibrium electronic distribution.33,48,49
3 Results and discussion
We focus on the optical response of interacting highly-doped graphene nanoribbons, all of which have finite widths in ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and are translationally invariant in ŷ, so that the potential can be decomposed in plane waves indexed by a wave vector q according to Φ(n,s)(R) = φ(n,s)(x)eisqy. The symmetry of such nanoribbon ensembles in y simplifies our calculations for normally-impinging plane-wave illumination with electric field amplitude Eext polarized along
and are translationally invariant in ŷ, so that the potential can be decomposed in plane waves indexed by a wave vector q according to Φ(n,s)(R) = φ(n,s)(x)eisqy. The symmetry of such nanoribbon ensembles in y simplifies our calculations for normally-impinging plane-wave illumination with electric field amplitude Eext polarized along ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , such that Φext = −xEext, and localized plasmon resonances can be optically excited in each ribbon. The nonlinear optical response is quantified by computing the induced charge density in eqn (9), from which the induced dipole moment (per unit length along ŷ) of the combined system
, such that Φext = −xEext, and localized plasmon resonances can be optically excited in each ribbon. The nonlinear optical response is quantified by computing the induced charge density in eqn (9), from which the induced dipole moment (per unit length along ŷ) of the combined system 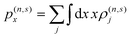 yields the effective polarizability per unit length α(n,s) ≡ p(n,s)x/(Eext)n and the susceptibility
yields the effective polarizability per unit length α(n,s) ≡ p(n,s)x/(Eext)n and the susceptibility 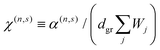 , where dgr = 0.33 nm is the inter-layer spacing of graphite, commonly used to estimate the thickness of graphene.25
, where dgr = 0.33 nm is the inter-layer spacing of graphite, commonly used to estimate the thickness of graphene.25
The archetypical system in which to explore the nonlinear optical response associated with interacting localized 2D plasmons is a pair (N = 2) of co-planar (z1 = z2) graphene nanoribbons separated by a distance d, as illustrated schematically in Fig. 1a, where the ribbons have independent widths (W1 and W2), Fermi energies (EF1 and EF2), and damping rates (γ1 and γ2) that lead to distinct plasmon resonances (ωp1 and ωp2). For an isolated structure (j = j′) of size Wj and Fermi energy EFj, the self-consistent relation for the scalar potential in eqn (5) reduces to the eigenvalue problem 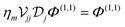 , from which the eigenvalues ηm determine the plasmon resonances
, from which the eigenvalues ηm determine the plasmon resonances
| | 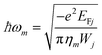 | (16) |
in the Drude conductivity model for graphene (neglecting losses). Following the prescription in the ESI,
† the first three finite eigenvalues are computed as
η1 = −0.0689,
η2 = −0.0289, and
η3 = −0.0184. The plasmon resonance condition of
eqn (16) sets the properties of graphene nanoribbon dimers that can simultaneously support plasmons at fundamental and harmonic frequencies of the incoming field, a configuration that we explore in
Fig. 1b for ribbons with widths
W1 = 160 nm and
W2 = 40 nm at a common doping level
EF1 =
EF2 = 0.4 eV, where both the linear optical response (here quantified by the absorption cross section) and SHG susceptibility (in logarithmic scale) are presented for several values of the co-planar ribbon separation
d. Importantly, besides the enhancement of SHG provided by matching the lowest-order dipolar plasmon modes at both input and output frequencies, the dimer configuration provides the symmetry-breaking required to induce a nonvanishing dipolar second-order response. The influence of nonlocal effects is clearly enhanced by bringing the ribbons closer together, such that the dipolar SHG response intensifies with the stronger field gradients produced by near field coupling.
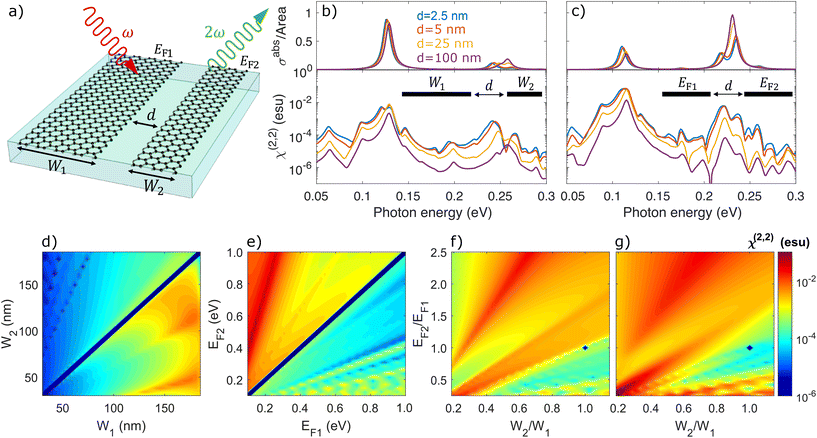 |
| | Fig. 1 Second-harmonic generation in co-planar asymmetric nanoribbon pairs. (a) Schematic illustration of second-harmonic generation (SHG) in two co-planar graphene nanoribbons separated by a distance d and characterized by widths Wj, Fermi energies EFj, and damping rates γj for j∈{1, 2}. (b) The effect of inter-ribbon interaction is explored in both the linear absorption cross section (upper panel) and the SHG susceptibility (lower panel) by varying the separation distance d for a dimer formed by arranging ribbons of width W1 = 160 nm and W2 = 40 nm at the same doping EFj = 0.4 eV, such that the frequency of the lowest-order dipolar plasmon resonance in ribbon j = 1 is half of that in ribbon j = 2 (i.e., frequency ∝Wj1/2). (c) Similar to (b), but for ribbons with equal width Wj = 100 nm and different dopings EF1 = 0.2 eV and EF2 = 0.8 eV. (d–f) SHG from co-planar ribbons spaced d = 25 nm apart when: (d) the ribbons have the same doping EF1 = EF2 = 0.4 eV and varying widths Wj; (e) the ribbons have equal widths W1 = W2 = 100 nm and varying doping levels EFj; (f) both the width and doping of ribbon j = 2 are changed. (g) Similar to (f), but for a small ribbon separation d = 2.5 nm. In panels (d–g), the impinging light frequency is maintained at the lowest-order dipolar plasmon resonance frequency ħω = (−e2EF1/πη1W1)1/2. Results are obtained for an inelastic broadening ħγ1 = ħγ2 = 10 meV and a homogeneous environment with permittivity ε = 1. | |
In an alternative approach to triggering SHG, we explore in Fig. 1c the response of a co-planar graphene nanoribbon dimer formed by ribbons with a common width W1 = W2 = 100 nm but unequal doping levels EF1 = 0.2 eV and EF2 = 0.8 eV. Interestingly, although W1 + W2 is preserved in the spectra of panels (b) and (c), roughly one order of magnitude improvement in the SHG yield manifests in the latter case within the same excitation energy window, presumably due to the larger overall Drude weight for the ribbon supporting a plasmon resonance at the second harmonic frequency. We also note the increased spectral splitting in the high-energy dipolar plasmon resonance of the j = 2 ribbon in both scenarios, which is attributed to hybridization with a higher-order mode supported by the j = 1 ribbon.50 More specifically, analysis of the resonance condition in eqn (16) reveals that the spectral splitting in Fig. 1c is a consequence of hybridization between the first- (η1) and third-order (η3) dipolar (bright) modes.
To identify optimal configurations for plasmon-enhanced SHG in co-planar ribbon dimers, we present the SHG response while (passively) sweeping over the ribbon widths Wj at fixed doping EFj = 0.4 eV in Fig. 1d and when (actively) varying the doping levels EFj of ribbons with fixed width Wj = 100 nm in Fig. 1e, such that in both cases the ribbons are separated by d = 25 nm and the impinging optical frequency is fixed to the plasmon resonance in the j = 1 ribbon (i.e., ω = ωp1). The broad parameter sweep encompasses situations in which the symmetry of the ribbon dimer in the polarization direction quenches the dipolar SHG response while also probing the double-resonance condition (e.g., ωp2 = 2ωp1) explored in Fig. 1b and c. We furthermore consider configurations in which the light frequency is tuned to the plasmon resonance specified by the attributes of the j = 1 ribbon, while both the width and doping of the second ribbon are varied according to Fig. 1f and g for separation distances d = 25 nm and d = 2.5 nm, respectively, that modify the inter-ribbon interaction. Our findings reveal that the SHG response can be amplified when multiple plasmon modes of the nanoribbon are resonant at either the fundamental or second-harmonic frequency, while the nonlinear response can be altered by orders of magnitude with only small variations in the Fermi energy of only one ribbon in a heterostructure.
While co-planar ribbons provide the required symmetry-breaking to trigger strong SHG, the inter-ribbon coupling is localized at the ribbon edges. Vertical stacking thus presents an alternative configuration to interface nanoribbons over a larger cross-sectional area, as illustrated schematically in Fig. 2a. The optical response of a stacked nanoribbon pair is presented in Fig. 2b for ribbons of width W1 = 160 nm and W2 = 40 nm with equal doping EF1 = EF2 = 0.4 eV, so that the lowest-order dipolar plasmon resonances satisfy ωp2 = 2ωp1 as in Fig. 1b. The linear absorption cross section reveals strong hybridization of the dipolar plasmon resonance as the ribbon separation parameter d decreases, while the SHG susceptibility χ(2,2) presents peaks of similar magnitude as those obtained in the co-planar configuration that emerge at the plasmon resonances. We attribute this behaviour to the greater nanoribbon interaction area available in the stacked geometry, which ultimately leads to larger hybridization effects.
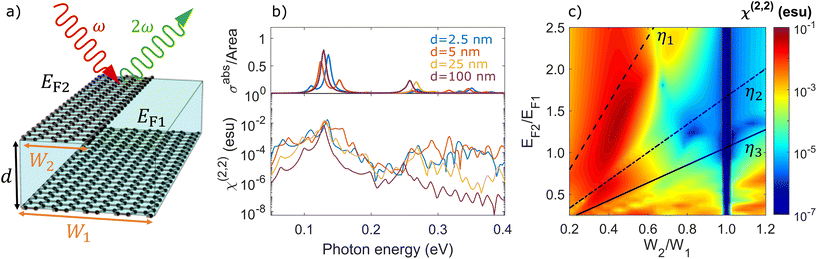 |
| | Fig. 2 Second-harmonic generation in stacked nanoribbon pairs. (a) Schematic of parallel graphene nanoribbons separated by a vertical distance d and aligned on one edge. Ribbon j∈{1, 2} is characterized by a width Wj and Fermi energy EFj. (b) Linear absorption cross section (upper panel) and SHG susceptibility (lower panel) of a stacked nanoribbon pair with W1 = 160 nm, W2 = 40 nm, and EF1 = EF2 = 0.4 eV for different separation distances. (c) SHG susceptibility of a stacked ribbon pair separated by d = 25 nm when the illumination frequency is fixed to the lowest-order dipolar plasmon resonance of ribbon j = 1 with W1 = 160 nm and EF1 = 0.4 eV as the width and doping of ribbon j = 2 are varied. Results are obtained for self-standing ribbons and a damping ħγj = 10 meV. | |
In Fig. 2c we maintain W1 = 160 nm and EF1 = 0.4 eV in the first ribbon and fix the illumination frequency to the lowest-order dipolar plasmon resonance (ℏωp1 = 0.13 eV) while varying the width and doping of ribbon j = 2 in order to explore the optimal second-harmonic response in the stacked configuration. Note that the dip in SHG response at W2 = W1 = 160 nm corresponds to an inversion-symmetric heterostructure, independent of the chosen Fermi energies. Prominent features in the SHG response correspond to overlap of the leading bright modes with the second harmonic frequency in ribbon j = 2. Consequently, although not radiating into the far field, the second-order ribbon eigenmode may still contribute significantly to the SHG response. Analogously, the large SHG below EF2 = 0.2 eV in Fig. 2c originates in coalescing higher-order modes. In particular, when the illumination frequency matches the dipolar plasmon resonance of ribbon j = 1, an enhancement in harmonic generation at sω emerges when the condition EF2/EF1 = s2W2ηm/W1η1 is met for eigenvalues ηm. We indicate the resonance conditions for the first three finite ribbon eigenmodes in Fig. 2c by black dashed, dot-dashed, and solid lines, which however do not match perfectly with maxima in the SHG response due to hybridization effects. Larger ribbon separations would limit mode hybridization, thus matching the optimal SHG response with the aforementioned condition, as illustrated in Fig. S2 in the ESI.† Furthermore, the optimal horizontal alignment in stacked ribbon dimers comprised of ribbons with constant width and different doping levels has been analyzed in Fig. S3 in the ESI,† and underscores the resonant enhancement of SHG that occurs when ωp2 = 2ωp1.
Now, turning our attention to the third-order response, we investigate THG in a system formed by three interacting graphene ribbons with independent widths Wj and doping levels EFj for j∈{1, 2, 3}, separated by a common horizontal gap distance d, as depicted in Fig. 3a. In such a nanoribbon triad, each of the three ribbons may have a distinct plasmon resonance frequency ωpj that we can tune actively or passively to realize a system sustaining plasmon resonances at the fundamental, second, and third harmonic frequencies of the impinging light. In Fig. 3b, we present the absorption cross section (upper panel) and THG susceptibility χ(3,3) (lower panel) for ribbons of a fixed doping EFj = 0.45 eV and widths W1 = 220 nm, W2 = 55 nm, and W3 = 25 nm at different horizontal separations d, which simultaneously satisfy the condition ωp2 = 2ωp1 and ωp3 = 3ωp1, where the solid curves show the results for three parallel ribbons and the black-dotted curves are calculated for a single ribbon with a width equal to the sum of the three ribbons. The same triple-resonance condition is obtained for ribbons of equal width Wj = 100 nm and Fermi energies EF1 = 0.1 eV, EF2 = 0.4 eV, and EF3 = 0.9 eV, a configuration that is shown in Fig. 3c to exhibit plasmon mode interference and stronger THG at lower frequencies. In particular, the splitting of the two high-energy modes in Fig. 3c is observed in the linear response, which arises due to mixing with the dark mode of both ribbon j = 1 and ribbon j = 2. Comparing Fig. 3b with Fig. 3c, we conclude that the configuration with constant width is superior to the configuration with constant doping by almost one order of magnitude, and we emphasize that the sum of the widths have been preserved on both cases. Furthermore, Fig. 3b indicates that a single ribbon with the combined width of the triad displays similar THG response at ħω ≈ 0.1 eV, but is several orders of magnitude smaller at larger excitation energies.
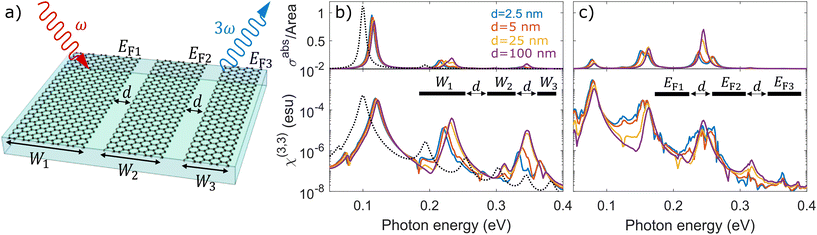 |
| | Fig. 3 Third-harmonic generation in a co-planar nanoribbon triad. (a) Schematic of co-planar graphene ribbons of width Wj and doping EFj for j∈{1, 2, 3}, separated by a common gap distance d. (b) Linear absorption cross section (upper panel) and THG response when ribbons of width W1 = 220 nm, W2 = 55 nm, and W3 = 25 nm are equally-doped to EFj = 0.45 eV for different gap distances d. (c) Same as in (b), but for ribbons of equal width Wj = 100 nm and different doping levels EF1 = 0.1 eV, EF2 = 0.4 eV and EF3 = 0.9 eV. Results are obtained for self-standing ribbons and damping ħγj = 10 meV. | |
An alternative approach to a system suited to fulfill the triple-resonance condition is that of three graphene ribbons vertically separated by a distance d, as illustrated schematically in Fig. 4a. Neglecting hybridization effects, the triple-resonance condition is assured by choosing the same material parameters as for the previously considered co-planar THG system, from which we obtain the spectra shown in Fig. 4b (4c) for constant doping level (width) and different widths (doping levels). In analogy to SHG from two vertically separated ribbons, the increased overlap of graphene material for the three stacked ribbons leads to more significant plasmon hybridization, as revealed in Fig. 4c by the blueshift of the lowest-order dipolar resonances with decreasing vertical separation distance d. Interestingly, for the equally-doped ribbon triad, only the THG signal associated with the dipolar plasmon resonance of the middle ribbon changes substantially as the separation is reduced (see the lower panel of Fig. 4b), while all dipolar resonances in the THG response are modified for ribbons of equal width (see the lower panel of Fig. 4c). The latter situation is attributed to the decreasing oscillator strength of the plasmon resonance at lower energies as the ribbons are brought closer together, approaching the limit of a single ribbon with a net Drude weight 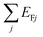 .51 The dotted blue line in the lower panels of Fig. 4b and 4c show the optical response when the cascaded contribution is neglected for closely spaced ribbons with d = 2.5 nm, i.e., setting j(2,\{ 1,2\} )NL = 0 in eqn (13). The cascaded effect seems to have the largest impact at high excitation energies in the system with constant doping, while the opposite trend is reported in the system with constant ribbon width.
.51 The dotted blue line in the lower panels of Fig. 4b and 4c show the optical response when the cascaded contribution is neglected for closely spaced ribbons with d = 2.5 nm, i.e., setting j(2,\{ 1,2\} )NL = 0 in eqn (13). The cascaded effect seems to have the largest impact at high excitation energies in the system with constant doping, while the opposite trend is reported in the system with constant ribbon width.
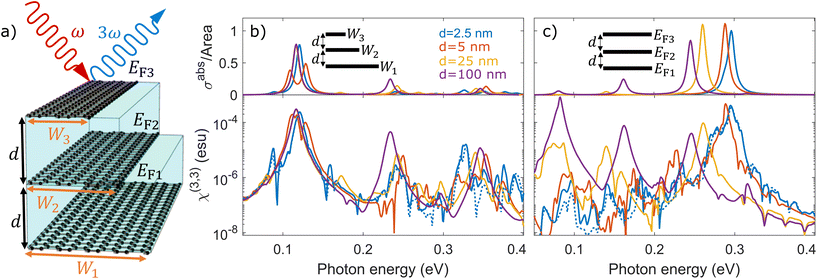 |
| | Fig. 4 Third-harmonic generation in stacked nanoribbon triads. (a) Schematic illustration of three stacked ribbons vertically separated by the same distance d and with independent widths Wj and dopings EFj for j∈{1, 2, 3}. (b) Linear and THG response of a stair-like configuration formed by combining ribbons of widths W1 = 220 nm, W2 = 55 nm, and W3 = 25 nm at the same doping EFj = 0.45 eV. The left-most edges of the ribbons are vertically aligned. (c) Similar to (b) but for equal widths Wj = 100 nm and different doping levels EF1 = 0.1 eV, EF2 = 0.4 eV, and EF3 = 0.9 eV. Note that the nanoribbon parameters in both (b) and (c) are chosen to keep a constant total width 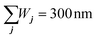 and satisfy the triple-resonance condition ωp1 = ωp2/2 = ωp3/3. The dotted curves indicate the same system as the solid curves (distinguishable only for d = 2.5 nm), but omitting nonlocal terms in the calculation. The phenomenological damping of graphene is set to ħγj = 10 meV and the dielectric environment is ε = 1. and satisfy the triple-resonance condition ωp1 = ωp2/2 = ωp3/3. The dotted curves indicate the same system as the solid curves (distinguishable only for d = 2.5 nm), but omitting nonlocal terms in the calculation. The phenomenological damping of graphene is set to ħγj = 10 meV and the dielectric environment is ε = 1. | |
To further enhance the electric field gradients that give rise to even-ordered nonlinear optical effects, we may introduce additional asymmetry in graphene heterostructures by interfacing electron- and hole-doped nanoribbons. In particular, the nonlocal intraband SHG conductivity of graphene in eqn (11) and (14) exhibits a dependence on the sign of the Fermi energy, suggesting that the induced charge associated with SHG should exhibit additional dipolar character when ribbons of opposite doping interact. In Fig. 5 we consider a dimer comprised of staggered ribbons and compare the harmonic generation produced when the doping charge level is equal or opposite for various inter-ribbon separations. While the same linear response appears in Fig. 5a for electron and hole doping, a strong SHG signal emerges from the dimer of oppositely-doped ribbons in Fig. 5b, which vanishes in the dimer of equally-doped ribbons (not shown). The resulting THG yield for the equally-doped ribbons in Fig. 5c differs from that of the oppositely-doped dimer in Fig. 5d for the smallest separation distance considered due to a significant cascaded nonlinear response, particularly for photon energies near the lowest-order dipolar plasmon resonance of the individual ribbons that in this case are strongly hybridized.
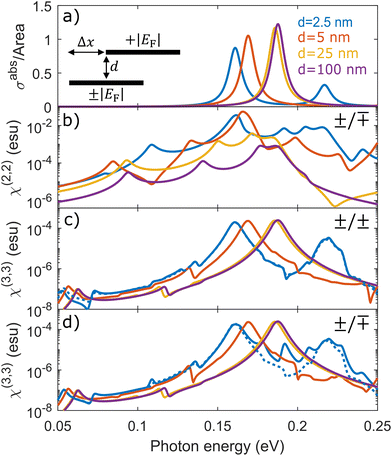 |
| | Fig. 5 Harmonic generation in equally- and oppositely-doped graphene nanoribbon dimers. (a) Linear optical response of staggered graphene nanoribbons with the same width W = 100 nm offset by Δx = 50 nm and separated vertically by a distance d. The response is independent of whether the ribbons are equally or oppositely doped to a Fermi level |EF| = 0.5 eV. The corresponding SHG response (b) is nonvanishing only for oppositely-doped ribbons, while THG spectra appear in each case and are shown for equally-doped (c) and opppositely-doped (d) ribbons, including (solid curves) and omitting (dashed curves) the cascaded contribution. We choose ħγj = 10 meV and ε = 1 in all cases. | |
4 Conclusions
The strong intrinsic nonlinear optical response of graphene can be further enhanced by its highly-confined and electrically-tunable plasmon resonances, which are conveniently excited by far-field illumination in subwavelength structures. The semianalytical method we introduce here enables explorations over a wide parameter space to reveal optimal configurations for harmonic generation from interacting graphene nanostructures. We find the nonlinear efficiency to depend crucially on nonlocal effects in the optical response. While pristine graphene does not produce an even-ordered response due its centrosymmetric crystal structure, the breaking of symmetry in patterned morphologies is predicted here to produce intense SHG when the impinging light frequency ω matches one or more plasmon resonances ωps (i.e., when ω = ωps/s for s = 1 and/or s = 2). Similar conclusions apply to THG, which is dominated by a local nonlinear response but can be sensitive to nonlocal effects through the cascaded second-order wave mixing of fundamental and second-harmonic frequency components in the near field. In practice, the heterostructures under consideration could be fabricated by inserting passive dielectric spacers such as hexagonal boron nitride with a prescribed number of atomic layers to define the vertical spacing. In addition, each graphene plane could be lithographically patterned to achieve the desired lateral spacing. Our findings underscore the importance of nonlinear near-field interactions and their relatively untapped potential to develop efficient nano-optical devices, along with the appeal of graphene as an actively-tunable plasmonic material in subwavelength heterostructures to independently tune different optical resonators and control nonlinear optical phenomena.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. R. E. and F. J. G. A. acknowledge support from ERC (Advanced Grant 789104-eNANO), the Spanish MINECO (MAT2017-88492-R and SEV2015-0522), the Catalan CERCA Program, and Fundació Privada Cellex. J. D. C. is a Sapere Aude research leader supported by VILLUM FONDEN (grant no. 16498) and Independent Research Fund Denmark (grant no. 0165-00051B). The Center for Polariton-driven Light–Matter Interactions (POLIMA) is funded by the Danish National Research Foundation (project no. DNRF165).
References
- W. L. Barnes, A. Dereux and T. W. Ebbesen, Nature, 2003, 424, 824–830 CrossRef CAS.
- M. Kauranen and A. V. Zayats, Nat. Photonics, 2012, 6, 737–748 CrossRef CAS.
- D. K. Gramotnev and S. I. Bozhevolnyi, Nat. Photonics, 2014, 8, 13–22 CrossRef CAS.
- J. Butet, P.-F. Brevet and O. J. F. Martin, ACS Nano, 2015, 9, 10545–10562 CrossRef CAS.
-
S. A. Maier, Plasmonics: fundamentals and applications, Springer Science & Business Media, 2007 Search PubMed.
- D. K. Gramotnev and S. I. Bozhevolnyi, Nat. Photonics, 2010, 4, 83–91 CrossRef CAS.
-
R. W. Boyd, Nonlinear optics, Academic press, 2020 Search PubMed.
- M. I. Stockman, Opt. Express, 2011, 19, 22029–22106 CrossRef PubMed.
- A. Krasnok, M. Tymchenko and A. Alù, Mater. Today, 2018, 21, 8–21 CrossRef CAS.
- J. Shi, Q. Guo, Z. Shi, S. Zhang and H. Xu, Appl. Phys. Lett., 2021, 119, 130501 CrossRef CAS.
- J. B. Khurgin, Nat. Nanotechnol., 2015, 10, 2–6 CrossRef CAS PubMed.
- S. V. Boriskina, T. A. Cooper, L. Zeng, G. Ni, J. K. Tong, Y. Tsurimaki, Y. Huang, L. Meroueh, G. Mahan and G. Chen, Adv. Opt. Photonics, 2017, 9, 775–827 CrossRef.
- A. M. Brown, M. T. Sheldon and H. A. Atwater, ACS Photonics, 2015, 2, 459–464 CrossRef CAS.
- R. A. Maniyara, D. Rodrigo, R. Yu, J. Canet-Ferrer, D. S. Ghosh, R. Yongsunthon, D. E. Baker, A. Rezikyan, F. J. García de Abajo and V. Pruneri, Nat. Photonics, 2019, 13, 328–333 CrossRef CAS.
- F. J. García de Abajo, ACS Photonics, 2014, 1, 135–152 CrossRef.
-
P. A. D. Gonçalves and N. M. R. Peres, An introduction to graphene plasmonics, World Scientific, 2016 Search PubMed.
- F. H. L. Koppens, D. E. Chang and F. J. García de Abajo, Nano Lett., 2011, 11, 3370–3377 CrossRef CAS PubMed.
- L. Ju, B. Geng, J. Horng, C. Girit, M. Martin, Z. Hao, H. A. Bechtel, X. Liang, A. Zettl, Y. R. Shen and F. Wang, Nat. Nanotechnol., 2011, 6, 630–634 CrossRef CAS PubMed.
- S. Kim, M. S. Jang, V. W. Brar, Y. Tolstova, K. W. Mauser and H. A. Atwater, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- J. Sloan, N. Rivera, M. Soljačić and I. Kaminer, Nano Lett., 2018, 18, 308–313 CrossRef CAS PubMed.
- S. A. Mikhailov, Europhys. Lett., 2007, 79, 27002 CrossRef.
- A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef.
- A. V. Gorbach, Phys. Rev. A, 2013, 87, 013830 CrossRef.
- J. D. Cox and F. J. García de Abajo, Acc. Chem. Res., 2019, 52, 2536–2547 CrossRef CAS PubMed.
- E. Hendry, P. J. Hale, J. Moger, A. K. Savchenko and S. A. Mikhailov, Phys. Rev. Lett., 2010, 105, 097401 CrossRef CAS PubMed.
- S.-Y. Hong, J. I. Dadap, N. Petrone, P.-C. Yeh, J. Hone and R. M. Osgood Jr., Phys. Rev. X, 2013, 3, 021014 Search PubMed.
- G. Soavi, G. Wang, H. Rostami, D. G. Purdie, D. D. Fazio, T. Ma, B. Luo, J. Wang, A. K. Ott, D. Yoon, S. A. Bourelle, J. E. Muench, I. Goykhman, S. D. Conte, M. Celebrano, A. Tomadin, M. Polini, G. Cerullo and A. C. Ferrari, Nat. Nanotechnol., 2018, 13, 583–588 CrossRef CAS PubMed.
- T. Jiang, D. Huang, J. Cheng, X. Fan, Z. Zhang, Y. Shan, Y. Yi, Y. Dai, L. Shi, K. Liu, C. Zeng, J. Zi, J. E. Sipe, Y.-R. Shen, W.-T. Liu and S. Wu, Nat. Photonics, 2018, 12, 430–436 CrossRef CAS.
- Y. Zhang, D. Huang, Y. Shan, T. Jiang, Z. Zhang, K. Liu, L. Shi, J. Cheng, J. E. Sipe, W.-T. Liu and S. Wu, Phys. Rev. Lett., 2019, 122, 047401 CrossRef PubMed.
- T. J. Constant, S. M. Hornett, D. E. Chang and E. Hendry, Nat. Phys., 2016, 12, 124–127 Search PubMed.
- M. M. Jadidi, J. C. König-Otto, S. Winnerl, A. B. Sushkov, H. D. Drew, T. E. Murphy and M. Mittendorff, Nano Lett., 2016, 16, 2734–2738 CrossRef CAS PubMed.
- D. Kundys, B. V. Duppen, O. P. Marshall, F. Rodriguez, I. Torre, A. Tomadin, M. Polini and A. N. Grigorenko, Nano Lett., 2018, 18, 282–287 CrossRef CAS PubMed.
- I. A. Calafell, L. A. Rozema, D. Alcaraz Iranzo, A. Trenti, P. K. Jenke, J. D. Cox, A. Kumar, H. Bieliaiev, S. Nanot, C. Peng, D. K. Efetov, J.-Y. Hong, J. Kong, D. R. Englund, F. J. García de Abajo, F. H. L. Koppens and P. Walther, Nat. Nanotechnol., 2021, 16, 318–324 CrossRef PubMed.
- M. T. Manzoni, I. Silveiro, F. J. García de Abajo and D. E. Chang, New J. Phys., 2015, 17, 083031 CrossRef.
- B. Jin, T. Guo and C. Argyropoulos, J. Opt., 2017, 19, 094005 CrossRef.
- J. W. You and N. C. Panoiu, Phys. Rev. B, 2020, 102, 121403 CrossRef CAS.
- D. Alcaraz Iranzo, S. Nanot, E. J. C. Dias, I. Epstein, C. Peng, D. K. Efetov, M. B. Lundeberg, R. Parret, J. Osmond, J.-Y. Hong, J. Kong, D. R. Englund, N. M. R. Peres and F. H. L. Koppens, Science, 2018, 360, 291–295 CrossRef CAS PubMed.
- Q. Zhang, G. Hu, W. Ma, P. Li, A. Krasnok, R. Hillenbrand, A. Alù and C.-W. Qiu, Nature, 2021, 597, 187–195 CrossRef CAS PubMed.
- S. G. Menabde, J. T. Heiden, J. D. Cox, N. A. Mortensen and M. S. Jang, Nanophotonics, 2022, 11, 2433–2452 CrossRef CAS.
- Z. Xu, D. Wu, Y. Liu, C. Liu, Z. Yu, L. Yu and H. Ye, Nanoscale Res. Lett., 2018, 13, 1–8 CrossRef CAS PubMed.
- M. Yankowitz, Q. Ma, P. Jarillo-Herrero and B. J. LeRoy, Nat. Rev. Phys., 2019, 1, 112–125 CrossRef CAS.
- I.-H. Lee, D. Yoo, P. Avouris, T. Low and S.-H. Oh, Nat. Nanotechnol., 2019, 14, 313–319 CrossRef CAS PubMed.
- T. Christensen, W. Yan, A.-P. Jauho, M. Wubs and N. A. Mortensen, Phys. Rev. B, 2015, 92, 121407(R) CrossRef.
- J. D. Cox, R. Yu and F. J. García de Abajo, Phys. Rev. B, 2017, 96, 045442 CrossRef.
- Y. Wang, M. Tokman and A. Belyanin, Phys. Rev. B, 2016, 94, 195442 Search PubMed.
- J. L. Cheng, N. Vermeulen and J. E. Sipe, Sci. Rep., 2017, 7, 1–11 CrossRef PubMed.
- D. A. Smirnova and A. S. Solntsev, Phys. Rev. B, 2015, 92, 155410 CrossRef.
- B. V. Duppen, A. Tomadin, A. N. Grigorenko and M. Polini, 2D Mater., 2016, 3, 015011 CrossRef.
- A. I. Berdyugin, N. Xin, H. Gao, S. Slizovskiy, Z. Dong, S. Bhattacharjee, P. Kumaravadivel, S. Xu, L. A. Ponomarenko, M. Holwill, D. A. Bandurin, M. Kim, Y. Cao, M. T. Greenaway, K. S. Novoselov, I. V. Grigorieva, K. Watanabe, T. Taniguchi, V. I. Fal'ko, L. S. Levitov, R. K. Kumar and A. K. Geim, Science, 2022, 375, 430–433 CrossRef CAS PubMed.
- R. Yu, J. D. Cox, J. R. M. Saavedra and F. J. García de Abajo, ACS Photonics, 2017, 4, 3106–3114 CrossRef CAS.
- D. Rodrigo, A. Tittl, O. Limaj, F. J. García de Abajo, V. Pruneri and H. Altug, Light: Sci. Appl., 2017, 6, e16277–e16277 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
 a,
A.
Rodríguez Echarri
a,
A.
Rodríguez Echarri
 b,
F. Javier
García de Abajo
b,
F. Javier
García de Abajo
 bc and
Joel D.
Cox
bc and
Joel D.
Cox
 *ad
*ad
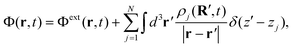
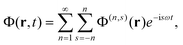
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ(1,1)jE(1,1)j, from which the charge density can be expressed in terms of the potential as
σ(1,1)jE(1,1)j, from which the charge density can be expressed in terms of the potential as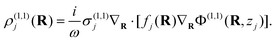
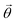 that parametrizes a 2D structure, such that
that parametrizes a 2D structure, such that 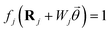 within structure j and vanishes elsewhere, effectively defining its geometry in terms of a characteristic size Wj (here taken as the ribbon width) and location rj = (Rj, zj) (e.g., the center of mass). Combining eqn (1) and (4), the potential in structure j is found to satisfy the self-consistent relation
within structure j and vanishes elsewhere, effectively defining its geometry in terms of a characteristic size Wj (here taken as the ribbon width) and location rj = (Rj, zj) (e.g., the center of mass). Combining eqn (1) and (4), the potential in structure j is found to satisfy the self-consistent relation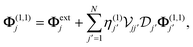
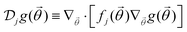 , while the dimensionless parameter η(s)j = iσ(1,s)j/sωWj contains all the frequency and material dependence entering the intrinsic conductivity. In effect, the Coulomb integral
, while the dimensionless parameter η(s)j = iσ(1,s)j/sωWj contains all the frequency and material dependence entering the intrinsic conductivity. In effect, the Coulomb integral 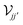 yields the potential produced at
yields the potential produced at 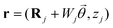 in ribbon j by the charge at
in ribbon j by the charge at 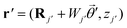 in ribbon j′. The system of eqn (5) can then be solved by constructing a block matrix spanning discretized real space elements: indeed, defining the potential in each structure as
in ribbon j′. The system of eqn (5) can then be solved by constructing a block matrix spanning discretized real space elements: indeed, defining the potential in each structure as 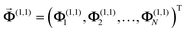 (similarly for
(similarly for 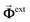 ), the self-consistent solution for the combined system is
), the self-consistent solution for the combined system is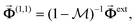
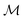 is a square block matrix comprised of matrices
is a square block matrix comprised of matrices 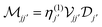 , here defined by representing the operators
, here defined by representing the operators 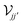 and
and 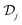 on a real space grid, while 1 denotes the identity matrix. In the ESI† we provide details on the spatial representation of the operators
on a real space grid, while 1 denotes the identity matrix. In the ESI† we provide details on the spatial representation of the operators 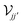 and
and 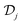 leading to the block matrix equation of eqn (6) for nanoribbons.
leading to the block matrix equation of eqn (6) for nanoribbons.
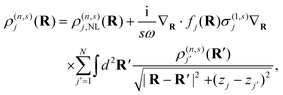
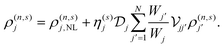
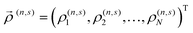 , the solution of eqn (8) can also be expressed in block-matrix form as
, the solution of eqn (8) can also be expressed in block-matrix form as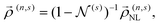
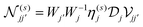 may be constructed by representing the operators
may be constructed by representing the operators 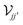 and
and 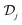 as matrices spanning discrete real-space elements in the 2D structures j and j′. In the ESI† we provide further details on the derivation of eqn (9) for the specific case of ribbons with translational symmetry in one dimension, which leads to a dependence of
as matrices spanning discrete real-space elements in the 2D structures j and j′. In the ESI† we provide further details on the derivation of eqn (9) for the specific case of ribbons with translational symmetry in one dimension, which leads to a dependence of 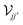 and
and 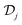 on the harmonic index s. In analogy to
on the harmonic index s. In analogy to 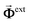 in eqn (6), the vector
in eqn (6), the vector 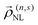 in eqn (9) acts as the external source of nonlinear response in the system, and depends on the specific definition of the nonlinear current j(n,s)NL.
in eqn (9) acts as the external source of nonlinear response in the system, and depends on the specific definition of the nonlinear current j(n,s)NL.
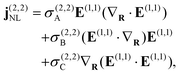
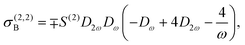
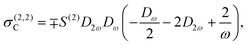
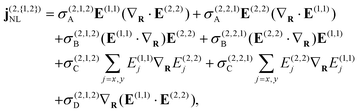
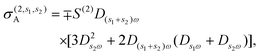
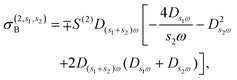
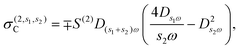
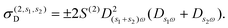
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and are translationally invariant in ŷ, so that the potential can be decomposed in plane waves indexed by a wave vector q according to Φ(n,s)(R) = φ(n,s)(x)eisqy. The symmetry of such nanoribbon ensembles in y simplifies our calculations for normally-impinging plane-wave illumination with electric field amplitude Eext polarized along
and are translationally invariant in ŷ, so that the potential can be decomposed in plane waves indexed by a wave vector q according to Φ(n,s)(R) = φ(n,s)(x)eisqy. The symmetry of such nanoribbon ensembles in y simplifies our calculations for normally-impinging plane-wave illumination with electric field amplitude Eext polarized along ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , such that Φext = −xEext, and localized plasmon resonances can be optically excited in each ribbon. The nonlinear optical response is quantified by computing the induced charge density in eqn (9), from which the induced dipole moment (per unit length along ŷ) of the combined system
, such that Φext = −xEext, and localized plasmon resonances can be optically excited in each ribbon. The nonlinear optical response is quantified by computing the induced charge density in eqn (9), from which the induced dipole moment (per unit length along ŷ) of the combined system 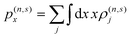 yields the effective polarizability per unit length α(n,s) ≡ p(n,s)x/(Eext)n and the susceptibility
yields the effective polarizability per unit length α(n,s) ≡ p(n,s)x/(Eext)n and the susceptibility 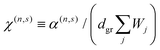 , where dgr = 0.33 nm is the inter-layer spacing of graphite, commonly used to estimate the thickness of graphene.25
, where dgr = 0.33 nm is the inter-layer spacing of graphite, commonly used to estimate the thickness of graphene.25
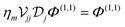 , from which the eigenvalues ηm determine the plasmon resonances
, from which the eigenvalues ηm determine the plasmon resonances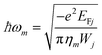
 .51 The dotted blue line in the lower panels of Fig. 4b and 4c show the optical response when the cascaded contribution is neglected for closely spaced ribbons with d = 2.5 nm, i.e., setting j(2,\{ 1,2\} )NL = 0 in eqn (13). The cascaded effect seems to have the largest impact at high excitation energies in the system with constant doping, while the opposite trend is reported in the system with constant ribbon width.
.51 The dotted blue line in the lower panels of Fig. 4b and 4c show the optical response when the cascaded contribution is neglected for closely spaced ribbons with d = 2.5 nm, i.e., setting j(2,\{ 1,2\} )NL = 0 in eqn (13). The cascaded effect seems to have the largest impact at high excitation energies in the system with constant doping, while the opposite trend is reported in the system with constant ribbon width.