Open Access Article
Open Access ArticleQuantifying vibronic coupling with resonant inelastic X-ray scattering
Keith
Gilmore
 ab
ab
aPhysics Department and IRIS Adlershof, Humboldt-Universität zu Berlin, Zum Großen Windkanal 2, 12489 Berlin, Germany. E-mail: kgilmore@physik.hu-berlin.de
bEuropean Theoretical Spectroscopy Facility (ETSF), Berlin, Germany
First published on 13th December 2022
Abstract
Electron–phonon interactions are fundamental to the behavior of chemical and physical systems. Various methods exist to quantify these interactions, however, none are entirely satisfactory for crystalline materials with dispersive phonons. In recent years, resonant inelastic X-ray scattering (RIXS) has been proposed as a new technique that can probe momentum-dependent electron–phonon interactions in crystalline materials with better resolution with respect to the phonon mode and momentum as well as the electronic orbital and momentum. We first summarize theoretical progress on understanding and interpreting RIXS measurements of vibronic coupling, and then outline a path toward eventual predictive first-principles calculations of the phonon contribution to RIXS spectra in the case of dispersive phonons. Particular attention is given to the relation between the coupling constant measured by RIXS, which relates to exciton–phonon scattering, and the standard electron–phonon coupling probed by transport measurements. We discuss first-principles calculation of this exciton–phonon coupling parameter. Example calculations are provided for crystalline MgO.
I. Introduction
Vibronic interactions are an inescapable aspect of various phenomena in chemistry and condensed matter physics. Bond lengths and angles are altered during chemical reactions as electrons fill or empty bonding and anti-bonding orbitals. Bond angles respond to the occurrence of degenerate electronic levels by distorting so as to break this degeneracy through the Jahn-Teller effect. Photoabsorption excites vibrational modes, can cause dissociation of molecules and can also induce isomer changes. Understanding and predicting these responses starts with quantitatively characterizing the ground- and excited-state potential energy surfaces (PESs) of molecules.In condensed matter systems, accounting for electron–phonon interactions (EPIs) is essential for understanding many physical properties. Electron–phonon scattering is a major contributor to electrical and spin transport properties in metals and to carrier mobilities in semiconductors. As such, it is an important factor in the various Hall effects. In semiconductors, EPIs can cause the formation of polarons and provide critical assistance to optical absorption within indirect band-gap materials. For metals, interactions between the electrons and lattice can manifest through the Kohn anomaly and spontaneously break degeneracies through the Peierls instability and the formation of charge density waves. They are also responsible for the attractive force between electrons that leads to Cooper pairing and BCS superconductivity.
The impact and importance of these vibronic interactions depends primarily on the strength of the electron–phonon coupling (EPC). For most material properties, such as resistivity and conventional BCS superconductivity, the momentum dependence of the electron–phonon coupling is not particularly important. However, the strength of the EPI near Fermi surface nesting wavevectors can be quite important, for example, for charge density wave ordering.1 The momentum dependence of electron–phonon coupling is likely also relevant to understanding unconventional, anisotropic superconductivity for which it may play an assisting role.2,3 These considerations provide strong motivation for accurately quantifying EPI strengths of crystalline materials throughout the Brillouin zone.
Quantifying the electron–phonon coupling (EPC) strength throughout the Brillouin zone is an outstanding problem. Raman and infrared methods are standard techniques,4–6 but are limited to probing the zone center. Angle-resolved photoemisison spectroscopy (ARPES) measures EPC with sensitivity to the electron momentum, but is averaged over the phonon momentum.7 Recent work on time-resolved ARPES is promising,8 though it is not yet a standard technique. Scattering techniques, including inelastic neutron scattering (INS)9,10 and inelastic X-ray scattering (IXS),11 in principle provide access to the momentum resolved EPC through the linewidth of the phonon excitation peaks. For phonon momenta with weak EPC, peak linewidths are narrow and the coupling strength can be reliably extracted. However, for phonon momenta with strong coupling – the most important regions – the peaks broaden significantly and accurate quantification of the coupling strength becomes challenging.
Resonant inelastic X-ray scattering (RIXS) is a relatively new technique that holds considerable promise for quantifying electron–phonon coupling throughout the Brillouin zone with unique specificity. RIXS measurements involve scattering X-rays that are tuned in energy to a particular core-level resonance of a sample.12 It is typical to approximate the RIXS cross section by the Kramers–Heisenberg equation
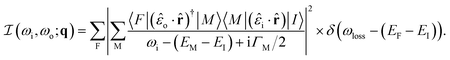 | (1) |
One refers to the initial-state I, which is typically the ground-state, virtual intermediate-states M with lifetimes ΓM/2 for which an electron from a particular core-level has been promoted to the conduction band, and final-states F that could be the ground-state (giving the elastic contribution) or a state with some low-energy excitation (giving inelastic contributions). The incident (outgoing) photon has energy ωi (ωo) and polarization vector ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) i (
i (![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) o). The energy transferred to the sample is ωloss = ωi − ωo and there is an implied momentum transfer q. The excitation left in the final-state could range from a charge-transfer excitation or plasmon (∼10 eV), a local orbital excitation (∼1 eV), a spin-wave (≲300 meV), a phonon (≲200 meV), or other composite excitations.
o). The energy transferred to the sample is ωloss = ωi − ωo and there is an implied momentum transfer q. The excitation left in the final-state could range from a charge-transfer excitation or plasmon (∼10 eV), a local orbital excitation (∼1 eV), a spin-wave (≲300 meV), a phonon (≲200 meV), or other composite excitations.
A few factors contribute to the power and versatility of RIXS. The core-level resonance condition makes the technique element and orbital selective allowing different sites and orbitals of a sample to be probed independently. Controlling the polarization of the incident and outgoing photons permits one to distinguish electronic and spin excitations,13 and to further differentiate between specific orbitals. Despite the negligible momentum carried by soft X-ray photons, the scattering nature of the technique permits the controllable transfer of considerable momentum to the sample, allowing the mapping of dispersion relations.14,15 Finally, due to the high cross-section of resonant X-ray scattering, the technique is sensitive to much smaller sample volumes than INS. This allows, e.g. measurement of spin-wave dispersions in films as thin as only a few monolayers.16
RIXS has two main limitation. First, while the experimental instrumentation is maturing rapidly, the present energy resolution of about 20 meV is considerably poorer than INS. Second, the scattering process is more complicated, which makes accurate interpretation of the data challenging. This is further exacerbated by the typical application of the technique to strongly correlated materials, which introduces challenges for making rigorous comparisons with calculations. Nevertheless, progress is being made on the computational and theoretical side,17 even in the context of first-principles calculations.18,19
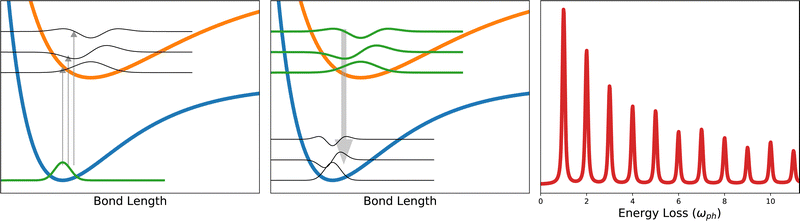
Fig. 1 illustrates the essential aspects of phonon generation during a RIXS measurement, taking the example of a system with a single active local vibrational mode. Invoking the Born–Oppenheimer approximation, each electronic configuration will present some potential energy surface for the vibrational dynamics. Absorption of a soft X-ray causes a vertical transition between the ground- and excited-state potential energy surfaces. Quantum mechanically, the initial-state vibrational wavefunction projects onto the vibrational eigenstates of the excited-state PES and then evolves accordingly for the duration of the core–hole lifetime. Classically, vibrational dynamics are initiated by the excited-state force that corresponds to the slope of the excited-state PES at the ground-state (equilibrium) mode coordinate. During the radiative transition back to the ground-state PES, the temporally evolved vibrational wavepacket projects back onto the vibrational eigenstates of the ground-state PES, having non-negligible overlap with multiple low vibrational levels. The resulting RIXS loss spectrum appears as a series of peaks separated by the ground-state vibrational frequency. The intensities of the peaks generally decrease with increases vibrational level, though this need not be strictly monotonic.
A primary objective of performing vibrational RIXS measurements on molecules or other, e.g. condensed-phase systems exhibiting localized vibrational modes, is to determine their potential energy surfaces.20–23 One often observes a large number of vibrational peaks in the RIXS loss spectrum spaced at integer multiples of the vibrational energy. Treating small molecules such as oxygen and acetone, Schreck et al.24 showed that anharmonic frequency shifts appear for higher oscillator levels and that these deviations allow precise fitting of the ground-state PES to a Morse potential. Work is ongoing to similarly characterize excited-state potential energy surfaces by probing vibrational progressions accompanying RIXS final-states with valence electronic excitations.25
Interpreting and modeling vibrational excitations in crystalline solids with delocalized, dispersive phonons is a considerably more complicated task than for materials with localized vibrational modes. One is confronted with the full, momentum-dependent electronic and phononic band structures. The activation of several dispersive phonon modes leads to more complex, broadened spectra that often do not have such well defined peaks.26–29
Rather than seeking to map a PES, the physical quantity of most interest when probing crystalline materials with dispersive phonons is typically the electron–phonon coupling strength. This quantity is encoded in the relative peak intensities. Accurately extracting electron–phonon coupling strengths of crystalline systems with dispersive phonons from the relative peak intensities of the phonon peaks of RIXS spectra is non-trivial and remains an open question.17,30–32 We focus on addressing this challenge in the present work.
Much of the analysis of the phonon features in RIXS spectra of periodic systems utilizes a simplified model presented by Ament et al. that approximates the problem as a displaced harmonic oscillator.33 This model and the accompanying analysis are presented in the Section II A. In Section II B and II C we present some simple extensions of this basic model that demonstrate the difficulty of using this description to accurately extract the electron–phonon coupling constant. In Section III, we introduce an alternative, Green's function based approach that is suitable for first-principles calculations. This begins with calculating the purely electronic X-ray absorption and RIXS spectra via the Bethe–Salpeter equation, which we describe in Section III A. From there, we discuss how to incorporate vibronic interactions as a self-energy built through a cumulant expansion. This is done for X-ray absorption in Section III B and for RIXS in Section III C. Finally, we comment in Section IV that the coupling constant extracted from a RIXS measurement is better viewed as exciton–phonon coupling than the usual electron–phonon coupling initially sought. Prescriptions for calculating this exciton–phonon parameter from first-principles and relating it to the desired electron–phonon coupling are provided. Some numerical expositions of the theoretical formalism are provided for crystalline MgO. We summarize the work in the conclusions.
II. Einstein oscillators
A. Displaced oscillator model
Given the complexity of evaluating the Kramers–Heisenberg expression for fully general electron–phonon interactions, interpretations of the phonon contribution to RIXS for solids have relied heavily on a simplified model put forward in the foundational work of Ament et al.33 This model is based on a Holstein Hamiltonian with a single localized electronic level coupled to a single Einstein oscillator. This picture was partially motivated by consideration of RIXS experiments tuned to the copper L-edge excitation of cuprates for which a core electron is promoted into the single empty and localized dx2−y2 orbital of a copper site. Defining the energy of the electronic transition as ε0 and the vibrational energy as ωph, the Hamiltonian isH = ε0ĉ†ĉ + ωph![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) † †![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) + Mĉ†ĉ( + Mĉ†ĉ(![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) + + ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †) †) | (2) |
![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †(
†(![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) ) designate the creation (annihilation) operators for the electron and oscillator, respectively, and M is the vibronic coupling strength. It is common to refer to the reduced vibronic coupling strength g = M2/ωph2. The Hamiltonian in eqn (2) may be diagonalized by applying a Lang–Firsov canonical transformation
) designate the creation (annihilation) operators for the electron and oscillator, respectively, and M is the vibronic coupling strength. It is common to refer to the reduced vibronic coupling strength g = M2/ωph2. The Hamiltonian in eqn (2) may be diagonalized by applying a Lang–Firsov canonical transformation ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = e
= e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) He−
He−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) using the generating function
using the generating function 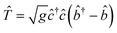 with the result that
with the result that ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) = ωph(
= ωph(![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †
†![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) − g).34 This amounts to a displaced harmonic oscillator where the resonance condition is shifted by the product of the dimensionless coupling strength and the vibrational frequency, gωph.
− g).34 This amounts to a displaced harmonic oscillator where the resonance condition is shifted by the product of the dimensionless coupling strength and the vibrational frequency, gωph.
Using the above canonical transformation, and assuming the system begins in the zero oscillator level, the RIXS amplitude for leaving n phonons in the final state becomes
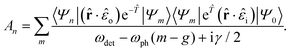 | (3) |
We assume that the vibronic states |Ψ〉 = |ϕ〉|χ〉 are factorizable into electronic |ϕ〉 and vibrational |χ〉 parts. Since the electronic space is limited to the ground-state and a single excited level, the subscripts n and m simply indicate the oscillator levels of the final and intermediate states, respectively. Within the denominator, ωdet = ωi − ε0 is the detuning between the incident photon energy and the electronic resonance, and γ/2 is the inverse lifetime of the core–hole-excited intermediate state.
The numerator of eqn (3) consists of Franck–Condon factors for the overlaps of the nuclear wavefunctions. With this substitution, the RIXS amplitude corresponding to a final state with n phonons reduces to
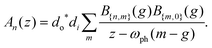 | (4) |
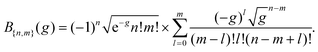 | (5) |
In eqn (4), the factors of d are the dipole matrix elements and z = ωdet + iγ/2. This simplified model for describing vibrational excitations during photon scattering experiments, often attributed to,33 in fact has long been applied to optical Raman scattering experiments.35–37
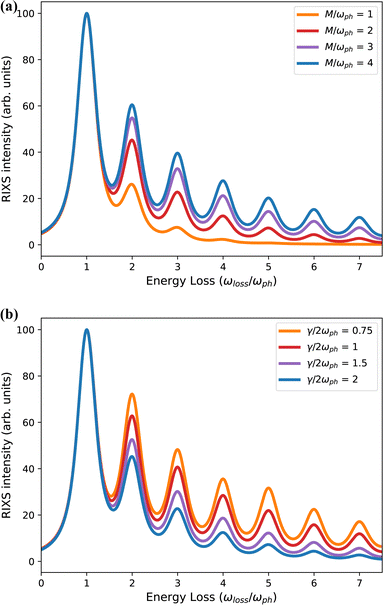
As shown in Fig. 2, eqn (4) results in a RIXS signal that consists of a series of peaks spaced by the vibrational energy, ωph. The intensities of the peaks depend on the vibronic coupling strength g (or M), the detuning from resonance ωdet and the lifetime of the intermediate-state (γ/2)−1. The detuning is fixed experimentally by selecting the incident photon energy during the measurement. The lifetime is sometimes left as a free parameter or roughly approximated, however, it is generally known38 and should be fixed accordingly. With the detuning and core–hole lifetime properly fixed, the coupling strength is the sole free parameter and is obtained by fitting the relative intensities of the first and second phonon harmonics to experimental results.30,33 Within this simple model, the coupling strength can be physically interpreted as related to the displacement distance between the equilibrium positions of the ground- and excited-state harmonic potentials.
Fig. 2 demonstrates that the intensities of the higher phonon harmonics increase when either the coupling strength g increases or when the core–hole lifetime becomes longer. Conceptually, the amount of spectral intensity transferred from the elastic line to the phonon peaks depends on the total impulse applied during the intermediate state. This quantity is a combination of the vibronic coupling strength and the intermediate state lifetime and can be expressed as the dimensionless quantity 2M/γ, which is often a better metric of the effective RIXS coupling strength than g = (M/ωph)2.30,39 This observation underscores the point that an erroneous value of the intermediate state lifetime leads to a misanalysis of the coupling strength. To properly quantify the vibronic coupling, it is important to recognize that the denominator of eqn (4) contains γ/2, the half width at half maximum of the absorption lineshape, not the full width at half maximum.
A common misconception within the condensed matter RIXS community, reinforced by Fig. 2, is that peak intensities of the phonon harmonics decrease monotonically. Evidence to the contrary exists for small molecules, such as O2.25 Small organic molecules present an unusual combination of strong coupling strength and long core–hole lifetime, making the product of the two, the effective impulse 2M/γ, unusually large. This, combined with large phonon frequencies, can yield a non-monotonic decay of the phonon harmonics. However, non-monotonic behavior can also occur when more than one phonon mode is active, or when contributions from different points in the Brillouin zone are important.
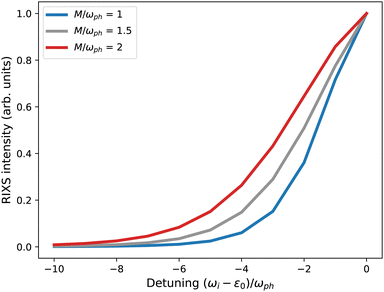
For some experimental RIXS data on crystalline materials, phonon harmonics beyond the first are not well resolved. In these cases, it may appear impossible to quantify the vibronic coupling strength. However, Rossi et al.40 and Braicovich et al.30 have recently demonstrated an alternative approach for quantifying the coupling strength based on the intensity decay of the first harmonic peak with respect to detuning the incident photon energy below the electronic resonance. The intensity of the first phonon harmonic is given by
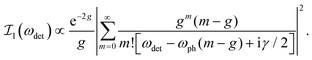 | (6) |
As demonstrated by those authors, and summarized in Fig. 3, the coupling strength g may be obtained by measuring the intensity of the first phonon harmonic at several detuning values and fitting the intensity decay with eqn (6). This approach requires that the electronic resonance under consideration is well isolated in energy from any other transition otherwise it becomes problematic to clearly define the detuning value. Further, the vibronic coupling shifts the resonance by gωph, which becomes significant when either the vibronic coupling or phonon frequency is large.39 These considerations complicate the use of detuning to accurately quantify the coupling constant and the efficacy of this technique remains unclear.41
The original displaced oscillator model for describing phonon features in RIXS spectra presented by Ament et al.33 established the basis for interpreting phonon excitations for the condensed matter community and has been widely applied to experimental RIXS data.26–28,42,43 Despite this widespread embrace, the model has important limitations. Specifically, it is restricted to a single localized vibrational mode coupled to a single localized electronic state. In the next subsections we explore the impact of relaxing some limitations of this model. Section II B allows different vibrational frequencies for the ground and excited states – the displaced and distorted harmonic oscillator – while Section II C introduces a second local vibrational mode. This still leaves important aspects unaddressed, such as generalizing the local nature of the electronic state and vibrational mode to itinerant electrons and extended phonons, respectively. Monciu et al.32 recently considered the impact of electron itinerancy while Dashwood et al. included the momentum dependence of phonons.31
B. Displaced and distorted oscillator
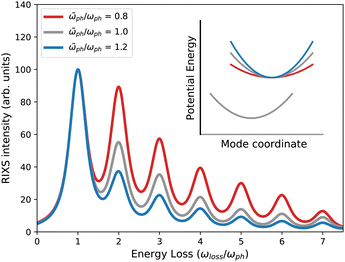
Thus far, we have assumed that the vibrational frequency is unchanged between the ground and core-excited states and the system maps onto the simple displaced harmonic oscillator model. For the case of molecules, it is clear that the core-excited state PES can differ radically from the ground-state PES; in some cases, the excited-state may be dissociative. In periodic solids, the ground-state vibrational modes correspond to delocalized phonons. The frequency of these phonon modes remains unchanged in the intermediate state, however the core-excited site may be viewed as a transient impurity that induces local vibrations. The vibrational frequency of these local modes may differ significantly from similarly displacive, e.g. optical phonon modes appearing in the RIXS final state.44,45 To illustrate the complexity this introduces while staying as close as possible to the model studied in the previous section, we assume that the vibrational modes for both the ground and core-excited states are local, harmonic modes, but with different frequencies. We may write the following effective Hamiltonian for this case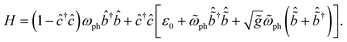 | (7) |
Tildes in the above expression indicate values corresponding to the RIXS intermediate state for which 〈ĉ†ĉ〉 = 1. In the initial and final state 〈ĉ†ĉ〉 = 0 and the Hamiltonian reduces to just the ground-state oscillator term with frequency ωph. In the intermediate state local vibrational modes with frequency ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ph are created (destroyed) by the operator
ph are created (destroyed) by the operator 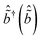 . This model corresponds to the displaced and distorted harmonic oscillator.
. This model corresponds to the displaced and distorted harmonic oscillator.
The phonon contribution to the RIXS signal for the displaced and distorted harmonic oscillator may be obtained by generalizing the canonical transformation presented in Section II A. Accounting first for the displaced aspect of the excited-state oscillator, we use the generating function 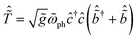 to write the RIXS amplitudes as
to write the RIXS amplitudes as
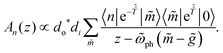 | (8) |
This expression differs from eqn (3) due to the different intermediate state vibrational modes |![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) 〉, altered frequencies
〉, altered frequencies ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) ph arising from the change in curvature of the excited-state vibrational surface, and the modified transformation operator. We write the coupling strength as
ph arising from the change in curvature of the excited-state vibrational surface, and the modified transformation operator. We write the coupling strength as ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) to stress the difference from the previous section.
to stress the difference from the previous section.
We treat the distorted aspect of the excited-state oscillator by introducing a map between the two vibrational bases, defined as the transformation 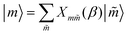 where
where 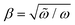 quantifies the change in the oscillator frequency. Analytic expressions for Xm
quantifies the change in the oscillator frequency. Analytic expressions for Xm![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) (β) have been derived by various methods.46–50 The result in terms of Hermite polynomials Hj is
(β) have been derived by various methods.46–50 The result in terms of Hermite polynomials Hj is
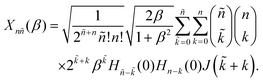 | (9) |
This expression introduces the factor
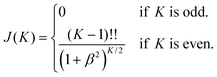 | (10) |
Substituting these transformation matrices into the expression for the RIXS amplitudes in eqn (8) gives
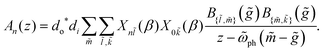 | (11) |
The impact of the difference in curvature between the ground- and excited-state PESs on the relative intensities of the phonon progression in the RIXS signal depends on two considerations. A steeper slope of the excited-state PES yields a larger vibronic coupling strength. However, the difference in curvature between the two vibrational surfaces also changes the Franck–Condon overlap factors. Fig. 4 shows the resulting phonon intensities for a given set of model parameters.
C. Two displaced oscillators
In many cases, more than one vibrational mode will be excited during a RIXS experiment. For this scenario, the Holstein Hamiltonian of eqn (2) becomes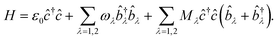 | (12) |
We can again convert this Hamiltonian into the diagonal form of a two-dimensional displaced harmonic oscillator by applying a Lang–Firsov canonical transformation with the generalized transformation matrix 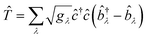 .39 Evaluating the overlap of ground-state and excited-state vibrational wavepackets introduces the following products of Franck–Condon factors
.39 Evaluating the overlap of ground-state and excited-state vibrational wavepackets introduces the following products of Franck–Condon factors
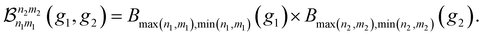 | (13) |
With these Franck–Condon products, the RIXS amplitudes for the double-mode case are
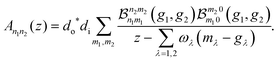 | (14) |
Further generalization to a higher number of vibrational modes is straight-forward.
III. Green's function approach
The numerical cost of calculating the phonon contribution to the RIXS cross section by wavefunction methods becomes prohibitive for periodic systems due to the need to account for momentum transfer between the electronic and vibrational systems. Setting up the vibronic Hamiltonian necessitates sampling the exciton and phonon states, as well as the momentum-dependent exciton–phonon coupling strengths, throughout the Brillouin zone. Such calculations may be feasible with respect to computational cost. The much larger challenge would be to diagonalize the resulting Hamiltonian as its Hilbert space expands rapidly when adjoining the phonon modes to the electronic degrees of freedom. In this situation, Green's function methods become advantageous.Devereaux et al. presented a formal Green's function description of the phonon RIXS signal for a model representative of 2-dimensional cuprates, including finite momentum transfer.17 This work provided valuable insight into the phonon excitation process during a RIXS measurement, including a description of the momentum transfer and phonon mode dependencies. However, the formalism and accompanying numerical results only included single phonon diagrams limiting the quantitative application of the work. Although the detuning method described in the previous section offers a means for quantifying the vibronic coupling strength using only the first harmonic, the numerical restriction to single phonon terms is insufficient for accurate quantification even in the weak coupling limit.51 One reason for this is that the intermediate-state vibronic coupling strength is typically strong even when the ground-state coupling is weak. This drives vibrational modes into high occupation levels in the intermediate-state, which has a significant impact on the intensity of the first harmonic peak in the final state.51 The intermediate-state phonon scattering also mixes modes at different q vectors making the intensity of the first harmonic peak dependent on the vibronic coupling strength throughout the Brillouin zone and invalidating a picture in which each q-point may be evaluated independently.31 Given the expectation that the intermediate-state coupling strength is strong even when the ground-state coupling is weak, it is essential to treat these vibronic contributions to high order. In this section, we review an alternate Green's function formulation of the RIXS cross section that sums phonon contributions to infinite order in the intermediate state and to arbitrary order in the final state.31,39,51
The objective of this and the next section is to establish a foundation for a many-body perturbation theory description of the RIXS phonon excitation spectrum that is suitable for first-principles calculations. We begin in Section III A by describing the electronic excitation process in the absence of phonon interactions. This is done within the context of the Bethe–Salpeter equation (BSE), which is appropriate for describing excitonic states in weakly to moderately correlated systems. In Section III B we introduce a vibronic interaction into the BSE at an approximate level and demonstrate how to generate phonon sidebands within an X-ray absorption calculation via use of a cumulant Green's function. In Section III C we extend these concepts to the RIXS scattering process. Finally, in Section IV, we argue that RIXS probes an effective exciton–phonon scattering process, present two approaches for numerically evaluating such coupling constants from first-principles, and relate this exciton–phonon scattering to the usual electron–phonon coupling constants.
A. Bethe–Salpeter equation
Solving the Bethe–Salpeter equations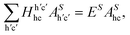 | (15) |
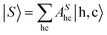 within a two-particle approximation that consist of linear combinations of electron (c) and hole (h) pairs with coefficients AShc and energies ES. The contribution of a given electron–hole pair |h,c〉 to the eigenstate |S〉 is quantified by AShc. For the RIXS intermediate state, c specifies the band index and wavevector for the conduction electron and h corresponds to a set of atomic quantum numbers for the core-level hole state, depending on the particular resonance selected (h runs over the occupied valence bands for the RIXS final state or in the case of optical absorption).
within a two-particle approximation that consist of linear combinations of electron (c) and hole (h) pairs with coefficients AShc and energies ES. The contribution of a given electron–hole pair |h,c〉 to the eigenstate |S〉 is quantified by AShc. For the RIXS intermediate state, c specifies the band index and wavevector for the conduction electron and h corresponds to a set of atomic quantum numbers for the core-level hole state, depending on the particular resonance selected (h runs over the occupied valence bands for the RIXS final state or in the case of optical absorption).
The elements of the Bethe–Salpeter Hamiltonian
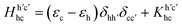 | (16) |
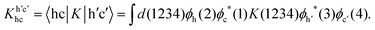 | (17) |
Numerical indices represent combined space-spin-time variables. The interaction kernel
| K(1234) = −iδ(12)δ(34)v(1,4) + iδ(14)δ(23)W(1,2) | (18) |
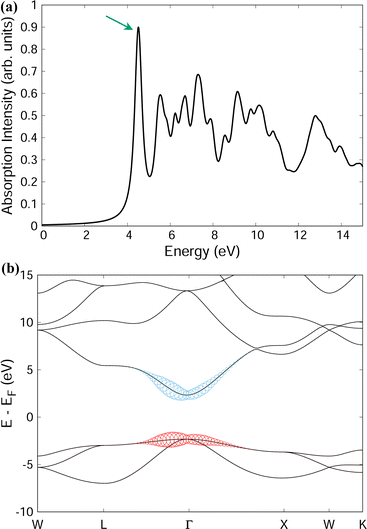
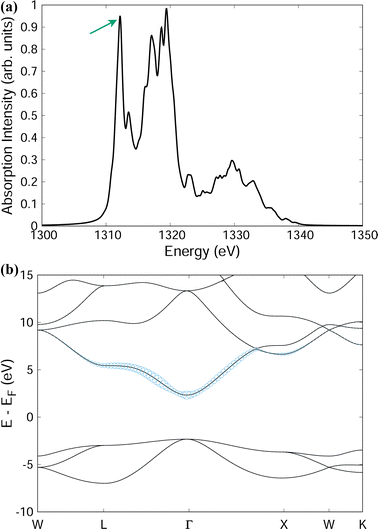
To present the power of the Bethe–Salpeter method Fig. 5 and 6 present example spectra of the optical and X-ray absorption spectra, respectively, of MgO in the rocksalt crystal structure. In addition to the absorption spectra, solution of HBSE also yields the weights AShc of the corresponding exciton eigenstates. Selecting a specific exciton eigenstate, indicated by the arrows in Fig. 5(a), (b) and 6(a), (b) show the band structure decomposition of the exciton. For optical absorption into the lowest bright exciton state, both the electron and hole are largely confined to a region around the Γ-point. This suggests the excitonic state is somewhat dispersed in real-space. For the case of a core excitation (from the Mg 1s shell), the excited electron component of the lowest energy bright exciton is quite dispersed in k-space. This is consistent with the notion of a bound exciton localized in real-space.
We introduce some basic nomenclature before proceeding further. Neglecting phonons for the moment, we designate the purely electronic absorption coefficient as μ0(ω) and use the corresponding electron–hole propagator 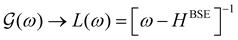 where HBSE is the Bethe–Salpeter Hamiltonian for the electron–hole interaction. At a formal level, the exciton propagator L(ω) can be expressed in terms of the bare electron–hole propagator L0(ω) via a Dyson equation with the interaction kernel K. In the next subsection we introduce phonons and obtain the full X-ray absorption coefficient μ(ω) including vibronic interactions. Λ(ω) will designate the corresponding phonon-dressed exciton propagator.
where HBSE is the Bethe–Salpeter Hamiltonian for the electron–hole interaction. At a formal level, the exciton propagator L(ω) can be expressed in terms of the bare electron–hole propagator L0(ω) via a Dyson equation with the interaction kernel K. In the next subsection we introduce phonons and obtain the full X-ray absorption coefficient μ(ω) including vibronic interactions. Λ(ω) will designate the corresponding phonon-dressed exciton propagator.
B. Vibronic coupling in XAS
Phonons and vibronic interactions can impact absorption spectra in various ways. One can generally separate these interactions into initial-state and final-state effects. Initial-state effects relate to structural disorder and atomic displacements caused, e.g. by thermal motion. Such atomic displacements impact spectra by modifying the quasiparticle energy levels, orbital hybridization, breaking local symmetries and lifting degeneracies. The impact of these atomic displacements have been studied by basing spectral calculations on disordered structures generated from molecular dynamics simulations58–60 and from thermally sampled phonon mode displacements.61,62 Initial-state vibrational interactions tend to cause broadening of spectral features, which can be extreme for some small organic molecules, but they can also activate otherwise optically-dark transitions.In the present work, we assume that atoms are located at their equilibrium positions in the initial state and focus on the contribution of vibronic interactions in the final-state. Final-state vibronic interactions generate phonon satellite peaks to the main electronic transitions. These satellite features may be distinguishable when experimental and lifetime resolutions allow. More often, they appear as an asymmetric broadening of the electronic transitions.44,45 Our objective is to study the phonon contribution to RIXS spectra due to final-state effects that occur within the intermediate state of the RIXS scattering process.
To illustrate our method, we first consider the Green's function representation of the X-ray absorption cross section
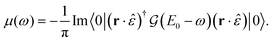 | (19) |
The argument of the Green's function is references with respect to the ground-state energy, E0. Absorption of an X-ray creates a photoelectron and core–hole, which may interact with each other and with the lattice. One can either first treat the lattice scattering of the electron and hole individually and then include the Coulomb interactions of the phonon–dressed electron and hole,63 or consider first the electron–hole binding and then incorporate lattice interactions as an exciton–phonon scattering process.64–66 When excitonic effects near the threshold of a core-level excitation are strong, excitonic binding can occur on a time-scale faster than the phonon dynamics. This motivates following the second approach.
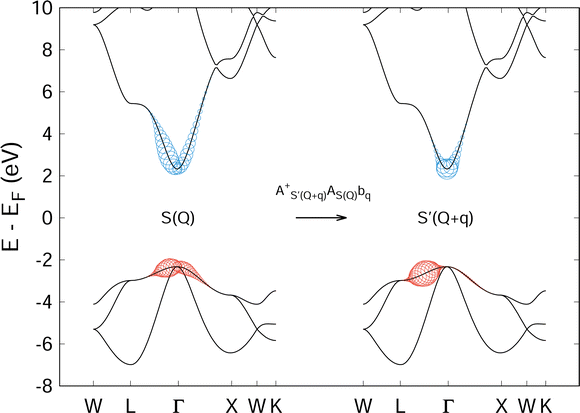
At optical and soft X-ray energies, photons carry negligible momentum, as do the excitons they create. However, phonons can subsequently scatter excitons to states of finite momentum. We designate these states as |S(Q)〉 where Q is the center of mass momentum of the electron–hole pair. (A numerical example of a finite momentum exciton state for MgO is provided in Fig. 7 and will be discussed in further detail in Section IV). To simplify notation, we will not always explicitly write the exciton momentum when Q = 0.
Starting from the phonon-free exciton propagator L(ω) and the corresponding excitonic eigenstates S, we construct a phonon-dressed exciton propagator Λ(ω) such that the full absorption spectrum, including both excitonic effects and exciton-lattice scattering, is given by
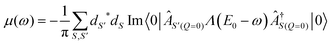 | (20) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) )|0〉 are again the dipole matrix elements. The operator
)|0〉 are again the dipole matrix elements. The operator 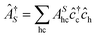 (
(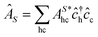 ) creates (annihilates) an exciton in state S.
) creates (annihilates) an exciton in state S.
Since it is critical to obtain a dressed exciton Green's function that gives a spectral function with good phonon satellite structure it is important to build Λ(ω) from the bare, phonon-free exciton propagator L(ω) not via the usual Dyson equation, but using the following cumulant representation in the time-domain
| Λ(S,t) = L(S,t)eC(S,t). | (21) |
Up to second-order, the cumulant may be expanded as
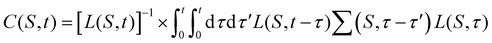 | (22) |
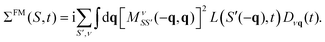 | (23) |
This expression contains a factor of the phonon propagator Dνq for mode ν and momentum q, and the exciton–phonon scattering matrix elements 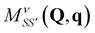 . We discuss the latter in more detail in Section IV.
. We discuss the latter in more detail in Section IV.
C. Vibronic coupling in RIXS
We now generalize the cumulant Green's function procedure to the evaluation of the Kramers–Heisenberg equation for the phonon contribution to RIXS spectra. It is useful to observe that while the intermediate state typically accesses high oscillator levels, only a few phonon levels are observed in the RIXS final state. Therefore, it is advantageous to employ a mixed Green's function and wavefunction representation of the RIXS cross section that maintains an explicit summation of a limited number of final oscillator levels, but replaces the summation over the intermediate states with a Green's function. In this mixed notation we express the RIXS cross-section in terms of vibrationally off-diagonal elements of the dressed exciton propagator Λ(nF) that are evaluated between the vibrational ground-state and the nF vibrational level. Writing nF → n for simplicity of notation, we have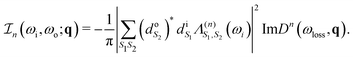 | (24) |
When the final-state contains no phonon excitations (n = 0) we recover the XAS exciton propagator 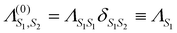 . The exciton propagators corresponding to the one- and two-phonon final states, expressed in the time-domain, are
. The exciton propagators corresponding to the one- and two-phonon final states, expressed in the time-domain, are
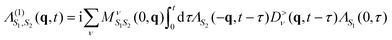 | (25) |
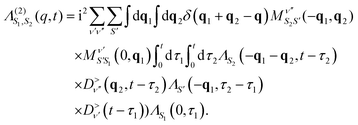 | (26) |
Higher order terms can be constructed using the standard diagrammatic rules that each vertex contributes a factor of 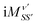 while factors of ΛS and
while factors of ΛS and 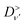 are added for each exciton or phonon line, respectively. Eqn (26) makes it clear that for a given momentum transfer q the intensity of higher harmonic peaks depend on the vibronic coupling at all points throughout the Brillouin zone. E.g. at the second harmonic all phonon pairs with momenta q1 + q2 = q will contribute. Although not explicit in eqn (25), this dependence on the coupling strength at all points in the Brillouin zone holds for the first harmonic as well. This dependence on all q-points occurs even for the first harmonic because the exciton propagator ΛS is dressed by virtual phonons appearing in the intermediate state, and is thus coupled to phonons throughout the Brillouin zone.
are added for each exciton or phonon line, respectively. Eqn (26) makes it clear that for a given momentum transfer q the intensity of higher harmonic peaks depend on the vibronic coupling at all points throughout the Brillouin zone. E.g. at the second harmonic all phonon pairs with momenta q1 + q2 = q will contribute. Although not explicit in eqn (25), this dependence on the coupling strength at all points in the Brillouin zone holds for the first harmonic as well. This dependence on all q-points occurs even for the first harmonic because the exciton propagator ΛS is dressed by virtual phonons appearing in the intermediate state, and is thus coupled to phonons throughout the Brillouin zone.
Dashwood et al.31 applied a preliminary implementation of the above Green's function method to reproduce the phonon features measured in graphite for a range of detunings across both the σ* and π* resonances. This allowed a quantitative determination of the momentum-dependent vibronic coupling strengths across the Brillouin zone. Furthermore, the authors demonstrated that combining RIXS experiment and the computational technique just described can easily discern different coupling strengths for different electronic excitations, i.e. to the π* versus σ* excitation in graphite.
IV. Exciton–phonon coupling
The main objective of measuring the phonon excitations of periodic systems with RIXS is to quantify the electron–phonon coupling strength throughout the Brillouin zone. Within the framework of density functional perturbation theory and linear response, the electron–phonon coupling matrix elements are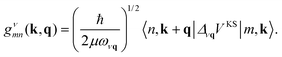 | (27) |
In this expression, ΔνqVKS is the variation of the Kohn–Sham potential due to a lattice distortion by the normal-mode coordinates of a phonon of mode ν, momentum q and energy ωνq. The average ion mass of the crystal is μ. The electron–phonon coupling strength is
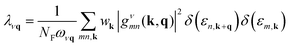 | (28) |
While gνmn(k,q) and λνq relate to the coupling of phonons to a single electron, such as determined through transport measurements, the electron–lattice interaction that occurs during a RIXS measurement involves the generation of phonons through the perturbation caused by the intermediate-state core-conduction exciton. This scattering of excitonic states with lattice vibrations may be expressed by the following vibronic Hamiltonian
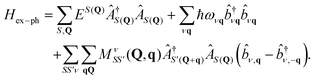 | (29) |
The last term represents scattering of an exciton from state S with center of mass momentum Q to the state S′ with momentum Q + q by a phonon of mode ν and momentum q. Phonon creation (annihilation) operators are given by 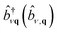 . An example calculation of this scattering process is presented in Fig. 7 for the scattering of a valence-conduction exciton (e.g. optical excitation) in MgO.
. An example calculation of this scattering process is presented in Fig. 7 for the scattering of a valence-conduction exciton (e.g. optical excitation) in MgO.
In analogy to the electron–phonon matrix elements in eqn (27), the exciton–phonon matrix elements can be written as
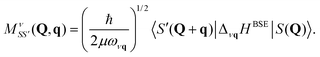 | (30) |
The expression involves evaluating the phonon-induced variation of the Bethe–Salpeter Hamiltonian between exciton states. Improving the quantitative understanding of RIXS measurements requires developing practical methodology to calculate these exciton–phonon matrix elements and finding a relation between them and the usual electron–phonon matrix elements.
The most direct approach to evaluating the exciton–phonon matrix elements in eqn (30) is to employ supercells to perform ground-state and Bethe–Salpeter calculations with finite atomic displacements along particular phonon normal modes. The energy of the excited-state vibrational surface may be expressed as ES(R) = E0(R) + ΩS(R) where E0(R) is the ground-state energy and ΩS(R) is the excitation energy. The position vector R = R0 + δu is restricted to small displacements δu around the equilibrium positions R0. The variation of the excited-state energy with respect to atomic displacements gives the excited-state force
| F(δu) = ∂RES|R = [∂RE0 + ∂RΩS]|R. | (31) |
Ismail–Beigi and Louie performed such finite displacement GW-BSE calculations to determine the optical excited-state forces for the CO molecule64 while Tinte and Shirley calculated the BSE forces for core excitations at the Ti site of SrTiO344 and Geondzhian and Gilmore reported similar calculations for core excitations at the oxygen site of acetone.51 These results, particularly for SrTiO3, reveal that exciton–phonon coupling values can differ noticeably from expectations based on normal electron–phonon coupling values. Such supercell calculations are typically limited by computational costs to a few high symmetry points in the Brillouin zone. It would be desirable in the future to develop methods analogous to density functional perturbation theory for calculating these excited-state forces for any q using only the primitive cell. Promising work in this direction, such as the quantitative description of polaron clouds from unit cell calculations,67,68 is ongoing.
Under the assumption that atomic displacements primarily impact the electron wavefunctions while the variation of the BSE interaction kernel may be neglected to first order, the exciton–phonon coupling constant may be expressed in terms of the usual electron–phonon coupling constants gνmn(k,q) as65,66
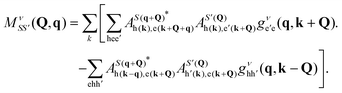 | (32) |
In this expression, h and e designate single particle states where h runs over all occupied, core states of the appropriate core level while e runs over unoccupied, conduction levels. This simplification treats exciton–phonon scattering as a superposition of electron–phonon and hole–phonon scattering events, weighted by the coefficients of the exciton wavefunctions. Fig. 8 provides a visual interpretation of these scattering processes for the case of a valence-conduction exciton in MgO.
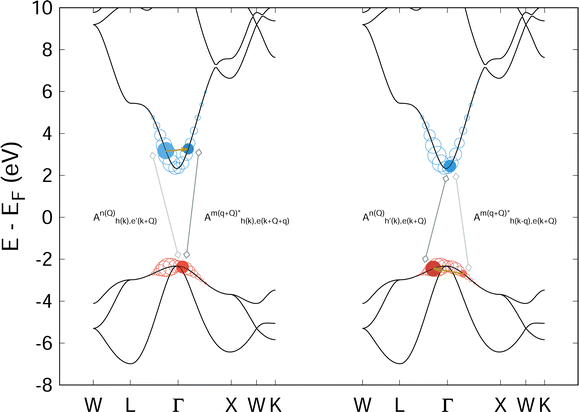 | ||
| Fig. 8 Schematic representation of eqn (32) for the lowest energy bright optical exciton in MgO. In each bandstructure diagram, the colored circles indicate the weight of a given k-point and band index to the electron (blue) or hole (red) portion of the exciton wavefunction. The left portion of the figure highlights two particular conduction band states (filled blue circles) to depict the electron–phonon scattering process while the highlighted hole state acts as a spectator. The right side provides a similar representation of the hole–phonon scattering process with a spectator electron state. Eqn (32) sums over all such combinations, weighted by the amplitudes of the corresponding excitonic wavefunctions. | ||
Eqn (32) provides a route toward predictive, first-principles evaluation of the exciton–phonon coupling constant based on standard many-body perturbation theory techniques. Nevertheless, it presents some challenges and, even within the present simplifying assumptions, indicates that the exciton–phonon coupling is a more complicated object than the normal electron–phonon coupling parameter. First, the exciton–phonon parameter includes a summation over all electron–phonon coupling values, weighted by their contribution to the given excitonic state. Second, numerical convergence of eqn (32) likely requires dense k-point sampling of the excitonic state. Third, the contribution of coupling between the core–hole and phonons appears with equal weight as compared to the conduction level electron–phonon coupling and must be carefully evaluated. Considerable work remains to address these numerical challenges.
The approximation made in eqn (32) for the exciton–phonon coupling constant assumes that the electron and hole scatter with phonons independently. Each scattering event creates or destroys a phonon and must conserve energy and momentum. In eqn (32) and Fig. 8, this energy and momentum conservation applies microscopically to each e − e′ and h − h′ scattering process. On the other hand, for eqn (30) and Fig. 7, the kinetic constraint is applied macroscopically to the entire exciton state, i.e. energy and momentum conservation is applied globally to S and S' and not to the individual electron and hole states of which they are comprised. By comparing Fig. 7 and 8, one can see that the two descriptions of exciton–phonon scattering involve different accessible scattering phase-spaces. Thus, while eqn (32) provides a practicable route toward obtaining the exciton–phonon coupling from the electron–phonon coupling, the numerical results may be less reliable than those obtained directly from eqn (30).
Eqn (32) assumes that the variation of the BSE interaction kernel with respect to finite atomic displacements is negligible. This approximation appears reasonable when the excitonic binding energy is small.69 However, with larger excitonic binding energy, as expected for core-level excitons at resonance, this picture may break down. In this case, the kinetically available phase-space for exciton–phonon scattering will differ noticeably from that of electron–phonon scattering65 and it will be necessary to numerically evaluate eqn (30).
V. Conclusion
The typical objective of using resonant inelastic X-ray scattering to measure phonon excitations in periodic solids is to quantify the electron–phonon coupling strength at different points in reciprocal space. The capability to do so has not yet been rigorously demonstrated. Most data analysis still relies on the basic displaced Einstein oscillator model. We have shown that simple extensions of this model – to two vibrational modes, or to allow a change in oscillator frequency between the ground- and excited-states – can noticeably impact the value of the vibronic coupling extracted from fitting experimental data. Furthermore, since the model is based on a local electronic level and a local Einstein oscillator, it does not offer access to the q-dependence of the coupling strength.We have presented a Green's function based description of the phonon contribution to RIXS that is suitable for first-principles calculations. The methodology combines a density functional theory based Bethe–Salpeter equation solution for the purely electronic component of the absorption and emission processes with a phonon contribution to the electronic self-energy generated using a cumulant Green's function approach. This formulation of the phonon contribution to RIXS incorporates the full momentum dependence of both the electronic states and the phonon modes and limits computational costs from becoming prohibitive by avoiding an explicit summation over intermediate states.
The RIXS calculations still require a momentum-dependent vibronic coupling parameter as input. Within our description, this is in fact an exciton–phonon interaction parameter. Under the assumption that the variation of the BSE interaction kernel with respect to small atomic displacements may be neglected, the exciton–phonon interaction relates to the usual electron–phonon coupling constants and can be numerically obtained from them. When the variation of the BSE interaction kernel cannot be neglected, we demonstrate that the exciton–phonon coupling parameter can be calculated directly through the use of supercells and finite displacements. The method described herein is practical to implement and will allow for rigorous testing of the theoretical understanding of phonon excitations in RIXS measurements.
Conflicts of interest
There are no conflicts to declare.Appendix computational details
All first-principles Bethe–Salpeter equation (BSE) calculations for MgO were performed with the Exciting code.70,71 Exciting is an all-electron density functional theory (DFT) code that employs periodic boundary conditions and the full-potential linearized augmented plane wave basis.The lattice constant of MgO was set to 7.96 Å. This value was then checked with a structural relaxation calculation. The ground-state electron density was obtained using the PBEsol approximation to the exchange–correlation potential and 8 × 8 × 8 k-point sampling. The BSE calculations used 6 × 6 × 6 k-point sampling, 60 empty bands for the BSE basis and 30 empty bands for the screening response. The BSE calculations for both the optical and X-ray absorption spectra were performed on the DFT electronic structure without GW corrections or a scissor shift. The X-ray absorption spectrum was shifted by +57 eV to align the first peak with the experimentally observed absorption onset of the Mg K-edge.
The code used to generate the phonon RIXS spectra for the harmonic oscillator models (displaced, displaced and distorted, and double oscillator) is available here https://github.com/geonda/rixs.phonons.
Acknowledgements
The author thanks Andrey Geondzhian and Kari Ruotsalainen for valuable discussions.References
- M. D. Johannes, Mazin II. Fermi surface nesting and the origin of charge density waves in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165135, DOI:10.1103/PhysRevB.77.165135.
- N. Bulut and D. J. Scalapino, dx2−y2 symmetry and the pairing mechanism, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14971–14973, DOI:10.1103/PhysRevB.54.14971.
- S. Y. Savrasov and O. K. Andersen, Linear-Response Calculation of the Electron–Phonon Coupling in Doped CaCuO2, Phys. Rev. Lett., 1996, 77, 4430–4433, DOI:10.1103/PhysRevLett.77.4430.
- P. Zhou, K. A. Wang, P. C. Eklund, G. Dresselhaus and M. S. Dresselhaus, Raman-scattering study of the electron–phonon interaction in M3 C60 (M = K,Rb), Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 8412–8417, DOI:10.1103/PhysRevB.48.8412.
- B. Schrader, in Infrared and Raman Spectroscopy: Methods and Applications, ed. B. Schrader, VCH Publishers, Weinheim, Germany, 1995 Search PubMed.
- P. Larkin, Infrared and Raman Spectroscopy: Principles and Spectral Interpretation, Elsevier, Amsterdam, Netherlands, 2011 Search PubMed.
- T. Cuk, D. H. Lu, X. J. Zhou, Z. X. Shen, T. P. Devereaux and N. Nagaosa, A review of electron–phonon coupling seen in the high-Tc superconductors by angle-resolved photoemission studies (ARPES), Phys. Status Solidi B, 2005, 242, DOI:10.1002/pssb.200404959.
- M. X. Na, A. K. Mills, F. Boschini, M. Michiardi, B. Nosarzewski and R. P. Day, et al., Direct determination of mode-projected electron–phonon coupling in the time domain, Science, 2019, 366(6470), 1231–1236, DOI:10.1126/science.aaw1662.
- B. N. Brockhouse and A. T. Stewart, Normal Modes of Aluminum by Neutron Spectrometry, Rev. Mod. Phys., 1958, 30, 236–249, DOI:10.1103/RevModPhys.30.236.
- P. B. Allen, Neutron Spectroscopy of Superconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 2577–2579, DOI:10.1103/PhysRevB.6.2577.
- A. Q. Baron, High-resolution inelastic X-ray scattering 1: Context, spectrometers, samples, and superconductors, Synchrotron Light Sources and Free-Electron Lasers, Springer, Switzerland, 2016 Search PubMed.
- L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Resonant Inelastic X-ray Scattering Studies of Elementary Excitations, Rev. Mod. Phys., 2010, 83, 705–767, DOI:10.1103/RevModPhys.83.705.
- L. J. P. Ament, G. Ghiringhelli, M. M. Sala, L. Braicovich and J. van den Brink, Theoretical Demonstration of How the Dispersion of Magnetic Excitations in Cuprate Compounds can be Determined Using Resonant Inelastic X-Ray Scattering, Phys. Rev. Lett., 2009, 103, 117003, DOI:10.1103/PhysRevLett.103.117003.
- L. Braicovich, J. van den Brink, V. Bisogni, M. M. Sala, L. J. P. Ament and N. B. Brookes, et al., Magnetic Excitations and Phase Separation in the Underdoped La2−xSrxCuO4 Superconductor Measured by Resonant Inelastic X-Ray Scattering, Phys. Rev. Lett., 2010, 104, 077002, DOI:10.1103/PhysRevLett.104.077002.
- X. Lu, P. Olalde-Velasco, Y. Huang, V. Bisogni, J. Pelliciari and S. Fatale, et al., Dispersive magnetic and electronic excitations in iridate perovskites probed by oxygen K-edge resonant inelastic X-ray scattering, Phys. Rev. B, 2018, 97, 041102, DOI:10.1103/PhysRevB.97.041102.
- J. Pelliciari, S. Lee, K. Gilmore, J. Li, Y. Gu and A. Barbour, et al., Tuning Spin Excitations in Magnetic Films by Confinement, Nat. Mater., 2021, 20, 188–193 CrossRef CAS PubMed.
- T. P. Devereaux, A. M. Shvaika, K. Wu, K. Wohlfeld, C. J. Jia and Y. Wang, et al., Directly Characterizing the Relative Strength and Momentum Dependence of Electron–Phonon Coupling Using Resonant Inelastic X-ray Scattering., Phys. Rev. X, 2016, 6, 041019, DOI:10.1103/PhysRevX.6.041019.
- A. Hariki, M. Winder, T. Uozumi and J. Kuneš, LDA + DMFT approach to resonant inelastic X-ray scattering in correlated materials, Phys. Rev. B, 2020, 101, 115130, DOI:10.1103/PhysRevB.101.115130.
- K. Gilmore, J. Pelliciari, Y. Huang, J. J. Kas, M. Dantz and V. N. Strocov, et al., Description of Resonant Inelastic X-Ray Scattering in Correlated Metals, Phys. Rev. X, 2021, 11, 031013, DOI:10.1103/PhysRevX.11.031013.
- A. Pietzsch, Y. P. Sun, F. Hennies, Z. Rinkevicius, H. O. Karlsson and T. Schmitt, et al., Spatial Quantum Beats in Vibrational Resonant Inelastic Soft X-ray Scattering at Dissociating States in Oxygen, Phys. Rev. Lett., 2011, 106, 153004, DOI:10.1103/PhysRevLett.106.153004.
- V. Vaz da Cruz, E. Ertan, R. C. Couto, S. Eckert, M. Fondell and M. Dantz, et al., A study of the water molecule using frequency control over nuclear dynamics in resonant Xray scattering, Phys. Chem. Chem. Phys., 2017, 19, 19573–19589, 10.1039/C7CP01215B.
- R. C. Couto, V. V. Cruz, E. Ertan, S. Eckert, M. Fondell and M. Dantz, et al., Selective gating to vibrational modes through resonant X-ray scattering, Nat. Commun., 2017, 8, 14165, DOI:10.1038/ncomms14165.
- E. Ertan, V. Kimberg, F. Gel’Mukhanov, F. Hennies, J. E. Rubensson and T. Schmitt, et al., Theoretical simulations of oxygen K-edge resonant inelastic X-ray scattering of kaolinite, Phys. Rev. B, 2017, 95(14), 144301 CrossRef.
- S. Schreck, A. Pietzsch, B. Kennedy, C. Såthe, P. S. Miedema and S. Techert, et al., Ground state potential energy surfaces around selected atoms from resonant inelastic Xray scattering, Sci. Rep., 2016, 7(May 2015), 20054 CrossRef PubMed.
- F. Hennies, A. Pietzsch, M. Berglund, A. Föhlisch, T. Schmitt and V. Strocov, et al., Resonant Inelastic Scattering Spectra of Free Molecules with Vibrational Resolution, Phys. Rev. Lett., 2010, 104, 193002, DOI:10.1103/PhysRevLett.104.193002.
- S. Moser, S. Fatale, P. Krüger, H. Berger, P. Bugnon and A. Magrez, et al., Electron–phonon coupling in the bulk of anatase TiO2 measured by resonant inelastic X-ray spectroscopy, Phys. Rev. Lett., 2015, 115(9), 096404 CrossRef CAS PubMed.
- S. Fatale, S. Moser, J. Miyawaki, Y. Harada and M. Grioni, Hybridization and electron–phonon coupling in ferroelectric BaTiO3 probed by resonant inelastic X-ray scattering, Phys. Rev. B, 2016, 94(19), 195131 CrossRef.
- D. Meyers, K. Nakatsukasa, S. Mu, L. Hao, J. Yang and Y. Cao, et al., Decoupling Carrier Concentration and Electron–Phonon Coupling in Oxide Heterostructures Observed with Resonant Inelastic X-ray Scattering, Phys. Rev. Lett., 2018, 121, 236802, DOI:10.1103/PhysRevLett.121.236802.
- A. Geondzhian, A. Sambri, G. M. De Luca, R. Di Capua, E. Di Gennaro and D. Betto, et al., Large Polarons as Key Quasiparticles in SrTiO3 and SrTiO3-Based Heterostructures, Phys. Rev. Lett., 2020, 125, 126401, DOI:10.1103/PhysRevLett.125.126401.
- L. Braicovich, M. Rossi, R. Fumagalli, Y. Peng, Y. Wang and R. Arpaia, et al., Determining the electronphonon coupling in superconducting cuprates by resonant inelastic X-ray scattering: Methods and results on Nd1+xBa2xCu3O7, Phys. Rev. Res., 2020, 2, 023231, DOI:10.1103/PhysRevResearch.2.023231.
- C. D. Dashwood, A. Geondzhian, J. G. Vale, A. C. Pakpour-Tabrizi, C. A. Howard and Q. Faure, et al., Probing Electron–Phonon Interactions Away from the Fermi Level with Resonant Inelastic X-ray Scattering, Phys. Rev. X, 2021, 11, 041052, DOI:10.1103/PhysRevX.11.041052.
- K. Bieniasz, S. Johnston and M. Berciu, Beyond the singlesite approximation modeling of electron–phonon coupling effects on resonant inelastic X-ray scattering spectra, SciPost Phys., 2021, 11, 062, DOI:10.21468/SciPostPhys.11.3.062.
- L. J. P. Ament, M. van Veenendaal and J. van den Brink, Determining the electron–phonon coupling strength from Resonant Inelastic X-ray Scattering at transition metal L-edges, EPL, 2011, 95(2), 27008 CrossRef . Available from: https://stacks.iop.org/0295-5075/95/i=2/a=27008..
- I. G. Lang and Y. A. Firsov, Kinetic Theory of Semiconductors with Low Mobility, Sov. Phys. JETP, 1963, 16(5), 1301 Search PubMed . Available from: https://www.jetp.ac.ru/cgi-bin/e/index/e/16/5/p1301?a=list.
- P. M. Champion, G. M. Korenowski and A. C. Albrecht, On the vibronic theory of resonance Raman scattering, Solid State Commun., 1979, 32(1), 7–12 CrossRef CAS . Available from: https://www.sciencedirect.com/science/article/pii/0038109879909876.
- P. B. Allen and V. Perebeinos, Self-Trapped Exciton and Franck–Condon Spectra Predicted in LaMnO3, Phys. Rev. Lett., 1999, 83, 4828–4831, DOI:10.1103/PhysRevLett.83.4828.
- V. Perebeinos and P. B. Allen, Multiphonon resonant Raman scattering predicted in LaMnO3 from the Franck–Condon process via self-trapped excitons, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 085118, DOI:10.1103/PhysRevB.64.085118.
- M. O. Krause and J. H. Oliver, Natural widths of atomic K and L levels, K X-ray lines and several KLL Auger lines, J. Phys. Chem. Ref. Data, 1979, 8(2), 329–338, DOI:10.1063/1.555595.
- A. Geondzhian and K. Gilmore, Generalization of the Franck–Condon model for phonon excitations by resonant inelastic X-ray scattering, Phys. Rev. B, 2020, 101, 214307, DOI:10.1103/PhysRevB.101.214307.
- M. Rossi, R. Arpaia, R. Fumagalli, M. Moretti Sala, D. Betto and K. Kummer, et al., Experimental Determination of Momentum-Resolved Electron–Phonon Coupling, Phys. Rev. Lett., 2019, 123, 027001, DOI:10.1103/PhysRevLett.123.027001.
- Y. Y. Peng, Doping-dependence of the electronphonon coupling in two families of bilayer superconducting cuprates, Phys. Rev. B, 2022, 105, 115105, DOI:10.1103/PhysRevB.105.115105.
- J. G. Vale, C. D. Dashwood, E. Paris, L. S. I. Veiga, M. Garcia-Fernandez and A. Nag, et al., High-resolution resonant inelastic X-ray scattering study of the electron–phonon coupling in honeycomb α-Li2IrO3, Phys. Rev. B, 2019, 100, 224303, DOI:10.1103/PhysRevB.100.224303.
- X. Feng, S. Sallis, Y. C. Shao, R. Qiao, Y. S. Liu and L. C. Kao, et al., Disparate Exciton–Phonon Couplings for Zone-Center and Boundary Phonons in Solid-State Graphite, Phys. Rev. Lett., 2020, 125, 116401, DOI:10.1103/PhysRevLett.125.116401.
- S. Tinte and E. L. Shirley, Vibrational effects on SrTiO3 Ti 1s absorption spectra studied using first-principles methods, J. Phys.: Condens. Matter, 2008, 20(36), 365221 CrossRef.
- K. Gilmore and E. L. Shirley, Numerical quantification of the vibronic broadening of the SrTiO3 Ti L-edge spectrum, J. Phys.: Condens. Matter, 2010, 22(31), 0–5 CrossRef CAS PubMed.
- W. Witschel, Harmonic oscillator integrals, J. Phys. B: At. Mol. Phys., 1973, 6(3), 527–534, DOI:10.1088/0022-3700/6/3/021.
- K. Nishikawa, Exact calculations of Franck–Condon overlaps and of matrix elements of some potentials by means of the coherent state representation, Int. J. Quantum Chem., 1977, 12(5), 859–873, DOI:10.1002/qua.560120509.
- A. Palma and J. Morales, Franck–condon factors and ladder operators. I. harmonic oscillator, Int. J. Quantum Chem., 1983, 24(S17), 393–400, DOI:10.1002/qua.560240843.
- J. L. Chang and Y. T. Chen, Ab initio calculations of low-lying electronic states of vinyl chloride, J. Chem. Phys., 2002, 116(17), 7518–7525, DOI:10.1063/1.1466828.
- T. Sattasathuchana, Calculation of Multidimensional Franck–Condon factors within the harmonic oscillator approximation for both gas phase and solution phase, University of Zurich, 2016 DOI:10.5167/uzh-134901.
- A. Geondzhian and K. Gilmore, Demonstration of resonant inelastic X-ray scattering as a probe of exciton–phonon coupling, Phys. Rev. B, 2018, 98, 214305, DOI:10.1103/PhysRevB.98.214305.
- E. L. Shirley, Ab Initio Inclusion of Electron–Hole Attraction: Application to X-ray Absorption and Resonant Inelastic X-ray Scattering, Phys. Rev. Lett., 1998, 80, 794–797, DOI:10.1103/PhysRevLett.80.794.
- S. Albrecht, L. Reining, R. Del Sole and G. Onida, Ab Initio Calculation of Excitonic Effects in the Optical Spectra of Semiconductors, Phys. Rev. Lett., 1998, 80, 4510–4513, DOI:10.1103/PhysRevLett.80.4510.
- M. Rohlfing and S. G. Louie, Excitonic Effects and the Optical Absorption Spectrum of Hydrogenated Si Clusters, Phys. Rev. Lett., 1998, 80, 3320–3323, DOI:10.1103/PhysRevLett.80.3320.
- M. Rohlfing and S. G. Louie, Electron–Hole Excitations in Semiconductors and Insulators, Phys. Rev. Lett., 1998, 81, 2312–2315, DOI:10.1103/PhysRevLett.81.2312.
- G. Onida, L. Reining and A. Rubio, Electronic excitations: density-functional versus many-body Green'sfunction approaches, Rev. Mod. Phys., 2002, 74, 601–659, DOI:10.1103/RevModPhys.74.601.
- K. Gilmore, J. Vinson, E. L. Shirley, D. Prendergast, C. D. Pemmaraju and J. J. Kas, et al., Efficient implementation of core-excitation Bethe–Salpeter equation calculations, Comput. Phys. Commun., 2015, 197, 315901, DOI:10.1016/j.cpc.2015.08.014.
- J. Niskanen, C. J. Sahle, K. Gilmore, F. Uhlig, J. Smiatek and A. Föhlisch, Disentangling structural information from core-level excitation spectra, Phys. Rev. E, 2017, 96, 013319, DOI:10.1103/PhysRevE.96.013319.
- J. Niskanen, M. Fondell, C. J. Sahle, S. Eckert, R. M. Jay and K. Gilmore, et al., Compatibility of quantitative X-ray spectroscopy with continuous distribution models of water at ambient conditions, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(10), 4058–4063 CrossRef CAS PubMed . Available from: https://www.pnas.org/content/116/10/4058.
- S. Petitgirard, C. J. Sahle, C. Weis, K. Gilmore, G. Spiekermnn and J. S. Tse, et al., Magma properties at deep Earth's conditions from electronic structure of silica, Geochem. Perspect. Lett., 2019, 9, 32–37 CrossRef . Available from: https://www.geochemicalperspectivesletters.org/article1902.
- J. Vinson, T. Jach, W. T. Elam and J. D. Denlinger, Origins of extreme broadening mechanisms in near-edge X-ray spectra of nitrogen compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205207, DOI:10.1103/PhysRevB.90.205207.
- R. Nemausat, D. Cabaret, C. Gervais, C. Brouder, N. Trcera and A. Bordage, et al., Phonon effects on X-ray absorption and nuclear magnetic resonance spectroscopies, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 144310, DOI:10.1103/PhysRevB.92.144310.
- A. Marini, Ab Initio Finite-Temperature Excitons, Phys. Rev. Lett., 2008, 101, 106405, DOI:10.1103/PhysRevLett.101.106405.
- S. Ismail-Beigi and S. G. Louie, Excited-State Forces within a First-Principles Green's Function Formalism, Phys. Rev. Lett., 2003, 90, 076401, DOI:10.1103/PhysRevLett.90.076401.
- G. Antonius and S. G. Louie, Theory of the exciton–phonon coupling, Phys. Rev. B, 2022, 105, 085111, DOI:10.1103/PhysRevB.105.085111.
- H. Y. Chen, D. Sangalli and M. Bernardi, Exciton–Phonon Interaction and Relaxation Times from First Principles, Phys. Rev. Lett., 2020, 125, 107401, DOI:10.1103/PhysRevLett.125.107401.
- W. H. Sio, C. Verdi, S. Poncé and F. Giustino, Polarons from First Principles, without Supercells, Phys. Rev. Lett., 2019, 122, 246403, DOI:10.1103/PhysRevLett.122.246403.
- W. H. Sio, C. Verdi, S. Poncé and F. Giustino, Ab initio theory of polarons: Formalism and applications, Phys. Rev. B, 2019, 99, 235139, DOI:10.1103/PhysRevB.99.235139.
- Z. Li, G. Antonius, M. Wu, F. H. da Jornada and S. G. Louie, Electron–Phonon Coupling from Ab Initio Linear-Response Theory within the GW Method: Correlation-Enhanced Interactions and Superconductivity in Ba1−xKxBiO3, Phys. Rev. Lett., 2019, 122, 186402, DOI:10.1103/PhysRevLett.122.186402.
- A. Gulans, S. Kontur, C. Meisenbichler, D. Nabok, P. Pavone and S. Rigamonti, et al., Exciting: a fullpotential all-electron package implementing densityfunctional theory and many-body perturbation theory, J Phys: Condens Matter., 2014, 26, 363202, DOI:10.1088/0953-8984/26/36/363202.
- C. Vorwerk, B. Aurich, C. Cocchi and C. Draxl, Bethe–Salpeter equation for absorption and scattering spectroscopy: implementation in the exciting code, Electron. Struct., 2019, 1, 037001, DOI:10.1088/2516-1075/ab3123.
| This journal is © the Owner Societies 2023 |