Open Access Article
Open Access ArticleEfficiency of thermo–photocatalytic production of hydrogen from biomolecules: a multifaceted perspective
María Natividad
Gómez-Cerezo†
,
Irene
Barba-Nieto†
,
Marcos
Fernández-García
 * and
Anna
Kubacka
*
* and
Anna
Kubacka
*
Instituto de Catálisis y Petroleoquímica. CSIC. C/ Marie Curie, 2. 28049 Madrid, Spain. E-mail: mfg@icp.csic.es; ak@icp.csic.es
First published on 26th August 2022
Abstract
Measuring and interpreting the efficiency of a thermo–photocatalytic reaction is key in the quest to define synergy for chemical reactions taking place under dual thermo–photo excitation. The analysis of the efficiency parameter requires multiple facets of the problem to be taken into account, demanding a detailed study of the chemical, photon and global energy balances of the reaction. This manuscript discussed how to approach such a goal, starting from using mathematical frameworks for the measurement of the three mentioned facets of the efficiency parameter with the help of the corresponding excess functions and ending with the interpretation of synergy through an adequate physico-chemical investigation using modern operando spectroscopic and theoretical tools.
1. Hydrogen production using light and heat
Hydrogen is a key molecule for the chemical industry, and is used in numerous processes to generate useful compounds, as well as for energy production. Both application areas but particularly the second would be promoted within the context of the environmentally respectful economy expected for the near future. The benefits of utilizing hydrogen as an energy source in transportation, household and industrial environments would come mainly from (i) a potentially unlimited supply due to its highest mass abundance on Earth compared to other chemical elements, (ii) its significant energy storage capacity, nearly three times higher per volume unit than those of other classic sources such as methane, and iii) the control of carbon-related emission and pollution, which can take place at the initial step of the generation of the fuel and not when energy is released (zero-emissivity). Independently of its final use, green hydrogen is expected to be produced massively in the near future from carbon neutral and environmentally benign processes. Catalysis plays an essential role in a significant number of processes considering green hydrogen generation.1,2 In particular, the green generation of hydrogen using conventional catalysts and molecules from bio-resources, such as water, alcohols, acetic acid and others, appears as a hot research field subjected to intensive research. Yet, building up a commercial technology will require a significant improvement to compete with the well-established (and gray but not green) methane dry reforming process.3,4 The more environmentally benign energy-intensive water-electrolysis would also be a benchmark reference if combined with a solar (photo-voltaic) energy supply. Nevertheless, at present, the water electrolysis economic viability is restricted by the need of more efficient and stable membranes as well as working around the clock, which in turn would require other energy sources in addition to the sun.5Within the context of hydrogen production from natural resources, photocatalysis appeared as an attractive possibility as it works at room temperature and pressure.6,7 Ideally, hydrogen can be produced photocatalytically from water but, independently of catalytic aspects, the separation cost of hydrogen and oxygen could make the cost of the technology prohibitive.8,9 Unless newly developed efficient (not currently achievable) photocatalysts can produce the two gases separately, at two different physical locations even from the initial stage of the reaction, the use of water as the hydrogen source may not find application as a competing technology.5 Therefore, the use of broadly available and cheap bio-resources such as methanol, ethanol and others in water as the primary target(s) of the process appears as a rather convenient alternative.10,11 However, as is well-known, the efficiency of the corresponding hydrogen production photocatalytic processes is limited, restraining their industrial applications.
A potential pathway to eliminate or overcome the mentioned drawbacks of thermal and photocatalytic processes to generate hydrogen from bio-molecules would come from the synergistic use of both types of processes. Combining thermal and photonic energies into single catalytic processes has been shown to be effective for many chemical reactions and, particularly, hydrogen production.12–19 The simultaneous use of thermal and photonic energies within a single catalytic process can primarily depend on the way by which the energy is supplied. Thermal energy can be supplied as customarily carried out in thermal catalysis using heat suppliers or can be obtained from light and, particularly, using infrared region. Thermal conductivity (and also, frequently, convection taking place though fluidized phases) is (are) the most significant relevant mode(s) of heat handling and transfer in conventional reactors while the complex de-excitation of light is the main physico-chemical process related to heat handling in photoreactors. Note that photoreactors have thus an inherent thermal effect which cannot be decoupled. On the other hand, it is obvious that the “pure” heat (thermal conductivity/convectivity) related effects are essentially non-local in conventional heat-supplying reactors (yet local type effects, e.g. hot spots, can be obtained using chemical-related effects such as those present in auto-thermal reforming reactions) while well-defined (nanometric) localized type effects can be obtained using light if the corresponding “active” catalyst component has a characteristic nanometer dimension. De-excitation of light involves radiative and non-radiative channels, all of potential relevance in photo-thermal reactions, and strongly dependent on the nature of catalysts, particularly of the presence of metallic or semiconducting components. Thus, photon-induced charge carrier species suffer de-excitation processes via (radiative) “direct” emission of photons. Non-radiative recombination can occur via electron-related (electron–electron scattering) phenomena in metallic (plasmonic or not) components while de-excitation via lattice phonons could occur in all systems but is particularly significant for semiconductor phases.14,16,20,21 Although out of the scope of this work, we note that the complex physical and chemical mechanisms of the light–matter interaction under thermo–photo excitation are described in previous literature review articles.20,22
From the previous discussion, we highlight that light and heat phenomena (even in the so-called pure photocatalytic processes) are intimately inter-related and that there is no obvious way of classifying the dual-excited materials as photo- or thermo-assisted thermo/photocatalytic solids or truly thermo–photocatalysts. Yet, a simple picture may evolve from the nature of the rate determining step (RDS) of the reaction. A RDS resembling the thermo/photo single source counterpart can be defined as dominated by such phenomena (and assisted by the other one) while a completely new RDS (and thus reaction mechanism) would imply a novel thermo–photo process.12–14,16,17 Of course, the kinetic analysis of a thermo–photo-dependent reaction is not obvious although some rigorous studies are available where the temperature dependence of both the optical and chemical properties of the systems is, at least, partially accounted for.23–25 Nonetheless, the complexity of any thermo–photo reaction mechanism and kinetics makes this a really open field for research.
In this perspective contribution, we focus on the specific problem of analyzing the efficiency of the thermo–photo production of hydrogen from bio-molecules. Whatever the exact physical mechanism of heat handling and transfer in a thermo–photocatalyst, a previous problem to be solved is the simultaneous and, hopefully, synergistic use of light and heat by a catalytic solid. It is obvious that the complexity inherent to a dual excitation catalytic process demands synergy for practical applications.21 The accurate measurement of the efficiency when using two energy sources is therefore required to establish the synergy of the catalytic process and appears as an essential physico-chemical aspect of the dual thermo–photocatalysis research field. Such a field is currently subjected to intense scrutiny. As will be detailed here, most active thermo–photocatalytic systems correspond to photo-responsive oxide semiconductors, such as titania, ceria, zinc or indium oxides and others, promoted by metals or other co-catalysts.12–19,25 The key role of the photo-active oxides in the heat–light interaction is primarily understood considering the phenomena taking place in an oxide semiconductor. Of course, the presence of a co-catalyst of a different chemical nature should also be considered.
Although challenging, the quantitative assessment of a thermo–photocatalytic reaction has been approached in several contributions. To provide a framework to rationalize the existing results to measure and interpret thermo–photo activity, we will explore this problem from a complete perspective, considering the chemical–catalytic, photonic and energetic points of view. We summarized the proposed approach for the measurement of thermo–photo activity in Fig. 1. The primary objective is thus to define how we can assure that a catalyst is an useful thermo–photocatalytic system. In particular, as a result of the mentioned multi-faceted perspective to approach the problem (Fig. 1), we expect to highlight how the utility of the process with respect to (parent) more conventional, single-source processes for hydrogen generation from bio-molecules can be established.
 | ||
| Fig. 1 Schematic representation of a hydrogen thermo-photoproduction process: energy sources, catalyst, chemical reaction(s) and efficiency observables. | ||
Within this contribution, the chemical-catalytic view would drive us to pinpoint case examples considering the most relevant studies analyzing the functional properties of highly active solids utilized in the field. Any active catalytic material is defined by the corresponding active center, the reaction mechanism and thermodynamic and kinetic parameters. As is well-known, a complete knowledge of the catalytic “problem” is a rather complex task in conventional catalysis but the current (experimental and theoretical) capabilities limit a full interpretation in the thermo–photo research field. This is intimately connected with the complex light–heat interplay previously mentioned. The analysis of exclusive photon-related aspects of thermo–photoreactions is also a challenging task. We can however understand such aspects considering the close parallelism with the corresponding photocatalytic reaction(s). Starting from the IUPAC-defined photonic yield and quantum efficiency of a photocatalytic process,26 the literature defines analogs for thermo–photoreactions to accurately express and measure what is the chemical fate of each photon impinging or absorbed by a solid at the reaction temperature. The corresponding results for case examples would also shed light on the understanding of the thermo–photo-phenomenon. Finally, the analysis of the global energy efficiency is considered to render a robust (global) estimation of the goodness of any thermo–photocatalytic material. The measurement of such a type of parameter appears critical to provide evidence of synergistic effects and calibrate the potential benefits of the technology both to expand thermal-based conventional chemical processes as well as to open the use of alternative sources such as the sun as a dual source of heat and light in chemical processes of industrial interest. Yet, besides analyzing efficiency observables reported in the literature, we present a mathematical framework to interpret them and to provide information about the physico-chemical mechanism(s) behind the phenomenon.
In short, in this contribution, we attempt to provide an overall view of the most exciting results reported in the literature covering the above mentioned chemical, photonic and energy-related fundamental aspects of the thermo–photocatalytic production of hydrogen from bio-molecules. The corresponding information as well as an unified view of the problem are completely absent in the literature12–14,16–19 and are of critical significance in order to assess synergy in dual thermo–photocatalytic processes. We would like to stress the fact that the framework provided for the measurement, analysis and interpretation of the efficiency is general for any thermo–photo reaction and that the catalytic process studied here can also be viewed as a case example to generalize the results of this perspective contribution.
2. Thermo–photoefficiency
2.1. Measuring and reporting the reaction rate and photonic and energy efficiencies
| re = rTP − (rP + rT) | (1) |
| re = rTP/(rP + rT) | (2) |
This excess rate can be defined as a synergistic rate when positive. Alternatively, the plot of the corresponding (thermo and thermo–photo) rates evolution vs. temperature can provide similar information. Of course, measuring a reaction rate (as well as any other efficiency parameter) should be carried out considering adequate rules in order to provide information.
Discussing this last point in a general context, we can note that measuring a true thermo–photorate requires a number of minimal conditions. Ideally, as a first critical point, to carry out a thermo–photoreaction, a catalyst body or bed with full access to light is highly desirable. In order to address this issue, we detailed below the relevant physico-chemical phenomena under dual thermal and optical excitation as a function of light–matter interaction characteristics in the reaction system (catalyst, reaction medium and reactor). Note that these phenomena are independent of the solid nature, whether it is a semiconductor, a metal or any other type of material. So, we will start with a general description of the relevant physico-chemical phenomena for light–catalyst interactions, valid for any thermo–photocatalyst, particularly those mentioned in point 1 of this contribution. The mathematical formulation of all optical (opto-electronic) events of significance in the thermo–photocatalytic processes is subsequently addressed in Section 2.1.2.
As discussed in the literature, two well differentiated situations of the problem of maximizing the light use by a catalytic material can take place as a function of interaction between light and the catalytic solid. The first is the so-called homogeneous case, where the light–matter interaction is mathematically handled considering the catalyst and the medium of the reaction as a single entity. Liquid phase catalyst suspensions are typical cases, where light absorption, emission and scattering are the dominant optical (opto-electronic) events. Refraction at reactor walls should also be considered. The micrometric secondary particle size of most of the catalytic solids and the mean free path of light in “photocatalytic solids” (also micrometric but strongly solid and wavelength dependent in the range of ca. 250–1200 nm, e.g. the typical UV-visible–near-IR range useful for catalysis) point out the practical impossibility for light to access all possible active sites of the catalyst. In an important number of cases, the inner part of the secondary particle size does not receive significant light intensity. In the literature, this is reported as the dead or void volume problem or the shadowing effect.27–31
The second case is the so-called heterogeneous system, where the interaction of light with the catalysts can be isolated from (other) physical phenomena taking place in the reaction medium. In this case, light absorption/transmittance, reflection, emission and, to a somewhat lower extent, refraction at reactor walls are the main optical events taking place. Refraction is significantly less critical for the air–glass–air case than the one corresponding to the air–glass–water. Scattering is negligible in this case expect for specific cases, for example, with catalytic solids having fractal porosity specifically designed to maximize scattering.32 Gas phase reactions (when the medium is optically inert) using solid films are the archetypal cases of (light–catalyst) heterogeneous systems. For such types of systems, an optical depth can be defined to limit the main dead volume problems.33,34 In short, with generality, in almost all reactor designs and independently of the light–matter interaction details, a gradual degradation of the light through the optically active system (away from the light source and/or considering the inner parts of the secondary particle) takes place and may trigger the “waste” of a fraction of the catalytic solid. For all heterogeneous and homogeneous cases, the latter can be truly calculated from the interplay of the light–matter interaction and the mass transport of the reactants/products through the solid.32,34
As a second important point, if the reaction is either exothermic, non-radiative de-excitation dominates (particularly if taking place in local nanometric nature, rendering hot stops), light includes a significant IR contribution, and/or, in general, thermo–photo experiments are studied, the presence of thermal gradients could additionally occur and be solved (or more properly speaking, minimized) as customarily carried out in thermal catalysis, limiting heat-transfer effects. This last issue unveils the second critical point to carry out thermo–photoreactions, that is, the difficulty of obtaining a uniform and stable temperature through the (thermo–photocatalytic) reactor and, thus, directly connects with the issue of defining the temperature of the catalyst active region when light is one of the excitation sources.16,22
From our previous discussion, it appears obvious that controlling the morphological properties of a powder catalyst can minimize transport (mass and thermal) effects, related to the mentioned interplay between the light–matter interaction and mass–heat transfer effects, in the homogeneous (light-matter) case. Note that the secondary particle size (as mentioned, a highly relevant morphological property in this context) is catalyst and medium dependent for liquid phase reactions, so it is defined by the experimental conditions utilized in the reaction. In the case of using the powder catalyst in a film, selecting the appropriate thickness of the bed can do the same job and would allow the control of transport effects. Alternatively, due to the complexity of the physical problem, almost unavoidable constraints inherent to a catalytic process with dual excitation (and connected with materials, the reaction medium and reactor) can trigger the existence of transport issues. For example, this is a frequent case when a conventional thermal source and light excitation will reach a (non-optimized from the “optical” perspective) catalyst bed from opposite sides. In these types of (heterogeneous) systems, experimental measurements can be carried out to check the potential thermal gradient taking place as well as to obtain an average effective temperature to be used for comparison with single-source thermal catalysis.35,36 We can mention here advances in the nanometric-scale measurements of temperature as potentially useful in this context, but the complexity of the experimental methods (scanning microscopy coupled with temperature nanoprobes, IR nano-thermography, etc.) makes them hard to implement for the analysis of photo-reactors working under relevant catalytic conditions.
So, care should be taken to analyze the potential limited use of light intensity supplied and/or the uniformity of the temperature under dual thermo–photo excitation. The brief discussion just presented pointed out how to carry out meaningful measurements of a thermo–photocatalytic reaction. A simple summary of the useful reaction rate reports concerning the thermo–photo production of hydrogen is presented in Fig. 2. Typical results report the observable vs. temperature of the reaction under dark (thermal) and illuminated (thermo–photo) conditions. The representative works concerning titania-based systems for the methanol steam reforming reaction are presented in Fig. 2A–D. Metal loaded on bare titania37 as well as composite oxides having titania as one (main) component are considered.38,39 Other titania based materials render rather similar results.25,40–43 As can be seen (particularly using the excess function presented in panel 2D for a series of catalysts), the titania-based oxides promoted by metals are active thermo–photocatalysts. This reaction can be carried out at temperatures typical of the thermal (alone) reaction but with clear advantages coming from the combination of light and heat energy sources. Similarly, more complex catalytic formulations based on Cu–Zn–Ti44 as well as Cu–Zn–Zr45 composite materials provide good activity in the same reaction (Fig. 2D and E).
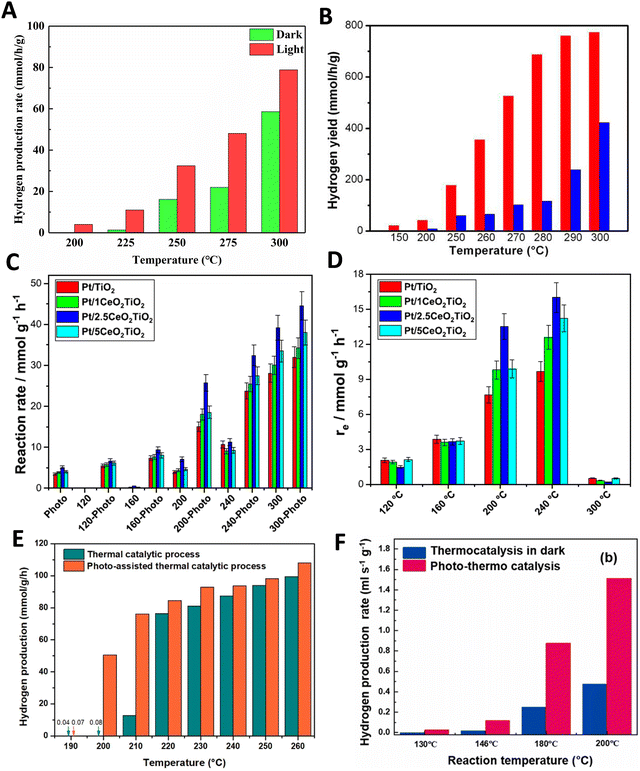 | ||
| Fig. 2 Dark (thermo) and illuminated (thermo-photo) reaction rates for hydrogen production as a function of the temperature using methanol:water mixtures. (A) Using a Cu/CeOx/TiO2 catalyst. Reproduced with permission from ref. 37. Copyright Elsevier. (B) Using a black Pt/ TiO2 catalyst. Reproduced with permission from ref. 36. Copyright ACS. (C and D) Using a series of Pt/CeOx/TiO2 catalysts. Reproduced with permission from ref. 38. Copyright Elsevier. (E) Using a CuOx/ZnO/TiO2 catalyst. Reproduced with permission from ref. 43. Copyright Elsevier. (F) Using a CuOx/ZnO/CrOx catalyst. Reproduced with permission from ref. 44. Copyright Elsevier. | ||
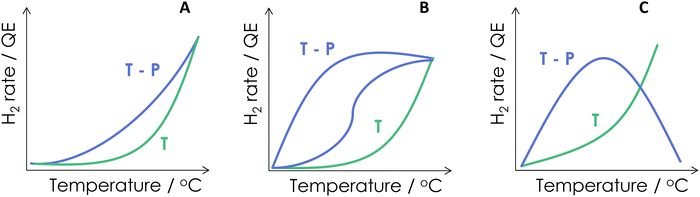
As a summary of the reported literature, the benefits of combining energy sources are presented schematically in Fig. 3. Of course, this figure summarized cases where synergy is observed. Many traditional catalytic systems employed for hydrogen generation would not be able to do it under dual excitation. Fig. 3 shows three different cases. Panel A illustrates a case where a relatively limited yet positive effect can be obtained from the dual-energy reaction vs. the single source(s). This appears the case presented in Fig. 2A. The most common case reported in the literature is nevertheless presented in Fig. 3B, where a strong positive effect can be observed. This frequent case is reflected in the activity data of several works included in the remaining panels of Fig. 2(B–F). The positive effect can show a behavior having one or two different regions. Another case (which will be illustrated using photon efficiency calculations) can occur. Fig. 3C displays the case of a thermo–photocatalyst with both positive and negative excess rate(s) as a function of the temperature. The existence of two well differentiated regions may indicate, in one way or other, a change of the reaction mechanism and/or effects related to surface coverages of active or poisoning species. Alternative interpretations based on the presence of more than one active center may also be envisaged.
Before discussing the photonic-type efficiency we would like to briefly address the question of reporting the turnover number or frequency (TON/TOF). Although the IUPAC provides definitions of such observables for a light-triggered reaction,26 a real problem in providing meaningful results is the impossibility, with the current technical capability, to define accurately the active center of any photo-triggered catalytic reaction.46 This can be obviously extended to any thermo–photocatalyst having synergy between excitation sources. Therefore, for the purposes of achieving the quantitative measurement of activity, the TON/TOF observables of thermo–photocatalytic processes would be of little utility or, more precisely, would include additional and unavoidable error sources not easily appraisable with respect to rigorously measured reaction rates. Such sources come out from the currently available, poor quantitative estimation(s) of the active center surface density for a (light-triggered) catalyst. Nowadays, common procedures to estimate such a parameter use, in one way or other, titration procedures of surface species, particularly hydroxyl groups. This assumes that the hydroxyl (or other titrated species such as superoxide) entity is the charge carrier species involved in the RDS as well as an univocal relationship with the active center. The latter dismisses the chemical (different surface hydroxyl species) as well as the energy (after light excitation) distributions of the radical species, which cannot be clearly established and, therefore, obscure the analysis of the (relevant properties of the) specific radical species directly linked with the active center and thermo–photoactivity.47,48 The analysis of the active center surface density can also be approached with the help of single-particle single-event techniques based on space and time-resolved photoemission, photoluminescence, transient absorption and/or positron annihilation spectroscopies. Yet the experimental conditions to carry out these measurements are far from conditions taking place in thermo–photo reactors and this limits the reliability of the results.49–51
As described previously, to calculate the photon-related efficiency, two well differentiated situations are considered when light interacts with matter. For pseudo-homogeneous cases, we need to solve the radiative transfer eqn (3), which provides the intensity at each point of the reactor 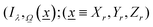 ; r refers to the reactor):
; r refers to the reactor):
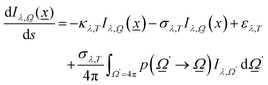 | (3) |
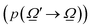 were used.32,52 Of course, the intensity would also depend on the temperature and, as usual catalytic processes are isothermal, it is normally analyzed at (a single) reaction temperature. Except the emissivity-type factor, considered negligible, the other three are common to single source photocatalytic experiments and are obtained by the measurement of the optical properties of the solid (as said, carried out at the reaction temperature experimentally utilized).53 The emissivity-type factor cannot be easily obtained experimentally under the relevant conditions taking place in a thermo–photoreactor, e.g. in the presence of a reactive mixture. It can be calculated using the Stefan–Boltzmann law as defined in eqn (4).
were used.32,52 Of course, the intensity would also depend on the temperature and, as usual catalytic processes are isothermal, it is normally analyzed at (a single) reaction temperature. Except the emissivity-type factor, considered negligible, the other three are common to single source photocatalytic experiments and are obtained by the measurement of the optical properties of the solid (as said, carried out at the reaction temperature experimentally utilized).53 The emissivity-type factor cannot be easily obtained experimentally under the relevant conditions taking place in a thermo–photoreactor, e.g. in the presence of a reactive mixture. It can be calculated using the Stefan–Boltzmann law as defined in eqn (4).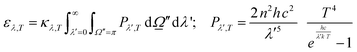 | (4) |
Eqn (3) is solved for each reaction temperature tested (if more than one used) and for all relevant (defined by the source) wavelengths, providing the intensity of light at each point of the reactor. Of course, even for a single temperature, solving eqn (3) rigorously (that is, numerically, reaching spectral, directional and dimensional stability)54,55 requires a rather time-consuming self-consistent, iterative process. In any case, after obtaining the intensity, we can calculate the corresponding photon efficiency observables. Eqn (5) renders the rate of photon absorption, ea, which directly allows the calculation of the quantum efficiency, QE, with the help of the reaction rate (r) and the rate of photon absorption, calculated as average values over the entire reactor.
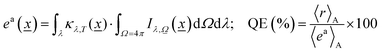 | (5) |
An excess photonic efficiency can be calculated from the quantum efficiency (eqn (5)) or the photonic yield by substituting the rate by the excess rate described in eqn (1). Notice that the photonic yield would use, as required by the IUPAC, the impinging irradiance (correctly measured in units of Einstein m−2 s−1) at the internal part of the reactor window facing the light source, instead of the rate of photon absorption.26 An adequate experimental procedure should be set up. However, reports on the photonic yield usually in the literature are frequently not correct as, customarily, they utilized very simple measurements of the light source intensity without considering the light spectral distribution as well as dismissing the reactor wall(s) effects. These simplifications can lead to a systematic and significant error for the photonic yield evaluation.
For (light–mater interaction) heterogeneous systems, the (excess or not) quantum efficiency calculation can be carried out using eqn (6) for the rate of photon absorption.32,33
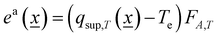 | (6) |
Similar to the discussion of the reaction rate illustrated by the results summarized in Fig. 2, the analysis of the photon efficiency further confirms the useful catalytic consequences of utilizing dual-excitation in catalytic processes for hydrogen production from bio-molecules. Fig. 4 shows the representative examples using titania-based materials. In the case of Cu, Pd and PdCu promoted titania-based catalysts (Fig. 4A and B),59,60 we can observe the characteristic behavior schematically depicted in Fig. 3C. The positive photonic efficiency excess (called the synergy in the corresponding plot) is shown to turn down to a negative effect when the temperature increases above ca. 300 °C. Other works carried out a complete study of the spectral and temperature effects on photon-related issues and reported the quantum efficiency observable corrected for temperature effects.39,41Fig. 4C and D show a case where the quantum efficiency excess is reported for a series of titania-based samples promoted with different quantities of ruthenium at the surface. The quantum efficiency appears always positive for the whole range of temperatures explored. In all cases presented in Fig. 4, an excess higher than 25–30% is detected in the use of photons at specific temperatures. The maximum thermo–photoactivity is reached ca. 50–100 °C degrees below the thermo-alone one.
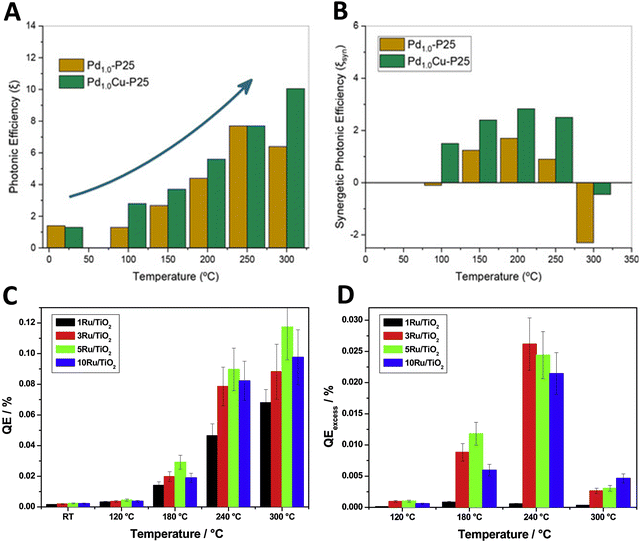 | ||
| Fig. 4 Dark (thermo) and illuminated (thermo-photo) photonic-type efficiency as a function of temperature for hydrogen production using methanol:water mixtures. Bare (A) and excess (B) photonic yields of PdCu/TiO2 and reference catalysts. Reproduced with permission from ref. 55. Copyright Wiley. Bare (C) and excess (D) quantum efficiency (QE) for a series of Ru/TiO2 catalysts. Reproduced with permission from ref. 40. Copyright Elsevier. | ||
Before ending with the study of the chemical and photonic efficiencies, we note that a case deserving further discussion occurs when solar light is directly used as the source of light and heat. If optical-responsive oxides (or any semiconductor) are utilized, the band gap red shift experienced under temperature would need to be considered. This is typically relevant when using visible wavenumbers and, for example, titania, and would need to be taken into account through the spectral absorption coefficient or the fraction of light absorbed which, as stated in eqn (3) and (6), both show dependence with the temperature.40 In addition and as discussed previously, the use of a source having an IR contribution makes rather complex to define a reaction temperature which can be accurately measured. Yet, liquid phase reactions may limit the effect of temperature gradients by obvious thermal effect(s) of the fluid phase in contact with the catalyst. Note, on the other hand, that using fluid phases, particularly water, may interfere (absorption of the excitation light) and be at odds of utilizing the IR contribution for chemical purposes. In any case, a study with some details on this issue utilized Pt supported on a morphology-controlled plasmonic TiO2/TiN for hydrogen thermo–photoproduction from methanol in the liquid phase. The work was able to prove the existence of relatively small temperature gradient effects at an illumination intensity below 1 sun (ca. 100 mW cm−2).61 The control of the surface temperature is nevertheless a point of intense debate for plasmonic photocatalysts.22,62 In any case, Fig. 5A displays the rate (normalized by a constant considering the amount of Pt of the catalyst) behavior under thermo–photo and dark conditions. Under the relatively well controlled temperature conditions of the experiment, the mentioned study also illustrates (Fig. 5B) that the excess reaction rate (here defined as “hot electron” –Hot e, measured at two different temperatures called IT and a higher one, FT) has a power-like dependence on light intensity, a feature compatible, according to the authors, with electron-driven chemical reactions, directly reflecting the critical contribution of the hot electrons created after illumination of the composite (plasmonic) solid. This point was also supported by the analysis of the “action” spectrum, that is, the catalytic response vs. illumination wavelength, which shows a strong resemblance of the plasmon behavior vs. wavelength. The parallel analysis of the corresponding “hot electron” excess contribution to the photonic yield (called the apparent quantum efficiency in Fig. 5C) rendered a relatively flat (or mildly increasing) dependence on light intensity. Although the variation of the excess photonic yield is relatively flat, its importance (e.g. relative contribution to the thermo–photo observable) increases significantly with light intensity, increasing from ca. 28% at 1 sun to ca. 35–45% at above 5 suns.61 It should be noted that an obvious interpretation was presented in the work to rationalize the photonic efficiency behavior but the result highlights the fact that light intensity strongly affects the (chemical and photonic) performance of thermo-photocatalysts. This allows highlighting the mutual effects of temperature and light on chemical variables. Such a complex scenario will be discussed in detail in Section 2.2.
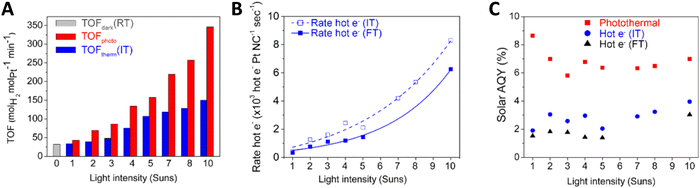 | ||
| Fig. 5 TOF (A), excess reaction rate (B) and photonic yield (called the apparent quantum efficiency, AQE, (C)) vs. irradiance intensity for a Pt/TiO2/TiN catalyst. The excess function is called “Hot e−”. Observables are presented at two different temperatures (called IT, intermediate temperature, and FT, the final temperature of the reaction) in the panels. Reproduced with permission from ref. 56. Copyright ACS. | ||
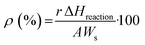 | (7) |
Here, r is the (excess or not) reaction rate (mol s−1), ΔHreaction is the standard enthalpy of the reaction (J mol−1), Ws is the energy supplied per surface area unit (W m−2) and A is the surface area of the catalyst subjected to the reaction. These last two parameters can be easily reformulated for liquid phase reactions as the energy supplied per unit volume and the reactor volume, respectively. The first parameter should be measured using specific procedures with the help of radiometry and actinometry.55,64
Of course, the energy supplied, e.g. the denominator of eqn (7), should consider a single, when solar or IR-containing light, or dual, when light is combined with conventional heating, source for the reaction. In case that the reaction can be considered an equilibrium, like methane dry reforming or the water gas shift reaction, the numerator of eqn (7) would include the rates and standard enthalpy of formation for all molecules involved in such a chemical equilibrium 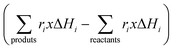 .
.
For liquid-phase methanol reforming and a Pt/TiO2 catalysis, the use of a full solar light according to eqn (7) renders a value of 0.36% at a temperature of ca. 54 °C.65 The same reaction but carried out in the gas phase using ZnCu/SiO2 reached a 1.2% energy efficiency under 7.9 suns (temperature ca. 250 °C).66 For the water gas shift reaction carried out using a CuOx/ZnO/Al2O3 catalyst under 1 sun illumination (simulated sunlight), a value of 2.86% was obtained at a temperature of ca. 270 °C.67 For the dry reforming of methane and temperatures above 700 °C obtained under simulated sunlight, catalysts such as Ni/La2O3/SiO268 or NiCo/Co–Al2O369 reached values of 20.3 and 29.7% for the energy efficiency, respectively. This glimpse on literature reports concerning the energy efficiency observable clearly points out a strong dependence on the reaction medium (liquid or gas phase) and nature (three reactions were shown here) and typical range of achievable and useful temperatures to run the coupling of energy excitations. The corresponding values also show excess from pure thermal ones at the same temperature by values above 25–50%.
Summarizing, for the analysis of synergy for dual-excitation catalytic processes, a critical point evolving from eqn (1), (5) and (7) is that chemical, photonic and global energy excess functions can be accurately calculated and reported. We note that all parameters mentioned should be measured under adequate (transport free) kinetic conditions. In other case, careful modelling of transport effects is required to obtain meaningful observables. Note also that deactivation may complicate the measurements and would require the analysis of the catalyst at different time spots or physico-chemical conditions. On the other hand, we stress that the survey of the literature here presented confirms using the chemical (reaction rate), photonic (photonic yield or quantum efficiency) or global-energy efficiencies that a number of different catalysts can lead to a significant advantage for hydrogen production from bio-molecules under dual excitation, irrespective of the perspective. Notably, this appeared the case for titania-based systems promoted with noble and non-noble components.
2.2. Interpretation of excess functions
To interpret the physico-chemical basis of the thermo–photobehavior of active catalysts for hydrogen production, we would first provide a relatively simple framework to rationalize the kinetics of any thermo–photoreaction and thus the reaction rate. As is well-known from the review papers of light-triggered reaction,55,64 any reaction rate is a function of chemical and light-related variables. Extending this for a thermo–photoreaction, the corresponding (excess or not) rate can be expressed with generality as eqn (8).| r = f(ki(T),ki(T),ea(T);Ci) | (8) |
The rate (r) is a function (described as f(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) in eqn (8)) of: (i) temperature (T), (ii) chemical variables, defined always by the concentration of reactants, the adsorption constants (Ki) and the kinetic constants of relevant steps (ki), and (iii) light-related variables, described by a single observable, the rate of photon absorption (ea). The rate also shows dependence on an additional optical property, the primary quantum yield, which however is a constant for the system (therefore not considered explicitly in eqn (8)).64 It is somewhat obvious or, in other words, directly comes from eqn (5), that the same functional dependence can be expressed for the “photon-related” efficiency as it would have a similar functional dependence in the majority of cases. Only in specific cases (e.g. a rate owing to the separation of chemical/light-related variables and linear dependence on ea), a measurement of the quantum efficiency will lack dependence on the rate of photon absorption.64 Similarly, eqn (7) implies that the above discussion of the rate dependence applies to global energy excess function considerations.
) in eqn (8)) of: (i) temperature (T), (ii) chemical variables, defined always by the concentration of reactants, the adsorption constants (Ki) and the kinetic constants of relevant steps (ki), and (iii) light-related variables, described by a single observable, the rate of photon absorption (ea). The rate also shows dependence on an additional optical property, the primary quantum yield, which however is a constant for the system (therefore not considered explicitly in eqn (8)).64 It is somewhat obvious or, in other words, directly comes from eqn (5), that the same functional dependence can be expressed for the “photon-related” efficiency as it would have a similar functional dependence in the majority of cases. Only in specific cases (e.g. a rate owing to the separation of chemical/light-related variables and linear dependence on ea), a measurement of the quantum efficiency will lack dependence on the rate of photon absorption.64 Similarly, eqn (7) implies that the above discussion of the rate dependence applies to global energy excess function considerations.
To consider the interpretation of eqn (8), a first critical point is that chemical and light related variables are usually inter-related and cannot be studied separately. In the mathematical form, with generality, there is no separation of variables and, therefore, they cannot be studied independently. From an experimental point of view, this means that, to run thermo–photocatalytic experiments, the adequate experimental design should consider both types of variables together.23 Second, as explicitly declared in eqn (8), both types of variables, and not only chemical ones, depend on temperature. We should note that the dependence of optical variables may be less significant than that of chemical ones for typical catalytic reactions. Running at relatively low temperatures, say below 500 °C, and considering limited temperature ranges may allow dismissing the thermal-dependence of optical variables. Nevertheless, this would not be a general case and should be tested carefully for each experiment reported. Third, the light dependence cannot be represented by the intensity of the light source (spectral irradiance) as the rate of photon absorption is a complex observable depending on the catalyst–medium optoelectronic properties. Section 2.1 makes a brief yet exhaustive analysis of this issue for heterogeneous and homogenous type catalytic systems and eqn (4) and (6) summarize the general dependence of the rate of photon absorption on physico-chemical variables. These three points are usually dismissed in the corresponding analyses presented in literature reports. For example, in Section 2.1, we mentioned the analysis of thermal and optolectronic effects in plasmonic materials and most experimental considerations of light-related variables to date reported in literature sources do not account for the adequate variables (particularly the rate of photon absorption) to analyze the efficiency and dismiss (without full justification) the dependence of some (mostly optical) variables on temperature.
Eqn (8) and the corresponding kinetic governing equations would thus be a tool for interpreting excess function(s) in a quantitative way. Differences between the results concerning thermal-alone (more rigorously the sum of thermal and photo alone) and thermo–photo conditions would be the main tool to interpret excess functions and synergy for thermo–photo applications.
To interpret synergy, the literature mainly describes the use of in situ spectroscopies as well as isotopic kinetic studies. Corresponding works have shed light on the mechanism/kinetics of hydrogen thermo–photoproduction from bio-molecules. Vibrational (infrared) spectroscopy is a frequently applied tool by researchers to interrogate the system under reaction conditions. In Fig. 6, we summarize two representative studies using Pt/CeOx/TiO239 and CuO/ZnO/ZrO245 systems. Relatively similar results can be encountered in works concerning Cu/TiO2,59,70 PdCu/TiO2,60 Ru/RuOx/TiO2,41 and Cu/CeOx/TiO2.38 The methanol reforming reaction was the subject of analysis in all cases. The infrared spectra shown in Fig. 6(A and C) are recorded at fixed temperatures under dark (also called thermal) and thermo–photo (also called photo-assisted) conditions. In all the studies mentioned, methanol evolves in a step-way forming aldehyde-type, formate-type and, finally, carbon dioxide moieties. At each oxidation step, hole-related species are consumed and protons are concomitantly formed to the carbon-containing species. Such protons would produce the desired hydrogen with the participation of electrons. It should be noted that, to generate formate type species (and thus carbon dioxide), water is required and the resulting protons are then provided by the two molecules, methanol and water. The step-way path is the main path of the reaction according to all literature sources and is graphically presented in numerous works (it is in fact illustrated in Fig. 6B and D). In addition to this main path, other reactions and products can be detected. Mostly, decarbonylation type reactions (of aldehyde and carboxylate type entities) generating carbon monoxide and the interaction of formate-type species and methanol with the generation of methyl formate can be observed (Fig. 6B). Carbon monoxide would subsequently be involved in a water gas shift step, generating additional hydrogen and carbon dioxide. Although complex, this appears a general or basic mechanism, common to all reported works.38–41,45,59,60,70
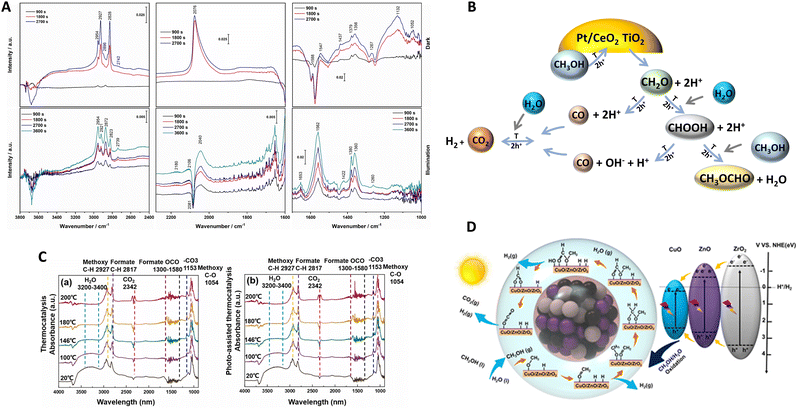 | ||
| Fig. 6 Infrared spectra under dark (thermo) and illuminated (thermo-photo) conditions using methanol:water reaction mixtures (A and C). Schematic representation of the corresponding catalyst and catalytic process (B and D). Reproduced with permission from ref. 38 (Copyright Elsevier; panels A and B) and ref. 44 (Copyright Elsevier; panels C and D). | ||
Comparing dark and illuminated conditions, the works highlight the promotion of different intermediates under thermo–photo conditions. Specifically, under thermo–photo conditions, most of the active materials promote formate production,38,39,45 while a few described the significant promotion of formaldehyde41 and/or the water gas shift reaction.39,60 For formaldehyde or formate production enhancement, a hole attack would increase the activation of the corresponding precursor entities. For the water gas shift, specific metal entities appear critical and activated under thermo–photo conditions, a fact which may be related to the different electronic densities achieved under illumination conditions with respect to the dark one. Other works emphasize additional thermo–photo effects on product desorption, facilitating the concomitant generation of hydrogen in an indirect way.43 A similar reaction mechanism but from formic acid as the initial reactant instead of an alcohol has been shown to occur with Ru/TiO2.71 As for the methanol case, the formate type species, decarbonylation type reactions leading to CO as well as the generation of carbon dioxide were promoted under thermo–photo conditions.
For methanol reforming, the spectroscopic-based interpretation can be complemented with information from isotopic-based kinetic studies. Illustrative studies were carried out for Ni and Ru supported on TiO2.72,73Fig. 7 exemplifies the isotopic studies and their interpretation. The analysis of KIE (kinetic isotope effect) for pure photoconditions (Fig. 7A) indicates that alcohol oxidation is involved in the rate determining step. Fig. 7B describes this sacrificial molecule oxidation pathway with the specific intermediates detected by the authors. The mechanism proposed is essentially the same step-wise mechanism presented in Fig. 6. Under thermo–photoconditions, the isotopic-labelled catalytic studies (Fig. 7C) show effects on carbon-containing moieties. Fig. 7D graphically illustrates the promotion (among others) of CO and CO2 generation but also a marked increase in water reduction with the concomitant generation of hydrogen. In this case, the new effect of water (leading to its reduction) for the thermo–photo production of hydrogen is proposed to be a pure thermal effect. KIE based studies were also carried out for plasmonic based systems and provided information about the nature of the reaction, indicating the important promotion of hot-carrier mediated steps taking place for hydrogen production under thermo–photo conditions.61,66,74 These KIE studies used the technique to a simpler level than the one presented in Fig. 7. In any case, the examples selected here illustrate that isotopic studies can be particularly useful to complete spectroscopic work, with relevant information about the molecules and key reaction steps involved in controlling kinetics.
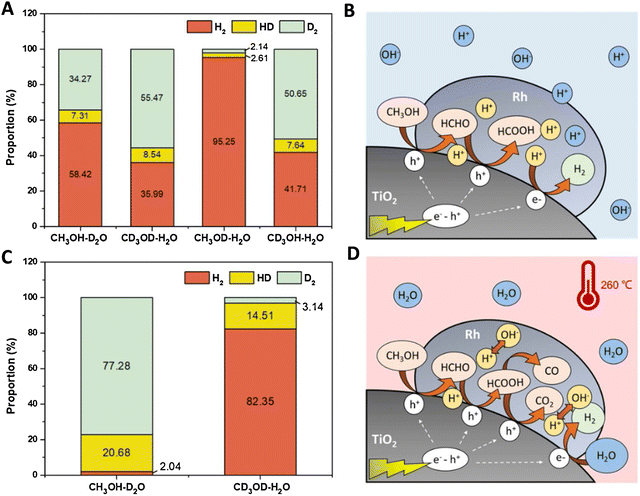 | ||
| Fig. 7 Results from isotopic labelling experiments (A and C) and schematic process representation of the reaction mechanism (C and D) of a Ru/TiO2 catalyst using a methanol:water mixture. Thermo (A and B) and thermo–photo (B and D) conditions are tested. Reproduced with permission from ref. 67. Copyright Elsevier. | ||
We can complete the discussion of the interpretation of synergy highlighting a few ideas connected with the analysis of the active center of a thermo–photo reaction. As mentioned in Section 2.1, this is a rather complex task for dual-excitation catalysts. So, the up-to-date results only provided incomplete and rather limited information. Advanced approaches were used to analyze the catalytic solids under reaction conditions (the simultaneous use of light and heat) utilizing TAP-type (temporary analysis of products) kinetic schemes and techniques like X-ray absorption (XAS) or XPS. Note that, for bulk-sensitive techniques like XAS, matching the technique probe depth and the light “penetration” depth (the characteristic dimension perpendicular to light propagation in the micro-size range from the UV to the near-IR range) in the measurement reactor subjected to scrutiny is a must if useful results are aimed to be obtained.39,75 Single particle spectroscopic tools can also contribute in this context but can be hardly applied under real thermo–photo reaction conditions. Finally, the contribution of theoretical tools with an appropriate study of excited states as well as electric-field local properties can be pointed out as valuable tools for thermo–photo active center interrogation.74,76,77
From the previous discussion, it appears evident that a full interpretation of the thermo–photophenomenon would require a step forward. The current status of research renders useful pieces of information to interpret excess functions but assembling the complete puzzle is a complicated work that needs to be done. Using the above mentioned information about relevant mechanistic and kinetic details, a full spectro-kinetic scheme braiding information from vibrational and kinetic-KIE tools could decisively contribute to interpreting excess functions and activity. This would consider a careful experimental design of catalytic data, with the adequate handling of chemical and light related variables, together with a physico-chemical grounded kinetic formalism. Also, new operando spectroscopic techniques using, for example, ambient pressure XPS or micro-XAS under dual excitation, and advanced theoretical studies with the complete analysis of excited electronic states would address fundamental questions about the reaction center from both the solid and reactant–solid perspectives. In brief, the quantitative structure–activity links achieved in this way will ultimately uncover and interpret light–heat effects in the rate determining step (interpreting energy of activation), coverage of surface species (intermediates, poisons, etc.) and reactant reaction orders, as well as the functional details of the active center behavior which should allow a complete understating of synergy in thermo–photo reactions.
3. Conclusions
Thermo–photo production of hydrogen from bio-molecules is a research field quickly expanding. However, the technical issues inherent to the measurement of catalytic observables under dual excitation are rather challenging. This together with the need of the precise analysis of efficiency to demonstrate synergy (and thus the potential application in industry) trigger us to provide a general framework for measuring and interpreting thermo–photo data for hydrogen production. The framework presented can nevertheless be applied to any thermo–photo reaction and thus has a general validity.The mentioned framework first analyzed the synergy for all possible facets of the problem, that is chemical, photonic and global energy. The mathematical formalism(s) to analyze the synergy was outlined and a careful methodology was described to measure the reaction rate, the quantum efficiency (and photonic yield) and energy observables. The corresponding figures of merit to quantitatively appraise the corresponding excess functions were presented and discussed to highlight their importance. We stress that the three facets of the problem should be studied together, as they are rather complementary and informative, and, as a whole, would serve as a critical (quantitative and general) tool to compare among thermo–photocatalysts. The interpretation of thermo–photo synergy, uncovered by the excess functions, was also addressed. The subtle interplay between the chemical and photonic variables at the reaction temperature was analyzed and the corresponding mechanism(s) (structural and mechanistic/kinetic) were targeted and explained with the help of nowadays available information as well as the envisaged future spectroscopic and theoretical tools aiming to render a full understanding of the phenomenon.
In sum, the analysis and interpretation of synergy was carried out with the help of the experimental evidence tackling the problem and an adequate mathematical formalism. The contribution also aimed to provide some guidelines for future research in order to unveil the true nature of thermo–photocatalytic processes. It is expected that the proposed guidelines would contribute to a more efficient investigation in the field.
Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors acknowledge financial support through the grant PID2019-105490RB-C31 funded by MCIN/AEI/ 10.13039/501100011033 and, as appropriate, by “ERDF A way of making Europe”, by the “European Union”. I. B.-N. and M. N. G.-C. would like to thank MICIN for, respectively, doctoral FPI (BES-2017-080069) and post-doctoral JyD (FJC2019-039969) fellowships. M. F. G. is fully indebted to Prof. F. Fernández-Martín for general discussions.References
- E. C. Okonkwo, M. Al-Breiki, Y. Bicer and T. Al-Ansari, Int. J. Hydrogen Energy, 2021, 46, 35525–35549 CrossRef CAS
.
- T. Vezirolu and F. Barbir, Int. J. Hydrogen Energy, 1992, 17, 391–404 CrossRef
.
- L. V. Mattos, G. Jacobs, B. H. Davis and F. B. Noronha, Chem. Rev., 2012, 112, 4094–4123 CrossRef CAS PubMed
.
- U. Mondal and G. D. Yadav, Green Chem., 2021, 23, 8361–8405 RSC
.
- H. Idriss, Energy Technol., 2021, 9, 2000843 CrossRef CAS
.
- Y. Zhao, Y. Li and L. Sun, Chemosphere, 2021, 276, 130201 CrossRef CAS PubMed
.
- A. Kubacka, M. Fernández-García and G. Colón, Chem. Rev., 2012, 112, 1555–1614 CrossRef CAS PubMed
.
- S. Alsayegh, J. R. Johnson, B. Ohs, J. Lohaus and M. Wessling, Int. J. Hydrogen Energy, 2017, 42, 6000–6011 CrossRef CAS
.
- S. Alsayegh, J. R. Johnson, X. Wei, B. Ohs, J. Lohaus and M. Wessling, Int. J. Hydrogen Energy, 2017, 42, 21793–21805 CrossRef CAS
.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570 CrossRef CAS PubMed
.
- H. H. Do, D. L. T. Nguyen, X. C. Nguyen, T.-H. Le, T. P. Nguyen, Q. T. Trinh, S. H. Ahn, D.-V. N. Vo, S. Y. Kim and Q. Van Le, Arab. J. Chem., 2020, 13, 3653–3671 CrossRef CAS
.
- V. Nair, M. J. Muñoz-Batista, M. Fernández-García, R. Luque and J. C. Colmenares, ChemSusChem, 2019, 12, 2098–2116 CrossRef CAS
.
- S. Tang, X. Xing, W. Yu, J. Sun, Y. Xuan, L. Wang, Y. Xu, H. Hong and H. Jin, iScience, 2020, 23, 101012 CrossRef CAS PubMed
.
- K. Czelej, J. C. Colmenares, K. Jabłczyńska, K. Ćwieka, Ł. Werner and L. Gradoń, Catal. Today, 2021, 380, 156–186 CrossRef CAS
.
- K. Ćwieka, K. Czelej, J. C. Colmenares, K. Jabłczyńska, Ł. Werner and L. Gradoń, ChemCatChem, 2021, 13, 4458–4496 CrossRef
.
- I. Barba-Nieto, N. Gómez-Cerezo, A. Kubacka and M. Fernández-García, Catal. Sci. Technol., 2021, 11, 6904–6930 RSC
.
- N. Keller, J. Ivanez, J. Highfield and A. M. Ruppert, Appl. Catal. B Environ., 2021, 296, 120320 CrossRef CAS
.
- D. Wang, R. Chen, X. Zhu, D. Ye, Y. Yang, Y. Yu, J. Li, Y. Liu, H. Zhao and Q. Liao, J. Phys. Chem. Lett., 2022, 13, 1602–1608 CrossRef CAS
.
- W. Ouyang, C. Yao, K. Ye, Y. Guo, L. Li and Z. Lin, Int. J. Hydrogen Energy, 2022, 47, 19989–19998 CrossRef CAS
.
- M. Ghoussoub, M. Xia, P. N. Duchesne, D. Segal and G. Ozin, Energy Environ. Sci., 2019, 12, 1122–1142 RSC
.
- S. Fang and Y. H. Hu, Chem. Soc. Rev., 2022, 51, 3609–3647 RSC
.
- D. Mateo, J. L. Cerrillo, S. Durini and J. Gascon, Chem. Soc. Rev., 2021, 50, 2173–2210 RSC
.
- M. J. Muñoz-Batista, A. M. Eslava-Castillo, A. Kubacka and M. Fernández-García, Appl. Catal. B Environ., 2018, 225, 298–306 CrossRef
.
- Y. Cho, A. Yamaguchi, A. Sinaga, Y. Yang and M. Miyauchi, Appl. Catal. A Gen, 2022, 118772 CrossRef CAS
.
- M. Lyulyukin, N. Kovalevskiy, I. Prosvirin, D. Selishchev and D. Kozlov, J. Photochem. Photobiol., A, 2022, 425, 113675 CrossRef CAS
.
- S. E. Braslavsky, A. M. Braun, A. E. Cassano, A. V. Emeline, M. I. Litter, L. Palmisano, V. N. Parmon and N. Serpone, Pure Appl. Chem., 2011, 83, 931–1014 CrossRef CAS
.
- Y. Du, M. Liu and L. Guo, J. Photonics Energy, 2021, 11, 016501 CAS
.
- J. Tan, Y. Xie, F. Wang, L. Jing and L. Ma, Int. J. Heat Mass Transfer, 2017, 115, 1103–1112 CrossRef CAS
.
- F. Pellegrino, L. Pellutiè, F. Sordello, C. Minero, E. Ortel, V.-D. Hodoroaba and V. Maurino, Appl. Catal. B Environ., 2017, 216, 80–87 CrossRef CAS
.
- A. Tolosana-Moranchel, C. Pecharromán, M. Faraldos and A. Bahamonde, Chem. Eng. J., 2021, 403, 126186 CrossRef CAS
.
- M. de los, M. Ballari, R. Brandi, O. Alfano and A. Cassano, Chem. Eng. J., 2008, 136, 242–255 CrossRef
.
- A. Kubacka, I. Barba-Nieto, U. Caudillo-Flores and M. Fernández-García, Curr. Opin. Chem. Eng., 2021, 33, 100712 CrossRef
.
- M. J. Muñoz-Batista, A. Kubacka, A. B. Hungría and M. Fernández-García, J. Catal., 2015, 330, 154–166 CrossRef
.
- N. Padoin and C. Soares, Chem. Eng. J, 2017, 310, 381–388 CrossRef CAS
.
- X. Zhang, X. Li, M. E. Reish, D. Zhang, N. Q. Su, Y. Gutiérrez, F. Moreno, W. Yang, H. O. Everitt and J. Liu, Nano Lett., 2018, 18, 1714–1723 CrossRef CAS PubMed
.
- X. Li, X. Zhang, H. O. Everitt and J. Liu, Nano Lett., 2019, 19, 1706–1711 CrossRef CAS
.
- B. Han and Y. H. Hu, J. Phys. Chem. C, 2015, 119, 18927–18934 CrossRef CAS
.
- X. Liu, C. Bao, Z. Zhu, H. Zheng, C. Song and Q. Xu, Int. J. Hydrogen Energy, 2021, 46, 26741–26756 CrossRef CAS
.
- U. Caudillo-Flores, I. Barba-Nieto, M. J. Muñoz-Batista, D. Motta Meira, M. Fernández-García and A. Kubacka, Chem. Eng. J, 2021, 425, 130641 CrossRef CAS
.
- Y. Khani, P. Tahay, F. Bahadoran, N. Safari, S. Soltanali and A. Alavi, Appl. Catal. A Gen, 2020, 594, 117456 CrossRef CAS
.
- U. Caudillo-Flores, G. Agostini, C. Marini, A. Kubacka and M. Fernández-García, Appl. Catal. B Environ., 2019, 256, 117790 CrossRef
.
- L. Huaxu, W. Fuqiang, C. Ziming, H. Shengpeng, X. Bing, G. Xiangtao, L. Bo, T. Jianyu, L. Xiangzheng, C. Ruiyang, L. Wen and L. Linhua, Int. J. Hydrogen Energy, 2017, 42, 12133–12142 CrossRef
.
- L. Li, W. Ouyang, Z. Zheng, K. Ye, Y. Guo, Y. Qin, Z. Wu, Z. Lin, T. Wang and S. Zhang, Chinese J. Catal., 2022, 43, 1258–1266 CrossRef CAS
.
- Z. Sun, S. Fang, Y. Lin and Y. H. Hu, Chem. Eng. J., 2019, 375, 121909 CrossRef CAS
.
- X. Yu, L. Yang, Y. Xuan, X. L. Liu and K. Zhang, Nano Energy, 2021, 84, 105953 CrossRef CAS
.
- M. Melchionna and P. Fornasiero, ACS Catal., 2020, 10, 5493–5501 CrossRef CAS
.
- T. R. Eaton, M. P. Campos, K. A. Gray and J. M. Notestein, J. Catal., 2014, 309, 156–165 CrossRef CAS
.
- B. H. Simpson and J. Rodríguez-López, Electrochim. Acta, 2015, 179, 74–83 CrossRef CAS
.
- C. Luo, X. Ren, Z. Dai, Y. Zhang, X. Qi and C. Pan, ACS Appl. Mater. Interfaces, 2017, 9, 23265–23286 CrossRef CAS
.
- U. Caudillo-Flores, M. J. Muñoz-Batista, A. Kubacka and M. Fernández-García, ChemPhotoChem, 2018, 2, 777–785 CrossRef CAS
.
- U. Caudillo-Flores, I. Barba-Nieto, M. J. Muñoz-Batista, A. Kubacka and M. Fernández-García, Top. Curr. Chem., 2019, 377, 24 CrossRef PubMed
.
- Á. García-Gil, C. Casado, C. Pablos and J. Marugán, Chem. Eng. J., 2019, 376, 120194 CrossRef
.
- M. L. Satuf, R. J. Brandi, A. E. Cassano and O. M. Alfano, Ind. Eng. Chem. Res., 2005, 44, 6643–6649 CrossRef CAS
.
- F. Parrino, V. Loddo, V. Augugliaro, G. Camera-Roda, G. Palmisano, L. Palmisano and S. Yurdakal, Catal. Rev., 2019, 61, 163–213 CrossRef CAS
.
- U. Caudillo-Flores, M. J. Muñoz-Batista, M. Fernández-García and A. Kubacka, Catal. Rev., 2022, 1–55 CrossRef
.
- G. Wang, Y. Zhang, D. Zhang and J. Fan, Int. J. Miner. Metall. Mater., 2012, 19, 179–184 CrossRef CAS
.
- I. Setién-Fernández, T. Echániz, L. González-Fernández, R. B. Pérez-Sáez, E. Céspedes, J. A. Sánchez-García, L. Álvarez-Fraga, R. Escobar Galindo, J. M. Albella, C. Prieto and M. J. Tello, Sol. Energy Mater. Sol. Cells, 2013, 117, 390–395 CrossRef
.
- A. Kubacka, U. Caudillo-Flores, I. Barba-Nieto and M. Fernández-García, Appl. Catal. A Gen, 2021, 610, 117966 CrossRef CAS
.
- F. Platero, A. López-Martìn, A. Caballero and G. Colón, ChemCatChem, 2021, 13, 3878–3888 CrossRef CAS
.
- A. López-Martín, F. Platero, A. Caballero and G. Colón, ChemPhotoChem, 2020, 4, 630–637 CrossRef
.
- S. Rej, L. Mascaretti, E. Y. Santiago, O. Tomanec, Š. Kment, Z. Wang, R. Zbořil, P. Fornasiero, A. O. Govorov and A. Naldoni, ACS Catal., 2020, 10, 5261–5271 CrossRef CAS
.
- P. Verma, Y. Kuwahara, K. Mori, R. Raja and H. Yamashita, EnergyChem, 2022, 4, 100070 CrossRef CAS
.
- J. Hong, C. Xu, B. Deng, Y. Gao, X. Zhu, X. Zhang and Y. Zhang, Adv. Sci., 2022, 9, 2103926 CrossRef CAS PubMed
.
- M. J. Muñoz-Batista, M. M. Ballari, A. Kubacka, O. M. Alfano and M. Fernández-García, Chem. Soc. Rev., 2019, 48, 637–682 RSC
.
- X. Liu, L. Ye, Z. Ma, C. Han, L. Wang, Z. Jia, F. Su and H. Xie, Catal. Commun., 2017, 102, 13–16 CrossRef CAS
.
- S. Luo, H. Lin, Q. Wang, X. Ren, D. Hernández-Pinilla, T. Nagao, Y. Xie, G. Yang, S. Li, H. Song, M. Oshikiri and J. Ye, J. Am. Chem. Soc., 2021, 143, 12145–12153 CrossRef CAS PubMed
.
- C. Shi, D. Yuan, L. Ma, Y. Li, Y. Lu, L. Gao, X. San, S. Wang and G. Fu, J. Mater. Chem. A, 2020, 8, 19467–19472 RSC
.
- G. Zhang, S. Wu, Y. Li and Q. Zhang, Appl. Catal. B Environ., 2020, 264, 118544 CrossRef
.
- S. Wu, Y. Li, Q. Zhang, Q. Hu, J. Wu, C. Zhou and X. Zhao, Adv. Energy Mater., 2020, 10, 2002602 CrossRef CAS
.
- F. Platero, A. Caballero and G. Colón, Appl. Catal., A, 2022, 643, 118804 CrossRef CAS
.
- J. Ivanez, P. Garcia-Munoz, A. M. Ruppert and N. Keller, Catal. Today, 2021, 380, 138–146 CrossRef CAS
.
- S. Fang, Y. Liu, Z. Sun, J. Lang, C. Bao and Y. H. Hu, Appl. Catal. B Environ., 2020, 278, 119316 CrossRef CAS
.
- S. Fang, Z. Sun and Y. H. Hu, ACS Catal., 2019, 9, 5047–5056 CrossRef CAS
.
- Y. Liu, Z. Zhang, Y. Fang, B. Liu, J. Huang, F. Miao, Y. Bao and B. Dong, Appl. Catal. B Environ., 2019, 252, 164–173 CrossRef CAS
.
- M. J. Muñoz-Batista, D. Motta Meira, G. Colón, A. Kubacka and M. Fernández-García, Angew. Chem., Int. Ed., 2018, 57, 1199–1203 CrossRef PubMed
.
- C. Sousa, S. Tosoni and F. Illas, Chem. Rev., 2013, 113, 4456–4495 CrossRef CAS
.
- B. Samanta, Á. Morales-García, F. Illas, N. Goga, J. A. Anta, S. Calero, A. Bieberle-Hütter, F. Libisch, A. B. Muñoz-García, M. Pavone and M. Caspary Toroker, Chem. Soc. Rev., 2022, 51, 3794–3818 RSC
.
Footnote |
| † These two authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |