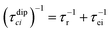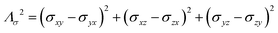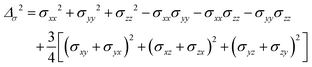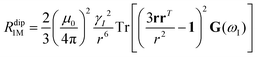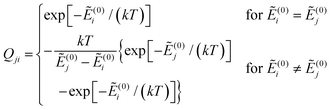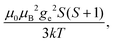Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The evolution of paramagnetic NMR as a tool in structural biology
Enrico
Ravera
 abc,
Lucia
Gigli
abc,
Lucia
Gigli
 abc,
Letizia
Fiorucci
abc,
Letizia
Fiorucci
 abc,
Claudio
Luchinat
abc,
Claudio
Luchinat
 abc and
Giacomo
Parigi
abc and
Giacomo
Parigi
 *abc
*abc
aMagnetic Resonance Center (CERM), University of Florence, via Luigi Sacconi 6, Sesto Fiorentino, 50019, Italy
bDepartment of Chemistry “Ugo Schiff”, University of Florence, via della Lastruccia 3, Sesto Fiorentino, 50019, Italy
cConsorzio Interuniversitario Risonanze Magnetiche Metallo Proteine (CIRMMP), via Luigi Sacconi 6, Sesto Fiorentino, 50019, Italy. E-mail: parigi@cerm.unifi.it
First published on 28th June 2022
Abstract
Paramagnetic NMR data contain extremely accurate long-range information on metalloprotein structures and, when used in the frame of integrative structural biology approaches, they allow for the retrieval of structural details to a resolution that is not achievable using other techniques. Paramagnetic data thus represent an extremely powerful tool to refine protein models in solution, especially when coupled to X-ray or cryoelectron microscopy data, to monitor the formation of complexes and determine the relative arrangements of their components, and to highlight the presence of conformational heterogeneity. More recently, theoretical and computational advancements in quantum chemical calculations of paramagnetic NMR observables are progressively opening new routes in structural biology, because they allow for the determination of the structure within the coordination sphere of the metal center, thus acting as a loupe on sites that are difficult to observe but very important for protein function.
Introduction
NMR spectroscopy has long proven a powerful technique for determining the structure of biological macromolecules. X-ray diffraction structures account for 87% of the protein data bank (PDB), and to date, the number of electron microscopy and NMR structures has become comparable (5.6% vs. 7.2%). However, X-ray and cryo-electron microscopy require crystallization and rapid freeze treatment, respectively, whereas NMR is performed in solution or on sedimented samples and thus has the advantage to operate at higher temperatures and in close to biologically relevant conditions.1 Furthermore, NMR remains the method of choice for the investigation of dynamics. The presence of a paramagnetic metal ion can provide an additional source of valuable information, at a level that is often hardly accessible with other techniques: paramagnetic centers affect the NMR spectra of proteins in ways that depend (besides on the type of paramagnetic metal) on the fine (sub-Å) detail of the coordination environment of the metal ion and of the distribution of protein nuclei, even if these are nanometers away from the metal.The major paramagnetic NMR effects, due to the dipole–dipole interaction between nuclear and electron magnetic moments, are the changes with respect to the values measured for an analogue diamagnetic system in (i) nuclear relaxation rates, called paramagnetic relaxation enhancements (PREs), (ii) NMR shifts of the protein nuclei, called hyperfine shifts, and (iii) coupling constants between paired nuclei, called paramagnetic residual dipolar couplings (pRDCs). Hyperfine shifts are composed of pseudocontact shifts (PCSs) and, in the presence of unpaired electron spin density onto the observed nuclei, Fermi-contact shifts (FCSs). All these paramagnetic effects report on the structural details of the protein and on the variability thereof in the NMR time scale and are thus increasingly used as structural restraints.
The obtainment of the paramagnetic NMR restraints depends critically on the electronic structure of the paramagnetic center; they are in general measured as the difference of a given observable for the same protein with and without the paramagnetic metal that can be (i) replaced by a diamagnetic metal ion, (ii) reduced to a diamagnetic state, or (iii) removed from the protein.
The first protein structure calculations taking advantage of paramagnetic NMR restraints date back to the nineties. PREs were included in solution structure protocols in the first solution structures of paramagnetic proteins.2 The introduction of PCSs in structural determination was demonstrated in 1996,3 and shortly afterwards pRDCs were introduced.4,5 These two classes of restraints, combined with paramagnetic cross-correlated relaxation rates,6,7 allowed us to obtain the first backbone structure of a protein only relying on paramagnetic restraints.8,9 Also PREs measured through tailored experiments even for nuclei close to the paramagnetic center could be used to determine the structure of a small protein.10 These examples show the importance and the relevance of the structural information contained in these restraints. When dealing with paramagnetic proteins, paramagnetic NMR restraints should thus be always included in protein structure calculation protocols together with all other available restraints, mainly distance restraints determined from NOEs (nuclear Overhauser effects) and dihedral angle restraints from NMR chemical shifts.
Important advances have been made in the last few years regarding the protein structure refinement strategies through paramagnetic data, the theory of paramagnetic NMR shift and relaxation, the calculation from first-principles of quantum mechanics of hyperfine shifts, and the implementation of tools for their use as structural restraints. Some of the main achievements will be discussed in the following sections in light of the new perspectives they are disclosing.
The electron–nucleus interaction: the origin of relaxation and shift
The electron–nucleus or hyperfine interaction can be divided into two contributions, one arising from the interaction of the nuclear magnetic moment with the unpaired electron spin density (ρI) residing on it (called Fermi-contact interaction) and due to both direct electron spin delocalization and spin polarization, and another arising from the through-space interaction of the nuclear magnetic moment with the electron magnetic moment (called dipolar interaction).11,12 This second term comprises the nuclear spin–electron spin interaction as well as the interaction between the nuclear spin and the electron orbital magnetic moment.13,14Given that electron relaxation occurs orders of magnitude faster than nuclear relaxation, the nucleus senses fluctuating fields originating from the hyperfine interaction, and further nuclear spin relaxation mechanisms become available (PRE, vide infra). Because in the presence of a magnetic field, the electron spin magnetic moment (for Fermi-contact interaction) and the overall electron magnetic moment (for dipolar interaction) are not null due to the different population of the electronic states, the nuclear resonances shifted (hyperfine shift, vide infra).
The paramagnetic relaxation enhancements
Nuclear relaxation rates in paramagnetic metalloproteins depend on several relaxation mechanisms all related to the presence of the paramagnetic center which add to the diamagnetic relaxation rates. One relaxation mechanism depends on the modulation of the dipole coupling with the electron spin according to the Solomon equations:15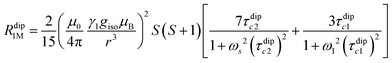 | (1a) |
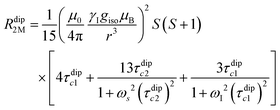 | (1b) |
where τr and τei are the reorientation time and the longitudinal (i = 1) and transverse (i = 2) electron relaxation times, respectively. In the case of lanthanoids and actinoids, the J quantum number substitutes the S quantum number and gJ substitutes giso. These equations are derived from a number of assumptions, which include (but are not limited to): (i) the point-dipole approximation for the electron spin, (ii) isotropic molecular reorientations, (iii) isotropic g tensors and an electron Zeeman interaction much larger, at the field of interest, than zero-field splitting (ZFS), and hyperfine coupling between the electron spin and metal nuclear spin (for paramagnetic metals with I > 0). Recent experimental works have shown that in some cases these assumptions cannot be safely made even at high magnetic fields, and tools for managing experimental data have been proposed (see later).
When electron relaxation times are very short, nuclear relaxation caused by the Solomon equations is modest, and significant contributions to nuclear relaxation can arise from the modulation of the dipole–dipole interaction between the nuclear magnetic moment and the averaged electron magnetic moment (Curie spin relaxation). This contribution depends on the molecular reorientation time and on the magnetic susceptibility, and, in the case of isotropic χ tensors, Curie spin PREs are given by:16
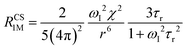 | (2a) |
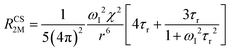 | (2b) |
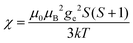 (spin-only approximation). In lanthanoids, because the spin–orbit coupling energy is generally larger than the effect of the crystal field, S is substituted by the spin–orbit coupled quantum number J, ge by the Landé g-factor gJ, and the isotropic χ becomes
(spin-only approximation). In lanthanoids, because the spin–orbit coupling energy is generally larger than the effect of the crystal field, S is substituted by the spin–orbit coupled quantum number J, ge by the Landé g-factor gJ, and the isotropic χ becomes 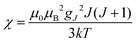 .
.
The anisotropy of χ affects the Curie spin PREs,17 which can be calculated, as recently shown,18 with the following expression:
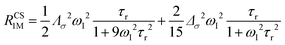 | (3a) |
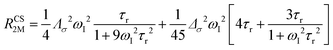 | (3b) |
where σ is the dipolar shielding tensor:
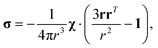 | (4) |
As already indicated, eqn (1) for PREs is derived from the isotropic g tensor and from the absence of ZFS and hyperfine coupling between unpaired electron(s) and metal nuclear magnetic moment. The latter effects can significantly affect the energy of electronic spin transitions, in such a way that sizably different rates are calculated, depending, for instance, on the magnitude of the ZFS energy with respect to the Zeeman energy, as well as on the position of the nucleus with respect to the axes of the ZFS tensor, with origin on the metal ion. Therefore, for systems with large ZFS, PREs have a structural dependence not limited to the metal–nuclear distance (as in eqn (1)), but comprising also the spherical angles defining the metal–nucleus direction in the ZFS frame.19–22
The evidence of the angular dependence of PREs has been obtained experimentally for a paramagnetic lanthanoid(III) complex with a large static ZFS.18 PRE data, measured at 1 T, could in fact not be satisfactorily fitted using the Solomon equation (eqn (1a)) and showed a dependence on the direction of the r vector. PRE values were found to correlate with the sign of the PCSs, and thus to depend on the sign and orientation of the Δχ tensor, and could be nicely fitted using the parametric equation:
The hyperfine shift
The analysis of the NMR spectra of a paramagnetic system passes through the evaluation of the hyperfine shifts, which correspond to the differences in the NMR shifts collected for the paramagnetic system and its diamagnetic analogue.In solution, both the Fermi-contact and the dipolar contributions are averaged by molecular tumbling, which causes sampling of all molecular orientations with respect to the applied magnetic field. The rotational average of the dipolar shift is called PCS and is commonly analysed in terms of its dependence on a symmetric, traceless tensor (Δχ), corresponding to the anisotropic part of the magnetic susceptibility tensor, χ.23
In the point-dipole approximation, the equations for PCSs and FCSs in isotropic solutions are:
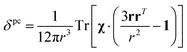 | (5) |
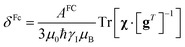 | (6) |
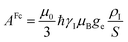 | (7) |
Because the term (3rrT/r2 − 1) appearing in eqn (5) is traceless, δpc is only determined by the susceptibility anisotropy Δχ = χ − χiso1, where χiso = Tr(χ)/3, whereas δFc depends on the overall χ tensor. In the reference frame where the Δχ tensor is diagonal, eqn (5) becomes
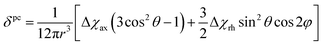 | (8) |
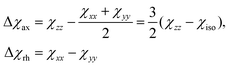 | (9) |
Using a modern quantum chemistry (QC) formalism, in the spin Hamiltonian approximation, at high temperature (μBB0 ≪ kT) and for a system with a singly-populated non-degenerate ground multiplet, the paramagnetic susceptibility tensor can be written in the form
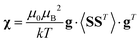 | (10) |
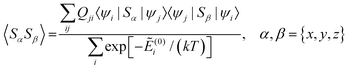 | (11) |
and Ẽ(0)i is the energy of the state |ψi〉 at zero magnetic field. In the approximation to the first order in D/(kT), this provides32
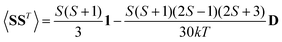 | (12) |
A question recently was raised on the correctness of eqn (5) and (10), i.e. in the derivation of the relationship between the tensor used to describe the PCSs, and the g and D tensors.33–41 PCSs can in fact be calculated using QC approaches as a part of total hyperfine shifts.34,39,40,42–48 Using the effective spin Hamiltonian framework, it was first clarified that if the contribution of the orbital angular momenta of electrons to the PCSs is not correctly included in the first-principles QC treatment, a different expression for the PCSs is obtained.49 The validity of eqn (5) and (10) was finally demonstrated50,51 using the QC formulation of hyperfine shifts to be proportional to the second derivative of the thermally averaged Helmholtz free energy F with respect to the magnetic field and the nuclear magnetic moment, calculated at zero magnetic field and zero magnetic moment.52 In the effective spin Hamiltonian framework, the PCSs can in fact be written as
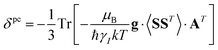 | (13) |
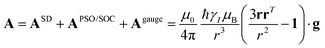 | (14) |
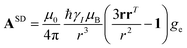 and
and 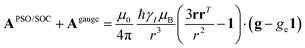 . This derivation confirms the validity of the classical equations for PCSs and thus paves the way for their predictions from the χ tensors which can possibly be calculated through QC tools.
. This derivation confirms the validity of the classical equations for PCSs and thus paves the way for their predictions from the χ tensors which can possibly be calculated through QC tools.
The relationships between PCSs, the Δχ tensor and the g tensor were also experimentally demonstrated to be correctly described by eqn (5) and (10) for some copper(II) proteins, where the g tensor could be measured through EPR under the same conditions of the NMR experiments.53
Eqn (5) for PCSs is valid in the point-dipole approximation, which assumes that the unpaired electron(s) are localized onto the paramagnetic atom. If, on the contrary, the unpaired electron spin(s) are spread over the ligand atoms through molecular orbital overlap, PCS values should be calculated from integration performed over space by considering the actual electron density distribution.25 In the assumption that the χ tensor is independent of the electron spin positions, a relationship – called the Inverse Kuprov Equation – was recently found that permits to recover the electron density distribution, under some regularization conditions, from the experimental PCSs and the atomic coordinates of the molecule.25,54
The paramagnetic residual dipolar couplings
The anisotropy of the magnetic susceptibility causes partial self-orientation of paramagnetic molecules. In fact, the probabilities for different molecular orientations with respect to the magnetic field are not equal and depend on the anisotropy of the χ tensor. The principal components of the self-alignment tensor are given by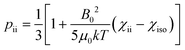 .12,55 This partial self-alignment of the molecules causes a non-null average of the energy of the dipole–dipole interaction between the nuclear magnetic moments, and thus this results in a paramagnetic contribution to their 1J coupling. Therefore, pRDCs are usually calculated from the differences of the J-couplings measured for paramagnetic and diamagnetic samples (assuming negligible dynamic frequency shifts12). As a result, pRDCs and PCSs depend on the same magnetic susceptibility anisotropy tensor Δχ of the paramagnetic metal ion, and are thus often analyzed jointly. Nevertheless, as the dependences on the structural parameters are different, PCSs and pRDCs bear complementary information. In the reference frame where the Δχ tensor is diagonal, pRDCs are equal to
.12,55 This partial self-alignment of the molecules causes a non-null average of the energy of the dipole–dipole interaction between the nuclear magnetic moments, and thus this results in a paramagnetic contribution to their 1J coupling. Therefore, pRDCs are usually calculated from the differences of the J-couplings measured for paramagnetic and diamagnetic samples (assuming negligible dynamic frequency shifts12). As a result, pRDCs and PCSs depend on the same magnetic susceptibility anisotropy tensor Δχ of the paramagnetic metal ion, and are thus often analyzed jointly. Nevertheless, as the dependences on the structural parameters are different, PCSs and pRDCs bear complementary information. In the reference frame where the Δχ tensor is diagonal, pRDCs are equal to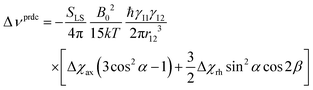 | (15) |
In the presence of paramagnetic tags attached to proteins with some degrees of flexibility, the pRDCs are significantly smaller than the values that are calculated for rigid systems using the Δχ tensor. In turn, when pRDCs are analysed using eqn (15) with SLS = 1, as routinely done, “effective Δχ tensors” are obtained that may be significantly smaller than the real Δχ tensors. The different sizes of PCS-derived and pRDC-derived Δχ tensors can be in fact used to pinpoint the occurrence of tag mobility.
Relation between PCSs and RDCs
PCSs and pRDCs can be fitted against the same molecular structural models to obtain the magnetic susceptibility anisotropy tensors, Δχ, on which they depend (see eqn (5) and (15)), using programs like FANTEN57 or NUMBAT.58 Because PCSs and pRDCs depend on the same tensor, they can fit simultaneously, provided that the biomolecular structure is rigid, and a slight possible reduction in the orienting tensor (SLS < 1) is allowed for, taking into account some local mobility of the coupled nuclei vectors.Magnetic susceptibility anisotropy and electron relaxation rates of paramagnetic metals
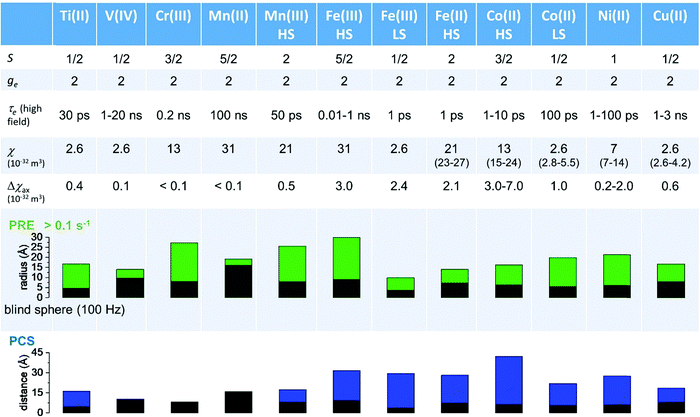
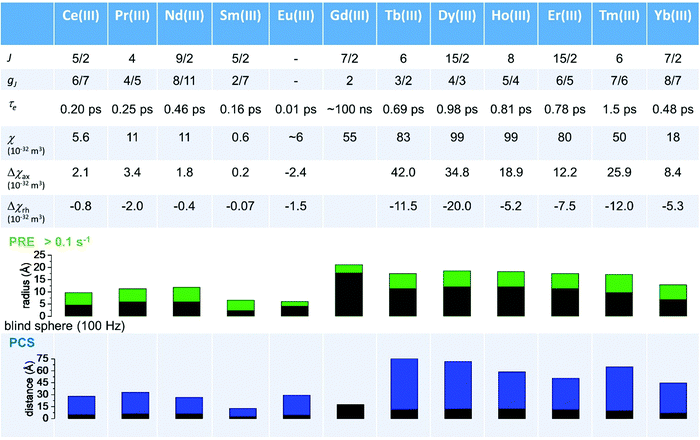
As seen in the previous sections, the magnitudes of PCSs and pRDCs increase with the anisotropy of magnetic susceptibility, whereas PREs are the functions of the electron relaxation time and of the overall magnetic susceptibility (besides of the molecular reorientation time). Magnetic susceptibility anisotropies and electron relaxation times in turn depend on the presence of excited states close in energy (with respect to kT) to the ground state, which makes spin–orbit coupling efficient. Metal ions with low-lying excited states thus have (i) very efficient electron relaxation mechanisms, so that their electron relaxation times are very short, and (ii) very anisotropic g tensors, so that their magnetic susceptibility anisotropies are very large. Therefore, these systems originate from small Solomon contributions to PREs and large PCSs and pRDCs. Conversely, systems with excited states far in energy from the ground state have long electron relaxation times and small magnetic susceptibility anisotropies, so that Solomon contributions to PREs are large and PCSs and pRDCs are small. Fig. 1 and 2 show the typical values of τe, χ and Δχ for the first row transition metal ions and lanthanoids. The figures also show the maximum distances from the nuclei of the paramagnetic metal (those in axial position) experiencing a PCS as small as 0.05 ppm. These distances are calculated from the expression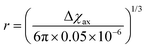 .
.
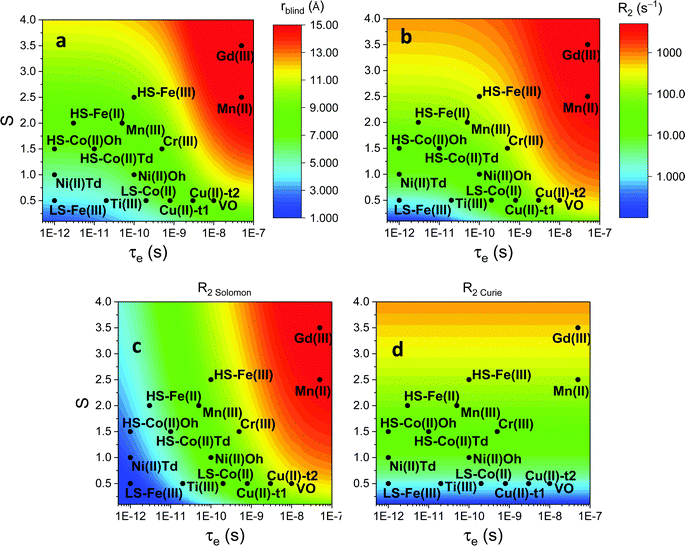
Large PREs determine the presence of a blind sphere around the paramagnetic metal, where nuclear signals are undetectable in standard NMR experiments due to the excessive paramagnetic line broadening. Curie relaxation can sizably contribute to the PREs in large molecules (due to the large τr), as in metalloproteins, especially in the case of late lanthanoids, when χ is quite large. Fig. 3 and 4 show typical R21H PREs for a proton at 10 Å from the metal, in a molecule with the τr of 10 ns, at 900 MHz, and the radius of the 1H blind spheres for the different metal ions. Blind sphere radii are also shown in Fig. 1 and 2 together with the radii of the spheres containing nuclei with R11H PREs larger than 0.1 s−1 (taken as detection limit).
 | ||
| Fig. 3 (a) Typical radii of 1H blind spheres at 900 MHz (paramagnetic linewidths ≥100 Hz), for molecules with the τr of 10 ns and typical values of the electron relaxation times of paramagnetic metal ions. (b) 1H R2 PREs and their Solomon (c) and Curie (d) contributions at 900 MHz, for a proton at 10 Å from the metal, in a molecule with the τr of 10 ns. Besides transition metal ions, only gadolinium(III) is shown in this figure; other lanthanoids, differing in their g-values, are reported in Fig. 4. Metals are labeled as LS: low spin; HS: high spin; t1: type-1; t2: type-2; Td: tetrahedral coordination; Oh: octahedral coordination. | ||
 | ||
| Fig. 4 Typical radii of 1H blind spheres of lanthanoid(III) ions (paramagnetic linewidths ≥100 Hz, left panel), and 1H R2 PRE (right panel), due to Curie relaxation, for a proton at 10 Å from the lanthanoid ion, at 900 MHz. The electron relaxation times τe are set to 1 ps and τr to 10 ns. Gadolinium(III), with τe several orders of magnitude larger, is shown in Fig. 3. | ||
Lanthanoid binding tags rigidly attached to diamagnetic systems59–62 or specific lanthanoid-binding sites introduced in diamagnetic proteins63 are conveniently used for the generation of paramagnetic data to be used as structural restraints in the study of diamagnetic biomolecules. It was recently made clear that the choice of the lanthanoid ligand can significantly affect the magnitude of the magnetic susceptibility anisotropy, and thus of the PCSs, even in the assumption of a completely rigid attachment to the biomolecule. The need for a rigid attachment of the paramagnetic site is mandatory for avoiding conformational averaging effects at the origin of a reduction in the “effective” Δχ tensor (see above – although an average tensor may even not be defined when the position of the metal with respect to the molecule changes), and thus on the measured PCSs and pRDCs.64
The dependence of the Δχ tensor on the coordination environment of lanthanoid ions, usually neglected due to the assumption that the ligand field splitting is small compared to the large spin–orbit coupling of lanthanoids, originates from the observation that in lanthanoid complexes, ligand field splittings are commonly larger than kT at room temperature,65 and the electron density distribution is not spherical in f orbitals, except that for gadolinium(III). The Δχ tensor has been shown to depend on the compliance of the single-ion electron density with the crystal field environment in which it is placed. The (2J + 1)-fold degeneracy of the ground state can in fact be removed by the surrounding crystal field, so that the electronic structure of the ground state is linked to the strength and symmetry of the ligand field.66,67 In turn, a proper choice of the coordination environment of the lanthanoid ion can increase the performance of lanthanoid tags.
As described in ref. 66 and 67, there are two general optimum ligand architectures providing a highly anisotropic ground state depending on whether the basic overall shape of the free-ion electron density is oblate, as for Ce3+, Pr3+, Nd3+, Tb3+, Dy3+ and Ho3+, or prolate, as for Pm3+, Sm3+, Er3+, Tm3+ and Yb3+. The magnetic susceptibility anisotropy of an oblate ion is maximized by a crystal field for which the ligand electron density is concentrated above and below the xy plane (see Fig. 5), so that the ground state corresponds to the configurations that minimize repulsive charge contacts between ligand and f-electron charge clouds. This configuration corresponds to the mJ state with the highest value. At the same time, states with low mJ values force the f-electron charge cloud into direct contact with the ligands, thus having a high energy. Conversely, the magnetic susceptibility anisotropy of a prolate ion is maximized by an equatorial coordination geometry so that the ground state, minimizing the charge contact with the axially located f-element electron density, corresponds to the mJ state with the highest value. Also the main direction (z axis) of the Δχ tensor depends on the non-spherical electron density distribution of the lanthanoid ion and on the ligand atom positions,68,69 so as it may be oriented differently for the different lanthanoids, even if they are bound by the same ligand and, likewise, it may be oriented differently for different ligands, even if bound to the same lanthanoid ion. Careful engineering can lead to ligands preserving an almost completely axial susceptibility even at room temperature in solution. For example, a dysprosium(III) complex is available with Δχax = 2.16 × 10−30 m3, which is more than 220% of its isotropic magnetic susceptibility, and Δχrh = 2.17 × 10−32 m3, which is less than 3% of its isotropic value.70
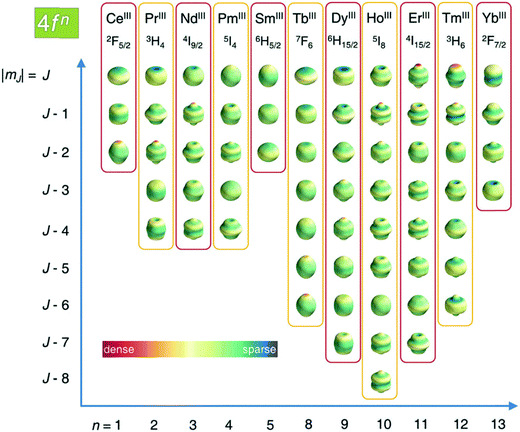 | ||
| Fig. 5 Charge density angular distribution for lanthanoid(III) 4f shells for the different mJ states. Reproduced from ref. 66 with permission from the Royal Society of Chemistry. | ||
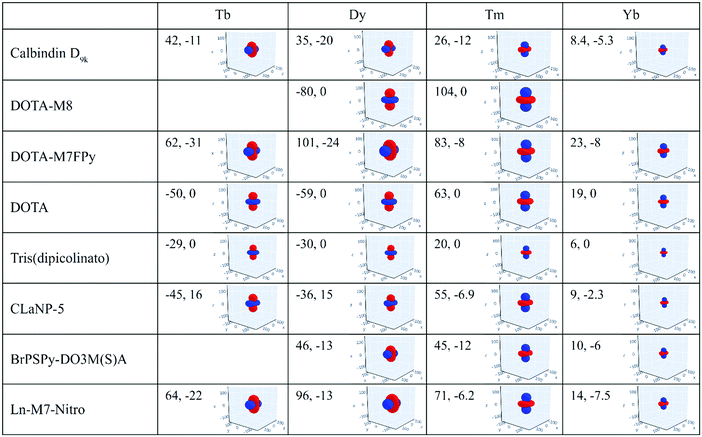
The magnetic susceptibility anisotropy values obtained for lanthanoids in calbindin D9k, reported in Fig. 2, can be compared to the values obtained for some DOTA-based complexes, for tris(dipicolinato)lanthanoids (dipic = pyridine-2,6-dicarboxylate), and for some widely used and efficient lanthanoid-binding tags, shown in Fig. 6. The anisotropy values were determined from the shifts of the ligand nuclei in the case of the DOTA,71 DOTA-M8,72 DOTA-M7FPy72 and tris(dipicolinato)73,74 complexes, and from the nuclear shifts of the attached proteins in the case of the tags CLaNP-5,28,75 BrPSPy-DO3M(S)A76 and Ln-M7-Nitro.77 In the case of the proteins with paramagnetic tags, the shifts may be reduced to some extent by a non-completely rigid attachment of the tag.
The data show that if the DOTA-based tags providing the largest anisotropies could be rigidly attached to proteins, PCSs could be detected for nuclei at larger distances than expected from the Δχ of the same ions in calbindin D9k, and higher, and thus more accurate, pRDCs could be measured, thus extending the perspectives for their use in the structural determination of biomolecular systems.
Paramagnetic structural restraints
Paramagnetic restraints efficiently provide structural information throughout the whole macromolecular system, or a large part of it because of their long-range nature. This feature becomes particularly relevant when paramagnetic restraints are used in integration with the data obtained using other techniques, and can help in removing assignment ambiguities.11,78–82 Besides the use for de novo structural determination, the interest towards paramagnetic restraints has increased in the last decades,83 thanks to other notable implications of their use in (e.g.) detecting transient interactions, conformational changes, etc.Paramagnetic restraints in the protein structure calculation
Determination of the traditional structure by NMR suffers from the lack of long-range observables. The collected PCSs, pRDCs and PREs can thus be used for the calculation of de novo structure or for the refinement of structures together with dihedral angle restraints and other diamagnetic restraints in programs like PARAMAGNETIC-CYANA84,85 or Xplor-NIH.86,87 For instance, the solution structure of the protein calbindin D9k could be refined using paramagnetic data from lanthanoid ions substituted in the second calcium binding site of the protein, with an increase in resolution not only in the close proximity of the paramagnetic center but along the overall protein backbone chain.88 A further insight into the structure of calbindin D9k with the thulium(III) ion substituting one calcium(II) ion arose from the application of the Inverse Kuprov Equation: a probability density distribution of the paramagnetic center was reconstructed, providing a better agreement with the experimental data than calculated from the point-dipole approximation.25PCSs can efficiently guide the reconstruction of protein conformations in the ROSETTA fragment assembly method,24 especially when multiple paramagnetic metals positioned in different places on the protein surface are used.89,90 Also PREs showed usefulness to recover protein structures in molecular fragment searching protocols, when used in conjunction with diamagnetic RDCs and/or backbone dihedral angles.91,92 In microcrystalline protein samples, PCSs have been used to obtain unambiguous signal assignments in solid-state NMR spectra, allowing for determining high-resolution protein structure,93,94 as well as for determining the relative positions of the protein molecules in the crystal.31
Interdomain position reorganization in solution and crystals
Also the solution structure of calmodulin in complex with the calmodulin-binding peptide of the death-associated protein kinase could be determined using PCSs and pRDCs from three different lanthanoids substituted into the second binding site of the N-terminal domain of the N60D mutant of the protein.95 The calculated structure shows a different arrangement of the two domains with respect to the crystal structure: this is due to the absence of inter-protein contacts that are present in the crystal. Indeed, this solution structure resulted in better agreement with the crystal structure of calmodulin in complex with the whole kinase protein96 than with the crystal structure of calmodulin bound to the peptide (Fig. 7a).97 The steric hindrance of the whole protein in the crystal prevents the formation of H-bonds and salt bridges between different calmodulin molecules, thus allowing the latter to have a conformation more similar to the solution structure. The residual discrepancy between the paramagnetic data and the solution structure can be attributed to a limited but significant interdomain mobility.98 In general, the achievement of a good fit of the experimental PCSs and pRDCs30,57,97 is an indication of a good accuracy of the protein structure (Fig. 7b).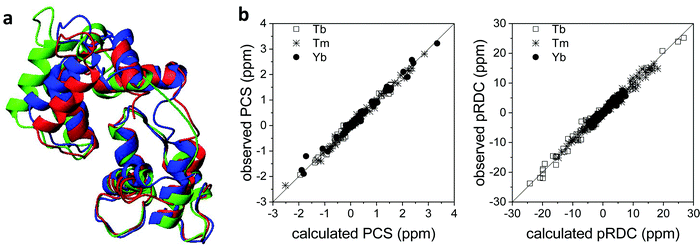 | ||
| Fig. 7 (a) X-ray structure (PDB entry 1YR5, in red) and refined solution structure (PDB entry 2K61, in blue) of the peptide-bound calmodulin, and X-ray structure of calmodulin in complex with the whole kinase protein (PDB entry 2X0G, in green). (b) Best fit of PCSs and pRDCs for the refined solution structure, calculated using FANTEN57 and a common Δχ tensor for each paramagnetic metal ion. | ||
Paramagnetic data for protein structural refinement in integrative structural biology
The long-range nature of paramagnetic restraints is particularly appealing to validate, and possibly refine, structures obtained from X-ray data, cryo-electron microscopy, or homology modeling. X-ray crystallography, in particular, provides very precise protein structures, which can, however, suffer from crystal packing forces. Therefore, they can be inaccurate models, to some extent, in solution, where these interactions are abolished. Furthermore, crystal structures are affected by “structural noise”,99 depending on the resolution of the X-ray reflections and on the structural refinement protocol employed, which may result in a lower accuracy of local structural details than that contained in NMR data. The high accuracy, despite their sparsity, of paramagnetic restraints makes them fully complementary to X-ray data for achieving a more accurate structural description of the biomolecules, also because NMR data provide direct information on local details, in the form of interatomic distances or orientations of vectors connecting chemically bound nuclei.30The information contained in PCSs and pRDCs are of different kinds. On the one hand, PCSs are barely affected by small structural inaccuracies, so that they are nicely fitted when the structural model is in overall agreement with the biomolecular structure in solution. Their fit provides a very robust estimation of the magnetic susceptibility anisotropy tensor, being determined by several tens, or hundreds, of PCS values. On the other hand, pRDCs, which are sensitive to even small local inaccuracies in the orientation of nuclear pairs, hardly agree with the susceptibility tensor obtained from PCSs unless the molecular structure is a very accurate model for the protein in solution. For instance, the pRDCs measured for the catalytic domain of matrix metalloproteinase-1 (MMP1), attached with the CLaNP-5 tag62 with either one of the three paramagnetic lanthanoids Tb3+, Tm3+ and Yb3+, provide an agreement with the crystallographic structure much poorer than that expected from the experimental errors of the data (Fig. 8), despite the very good fit of the PCS data.29 This disagreement could be due to either some protein structural rearrangements on passing from the crystal state to the solution state, or to some inaccuracy in the nuclear coordinates determined from X-ray data (structural noise). Actually, the second case seems more plausible for this system because the disagreement of pRDCs could be solved by very small conformational adjustments, within the indeterminated X-ray data. Similarly, the disagreement between the diamagnetic RDCs measured for the protein ubiquitin and its crystal structure could be accommodated within the structural noise of the X-ray data,29 and even for sub-atomic resolution structures of lysozyme100 RDC restraints could be accommodated within the X-ray structural noise without the need for invoking conformational averaging.
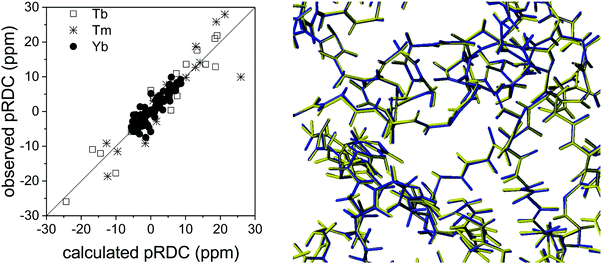 | ||
| Fig. 8 Best fit agreement of experimental pRDCs measured for the catalytic domain of matrix metalloproteinase-1 with the crystallographic structure (PDB entry 3SHI) (2.2 Å resolution) and superposition of original (in blue) and refined (in yellow) structures. | ||
The paramagnetic data can thus be used to assess how accurately crystal structures represent solution structures and to improve them by simultaneous refinements through NMR and X-ray data. PCSs and pRDCs can be fitted, using the same Δχ tensor for each metal ion, together with X-ray data using the program REFMAC-NMR29 developed within REFMAC5 from CCP4.101 The program provides a refined structure, resulting from the combined use of the information on the heavy atom positions mainly contained in X-ray reflections, and on nuclear (mostly hydrogen) positions and bond orientations of nuclear pairs contained in PCSs and pRDCs. If this structure is in good agreement with both X-ray data (in terms of R and R-free values) and NMR data (in terms of Q-factor), it can be concluded that there are no inconsistencies between the crystal and the solution structures, and thus the refinement performed with both NMR and X-ray data provides a more reliable structural model.102 On the other hand, the presence of some NMR data which do not match the values predicted by the refined conformation within their error is an indication of minor inconsistencies, i.e., of local conformational rearrangements between the solution and the solid states (or the presence of conformational heterogeneity in solution) in specific regions of the protein.30,102
In the case of the catalytic domain of MMP1, REFMAC-NMR provides a refined structure with a backbone root mean square deviation from the original model of only 0.04 Å (Fig. 8), in full agreement with the X-ray reflections and a significant overall improvement in the agreement of the NMR data, the Q-factor of the pRDCs decreasing from 0.41 to 0.16.29 This example shows the high accuracy in defining structural details that these NMR data can provide.
For systems composed of multiple domains, the evaluation of the Δχ tensors determined from the fit of PCSs and/or pRDCs measured for each domain provides a simple but powerful way for assessing their relative arrangement in solution. Several situations can be encountered.
1. If both sizes and orientations of the tensors coincide, the crystal conformation is maintained in solution.
2. If only the sizes coincide, and not the orientations, the relative arrangements of the refined domains in solution can be retrieved by superimposing the anisotropy tensors.57 As an example, a cobalt(II) binding tag was attached to the N-terminal domain of the homodimeric protein STAT4. The PCSs permitted to refine the monomeric structure80 and to determine the arrangement of the monomeric subunits. Sub-stoichiometric addition of the paramagnetic metal in this case permitted to disrupt the symmetry in the NMR spectra of the protein.103 Data from multiple paramagnetic ions or from ions located in multiple positions are often needed to identify the correct conformation among the possible degenerate solutions.104,105
3. Finally, if the tensors differ both in size and in orientation, interdomain mobility occurs and thus conformational averaging takes place.64 In these conditions, the measured PCSs, pRDCs and PREs are population-weighted averaged over all sampled conformations (PREs may also depend on the time of interconversion between the different conformations).106,107 Several approaches have been developed to recover some information on the experienced conformations, although the reconstruction of the real structural ensemble is impossible due to the inherent presence of degenerate solutions.64,108–113
PREs, providing very sensitive information on the distance between the observed nucleus and the paramagnetic metal ion (eqn (1) and (2)), have been found to be very useful to monitor the occurrence of structural mobility in solution. In particular, PREs can detect the presence of less (few percent) populated conformational states when the latter imply metal–nuclear distances much shorter than in the more populated conformational states.114 In the presence of two states, in fact, if their exchange rate is faster than the difference in relaxation rates and slower than the reorientation time of the system, the measured PREs are population weighted averages of the PREs in the two states. Along the same lines, PREs have been used to detect the presence of transient, sparsely populated, protein–protein encounter complexes, and to identify the patches of protein residues that come into short-lived close contact with one another.115–117 Such sensitivity of PREs to lowly populated structural states is an extraordinary informative tool for the characterization of transient states in solution. Paramagnetic restraints can also be used in HADDOCK118 for driving docking calculations of protein complexes.
Coupling QC calculations to paramagnetic data analysis
Quantum chemical methods for the calculation of hyperfine shifts and relaxation rates are becoming increasingly accessible and can now be included in the toolkit for protein structural calculations. The hyperfine shifts of the two high-spin pentacoordinate nickel(II) complexes, NiSAL-MeDPT and NiSAL-HDPT (SAL = salicylaldiminate; DPT = dipropylenetriamine), composed of both PCSs and FCSs, could, for instance, be calculated119 using the ORCA quantum chemistry package120,121 and the NiSAL-MeDPT structure after refinement at the density functional theory (DFT) level. PCSs were calculated from eqn (5) and the Δχ tensors obtained using state-averaged complete active space self-consistent field (SA-CASSCF),122 accounting for the dynamic correlations by N-electron valence perturbation theory to the second order (NEVPT2),123 and FCSs were calculated using the Fermi contact coupling constant and the isotropic g values obtained from DFT calculations. The calculated hyperfine shifts agree very well with the experimental shifts of both complexes (Fig. 9). The accuracy of the calculations allowed for a swap in the assignment of the methylene signals previously reported,124 and for a refinement of the NiSAL-HDPT structure using the structure of NiSAL-MeDPT as a starting template.119 The small discrepancies between the calculated shifts and the shifts measured for the HDPT derivative, for which a structure is not experimentally available, were finally rationalized in terms of minor structural changes.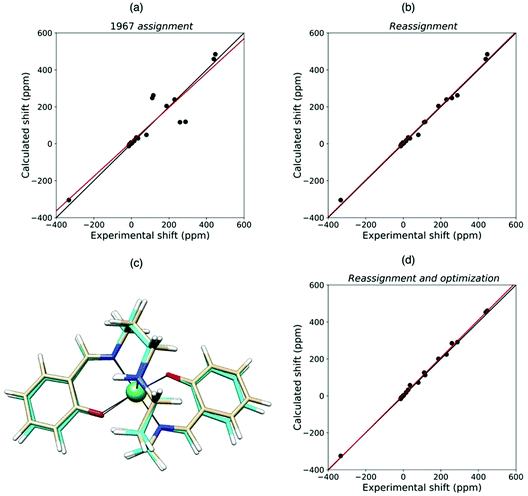 | ||
| Fig. 9 Agreement between experimental and QC calculated shifts of NiSAL-HDPT, with the assignment previously reported (a),124 and the theory-based reassignment (b). Comparison between initial (beige) and DFT-optimized (cyan) structures (c) and agreement between the experimental and QC calculated shifts for the refined structure (d). | ||
As it is clear from eqn (5), PCSs depend on the magnitude and orientation of the Δχ tensor, which in turn reflects the very fine details of the coordination geometry of the paramagnetic metal ion. For instance, in cobalt(II)-substituted human carbonic anhydrase II, the cobalt(II) ion is essentially tetracoordinated when the enzyme is free in water or bound to sulfonamides, and pentacoordinated in the presence of ligands such as oxalate, where two oxygen atoms of the ligand complete the coordination environment.125 Indeed, the magnetic susceptibility anisotropy changes dramatically in the two cases.126
It was recently figured out that PCSs can be used not only for refining protein structures at the positions of the observed nuclei but also around the paramagnetic center, thus recovering accurate conformational details about the metal ligand positions. In fact, recently, for the first time, it was shown that the paramagnetic Δχ tensor of a large metalloprotein can be calculated ab initio with advanced quantum-chemical approaches using only a structural model of the metal coordination site.33 Using the effective spin Hamiltonian (valid when all orbital excited states are sufficiently more in energy from the ground state with respect to the energy of the thermal bath), the Δχ tensor can also be determined from the g and the ZFS (D) tensors (see eqn (10)–(12)).12,23,41,127 From the knowledge of the Δχ tensor and of the protein coordinates, it is easy to predict the PCSs in the point-dipole approximation. A good matching between predicted and experimental PCSs is thus a clear indication of a good prediction of the Δχ tensor.
Conversely, as the magnetic susceptibility tensor is very sensitive to the details of the coordination geometry of the paramagnetic metal ion, the PCSs, measured for nuclei far from the paramagnetic metal, can be used to refine the molecular structure around the metal ion.82 This approach offers the possibility to overcome one of the most important limitations of paramagnetic NMR, which is the large line broadening often affecting the signals of nuclei in the immediate vicinity of the paramagnetic center, responsible for the presence of a blind sphere. The knowledge of the metal coordination environment at the highest possible resolution is crucial to understand structure–activity relationships for metal ions in proteins and for the successful use of docking strategies for drug discovery.128,129
This approach has been tested to refine the structure in solution of the catalytic domain of the human matrix metalloproteinase-12, where the catalytic zinc(II) ion was substituted with the paramagnetic high spin cobalt(II) ion (CoMMP12), coordinated by the N-isobutyl-N-[4-methoxyphenylsulphonyl]glycyl hydroxamic acid (NNGH) inhibitor. The cobalt(II) ion coordinates three histidines through their nitrogen atoms, and the inhibitor NNGH through the oxygen atoms of its hydroxamic moiety. A Δχ tensor was obtained using FANTEN57 from the best fit of the PCS data measured for this protein and the X-ray structure of the NNGH-inhibited zinc(II) protein at 1.34 Å resolution (PDB entry 5LAB33), with cobalt(II) replacing zinc(II). The high quality of this fit indicates the good accuracy of the crystallographic model in representing the overall structure of the protein in solution, as well as of the Δχ tensor because it is determined from several hundreds of 13C PCSs.130 A magnetic susceptibility tensor was also calculated with ORCA120,121 from the coordinates of the metal ligands taken from the same X-ray structure of the protein. The anisotropy of this QC calculated susceptibility tensor was not found in agreement with the Δχ tensor obtained from the fit of the PCSs. On the other hand, relativistic CASSCF calculations, with second-order perturbation theory corrections, implemented in ORCA, have been shown to be quite reliable in predicting the magnetic properties of transition metal complexes and their temperature dependencies in a number of cases.119,131,132 Therefore, starting from the crystallographic model of the cobalt(II) coordination cage, a structural refinement procedure was implemented so as to obtain a susceptibility tensor from ORCA in good agreement with the PCSs-derived anisotropy tensor.133 The structural refinement was performed by adjusting, through a steepest descent search, 19 degrees of freedom among coordination bond lengths, angles and dihedral angles, selected in a way to avoid altering the structure of the ligands themselves. The calculations also showed that an additional proton in the structure of NNGH should be included (implying that the hydroxamic acid moiety, and not the hydroxamate moiety, coordinates the cobalt(II) ion). This procedure permitted to refine the structure of the metal coordination site in solution to picometer precision (Fig. 10).
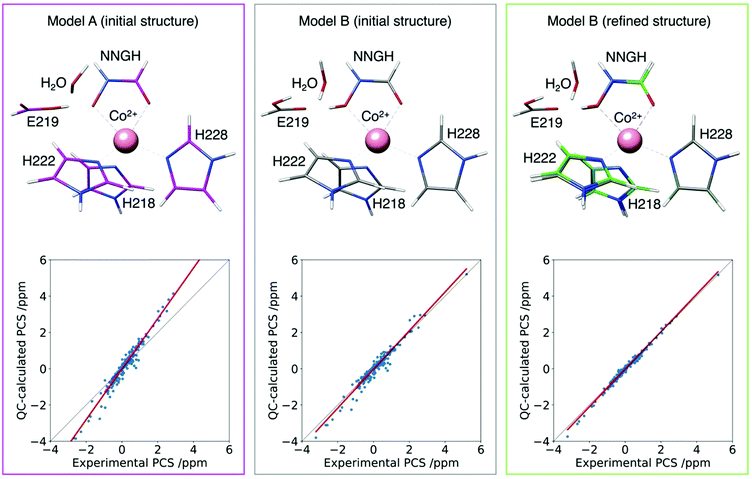 | ||
| Fig. 10 Agreement between experimental and QC calculated PCSs for the CoMMP-12 protein structure (PDB entry 5LAB) with the hydroxamate (model A initial structure) or the hydroxamic acid moieties of the NNGH inhibitor, before (model B initial structure) and after (model B refined structure) geometry refinement. The refined structure (green) is superimposed to the initial one (grey) to highlight the subtle structural differences. | ||
In summary, having clarified the QC terms to be included in the hyperfine coupling tensor, and thus having confirmed the dependency of PCSs on the χ tensor from first principles, QC tools can now be used for an accurate prediction of the χ tensor from a structural model of the metal coordination cage, and consequently for an accurate prediction of the PCSs of all protein nuclei from the knowledge of the protein structure, in the point-dipole approximation. The χ tensor can be predicted from relativistic CASSCF/NEVPT2 calculations for metal ions like cobalt(II) and nickel(II). Current challenges are now: (i) to extend the applicability of the QC tools to the robust and efficient prediction of the χ tensor of other paramagnetic metal ions, including lanthanoids(III),121,134–136 and (ii) to accurately predict PCSs outside the point-dipole approximation.54
Also FCSs can be used for the refinement of the metal coordination site to a similar precision. In fact, FCSs depend on the electron spin densities delocalized onto the nuclei, and in turn on the coordination geometry of the paramagnetic metal ion. It has been recently shown that the FCSs measured for 1H, 13C and 15N nuclei of the cobalt(II) ligands in solid-state NMR spectra of the human protein superoxide dismutase 1, in a microcrystalline form and containing a cobalt(II) ion, allowed for the determination of the high-resolution structure of the metal coordination sphere at picometer resolution in the precision of the bond lengths and ±1° resolution of bond angles.137 A structural model could, in fact, be selected within an ensemble of X-ray structures so as to achieve the best agreement of the measured FCSs with those calculated from the molecular structures using DFT. The structural precision so achieved was enough to correlate the coordination geometry with the unreactive nature of the metal center in these proteins, where it plays a purely structural role.
In perspective, QC calculations of hyperfine shifts are expected to increase in importance and popularity with the increase in computational power, which will extend the applicability of the approach for the structural refinements of proteins even when starting from more distant initial models.
Paramagnetic restraints to monitor protein dynamics
A challenging objective of structural biology is the characterization of the conformational variability which can be exploited by biomolecular systems to perform their biological function. Experimental NMR data are averaged values reflecting this structural variability. Recovering information on the different conformations from these averaged data is a quite cumbersome, ill-posed, inverse problem, which can be tackled in a number of ways112,113,138 but always without the possibility of reconstructing a single structural ensemble if a priori assumptions are not introduced. In the case of systems composed of multiple structured domains which can reorient with respect to one another, the most used approaches either rely on the Occam's razor139 (or maximum parsimony) principle or on the maximum entropy principle, aiming at identifying the least populated structural ensembles and the broadest and flattest probability distribution, respectively.112,113,138 Alternatively, one can rely on unbiased molecular dynamics simulations reweighted in order to achieve an agreement with the experimental data. From a yet different perspective, the maximum occurrence approach27,28,112,116,138,140 has been proposed to extract the information contained in the averaged data without any prior assumption or calculation. This approach provides the largest weight possible for each allowed conformation, independently from all other conformations present in the ensemble, and is achieved at the cost of giving up the reconstruction of structural ensembles.Paramagnetic NMR data contain averaged structural information which can be very useful for monitoring the conformational variability of the biomolecular system.64 For instance, in multidomain proteins, pRDCs are very sensitive to the mobility of a metal-free domain with respect to another domain containing a paramagnetic metal; PREs are very sensitive to even very lowly populated conformations with some nuclei close to the paramagnetic metal, and PCSs are sensitive to both reorientations and translations.
As an example, PCSs and RDCs, complemented by SAXS data, measured for the protein matrix metalloproteinase-1 allowed for the recovery of the mostly populated conformations within the wide structural ensemble experienced by the protein due to the long flexible linker connecting the catalytic and the hemopexin-like domain.28 These conformations differ largely from the structures obtained by X-ray crystallography.
Conclusions and perspectives
Recent technological advancements, which comprise cryo-electron microscopy and computational methods for structure prediction,141 offer new tools for the structural characterization of biomolecules, in addition to NMR and X-ray crystallography. Nevertheless, only paramagnetic NMR can offer a spatial resolution on the picometer scale. Therefore, although other techniques can be more advantageous in terms of high-throughput and automation, structural validation and refinement in solution through NMR studies are still crucial for many applications. We thus envision that paramagnetic NMR data, rather than being used for ab initio structure calculations, will be increasingly combined with experimental data from different sources in integrative structural biology approaches.Challenging applications of paramagnetic NMR in structural biology are mainly expected in the following fields:
(1) Refinement of molecular models obtained from other techniques (X-ray crystallography, cryoelectron microscopy, artificial intelligence –AI– predictions). Paramagnetic data offer precious information with an accuracy hardly available using the other techniques and an unprecedented level of detail. Paramagnetic data, in fact, despite their long range nature, provide immediate information about short-range inter-atom distances and bond orientations and can probe the dynamics experienced in solution. Therefore, they are highly suitable to refine conformational models determined using techniques not allowing for such accurate local structural details, and to evaluate the presence of conformational averaging. This approach can improve X-ray structures, which can be affected by structural noise and can be from slightly to significantly inaccurate in solution due to the presence of crystal packing forces, as well as models determined by cryoelectron microscopy and by computational methods for predicting the protein structure, like AlphaFold.142 Structures determined by cryoelectron microscopy can, in fact, suffer from low resolution, especially in the case of small biomolecules, and can be inaccurate in solution, and the accuracy of AlphaFold structures may need to be improved depending on the required level of structural details.
(2) Evaluation and characterization of the conformational dynamics relevant to functions in systems exploiting structural heterogeneity. In all cases, no or very limited insights into conformational dynamics are obtained using other structural techniques (X-ray crystallography, cryoelectron microscopy, AI predictions). NMR is an irreplaceable technique in this respect, and paramagnetic NMR, in particular, can provide very informative data.
(3) Monitoring of protein–protein interactions and protein–drug interactions in solution. Paramagnetic data can allow for monitoring the presence of interactions between proteins, even if transient and elusive,116 as well as between proteins and small paramagnetic molecules, even with a low binding affinity. These studies are crucial for the understanding of protein biological functions and for the development of drugs.
(4) Refinement of the metal coordination site of paramagnetic proteins, also taking advantage of the available QC tools. The improvement in QC predictions of paramagnetic NMR data and the development of computational tools for the exploitation of QC data are challenging fields of research. Thanks to QC computations, it can, in fact, be possible to improve the biomolecular structures to a resolution unachievable by any other techniques.143 Such an accuracy may be needed, for instance, for a thorough understanding of structure–activity relationships and in drug discovery. For a routinary and reliable use of QC tools, much work is still needed for the improvement of the prediction tools, for the whole range of paramagnetic metal ions, in terms of accuracy and computational time, and for cross validation of the predicted data. In parallel, efficient protocols for structural refinement should be implemented. To be noted, the accuracy of X-ray atomic coordinates in the immediate vicinity of a metal ion can sometimes be compromised by phase problems, and AlphaFold is not yet optimized for the structural modeling of metalloproteins.
(5) High magnetic fields represent a challenge not only for relaxation (eqn (2) and (3)) but also because of the span in frequencies that are associated with large hyperfine shifts. Efforts are currently being devoted to the development of pulses that can efficiently cover the full spectral width,144 as well as for methods that allow for reducing the massive phase distortion that occurs as a result of pulse imperfections and dead time.145
(6) When discussing the use of high fields, it is mandatory to mention the use of solid-state NMR, where the absence/reduction of incoherent molecular tumbling yields an effective reduction of the Curie-spin relaxation146,147 and, in parallel, the appearance of a “powder pattern” reflects the geometry and the anisotropy of the interaction of the nuclear spin with the “Curie Spin”, and encodes highly relevant structural/dynamical information.11,127,148–150
The possibility of providing structural information in solution with an increasing level of detail, in conjunction with the possibility of characterizing biomolecular dynamics, is expected to further increase the number of users and applications of paramagnetic NMR, and to foster the development of computational tools and automated protocols for integrated data analysis. These advancements will keep paramagnetic NMR vital in the foreseeable future, contributing to solve challenging and important biological problems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Fondazione Cassa di Risparmio di Firenze and the Italian Ministero dell’Istruzione, dell’Università e della Ricerca through the “Progetto Dipartimenti di Eccellenza 2018–2022” to the Department of Chemistry “Ugo Schiff” of the University of Florence. The authors acknowledge the support and the use of resources of Instruct-ERIC, a landmark ESFRI project, and specifically the CERM/CIRMMP Italy center.Notes and references
- E. Luchinat and L. Banci, In-Cell NMR in Human Cells: Direct Protein Expression Allows Structural Studies of Protein Folding and Maturation, Acc. Chem. Res., 2018, 51, 1550–1557 CrossRef CAS PubMed.
- I. Bertini, M. M. J. Couture, A. Donaire, L. D. Eltis, I. C. Felli, C. Luchinat, M. Piccioli and A. Rosato, The solution structure refinement of the paramagnetic reduced HiPIP I from Ectothiorhodospira halophila by using stable isotope labeling and nuclear relaxation, Eur. J. Biochem., 1996, 241, 440–452 CrossRef CAS PubMed.
- L. Banci, I. Bertini, K. L. Bren, M. A. Cremonini, H. B. Gray, C. Luchinat and P. Turano, The use of pseudocontact shifts to refine solution structures of paramagnetic metalloproteins: Met80Ala cyano-cytochrome c as an example, J. Biol. Inorg. Chem., 1996, 1, 117–126 CrossRef CAS.
- L. Banci, I. Bertini, J. G. Huber, C. Luchinat and A. Rosato, Partial orientation of oxidized and reduced cytochrome b5 at high magnetic fields: magnetic susceptibility anisotropy contributions and consequences for protein solution structure determination, J. Am. Chem. Soc., 1998, 120, 12903–12909 CrossRef CAS.
- J. R. Tolman, J. M. Flanagan, M. A. Kennedy and J. H. Prestegard, Nuclear magnetic dipole interactions in field-oriented proteins: information for structure determination in solution, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 9279–9283 CrossRef CAS PubMed.
- I. Bertini, J. Kowalewski, C. Luchinat and G. Parigi, Cross-correlation between the dipole–dipole interaction and the Curie spin relaxation. The effect of anisotropic magnetic susceptibility, J. Magn. Reson., 2001, 152, 103–108 CrossRef CAS PubMed.
- I. Bertini, G. Cavallaro, M. Cosenza, R. Kümmerle, C. Luchinat, M. Piccioli and L. Poggi, Cross Correlation Rates Between Curie Spin and Dipole–Dipole relaxation in Paramagnetic Proteins: the Case of Cerium Substituted Calbindin D9k, J. Biomol. NMR, 2002, 23, 115–125 CrossRef CAS PubMed.
- J. C. Hus, D. Marion and M. Blackledge, De novo determination of protein structure by NMR using orientational and long-range order restraints, J. Mol. Biol., 2000, 298, 927–936 CrossRef CAS PubMed.
- R. Barbieri, C. Luchinat and G. Parigi, Backbone-only protein solution structures with a combination of classical and paramagnetism-based constraints: a method that can be scaled to large molecules, Chem. Phys. Chem., 2004, 21, 797–806 CrossRef PubMed.
- I. B. Trindade, M. Invernici, F. Cantini, R. O. Louro and M. Piccioli, PRE-driven protein NMR structures: an alternative approach in highly paramagnetic systems, FEBS J., 2021, 288, 3010–3023 CrossRef CAS PubMed.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, NMR of paramagnetic molecules: applications to metallobiomolecules and models, Elsevier, 2017 Search PubMed.
- G. Parigi, E. Ravera and C. Luchinat, Magnetic susceptibility and paramagnetism-based NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115, 211–236 CrossRef CAS PubMed.
- J. S. Griffith, The theory of transition-metal ions, Cambridge University Press, Cambridge, 1961, vol. 1 Search PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Metal Ions, Clarendon Press, Oxford, 1970 Search PubMed.
- I. Solomon, Relaxation Processes in a System of Two Spins, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- M. Gueron, Nuclear relaxation in macromolecules by paramagnetic ions: a novel mechanism, J. Magn. Reson., 1975, 19, 58–66 CAS.
- A. J. Vega and D. Fiat, Nuclear relaxation processes of paramagnetic complexes The slow-motion case, Mol. Phys., 1976, 31, 347–355 CrossRef CAS.
- E. A. Suturina, K. Mason, C. F. G. C. Geraldes, N. F. Chilton, D. Parker and I. Kuprov, Lanthanide-induced relaxation anisotropy, Phys. Chem. Chem. Phys., 2018, 20, 17676–17686 RSC.
- I. Bertini, O. Galas, C. Luchinat and G. Parigi, A computer program for the calculation of paramagnetic enhancements of nuclear relaxation rates in slowly rotating systems, J. Magn. Reson., Ser. A, 1995, 113, 151–158 CrossRef CAS.
- I. Bertini, J. Kowalewski, C. Luchinat, T. Nilsson and G. Parigi, Nuclear spin relaxation in paramagnetic complexes of S = 1: electron spin relaxation effects, J. Chem. Phys., 1999, 111, 5795–5807 CrossRef CAS.
- J. Kowalewski, D. Kruk and G. Parigi, NMR relaxation in solution of paramagnetic complexes: recent theoretical progress for S > 1, Adv. Inorg. Chem., 2005, 57, 41–104 CrossRef CAS.
- I. Bertini, C. Luchinat, M. Mancini and G. Spina, The electron-nucleus dipolar coupling. The effect of zero-field splitting of an S = 3/2 manifold, J. Magn. Reson., 1984, 59, 213–222 CAS.
- R. J. Kurland and B. R. McGarvey, Isotropic NMR shifts in transition metal complexes: calculation of the Fermi contact and pseudocontact terms, J. Magn. Reson., 1970, 2, 286–301 CAS.
- C. Schmitz, R. Vernon, G. Otting, D. Baker and T. Huber, Protein structure determination from pseudocontact shifts using ROSETTA, J. Mol. Biol., 2012, 416, 668–677 CrossRef CAS PubMed.
- E. A. Suturina and I. Kuprov, Pseudocontact shifts from mobile spin labels, Phys. Chem. Chem. Phys., 2016, 18, 26412–26422 RSC.
- G. Pintacuda, M. John, X.-C. Su and G. Otting, NMR Structure Determination of Protein−Ligand Complexes by Lanthanide Labeling, Acc. Chem. Res., 2007, 40, 206–212 CrossRef CAS PubMed.
- L. Gigli, W. Andrałojć, A. Dalaloyan, G. Parigi, E. Ravera, D. Goldfarb and C. Luchinat, Assessing protein conformational landscapes: integration of DEER data in Maximum Occurrence analysis, Phys. Chem. Chem. Phys., 2018, 20, 27429–27438 RSC.
- L. Cerofolini, G. B. Fields, M. Fragai, C. F. G. C. Geraldes, C. Luchinat, G. Parigi, E. Ravera, D. I. Svergun and J. M. C. Teixeira, Examination of Matrix Metalloproteinase-1 in Solution: A Preference for the Pre-Collagenolysis State, J. Biol. Chem., 2013, 288, 30659–30671 CrossRef CAS PubMed.
- M. Rinaldelli, E. Ravera, V. Calderone, G. Parigi, G. N. Murshudov and C. Luchinat, Simultaneous use of solution NMR and X-ray data in REFMAC5 for joint refinement/detection of structural differences, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2014, 70, 958–967 CrossRef CAS PubMed.
- A. Carlon, E. Ravera, W. Andrałojć, G. Parigi, G. N. Murshudov and C. Luchinat, How to tackle protein structural data from solution and solid state: an integrated approach, Prog. Nucl. Magn. Reson. Spectrosc., 2016, 92–93, 54–70 CrossRef CAS PubMed.
- C. Luchinat, G. Parigi, E. Ravera and M. Rinaldelli, Solid state NMR crystallography through paramagnetic restraints, J. Am. Chem. Soc., 2012, 134, 5006–5009 CrossRef CAS PubMed.
- B. Bleaney, Nuclear magnetic resonance shifts in solution due to lanthanide ions, J. Magn. Reson., 1972, 8, 91–100 CAS.
- L. Benda, J. Mareš, E. Ravera, G. Parigi, C. Luchinat, M. Kaupp and J. Vaara, Pseudo-Contact NMR Shifts over the Paramagnetic Metalloprotein CoMMP-12 from First Principles, Angew. Chem., Int. Ed., 2016, 55, 14713–14717 CrossRef CAS PubMed.
- A. Mondal, M. W. Gaultois, A. J. Pell, M. Iannuzzi, C. P. Grey, J. Hutter and M. Kaupp, Large-Scale Computation of Nuclear Magnetic Resonance Shifts for Paramagnetic Solids Using CP2K, J. Chem. Theory Comput., 2018, 14, 377–394 CrossRef CAS PubMed.
- J. Mareš and J. Vaara, Ab initio paramagnetic NMR shifts via point-dipole approximation in a large magnetic-anisotropy Co(II) complex, Phys. Chem. Chem. Phys., 2018, 20, 22547–22555 RSC.
- J. Chyba, M. Novák, P. Munzarová, J. Novotný and R. Marek, Through-Space Paramagnetic NMR Effects in Host–Guest Complexes: Potential Ruthenium(III) Metallodrugs with Macrocyclic Carriers, Inorg. Chem., 2018, 57, 8735–8747 CrossRef CAS PubMed.
- P. Srb, M. Svoboda, L. Benda, M. Lepšík, J. Tarábek, V. Šícha, B. Grüner, K. Grantz-Šašková, J. Brynda, P. Řezáčová, J. Konvalinka and V. Veverka, Capturing a dynamically interacting inhibitor by paramagnetic NMR spectroscopy, Phys. Chem. Chem. Phys., 2019, 21, 5661–5673 RSC.
- A. V. Arbuznikov, J. Vaara and M. Kaupp, Relativistic spin–orbit effects on hyperfine coupling tensors by density-functional theory, J. Chem. Phys., 2004, 120, 2127–2139 CrossRef CAS PubMed.
- T. O. Pennanen and J. Vaara, Nuclear magnetic resonance chemical shift in an arbitrary electronic spin state, Phys. Rev. Lett., 2008, 100, 133002 CrossRef PubMed.
- B. Martin and J. Autschbach, Temperature dependence of contact and dipolar NMR chemical shifts in paramagnetic molecules, J. Chem. Phys., 2015, 142, 054108 CrossRef PubMed.
- A. J. Pell, G. Pintacuda and C. P. Grey, Paramagnetic NMR in solution and the solid state, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed.
- J. Vaara, S. A. Rouf and J. Mareš, Magnetic Couplings in the Chemical Shift of Paramagnetic NMR, J. Chem. Theory Comput., 2015, 11, 4840–4849 CrossRef CAS PubMed.
- B. Martin and J. Autschbach, Kohn–Sham calculations of NMR shifts for paramagnetic 3d metal complexes: protocols, delocalization error, and the curious amide proton shifts of a high-spin iron(II) macrocycle complex, Phys. Chem. Chem. Phys., 2016, 18, 21051–21068 RSC.
- S. A. Rouf, J. Mareš and J. Vaara, 1H Chemical Shifts in Paramagnetic Co(II) Pyrazolylborate Complexes: A First-Principles Study, J. Chem. Theory Comput., 2015, 11, 1683–1691 CrossRef CAS PubMed.
- J. Autschbach, Annual Reports in Computational Chemistry, Elsevier, 2015, vol. 11, pp. 3–36 Search PubMed.
- J. Autschbach, S. Patchkovskii and B. Pritchard, Calculation of Hyperfine Tensors and Paramagnetic NMR Shifts Using the Relativistic Zeroth-Order Regular Approximation and Density Functional Theory, J. Chem. Theory Comput., 2011, 7, 2175–2188 CrossRef CAS PubMed.
- P. Hrobárik, R. Reviakine, A. V. Arbuznikov, O. L. Malkina, V. G. Malkin, F. H. Köhler and M. Kaupp, Density functional calculations of NMR shielding tensors for paramagnetic systems with arbitrary spin multiplicity: validation on 3d metallocenes, J. Chem. Phys., 2007, 126, 024107 CrossRef PubMed.
- T. O. Pennanen and J. Vaara, Density-functional calculations of relativistic spin–orbit effects on nuclear magnetic shielding in paramagnetic molecules, J. Chem. Phys., 2005, 123, 174102 CrossRef PubMed.
- G. Parigi, L. Benda, E. Ravera, M. Romanelli and C. Luchinat, Pseudocontact shifts and paramagnetic susceptibility in semiempirical and quantum chemistry theories, J. Chem. Phys., 2019, 150, 144101 CrossRef PubMed.
- L. Lang, E. Ravera, G. Parigi, C. Luchinat and F. Neese, Solution of a Puzzle: High-Level Quantum-Chemical Treatment of Pseudocontact Chemical Shifts Confirms Classic Semiempirical Theory, J. Phys. Chem. Lett., 2020, 11, 8735–8744 CrossRef CAS PubMed.
- L. Lang, E. Ravera, G. Parigi, C. Luchinat and F. Neese, Theoretical analysis of the long-distance limit of NMR chemical shieldings, J. Chem. Phys., 2022, 156, 154115 CrossRef CAS PubMed.
- W. Van den Heuvel and A. Soncini, NMR chemical shift as analytical derivative of the Helmholtz free energy, J. Chem. Phys., 2013, 138, 054113 CrossRef PubMed.
- L. Cerofolini, J. M. Silva, E. Ravera, M. Romanelli, C. F. G. C. Geraldes, A. L. Macedo, M. Fragai, G. Parigi and C. Luchinat, How Do Nuclei Couple to the Magnetic Moment of a Paramagnetic Center? A New Theory at the Gauntlet of the Experiments, J. Phys. Chem. Lett., 2019, 3610–3614 CrossRef CAS PubMed.
- G. T. P. Charnock and I. Kuprov, A partial differential equation for pseudocontact shift, Phys. Chem. Chem. Phys., 2014, 16, 20184–20189 RSC.
- I. Bertini, C. Luchinat and G. Parigi, Magnetic susceptibility in paramagnetic NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 249–273 CrossRef CAS.
- G. Lipari and A. Szabo, Model-Free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity, J. Am. Chem. Soc., 1982, 104, 4546–4559 CrossRef CAS.
- M. Rinaldelli, A. Carlon, E. Ravera, G. Parigi and C. Luchinat, FANTEN: a new web-based interface for the analysis of magnetic anisotropy-induced NMR data, J. Biomol. NMR, 2015, 61, 21–34 CrossRef CAS PubMed.
- C. Schmitz, M. J. Stanton-Cook, X.-C. Su, G. Otting and T. Huber, Numbat: an interactive software tool for fitting Δχ-tensors to molecular coordinates using pseudocontact shifts, J. Biomol. NMR, 2008, 41, 179–189 CrossRef CAS PubMed.
- C. Nitsche and G. Otting, Pseudocontact shifts in biomolecular NMR using paramagnetic metal tags, Prog. Nucl. Magn. Reson. Spectrosc., 2017, 98–99, 20–49 CrossRef CAS PubMed.
- X.-C. Su and G. Otting, Paramagnetic labelling of proteins and oligonucleotides for NMR, J. Biomol. NMR, 2010, 46, 101–112 CrossRef CAS PubMed.
- D. Joss and D. Häussinger, Design and applications of lanthanide chelating tags for pseudocontact shift NMR spectroscopy with biomacromolecules, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115, 284–312 CrossRef CAS PubMed.
- P. H. Keizers, J. F. Desreux, M. Overhand and M. Ubbink, Increased paramagnetic effect of a lanthanide protein probe by two-point attachment, J. Am. Chem. Soc., 2007, 129, 9292–9293 CrossRef CAS PubMed.
- S. Mekkattu Tharayil, M. C. Mahawaththa, C.-T. Loh, I. Adekoya and G. Otting, Phosphoserine for the generation of lanthanide-binding sites on proteins for paramagnetic nuclear magnetic resonance spectroscopy, Magn. Reson., 2021, 2, 1–13 CrossRef.
- M. Fragai, C. Luchinat, G. Parigi and E. Ravera, Conformational freedom of metalloproteins revealed by paramagnetism-assisted NMR, Coord. Chem. Rev., 2013, 257, 2652–2667 CrossRef CAS.
- D. Parker, E. A. Suturina, I. Kuprov and N. F. Chilton, How the Ligand Field in Lanthanide Coordination Complexes Determines Magnetic Susceptibility Anisotropy, Paramagnetic NMR Shift, and Relaxation Behavior, Acc. Chem. Res., 2020, 53, 1520–1534 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Symmetry strategies for high performance lanthanide-based single-molecule magnets, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078–2085 RSC.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Magnetic Anisotropy in a Dysprosium/DOTA Single-Molecule Magnet: Beyond Simple Magneto-Structural Correlations, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, An electrostatic model for the determination of magnetic anisotropy in dysprosium complexes, Nat. Commun., 2013, 4, 2551 CrossRef PubMed.
- F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, A dysprosium single molecule magnet outperforming current pseudocontact shift agents, Chem. Sci., 2022, 13, 5860–5871 RSC.
- M. P. M. Marques, C. F. G. C. Geraldes, A. D. Sherry, A. E. Merbach, H. Powell, D. Pubanz, S. Aime and M. Botta, NMR conformational study of the lanthanide(III) complexes of DOTA in aqueous solution, J. Alloys Compd., 1995, 225, 303–307 CrossRef CAS.
- R. Vogel, T. Müntener and D. Häussinger, Intrinsic anisotropy parameters of a series of lanthanoid complexes deliver new insights into the structure-magnetism relationship, Chem, 2021, 7, 3144–3156 CAS.
- M. Sugita, N. Ishikawa, T. Ishikawa, S. Koshihara and Y. Kaizu, Static Magnetic-Field-Induced Phase Lag in the Magnetization Response of Tris(dipicolinato)lanthanides, Inorg. Chem., 2006, 45, 1299–1304 CrossRef CAS PubMed.
- B. Bleaney, C. M. Dobson, B. A. Levine, R. B. Martin, R. J. P. Williams and A. V. Xavier, Origin of lanthanide nuclear magnetic resonance shifts and their uses, J. Chem. Soc., Chem. Commun., 1972, 791b–793b RSC.
- P. H. J. Keizers, A. Saragliadis, Y. Hiruma, M. Overhand and M. Ubbink, Design, Synthesis, and Evaluation of a Lanthanide Chelating Protein Probe: CLaNP-5 Yields Predictable Paramagnetic Effects Independent of Environment, J. Am. Chem. Soc., 2008, 130, 14802–14812 CrossRef CAS PubMed.
- B. Ma, J.-L. Chen, C.-Y. Cui, F. Yang, Y.-J. Gong and X.-C. Su, Rigid, Highly Reactive and Stable DOTA-like Tags Containing a Thiol-Specific Phenylsulfonyl Pyridine Moiety for Protein Modification and NMR Analysis**, Chem. – Eur. J., 2021, 27, 16145–16152 CrossRef CAS PubMed.
- D. Joss, F. Winter and D. Häussinger, A novel, rationally designed lanthanoid chelating tag delivers large paramagnetic structural restraints for biomolecular NMR, Chem. Commun., 2020, 56, 12861–12864 RSC.
- I. Bertini, K. S. McGreevy and G. Parigi, NMR in systems biology, Wiley, 2012 Search PubMed.
- in Recent developments in biomolecular NMR, ed. M. Clore and J. Potts, RSC Publ, Cambridge, 2012 Search PubMed.
- V. Gaponenko, S. P. Sarma, A. S. Altieri, D. A. Horita, J. Li and R. A. Byrd, Improving the accuracy of NMR structures of large proteins using pseudocontact shifts as long/range restraints, J. Biomol. NMR, 2004, 28, 205–212 CrossRef CAS PubMed.
- J. Koehler and J. Meiler, Expanding the utility of NMR restraints with paramagnetic compounds: background and practical aspects, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 59, 360–389 CrossRef CAS PubMed.
- E. Ravera, G. Parigi and C. Luchinat, Perspectives on paramagnetic NMR from a life sciences infrastructure, J. Magn. Reson., 2017, 282, 154–169 CrossRef CAS PubMed.
- E. Ravera, G. Parigi and C. Luchinat, What are the methodological and theoretical prospects for paramagnetic NMR in structural biology? A glimpse into the crystal ball, J. Magn. Reson., 2019, 306, 173–179 CrossRef CAS PubMed.
- S. Balayssac, I. Bertini, C. Luchinat, G. Parigi and M. Piccioli, 13C direct detected NMR increases the detectability of residual dipolar couplings, J. Am. Chem. Soc., 2006, 128, 15042–15043 CrossRef CAS PubMed.
- P. Guentert, Automated NMR structure calculation with CYANA, Methods Mol. Biol., 2004, 278, 353–378 Search PubMed.
- L. Banci, I. Bertini, G. Cavallaro, A. Giachetti, C. Luchinat and G. Parigi, Paramagnetism-based restraints for Xplor-NIH, J. Biomol. NMR, 2004, 28, 249–261 CrossRef CAS PubMed.
- C. D. Schwieters, J. J. Kuszewski, N. Tjandra and G. Marius Clore, The Xplor-NIH NMR molecular structure determination package, J. Magn. Reson., 2003, 160, 65–73 CrossRef CAS PubMed.
- I. Bertini, A. Donaire, B. Jimnez, C. Luchinat, G. Parigi, M. Piccioli and L. Poggi, Paramagnetism-based Versus Classical Constraints: An Analysis of the Solution Structure of Ca Ln Calbindin D9k, J. Biomol. NMR, 2001, 21, 85–98 CrossRef CAS PubMed.
- B.-B. Pan, F. Yang, Y. Ye, Q. Wu, C. Li, T. Huber and X.-C. Su, 3D structure determination of a protein in living cells using paramagnetic NMR spectroscopy, Chem. Commun., 2016, 52, 10237–10240 RSC.
- H. Yagi, K. B. Pilla, A. Maleckis, B. Graham, T. Huber and G. Otting, Three-dimensional protein fold determination from backbone amide pseudocontact shifts generated by lanthanide tags at multiple sites, Struct. Lond. Engl. 1993, 2013, 21, 883–890 CAS.
- K. B. Pilla, J. K. Leman, G. Otting and T. Huber, Capturing Conformational States in Proteins Using Sparse Paramagnetic NMR Data, PLoS One, 2015, 10, e0127053 CrossRef PubMed.
- M. J. Berardi, W. M. Shih, S. C. Harrison and J. J. Chou, Mitochondrial uncoupling protein 2 structure determined by NMR molecular fragment searching, Nature, 2011, 476, 109–113 CrossRef CAS PubMed.
- I. Bertini, A. Bhaumik, G. De Paepe, R. G. Griffin, M. Lelli, J. R. Lewandowski and C. Luchinat, High-Resolution Solid-State NMR Structure of a 17.6 kDa Protein, J. Am. Chem. Soc., 2010, 132, 1032–1040 CrossRef CAS PubMed.
- A. Bhaumik, C. Luchinat, G. Parigi, E. Ravera and M. Rinaldelli, NMR crystallography on paramagnetic systems: solved and open issues, CrystEngComm, 2013, 15, 8639–8656 RSC.
- I. Bertini, P. Kursula, C. Luchinat, G. Parigi, J. Vahokoski, M. Willmans and J. Yuan, Accurate solution structures of proteins from X-ray data and minimal set of NMR data: calmodulin peptide complexes as examples, J. Am. Chem. Soc., 2009, 131, 5134–5144 CrossRef CAS PubMed.
- I. de Diego, J. Kuper, N. Bakalova, P. Kursula and M. Wilmanns, Molecular Basis of the Death-Associated Protein Kinase-Calcium/Calmodulin Regulator Complex, Sci. Signal., 2010, 3, ra6.1–ra6.9 Search PubMed.
- A. Carlon, E. Ravera, G. Parigi, G. N. Murshudov and C. Luchinat, Joint X-ray/NMR structure refinement of multidomain/multisubunit systems, J. Biomol. NMR, 2019, 73, 265–278 CrossRef CAS PubMed.
- W. Andrałojć, C. Luchinat, G. Parigi and E. Ravera, Exploring Regions of Conformational Space Occupied by Two-Domain Proteins, J. Phys. Chem. B, 2014, 118, 10576–10587 CrossRef PubMed.
- M. Zweckstetter and A. Bax, Evaluation of uncertainty in alignment tensors obtained from dipolar couplings, J. Biomol. NMR, 2002, 23, 127–137 CrossRef CAS PubMed.
- A. Schirò, A. Carlon, G. Parigi, G. Murshudov, V. Calderone, E. Ravera and C. Luchinat, On the complementarity of X-ray and NMR data, J. Struct. Biol.: X, 2020, 4, 100019 Search PubMed.
- G. N. Murshudov, P. Skubák, A. A. Lebedev, N. S. Pannu, R. A. Steiner, R. A. Nicholls, M. D. Winn, F. Long and A. A. Vagin, REFMAC5 for the refinement of macromolecular crystal structures, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2011, 67, 355–367 CrossRef CAS PubMed.
- A. Carlon, E. Ravera, J. Hennig, G. Parigi, M. Sattler and C. Luchinat, Improved Accuracy from Joint X-ray and NMR Refinement of a Protein–RNA Complex Structure, J. Am. Chem. Soc., 2016, 138, 1601–1610 CrossRef CAS PubMed.
- V. Gaponenko, A. S. Altieri, J. Li and R. A. Byrd, Breaking symmetry in the structure determination of (large) symmetric protein dimers, J. Biomol. NMR, 2002, 24, 143–148 CrossRef CAS PubMed.
- M. Longinetti, G. Parigi and L. Sgheri, Uniqueness and degeneracy in the localization of rigid domains in paramagnetic proteins, J. Phys. A: Math. Gen., 2002, 35, 8153–8169 CrossRef CAS.
- W. Andrałojć, K. Berlin, D. Fushman, C. Luchinat, G. Parigi, E. Ravera and L. Sgheri, Information content of long-range NMR data for the characterization of conformational heterogeneity, J. Biomol. NMR, 2015, 62, 353–371 CrossRef PubMed.
- N. J. Anthis, M. Doucleff and G. M. Clore, Transient, Sparsely Populated Compact States of Apo and Calcium-Loaded Calmodulin Probed by Paramagnetic Relaxation Enhancement: Interplay of Conformational Selection and Induced Fit, J. Am. Chem. Soc., 2011, 133, 18966–18974 CrossRef CAS PubMed.
- M. A. Hass and M. Ubbink, Structure determination of protein–protein complexes with long-range anisotropic paramagnetic NMR restraints, Curr. Opin. Struct. Biol., 2014, 24, 45–53 CrossRef CAS PubMed.
- E. Ravera, L. Salmon, M. Fragai, G. Parigi, H. Al-Hashimi and C. Luchinat, Insights into Domain–Domain Motions in Proteins and RNA from Solution NMR, Acc. Chem. Res., 2014, 47, 3118–3126 CrossRef CAS PubMed.
- G. M. Clore, Exploring sparsely populated states of macromolecules by diamagnetic and paramagnetic NMR relaxation, Protein Sci. Publ. Protein Soc., 2011, 20, 229–246 CrossRef CAS PubMed.
- L. Russo, M. Maestre-Martinez, S. Wolff, S. Becker and C. Griesinger, Interdomain Dynamics Explored by Paramagnetic NMR, J. Am. Chem. Soc., 2013, 135, 17111–17120 CrossRef CAS PubMed.
- C. Camilloni and M. Vendruscolo, Using Pseudocontact Shifts and Residual Dipolar Couplings as Exact NMR Restraints for the Determination of Protein Structural Ensembles, Biochemistry, 2015, 54, 7470–7476 CrossRef CAS PubMed.
- E. Ravera, L. Sgheri, G. Parigi and C. Luchinat, A critical assessment of methods to recover information from averaged data, Phys. Chem. Chem. Phys., 2016, 18, 5686–5701 RSC.
- M. Bonomi, G. T. Heller, C. Camilloni and M. Vendruscolo, Principles of protein structural ensemble determination, Curr. Opin. Struct. Biol., 2017, 42, 106–116 CrossRef CAS PubMed.
- J. Iwahara and G. M. Clore, Detecting transient intermediates in macromolecular binding by paramagnetic NMR, Nature, 2006, 440, 1227–1230 CrossRef CAS PubMed.
- L. Deshmukh, J. M. Louis, R. Ghirlando and G. M. Clore, Transient HIV-1 Gag–protease interactions revealed by paramagnetic NMR suggest origins of compensatory drug resistance mutations, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12456–12461 CrossRef CAS PubMed.
- W. Andrałojć, Y. Hiruma, W.-M. Liu, E. Ravera, M. Nojiri, G. Parigi, C. Luchinat and M. Ubbink, Identification of productive and futile encounters in an electron transfer protein complex, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E1840–E1847 CrossRef PubMed.
- J. Schilder, F. Löhr, H. Schwalbe and M. Ubbink, The cytochrome c peroxidase and cytochrome c encounter complex: the other side of the story, FEBS Lett., 2014, 588, 1873–1878 CrossRef CAS PubMed.
- S. J. de Vries, M. van Dijk and A. M. Bonvin, The HADDOCK web server for data-driven biomolecular docking, Nat. Protoc., 2010, 5, 883–897 CrossRef CAS PubMed.
- E. Ravera, L. Gigli, B. Czarniecki, L. Lang, R. Kümmerle, G. Parigi, M. Piccioli, F. Neese and C. Luchinat, A Quantum Chemistry View on Two Archetypical Paramagnetic Pentacoordinate Nickel(II) Complexes Offers a Fresh Look on Their NMR Spectra, Inorg. Chem., 2021, 60, 2068–2075 CrossRef PubMed.
- F. Neese, The ORCA program system: The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, The complete active space SCF (CASSCF) method in a Newton–Raphson formulation with application to the HNO molecule, J. Chem. Phys., 1981, 74, 2384–2396 CrossRef.
- C. Angeli and R. Cimiraglia, Multireference perturbation configuration interaction V. Third-order energy contributions in the Møller–Plesset and Epstein–Nesbet partitions, Theor. Chem. Acc., 2002, 107, 313–317 Search PubMed.
- G. N. La Mar and L. Sacconi, Proton magnetic resonance studies of high-spin nickel(II) complexes with pentadentate Schiff bases, J. Am. Chem. Soc., 1967, 89, 2282 CrossRef CAS.
- I. Bertini and C. Luchinat, Cobalt(II) as a probe of the structure and function of carbonic anhydrase, Acc. Chem. Res., 1983, 16, 272–279 CrossRef CAS.
- L. Cerofolini, T. Staderini, S. Giuntini, E. Ravera, M. Fragai, G. Parigi, R. Pierattelli and C. Luchinat, Long-range paramagnetic NMR data can provide a closer look on metal coordination in metalloproteins, J. Biol. Inorg. Chem., 2018, 23, 71–80 CrossRef CAS PubMed.
- B. J. Walder, A. M. Patterson, J. H. Baltisberger and P. J. Grandinetti, Hydrogen motional disorder in crystalline iron group chloride dihydrates, J. Chem. Phys., 2018, 149, 084503 CrossRef PubMed.
- I. V. Korendovych and W. F. DeGrado, Catalytic efficiency of designed catalytic proteins, Curr. Opin. Struct. Biol., 2014, 27, 113–121 CrossRef CAS PubMed.
- S. Signorella, C. Palopoli and G. Ledesma, Rationally designed mimics of antioxidant manganoenzymes: role of structural features in the quest for catalysts with catalase and superoxide dismutase activity, Coord. Chem. Rev., 2018, 365, 75–102 CrossRef CAS.
- S. Balayssac, I. Bertini, A. Bhaumik, M. Lelli and C. Luchinat, Paramagnetic shifts in solid-state NMR of proteins to elicit strucutral information, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17284–17289 CrossRef CAS PubMed.
- E. A. Suturina, J. Nehrkorn, J. M. Zadrozny, J. Liu, M. Atanasov, T. Weyhermüller, D. Maganas, S. Hill, A. Schnegg, E. Bill, J. R. Long and F. Neese, Magneto-Structural Correlations in Pseudotetrahedral Forms of the [Co(SPh)4]2− Complex Probed by Magnetometry, MCD Spectroscopy, Advanced EPR Techniques, and ab Initio Electronic Structure Calculations, Inorg. Chem., 2017, 56, 3102–3118 CrossRef CAS PubMed.
- P. Kumar, D. J. SantaLucia, K. Kaniewska-Laskowska, S. V. Lindeman, A. Ozarowski, J. Krzystek, M. Ozerov, J. Telser, J. F. Berry and A. T. Fiedler, Probing the Magnetic Anisotropy of Co(II) Complexes Featuring Redox-Active Ligands, Inorg. Chem., 2020, 59, 16178–16193 CrossRef CAS PubMed.
- E. Ravera, L. Gigli, E. A. Suturina, V. Calderone, M. Fragai, G. Parigi and C. Luchinat, A High-Resolution View of the Coordination Environment in a Paramagnetic Metalloprotein from its Magnetic Properties, Angew. Chem., Int. Ed., 2021, 60, 14960–14966 CrossRef CAS PubMed.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets, Coord. Chem. Rev., 2015, 289–290, 177–214 CrossRef CAS.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, Molcas 8: new capabilities for multiconfigurational quantum chemical calculations across the periodic table, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- P. P. Hallmen, H.-J. Werner, D. Kats, S. Lenz, G. Rauhut, H. Stoll and J. van Slageren, Toward fast and accurate ab initio calculation of magnetic exchange in polynuclear lanthanide complexes, Phys. Chem. Chem. Phys., 2019, 21, 9769–9778 RSC.
- A. Bertarello, L. Benda, K. J. Sanders, A. J. Pell, M. J. Knight, V. Pelmenschikov, L. Gonnelli, I. C. Felli, M. Kaupp, L. Emsley, R. Pierattelli and G. Pintacuda, Picometer Resolution Structure of the Coordination Sphere in the Metal-Binding Site in a Metalloprotein by NMR, J. Am. Chem. Soc., 2020, 142, 16757–16765 CrossRef CAS PubMed.
- D. M. Selegato, C. Bracco, C. Giannelli, G. Parigi, C. Luchinat, L. Sgheri and E. Ravera, Comparison of Different Reweighting Approaches for the Calculation of Conformational Variability of Macromolecules from Molecular Simulations, ChemPhysChem, 2021, 22, 127–138 CrossRef PubMed.
- G. M. Clore and C. D. Schwieters, How Much Backbone Motion in Ubiquitin Is Required To Account for Dipolar Coupling Data Measured in Multiple Alignment Media as Assessed by Independent Cross-Validation?, J. Am. Chem. Soc., 2004, 126, 2923–2938 CrossRef CAS PubMed.
- I. Bertini, A. Giachetti, C. Luchinat, G. Parigi, M. V. Petoukhov, R. Pierattelli, E. Ravera and D. I. Svergun, Conformational space of flexible biological macromolecules from average data, J. Am. Chem. Soc., 2010, 132, 13553–13558 CrossRef CAS PubMed.
- G. Masrati, M. Landau, N. Ben-Tal, A. Lupas, M. Kosloff and J. Kosinski, Integrative Structural Biology in the Era of Accurate Structure Prediction, J. Mol. Biol., 2021, 433, 167127 CrossRef CAS PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Highly accurate protein structure prediction with AlphaFold, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- G. Parigi, E. Ravera and C. Luchinat, Paramagnetic effects in NMR for protein structures and ensembles: studies of metalloproteins, Curr. Opin. Struct. Biol., 2022, 74, 102386 CrossRef CAS PubMed.
- S. Asami, W. Kallies, J. C. Günther, M. Stavropoulou, S. J. Glaser and M. Sattler, Ultrashort Broadband Cooperative Pulses for Multidimensional Biomolecular NMR Experiments, Angew. Chem., Int. Ed., 2018, 57, 14498–14502 CrossRef CAS PubMed.
- E. Ravera, Phase distortion-free paramagnetic NMR spectra, J. Magn. Reson. Open, 2021, 8–9, 100022 CrossRef.
- G. Kervern, S. Steuernagel, F. Engelke, G. Pintacuda and L. Emsley, Absence of Curie relaxation in paramagnetic solids yields long 1H coherence lifetimes, J. Am. Chem. Soc., 2007, 129, 14118–14119 CrossRef CAS PubMed.
- L. Gigli, S. Di Grande, E. Ravera, G. Parigi and C. Luchinat, NMR for Single Ion Magnets, Magnetochemistry, 2021, 7, 96 CrossRef CAS.
- A. Nayeem and J. P. Yesinowski, Calculation of magic-angle spinning nuclear magnetic resonance spectra of paramagnetic solids, J. Chem. Phys., 1988, 89, 4600–4608 CrossRef CAS.
- G. Kervern, A. D’Aléo, L. Toupet, O. Maury, L. Emsley and G. Pintacuda, Crystal-Structure Determination of Powdered Paramagnetic Lanthanide Complexes by Proton NMR Spectroscopy, Angew. Chem., Int. Ed., 2009, 48, 3082–3086 CrossRef CAS PubMed.
- T. Le Marchand, T. Schubeis, M. Bonaccorsi, P. Paluch, D. Lalli, A. J. Pell, L. B. Andreas, K. Jaudzems, J. Stanek and G. Pintacuda, 1H-Detected Biomolecular NMR under Fast Magic-Angle Spinning, Chem. Rev., 2022, 122, 9943–10018 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |