Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting Coulomb explosion fragment angular distributions using molecular ground-state vibrational motion
Louis
Minion
 a,
Jason W. L.
Lee
a,
Jason W. L.
Lee
 b and
Michael
Burt
b and
Michael
Burt
 *a
*a
aDepartment of Chemistry, University of Oxford, 12 Mansfield Road, Oxford OX1 3TA, UK. E-mail: michael.burt@chem.ox.ac.uk
bDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany
First published on 26th April 2022
Abstract
Laser-induced Coulomb explosions can be used to identify gas-phase molecular structures through correlations between fragment ion trajectories. This report presents a model for predicting these outcomes, which first establishes the neutral equilibrium geometry of a target molecule using electronic structure calculations, and then samples a probability distribution of potential ground-state configurations by allowing for zero-point vibrational motion. Candidate structures are assumed to explode instantaneously into charged fragments, and the simulated ion trajectories are correlated using recoil-frame covariance analysis. The effects of detection efficiency and fluctuating experimental conditions are also considered. The results were found to match experimental data, indicating that Coulomb explosion fragment angular distributions produced from highly-charged ions depend largely on the internal motion of the target molecule.
1 Introduction
Molecules exposed to intense femtosecond laser pulses can lose multiple electrons, producing unbound states that explode with fragment trajectories that are largely directed by Coulombic interactions.1 With increasing charge, the parent ion explosion occurs more abruptly and the fragment momenta begin to resemble purely electrostatic repulsion.2,3 The molecular structure at the time of its Coulomb explosion can therefore be established from the relative product trajectories. This method has been used to distinguish structural and chiral isomers of small gas-phase ions, and has been combined with femtosecond pump-probe spectroscopy to explore structural and reaction dynamics.4–9 Due to Coulomb's law, the fragment kinetic energies are acutely sensitive to changes in molecular geometry, which can allow excited states to be distinguished from ground state molecules or other competing reactions, so long as the relevant structures are distinct.10Despite the potential of Coulomb explosion imaging, its generality as a structural determination tool has limits. One challenge is accurately correlating the fragment momenta. For small molecules, this can be done directly through coincidence counting.4–6,8 However, this restricts the upper event rate limit to about one Coulomb explosion per laser pulse to avoid false correlations, which considerably lengthens the time required to sample the full probability distribution of reaction outcomes. For experiments that are limited by repetition rates, covariance analysis becomes a more practical alternative. This method relies on determining statistical dependencies between fragments from a large data set,11–13 and can handle event rates that are ten to a thousand times higher than coincidence conditions.14,15 For this reason, covariance analysis is often applied at intense light sources, such as free electron lasers, that ionize large numbers of molecules within a single pulse.
A second complication arises when interpreting relative fragment trajectories. Coulomb explosions can result in the creation of significant amounts of identical cations. As the ensemble of molecules being studied contains different vibrational phases, successive laser pulses are not matched with a unique geometry and the fragments are emitted with angular distributions that can overlap. This angular blurring is apparent even in reasonably rigid structures, such as aromatic molecules, and therefore limits the number of fragment trajectories that can be experimentally distinguished for a given ion.9 In principle, the rotations of molecular fragments during a Coulomb explosion could also affect these momenta. However, rotational periods are generally long (>10−13 s) relative to the laser-induced fragmentation (∼10−14 s) and so the axial-recoil approximation is usually assumed to hold.16 Prompt Coulomb explosions can therefore be applied to predict structural information even when segments of the original bonding framework survive.17,18
Given the uncertainty in mapping ionic fragment momenta to neutral ground-state structures, a variety of computational approaches have been developed to simulate Coulomb explosion dynamics. For the simplest molecules, such as H2+, the product momenta can be determined by solving the time-dependent Schrödinger equation in the presence of a strong laser field and projecting the result onto a Coulombic potential energy surface.19 Good agreement with the Schrödinger equation can also be obtained in multielectron systems using the strong-field approximation, which considers the effect of the laser field on a photodetached electron.20,21 Field-free methods have also proven useful. For example, one-dimensional ab initio potential energy curves calculated for CH3I have broadly reproduced Coulomb explosion data,22 as have molecular dynamics simulations for aromatic molecules, including C60.23,24
This report presents a field-free ab initio framework for predicting Coulomb explosion fragment trajectories from neutral ground-state structures, and applies it to assess the efficacy of Coulomb explosion imaging as a structural analysis method, subject to the constraints outlined above. The model assumes an instantaneous Coulomb explosion of a charged parent ion, whose initial geometry and reaction channel are selected from a probability distribution of neutral ground-state structures in different zero-point vibrational phases. Experimental considerations including event rate, detection efficiency, and noise are also accounted for, and the output is interpreted using covariance analysis. The following sections detail this model, verify it against experiments on 3,5-difluoroiodobenzene, and discuss the advantages and limitations of Coulomb explosion fragment covariance analysis when applied to complex molecules.
2 Methods
2.1 Coulomb explosion modeling
Coulomb explosions were modeled by assuming instantaneous fragmentation and electrostatic repulsion. The validity of this approximation will be greatest when using ultrashort laser pulses to produce highly-charged parent ions, due to the increasing likelihood of a prompt explosion. It also improves when considering heavier nuclei, as they move relatively slowly along their laser-distorted potential energy surfaces with trajectories that are harder to perturb.19 For a given parent molecule, the equilibrium geometry at the time of the explosion was specified to be the lowest energy neutral isomer determined using the B3LYP density functional method with 6-311G or SDD basis sets, as implemented by Gaussian 09.25 The product ions were then selected from a probability distribution of possible reaction outcomes and modeled as point charges with initial positions defined by the equilibrium structure and the fragment centers-of-mass. In the examples reported here, a single charge was assigned to each atom to ensure purely Coulombic repulsion. However, it is worth noting that this step can be improved using experimental results, for example by comparing relative signal intensities in a mass spectrum, as well as their correlations, to identify the most likely fragmentation channels. The resulting trajectories were calculated using Newton's second law with Coulombic forces between particles, such that, for n fragments, the forces![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ij arising from pairwise interactions between ions i and j with masses m, charges q, and internuclear distances
ij arising from pairwise interactions between ions i and j with masses m, charges q, and internuclear distances ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij were given by the following expression, where k is the Coulomb constant:
ij were given by the following expression, where k is the Coulomb constant: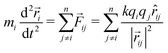 | (1) |
For most systems, the above equation is a many-body problem. A fourth-order explicit Runge–Kutta algorithm from the SciPy package was therefore used to determine numerical solutions, with the ion masses and positions from the electronic structure calculation as initial conditions.26 The dynamic fragment trajectories during the explosion were evaluated for up to 10 ns, with time steps determined by the equation solver, at which point the products were far enough apart for the Coulombic interactions to be negligible.
This method produces Coulomb explosion fragments from an oriented and static structure. However, in typical experiments molecules will be isotropic or aligned relative to a laser polarization axis, and will exist in one of many configurations due to vibrations. To account for these factors, the fragment positions were collectively rotated before each Coulomb explosion, either using a random angle or a confined distribution to simulate alignment. The harmonic vibrational frequencies ω and reduced masses μ were also calculated for the equilibrium structures and used to determine the likely motion imparted to individual atoms from each normal mode. Unperturbed molecules were assumed to be in their ground vibrational states, and the probability of finding the nuclei in a specific arrangement was determined using the harmonic oscillator wavefunctions ψ0(z) for each mode.
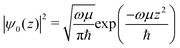 | (2) |
The above equation is a normal distribution where z represents the displacement from equilibrium for a particular mode. Its standard deviation is 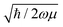 , where ħ is the reduced Planck constant. In this way, the likelihood of a vibration extending beyond the classical turning points is equal to the 16% tunneling probability of a ground-state harmonic oscillator.
, where ħ is the reduced Planck constant. In this way, the likelihood of a vibration extending beyond the classical turning points is equal to the 16% tunneling probability of a ground-state harmonic oscillator.
The z parameter is sampled for each mode and used to determine new atomic positions for every explosion. Repeating this procedure for multiple laser shots produces a three-dimensional distribution of fragments whose densities at particular spatial coordinates are weighted by the ground-state vibrational wavefunctions of the equilibrium structure. For isotropic molecules, the ions appear as nested spherical shells with radii that depend on their kinetic energies. To imitate particle detection in a velocity-map imaging mass spectrometer, the fragments were additionally simulated to accelerate along a defined axis using a uniform electric field, and projected onto a plane representing a position-sensitive detector. Each ion is therefore assigned image coordinates as well as a time-of-flight that depends on its mass-to-charge ratio. This produces two-dimensional ion images for each fragment that are used for covariance analysis.
2.2 Experimental variance
The covariances between co-fragments should be independent of experimental noise. However, fluctuating parameters often introduce unimportant correlations that overshadow these. Variations in a Coulomb explosion experiment, such as in the gas density within the laser interaction volume, or the laser pulse energy and pointing stability, can significantly change the number of ions generated per experimental cycle. This makes all ions appear correlated, as a rise in intensity means more of them are being generated together and vice versa.To simulate this noise, the fluctuating experimental conditions are considered using the method of Mikosch and Patchkovskii.14 The experimental event rate v is sampled from a normal distribution centered on the mean value. Choosing a large standard deviation σ leads to greater variability in the shot-to-shot event rate, whereas a value of zero yields a completely stable experiment.
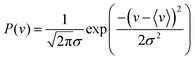 | (3) |
The number of molecules m fragmented by a laser pulse is then chosen from a Poisson distribution using the sampled event rate.
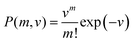 | (4) |
The fragments generated from each exploding molecule are chosen using a probability distribution that reflects the possible outcomes. As discussed above, this can be as simple as assigning a single charge to each atom and assuming a purely Coulombic repulsion, or be informed by experimental results. Each ion is also given an imperfect detection efficiency to better approximate typical experiments. The result of these adaptations is that the simulated ion images are produced with a level of noise that can be tuned by the σ parameter in eqn (3).
2.3 Recoil-frame covariance analysis
Correlations between the simulated Coulomb explosion images are determined using recoil-frame covariance analysis.27–29 This places the expected angular distribution of one fragment in the reference frame of a recoiling co-fragment, producing ion images that can be intuitively compared to the geometry of a parent molecule at the time of its explosion. To our knowledge, this method has only been qualitatively described, so a detailed description is provided here.Covariance measures how relative changes in random variables correlate. For a data set comprising m random variables, the variances and covariances can be quickly assessed by constructing an m× m variance–covariance matrix S:
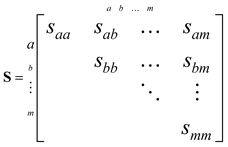 | (5) |
The main diagonal of this matrix contains the variances of each variable, and the remaining symmetric elements are the covariances.30 For two particular variables a and b that are randomly distributed, these can be defined as:
| var(a) = saa = 〈(a − 〈a〉)2〉 = 〈a2〉 − 〈a〉2 | (6) |
| cov(a, b) = sab = 〈(a − 〈a〉)(b − 〈b〉)〉 = 〈ab〉 − 〈a〉〈b〉 | (7) |
In the context of Coulomb explosion imaging with time-stamping sensors, the measured variables include the times-of-arrival (t) and spatial coordinates (x, y) of each detected fragment. Correlations between ion time-of-flight signals can be determined using the method described by Frasinski, where two identical one-dimensional time-of-flight spectra are used to produce a variance–covariance matrix11St, as shown below. The off-diagonal elements of these covariance maps reveal which ions are produced from the same reaction channels, and approximate the results of coincidence counting experiments.
 | (8) |
In a similar manner, variance–covariance matrices can be constructed from ion image coordinates.31–33 This is useful for determining structural information from velocity-mapped images of Coulomb explosion fragments, as the resulting covariance maps contain the relative fragment recoil directions. In essence, this application extends time-of-flight covariance analysis to higher dimensions. The spatial coordinate covariances between two ion images create a four-dimensional array that must be reduced for further interpretation. For example, Stapelfeldt and coworkers demonstrated an angular covariance mapping method that transforms the spatial x and y coordinates of detected ions into a range of polar angles θ, which are then used to create a two-dimensional map,31 as in eqn (8). Subsequent work by Brouard and Stapelfeldt instead used both polar coordinates (r, θ) to produce recoil-frame covariance maps that preserve the fragment velocity information, and hence retain the outward appearance of ion images, while rotating the data into a common reference frame.27,28
As an example of recoil-frame covariance analysis, consider the fragmentation of a heteronuclear diatomic molecule into two ions A and B. With an i × j pixel time-stamping detector, the ion imaging data will be recorded as xiyjtA or xiyjtB coordinates. The complete ion imaging variance–covariance matrix Sxy for these observables will be 16-dimensional (using x, y, tA and tB), and can be shaped into four block matrices that represent the pixel-to-pixel variances and covariances of the two ion images.
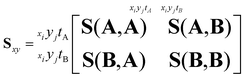 | (9) |
The upper right quadrant contains the covariances of A with B, and the lower left quadrant is its transpose. Only one is needed to determine the relative behaviour of the two ions, which simplifies the above matrix to:
 | (10) |
This is an ij × ij matrix where each row contains the covariances of a unique A pixel with every B pixel. As the data it contains is effectively four-dimensional, with the A and B images each contributing two degrees of freedom, it is convenient to reduce the output to a two-dimensional image. In this case, B is chosen as the reference ion to remain consistent with previous work.34 Integrating each A pixel over all B pixels produces a single column where each element is the total covariance of an A pixel due to the collective B pixels. This is shown below, where the i and j coordinates of the B ions have been relabeled as v and w for clarity in the following equations.
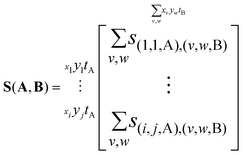 | (11) |
Reshaping this column into an i × j array yields the covariance map Cov(A,B) of A with respect to B.† As S(A,B) and S(B,A) are transposes, the same data can also be reshaped to produce the covariance map Cov(B,A).
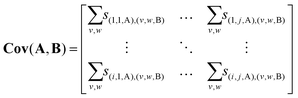 | (12) |
Using eqn (7), the elements of this result can be written as two terms that represent n observations. The first is the expected coincidence count of a particular A pixel with every B pixel:
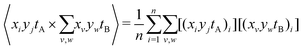 | (13) |
The second is the expected value of an A pixel multiplied with the expected summed intensity due to every B pixel:
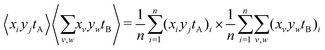 | (14) |
With these definitions in mind, Cov(A,B) is typically written as:
| Cov(A,B) = 〈AB〉 − 〈A〉〈B〉 | (15) |
However, eqn (13) and (14) demonstrate that this is a convenient abuse of notation, as A and B are defined differently despite being intended to represent two ion images. The 〈AB〉 and 〈A〉〈B〉 terms must also be weighted to ensure they are comparable. For example, it is useful to consider Cov(A,B) as the expected distribution of A ions per shot with respect to a single reference ion. Since the number of observed events n is not necessarily equal to the number of laser shots used to measure them, the 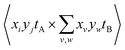 terms should be normalized to the number of reference ions on a shot-by-shot basis, to avoid overcounting the number of A ions. However, as the
terms should be normalized to the number of reference ions on a shot-by-shot basis, to avoid overcounting the number of A ions. However, as the 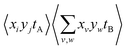 terms are proportional to the average amounts of A and B per shot, they must also be divided by
terms are proportional to the average amounts of A and B per shot, they must also be divided by 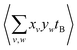 to ensure that the magnitude of Cov(A,B) represents one reference ion.
to ensure that the magnitude of Cov(A,B) represents one reference ion.
Fig. 1 illustrates 〈AB〉, 〈A〉〈B〉, and Cov(A,B) for the fragmentation of a freely rotating heteronuclear diatomic molecule. These were created by simulating the isotropic Coulomb explosion of IBr into I+ and Br+ over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots and projecting the output as ion images (A+ and B+ in Fig. 1a, respectively). The left-hand column of Fig. 1b was produced with a detection efficiency of 0.6, and using eqn (4) to define a Poissonian event rate with v = 10. The right-hand column was made the same way, but with perfect detection efficiency and an invariant rate of v = 1.
000 laser shots and projecting the output as ion images (A+ and B+ in Fig. 1a, respectively). The left-hand column of Fig. 1b was produced with a detection efficiency of 0.6, and using eqn (4) to define a Poissonian event rate with v = 10. The right-hand column was made the same way, but with perfect detection efficiency and an invariant rate of v = 1.
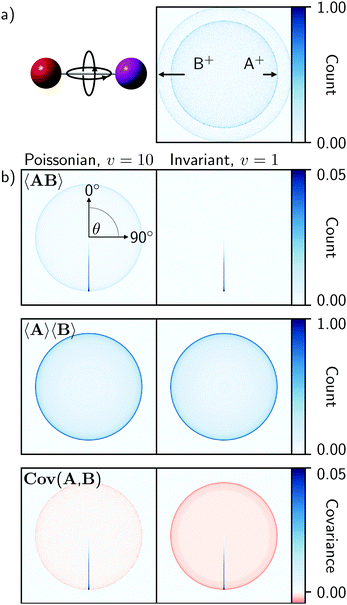 | ||
Fig. 1 (a) Simulated Coulomb explosion images of fragments A+ and B+ from a freely rotating heteronuclear diatomic molecule (IBr, with I![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) A and B A and B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Br), composed using 50 Br), composed using 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots with a detection efficiency of 0.6. (b) Covariance analysis of this data, created with either a Poissonian event rate of v = 10 (eqn (3) or an invariant rate of v = 1, illustrates the expected coincidence images 〈AB〉, averaged images 〈A〉〈B〉, and recoil-frame covariance images Cov(A,B) when B+ is chosen as the reference ion. The band of positive covariances extending from the center of the covariance images at 180° represents the spherically symmetric two-body fragmentation. Each image is normalized to its maximum value. 000 laser shots with a detection efficiency of 0.6. (b) Covariance analysis of this data, created with either a Poissonian event rate of v = 10 (eqn (3) or an invariant rate of v = 1, illustrates the expected coincidence images 〈AB〉, averaged images 〈A〉〈B〉, and recoil-frame covariance images Cov(A,B) when B+ is chosen as the reference ion. The band of positive covariances extending from the center of the covariance images at 180° represents the spherically symmetric two-body fragmentation. Each image is normalized to its maximum value. | ||
As the data is isotropic, the xiyjtA and xiyjtB events were transformed into polar coordinates and rotated into a common recoil frame with B+ as the reference ion. For the 〈AB〉 images, the A+ ions were rotated relative to each coincident B+ ion shot-by-shot, while the 〈A〉〈B〉 representations were rotated after the summation in eqn (14), as the coincidence information is necessarily lost during this process. In the 〈AB〉 coincidence images, the spherically symmetric two-body fragmentation of the molecule produces an intense line that extends from the image center at 180° from the reference ion, and which reaches a maximum at the radius that corresponds to the kinetic energy of the A+ fragment. The Poissonian data additionally exhibits an isotropic feature at the same radius that decreases in intensity towards the center of the image. This arises from false coincidences caused by the higher event rate. By contrast, the 〈A〉〈B〉 images are qualitatively identical for both data sets. These represent the expected distributions of all A+ ions relative to B+ as the recoil direction, and therefore appear as two-dimensional projections of the spherically symmetric data.
The recoil-frame covariance maps are simply the difference of 〈AB〉 with respect to 〈A〉〈B〉 and therefore exhibit positive and negative values in regions where true and false coincidences are respectively expected. Positive covariances represent the distribution of fragment ions that are correlated with respect to the reference ion. The interpretation of negative covariances is slightly more complicated, and is often the source of ambiguity in photofragmentation experiments.12,35 Under gas-phase conditions, parent ion fragmentation pathways are statistically independent, meaning that fragment covariances should be positive within the same channel but zero otherwise, even for competing channels. With this in mind, negative covariances would not normally be expected in time-of-flight or angular covariance maps, unless fluctuations in an experimental parameter such as laser pulse energy influenced the observed outcomes. However, recoil-frame covariance analysis necessarily introduces negative covariances, as the average distribution of A+ with respect to B+ is subtracted from the recoil-frame coincidences of A+ and B+.
3 Discussion
To verify the model described in Sections IIA and IIB, it was used to simulate and compare the Coulomb explosion of 3,5-difluoroiodobenzene with previously reported data.9 This molecule was chosen for its symmetry, which results in clear structural features following covariance analysis, and because its size requires a relatively large number of vibrational modes (30) to be considered. When subjected to intense 35 fs laser pulses at 800 nm (I0 = 3.0 × 1014 W cm−2), the parent molecule primarily fragments into atomic ions. For this reason, the molecule was assumed to undergo purely Coulombic fragmentation and a single charge was assigned to each atom in the simulation. This may overestimate the average parent ion charge state, but will not lead to any significant deviations between the experimental and simulated fragment angular distributions as the former reaction is expected to be Coulombic.36 In the experiment, the molecules were also adiabatically aligned along their C–I bond axes using 10 ns laser pulses at 1064 nm (I0 = 5.0 × 1011 W cm−2), which restricted their orientations to a narrow angular distribution with 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 = 0.83. The simulated Coulomb explosion trajectories were therefore confined in the same way.
θ〉 = 0.83. The simulated Coulomb explosion trajectories were therefore confined in the same way.
The experimental and simulated covariances between the aromatic substituent fragments (H+, F+, and I+) are shown in the top and bottom rows of Fig. 2. In each case, the positive covariances, which represent the relative fragment recoil angles, confirm the structural isomer of the parent molecule. The negative covariances arise due to the recoil-frame rotation of the data, as described above. The qualitative agreement of the fragment angular distributions and the areas of positive and negative covariance are excellent. Fig. 3 demonstrates that the angular distributions are essentially identical for the two Cov(F+,I+) images. The simulated recoil angles are 121° ± 10°, compared with 121° ± 7° experimentally. Similar agreement is seen for the other covariance images, as shown in Table 1. In this example, the simulated data included 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots, however it is worth noting that the discrete Fréchet distance between this data and the experimental curve in Fig. 3 varied by less than 5% when the simulation was modified to include 1000 to 50
000 laser shots, however it is worth noting that the discrete Fréchet distance between this data and the experimental curve in Fig. 3 varied by less than 5% when the simulation was modified to include 1000 to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots, which indicates that this model efficiently converged on the experimental results.
000 laser shots, which indicates that this model efficiently converged on the experimental results.
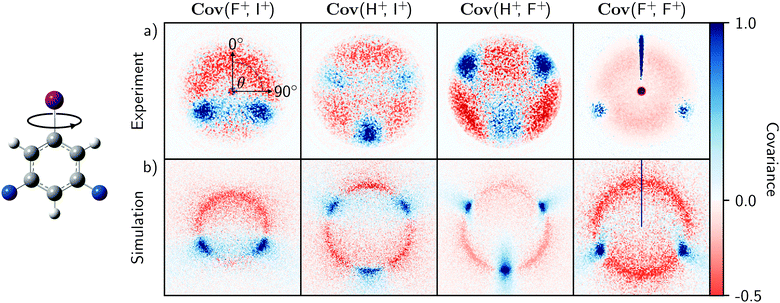 | ||
| Fig. 2 Recoil-frame covariance images Cov(A,B) of fragment pairs produced from the experimental (a) and simulated (b) Coulomb explosions of 3,5-difluoroiodobenzene molecules aligned along their carbon–iodine bond axes. Each displays the velocity distribution of a fragment ion A relative to a reference ion B recoiling at 0°. The experimental images were created from the data used in ref. 9. The predicted images were simulated from 5000 laser shots using the model described in the text with an event rate of 10 and perfect detection efficiency. | ||
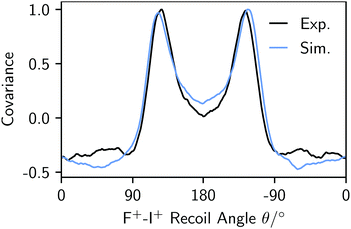 | ||
| Fig. 3 Experimental (black) and simulated (blue) F+–I+ angular distributions from the analogous Cov(F+,I+) images in Fig. 2. | ||
The agreement between experiment and theory is striking, and justifies the initial assumption that the parent ion undergoes Coulombic fragmentation. It also demonstrates that Coulomb explosion fragment angular distributions can largely be predicted by the equilibrium vibrational motion of the parent molecule, so long as the explosion is relatively brisk. In reality, the ionization and dissociation mechanisms taking place during a Coulomb explosion are complex and depend on the strength of the applied laser field. They initially take place on laser-distorted potential energy surfaces, with ionization rates that can depend on the orientation of the molecule with respect to the laser polarization axis, as well as the tunneling times of the bound electrons.38–40 This model ignores these factors, meaning that bond softening and structural rearrangements of the parent molecule are not accounted for.41,42 The simulated kinetic energies, which also depend on accurate knowledge of the parent ion charge state, were therefore scaled to the experimental results in Fig. 2 for clarity.
For 3,5-difluoroiodobenzene, the match between experimental and simulated recoil angles suggests that contributions to nuclear motion from accessible neutral or charged excited states are similar to those of the equilibrium geometry. This will not generally be true if the parent structure significantly changes during the explosion. For example, Légaré et al. established that for the Coulomb explosion of D2O, the time spent on a linear D2O+ potential surface during the explosion resulted in a wider bond angle being observed than would be expected from purely ground state motion through successive charge states.40 Allowing less time for nuclear motion, for instance by using shorter laser pulses or higher initial charge states to promote rapid fragmentation, should therefore improve the applicability of this model.2,3 Fragment recoil angles measured from the explosions of large molecules are also not necessarily representative of the corresponding bond angles, as electrostatic repulsion from other fragments can significantly impact the resulting trajectories (i.e. for a generic internal angle ∡ABC, where each constituent is a singly-charged cation, the angle will appear wider than expected due to repulsion between A+ and C+). Correcting for these contributions can in principle allow the bond angles at the time of the explosion to be measured, as well as their variation due to internal motion.
The effect of the experimental variability parameter σ, which characterizes fluctuating event rates, was also assessed using the 3,5-difluoroiodobenzene data. To understand its effect, it is first worth considering how noise influences observations of competing outcomes from a Poisson distribution of fragmentation events.14 When measuring covariance between two ions A+ and B+, there are three measurable outcomes of interest with discrete probabilities PAB: both ions can be detected in coincidence (P11) or individually in the absence of the other (P01 or P10). The relative probabilities per laser shot will depend on the detection efficiencies ξ of each ion as well as the fraction of events that produce them. For a generic mass spectrum containing A+, B+, and other fragments, the normalized fractions of events that produce each ion f(M) can be described by the following, where M is the set of reaction outcomes with probabilities PM that produce a particular ion:
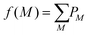 | (16) |
Ion imaging further allows each f(M) to be subdivided into normalized contributions fM(T) that correspond to the kinetic energy ranges of particles detected from events involving the ion of interest:
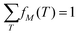 | (17) |
| P11 = f(A)fA(B)ξAξB | (18) |
| P10 = f(A)ξA − f(A)fA(B)ξAξB | (19) |
| P01 = f(B)ξB − f(A)fA(B)ξAξB | (20) |
Using the theory derived by Mikosch and Patchkovskii,14 the covariance can be expressed as moments of the unconditional probability distribution governing the above outcomes:
| cov(A, B) = 〈v〉P11 + σ2〈v〉2(P11 + P10)(P11 + P01) | (21) |
Substituting eqn (18)–(20) into the above allows the covariance to be split into true (cov(t)) and false (cov(f)) components:
| cov(t) = 〈v〉f(A)fA(B)ξAξB(1 + σ2〈v〉f(A)) | (22) |
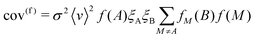 | (23) |
These contributions reveal several properties of experimental noise: first, when σ = 0, the covariance reduces to the product of the event rate and the likelihood of detecting two fragments in coincidence; second, σ introduces false correlations between uncorrelated ions, this varies with the square of the event rate and will therefore overshadow the true covariance for large products of σ and ν; third, perfect detection efficiency does not eliminate false covariance, so an unstable experiment will never converge on the true covariance.
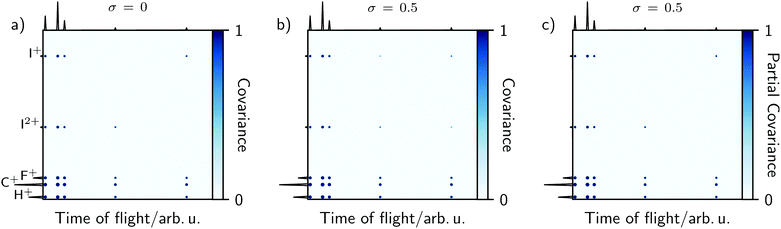
The simulation of 3,5-difluoroiodobenzene in Fig. 2 assumed that every fragmentation event was the same. To demonstrate the effect of σ, the initial conditions were therefore modified to consider that Coulomb explosions can result in both I+ and I2+. These must be uncorrelated since only one iodine fragment can be created per event, but shot-to-shot pulse fluctuations can produce indirect correlations due to the dependence between intensity and the measured ion count.12 As described in eqn (22) and (23), a large σ will yield non-zero covariance between I+ and I2+. Fig. 4a and b demonstrate this by comparing time-of-flight variance–covariance matrices simulated over 5000 laser shots with ν = 20, equal probabilities for the two channels, and σ = 0 or 0.5. The former shows no covariance between I+ and I2+, whereas the latter does.
The indirect correlations can be removed from Fig. 4b by calculating the partial variance–covariance matrix for the two ions, using σ as the common parameter responsible for their appearance:
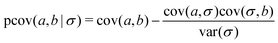 | (24) |
The result is shown in Fig. 4c, which is effectively identical to Fig. 4a where there are zero indirect correlations.
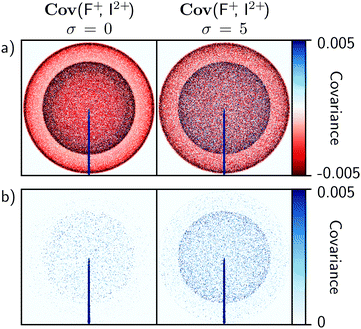
The influence of σ on recoil-frame covariance images is less significant than in time-of-flight covariance analysis. To demonstrate this, the simulation was adjusted to consider the Coulomb explosion of 3,5-difluoroiodobenzene into two equally probable channels: one resulting in the formation of I+ and F+, and the other in I2 + and F+. With σ = 0, one would expect the recoil-frame covariance images involving F+ to be similar to Fig. 1. For example, the Cov(F+, I2+) image in Fig. 5a exhibits an intense line of positive covariance at 180° due to back-to-back recoil, along with two isotropic negative features at high and low kinetic energies corresponding to false coincidences involving I2+ or I+, respectively. Increasing σ will again produce false correlations between ions. However, compared with time-of-flight covariance analysis these are spread over additional degrees of freedom due to the number of pixels available, which dilutes their impact.
Fig. 5 demonstrates the above effect for σ = 0 and 5. The results are plotted on the same intensity scale, and show that false correlations begin to appear as positive covariance when σ is increased. Due to their nature, these appear as isotropic distributions with kinetic energies that correspond to the two Coulomb explosion channels involving I2+ or I+. Compared with the false correlations observed in the time-of-flight covariance analysis in Fig. 4b, these features are effectively insignificant, and demonstrate that recoil-frame covariance imaging has an inherent advantage in that it mitigates the effects of experimental instabilities.
4 Conclusions
The above outcomes demonstrate that prompt Coulomb explosions of highly-charged ions can be modeled by assuming instantaneous fragmentation and electrostatic repulsion of ab initio determined structures. The reported model draws input geometries from a probability distribution of neutral ground-state structures in different zero-point vibrational phases. The resulting simulated fragment angular distributions match experimental reference data to a high degree of precision, demonstrating that the fragment trajectories of a target molecule are extensively driven by its internal motion.9 The accuracy of this model depends on the extent of nuclear motion during an explosion, and should consequently improve for experiments that use short laser pulses, or which initially place the parent molecule in a highly-charged state.2,3,36 The model itself can also be refined, for example by using Wigner sampling to better determine initial conditions, or by incorporating ab initio calculations of the parent ion potential energy surfaces or fragment trajectories.36,40,43The inclusion of experimental variance in the above model is also a useful tool, as it allows the effect of experimental event rate, detection efficiency, and noise to be examined. Systematic instabilities can introduce false correlations between Coulomb explosion fragments. When using covariance analysis, the magnitude of these false features depends on the product of the experimental variance and the square of the event rate. This effect cannot be reduced by enhancing the detection efficiency of the experiment, but can be counteracted by providing additional degrees of freedom to disperse the noise. For this reason, recoil-frame covariance analysis is better suited for these experiments than time-of-flight covariance analysis. It is therefore particularly beneficial for time- or sample-limited experiments at intense light sources, as it allows for higher event rates than coincidence methods and hence for more efficient use of these facilities.
The ability of Coulomb explosion imaging to probe molecular structures with non-resonant ionization is compelling, and a detailed understanding of the limitations imposed by vibrational motion and other factors will benefit the design of future experiments. For example, ring-opened gas-phase products prepared by resonant photon absorption are difficult to characterize due to their vibrational excitation and instability.44 Coulomb explosion imaging can in principle circumvent this problem by directly correlating the product momenta of fragments from the ring-opened structures, so long as the relevant product angular distributions are distinct. This condition will be easier to fulfill for small and rigid molecules, which suggests a size limit for using Coulomb explosion imaging to characterize molecular structures. Large and flexible organic molecules will produce several identical fragment ions whose fragment angular distributions overlap and obscure one another due to the large number of vibrational modes available, and are unlikely to make good targets. On the other hand, the vibrational motion dependence infers that molecules with low-frequency modes, such as metal clusters, are much more promising targets for this approach. In a similar manner, coherently exciting Franck–Condon active vibrational modes may also help to reduce the complexity introduced by out-of-phase ground-state vibrations. The continued development of Coulomb explosion imaging for small and geometrically regular structures is therefore likely to have wide-ranging applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge support from the UK EPSRC (EP/S028617/1) and the use of the University of Oxford Advanced Research Computing (ARC) facility (https://dx.doi.org/10.5281/zenodo.22558). A CC-BY licence is applied to the author accepted manuscript arising from this submission, in accordance with UKRI open access conditions. L. M. thanks Balliol College, Oxford, for their support, and M. B. is additionally grateful to the groups of H. Stapelfeldt and M. Brouard for the original collection of the Coulomb explosion imaging data used in Fig. 2. M. B. and J. W. L. L. would also like to recognise John Eland for his pioneering role in interpreting particle correlations, as well as for our insightful and enjoyable discussions about covariance analysis.References
- H. Stapelfeldt, E. Constant and P. B. Corkum, Phys. Rev. Lett., 1995, 74, 3780 CrossRef CAS PubMed.
- J. H. Sanderson, T. Nishide, H. Shiromaru, Y. Achiba and N. Kobayashi, Phys. Rev. A, 1999, 59, 4817 CrossRef CAS.
- H. Shiromaru, T. Nishide, T. Kitamura, J. H. Sanderson, Y. Achiba and N. Kobayashi, Phys. Scr., 1999, T80A, 110 CrossRef CAS.
- T. Kitamura, T. Nishide, H. Shiromaru, Y. Achiba and N. Kobayashi, J. Chem. Phys., 2001, 115, 5 CrossRef CAS.
- M. Pitzer, M. Kunitski, A. S. Johnson, T. Jahnke, H. Sann, F. Sturm, L. P. H. Schmidt, H. Schmidt-Böcking, R. Dörner, J. Stohner, J. Kiedrowski, M. Reggelin, S. Marquardt, A. Schießer, R. Berger and M. S. Schöffler, Science, 2013, 341, 1096 CrossRef CAS PubMed.
- H. Ibrahim, B. Wales, S. Beaulieu, B. E. Schmidt, N. Thiré, E. P. Fowe, É. Bisson, C. T. Hebeisen, V. Wanie, M. Giguére, J.-C. Kieffer, M. Spanner, A. D. Bandrauk, J. Sanderson, M. S. Schuurman and F. Légaré, Nat. Commun., 2014, 5, 4422 CrossRef CAS PubMed.
- J. D. Pickering, K. Amini, M. Brouard, M. Burt, I. J. Bush, L. Christensen, A. Lauer, J. H. Nielsen, C. S. Slater and H. Stapelfeldt, J. Chem. Phys., 2016, 144, 161105 CrossRef PubMed.
- U. Ablikim, C. Bomme, H. Xiong, E. Savelyev, R. Obaid, B. Kaderiya, S. Augustin, K. Schnorr, I. Dumitriu, T. Osipov, R. Bilodeau, D. Kilcoyne, V. Kumarappan, A. Rudenko, N. Berrah and D. Rolles, Sci. Rep., 2016, 6, 1 CrossRef PubMed.
- M. Burt, K. Amini, J. W. L. Lee, L. Christiansen, R. R. Johansen, Y. Kobayashi, J. D. Pickering, C. Vallance, M. Brouard and H. Stapelfeldt, J. Chem. Phys., 2018, 148, 091102 CrossRef.
- T. Endo, S. P. Neville, V. Wanie, S. Beaulieu, C. Qu, J. Deschamps, P. Lassonde, B. E. Schmidt, H. Fujise, M. Fushitani, A. Hishikawa, P. L. Houston, J. E. Bowman, M. S. Schuurman, F. Légaré and H. Ibrahim, Science, 2020, 370, 1072 CrossRef CAS PubMed.
- L. J. Frasinski, K. Codling and P. A. Hatherly, Science, 1989, 246, 1029 CrossRef CAS PubMed.
- L. J. Frasinski, J. Phys. B, 2016, 49, 152004 CrossRef.
- V. Zhaunerchyk, L. J. Frasinski, J. H. D. Eland and R. Feifel, Phys. Rev. A, 2014, 89, 053418 CrossRef.
- J. Mikosch and S. Patchkovskii, J. Mod. Opt., 2013, 60, 1426 CrossRef CAS.
- J. Mikosch and S. Patchkovskii, J. Mod. Opt., 2013, 60, 1439 CrossRef CAS.
- L. D. A. Siebbeles, M. Glass-Maujean, O. S. Vasyutinskii, J. A. Beswick and O. Roncero, J. Chem. Phys., 1994, 100, 3610 CrossRef CAS.
- M. Pitzer, G. Kastirke, M. Kunitski, T. Jahnke, T. Bauer, C. Goihl, F. Trinter, C. Schober, K. Henrichs, J. Becht, S. Zeller, H. Gassert, M. Waitz, A. Kuhlins, H. Sann, F. Sturm, F. Wiegandt, R. Wallauer, L. P. H. Schmidt, A. S. Johnson, M. Mazenauer, B. Spenger, S. Marquardt, S. Marquardt, H. Schmidt-Böcking, J. Stohner, R. Dörner, M. Schöffler and R. Berger, ChemPhysChem, 2016, 17, 2465 CrossRef CAS PubMed.
- G. A. Cooper, S. T. Alavi, W. Li, S. K. Lee and A. G. Suits, J. Phys. Chem. A, 2021, 125, 5481 CrossRef CAS PubMed.
- S. Chelkowski, P. B. Corkum and A. D. Bandrauk, Phys. Rev. Lett., 1999, 82, 3416 CrossRef CAS.
- H. R. Reiss, Phys. Rev. A, 1980, 22, 1786 CrossRef CAS.
- M. Wickenhauser, X. M. Tong, D. G. Arbó, J. Burgdörfer and C. D. Lin, Phys. Rev. A, 2006, 74, 041402 CrossRef.
- M. E. Corrales, G. Gitzinger, J. González-Vázquez, V. Loriot, R. de Nalda and L. Bañares, J. Phys. Chem. A, 2012, 116, 2669 CrossRef CAS PubMed.
- J. Kou, V. Zhakhovskii, S. Sakabe, K. Nishihara, S. Shimizu, S. Kawato, M. Hashida, K. Shimizu, S. Bulanov, Y. Izawa, Y. Kato and N. Nakashima, J. Chem. Phys., 2000, 112, 5012 CrossRef CAS.
- S. Shimizu, V. Zhakhovskii, F. Sato, S. Okihara, S. Sakabe, K. Nishihara, Y. Izawa, T. Yatsuhashi and N. Nakashima, J. Chem. Phys., 2002, 117, 3180 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. Carey, I. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261 CrossRef CAS PubMed.
- C. S. Slater, S. Blake, M. Brouard, A. Lauer, C. Vallance, J. J. John, R. Turchetta, A. Nomerotski, L. Christensen, J. H. Nielsen, M. P. Johansson and H. Stapelfeldt, Phys. Rev. A, 2014, 89, 011401 CrossRef.
- C. S. Slater, S. Blake, M. Brouard, A. Lauer, C. Vallance, C. S. Bohun, L. Christensen, J. H. Nielsen, M. P. Johansson and H. Stapelfeldt, Phys. Rev. A, 2015, 91, 053424 CrossRef.
- C. Vallance, D. Heathcote and J. W. L. Lee, J. Phys. Chem. A, 2021, 125, 1117 CrossRef CAS PubMed.
- K. V. Mardia, J. T. Kent and J. M. Bibby, Multivariate Analysis, Academic Press, 1979 Search PubMed.
- J. L. Hansen, J. H. Nielsen, C. B. Madsen, A. T. Lindhardt, M. P. Johansson, T. Skrydstrup, L. B. Madsen and H. Stapelfeldt, J. Chem. Phys., 2012, 136, 204310 CrossRef PubMed.
- L. Christensen, J. H. Nielsen, C. S. Slater, A. Lauer, M. Brouard and H. Stapelfeldt, Phys. Rev. A, 2015, 92, 033411 CrossRef.
- L. Christensen, L. Christiansen, B. Shepperson and H. Stapelfeldt, Phys. Rev. A, 2016, 94, 023410 CrossRef.
- J. W. L. Lee, D. S. Tikhonov, P. Chopra, S. Maclot, A. L. Steber, S. Gruet, F. Allum, R. Boll, X. Cheng, S. Düsterer, B. Erk, D. Garg, L. He, D. Heathcote, M. Johny, M. M. Kazemi, H. Köckert, J. Lahl, A. K. Lemmens, D. Loru, R. Mason, E. Müller, T. Mullins, P. Olshin, C. Passow, J. Peschel, D. Ramm, D. Rompotis, N. Schirmel, S. Trippel, J. Wiese, F. Ziaee, S. Bari, M. Burt, J. Küpper, A. M. Rijs, D. Rolles, S. Techert, P. Eng-Johnsson, M. Brouard, C. Vallance, B. Manschwetus and M. Schnell, Nat. Commun., 2021, 12, 1 CrossRef CAS PubMed.
- L. Frasinski, J. Phys. B, 1993, 26, 2225 CrossRef CAS.
- W. Zhou, L. Ge, G. A. Cooper, S. W. Crane, M. H. Evans, M. N. R. Ashfold and C. Vallance, J. Chem. Phys., 2020, 153, 184201 CrossRef CAS PubMed.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989 CrossRef CAS.
- L. V. Keldysh, Sov. Phys. JETP, 1965, 20, 1307 Search PubMed.
- I. V. Litvinyuk, K. F. Lee, P. W. Dooley, D. M. Rayner, D. M. Villeneuve and P. B. Corkum, Phys. Rev. Lett., 2003, 90, 233003 CrossRef CAS PubMed.
- F. Légaré, K. F. Lee, I. V. Litvinyuk, P. W. Dooley, S. S. Wesolowski, P. R. Bunker, P. Dombi, F. Krausz, A. D. Bandrauk, D. M. Villeneuve and P. B. Corkum, Phys. Rev. A, 2005, 71, 013415 CrossRef.
- P. H. Bucksbaum, A. Zavriyev, H. G. Muller and D. W. Schumacher, Phys. Rev. Lett., 1990, 64, 1883 CrossRef CAS PubMed.
- W. A. Bryan, J. H. Sanderson, A. El-Zein, W. R. Newell, P. F. Taday and A. J. Langley, J. Phys. B, 2000, 33, 745 CrossRef CAS.
- E. Wigner, Phys. Rev., 1932, 40, 749 CrossRef CAS.
- B. Marchetti, T. N. V. Karsili, O. Kelly, P. Kapetanopoulos and M. N. R. Ashfold, J. Chem. Phys., 2015, 142, 224303 CrossRef PubMed.
Footnote |
| † Here Cov(A, B) and cov(a, b) indicate a matrix or element, respectively. |
| This journal is © the Owner Societies 2022 |