Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient neutralization of core ionized species in an aqueous environment
Eetu
Pelimanni
 *a,
Andreas
Hans
*a,
Andreas
Hans
 ab,
Emilia
Heikura
ab,
Marko
Huttula
ab,
Emilia
Heikura
ab,
Marko
Huttula
 a and
Minna
Patanen
a and
Minna
Patanen
 a
a
aNano and Molecular Systems Research Unit, Faculty of Science, University of Oulu, Box 3000, FI-90014, Finland. E-mail: eetu.pelimanni@oulu.fi
bUniversität Kassel, Institut für Physik und CINSaT, Heinrich-Plett-Straße 40, 34132, Kassel, Germany
First published on 27th April 2022
Abstract
Core ionization dynamics of argon–water heteroclusters ArM[H2O]N are investigated using a site and process selective experimental scheme combining 3 keV electron irradiation with Auger electron–ion–ion multi-coincidence detection. The formation of Ar 2p−1 vacancies followed by non-radiative decay to intermediate one-site doubly ionized states Ar2+(3p−2)−ArM−1[H2O]N and subsequent redistribution of charge to the cluster environment are monitored. At low argon concentrations the emission of an [H2O]n′H+/[H2O]n′′H+ ion pair is the dominant outcome, implying on high efficiency of charge transfer to the water network. Increasing the condensation fraction of argon in the mixed clusters and/or to pure argon clusters is reflected as a growing yield of Arm′+/Arm′′+ ion pairs, providing a fingerprint of the precursor heterocluster beam composition. The coincident Auger electron spectra, resolved with better than 1 eV resolution, show only subtle differences and thereby reflect the local nature of the initial Auger decay step. The results lead to better understanding of inner shell ionization processes in heterogeneous clusters and in aqueous environments in general.
1 Introduction
Inner shell ionization is one of the central primary interaction mechanisms between X-rays or high energy particles and matter, followed by complex charge and energy redistribution dynamics and radiolysis. These processes are fundamental in nature, in radiotherapy, and also widely exploited in various spectroscopic material characterization techniques with atomic specificity.1 Concerning ionization of hydrated atoms/molecules in particular, unique insights to the effect of neighbouring water molecules have been obtained from recent experiments on pure and doped water clusters.2–7 Generally, molecules neighbouring the primary ionization site influence the electronic decay cascade for example by opening non-local decay pathways, enable the exchange of charge and vibrational energy, and may open or close specific fragmentation channels. As condensed yet spatially confined samples, in gas phase clusters the reaction products (electrons and ions) can be probed using the same electron and ion spectroscopic methods that have been well-established in single molecule studies, building understanding of the role of the environment. In hydrated clusters, both suppression3,7 and increase5,6 of radiation damage have been reported compared to the free molecule case.The properties of clusters are intermediate to those of free molecules and macroscopic matter, with energetics of the transition states, number of degrees of freedom and mobility during the fragmentation process (structural reorganization) being sensitive to the size and composition of the probed system.5 In core ionization, charge and energy distribution to the water network are connected to the core vacancy being filled via (a cascade of) local or interatomic non-radiative decay channels that lead to multiply ionized states.4,7 In-depth understanding of the detailed mechanisms and energetics can be obtained especially from the application of multi-particle coincidence detection schemes, i.e., simultaneous detection of the emitted electron(s) and ion(s), as demonstrated, e.g., in recent work using X-ray ionization,7 and in the present work using high energy electron ionization.
In this work, we investigate inner shell ionization dynamics in argon–water clusters. These heterogeneous systems are composed of adjacent domains of a hydrogen bonded network of water molecules and van der Waals bonded inert gas atoms. When the number of argon atoms is sufficiently high, core–shell (water–argon, respectively) type configuration can also take place.2,8,9 The example structure illustrated in the abstract figure is taken from Lu et al.9 Mass spectroscopic studies of argon–water clusters, mainly upon (inner/outer) valence ionization, have been previously carried out at least by Shinohara et al.,10 Jongma et al.,11 Golan and Ahmed,12 and Kočišek et al.2 It has been found that ionization of the argon matrix can act as a mediator for water cluster ionization, and also provide cooling for the water cluster cation via neutral evaporation.2,11,12 Excitonic charge transfer reactions from argon to water were observed with resonant VUV excitation by Golan and Ahmed,12 while low energy electron irradiation was examined by Kočišek et al.2
In the present experiment, we exploit high energy (3 keV) electron irradiation to induce core ionization from the 2p-core level of an Ar-site, followed by L2,3M2,3M2,3 Auger decay to a one-site doubly ionized state Ar2+(3p−2)−ArM−1[H2O]N. This process and the following redistribution of charge within the cluster are unambiguously singled out using an Auger electron–ion–ion multi-coincidence detection scheme. Overall, the high energy resolution detection of the Auger electron in coincidence with the ions provides not only elemental selectivity but also information on the localization of the initial ionization site (surface/bulk), the initial electronic decay step (L2,3M2,3M2,3) and the potential influence of neighbouring water molecules to it (local vs. non-local decay).
To clarify the notation used throughout this paper, the neutral parent clusters ArM[H2O]N are denoted with uppercase “M” and “N” (M, N = 1, 2, 3,…), while corresponding lowercase “m” and “n” (m, n = 1, 2, 3,…) are used for the ionic fragments Arm+ and [H2O]nH+. In general m ≤ M and n ≤ N − 1 due to cluster fragmentation, which in the case of electron ionization is often extensive so that in practice m ≪ M and n ≪ N.13,14 When referring to a pair of fragments originating from the same parent cluster, apostrophes are added for further distinction, e.g., Arm′+/Arm′′+ and [H2O]n′H+/[H2O]n′′H+, where m′ + m′′ ≤ M and n′ + n′′ ≤ N − 2.
2 Experimental
The set-up consists of a Scienta SES-200 hemispherical deflection analyzer (HDA), a Wiley–McLaren type time-of-flight mass spectrometer (TOFMS) with a focusing lens field,16,17 and a SPECS EQ 22-35 electron gun (EG), all of which were installed at 90° angles with respect to each other. Argon–water heteroclusters were produced in a continuous adiabatic expansion of a mixture of argon and water vapor through a conical nozzle, with a reservoir of liquid water (Milli-Q) in the gas line providing the humidification. The nozzle had a diameter of 25 μm, a half opening angle of 20°, and a 5 mm long expansion cone. Clusters were generated at three different source conditions by varying the expansion pressure between 4.5 bar, 6 bar, and 10 bar. Only the argon feed pressure was varied, while in all three cases the water reservoir was kept at room temperature and the nozzle at 40 °C. The clusters passed through a skimmer (0.3 mm orifice diameter) and then the repeller plate of the TOFMS (a solid plate with a central few mm wide pinhole for the clusters) to the interaction region. As such the initial cluster velocity was readily directed towards the ion detector, which together with the lens field resulted in a high ion collection efficiency. During measurements the pressure was in the 10−4–10−3 mbar regime in the expansion chamber, and in the 10−8–10−7 mbar regime in the analysis chamber.Non-coincident Auger electron spectra were measured by operating the HDA in the conventional scanning mode. In turn, in the coincidence measurements static voltages were kept so that only electrons with kinetic energies (KE) within an ∼8 eV wide window (203–211 eV) in the Ar L2,3M2,3M2,3 regime were collected. A pass energy of 100 eV and a 2.5 mm entrance slit were used, resulting in a kinetic energy resolution of ∼0.6 eV. The kinetic energy scale was calibrated to the L3M2,3M2,3 (1S0) atomic peak at 201.11 eV.15 A continuous 3 keV electron beam crossed the cluster beam in the normally field free interaction region, and each detected electron in the HDA triggered an extraction field pulse for the ions. Bipolar pulses were applied to the repeller plate (+195 V, 5.4 μs/−30 V, 57 μs), with the negative after-pulse reducing the ion background. Protons are not considered in the present analysis, as the measurement of very short TOFs was prohibited by extraction pulse induced noise in the ion detector. Position sensitive detectors were used in both analyzers, with a RoentDek HEX75 microchannel plate/3-layer delay line anode detector in the TOFMS, and a Quantar 3395A microchannel plate/resistive anode detector in the HDA. A RoentDek TDC8HP card was used for ion data acquisition, together with an ATC1 add-on card (with ADCs) for recording also the electron positions.
A low event rate of <10 electrons per s was used to minimize the false coincidence yield, with a data acquisition time of ∼1–4 weeks for each expansion pressure. The data analysis was carried out using the CoboldPC (RoentDek Handels GmbH) and the Igor Pro 8 (WaveMetrics, Inc.) softwares, the latter with the curve-fitting package SPANCF.18,19 False coincidences were subtracted using a “random” trigger reference method, the details of which can be found elsewhere.20 The “random” trigger reference was conveniently obtained from the randomly observed dark counts at the electron detector. While dark counts were observed throughout the detector surface, electrons from the narrow cluster beam were concentrated only at the center of the detector (due to the spatial focusing effect of the electrostatic lens). Hits at the center were thus considered as the electron coincidence statistics, and hits at the edges as the random statistics.
3 Results and discussion
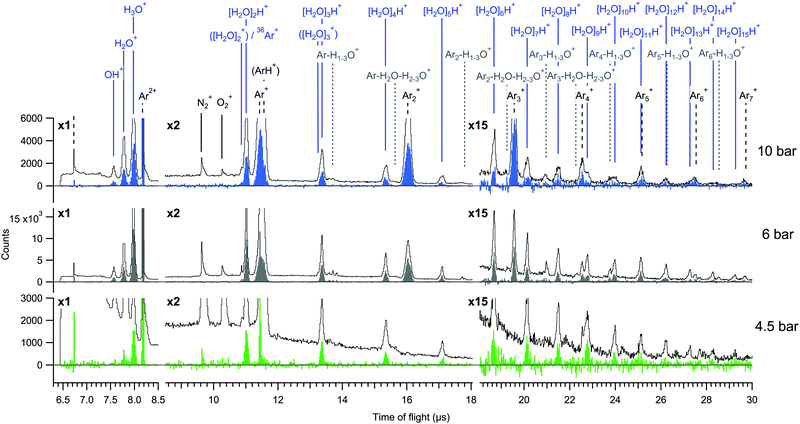
For an overview of the induced Auger transitions, non-coincident electron spectra measured at a broad kinetic energy range from argon atoms, argon clusters and argon–water clusters are shown in Fig. 1. The rich structure emerges from the decay of L1,2,3−1 states to various doubly and triply ionized final state configurations, for which detailed assignments can be found elsewhere.15 The present electron–ion coincidence measurements were targeted to the strongest features at 203–211 eV, involving L2,3M2,3M2,3 transitions to final states with 3p−2 configuration. Overlapping contributions from L1 ionization to triply ionized states are weak in this region. The coincidence yield of Ar3+ was observed to be lower than 4% of the value for Ar2+ (as determined from the coincident time of flight spectra shown in Fig. 2).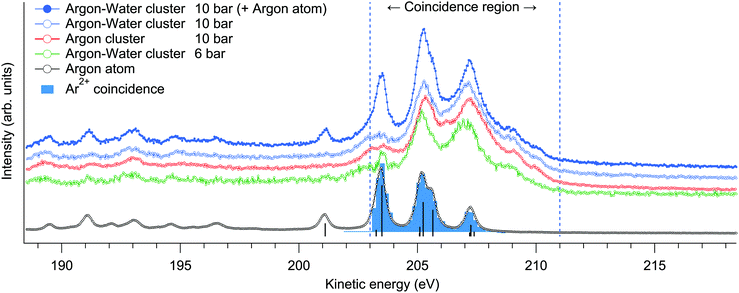 | ||
| Fig. 1 Overview Auger electron spectra resulting from Ar L-shell ionization measured in non-coincident scanning mode (lines). The L2,3M2,3M2,3 transitions in Ar atoms are also designated (sticks).15 The same features in clusters, targeted in the electron–ion coincidence measurements, are broader and found at slightly higher kinetic energies. | ||
Multiply charged ions are not observed from argon clusters21 or argon–water clusters where the charge is efficiently transferred to neighbouring sites. This becomes apparent from the Ar2+-coincident electron spectrum shown in Fig. 1, which although extracted from the cluster measurement, is essentially identical with the non-coincident electron spectrum of atomic Ar and thus originates only from the uncondensed fraction of Ar in the interaction region.
The total electron-coincident ion time-of-flight spectra are shown in Fig. 2, where all events are included irrespective of the number of detected ions in each event. The spectra are shown both before and after subtraction of false coincidences. The expression for the subtraction is It = Ie − (Ne/Nr)·Ir, where It is the true (t) ion statistics (color filled spectra), Ie (line spectra) and Ir are the statistics of all ions obtained with electron (e) and random (r) triggered events, and Ne and Nr are the numbers of electron and random triggered events for normalization.20 In the true ion statistics, it is seen that the continuous background as well as obvious false coincidence peaks such as the N2+ and O2+ traces from residual air are cleanly eliminated.
The mass spectra are dominated by two main series of fragments, [H2O]nH+ and Arm+. Some of the Arm+ ions might also be of the type ArmH+ as previously reported,2 but in our measurement these are not clearly distinguishable due to broadening of the peaks by ion momentum. In previous investigations of argon–water clusters also [H2O]n+ (n ≤ N) water cluster ions have been observed as cluster cooling by evaporation of the argon atoms allows the OH radical to be retained in the water cluster.10,11,22 In contrast, we do not observe significant contributions from them at any pressure, which may be due to large excess energies remaining in the clusters after (double) ionization and/or to the average cluster size being smaller in the present experiment.2,10 Mixed species containing both argon and water (e.g. Arm+−H1–3O+) have also only minimal yields. Potential origins of such species have been discussed in other works.2,10
Regarding the cluster size, conventional scaling law approaches for mean size estimation are not readily applicable for the mixed gas expansion.2 We however note that the values calculated for pure argon expansions are 〈M〉 = 9 (4.5 bar), 〈M〉 = 14 (6 bar) and 〈M〉 = 32 (10 bar) atoms per cluster on average.23 Although the presence of water molecules changes the condensation dynamics, based on these we suspect that the true sizes are on the order of few to few tens of atoms and/or molecules per cluster. Relatively small mean sizes are supported also by the fact that the 4.5 bar measurement is close to the minimum pressure where clusters were observed. A reliable size estimate from the relatively small fragment sizes observed in the mass spectrum is prohibited since significant fragmentation is expected.24
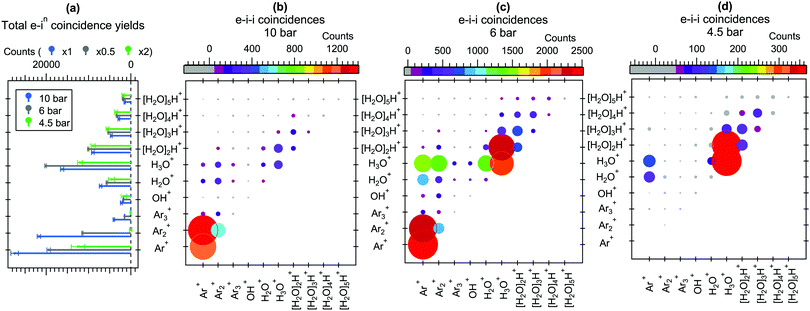
For better comparison of the relative ion yields at different expansion pressures, the true coincidence yields extracted from the peak areas of these spectra are presented in Fig. 3(a). The relative strong yield of protonated water cluster fragments readily indicates that final charge localization to water is favoured over argon, particularly in the 4.5 bar measurement. Interestingly, when this is combined with the removal of excess energy after ionization by strong Ar evaporation,2,11 the mere presence of argon in the precursor clusters generated at 4.5 bar is not readily apparent from the mass spectrum alone, but is only revealed by the combined information from the Auger electrons. Note that the remaining “true” intensity in Ar+ at 4.5 bar peaking at a sharp TOF distribution (Fig. 2) is attributed to be mostly due to a very slight inaccuracy in subtracting the exceptionally high number of false coincidences for this peak. At higher pressures a clear but rapidly decaying series of coincident Arm+ peaks appears alongside the [H2O]nH+ series, reflecting an increasing number of pure argon clusters and/or increasing fraction of argon (layer thickness) in the heterogeneous clusters.
Further insight to the origin of the mass spectrum and the cluster beam composition can be obtained from the electron–ion–ion correlations shown in Fig. 3(b–d). In these correlation maps, the colour and size of each circle indicates the number of true counts for the pair of ions specified at the horizontal and vertical axes. Note that the presentation is distinct from the traditional “TOF 1 vs. TOF 2”-maps, also in that the ions are not ordered as a function of TOF (or m/z). These statistics were obtained using eqn (5) of ref. 20, which is not repeated here in detail due to its lengthiness. Qualitatively, the overall ion pair statistics consist of four types of events, where the first (1) and second (2) ion are either true(1)/true(2), true(1)/false(2), false(1)/true(2) or false(1)/false(2). To obtain the true(1)/true(2) statistics presented here, the other three contributions have been subtracted from the overall electron triggered statistics. Note that the intensities of ion pairs in the diagonals (e.g. H3O+/H3O+) are underestimated due to the reduced detection efficiency of two ions arriving nearly simultaneously to the detector, and as mentioned above, some additional uncertainty is involved in the Ar+/X+ pairs due to the high number of Ar+ false coincidences.
It is seen in Fig. 3(b–d) that the Arm+ and [H2O]nH+ series originate mainly from Arm′+/Arm′′+ and [H2O]n′H+/[H2O]n′′H+ ion pair formation, respectively. However, in all three pressures Arm+ ions rarely coincide with the protonated [H2O]nH+ (n > 1) fragments, suggesting that as long as the number of water molecules in the cluster is sufficiently high (and perhaps the number of Ar atoms is sufficiently low, keeping in mind the core–shell structure at large sizes), both charges are efficiently transferred to the water network. Some Arm+/H2O+ and Arm+/H3O+ pairs appear, which likely originate mostly from clusters where just one or a couple of water molecules were present.
Charge transfer to water appears justified by the much lower ionization energy of water, but the details of this process can be further considered. The fastest route for transferring the charge to a neighbouring site would be directly after ionization via core-level intermolecular coulombic decay (core-ICD) to delocalized final states. The probability of core-ICD strongly depends on the species, the interatomic distance, orbital overlap, and transition energy.4 The importance of this process was recently emphasized for hydrated biomolecules, where core-ICD rates may compete and even surpass local Auger decay.7 In comparison, lower contributions of just few % of the total decay rate have been observed, e.g., for solvated ions,25,26 and even smaller rates can be expected for van der Waals bonded species. In pure argon clusters, Ar 2p−1 states predominantly decay via a local Auger process, with the branching ratio of core-ICD being <1% (appearing in the 212–218 eV kinetic energy range).27 To see if the presence of neighbouring water molecules changes this situation in the present mixed argon–water case, non-coincident Auger electron spectra were measured at a broad kinetic energy range from 146 to 231 eV from mixed argon–water clusters and from pure argon clusters at 10 bar expansions (Fig. 1 shows parts of these spectra, after subtraction of the uncondensed atomic contribution). Any core-ICD channels involving the 1b1, 3a1, 1b2 or 2a1 electrons should occur in this energy range, but essentially identical non-coincident spectra are however obtained. Moreover, below we discuss also the ion-coincident electron spectra (Fig. 4), which likewise clearly show that a significant fraction of the coincident electrons indeed belong to the main features corresponding to local Auger decay. These suggest that decay rates via core-ICD channels are not substantial in the present conditions, and that charge transfer dynamics occurring well after the first local Auger emission step appear to drive the fragmentation process. Hence, before fragmentation, an intermediate state is formed with a doubly charged argon site in the cluster. It should be emphasised, however, that this competing interatomic mechanism is not ruled out in general. Given that core-ICD was observed in the pure argon cluster case and for other hydrated species,7,25–27 it seems reasonable to expect it to be possible in the present argon–water system as well even if it is not prominent after Ar 2p ionisation compared to local Auger decay. Note that a small overlapping contribution from core-ICD is difficult to extract from the present electron spectrum due to the large number of overlapping states (except in the case that a specific ionic fragment would originate explicitly from this process). The composition of the Auger electron spectrum is discussed in more detail below.
The subsequent charge redistribution steps are not reflected in the present measurements and further work is needed for their precise determination. However, a brief discussion can be given. In pure argon clusters, the here probed L2,3M2,3M2,3 decay leads to an intermediate non-dissociative one-site dicationic state, which subsequently decays via Radiative Charge Transfer (RCT): [Ar2+(3p−2)−Ar] → Ar+(3p−1) + Ar+(3p−1) + hν.27,28 This radiative transition dominates since non-radiative decay channels (causing further ionization) are energetically forbidden. Thus, this should be the predominant process producing the here observed Arm′+/Arm′′+ ion pairs. The energy released in this process is up to around ∼10.7 eV,27 and couple eV larger in the mixed cluster case if the highest occupied molecular orbital (HOMO) of a neutral water molecule contributes to the charge transfer (given its ∼3.5 eV lower ionization energy compared to Ar). It is not fully clear whether third ionization could occur in the heterogeneous environment, but here we have limited the analysis only up to 2 ion correlations. Third ionization could occur also due to inelastic scattering of the electrons on their way out of the cluster. The coincidence detection excludes this possibility for the Auger electron (discussed further below), but does not explicitly rule it out for the primary impacting electron nor for the initially ionized 2p-electron which are not measured. It was recently observed that in argon–nitrogen heteroclusters,29 the above mentioned RCT channel occurring in pure argon clusters was efficiently quenched by competing nonradiative direct single charge transfer (SCT) to Ar+−N2+* states with crossing potential energy curves. Similar mechanisms may then play a role in other heterosystems as well, potentially also in the present case.
Kočišek et al.2 have also discussed charge transfer mechanisms from argon to water after electron ionization from the threshold region up to 80 eV electrons. They also reported that in their experiment surface ionization was dominant so that the argon atoms effectively shielded the internal water cluster. In comparing the results, it should be noted that our clusters are likely to be smaller than those in the experiment of Kočišek et al.,2 considering differences in the expansion conditions and the mass spectra. Additionally, the probe depth should be considered as the inelastic mean free path (IMFP) of electrons varies largely in the considered energy range. The energy of the here probed Auger electrons (∼200 eV) settles close to the minimum of the IMFP curve in water, where the IMFP is ∼1 nm.30 In turn, the IMFP of the incident 3 keV electrons in water is significantly larger, around 10 nm (note that the IMFP rises steeply also for low energy electrons).30 These values suggest that in our experiment the incident electrons should relatively easily penetrate into the cluster, while inelastic scattering of the outgoing Auger electron is more probable since its IMFP is roughly comparable to the cluster size.
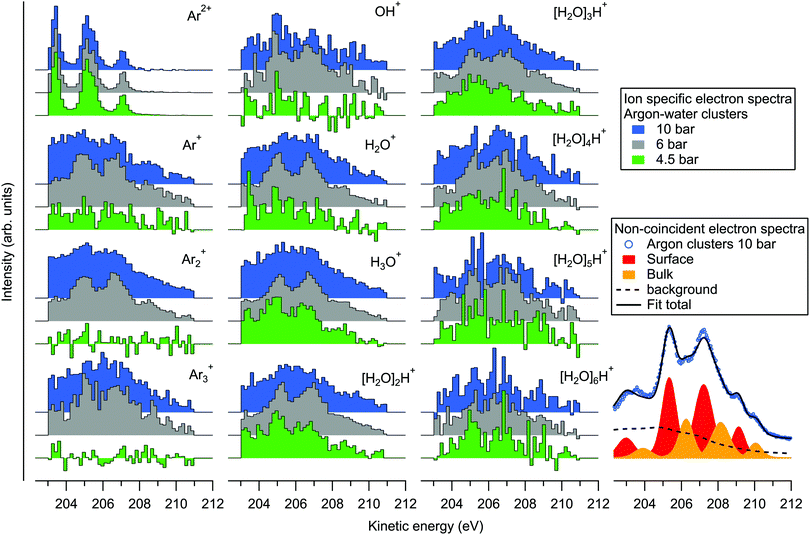
Since the kinetic energy of the Auger electron depends on the final state polarization screening efficiency by the environment, initial coordination of the ionization sites should be reflected as fine structure in the Auger electron spectra. On the bottom right of Fig. 4 we show an example fit of the non-coincident spectrum measured at 10 bar. The fit is performed by first fitting the atomic L2,3M2,3M2,3 spectrum (for simplicity, with 4 peak profiles), and applying the result to the cluster spectrum with fixed intensity ratios and energy splittings, but with broadened profiles that are also shifted in energy. It is seen that the experimental spectrum can be reasonably well reproduced with two sets of peaks, which have been previously assigned to surface (lower KE) and bulk (higher KE) coordinated atoms.31 The respective KE shifts from the atomic spectrum are ∼1.9 and 2.8 eV. Besides the main lines, a Shirley-like cumulative profile is simultaneously applied in the fit to account for the non-constant background and potential minor contributions from overlapping structures. This profile was selected given that the main Auger lines lose intensity to lower kinetic energies due to inelastic intracluster scattering (ionization or excitation of the same or neighbouring sites) of the incident electron, the ionized 2p electron or the Auger electron itself.31,32 Note that some processes like “shake” transitions and post-collision interaction may also increase the Auger electron energy.32 While the applied profile is therefore somewhat arbitrary (in other works simple line profiles have also been used31,32), a detailed account of these processes is beyond the scope of this work. As noted above, ionization by inelastic scattering of the Auger electron leading to triply ionized states can be ruled out since corresponding spectral features would be out of the coincidence detection window. The minimum energy loss in this Auger electron induced shake-off process is ≳ 10 eV (adiabatic ionization energy of a neutral Ar or an H2O site33) and therefore these electrons lie outside (lower kinetic energy side) of the monitored kinetic energy region. Other processes may still contribute in the monitored region, however, although their intensities appear much weaker than the normal Auger lines.
On the left part of Fig. 4 we show the ion-specific electron spectra, obtained by taking the events where exactly one of the designated ions was detected (along with 0, 1, 2, … other types of ions), and then subtracting the false coincidence background (see eqn (3) and related discussion in ref. 20 for details). While the data are thus not filtered to specific ion–ion correlations, the origins of the individual ions are however implied in the ion–ion correlations discussed above. Firstly, the electron spectra obtained in coincidence with the Ar2+ ion are shown on the top left. The obtained spectra are practically identical at all three pressures, resembling the non-coincident spectrum of argon atoms. These ions thus originate from the uncondensed fraction of argon atoms in the cluster jet, as was already noted above. The rest of the plots show electron spectra that were obtained in coincidence with various ions originating from the clusters. As expected, the profiles appear broadened and shifted to higher kinetic energies compared to the atomic spectrum.
Considering if the efficiency of charge localization to water depends on the initial coordination site of the ionized argon atom in the cluster (e.g., an atom adjacent to a water molecule vs. a surface atom with multiple atomic layers in between), it is remarkable that differences between the Arm+ and [H2O]nH+ coincident electron spectra are overall relatively subtle. All of the spectra show similarly broad energy distributions, and with increasing stagnation pressure the increasing mean cluster size and compositional diversity broadens the energies similarly for both Arm+ and [H2O]nH+. Above we also noted that the non-coincident spectra between pure and heterogeneous clusters measured at 10 bar (Fig. 1) are virtually indistinguishable. The coincident electron spectra appear also rather similar to the non-coincident measurement at 6 bar, as one might expect, but there is some discrepancy between the coincident and non-coincident electron spectra measured at 10 bar (the 4.5 bar non-coincident spectrum was not measured). Particularly the spectra of the smallest fragments appear less resolved, and weighted to lower kinetic energies. The reason for this discrepancy at 10 bar is not fully clear, but one can speculate that the decreasing detection efficiency of ions with increasing mass may play a more significant role here, and that the smallest fragments might be more likely to coincide with inelastically scattered electrons. Clearly, the charge transfer dynamics (and therein the efficiency of charge migration to water) are subject also to any transient nuclear dynamics occurring during and after the lifetime of the intermediate dicationic state (which in pure argon clusters was reported to be up to several ns34), which could be an interesting subject of further theoretical work on the matter.
4 Conclusions
In this experiment, we have combined the production of aqueous heteroclusters in an adiabatic expansion, core ionization by a compact electron source, and site and process selective Auger electron–ion–ion multi-coincidence detection with high resolution hemispherical electron and ion time of flight analyzers. Argon–water heteroclusters were investigated with 3 keV electron ionization by selectively monitoring the formation of 2p core level vacancies on Ar-sites, Auger decay to Ar 3p−2 intermediate states and subsequent charge redistribution to the environment. The coincidence scheme was of particular importance in singling out the core level process, which for few keV electrons has an order of magnitude lower cross section than valence ionization35 (while with soft X-rays, e.g., in synchrotron and free electron laser experiments the Ar 2p cross section is an order of magnitude higher than the valence36,37).Multi-ion detection allowed breakdown of the mass spectrum mainly to the formation of [H2O]n′H+/[H2O]n′′H+ and Arm′+/Arm′′+ ion pairs, with relative yields correlating strongly with the precursor cluster composition. It was found that in low argon concentrations the production of Arm+ ions was effectively suppressed by the combined effects of charge transfer to water and Ar evaporation, but with the applied electron–ion coincidence scheme it was still possible to reveal the presence of argon in the precursor clusters. This observation also emphasizes that, generally, care should be taken in assessing the precursor cluster composition from mass spectroscopy alone. The large number of emitted [H2O]n′H+/[H2O]n′′H+ ion pairs with close to negligible yield of Arm+ ions at low argon concentrations also demonstrates how multiply charged species can be efficiently neutralized by charge migration to the surrounding water molecules. This contributes to the significant interest presently given in assessing the detailed dynamics and outcome of inner shell ionization processes in hydrated clusters, and aqueous environments in general.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support by the Academy of Finland, the Finnish Cultural Foundation (North Ostrobothnia Regional fund) and the Tauno Tönning Foundation.References
- P. Willmott, An introduction to synchrotron radiation: techniques and applications, John Wiley & Sons, 2019 Search PubMed.
- J. Kočišek, J. Lengyel, M. Fárnk and P. Slavíček, J. Chem. Phys., 2013, 139, 214308 Search PubMed.
- P. Markush, P. Bolognesi, A. Cartoni, P. Rousseau, S. Maclot, R. Delaunay, A. Domaracka, J. Kočišek, M. C. Castrovilli, B. A. Huber and L. Avaldi, Phys. Chem. Chem. Phys., 2016, 18, 16721–16729 RSC.
- T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling, P. V. Demekhin, K. Gokhberg, L. S. Cederbaum, A. Ehresmann, A. Knie and A. Dreuw, Chem. Rev., 2020, 120, 11295–11369 CrossRef CAS PubMed.
- E. Wang, X. Ren, W. Baek, H. Rabus, T. Pfeifer and A. Dorn, Nat. Commun., 2020, 11, 1–7 CrossRef PubMed.
- A. R. Milosavljević, K. Jänkälä, M. L. Ranković, F. Canon, J. Bozek, C. Nicolas and A. Giuliani, Phys. Chem. Chem. Phys., 2020, 22, 12909–12917 RSC.
- A. Hans, P. Schmidt, C. Küstner-Wetekam, F. Trinter, S. Deinert, D. Bloß, J. H. Viehmann, R. Schaf, M. Gerstel, C. M. Saak, J. Buck, S. Klumpp, G. Hartmann, L. S. Cederbaum, N. V. Kryzhevoi and A. Knie, J. Phys. Chem. Lett., 2021, 12, 7146–7150 CrossRef CAS PubMed.
- E. Borges, G. Ferreira and J. Braga, Int. J. Quantum Chem., 2008, 108, 2523–2529 CrossRef CAS.
- W. Lu, R. B. Metz, T. P. Troy, O. Kostko and M. Ahmed, Phys. Chem. Chem. Phys., 2020, 22, 14284–14292 RSC.
- H. Shinohara, N. Nishi and N. Washida, J. Chem. Phys., 1986, 84, 5561–5567 CrossRef CAS.
- R. T. Jongma, Y. Huang, S. Shi and A. M. Wodtke, J. Phys. Chem. A, 1998, 102, 8847–8854 CrossRef CAS.
- A. Golan and M. Ahmed, J. Phys. Chem. Lett., 2012, 3, 458–462 CrossRef CAS PubMed.
- C. Bobbert, S. Schütte, C. Steinbach and U. Buck, Eur. Phys. J. D, 2002, 19, 183–192 CAS.
- S. Schütte and U. Buck, Int. J. Mass Spectrom., 2002, 220, 183–192 CrossRef.
- H. Pulkkinen, S. Aksela, O. Sairanen, A. Hiltunen and H. Aksela, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 3033 CrossRef CAS.
- E. Kokkonen, PhD thesis, University of Oulu, 2017.
- E. Kokkonen, K. Jänkälä, M. Patanen, W. Cao, M. Hrast, K. Bučar, M. Žitnik and M. Huttula, J. Chem. Phys., 2018, 148, 174301 CrossRef CAS PubMed.
- E. Kukk, G. Snell, J. D. Bozek, W.-T. Cheng and N. Berrah, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 63, 062702 CrossRef.
- E. Kukk, K. Ueda, U. Hergenhahn, X.-J. Liu, G. Prümper, H. Yoshida, Y. Tamenori, C. Makochekanwa, T. Tanaka, M. Kitajima and H. Tanaka, Phys. Rev. Lett., 2005, 95, 133001 CrossRef CAS PubMed.
- G. Prümper and K. Ueda, Nucl. Instrum. Methods Phys. Res., Sect. A, 2007, 574, 350–362 CrossRef.
- H. Fukuzawa, Y. Li, D. You, Y. Sakakibara, S. Yamada, Y. Ito, T. Takanashi, M. Oura, N. Saito and K. Ueda, Phys. Rev. A, 2019, 99, 042505 CrossRef CAS.
- K. Mizuse and A. Fujii, J. Phys. Chem. A, 2013, 117, 929–938 CrossRef CAS PubMed.
- U. Buck and R. Krohne, J. Chem. Phys., 1996, 105, 5408–5415 CrossRef CAS.
- J. Lengyel, A. Pysanenko, V. Poterya, J. Kočišek and M. Fárnk, Chem. Phys. Lett., 2014, 612, 256–261 CrossRef CAS.
- W. Pokapanich, N. V. Kryzhevoi, N. Ottosson, S. Svensson, L. S. Cederbaum, G. Öhrwall and O. Björneholm, J. Am. Chem. Soc., 2011, 133, 13430–13436 CrossRef CAS PubMed.
- G. Gopakumar, E. Muchová, I. Unger, S. Malerz, F. Trinter, G. Öhrwall, F. Lipparini, B. Mennucci, D. Ceolin, C. Caleman, I. Wilkinson, B. Winter, P. Slavíček, U. Hergenhahn and O. Björneholm, Phys. Chem. Chem. Phys., 2022, 24, 8661–8671 RSC.
- A. Hans, C. Küstner-Wetekam, P. Schmidt, C. Ozga, X. Holzapfel, H. Otto, C. Zindel, C. Richter, L. S. Cederbaum, A. Ehresmann, U. Hergenhahn, N. V. Kryzhevoi and A. Knie, Phys. Rev. Res., 2020, 2, 012022 CrossRef CAS.
- N. Saito, Y. Morishita, I. H. Suzuki, S. Stoychev, A. Kuleff, L. S. Cederbaum, X.-J. Liu, H. Fukuzawa, G. Prümper and K. Ueda, Chem. Phys. Lett., 2007, 441, 16–19 CrossRef CAS.
- C. Küstner-Wetekam, X. Hu, L. Marder, P. Schmidt, C. Ozga, C. Zindel, H. Otto, Y. Peng, J. Wang, C. Richter, N. Sisourat, U. Hergenhahn, A. Knie, A. Ehresmann, Y. Wu and A. Hans, Phys. Rev. A, 2021, 104, 042802 CrossRef.
- H. Shinotsuka, B. Da, S. Tanuma, H. Yoshikawa, C. Powell and D. R. Penn, Surf. Interface Anal., 2017, 49, 238–252 CrossRef CAS PubMed.
- M. Lundwall, M. Tchaplyguine, G. Öhrwall, A. Lindblad, S. Peredkov, T. Rander, S. Svensson and O. Björneholm, Surf. Sci., 2005, 594, 12–19 CrossRef CAS.
- M. Lundwall, A. Lindblad, G. Öhrwall, S. Svensson and O. Björneholm, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 065201 CrossRef.
- E. Pelimanni, L. Hautala, A. Hans, A. Kivimäki, M. Kook, C. Küstner-Wetekam, L. Marder, M. Patanen and M. Huttula, J. Phys. Chem. A, 2021, 125, 4750–4759 CrossRef CAS PubMed.
- C. Ozga, C. Honisch, P. Schmidt, X. Holzapfel, C. Zindel, C. Küstner-Wetekam, C. Richter, U. Hergenhahn, A. Ehresmann, A. Knie and A. Hans, Rev. Sci. Instrum., 2021, 92, 045110 CrossRef CAS PubMed.
- L. Jha, S. Kumar and B. Roy, Eur. Phys. J. D, 2006, 40, 101–106 CrossRef CAS.
- J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155 CrossRef CAS.
- J. Yeh, Atomic Calculation of Photoionization Cross-sections and Asymmetry Parameters, Gordon & Breach Science, Publishers, 1993 Search PubMed.
| This journal is © the Owner Societies 2022 |