Advances in modelling X-ray absorption spectroscopy data using reverse Monte Carlo
Andrea
Di Cicco†
 *a and
Fabio
Iesari†
*a and
Fabio
Iesari†
 b
b
aPhysics Division, School of Science and Technology, Camerino University, 62032 Camerino, MC, Italy. E-mail: andrea.dicicco@unicam.it
bAichi Synchrotron Radiation Center, 489-0965 Seto, Aichi, Japan. E-mail: fabio.iesari@aichisr.jp
First published on 28th February 2022
Abstract
Modern extended X-ray absorption fine structure (EXAFS) analysis is based on multiple-scattering calculations. Those calculations are carried out for fixed atomic configurations and proper account of the thermal and static disorder, corresponding to well-defined pair and higher-order distribution functions, can be obtained using different methods. The application of the Reverse Monte Carlo (RMC) method is able to provide tridimensional models of the atomic structure compatible with a given set of experimental data, producing useful and consistent structural models. This method has been proposed and applied also to EXAFS data by several authors in the last 25 years and has been fully implemented in the framework of the RMC-GnXAS method for EXAFS data-analysis. Here we present the extension and application of this method to multiple-edge studies of molecules, crystalline solids and liquids, including the long-range constraints provided by other techniques (e.g. diffraction). The potential and possible weaknesses of the RMC method are discussed, as well as the importance of accounting for the effect of noise levels in XAFS data. Results of RMC refinements are reported for several exemplary cases including Br2 and GeI4 molecular gases, crystalline Ge and AgBr, amorphous Ge and liquid AgBr. Those applications show the general interest for this method, and the importance of combining multiple set of data for improving the accuracy of the structural refinement both at short and long range.
1 Introduction
Modern XAS (X-ray Absorption Spectroscopy) analysis is based on the comparison of experimental data with accurate multiple-scattering calculations.1,2 Those calculations are carried out for fixed atomic configurations and proper account of the thermal and static disorder is usually performed using model distribution functions composed of several distinct peaks (“peak-fitting” approach).1–3 The standard XAS structural refinement is then based in refining the short-range distribution functions as a sum of individual peaks associated with well-defined bonding distances corresponding to first and further neighbors for the pair (g2) and higher-order (gn, n > 2) distribution functions,3 an approach easily justified for molecules and ordered condensed matter. Depending on the particular shape of the peak functions (Gaussian for example) selected structural parameters can be optimized for a given set of experimental data, e.g. average distance R, variance σR2 (mean-square relative displacement), coordination number N, using different refinement techniques. This “peak-fitting” approach has proven to be very powerful reducing the structural problem to the derivation of a limited number of unknowns. However, the problem of defining suitable model functions still holds also in simple crystalline cases. Gaussian shapes correspond to harmonic vibrations in solids, but visible deviations have been observed and studied even at moderate temperatures, resulting in asymmetric peaks of the radial distribution. Cumulant expansion models were introduced in early times (see ref. 4–6) to account for moderate disorder. The use of analytical non-Gaussian functions modelling the g(r) peaks was developed (see ref. 7 and 8 and refs. therein) and proved to be successful for moderate and large deviations from a Gaussian shape.Among different XAS data-analysis methods, the GnXAS ab initio suite of programs has been designed to produce accurate simulations of the γ(n) MS XAS n-body signals associated with the n-body distribution functions gn describing the local structure around selected photoabsorbing atoms.2,3 The accuracy of the data-analysis was widely tested on several crystalline and molecular cases, and the above-mentioned “peak-fitting” scheme has been used also in highly disordered substances, such as amorphous or liquid matter.9 In these systems, short-range peaks of the n-body distribution functions are usually merged into a long-range tail and a meaningful XAS data-analysis can be only carried out using suitable physical constraints.10,11 The application of this methodology has been shown to be successful in describing the short-range pair distribution function of “simple” elemental melts, ionic binary liquids and aqueous solutions (see ref. 10, 12–16 and the review paper17).
The “peak-fitting” approach have obvious advantages being particularly simple for routine applications in XAS data-analysis, providing also directly robust estimates for important average structural parameters. However, a consistent description of the local structure in terms of the gn distribution functions in both ordered and disordered systems rather requires the development of realistic tridimensional models of the atomic structure.
We have recently developed a strategy to incorporate the accurate simulations provided by the GnXAS suite of programs within a Reverse Monte Carlo (RMC) scheme18,19 for XAS structural refinement. Applications of the RMC method for XAS data-analysis were originally suggested by Gurman and McGreevy19, and also applied by other researchers mainly to disordered substances.20,21 More recently, a modified RMC approach using simulated annealing and wavelet transforms analysis was proposed for crystalline systems.22
Our advanced suite of programs, called RMC-GnXAS,23–25 was originally designed to apply the RMC algorithm for calculating the XAS signal starting from ensembles of either molecular replicas or box with cyclic boundary conditions. In the latter case, the RMC refinement is applied both to XAS experimental data and the g(r) curve obtained by diffraction techniques, so that XAS data probe the local structure around photoabsorbing centers, while diffraction data provide the necessary medium and long-range constraints. Several initial applications regarded liquid systems under high temperature and/or high pressure conditions.23,24,26–28 In this manuscript, we present the extension and application of the RMC-GnXAS approach to multiple-edge studies of exemplary molecules, crystalline solids and disordered systems (glasses and liquids), including also relativistic effects29 in the multiple-scattering calculations. The potential and the possible weaknesses of the RMC method are discussed, including a specific example of the effect of the experimental noise levels on the derived distribution functions.
2 Background
In its original presentation, Reverse Monte Carlo is an “inverse” modelling technique introduced by McGreevy and Pustzai18 as an application of the Metropolis Monte Carlo (MMC) algorithm. This application was conceived to produce a series of three-dimensional structural models compatible with X-ray and neutron scattering experimental data, but can be easily applied to other experimental data. The basic idea of an iterative technique reconstructing a model structure dates back to early attempts (see for example30) but it became feasible and popular only with the increasing availability of large computing resources.In standard RMC methods31 we assume that the experimental data under consideration contain only statistical noise following a normal distribution, so that the difference between experimental (AE) and calculated (AC) structure factors for the ‘real’ model of a given system will be a Gaussian random variable ei = AE(qi) − AC(qi), where i runs over the experimental data points. The original method was developed for diffraction data, but what follows can be applied to any experimental technique for which the calculated signal AC depends upon the atomic coordinates. The total probability distribution is the product of the individual Gaussian distributions for each point i. Modelling the structure of the system requires the construction of a statistical ensemble of atoms whose calculated signal AC satisfies the total probability distribution. A simple calculation31 shows that that this is obtained properly defining the variable 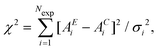 where σi is the standard deviation of each data point i and Nexp is the total number of data points. In this way, the total probability function is found to be proportional to exp(−χ2/2) and it can be immediately seen that χ2/2 plays the same role of U/kBT in the classic Metropolis Monte Carlo procedure which generates atomic configurations following the Boltzmann distributions of energies for a given energy potential U and temperature T.
where σi is the standard deviation of each data point i and Nexp is the total number of data points. In this way, the total probability function is found to be proportional to exp(−χ2/2) and it can be immediately seen that χ2/2 plays the same role of U/kBT in the classic Metropolis Monte Carlo procedure which generates atomic configurations following the Boltzmann distributions of energies for a given energy potential U and temperature T.
It is important here to stress the role played by the experimental noise (standard deviations σi) that must be used to drive the RMC refinement following the correct probability distribution. On the other hand, interatomic potentials are not used for standard RMC and very few assumptions on the structure are required. Of course, the temperature of the measurements T is not explicitly introduced in the refinement process (it acts obviously on the experimental data, collected at a given temperature). In principle only number density and chemical composition are needed for RMC modelling, although physical constraints are usually introduced, as discussed in more detail in the original papers (see ref. 32 for a review) and in the following sections.
Having defined the correct random variable, the RMC refinement proceeds similarly to a standard Metropolis Monte Carlo procedure for which there is a common theoretical background. An initial configuration, generated with or without periodic boundary conditions (see next sections) is used to calculate the signal AC to be compared with the experimental data AE. The variable 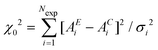 is calculated for the initial structure. Then one atom is moved at random and again the variable
is calculated for the initial structure. Then one atom is moved at random and again the variable 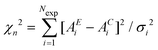 is calculated. The atom move is accepted if χn2 ≤ χ02. If χn2 > χ02 the move is accepted with probability e−(χn2−χ02)/2 (rejected otherwise). The atom moves are repeated until χ2 will oscillate around an equilibrium value, typically the number of points when χ2 really represents a statistical χ2-like random variable.
is calculated. The atom move is accepted if χn2 ≤ χ02. If χn2 > χ02 the move is accepted with probability e−(χn2−χ02)/2 (rejected otherwise). The atom moves are repeated until χ2 will oscillate around an equilibrium value, typically the number of points when χ2 really represents a statistical χ2-like random variable.
The resulting equilibrium atomic configurations are those consistent with the experimental data under consideration, within the experimental uncertainty. Independent configurations generated during the RMC procedure can be collected and used for producing average quantities related to the structure evaluating the fluctuations of a given model. Of course, the model structure can not be considered unique and we can only say that it is compatible with the set of experimental data under consideration. One of the main strengths of RMC is that it can be applied formally to data of a variety of experimental techniques, providing different and more stringent constraints for determining the structure of molecular, ordered and disordered condensed systems. Finally, the outcome is a set of three-dimensional structural models for the investigated system on which a full statistical analysis can performed to derive the pair distribution functions, the distribution of bond angles and to identify specific local atomic arrangements.
3 Methodology
In our current implementation of the RMC method it is possible to refine not only the XAFS signals, but also partial or total pair distribution functions, which can be obtained by X-ray/neutron diffraction experiments or computer simulations. This feature is used to provide a suitable constraint for the long-range order of the system, since XAFS is mainly sensitive to the local structure around the photo-absorber sites. Here we briefly review the workflow of the RMC-GnXAS program (for more information see ref. 24 and 33).For creating the initial configuration two different strategies24 are used. The first standard choice consists in creating a box of well-defined density with periodic boundary conditions, used for bulk systems like solids and liquids. In this case, one can start from a crystal unit cell, defining also the atomic density (which is usually fixed), repeated in space to create a super-cell with a large number of independent atomic sites. The second strategy consists in creating many replicas of a given ensemble of atoms, without introducing periodic boundary conditions. This second option is very useful to describe isolated molecules or small nano-particles. Structural quantities and signals are averaged over the different replicas in order to reproduce the thermal disorder.
After constructing the initial configuration, the starting XAFS signals and radial distribution functions are calculated. The initial residual is therefore estimated, according to:
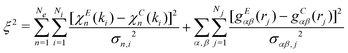 | (1) |
Having defined the terms in eqn (1) the typical RMC iterative algorithm then starts. One by one, each atom in the configuration is moved randomly with a possible maximum displacement and the new position is retained or discarded accordingly to the Metropolis sampling. Additional constraints can be also introduced: if the distance between two atoms become smaller than a pre-defined minimum distance the move is rejected (hard-sphere model), and for molecular cases a maximum distance can also be imposed to avoid that the molecule breaks apart. After all atoms have been moved (this is what we consider a RMC move), the maximum distance displacement is increased or decreased depending on the acceptance rate for the moves (decreased if less than 50% of moves were accepted) and the process is then repeated. After some number of RMC moves, the residual reaches a minimum value around which it will oscillate, indicating that convergence to an equilibrium structure is reached. A series of equilibrium configurations is then saved for structural analysis.
The indipendent signals χEn(ki) and gEαβ(rj) contribute in the same form to the two terms defining the residual function in eqn (1). The first term is related to the XAFS signals while the second can include X-ray or neutron diffraction data using suitable radial distribution retrieval schemes applied to the experimental structure factors. The pair distributions related to the second term can be also obtained directly by MD or MC computer simulations. For both terms the floating variables used in RMC refinements are the atomic coordinates.
As also described in previous publications,24,33,34 the practical implementation of the RMC-GnXAS refinement is carried out using directly the raw XAFS signals χEn(ki) obtained by a preliminary data-analysis performed using the fitheo program (GnXAS suite) using a suitable structural model. The extraction of the χEn(ki) signals is done by a suitable modeling of the background and normalization functions, as usual within the GnXAS fitting procedures3 and is considered to be accurate for the successive refinement purposes. Moreover, the pre-analysis provides also estimates for the values of relevant XAFS non-structural parameters (amplitude reduction factor S02, difference between energy scales of simulated and experimental data E0, experimental energy resolution). Those parameters are presently kept fixed in the RMC-GnXAS refinement, limiting the floating variables to the atomic coordinates which also define automatically the pair and higher-order distributions. An extension of the present scheme incorporating XAFS non-structural parameters (and background modeling) is conceptually possible and technically feasible but the present option is to treat the XAFS signals similarly to ND or XRD data, for which only the final result of the extraction of the structure factor (and g(r)) are usually reported and employed in RMC. In the present RMC-GnXAS applications to condensed systems we have also opted to keep constant the density and cell parameters, so that only the atomic fractional coordinates are used as floating variables.
The typical size of the ensemble of atoms and the accuracy of the structural parameters that can be obtained are important features of the simulation process. Details on configuration sizes and on the typical uncertainty on average structural quantities in simple monoatomic systems have been given in ref. 24. Typical configuration sizes are generally in the 103–104 range for the number of atoms, whereas larger ensembles are not found to improve the quality of the refinement on simple test cases. The uncertainty on selected structural parameters (for example, a given bond distance) can be evaluated looking at the fluctuations observed during the RMC procedure.24 It must be stressed again that the three dimensional structure produced by RMC is simply a model consistent with the available data and constraints, and is not unique. Other methods producing structural models equally consistent with the available data and constraints are equally acceptable. Of course, increasing the number of experimental data and constraints is likely to reduce the number of acceptable structural models. Therefore, the inclusion of multiple-edge XAFS data and pair distribution constraints obtained by diffraction, for example, is likely to produce more stable structural models for the given substance under consideration.
Another interesting question is how much the energy extension and the noise of the experimental XAFS data are affecting the RMC structural refinement and the average structural quantities of interest. The answer is basically related to the definition of the χ2-like random variable for RMC refinement (see eqn (1)) which contains both noise functions and wave-vector extensions of the experimental data. Clearly, higher levels of noise will correspond to easier adjustments of the χ2-like function that in the limit of infinite noise is of course insensitive to the particular model structure. Therefore, larger fluctuations for the atomic configurations of the models will be expected for higher noise levels. An example of the effect of an increasing noise in XAFS data of molecular Br2 is given in the next sections. The question about the energy extension is more subtle. Eqn (1) contains a simple summation over the energy points indicating a more stringent constraint for the structural model increasing the number of points (energy limit for regularly spaced signals). However, there is a natural decay in the amplitude and a typical frequency of the oscillating XAFS signals so that the effect of the choice of a given energy (or wave vector k) extension in XAFS may be system-dependent and need more detailed studies.35
4 Examples of molecular systems
4.1 Gas-phase bromine
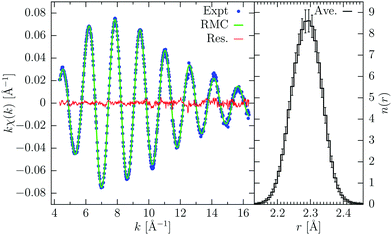
Gaseous bromine, Br2, is a simple diatomic molecule: being the simplest system we can study, it is often used as benchmark case for various tests. The Br K-edge XAFS signal is completely determined by the distribution of the molecular bond distances, consisting in an approximately Gaussian peak centered at r = 2.289 Å and standard deviation σ2 = 0.0019 Å2 (see ref. 24 and references therein). For the RMC refinements we used 2500 replicas for reproducing the k-weighted XAFS signal, which was extracted from the experimental data by a conventional XAFS peak-fitting procedure using GnXAS. In this way we also obtained the values of the non-structural parameters, which are not refined during the RMC process: the energy difference between experimental and theoretical scale, E0 − Ee = 2.0 eV, and the reduction factor S02 = 1.00. Lower and upper limit to the Br–Br distance were imposed at 2.0 and 2.55 Å respectively. After few moves, the RMC simulation already converged and after reaching equilibrium we accumulated 1000 moves to calculate average quantities. The RMC calculated signal and the corresponding number distribution n(r) are shown in Fig. 1. The average distance and Debye–Waller like factor calculated from RMC coordinates are, respectively, R = 2.2889(2) Å and σR2 = 2.03(5) × 10−3 Å2, in agreement with previous results. The deviations are calculated as maximum and minimum values between different RMC equilibrium configurations, therefore these values represent the oscillations of the average quantities during the RMC process. Of course, they account only for statistical fluctuations and do not consider possible non-statistical (systematic) errors possibly present in both experiments and MS calculations.The obtained results on the average structure of molecular bromine are in nice agreement with previous determinations. However, we can use this simple case to investigate how the noise on the experimental data affects the results of the RMC refinement. Noise enters into the RMC procedure not only in the fluctuations of the data under consideration, but also in the definition of the residual (σ2 in eqn (1)). A higher value of the noise produces lower values of the residual χ2-like function (ξ2), which implies a higher probability of accepting moves increasing the residual function and therefore a more disordered structure. In other words, as mentioned above, the role of the noise is equivalent to the temperature factor kBT in Metropolis Monte Carlo (MMC) method.32
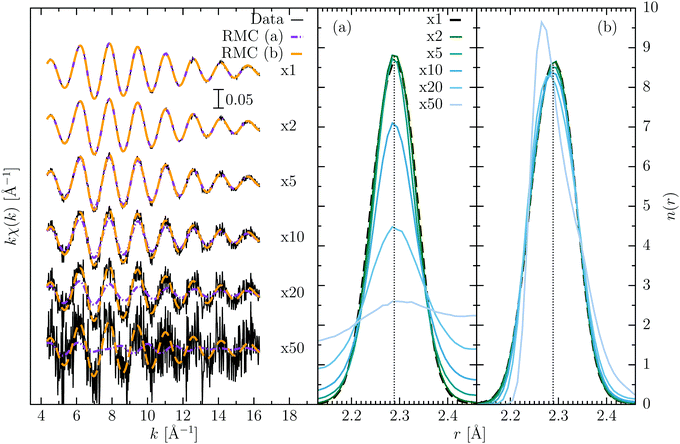
In this test, we have gradually increased the noise present in the original data. For the k-weighted XAFS signal under consideration, noise has been estimated to be of the order of σ2 ≃ 10−6. We have then added artificially increasing levels of random noise (from ×2 to ×50 the original one) and run specific RMC refinements for each of them. The RMC procedures were applied in two different ways: the first case (a) is one where the noise σi2 is correctly estimated and inserted in eqn (1); the second case (b) in which we used the original values for the noise σi2 (≃10−6) independently of the actual level of noise included in the XAFS data.
Fig. 2 shows the XAFS data incorporating different levels of noise, and the results of the analysis in the two different scenarios (a) and (b). When the level of noise is still close to the original one, the results are similar and close to the original data, but as the noise increases two different behaviors occur. For case (a), the quality of the fit decreases strongly when the noise reaches higher values (>10−5). The bond distance distribution appears to be broadened, similarly, as stated before, to having defined an increased formal “temperature”. The peak position still remains at the correct value indeed. This is to be expected if we think at the extreme case where the noise is much greater than the signal: there should be nothing to fit and the distribution is flat, being unsensitive to the XAFS data. For case (b) instead, the use of an artificially lower noise, as compared to that applied to the XAFS data, produces a better refinement of the noisy XAFS data, being more stringent the condition related to eqn (1). The pair distribution in this case seems more stable but becomes progressively skewed as compared to the original curve for high levels of noise. What happens in this case is that the configuration freezes around a minimum from which it hardly moves. We have also tried a third approach, where the noise was slowly reduced to the value of 10−6 during the RMC refinement (similar to a sort of annealing process), but the final results were basically identical to case (b). All the calculations started from the same starting configuration, and we additionally tested that the final results do not change if a different initial configuration were used.
It is difficult to clearly state which is the more advisable procedure for reliable RMC refinements accounting for the noise, since each method has its drawbacks. Using a correctly estimated noise, as defined in the mathematical background of RMC exposed in Sec. 2, we found results in agreement with the general rule of RMC of finding the most disordered structure that reproduces the data, but in the case of highly noisy data an artificially lower noise may be a more clever strategy to obtain more realistic distributions. Although in this case, deviations from the correct structure could occur. A manuscript with a more in-depth investigation and discussion about this topic is in preparation by the authors.35
4.2 Gas-phase GeI4
As an example of multi-atomic molecule we consider gaseous GeI4, a five atom molecule with tetrahedral (Td) symmetry. This case was also examined in a previous article.36 Here, we have here repeated the calculations with a larger number of atoms, using a total of 4000 replicas (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms). The gas-phase molecule XAS spectra was measured at about T ≃ 553 K at the I K-edge. A standard peak-fitting procedure was carried out on the data in order to extract the XAFS structural signal and obtain the non-structural parameters, the energy shift E0 − Ee = 5.8 eV and S02 = 1.00. The data consisted in a total of NXAS = 743 points.
000 atoms). The gas-phase molecule XAS spectra was measured at about T ≃ 553 K at the I K-edge. A standard peak-fitting procedure was carried out on the data in order to extract the XAFS structural signal and obtain the non-structural parameters, the energy shift E0 − Ee = 5.8 eV and S02 = 1.00. The data consisted in a total of NXAS = 743 points.
RMC refinements were carried using the extracted XAFS signal (collected at a temperature T = 553 K) together with number distributions obtained by electron diffraction data,37 available at T = 350 K (Δr = 0.01 Å spacing, N = 285 points). Additional constraints on closest and maximum distances were used to avoid intra-molecular separations: for Ge–I atoms, 2.15 and 3.00 Å, for I–I atoms, 3.20 and 4.85 Å, respectively. After an initial run to reach convergence (achieved after 50 moves), the RMC refinement was kept running for 1000 steps saving the coordinates every 10 steps, for a total of 100 equilibrium configurations from which we calculated the average quantities shown in Fig. 3.
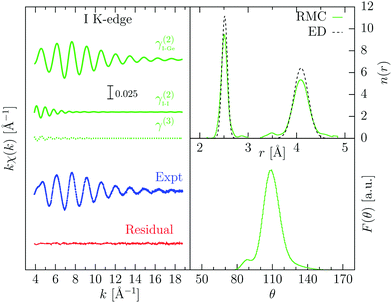 | ||
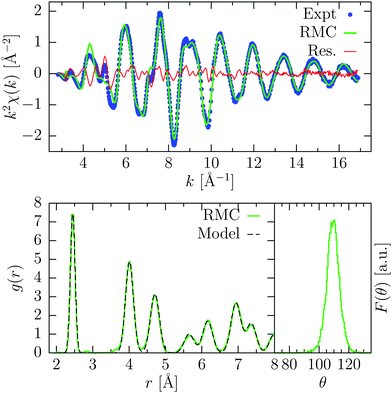
| Fig. 3 RMC refinement of gas-phase GeI4 XAFS data (T = 553 K). On the left: experimental I K-edge XAFS signal (Expt, blue dots), and calculated signals from RMC coordinates showing the contributions of different atomic configurations (green lines I–I, I–Ge, and I–Ge–I, see text). The almost flat residual is shown as a red line. Top right: number distribution function n(r) obtained from averaging 100 RMC configurations, compared with ED data (ref. 37). The broadening of the peaks is assigned to the different temperature between the two experiments. Bottom right: bond-angle distribution from the central Ge atom. The main peak centered around 109° indicates a tetrahedral configuration. | ||
The refinement of the EXAFS signal is excellent as indicated by the almost flat residual in Fig. 3. The main contribution to the XAFS signal comes from the two-body γ2 I–Ge contribution, although I–I contributions are also important to reproduce oscillations in the lower k region of the spectra as shown in Fig. 3. The three-body term I–Ge–I is almost negligible. The number density distribution obtained from RMC agrees well with the previous one determined by ED, although the peaks are broader, due to the higher temperature of the XAFS experiment. Average cumulants for the distributions of the two peaks have been calculated from atomic coordinates. For the Ge–I peak, the average distance is R1 = 2.507(1) Å and the standard deviation σ12 = 5.13(4) × 10−3 Å2; while for the I–I peak, R2 = 4.084(1) Å and σ22 = 35.0(4) × 10−3 Å2. The bond-angle distribution centered on the Ge atoms (bottom right of Fig. 3) shows a well-defined peak centered around 109.3°, close to the ideal tetrahedral angle, with a standard deviation of about 9.5°.
Overall the results agree nicely with previously published data,36 confirming our previous finding that increasing the number of atoms does not improve the RMC refinement after reaching sufficient accuracy.24
5 Examples of crystalline systems
5.1 Germanium
Germanium is an important semiconductor material with a wide range of applications. Its crystal configuration at ambient condition is the diamond structure, where atoms form covalent bonds with their 4 nearest neighbors in a typical tetrahedral configuration corresponding to a bond-angle of about 109.47°. Ge also possesses a rich phase diagram upon increasing pressure, where the tetrahedral structure is broken in favor of more dense and metallic phases and meta-stable phases upon decompression.38The c-Ge K-edge XAFS spectrum collected at room temperature (experimental details can be found in ref. 7) is mainly composed by the two-body MS terms related to the first three coordination shells (first three peaks of the radial distribution), while three-body oscillations can be considered negligible. RMC simulations can be used in this case to obtain information about the bond-angle distribution also including contributions from long-distance shells using suitable additional constraints, since the amplitude of the XAFS signals decreases as 1/r2 and is also strongly damped by thermal disorder.
A starting configuration of 1728 atoms was created by combining 6 × 6 × 6 unit cells of diamond Ge with a lattice parameter value of 5.658 Å, in agreement with literature data at room temperature (see ref. 7 and refs. therein). From the pre-analysis we also obtained the non-structural parameters S02 = 0.8595 and E0 − Ee = −0.5 eV. The extracted XAFS signal consisted in a total of 600 points and the estimated noise for the k2-weighted data estimated to be of the order σ2 ≃ 10−4.
Before running the RMC simulation of XAFS data, an initial refinement was run using a model pair distribution function. Position and area of the peaks were a consequence of distances and coordination numbers related to the diamond crystal structure with the given lattice parameter. The widths of the peaks are due to the correlated vibrations of the atoms (Debye–Waller-like factors σR2) for which we can find several different approximations for increasing shell distances. In our case, we used values obtained by DFT39 for the first three shells, σR2 = 3.98, 11.91, 15.03 × 10−3 Å2 respectively. The Debye–Waller-like of farther shells were fixed to 18 × 10−3 Å2, corresponding to the limiting case of uncorrelated vibrations. The RMC refinement using the resulting g(r) (Δr = 0.025 Å, N = 240 points) was carried out for 500 RMC moves, and the final configuration was used as the starting configuration for the subsequent full RMC analysis. The noise function for g(r) data was chosen to account for pair statistics (see Section 3). The XAFS signals of crystalline Ge were calculated up to a cut-off distance of 7.8 Å with a Gaussian smoothing of 0.3 Å. A closest distance constraint was also imposed, so that atoms could not become closer than 2 Å.
The results of the full RMC simulation are shown in Fig. 4. We can see that the XAFS signal is well reproduced, with some small high-frequency oscillations in the residual and a feature in the lower k-range, around 5 Å−1, that could be associated with an additional multiple-electron excitation in the background.
The pair distribution function obtained by RMC agrees closely to the model distribution previously mentioned, showing that the latter one was a good approximation to the thermal disorder present in crystalline Ge at room temperature. The first nearest-neighbor distribution was found to show an average distance R = 2.4502(4) Å and standard deviation σ2 = 3.26(2) × 10−3 Å, in agreement with previous findings.7 The bond-angle distribution of the first nearest-neighbors is also shown in Fig. 4, where we observe a clear peak centered around 109.4° (tetrahedral angle), with a standard deviation σ = 4.1.
In Fig. 5 we show the results of a RMC refinement using only the XAFS experimental data. In this case, we have used only the first sum in eqn (1). As expected, the residual in this case slightly improves, although some minor disagreements still remain. Looking at the pair distribution function obtained, we see the appearance of small bumps around 2.9, 3.5 and 5.4 Å which are not compatible with the diamond structure, which is found to be very disordered at large distances. On the other hand, the first peak is almost identical, because of the high sensitivity of XAFS at short distances. This finding confirms that for crystalline materials, whose average structure is known, the inclusion of a model distribution (obtained by experiments or simulations) can avoid the appearance of unphysical features related to the intrinsic sensitivity of XAFS to the local structure within a few Å around photoabsorbing sites.
5.2 Silver bromide
An interesting example of the application of RMC to a multiatomic condensed system is Silver Bromide (AgBr). Very good multiple-edge XAFS data have been collected at the ESRF (BM29) and analyzed several years ago8 using the peak-fitting technique and showing that useful structural information can be obtained both for crystalline and liquid phases. In particular, clear evidence for an asymmetric distribution of the first-neighbor distances was found in crystalline AgBr, and for an increasing skewness with temperature. Moreover, the structure of liquid AgBr was studied by using proper constraints for the medium and long-range correlations as described in ref. 8, 10, 14 and 17.As mentioned above, RMC XAFS data-analysis offers the possibility of overcoming the peak-fitting technique producing realistic models for the tridimensional structure, without the limitation of a given functional form for the radial and higher-order distribution functions. This may be interesting for the AgBr case for which we can put to a test particular features like the strong asymmetry of the first-neighbour distribution in crystalline AgBr and the shape of the radial distributions in liquid AgBr as shown in the next sections.
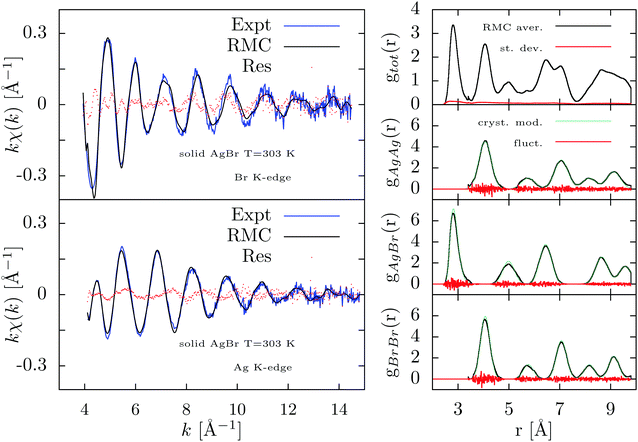
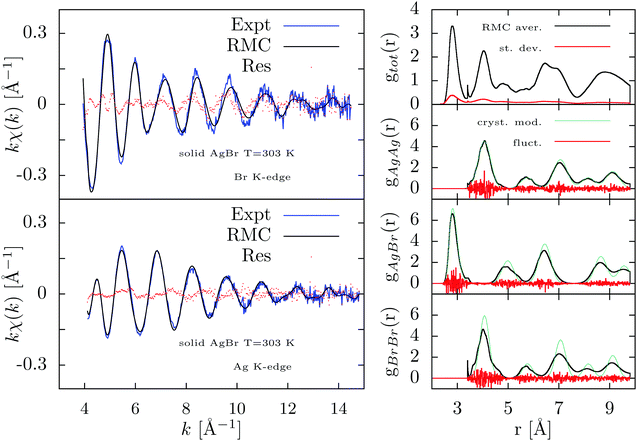
The starting model for the RMC XAFS data-analysis of solid AgBr has been a box containing 125 cubic unit cells (5 × 5 × 5) for a total of 1000 atoms. The atomic positions have been initially adjusted to model a realistic radial distribution function by RMC, using the known density of solid AgBr at 303 K (lattice parameter a = 5.7745 Å corresponding to ∼ 0.04155 atoms Å−3) and suitable estimates for the variances σn2 of the peaks (n = 1, 2, 3,…) of the radial distribution function g(r) corresponding to specific coordination shells (Ag–Ag, Ag–Br, Br–Br) in crystalline AgBr (see right-hand panels of Fig. 6 and 7 as an example). For this investigation, evaluation of the variances (mean-square relative displacements) associated with Ag–Ag, Ag–Br, and Br–Br distances (shells) was carried out using a simple model for atomic vibrations. The known difference in Debye–Waller factors related to Ag and Br positions40 and a simplified Keating dispersion model,41,42 within the Debye approximation43,44 (Debye temperature θD ∼ 140 K), was used to model the increase of the variances with distance, taking into account the results of previous XAFS investigations8 indicating precise values for the first-neighbor distribution (R = 2.893 Å, σ12 = 0.0285 Å2, skewness β1 = 0.67).
Subsequently, we have performed RMC refinements including directly the XAFS data collected at both Br and Ag K-edges of crystal AgBr at 303 K. The XAFS structural signals χ(k) were extracted for both edges using the GnXAS suite of programs and used subsequently with a k2 weight (k2χ(k), 422 and 424 data points for Br and Ag K-edge respectively). In this work we have kept fixed the background and normalization functions as well as the values of all the relevant non-structural parameters (Edge energy, S02, experimental resolution) as described in a previous work.8 More details about the XAFS data-analysis of AgBr using GnXAS can be found elsewhere.8
Here we show the main results obtained by RMC XAFS refinements either using a long-distance radial distribution constraint provided by realistic g(r) models (Fig. 6) or without those constraints (Fig. 7).
The RMC refinements were carried out using rather standard prescriptions regarding other constraints such as the density (kept fixed to the initial value) and closest approach distance limits. Choice of the closest approach distances is usually not obvious and in this case they were inferred by the starting radial distribution model (2.35 Å for AgBr and 3.4 Å for BrBr and AgAg distances). Shorter distances were not allowed in the final model. An important factor in those multiple data-set RMC refinements is the noise function to be used, that should reproduce the actual uncertainty of the data in order to mimic the χ2 statistical function. The noise functions adopted for XAFS data correspond to the statistical fluctuations of the data and were estimated by a specific program (noise).33,34 When using the radial distributions as a further long-distance constraint, the noise function was calibrated to account for pair statistics, so that the typical fluctuations are inversely proportional to the number of pair distances found in a given radial bin. For a constant radial mesh (in this case points were equally spaced Δr = 0.01 Å), fluctuations are obviously higher at short distances and the noise function is inversely proportional to r2.33,34 The global cut-off distance was set to 9.8 Å while XAFS simulations were carried out using a smoothing half-Gaussian window centered at Rwin = 8.7 Å with standard deviation ΔR = 0.3 Å (this is important to avoid truncation and side effects at long distances). We verified that other choices of these parameters in reasonable ranges (Rwin ∼ 5–9 Å and ΔR ∼ 0.3–0.5 Å) do not affect final results.
We have allowed a total of 104 RMC moves for each atom, corresponding to a total of 107 refinement attempts, verifying convergence to a given minimum.24 As the expected residual value corresponds to the number of data points, this turns out to be different when including the radial distributions (gBrBr, gAgBr, gAgAg each one 780 points). In the present RMC procedure, the expected residual value was 3186 when including the medium/long-range constraint associated with the three partial radial distributions and 846 when considering only the XAFS signals.
In Fig. 6 we report the results of the RMC refinement considering both the XAFS signals and the radial distribution constraints. The agreement among RMC simulations and experimental XAFS data is pretty good as shown in the left panels of Fig. 6 although the residual curves indicate that there is still some unexplained signal especially for the Br K-edge. The resulting partial and total distribution functions, averaged over the last 2000 RMC moves and shown in the right-hand panel of Fig. 6, indicate only small intrinsic fluctuations and minor differences as compared to the g(r) models. Due to the different vibrational amplitudes at Ag and Br sites,40 the peaks of the partial gAgAg distribution are broader than those of the gBrBr one. The crystalline structure is obviously retained.
In Fig. 7 we show the results of the RMC refinement carried out only considering the XAFS signals reported in the left panels. There is a visible slight improvement in the agreement obtained in this unconstrained refinement, but we observe much larger fluctuations (as compared to Fig. 6) in the reconstructed radial distributions reported in the right-hand panels of Fig. 7. Moreover, the peaks of the gAgBr and gBrBrradial distributions (averaged over the last 2000 RMC moves) are largely broadened departing also for simple Gaussian profiles. The resulting distributions are not compatible with previous data indicating different vibrational amplitudes for Ag and Br40 ions although the first-neighbor AgBr peak (the only one strongly constrained by XAFS) is in agreement with the constrained RMC refinement of Fig. 6 and with previous investigations.8 These results reflect naturally the short-range nature of XAFS data, for which accurate information can be obtained only for short distances, and the fact that RMC converge to the most disordered structure (higher Entropy) compatible with the given set of data under consideration.
6 Disordered systems
6.1 Amorphous germanium
Another interesting application of RMC is the study of amorphous and glassy materials. As explained in the introduction, this is particularly useful for the analysis of XAFS data, where the standard peak-fitting procedure presents some limitations. Germanium, which we have shown in the previous section in the crystalline phase, has also a glassy phase at ambient conditions, with a low-density to high-density transition upon application of pressure.45 XAFS data of amorphous Ge (a-Ge) were collected at room temperature.7For the initial configuration, we used 6 × 6 × 6 unit cell of diamond structure with a lattice parameter a = 5.737 Å, in order to reproduce the experimental value of the density for a-Ge (ρ = 0.04236 atoms Å−3). An initial refinement was carried out using only a pair distribution function obtained from X-ray diffraction data46 as a constraint for a total of 104 steps, to make sure that the initial crystal structure became completely amorphous. The binning step for determining the g(r) is Δr = 0.025 Å, resulting in N = 240 data points. The last configuration obtained was used as starting position for the RMC refinement including XAFS data.
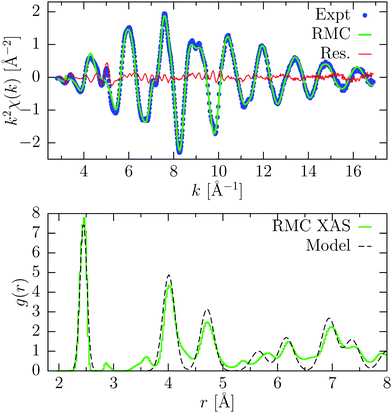
RMC results for a-Ge are shown in Fig. 8. The RMC simulation was extended to 1500 RMC moves and convergence was achieved after about 50 moves. The experimental XAFS signal consisted of NXAS = 658 points and was reproduced quite accurately. The XAFS signal is described mainly by a single well-defined oscillation, associated with first nearest-neighbors at an average distance R = 2.470(1) Å and bond variance σ2 = 5.1(1) × 10−3 Å2, calculated directly from the RMC coordinates of the atoms in the range 2.25–2.70 Å, and in close agreement with previously published results.7 The shape of the first g(r) peak is therefore mainly determined by refining the XAFS data. This explains the differences observed in the first peak with the model obtained from XRD, which is less sensitive to short-range ordering. At higher distance instead, the pair distribution function follows closely the XRD model, since EXAFS contributions are strongly damped (see Fig. 8, RMC XAS + XRD). In this way, we exploit the complementarity of the two techniques, because the XRD data probe the intermediate and long-range structure, while XAFS is more sensitive to the short-range. In fact, without the additional constraint of the pair distribution function, the resulting g(r) obtained by RMC reported in Fig. 8 (RMC XAS, lower panel) shows a practically featureless long-distance tail and is not reproducing at all the existing XRD data. On the other hand, the XAFS data are nicely reproduced with similar values for the first-neighbor distribution (R = 2.472(2) Å and width σR2 = 5.4(4) × 10−3 Å2).
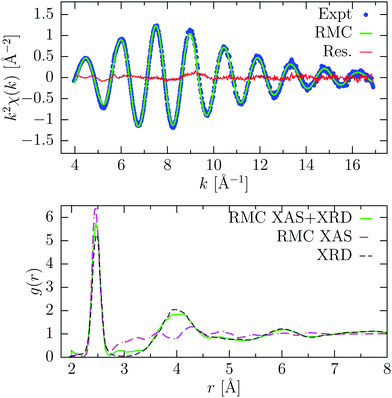 | ||
| Fig. 8 Result of RMC refinement for amorphous Ge at room temperature. Top panel: experimental K-edge XAFS signal (Expt, blue points) and average signal obtained from RMC coordinates after convergence (RMC, green line) using both XAS and XRD data. The difference spectrum is also shown (Res., red line). Bottom panel: pair distribution function g(r) obtained from RMC considering only XAFS data (RMC XAS, magenta dashed-dotted line), or using both XAFS and XRD data (RMC XAS + XRD, green solid line). The g(r) obtained by X-ray diffraction46 (XRD, dashed) is also shown. | ||
6.2 Molten silver bromide
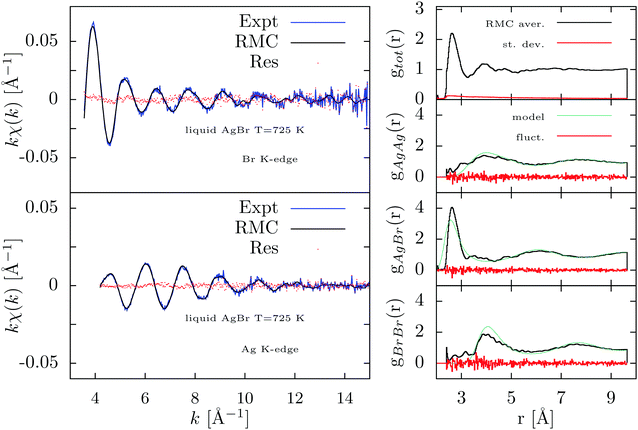
As anticipated in the previous sections, we have performed a RMC-GnXAS refinement of multiple-edge XAFS data of liquid AgBr. Previously, the structure of liquid AgBr was investigated by XAFS8 using proper constraints for the medium and long-range correlations as described in ref. 10, 14 and 17. Specific g(r) functions obtained by neutron diffraction47 or molecular-dynamics simulations48 were used for reproducing the structure beyond the first-neighbor distribution. Low-noise XAFS data of liquid AgBr at 725 K were collected at the ESRF (BM29) and are here re-analyzed by RMC-GnXAS using basically the same strategy illustrated above for solid AgBr.The starting model for the RMC-GnXAS data-analysis of liquid AgBr has been again a box containing 125 cubic unit cells (5 × 5 × 5) for a total of 1000 atoms. The atomic positions have been initially adjusted using a specific RMC procedure applied only to given radial distribution functions, in this case taken from ref. 48 using the known atomic density for the liquid phase at 725 K (ρ ∼ 0.0354 atoms Å−3). This initial procedure introduces the necessary spread in atomic positions for a typically highly disordered phase facilitating the successive refinement using XAFS data. We have then performed RMC refinements including directly the XAFS data of liquid AgBr collected at both Br and Ag K-edges. The XAFS structural signals χ(k) were extracted for both edges using the GnXAS suite of programs and used subsequently with a k1 weight (kχ(k), 456 and 438 data points for Br and Ag K-edge respectively). Similarly to the case of solid AgBr, we have used the same background and normalization functions, as well as the values of all the relevant non-structural parameters (Edge energy, S02, experimental resolution), as reported in a previous work.8
The RMC-GnXAS refinements were carried out using typical constraints such as the given atomic density and closest approach distance limits. The closest approach distances were chosen to be 2.05 Å for AgBr and 2.4 Å for BrBr and AgAg distances, allowing rather short distances as expected in this liquid ionic system. The noise functions adopted for XAFS data were estimated to reproduce the statistical fluctuations of the data as in previous cases. The noise function applied to the model radial distribution functions was calibrated as usual to account for pair statistics.33,34 In this specific application, we have used a constant radial mesh (in this case points were equally spaced Δr = 0.02 Å). The global cut-off distance was set to 9.65 Å while XAFS simulations were carried out using a smoothing half-Gaussian window centered at 8.5 Å with standard deviation 0.4 Å.
We have allowed a total of 104 RMC moves for each atom, corresponding to a total of 107 refinement attempts, verifying convergence to a given minimum.24 The expected residual value correspond to the total number of data points (2040) including the radial distributions (gBrBr,gAgBr,gAgAg total of 1146 points).
In Fig. 9 we report the results of the present RMC-GnXAS refinement of liquid AgBr. The agreement between RMC simulations and experimental XAFS data is rather spectacular as shown in the left panels of Fig. 9 where the residual curves are substantially dominated by statistical noise. The RMC residual has been found to converge near to the expected value quite rapidly, typically within 100 RMC moves (105 atom moves) over the total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 of the entire run. The resulting partial and total distribution functions, averaged over the last 2000 RMC moves and shown in the right-hand panel of Fig. 9, indicate small intrinsic fluctuations with the possible exception of the short-range side of the gAgAg distribution.
000 of the entire run. The resulting partial and total distribution functions, averaged over the last 2000 RMC moves and shown in the right-hand panel of Fig. 9, indicate small intrinsic fluctuations with the possible exception of the short-range side of the gAgAg distribution.
The results obtained here nicely reproduce those obtained for the shape of the short-range gAgBr peak using the more standard peak-fitting technique reported in ref. 8. The first-neighbor Ag–Br distribution results to be narrower than the current models for the liquid structure based on neutron diffraction47 and molecular-dynamics calculations48,49 as also previously noted. The shape of the first Ag–Br peak is determined very accurately as shown by the small fluctuations reported in the right-hand panel of Fig. 9 and reflects the exceptional short-range XAFS sensitivity. On the other hand, larger fluctuations are observed for the gAgAg and gBrBr functions, as a consequence of the decreased sensitivity at medium and large distances.
Presence of Ag–Ag and Br–Br distances in the short-range side below 4 Å confirms the occurrence of an almost structureless and broad distribution that can be typical of these ionic liquids. The long range structure found in this RMC refinement is compatible with the structural model used here48 while larger deviations are observed at intermediate distances.
Generally speaking, the results obtained here confirm that the current MD models (see for example ref. 48 and 49) for the first-neighbor Ag-Br distribution are broader and clearly shifted toward shorter distances, indicating the need of developing more accurate models for the interaction potential, particularly for the short-range repulsive part. The same holds for the results of neutron diffraction experiments, also analyzed using RMC, providing accurate information on medium-range order, but less precise at short distances.8,14
7 Conclusions
In this work, we have presented a detailed account of the application of the Reverse Monte Carlo refinement methods for XAFS structural refinements in exemplary molecular and condensed systems. The method used is an application of the original RMC technique based rigorously on the Metropolis Monte Carlo algorithm, using XAFS calculations performed by the advanced RMC-GnXAS programs. This approach has been used for multiple-edge studies of molecules, crystalline solids as well as glasses and liquids, including the long-range constraints provided by other techniques (e.g. diffraction). The RMC-GnXAS method has been developed to consider naturally a combination of experimental XAFS data and model pair distribution functions, including directly the noise of the experimental data in the random variable to be minimized in the Monte Carlo iterative process.The detailed usage, potential and possible weaknesses of the RMC method are discussed looking also at specific exemplary applications like gaseous Br2 and GeI4, crystalline Ge and AgBr, as well as amorphous Ge and liquid AgBr. A specific study on the effect of noise levels in XAFS data on the derived distribution functions is presented for gaseous Br2, showing how the accuracy of structural results depend on accounting data fluctuations. The importance of the long-range constraints in RMC refinement of XAFS data is also discussed in this work with specific examples. The lack of these constraints results in largely disordered structures for distances beyond the first coordination shells, in agreement with the short-range nature of the XAFS technique.
The method and applications reported in this work highlight the general interest of the RMC technique applied to XAFS data within the RMC-GnXAS scheme, and the importance of combining multiple set of data for improving the accuracy of the structural refinements both at short and long range.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. I. acknowledges financial support from the Japan Science and Technology Agency Core Research for Evolutional Science and Technology (CREST) program grant number JPMJCR1861.Notes and references
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- A. Filipponi, A. Di Cicco and C. R. Natoli, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15122–15134 CrossRef CAS PubMed.
- A. Filipponi and A. Di Cicco, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15135 CrossRef CAS PubMed.
- G. Bunker, Nucl. Instr. Methods, 1983, 207, 437–444 CrossRef CAS.
- S. A. Beccara, G. Dalba, P. Fornasini, R. Grisenti, F. Pederiva, A. Sanson, D. Diop and F. Rocca, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 140301 CrossRef.
- S. W. T. Price, N. Zonias, C.-K. Skylaris, T. I. Hyde, B. Ravel and A. E. Russell, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075439 CrossRef.
- A. Filipponi and A. Di Cicco, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12322–12336 CrossRef CAS PubMed.
- A. Di Cicco, M. Taglienti, M. Minicucci and A. Filipponi, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 12001–12013 CrossRef CAS.
- A. Di Cicco, Radiat. Phys. Chem., 2020, 175, 108077 CrossRef CAS.
- A. Filipponi, J. Phys.: Condens. Matter, 1994, 6, 8415–8427 CrossRef CAS.
- A. Trapananti and A. Di Cicco, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 014101 CrossRef.
- P. D'Angelo, A. Di Nola, A. Filipponi, N. V. Pavel and D. Roccatano, J. Chem. Phys., 1994, 100, 985–994 CrossRef.
- A. Di Cicco, M. J. Rosolen, R. Marassi, R. Tossici, A. Filipponi and J. Rybicki, J. Phys.: Condens. Matter, 1996, 8, 10779–10797 CrossRef CAS.
- A. Di Cicco, M. Minicucci and A. Filipponi, Phys. Rev. Lett., 1997, 78, 460–463 CrossRef CAS.
- A. Filipponi, A. Di Cicco and S. De Panfilis, Phys. Rev. Lett., 1999, 83, 560–563 CrossRef CAS.
- P. D'Angelo and N. V. Pavel, J. Chem. Phys., 1999, 111, 5107–5115 CrossRef.
- A. Filipponi, J. Phys.: Condens. Matter, 2001, 13, R23 CrossRef CAS.
- R. L. McGreevy and L. Pusztai, Mol. Sim., 1988, 1, 359–367 CrossRef.
- S. J. Gurman and R. L. McGreevy, J. Phys.: Condens. Matter, 1990, 2, 9463–9473 CrossRef.
- Y. Wang, K. Lu and C. Li, Phys. Rev. Lett., 1997, 79, 3664–3667 CrossRef CAS.
- M. Winterer, J. Appl. Phys., 2000, 88, 5635–5644 CrossRef CAS.
- J. Timoshenko, A. Kuzmin and J. Purans, Comput. Phys. Commun., 2012, 183, 1237–1245 CrossRef CAS.
- A. Di Cicco, A. Trapananti, S. Faggioni and A. Filipponi, PRL, 2003, 91, 135505-1–135505-4 Search PubMed.
- A. Di Cicco and A. Trapananti, J. Phys.: Condens. Matter, 2005, 17, S135–S144 CrossRef CAS.
- A. Di Cicco, A. Trapananti and A. Filipponi, Phys. Scripta, 2004, T115, 882–884 Search PubMed.
- A. Di Cicco, A. Trapananti, E. Principi, S. De Panfilis and A. Filipponi, Appl. Phys. Lett., 2006, 89, 221912 CrossRef.
- A. Di Cicco and A. Trapananti, J. Non-Cryst. Sol., 2007, 353, 3671–3678 CrossRef CAS.
- A. Di Cicco, F. Iesari, S. De Panfilis, M. Celino, S. Giusepponi and A. Filipponi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060102 CrossRef.
- N. Hara, A. Di Cicco, G. Tchoudinov, K. Hatada and C. R. Natoli, Symmetry, 2021, 13, 1021 CrossRef CAS.
- R. Kaplow, T. A. Rowe and B. L. Averbach, Phys. Rev., 1968, 168, 1068–1079 CrossRef CAS.
- R. McGreevy, M. A. Howe, D. Keen and K. N. Clausen, IOP Conf. Series, 1990, pp. 165–184 Search PubMed.
- R. L. McGreevy, J. Phys.: Condens. Matter, 2001, 13, R877–R913 CrossRef CAS.
- F. Iesari, K. Hatada, A. Trapananti, M. Minicucci and A. Di Cicco, in Multiple Scattering Theory for Spectroscopies, ed. D. Sébilleau, K. Hatada and H. Ebert, Springer International Publishing, 2018, vol. 204 of Springer Proceedings in Physics, pp. 221–256 Search PubMed.
- GNXAS. Extended suite of programs for advanced X-ray absorption data-analysis: methodology and practice, ed. A. Di Cicco, TASK publishing ISBN 978-83-908112-8-4, Gdansk, Poland, 2009.
- F. Iesari and A. Di Ciccoet al., under preparation.
- A. Di Cicco, F. Iesari, A. Trapananti, P. DAngelo and A. Filipponi, J. Chem. Phys., 2018, 148, 094307 CrossRef.
- N. Giricheva, G. Girichev, S. Shlykov, V. Titov and T. Chusova, Zhurnal Strukturnoi Khimii, 1986, 29, 50–54 Search PubMed.
- F. Coppari, J. Chervin, A. Congeduti, M. Lazzeri, A. Polian, E. Principi and A. Di Cicco, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115213 CrossRef.
- F. D. Vila, J. J. Rehr, H. H. Rossner and H. J. Krappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014301 CrossRef.
- S. Hull and D. A. Keen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 750–761 CrossRef CAS.
- A. Di Cicco, A. Bianconi and N. Pavel, Solid State Commun., 1987, 61, 635–639 CrossRef CAS.
- C. B. Walker and D. T. Keating, Acta Crystallogr., 1961, 14, 1170–1176 CrossRef.
- E. Sevillano, H. Meuth and J. J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 4908–4911 CrossRef CAS.
- S. K. Joshi and S. S. Mitra, Proc. Phys. Soc. (1958-1967), 1960, 76, 295–298 CrossRef CAS.
- G. Mancini, M. Celino, F. Iesari and A. D. Cicco, J. Phys.: Condens. Matter, 2015, 28, 015401 CrossRef PubMed.
- R. J. Temkin, W. Paul and G. A. N. Connell, Adv. Phys., 1973, 22, 581–641 CrossRef CAS.
- D. A. Keen, W. Hayes and R. L. McGreevy, J. Phys.: Condens. Matter, 1990, 2, 2773–2786 CrossRef CAS.
- C. Tasseven, J. Trullàs, O. Alcaraz, M. Silbert and A. Giró, J. Chem. Phys., 1997, 106, 7286–7294 CrossRef CAS.
- V. Bitrián and J. Trullàs, J. Phys. Chem. B, 2006, 110, 7490–7499 CrossRef PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2022 |