Multi-electron excitation contributions towards primary and satellite states in the photoelectron spectrum†
Received
13th October 2021
, Accepted 28th February 2022
First published on 1st March 2022
Abstract
The computation of Dyson orbitals and corresponding ionization energies has been implemented within the equation of motion coupled cluster singles, doubles and perturbative triples (EOM-CC3) method. Coupled to an accurate description of the electronic continuum via a time-dependent density functional approach using a multicentric B-spline basis, this yields highly accurate photoionization dynamical parameters (cross-sections, branching ratios, asymmetry parameters and dichroic coefficients) for primary (1h) states as well as satellite states of (2h1p) character. Illustrative results are presented for the molecular systems H2O, H2S, CS, CS2 and (S)-propylene oxide (a.k.a. methyloxirane).
1 Introduction
Significant advancements in high-resolution photoelectron spectroscopy have led to a renewed quest for accurate theoretical assignments, in particular of the high energy region of the photoelectron spectrum, comprising low intensity peaks.1,2 Under the sudden approximation limit,3 the photoelectron is assumed to be removed instantaneously from the system, without allowing for the other electrons to adjust to the hole potential. Under such circumstances, there is a finite probability of ionic state to be in its excited state, generating a satellite in the photoelectron spectrum. Starting from the initial state N-electron configuration, these satellite states are attributed to multi-electron excitations of 2h1p (two-hole one-particle) or higher order character.4 The appearance of satellites in the theoretical spectra is guided by both correlation and relaxation effects, the former describing the multi-electron excitation character, whereas the latter accounts for the rearrangement of the orbitals around the ionized hole. However, these two effects are inseparable to a certain degree.4–6
For the theoretical description of the shake-up satellite states, a method capable of capturing many-body effects is thus required. Based on Koopmans theorem, only primary (1h) states are accessible. This “breakdown of the molecular orbital picture” in molecular photoionization due to correlation effects was pointed out decades ago, see e.g. the work of Cederbaum and collaborators.4,7,8 Ever since, numerous efforts have been directed towards the development of theoretical methods that go beyond the simple Koopmans' picture of the process. The literature on the subject is vast and steadily growing. Without any ambition to give an exhaustive account, and starting from the correlated description of the bound states, we mention here various Green's function (GF) methods (see, e.g., ref. 9 for a recent review) like the Dyson and non-Dyson variants of the Algebraic Diagrammatic Construction to third order (ADC3),10–12 and the ‘outer valence’ GF approach (OVGF),13 see also ref. 14; the symmetry-adapted-cluster configuration interaction general-R (SACCI-R) approach;15,16 the Configuration Interaction (CI) method;17 multiconfigurational approaches like complete active space self-consistent field (CASSCF),18 restricted active space SCF (RASSCF) and CAS/RAS with a second-order perturbation theory (CASPT2/RASPT2).5,6,19–24
Popular correlated frameworks to compute molecular properties and spectra, including photoelectron spectra and photoionisation dynamical properties,25–29 are coupled cluster response theory (CCRT)30,31 and the equation of motion (EOM) coupled cluster method.32–35 CCRT provides size-intensive excitation energies and transition moments;30,31 EOM-CC32–35 gives the same excitation energies as CCRT, but the transition moments are different and not strictly size-intensive. On the other hand, the computational cost of EOM transition moments is less demanding than for CCRT and the size-intensivity errors are expected to be small. We therefore here use equation of motion coupled cluster singles, doubles and perturbative triples (EOM-CC3)36–40 ionization energies and corresponding Dyson orbitals13,25,41–44 to represent such transitions. The 2h1p satellites are in principle also attainable at the EOM coupled cluster singles and doubles (EOM-CCSD)25,27,32–34 level; however, their ionization energies can be rather overestimated.45 The triples' correction is the basic requirement for the precise calculation of both ionization energies and corresponding intensities. The square norms of the Dyson orbitals13,41–43 are proportional to the intensities of the photoelectron spectrum. Thus, it can be considered that the satellite state borrows intensity from the primary states that are mixed into it, leading to a decrease in intensity of the primary ionized states. In some cases, especially for transition metal complexes,46 it becomes difficult to distinguish between primary and satellite states.
The simulation of the individual-channel photoionization observables additionally requires an explicit description of the outgoing electron in conjunction with the bound state of the system. A popular strategy to evade this is to reconstruct the total cross-section from purely bound-state pseudo-spectral representations spanning over the post-ionization region using Stieltjes Imaging or Padé approximant techniques.47–54 However, these techniques are limited by the lack of proper asymptotic boundary conditions, which are needed to compute individual channel photoionization observables.
Several strategies have been developed to account for the continuum electrons. A straightforward method is to use simple analytic functions like plane waves and Coulomb waves.26 Though conceptually simple, these methods fail to reproduce complex phenomena like the appearance of Cooper minima or shape resonances.27 More accurate approaches determine the continuum orbitals numerically using stationary conditions formulated within the R-matrix,55,56 Schwinger variational,57,58 complex Kohn59 and least-square or Galerkin methods.60,61 While grid methods can be easily implemented in one-center expansion (OCE) approaches,62 current trend is to employ a multicenter basis set, with a long range OCE and a small number of additional functions centered on the nuclei, in the spirit of the linear combination of atomic orbitals (LCAO) approach. For the one center radial functions, B-splines56,60,63,64 or similar finite elements65 are popular. A hybrid approach joining short-range Gaussians and long-range B-splines overlapping over an intermediate interval has also been shown viable.66,67 Gaussians or the same B-splines are used for the LCAO part.
As anticipated, we here present a study on the effect of the inclusion of triple excitations in the bound state description on both the primary and satellite ionized states. For this purpose, firstly the EOM-CC3 Dyson orbitals have been implemented in the eT software package.68 In order to account for the outgoing electron, multicentric B-spline time-dependent density functional theory is used.45 The Dyson orbitals are utilized not only to estimate the intensities in the photoelectron spectra, but first and foremost to compute the single-particle photoelectron matrix elements needed to obtain the photoionization observables.5,25,27
In Section 2, we detail the composite theoretical approach, with emphasis on the implementation of the EOM-CC3 Dyson orbital. The computational protocol used is described in Section 3. In Section 4, the devised formalism is validated by studying the valence ionization dynamics of simple molecules like H2O, H2S, CS, CS2 and (S)-C3H6O. Emphasis on the inner valence region of the spectra is given due to the presence of multiple closely-lying ionized states of substantial 2h1p nature. Comparison of CCSD and CC3 coupled to TD-DFT for the bound and continuum part, respectively, has been presented wherever deemed meaningful. Section 5 summarizes our findings.
2 Theory
The key quantity encapsulating all the information of the initial (ΨNi) and final composite state (Φf) of the system is given by the photoelectron matrix element,| | Dif = 〈ΨNi|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |Φf〉. |Φf〉. | (1) |
In eqn (1), ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) is the electric dipole moment. The most general approach is to expand Φf in a CI-type fashion, called the “close-coupling” form.69 A number of close-coupling implementations are available, and can give accurate results for small molecules, especially close to threshold.56,58,66,67 However, ab initio computations using the full expansion are computationally expensive and often unnecessary. We have restricted ourselves to the single channel approximation, where the final composite state is represented by the anti-symmetrized product of the photoelectron and the bound ionized state accessible at that particular energy
is the electric dipole moment. The most general approach is to expand Φf in a CI-type fashion, called the “close-coupling” form.69 A number of close-coupling implementations are available, and can give accurate results for small molecules, especially close to threshold.56,58,66,67 However, ab initio computations using the full expansion are computationally expensive and often unnecessary. We have restricted ourselves to the single channel approximation, where the final composite state is represented by the anti-symmetrized product of the photoelectron and the bound ionized state accessible at that particular energy| | 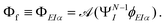 | (2) |
Under these assumptions, the photoelectron matrix element in eqn (1) boils down to a single particle photoelectron matrix element, given by| | Dif = 〈ϕDif|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |ϕEIα〉. |ϕEIα〉. | (3) |
All information about the bound initial N-electron and final (N − 1)-electron states is now compressed into the orbital function ϕDif, called the Dyson orbital.41–43 From now onward, we will drop the suffix if from ϕDif. For details on how to obtain the above simplified expression, we refer to, e.g., ref. 45 and the supplementary information file of ref. 27.
2.1 EOM-CC3 Dyson orbitals
The coupled cluster (CC) wave function is defined by| | 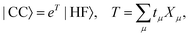 | (4) |
where the cluster operator T is composed of the excitation operator Xμ and the amplitudes tμ. The excitation operator consists of strings of singlet excitation operators, Eai, and maps the Hartree–Fock determinant into excited determinants |μ〉. We use the standard notation where indices i, j, k,… refer to occupied, a, b, c,… to virtual, and p, q, r,… to general orbitals. The hierarchy of coupled cluster methods is obtained by truncating the cluster operator at a certain number of excitations.70 We introduce the similarity transformed Hamiltonian,| | ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = e−THeT, = e−THeT, | (5) |
where the electronic (spin-free) Hamiltonian, H, in second quantization is defined as70| | 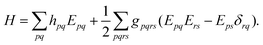 | (6) |
The amplitudes are obtained by solving the projected coupled cluster equations70| | 〈μ|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |HF〉 = Ωμ = 0, |HF〉 = Ωμ = 0, | (7) |
and the energy is given as| | ECC = 〈HF|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |HF〉. |HF〉. | (8) |
The projection space is generated by the contravariant excitation operator, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) μ, such that the determinants are biorthogonal to the determinants created by the cluster operator
μ, such that the determinants are biorthogonal to the determinants created by the cluster operator| | 〈μ| = 〈HF|![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) μ, |ν〉 = Xμ|HF〉, 〈μ|ν〉 = δμ,ν. μ, |ν〉 = Xμ|HF〉, 〈μ|ν〉 = δμ,ν. | (9) |
In EOM-CC theory,32 additional operators, Lm and Rm, are introduced that generate the m-th EOM states, 〈Lm| and |Rm〉:| | 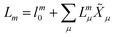 | (10) |
| | 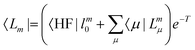 | (11) |
| | 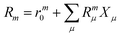 | (12) |
| | 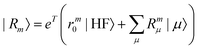 | (13) |
The additional parameters are determined as left and right eigenvectors of the similarity transformed Hamiltonian| | ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) TLm = EmLm TLm = EmLm | (14) |
| | ![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Rm = EmRm, Rm = EmRm, | (15) |
where the eigenvalue, Em, corresponds to the total energy of the state. Assuming that the ground state equations have been solved, the Hamiltonian matrix has the following form| | 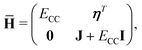 | (16) |
where J is the Jacobian, Jμν = 〈μ|[![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ,Xν]|HF〉 (also known as A) and ην = 〈 HF|[
,Xν]|HF〉 (also known as A) and ην = 〈 HF|[![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ,Xν]|HF〉. From the structure of the Hamiltonian matrix and the biorthonormality of the states, we find the left and right ground state solutions
,Xν]|HF〉. From the structure of the Hamiltonian matrix and the biorthonormality of the states, we find the left and right ground state solutions| | 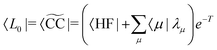 | (17) |
| | | |R0〉 = |CC〉 = eT|HF〉, | (18) |
where the multipliers, λμ, are determined from λTJ = −η. The excited states are obtained as| | 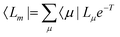 | (19) |
| | 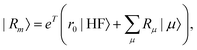 | (20) |
where m is larger than 0 and the superscript was removed from the amplitudes for simplicity. The parameter r0 is defined as 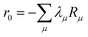 to ensure biorthogonality to the left ground state,
to ensure biorthogonality to the left ground state, 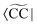 . Transition properties for a one-electron operator (in second quantization)
. Transition properties for a one-electron operator (in second quantization) 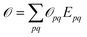 are given as biorthogonal expectation values,
are given as biorthogonal expectation values,| | 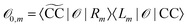 | (21) |
expressed in terms of transition densities| | 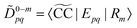 | (22) |
| | | Dm−0pq = 〈Lm|Epq|CC〉. | (23) |
In order to obtain the CC3 equations, we divide the Hamiltonian into a one-particle operator (F) and a fluctuation potential (U),The single excitation amplitudes are considered zeroth order parameters as they are crucial for orbital relaxation, while double and triple excitation amplitudes are first and second order in the perturbation, U, respectively. Introducing the perturbation expansion into the expression for the energy of the EOM states,| | Em = LTm![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Rm Rm | (25) |
and neglecting terms of fifth order and higher, yields the CC3 equations. Details about the derivation of the explicit terms and their implementation can be found in ref. 37, 38 and 40.
In EOM CC theory, ionization energies can be rigorously obtained by replacing the singlet excitation operators, ![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) μ and Xμ, in eqn (10) and (12) by particle nonconserving excitation operators like 1h, 2h1p,… operators, which defines the EOM-CC method for ionization potentials, EOM-IP-CC.33 However, as proposed by Stanton and Gauss,71 we can also compute the ionization energies by including a bath orbital in the virtual orbital space which does not interact with the other orbitals, and then projecting out all excitations that do not include the bath orbital during the solution of the eigenvalue equation.72 This approach has the advantage of requiring only a small modification to an existing EOM-CC code for excitation energies (EOM-EE-CC). As a disadvantage, its scaling is the same as EOM-CC for excitation energies, whereas a rigorous implementation of EOM-IP-CC scales one order less with the number of virtual orbitals (nv).
μ and Xμ, in eqn (10) and (12) by particle nonconserving excitation operators like 1h, 2h1p,… operators, which defines the EOM-CC method for ionization potentials, EOM-IP-CC.33 However, as proposed by Stanton and Gauss,71 we can also compute the ionization energies by including a bath orbital in the virtual orbital space which does not interact with the other orbitals, and then projecting out all excitations that do not include the bath orbital during the solution of the eigenvalue equation.72 This approach has the advantage of requiring only a small modification to an existing EOM-CC code for excitation energies (EOM-EE-CC). As a disadvantage, its scaling is the same as EOM-CC for excitation energies, whereas a rigorous implementation of EOM-IP-CC scales one order less with the number of virtual orbitals (nv).
Dyson orbitals can be described as the overlap between a N-electron wave function and a (N − 1)-electron wave function.13,25,41,42 Expressing a Dyson orbital, ϕD, in terms of molecular orbitals, ϕp, gives
| | 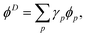 | (26) |
where the expansion coefficients are defined as
for general (
N − 1) and
N electron states, Ψ
N−1 and Ψ
N. The squared norm of the Dyson orbital is called the pole strength,
RF,
| | 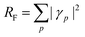 | (28) |
which is related to the intensity of the bands in the photoelectron spectrum. As coupled cluster is a non-Hermitian theory, two Dyson orbitals are obtained corresponding to the left and right ionized state for a given ionization potential
| | 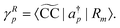 | (30) |
In analogy to the EOM-CC transition strength,
73,74 we define the pole strength as
27,45| | 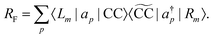 | (31) |
Due to the biorthonormality of the EOM states, the pole strength assumes values between zero and one, while the norms of individual left and right Dyson orbitals depend on the norm of the corresponding ionized states, which can be significantly larger than one. If
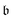
denotes the bath orbital,
eqn (29) and (30) can be rewritten as
| | 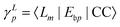 | (32) |
| | 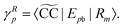 | (33) |
These expressions demonstrate that the left/right Dyson orbitals can be obtained as the row/column corresponding to the bath orbital of the EOM CC transition densities
Dm−0 and
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 0−m
0−m.
25 As the bath orbital is part of the virtual orbital space, only two of the four blocks of
Dm−0 and
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 0−m
0−m need to be constructed. Additionally, the ground state amplitudes
t and multipliers
λ are zero if one of their indices corresponds to the bath orbital. Therefore, the CC3 contribution to the right Dyson orbital consists of only four terms, and there is only a single term for the left Dyson orbital. We list these additional terms as follows (where we also use the symbol += to highlight that these terms are added to the CCSD-like ones):
| | 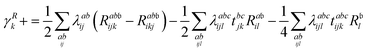 | (34) |
| | 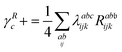 | (35) |
| | 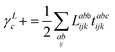 | (36) |
The CC3 ionization energies and Dyson orbitals have been implemented in a development version of the
eT program package
68 using a bath orbital. The bath orbital is added to the virtual space after the Hartree–Fock step and its corresponding integrals are set to zero. For a description of the algorithms to solve for the ground state, the excited states and transition densities we refer to ref.
40.
Table S1 (ESI†) summarizes the scaling per iteration to obtain the ground state amplitudes, t and λ, the excited state parameters, L and R, as well as the cost per left/right Dyson orbital as implemented in eT. In the current implementation, the Jacobian transformation of a trial vector is carried out in a triple loop over the occupied indices i, j, k. This allows us to use the full permutational symmetry of the triples amplitudes while keeping a dense block of the virtual indices for efficient matrix–matrix multiplications.75,76 For the ionized states this algorithm computes some unnecessary terms scaling as 8nv4no3 floating point operations (FLOP), because all amplitudes Lμ and Rμ that do not involve the bath orbital are zero. Switching to a loop over the virtual orbitals the scaling for the ionized states could be reduced to 8nv3no3 FLOP. However, the computation of the ground state parameters and the left Dyson orbitals would still scale as shown in Table S1 (ESI†) and the cost for the right Dyson orbitals could only be reduced to 6nv4no3 FLOP. For large systems and if many ionized states are requested, the savings would be significant, but for the systems considered in this work the scaling was not an issue and the optimization of the code is deferred.
2.2 Multicentric B-spline TD-DFT
In order to describe continuum orbitals, conventional  Gaussian type or Slater type orbitals are not very accurate, despite efforts to adapt them.77–79 Instead, we use a highly flexible linear combination of primitive B-spline functions (ζ),
Gaussian type or Slater type orbitals are not very accurate, despite efforts to adapt them.77–79 Instead, we use a highly flexible linear combination of primitive B-spline functions (ζ),| | 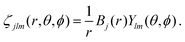 | (37) |
Within the Kohn–Sham (KS) static-exchange DFT approach, the Schrödinger equation has the form,
| | HKSϕi = εiϕi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ; i = 1, 2,…, n ; i = 1, 2,…, n | (38) |
where,
| | 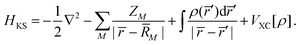 | (39) |
In the above expressions,
ρ is the ground state electron density obtained from a preliminary conventional SCF calculation,
ZM and
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) M
M are the atomic number and nuclear coordinate, respectively.
VXC is the exchange–correlation potential. As previously shown, the LB94 functional outperforms the LDA or GGA functionals for simulating KS photoionization, due to the correct asymptotic Coulomb behaviour.
80 The continuum KS orbitals are then extracted as the eigenfunctions of the Hamiltonian in
eqn (39), with given positive eigenvalue equal to the kinetic energy (
E) of the photoelectron. The problem is recast as to obtain the eigenvectors (
c) with a minimum modulus eigenvalue (
a) of the energy-dependent matrix
A†A(
E),
| | | A†A(E)c = ac, A(E) = H − ES, | (40) |
where
H and
S are the Hamiltonian and overlap matrices, respectively.
64,81
The natural extension of the KS-DFT approach to include interchannel coupling effects while still restricting the bound states to a single determinant representation is the TD-DFT method within the linear response formalism. The linear response of the electron density (δρ) due to an external potential is evaluated following the scheme by Zangwill and Soven.82 The effective self-consistent field potential (VSCF) is the sum of the external potential (μext) and Coulomb and exchange–correlation screening. Using the adiabatic local density approximation (ALDA)82 for the exchange–correlation kernel, the effective potential becomes,
| | 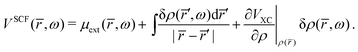 | (41) |
The response density is obtained from the KS dielectric susceptibility (
χ) and the effective potential as,
| | 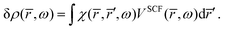 | (42) |
Inserting
eqn (42) in
eqn (41) gives the integral equation,
| | 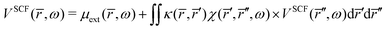 | (43) |
where,
| | 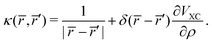 | (44) |
Eqn (43) is solved with respect to
VSCF, avoiding the need for a self-consistent procedure.
64
2.3 Photoionization observables
Once the Dyson orbitals and the continuum orbitals are known, all photoionization parameters can be computed. The photoelectron matrix element (eqn (3)) is related to the differential photoionization cross-section| | 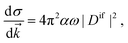 | (45) |
where α is the fine structure constant, ω is the photon energy and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is the momentum of the photoelectron in the molecular frame. Following the mathematical manipulations proposed by Chandra,83 one obtains
is the momentum of the photoelectron in the molecular frame. Following the mathematical manipulations proposed by Chandra,83 one obtains| | 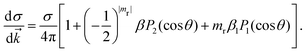 | (46) |
It is evident from eqn (46) that the angular distribution of the photoelectron is guided by three parameters, namely the partial cross-section (σ), the asymmetry parameter (β) and the photoelectron dichroic parameter (β1). The light polarization, mr, can have values 0 (linearly polarized light), +1 (left circularly polarized light) and −1 (right circularly polarized light); Pi are the Legendre polynomials of order i and θ is the angle between the photoelectron moment and the light polarization, for linear polarization, or light propagation, for circular polarization. Additionally, we report the branching ratio, which is defined as the ratio between the partial photoionization cross-section of an individual channel and the sum of the partial cross-sections of all ionization channels considered.
3 Computational details
Experimental geometries from the NIST database84 have been used for H2O, H2S, CS and CS2. The geometry of (S)-methyloxirane was taken from a previous work.85 The Dyson orbitals were obtained from the eT program package68 using the aug-cc-pVTZ basis set for H2O, H2S, CS and (S)-methyloxirane and the aug-cc-pVDZ set for CS2. The ground state electronic densities were computed with the ADF software,86 using the LB94 exchange–correlation functional and DZP basis set.87 Occupied and continuum orbitals were obtained solving eqn (38) in a basis of B-spline functions. A long range expansion of the B-spline functions with angular momentum Lmax is placed at the origin of the coordinate system (center of mass), up to a maximum radial grid length of Rmax with nstep grid points. Additional off-center functions were placed on the non-center atoms with an angular momentum of lmax and radial grid length of rmax. The parameters used are listed in Table S2 (ESI†). This choice of parameters ensured accurate convergence of the photoionization observables. The projected bound (Dyson) and continuum orbitals on the multicentric B-spline basis, and finally the photoionization observables were obtained using the Tiresia code.63 Dyson orbital plots were prepared with UCSF ChimeraX.88
4 Results and discussions
4.1 Water
We start by showcasing the applicability and performance of our implementation of the EOM-CC3 ionization energy and Dyson orbitals in the case of the H2O molecule. The importance of incorporating triple excitations is evaluated for the outer and inner valence regions of the photoelectron spectrum.
A comparison of the ionization energies and spectral strengths computed at EOM-CCSD and EOM-CC3 level is reported in Table 1, with details on the dominant amplitudes and percentage of singles character (%|R1|) in the right ionization vectors. Fig. 1 is a rendering of the photoelectron spectrum of each method based on the tabulated data, compared vis-à-vis with experimental data from ref. 90 for the whole spectrum, and from ref. 89 for the inner region satellite. The three lowest ionization energies correspond to primary ionizations, characterised by electron ejection from a particular molecular orbital. The corresponding Dyson orbitals are also equivalent to the dominant molecular orbital. No significant difference in ionization energy is observed upon inclusion of the perturbative triples excitations. However, a consistent decrease in pole strengths RF is reported at the EOM-CC3 level, in comparison to EOM-CCSD. This gives way for redistribution of the intensity among satellite peaks.
Table 1 H2O. Comparison of ionization energies (IE, in eV) and pole strengths. Experimental results are taken from ref. 89. The percentage of singles character (%|R1|) in the right EOM-CCSD ionization vectors is given in parenthesis beside the computed IEs. The notation i−1(j−1a) is used to specify, respectively, the ionization and the excitation (in parenthesis) components of the 1p transitions (where i, j and a indicate specific molecular orbitals). Only configurations having amplitudes 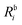 and
and 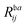 greater than 0.3 and 0.4, respectively, are listed. The HF ground-state electronic configuration is 1a212a211b223a211b21
greater than 0.3 and 0.4, respectively, are listed. The HF ground-state electronic configuration is 1a212a211b223a211b21
| Peak |
EOM-CCSD/aug-cc-pVTZ |
EOM-CC3/aug-cc-pVTZ |
Exp89 |
| IE (%|R1|) |
R
F
|
Dominant amplitudes |
IE |
R
F
|
Dominant amplitudes |
IE (intensity) |
| X 2B1 |
12.62 (95%) |
0.9149 |
1b−11 |
12.67 |
0.8839 |
1b−11 |
12.20 |
| A 2A1 |
14.83 (96%) |
0.9155 |
3a−11 |
14.89 |
0.8838 |
3a−11 |
15.00 |
| B 2B2 |
19.00 (97%) |
0.9250 |
1b−12 |
19.04 |
0.8990 |
1b−12 |
18.51 |
|
|
|
|
|
26.09 |
0.0076 |
1b−214a1, 1b−216a1 |
|
|
|
|
|
|
26.11 |
0.0034 |
3a−11(1b−114a1), 1b−11(3a−114a1) |
|
|
|
|
|
|
27.70 |
0.0019 |
1b−11(3a−114a1), 3a−11(1b−114a1) |
|
|
|
|
|
|
29.88 |
0.0066 |
1b−11(3a−115a1), 3a−11(1b−115a1) |
|
|
|
|
|
|
30.02 |
0.0121 |
3a−11(1b−112b1), 1b−11(3a−112b1) |
|
|
|
|
|
|
30.33 |
0.0143 |
1b−212b1 |
|
|
|
|
|
|
30.68 |
0.0025 |
1b−212b1, 3a−11(1b−114a1) |
|
|
|
|
|
|
30.73 |
0.0654 |
1b−214a1 |
|
|
|
|
|
|
30.80 |
0.0081 |
3a−214a1, 3a−216a1 |
|
|
|
32.80 (72%) |
0.6876 |
2a−11 |
31.93 |
0.1327 |
2a−11, 1b−11(3a−112b1), 3a−11(1b−112b1) |
32.20 (0.58) |
|
|
|
|
|
32.08 |
0.0017 |
1b−12(3a−114a1), 1b−12(3a−116a1) |
|
|
|
|
|
|
32.09 |
0.0021 |
1b−12(1b−114b2), 3a−11(1b−115a1) |
|
|
|
|
|
|
32.22 |
0.0093 |
1b−117a1 |
|
|
|
|
|
|
32.58 |
0.3024 |
2a−11, 1b−11(3a−112b1) |
|
|
|
|
|
|
32.60 |
0.0013 |
1b−11(3a−114a1), 3a−11(1b−114a1) |
|
|
|
|
|
|
32.96 |
0.0017 |
3a−11(1b−113b1), 1b−11(3a−113b1) |
|
|
|
|
|
|
33.45 |
0.0771 |
2a−11, 1b−218a1 |
|
|
|
|
|
|
33.47 |
0.0124 |
1b−11, 1b−11(1b−125a1), 1b−213b1 |
|
|
|
|
|
|
34.33 |
0.0133 |
1b−12, 1b−12(1b−112b1), 1b−11(1b−122b1) |
|
|
|
|
|
|
34.50 |
0.0353 |
2a−11, 3a−214a1, 1b−12(3a−115a1) |
|
|
|
|
|
|
34.87 |
0.0089 |
3a−215a1 |
|
|
|
35.14 (17%) |
0.1526 |
2a−11, 1b−216a1 |
35.05 |
0.0155 |
2a−11, 1b−11(3a−113b1), 3a−11(1b−113b1) |
35 (0.18) |
|
|
|
|
|
35.07 |
0.0012 |
1b−12(1b−115a1), 1b−11(3a−118a1) |
|
|
|
|
|
|
35.59 |
0.0112 |
2a−11, 3a−214a1 |
|
|
|
|
|
|
35.78 |
0.0058 |
1b−12(1b−112b1), 1b−11(1b−122b1) |
|
|
|
|
|
|
35.93 |
0.0471 |
2a−11, 3a−11(1b−125a1), 1b−219a1 |
|
|
|
|
|
|
36.14 |
0.0358 |
2a−11, 1b−219a1 |
|
|
|
|
|
|
36.15 |
0.0043 |
1b−12(3a−115a1), 3a−11(1b−125a1) |
|
|
|
|
|
|
36.45 |
0.0049 |
2a−11, 1b−11(1b−121a2), 1b−12(1b−111a2) |
|
|
|
|
|
|
36.62 |
0.0025 |
1b−12(1b−113b2), 1b−11(1b−125a1) |
|
 |
| | Fig. 1 H2O. Comparison of experimental and computed photoelectron spectrum. Experimental results are taken from ref. 90 and 89. | |
In the experiment,89 three peaks were identified in the inner valence region at 32.2, 35.0 and 38.9 eV, with the last one being an order of magnitude weaker than the first two. We have computed the ionization spectrum of H2O up to 37 eV using both EOM-CCSD and EOM-CC3 methods, in order to characterise the first two satellite bands. As envisaged, the inner valence ionization region comprises more low intensity peaks at the EOM-CC3 level, versus only two peaks obtained at the EOM-CCSD level (at 32.80 and 35.14 eV). The two ionized states obtained at the EOM-CCSD level have corresponding Dyson orbitals with major contribution from the 2a1 molecular orbital.
The corresponding 2a1 Hartree–Fock/aug-cc-pVTZ molecular orbital energy is 36.82 eV. Somewhat surprisingly, the energies of these two EOM-CCSD ionizations agree well with the experimental observation. Nevertheless, the spectral strength of the primary (2a1)−1 band is overestimated while that of the second, satellite peak is underestimated.
Due to the inclusion of approximate triple excitations at the EOM-CC3 level, the description of 2h1p states is significantly improved. This results in reduced ionization energies for these states. Therefore, there appear multiple satellite states in the high energy region of the spectrum, not only of (2a1)−1 character. The photoelectron spectrum in the inner valence region is not well resolved, and is rather a broad feature, see Fig. 1. Thus, it is reasonable that it envelopes numerous low intensity peaks. The energy region between 26.09 eV and 30.80 eV consists of multiple very low intensity satellites of (1b1)−1, (3a1)−1 (1b2)−1, the total intensity of these peaks being approximately 0.12. The first ionized state of contribution from (2a1)−1 ionization arises at 31.93 eV. The peaks between 31–34 eV and 34–37 eV have an overall spectral intensity of about 0.56 and 0.18, which is in excellent agreement with the experimental monopole strengths of 0.58 and 0.18,89 respectively.
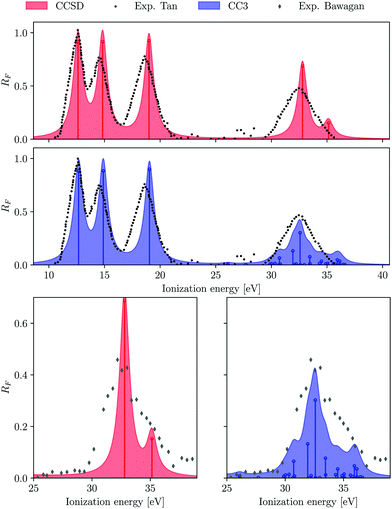
The photoionization observables for the primary peaks, generated using the B-spline TD-DFT continuum orbitals and the EOM-CCSD and EOM-CC3 Dyson orbitals for the bound part, are shown in Fig. 2. They are indistinguishable, when comparing the two CC methods. This is also reasonable given that even at the EOM-CCSD level, the agreement with the experimental results is quite accurate, not leaving much scope for improvement. However, a slight variance is noticed for the A 2A1 band (middle row in Fig. 2) near the ionization threshold. The partial cross-section computed using EOM-CC3 Dyson orbitals clearly is a better match with the experimental observations. The sharp features obtained in the near-threshold region are due to autoionization resonances, which are not seen in the experiment due to vibrational motion. The features are attributed to discrete excitations to Rydberg states lying in the electronic continuum of the lowest-energy ionization channel. The partial cross-section and asymmetry parameters for the 2a−11 region are shown in Fig. S1 (ESI†).
 |
| | Fig. 2 H2O. Partial cross-section σ (left panels) and asymmetry parameter β (right panels) for the primary ionization channels obtained using EOM-CCSD and EOM-CC3 Dyson orbital descriptions of the bound state. B-spline TD-DFT is used for the continuum orbital description. Experimental results are taken from ref. 90–92. | |
4.2 Carbon monosulphide
The CS molecule is a favourite test case for theory due to the presence of experimentally well characterized primary and satellite peaks. The experimental photoelectron spectrum of CS exhibits four well separated peaks between 10–18 eV.93 The calculated ionization energies are listed in Table 2. The two lowest-energy spectral peaks are assigned to ionizations from the HOMO (7σ) and HOMO−1 (2π) molecular orbitals, respectively. As they are dominantly 1h type ionizations, the Dyson orbitals are essentially equivalent to the corresponding molecular orbitals as predicted by Koopmans' theorem.
Table 2 CS. Comparison of Koopmans' theorem Hartree–Fock (HF) molecular orbital energies, EOM-CCSD and EOM-CC3 ionization energies (IE), percentage of singles character (%|R1|), and spectral strengths (RF) obtained using the aug-cc-pVTZ basis set. All energies are reported in eV. Experimental results are taken from ref. 93. The corresponding photoelectron spectrum is shown in Fig. S2 (ESI). The “major MO” is the orbital contributing the most to the Dyson orbital. The HF electronic configuration for the ground state is 1σ22σ23σ24σ21π45σ26σ27σ22π4
| Peak |
Major MO |
HF |
EOM-CCSD |
EOM-CC3 |
Exp93 |
| IE |
IE (%|R1|) |
R
F
|
Dominant amplitude |
IE (%|R1|) |
R
F
|
Dominant amplitude |
IE |
| X 2Σ |
7σ |
12.82 |
11.52 (96) |
0.8672 |
7σ−1 |
11.29 (94) |
0.8330 |
7σ−1 |
11.33 |
| A 2Π |
2π |
12.60 |
13.06 (98) |
0.9091 |
2π−1 |
12.94 (97) |
0.8812 |
2π−1 |
12.79 |
| B 2Σ |
|
|
17.26 (90) |
0.7683 |
6σ−1 |
16.54 (67) |
0.4093 |
6σ−1, 2π−1(7σ−13π) |
15.84 |
| C 2Σ |
6σ |
18.83 |
20.32 (37) |
0.1056 |
6σ−1, 2π−1(7σ−13π) |
18.40 (73) |
0.4000 |
6σ−1, 2π−1(7σ−13π) |
18.0 |
In CS, the complexity arises in accurately simulating the third and fourth peak. They both originate due to (6σ)−1 transition. The 6σ Hartree–Fock molecular orbital energy is 18.83 eV, significantly higher than the third experimental ionization energy (15.84 eV), but comparable to the fourth one at 18.0 eV. The Koopmans description is clearly failing for CS. At the EOM-CCSD level, the two 6σ peaks are captured but at much higher energy and with a larger separation of 3.06 eV between them, in contrast to an experimental gap of 2.16 eV. Furthermore, experimentally the intensities of the third and fourth bands are comparable, whereas, at the CCSD level, the third has a much larger spectral strength than the fourth one. EOM-CC3 significantly improves the ionization energies as well as the intensity distribution between the third and fourth peak (see Fig. S2, ESI†). As also shown in Table 2 and Table S4 (ESI†), considerable differences exist in the singles character and in the dominant amplitudes of the last two ionized states at the CCSD and CC3 levels.
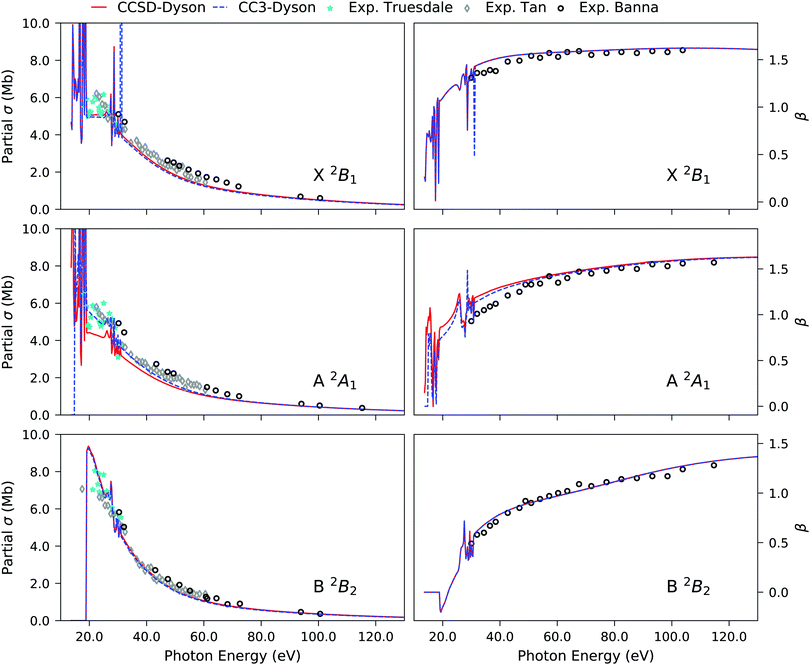
In line with our findings for H2O, we observe that CC3 allows for more redistribution of spectral intensities from the primary to the satellite peaks, thereby reducing the RF values of the primary Dyson orbitals in comparison to the CCSD values. A comparison of the photoionization observables computed using EOM-CCSD and EOM-CC3 Dyson orbitals is presented in Fig. 3. The overall spectral shape is the same for the primary ionization bands (X and A). Significantly different partial cross sections and asymmetry parameters have been obtained for the B 2Σ and C 2Σ band using the CCSD and CC3 Dyson orbitals. We note however that it is difficult to further comment on the correctness of the bound state description for the B 2Σ and C 2Σ band due to lack of experimental observations to corroborate our findings. The overall asymmetry parameter profiles for the B and C bands are distinct, indicating differences in the nature of the underlying transitions. This also aligns with the findings reported in ref. 5, obtained using CASSCF Dyson orbitals for the description of the bound part.
 |
| | Fig. 3 CS. Partial cross section and asymmetry parameters computed using EOM-CCSD and EOM-CC3 Dyson orbitals with the B-spline TD-DFT continuum description. Basis set aug-cc-pVTZ. | |
4.3 Hydrogen sulphide
The computed EOM-CC3/aug-cc-pVTZ photoelectron spectral data of H2S are listed in Table 3, together with EOM-CCSD/aug-cc-pVTZ data. HF results are reported in Table S8 (ESI†), along with CCSD and CC3 results with a smaller basis set. The experimental spectrum94 is split into two parts, an outer valence region between 10–17 eV and an inner valence region above 19 eV characterized by low intensity, closely-spaced, peaks. The photoelectron spectrum of the inner valence region is shown in Fig. S5 (ESI†).
Table 3 H2S. Ionization energies (IE, in eV) and intensities computed using EOM-CCSD and EOM-CC3/aug-cc-pVTZ. Experimental results are taken from ref. 94 and 95. The “major MO” is the orbital contributing the most to the Dyson orbital. The HF ground-state configuration is 1a212a211b223a211b214a212b225a212b21
| Peak |
Major MO |
EOM-CCSD |
EOM-CC3 |
Exp94 |
Exp95 |
| IE (%|R1|) |
R
F
|
Dominant ampl. |
IE (%|R1|) |
R
F
|
Dominant ampl. |
IE |
IE |
Intensity |
| X 2B1 |
2b1 |
10.42 (98) |
0.9291 |
2b−11 |
10.38 (98) |
0.9051 |
2b−11 |
10.5 |
10.50 |
|
| A 2A1 |
5a1 |
13.43 (98) |
0.9128 |
5a−11 |
13.40 (97) |
0.8935 |
5a−11 |
13.4 |
13.10 |
|
| B 2B2 |
2b2 |
15.69 (98) |
0.9141 |
2b−12 |
15.64 (97) |
0.8927 |
2b−12 |
15.6 |
15.60 |
|
|
|
2b2 |
21.98 (4) |
0.0019 |
2b−215b2, 2b−214b2 |
19.35 (7) |
0.0047 |
2b−215b2, 2b−214b2 |
|
18 |
0.018 |
|
|
4a1 |
22.41 (68) |
0.4130 |
4a−11, 2b−219a1 |
20.29 (28) |
0.0709 |
4a−11, 2b−219a1, 2b−218a1, 2b−216a1 |
20 |
19.9 |
0.059 |
|
|
4a1 |
24.35 (54) |
0.2617 |
4a−11, 2b−218a1 |
22.27 (50) |
0.2268 |
4a−11, 2b−216a1 |
22.1 |
22.08 |
0.210 |
|
|
2b1 |
|
|
|
22.62 (2) |
0.0007 |
2b−11(5a−118a1), 2b−11(5a−116a1), |
22.7 |
22.68 |
0.060 |
|
|
|
|
|
|
|
|
2b−11(5a−119a1) |
|
|
|
|
|
4a1 |
26.26 (17) |
0.0232 |
2b−219a1, 2b−216a1 |
23.26 (34) |
0.1026 |
4a−11, 2b−2110a1 |
23.05 |
23.00 |
0.030 |
|
|
4a1 |
|
|
|
23.72 (41) |
0.1576 |
4a−11, 2b−2110a1 |
23.31 |
23.43 |
0.190 |
The primary ionization features are due to ionization from the 2b1, 5a1 and 2b2 molecular orbitals, which are plotted in Fig. S4 (ESI†). The corresponding Dyson orbitals of these three ionizations resemble the molecular orbitals, with dominant contributions from the central sulphur atom, as shown in Fig. 4, in the order of X > A > B, as previously discussed.45,94 The Dyson orbital of the X band is a pure S(3p) lone-pair orbital, orthogonal to the molecular plane. That of the B band is of S–H σ bonding type. Ionizations from 3p atomic orbitals of third row elements are known to exhibit Cooper minima at around 40 eV. The depth of the minimum in the asymmetry parameter of the first three bands, shown in Fig. 5, correlates with the extent of the contribution from the sulphur 3p orbital to the Dyson orbital. The X band, having the deepest minimum, has the largest contribution from the S(3p) orbital, while the B band exhibits, amongst the three, the smallest contribution and the most shallow minimum.
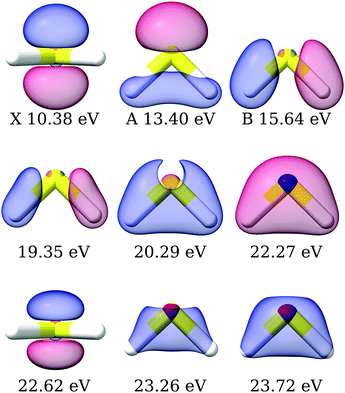 |
| | Fig. 4 H2S: right Dyson orbitals for the satellite states computed using EOM-CC3/aug-cc-pVTZ. The first row is plotted with isovalue 0.1, the second row with isovalues 0.01, 0.03 and 0.05, respectively, and the third row with isovalues 6 × 10−3, 0.05, 0.05. The molecular orbitals corresponding to the X, A and B bands according to Koopmans' theorem are plotted in Fig. S4 (ESI†). | |
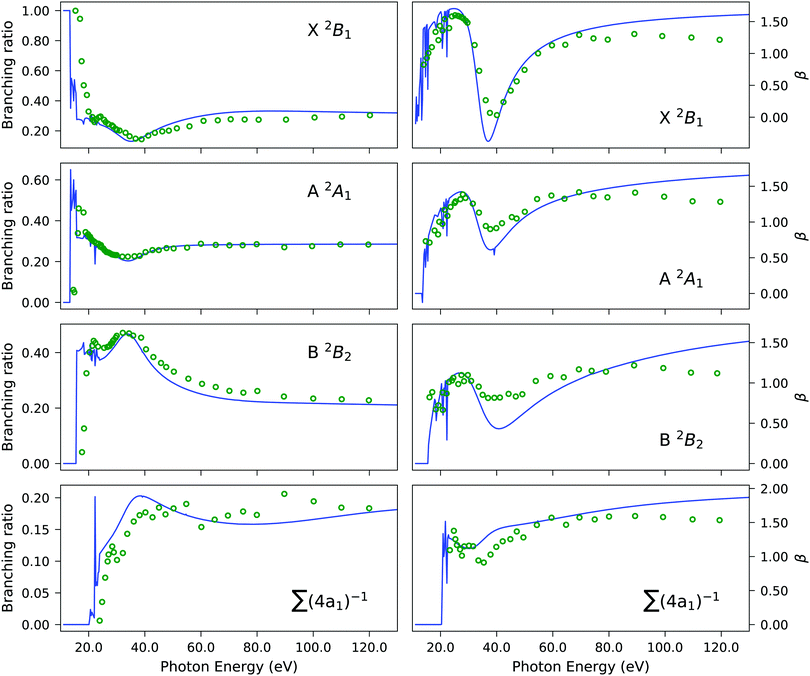 |
| | Fig. 5 H2S. Branching ratio (left panels) and asymmetry parameter β (right panels) obtained using the EOM-CC3/aug-cc-pVTZ Dyson orbital description of the bound state with the B-spline TD-DFT continuum (solid blue line) versus experiment (green circles). The summation in the bottom panels refers to the four 4a1 states listed in Table 3. The experimental results were re-digitized from ref. 94. | |
Experimentally, the inner valence region is attributed to ionizations from the 4a1 molecular orbital. Our CC3 calculations reveal six ionization channels in this energy span, of which four have 4a1, one 2b1 and one 2b2 as major contributors to the Dyson orbital.
The Dyson orbitals are shown in Fig. 4. As the satellites have pronounced 2h1p excitation character, the schematic representation of the Dyson orbitals of 4a1 molecular orbital parentage does not have an unambiguous one-to-one correspondence to the dominant molecular orbital. In the bottom panels of Fig. 5, the branching ratio and asymmetry parameter for the composite ionization channels arising from the 4a1 molecular orbital have been reported. Here, we do not take into consideration the very weak satellite states of B1 and B2 symmetry, as the experimental results (green dots) are for 4a1 ionization channels. For the asymmetry parameter of the individual satellite ionization channels, see Fig. S6 (ESI†). The minimum in the asymmetry parameter β is computed to be at a slightly lower photon energy, and the depth of the minimum is underestimated, as shown in the bottom right panel of Fig. 5. The experimental branching ratio for the satellite state shows oscillations above 60 eV. On the contrary, our simulations produce an almost flat structure. This is reasonable as we have only taken into account ionizations up to 25 eV, thereby neglecting contributions from all higher-energy ionization channels.
4.4 Carbon disulphide
The computed and experimental ionization energies and spectral strengths of CS2 are reported in Table 4 and Table S9 (ESI†). The four outermost primary ionizations are simple and already well described at the EOM-CCSD level.45 Here, we focus on the fifth band, which has been experimentally characterized to be of 2Πu symmetry. According to Koopmans' theorem, the fifth band should be due to pure ionization from the 4σu orbital, which, on the other hand, has a much higher ionization energy. Even though at the EOM-CCSD level we do obtain an ionization at 17.78 eV, which is comparable to the experimental position, its intensity is significantly underestimated. This is also translated to the partial cross-section, which is also underestimated by an order of magnitude in comparison to experiment, as shown in Fig. 6. However, an appreciable agreement is seen for the asymmetry parameter due to the correct symmetry of the underlying transition. An earlier analysis of the ionization vector also revealed that the CCSD ionization at 17.78 eV has exclusively double excitation character, so we expect it to move significantly upon inclusion of triple excitations.45 Another 2Πu state is obtained at 21.68 eV, with a sizeable amount of single excitation character.
Table 4 CS2. Ionization energies (in eV) and pole strengths computed using EOM-CCSD and EOM-CC3 with the aug-cc-pVDZ basis set. Experimental results are taken from ref. 96. The corresponding photoelectron spectrum is shown in Fig. S7. HF ground state configuration 1σ2u1σ2g2σ2g2σ2u3σ2g3σ2u4σ2g1π4g1π4u5σ2g4σ2u6σ2g5σ2u2π4u2π4g
| Peak |
Major |
EOM-CCSD |
EOM-CC3 |
Exp |
| MO |
IE (%|R1|) |
R
F
|
Dominant ampl. |
IE (%|R1|) |
R
F
|
Dominant ampl. |
IE96 |
| X 2Πg |
2πg |
9.90 (98) |
0.8970 |
2π−1g |
9.84 (97) |
0.8630 |
2π−1g |
10.1 |
| A 2Πu |
2πu |
13.20 (93) |
0.8250 |
2π−1u |
12.74 (86) |
0.6993 |
2π−1u, 2π−2g3πu |
12.9 |
| B 2Σu |
5σu |
14.45 (96) |
0.8734 |
5σ−1u |
14.20 (94) |
0.8240 |
5σ−1u |
14.6 |
|
2Πu |
2πu |
17.78 (14) |
0.0136 |
2π−2g3πu |
14.74 (23) |
0.0290 |
2π−2g3πu |
|
|
2Πu |
2πu |
|
|
|
15.82 (8) |
0.0056 |
2π−2g3πu |
|
| C 2Σg |
6σg |
16.42 (93) |
0.8140 |
6σ−1g |
15.93 (86) |
0.6798 |
6σ−1g |
16.2 |
| D 2Πu |
2πu |
21.68 (32) |
0.0573 |
2π−1u, 2π−2g3πu |
17.60 (43) |
0.1480 |
2π−1u, 2π−2g3πu |
17.2 |
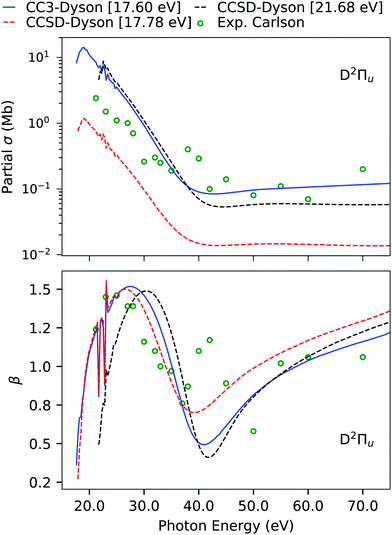 |
| | Fig. 6 CS2. Individual channel photoionization cross-section σ and asymmetry parameter β of the D band computed using B-spline TD-DFT continuum orbitals with Dyson orbitals computed using the aug-cc-pVDZ basis set. The experimental results (green dots) are from ref. 96. The CCSD results were also reported in ref. 45, together with CCSDR(3) corrected counterparts. | |
Indeed, using EOM-CC3, the ionization energy is considerably lowered from 17.78 eV to 14.74 eV, and the other 2Πu satellite at 21.68 eV moves down to 17.60 eV. While the ionization energy of this latter peak is still overestimated, the agreement with the fifth band of the experiment is substantially improved. The photoionization cross-section and asymmetry parameter computed using this 21.68 eV EOM-CCSD Dyson orbital provide a good match with experiment. However, in case of the asymmetry parameter, it is difficult to comment on the performance of the Dyson orbital treatment as the experimental results are scattered.
4.5 Methyloxirane
As final example, Fig. 7 illustrates the results of our approach for the photoelectron circular dichroic parameter, β1, of (S)-methyloxirane, a prototypical chiral molecule. We study the six lowest-energy ionization channels, which are characterized as ionization from one particular molecular orbital. The computed photoelectron spectral details are reported in Table S10 (ESI†). The corresponding EOM-CC3 Dyson orbitals are shown in Fig. S11 (ESI†). It has been shown previously,27 that Koopmans' theorem-based Hartree–Fock molecular orbitals fail to reproduce the experimental trends in the near-threshold region. Here, we see that our combined method matches the experimental data well. Not surprisingly, since all six channels correspond to primary ionizations, the CC3 and CCSD results are very similar, as it can be appreciated from Fig. S12 (ESI†). Also, static DFT and TD-DFT representations of the continuum yield photoelectron dichroic parameters of similar quality, as seen in Fig. S12 (ESI†).
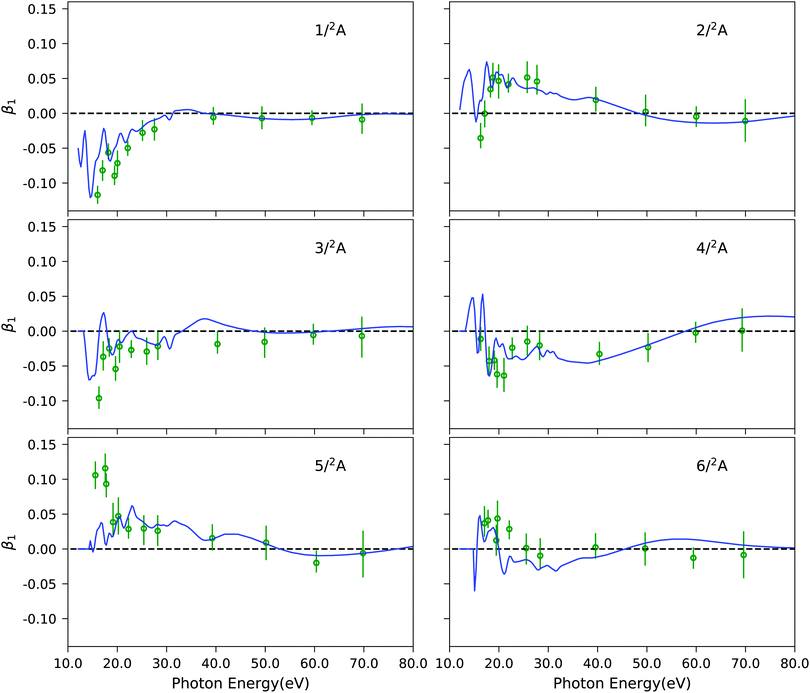 |
| | Fig. 7 C3H6O: photoelectron circular dichroic parameter β1 computed using EOM-CC3/aug-cc-pVTZ Dyson orbitals and B-spline TD-DFT continuum orbitals, shown by blue lines. Experimental results (green dots) were taken from ref. 97. The spectral features are convoluted using Gaussian broadening of full width at half maximum of 1.0 eV. | |
5 Conclusions
In summary, we have devised a technique combining EOM-CC3 Dyson orbital coefficients to describe the bound state character of the system with B-spline TD-DFT continuum orbitals, allowing for the accurate simulation of photoelectron spectra and photoionization dynamical observables, namely partial cross-sections, asymmetry parameters, branching ratios and photoelectron dichroic parameters. The study involved two main components, the implementation of the EOM-CC3 Dyson orbital coefficients and their interface with the B-spline (TD-)DFT continuum for the computation of the spectroscopic parameters.
A detailed investigation of the outer as well as inner valence region of the photoelectron spectrum of exemplary molecular systems has been carried out. For outer valence ionizations, CCSD results are already accurate, and CC3 brings little improvement. The accuracy of CCSD may be gauged by the pole strengths RF of the individual ionizations, and the percentage of 1h states. As a rule of thumb, CCSD results may be considered accurate when RF > 0.85 and the 1h-percentage >0.90.
The perturbative triples correction is necessary for reproducing complex satellite bands of higher order excitation character. The inner valence region of the spectrum comprising satellite peaks is a direct probe of correlation effects and quite challenging to accurately reproduce theoretically. Recent developments in experimental facilities have made it possible to capture such low intensity features with high accuracy, giving impetus to concomitant theoretical advancements. Even though EOM-CCSD is capable of describing 2h1p ionizations, the ionization energy is often highly overestimated making it difficult to assign the ionized states to the corresponding experimental bands. This is extensively corrected at the EOM-CC3 level. The proposed EOM-CC3 Dyson orbital treatment of the bound state in conjunction with B-spline TD-DFT continuum orbitals constitutes a state-of-the-art theoretical methodology capable of quantitative comparison with experiments.
The presented protocol is general and can be extended and applied to investigate sophisticated experimental observations. For instance, open-shell systems could be studied using the method. Core ionization spectra will also be studied in the future, as they are known to exhibit a plethora of satellite peaks, difficult to handle using only singles and doubles excitations. The method can also be suitably extended to include nuclear dynamic effects, in order to describe vibrationally resolved photoelectron spectral features.
Author contributions
S. C., H. K. and P. D. conceptualized and supervised the project. A. C. P. implemented the EOM-CCSD and EOM-CC3 Dyson orbitals in the eT program package. T. M. developed the composite methodology interfacing the B-spline Tiresia code and the eT program. T. M., A. C. P., S. C. and P. D. carried out the calculations and validation. All authors contributed to the writing of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We acknowledge support from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie European Training Network COmputational Spectroscopy In Natural sciences and Engineering (COSINE), Grant Agreement No. 765739 (T. M., A. C. P., H. K. and S. C.); from the Independent Research Fund Denmark-DFF-FNU RP2, Grant no. 7014-00258B (S. C.) and from the Research Council of Norway through FRINATEK project 275506, Theolight (H. K. and S. C.). The results leading to this publication have also been funded by CA18222 COST Action (AttoChem) – Horizon 2020 Framework Programme of the European Union.
References
-
F. Merkt, S. Willitsch and U. Hollenstein, High-resolution Photoelectron Spectroscopy, in Handbook of High-resolution Spectroscopy, ed. M. Quack and F. Merkt, John Wiley & Sons, Ltd, 2011 Search PubMed.
- M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martín, Chem. Rev., 2017, 117, 10760–10825 CrossRef CAS.
- R. L. Martin and D. A. Shirley, J. Chem. Phys., 1976, 64, 3685–3689 CrossRef CAS.
- L. S. Cederbaum, W. Domcke, J. Schirmer and W. Von Niessen, Adv. Chem. Phys., 1986, 65, 115–159 CAS.
- A. Ponzi, C. Angeli, R. Cimiraglia, S. Coriani and P. Decleva, J. Chem. Phys., 2014, 140, 204304 CrossRef PubMed.
- A. Ponzi, N. Quadri, C. Angeli and P. Decleva, Phys. Chem. Chem. Phys., 2019, 21, 1937–1951 RSC.
- L. S. Cederbaum, J. Schirmer, W. Domcke and W. von Niessen, J. Phys. B: At. Mol. Phys., 1977, 10, L549–L553 CrossRef CAS.
- L. S. Cederbaum, J. Schirmer, W. Domcke and W. Von Niessen, Int. J. Quantum Chem., 1978, 14, 593–601 CrossRef CAS.
- D. Danovich, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 377–387 CAS.
- W. von Niessen, J. Schirmer and L. S. Cederbaum, Comput. Phys. Rep., 1984, 1, 57–125 CrossRef CAS.
- J. Schirmer, A. B. Trofimov and G. Stelter, J. Chem. Phys., 1998, 109, 4734–4744 CrossRef CAS.
- A. B. Trofimov and J. Schirmer, J. Chem. Phys., 2005, 123, 144115 CrossRef CAS PubMed.
-
J. V. Ortiz, Adv. Quantum Chem., Academic Press, 1999, vol. 35, pp. 33–52 Search PubMed.
- E. Opoku, F. Pawłowski and J. V. Ortiz, J. Chem. Phys., 2021, 155, 204107 CrossRef CAS.
- M. Ehara, M. Ishida and H. Nakatsuji, J. Chem. Phys., 2001, 114, 8990–8999 CrossRef CAS.
- Q. Tian, J. Yang, Y. Shi, X. Shan and X. Chen, J. Chem. Phys., 2012, 136, 094306 CrossRef PubMed.
- A. D. O. Bawagan and E. R. Davidson, Adv. Chem. Phys., 1999, 110, 215–263 CAS.
- B. O. Roos, Adv. Chem. Phys., 1987, 399–445 CAS.
- K. Andersson, P. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- P.-Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109 CrossRef.
- V. Sauri, L. Serrano-Andrés, A. R. M. Shahi, L. Gagliardi, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 153–168 CrossRef CAS.
- G. Grell, S. Bokarev, B. Winter, R. Seidel, E. Aziz, S. Aziz and O. Kühn, J. Chem. Phys., 2015, 143, 074104 CrossRef PubMed.
- G. Grell and S. I. Bokarev, J. Chem. Phys., 2020, 152, 074108 CrossRef CAS PubMed.
- B. N. C. Tenorio, A. Ponzi, S. Coriani and P. Decleva, Molecules, 2022, 27, 1203 CrossRef CAS PubMed.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef.
- S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540 CrossRef CAS PubMed.
- T. Moitra, A. Ponzi, H. Koch, S. Coriani and P. Decleva, J. Phys. Chem. Lett., 2020, 11, 5330–5337 CrossRef CAS PubMed.
- M. L. Vidal, A. I. Krylov and S. Coriani, Phys. Chem. Chem. Phys., 2020, 22, 2693–2703 RSC.
- M. L. Vidal, A. I. Krylov and S. Coriani, Phys. Chem. Chem. Phys., 2020, 22, 3744–3747 RSC.
- H. Koch and P. Jørgensen, J. Chem. Phys., 1990, 93, 3333–3344 CrossRef CAS.
- H. Koch, H. J. A. Jensen, P. Jørgensen and T. Helgaker, J. Chem. Phys., 1990, 93, 3345–3350 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- S. Coriani, F. Pawłowski, J. Olsen and P. Jørgensen, J. Chem. Phys., 2016, 144, 024102 CrossRef PubMed.
- R. J. Bartlett, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 126–138 CAS.
- H. Koch, O. Christiansen, P. Jørgensen, A. M. Sanchez de Merás and T. Helgaker, J. Chem. Phys., 1997, 106, 1808–1818 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1996, 105, 1451–1459 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1995, 103, 7429–7441 CrossRef CAS.
- R. H. Myhre and H. Koch, J. Chem. Phys., 2016, 145, 044111 CrossRef.
- A. C. Paul, R. H. Myhre and H. Koch, J. Chem. Theory Comput., 2021, 17, 126 Search PubMed.
- J. V. Ortiz, J. Chem. Phys., 2020, 153, 070902 CrossRef CAS PubMed.
- A. I. Krylov, J. Chem. Phys., 2020, 153, 080901 CrossRef CAS PubMed.
- M. Díaz-Tinoco, H. H. Corzo, F. Pawłowski and J. V. Ortiz, Mol. Phys., 2019, 117, 2275–2283 CrossRef.
- V. Pomogaev, S. Lee, S. Shaik, M. Filatov and C. H. Choi, J. Phys. Chem. Lett., 2021, 12, 9963–9972 CrossRef CAS PubMed.
- T. Moitra, S. Coriani and P. Decleva, J. Chem. Theory Comput., 2021, 17, 5064–5079 CrossRef CAS.
- T. Fukumi, J. Chem. Phys., 1981, 75, 3743–3745 CrossRef CAS.
-
F. Müller-Plathe and G. H. Diercksen, Molecular photoionisation cross sections by moment theory. An introduction, in Electronic Structure of Atoms, Molecules and Solids. Proceeding of the II Escola Brasileira de Estructure Eletronica, Olinda, Brazil, July 17–22, 1989, ed. S. Canuto, J. D'Albuquerque e Castro and F. J. Paixao, World Scientific, Olinda, Brazil, 1990, pp. 1–29 Search PubMed.
- J. Cukras, S. Coriani, P. Decleva, O. Christiansen and P. Norman, J. Chem. Phys., 2013, 139, 094103 CrossRef.
- J. Cukras, P. Decleva and S. Coriani, J. Chem. Phys., 2014, 141, 174315 CrossRef PubMed.
- B. N. C. Tenorio, M. A. C. Nascimento, S. Coriani and A. B. Rocha, J. Chem. Theory Comput., 2016, 12, 4440–4459 CrossRef CAS PubMed.
- B. N. C. Tenorio, T. Moitra, M. A. C. Nascimento, A. B. Rocha and S. Coriani, J. Chem. Phys., 2019, 150, 224104 CrossRef PubMed.
-
B. N. C. Tenorio, S. Coriani, A. B. Rocha and M. A. C. Nascimento, Photoionization and Photodetachment Cross Sections Based on L2 Basis Sets: Theory and Selected Examples, in Advances in Methods and Applications of Quantum Systems in Chemistry, Physics, and Biology, ed. A. V. Glushkov, O. Y. Khetselius, J. Maruani and E. Brändas, Springer International Publishing, Springer, 2021, pp. 151–179 Search PubMed.
- S. P. Neville, V. Averbukh, M. Ruberti, R. Yun, S. Patchkovskii, M. Chergui, A. Stolow and M. S. Schuurman, J. Chem. Phys., 2016, 145, 144307 CrossRef PubMed.
- T. Moitra, S. Coriani and B. N. C. Tenorio, Mol. Phys., 2021, e1980235 CrossRef.
-
P. G. Burke, R-matrix theory of atomic collisions: application to atomic, molecular and optical processes, Springer, 2011 Search PubMed.
- Z. Mašín, J. Benda, J. D. Gorfinkiel, A. G. Harvey and J. Tennyson, Comput. Phys. Commun., 2020, 249, 107092 CrossRef.
- M. B. Amar and F. C. Farnoux, J. Phys. B: At. Mol. Phys., 1983, 16, 2339–2358 CrossRef.
- R. R. Lucchese, K. Takatsuka and V. McKoy, Phys. Rep., 1986, 131, 147–221 CrossRef.
-
T. N. Rescigno, C. W. McCurdy, A. E. Orel and B. H. Lengsfield, in The Complex Kohn Variational Method, ed. W. M. Huo and F. A. Gianturco, Springer US, Boston, MA, 1995, pp. 1–44 Search PubMed.
- M. Brosolo, P. Decleva and A. Lisini, Chem. Phys., 1994, 181, 85–95 CrossRef CAS.
- C. F. Fischer and M. Idrees, J. Phys. B: At., Mol. Opt. Phys., 1990, 23, 679–691 CrossRef CAS.
- P. V. Demekhin, A. Ehresmann and V. L. Sukhorukov, J. Chem. Phys., 2011, 134, 024113 CrossRef.
- D. Toffoli, M. Stener, G. Fronzoni and P. Decleva, Chem. Phys., 2002, 276, 25–43 CrossRef CAS.
- M. Stener, G. Fronzoni and P. Decleva, J. Chem. Phys., 2005, 122, 234301 CrossRef CAS PubMed.
- V. P. Majety, A. Zielinski and A. Scrinzi, New J. Phys., 2015, 17, 063002 CrossRef.
- C. Marante, M. Klinker, I. Corral, J. González-Vázquez, L. Argenti and F. Martín, J. Chem. Theory Comput., 2017, 13, 499–514 CrossRef CAS.
- M. Klinker, C. Marante, L. Argenti, J. González-Vázquez and F. Martín, J. Phys. Chem. Lett., 2018, 9, 756–762 CrossRef CAS PubMed.
- S. D. Folkestad, E. F. Kjønstad, R. H. Myhre, J. H. Andersen, A. Balbi, S. Coriani, T. Giovannini, L. Goletto, T. S. Haugland, A. Hutcheson, I.-M. Høyvik, T. Moitra, A. C. Paul, M. Scavino, A. S. Skeidsvoll, Å. H. Tveten and H. Koch, J. Chem. Phys., 2020, 152, 184103 CrossRef CAS PubMed.
-
R. Nesbet, Variational Methods in Electron-Atom Scattering Theory, Plenum Press, New York, 1980 Search PubMed.
-
T. Helgaker, P. Jørgensen and J. Olsen, Molecular electronic-structure theory, John Wiley & Sons, Ltd, 2000, pp. 1–908 Search PubMed.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1999, 111, 8785 CrossRef CAS.
- S. Coriani and H. Koch, J. Chem. Phys., 2015, 143, 181103 CrossRef PubMed.
- J. F. Stanton, J. Chem. Phys., 1994, 101, 8928–8937 CrossRef CAS.
- S. V. Levchenko, T. Wang and A. I. Krylov, J. Chem. Phys., 2005, 122, 224106 CrossRef PubMed.
- D. A. Matthews, J. Gauss and J. F. Stanton, J. Chem. Theory Comput., 2013, 9, 2567–2572 CrossRef CAS PubMed.
- D. A. Matthews and J. F. Stanton, J. Chem. Phys., 2015, 142, 064108 CrossRef PubMed.
- C.-h. Yu, R. M. Pitzer and C. W. McCurdy, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 2134–2141 CrossRef CAS PubMed.
- R. Matsuzaki and S. Yabushita, J. Comput. Chem., 2017, 38, 2030–2040 CrossRef CAS PubMed.
- A. Ammar, A. Leclerc and L. U. Ancarani, J. Comput. Chem., 2020, 41, 2365–2377 CrossRef CAS PubMed.
- M. Stener, S. Furlan and P. Decleva, J. Phys. B-At. Mol. Opt., 2000, 33, 1081–1102 CrossRef CAS.
- C. Froese Fischer and M. Idrees, Comput. Phys., 1989, 3, 53–58 CrossRef.
- A. Zangwill and P. Soven, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 21, 1561–1572 CrossRef CAS.
- N. Chandra, J. Phys. B: At. Mol. Phys., 1987, 20, 3405–3415 CrossRef CAS.
-
NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, Release 20 August 2019.
- D. Di Tommaso, M. Stener, G. Fronzoni and P. Decleva, ChemPhysChem, 2006, 7, 924–934 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, E. C. Meng, G. S. Couch, T. I. Croll, J. H. Morris and T. E. Ferrin, Protein Sci., 2021, 30, 70–82 CrossRef CAS PubMed.
- A. Bawagan, L. Lee, K. Leung and C. Brion, Chem. Phys., 1985, 99, 367–382 CrossRef CAS.
- K. H. Tan, C. E. Brion, P. E. V. der Leeuw and M. J. van der Wiel, Chem. Phys., 1978, 29, 299–309 CrossRef CAS.
- M. S. Banna, B. H. McQuaide, R. Malutzki and V. Schmidt, J. Chem. Phys., 1986, 84, 4739–4744 CrossRef CAS.
- C. M. Truesdale, S. Southworth, P. H. Kobrin, D. W. Lindle, G. Thornton and D. A. Shirley, J. Chem. Phys., 1982, 76, 860–865 CrossRef CAS.
- N. Jonathan, A. Morris, M. Okuda, K. J. Ross and D. J. Smith, Faraday Discuss. Chem. Soc., 1972, 54, 48–55 RSC.
- P. Baltzer, L. Karlsson, M. Lundqvist, B. Wannberg, D. M. P. Holland and M. A. MacDonald, Chem. Phys., 1995, 195, 403–422 CrossRef CAS.
- M. Y. Adam, A. Naves de Brito, M. P. Keane, S. Svensson, L. Karlsson, E. Källne and N. Correia, J. Electron Spectrosc. Relat. Phenom., 1991, 56, 241–257 CrossRef CAS.
- T. A. Carlson, M. O. Krause and F. A. Grimm, J. Chem. Phys., 1982, 77, 1701–1709 CrossRef CAS.
- S. Stranges, S. Turchini, M. Alagia, G. Alberti, G. Contini, P. Decleva, G. Fronzoni, M. Stener, N. Zema and T. Prosperi, J. Chem. Phys., 2005, 122, 244303 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04695k |
| ‡ These authors contributed equally to this work. |
|
| This journal is © the Owner Societies 2022 |
 a,
Alexander C.
Paul‡
a,
Alexander C.
Paul‡
 b,
Piero
Decleva
b,
Piero
Decleva
 c,
Henrik
Koch
c,
Henrik
Koch
 *bd and
Sonia
Coriani
*bd and
Sonia
Coriani
 *ab
*ab
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |Φf〉.
|Φf〉.![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) is the electric dipole moment. The most general approach is to expand Φf in a CI-type fashion, called the “close-coupling” form.69 A number of close-coupling implementations are available, and can give accurate results for small molecules, especially close to threshold.56,58,66,67 However, ab initio computations using the full expansion are computationally expensive and often unnecessary. We have restricted ourselves to the single channel approximation, where the final composite state is represented by the anti-symmetrized product of the photoelectron and the bound ionized state accessible at that particular energy
is the electric dipole moment. The most general approach is to expand Φf in a CI-type fashion, called the “close-coupling” form.69 A number of close-coupling implementations are available, and can give accurate results for small molecules, especially close to threshold.56,58,66,67 However, ab initio computations using the full expansion are computationally expensive and often unnecessary. We have restricted ourselves to the single channel approximation, where the final composite state is represented by the anti-symmetrized product of the photoelectron and the bound ionized state accessible at that particular energy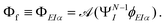
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |ϕEIα〉.
|ϕEIα〉.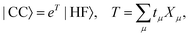
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = e−THeT,
= e−THeT,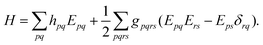
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |HF〉 = Ωμ = 0,
|HF〉 = Ωμ = 0,![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |HF〉.
|HF〉.![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) μ, such that the determinants are biorthogonal to the determinants created by the cluster operator
μ, such that the determinants are biorthogonal to the determinants created by the cluster operator![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) μ, |ν〉 = Xμ|HF〉, 〈μ|ν〉 = δμ,ν.
μ, |ν〉 = Xμ|HF〉, 〈μ|ν〉 = δμ,ν.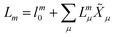
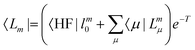
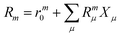
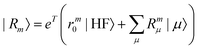
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) TLm = EmLm
TLm = EmLm![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Rm = EmRm,
Rm = EmRm,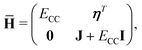
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ,Xν]|HF〉 (also known as A) and ην = 〈 HF|[
,Xν]|HF〉 (also known as A) and ην = 〈 HF|[![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ,Xν]|HF〉. From the structure of the Hamiltonian matrix and the biorthonormality of the states, we find the left and right ground state solutions
,Xν]|HF〉. From the structure of the Hamiltonian matrix and the biorthonormality of the states, we find the left and right ground state solutions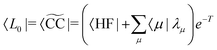
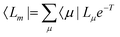
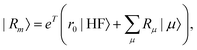
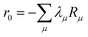 to ensure biorthogonality to the left ground state,
to ensure biorthogonality to the left ground state, 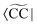 . Transition properties for a one-electron operator (in second quantization)
. Transition properties for a one-electron operator (in second quantization) 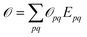 are given as biorthogonal expectation values,
are given as biorthogonal expectation values,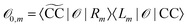
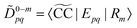
![[H with combining macron]](https://www.rsc.org/images/entities/b_char_0048_0304.gif) Rm
Rm![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) μ and Xμ, in eqn (10) and (12) by particle nonconserving excitation operators like 1h, 2h1p,… operators, which defines the EOM-CC method for ionization potentials, EOM-IP-CC.33 However, as proposed by Stanton and Gauss,71 we can also compute the ionization energies by including a bath orbital in the virtual orbital space which does not interact with the other orbitals, and then projecting out all excitations that do not include the bath orbital during the solution of the eigenvalue equation.72 This approach has the advantage of requiring only a small modification to an existing EOM-CC code for excitation energies (EOM-EE-CC). As a disadvantage, its scaling is the same as EOM-CC for excitation energies, whereas a rigorous implementation of EOM-IP-CC scales one order less with the number of virtual orbitals (nv).
μ and Xμ, in eqn (10) and (12) by particle nonconserving excitation operators like 1h, 2h1p,… operators, which defines the EOM-CC method for ionization potentials, EOM-IP-CC.33 However, as proposed by Stanton and Gauss,71 we can also compute the ionization energies by including a bath orbital in the virtual orbital space which does not interact with the other orbitals, and then projecting out all excitations that do not include the bath orbital during the solution of the eigenvalue equation.72 This approach has the advantage of requiring only a small modification to an existing EOM-CC code for excitation energies (EOM-EE-CC). As a disadvantage, its scaling is the same as EOM-CC for excitation energies, whereas a rigorous implementation of EOM-IP-CC scales one order less with the number of virtual orbitals (nv).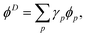
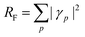
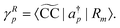
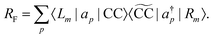
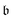 denotes the bath orbital, eqn (29) and (30) can be rewritten as
denotes the bath orbital, eqn (29) and (30) can be rewritten as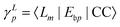
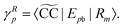
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 0−m.25 As the bath orbital is part of the virtual orbital space, only two of the four blocks of Dm−0 and
0−m.25 As the bath orbital is part of the virtual orbital space, only two of the four blocks of Dm−0 and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 0−m need to be constructed. Additionally, the ground state amplitudes t and multipliers λ are zero if one of their indices corresponds to the bath orbital. Therefore, the CC3 contribution to the right Dyson orbital consists of only four terms, and there is only a single term for the left Dyson orbital. We list these additional terms as follows (where we also use the symbol += to highlight that these terms are added to the CCSD-like ones):
0−m need to be constructed. Additionally, the ground state amplitudes t and multipliers λ are zero if one of their indices corresponds to the bath orbital. Therefore, the CC3 contribution to the right Dyson orbital consists of only four terms, and there is only a single term for the left Dyson orbital. We list these additional terms as follows (where we also use the symbol += to highlight that these terms are added to the CCSD-like ones):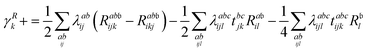
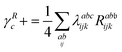
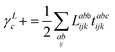
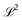 Gaussian type or Slater type orbitals are not very accurate, despite efforts to adapt them.77–79 Instead, we use a highly flexible linear combination of primitive B-spline functions (ζ),
Gaussian type or Slater type orbitals are not very accurate, despite efforts to adapt them.77–79 Instead, we use a highly flexible linear combination of primitive B-spline functions (ζ),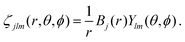
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ; i = 1, 2,…, n
; i = 1, 2,…, n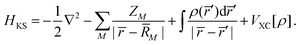
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) M are the atomic number and nuclear coordinate, respectively. VXC is the exchange–correlation potential. As previously shown, the LB94 functional outperforms the LDA or GGA functionals for simulating KS photoionization, due to the correct asymptotic Coulomb behaviour.80 The continuum KS orbitals are then extracted as the eigenfunctions of the Hamiltonian in eqn (39), with given positive eigenvalue equal to the kinetic energy (E) of the photoelectron. The problem is recast as to obtain the eigenvectors (c) with a minimum modulus eigenvalue (a) of the energy-dependent matrix A†A(E),
M are the atomic number and nuclear coordinate, respectively. VXC is the exchange–correlation potential. As previously shown, the LB94 functional outperforms the LDA or GGA functionals for simulating KS photoionization, due to the correct asymptotic Coulomb behaviour.80 The continuum KS orbitals are then extracted as the eigenfunctions of the Hamiltonian in eqn (39), with given positive eigenvalue equal to the kinetic energy (E) of the photoelectron. The problem is recast as to obtain the eigenvectors (c) with a minimum modulus eigenvalue (a) of the energy-dependent matrix A†A(E),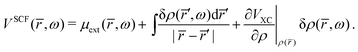
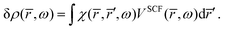
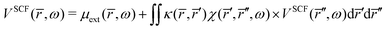
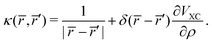
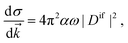
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is the momentum of the photoelectron in the molecular frame. Following the mathematical manipulations proposed by Chandra,83 one obtains
is the momentum of the photoelectron in the molecular frame. Following the mathematical manipulations proposed by Chandra,83 one obtains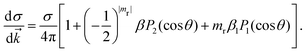
 and
and 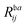 greater than 0.3 and 0.4, respectively, are listed. The HF ground-state electronic configuration is 1a212a211b223a211b21
greater than 0.3 and 0.4, respectively, are listed. The HF ground-state electronic configuration is 1a212a211b223a211b21







