Multi-stimulus linear negative expansion of a breathing M(O₂CR)₄-node MOF

Abstract

The metal–organic framework (Me₂NH₂)₂[Cd(NO₂BDC)₂] (SHF-81) comprises flattened tetrahedral Cd(O₂CR)₄²⁻ nodes, in which Cd(II) centres are linked via NO₂BDC²⁻ ligands (2-nitrobenzene-1,4-dicarboxylate) to give a doubly interpenetrated anionic network, with charge balanced by two Me₂NH₂⁺ cations per Cd centre resident in the pores. The study establishes that this is a twinned α-quartz-type structure (trigonal, space group P3_x21, x = 1 or 2), although very close to the higher symmetry β-quartz arrangement (hexagonal, P6_x22, x = 2 or 4) in its as-synthesised solvated form [Cd(NO₂BDC)₂]·2DMF·0.5H₂O (SHF-81-DMF). The activated MOF exhibits very little N₂ uptake at 77 K, but shows significant CO₂ uptake at 273–298 K with an isosteric enthalpy of adsorption (ΔH_ads) at zero coverage of −27.4 kJ mol⁻¹ determined for the MOF directly activated from SHF-81-DMF. A series of in situ diffraction experiments, both single-crystal X-ray diffraction (SCXRD) and powder X-ray diffraction (PXRD), reveal that the MOF is flexible and exhibits breathing behaviour with observed changes as large as 12% in the a- and b-axes (|Δa|, |Δb| < 1.8 Å) and 5.5% in the c-axis (|Δc| < 0.7 Å). Both the solvated SHF-81-DMF and activated/desolvated SHF-81 forms of the MOF exhibit linear negative thermal expansion (NTE), in which pores that run parallel to the c-axis expand in diameter (a- and b-axis) while contracting in length (c-axis) upon increasing temperature. Adsorption of CO₂ gas at 298 K also results in linear negative expansion (Δa, Δb > 0; Δc < 0; ΔV > 0). The largest change in dimensions is observed during activation/desolvation from SHF-81-DMF to SHF-81 (Δa, Δb < 0; Δc > 0; ΔV < 0). Collectively the nine in situ diffraction experiments conducted suggest the breathing behaviour is continuous, although individual desolvation and adsorption experiments do not rule out the possibility of a gating or step at intermediate geometries that is coupled with continuous dynamic behaviour towards the extremities of the breathing amplitude.

---

Introduction

Extensive interest in metal–organic frameworks (MOFs) over the past two decades has centred on their modular design and the wide range of applications that exploit their molecular-scale porosity, including selective gas adsorption/separation,^1–3 catalysis,^4–6 energy storage and conversion,⁷ sensing,^8,9 and drug delivery. Most reported MOFs are ostensibly rigid materials, which possess empty pores or channels that, after activation, can be used to encapsulate small-molecule guests under certain conditions. There are, however, a growing number of MOFs that exhibit often reversible flexible behaviour in response to external stimuli. There is much interest in understanding this behaviour and in the development of applications related to the differential responses to changes in stimuli such as guest inclusion, light, temperature or pressure.^10–16 In particular, so-called “breathing” behaviour, in which framework flexibility enables the reversible contraction and expansion of pores, is very attractive due to the potential for selective guest inclusion, for example in the field of gas separation,¹⁷ but also increasingly in other areas such as catalysis,¹⁸ modulation of photophysical behaviour,¹⁹ or energy storage and mechanical response.^20,21

Almost all “breathing” MOFs are reported to exist in two or more discrete states with different pore dimensions, at least a narrow-pore and a wide-pore (open and closed) form. Such MOFs include the archetypical MIL-53 family²² and those based on DMOF,²³ and can involve multiple intermediate states, such as in the case of Co(bdp)²⁴ (bdp = benzenedipyrazolate). In the examples noted, flexibility arises from hinge-like deformations in metal–ligand coordination, and often leads to gated adsorption of gases, although in other framework materials gating can arise from the deformation of flexible ligands.²⁵ In contrast to the growing number of published MOFs that exhibit the aforementioned discrete flexibility, there are very few materials that have been shown to exhibit continuous dynamic behaviour. Examples include the MIL-88 family,²⁶ which display this property under solvent uptake, and SHF-61, which displays a continuous pore-closing mechanism during activation to remove DMF.²⁷

A growing area of interest in the context of cooperative phenomena in framework materials is the anomalous mechanical response associated with phenomena such as negative thermal expansion (NTE),²⁸ negative linear compressibility (NLC)²⁹ and auxetic behaviour,³⁰ which have been concisely introduced by Goodwin and colleagues (Fig. 1),³¹ and have potential for applications in composite materials with thermally adjustable expansion (NTE) or pressure sensors (NLC and auxetic materials). In their report, Goodwin and co-workers undertook neutron powder diffraction (NPD) studies over a wide temperature range for two perdeuterated quartz-like MOFs after prior activation.³¹ These studies illustrated uniaxial NTE behaviour for D[In(BDC-d₄)₂] and uniaxial positive thermal expansion (PTE) for [Zn(isonicotinate)₂], and geometric criteria were developed for the prediction of these behaviours in other related MOFs.

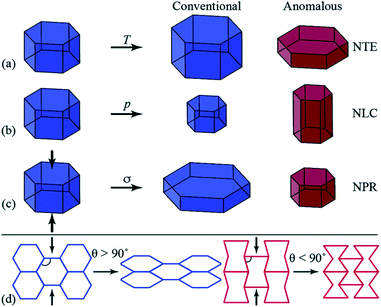Fig. 1 Diagrammatic representation of anomalous mechanics for materials exhibiting (a) uniaxial negative thermal expansion (NTE), contraction in one direction upon heating (T); (b) negative linear compressibility (NLC), expansion in one direction under hydrostatic pressure (p); and (c) auxetic response upon axial compression (σ, indicated by the arrows), whereby a negative Poisson’s ratio (NPR) is observed. (d) Honeycomb frameworks with different geometries (framework angle, θ) exhibit contrasting mechanical responses to axial compression. Reproduced from ref. 31 with permission of The Royal Society of Chemistry.

Here we report a new example of continuous breathing and uniaxial expansion/contraction behaviour in the MOF (Me₂NH₂)₂[Cd(NO₂BDC)₂]·2DMF·0.5H₂O (SHF-81-DMF) (NO₂BDC²⁻, 2-nitrobenzene-1,4-dicarboxylate (2-nitroterephthalate); SHF, Sheffield Framework), for which this anisotropic flexible response can be accessed by different stimuli. Specifically, we describe the dynamic framework responses to stimulation by activation (solvent loss), gas adsorption or change in temperature. Structural insight into the flexible behaviour is provided by extensive single-crystal and powder X-ray diffraction studies. Originally reported as a static MOF,³² we demonstrate that this material is unusual, not only in its dynamic behaviour, but in that this behaviour can be documented by single-crystal X-ray diffraction. SHF-81-DMF comprises two identical interpenetrated networks of qtz topology (i.e. based on the quartz network). The networks are constructed from Cd²⁺ ions, which serve as distorted tetrahedral Cd(O₂CR)₄²⁻ nodes, connected via nitroterephthalate linkers that coordinate the metal centres in a chelating manner. The anionic framework contains charge-balancing dimethylammonium cations, DMF and water molecules in its triangular channels.

Experimental

General

Reagents and solvents were obtained from Sigma-Aldrich, Alfa Aesar, Acros Organics, Fisher Scientific, Fluorochem or Manchester Organics, and were used without additional purification. Samples used for elemental analysis, thermogravimetric analysis and laboratory powder X-ray diffraction were ground into a powder using a mortar and pestle immediately prior to analysis, to ensure consistency of solvent content in the bulk material. For solution-phase NMR spectroscopic characterisation, the sample (ca. 3 mg) was acid-digested in 50 μL deuterium chloride (35% in D₂O) in 1 mL DMSO-d₆. Thermogravimetric analysis was performed in air using a PerkinElmer Pyris1 Thermogravimetric Analyser. Elemental analysis was performed by combustion in pure oxygen using a PerkinElmer 2400 CHNS/O Series II Analyser or an Elementar Vario MICRO cube analyser. NMR spectroscopy (400 MHz) was performed using Bruker AVANCE III 400 HD or AVANCE 400 HD spectrometers.

Synthesis

Cadmium nitrate hexahydrate (0.3072 g, 0.993 mmol), 2-nitroterephthalic acid (0.4210 g, 1.994 mmol), dimethylamine hydrochloride (8.0 mg, 98 μmol) and N,N-dimethylformamide (DMF) (10 mL) were stirred for ca. 5 min (until dissolution of the solids) in a 23 mL Teflon vessel. The Teflon vessel was then sealed inside a stainless steel autoclave, heated to 130 °C at a rate of 1 °C min⁻¹ and held at 130 °C for 24 h. The vessel was then cooled to room temperature at a rate of 0.1 °C min⁻¹ and the product (orange crystalline needles; 0.5621 g, 0.738 mmol, 74%) was washed with DMF and stored under DMF. Found: C, 40.16%; H, 4.74%; N, 10.74%. Expected: C, 40.14%; H, 4.79%; N, 10.80%. Yield and expected elemental analysis calculated using the formula: [Me₂NH₂]₂[Cd(NO₂BDC)₂]·2DMF·0.5H₂O. Phase purity of the sample was confirmed by Pawley fitting of PXRD data (Fig. S5†). Further details of characterisation by TGA and by solution-phase NMR spectroscopy following acid digestion are provided in the ESI.†

Gas adsorption

Gravimetric CO₂ adsorption measurements were made using an Intelligent Gravimetric Analyser (IGA-003) supplied by Hiden Isochema Ltd, which was thermally regulated via active computer control. A computer algorithm was applied to monitor the approach to equilibrium at each pressure step. Prior to measurements, the sample was activated at room temperature under ultra-high vacuum (10⁻⁸ bar) until constant mass was attained. Adsorption isotherms for CO₂ were measured at 273, 288 and 298 K and used to determine the isosteric enthalpy of adsorption (see Fig. S11 and S12†). Volumetric N₂ adsorption was performed on a Micromeritics ASAP 2020Plus Analyser. The sample (ca. 100 mg) was desolvated at 80 °C under vacuum overnight (ca. 16 hours) using standard Schlenk techniques, transferred to the analyser and degassed for a further 16 hours under vacuum at 80 °C prior to analysis. Nitrogen uptake was performed at 77 K using a liquid N₂ bath for temperature control (Fig. S10†).

Powder X-ray diffraction

Laboratory powder X-ray diffraction (PXRD) experiments were performed using a Bruker D8 Advance diffractometer equipped with Göbel mirrors, and recorded in the range 3° < 2θ < 60° using Cu-K_α radiation. Data collection was performed with Debye–Scherrer geometry, with a rotating capillary stage. Samples were loaded in 0.7 mm borosilicate capillaries. Temperature was either ambient (routine collections), or controlled using an Oxford Cryosystems Cryostream Plus device. Synchrotron powder X-ray diffraction data were collected at Beamline I11, Diamond Light Source using a wide-angle position-sensitive detector comprising 18 Mythen-2 modules.^33,34 Samples were packed into 0.7 mm quartz capillaries built into a gas cell to allow sample evacuation and CO₂ uptake. A pair of scans was collected for each measurement, related by a 0.25° detector offset, to account for gaps between modules. At each gas pressure four such pairs of patterns were summed to give the final pattern used for analysis. All powder diffraction data were analysed by Pawley refinement,³⁵ using TOPAS 4.1.³⁶

Single-crystal X-ray diffraction

Laboratory single-crystal X-ray diffraction (SCXRD) experiments were performed using either a Bruker APEX-II CCD diffractometer with 3-circle SMART or 4-circle KAPPA platform and a Mo-K_α sealed-tube X-ray source, or a Bruker D8 Venture diffractometer with a PHOTON 100 dual-CMOS chip detector, operating with a Cu-K_α IμS microfocus X-ray source. Data were processed using the APEX-3 suite of programs.³⁷ Sample temperature was maintained using an Oxford Cryosystems Cryostream 700 or CryostreamPlus 700 device. Samples were mounted directly from the mother liquor, unless stated otherwise. Absorption correction was performed using empirical methods (SADABS) based on symmetry-equivalent reflections combined with measurements at different azimuthal angles.³⁸ Synchrotron SCXRD data were recorded at Beamline I19, Diamond Light Source. The crystal was carefully glued to a Mylar loop, ensuring minimum coverage of the crystal with glue, and loaded into a 1.0 mm quartz capillary built into a gas cell to allow CO₂ uptake. A minimum of one hemisphere of data was collected using three 132° and one 180° omega scans, with 0.4° slicing, on a Newport diffractometer using a Pilatus 300 K detector.³⁹ Data processing and absorption correction was performed using Rigaku Oxford Diffraction CrysalisPro.⁴⁰ Crystal structures were solved and refined against F² values the program SHELXL⁴¹ implemented via OLEX-2.⁴² All non-hydrogen atoms were refined anisotropically except for some of the structures in which positional disorder of the cations or orientational disorder of the linker ligand was required. Crystallographic restraints and constraints were applied to some structures where necessary. Positions of hydrogen atoms were calculated with idealised geometries and refined using a riding model with isotropic displacement parameters. The PLATON function SQUEEZE⁴³ was applied in some cases to determine the contribution to the structure factors of the unmodelled electron density of solvent molecules and/or the cations in the MOF pores, where otherwise poor convergence of the least-squares refinement resulted.

Results & discussion

Synthesis, crystal structure & bulk-phase characterisation

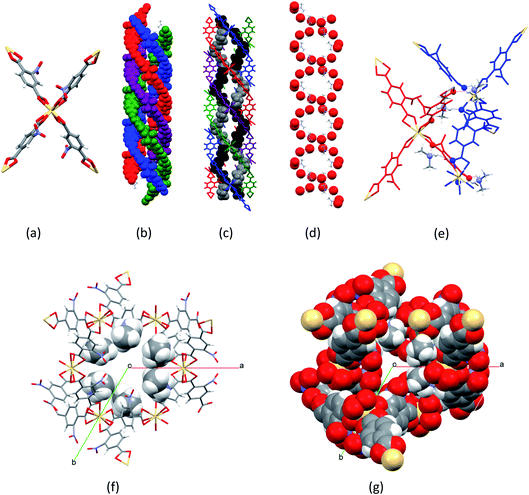
[Me₂NH₂]₂[Cd(NO₂BDC)₂]·2DMF·0.5H₂O (SHF-81-DMF) was prepared by a modification of the reported solvothermal procedure,³² which, in our hands, had yielded no product. Our procedure uses a different stoichiometry of reactants, milder conditions and a considerably shorter reaction time, and is further facilitated by adding to the reaction mixture 0.05 equivalents of [Me₂NH₂]Cl, which may have a templating effect, enabling a 74% yield. The majority of NMe₂H₂⁺ cations present in the crystalline product, however, result from in situ hydrolysis of DMF. We note that precise control of the water content in the reaction mixture was not attempted. The composition and phase purity of the product were established by a combination of elemental analysis, thermogravimetric analysis (Fig. S4†), ¹H and ¹³C NMR spectroscopy of acid-digested material (Fig. S1–S3†) and PXRD (Fig. S5†); the crystal structure was determined by SCXRD. The composition of the solvated form of the MOF (SHF-81-DMF) is presented henceforth as [Me₂NH₂]₂[Cd(NO₂BDC)₂]·2DMF·0.5H₂O, which closely approximates consistent compositions determined by the aforementioned range of characterisation techniques.

The crystal structure of SHF-81-DMF (Fig. 2) consists of a doubly interpenetrated qtz network constructed from 8-coordinate cadmium(II) ions, which serve as network nodes, each chelated by four nitroterephthalate (NO₂BDC²⁻) linkers to give a flattened pseudo-tetrahedral node geometry (Fig. 2a). The two networks give rise to a quadruple helix arrangement along the c-axis, in which every second helix component is connected to the same network (Fig. 2b). Triangular channels run parallel to the c-axis and are lined by inwardly oriented nitro groups (Fig. 2f and g). Within these channels the Me₂NH₂⁺ cations are arranged in a double helix arrangement of opposite handedness to the framework helices, each cation forming N–H⋯O hydrogen bonds to carboxylate oxygens associated with two Cd(O₂CR)₄²⁻ nodes (Fig. 2c–e). The channels are further occupied by DMF and water molecules, established from bulk-phase characterisation but not modelled crystallographically.

Fig. 2 Crystal structure of doubly-interpenetrated [Me₂NH₂]₂[Cd(NO₂BDC)₂]·2DMF·0.5H₂O (SHF-81-DMF) framework structure at 100 K, showing (a) Cd(O₂CR)₄²⁻ node; (b) quadruple helix arrangement of the framework along the c-axis (vertical) (blue and purple helices are part of one network; red and green helices are part of the other network); (c) quadruple helix arrangement of the framework, showing the double helix arrangement of the Me₂NH₂⁺ cations (black and grey) in the channels; (d) double helix arrangement of Me₂NH₂⁺ cations along the c-axis, emphasising framework carboxylate oxygens (red) which accept N–H⋯O hydrogen bonds from the cations and adopt a double-helix arrangement to match that of the cations; (e) N–H⋯O hydrogen bonds from the cations linking two networks, shown in red and blue (N, H and O atoms are emphasised); (f) view down the c-axis of a triangular channel, showing inwardly oriented nitro groups and the location of cations (shown in space-filling representation); (g) view down the c-axis of a triangular channel (all atoms in space-filling representation). Atom colours for parts (a), (d), (f) and (g): Cd, beige; O, red; N, blue; C, grey; H, white.

The crystal structure is modelled as a merohedral twin in trigonal space group P3_x21 (x = 1 or 2; crystals of each enantiomorph are present in any given batch). Twinning occurs via a 2-fold rotation about the c-axis, with the contribution of the twin domains refining to 0.51(1) : 0.49(1). This is an analogous description to that of Dauphiné twins in α-quartz,⁴⁴ which adopts the same trigonal space group(s). It is also possible to refine a structural model for SHF-81-DMF in hexagonal space group P6_x22 (x = 2 or 4; crystals of each enantiomorph are present in any given batch), the space group adopted by β-quartz⁴⁴ and reported for the analogous MOF QMOF-2 (vide supra),⁴⁵ but this model gives poorer indices of fit (R1, wR2, R_int) and has a number of other unsatisfactory features. The hexagonal model requires two-fold rotational disorder of the nitroaromatic moieties (C₆H₃NO₂), which in the simplest model can be described in terms of disorder of the nitro group across two adjacent ring positions; cations or solvent molecules could not be modelled. The twinned trigonal model, in contrast, does not require this disorder to be invoked for the nitro substituents and allows modelling of the ordered network of cations that shows the hydrogen bonding arrangement along the channels (Fig. 2c–e). The previous report of the crystal structure used a model in hexagonal space group P6₂22 and suffers the same deficiencies as our refinements in the space group.³² The necessity of the twinned trigonal model becomes more apparent upon desolvation of the MOF to generate SHF-81, for which a hexagonal model no longer provides an approximate fit (vide infra). Thus, SHF-81 adopts a Dauphiné twin α-quartz structure, whereas SHF-81-DMF adopts the same type of structure, but one that lies much closer to the β-quartz structure.

Activation studies: discovery of flexible behaviour

The TGA studies of SHF-81-DMF are consistent with stepwise removal of solvent from 80–130 °C, followed by cation degradation via loss of Me₂NH at 230–280 °C, behaviour that compares well with that previously reported for the MOF SHF-61-DMF [Me₂NH₂][In(NH₂BDC)₂]·1.75DMF·1.25H₂O.²⁷ Heating a sample of SHF-81-DMF in powder form at 80 °C under dynamic vacuum for 16 h resulted in desolvation, but retention of the Me₂NH₂⁺ cations, yielding [Me₂NH₂]₂[Cd(NO₂BDC)₂] (SHF-81), as indicated by ¹H NMR spectroscopy following acid digestion (Fig. S6†). PXRD data show that the material is still a single phase; the Pawley fits indicate substantial changes in unit cell dimensions determined at 295 K (Table 1; SHF-81-DMF, Fig. S5;†SHF-81, Fig. S7†) and suggest anisotropic breathing behaviour that involves contraction of the framework along the equivalent a- and b-axes, but expansion along the c-axis. A breathing response of similar magnitude was also achieved in single crystals of SHF-81-DMF by heating on a glass slide in a temperature-controlled oven at 100 °C for 1 h. SCXRD data were collected at 100 K and 195 K and used in crystal structure refinements for SHF-81 (Table 1). Comparisons of unit cell data across the three temperatures, in either the solvated or activated/desolvated state, also indicate an anisotropic thermal expansion, consistent with the dynamic framework behaviour associated with activation and with the linear NTE behaviour of the analogous MOF QMOF-2,⁴⁵ reported as D[In(BDC-d₄)₂].³¹

Table 1 Unit cell parameters for solvated SHF-81-DMF and activated/desolvated SHF-81

Technique	Temperature		a/Å	c/Å	V/Å^3
a Data for solvated SHF-81-DMF were collected on crystals that adopted space group P3221; data for desolvated SHF-81 were collected on separate crystals that adopted space group P3121. b Pawley refinements using space group P3121.
SCXRD^a	100 K	SHF-81-DMF	14.8922(7)	12.7663(6)	2452.0(3)
		SHF-81	13.619(1)	13.229(1)	2124.9(5)
	195 K	SHF-81-DMF	15.0467(5)	12.6619(4)	2482.6(2)
		SHF-81	13.7702(3)	13.2048(3)	2168.4(1)
PXRD^b	298 K	SHF-81-DMF	15.3550(3)	12.5133(4)	2555.1(1)
		SHF-81	13.931(2)	13.148(3)	2209.6(9)

---

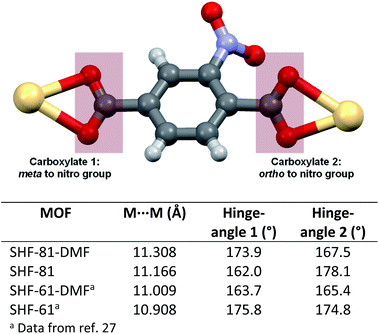
The change in the unit cell parameters upon activation of the MOF is consistent with narrowing and lengthening of the channels in the material, which run parallel to the c-axis (Fig. 2). The flexibility of the framework can be viewed at a local level in terms of the hinge-like motion of the nitroterephthalate ligands (NO₂BDC²⁻) described in terms of rotation of the ligand about the O⋯O vector of its carboxylate groups (Fig. 3). The crystal structures contain one independent ligand with two crystallographically distinct carboxylate groups. Upon desolvation,‡ the hinge angle at the carboxylate group ortho to the nitro substituent increases from 167.5° to 178.1°, whereas at the other carboxylate group the hinge angle decreases from 173.9° to 162.0°; the Cd⋯Cd distance is reduced by only approx. 0.14 Å (11.3084(4) to 11.1662(8) Å). The magnitudes of the changes are similar to those of the flexible diamondoid MOF SHF-61,²⁷ which is based on distorted tetrahedral In(O₂CR)₄⁻ nodes linked by aminoterephthalate ligands.

Fig. 3 Carboxylate coordination for NO₂BDC²⁻ to consecutive Cd centres in the framework SHF-81. Analogous coordination is found for NH₂BDC²⁻ to consecutive In centres in the framework SHF-61. Tabulated hinge angles at the two carboxylate groups (meta and ortho to the ring substituent) are defined as the angle M⋯(OO centroid)⋯(C₆ ring centroid). Where disorder of the carboxylate group has been modelled, the angles refer to the major component of the model. All single-crystal structures at 100 K (except SHF-61 at 105 K).

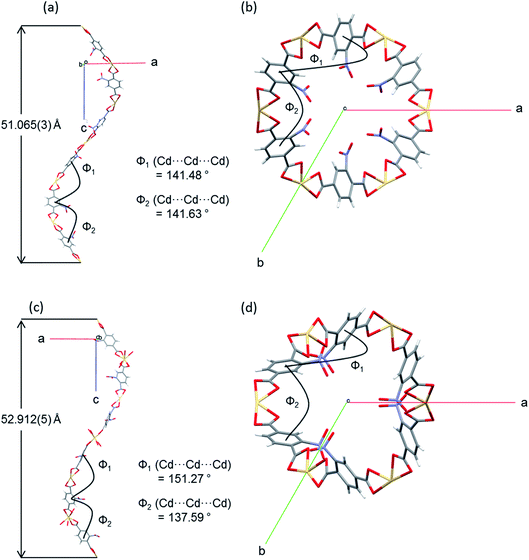
The flexibility of the framework and its relationship to the changes in unit cell dimensions can be seen more readily by consideration of the framework angles defined by Cd nodes (Cd⋯Cd⋯Cd). The crystal structures contain one crystallographically unique Cd centre, which resides on a 2-fold rotation axis in the P3_x21 space group. There are two unique alternating Cd⋯Cd⋯Cd angles (φ₁, φ₂) that propagate the helical chains, with each turn of the helix comprising six Cd(II) centres and six NO₂BDC²⁻ ligands (Fig. 4 and Fig. S8†). In the hexagonal β-quartz structure φ₁ = φ₂, but in the lower symmetry α-quartz structure φ₁ ≠ φ₂. In SHF-81-DMFφ₁ = 141.48° and φ₂ = 141.63°, confirming that the structure is close to the β-quartz type, but upon desolvation/activation the angles change to φ₁ = 151.27° and φ₂ = 137.59°, which very clearly indicates an α-quartz type structure. This change lengthens the helix pitch from 51.065(3) to 52.912(5) Å (4 × c-axis length) and results in three of the six Cd(II) centres in each helical turn moving towards the centre of a given channel and three moving away, in an alternating pattern (Fig. 4c and d). Of the six Cd⋯Cd⋯Cd angles that can be defined around each tetrahedral network node associated with a Cd(II) centre (Fig. S8†), local 2-fold rotational symmetry requires that four are unique. The remaining two unique angles change from φ₃ = 82.36° and φ₄ = 110.47° in SHF-81-DMF to φ₃ = 75.15° and φ₄ = 115.83° in SHF-81. The changes in Cd⋯Cd⋯Cd angles upon activation/desolvation are also reflected in changes in the distances between consecutive nitro groups along each chain. As measured by the N⋯N separations, these change from 7.153 and 11.662 Å in SHF-81-DMF to 8.699 and 10.821 Å in SHF-81 (distances for major components of the rotationally disordered nitroaromatic group in SHF-81 are listed).

Fig. 4 A single turn of a helix viewed perpendicular and parallel to the c-axis, along which the helices and accompanying pores propagate, shown with dimensions for alternating Cd⋯Cd⋯Cd angles (φ₁, φ₂) and the helix pitch, for (a) and (b) SHF-81-DMF; (c) and (d) SHF-81. Single-crystal structures determined at 100 K.

In situ diffraction studies of framework dynamic response to multiple stimuli: activation, CO₂ adsorption and temperature

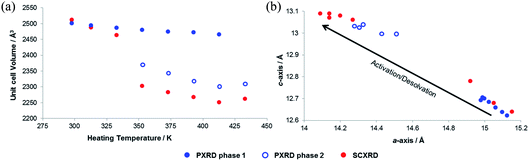
In order to explore the initial findings, in situ diffraction studies were conducted to examine the response of the framework to different stimuli in more detail. We examined (i) activation of SHF-81-DMF and the dynamic structural response to pore-solvent removal, (ii) adsorption of CO₂ gas by activated SHF-81 and the resultant dynamic framework response, and (iii) the uniaxial NTE response to change of temperature in both SHF-81-DMF and its activated/desolvated counterpart SHF-81.

Activation of SHF-81-DMF. Sequences of SCXRD and PXRD experiments were conducted to monitor the changes in structure of the framework of SHF-81-DMF upon heating to remove the pore solvent. In each case the sample (single crystal on a MiTeGen mount or powder in a capillary) was heated to a specified temperature for 30 min then returned to 298 K and allowed to equilibrate for 5 min before measurement either of diffraction intensities on a fixed number of frames (SCXRD) or of a powder pattern, which were then indexed and used to determine the unit cell dimensions by standard least-squares methods. Each study comprised a series of sequential measurements conducted in this manner after heating at progressively higher temperatures, ranging from 298 K to 433 K.

In both studies, progressive heating at higher temperatures results in gradual contraction of the equivalent a- and b-axes and expansion of the c-axis, i.e. area negative expansion, leading to a gradual reduction in unit cell volume (Fig. 5). The sequence of lattice parameters determined suggests a continuous breathing behaviour, although it is noted that a more substantial change occurs for both studies between the measurement following heating at 333 K and that following heating at 353 K. For the SCXRD study, there is a substantial change in the unit cell of the crystal studied at this point (Table S3†), whereas for the PXRD study initially only a small fraction of the sample undergoes this change (Fig. S9 and Table S4†). Thus, after heating the powder sample to 333 K, two phases of the MOF are required for a satisfactory Pawley fit (Table S5†), the second (minor) phase having the more closed-pore structure (smaller a-axis, larger c-axis). Upon subsequent heating steps, both phases show further progression along the anisotropic deformation pathway (a-axis decreasing, c-axis increasing) and the second phase increases in relative proportion. After heating at 433 K, all the material is converted into the more closed-pore phase and a single-phase fit to the pattern can be obtained.

Fig. 5 Progressive changes (a) in unit cell volume (determined at 298 K) as a sequential function of heating temperature, and (b) in lattice parameters during activation/desolvation of SHF-81-DMF from in situ SCXRD and PXRD studies.

Adsorption of CO₂ by SHF-81. Volumetric adsorption of N₂ gas by SHF-81 at 77 K indicated minimal adsorption (≈3 cm³ g⁻¹, Fig. S10†), whereas gravimetric measurements of CO₂ adsorption conducted at 273 K, 288 K and 298 K (Fig. 6a and Fig. S11†) indicated substantial adsorption (4.4 mmol g⁻¹ at 19 bar CO₂ (p/p₀ 0.52), 273 K; 3.6 mmol g⁻¹ at 19 bar CO₂ (p/p₀ 0.31), 298 K) and an isosteric enthalpy of adsorption, ΔH_ads (i.e. adsorption at zero surface coverage) of −27.4 kJ mol⁻¹ (Fig. S12†). One might infer substantial selectivity of adsorption of CO₂ over N₂ from these results, but further studies would be needed to quantify this. Our focus, however, has been to investigate whether CO₂ adsorption is a stimulus for anisotropic framework breathing that follows the reverse pathway observed for activation/desolvation. Thus, in situ synchrotron X-ray diffraction experiments were conducted at Diamond Light Source to study the effects of adsorption using PXRD at 298 K (0–50 bar CO₂, Fig. S13 and Table S6†) and SCXRD at 298 K (0–40 bar CO₂, Table S7†).

Fig. 6 (a) Gravimetric CO₂ adsorption isotherms at 273, 288 and 298 K for SHF-81 (activated from SHF-81-DMF). Unit cell volume of SHF-81 as a function of CO₂ pressure during (b) in situ SCXRD study at 298 K and (c) in situ PXRD study at 298 K. Lattice parameters for SHF-81 as a function of increasing CO₂ pressure during (d) in situ SCXRD study at 298 K and (e) in situ PXRD study at 298 K. The dotted line in (b) is a guide to the eye, and illustrates the likely inflexion point slightly below p/p₀ 0.6. The arrows in (d) and (e) represent the direction of change for increasing CO₂ pressure (adsorption).

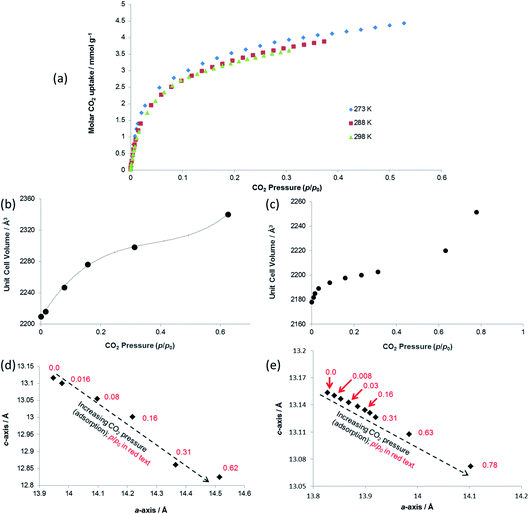
Both PXRD and SCXRD studies at 298 K show a small but rapid increase in unit cell volume at lower pressures (p/p₀ < 0.1, p < 6 bar CO₂), followed by a shallower increase until p/p₀ ≈ 0.6 (p ≈ 37 bar CO₂) and a further steep increase at p/p₀ > 0.6 (Fig. 6b and c), suggesting a potential gating of adsorption in the higher pressure range. The gravimetric adsorption data, which due to instrument limitations could not exceed a pressure of 20 bar, cover only the region of the diffraction studies at pressure below this apparent gating. The plots of a- vs. c-axis lengths show an increase in a-axis and decrease in c-axis length as CO₂ pressure is increased, consistent with the same framework breathing behaviour observed during the activation/desolvation of SHF-81-DMF, although with geometric changes in the opposite direction, i.e. negative linear expansion as CO₂ is adsorbed into the MOF pores. The range of changes in unit cell axis lengths and volume match reasonably well with those in the activation/desolvation study in the more closed-pore region of that study. Further studies (both adsorption and diffraction) at higher CO₂ pressures and/or lower temperatures (enabling higher p/p₀) would shed light on whether the geometries during the apparent adsorption gate are consistent with the observed step in observed geometries during activation/desolvation.

Temperature-dependence of framework flexibility in SHF-81 and SHF-81-DMF. A series of five variable-temperature X-ray diffraction experiments (VT1–VT4, SCXRD; VT5, PXRD) were conducted to provide further detail on the thermally induced flexibility of the framework. Study VT1 comprised sequential full SCXRD data collections using one crystal of SHF-81-DMF at 170, 140 and 100 K, including crystal structure refinements, and augments the data in Table 1. Other studies involved collection of only sufficient intensity data for accurate unit cell determination. Data were collected on two separate crystals of SHF-81-DMF at sequentially lower temperatures in studies VT2 (160–85 K) and VT3 (300–90 K). Data were collected on a crystal of activated/desolvated SHF-81 at sequentially higher temperatures in study VT4 (85–300 K). Study VT5 comprised PXRD data for SHF-81-DMF in temperature steps from 300 K to 90 K and then, using the same steps, returning from 90 K to 300 K. Unit cell data for studies VT1–VT5 are presented together with earlier data (Table 1) for SHF-81-DMF and SHF-81 at different temperatures in Fig. 7. Data for the structurally closely related MOF QMOF-2, for which a prior study of linear NTE has been reported,³¹ are included for comparison.

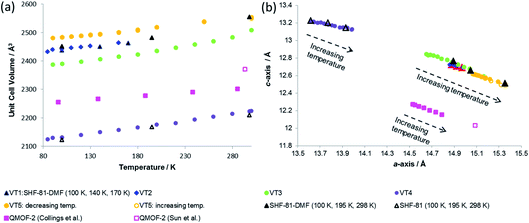Fig. 7 (a) Unit cell volume as a function of temperature and (b) lattice parameters during in situ SCXRD (VT2, VT3, SHF-81-DMF; VT4, SHF-81) and PXRD (VT5, SHF-81-DMF) studies. Data for full crystal structure determinations of SHF-81-DMF and SHF-81 at different temperatures are included, as are data for the previously reported VT-NPD study³¹ of desolvated QMOF-2 and single-crystal structure determination⁴⁵ of solvated QMOF-2 (note: the linear NTE behaviour of QMOF-2 was studied in the temperature range 12–285 K; data for the two studies conducted below 80 K are excluded from (a) for clarity of presentation, but studies over the full temperature range are included in (b)).

Both solvated SHF-81-DMF and activated/desolvated SHF-81 exhibit linear NTE, wherein the c-axis (channel length) decreases with increasing temperature, whereas the a- and b-axes (channel width) increase. The geometric changes involved are analogous to those described in the earlier sections. Qualitatively similar thermally induced changes are observed for QMOF-2. It is notable, however, that despite the similarities in structure between SHF-81/SHF-81-DMF and QMOF-2, the latter has a shorter helical pitch along the channels (shorter c-axis) and displays a smaller range of dynamic motion.

General discussion

The similarity in linear NTE behaviour of SHF-81-DMF/SHF-81 and QMOF-2 is understandable given their shared framework topology, doubly interpenetrated networks and analogous M(O₂CR)₄ⁿ⁻ network nodes and linker ligands (NO₂BDC²⁻ and BDC²⁻). Goodwin and co-workers have established that in quartz-like networks such as these the occurrence of linear NTE or PTE can be predicted geometrically based on the c/a ratio, ρ.³¹ For ρ < ρ_critical linear NTE occurs, whereas for ρ > ρ_critical linear PTE should be expected. For these MOFs, ρ_critical = 0.53; ρ = 0.82–0.85 for QMOF-2, ρ = 0.81–0.86 for SHF-81-DMF and ρ = 0.94–0.97 for SHF-81 over the temperature ranges studied, consistent with the linear NTE behaviour observed.

There is a marked difference in range of dynamic motion exhibited by the two MOFs, despite the frameworks being constructed with analogous ligands of the same length. The thermal expansion is of similar magnitude (Table 2) for both solvated SHF-81-DMF and desolvated SHF-81, and compares well with that of QMOF-2; there appears, however, to be a somewhat greater expansion for SHF-81-DMF in study VT3, which is likely to be a slightly desolvated crystal, based on the lattice parameters involved. The dynamic range resulting from activation/desolvation of SHF-81-DMF to SHF-81 is, however, markedly greater (approx. four-fold) than that reported for QMOF-2 (Table 2). This could be a consequence of a number of factors, most obviously incomplete activation/desolvation for QMOF-2, as noted in the reported study.³¹ There are a number of other differences between the two MOFs, notably the differences in metal–ligand bonding, wherein the In^III–O bonds in QMOF-2 are 0.05–0.2 Å shorter than the Cd^II–O bonds in SHF-81-DMF/SHF-81,⁴⁶ which may lead to differences in how facile the carboxylate hinge-deformation integral to the breathing motion is. The dicarboxylate linker ligands also differ in the presence of the nitro substituent, which will have an electronic effect on metal–ligand bonding and a steric effect on channel dimensions. A final area of difference is the nature of the charge-balancing cation in the pore. In the case of SHF-81-DMF/SHF-81, SCXRD and ¹H NMR evidence indicate that the MOF retains two Me₂NH₂⁺ cations per Cd(II) centre during the studies conducted. This situation is less clear, however, for QMOF-2. The original report provides a formula of H[In(BDC)₂]·nH₂O,⁴⁵ although the synthetic route used will inevitably generate Me₂NH₂⁺ cations. Closer inspection of the reported IR spectrum suggests the presence of ν(N–H) bands (at 3224 cm⁻¹) consistent with such cations, and TGA data include a mass loss at 220–250 °C consistent with loss of Me₂NH from the cations, as also documented for SHF-81 and other dimethylammonium-containing MOFs.²⁷ The fully deuterated QMOF-2 used in the thermal expansion study was prepared in an analogous manner to the original QMOF-2, and most likely has a composition of (CD₃)₂ND₂[In(BDC-d₄)₂]·n(DMF-d₇)·m(D₂O). Upon activation, although the reported composition is D[In(BDC-d₄)₂]·guest,³¹ it is likely that (CD₃)₂ND₂⁺ cations remain, given the activation procedure used.⁴⁷

Table 2 Comparison of changes in lattice parameters for SHF-81-DMF, SHF-81 and QMOF-2 as a consequence of (i) increasing temperature and (ii) desolvation

Thermal
MOF	Δa (Å)	Δc (Å)	Diffraction technique	Temperature range (increasing)	Notes
a Based on the range of unit cell dimensions it is most likely that this study is based on a partially desolvated crystal. b The authors note that D[In(BDC-d4)2] is not fully desolvated, as demonstrated by Rietveld fits.^31 c A range of temperatures that most closely matches the current studies is selected (full temperature range is 12–285 K). d Calculated based on differences between SCXRD unit cell for solvated H[In(BDC)2] at 293 K (ref. 45) and PND unit cell for (partially) desolvated D[In(BDC-d4)2] at 285 K.^31
SHF-81-DMF	0.52	−0.25	SCXRD	90–300 K	VT3
SHF-81-DMF	0.29	−0.13	PXRD	90–300 K	VT5
SHF-81	0.34	−0.083	SCXRD	90–300 K	VT4
QMOF-2^b	0.20	−0.095	NPD	96–285^c K	Ref. 31

---

Desolvation
MOF	Δa (Å)	Δc (Å)	Diffraction technique	Temperature used for comparison	Notes
SHF-81-DMF	−1.42	0.63	PXRD	298 K
SHF-81-DMF	−1.28	0.54	SCXRD	195 K
SHF-81-DMF	−1.28	0.46	SCXRD	100 K
QMOF-2	−0.30	0.12	NPD	285–293^d K	Partial desolvation^b

---

The differences in behaviour between the SHF-81 and QMOF-2 systems suggest the possibility of tuning the dynamic behaviour by changing the nature of the substituent on the BDC²⁻ ligand, through the use of mixed ligand MOFs and/or by changing the number and nature of the charge-balancing cations that reside in the MOF pores. The potential advantages and applications that many arise in the future from tuning anisotropic and negative expansion behaviour have been discussed by others. With that in mind, we note that a number of other analogues of these MOFs have been reported,^32,48 although this is a phase-rich area of MOF materials and to date, in our hands, many of these have proven challenging to isolate in phase-pure form on a practical scale.

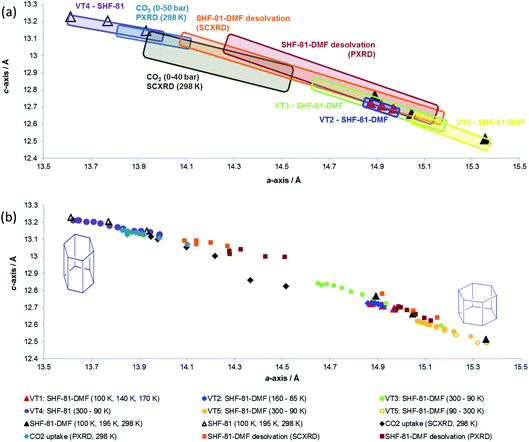
Data from all diffraction studies are combined in Fig. 8 to convey the change in lattice parameters associated with the full range of breathing behaviour collectively probed by different stimuli. Notably, there are data points across the full range of lattice parameters 15.4 Å > a > 13.6 Å and 12.5 Å < c < 13.2 Å that lie approximately along a single line, suggesting the potential for a continuous breathing motion within this range of geometries with a negative correlation between a- and c-axis lengths. Activation/desolvation of SHF-81-DMF results in the largest changes, which span most of the full range of accessible dimensions. The CO₂ adsorption studies and thermal studies (90–300 K) give rise to changes of framework dimensions of similar magnitude, but smaller than those observed due to activation/desolvation. Although in principle higher pressures of CO₂ could be applied, the PXRD study reached p/p₀ of 0.8, which may suggest that CO₂ is not as effective an adsorbate for opening the MOF pores as the DMF/H₂O solvent, consistent with the modest CO₂ adsorption enthalpy for SHF-81. Further investigations with a wider variety of adsorbates would be needed to describe the MOF performance more completely.

Fig. 8 Combined plots showing change in lattice parameters as a function of different stimuli: activation/desolvation, CO₂ adsorption and temperature. (a) Each in situ diffraction study is represented by a rectangular box that encloses all data points associated with that study. Individual SCXRD studies at different temperatures (six SHF-81-DMF; three SHF-81) are denoted by triangular markers. (b) All individual data points associated with each study are shown. Colours and shapes of markers for individual data points are denoted in the legend.

It is also apparent, particularly from the representation of the in situ studies in Fig. 8a, that what appear to be analogous studies are in fact conducted on samples in different initial states. Thus, thermal studies VT2, VT3 and VT5 clearly involve samples with different levels of partial desolvation, although all were ostensibly solvated SHF-81-DMF. The two in situ activation/desolvation studies, although starting at a similar point (slightly desolvated SHF-81-DMF), have endpoints with different geometries, the single-crystal sample being the more desolvated. This is most likely a consequence of the greater difficulty in solvent removal from the powder sample, as a consequence of its containment within a capillary. Study VT4 and the two CO₂ adsorption studies have starting dimensions that suggest that these samples are a little more desolvated than the endpoints of the two desolvation studies. The difference in starting point between the two CO₂ adsorption studies (the PXRD sample is slightly more closed – smaller a-axis, larger c-axis) may be a factor in governing the smaller change in dimensions observed for the PXRD study than the SCXRD study. These observations indicate the challenges in clearly defining initial and final states in dynamic studies, such as this. The collective value of conducting a series of studies, using different stimuli and also different initial and final states, is also clearly demonstrated.

Conclusions

The MOF [Me₂NH₂]₂[Cd(NO₂BDC)₂]·2DMF·0.5H₂O (SHF-81-DMF) can be synthesised in good yield solvothermally by addition of a sub-stoichiometric amount (0.05 equiv.) of [Me₂NH₂]Cl. The MOF adopts a Dauphiné twinned α-quartz structure (trigonal, P3_x21, x = 1, 2) that deviates slightly from the higher symmetry β-quartz structure (hexagonal, P6_x22, x = 2, 4). Direct activation by heating to remove pore solvent reveals that the MOF is flexible and exhibits breathing behaviour. A series of in situ PXRD and SCXRD studies demonstrated that three stimuli – (i) activation/desolvation, (ii) CO₂ adsorption and (iii) temperature – each led to breathing behaviour that is characterised by changes in the a-axis (b-axis) and c-axis dimensions that are opposite in sign, with magnitudes as large as |Δa|, |Δb| < 1.8 Å and |Δc| < 0.7 Å. The a- and b-axes quantify the width of pores, which run parallel to the c-axis and are defined by framework helices that increase in pitch as they narrow in diameter, and vice versa, during the reversible breathing behaviour. The thermal response of the MOF, either as solvated SHF-81-DMF or desolvated SHF-81, is described as linear negative thermal expansion. Adsorption of CO₂ by SHF-81 can also be described as negative linear expansion, whereas activation/desolvation results in the reverse of the dynamic behaviour associated with adsorption. Comparison with the related β-quartz MOF H[In(BDC)₂]·guest (QMOF-2), which contains analogous building blocks and M(O₂CR)₄ⁿ⁻ nodes and also exhibits linear NTE behaviour, suggests that there is an opportunity for tuning this behaviour based upon choice of metal ion and ligand potentially in a large family of related MOFs. We are actively exploring this potential.

Conflicts of interest

There are no conflicts of interest.

Acknowledgements

We are grateful to the University of Sheffield for a PhD studentship (DW) and to the Leverhulme Trust for support for TMR. We thank EPSRC for support of X-ray diffraction and NMR spectroscopy facilities at University of Sheffield and Diamond Light Source for beam time at beamlines I19 and I11.

References

1. D. M. D’Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082.
2. L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314.
3. M. P. Suh, H. J. Park, T. K. Prasad and D. Lim, Chem. Rev., 2012, 112, 782–835.
4. A. Corma, H. Garcia and F. X. Llabres i Xamena, Chem. Rev., 2010, 110, 4606–4655.
5. Y. Liu, W. Xuan and Y. Cui, Adv. Mater., 2010, 22, 4112–4135.
6. J. Liu, L. Chen, H. Cui, J. Zhang, L. Zhang and C.-Y. Su, Chem. Soc. Rev., 2014, 43, 6011–6061.
7. Y. Zhao, Z. Song, X. Li, Q. Sun, N. Cheng, S. Lawes and X. Sun, Energy Storage Materials, 2016, 2, 35–62.
8. L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125.
9. E. Barea, C. Montoro and J. A. R. Navarro, Chem. Soc. Rev., 2014, 43, 5419–5430.
10. S. Kitagawa and K. Uemura, Chem. Soc. Rev., 2005, 34, 109–119.
11. S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695–704.
12. G. Férey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380–1399.
13. C. R. Murdock, B. C. Hughes, Z. Lu and D. M. Jenkins, Coord. Chem. Rev., 2014, 258–259, 119–136.
14. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096.
15. G. Fraux and F.-X. Coudert, Chem. Commun., 2017, 53, 7211–7221.
16. I. E. Collings and A. L. Goodwin, J. Appl. Phys., 2019, 126, 181101.
17. L. Li, R.-B. Lin, R. Krishna, X. Wang, B. Li, H. Wu, J. Li, W. Zhou and B. Chen, J. Am. Chem. Soc., 2017, 139, 7733–7736.
18. S. Yuan, L. Zou, H. Li, Y.-P. Chen, J. Qin, Q. Zhang, W. Lu, M. B. Hall and H.-C. Zhou, Angew. Chem., Int. Ed., 2016, 55, 10776–10780.
19. X.-Y. Dong, H.-L. Huang, J.-Y. Wang, H.-Y. Li and S.-Q. Zang, Chem. Mater., 2018, 30, 2160–2167.
20. P. G. Yot, L. Vanduyfhuys, E. Alvarez, J. Rodriguez, J.-P. Itié, P. Fabry, N. Guillou, T. Devic, I. Beurroies and P. L. Llewellyn, Chem. Sci., 2016, 7, 446–450.
21. J. Troyano, A. Carné-Sánchez, J. Pérez-Carvajal, L. León-Reina, I. Imaz, A. Cabeza and D. Maspoch, Angew. Chem., Int. Ed., 2018, 57, 15420–15424.
22. (a) C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526; (b) P. L. Llewellyn, P. Horcajada, G. Maurin, T. Devic, N. Rosenbach, S. Bourrelly, C. Serre, D. Vincent, S. Loera-Serna, Y. Filinchuk and G. Férey, J. Am. Chem. Soc., 2009, 131, 13002–13008.
23. (a) Z. Wang and S. M. Cohen, J. Am. Chem. Soc., 2009, 131, 16675–16677; (b) J. S. Grosch and F. Paesani, J. Am. Chem. Soc., 2012, 134, 4207–4215; (c) S. Henke, A. Schneemann, A. Wütscher and R. A. Fischer, J. Am. Chem. Soc., 2012, 134, 9464–9474.
24. (a) H. J. Choi, M. Dincă and J. R. Long, J. Am. Chem. Soc., 2008, 130, 7848–7850; (b) J. A. Mason, J. Oktawiec, M. K. Taylor, M. R. Hudson, J. Rodriguez, J. E. Bachman, M. I. Gonzalez, A. Cervellino, A. Guagliardi, C. M. Brown, P. L. Llewellyn, N. Masciocchi and J. R. Long, Nature, 2015, 527, 357–361; (c) M. K. Taylor, T. Runčevski, J. Oktawiec, M. I. Gonzalez, R. L. Siegelman, J. A. Mason, J. Ye, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2016, 138, 15019–15026; (d) M. K. Taylor, T. Runčevski, J. Oktawiec, J. E. Bachman, R. L. Siegelman, H. Jiang, J. A. Mason, J. D. Tarver and J. R. Long, J. Am. Chem. Soc., 2018, 140, 10324–10331.
25. (a) A. P. Katsoulidis, K. S. Park, D. Antypov, C. Martí-Gastaldo, G. J. Miller, J. E. Warren, C. M. Robertson, F. Blanc, G. R. Darling, N. G. Berry, J. A. Purton, D. J. Adams and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2014, 53, 193–198; (b) A. P. Katsoulidis, D. Antypov, G. F. S. Whitehead, E. J. Carrington, D. J. Adams, N. G. Berry, G. R. Darling, M. S. Dyer and M. J. Rosseinsky, Nature, 2019, 565, 213–217; (c) S. Krause, V. Bon, I. Senkovska, U. Stoeck, D. Wallacher, D. M. Többens, S. Zander, R. S. Pillai, G. Maurin, F.-X. Coudert and S. Kaskel, Nature, 2016, 532, 348–352.
26. (a) C. S. C. Mellot-Draznieks, S. Surblé, N. Audebrand, Y. Filinchuk and G. Férey, Science, 2007, 315, 1828–1831; (b) P. Horcajada, F. Salles, S. Wuttke, T. Devic, D. Heurtaux, G. Maurin, A. Vimont, M. Daturi, O. David, E. Magnier, N. Stock, Y. Filinchuk, D. Popov, C. Riekel, G. Férey and C. Serre, J. Am. Chem. Soc., 2011, 133, 17839–17847.
27. E. J. Carrington, C. A. McAnally, A. J. Fletcher, S. P. Thompson, M. Warren and L. Brammer, Nat. Chem., 2017, 9, 882–887.
28. A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794–797.
29. (a) R. Baughman, S. Stafstrom, C. Cui and S. Dantas, Science, 1998, 279, 1522–1524; (b) A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. van der Lee, L. Peters, A. L. Thompson, V. Dmitriev, J. Haines and A. L. Goodwin, Nat. Mater., 2013, 12, 212–216; (c) A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465.
30. J. N. Grima, R. Gatt, V. Zammit, J. J. Williams, K. E. Evans, A. Alderson and R. I. Walton, J. Appl. Phys., 2007, 101, 086102.
31. I. E. Collings, M. G. Tucker, D. A. Keen and A. L. Goodwin, CrystEngComm, 2014, 16, 3498–3506.
32. X.-F. Wang, Y.-B. Zhang and Y.-Y. Lin, CrystEngComm, 2013, 15, 3470–3477.
33. S. P. Thompson, J. E. Parker, J. Potter, T. P. Hill, A. Birt, T. M. Cobb, F. Yuan and C. C. Tang, Rev. Sci. Instrum., 2009, 80, 075107.
34. S. P. Thompson, J. E. Parker, J. Marchal, J. Potter, A. Birt, F. Yuan, R. D. Fearn, A. R. Lennie, S. R. Street and C. C. Tang, J. Synchrotron Radiat., 2011, 18, 637–648.
35. G. S. Pawley, J. Appl. Crystallogr., 1981, 14, 357–361.
36. (a) A. A. Coelho, TOPAS Academic Version 4.1, 2007, see http//www.topas-academic.net; (b) A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218; (c) A. A. Coelho, J. Evans, I. Evans, A. Kern and S. Parsons, Powder Diffr., 2011, 26, S22–S25.
37. APEX3, Bruker AXS Inc., Madison, Wisconsin, USA, 2016.
38. (a) SADADS, empirical absorption correction program, based on the method of Blessing^38b L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, J. Appl. Crystallogr., 2015, 48, 3–10 ; (b) R. H. Blessing, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 33–38.
39. H. Nowell, S. A. Barnett, K. E. Christensen, S. J. Teat and D. R. Allan, J. Synchrotron Radiat., 2012, 19, 435–441.
40. CrysAlis^PRO, Rigaku Oxford Diffraction.
41. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
42. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
43. A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18.
44. (a) A. F. Wright and M. S. Hehmann, J. Solid State Chem., 1981, 36, 371–380; (b) K. Kihara, Eur. J. Mineral., 1990, 2, 63–77; (c) J. Van Landuyt, G. Van Tendeloo, S. Amelinckx and M. B. Walker, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 2986–2992.
45. J. Sun, L. Weng, Y. Zhou, J. Chen, Z. Chen, Z. Liu and D. Zhao, Angew. Chem., Int. Ed., 2002, 41, 4471–4473.
46. SHF-81-DMF: Cd–O bond lengths 2.314–2.494 Å; QMOF-2 (ref. 45): In–O bond lengths 2.267–2.282 Å.
47. (a) Kang and coworkers report^47b that Me₂NH₂⁺ cations lose Me₂NH at approximately 250–300 °C in as-synthesised QMOF-2 (TGA measurements), but also report that Me₂NH loss occurs by heating at 60 °C under vacuum for an unspecified time period, after first exchanging pore-solvent with CH₂Cl₂ (by an unspecified procedure); (b) W. Ji, H. Hu, W. Zhang, H. Huang, X. He, X. Han, F. Zhao, Y. Liu and Z. Kang, Dalton Trans., 2013, 42, 10690–10693.
48. M. Krüger, M. Albat, A. K. Inge and N. Stock, CrystEngComm, 2017, 19, 4622–4628.

---

Footnotes

† Electronic supplementary information (ESI) available: Further details on all experimental studies can be found in the supporting information, including synthesis and characterisation, and all SCXRD and PXRD studies. CCDC 2013011–2013023. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0fd00089b

‡ Distances and angles used in the section to quantify changes in crystal structure upon desolvation/activation are those for the crystal structures of SHF-81-DMF and SHF-81 at 100 K.

---