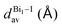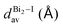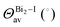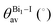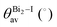Open Access Article
Open Access ArticleNovel zero-dimensional lead-free bismuth based perovskites: from synthesis to structural and optoelectronic characterization†
Mailde S.
Ozório
 a,
Willian X. C.
Oliveira
a,
Willian X. C.
Oliveira
 b,
Julian F. R. V.
Silveira
a,
Ana Flávia
Nogueira
*c and
Juarez L. F.
Da Silva
b,
Julian F. R. V.
Silveira
a,
Ana Flávia
Nogueira
*c and
Juarez L. F.
Da Silva
 *a
*a
aSão Carlos Institute of Chemistry, University of São Paulo, PO Box 780, 13560-970, São Carlos, SP, Brazil. E-mail: anafla@unicamp.br; juarez_dasilva@iqsc.usp.br
bDepartamento de Qumica, Instituto de Cincias Exatas, Universidade Federal de Minas Gerais, PO Box 6154, 13083-970, Belo Horizonte, MG, Brazil
cInstitute of Chemistry, University of Campinas, PO Box 6154, 13083-970 Campinas, SP, Brazil
First published on 3rd November 2020
Abstract
Despite high photo-conversion efficiency, the short long-term stability and toxicity issues have prevented lead-based perovskites from becoming the standard in high efficiency solar cells. Hence, lead-free perovskites with low inorganic framework dimensionality have attracted great attention because of their optoelectronic properties and superior stability. In this work, we present a combined experimental and theoretical investigation of the structural and optoelectronic properties of three novel highly stable zero-dimensional perovskites (discrete connectivity of the inorganic framework), where fused octahedra [BixIy]z− are interspersed by large organic cations: H2bpy2+ for 1, Hdmphen+ for 2 and the combination of H2terpy+2 and Hterpy+ for 3 (bpy = 4,4-bipyridine, dmphen = 2,9-dimethyl-1,10-phenanthroline, terpy = 2,2′;6′,2′′-terpyridine). In each of these compounds, the inorganic moieties display different morphologies, either edge-sharing bi-octahedra (Bi2I104−, 1), face-sharing bi-octahedra (Bi2I93−, 2) or isolated octahedra (BiI63−, 3). The consistent results of experimental and theoretical characterization reveal that distortions in the coordination octahedra are most prominent as the number of shared iodide species increases. The experimental optical response presents similar trends between all three materials, which is dominated by transitions inside the octahedron, while the transitions between cations and anionic bismuth-iodide clusters displayed very low intensity at a lower photon energy, an aspect that was described qualitatively well by theoretical characterization. Overall, these materials show different potential prospects, such as application in hybrid dimensional materials, acting as dielectrics for instance, or as a source of Bi for the synthesis of other lead-free perovskites.
I Introduction
Lead-based halide perovskites, APbI3, have emerged as a promising material for low cost solution processed optoelectronic devices,1–3 displaying tunable energy band gaps,4–6 expressive light harvesting7 and high exciton lifetime.6 However, commercialization has been hindered due to lead toxicity and instability caused by moisture, heat and extended light exposure.8 One of the avenues to address these issues is to move towards lower dimensional perovskites, where the octahedra are interspersed in one or more directions by organic cations, creating octahedral planes (2D),9 threads (1D),10 or simply small interspersed octahedral clusters (0D).11Moving towards low dimensional systems opens possibilities for different interstitial cations inside the octahedron, and one of the most prominent is Bi(III), which has a similar electronic configuration to lead but is non-toxic. Additionally, bismuth(III)-based perovskites can be straightforwardly prepared via solution processing or solid state reactions. Within this prospect, several studies have explored lower dimensional Bi-based perovskites for numerous applications, such as solar cells,12,13 broad range emission,11 X-ray imaging,14 capacitors15 and photodetectors.16 For instance, in the context of photovoltaics, Cs3Bi2I9 and MA3BiI9 (MA = methylammonium), both 0D perovskites with two face-sharing Bi2I93− octahedra, resulted in devices with a power conversion efficiency (PCE) of 3.20%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 and 1.64%,12 respectively.
13 and 1.64%,12 respectively.
Overall, low dimensional perovskites exhibited improved stability as a result of hydrophobic interactions between the octahedra and the cations, which can prevent water/oxygen physisorption.8 However, long range octahedra–cation interactions have led to decreased power conversion efficiency,17 especially when compared to 3D configurations, which is caused by low carrier mobility due to quantum confinement derived from the organic components' interspersion. Hybrid dimensional constructions are possible alternatives in which this problem can be averted for superior power conversion,17 but, to that end, it is necessary to have a fundamental understanding of lower dimensional perovskites, and 0D perovskites have higher structural flexibility to be part of these constructions.18 Therefore, there is great interest to design new 0D perovskites for photovoltaic applications.
In this work, we combined several experimental techniques and density functional theory (DFT) calculations to characterize the structural, electronic and optical properties of three novel 0D lead-free bismuth-based perovskites, namely, (H2bpy)2[Bi2I10] (1, C20H20N4Bi2I10), (Hdmphen)3[Bi2I9] (2, C42H39N6Bi2I9) and Hterpy(H2terpy)[BiI6]·2H2O (3, C30H25N6BiI6.2H2O), where bpy = 4,4-bipyridine, dmphen = 2,9-dimethyl-1,10-phenanthroline, and terpy = 2,2′;6′,2′′-terpyridine, in which the octahedral morphology and orientation change from one system to another.
These novel materials were characterized, and DFT calculations accurately predicted their structural properties by revealing higher distortions in face-sharing octahedra, followed by edge-sharing octahedra, and finally, by isolated octahedra. The experimental results reveal optical band gaps of about 2.2 eV for all systems, while the theoretical calculations capture this behavior qualitatively, identifying the most significant transitions as the ones between Bi and I species, while cation–anion transitions present low intensity due to low charge transfer. This limits standalone applications in photovoltaic devices, but the possibility of application in hybrid dimensional perovskites as a coating to protect against moisture and UV radiation can aid the overall development of photovoltaic technology.
II Experimental synthesis and characterization
A Synthesis
In this work, 4,4′-bipyridine (bpy), 2,9-dimethyl-1,10-phenanthroline (DMPHEN) hemihydrate, 2,2′;6′,2′′-terpyridine (terpy), hydriodic acid, Bi(NO3)3·5H2O, dimethylformamide (DMF), and ethanol were used without any purification. Nitrates and hydriodic acid react vigorously under heat, producing toxic nitrogen oxide gases and iodide vapour. Thus, the reactions were performed on a mmol scale for the sake of safety.(H2bpy)2[Bi2I10] (1). The synthetic procedure for 1 used 970 m (2.0 mmol) of Bi(NO3)·5H2O, 20.0 mL of water, 5.0 mL of HI, 312 mg of 4,4′-bipyridine, 20 mL of ethanol and 20 mL of DMF. Red block crystals were obtained. Yield: 68% (678 mg, 0.338 mmol). Exp. [calc.] for C20H20N4Bi2I10: C 11.79 (11.99), H 1.38 (1.01), N 2.71 (2.80), Bi 20.91 (20.86%). IV (KBr): 3081 (νC–H), 2463 (νN–H⋯N intermolecular), 1641 (νC
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH–C), 1596 (νC
NH–C), 1596 (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C). 1 H NMR: 5.379 (s, NH), 8.122 (dd, 4H, Ph–H, J = 4.8 Hz, j = 1.8 Hz), 9.118 (dd, 4H, Ph–H, J = 4.8 Hz, j = 1.8 Hz) ppm.
C). 1 H NMR: 5.379 (s, NH), 8.122 (dd, 4H, Ph–H, J = 4.8 Hz, j = 1.8 Hz), 9.118 (dd, 4H, Ph–H, J = 4.8 Hz, j = 1.8 Hz) ppm.
(Hdmphen)3[Bi2I9] (2). For 2 was used 1.23 g (6.0 mmol) of 2,9-dimethyl-1,10-phenanthroline hemihydrate and 80 mL of DMF instead. The product was obtained as red lamellar crystals. Yield: 91% (1.99 g, 0.909 mmol). Exp. [calc.] for C42H39N6Bi2I9: C 25.00 (25.06), H 1.88 (1.80), N 3.80 (3.84), Bi 19.01 (19.10%). IV (KBr): 3044 and 2915 (νC–H), 2463 (νN–H⋯N intermolecular), 1657 and 1625 (νC
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH–C), 1602 (νC
NH–C), 1602 (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) cm−1. 1H NMR: 2.924 (s, 6H, CH3), 7.905 (d, 2H, Ph–H, J = 8.5), 8.104 (s, 2H, Ph–H), 8.698 (d, 2H, Ph–H, J = 8.3) ppm.
C) cm−1. 1H NMR: 2.924 (s, 6H, CH3), 7.905 (d, 2H, Ph–H, J = 8.5), 8.104 (s, 2H, Ph–H), 8.698 (d, 2H, Ph–H, J = 8.3) ppm.
(H2terpy)(Hterpy)[BiI6]·2H2O (3). For the synthesis of 3 the following amounts of reagents were used: 485 mg (1.0 mmol) of Bi(NO3)·5H2O, 2.5 mL of HI, 30 mL of water, 700 mg (3.0 mmol) of 2,2′;6′,2′′-terpyridine, 10 mL of ethanol and 20 mL of water. Orange needle-like crystals were obtained. Yield: 54% (780 mg; 0.542 mmol). Exp. [calc.] for C30H29N6O2BiI6: C 24.25 (24.41), H 2.12 (1.98), N 5.55 (5.69), Bi 13.96 (14.16%) IV (KBr): 3066 and 2960 (νC–H), 2762 and 2413 (νN–H⋯N intermolecular), 1635 (νC
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH–C), 1598 (νC
NH–C), 1598 (νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) cm−1. 1H NMR: 7.090 (s, NH), 7.907 (td, 2H, Ph–H, J = 6,4, j = 0.88 Hz), 8.348 (t, 1H, Ph–H, J = 7.8 Hz), 8.485 (td, 2H, Ph–H, J = 8.0 Hz, j = 1.5 Hz), 8.636 (d, 2H, Ph–H, J 8.0 Hz), 8.484 (dd, 4H, Ph–H, J = 5.6 Hz, j = 3.8 Hz) ppm.
C) cm−1. 1H NMR: 7.090 (s, NH), 7.907 (td, 2H, Ph–H, J = 6,4, j = 0.88 Hz), 8.348 (t, 1H, Ph–H, J = 7.8 Hz), 8.485 (td, 2H, Ph–H, J = 8.0 Hz, j = 1.5 Hz), 8.636 (d, 2H, Ph–H, J 8.0 Hz), 8.484 (dd, 4H, Ph–H, J = 5.6 Hz, j = 3.8 Hz) ppm.
B Chemical characterization
Nuclear magnetic resonance (NMR) spectra were obtained with a Bruker AVANCE-III 400 Nanobay spectrometer, using dry dimelthylsulfoxide-d6 as a solvent. Chemical shifts (δ) were reported in ppm and referenced to TMS, Si(CH3)4, as the internal standard. Infra-red (IR) spectra were recorded on a PerkinElmer 882 spectrometer in the range 4000 to 400 cm−1 with a spectral resolution of 4 cm−1 by using dry KBr pellets. Elemental analyses (C, H, N) were performed using a PerkinElmer 2400 analyzer. Thermogravimetric analysis (TG/DTA) was carried out with a Shimadzu TG/DTA 60 under a dry synthetic atmosphere at a heating rate of 10 from room temperature to 700. The bismuth content was determined via atomic absorption using a Varian AA240FS spectrophotometer. Elemental analyses (C, H, N) were performed with a PerkinElmer 2400 analyzer. Photo-luminescence (PL) spectra were recorded using a spectofluorimeter Varian Cary Eclipse using the same solid state samples mounted in FTO glass used for the UV-vis spectra experiments. The samples were excited at 350 nm and the luminescence recorded from 400–650 nm to avoid harmonics from the light source. TG/DTA curves with their interpretation and NMR, IR and PL spectra can be found in the ESI.†C Single crystal X-ray diffraction
Single crystal X-ray diffraction (XRD) data were collected using a Bruker-AXS Kappa Duo diffractometer with an APEX II CCD detector and Mo-Kα radiation at 150 K. CrysAlis CCD and CrysAlisRED19 were used for cell refinement and data indexing, integration, reduction and absorption correction. Structure solution and refinements were performed using SHELXL-2018.20 Non-hydrogen and hydrogen atoms were refined anisotropically and isotropically, respectively. All CH hydrogen atoms were added to their corresponding carbons following a riding model with fixed bond lengths and angles. In the case of NH and water hydrogen atoms, before their constraining, they were firstly found from the difference Fourier map and checked for suitable orientation of hydrogen bonds.Hydrogen atoms had their isotropic atomic displacement parameters set to 1.2 × Uiso(C/N) or 1.5 × Uiso(O). Compound 3 exhibits disorder associated with hydrogen atoms in protonated terpyridine and water molecules. For terpyridine, the H1 and H3 atoms have half occupancy, and, for water, H1 was split in two positions (H1A and H1B) with equal occupancies. The complete X-ray diffraction data set for the structures of perovskites 1, 2, and 3 is available under CCDC number codes 1996480, 1996481 and 1996482,† respectively, and is reported in Table S1, in the ESI.† Selected bond geometries, showcasing the length, angle and/or proper symmetry operations, can be seen in Tables S2, S3 and S4 (ESI†), for 1, 2 and 3, respectively.
D Ultraviolet-visible spectroscopy
All optical characterization was performed using thin films deposited on glass supported fluorine doped tin oxide (FTO). For film deposition 40 μL of saturated dimethylformamide solution was spin coated for 60 at 3000 rpm. Ultraviolet-visible (UV-vis) spectra were recorded using Agilent Cary 60 equipment in the 800 nm to nm range. The optical band gap was estimated by Tauc plots using solid state absorption spectra and the direct band gap approximation.III Theoretical approach and computational details
Our total energy calculations are based on DFT calculations with the semilocal Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional,21 as implemented in version 5.4.1 of the Vienna ab initio simulation package (VASP),22,23 where the Kohn–Sham equations are solved using the frozen-core projector augmented-wave (PAW) method.24,25 To improve the description of the weak van der Waals (vdW) interactions, we considered the vdW D3 correction proposed by Grimme et al.,26 which is important to include due to the stacking of the organic cations seen in compounds 1, 2, and 3, Fig. 1.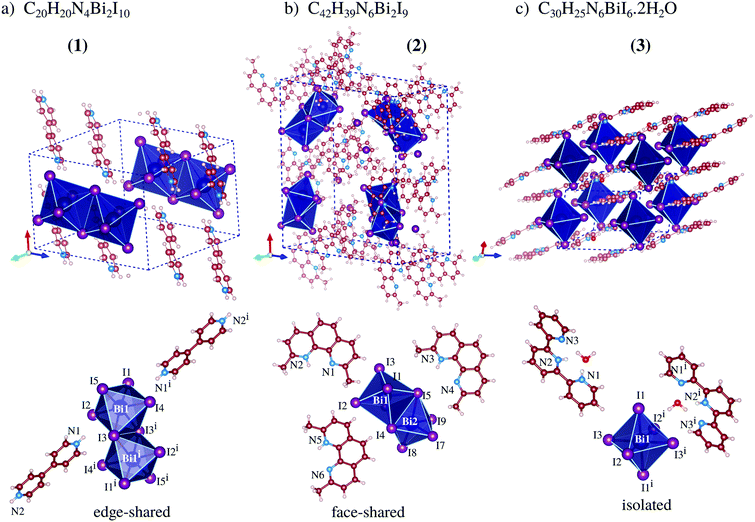 | ||
| Fig. 1 Experimental crystal structures of perovskites 1, 2 and 3, where the dashed-lines indicate the unit cell, while the octahedra show the frames formed by the BiI6 ions. | ||
To improve the description of the energy band-gaps, which is fundamental to compare with the experimental results, we employed the hybrid Heyd–Scuseria–Ernzerhof27 (HSE06) exchange–correlation functional, which replaces 25% of the PBE exchange with the non-local Fock exchange term. Due to the higher computational cost of DFT-HSE06 calculations as implemented in VASP, our HSE06 calculations were performed using frozen PBE optimized structures with a reduced k-density of 20 Å−1. It has been shown in several studies that HSE06 yields an almost rigid shift of the conduction band compared with PBE results, and hence the same shift is expected in the absorption coefficient spectra.
The equilibrium configurations were obtained via stress-tensor calculations and using a plane-wave cutoff energy of 841.82 eV due to the slow convergence of the stress-tensor as a function of the number of plane-waves, while for the total energy calculations, density of states, band structure, and optical properties we employed a plane-wave cutoff energy of 473.53 eV. The atomic force and total energy convergence criteria were 0.025 eV Å−1 and 10−5 eV, respectively, while for the Brillouin zone sampling we employed a k-point density of 20 Å−1 for the stress-tensor, which generated k-point meshes of 2 × 2 × 2, 1 × 2 × 1, and 2 × 2 × 2 for 1, 2 and 3, respectively. For density of states and optical property calculations, we considered twice the k-point density of the stress-tensor calculations, which yields k-meshes of 5 × 4 × 4, 2 × 4 × 2, and 5 × 5 × 4, respectively. Further technical details are reported within the ESI.†
IV Experimental results
A Comments on the synthesis and chemical characterization
All compounds were synthesized with a very straightforward and easy procedure, with good or very good yield. From the chemical characterization, one can find that the compounds are pure and the proposed compositions, based on their crystal structures, are representative of the bulk material. From a structural point of view, although using a similar synthetic path, the compositions and in particular the bismuth-iodide anion complexes are completely different, the organic cation being most likely responsible for the crystal engineering.Finally, the compounds could be manipulated, stored and almost all characterizations performed under a regular atmosphere, showing long term stability, being stable in the presence of oxygen and atmospheric humidity. The TG/DTA curves also exhibit stability from room temperature until 250 °C for 1, 100 °C for 2 and 130 °C for 3, with no weight loss, indicating that the materials are also thermally stable.
B Crystal structure description
From our results, compound 1 crystallizes in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and is formed by one bi-octahedra [Bi2I10]4− unit and two moieties of H2bpy2+, Fig. 1a, where the crystal packing is mainly ruled by non-classical NH⋯I hydrogen bonds. The anionic complex is built up from two square-based pyramid [BiI5]2− fused to a basal iodide, which fills the neighboring bismuth(III) free apical position, culminating in edge-sharing octahedra. The edge-sharing complexes for bismuth-iodine systems are most likely to be formed when the organic cation is doubly positively charged at opposite ends, observed in the literature for cations based on 1,3-propanediamine,16 1,4-phenylenediamine,28,29 4,4′-diaminobiphenyl,30etc.31–37 Additionally, viewing along the crystallographic c-axis, one can observe that the organic cations are packed sandwiching a layer of bismuth dimers, producing supramolecular perovskites (Fig. S10, ESI†).
space group and is formed by one bi-octahedra [Bi2I10]4− unit and two moieties of H2bpy2+, Fig. 1a, where the crystal packing is mainly ruled by non-classical NH⋯I hydrogen bonds. The anionic complex is built up from two square-based pyramid [BiI5]2− fused to a basal iodide, which fills the neighboring bismuth(III) free apical position, culminating in edge-sharing octahedra. The edge-sharing complexes for bismuth-iodine systems are most likely to be formed when the organic cation is doubly positively charged at opposite ends, observed in the literature for cations based on 1,3-propanediamine,16 1,4-phenylenediamine,28,29 4,4′-diaminobiphenyl,30etc.31–37 Additionally, viewing along the crystallographic c-axis, one can observe that the organic cations are packed sandwiching a layer of bismuth dimers, producing supramolecular perovskites (Fig. S10, ESI†).
The Bi–I bonds spread from 2.9508(5) to 3.2562(5) Å, and we noticed that shared iodide ions have elongated Bi–I bonds, e.g., Bi1–I3 = 3.2062(5) Å and I3–Bi1i = 3.2562(5) Å, while the bridge angle Bi1–I3–Bi1i = 95.29(1)°. As expected from the differences in the asymmetrical bridge and bond lengths (e.g., 0.22 Å), the octahedron is distorted, and hence the out-of bridge plane iodine ligands are slightly bent towards each other with lower bond angle (I2–Bi1–I4 = 176.25(1)°). The intermetallic distance (Bi1⋯Bi1i) is equal to 4.7758(5) Å.
Furthermore, the H2bpy2+ units interact with terminal iodide anions with intermolecular distances between 2.921 Å and 3.086 Å [see Fig. S5a (ESI†); N1–H1⋯I3 and N2–H2⋯I4ii, respectively]. The metal complexes are close to each other, the closest separated by only 4.2045(7) Å concerning the I2⋯I2iii interaction, and 4.5573(5) and 4.9860(6) Å in the I5⋯I5iv and I4⋯I4v contact, respectively. Unexpectedly, there is no clear stacking of aromatic rings since all H2bpy2+ cations are surrounded by [Bi2I10]4− units, see Fig. 1a.
Compound 2, which crystallizes in the orthorhombic structure, with space group Pna21, is composed of three monovalent 2,9-dimethyl-1,10-phenanthroline cations for each of the [Bi2I9]3− units, Fig. 1b, which are composed of two octahedral complexes fused on one face. The Hdmphen+ cations have three fused aromatic rings, displaying great surface area and planarity, facilitating the stacking along the crystallographic b-axis with an average distance of 3.5(2) Å, twisted in relation to each other also due the methyl group steric hindrance effect (Fig. S10, ESI†). The presence of methyl groups in the 1 and 10 positions introduces steric hindrance, which weakens the hydrogen bonds, and is hence competitive with stacking. Furthermore, [Bi2I9]3− can be seen occupying the voids left from Hdmphen+ stacking, but contacts close to complexes create a supramolecular chain almost perpendicular to the organic moiety stacking where the shortest distance between the anions is equal to 3.667(1) Å [I1⋯I8iii].
As observed for 1, the bridge iodide ligands have larger bond lengths than other ones. The bond lengths vary between 3.1471(9) and 3.3590(8) Å [Bi1–I5 and Bi2–I6] and 3.1471(9) and 3.012(1) Å [Bi21I8 and Bi21I9], for shared and non-shared ligands. As expected of face-sharing dimers, the octahedra are eclipsed, but slightly twisted with an average twist angle of 2.0(5) Å. The intermetallic distance in this complex is 4.2175(7) Å [Bi1⋯Bi2]. Some weak hydrogen bonds are observed, with an interaction distance of 2.967 Å.
As can be seen in Fig. 1c, the crystal structure of perovskite 3 is build up by one [BiI6]3− complex, two protonated 2,2′:6,2′′-terpyridine molecules, and two water molecules. The structure crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and the packing is ruled by the π-stacking among terpy cations and the bismuth-based units form a monometallic octahedron complex with almost regular geometry. The bismuth complexes are packed parallel to the a-axis, which creates a supramolecular 1D-like chain (pseudo-1D perovskite, Fig. S11, ESI†). In this array, the distance between the metallic atoms is 10.947(2) Å and the chains are spaced 10.822(2) Å from each other.
and the packing is ruled by the π-stacking among terpy cations and the bismuth-based units form a monometallic octahedron complex with almost regular geometry. The bismuth complexes are packed parallel to the a-axis, which creates a supramolecular 1D-like chain (pseudo-1D perovskite, Fig. S11, ESI†). In this array, the distance between the metallic atoms is 10.947(2) Å and the chains are spaced 10.822(2) Å from each other.
In contrast with compounds 1 and 2, the Bi–I bond lengths are very close to each other as there are no shared octahedrons, e.g., 3.0899(7) Å [Bi1–I1], 3.0737(8) Å [Bi1–I2] and 3.080(7) Å [Bi1–I3]. Further, similar to 2, in 3 the protonated part of terpy has great steric hindrance and no other terpy molecule nor bismuth complex can interact with it. Thus, only a small molecule such as water is able to occupy the available void. The water molecules are trapped along the [BiI6]3− complex in the voids caused by terpy packing, creating a local hydrogen bond net. The great amount of hydrogen bond donors avoids the iodide being shared, leading to a mononuclear bismuth complex, also observed for similar systems in the literature.38–41
Although only one terpy unit is present in the asymmetric unit of this compound, half of them are doubly protonated (H2terpy2+), and the other half singly protonated (Hterpy+). In the difference Fourier map the second hydrogen atom was hardly found around the N1 or N3 atoms, suggesting that both can be protonated, and thus the occupancy of H1 and H3 was fixed as 0.25, for the sake of charge equilibrium. Due to the strong intramolecular hydrogen bond and the three basic nitrogen atoms, multiple protonations occurred, but, also, due to the proximity of hydrogen atoms in the double protonated units and their almost planar structure in the solid-state, an HI molecule is lost at very low temperatures, as seen in the thermal analysis of 3. The crystallization of water molecules assisted the stabilization of protonated terpy units, adding a negative pole very close to the charged atoms. Following the double position of the second acidic hydrogen (H1 and H3) added to the terpy unit, the water hydrogen atom was split in two possible positions to interact with the non-protonated nitrogen atom, both with equal occupancy. The planarity of terpy is verified by the angle of the external pyridine rings, which is equal to 11.1(5)°. The protonated terpy units interact with a nearby one packing the inner and one outer pyridine ring with a mean plane distance of 3.469(2) Å.
C UV-vis absorption
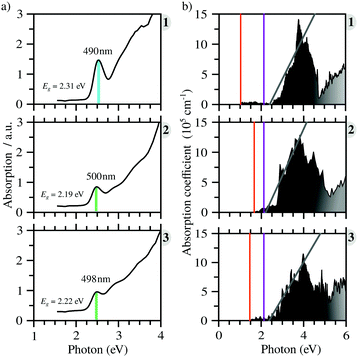
All compounds exhibit similar optical behavior with a broad absorption band in the visible and UV region in a solid-state thin film, see Fig. S1–S3 (ESI†), with no emission observed between UV and near-IR when exciting them using UV or near-UV visible light. The absorption maximum in the visible region for all materials occurs between 490 nm and 500 nm, with a bandwidth around 80 nm. The films deposited onto glass presented an orange color, in agreement with the visible absorption. It is associated with anion complex charge transfer, I(p) → Bi(p), just as seen for Cs3Bi2I9, which has an absorption maximum at 494 nm.42 The small changes in the absorption maximum are mostly due to the complex geometry, which slightly changes the charge density over the iodide atoms, combined with hydrogen bonds towards the anionic complexes. Down from 450 nm the absorption increases again, referring to n → π* and π → π* transitions of very conjugated organic cations. The more conjugated the cation, the greater the absorption in the UV and near-UV region, increasing the ratio of the absorption at the maximum in the visible region and UV region from 1 to 3.In order to determine these materials’ potential as semiconductors, the band-gap was estimated using Tauc plots from the absorption spectra. All three compounds’ Tauc plots were best fitted when a direct band gap was considered, presenting a narrow edge near 2.2 eV, Fig. 2. The estimated optical band gaps are 2.31 eV for 1, 2.19 eV for 2 and 2.22 eV for 3.
V Theoretical results
A Structural properties
The greatest uncertainties regarding the X-ray experimental structures originated in the low accuracy of the position of the hydrogen atoms. Perovskite 1 contains fully protonated H2bpy2+ units, which removes the need for guesswork to determine the position of the hydrogen atoms, and although perovskite 2 has six degrees of freedom regarding the position of the hydrogen in one of two sites in each of the three Hdmphen+ units, this likely has little bearing on the overall structure, due to the sites being symmetrical. Perovskite 3, on the other hand, not only has more degrees of freedom in the H2terpy2+ and Hterpy+ pair, but also has two water molecules in the crystal structure, interacting via hydrogen bonds with the organic molecules. This aspect, if not properly modeled, can induce steric effects and lead to multiple configurations with different energy and lattice parameters.To address this concern, we employed multiple initial configurations of perovskite 3 for the stress-tensor calculations, varying the position of the hydrogens between the two units, as well as the initial position of the hydrogens of the water molecules, which can affect the optimization procedure in the stress-tensor calculations, resulting in local minima. As shown in Table 1, the lattice parameters (a0, b0, c0, α, β, and γ) displayed very low deviation from the experimental results, ranging from −1.3% to 1.0%, a very solid result that validates the method employed. It is noticeable that, as predicted, different initial configurations of perovskite 3 resulted in other higher energy structures, with different lattice parameters. The lattice parameter deviations within this set were as high as 8%, which reaffirms the need to properly address the uncertainties regarding the position of hydrogen atoms in complex systems, see the ESI.†
Analysis of the local structure parameters reveals little deviation from the experimental ones, with the exception of ECNBi, with deviations as high as 2% for perovskite 1 and 6% for perovskite 2, indicating a small but consistent discrepancy in dealing with fused octahedra. It is noticeable that the local parameter analysis identified increasing deviations from the perfect octahedron as the number of shared halides increases, with perovskite 2, which has face-sharing octahedra, displaying the largest deviation, followed by compound 1, which has edge-sharing octahedra, and finally by perovskite 3, which has isolated octahedra, and displays virtually no local distortions. As the discrepancies noted earlier also increase with the magnitude of the octahedron fusion, calculations employing larger, more complex fused octahedra are susceptible to even greater deviations.
| E optg,PBE+D3 | Eoptg,HSE06 | E optg,Exp. | |
|---|---|---|---|
| 1 | 2.30 | 3.10 | 2.31 |
| 2 | 2.20 | 3.00 | 2.19 |
| 3 | 2.25 | 3.09 | 2.22 |
B Electronic structure
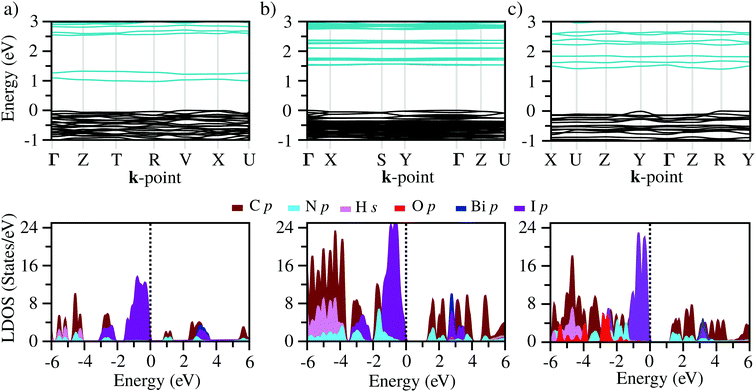
The band structures of the three compounds are nearly flat for most of the bands, Fig. 2, which is a consequence of the discrete nature of the inorganic moiety, which occurs as the octahedra are surrounded by the large organic cations, and the predominantly long range interactions between cations and anions severely decrease the carrier mobility. Although the bands look equally flat for all compounds, we found substantially larger electron and hole effective masses for compound 2, which can be explained by the larger isolation of the octahedra compared with compounds 1 and 3. All materials are semiconductors with PBE + D3 (HSE06, frozen PBE + D3 structures) fundamental energy band gaps of 0.98 eV (1.80 eV), 1.53 eV (2.35 eV), and 1.41 eV (2.24 eV), respectively, for perovskites 1, 2 and 3, and, as expected, the HSE06 results are larger due to the non-local Fock exchange. The valence band maxima (VBM) are located at V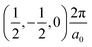 , Γ
, Γ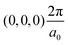 , and R
, and R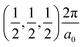 , respectively, while the conduction band minima (CBM) are located at R
, respectively, while the conduction band minima (CBM) are located at R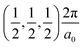 , between Γ–X
, between Γ–X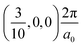 , and R
, and R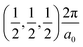 , respectively; as such perovskites 1 and 2 have indirect band gaps, while perovskite 3 has a direct band gap. Analysis of the density of states reveals that all materials have similar contributions to both the VBM and CBM; the former is almost solely comprised of I p-states, while the latter has contributions from both C p and N p-states. The main difference between these materials is the presence of punctual CBM states in compounds 1 and 3, while 2 has more bundled CBM states.
, respectively; as such perovskites 1 and 2 have indirect band gaps, while perovskite 3 has a direct band gap. Analysis of the density of states reveals that all materials have similar contributions to both the VBM and CBM; the former is almost solely comprised of I p-states, while the latter has contributions from both C p and N p-states. The main difference between these materials is the presence of punctual CBM states in compounds 1 and 3, while 2 has more bundled CBM states.
C Optical properties
From the calculated absorption coefficient spectra, which include only direct transitions from the valence to the conduction band, we found optical PBE + D3 band gaps of 1.01 eV, 1.53 eV, and 1.41 eV for 1, 2, and 3, respectively. This indicates the first onset of optical activity, but, as can be seen in the absorption coefficient theoretical data, Fig. 3(b), this initial activity, the fruit of the cation–anion transitions, is insignificant compared to the absorption noticed at about 2.5 eV, which can be associated via the density of states with I(p) → Bi(p) intra-octahedral transitions. This is corroborated by the fact that the perovskite Cs3Bi2I9 has a similar optical gap to our systems, despite their differences.42 This different intensity of intra-octahedral and cation–anion transitions is likely due to poor carrier mobility due to the nature of the interactions between the cation and anion. Analogously to the experimental procedure of extrapolating to obtain the optical gap, we can use a similar procedure to capture the onset of the most significant transitions, resulting, similarly to the experimental results, in all optical band gaps being approximately the same (Table 2).After application of the HSE06 shift to the data in order to improve the description of the band gap, the theoretical optical band gaps, while still remaining close to one another, are shifted to the 3 eV region, leading to a quantitative discrepancy between the experimental and theoretical data. This discrepancy is most likely associated with a combination of limitations of the theoretical calculations, which consider perfect crystal structures, and the experimental sample may contain defects which can likely introduce mid-gap states that can justify the smaller optical band gaps.
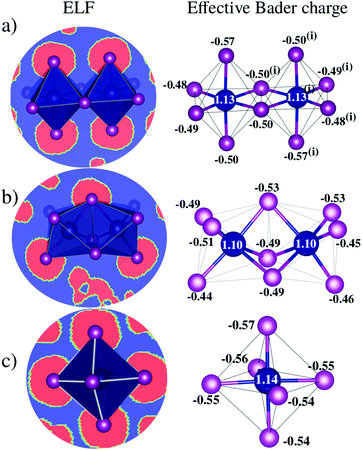
D Charge transfer analysis
Bader charge analysis reveals that Bi–I bonds display ionic behavior in all configurations, Fig. 4, regardless of the shape of the octahedra (face-sharing, edge-sharing, or isolated). The little difference between BixIyδ− moieties is likely associated with the long distance interactions; for example, in perovskite 1, charge accumulation is observed in the two iodides transversely symmetric in the apical position (Iap.), resulting in 0.08 higher charge than the iodide average observed on the other iodide ions, which is associated with the weak –NH⋯Iap. hydrogen bond with the H2bpy2+ cation. These small differences justify the similar optical behavior of these systems and corroborate the fact that transitions inside the octahedron are most responsible for the optical activity.VI Conclusions
Three novel perovskite materials were synthesized and characterized via a combination of experimental and theoretical techniques. The compounds exhibited remarkable stability being stored under room conditions. The results showed that octahedra with an increased number of shared iodides display a greater degree of structural deformation, an aspect that was corroborated by theoretical calculations successfully.Analysis of the optical properties revealed all three materials to have a similar behavior, with similar optical band gaps of around 2.2 eV. The transitions around the fundamental band edge present low intensity and the most significant transitions observed were inside the octahedra, which justifies why the three different materials would present similar optical responses. Theoretical calculations were able to predict this behavior only in a qualitative sense, but the values of the optical band gap deviated consistently by about 1 eV, which is likely due to limitations of the calculations and employment of a perfect model without defects, an aspect that could, in an experimental sample, affect the band gap.
Overall, this work was able to capture an atomic level understanding of these materials, and while their use in photovoltaics is limited due to the low carrier mobility, this study will hopefully inspire further studies of 0D perovskites for novel applications, such as dielectrics for capacitors or bismuth-iodide sources for double halide lead-free perovskite preparation soluble in a wide solvent range.
Author statement
First authors: Mailde S. Ozório (theoretical) and Willian X. C. Oliveira (experimental). Corresponding authors: Juarez L. F. Da Silva (theoretical) and Ana Flávia Nogueira (experimental).Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors gratefully acknowledge support from FAPESP (São Paulo Research Foundation) and Shell, Grant Numbers 2017/11631-2, 2017/11986-5, and 2018/21401-7, and the strategic importance of the support given by ANP (Brazil's National Oil, Natural Gas and Biofuels Agency) through the R&D levy regulation. This study was financed in part by the National Council for Scientific and Technological Development (CNPq). W. X. C. Oliveira and A. F. Nogueira are thankful for Brazil's Coordination for the Improvement of Higher Education Personnel (CAPES) for postdoc scholaship (CAPES Thesis Award - Brazilian Best Thesis in Chemistry 2017). The authors also acknowledge the National Laboratory for Scientific Computing (LNCC/MCTI, Brazil) for providing HPC resources of the SDumont supercomputer, which have contributed to the research results reported within this paper. URL: http://sdumont.lncc.br. The authors are thankful also for the infrastructure provided to our computer cluster by the Department of Information Technology – Campus São Carlos. The research was developed with the help of HPC resources provided by Information Technology Superintendence of the University of São Paulo.References
- M. Alaaeddin, S. Sapuan, M. Zuhri, E. Zainudin and F. M. AL-Oqla, Photovoltaic Applications: Status and Manufacturing Prospects, Renewable Sustainable Energy Rev., 2019, 102, 318–332, DOI:10.1016/j.rser.2018.12.026
.
- Y. Wei, Z. Cheng and J. Lin, An Overview on Enhancing the Stability of Lead Halide Perovskite Quantum Dots and Their Applications in Phosphor-Converted LEDs, Chem. Soc. Rev., 2019, 48, 310–350, 10.1039/c8cs00740c
.
- Y. Wang, M.-L. Gao, J.-L. Wu and X.-W. Zhang, Metal Halide Perovskite Photodetectors: Material Features and Device Engineering, Chin. Phys. B, 2019, 28, 018502, DOI:10.1088/1674-1056/28/1/018502
.
- L. Wang, G. D. Yuan, R. F. Duan, F. Huang, T. B. Wei, Z. Q. Liu, J. X. Wang and J. M. Li, Tunable Bandgap in Hybrid Perovskite CH3NH3Pb(Br3−yXy) Single Crystals and Photodetector Applications, AIP Adv., 2016, 6, 045115, DOI:10.1063/1.4948312
.
- D. Dong, H. Deng, C. Hu, H. Song, K. Qiao, X. Yang, J. Zhang, F. Cai, J. Tang and H. Song, Bandgap Tunable Csx(CH3NH3)1−xPbI3 Perovskite Nanowires by Aqueous Solution Synthesis for Optoelectronic Devices, Nanoscale, 2017, 9, 1567–1574, 10.1039/c6nr06636d
.
- D. Ju, Y. Dang, Z. Zhu, H. Liu, C.-C. Chueh, X. Li, L. Wang, X. Hu, A. K.-Y. Jen and X. Tao, Tunable Band Gap and Long Carrier Recombination Lifetime of Stable Mixed CH3NH3PbxSn1−xBr3 Single Crystals, Chem. Mater., 2018, 30, 1556–1565, DOI:10.1021/acs.chemmater.7b04565
.
- G. Lucarelli, F. D. Giacomo, V. Zardetto, M. Creatore and T. M. Brown, Efficient Light Harvesting from Flexible Perovskite Solar Cells under Indoor White Light-Emitting Diode Illumination, Nano Res., 2017, 10, 2130–2145, DOI:10.1007/s12274-016-1402-5
.
- R. Wang, M. Mujahid, Y. Duan, Z.-K. Wang, J. Xue and Y. Yang, A Review of Perovskites Solar Cell Stability, Adv. Funct. Mater., 2019, 29, 1808843, DOI:10.1002/adfm.201808843
.
- T. Zhou, M. Wang, Z. Zang, X. Tang and L. Fang, Two-Dimensional Lead-Free Hybrid Halide Perovskite Using Superatom Anions with Tunable Electronic Properties, Sol. Energy Mater. Sol. Cells, 2019, 191, 33–38, DOI:10.1016/j.solmat.2018.10.021
.
- W. Zhang, K. Tao, C. Ji, Z. Sun, S. Han, J. Zhang, Z. Wu and J. Luo, C6H13N)2BiI5: A One-Dimensional Lead-Free Perovskite-Derivative Photoconductive Light Absorber, Inorg. Chem., 2018, 57, 4239–4243, DOI:10.1021/acs.inorgchem.8b00152
.
- R. Zhang, X. Mao, Y. Yang, S. Yang, W. Zhao, T. Wumaier, D. Wei, W. Deng and K. Han, Air-Stable, Lead-Free Zero-Dimensional Mixed Bismuth-Antimony Perovskite Single Crystals with Ultra-broadband Emission, Angew. Chem., Int. Ed., 2019, 58, 2725–2729, DOI:10.1002/anie.201812865
.
- Z. Zhang, X. Li, X. Xia, Z. Wang, Z. Huang, B. Lei and Y. Gao, High-Quality (CH3NH3)3Bi2I9 Film-Based Solar Cells: Pushing Efficiency up to 1.64%, J. Phys. Chem. Lett., 2017, 8, 4300–4307, DOI:10.1021/acs.jpclett.7b01952
.
- F. Bai, Y. Hu, Y. Hu, T. Qiu, X. Miao and S. Zhang, Lead-free, Air-Stable Ultrathin Cs3Bi2I9 Perovskite Nanosheets for Solar Cells, Sol. Energy Mater. Sol. Cells, 2018, 184, 15–21, DOI:10.1016/j.solmat.2018.04.032
.
- Y. Liu, Z. Xu, Z. Yang, Y. Zhang, J. Cui, Y. He, H. Ye, K. Zhao, H. Sun, R. Lu, M. Liu, M. G. Kanatzidis and S. F. Liu, Inch-Size 0D-Structured Lead-Free Perovskite Single Crystals for Highly Sensitive Stable X-Ray Imaging, Matter, 2020, 3, 180–196, DOI:10.1016/j.matt.2020.04.017
.
- J. K. Pious, M. L. Lekshmi, C. Muthu, R. B. Rakhi and V. C. Nair, Zero-Dimensional Methylammonium Bismuth Iodide-Based Lead-Free Perovskite Capacitor, ACS Omega, 2017, 2, 5798–5802, DOI:10.1021/acsomega.7b00973
.
- J. K. Pious, A. Katre, C. Muthu, S. Chakraborty, S. Krishna and V. C. Nair, Zero-Dimensional Lead-Free Hybrid Perovskite-like Material with a Quantum-Well Structure, Chem. Mater., 2019, 31, 1941–1945, DOI:10.1021/acs.chemmater.8b04642
.
- J. Zhang, D. Bai, Z. Jin, H. Bian, K. Wang, J. Sun, Q. Wang and S. F. Liu, 3D-2D-0D Interface Profiling for Record Efficiency All-Inorganic CsPbBrI2 Perovskite Solar Cells with Superior Stability, Adv. Energy Mater., 2018, 8, 1703246, DOI:10.1002/aenm.201703246
.
- J. Fan, Y. Ma, C. Zhang, C. Liu, W. Li, R. E. I. Schropp and Y. Mai, Thermodynamically Self-Healing 1D-3D Hybrid Perovskite Solar Cells, Adv. Energy Mater., 2018, 8, 1703421, DOI:10.1002/aenm.201703421
.
-
O. Rigaku, CrysAlis PRO, Rigaku Oxford Diffraction, Yarnton, England, 2015 Search PubMed
.
- G. M. Sheldrick, SHELXT-Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8, DOI:10.1107/s2053273314026370
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/physrevlett.77.3865
.
- G. Kresse and J. Hafner, Ab-Initio Molecular Dynamics for Open-Shell Transition Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118, DOI:10.1103/physrevb.48.13115
.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab-Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/physrevb.54.11169
.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979, DOI:10.1103/physrevb.50.17953
.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775, DOI:10.1103/physrevb.59.1758
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H–Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215, DOI:10.1063/1.1564060
.
- C. Hrizi, A. Samet, Y. Abid, S. Chaabouni, M. Fliyou and A. Koumina, Crystal structure, vibrational and optical properties of a new self-organized material containing iodide anions of bismuth(III), [C6H4(NH3)2]2Bi2I10·4H2O, J. Mol. Struct., 2011, 992, 96–101, DOI:10.1016/j.molstruc.2011.02.051
.
- C. Hrizi, A. Trigui, Y. Abid, N. Chniba-Boudjada, P. Bordet and S. Chaabouni, α- to β-[C6H4(NH3)2]2Bi2I10 reversible solid-state transition, thermochromic and optical studies in the p-phenylenediamine-based iodobismuthate(III) material, J. Solid State Chem., 2011, 184, 3336–3344, DOI:10.1016/j.jssc.2011.10.004
.
- L. Dobrzycki and K. Woźniak, 1D vs. 2D crystal architecture of hybrid inorganic–organic
structures with benzidine dication, J. Mol. Struct., 2009, 921, 18–33, DOI:10.1016/j.molstruc.2008.12.027
.
- F. Li, H.-D. Yin, J. Zhai and D.-Q. Wang, Bis(4,4′-bipyridinium) di-μ-bromo-bis[tetrabromobismuthate(iii)], Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m1387–m1389, DOI:10.1107/s1600536806018678
.
- Y. Chen, Z. Yang, C.-X. Guo, C.-Y. Ni, Z.-G. Ren, H.-X. Li and J.-P. Lang, Iodine-Induced Solvothermal Formation of Viologen Iodobismuthates, Eur. J. Inorg. Chem., 2010, 5326–5333, DOI:10.1002/ejic.201000755
.
- S. A. Adonin, M. E. Rakhmanova, A. I. Smolentsev, I. V. Korolkov, M. N. Sokolov and V. P. Fedin, Binuclear Bi(III) halide complexes with 4,4′-ethylenepyridinium cations: luminescence tuning by reversible solvation, New J. Chem., 2015, 39, 5529–5533, 10.1039/c5nj00889a
.
- B.-G. Chen, Organic/Bismuth Iodides Hybrids: Structural Perturbation of Substitutes and Their Photocurrent Response Properties, J. Cluster Sci., 2016, 28, 983–994, DOI:10.1007/s10876-016-1089-5
.
- S. A. Adonin, M. I. Rakhmanova, D. G. Samsonenko, M. N. Sokolov and V. P. Fedin, Hybrid salts of binuclear Bi(III) halide complexes with 1, 2-bis(pyridinium)ethane cation: Synthesis, structure and luminescent behavior, Inorg. Chim. Acta, 2016, 450, 232–235, DOI:10.1016/j.ica.2016.06.010
.
- E. A. Kovalenko, D. V. Kochelakov, D. G. Samsonenko and V. P. Fedin, Crystal Structure of Binuclear Bismuth Complex [H2dabco]2[Bi2Br10]4H2O, J. Struct. Chem., 2018, 59, 193–196, DOI:10.1134/s0022476618010304
.
- I. D. Gorokh, S. A. Adonin, D. G. Samsonenko, M. N. Sokolov and V. P. Fedin, Mono- and Binuclear Chloride and Bromide Complexes of Bi(III) with Double-Charged Cations Based on Pyridine: Syntheses and Crystal Structures, Russ. J. Coord. Chem., 2018, 44, 502–506, DOI:10.1134/s1070328418080031
.
- G. Bator, T. Zeegers-Huyskens, R. Jakubas and J. Zaleski, Structure and phase transitions in guanidinium halogenobismuthates(III), J. Mol. Struct., 2001, 570, 61–74, DOI:10.1016/s0022-2860(01)00490-2
.
- N. Elfaleh and S. Kamoun, Structural characterization, vibrational studies and optical properties of a new luminescent organic-inorganic material C6H20N3]BiI6·H2O, J. Organomet. Chem., 2016, 819, 95–102, DOI:10.1016/j.jorganchem.2016.06.029
.
- M. Li, M. Xia and H. Xiao, Centrosymmetric Versus Noncentrosymmetric: Structural and Optical Studies on Inorganic-Organic Hybrid Compounds of Bismuth Thiourea Iodide Resulting from Acid Effect, ChemistrySelect, 2017, 2, 5882–5886, DOI:10.1002/slct.201701038
.
- S. Li, L. Chen and Y. Xiang, Synthesis, crystal structures and characterization of two novel organic-inorganic hybrid compounds (C5NH6)6Bi4Br18 and [C(NH2)3]3BiI6, J. Mol. Struct., 2017, 1130, 617–622, DOI:10.1016/j.molstruc.2016.11.025
.
- B.-B. Yu, M. Liao, J. Yang, W. Chen, Y. Zhu, X. Zhang, T. Duan, W. Yao, S.-H. Wei and Z. He, Alloy-induced Phase Transition and Enhanced Photovoltaic Performance: the Case of Cs3Bi2I9−xBrx Perovskite Solar Cells, J. Mater. Chem. A, 2019, 7, 8818–8825, 10.1039/c9ta01978b
.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and theoretical procedures, supporting results and analyses are reported. Further, additional data, etc., can be obtained directly from the authors. CCDC 1996480–1996482. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ma00791a |
| This journal is © The Royal Society of Chemistry 2020 |