An efficient multi-doping strategy to enhance Li-ion conductivity in the garnet-type solid electrolyte Li7La3Zr2O12†
Yedukondalu
Meesala
a,
Yu-Kai
Liao
b,
Anirudha
Jena
ac,
Nai-Hsuan
Yang
a,
Wei Kong
Pang
 d,
Shu-Fen
Hu
d,
Shu-Fen
Hu
 *b,
Ho
Chang
*c,
Chia-Erh
Liu
e,
Shih-Chieh
Liao
e,
Jin-Ming
Chen
e,
Xiangxin
Guo
*f and
Ru-Shi
Liu
*b,
Ho
Chang
*c,
Chia-Erh
Liu
e,
Shih-Chieh
Liao
e,
Jin-Ming
Chen
e,
Xiangxin
Guo
*f and
Ru-Shi
Liu
 *ac
*ac
aDepartment of Chemistry, National Taiwan University, Taipei 106, Taiwan. E-mail: rsliu@ntu.edu.tw
bDepartment of Physics, National Taiwan Normal University, Taipei 116, Taiwan. E-mail: sfhu.hu@gmail.com
cDepartment of Mechanical Engineering, Graduate Institute of Manufacturing Technology, National Taipei University of Technology, Taipei 106, Taiwan. E-mail: f10381@ntut.edu.tw
dInstitute for Superconducting & Electronic Materials, University of Wollongong, NSW 2522, Australia
eMaterial and Chemical Research Laboratories, Industrial Technology Research Institute, Hsinchu 300, Taiwan
fCollege of Physics, Qingdao University, Qingdao 266071, China. E-mail: xxguo@qdu.edu.cn
First published on 9th March 2019
Abstract
Lithium-ion (Li+) batteries suffer from problems caused by the chemical instability of their organic electrolytes. Solid-state electrolytes that exhibit high ionic conductivities and are stable to lithium metal are potential replacements for flammable organic electrolytes. Garnet-type Li7La3Zr2O12 is a promising solid-state electrolyte for next-generation solid-state Li batteries. In this study, we prepared mono-, dual-, and ternary-doped lithium (Li) garnets by doping tantalum (Ta), tantalum–barium (Ta–Ba), and tantalum–barium–gallium (Ta–Ba–Ga) ions, along with an undoped Li7La3Zr2O12 (LLZO) cubic garnet electrolyte, using a conventional solid-state reaction method. The effect of multi-ion doping on the Li+ dynamics in the garnet-type LLZO was studied by combining joint Rietveld refinement against X-ray diffraction and high-resolution neutron powder diffraction analyses with the results of Raman spectroscopy, scanning electron microscopy, energy-dispersive X-ray spectroscopy, and multinuclear magic angle spinning nuclear magnetic resonance. Our results revealed that Li+ occupancy in the tetrahedrally coordinated site (24d) increased with increased multi-ion doping in LLZO, whereas Li+ occupancy in the octahedrally coordinated site (96h) remained constant. Among the investigated compounds, the ternary-doped garnet structure Li6.65Ga0.05La2.95Ba0.05Zr1.75Ta0.25O12 (LGLBZTO) exhibited the highest total ionic conductivity of 0.72 and 1.24 mS cm−1 at room temperature and 60 °C, respectively. Overall, our findings revealed that the dense microstructure and increased Li+ occupancy in the tetrahedral-24dLi1 site played a key role in achieving the maximum room-temperature Li-ion conductivity in the ternary-doped LGLBZTO garnet, and that the prepared ternary-doped LGLBZTO was a potential solid electrolyte for Li-ion batteries without polymer adhesion.
Introduction
Inorganic solid-state electrolytes (SEs) for all-solid-state Li-ion batteries (ASSLIB) are promising replacements for the flammable, toxic, flowing, and volatile organic liquid-based electrolytes due to their great safety, high performance, and reliability.1,2 Moreover, SEs are sufficiently stable in contact with Li metal, and can address the well-known problems of conventional batteries, such as explosion hazards due to an internal short circuit (dendrites) and thermal runaway.3,4 However, the challenge is in the design of appropriate solid electrolytes with high ionic conductivity (>10−4 S cm−1), negligible electronic conductivity, and good electrochemical stability.5–8 A garnet-like material of the stoichiometry Li7La3Zr2O12 (LLZO) was first discovered as a fast Li+ conductor by Murugan et al. in 2007.9 The LLZO SE material has been a research hotspot due to its relatively high Li-ion conductivity (2 × 10−4 S cm−1) at room temperature, wide electrochemical window (>5 V vs. Li+/Li), and good compatibility with Li anodes.10,11 However, LLZO crystallizes as two polymorphs: a thermodynamically stable tetragonal polymorph with ordered Li+ distribution (space group: I41/acd, no. 142)12 and a high-temperature stable cubic polymorph with highly disordered Li+ distribution (space group: Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d, no. 230).12,13 The Li+ ions in the cubic phase partially occupied the tetrahedral-24dLi1 and distorted octahedral-96hLi2 sites, whereas the Li+ ions in the tetragonal polymorph fully occupied three crystallographic sites: tetrahedral-8a (Li1), distorted octahedral-16f (Li2), and 32g (Li3).12,13 As a result of the disordered Li+ distribution and partial occupation in the cubic phase, the Li-ion conductivity of the cubic phase is about two orders of magnitude higher than that of the tetragonal counterpart at room temperature.14,15 Hence, many studies focused on the optimization of the garnet cubic phase by promoting a disordered Li+ framework and on the improvement of the Li-ion conductivity (ranging from ∼10−4 S cm−1 to 10−3 S cm−1) at room temperature.6 Geiger et al. noticed the highly conductive cubic polymorph along with the tetragonal polymorph when LLZO was synthesized in an Al-containing crucible; LLZO sintered in a Pt-crucible yielded solely a tetragonal phase.16 They argued that the unintentional doping of Al from the crucible into the LLZO framework at the Li site during the high-temperature sintering stabilized the cubic polymorph. Many studies investigated the role of Al in achieving a fast ionic cubic conductor by intentionally adding Al into the LLZO garnet during the synthesis.14,17–19 However, the preferential site (tetrahedral-24dLi1 or octahedral-96hLi2 sites) for Al ions remains unclear. The formation of a highly conductive cubic polymorph from an alumina crucible often requires high sintering temperatures (>1200 °C) and a long sintering time, which may cause substantial Li loss from the sample.20,21 A trivalent doping cation (Ga3+), as a substitute for Li+, was found to stabilize a similar cubic phase and improve the Li-ion conductivities compared with Al3+.22,23 Moreover, Ga doping can stabilize the cubic phase at a low synthesis temperature of about 1000 °C (sintering temperature is about 1100 °C).24
d, no. 230).12,13 The Li+ ions in the cubic phase partially occupied the tetrahedral-24dLi1 and distorted octahedral-96hLi2 sites, whereas the Li+ ions in the tetragonal polymorph fully occupied three crystallographic sites: tetrahedral-8a (Li1), distorted octahedral-16f (Li2), and 32g (Li3).12,13 As a result of the disordered Li+ distribution and partial occupation in the cubic phase, the Li-ion conductivity of the cubic phase is about two orders of magnitude higher than that of the tetragonal counterpart at room temperature.14,15 Hence, many studies focused on the optimization of the garnet cubic phase by promoting a disordered Li+ framework and on the improvement of the Li-ion conductivity (ranging from ∼10−4 S cm−1 to 10−3 S cm−1) at room temperature.6 Geiger et al. noticed the highly conductive cubic polymorph along with the tetragonal polymorph when LLZO was synthesized in an Al-containing crucible; LLZO sintered in a Pt-crucible yielded solely a tetragonal phase.16 They argued that the unintentional doping of Al from the crucible into the LLZO framework at the Li site during the high-temperature sintering stabilized the cubic polymorph. Many studies investigated the role of Al in achieving a fast ionic cubic conductor by intentionally adding Al into the LLZO garnet during the synthesis.14,17–19 However, the preferential site (tetrahedral-24dLi1 or octahedral-96hLi2 sites) for Al ions remains unclear. The formation of a highly conductive cubic polymorph from an alumina crucible often requires high sintering temperatures (>1200 °C) and a long sintering time, which may cause substantial Li loss from the sample.20,21 A trivalent doping cation (Ga3+), as a substitute for Li+, was found to stabilize a similar cubic phase and improve the Li-ion conductivities compared with Al3+.22,23 Moreover, Ga doping can stabilize the cubic phase at a low synthesis temperature of about 1000 °C (sintering temperature is about 1100 °C).24
Recent studies demonstrated that doping of supervalent cations (Ta5+, Nb5+, Sb5+, and Bi5+ at the Zr4+ site) into the garnet-type LLZO remarkably improved the Li-ion conductivities at room temperature.25–29 The doping alters the structure by creating Li+ vacancies for charge neutrality and by increasing the disorderliness in the framework, thereby promoting the stabilization of a highly conductive cubic phase. In contrast, partial substitution of low-valent alkaline earth metal cations (Ca2+, Sr2+, and Ba2+) at the La3+ site in the LLZO garnet framework has a substantial effect on Li-ion conductivities.30,31 Divalent doping at the La site increases the Li+ concentration in the framework, which leads to improved Li-ion conductivities. Additionally, replacement of La3+ with large sized dopant ions expands the lattice, enlarging the bottleneck size for Li+ migration, thereby increasing the Li-ion conductivities.32 In strategic doping in the LLZO garnet, each doping ion has an important role in modifying the garnet framework. Thus, choosing the doping ion can effectively enhance the Li-ion conductivity in LLZO. Recently, a simultaneous multi-doping strategy in LLZO resulted in enhanced ionic conductivity (ranging from ∼10−4 cm−1 to 10−3 S cm−1) at room temperature.33 However, further endeavors are still needed to investigate the site preference and role of each dopant ion with respect to the Li+ dynamics in doped LLZO systems. We aim to identify the preferred site of the dopant ions, preferred Li occupancy in the 24dLi1/96hLi2 sites, and the role of the dopants in the Li-ion conduction by using neutron diffraction techniques.
Therefore, in this paper, we used a multi-doping strategy for tuning the conductivity of LLZO by substituting aliovalent ions (e.g., partial substitution of Li+ by Ga3+, La3+ by Ba2+, and Zr4+ by Ta5+) in LLZO. The effects of the doping ions on Li+ mobility and Li-ion conductivity were investigated via joint Rietveld refinement against X-ray diffraction (XRD) and high-resolution neutron powder diffraction (NPD) analysis that conclusively gives information on Li occupancy. A joint XRD and NPD Rietveld refined analysis, together with the results of Raman and solid-state nuclear magnetic resonance (NMR) spectroscopy, scanning electron microscopy (SEM), and energy-dispersive X-ray spectroscopy (EDX). The simultaneous multi-doping approach has the potential to improve the Li-ion conductivity in LLZO. The prepared garnet-type electrolyte was successfully tested in ASSLIBs with LFP as the cathode.
Experimental section
Solid electrolyte synthesis
Density and structure characterization
The ceramic density values were obtained through the Archimedes method with water for measurement. The ceramic densities of the pellets were estimated based on a theoretical density of 5.107 g cm−3. The phase purity of the doped LLZO powder sintered at 900 °C and the multi-sintered pellets at different temperatures was determined using X-ray powder diffraction (XRD) through a Bruker D2 Phaser with CuKα radiation (λ = 1.5405 Å). All diffraction patterns were recorded in the range of 10° < 2θ < 80° with a step size of 0.015°. The applied voltage and current were 30 kV and 30 mA, respectively. The synchrotron X-ray powder diffraction (SXRD) patterns were recorded from the 01C2 beamline with 25 keV X-rays at the National Synchrotron Radiation Research Center in Taiwan. An X-ray beam with a wavelength of 0.774916(1) Å was used, and the data were recorded between 5° < 2θ < 45°. Neutron powder diffraction (NPD) data were obtained using the beamline ECHIDNA at the Australian Nuclear Science and Technology Organization. The neutron beam wavelength was determined to be 1.62362(4) Å using the La11B6 NIST standard reference material (SRM660b). GSAS software was employed to analyze the NPD data. The Al occupancy at the tetrahedral-24d site was fixed at 0.06, which is close to the theoretical value derived from 1 wt% addition of Al2O3.20 The morphologies and microstructures of the doped LLZO pellets were analyzed using a field-emission scanning electron microscopy (FE-SEM) system by operating JEOL JSM-7610F at 15 kV. The samples were platinum-sputtered to eliminate any charge effect. The elemental composition and the presence of all common elements were obtained using energy dispersive X-ray spectroscopy (EDS). The mirror-polished pellets were gently broken into small pieces in an argon-filled glovebox and quickly moved for the analysis to minimize air exposure. To obtain more detailed structural information around Li and Ga environments, 7Li and 71Ga MAS NMR data were collected, respectively, at room temperature by using a Bruker Avance III spectrometer equipped with a 3.2 mm MAS probe head. The frequencies used for the 7Li and 71Ga nuclei were 155.5 and 121.951 MHz, respectively, by applying an external magnetic field of 14.1 T. The spinning speed of the samples was 12 kHz, and spectra were recorded after a single pulse irradiation (2–6 μs). The chemical shifts of 7Li and 71Ga were calibrated with 1 M LiCl and Ga(NO3)3, respectively. The spinning rate, position, line width, and intensity of components were automatically determined.Conductivity measurements
The AC impedance of the SEs was determined using a Solartron SI1260 impedance/gain-phase analyzer in the frequency range of 10 MHz to 0.1 Hz, with a signal amplitude of 0.1 V. All the doped LLZO pellets used in the electrochemical measurements have a thickness of 1.0–2.0 mm unless otherwise specified. The mirror-polished pellets were sputtered with Au as the blocking electrode on both sides and placed into a Swagelok cell in the Au|LLZO|Au configuration for electrochemical studies. The assembled cell was then connected with electrical wires to the impedance spectrometer. To measure the conductivity versus temperature, the AC impedance of the cells was measured from 20–120 °C. The cell was equilibrated for 1 h at each measurement. The impedance data were analyzed using Z Plot and Z View software packages. All impedance data were fitted with an equivalent circuit of the R(R//CPE)(R//CPE) model.Fabrication of all-solid-state Li-ion batteries
A cathode slurry was prepared by mixing LiFePO4, polyvinylidene fluoride (PVDF), KS6 carbon black, and bis-trifluoromethane sulfonamide (LiTFSI) as a lithium salt in the weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 by using an appropriate amount of NMP.34 Notably, the mixture of Li salt (LiTFSI) and the binder (PVDF) can form a polymer electrolyte.35 The slurry was homogeneously ground using a mortar and pestle for 30 min. The well-mixed slurry was spread equally on one side of a SE pellet followed by vacuum drying at 120 °C for 12 h. On the other side of the SE pellet pressed Li foil (thickness of around 20 μm) was placed as a negative electrode. The active material loading of the cathode was 2–3 mg cm−2.
7 by using an appropriate amount of NMP.34 Notably, the mixture of Li salt (LiTFSI) and the binder (PVDF) can form a polymer electrolyte.35 The slurry was homogeneously ground using a mortar and pestle for 30 min. The well-mixed slurry was spread equally on one side of a SE pellet followed by vacuum drying at 120 °C for 12 h. On the other side of the SE pellet pressed Li foil (thickness of around 20 μm) was placed as a negative electrode. The active material loading of the cathode was 2–3 mg cm−2.
Electrochemical measurements
For the electrochemical studies, the SE pellet with Li foil was sealed in a Swagelok cell in an argon glovebox. The cell was tested at room temperature between 2.7 and 3.8 V by using a potentiostat/galvanostat (Arbin BT2000) under open-air conditions.Results and discussion
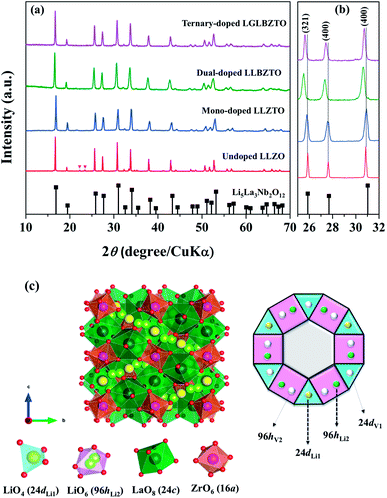
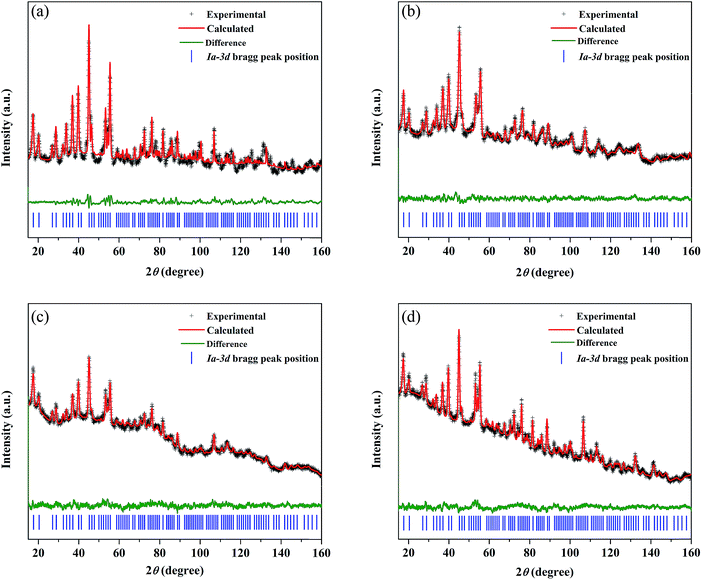
The synthesized LLZO powders calcined at 900 °C for 12 h, uniaxially pressed pellets sintered at 1130 °C for 18 h, and hot-pressed pellets at 1100 °C for 1 h were analyzed via X-ray diffraction (XRD) using CuKα radiation in the range of 10° < 2θ < 80° with a step size of 0.015°. Fig. 1 shows the room temperature XRD data for the Li7La3Zr2O12 (undoped LLZO), Li6.75La3Zr1.75Ta0.25O12 (mono-doped LLZTO), Li6.8La2.95Ba0.05Zr1.75Ta0.25O12 (dual-doped LLBZTO), and Li6.65Ga0.05La2.95Ba0.05Zr1.75Ta0.25O12 (ternary-doped LGLBZTO) powders after calcination at 900 °C for 12 h. XRD analysis revealed that all the diffraction peaks of the undoped LLZO and multi-doped LLZOs powders were well indexed with the standard compound (garnet-type with cubic structure Li5La3Nb2O12 (PDF45-0109)), indicating that the garnet framework can accommodate aliovalent ions of different sizes in the multi-doped LLZO structure without modifying the symmetry.16,36 By contrast, additional weak diffraction peaks corresponding to a minor impurity phase (LiAlO2, PDF73-1338) were observed only for the undoped LLZO sample, which may be due to the addition of Al during the synthesis. However, no other peaks were observed for the mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO samples. Doping of supervalent Ta5+ and Ga3+ and low-valent Ba2+ at the Zr4+, Li+, and La3+ sites, respectively, into the garnet structure led to a disordered structure, either by creating or filling Li+ vacancies to form a pure cubic phase without any tetragonal or other detectable impurities. In the close inspection of the XRD pattern, the peaks between 25° and 32° appear to be shifted with multi-ion doping (Fig. 1b). For the mono-doped LLZTO, the diffraction peaks slightly shifted toward higher angles, suggesting a decrease in both the Li+ concentration and lattice constants with increased Ta5+ doping at the Zr4+ site. Compared with undoped LLZO, the diffraction peaks for dual-doped LLBZTO and ternary-doped LGLBZTO shifted toward lower angles, which indicated increased lattice parameters. In general, the intensity of the diffraction peaks reduces significantly with the increase in dopant concentration, indicating a loss of crystallinity due to lattice distortion. Multi-doping of larger sized dopant ions into the garnet framework expands the lattice size and induces a strain into the system. As can be seen from the XRD patterns of multi-doped LLZO (Fig. 1), the diffraction peaks get broadened with doping, suggesting a significant lattice-defect formation by multi-ion doping. The lattice parameters were evaluated using both XRD and NPD Rietveld refined analysis (vide infra). The diffraction peaks widened with increased multi-ion doping in LLZO. The Rietveld refinements of the XRD patterns of the analyzed samples are shown in Fig. S1–S4.† The XRD refined crystallographic parameters are summarized in Table S1.† During structure Rietveld refinement, zero shift error, background parameters, absorption correction parameters, occupation parameters, histogram scale factors, pseudo-Voigt coefficient, and lattice constants were refined followed by the atomic displacement parameters. Then, isotropic thermal parameters were freely refined. Refinement results revealed that all the garnet samples were indexed to a highly conductive cubic phase with the space group of Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d and the lattice constants agreed well with the literature.9 The structure of a cubic LLZO unit cell with the connectivity pattern of tetrahedral-24dLi1 and octahedral-96hLi2 sites projected on 2D is shown in Fig. 1c. The garnet-type cubic LLZO structure is composed of edge-sharing dodecahedral La(1)O8 and La(2)O8 units (green, 24c site) occupied by La3+ at the central site, and octahedral ZrO6 units (orange, 16a site) occupied by Zr4+ at the central site. Li+ ions occupied two crystallographic sites: tetrahedral-24dLi1 sites represented by yellow spheres and distorted octahedral-96hLi2 sites represented by green spheres.
d and the lattice constants agreed well with the literature.9 The structure of a cubic LLZO unit cell with the connectivity pattern of tetrahedral-24dLi1 and octahedral-96hLi2 sites projected on 2D is shown in Fig. 1c. The garnet-type cubic LLZO structure is composed of edge-sharing dodecahedral La(1)O8 and La(2)O8 units (green, 24c site) occupied by La3+ at the central site, and octahedral ZrO6 units (orange, 16a site) occupied by Zr4+ at the central site. Li+ ions occupied two crystallographic sites: tetrahedral-24dLi1 sites represented by yellow spheres and distorted octahedral-96hLi2 sites represented by green spheres.
Raman measurements were performed on the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO in the range of 50–1200 cm−1 at room temperature and the results are shown in Fig. 2. In the Raman spectra, the low frequency region (<300 cm−1) vibrational bands can be assigned to the LiO6 octahedral unit (96hLi2 position), the middle-frequency region (300–550 cm−1) vibrational bending modes can be assigned to the LiO4 tetrahedral unit (24dLi1 position), and the high-frequency region (>550 cm−1) bands correspond to the stretching mode of the ZrO6 octahedral unit (16a position).37 The Raman spectra of the undoped and multi-doped LLZO overlapped with the cubic phase of LLZO garnets reported in the literature.37–41 Tietz et al. reported that the band near 645 cm−1 corresponds to the stretching mode of the ZrO6 octahedral unit.37 Thompson et al. found an additional band near 750 cm−1 in Li6.5La3Zr1.5Ta0.5O12 with the partial substitution of Zr4+ with Ta5+.39 They suggested that the additional band was attributed to the stretching mode of the TaO6 octahedral unit due to its increased intensity at a high Ta5+ concentration. In our investigation, for the multi-doped LLZO, the band corresponding to the stretching mode of the Zr–O bond and an additional band corresponding to the Ta–O unit appeared at 625 and 720 cm−1, respectively. In the low frequency region of the Raman spectra, the two narrow bands that appeared below 200 cm−1 belonged to Li–O bonding peaks of the cubic LLZO garnet. Such peaks were split in the tetragonal LLZO due to the reduction in symmetry. The highly intense Raman peak that corresponds to the vibration mode of CO32− generally appears at 1090 cm−1 was not observed in the undoped and multi-doped LLZO; such a finding indicated that the pellets were free from Li2CO3.41
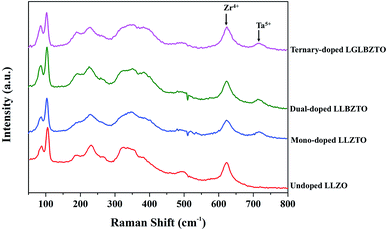 | ||
| Fig. 2 Raman spectra of the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO in the range of 50–800 cm−1. | ||
The ceramic densities of the undoped and multi-doped LLZO hot-press pellets were calculated using the formula ρexp/ρtheo, where ρexp is the experimental density measured through the Archimedes method, and ρtheo is the theoretical density (5.107 g cm−3) of cubic LLZO.16 The ρexp of the doped LLZO samples was calculated by using eqn (1).
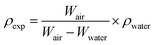 | (1) |
| Garnet | Density (g cm−3) | Ceramic density (%) | σ total (S cm−1) | E a (eV) |
|---|---|---|---|---|
| LLZO | 4.939 | 96.7 | 2.4 × 10−4 | 0.34 |
| LLZTO | 5.086 | 99.6 | 4.3 × 10−4 | 0.32 |
| LLBZTO | 5.091 | 99.7 | 6.5 × 10−4 | 0.29 |
| LGLBZTO | 5.137 | 99.9 | 7.2 × 10−4 | 0.28 |
The influence of doping multiple ions (Ga, Ba, and Ta) on the morphology of doped LLZO samples was examined using field emission scanning electron microscopy (FE-SEM). Fig. S5† shows the FE-SEM images of the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO obtained at room temperature along with the optical image of LGLBZTO with 0.5 mm thickness. Substantial changes in the morphology of the microstructure were observed between the undoped LLZO and multi-doped LLZO samples. The SEM image of the undoped LLZO revealed that the grains were not connected well with each other. Furthermore, there were irregular pores among the grains, which is consistent with the low density of the undoped LLZO. By contrast, the SEM images of the mono-doped LLZTO and dual-doped LLBZTO exhibited a dense and homogeneous morphology without any noticeable pores among the grains, which are reduced owing to their grain growth and mergence. A close inspection of the ternary-doped LGLBZTO revealed that mixtures of small and large grains were present in the microstructure. The microstructure appeared to be highly dense and compact due to the filling of the gaps between large grains by small grains. This result corroborated the high density of the ternary-doped LGLBZTO, which was close to the theoretical density. The fabrication of differently sized grains by mixing large particles with small particles resulted in the dense microstructure.43 Almost no porosity was detected for the dual-doped LLBZTO and ternary-doped LGLBZTO. Hence, multi-doped LLZO samples are expected to exhibit high Li-ion conductivities. The letters “LGLBZTO” behind the pellet can be seen clearly, which indicates the translucent nature of the pellet with reduced grain boundaries. The particle size distributions for the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO were measured at room temperature. The d(0.1), d(0.5), and d(0.9) of the undoped and multi-doped LLZO particles substantiated the SEM microstructure (Table S2†).
EDX mapping was carried out for the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO samples to detect the respective dopants and their composition on grains and grain boundaries (Fig. 3). EDX analysis revealed that Al was exclusively found in the undoped LLZO sample at the grain boundaries. The localization of O, La, Zr, and dopant ions (Ta, Ba, and Ga) was uniformly distributed among the crystal grains. Furthermore, a predominant distribution of Ga, Ba, and Ta was observed mainly inside the grains in the EDX maps, which confirmed the inclusion of dopant ions in the garnet lattice.
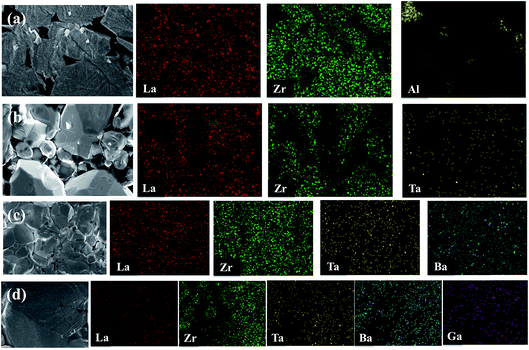 | ||
| Fig. 3 SEM images and corresponding EDX maps of La, Zr, Al, Ta, Ba, and Ga for (a) undoped LLZO, (b) mono-doped LLZTO, (c) dual-doped LLBZTO, and (d) ternary-doped LGLBZTO. | ||
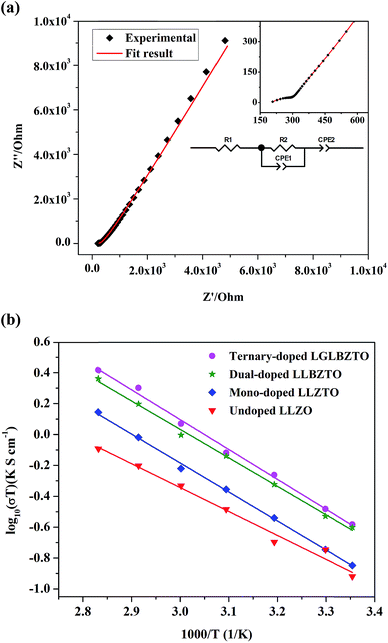
To study the effect of doping on Li+ transportation, the ionic conductivities of the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO were measured using the AC impedance technique with Au as the blocking electrode. A typical Nyquist impedance plot for the ternary-doped LGLBZTO (Li6.65Ga0.05La2.95Ba0.05Zr1.75Ta0.25O12) with the Au|LGLBZTO|Au configuration was recorded at room temperature (Fig. 4a). The undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO all showed one partially depressed semicircle at the high-frequency region with a low-frequency diffusion spike. This semicircle can be assigned as the total impedance, including the contribution from bulk and grain boundary impedances, and the low-frequency spike can be attributed to Li+ blocking at the electrode/electrolyte interface. The impedance data were fitted using an equivalent circuit model consisting of (Rb)(RgbCPEgb)(CPE). The right intercept of the semicircle on the real axis at the high-frequency region represents the bulk resistance of the sample, which is denoted as Rb in the equivalent circuit. Rgb is the grain boundary resistance; CPEgb and CPE are the constant phase element contributions attributed to the grain boundary capacitance and the diffusion capacitance at the electrode/electrolyte interface, respectively. The diameter of the semicircle at the middle frequency region corresponds to the total resistance, which is the sum of the resistance of the grain and grain boundary response (Rb + Rgb). The contributions of grain and grain boundary responses were difficult to distinguish from the impedance spectra. The total Li-ion conductivity of the specimen, σt (S cm−1), was achieved using the total resistance normalized with respect to the thickness and cross-sectional area of the specimen. The ionic conductivities of the undoped and multi-doped LLZO samples were calculated from eqn (2):
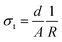 | (2) |
The Li-ion conductivity of the LLZO cubic garnet depends on various key factors, such as (i) mobile Li+ concentration, (ii) Li+ vacancy (VLi) concentration, (iii) bottleneck size for Li+ migration, (iv) coulombic repulsion between the Li+–Li+ pair, and (v) specimen microstructure.40,45–49 It is well known that the nominal cubic garnet-type structure, Li7La3Zr2O12, is not stable at room temperature due to the high coulombic repulsion between the Li+–Li+ pair.50 In the mono-doped LLZTO, the substitution of high valence Ta5+ for Zr4+ led to Li+ vacancies and reduced Li+ concentration for charge compensation, which promoted the Li+ motion in the LLZTO framework. The substitution of Ta5+ for Zr4+ reduced the coulombic repulsion between the Li+–Li+ pair by creating Li+ vacancies. As a result, the mono-doped LLZTO showed conductivity higher than that of the undoped LLZO. Although VLi can promote ionic conductivity, there should be an optimal VLi. The excess increment of VLi may result in reduced mobile Li+ concentration in the garnet framework, which might result in low conductivities. The dual substitution strategy can improve the Li+ dynamics in Sb–Ba co-doped LLZO.51 In the dual-doped LLBZTO, the substitution of Ta5+ for Zr4+ and Ba2+ for La3+ may lead to optimal Li+ concentration. Furthermore, the larger ionic radius r of Ba2+ than that of La3+ may cause lattice expansion, which enlarged the bottleneck size for Li+ migration and thereby resulted in a conductivity higher than that of the undoped LLZO and mono-doped LLZTO.
The Li rearrangement took place between the tetrahedral-24dLi1 and octahedral-96hLi2 sites due to the electrostatic repulsion of either the Li+–Li+ pair or Li+-dopant ion pair in the LLZO framework.48 The strong electrostatic repulsion of the Li+-dopant ion pair may affect the neighboring Li+ sites, which can lead to the high mobility of Li+. Therefore, the coulombic interaction between Li+ and dopant cations is a determining factor for Li-ion conductivity. Strategic doping of ions at the Li sites in LLZO may create strong coulombic repulsion between dopant ions and Li+, which can influence the mobility of Li+. In the ternary-doped LGLBZTO, the substitution of Ta5+ for Zr4+, Ba2+ for La3+, and immobile Ga3+ for Li+ created a strong coulombic repulsion at the Li sites, in addition to the enlarged bottleneck size from Ba doping. Hence, we can expect a high conductivity for the ternary-doped LGLBZTO, attributed to the enhanced Li+ mobility arising from the coulombic repulsion between Li+ ions and dopant Ga ions. With the increased amount of doped ions, the total conductivity linearly increased. The optimum total ionic conductivity (σt) achieved for the ternary-doped LGLBZTO (Li6.65Ga0.05La2.95Ba0.05Zr1.75Ta0.25O12) was 0.72 and 1.24 mS cm−1 at room temperature and 60 °C, respectively.
The Nyquist plot of a symmetric lithium cell with the configuration of Li|LGLBZTO|Li was recorded at room temperature and 60 °C (Fig. S6†). The symmetrical cell showed two depressed semicircles with an inclined line. The first semicircle at high-frequencies shows a bulk resistance (R1 + R2) of ∼203 Ω and ∼140 Ω at room temperature and 60 °C, respectively, corresponding to the solid electrolyte. The second depressed semicircle attributed to the interfacial resistance (R3) of ∼8551 Ω and ∼1912 Ω at room temperature and 60 °C, respectively, between the solid electrolyte and Li electrode was observed at middle frequencies. The decreased interfacial resistance at 60 °C could be attributed to the formation of better contact between the solid electrolyte and Li metal.
The total ionic conductivity varies linearly with inverse temperature; the activation energy Ea can be extracted from the Arrhenius plots using the following equation:
| σtotal = σ0e−Ea/KT | (3) |
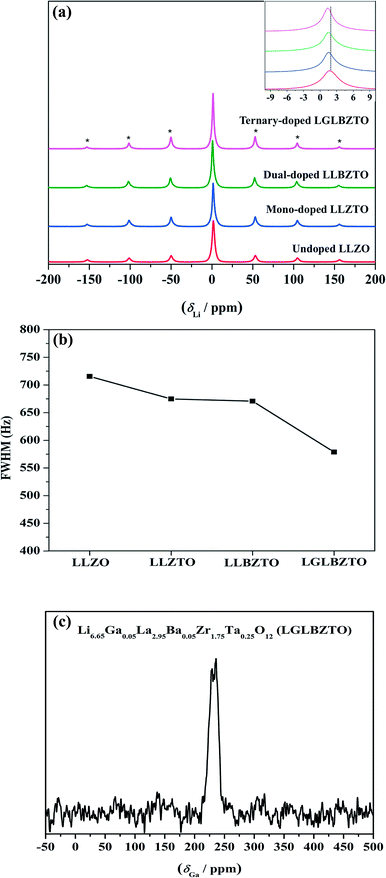
Solid-state magic angle spinning NMR (MAS NMR) studies were performed to elucidate the differences in the local structural features of garnet LLZO. The solid-state 7Li MAS NMR spectra of the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO were recorded at room temperature (Fig. 6). All investigated garnet compounds showed a single central transition at 1.5 ppm due to the −1/2 ↔ 1/2 transition along with three other satellite peaks (−5/2 ↔ 5/2, −3/2 ↔ 3/2, and −1/2 ↔ 1/2 transitions) corresponding to the spinning sidebands. The 7Li MAS NMR results are consistent with the reported garnet-type compounds in the literature.52,53 The central transition peak of the undoped LLZO at 1.7 ppm slightly shifted to the shielded region for the multi-doped LLZO with an increased amount of doped ions (Fig. 6a inset). In general, the full width at half-maximum (FWHM) of the central 7Li transition was governed by the strength of homonuclear (7Li–7Li) dipole–dipole interactions and Li+ migration ability.54Fig. 6b shows an apparent decrease in the FWHM of the 7Li MAS NMR spectra with multi-ion doping in the LLZO framework. A narrow line width of the central transition was observed for the ternary-doped LGLBZTO, indicating weak homonuclear (7Li–7Li) dipole–dipole interactions which may be attributed to the increased Li+ migration ability. However, spin-lattice relaxation times (T1) could give further insight into the diffusion behavior of Li in the LLZO garnet. Systematic variable temperature NMR studies are required to understand the Li+ dynamics and their coordination geometry in the undoped and multi-doped LLZO samples.55
71Ga (spin quantum number, I = 3/2) MAS NMR measurement was carried out to evaluate the crystallographic site and symmetry of the Ga environment in the garnet structure. The 71Ga MAS NMR spectrum of the ternary-doped LGLBZTO powder recorded at room temperature is shown in Fig. 6c. The sample showed one broad signal in the range of 210–255 ppm in the 71Ga MAS spectrum, indicating that the Ga ions in ternary-doped LGLBZTO were located in a single structural site (tetrahedral coordination Li24d site). Furthermore, the NPD results confirmed the site occupancy for Ga (vide infra). The small peaks at around 170 and 300 ppm were the spinning sidebands. The signal at 107–222 ppm corresponds to the tetrahedral environment.56,57 In an octahedral environment, the Ga signal shifted up field and appeared within 80 and −42 ppm.56–58
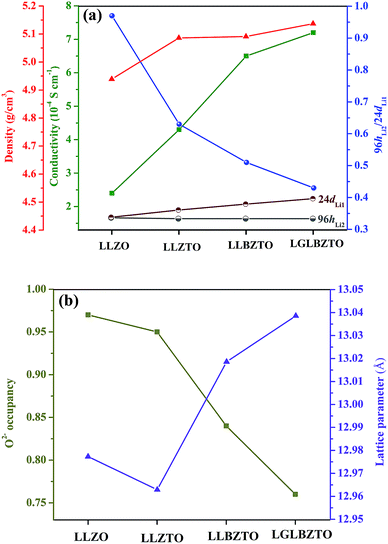
NPD, which offers high sensitivity towards light elements (e.g., Li and O) in the presence of heavy elements, was carried out to investigate the influence of doping aliovalent ions Ga3+, Ba2+, and Ta5+ at the Li+, La3+, and Zr4+ sites, respectively, on the Li+ distribution in the garnet structure LLZO. Room temperature NPD data were collected for the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO powders calcined at 900 °C for 12 h. Fig. 7 displays the corresponding Rietveld refinement plots. The refined structural parameters are summarized in Table 2. The Rietveld refinements were analyzed using the general structure analysis system (GSAS-II). The La3+, Zr4+, and O2− ions in the garnet structure were considered to occupy the dodecahedral 24c, octahedral 16a, and octahedral 96h sites, respectively. The Li+ ions were located on two sites: tetrahedral-24dLi1 and distorted octahedral-96hLi2. Ba2+ and Ta5+ were partially substituted at dodecahedral 24c (La3+) and octahedral 16a (Zr4+) sites with similar ionic radii, respectively, without blocking the Li+ transport path in the garnet framework.59 NPD measurements confirmed that Ga3+ was preferentially located at the tetrahedral-24dLi1 (r = 0.59 Å) site rather than at the octahedral-96hLi2 (r = 0.76 Å) site due to the small ionic radius of Ga3+ (r = 0.47 Å in a tetrahedral coordination).22,40,60,61 The slightly large lattice parameters in the dual-doped LLBZTO and ternary-doped LGLBZTO can be explained by the substitution of Ba2+ with larger doping ionic radius (r = 1.42 Å in VIII co-ordination) for the smaller La3+ (r = 1.16 Å in VIII coordination) in the LLZO system. The reduced lattice constant observed for the mono-doped LLZTO was due to the smaller doping ionic radius of Ta5+ (r = 0.64 Å in VI coordination) than that of Zr4+ (r = 0.72 Å in VI coordination).62 The refined lattice parameters, Li occupancy at the tetrahedral-24dLi1 and octahedral-96hLi2 sites, the ratio of octahedral-96hLi2 to tetrahedral-24dLi1, O2− occupancy at the 96h site, and unit-cell volumes of the undoped and multi-doped LLZOs are presented in Table 3. The supervalent cation substitution, either Ta5+ at the Zr4+ site or Ga3+ at the Li+ site, leads to the stabilization of a highly conductive cubic polymorph. In our NPD refinement, the occupancy of Li at the tetrahedral-24dLi1 site increased with an increased number of doped ions, whereas the Li occupancy at the octahedral-96hLi2 site remained constant. In the undoped LLZO, the lithium ions reside equally at octahedral-96hLi2 (0.36(5)) and tetrahedral-24dLi1 (0.35(3)) sites. Upon doping multiple elements, an increase of Li occupancy at the tetrahedral-24dLi1 site was observed. The occupancy of lithium in the tetrahedral-24dLi1 sites increased from 0.36(5) to 0.77(5) with ternary element doping. Thus, the tetrahedral-24dLi1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) octahedral-96hLi2 Li occupancy ratio increased with an increased number of doped ions. It is generally believed that the immobile Al dopant in the garnet framework occupying the Li sites may cause blocking of the Li+ transport in Al-doped LLZO garnets.20 Shin et al. reported that upon doping of tantalum into the Al-doped LLZO garnet, the blocking immobile Al shifts from the tetrahedral-24dLi1 to octahedral-96hLi2 site, thereby providing more open space for Li ion transport.63 We believe that multi-ion doping into the garnet framework caused structural alteration and provides more space in the tetrahedral-24dLi1 site. The lithium ion mobility at the tetrahedral-24dLi1 sites plays an important role in the total ionic conductivity in garnet-type structures.64,65 Additionally, a reduction in oxygen defects with an increased amount of doped ions was observed from the Rietveld analysis. The decrease in oxygen occupancy created a positive hole for Li+ hopping. Wu, J.-F. et al.,40,61 Rettenwander, D. et al.66 and Jalem, R. et al.65 reported that the electrochemical properties improved with increased Li occupancy at the tetrahedral-24dLi1 site, which can serve as the trigger for Li-ion mobility in LLZO garnet-type systems. Recently, we found that the increased Li content along with the reduced oxygen defects can enhance the Li-ion conductivity in Al-doped LLZO by locally rearranging the oxygen atoms in the anionic framework during voltammetric treatment.67 The increased ionic conductivity with multi-ion doping can be ascribed to the partial occupancy of Li+ across the tetrahedral-24dLi1 and octahedral-96hLi2 sites, decreased Li occupancy ratio (96hLi2/24dLi1), and reduced oxygen defects.
octahedral-96hLi2 Li occupancy ratio increased with an increased number of doped ions. It is generally believed that the immobile Al dopant in the garnet framework occupying the Li sites may cause blocking of the Li+ transport in Al-doped LLZO garnets.20 Shin et al. reported that upon doping of tantalum into the Al-doped LLZO garnet, the blocking immobile Al shifts from the tetrahedral-24dLi1 to octahedral-96hLi2 site, thereby providing more open space for Li ion transport.63 We believe that multi-ion doping into the garnet framework caused structural alteration and provides more space in the tetrahedral-24dLi1 site. The lithium ion mobility at the tetrahedral-24dLi1 sites plays an important role in the total ionic conductivity in garnet-type structures.64,65 Additionally, a reduction in oxygen defects with an increased amount of doped ions was observed from the Rietveld analysis. The decrease in oxygen occupancy created a positive hole for Li+ hopping. Wu, J.-F. et al.,40,61 Rettenwander, D. et al.66 and Jalem, R. et al.65 reported that the electrochemical properties improved with increased Li occupancy at the tetrahedral-24dLi1 site, which can serve as the trigger for Li-ion mobility in LLZO garnet-type systems. Recently, we found that the increased Li content along with the reduced oxygen defects can enhance the Li-ion conductivity in Al-doped LLZO by locally rearranging the oxygen atoms in the anionic framework during voltammetric treatment.67 The increased ionic conductivity with multi-ion doping can be ascribed to the partial occupancy of Li+ across the tetrahedral-24dLi1 and octahedral-96hLi2 sites, decreased Li occupancy ratio (96hLi2/24dLi1), and reduced oxygen defects.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d)
d)
| Garnet | L.P./Å | GOF | R wp | Site | Occupancy | x | y | z | U iso/(Å2) |
|---|---|---|---|---|---|---|---|---|---|
| LLZO | 12.9773(2) | 1.97 | 7.11% | Li(24d) | 0.32(4) | 3/8 | 0 | 1/4 | 0.003(1) |
| Li(96h) | 0.36(2) | 0.690(2) | 0.578(2) | 0.094(2) | 0.003(1) | ||||
| Al(24d) | 0.06 | 3/8 | 0 | 1/4 | 0.01 | ||||
| La(24c) | 0.96(2) | 1/8 | 0 | 1/4 | 0.054(4) | ||||
| Zr(16a) | 0.99(3) | 0 | 0 | 0 | 0.048(4) | ||||
| O(96h) | 0.97(1) | 0.099(1) | 0.194(6) | 0.280(5) | 0.051(2) | ||||
| LLZTO | 12.9629(2) | 2.21 | 3.59% | Li(24d) | 0.52(4) | 3/8 | 0 | 1/4 | 0.066(1) |
| Li(96h) | 0.33(2) | 0.692(2) | 0.600(1) | 0.098(2) | 0.066(1) | ||||
| La(24c) | 0.96(9) | 1/8 | 0 | 1/4 | 0.026(1) | ||||
| Zr(16a) | 0.86(8) | 0 | 0 | 0 | 0.032(2) | ||||
| Ta(16a) | 0.11(8) | 0 | 0 | 0 | 0.032(2) | ||||
| O(96h) | 0.95(6) | 0.101(2) | 0.194(2) | 0.280(2) | 0.026(9) | ||||
| LLBZTO | 13.0186(6) | 2.14 | 2.09% | Li(24d) | 0.65(8) | 3/8 | 0 | 1/4 | 0.100(3) |
| Li(96h) | 0.33(2) | 0.697(3) | 0.585(3) | 0.131(4) | 0.066(1) | ||||
| La(24c) | 0.95(6) | 1/8 | 0 | 1/4 | 0.035(2) | ||||
| Ba(24c) | 0.07(1) | 1/8 | 0 | 1/4 | 0.035(2) | ||||
| Zr(16a) | 0.85(1) | 0 | 0 | 0 | 0.072(4) | ||||
| Ta(16a) | 0.15(1) | 0 | 0 | 0 | 0.072(4) | ||||
| O(96h) | 0.84(8) | 0.101(4) | 0.194(4) | 0.278(3) | 0.027(1) | ||||
| LGLBZTO | 13.03858(1) | 2.16 | 2.61% | Li(24d) | 0.77(5) | 3/8 | 0 | 1/4 | 0.040(7) |
| Li(96h) | 0.33(3) | 0.698(4) | 0.595(3) | 0.211(4) | 0.040(7) | ||||
| Ga(24d) | 0.04(6) | 3/8 | 0 | 1/4 | 0.040(7) | ||||
| La(24c) | 0.95(5) | 1/8 | 0 | 1/4 | 0.017(1) | ||||
| Ba(24c) | 0.04(9) | 1/8 | 0 | 1/4 | 0.017(1) | ||||
| Zr(16a) | 0.86(1) | 0 | 0 | 0 | 0.033(1) | ||||
| Ta(16a) | 0.14(1) | 0 | 0 | 0 | 0.033(1) | ||||
| O(96h) | 0.76(6) | 0.101(4) | 0.194(4) | 0.278(3) | 0.014(9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tetrahedral-24dLi1, and O2− occupancy at the 96h site of the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO
tetrahedral-24dLi1, and O2− occupancy at the 96h site of the undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO
| Garnet | LLZO | LLZTO | LLBZTO | LGLBZTO |
|---|---|---|---|---|
| a Lattice parameter. b Volume. | ||||
| L.P.a/Å | 12.9773(2) | 12.9629(2) | 13.0186(6) | 13.03858(1) |
| V /Å3 | 2178.7(1) | 2178.2(8) | 2207.3(3) | 2216.4(3) |
| 24dLi1 | 0.36(5) | 0.52(4) | 0.65(8) | 0.77(5) |
| 96hLi2 | 0.35(3) | 0.33(2) | 0.33(2) | 0.33(3) |
| 96hLi2/24dLi1 | 0.97 | 0.63 | 0.51 | 0.43 |
| O2− | 0.97(1) | 0.95(6) | 0.84(8) | 0.76(6) |
The viability of the garnet solid electrolyte for all-solid-state batteries was demonstrated by constructing a half-cell with Li metal, Li6.65Ga0.05La2.95Ba0.05Zr1.75Ta0.25O12 (ternary-doped LGLBZTO), and LiFePO4 as the active electrodes. To reduce the interfacial resistance between the electrolyte and cathode, bis-trifluoromethane sulfonamide Li salt was added to the cathode material. Fig. 8 shows the cycling performance of the half-cell with the ternary-doped LGLBZTO electrolyte, metallic Li anode, and LiFePO4 cathode. AC impedance measurements were conducted for the half-cells before and after the 5th lithiation/delithiation cycle at 60 °C to evaluate the cell resistance evolution (Fig. S7†). In all cases, two depressed semicircles were observed at high and middle frequencies, followed by an inclined line at lower frequency. The high/middle frequency behavior was attributed to the interfacial resistances between the electrolyte and electrodes.68 After the 5th cycle, the interfacial resistances for the half cells with undoped LLZO and multi-doped LLZOs are mildly increased. However, the increment in interfacial resistance between the electrolyte and electrodes decreased obviously with multi-ion doping. Galvanostatic charge–discharge curves were achieved within the cut off voltage range of 2.7–3.8 V against Li+/Li at 0.05C (1C = 170 mA h g−1) and 60 °C (Fig. 8a). The first charge and discharge capacities of 160.0 mA h g−1 and 146.8 mA h g−1, which correspond to approximately 94.1% and 86.4% of the theoretical capacity (170 mA h g−1), respectively, at 0.05C were achieved.
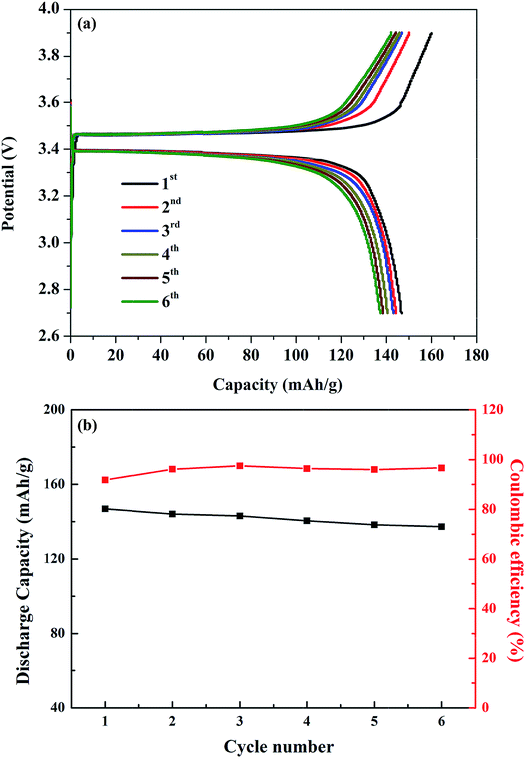 | ||
| Fig. 8 (a) Galvanostatic charge–discharge curves of the LFP/LGLBZTO/Li structured cell at 0.05C and 60 °C. (b) Capacity retention of the LFP/LGLBZTO/Li cell at 0.05C after 6 cycles. | ||
The first coulombic efficiency was 91.8%; however, the coulombic efficiency was increased in the following cycles, and was approximately 96.6% for the 6th cycle as can be seen in Fig. 8b. The gradual increase in the cell overpotential and the decrease in the discharge capacity were due to the rigid nature of the solid electrolyte and poor contact with electrodes during the cycling. Optimizing the electrolyte/electrode interfaces using various buffer layer coatings can solve such issues.
Conclusions
In summary, an efficient multi-doping strategy enhanced the Li-ion conductivity of the garnet-type solid electrolyte Li7La3Zr2O12. We synthesized undoped LLZO, mono-doped LLZTO, dual-doped LLBZTO, and ternary-doped LGLBZTO using the solid-state method. The synthesized garnet electrolytes were characterized via XRD, NPD, SEM, EDS mapping, and solid-state NMR techniques. The ceramic density of the synthesized garnets was near the theoretical density of LLZO. NPD Rietveld analysis revealed an increased Li+ occupancy at the tetrahedral-24dLi1 site with increased multi-ion doping in LLZO, whereas Li+ occupancy at the octahedral-96hLi2 site remained constant. The increased Li-ion conductivity with multi-ion doping can be ascribed to the dense microstructure, decreased 96hLi2/24dLi1 Li+ occupancy ratio, and reduced oxygen defects. The prepared ternary-doped LGLBZTO was tested for all solid-state Li+ cells with the Li|LGLBZTO|LFP configuration and the results showed a reasonable cyclability of over 6 cycles.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was financially supported by the Ministry of Science and Technology of Taiwan (contract no. MOST 107-2113-M-002-008-MY3 and MOST 106-2112-M-003-007-MY3) and the Material and Chemical Research Laboratories, Industrial Technology Research Institute, Hsinchu, Taiwan. W. K. Pang is grateful for the financial support of the Australian Research Council (ARC, FT160100251) and the University of Wollongong through the UIC International Links Grant Scheme 2018. The authors would also like to thank the staff members of the Australian Centre for Neutron Scattering, ANSTO, for their operation support.References
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- E. J. Cheng, A. Sharafi and J. Sakamoto, Electrochim. Acta, 2017, 223, 85–91 CrossRef CAS.
- A. W. Golubkov, D. Fuchs, J. Wagner, H. Wiltsche, C. Stangl, G. Fauler, G. Voitic, A. Thaler and V. Hacker, RSC Adv., 2014, 4, 3633–3642 RSC.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS.
- Y. Meesala, A. Jena, H. Chang and R.-S. Liu, ACS Energy Lett., 2017, 2, 2734–2751 CrossRef CAS.
- Z. Zhang, Y. Shao, B. V. Lotsch, Y.-S. Hu, H. Li, J. Janek, C. Nan, L. Nazar, J. Maier, M. Armand and L. Chen, Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213 CrossRef CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed.
- C. Cao, Z.-B. Li, X.-L. Wang, X.-B. Zhao and W.-Q. Han, Frontiers in Energy Research, 2014, 2, 25 CrossRef.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef CAS PubMed.
- J. Awaka, N. Kijima, H. Hayakawa and J. Akimoto, J. Solid State Chem., 2009, 182, 2046–2052 CrossRef CAS.
- J. Awaka, A. Takashima, K. Kataoka, N. Kijima, Y. Idemoto and J. Akimoto, Chem. Lett., 2011, 40, 60–62 CrossRef CAS.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg and A. Lotnyk, Phys. Chem. Chem. Phys., 2011, 13, 19378–19392 RSC.
- V. Thangadurai, S. Narayanan and D. Pinzaru, Chem. Soc. Rev., 2014, 43, 4714–4727 RSC.
- C. A. Geiger, E. Alekseev, B. Lazic, M. Fisch, T. Armbruster, R. Langner, M. Fechtelkord, N. Kim, T. Pettke and W. Weppner, Inorg. Chem., 2011, 50, 1089–1097 CrossRef CAS PubMed.
- S. Kumazaki, Y. Iriyama, K.-H. Kim, R. Murugan, K. Tanabe, K. Yamamoto, T. Hirayama and Z. Ogumi, Electrochem. Commun., 2011, 13, 509–512 CrossRef CAS.
- M. Kotobuki, K. Kanamura, Y. Sato and T. Yoshida, J. Power Sources, 2011, 196, 7750–7754 CrossRef CAS.
- E. Rangasamy, J. Wolfenstine and J. Sakamoto, Solid State Ionics, 2012, 206, 28–32 CrossRef CAS.
- D. Rettenwander, P. Blaha, R. Laskowski, K. Schwarz, P. Bottke, M. Wilkening, C. A. Geiger and G. Amthauer, Chem. Mater., 2014, 26, 2617–2623 CrossRef CAS PubMed.
- N. Bernstein, M. Johannes and K. Hoang, Phys. Rev. Lett., 2012, 109, 205702 CrossRef CAS PubMed.
- C. Bernuy-Lopez, W. Manalastas Jr, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef CAS.
- R. Jalem, M. Rushton, W. Manalastas Jr, M. Nakayama, T. Kasuga, J. A. Kilner and R. W. Grimes, Chem. Mater., 2015, 27, 2821–2831 CrossRef CAS.
- S. Song, B. Yan, F. Zheng, H. M. Duong and L. Lu, Solid State Ionics, 2014, 268, 135–139 CrossRef CAS.
- J. L. Allen, J. Wolfenstine, E. Rangasamy and J. Sakamoto, J. Power Sources, 2012, 206, 315–319 CrossRef CAS.
- S. Ohta, T. Kobayashi and T. Asaoka, J. Power Sources, 2011, 196, 3342–3345 CrossRef CAS.
- S. Ramakumar, L. Satyanarayana, S. V. Manorama and R. Murugan, Phys. Chem. Chem. Phys., 2013, 15, 11327–11338 RSC.
- T. Yang, Y. Li, W. Wu, Z. Cao, W. He, Y. Gao, J. Liu and G. Li, Ceram. Int., 2018, 44, 1538–1544 CrossRef CAS.
- R. Wagner, D. Rettenwander, G. n. J. Redhammer, G. Tippelt, G. Sabathi, M. E. Musso, B. Stanje, M. Wilkening, E. Suard and G. Amthauer, Inorg. Chem., 2016, 55, 12211–12219 CrossRef CAS PubMed.
- V. Thangadurai and W. Weppner, J. Am. Ceram. Soc., 2005, 88, 411–418 CrossRef CAS.
- A. Dumon, M. Huang, Y. Shen and C.-W. Nan, Solid State Ionics, 2013, 243, 36–41 CrossRef CAS.
- W. Bucheli, T. Durán, R. Jimenez, J. s. Sanz and A. Varez, Inorg. Chem., 2012, 51, 5831–5838 CrossRef CAS PubMed.
- L. Buannic, B. Orayech, J.-M. López Del Amo, J. Carrasco, N. A. Katcho, F. d. r. Aguesse, W. Manalastas, W. Zhang, J. Kilner and A. Llordés, Chem. Mater., 2017, 29, 1769–1778 CrossRef CAS.
- F. Du, N. Zhao, Y. Li, C. Chen, Z. Liu and X. Guo, J. Power Sources, 2015, 300, 24–28 CrossRef CAS.
- S. Rajendran, M. S. Song, M. S. Park, J. H. Kim and J. Y. Lee, Mater. Lett., 2005, 59, 2347–2351 CrossRef CAS.
- H. Hyooma and K. Hayashi, Mater. Res. Bull., 1988, 23, 1399–1407 CrossRef CAS.
- F. Tietz, T. Wegener, M. Gerhards, M. Giarola and G. Mariotto, Solid State Ionics, 2013, 230, 77–82 CrossRef CAS.
- G. Larraz, A. Orera and M. Sanjuan, J. Mater. Chem. A, 2013, 1, 11419–11428 RSC.
- T. Thompson, J. Wolfenstine, J. L. Allen, M. Johannes, A. Huq, I. N. David and J. Sakamoto, J. Mater. Chem. A, 2014, 2, 13431–13436 RSC.
- J.-F. Wu, E.-Y. Chen, Y. Yu, L. Liu, Y. Wu, W. K. Pang, V. K. Peterson and X. Guo, ACS Appl. Mater. Interfaces, 2017, 9, 1542–1552 CrossRef CAS PubMed.
- Y. Li, X. Chen, A. Dolocan, Z. Cui, S. Xin, L. Xue, H. Xu, K. Park and J. B. Goodenough, J. Am. Chem. Soc., 2018, 140, 6448–6455 CrossRef CAS PubMed.
- F. Shen, M. B. Dixit, X. Xiao and K. B. Hatzell, ACS Energy Lett., 2018, 3, 1056–1061 CrossRef CAS.
- L. Cheng, W. Chen, M. Kunz, K. Persson, N. Tamura, G. Chen and M. Doeff, ACS Appl. Mater. Interfaces, 2015, 7, 2073–2081 CrossRef CAS PubMed.
- C.-L. Tsai, V. Roddatis, C. V. Chandran, Q. Ma, S. Uhlenbruck, M. Bram, P. Heitjans and O. Guillon, ACS Appl. Mater. Interfaces, 2016, 8, 10617–10626 CrossRef CAS PubMed.
- W. G. Zeier, Dalton Trans., 2014, 43, 16133–16138 RSC.
- L. J. Miara, S. P. Ong, Y. Mo, W. D. Richards, Y. Park, J.-M. Lee, H. S. Lee and G. Ceder, Chem. Mater., 2013, 25, 3048–3055 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and S.-H. Yang, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- Y. Chen, E. Rangasamy, C. Liang and K. An, Chem. Mater., 2015, 27, 5491–5494 CrossRef CAS.
- Y. Zhang, J. Deng, D. Hu, F. Chen, Q. Shen, L. Zhang and S. Dong, Electrochim. Acta, 2019, 296, 823–829 CrossRef CAS.
- M. Xu, M. S. Park, J. M. Lee, T. Y. Kim, Y. S. Park and E. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 052301 CrossRef.
- Z. Cao, X. Cao, X. Liu, W. He, Y. Gao, J. Liu and J. Zeng, Ceram. Int., 2015, 41, 6232–6236 CrossRef CAS.
- L. van Wüllen, T. Echelmeyer, H.-W. Meyer and D. Wilmer, Phys. Chem. Chem. Phys., 2007, 9, 3298–3303 RSC.
- M. P. O'Callaghan, A. S. Powell, J. J. Titman, G. Z. Chen and E. J. Cussen, Chem. Mater., 2008, 20, 2360–2369 CrossRef.
- M. Forsyth, S. Wong, K. Nairn, A. Best, P. Newman and D. MacFarlane, Solid State Ionics, 1999, 124, 213–219 CrossRef CAS.
- A. Kuhn, M. Kunze, P. Sreeraj, H.-D. Wiemhöfer, V. Thangadurai, M. Wilkening and P. Heitjans, Solid State Nucl. Magn. Reson., 2012, 42, 2–8 CrossRef CAS PubMed.
- J. T. Ash and P. J. Grandinetti, Magn. Reson. Chem., 2006, 44, 823–831 CrossRef CAS PubMed.
- F. Blanc, D. S. Middlemiss, Z. Gan and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 17662–17672 CrossRef CAS PubMed.
- D. Massiot, T. Vosegaard, N. Magneron, D. Trumeau, V. Montouillout, P. Berthet, T. Loiseau and B. Bujoli, Solid State Nucl. Magn. Reson., 1999, 15, 159–169 CrossRef CAS PubMed.
- R. Inada, S. Yasuda, M. Tojo, K. Tsuritani, T. Tojo and Y. Sakurai, Frontiers in Energy Research, 2016, 4, 28 CrossRef.
- M. Howard, O. Clemens, E. Kendrick, K. Knight, D. Apperley, P. Anderson and P. Slater, Dalton Trans., 2012, 41, 12048–12053 RSC.
- J.-F. Wu, W. K. Pang, V. K. Peterson, L. Wei and X. Guo, ACS Appl. Mater. Interfaces, 2017, 9, 12461–12468 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- D. O. Shin, K. Oh, K. M. Kim, K.-Y. Park, B. Lee, Y.-G. Lee and K. Kang, Sci. Rep., 2015, 5, 18053 CrossRef CAS PubMed.
- D. Wang, G. Zhong, W. K. Pang, Z. Guo, Y. Li, M. J. McDonald, R. Fu, J.-X. Mi and Y. Yang, Chem. Mater., 2015, 27, 6650–6659 CrossRef CAS.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430 CrossRef CAS.
- D. Rettenwander, G. n. Redhammer, F. Preishuber-Pflügl, L. Cheng, L. Miara, R. Wagner, A. Welzl, E. Suard, M. M. Doeff and M. Wilkening, Chem. Mater., 2016, 28, 2384–2392 CrossRef CAS PubMed.
- Y.-T. Chen, A. Jena, W. K. Pang, V. K. Peterson, H.-S. Sheu, H. Chang and R.-S. Liu, J. Phys. Chem. C, 2017, 121, 15565–15573 CrossRef CAS.
- Y. Meesala, C.-Y. Chen, A. Jena, Y.-K. Liao, S.-F. Hu, H. Chang and R.-S. Liu, J. Phys. Chem. C, 2018, 122, 14383–14389 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Particle size distribution, microstructures, Rietveld refinement parameters, refined XRD spectra and impedance plots. See DOI: 10.1039/c9ta00417c |
| This journal is © The Royal Society of Chemistry 2019 |