Controlling the stereospecific bonding motif of Au–thiolate links

Abstract

Over the last decades, organosulfur compounds at the interface of noble metals have proved to be extremely versatile systems for both fundamental and applied research. However, the anchoring of thiols to gold remained an object of controversy for a long time. The RS–Au–SR linkage, in particular, is a robust bonding configuration that displays interesting properties. It is generated spontaneously at room temperature and can be used for the production of extended molecular nanostructures. In this work we explore the behavior of 1,4-bis(4-mercaptophenyl)benzene (BMB) on the Au(111) surface, which results in the formation of 2D crystalline metal–organic assemblies stabilized by this type of Au–thiolate bonds. We show how to control the thiolate's stereospecific bonding motif and thereby choose whether to form ordered arrays of Au₃BMB₃ units with embedded triangular nanopores or linearly stacked metal–organic chains. The former turn out to be thermodynamically favored structures and display confinement of the underneath Au(111) surface state. The electronic properties of single molecules as well as of the 2D crystalline self-assemblies have been characterized both on the metal–organic backbone and inside the associated pores.

---

Introduction

The production of monolayers of sulfur-containing organic compounds on noble metals was readily recognized long ago to be of great interest for the development of functional interfaces.^1–7 After decades of research, the interactions between organosulfur compounds and gold have in fact become textbook examples for strongly interacting metal–organic interfaces and the investigations on the interactions between organic sulfur, e.g. thiol (R-SH), and gold have shown a remarkable evolution with fruitful applications that span from biology^8–10 to drug- and medical-therapy^11–13 to materials sciences^14–18 or nanoplasmonics.^19–21

Such a broad range of applications rely on the strong Au–S connection that occurs on the metallic surface. While the hydrogenated R-SH group would only weakly interact through coordination-type bonds with gold via the S lone pair electrons,²² it is widely accepted that the Au–thiolate complex is formed after the dehydrogenation of the sulfhydryl group and the quenching of the resulting thiyl radical (RS˙) with gold.²³ Small²⁴ or flat lying arenethioles²⁵ have provided excellent examples to explore the direct anchoring point of the Au–S connections by its visualization with scanning probe microscopy (SPM) and lately the use of multi-functional aryl-thiols has additionally demonstrated the possibility of using RS–Au–SR type bonding schemes to create extended and complex molecular networks on surfaces.^26,27

In this work, combining low-temperature scanning tunneling microscopy and spectroscopy (LT-STM/STS), low energy electron diffraction (LEED), core level photoemission (XPS) and molecular modeling, we not only provide a detailed picture of the whole formation process of Au–thiolates, with the associated impact on the underlying Au(111), but further show the means to control the resulting stereospecific RS–Au–SR anchoring motifs. Using 1,4-bis(4-mercaptophenyl)benzene (BMB, Fig. 1a) we can thus choose whether to form regular arrays of triangular nanopores of Au₃BMB₃ with a well-defined size of ≈1.8 nm side length or wires of poly-[–S–Au–S–BMB–]–_n. The nanoporous Au₃BMB₃ turns out to be thermodynamically more stable on the gold surface than its linear counterpart and causes 2D quantum confinement of the Au(111) surface electrons, an interesting effect more commonly studied on the surfaces of Cu(111)^28,29 and Ag(111)^30,31 than on those of Au(111).³²

Fig. 1 (a) As-deposited, unreacted BMB molecules, 20 × 20 nm², V = 30 mV, I = 10 pA, T_depos = 120 K; (aⁱ) close-up 3.0 × 2.0 nm² of (a), and a molecular model of the fully hydrogenated BMB molecule; (aⁱⁱ) a close-up 3.0 × 2.0 nm² of (a), and a molecular model of the partially dehydrogenated BMB molecule; (aⁱⁱⁱ) a close-up 3.0 × 2.0 nm² of (a), and a molecular model of the fully dehydrogenated BMB molecule. (b) An aggregate of Au₃BMB₃ molecules obtained from (a) after annealing at RT (20 × 20 nm², V = 210 mV, I = 500 pA), with insets displaying close-up views of an open triangle and of a reactant molecule lacking a thiol/thiolate group on the right side; (bⁱ) a molecular model of an isolated Au₃BMB₃ complex and (bⁱⁱ) 3.0 × 3.0 nm² Laplace-filtered constant-height STM image with a CO-functionalized probe (U = 2 mV). (bⁱⁱⁱ) Laplace-filtered image of a probe particle model simulation of a Au₃BMB₃ complex. The reconstruction periodicity and the respective hcp and fcc sections are marked with arrows and labeled, respectively, for the as-deposited and thermalized sample, revealing the widening of the fcc sections and thereby the enhanced reconstruction periodicity for the latter.

Methods

Clean Au(111) surfaces were prepared in situ by repeated cycles of Ar+ sputtering (5 × 10⁻⁶ mbar, 800 eV) and annealing at 680 K. BMB molecules were purchased from Sigma Aldrich (nominal purity 95%) and used without further purification. The molecules were deposited, via sublimation, on the clean Au surface from the quartz crucible of a handmade Knudsen cell, heated at 380 K (440 K for the high deposition rate experiment). Scanning Tunneling Microscopy (STM) micrographs were performed with a commercial Scienta-Omicron low temperature system, operating in an ultrahigh vacuum (UHV) at 4.3 K. The STM tip was prepared ex situ by clipping a Pt/Ir wire (0.25 mm) and sharpened in situ by repeatedly indenting the tip a few nanometers (1 to 4 nm) into the Au surface while applying bias voltages from 2 V to 4 V between the tip and sample. In order to perform bond-resolving STM imaging, the tip apex was terminated with a CO molecule, directly picked up from the Au(111) surface, by positioning the sharp metal tip on top of it and applying a 500 ms bias pulse at −2 V (the inverted polarity of +2 V in turn controllably drops the CO back on to the surface). The imaging was then performed by measuring at constant height while applying a bias voltage within a 2.0 mV to 3.5 mV range to the tip. For spectroscopic measurements (both point spectra and conductance maps) the dI/dV signals were measured using a digital lock-in amplifier (Nanonis). STM images were analyzed by using WSxM software.³³ XPS analysis was performed with non-monochromatized Mg (K_α) radiation, collected by means of a SPECS Phoibos 100 hemispherical electron analyzer.

Large scale total energy Density Functional Theory (DFT) calculations of Au₃BMB₃ on the Au(111) surface were carried out by the local basis set Fireball code³⁴ using the general gradient approximation BLYP³⁵ and vdW-D3.³⁶ The Au₃BMB₃/Au(111) system was calculated with a rectangular (12 × 12) slab with two layers, consisting of 387 atoms in total. All atoms in the last layer were fixed. We used an optimized local basis set³⁷ H (R_C (s) = 5.42 a.u.), C (R_C (s) = 5.95 a.u.; R_C (s) = 5.95 a.u.), S (R_C (s) = 7.0 a.; R_C (s) = 7.0 a.u.) and Au (R_C (s) = 4.50 a.u.; R_C (s) = 5.60 a.u.; Au (R_C (d) = 4.30 a.u.). The precision of the Fireball calculations was carefully checked with the all-electron FHI-AIMS ab initio molecular simulations package³⁸ using the general gradient approximation PBE potential³⁹ and van der Waals interactions employing the Tkatchenko–Scheffler method with a light basis set.⁴⁰ Both methods provide very similar optimized structures of a free-standing Au₃BMB₃ model triangle. Also analysis of interaction energies of linear chains and triangles was performed using the FHI-AIMS code optimizing the 2D lattice vectors. In all calculations, the Brillouin zone was sampled with the Γ k-point only and the energy and force convergence were set to 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively.

The bond-resolved STM images of Au₃BMB₃ triangles acquired with a CO-tip at a low bias were simulated using the probe particle SPM model.⁴¹ The parameters of the probe particle were selected to mimic the CO-tip, using a monopole charge of −0.05e with a lateral stiffness of 0.24 N m⁻¹. The electrostatic force was included in the probe particle model calculations using the Hartree potential calculated by DFT. The dI/dV maps were calculated using the PP-STM code⁴² and using an s-wave probe and frontier orbitals of free-standing Au₃BMB₃ triangles as obtained from the Fireball code.

The electron-boundary-element-method (EBEM) was employed to extract the molecular potential landscape responsible for the confinement of the Shockley state within the Au₃BMB₃ nanoporous network. A triangular geometry is defined for each Au₃BMB₃ unit, and the potentials at the boundaries and inside nanopores were set to 0.6 eV and zero, respectively [see the ESI Fig. 3(a and b)†]. The reference binding energy and effective mass of the pristine Au(111) surface state were E_B = 0.485 eV and m_eff = 0.25m_e.⁴³ The energy and spatial dependence of the local density of states (LDOSs) were obtained for single and finite island of Au₃BMB₃ aggregates. A complementary electron-plane-wave-expansion (EPWE) method was also used to correlate the EBEM finite results with those obtained for the infinite nanoporous network. The details of EBEM and EPWE methods can be found in ref. 31, 44 and 45.

Results and discussion

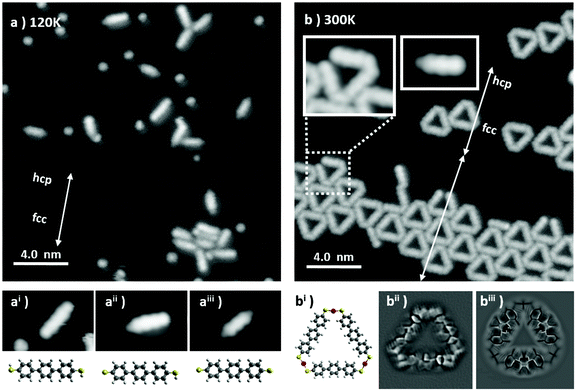
A representative STM image obtained after deposition of BMB on the Au(111) surface held at 120 K is shown in Fig. 1a. Scattered BMB molecules and disordered molecular aggregates are observed. A closer inspection of the molecules reveals a variability of their appearance, in particular at their extremities. While three central lobes remain a common molecular trait and are depictive of a quasi-flat lying geometry of a terphenil-core, the side lobes display two types of contrast, bright or dim (see the three different examples in Fig. 1aⁱ, aⁱⁱ and aⁱⁱⁱ). Such a behavior is associated with a partial dehydrogenation of the thiol groups (R–S–H) readily occurring during the condensation process. In line with a prior STM study on the thermal reactivity of benzenethiols on Au(111), the intact or undissociated thiol group is distinguished from the chemisorbed Au–thiolate (R–S–Au) by the characteristic bright and dim contrast, respectively, of the associated protrusions.²⁵ Thus, Fig. 1aⁱ, in which the terphenyl-core is sided by two bright lobes of homogeneous contrast, corresponds to the undissociated BMB molecule. Fig. 1aⁱⁱ shows a bis-mercapto moiety with bright and dim contrast on either side, in accordance with a partial molecular dehydrogenation. Finally, the molecule in Fig. 1aⁱⁱⁱ, sided by two dim protrusions, represents a fully dehydrogenated BMB. Noteworthily, isolated S atoms are also observed in Fig. 1a. The presence of these atoms will be further discussed below.

The scenario changes completely when the sample is allowed to thermalize at room temperature (RT) and cooled again for imaging. Triangular shaped molecular units appear on the surface as isolated objects or as clusters, both lying preferentially on the fcc regions of the Au(111) surface reconstruction. The clusters aggregate with a moderate lateral ordering and appear closely packed on widened fcc regions of the herringbone reconstruction (see Fig. 1b).

Within the triangular complexes the sides are discernible as terphenyl-units, while the bright connectors at the three vertexes fit with the S–Au–S bonding motif displayed in the molecular model of Fig. 1bⁱ. In order to corroborate the bonding structure of these units, constant height measurements with a CO-terminated STM tip were performed. Fig. 1bⁱⁱ shows a representative Laplace-filtered tunneling-current image of an isolated triangular unit. Intramolecular features are clearly identified and reveal that, within each terphenyl side, the central phenyl rings appear distorted. This results from their tilt angle with respect to the surface plane, imposed by the steric hindrance with the neighboring rings. Importantly, each S atom of the mercapto-residue connects one Au adatom and generates a cis-type S–Au–S coordination. Here the question arises whether the Au adatom is extracted from the surface or captured from freely diffusing Au adatoms at RT. However, the fact that the average fcp/hcp period of the Au(111) herringbone reconstruction is increased or otherwise modified in this sample implies a lower compression of the reconstructed surface layer, which in turn evidences the extraction of Au surface atoms for the thiolate–Au complex formation.

Further proof that the terphenyl-sides are linked through thiolate–Au complexes and not e.g., through disulfide bonds is obtained from theoretical calculations. Both options have been simulated and relaxed by DFT (Fig. S1†), revealing a formation energy of the Au₃BMB₃ complex several eV more favorable than that of the BMB₃ structure due to the presence of covalent Au–S bonds. Besides, the Au₃BMB₃ structure shows an excellent agreement with the experimental images. Proof of it is found in the simulations with the particle probe model,⁴¹ whose Laplace filtered image in Fig. 1bⁱⁱⁱ displays a notable similarity with the experimental data in Fig. 1bⁱⁱ. Particularly revealing is the presence of characteristic sharp edges at the presumable thiolate bonds of the Au₃BMB₃ structure due to the lateral relaxation of the CO-tip, which is completely missing in the case of the BMB₃ structure. From the total energy DFT simulations we can also deduce that the formation of strong covalent bonds between gold and sulfur atoms introduces a slight lateral distortion of the relatively soft BMB molecular units. These deformations are clearly visible in the high-resolution STM images acquired with the CO-tip.

It is also worth pointing out that, occasionally, incomplete triangles are found (Fig. 1b). A closer look at these metal organic complexes (see e.g. inset in Fig. 1b) evidences only three phenyl rings and the lack of a thiol/thiolate group at the open end, presumably associated with a thermal degradation occurring during the sublimation of the BMB powder. Similar findings can also be observed on single molecules like those in the second inset in Fig. 1b, clearly displaying three lobes associated with the three phenyl rings and a dim moiety on the left hand side attributed to a thiolate group, but a lack of any thiol or thiolate groups at the right hand side of the carbon backbone. Indeed, following the deposition at 120 K, it was found that a large amount of elemental sulfur adsorbs on the Au surface. In addition to single atoms or few-atom clusters, numerous 2D sulfur islands are also generated (Fig. S2a†). Combining STM and LEED on this sample (Fig. S2c and S2d†) it was found that S adsorbs in the well-known (√3 × √3) R30 phase,^46,47 not affecting the herringbone reconstruction of the underlying Au (Fig. S2b†). This phase is known to display limited stability, which may be the reason why we are able to observe it only at 4.3 K after its condensation on the Au surface held at 120 K. Finally, by letting the system thermalize to RT and cooling again to 4.3 K for imaging, a complete desorption of the atomic sulfur and a transformation of the scattered single molecules into the triangular metal–organic complexes are observed.

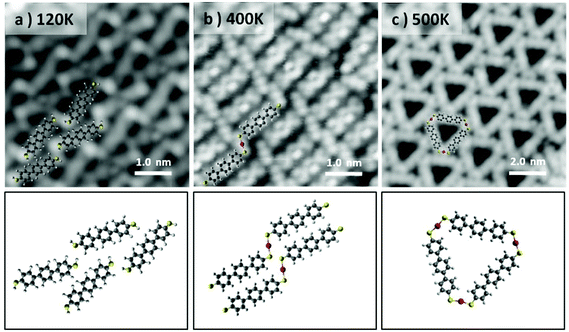
Considering the stereochemistry of the molecular product obtained in the sub-monolayer regime, and in particular focusing on the S–Au–S connectors of the molecular structure, it is remarkable that the cis-configuration of the system, which allows the formation of the triangle, occurs with such high specificity. We have explored the possibility to stabilize the trans-conformation of the S–Au–S connections in order to generate linear chains of poly-bis-mercaptobenzene. The control over the stabilization of specific bonding configuration, via surface coverage or temperature, has been extensively reported in the literature.⁴⁸ Examples include halogenated molecules^49–51 or thiols^26,27 on metallic surfaces. In particular the selective stabilization of chains or ring shaped structures has recently attracted much attention in the field of on-surface chemistry as a way to perform precise surface nanopatterning.

In our case, to obtain linear chains, the molecular deposition has been performed with a high molecular flux (by increasing the deposition rate to 300 monolayers per h), low temperature (the Au(111) surface being held at 120 K) and full monolayer (ML) coverage. As can be observed from the bright termini of the BMB molecules (Fig. 2a), under these conditions the –SH groups remain intact and the Au(111) reconstruction underneath the molecular layer is not affected (Fig. S3 and S4†). The molecule's bright ends attributed to thiol end groups disappear when the system is annealed to RT. Although in this temperature range the transformation of the overlayer into linear Au–thiolate chains does not occur quantitatively, the molecular arrangement loses its original periodicity and concurrently the surface morphology, i.e. the herringbone reconstruction, starts getting affected due to the cumulative extraction of surface atoms by the thiolates (Fig. S3†). When the system is brought to 400 K a full transformation into metal–organic chains is obtained and the Au(111) herringbone reconstruction is not observed anymore (Fig. S4†). The molecular layer appears as a series of long chains clearly bridged by a trans-conformation of the S–Au–S connectors (Fig. 2b). The chains extend over several tens of nanometers although their lateral order remains rather limited. Nonetheless this strategy reveals that the selective stabilization of the thiolate isomers is strictly dependent on the coverage and temperature processing parameters. The linear isomers, indeed, can be stabilized in a kinetic bottleneck, by increasing the initial density of the precursors. Finally, the metastability of the trans-organometallic chain is revealed when the system is annealed at 500 K. After the annealing, the system switches to the triangular nanopore array (Fig. 2c). The lower density of this phase readily denotes a substantial molecular desorption. Interestingly, the formation of small islands is observed concurrently with the phase change (Fig. S4†). We associate them with Au islands and rationalize their appearance as follows: the higher molecular density within the linear chains system induces the ablation of a higher number of Au atoms from the surface, compared with the triangular system. During the phase change, the decrease in molecular density, due to desorption, causes the excess Au atoms to aggregate as islands. These islands display an apparent height of 0.25 ± 0.06 nm, comparable to the height of a monatomic Au step (0.24 nm).

Fig. 2 Formation of the linear poly-[–S–Au–S–BMB–]_n at RT, in the high coverage regime and subsequent trans-to-cis isomerization into Au₃BMB₃ at higher temperatures on Au(111). (a) As-deposited (T_depos = 120 K), unreacted BMB molecules (5.0 × 5.0 nm², V = 50 mV, I = 80 pA). (b) Poly-[–S–Au–S–BMB–]_n obtained from (a) after thermalization at RT (5.0 × 5.0 nm², V = −100 mV, I = 300 pA). (c) Au₃BMB₃ obtained after annealing of (b) at 500 K (10.0 × 10.0 nm², V = −500 mV, I = 10 pA).

Annealing above 500 K the molecular overlayer undergoes degradation and desorbs almost entirely. These findings imply that the triangular complexes are more stable than their linear counterparts. To corroborate this hypothesis, we carried out total energy DFT simulations of linear and triangle structures and compared the formation energies of their 2D assemblies. First, we compared the formation energies of a single 1D chain and triangle (see Fig. S5†). Interestingly, the C–S–Au bond angles are similar, in both cases (and in the triangular complex calculated on Au(111)) ranging between 109.9° and 112.2°, but the individual chains turn out to be energetically slightly favorable by 18 meV per molecule. However, the situation changes when 2D assemblies are formed. After optimizing the lattice parameters for the free-standing assemblies, the binding energy per molecule turns out to be 230 meV larger for the triangle complexes. This indicates that it is the cumulative dispersion forces involved in the formation of the 2D molecular arrays which make the triangular aggregates substantially more stable than the chain-type aggregates.

Although XPS measurements employing Mg-K_α or Al-K_α radiation can be used for the study of sulfur–gold interactions,^52–54 most experiments do not provide data with sufficient signal to noise ratios to meticulously address tiny spectral features, especially if low coverages and small differences in chemical binding are concerned. In the low coverage experiment shown in Fig. 1, the extremely low density of the BMB molecule on the Au(111) surface would have made it virtually impossible to detect the molecular S 2p signal via Mg-K_α radiation. Therefore, at this stage, XPS measurements on the high coverage experiment are used as complementary pieces of evidence supporting that the adsorption of BMB molecules on Au(111) at 120 K occurs with intact thiol functionalities before the thermally induced collective generation of Au–thiolate complexes. The as-deposited system at 120 K shows the S 2p_3/2 peak at 163.3 eV (Fig. S3a†) characteristic of physisorbed or unbound thiol groups.^55–57 When the sample is annealed to RT an obvious chemical shift to lower binding energies is observed, namely 162.4 eV (Fig. S3b†). This value is in agreement with several studies with different precursors regarding the RT formation of the Au–thiolate.^27,57,58 It is worth pointing out that at 300 K the system is characterized mostly by BMB units with S atoms coordinating to surface atoms, but at the same time we observe the onset of the formation of linear BMB chains (with S atoms coordinated with extracted Au adatoms). By further increasing the annealing temperature to 450 K the chemisorbed sulfurs no longer coordinate to surface atoms but almost entirely to extracted adatoms. However, the virtually unchanged XPS spectrum reveals that once the covalent S–Au bond is formed, the coordination to Au surface atoms or to ablated Au adatoms results in S atoms with hardly distinguishable core levels.

In order to describe the 2D crystal lattice periodicity and to extract the adsorbate unit cell, LEED analysis was performed on the thermodynamically stable network of triangular complexes. The triangular units adsorb on the Au(111) by adopting two configurations, namely “up” and “down” as shown in Fig. 3a and both phases, related by a mirror plane, are observed to segregate during the formation of the closely packed molecular arrays (see unit cell representations and the boundary region highlighted with the yellow zig-zag line in Fig. 3a). Each “up” and “down” configuration includes three rotational domains, making up for the presence of a total of 6 epitaxially equivalent domains. The LEED pattern shows as a superposition of all domains, since they are probed simultaneously during the analysis. We have simulated the diffraction pattern for a superlattice characterized by the epitaxial matrix (8, 1/-1, 7), associated with a hexagonal unit cell with lattice vectors a = 2.17 nm and a 6.59° rotation with respect to the underlying substrate lattice, all in agreement with our STM images. In Fig. 3b and c the diffraction patterns have been simulated for each up and down configuration. Finally, when the two images are superimposed, an excellent fit with the experimental LEED pattern is obtained (Fig. 3d), confirming the commensurate epitaxy. The stabilization energy of the self-assembled long-range-ordered 2D nanostructures arises from the intermolecular interactions, as already evidenced in the calculations of Fig. S5,† while a favorable interplay of molecule–substrate interactions ensures the commensurability of this molecular layer with the underlying Au(111) surface.

Fig. 3 STM topography of a domain symmetry breaking of Au₃BMB₃, 10 × 10 nm², V = 260 mV, I = 400 pA. The yellow zig-zag line indicates the symmetry breaking region. Molecular models are superimposed on the STM topography and their mirror symmetry relation is indicated with a colored unit cell; (b) and (c) simulation of LEED patterns for the up and down domains, respectively; and (d) experimental LEED pattern at 51 eV with a superimposed LEED pattern simulation.

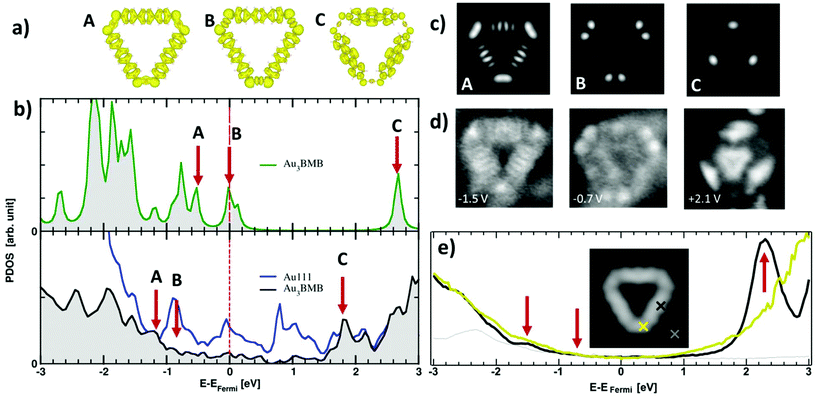
We have also probed the electronic properties of the Au₃BMB₃ complexes by STS and theoretical calculations, both on their metal–organic backbone and inside the pores. Regarding the former, Fig. 4b shows detailed density of states (DOS) calculations of fully optimized Au₃BMB₃ structures in a free-standing configuration (top) as well as adsorbed on Au(111) (bottom). The DOS of the free-standing complex displays well-defined orbitals, whose character is shown in Fig. 4a for the frontier states, involving unsaturated bonds in the coordination Au atoms that consequently appear around the Fermi level. Upon absorption on Au(111), the DOS appears broadened (Fig. 4b, lower panel) and the atomic orbitals of the complex Au atoms hybridize strongly with the surface atoms, causing an overall energy shift. However, the frontier orbitals are preserved and the same orbital character is now distinguished at lower energies (marked with arrows in Fig. 4b, bottom). The calculated DOS indeed shows a good agreement with our experimental data. On probing with STS on the terphenyl-units of the arms (black curve) we identify two clear resonances at −1.45 eV and +2.28 eV (Fig. 4e). Except for minor differences in energy due to size effects and the associated electron confinement,⁵⁹ the energies and local density of states distribution (Fig. 4d) very much resemble previous data on poly-paraphenylene on Au(111).⁶⁰ In contrast, spectra measured on the Au–thiolate connectors display a rather featureless signal, although evidencing a notable density of states within the previously mentioned terphenyl gap, including a shoulder around −0.7 eV (Fig. 4e). The corresponding conductance maps at −1.45 eV, −0.7 eV and +2.28 eV are shown in Fig. 4d. As mentioned above, while the maps at −1.45 eV and +2.28 eV resemble poly-paraphenylene orbitals,⁶⁰ the data at −0.7 eV reveal a spatially structured electronic density of states with the strongest weight around the Au–thiolate connection region. Notably, the three maps display a remarkable agreement with simulated dI/dV images (Fig. 4c) of the three frontier orbitals shown in Fig. 4a, providing a fully coherent picture of theory and experiment.

Fig. 4 (a) Simulated frontier orbitals A, B, and C of an isolated Au₃BMB₃ complex. (B) Calculated density of states of a free-standing (top) and adsorbed (bottom) Au₃BMB₃ complex, marked with arrows the energies associated with A, B and C orbitals. (c) Simulated dI/dV maps of A, B and C. (d) Experimental dI/dV maps measured at −1.5 eV, −0.7 eV and +2.1 eV. (e) Experimental dI/dV point spectra (V_rms = 15 mV at 731 Hz, closing feedback parameters V = 1 V, I = 200 pA) measured on the terphenyl arm (black), Au–thiolate region (yellow), and reference spectrum on the substrate (grey), as marked in the inset by the colored crosses superimposed to the STM topography of an isolated Au₃BMB₃ on Au(111) (3.5 × 3.5 nm², V = 50 mV, I = 100 pA).

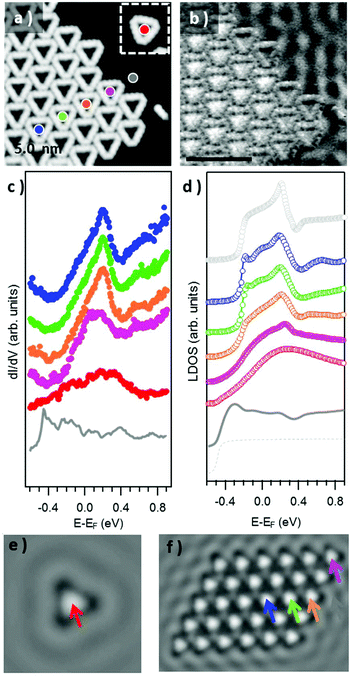
We now focus on the STS spectra recorded inside the pores. Interestingly, they reveal a substantially different signal from that detected on the bare Au(111) surface, in all cases evidencing the disappearance of the sharp Au(111) surface state onset at ≈−0.48 eV (grey spectrum in Fig. 5c), and the concomitant appearance of a broad signal at higher energies. Fig. 5c shows a comparative series of representative dI/dV spectra within isolated triangular units and differently positioned units within a 2D island. The signal within the isolated triangles is a broad band centered around +200 mV (red curve), which we assign, in line with previous reports on porous networks,^28–32,61 to electronic states associated with the confinement of the surface state electrons (n = 1 resonance). That is, the adsorbed Au₃BMB₃ complex acts as a scattering potential for the surface state electrons, which are thus confined into the nanopores and as a result upshifted in energy. However, there is also a certain transmission across such a scattering barrier, which partially accounts for the notable resonance width. Interestingly, when assembled into ordered arrays, these electronic states leaking through the confining barrier can couple with the states of the neighboring pores and end up forming well-defined bands.^28,32,61 This effect can be nicely observed by comparing the previous spectrum with the spectra on regular complex arrays. The triangular complex at the island edge is sided by other complexes at two of its sides and leaves only one side leaking electronic density of states toward the bare Au(111) surface. As a result, the pore's density of states readily appears to be much better defined than that for the isolated triangle, but still utterly different from that of the following complex toward the island interior, surrounded by neighbors on its three sides. For such “bulk” complexes a much sharper and clearly structured density of states appears in between about −200 meV and 230 meV (displaying a strong maximum at 205 meV). As mentioned above, the electronic states at discrete energies within the pores couple give rise to bonding and anti-bonding states. For extended arrays, these form a continuous band whose bandwidth (limited by bonding and antibonding states at the low and high energy sides, respectively) is proportional to the interaction between the pores. Although much weaker, as shown in Fig. 5c and d, it is also possible to observe the following quantum well state centered around 0.55 eV.

Fig. 5 (a) STM topography of an array of condensed triangular Au₃BMB₃ complexes (a single complex is displayed in the inset) obtained after annealing at 450 K (U = 210 mV, I = 400 pA) and (b) the corresponding conductance map recorded simultaneously (U_ac = 10 mV at 731 Hz). (c) STS point spectra recorded inside the pores of the single triangle and of the triangles forming a condensed island, at the locations marked with the corresponding colored dots in panel (a) (U_ac = 15 mV at 731 Hz). (d) Simulated LDOS spectra at the pore center of an isolated triangle (red), of triangles displaying one (orange), two (green), and three (blue, violet) neighbors within a finite molecular island, and for an infinite network (light grey). The LDOS close to an island and for the pristine Au(111) substrate are shown in dark solid and light dashed grey, respectively. Spatially resolved LDOS map evaluated at the resonance energy (E = 205 meV) for (e) an isolated triangle and (f) a molecular island.

In order to quantify the degree of inter-pore coupling, i.e. the strength of the confining potential, we performed EBEM simulations for an isolated triangle and for a finite molecular array (Fig. S6†). In the first approximation, we discard effective mass renormalization (m_eff = 0.25m_e), and use the band minimum of the Shockley surface state on pristine Au(111) as the energy reference (E_B = −0.485 eV). For a scattering potential of 0.6 eV, the onset of the surface state is upward shifted to −0.2 eV and the experimental resonance located at ≈0.2 eV is reproduced (Fig. 5(d)). The LDOS on the substrate close to the molecular island is only slightly modified (dashed grey) with an onset that nearly coincides with that of the pristine Au(111) surface state (solid grey). The evolution/narrowing of the resonance width by going from an isolated triangle (red) to a complex at an island edge displaying one (orange) or two (violet) neighbors and eventually to the interior of the network (green and blue) agrees remarkably well with the experiment. Indeed, even for such a small island, the LDOS at the network's interior largely resembles the calculated one for an infinite network as obtained from EPWE calculations (black curve). The spatial distributions of the n = 1 pore state at the resonance energy for both a single triangle and a finite molecular island are presented in 2D-LDOS maps in Fig. 5e and f, respectively. The good matching between the LDOS obtained from EBEM and EPWE calculations allows the estimation of an 80 meV zone-boundary gap (Fig. S6d†).

Conclusions

In conclusion, we report the controlled formation of stereospecific RS–Au–SR bonding motifs allowing for the selective stabilization of linear or porous Au–thiolate isomers. The investigation of the formation mechanism of covalent S–Au bonds starting from physisorbed thioles has revealed that the selective stabilization of the thiolate isomers is strictly dependent on the surface coverage and temperature. The linear isomers are thermodynamically less stable than their porous counterparts, but can be stabilized kinetically. Analysis of the electronic properties of the more stable porous arrays of Au₃BMB₃ has revealed that, besides the electronic states associated with the metal–organic backbone, the pores act as confinement barriers to the surface state electrons of the enclosed Au(111) patch. We can thus obtain 0-dimensional quantum dot states from single Au₃BMB₃ molecules, which can further couple into well-defined bands within extended ordered arrays of the Au–thiolate complexes. Interestingly, the finite size effects at the array's edges are unambiguously observed.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The project leading to this publication has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No 635919) and from the Spanish Ministry of Economy, Industry and Competitiveness (MINECO, Grant No. MAT2016-78293-C6-1-R). P. J. and A. C. acknowledge the support from Praemium Academie of the Academy of Science of the Czech Republic, MEYS LM2015087 and GACR 18-09914S and Operational Programme Research, Development and Education financed by the European Structural and Investment Funds and the Czech Ministry of Education, Youth and Sports (Project No. CZ.02.1.01/0.0/0.0/16_019/0000754). ZMA acknowledges Prof. Javier Garcia de Abajo for providing the EBEM-EPWE package.

References

1. R. G. Nuzzo and D. L. Allara, J. Am. Chem. Soc., 1983, 105, 4481–4483.
2. R. G. Nuzzo, B. R. Zegarski and L. H. Dubois, J. Am. Chem. Soc., 1987, 109, 733–740.
3. M. W. J. Beulen, B.-H. Huisman, P. A. van der Heijden, F. C. J. M. van Veggel, M. G. Simons, E. M. E. F. Biemond, P. J. de Lange and D. N. Reinhoudt, Langmuir, 1996, 12, 6170–6172.
4. Z. P. Yang, I. Engquist, J.-M. Kauffmann and B. Liedberg, Langmuir, 1996, 12, 1704–1707.
5. A. S. Dakkouri, D. M. Kolb, R. Edelstein-Shima and D. Mandler, Langmuir, 1996, 12, 2849–2852.
6. G. E. Poirier, Chem. Rev., 1997, 97, 1117–1128.
7. R. W. Carpick and M. Salmeron, Chem. Rev., 1997, 97, 1163–1194.
8. M. Azubel and R. D. Kornberg, Nano Lett., 2016, 16, 3348–3351.
9. F. Ghorbani, N. Attaran-Kakhki and A. Sazgarnia, Photodiagn. Photodyn. Ther., 2017, 17, 48–55.
10. C. J. Ackerson, P. D. Jadzinsky, J. Z. Sexton, D. A. Bushnell and R. D. Kornberg, Bioconjugate Chem., 2010, 21, 214–218.
11. M.-C. Bowman, T. E. Ballard, C. J. Ackerson, D. L. Feldheim, D. M. Margolis and C. Melander, J. Am. Chem. Soc., 2008, 130, 6896–6897.
12. D. A. Giljohann, D. S. Seferos, W. L. Daniel, M. D. Massich, P. C. Patel and C. A. Mirkin, Angew. Chem., Int. Ed., 2010, 49, 3280–3294.
13. Y. Bai, Y. Zhou, H. Liu, L. Fang, J. Liang and S. Xiao, ACS Appl. Nano Mater., 2018, 1, 969–976.
14. D. A. Boyd, Angew. Chem., Int. Ed., 2016, 55, 15486–15502.
15. C. Zeng, Y. Chen, C. Liu, K. Nobusada, N. L. Rosi and R. Jin, Sci. Adv., 2015, 1, e1500425.
16. J. R. Reimers, M. J. Ford, A. Halder, J. Ulstrup and N. S. Hush, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E1424–E1433.
17. T. Kamra, S. Chaudhary, C. Xu, L. Montelius, J. Schnadt and L. Ye, J. Colloid Interface Sci., 2016, 461, 1–8.
18. T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 1–15.
19. A. B. Serrano-Montes, D. Jimenez de Aberasturi, J. Langer, J. J. Giner-Casares, L. Scarabelli, A. Herrero and L. M. Liz-Marzán, Langmuir, 2015, 31, 9205–9213.
20. A. Lombardi, M. K. Schmidt, L. Weller, W. M. Deacon, F. Benz, B. de Nijs, J. Aizpurua and J. J. Baumberg, Phys. Rev. X, 2018, 8, 011016.
21. C. Goldmann, R. Lazzari, X. Paquez, C. Boissière, F. Ribot, C. Sanchez, C. Chanéac and D. Portehault, ACS Nano, 2015, 9, 7572–7582.
22. Y. Xue, X. Li, H. Li and W. Zhang, Nat. Commun., 2014, 5, 4348-1-9.
23. H. Häkkinen, Nat. Chem., 2012, 4, 443–455.
24. O. Voznyy, J. J. Dubowski, J. T. Yates and P. Maksymovych, J. Am. Chem. Soc., 2009, 131, 12989–12993.
25. P. Maksymovych and J. T. Yates, J. Am. Chem. Soc., 2008, 130, 7518–7519.
26. H. Walch, J. Dienstmaier, G. Eder, R. Gutzler, S. Schlögl, T. Sirtl, K. Das, M. Schmittel and M. Lackinger, J. Am. Chem. Soc., 2011, 133, 7909–7915.
27. A. Rastgoo-Lahrood, N. Martsinovich, M. Lischka, J. Eichhorn, P. Szabelski, D. Nieckarz, T. Strunskus, K. Das, M. Schmittel, W. M. Heckl and M. Lackinger, ACS Nano, 2016, 10, 10901–10911.
28. J. Lobo-Checa, M. Matena, K. Muller, J. H. Dil, F. Meier, L. H. Gade, T. A. Jung and M. Stohr, Science, 2009, 325, 300–303.
29. S. Wang, W. Wang, L. Z. Tan, X. G. Li, Z. Shi, G. Kuang, P. N. Liu, S. G. Louie and N. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245430.
30. F. Klappenberger, D. Kühne, W. Krenner, I. Silanes, A. Arnau, F. J. García de Abajo, S. Klyatskaya, M. Ruben and J. V. Barth, Nano Lett., 2009, 9, 3509–3514.
31. F. Klappenberger, D. Kühne, W. Krenner, I. Silanes, A. Arnau, F. J. García de Abajo, S. Klyatskaya, M. Ruben and J. V. Barth, Phys. Rev. Lett., 2011, 106, 026802.
32. K. Müller, M. Enache and M. Stöhr, J. Phys.: Condens. Matter, 2016, 28, 153003.
33. I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705.
34. J. P. Lewis, P. Jelínek, J. Ortega, A. A. Demkov, D. G. Trabada, B. Haycock, H. Wang, G. Adams, J. K. Tomfohr, E. Abad, H. Wang and D. A. Drabold, Phys. Status Solidi B, 2011, 248, 1989–2007.
35. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
36. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
37. M. A. Basanta, Y. J. Dappe, P. Jelínek and J. Ortega, Comput. Mater. Sci., 2007, 39, 759–766.
38. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396–1396.
40. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
41. P. Hapala, G. Kichin, C. Wagner, F. S. Tautz, R. Temirov and P. Jelínek, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085421.
42. O. Krejčí, P. Hapala, M. Ondráček and P. Jelínek, Phys. Rev. B, 2017, 95, 045407.
43. F. Reinert, G. Nicolay, S. Schmidt, D. Ehm and S. Hüfner, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 115415.
44. F. J. García de Abajo, J. Cordón, M. Corso, F. Schiller and J. E. Ortega, Nanoscale, 2010, 2, 717.
45. Z. M. A. El-Fattah, M. A. Kher-Elden, I. Piquero-Zulaica, F. J. G. de Abajo and J. E. Ortega, Phys. Rev. B, 2019, 99, 115443.
46. M. Yu, H. Ascolani, G. Zampieri, D. P. Woodruff, C. J. Satterley, R. G. Jones and V. R. Dhanak, J. Phys. Chem. C, 2007, 111, 10904–10914.
47. B. K. Min, A. R. Alemozafar, M. M. Biener, J. Biener and C. M. Friend, Top. Catal., 2005, 36, 77–90.
48. S. Clair and D. G. de Oteyza, Chem. Rev., 2019, 119, 4717–4776.
49. C. K. Krug, Q. Fan, F. Fillsack, J. Glowatzki, N. Trebel, L. J. Heuplick, T. Koehler and J. M. Gottfried, Chem. Commun., 2018, 54, 9741–9744.
50. Q. Fan, J. Dai, T. Wang, J. Kuttner, G. Hilt, J. M. Gottfried and J. Zhu, ACS Nano, 2016, 10, 3747–3754.
51. Q. Fan, T. Wang, J. Dai, J. Kuttner, G. Hilt, J. M. Gottfried and J. Zhu, ACS Nano, 2017, 11, 5070–5079.
52. Y. W. Yang and L. J. Fan, Langmuir, 2002, 18, 1157–1164.
53. T. Ishida, M. Hara, I. Kojima, S. Tsuneda, N. Nishida, H. Sasabe and W. Knoll, Langmuir, 1998, 14, 2092–2096.
54. D. A. Hutt, E. Cooper and G. J. Leggett, J. Phys. Chem. B, 1998, 102, 174–184.
55. D. G. Castner, K. Hinds and D. W. Grainger, Langmuir, 1996, 12, 5083–5086.
56. L. J. Cristina, G. Ruano, R. Salvarezza and J. Ferrón, J. Phys. Chem. C, 2017, 121, 27894–27904.
57. D. Nilsson, S. Watcharinyanon, M. Eng, L. Li, E. Moons, L. S. O. Johansson, M. Zharnikov, A. Shaporenko, B. Albinsson and J. Mårtensson, Langmuir, 2007, 23, 6170–6181.
58. J. Noh, E. Ito, K. Nakajima, J. Kim, H. Lee and M. Hara, J. Phys. Chem. B, 2002, 106, 7139–7141.
59. I. Piquero-Zulaica, A. Garcia-Lekue, L. Colazzo, C. K. Krug, M. S. G. Mohammed, Z. M. Abd El-Fattah, J. M. Gottfried, D. G. de Oteyza, J. E. Ortega and J. Lobo-Checa, ACS Nano, 2018, 12, 10537–10544.
60. N. Merino-Díez, A. Garcia-Lekue, E. Carbonell-Sanromà, J. Li, M. Corso, L. Colazzo, F. Sedona, D. Sánchez-Portal, J. I. Pascual and D. G. de Oteyza, ACS Nano, 2017, 11, 11661–11668.
61. I. Piquero-Zulaica, J. Lobo-Checa, A. Sadeghi, Z. M. A. El-Fattah, C. Mitsui, T. Okamoto, R. Pawlak, T. Meier, A. Arnau, J. E. Ortega, J. Takeya, S. Goedecker, E. Meyer and S. Kawai, Nat. Commun., 2017, 8, 787.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr04383g

‡ Present addresses: Center for Quantum Nanoscience, Institute for Basic Science (IBS), Seoul 03760, Republic of Korea and Department of Physics, Ewha Womans University, Seoul 03760, Republic of Korea.

---