Open Access Article
Open Access ArticleSurface-controlled dissolution rates: a case study of nanoceria in carboxylic acid solutions†
Eric A.
Grulke
 *a,
Matthew J.
Beck
*a,
Matthew J.
Beck
 *ab,
Robert A.
Yokel
*ab,
Robert A.
Yokel
 c,
Jason M.
Unrine
c,
Jason M.
Unrine
 d,
Uschi M.
Graham
d,
Uschi M.
Graham
 c and
Matthew L.
Hancock
c and
Matthew L.
Hancock
 a
a
aChemical & Materials Engineering, University of Kentucky, USA. E-mail: eric.grulke@uky.edu; m.beck@uky.edu
bCenter for Computational Sciences, University of Kentucky, USA
cPharmaceutical Sciences, University of Kentucky, USA
dPlant and Soil Sciences, University of Kentucky, USA
First published on 4th April 2019
Abstract
Nanoparticle dissolution in local milieu can affect their ecotoxicity and therapeutic applications. For example, carboxylic acid release from plant roots can solubilize nanoceria in the rhizosphere, affecting cerium uptake in plants. Nanoparticle dispersions were dialyzed against ten carboxylic acid solutions for up to 30 weeks; the membrane passed cerium-ligand complexes but not nanoceria. Dispersion and solution samples were analyzed for cerium by inductively coupled plasma mass spectrometry (ICP-MS). Particle size and shape distributions were measured by transmission electron microscopy (TEM). Nanoceria dissolved in all carboxylic acid solutions, leading to cascades of progressively smaller nanoparticles and producing soluble products. The dissolution rate was proportional to nanoparticle surface area. Values of the apparent dissolution rate coefficients varied with the ligand. Both nanoceria size and shape distributions were altered by the dissolution process. Density functional theory (DFT) estimates for some possible Ce(IV) products showed that their dissolution was thermodynamically favored. However, dissolution rate coefficients did not generally correlate with energy of formation values. The surface-controlled dissolution model provides a quantitative measure for nanoparticle dissolution rates: further studies of dissolution cascades should lead to improved understanding of mechanisms and processes at nanoparticle surfaces.
Environmental significanceDissolution of non-porous nanoparticles in aqueous media (ubiquitous in the environment) occurs at their surfaces. Dissolution is the first step in the biotransformation sequence of dissolution, transport, complexation, precipitation. The method described in this report requires nanoparticle size and shape distributions of the starting material as well as the total mass of nanoparticles added to the system. Model predictions can be validated against particle size and shape distributions for different experimental times. The method quantifies surface-controlled dissolution as an apparent rate coefficient, which can be used to interpret mechanisms. |
1. Introduction
Dissolution of naturally occurring and commercial solid metal oxide nanoparticles in the environment and in therapeutic applications can have important consequences for ecotoxicity and human health. Research on nanoparticle dissolution in aqueous systems has increased recently, even though the general problem has been known for some time.1 The silver nanoparticle dissolution rate is higher for smaller sizes.2 Silver loss appears to occur at the surface as there are few changes in the crystallite lattice parameters of the nanoparticle core. Silver nanoparticles may undergo shape changes3 and multistep oxidation of the partially oxidized silver atoms that form a surface monolayer.4 Its dissolution can be impacted by surface coatings,5,6 and has been modeled using first-7 and second-order kinetics.5 Dissolution has been observed for silica,2,8,9 copper,10 zinc-containing (ZnS,11 ZnO12–14), magnetite15 (Fe3O4), and ceria (nanoceria (CeO2)16,17) nanoparticles. Silica nanoparticle dissolution rates increase as particle size decrease,8 although Diedrich et al. reported that dissolution rates decrease with decreasing particle size due to changes in surface mechanisms.2 Zinc-containing nanoparticles have also been shown to have faster dissolution rates for smaller particle sizes.12,13 Nanoceria solubility has been measured as a function of pH in perchloric acid systems.18 Some researchers have recognized the need for dissolution rate data and dissolution rate constants as part of the risk assessment of nanomaterials.19 Nonetheless, there have been few attempts to develop rate models for dissolution processes under conditions linked to ecotoxicity or therapeutic applications.1.1 Ecotoxicity of nanoceria
It is well-known that plants secrete carboxylic acids from their root systems, which can complex metals in the rhizosphere, such as aluminum. Several researchers have shown that cerium can be taken into plant root systems. In the cucumber, only a portion of ceria nanoparticles formed Ce(III)–carboxyl complexes and showed no phytotoxicity.20 Nanoceria is known to dissolve and transform in acidic plant growth media.17 Citric acid coatings on nanoceria reduced its toxicity and cerium uptake in radish seedlings in water.21 Nanoceria can biotransform with the aid of organic acids after adsorption on cucumber root surfaces.22 Nanoceria dissolution at the radish root is enhanced by low molecular weight organic acids, e.g., succinic acid.23 Transformation of ceria nanoparticles in cucumbers appears to be influenced by phosphate.24 In general, there are not many studies on the effects of nanoceria size on ecotoxicity, which has been identified as a research gap.251.2 Therapeutic applications of nanoceria
Nanoceria surfaces are redox active and can cycle between Ce(III) and Ce(IV)26 as confirmed by DFT modelling of Fourier transform infrared (FTIR) absorption spectra of nanoceria particle surfaces.27 This auto-catalytic property leads to a number of commercial applications.28–30 In the life sciences, nanoceria might treat a number of therapeutic conditions, such as elevated oxidative stress and inflammation, cancer, radiation damage, bacterial infection, stroke-induced ischemia, and retinal degeneration.31 Nanoceria size is known to affect its hepatotoxicity. When HepG2 cells were exposed to nanoceria, the smaller, but not larger size, (8 vs. 58 nm nominal diameter) had metabolomic effects, increasing the concentrations of many lipids, especially fatty acids32 and altering pathways of mitochondrial function, apoptosis, and the tricarboxylic acid (Krebs) cycle.33 Smaller nanoceria cause aerobic glycolysis33 (the Warburg effect, important for oncology), for which high rates of glycolysis are followed by lactic acid fermentation even with abundant oxygen levels. Generally, nanoceria are only sparingly soluble in water, particularly at physiological pH (7.4).34 However, nanoceria can bioaccumulate in various organs (liver, spleen, bone marrow35). 30 nm nanoceria has been shown to biotransform36–38 to cerium phosphate (CePO4), possibly via a dissolution/recrystallization process. Cerium phosphate nanocrystals would have different reactivities with respect to oxidative stress and inflammation mechanisms, leading to loss of therapeutic benefits of nanoceria. Nanoceria has also been shown to have phosphatase activity39 and to react with organophosphates.40,411.3 Experimental design for measurement of long-term nanoceria dissolution rates
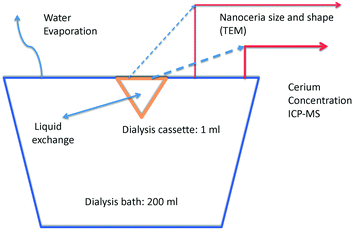
Solid particle dissolution is often controlled by mass transfer from the particle through the thin liquid film adjacent to its surface. For slowly dissolving solids, the rate-limiting mechanism can be breaking chemical interactions of surface atoms or molecules and forming ligand complexes that are soluble in the liquid phase.42,43 Nanoceria dissolution data were obtained for a series of aqueous carboxylic acid solutions at 37 °C and pH 4.5, conditions relevant to ecotoxicity and inside phagolysosomes. The carboxylic acids selected have structures related to citric acid, which is known to interact with nanoceria surfaces.44–47 Solubilized cerium was measured as a function of time. Dissolution rate coefficients, estimated using a surface-controlled process model, are expected to link to both nanoceria ecotoxicity and therapeutic applications. DFT was used to model the energy of formation for cerium-ligand complexes to assess whether the dissolution process is expected to proceed.One ml of nanoceria dispersion in iso-osmotic citric acid was loaded into a dialysis cassette (Slide-A-Lyzer®) that was placed in 200 ml of iso-osmotic solution containing a carboxylic acid or control ligand (Fig. 1). The nanoceria slowly dissolved into the dialysis cassette liquid, releasing salts that diffused across the cassette membrane, and into the bath. The 2 kDa molecular weight cut-off cassette membrane is known to prevent nanoceria particles ≳1 nm from passing, while permitting salts to diffuse.48,49 Samples from the bath and cassette were withdrawn periodically for Ce analysis by ICP-MS. Samples were also taken for nanoparticle size and shape determination by TEM. There can be water evaporation from the bath and solution flux between the cassette and the bath.
Dissolution experiments were carried out for 28 to 30 weeks. Bath Ce concentrations were measured each week by withdrawing 1 ml samples for ICP-MS analysis. Dialysis cassette Ce concentrations were determined by withdrawing 75 μL samples occasionally from the cassette. Additionally, 25 μL samples were occasionally withdrawn from the cassette for TEM imaging of the nanoparticles. Sampling removed Ce ions from the bath, nanoceria from the cassette, and Ce ions from the cassette, changing the amounts of nanoceria and Ce in the cassette, Ce in the bath, and Ce in the total system. The final cassette and bath volumes were measured. Evaporative losses from the bath changed its volume but removed only water. Cassette volume changes occurred due to a net flux of the bath solution either into or out of the cassette. Material balance equations are provided in ESI.†
The carboxylic acids studied were citric acid, analogs of citric acid with similar or related structures (glutaric, hydroxybutyric, lactic, malic, succinic, and tricarballylic acids), acetic acid, which is known to bind on nanoceria surfaces,50 and adipic and pimelic acids, which are known to bind solely to nanoceria's (100) crystallite face.51 Three control solutions were used: ammonium ion (a positively charged species), horseradish peroxidase/H2O2 (a free radical mediator reported to facilitate carbon nanotube dissolution52), and water (a substance that should have minimal effects). Carboxylic acid structures are shown in Fig. S1 (ESI†).
1.4 Surface-controlled dissolution rate
Early in the study, zero-, first-, and second-order kinetic models were applied to dissolution data. All of these models showed generally poor correspondence. There was good correspondence between data and prediction when a model for surface-controlled dissolution of solid particles43,53 was applied to the bath data. This model links the rate of solid dissolution from a spherical particle to its current surface area. It requires knowledge of the particle size and/or size distribution, the number of Ce atoms in a particle of a specific size, and the number of nanoceria particles in the cassette. It was assumed that Ce ion/carboxylic acid ligands do not reform nanoceria and that the chemical potential for dissolution does not change during the experiments. With these assumptions, the dissolution process is dependent only on the number of nanoceria particles in the cassette and their size. The apparent dissolution rate constant is estimated by nonlinear regression to minimize the differences between the measured Ce ion concentrations in the bath and the model predictions, using the discrete balances to adjust for nanoceria mass loss from the cassette, and Ce ion loss from the bath. Withdrawal of the dispersion changes the number of nanoparticles remaining in the cassette, but not their size. Furthermore, we assume that the dissolved Ce salts are sufficiently soluble in the aqueous phase so as to not create a thermodynamic barrier to CeO2 dissolution. The only identified report of a value reported its solubility to be 3.02 and 6.40 g L−1 in H2O at 20 and 90°, respectively,54 greater than the cerium concentration if all of the nanoceria in the dialysis cassette equally distributed throughout the dialysis/dissolution system (∼0.00250 g L−1).The loss rate of Ce ions from a nanoceria particle is:
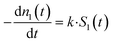 | (1) |
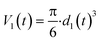 | (2) |
The nanoparticle surface area is:
| S1(t) = 4·π·r1(t)2 = π·d1(t)2 | (3) |
The number of Ce atoms in particles with initial size n1 is:
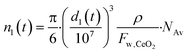 | (4) |
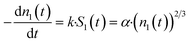 | (5) |
| α = k·π1/3·(6·Fw,ceria·1021/ρ·NAv)2/3 | (6) |
The factor α has units of (atoms)1/3 per h. The solution of eqn (6) is:
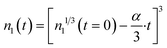 | (7) |
This equation gives negative values of n1(t) when the particle is fully dissolved. If desired, this can be corrected by applying the Heaviside step function.43Eqn (7) gives the number of Ce atoms remaining in a nanoparticle of size n1 at any time after the start of the experiment. For any two discrete sampling times, eqn (7) can be used to compute the difference, n(i + 1) − n(i), giving the net change in atoms/particle over that time interval. Details for the discrete material balances are shown in ESI.† Nanoceria size changes during growth and dissolution were imaged via HRTEM and analyzed using ImageJ and methods for particle size distributions by TEM.55–57
1.5 Two dissolution pathway elements: carboxylic acids binding to ceria surfaces and stability estimates for soluble Ce–carboxylic acid complexes
If nanoceria dissolves in aqueous carboxylic acids, then carboxylate ion binding to nanoparticle surfaces may be an important first step for the dissolution process. Carboxylic acids are known to adsorb on nanoceria surfaces in aqueous solutions. As examples, citric acid is used as the seed particle stabilizer for nanoceria synthesis method used in this work,45 and some unicarboxylic acid ligands have their maximum adsorption on ceria surfaces at pH 4.5.58 DFT shows that acetic acid binds in the bidentate chelating mode to oxidized ceria surfaces, but binds in both bidentate chelating and bridging modes to partially reduced ceria surfaces.50 Also, dissociated adsorption was more favorable on uncoordinated (high energy) corner sites.50 Some carboxylic acids preferentially adsorb to specific nanoceria crystal faces.50,59 On nanoceria surfaces composed mostly of Ce4+ species, acetate ions bind more strongly to the nanoparticles than water.60 The ‘outward-directed’ portion of adsorbed carboxylic acids might affect agglomeration of the nanoceria in aqueous dispersions.On the other end of the dissolution process pathway, it would be useful to know which stoichiometrically possible cerium–carboxylate complexes will be thermodynamically stable. Complexes of carboxylic acids with cerium and other lanthanides have been are reported in the patent and journal literature. Hawkins61 reported complexes of Ce(IV) coordinated with 2 anions of organic compounds, which could be used for clean combustion of hydrocarbon fuels and higher drying rates of paints. Kalsotra62 reported complexes of Ce(IV) with unicarboxylic acids. Other researchers have prepared Ce(III)–carboxylic acid complexes for a variety of applications.63–65 Azenha has reported that trivalent lanthanides can have bidentate coordinations with carboxylates, such as cerium(III) acetates.65 Therefore, it appears possible that cerium(IV)– or cerium(III)–carboxylic acid complexes can be formed. If Ce-bidentate carboxylic acid chelates are thermodynamically stable, polar groups on their non-complexing ‘tails’ might improve Ce-ligand solubilities in aqueous solutions.
2. Materials and experimental methods
2.1 Materials
The chemicals, their sources, purity, and CAS numbers were adipic acid, TCI, ≥99%, 124-04-9; ammonium nitrate, Fisher, ACS grade, 6484-52-2; citric acid monohydrate, Fisher, ACS grade, 5949-29-1; DL-3-hydroxybutyric acid sodium salt, Chem Impex Int'l Inc., 100.30%, 150-83-4 & 306-31-0; DL-malic acid, Alfa Aesar, 98%, 6915-15-7; glutaric acid, Acros organics, 99%,110-94-1; hydrogen peroxide 3% W/W, BDH chemicals, 7722-84-1; horseradish peroxide type II, Sigma, 150–250 U mg−1, 9003-99-0; lactic acid, TCI, ≥85%, 50-21-5; pimelic acid, Alfa Aesar, 98+%, 111-16-0; sodium acetate, VWR, ACS grade, 127-09-3; sodium azide, Sigma, 99.8%, 26628-22-8; sodium nitrate, BDH chemicals, ACS grade, 7631-99-4; succinic acid, TCI America, ≥99%,110-15-6; and tricarballylic acid, Alfa Aesar, 98%, 99-14-9. The electron microscopy grids were 200 mesh carbon support film on hexagonal copper square grids from Electron Microscopy Sciences. Pierce Biotechnology's 2 kD MWCO Slide-A-Lyzer™ dialysis cassettes were used. Trace metal grade concentrated nitric acid was from Fisher. ICP/DCP Ce ion standard solution was from Aldrich.2.2 Nanoceria synthesis and characterization
A polyhedral, polycrystalline citrate-coated nanoceria was synthesized using a hydrothermal approach.45 A 1.0 M CeCl3 solution with citric acid was reacted for 24 hours in excess 3.0 M ammonia water at 323 K. The temperature was increased to 353 K for 24 hours to crystallize the nanoceria. The solid product was dialyzed 5 times, 12 h each, against iso-osmotic citric acid at pH 7.4 to remove Ce and reactants not incorporated in the solid nanoceria product. Nanoceria primary and hydrodynamic particle sizes were determined by TEM using a 200 keV field emission analytical transmission electron microscope [JEOL JEM-2010F, Tokyo, Japan] and dynamic light scattering (DLS) using a 90Plus Nanoparticle Size Distribution Analyzer; Brookhaven Instruments Corp., Holtsville, NY. A sample of the citrate-coated nanoceria was dialyzed against ten volumes of water for 24 h with 3 changes of water, then dried. Nanoceria was stored at room temperature in the dark. The nanoceria dispersion was sterilized by autoclaving prior to introduction into the dialysis cassettes.2.3 Dissolution conditions
Nanoceria (containing ∼500 μg Ce) in 1 ml of iso-osmotic citric acid was introduced into dialysis cassettes immersed in 400 ml beakers containing 200 ml of aqueous carboxylic acid solutions plus 0.02% sodium azide as a bacteriostatic and fungistatic agent. This nanoceria concentration was used by Dahle, et al.16 The test solutions' pH and components are shown in Table S1.† Each condition, except water, was studied in duplicate, e.g., citric acid-1 and citric acid-2. The concentration of most ligands (110 mM) was based on the concentration of citric acid to produce an iso-osmotic solution, if it totally dissociated. Horseradish peroxidase (15 nmoles) was introduced into the cassette at pH 6.1, the pH of its maximal activity. H2O2 was added to the bath at the beginning of the experiment and each time the bathing medium was sampled. Determination of the osmotic strength of 110 mM citric acid revealed that it did not produce an iso-osmotic solution, presumably due to the lack of complete ionization (non-adherence to van't Hoff's law at this concentration). Sodium nitrate was added to all solutions (except water) to bring them to iso-osmotic strength. In a separate experiment, a Ce ligand (Ce nitrate) was allowed to diffuse across the membrane in order to compare its diffusion rate to the dissolution rates of nanoceria in the various carboxylic acid solutions. The Ce ligand should diffuse at least an order of magnitude faster than the dissolution rate for the bath and cassette solutions to be near equilibrium with each other. Ce ion concentration in the bath was measured using ICP-MS.2.4 Ce measurement
Samples containing nanoceria were digested with 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HNO3
1 HNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2 in Teflon vessels in a CEM MARS Xpress microwave digestion system (Matthews, NC, USA). Tb was added as an internal standard, and analyzed compared to external calibration standards. Ce was quantified by ICP-MS (Agilent 7500cx, Agilent Technologies, Inc., Santa Clara, CA).
H2O2 in Teflon vessels in a CEM MARS Xpress microwave digestion system (Matthews, NC, USA). Tb was added as an internal standard, and analyzed compared to external calibration standards. Ce was quantified by ICP-MS (Agilent 7500cx, Agilent Technologies, Inc., Santa Clara, CA).
2.5 Nanoceria size and shape distributions
Nanoceria size and shape distributions were obtained by acquiring TEM images of cassette dispersions,66 using automated methods for particle capture57 (ImageJ), comparing distribution statistics, fitting the parameters of reference distribution models,66 and evaluating bivariate correlations.56 These are programmed in R and have been implemented in a series of ShinyApp™ tools that are available on the web.67 Changes in size and shape distributions were quantified and compared to confirm nanoceria dissolution. Five particle size and shape descriptors were measured: area, equivalent circular diameter (ECD), Feret diameter (Feret; the maximum length of the particle), minimum Feret diameter (minFeret; the maximum width of the particle), and aspect ratio (aspectR = minFeret/Feret). The ECD is an appropriate choice to link with d1(t) in order to obtain n1(t) (eqn (4)) in the modeling exercises.Typically, 50 to 100 nanoceria particle images are analysed to produce repeatable size and shape distributions.
2.6 Computational methods
Density functional theory was used to estimate enthalpies of formation for possible Ce(IV) products to show whether their formation was thermodynamically favored. DFT methods have been used for a wide variety of energy calculations of lanthanides and carboxylic acids. Formation energies of possible Ce-ligand complexes were defined relative to the computed bulk energy per chemical unit of CeO2 and the energy of isolated acid molecules. The commercially available VASP planewave-pseudopotential code was used for all calculations.68 Pseudopotentials based on the Perdew–Burke–Ernzerhof (PBE) formalism were used for all atoms.69 Ce 4f5s5p5d6s and O 2p2s electrons were treated as valence electrons, in addition to the H 1s and C 2s2p electrons. The wavefunction was expanded in planewaves with an energy cutoff of 400 eV. These four conditions have previously been used for DFT computations of dissociated binding of acetic acid on nanoceria surfaces in water.50,70–72 Calculation cells of 2 nm on a side were used for all molecule and complex calculations; these cells were large enough to accommodate one CeO2 molecule plus carboxylic acid ligands, or a Ce–carboxylate ligand complex. A 1 × 1 × 1 k-point mesh centered at the Γ-point was used, yielding k-point densities of 2 k-points per nm, similar to those used previously for Ce-containing nanoparticles.73 The bulk CeO2 reference energy was calculated for a single CeO2 unit cell using a k-point density equivalent to that used in the molecule calculations (that is, 2 k-points per nm). Tests show that computed enthalpies are converged to within 0.1 eV with respect to k-point density. Initial atomic configurations were relaxed according to the calculated interatomic forces until binding energies were converged to 10−3 eV per atom or better.3. Results and discussion
3.1 Ce salt diffusivity through the cassette membrane
The rate of diffusion of Ce ligands through the membrane should be at least an order of magnitude faster than the dissolution rate of nanoceria so that the Ce ligand concentration in the bath is near its concentration in the cassette. Ce concentration in the bath was measured as a function of time (Mt) for comparison to the amount of Ce expected in the bath at equilibrium (Minf). See Fig. S2 (ESI†) to see the fits between datasets and the model for the diffusivity experiment. The half-time for the Ce nitrate diffusion process is 12.5 hours. The shortest dissolution half-life for nanoceria was 840 hours (seven weeks) in the presence of lactic acid. Using the half-life ratio, the membrane diffusion process is over 60 times faster than the nanoceria dissolution rate. The assumption that the Ce ion concentration in the bath is similar to that in the cassette appears sound.3.2 Dissolution effects on nanoceria size and shape distributions
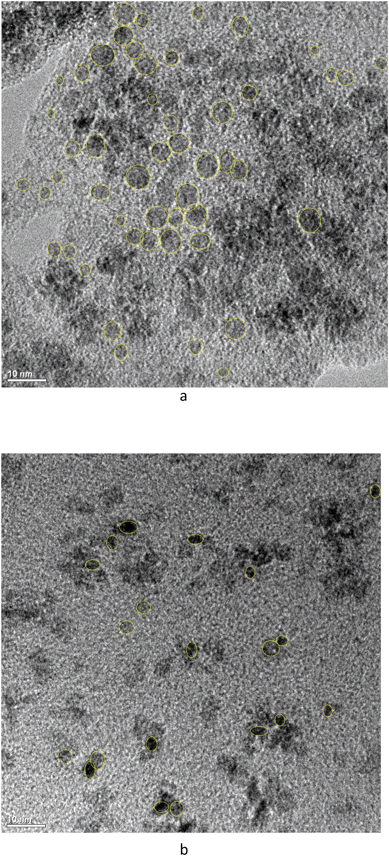
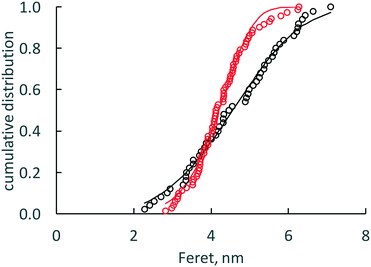
TEM images of cassette dispersions were used to evaluate dissolution effects on nanoceria size and shape distributions. Synthesis reproducibility with respect to nanoparticle size was good: Masui et al.45 reported an average nanoceria particle size of 3.9 nm (equivalent to a surface area of 211 m2 g−1) while this lab produced average nanoceria particle sizes of 4.24 nm (equivalent to a surface area of 196 m2 g−1). At this particle size, there is a mixture of Ce3+ and Ce4+ on the nanoceria surfaces.74Fig. 2a and b show nanoceria samples at t = 0 and t = 7 weeks, respectively. Nanoceria crystallites with clear edges were outlined using ellipses57 and analyzed using ImageJ software.66 The outlined particles were chosen such that the image was deemed to be a single crystallite with clear areal boundaries.57ANOVA analysis67 of each descriptor for the two samples of Fig. 2 show that the means of size and shape descriptor distributions are statistically different between the two datasets, except for the Feret diameter. Therefore, the average area and the average shape of nanoceria changes as it dissolves. Fig. 3 shows the two cumulative distributions with a Rosin–Rammler curve (often used for crystallization growth information) fitted to the data by nonlinear regression. The protocol is given in ESI.†
Table S2† also shows a comparison for the predicted diameter of an average nanoceria particle at seven weeks (shown in italics) for the two experimental trials with citric acid solutions. The measured change in the equivalent circular diameter was 12%, while those predicted using the model coefficients for each experiment were 11% and 13%. Thus, there is good correspondence between the nanoceria size predicted by the surface-controlled dissolution model and the ECD particle size as estimated from the particle area distribution. Additional TEM images of the nanoceria at several time points and for all carboxylic acids in the study can be found in Fig. 6 of Yokel et al.74
Bivariate plots are an alternative way to show differences in size and shape of nanoparticle populations.56Fig. 4 shows two contour plots of the aspect ratio as a function of nanoceria area for the citric 1 experiment, t = 0 and t = 7 weeks. The starting material (t = 0) appears to have two size clusters (area = 10 and 22 nm2) with the aspect ratio ranging from 0.65 to 0.98 for each of these. After seven weeks of dissolution, there are no particles with areas greater than 20 nm2, no apparent bimodal appearance to the area distribution, and an expanded aspect ratio range, 0.50 to 0.98. Bivariate analysis56 of the two datasets also confirms that they are different statistically. The p-values between the two plots were much less than 0.05. Therefore, particle area is being reduced and the remaining nanoceria have a lower average aspect ratio.
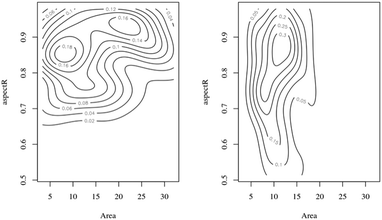 | ||
| Fig. 4 Aspect ratio/area (nm2) bivariate plots: starting sample (t = 0) = left side; seven week sample = right side. | ||
The current implementation of the model assumes spheroidal particles, but TEM images demonstrate asymmetric particles after dissolution. The change in aspect ratio appears to be driven by a reduction in nanoparticle width rather than nanoparticle length. As shown in Table S2,† the two Feret diameter distributions have mean values that are similar while the two minFeret diameter distributions have different mean values. Lu et al.75 reported the dissolution of nanoceria crystallines in radiolytic water, showing a transformation to lower oxygen coordinated phase, Ce2O3. Progressive, layer-by-layer, dissolution of nanoceria crystallites at one crystal face in strong acid resulted in a change in crystallite shape from a cube to a polyhedron (Fig. 2, frames g, h, i, and j of this reference). The particle size and shape distribution changes shown in Fig. 4 are consistent with a higher rate of dissolution at a specific crystallite face.
As exposure time increased, most nanoceria particle surfaces showed effects of rounding at crystallite edges and corners, likely due to the high energy sites at these locations. This is consistent with dissolution of nanoceria in vivo within both rat liver and spleen macrophages, previously reported by Graham et al.,36–38 and that caused significant particle rounding over time. Nanoceria surface structure near edges and corners is complex,27,73,76 which directly impacts the local redox potentials as well as the possible surface adsorption of water and carboxylic acid moieties into the distorted crystal lattice, accelerating the dissolution rate.
3.3 Analysis of model results
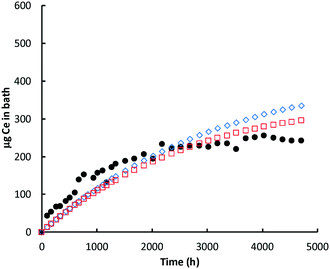 | ||
| Fig. 5 Ce (μg) in bath: glutaric acid. Black circles = ICP-MS data for bath; red open squares = model prediction Ce in the bath; blue open diamonds = cumulative amount of nanoceria dissolved. | ||
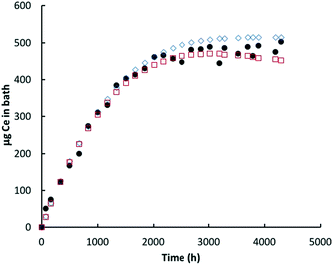 | ||
| Fig. 6 Ce (μg) in bath: lactic acid. Black circles = Ce in bath (ICP-MS data); red open squares = model prediction Ce in the bath; blue open diamonds = cumulative amount of nanoceria dissolved. | ||
In most experiments, there is an initial ‘burst’ of dissolution that is not captured by the model, which is based on the average nanoceria particle size. One likely cause of this difference is the assumption of an average particle size for the model. About 16% of the initial nanoceria introduced into the cassette has an ECD of 3 nm or less. Our estimates demonstrated that a model based on the empirical size distribution (binned into five fractions of 20% each and represented by their average size) provides a much better fit to the shapes of the bath Ce mass versus time plots. However, such a model would best be implemented when the minimum size of nanoceria in the bath solution is known. When this minimum stable size is reached, the unstable ceria nanoparticle should dissolve into the liquid phase. And, the minimum stable size might vary with each carboxylic acid, depending on its ability to stabilize small nanoceria particles. Such a model modification is expected to be done in future work.
Lactic acid solutions caused nearly complete dissolution of the nanoceria prior to the end of the 28 week sampling event. For both lactic acid experiments, the predicted Ce level in the bath decreased more rapidly with time than was predicted; notice that the red open squares in Fig. 6 go through a maximum and decrease with time. Sampling removed about 11% of the nanoceria from the cassette over the course of the lactic acid experiment. Because of the higher dissolution rate constant, the overall dissolution rate of nanoceria is less affected by the presence of the smallest size ‘bin’ and the model fits the initial data well. Nanoceria particles greater than the average have higher surface areas and greater loss rates of atoms per nanoparticle, per eqn (7). However, as their size becomes smaller, so does the surface area and the Ce atom loss rate, flattening the red square curve, and perhaps eliminating the maximum predicted by the model. This provides additional incentive to link the nanoceria surface area to particle size, shape, and crystallite facets.
| Key component | Dissolution rate constant, Ce atoms h−1 nm−2 |
|---|---|
| Controls | |
| Water, pH 6 | 0.00019 |
| Horseradish peroxidase | 0.00020 |
| Ammonium nitrate, pH 4.5 | 0.0030 |
| Carboxylic acids, pH 4.5 | |
| Glutaric acid | 0.0045 |
| Tricarballylic acid | 0.0046 |
| DL-3-Hydroxybutyric acid | 0.0050 |
| Pimelic acid | 0.0050 |
| Citric acid | 0.0057 |
| Acetic acid | 0.0057 |
| Adipic acid | 0.0062 |
| Succinic acid | 0.0072 |
| DL-Malic acid | 0.0075 |
| Lactic acid | 0.014 |
The ammonium system has a rate coefficient about 2/3rds of those of the slowest carboxylic acid system, showing that it affects nanoceria dissolution over 28 weeks. Since ammonia water plus citric acid was used in the synthesis of these nanoceria, it is not surprising that an ammonia solution at pH 4.5 in the absence of citric acid might permit the dissolution of nanoceria particles.
Carboxylic acid solutions accelerated dissolution and the ligand matters. The pKa's of the acids do not correlate with dissolution rate. All of the carboxylic acids caused measurable nanoceria dissolution over this time scale. Dissolution rates are partially controlled by the particle's surface area and occur layer-by-layer, as the particles are not porous. Since carboxylic acids are known to stabilize nanoceria during particle growth, it should not be surprising that they can influence nanoceria dissolution rates.
Vlasova and coworkers have shown that monocarboxylic acids, such as benzoic and cinnamic acids, are near their maximum surface complexation at pH 4.5, the level studied in this work. Carboxylic acids that complex with nanoceria surfaces are known to stabilize their dispersions. In related work, Yokel and co-workers74 (see Fig. 6 of this reference) have shown that lactic, malic, and succinic acids reduce agglomeration of nanoceria, while the rest of the carboxylic acids do not inhibit agglomeration. Surface complexation appears to be a dynamic equilibrium process that might slow rather than prevent dissolution.
Fig. 7 shows model predictions of the number of cerium atoms in the nanoceria particles of three carboxylic acids vs. time. Lactic acid had the highest dissolution rate coefficient and, by the end of 21 weeks, nanoceria was essentially depleted from the cassette. While the discrete balance shows that particles are still in the cassette, the computed number of Ce atoms per particle is quite low. At the end of 28 weeks, both the adipic acid and glutaric acid experiments still had nanoparticles with sizes observable by conventional TEM. The total Ce in the nanoceria is given by the product of the number of particles times the atoms in each particle.
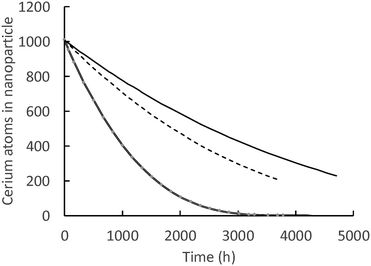 | ||
| Fig. 7 Number of Ce atoms in nanoparticles: solid line = glutaric acid, dashed line = adipic acid, double line = lactic acid. | ||
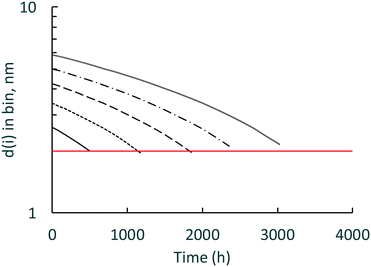
While the surface-controlled dissolution model can calculate down to one atom of Ce in a nanoceria particle, it is more likely that there is a lower size limit for a stable nanoceria particle in the various carboxylic acid solutions. Fig. 8 shows the calculated size of nanoceria (d(i)) for a lactic acid experiment. The nanoceria diameter decreases linearly with time, which is expected since the overall dissolution rate depends on the number of Ce atoms in the particle (n1(t)) to the 1/3rd power (eqn (7)).
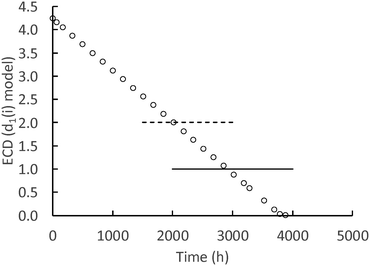 | ||
| Fig. 8 Calculated d1(i) (nm) for the lactic acid system. Open circles = predicted nanoceria diameter, dashed line = in vacuo stable particle,26 solid line = experimental fine particles by USAXS.77 | ||
Two reports suggest lower limits on the size of stable nanoceria particles. Reed and coworkers26 estimated the size of the smallest nanoceria particle as a truncated octahedron of ∼2 nm that is a surface-terminated cube of ∼2 × 2 × 2 nm, approximately Ce80O160 (no hydroxyls per an in vacuo assumption). This limit is illustrated in Fig. 8 by the dashed line crossing the d1(i) data. Assuming that a nanoceria particle less than this size would quickly ‘dissolve’, this would represent about 8% of the total Ce material for this dissolution experiment. A second potential limit for particle size was obtained by USAXS measurements for growing nanoceria particles by Allen et al.77 The measurements were done on a hydrothermal synthesis system based on Ce nitrate as the precursor and hexamethylene tetramine (HMT) as an agent for NH4 generation in situ. Their nanoceria product had particle sizes greater than 6 nm (octahedral or truncated octahedral morphologies, with (111) and (100) faces), but they also observed fine nanoparticles (termed ‘features’) in the order of ∼1 nm. It is possible that these represent ‘stable’, Ce/HMT complexes, but there are other explanations as well. This possible limiting size is shown as the solid line in Fig. 8 and would represent only 1.2% of the total Ce in the system.
Fig. 9 shows a dissolution cascade computed for lactic acid dissolution based on the measured initial particle size distribution binned into five elements of equal particle numbers, represented by an average size, and using a 2 nm value for the minimum size of a stable nanoparticle. After 7 weeks of dissolution (1176 hours), particles in the two lower particle sizes are predicted to dissolve. For the largest and smallest of these 5 bins, the nanoparticle surfaces areas differ by a factor of ∼6 so the large particles are dissolving at a much higher loss rate per particle. However, the smallest particles are much closer to the assumed minimal stable particle size and they disappear from the cassette first.
Our high resolution TEM images of a carbon support film that was passed through the bathing medium (citric acid = 110 mM, pH 4.5 after a 16 week dissolution period) detected a few isolated, subnano-scale particles associated with the carbon film (Fig. 10). These few crystallites were in the size range of ∼0.75–1 nm, which is in good agreement with Reed and coworker's findings that nanoceria below this size limit should be unstable.26 Ultrafine ‘features’ have also been reported by Allen and coworkers in nanoceria growth experiments.77 The ultrafine particles appear crystalline rather than amorphous and may represent the minimum stable size for CeO2 crystallites in the presence of citric acid. These ultra-fine particles are too small for EELS analysis to determine composition (CeO2 or Ce2O3). More work is needed to compare results for the other carboxylic acids. If ultrafine crystallites can associate with lacy carbon films (Fig. 10), then a similar uptake mechanism could also be present in vivo. Ultrafine crystallites could attach to a variety of surfaces, contributing to the long retention of nanoceria in mammalian organs35,78 that is not very well understood at this time.
3.4 Density functional theory: energy of formation of cerium ligand complexes
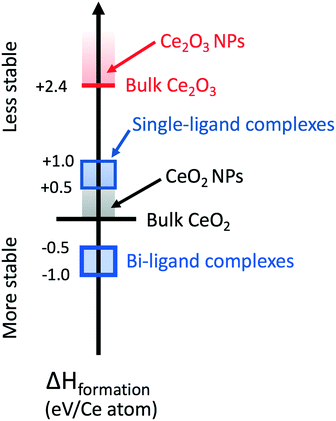
The dissolution experimental data place significant constraints on the possible atomistic mechanisms driving ligand-assisted nanoceria solubility. First, the dissolution of atoms from the surface must conserve the surface chemistry and charge as well as the conditions in the bath. Otherwise, the rate model of surface dissolution would require additional terms beyond simply the surface area of the solid particle in order to account for these changes over time. Secondly, experiments show that the ligands themselves must be directly involved in the dissolution mechanism (e.g. as a catalyst or as components in a chelated metal complex). Based on these constraints, we considered potential dissolution products from a thermodynamic perspective only, seeking to identify chelated metal complexes containing Ce(IV) that are more stable than the combination of precursor nanoceria (CeO2) and isolated acid molecules. These DFT calculations do not assume a particular charge state on Ce when computing the energy of either bulk CeO2 or Ce-containing molecules. Instead, the calculations allow redistribution of charge such that atoms in the computational system “relax” to their minimum energy state. Ce atoms coordinated to four O atoms have valence state Ce(IV), simply because stoichiometric CeO2 is most stable when each Ce atom transfers 1 electron to each of the 4 coordinated Os. Complexes containing Ce(III) could be formed, e.g., by adding an H atom to the double-bonded O, but doing so would imply that the CeO2 dissolution consumes H atoms, further implying that the pH of the solvent is time dependent—a situation not observed here. In addition, computing formation energies for single-ligand complexes with an additional H atom would require knowledge of the chemical potential of H in the system, which is beyond the scope of this paper.We considered the general dissolution of exactly one CeO2 formula unit to one and/or two ligand complexes of a subset of the acids examined experimentally. Computed formation energies are referenced to the energy of perfect, bulk CeO2. In all cases, complex cerium salts with one ligand have positive formation energies, meaning that they are not thermodynamically favored. Cerium salts with two ligand complexes have negative formation energies (shown as the blue square on the enthalpy of formation scale), indicating that the complexes are more stable than a reference state of bulk CeO2 and the isolated acid molecules. There is a thermodynamic driving force for dissolution and formation of a bi-ligand salt.
Fig. 11 shows DFT-computed enthalpy of formation scale for various precursors and products. Specific Ce(IV) di-carboxylic acid (“two-ligand”) complexes (blue block with thick border) are stable with respect to bulk CeO2 (black horizontal line). Single-ligand complexes have positive enthalpies of formation (blue block with thin border). In real systems, such as ceria nanoparticles, surface groups and defects will increase the energy of the ceria surface relative to that of the ideal bulk. Nanoceria particles (gray-colored band in Fig. 11) are less stable than perfect bulk ceria regardless of surface termination or defect concentration compared to the reference energy of bulk CeO2. If a particular combination of surface facets or defect arrangements rendered a ceria nanoparticle more stable than bulk ceria, then bulk ceria would spontaneously decompose into the nanoparticles.
Bulk Ce2O3 surfaces, shown as the red horizontal bar in Fig. 11, have a heat of formation of +2.4 eV/Ce atom. They are less stable with respect to bulk CeO2 surfaces. The surfaces of Ce2O3 nanoparticles will be less stable than their bulk counterpart and are indicated by the red-colored band. In O-rich conditions, surface Ce2O3 has a positive formation enthalpy and is unstable relative to CeO2. While the exact conditions of O availability in solution are complex, we expect that conditions are sufficiently O-rich for Ce2O3 to remain unstable with respect to CeO2. If this were not true, after long times we would expect to observe small ceria particles in the Ce2O3 structure. Variations in the relative abundance of Ce2O3 and CeO2 observed by EELS62 are only consistent with effects of decreasing particle size, and not with reduction of the nanoparticles in an O-poor environment.
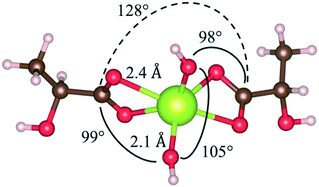
Fig. 12 shows the relaxed state for a double-lactic acid cerium complex, which has the most negative heat of formation as modelled. This complex is stoichiometrically equivalent to two acid molecules plus one CeO2 unit. The bond angles between the hydroxyl groups and the lactate groups are similar and the two lactate groups have a bond angle of 128°. The carboxylate ‘bonds’ should be considered an electron resonating between one oxygen and the other, that is, a bidentate bond. These calculations appear to be consistent with the results of Lu for bidentate binding of acetic acid to oxidized ceria surfaces50 and the results of Hawkins for Ce(IV) complexes with two ligands.61
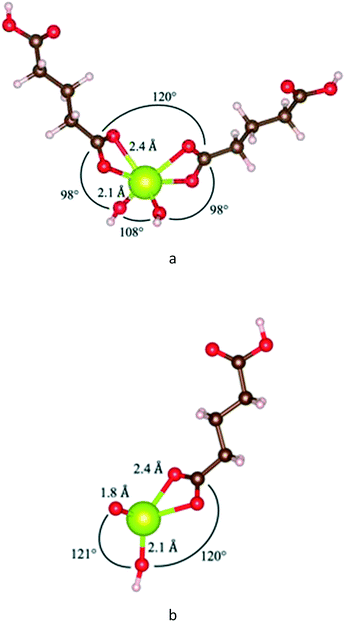
Fig. 13 shows relaxed states of double- and single-glutaric acid complexes with cerium. The single-glutaric acid complex is stoichiometrically equivalent to one acid molecule plus one CeO2 unit. These configurations yield Ce(IV) with a Ce![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, a hydroxyl, and coordinated with a carboxylic acid group, which has a positive enthalpy of formation and is not thermodynamically stable. Complexes containing Ce(III) could be formed, e.g., by adding an H atom to the double-bonded O but doing so would imply that CeO2 dissolution consumes H atoms, further implying that the pH of the solution is time dependent—a situation not observed here. In addition, computing formation energies for single-ligand complexes with an additional H atom would require knowledge of the chemical potential of H in the system, determination of which, for the present experimental conditions, is beyond the scope of this paper.
O bond, a hydroxyl, and coordinated with a carboxylic acid group, which has a positive enthalpy of formation and is not thermodynamically stable. Complexes containing Ce(III) could be formed, e.g., by adding an H atom to the double-bonded O but doing so would imply that CeO2 dissolution consumes H atoms, further implying that the pH of the solution is time dependent—a situation not observed here. In addition, computing formation energies for single-ligand complexes with an additional H atom would require knowledge of the chemical potential of H in the system, determination of which, for the present experimental conditions, is beyond the scope of this paper.
The relative instability of single-ligand Ce(IV) complexes does not rule out the possibility that such single-ligand Ce(IV) or Ce(III) complexes are formed (either as an intermediate state during dissolution or as a minority product), but rather that bi-ligand Ce(IV) complexes are preferred to deprotonated (and therefore Ce(IV)-containing) single-ligand complexes. In addition, previous experiments have examined various binding geometries of carboxyl groups to CeO2 surfaces and found that the bidentate chelating configuration is favoured over bridging and monodentate configurations. The present results are consistent with these findings, as the low-energy Ce–carboxyl configurations identified are bidentate chelating.
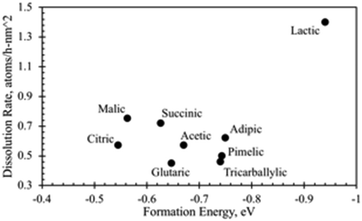
3.5 Comparison of heats of formation with dissolution rate coefficients
While the formation enthalpies of two-ligand complexes varies with the structure of the relevant acids, these variations do not fully explain differences in dissolution rates (Fig. 14). While the lactic acid complex does have the most negative formation energy (that is, the strongest thermodynamic driving force for complex formation, −0.94 eV per complex) and exhibits a high dissolution rate, the other acid complexes studied have formation energies and dissolution rates clustered with no obvious pattern. Succinic and glutaric acid complexes exhibit nearly identical formation energies, but significantly different dissolution rates, while the citric acid complex has a much less negative formation energy (that is, would be expected to be less thermodynamically stable) than adipic and pimelic acid complexes, but exhibits a similar dissolution rate. This implies that structural and conformational factors influence the dissolution rate mechanism in addition to thermodynamics.Yokel et al.74 provided descriptive interpretations on the differential effects of carboxylic acids on nanoceria dissolution, which are relevant to in vivo and environmental systems. EELS plots in this reference (Fig. 7) have been used to estimate quantitative changes in Ce3+/Ce4+ ratios of nanoceria surface over a 12 week period for citric acid solutions. EELS data were taken at both surface edges and the center (core) surface of nanoceria at each of three times (week 0, week 4, and week 12). Table 2 shows the diameters of the measured particles; the average particle diameter predicted by eqn (7); the estimated ratio of Ce3+/Ce4+ using the peak heights for the edge and core surfaces, and the fraction of ceria dissolved for each sample. It is well known that this ratio increases as particle size decreases. However, there are only modest changes in this ratio between edge and core surfaces, and between samples over the twelve week period. By week 12, over 50% of the nanoceria had dissolved with only moderate changes in edge and core Ce3+/Ce4+ ratios. The surface-controlled model still tracks the material balances of this dissolution experiment well, and the reference states selected for the heat of formation estimates (Fig. 11) are expected to be viable.
| Condition | Diameter, nm | Ce3+/Ce4+ ratio at surface | % Ce dissolved | ||
|---|---|---|---|---|---|
| Measured | Eqn (7) | Edge | Core | ||
| Week 0 | 4 | 4.24 | 1 | 1 | 0 |
| Week 4 | 3 | 3.89 | 1.1 | 1 | 22% |
| Week 12 | 2 | 3.21 | 1.3 | 1.2 | 52% |
4. Conclusions
The dialysis cassette experiment coupled with a surface-controlled dissolution model appears to be a sound method for estimating dissolution rate coefficients for nanoceria exposed to a variety of carboxylic acids. This model predicts that the number of atoms dissolved per unit time is directly proportional to nanoparticle surface areas; larger particles dissolve faster. The general approach could be extended to study the dissolution of other metal oxides and metals in various aqueous systems relevant to environmental and medical exposures. All of the carboxylic acid solutions dissolved nanoceria at pH 4.5, producing soluble products. Comparison of initial and seven week dissolution populations using TEM images verified that nanoceria size and shape varied due to dissolution. ANOVA and bivariate analysis of size and shape descriptor distributions confirmed that dissolution created statistically different nanoceria populations. The surface-controlled dissolution model fit the nanoceria dissolution data for all carboxylic acids and the experimental controls using the ECD descriptor to represent d1(t). Lactic acid solutions gave dissolution rate coefficients of 0.014 Ce atoms h−1 nm−2 with the coefficients of the other carboxylic acids ranging from 1/3 to 1/2 of this value.DFT calculations on possible soluble Ce–carboxylates showed that di-ligand complexes with the carboxylic acids of this study should be thermodynamically stable and would have bidentate bonding between cerium and ligand. Careful comparison of experimental and model results to nanoceria literature suggest that models of the dissolution process could be improved by: 1) better understanding of the lower size limit for stable nanoparticles in aqueous media, 2) implementing the model with empirical nanoparticle size distributions rather than an average diameter, 3) determining the dissolution rates of different crystallite surfaces in carboxylic acid solutions, which could lead to acentric shape distributions, 4) implementing particle shape in the dissolution model, and 5) confirming 3) with analyses of crystallite structure during the dissolution process. Estimates of the energy of formation for some possible dissolution products of CeO2 show that Ce(IV) complexed with two carboxylic acid ligands in bidentate structures would be thermodynamically possible. Since the dissolution rate coefficients do not seem to correlate with either pKa of the various carboxylic acids or estimates of the energy of formation for some possible dissolution products, it appears likely that nanoceria surface structures plus ligand adsorption mechanisms could contribute to the dissolution process.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Funding source
Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R01GM109195. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Shristi Shrestha provided ICP-MS Ce analysis results. The authors thank the Center for Computational Sciences for its support of the computational resources used for this project. The authors thank Thomas Chaney for his work on computing energy of formation for some possible cerium-ligand complexes.References
- A. A. Pohlman and J. G. McColl, Kinetics of metal dissolution from forest soils by soluble organic acids, J. Environ. Qual., 1986, 15, 86–92 CrossRef CAS.
- T. Diedrich, A. Dybowska, J. Schott, E. Valsami-Jones and E. H. Oelkers, The dissolution rates of SiO2 nanoparticles as a function of particle size, Environ. Sci. Technol., 2012, 46, 4909–4915 CrossRef CAS PubMed.
- R. D. Kent and P. J. Vikesland, Controlled Evaluation of Silver Nanoparticle Dissolution Using Atomic Force Microscopy, Environ. Sci. Technol., 2012, 46, 6977–6984 CrossRef CAS PubMed.
- B. Molleman and T. Hiemstra, Time, pH, and size dependency of silver nanoparticle dissolution: the road to equilibrium, Environ. Sci.: Nano, 2017, 4, 1314–1327 RSC.
- M. N. Martin, A. J. Allen, R. I. MacCuspie and V. A. Hackley, Dissolution, agglomerate morphology, and stability limits of protein-coated silver nanoparticles, Langmuir, 2014, 30, 11442–11452 CrossRef CAS PubMed.
- C. Liu, W. Leng and P. J. Vikesland, Controlled Evaluation of the Impacts of Surface Coatings on Silver Nanoparticle Dissolution Rates, Environ. Sci. Technol., 2018, 52, 2726–2734 CrossRef CAS PubMed.
- S.-F. Chen, H. Zhang and Q.-Y. Lin, Effect of different water conditions on dissolution of nanosilver, Water Sci. Technol., 2013, 68, 1745–1750 CrossRef CAS PubMed.
- J. Choi, N. S. Wang and V. Reipa, Photoassisted tuning of silicon nanocrystal photoluminescence, Langmuir, 2007, 23, 3388–3394 CrossRef CAS PubMed.
- J. D. Rimer, O. Trofymluk, A. Navrotsky, R. F. Lobo and D. G. Vlachos, Kinetic and Thermodynamic Studies of Silica Nanoparticle Dissolution, Chem. Mater., 2007, 19, 4189–4197 CrossRef CAS.
- S. Elzey and V. H. Grassian, Nanoparticle Dissolution from the Particle Perspective: Insights from Particle Sizing Measurements, Langmuir, 2010, 26, 12505–12508 CrossRef CAS PubMed.
- H. Zhang, B. Chen and J. F. Banfield, Particle size and pH effects on nanoparticle dissolution, J. Phys. Chem. C, 2010, 114, 14876–14884 CrossRef CAS.
- S.-W. Bian, I. A. Mudunkotuwa, T. Rupasinghe and V. H. Grassian, Aggregation and dissolution of 4 nm ZnO nanoparticles in aqueous environments: influence of pH, ionic strength, size, and adsorption of humic acid, Langmuir, 2011, 27, 6059–6068 CrossRef CAS PubMed.
- V. Kononenko, N. Repar, N. Marusic, B. Drasler, T. Romih, D. Drobne and S. Hocevar, Comparative in vitro genotoxicity study of ZnO nanoparticles, ZnO macroparticles and ZnCl2 to MDCK kidney cells: Size matters, Toxicol. In Vitro, 2017, 40, 256–263 CrossRef CAS PubMed.
- N. Odzak, D. Kistler and L. Sigg, Influence of daylight on the fate of silver and zinc oxide nanoparticles in natural aquatic environments, Environ. Pollut., 2017, 226, 1–11 CrossRef CAS PubMed.
- A. L. Swindle, A. S. Elwood-Madden, I. M. Cozzarelli and M. Benamara, Size-dependent reactivity of magnetite nanoparticles: a field-laboratory comparison, Environ. Sci. Technol., 2014, 48, 11413–11420 CrossRef CAS PubMed.
- J. T. Dahle, K. Livi and Y. Arai, Effects of pH and phosphate on CeO2 nanoparticle dissolution, Chemosphere, 2015, 119, 1365–1371 CrossRef CAS PubMed.
- F. Schwabe, R. Schulin, P. Rupper, A. Rotzetter, W. Stark and B. Nowack, Dissolution and transformation of cerium oxide nanoparticles in plant growth media, J. Nanopart. Res., 2014, 16, 2668–2678 CrossRef.
- T. V. Plakhova, A. Y. Romanchuk, S. N. Yakunin, T. Dumas, S. Demir, S. Wang, S. G. Minasian, D. K. Shuh, T. Tyliszczak, A. A. Shiryaev, A. V. Egorov, V. K. Ivanov and S. N. Kalmykov, Solubility of nanocrystalline cerium dioxide: Experimental data and thermodynamic modeling, J. Phys. Chem. C, 2016, 120, 22615–22626 CrossRef CAS.
- W. Utembe, K. Potgieter, A. B. Stefaniak and M. Gulumian, Dissolution and biodurability: important parameters needed for risk assessment of nanomaterials, Part. Fibre Toxicol., 2015, 12, 1–12 CrossRef CAS PubMed.
- Y. Ma, P. Zhang, Z. Zhang, X. He, Y. Li, J. Zhang, L. Zheng, S. Chu, K. Yang, Y. Zhao and Z. Chai, Origin of the different phytotoxicity and biotransformation of cerium and lanthanum oxide nanoparticles in cucumber, Nanotoxicology, 2015, 9, 262–270 CrossRef CAS PubMed.
- J. Trujillo-Reyes, A. R. Vilchis-Nestor, S. Majumdar, J. R. Peralta-Videa and J. L. Gardea-Torresdey, Citric acid modifies surface properties of commercial CeO2 nanoparticles reducing their toxicity and cerium uptake in radish (Raphanus sativus) seedlings, J. Hazard. Mater., 2013, 263, 677–684 CrossRef CAS PubMed.
- P. Zhang, Y. Ma, Z. Zhang, X. He, J. Zhang, Z. Guo, R. Tai, Y. Zhao and Z. Chai, Biotransformation of Ceria Nanoparticles in Cucumber Plants, ACS Nano, 2012, 6, 9943–9950 CrossRef CAS PubMed.
- W. Zhang, Y. Dan, H. Shi and X. Ma, Elucidating the mechanisms for plant uptake and in-planta speciation of cerium in radish (Raphanus sativus L.) treated with cerium oxide nanoparticles, J. Environ. Chem. Eng., 2017, 5, 572–577 CrossRef CAS.
- Y. Rui, P. Zhang, Y. Zhang, Y. Ma, X. He, X. Gui, Y. Li, J. Zhang, L. Zheng, S. Chu, Z. Guo, Z. Chai, Y. Zhao and Z. Zhang, Transformation of ceria nanoparticles in cucumber plants is influenced by phosphate, Environ. Pollut., 2015, 198, 8–14 CrossRef CAS PubMed.
- B. Collins, M. Auffan, A. C. Johnson, I. Kaur, A. A. Keller, A. Lazareva, J. R. Lead, X. Ma, R. C. Merrifield, C. Svendsen, J. C. White and J. M. Unrine, Environmental release, fate and ecotoxicological effects of manufactured ceria nanomaterials, Environ. Sci.: Nano, 2014, 1, 533–548 RSC.
- K. Reed, A. Cormack, A. Kulkarni, M. Mayton, D. Sayle, F. Klaessig and B. Stadler, Exploring the properties and application of nanoceria: is there still plenty of room at the bottom?, Environ. Sci.: Nano, 2014, 1, 390–405 RSC.
- X. Huang, B. Wang, E. A. Grulke and M. J. Beck, Toward tuning the surface functionalization of small ceria nanoparticles, J. Chem. Phys., 2014, 140, 074703 CrossRef PubMed.
- J. G. Dale, S. S. Cox, M. E. Vance and M. F. Hochella, Transformation of cerium oxide nanoparticles from a diesel fuel additive during combustion in a diesel engine, Environ. Sci. Technol., 2017, 51, 1973–1980 CrossRef CAS PubMed.
- Z. L. Wang and X. Feng, Polyhedral shapes of CeO2 nanoparticles, J. Phys. Chem. B, 2003, 107, 13563–13566 CrossRef CAS.
- S. D. Senanayake, D. Stacchiola and J. A. Rodriguez, Unique properties of ceria nanoparticles supported on metals: Novel inverse ceria/copper catalysts for CO oxidation and the water-gas shift reaction, Acc. Chem. Res., 2013, 46, 1702–1711 CrossRef CAS PubMed.
- C. Walkey, S. Das, S. Seal, J. Erlichman, K. Heckman, L. Ghibelli, E. Traversa, J. F. McGinnis and W. Self, Catalytic properties and biomedical applications of cerium oxide nanoparticles, Environ. Sci.: Nano, 2015, 2, 33–53 RSC.
- K. T. Kitchin, E. Grulke, B. L. Robinette and B. T. Castellon, Metabolomic effects in HepG2 cells exposed to four TiO2 and two CeO2 nanomaterials, Environ. Sci.: Nano, 2014, 1, 466–477 RSC.
- S.-F. Thai, K. A. Wallace, C. P. Jones, H. Ren, B. T. Castellon, J. Crooks, E. A. Grulke and K. T. Kitchin, Differential Genomic Effects on Signaling Pathways by Two Different CeO2 Nanoparticles in HepG2 Cells, J. Nanosci. Nanotechnol., 2015, 15, 9925–9937 CrossRef CAS PubMed.
- W.-S. Cho, R. Duffin, F. Thielbeer, M. Bradley, I. L. Megson, W. MacNee, C. A. Poland, C. L. Tran and K. Donaldson, Zeta potential and solubility to toxic ions as mechanisms of lung inflammation caused by metal/metal oxide nanoparticles, Toxicol. Sci., 2012, 126, 469–477 CrossRef CAS PubMed.
- R. A. Yokel, T. C. Au, R. MacPhail, S. S. Hardas, D. A. Butterfield, R. Sultana, M. Goodman, M. T. Tseng, M. Dan, H. Haghnazar, J. M. Unrine, U. M. Graham, P. Wu and E. A. Grulke, Distribution, Elimination, and Biopersistence to 90 Days of a Systemically Introduced 30 nm Ceria-Engineered Nanomaterial in Rats, Toxicol. Sci., 2012, 127, 256–268 CrossRef CAS PubMed.
- U. M. Graham, M. T. Tseng, J. B. Jasinski, R. A. Yokel, J. M. Unrine, B. H. Davis, A. K. Dozier, S. S. Hardas, R. Sultana, E. A. Grulke and D. A. Butterfield, In Vivo Processing of Ceria Nanoparticles inside Liver: Impact on Free-Radical Scavenging Activity and Oxidative Stress, ChemPlusChem, 2014, 79, 1083–1088 CrossRef CAS PubMed.
- U. M. Graham, G. Jacobs, R. A. Yokel, B. H. Davis, A. K. Dozier, M. E. Birch, M. T. Tseng, G. Oberdorster, A. Elder and L. DeLouise, in Modelling the Toxicity of Nanoparticles, ed. L. Tran, M. A. Banares and R. Rallo, Springer, Cham, Switzerland, 2017, pp. 71–100 Search PubMed.
- U. M. Graham, R. A. Yokel, A. K. Dozier, L. Drummy, K. Mahalingam, M. T. Tseng, M. E. Birch and J. Fernback, Analytical high-resolution electron microscopy reveals organ specific nanoceria bioprocessing, Toxicol. Pathol., 2018, 46, 47–61 CrossRef CAS PubMed.
- A. Dhall, A. Burns, J. Dowding, S. Das, S. Seal and W. Self, Characterizing the phosphatase mimetic activity of cerium oxide nanoparticles and distinguishing its active site from that for catalase mimetic activity using anionic inhibitors, Environ. Sci.: Nano, 2017, 4, 1742–1749 RSC.
- P. Janos, J. Henych, J. Pfeifer, N. Zemanova, V. Pilarova, D. Milde, T. Opletal, J. Tolasz, M. Maly and V. Stengl, Nanocrystalline cerium oxide prepared from a carbonate precursor and its ability to breakdown biologically relevant organophosphates, Environ. Sci.: Nano, 2017, 4, 1283–1293 RSC.
- P. Janos, I. Lovaszova, J. Pfeifer, J. Ederer, M. Dosek, T. Loucka, J. Henych, Z. Kolska, D. Milde and T. Opletal, Accelerated dephosphorylation of adenosine phosphates and related compounds in the presence of nanocrystalline cerium oxide, Environ. Sci.: Nano, 2016, 3, 847–856 RSC.
- G. Beauchamp, Dissolution kinetics of solids: application with spherical candy, J. Chem. Educ., 2001, 78, 523–524 CrossRef CAS.
- C. L. Forryan, O. V. Klymenko, C. M. Brennan and R. G. Compton, Reactions at the solid-liquid interface: surface-controlled dissolution of solid particles. The dissolution of potassium bicarbonate in dimethylformamide, J. Phys. Chem. B, 2005, 109, 2862–2872 CrossRef CAS PubMed.
- I. Allessandri, M. Ferroni and L. E. Depero, Plasmon-assisted, spatially resolved laser generation of transition metal oxides from liquid precursors, J. Phys. Chem. C, 2011, 115, 5174–5180 CrossRef.
- T. Masui, H. Hirai, N. Imanaka, G. Adachi, T. Sakata and H. Mori, Synthesis of cerium oxide nanoparticles by hydrothermal crystallization with citric acid, J. Mater. Sci. Lett., 2002, 21, 489–491 CrossRef CAS.
- M. F. P. da Silva, L. S. Soeira, K. R. P. Daghastianli, T. S. Marins, I. M. Cuccovia, R. S. Freire and P. C. Isolani, CeO2-catalyzed ozonation of phenol, J. Therm. Anal. Calorim., 2010, 102, 907–913 CrossRef.
- Y. Zhang, Y. Lin, C. Jing and Y. Qin, Formation and thermal decomposition of cerium-organic precursor for nanocrystalline cerium oxide powder synthesis, J. Dispersion Sci. Technol., 2007, 28, 1053–1058 CrossRef CAS.
- E. White, Technical Applications Scientist III, North American Protein Biology, Life Science Solutions, Personal communication to R. Yokel, 2018.
- S.-H. Yoon, Classifications of membranes according to pore size, http://onlinembr.info/membrane-process/classification-of-membranes-according-to-pore-size/, (accessed 17 July 2018) Search PubMed.
- Z. Lu, A. Karakoti, L. Velarde, W. Wang, P. Yang, S. Thevuthasan and H.-f. Wang, Dissociative Binding of Carboxylic Acid Ligand on Nanoceria Surface in Aqueous Solution: A Joint In Situ Spectroscopic Characterization and First-Principles Study, J. Phys. Chem. C, 2013, 117, 24329–24338 CrossRef CAS.
- E. Grulke, K. Reed, M. Beck, X. Huang, A. Cormack and S. Seal, Nanoceria: factors affecting its pro- and anti-oxidant properties, Environ. Sci.: Nano, 2014, 1, 429–444 RSC.
- B. L. Allen, P. D. Kichambare, P. Gou, I. I. Vlasova, N. Konduru, V. E. Kagan and A. Star, Biodegradation of single-walled carbon nanotubes through enzymatic catalysis, Nano Lett., 2008, 8, 3899–3903 CrossRef CAS PubMed.
- C. L. Forryan, O. V. Klymenko, C. M. Brennan and R. G. Compton, Heterogeneous kinetics of the dissolution of an inorganic salt, potassium carbonate, in an organic solvent, dimethylformamide, J. Phys. Chem. B, 2005, 109, 8263–8269 CrossRef CAS PubMed.
- T. P. Ezerskaya and K. A. Cherches, Solubility of citrate complex acids of cerium-group lanthanoids in water, Izv. Vyssh. Uchebn. Zaved., Khim. Khim. Tekhnol., 1973, 16, 648 CAS.
- E. A. Grulke, S. B. Rice, J. Xiong, K. Yamamoto, T. H. Yoon, K. Thomson, M. Saffaripour, G. J. Smallwood, J. W. Lambert, A. J. Stromberg, R. Macy, N. J. Briot and D. Qian, Size and shape distributions of carbon black aggregates by transmission electron microscopy, Carbon, 2018, 130, 822–833 CrossRef CAS.
- E. A. Grulke, X. Wu, Y. Ji, E. Buhr, K. Yamamoto, N. W. Song, A. B. Stefaniak, D. Schwegler-Berry, W. W. Burchett, J. W. Lambert and A. J. Stromberg, Differentiating gold nanorod samples using particle size and shape distributions from transmission electron microscope images, Metrologia, 2018, 55, 254–267 CrossRef CAS.
- E. A. Grulke, K. Yamamoto, K. Kumagai, I. Hausler, W. Osterle, E. Ortel, V.-D. Hodoroaba, S. C. Brown, C. Chan, J. Zheng, K. Yamamoto, K. Yashiki, N. W. Song, Y. H. Kim, A. B. Stefaniak, D. Schwegler-Berry, V. A. Coleman, A. K. Jamting, J. Herrmann, T. Arakawa, W. W. Burchett, J. W. Lambert and A. J. Stromberg, Size and shape distributions of primary crystallites in titania aggregates, Adv. Powder Technol., 2017, 28, 1647–1659 CrossRef CAS PubMed.
- N. N. Vlasova, L. P. Golovkova and N. G. Stukalina, Adsorption of organic acids on a cerium dioxide surface, Colloid J., 2015, 77, 418–424 CrossRef CAS.
- M. Taguchi, S. Takami, T. Naka and T. Adschiri, Growth Mechanism and Surface Chemical Characteristics of Dicarboxylic Acid-Modified CeO2 Nanocrystals Produced in Supercritical Water: Tailor-Made Water-Soluble CeO2 Nanocrystals, Cryst. Growth Des., 2009, 9, 5297–5303 CrossRef CAS.
- A. S. Karakoti, P. Yang, W. Wang, V. Patel, A. Martinez, V. Shutthanandan, S. Seal and S. Thevuthasan, Investigation of ligand-nanoparticle interface: Cryogenic approach for preserving surface chemistry, J. Phys. Chem. C, 2018, 122, 3582–3590 CrossRef CAS.
- I. M. Hawkins and H. H. K. Mauermann, US5449387A, 1995.
- B. L. Kalsotra, S. K. Gupta and R. N. Kapoor, Cerium(IV) carboxylates, Transition Met. Chem., 1976, 1, 158–161 CAS.
- T. M. Suranyi and V. Canic, Study of propionate, phthalate, and benzoate complexes of cerium(III), Glas. Hem. Drus. Beograd, 1977, 42, 537–544 CAS.
- A. L. C. S. do Nasciment, J. A. Teixeira, W. D. G. Nunes, F. X. Caomps, O. Treu-Filho, F. J. Caires and M. Ionashiro, Thermal behavior, spectroscopic study, and evolved gas analysis (EGA) during pyrolysis of picolinic acid, sodium picolinate and its light trivalent lanthanide complexes in solid state, J. Anal. Appl. Pyrolysis, 2016, 119, 242–250 CrossRef.
- M. E. Azenha, H. D. Burrows, S. M. Fonseca, M. L. Ramos, J. Rovisco, J. S. de Melo, A. J. F. N. Sobral and K. Kogej, Luminescence from cerium(III) acetate complexes in aqueous solution: considerations on the nature of carboxylate binding to tri-lanthanides, New J. Chem., 2008, 32, 1531–1535 RSC.
- S. B. Rice, C. Chan, S. C. Brown, P. Eschbach, L. Han, D. S. Ensor, A. B. Stefaniak, J. Bonevich, A. E. Vladar, A. R. H. Walker, J. Zheng, C. Starnes, A. Stromberg, J. Ye and E. A. Grulke, Particle size distributions by transmission electron microscopy: An interlaboratory comparison case study, Metrologia, 2013, 50, 663–678 CrossRef PubMed.
- J. W. Lambert and A. Stromberg, Statistical tools for analyzing nanoparticle size and shape distributions: ANOVA, curve fitting, and bivariate analysis, https://shiny.as.uky.edu/anova-app/, https://shiny.as.uky.edu/curve-fitting-app/, https://shiny.as.uky.edu/bivariate-fitting-app/ Search PubMed.
- G. Kresse and J. Furthmuller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Nolan, S. Grigoleit, D. C. Sayle, S. C. Parker and G. W. Watson, Density function theory studies of the structure and electronic structure of pure and defective low index surfaces of ceria, Surf. Sci., 2005, 576, 217–229 CrossRef CAS.
- C. Loschen, A. Migani, S. T. Bromley, F. Illas and K. M. Neyman, Density functional studies of model cerium oxide nanoparticles, Phys. Chem. Chem. Phys., 2008, 10, 5730–5738 RSC.
- T. M. Inerbaev, S. Seal and A. E. Masunov, Density functional study of oxygen vacancy formation and spin density distribution in octahedral ceria nanoparticles, J. Mol. Model., 2010, 2010, 1617–1623 CrossRef PubMed.
- X. Huang and M. J. Beck, Surface structure of catalytically-active ceria nanoparticles, Comput. Mater. Sci., 2014, 91, 122–133 CrossRef CAS.
- R. A. Yokel, M. Hancock, E. A. Grulke, J. M. Unrine, A. K. Dozier and U. M. Graham, Carboxylic acids accelerate acidic environment-mediated nanoceria dissolution, Nanotoxicology, 2019 DOI:10.1080/17435390.2018.1553251.
- Y. Lu, J. Geng, K. Wang, W. Zhang, W. Ding, Z. Zhang, S. Xie, H. Dai, F.-R. Chen and M. Sui, Modifying Surface Chemistry of Metal Oxides for Boosting Dissolution Kinetics in Water by Liquid Cell Electron Microscopy, ACS Nano, 2017, 11, 8018–8025 CrossRef CAS PubMed.
- X. Huang and M. J. Beck, Determining the Oxidation State of Small, Hydroxylated Metal-Oxide Nanoparticles with Infrared Absorption Spectroscopy, Chem. Mater., 2015, 27, 2965–2972 CrossRef CAS.
- A. J. Allen, V. A. Hackley, P. R. Jemian, J. Ilavsky, J. M. Raitano and S.-W. Chan, In situ ultra-small-angle X-ray scattering study of the solution-mediated formation and growth of nanocrystalline ceria, J. Appl. Crystallogr., 2008, 41, 918–929 CrossRef CAS.
- K. L. Heckman, W. DeCoteau, A. Estevez, K. J. Reed, W. Costanzo, D. Sanford, J. C. Leiter, J. Clauss, K. Knapp, C. Gomez, P. Mullen, E. Rathbun, K. Prime, J. Marini, J. Patchefsky, A. S. Patchefsky, R. K. Hailstone and J. S. Erlichman, Custom cerium oxide nanoparticles protect against a free radical mediated autoimmune degenerative desease in the brain, ACS Nano, 2012, 7, 10582–10596 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9en00222g |
| This journal is © The Royal Society of Chemistry 2019 |