Open Access Article
Open Access ArticleTransient IR spectroscopy of optically centrifuged CO2 (R186–R282) and collision dynamics for the J = 244–282 states
Michael E.
Ritter
 ,
Simone A.
DeSouza
,
Simone A.
DeSouza
 ,
Hannah M.
Ogden
,
Hannah M.
Ogden
 ,
Tara J.
Michael
,
Tara J.
Michael
 and
Amy S.
Mullin
and
Amy S.
Mullin
 *
*
Department of Chemistry and Biochemistry, University of Maryland College Park, College Park, Maryland 20742, USA. E-mail: mullin@umd.edu
First published on 5th April 2024
Abstract
Collisions of optically centrifuged CO2 molecules with J = 244–282 (Erot = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–30
800–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1) are investigated with high-resolution transient IR absorption spectroscopy to reveal collisional and orientational phenomena of molecules with hyper-thermal rotational energies. The optical centrifuge is a non-resonant optical excitation technique that uses ultrafast, 800 nm chirped pulses to drive molecules to extreme rotational states through sequential Raman transitions. The extent of rotational excitation is controlled by tuning the optical bandwidth of the excitation pulses. Frequencies of 30 R-branch ν3 fundamental IR probe transitions are measured for the J = 186–282 states of CO2, expanding beyond previously reported IR transitions up to J = 128. The optically centrifuged molecules have oriented angular momentum and unidirectional rotation. Polarization-sensitive transient IR absorption of individual rotational states of optically centrifuged molecules and their collision products reveals information about collisional energy transfer, relaxation kinetics, and dynamics of rotation-to-translation energy transfer. The transient IR probe also measures the extent of polarization anisotropy. Rotational energy transfer for lower energy molecules is discussed in terms of statistical models and a comparison highlights the role of increasing energy gap with J and angular momentum of the optically centrifuged molecules.
300 cm−1) are investigated with high-resolution transient IR absorption spectroscopy to reveal collisional and orientational phenomena of molecules with hyper-thermal rotational energies. The optical centrifuge is a non-resonant optical excitation technique that uses ultrafast, 800 nm chirped pulses to drive molecules to extreme rotational states through sequential Raman transitions. The extent of rotational excitation is controlled by tuning the optical bandwidth of the excitation pulses. Frequencies of 30 R-branch ν3 fundamental IR probe transitions are measured for the J = 186–282 states of CO2, expanding beyond previously reported IR transitions up to J = 128. The optically centrifuged molecules have oriented angular momentum and unidirectional rotation. Polarization-sensitive transient IR absorption of individual rotational states of optically centrifuged molecules and their collision products reveals information about collisional energy transfer, relaxation kinetics, and dynamics of rotation-to-translation energy transfer. The transient IR probe also measures the extent of polarization anisotropy. Rotational energy transfer for lower energy molecules is discussed in terms of statistical models and a comparison highlights the role of increasing energy gap with J and angular momentum of the optically centrifuged molecules.
I. Introduction
Molecules in high energy rotational states are observed in plasmas, as products of photodissociation and collisional energy transfer, and in exoplanet atmospheres, yet much remains to be understood about their behavior and properties.1–8 Of particular interest here is the collisional energy transfer behavior of molecules with large amounts of rotational energy. Linear molecules have rotational energies that increase essentially as the square of the rotational quantum number J, leading to increasing energy gaps between states as a function of J2. The role of energy gaps in statistical models of energy transfer of low energy molecules is well established, but we are yet to understand how large rotational energy gaps affect collisional energy transfer.9High energy rotational states of molecules cannot be populated using traditional optical approaches because selection rules for absorption and Raman processes limit changes in the rotational angular momentum to small ΔJ values. Recent advances in optical control of molecular rotation have led to new methods for controlling alignment, orientation, energy and directionality of molecular rotors.10–50 These techniques include using a pair of orthogonally polarized pulses of light with a time delay, a sequence of pulse trains with varying pulse lengths, and a pair of oppositely chirped pulses. The first two techniques can control a component of molecular motion but are limited to relatively low-J states.10–15 The third technique is the optical centrifuge which can prepare molecules in extreme rotational states and has been used to investigate the properties and dynamics for a number of systems.16–50
In the work reported here, we use a tunable optical centrifuge to prepare rotationally excited CO2 molecules and investigate their collision dynamics using high-resolution transient IR absorption spectroscopy. The collision studies focus on CO2 with J = 244–282 and rotational energies of Erot = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–30
800–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1. To perform these studies, we first used high-resolution transient IR absorption spectroscopy to identify line-center frequencies of 30 R-branch transitions with J = 186–282 of the CO2ν3 fundamental absorption band and then used the IR transitions to investigate the collision dynamics of the optically centrifuged CO2 molecules.
300 cm−1. To perform these studies, we first used high-resolution transient IR absorption spectroscopy to identify line-center frequencies of 30 R-branch transitions with J = 186–282 of the CO2ν3 fundamental absorption band and then used the IR transitions to investigate the collision dynamics of the optically centrifuged CO2 molecules.
Previously, high-resolution IR transitions for CO2 have been reported up to J = 128 in the HITRAN database.51,52 Transitions up to J = 146 have also been observed in dispersed IR emission from a flame, but populating high-J states by thermal heating leads to spectral broadening and congestion, making identification of state-resolved transition frequencies difficult.1 The HITEMP database reports transitions up to J = 200 based on semi-empirical calculations.53 The Carbon Dioxide Spectral Database at 4000 K (CDSD4000) reports IR absorption transitions for CO2 at 4000 K based on effective Hamiltonian calculations that include 41 vibrational states and 300 rotational states.54 For the IR transitions reported here, we used a combination of a third-order expansion of the rigid rotor model and the CDSD4000 as a guide for identifying the CO2 transition frequencies.
Spectral lines of high rotational states of CO2 are used to study combustion processes, and the atmospheres of Venus and exoplanets.5–8,55–57 These studies have relied on calculated transition frequencies to identify the high-J CO2 states. The new high-J transition frequencies reported here will serve as benchmark for future spectral calculations and databases.54,58
Previously, we have investigated collisions of optically centrifuged CO2 by probing P-branch transitions for states with J < 104.18,20,21,23,24 In the first of these studies in 2011, single-pass IR detection was used to investigate the collision dynamics of centrifuged CO2 molecules with 62 ≤ J ≤ 88.18 With the single-pass IR detection, a polarization-sensitive study of the J = 76 state of CO2 showed that even after 1000 collisions, there was a preference for population to remain in the original plane of rotation.20 In 2015, a J-dependent survey of CO2 states 0 ≤ J ≤ 100 showed that collisions of centrifuged molecules preferentially involve a translationally cool subset of molecules from the low-J states.21 This study measured large translational energies for states with J = 36–100 that result from collisions with optically centrifuged molecules. In 2017 and 2018, increased signal intensities from a multi-pass detection setup enabled studies of CO2J = 76–100. The first study highlighted the anisotropic kinetic energy release from collisions and orientational anisotropy values and decay rates that increase as a function of J.23 The second study identified the importance of rotational adiabaticity in collisions of centrifuged CO2 with buffer gases.24
The work presented here builds on the previous studies of optically centrifuged CO2 by extending the range of J-states up to J = 282. For comparison, the rotational energy of the J = 100 state is near 3930 cm−1 with a downward energy gap of ΔE = 150 cm−1, while the energy of the J = 282 state is 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 with a comparable energy gap of ΔE = 415 cm−1. Our dynamics studies use polarization-sensitive transient IR absorption to characterize the inverted rotational distribution of the centrifuged molecules, their polarization anisotropies, the kinetics of the state-resolved collisional relaxation, and the magnitude of rotation-to-translation energy transfer by measuring Doppler-broadened line profiles.
300 cm−1 with a comparable energy gap of ΔE = 415 cm−1. Our dynamics studies use polarization-sensitive transient IR absorption to characterize the inverted rotational distribution of the centrifuged molecules, their polarization anisotropies, the kinetics of the state-resolved collisional relaxation, and the magnitude of rotation-to-translation energy transfer by measuring Doppler-broadened line profiles.
II. Methods
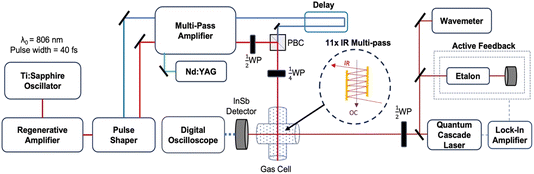
The experiments reported here were performed using an optical centrifuge laser system coupled to a high-resolution transient IR absorption spectrometer. The optical centrifuge instrument has been described in detail previously.1 The key features are presented here and a schematic diagram of the instrumentation is shown in Fig. 1.The optical centrifuge pulse uses an amplified ultrafast Ti:Sapphire laser system, which generates pulses of light centered at λ = 806 nm. The pulses are stretched in time from 40 fs to 100 ps and amplified in a regenerative amplifier. The temporal stretching induces a positive chirp. A pulse shaper spectrally splits the original pulses into pairs of pulses, one with λ > 806 nm denoted ω1 and the other with λ < 806 nm denoted ω2. A negative chirp is induced into ω2 such that the pair of pulses have an initial wavelength of λ0 = 806 nm and their optical frequency difference increases over the time of the pulse. The time-dependent frequency difference is the source of the sequential Raman transitions that lead to optically centrifuged molecules.
The oppositely chirped pulses are sent through a multi-pass amplifier, which is pumped by a 10 Hz Nd:YAG laser at λ = 532 nm, and are amplified to approximately 20 mJ per pulse each. Once amplified, the pair of pulses is recombined in space with a polarizing beam cube and in time with a delay stage. The recombined pairs of pulses are given opposite circular polarization with a ¼-wave plate, resulting in an optical field that angularly accelerates over the pulse duration. Gas-phase CO2 molecules that are trapped in the optical field through an induced-dipole interaction are angularly accelerated into extreme rotational states.
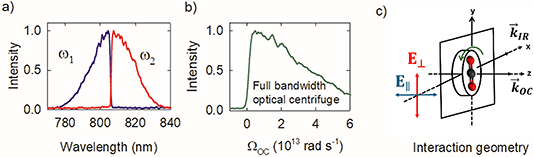
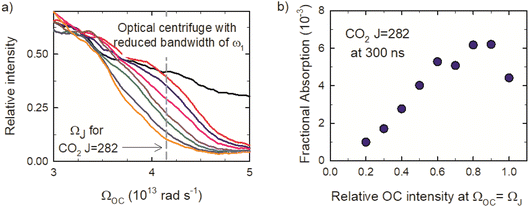
Fig. 2a shows the spectra of the pair of optical centrifuge pulses. The instantaneous angular frequency of the optical centrifuge trap is given by 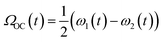 . Fig. 2b shows the intensity profile of the optical trap as a function of ΩOC, based on the intensity profile of ω1(t). The extent of rotational excitation in the optically centrifuged molecules is controlled by the spectral bandwidth of the optical centrifuge pulse. Optical centrifuge pulses with the full spectral bandwidth can populate CO2 rotational states near J = 360. Here we used reduced bandwidth pulses to preferentially populate rotational states with J ≤ 282. A tunable optical centrifuge trap is realized by removing a selected short wavelength portion of ω1 using a micrometer-controlled beam block.
. Fig. 2b shows the intensity profile of the optical trap as a function of ΩOC, based on the intensity profile of ω1(t). The extent of rotational excitation in the optically centrifuged molecules is controlled by the spectral bandwidth of the optical centrifuge pulse. Optical centrifuge pulses with the full spectral bandwidth can populate CO2 rotational states near J = 360. Here we used reduced bandwidth pulses to preferentially populate rotational states with J ≤ 282. A tunable optical centrifuge trap is realized by removing a selected short wavelength portion of ω1 using a micrometer-controlled beam block.
Fig. 2c shows the geometry of the interaction region for the centrifuged molecules. The optical centrifuge propagation vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) OC lies along the z-axis. Optically centrifuged molecules have unidirectional rotational motion within the x–y plane and orientated angular momenta along the z-axis. The IR probe beam is propagated along the x-axis with vector
OC lies along the z-axis. Optically centrifuged molecules have unidirectional rotational motion within the x–y plane and orientated angular momenta along the z-axis. The IR probe beam is propagated along the x-axis with vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) IR. A ½-wave plate controls the polarization of the IR probe, with ∥-polarization parallel to the z-axis (E∥) and ⊥-polarization (E⊥) perpendicular to the z-axis. The optical centrifuge beam is focused to a beam waist of ω0 = 52 μm. The IR beam is focused to a beam waist of 230 μm.
IR. A ½-wave plate controls the polarization of the IR probe, with ∥-polarization parallel to the z-axis (E∥) and ⊥-polarization (E⊥) perpendicular to the z-axis. The optical centrifuge beam is focused to a beam waist of ω0 = 52 μm. The IR beam is focused to a beam waist of 230 μm.
Individual rotational states of the centrifuged CO2 molecules are measured with high-resolution transient IR absorption spectroscopy from a λ = 4.5 μm quantum cascade laser (Daylight Solutions). The quantum cascade laser has a resolution of Δν ≤ 0.0002 cm−1. The IR output frequency is controlled via active feedback using a scanning Fabry–Perot etalon and a lock-in amplifier to tune over the CO2 transitions, while the wavelength is monitored on a wavemeter (Bristol Instruments) with a resolution of Δν ≤ 0.0004 cm−1. Inside the gas cell, the IR beam is overlapped with the optical centrifuge 11 times using an IR multipass (shown in the Fig. 1 inset) to increase signal-to-noise. Spectral features were measured with a 200 ns rise time InSb detector, while dynamics measurements used an InSb detector with a 70 ns rise time. The CO2 pressure used in this experiment is 2.95 Torr based on an equilibrium IR absorption measurement, corresponding to a gas kinetic collision time of ∼30 ns. Transient IR measurements at t = 120 ns represent CO2 molecules that have undergone approximately four gas-kinetic collisions.
III. Results and discussion
Here we describe the results of experiments that measure IR transition frequencies for CO2 (0001) ← (0000) R-branch transitions with J = 186–282 and use those transitions to investigate the collisional relaxation of optically centrifuged molecules with J = 244–282. We start with a description of line-center transition frequency measurements and compare the results to calculated transition frequencies from the CDSD4000 and predicted frequencies from an expansion of the rigid rotor model. We then use a reduced-bandwidth optical trap to preferentially populate CO2 rotational states with J ≤ 282.a. Transient IR spectroscopy of CO2 (0001) ← (0000) R-branch transitions for J = 186–282
New IR spectroscopy was needed to investigate the collision dynamics of optically centrifuged CO2. Here, we report 30 new IR R-branch ν3 fundamental transition frequencies for CO2 with 186 ≤ J ≤ 282. An earlier study on the spectroscopy of optically centrifuged N2O with 140 ≤ J ≤ 205 showed that a 3rd order polynomial expansion of the rigid rotor model is a reasonable approach for predicting IR transition frequencies of high-J states of N2O.26 We started with this approach as a guide to locating high-J CO2 transitions. The predicted high-J transitions are based on a 3rd order polynomial expansion in J(J + 1) of the (0000) and (0001) states of CO2 using energies for J ≤ 128 that is then extrapolated for high-J transitions.51,52 The expansion is shown in eqn (1).| Erot = BJ(J + 1) − D(J(J + 1))2 + H(J(J + 1))3 | (1) |
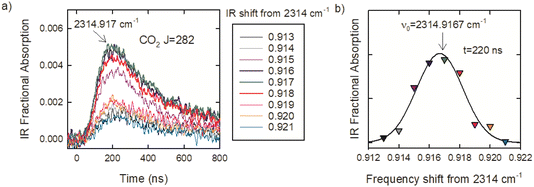
The optical centrifuge was used to populate CO2 rotational states with J values well above a 300 K distribution and transient IR absorption spectroscopy was used to identify the line center IR transition frequencies. CO2 in the ground vibrational state has only even J values because of nuclear spin statistics. Line-center transition frequencies (νobs) were determined by collecting transient absorption signals at discrete IR frequencies in steps of δν ≤ 0.003 cm−1. Fig. 3a shows the set of transient absorption signals used to identify the CO2 R282 transition near 2315 cm−1. Fig. 3b shows the fractional absorption intensities at t = 220 ns after the optical centrifuge pulse as a function of IR frequency. The data are fitted with a Gaussian function and the fit is used to identify the line-center transition frequency. For this transition, line-center frequency is νobs = 2314.9167 ± 0.003 cm−1. Such scans were collected for the 30 R-branch transitions reported here.
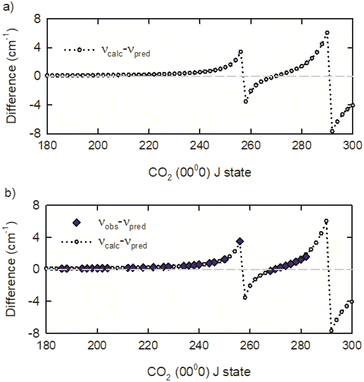
The observed IR R-branch transition frequencies for J ≤ 218 are within 0.01 cm−1 of the frequencies predicted by the 3rd order polynomial expansion in J(J + 1). The predicted values are denoted νpred. However, starting at R220 and going to R256, the observed transition frequencies deviate exponentially from the predicted values. The observed deviation for the R256 transition is 3.2 cm−1. An exponential fit of the spectral deviations predicted a frequency deviation for the R258 transition of 4.43 cm−1 but no transition was observed in this spectral region.
To identify the observed deviations for additional transitions, the predicted values from the 3rd order polynomial expansion were compared to transition frequencies from the effective Hamiltonian calculations CDSD4000.54 The transition frequency differences of νcalc and νpred are presented in Fig. 4a, showing that two spectral perturbations are present in the R-branch transitions near R258 and R292. Using the calculated frequencies as a guide, we observed the R268 to R282 transitions. The R258 to R266 transitions remain elusive, in part because of interference with strongly absorbing ambient CO2 lines. A comparison of the observed transition frequencies relative to the predicted values is shown in Fig. 4b. There is excellent agreement between the observed and calculated transition frequencies. Table 1 lists the transition frequencies measured in this study, along with calculated frequencies, deviations, and rotational energies Erot from the effective Hamiltonian calculations.
| J state | ν obs (±0.003 cm−1) | ν calc (cm−1) | Δ(νobs − νcalc) (cm−1) | E rot (cm−1) |
|---|---|---|---|---|
| a From Heff calculations by Tashkun and Perevalov in the CDSD4000.54 | ||||
| 186 | 2383.921 | 2383.914 | 0.008 | 13411.817 |
| 188 | 2383.070 | 2383.065 | 0.005 | 13697.486 |
| 194 | 2380.360 | 2380.365 | −0.005 | 14571.852 |
| 196 | 2379.421 | 2379.413 | 0.008 | 14869.078 |
| 198 | 2378.443 | 2378.435 | 0.008 | 15169.181 |
| 200 | 2377.441 | 2377.432 | 0.009 | 15472.156 |
| 202 | 2376.413 | 2376.402 | 0.011 | 15777.998 |
| 204 | 2375.359 | 2375.347 | 0.012 | 16086.702 |
| 212 | 2370.885 | 2370.87 | 0.015 | 17350.035 |
| 214 | 2369.704 | 2369.688 | 0.016 | 17672.972 |
| 218 | 2367.267 | 2367.247 | 0.020 | 18327.332 |
| 222 | 2364.730 | 2364.707 | 0.023 | 18992.972 |
| 226 | 2362.095 | 2362.071 | 0.024 | 19669.847 |
| 228 | 2360.743 | 2360.717 | 0.026 | 20012.485 |
| 234 | 2356.552 | 2356.522 | 0.030 | 21057.125 |
| 236 | 2355.113 | 2355.083 | 0.030 | 21410.896 |
| 238 | 2353.658 | 2353.625 | 0.033 | 21767.435 |
| 240 | 2352.186 | 2352.151 | 0.035 | 22126.738 |
| 244 | 2349.208 | 2349.172 | 0.036 | 22853.609 |
| 246 | 2347.712 | 2347.682 | 0.030 | 23221.164 |
| 250 | 2344.796 | 2344.78 | 0.016 | 23964.486 |
| 256 | 2341.879 | 2341.775 | 0.104 | 25099.903 |
| 268 | 2327.177 | 2327.168 | 0.009 | 27443.674 |
| 270 | 2325.475 | 2325.466 | 0.009 | 27843.681 |
| 272 | 2323.728 | 2323.73 | −0.002 | 28246.351 |
| 274 | 2321.958 | 2321.979 | −0.021 | 28651.677 |
| 276 | 2320.175 | 2320.227 | −0.052 | 29059.651 |
| 278 | 2318.398 | 2318.494 | −0.096 | 29470.268 |
| 280 | 2316.637 | 2316.803 | −0.166 | 29883.520 |
| 282 | 2314.920 | 2315.188 | −0.268 | 30299.400 |
To understand the vibrational states responsible for the perturbations, the CDSD4000 (0000) and (0001) energies were fit to a 3rd order polynomial expansion in J(J + 1) with J ≤ 300.54 The results were used to predict unperturbed high-J energies for both vibrational states. The deviations from the calculated and predicted energies are shown in Fig. 5. The (0000) state of CO2 shows no J-dependent structure, but the (0001) state shows distinct energy deviations near J = 259 and 293. This comparison shows that the (0001) state is coupled to other CO2 rovibrational states with energies near (0001) J = 259 and 293.
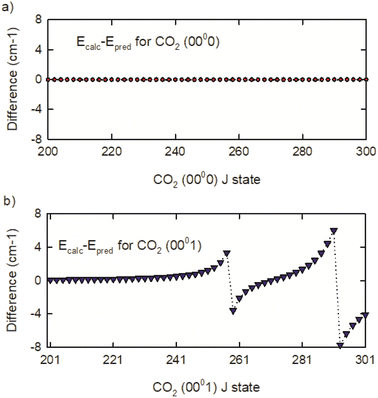 | ||
| Fig. 5 Differences of calculated and predicted energies for the (a) (0000) and (b) (0001) states of CO2. | ||
The Heff model accounts for three vibrational states of CO2 that interact with the (0001) state.54 The interacting vibrational states are (0330), (1110(1)), and (1110(2)) where (1) and (2) identify Fermi-mixed states. Based on this model, energy level crossings are present near the J = 259 rotational states of the (0001) and (0330) vibrational states and near the J = 291 rotational state of the (0001) and (1110(1)) vibrational states. The (1110(2)) state interacts indirectly through the (0330) state. Based on the effective Hamiltonian, the authors identify Fermi, Fermi + L-type, and Coriolis coupling as being responsible for the perturbations. While the perturbations affect the IR transition frequencies, they do not affect the rotational energies of the CO2 (0000) vibrational state, which is the topic of the dynamics measurements described in the next section.
b. State-resolved collisional relaxation of optically centrifuged CO2J = 244–282
Here, we present results of collisional relaxation experiments of optically centrifuged CO2 molecules with J = 244–282, using the IR transitions reported in the previous section. We used polarization-sensitive, high-resolution IR probing to characterize the distribution of the optically centrifuged molecules, their orientational properties, and their decay kinetics. For these measurements, the bandwidth of the ω1 optical pulse was reduced to limit the extent of CO2 rotational excitation to states with J > 282, thereby limiting the effect of downward collisions that populate the J = 244–282 states.![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) parallel to the z-axis and A(2)0 = −1 for
parallel to the z-axis and A(2)0 = −1 for ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) perpendicular to the z-axis.
perpendicular to the z-axis.
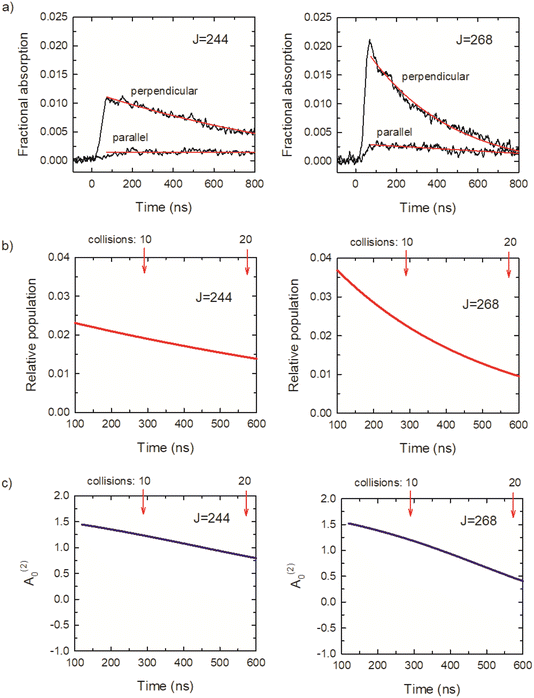
Fig. 7a shows transient absorption signals I⊥ and I∥ in black for CO2J = 244 and 268. The rise times of the transient signals are detector limited, showing that these states are prepared directly by the optical centrifuge pulse. Approximately 3 collisions having occurred at t = 100 ns, based on the average collision time of 29 ns at a pressure of 2.95 Torr. The ⊥-polarized data from t = 120 ns to 1 μs were fit to a 3-parameter exponential decay function, and the ∥-polarized data over the same time range were fit to a linear function. The results are shown in red in Fig. 7a. The fit parameters were used to determine the time-dependent population and alignment values, shown in Fig. 7b and c, based on the expressions above. The optical centrifuge pulses were adjusted to optimize population in the J = 268 state. Evidence of the population inversion for the centrifuged molecules is evident with the initial population for J = 268 twice that of J = 244. The ⊥-polarized signals are an order of magnitude larger than the ∥-polarized signals, indicating a significant polarization in both states. These features are representative of the transient absorption signals for the CO2J = 244–282 states.
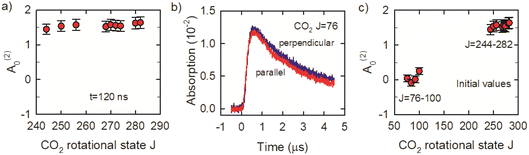
We now consider the J-dependence of the alignment in the x–y plane of optically centrifuged CO2 molecules with J = 244–282. Fig. 8a shows that the alignment moments at t = 120 ns are close to A(2)0 = 1.5, indicating a high degree of alignment relative to the excitation polarization of the optical centrifuge. We performed additional measurements for the CO2J = 76–100 states to check for evidence of alignment in the collision products. The J = 76–100 states are not populated directly in the optical centrifuge pulse; instead, they are populated through collisions of optically centrifuged molecules with the thermal bath. Fig. 8b shows the fractional absorption intensities I⊥ and I∥ for J = 76. These signals have rise times that are 6-fold longer than those for the J = 244–282 states, consistent with collision-induced population growth. The I⊥ and I∥ signals for J = 76–100 have similar intensities and decay rates. The alignment moment values for these states are close to zero, as shown in Fig. 8c, indicating that the collisions involve a broad range of scattering angles.
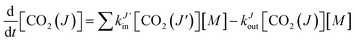 | (2) |
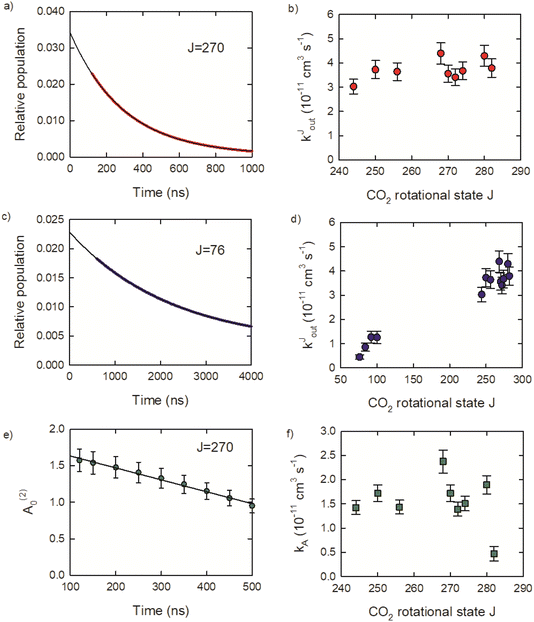
Relaxation rate constants were determined from decay lifetimes for individual rotational states with J = 244–282 by fitting the population to exponential decay functions. Fig. 9a shows the population decay (in red) for J = 270 along with the fit results in black. The J-dependent rate constants for these states are shown in Fig. 9b, with values of kJout = (4.3 ± 0.4) × 10−11 cm3 molecule−1 s−1 for J = 280 and kJout = (3.0 ± 0.3) × 10−11 cm3 molecule−1 s−1 for J = 244. These rate constants are an order of magnitude smaller than the Lennard-Jones collision rate constant kLJ = 3.7 × 10−10 cm3 molecule−1 s−1, showing that population loss does not occur on every collision for the J = 244–282 states.
Relaxation kinetics were also measured for several states with J = 76–100 to better characterize the overall collisional relaxation. These states are populated by the collisional cascade of the optically centrifuged molecules. The population decay for J = 76 is shown (in blue) in Fig. 9c, along with an exponential fit. Fig. 9d shows that the rate constants for J = 76, 84, 92 and 100 are significantly smaller than the values for J = 244–282, consistent with the overall relaxation process.
Without state-to-state cross sections, either from experiments or calculations, it is not possible to assess how the observed relaxation rate constants compare to predicted values from statistical models that have been used for lower J states. At present, the reported rate constants for CO2 relaxation are benchmarks for future studies. In a related study on CO(J) relaxation, however, we used master equation simulations to calculate the relaxation kinetics and rotational distributions of optically centrifuged CO with J ≤ 80, based on extrapolated rate constants from state-to-state measurements for J = 0–29.27,28 The simulations successfully reproduced the qualitative features of the experimental results, with the key exception that the calculated relaxation rate constants were 5 times larger than those measured in the experiments. The statistical model for the CO system considered the increasing energy gaps for high J states, but the effects of large angular momentum and short rotational periods were not included.
Here we consider the time-dependence of the molecular alignment in the x–y plane. The A(2)0 values for CO2J = 270 are shown in Fig. 9e as a function of time. Loss of alignment in the centrifuged molecules occurs through collisions and pseudo-first order kinetics were used to describe the time-evolution of A(2)0, such that (A(2)0)t/(A(2)0)t=0 = e−kA[M]t. The decay profiles are linear for the J = 244–282 states and rate constants were determined using (A(2)0)t/(A(2)0)t=0 = −kA[M]t.
The resulting kA values are near kA = 2 × 10−11 cm3 molecule−1 s−1 for J = 244–280. However, kA for J = 282 is four times smaller, with kA = 4.7 × 10−12 cm3 molecule−1 s−1. This result shows that while collisions reduce the alignment of the optically centrifuged molecules, the effect is less apparent for the highest populated state. The alignment decay for the J = 282 state results from collisions that reorient a subset of molecules originally prepared by the optical centrifuge, but does not include incoming signal from the relaxation of higher J states. There are no J states populated above J = 282 and up-collisions from lower J are unlikely given the relatively large energy gaps of 420 cm−1 or more. In this way, the J = 282 state is unique among the set of states investigated here.
We also find that the alignment decay rates are a factor of two times smaller than the population decay rates. This set of rate constants for population and alignment decay show that collisions of optically centrifuged CO2 are more likely to reduce the J quantum number of the centrifuged molecules than to induce large changes in the mJ projection quantum number (without accompanying changes in J) that lead to randomization of their spatial orientations.
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) and the symmetry axis (z), such that
and the symmetry axis (z), such thatA(2)0 = 〈2P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 = (3〈cos2 θ)〉 = (3〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 − 1), θ〉 − 1), | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is the second Legendre polynomial as a function of cos
θ) is the second Legendre polynomial as a function of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.59–61 The average values of cos2
θ.59–61 The average values of cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ were used to determine average mJ quantum numbers for the optically centrifuged molecules using the high-J-limiting vector model expression cos
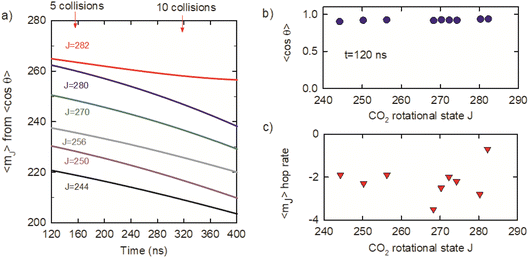
θ were used to determine average mJ quantum numbers for the optically centrifuged molecules using the high-J-limiting vector model expression cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = mJ/(J(J + 1))1/2. Fig. 10a shows the time evolution of 〈mJ〉 for the J = 244–282 states, along with the average number of collisions. The 〈mJ〉 values at t = 120 ns are slightly smaller than J and undergo collision-induced hops to lower mJ levels. Fig. 10b plots 〈cos
θ = mJ/(J(J + 1))1/2. Fig. 10a shows the time evolution of 〈mJ〉 for the J = 244–282 states, along with the average number of collisions. The 〈mJ〉 values at t = 120 ns are slightly smaller than J and undergo collision-induced hops to lower mJ levels. Fig. 10b plots 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 = mJ/(J(J + 1))1/2 as a function of J at t = 120 ns, showing that 〈mJ〉 > 0.9 (J(J + 1))1/2 for this set of states. The 〈mJ〉 hop rate is defined as the number of 〈mJ〉 hops per collision and Fig. 10c shows that hop rate is 2–3 hops per collision, on average. It is notable that the 〈mJ〉 hop rate for J = 282 is smaller than for the other J states. J = 282 is the highest state in the ensemble of centrifuged molecules and there are no states higher in energy to populate J = 282 through collisions. This result is consistent with our observation that J-changing collisions occur more readily than collisions that only induce changes in 〈mJ〉.
θ〉 = mJ/(J(J + 1))1/2 as a function of J at t = 120 ns, showing that 〈mJ〉 > 0.9 (J(J + 1))1/2 for this set of states. The 〈mJ〉 hop rate is defined as the number of 〈mJ〉 hops per collision and Fig. 10c shows that hop rate is 2–3 hops per collision, on average. It is notable that the 〈mJ〉 hop rate for J = 282 is smaller than for the other J states. J = 282 is the highest state in the ensemble of centrifuged molecules and there are no states higher in energy to populate J = 282 through collisions. This result is consistent with our observation that J-changing collisions occur more readily than collisions that only induce changes in 〈mJ〉.
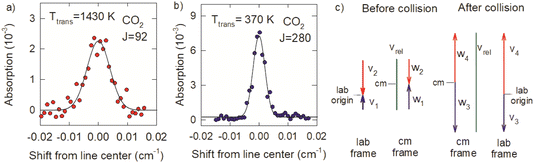
The Doppler profiles show that collisions of optically centrifuged CO2 molecules with thermal bath molecules are impulsive, leading to rotational excitation of the bath molecules and translational energy in both collision partners. The high degree of alignment of the centrifuged molecules in the x–y plane results in collision products that are scattered predominantly outward from the z-axis with cylindrical symmetry and the most effective collisions for energy transfer will have relative velocities that are in the x–y plane. Doppler profiles measured along the x-axis therefore characterize the maximum recoil velocities of the scattered molecules.
The difference in the Doppler broadening for J = 92 and J = 280 is an indication that the optically centrifuged molecules have lower initial velocities than the thermal bath molecules. Fig. 11c considers the velocity vectors before and after a head-on collision with a b = 0 impact parameter, in the lab frame and the center of mass (cm) frame. The lab frame velocities before the collision are v1 for the centrifuged molecule and v2 for the thermal bath molecule; the corresponding cm velocities are w1 and w2. After the collision, the cm velocities w3 (for the centrifuged molecule) and w4 (for the bath molecule) are equal and opposite. However, in the lab frame, v3 < v4 and the high-J collision products have narrower Doppler profiles.
Previous studies from our laboratory provide additional support that the centrifuged molecules have sub-thermal velocity distributions.21 In depletion measurements of CO2 following the optical centrifuge pulse, the J = 0 and J = 36 states have narrow Doppler profiles that correspond to translational temperatures of 130 and 140 K, respectively, showing that a translationally cool set of molecules are centrifuged to higher states. Further translational cooling may also take place during the optical centrifuge pulse through electrostriction in the focused laser beam. This phenomenon will be the focus of future investigations.
IV. Conclusions
We have investigated the spectroscopy and collision dynamics of optically centrifuged CO2 with rotational states J ≤ 282 using polarization-sensitive high-resolution transient IR absorption spectroscopy. For these studies, the optical centrifuge laser bandwidth was reduced so that the highest populated rotational state was J = 282. New IR fundamental ν3 R-branch transitions were measured using the optical centrifuge to populate high-J states of CO2. Except in regions of two spectral perturbations, the observed transitions were well predicted by extrapolating from low-J spectral constants of a third-order expansion of the rigid-rotor model.The nearly nascent distribution of the centrifuged molecules with J = 244–282 peaks at J = 268, and the centrifuged molecules have a high degree of alignment with the initial excitation polarization. The alignment moments for this set of optically centrifuged states are near A(2)0 = 1.5, which is near the maximum value of A(2)0 = 2. The centrifuged molecules are prepared with average angular momentum projection mJ quantum numbers that are within 90% of the J vector based on measured values of A(2)0. Through collisions, the centrifuged molecules gradually lose their alignment, but the anisotropy decay is slower than the population decay. Collisions lead to rotational excitation of thermal bath molecules, and transient measurements on the J = 76–100 states show that these collision products have a low degree of alignment.
The results presented here provide a clear picture of the rotation-to-translation energy transfer mechanism for molecules with large amounts of angular momentum. Our results reveal that collisions of centrifuged molecules impart rotational energy to thermal bath molecules, along with translational energy to both collision partners. A comparison of J-dependent Doppler profiles indicates that the centrifuged molecules initially have translational energies that are less than the thermal average, showing that the centrifuged molecules are prepared with relatively low kinetic energies. Collisional relaxation rate constants for the J = 244–282 states are near one-tenth the gas kinetic collision rate constant. Reduced collisional energy transfer rates are associated with increasing rotational energy gaps. Without state-to-state rate information for CO2–CO2 collisions, it is not possible to compare the rate results to statistical models. However, statistical models that work well for low-J CO–CO collisions overestimate the observed relaxation rate constants for high-J molecules, suggesting that angular momentum effects must also be considered. Future studies will take advantage of the tunability in the optical centrifuge to investigate CO2 collisional phenomena over a broader range of rotational states in order to elucidate J-dependent behavior in more detail.
These studies demonstrate the power of modern optical methods for generating and investigating molecules with large amount of controllable angular momentum. New IR spectral lines of high-J molecules will contribute to more accurate description of high energy molecules, and enable future investigations of high energy environments and remote atmospheres. The results reported here contribute to a growing body of work that highlight the impact of large amounts of angular momentum on collisional energy transfer, and the underlying principles that control molecular collisions.
Author contributions
Investigation: M. E. Ritter, S. A. DeSouza, H. M. Ogden, T. J. Michael, and A. S. Mullin; conceptualization: M. E. Ritter, S. A. DeSouza, H. M. Ogden, and A. S. Mullin; methodology: H. M. Ogden, and A. S. Mullin; formal analysis: M. E. Ritter, S. A. DeSouza, and A. S. Mullin; project administration and funding acquisition: A. S. Mullin; writing: M. E. Ritter, S. A. DeSouza, H. M. Ogden, and A. S. Mullin.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge Dr Valerii Perevalov for providing helpful insights to the observed spectral perturbation, Dr M. H. Alexander, P. J. Dagdigian, and J. T. Fourkas for provocative discussions on scattering dynamics, and Dr Kenneth G. McKendrick for his informative suggestions. The authors acknowledge research support from the US National Science Foundation through grants CHE-1800531 and CHE-2155135 and the University of Maryland.References
- D. Bailly, C. Camy-Peyret and R. Lanquetin, J. Mol. Spectrosc., 1997, 182, 10–17 CrossRef CAS.
- S. Hay, F. Shokoohi, S. Callister and C. Wittig, Chem. Phys. Lett., 1985, 118, 6–11 CrossRef CAS.
- A. S. Mullin, J. Park, J. Z. Chou, G. W. Flynn and R. E. Weston, Chem. Phys., 1993, 175, 53–70 CrossRef CAS.
- R. Aures, K.-H. Gericke, M. Kawasaki, C. Maul, Y. Nakano, G. Trott-Kriegeskorte and Z. Y. Wang, PhysChemComm, 2001, 4, 102–105, 10.1039/b108052k.
- J. Bailey, V. S. Meadows, S. Chamberlain and D. Crisp, Icarus, 2008, 197, 247–259 CrossRef.
- Q. Binauld, P. Rivière and A. Soufiani, Combust. Flame, 2018, 194, 128–134 CrossRef CAS.
- M. R. Swain, G. Tinetti, G. Vasisht, P. Deroo, C. Griffith, J. Bouwman, P. Chen, Y. Yung, A. Burrows, L. R. Brown, J. Matthews, J. F. Rowe, R. Kuschnig and D. Angerhausen, Astrophys. J., 2009, 704, 1616–1621 CrossRef CAS.
- G. Tinetti, P. Deroo, M. R. Swain, C. A. Griffith, G. Vasisht, L. R. Brown, C. Burke and P. McCullough, Astrophys. J. Lett., 2010, 712, L139–L142 CrossRef CAS.
- J. T. Yardley, Introduction to Molecular Energy Transfer, Academic Press, 1980 Search PubMed.
- Y. Ohshima and H. Hasegawa, Int. Rev. Phys. Chem., 2010, 29, 619–663 Search PubMed.
- G. Karras, M. Ndong, E. Hertz, D. Sugny, F. Billard, B. Lavorel and O. Faucher, Phys. Rev. Lett., 2015, 114, 103001 CrossRef CAS PubMed.
- O. Korech, U. Steinitz, R. J. Gordon, I. S. Averbukh and Y. Prior, Nat. Photonics, 2013, 7, 711–714 CrossRef CAS.
- K. Kitano, H. Hasegawa and Y. Ohshima, Phys. Rev. Lett., 2009, 103, 223002 CrossRef PubMed.
- C. Bloomquist, S. Zhdanovich, A. A. Milner and V. Milner, Phys. Rev. A, 2012, 86, 063413 CrossRef.
- M. Bitter and V. Milner, Phys. Rev. A, 2016, 93, 013420 CrossRef.
- J. Karczmarek, J. Wright, P. Corkum and M. Ivanov, Phys. Rev. Lett., 1999, 82, 3420–3423 CrossRef CAS.
- D. M. Villeneuve, S. A. Aseyev, P. Dietrich, M. Spanner, M. Y. Ivanov and P. B. Corkum, Phys. Rev. Lett., 2000, 85, 542–545 CrossRef CAS PubMed.
- L. W. Yuan, S. W. Teitelbaum, A. Robinson and A. S. Mullin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6872–6877 CrossRef CAS.
- L. W. Yuan, C. Toro, M. Bell and A. S. Mullin, Faraday Discuss., 2011, 150, 101–111 RSC.
- C. Toro, Q. N. Liu, G. O. Echebiri and A. S. Mullin, Mol. Phys., 2013, 111, 1892–1901 CrossRef CAS.
- M. J. Murray, H. M. Ogden, C. Toro, Q. N. Liu, D. A. Burns, M. H. Alexander and A. S. Mullin, J. Phys. Chem. A, 2015, 119, 12471–12479 CrossRef CAS PubMed.
- M. J. Murray, H. M. Ogden, C. Toro, Q. N. Liu and A. S. Mullin, ChemPhysChem, 2016, 17, 3692–3700 CrossRef CAS PubMed.
- M. J. Murray, H. M. Ogden and A. S. Mullin, J. Chem. Phys., 2017, 147, 154309 CrossRef PubMed.
- M. J. Murray, H. M. Ogden and A. S. Mullin, J. Chem. Phys., 2018, 148, 084310 CrossRef PubMed.
- H. M. Ogden, T. J. Michael, M. J. Murray, Q. N. Liu, C. Toro and A. S. Mullin, Phys. Chem. Chem. Phys., 2019, 21, 14103–14110 RSC.
- H. Ogden, T. Michael, M. Murray and A. Mullin, J. Quant. Spectrosc. Radiat. Transfer, 2020, 246, 106867 CrossRef CAS.
- T. J. Michael, H. M. Ogden and A. S. Mullin, J. Chem. Phys., 2021, 154, 134307 CrossRef CAS PubMed.
- M. R. Laskowski, T. J. Michael, H. M. Ogden, M. H. Alexander and A. S. Mullin, Faraday Discuss., 2022, 238, 87–102 RSC.
- A. Korobenko, A. A. Milner, J. W. Hepburn and V. Milner, Phys. Chem. Chem. Phys., 2014, 16, 4071–4076 RSC.
- A. Korobenko, A. A. Milner and V. Milner, Phys. Rev. Lett., 2014, 112, 113004 CrossRef PubMed.
- A. A. Milner, A. Korobenko, J. W. Hepburn and V. Milner, Phys. Rev. Lett., 2014, 113, 043005 CrossRef PubMed.
- A. A. Milner, A. Korobenko and V. Milner, New J. Phys., 2014, 16, 093038 CrossRef CAS.
- A. Korobenko, J. W. Hepburn and V. Milner, Phys. Chem. Chem. Phys., 2015, 17, 951–956 RSC.
- A. Korobenko and V. Milner, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 164004 CrossRef.
- A. A. Milner, A. Korobenko, J. Floss, I. S. Averbukh and V. Milner, Phys. Rev. Lett., 2015, 115, 033005 CrossRef CAS PubMed.
- A. A. Milner, A. Korobenko and V. Milner, Opt. Express, 2015, 23, 8603–8608 CrossRef CAS PubMed.
- A. A. Milner, A. Korobenko, K. Rezaiezadeh and V. Milner, Phys. Rev. X, 2015, 5, 031041 Search PubMed.
- A. Korobenko and V. Milner, Phys. Rev. Lett., 2016, 116, 183001 CrossRef CAS PubMed.
- A. A. Milner, A. Korobenko and V. Milner, Phys. Rev. A, 2016, 93, 053408 CrossRef.
- V. Milner and J. W. Hepburn, in Advances in Chemical Physics, ed. P. Brumer, S. A. Rice and A. R. Dinner, Wiley-Blackwell, Malden, 2016, vol. 159, pp. 395–412 Search PubMed.
- A. A. Milner, A. Korobenko, J. W. Hepburn and V. Milner, J. Chem. Phys., 2017, 147, 124202 CrossRef CAS PubMed.
- J. Floss, C. Boulet, J.-M. Hartmann, A. A. Milner and V. Milner, Phys. Rev. A, 2018, 98, 043401 CrossRef CAS.
- A. A. Milner, J. A. M. Fordyce, I. MacPhail-Bartley, W. Wasserman, V. Milner, I. Tutunnikov and I. S. Averbukh, Phys. Rev. Lett., 2019, 122, 223201 CrossRef CAS PubMed.
- I. MacPhail-Bartley, W. W. Wasserman, A. A. Milner and V. Milner, Rev. Sci. Instrum., 2020, 91, 045122 CrossRef CAS PubMed.
- I. Tutunnikov, J. Floss, E. Gershnabel, P. Brumer, I. S. Averbukh, A. A. Milner and V. Milner, Phys. Rev. A, 2020, 101, 021403(R) CrossRef.
- P. Amani, A. A. Milner and V. Milner, J. Chem. Phys., 2021, 155, 124201 CrossRef CAS PubMed.
- A. A. Milner and V. Milner, Phys. Rev. A, 2021, 103, L041103 CrossRef CAS.
- A. A. Milner, U. Steinitz, I. S. Averbukh and V. Milner, Phys. Rev. Lett., 2021, 127, 073901 CrossRef CAS PubMed.
- I. Tutunnikov, U. Steinitz, E. Gershnabel, J.-M. Hartmann, A. A. Milner, V. Milner and I. S. Averbukh, Phys. Rev. Res., 2022, 4, 013212 CrossRef CAS.
- T. Y. Chen, S. A. Steinmetz, B. D. Patterson, A. W. Jasper and C. J. Kliewer, Nat. Commun., 2023, 14, 3227 CrossRef CAS PubMed.
- S. A. Tashkun, V. I. Perevalov, R. R. Gamache and J. Lamouroux, J. Quant. Spectrosc. Radiat. Transfer, 2015, 152, 45–73 CrossRef CAS.
- I. E. Gordon, L. S. Rothman, C. Hill, R. V. Kochanov, Y. Tan, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, B. J. Drouin, J. M. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, V. I. Perevalov, A. Perrin, K. P. Shine, M. A. H. Smith, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, A. Barbe, A. G. Császár, V. M. Devi, T. Furtenbacher, J. J. Harrison, J. M. Hartmann, A. Jolly, T. J. Johnson, T. Karman, I. Kleiner, A. A. Kyuberis, J. Loos, O. M. Lyulin, S. T. Massie, S. N. Mikhailenko, N. Moazzen-Ahmadi, H. S. P. Müller, O. V. Naumenko, A. V. Nikitin, O. L. Polyansky, M. Rey, M. Rotger, S. W. Sharpe, K. Sung, E. Starikova, S. A. Tashkun, J. Vander Auwera, G. Wagner, J. Wilzewski, P. Wcislo, S. Yu and E. J. Zak, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 3–69 CrossRef CAS.
- L. S. Rothman, I. E. Gordon, R. J. Barber, H. Dothe, R. R. Gamache, A. Goldman, V. I. Perevalov, S. A. Tashkun and J. Tennyson, J. Quant. Spectrosc. Radiat. Transfer, 2010, 111, 2139–2150 CrossRef CAS.
- S. A. Tashkun and V. I. Perevalov, J. Quant. Spectrosc. Radiat. Transfer, 2011, 112, 1403–1410 CrossRef CAS.
- M. Paulec, M. Marciniak, K. Gross and D. Azevedo, Proc. SPIE, 2018, 10644, 2303982 Search PubMed.
- G. Tinetti, P. Drossart, P. Eccleston, P. Hartogh, A. Heske, J. Leconte, G. Micela, M. Ollivier, G. Pilbratt, L. Puig, D. Turrini, B. Vandenbussche, P. Wolkenberg, J. P. Beaulieu, L. A. Buchave, M. Ferus, M. Griffin, M. Guedel, K. Justtanont, P. O. Lagage, P. Machado, G. Malaguti, M. Min, H. U. Norgaard-Nielsen, M. Rataj, T. Ray, I. Ribas, M. Swain, R. Szabo, S. Werner, J. Barstow, M. Burleigh, J. Cho, V. C. du Foresto, A. Coustenis, L. Decin, T. Encrenaz, M. Galand, M. Gillon, R. Helled, J. C. Morales, A. G. Muñoz, A. Moneti, I. Pagano, E. Pascale, G. Piccioni, D. Pinfield, S. Sarkar, F. Selsis, J. Tennyson, A. Triaud, O. Venot, I. Waldmann, D. Waltham, G. Wright, J. Amiaux, J. L. Auguères, M. Berthé, N. Bezawada, G. Bishop, N. Bowles, D. Coffey, J. Colomé, M. Crook, P. E. Crouzet, V. Da Peppo, I. E. Sanz, M. Focardi, M. Frericks, T. Hunt, R. Kohley, K. Middleton, G. Morgante, R. Ottensamer, E. Pace, C. Pearson, R. Stamper, K. Symonds, M. Rengel, E. Renotte, P. Ade, L. Affer, C. Alard, N. Allard, F. Altieri, Y. André, C. Arena, I. Argyriou, A. Aylward, C. Baccani, G. Bakos, M. Banaszkiewicz, M. Barlow, V. Batista, G. Bellucci, S. Benatti, P. Bernardi, B. Bézard, M. Blecka, E. Bolmont, B. Bonfond, R. Bonito, A. S. Bonomo, J. R. Brucato, A. S. Brun, I. Bryson, W. Bujwan, S. Casewell, B. Charnay, C. C. Pestellini, G. Chen, A. Ciaravella, R. Claudi, R. Clédassou, M. Damasso, M. Damiano, C. Danielski, P. Deroo, A. M. Di Giorgio, C. Dominik, V. Doublier, S. Doyle, R. Doyon, B. Drummond, B. Duong, S. Eales, B. Edwards, M. Farina, E. Flaccomio, L. Fletcher, F. Forget, S. Fossey, M. Fränz, Y. Fujii, A. García-Piquer, W. Gear, H. Geoffray, J. C. Gérard, L. Gesa, H. Gomez, R. Graczyk, C. Griffith, D. Grodent, M. G. Guarcello, J. Gustin, K. Hamano, P. Hargrave, Y. Hello, K. Heng, E. Herrero, A. Hornstrup, B. Hubert, S. Ida, M. Ikoma, N. Iro, P. Irwin, C. Jarchow, J. Jaubert, H. Jones, Q. Julien, S. Kameda, F. Kerschbaum, P. Kervella, T. Koskinen, M. Krijger, N. Krupp, M. Lafarga, F. Landini, E. Lellouch, G. Leto, A. Luntzer, T. Rank-Lüftinger, A. Maggio, J. Maldonado, J. P. Maillard, U. Mall, J. B. Marquette, S. Mathis, P. Maxted, T. Matsuo, A. Medvedev, Y. Miguel, V. Minier, G. Morello, A. Mura, N. Narita, V. Nascimbeni, N. Nguyen Tong, V. Noce, F. Oliva, E. Palle, P. Palmer, M. Pancrazzi, A. Papageorgiou, V. Parmentier, M. Perger, A. Petralia, S. Pezzuto, R. Pierrehumbert, I. Pillitteri, G. Piotto, G. Pisano, L. Prisinzano, A. Radioti, J. M. Réess, L. Rezac, M. Rocchetto, A. Rosich, N. Sanna, A. Santerne, G. Savini, G. Scandariato, B. Sicardy, C. Sierra, G. Sindoni, K. Skup, I. Snellen, M. Sobiecki, L. Soret, A. Sozzetti, A. Stiepen, A. Strugarek, J. Taylor, W. Taylor, L. Terenzi, M. Tessenyi, A. Tsiaras, C. Tucker, D. Valencia, G. Vasisht, A. Vazan, F. Vilardell, S. Vinatier, S. Viti, R. Waters, P. Wawer, A. Wawrzaszek, A. Whitworth, Y. L. Yung, S. N. Yurchenko, M. R. Z. Osorio, R. Zellem, T. Zingales and F. Zwart, Exp. Astron., 2018, 46, 135–209 CrossRef.
- V. Wilquet, A. Mahieux, A. C. Vandaele, V. I. Perevalov, S. A. Tashkun, A. Fedorova, O. Korablev, F. Montmessin, R. Dahoo and J. L. Bertaux, J. Quant. Spectrosc. Radiat. Transfer, 2008, 109, 895–905 CrossRef CAS.
- X. C. Huang, R. S. Freedman, S. Tashkun, D. W. Schwenke and T. J. Lee, J. Mol. Spectrosc., 2023, 392, 111748 CrossRef CAS.
- R. N. Zare, Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics, Wiley-Interscience, 1988 Search PubMed.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Kluwer Academic/Plenum Publishers, 2nd edn, 1999 Search PubMed.
- U. Fano and J. H. Macek, Rev. Mod. Phys., 1973, 45, 553 CrossRef CAS.
- S. J. McGurk, K. G. McKendrick, M. L. Costen, D. I. G. Bennett, J. Klos, M. H. Alexander and P. J. Dagdigian, J. Chem. Phys., 2012, 136, 164306 CrossRef CAS PubMed.
- R. Uberna, R. D. Hinchliffe and J. I. Cline, J. Chem. Phys., 1995, 103, 7934–7945 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |