 Open Access Article
Open Access ArticleProtein sialylation affects the pH-dependent binding of ferric ion to human serum transferrin†
Tomislav
Friganović
 ,
Valentina
Borko
,
Valentina
Borko
 and
Tin
Weitner
and
Tin
Weitner
 *
*
Faculty of Pharmacy and Biochemistry, University of Zagreb, Ante Kovačića 1, 10000 Zagreb, Croatia. E-mail: tin.weitner@pharma.unizg.hr
First published on 11th June 2024
Abstract
Physiological or pathophysiological changes lead to posttranslational changes in the sialic acid content of human serum transferrin (hTf), an essential mediator of iron transport in the human body, resulting in a significantly increased concentration of desialylated hTf. The intrinsic fluorescence quenching upon binding of iron to hTf was successfully modeled using the binding polynomial for two iron-binding sites, allowing measurements in a high-throughput format. Removal of sialic acid residues resulted in a 3-fold increase in iron binding affinity for both sites of hTf at pH 7.4. The pH-dependence of iron binding showed significant differences in equilibrium constants, resulting in a 10-fold increase in binding affinity for desialylated hTf at pH 5.9. The changes in hTf sialylation apparently result in tuning of the stability of the conformational state, which in turn contributes to the stability of the diferric hTf. The observed differences in the conditional thermodynamic equilibrium constants suggest that the desialylated protein has a higher preference for diferric hTf over monoferric hTf species down to pH 6.5, which may also influence the interaction with transferrin receptors that preferentially bind to diferric hTf. The results suggest a link between changes in hTf glycan structure and alterations in iron binding equilibrium associated with tissue acidosis.
Introduction
Human serum transferrin (hTf), the primary iron transport protein in the human body, is a globular glycoprotein with an approximate molecular weight of 79 kDa that is predominantly produced in the liver.1,2 This highly glycosylated protein is bilobal, with each lobe—the N-lobe containing 336 amino acids and the C-lobe containing 343—harbouring a thermodynamically distinct binding site for iron(III) ions.3 The lobes are interconnected by a short peptide and stabilized by 19 intra-chain disulfide bonds.4 Structurally, the N-lobe consists of 14 helices and 13 strands, while the C-lobe is composed of 17 helices and 13 strands.5Transferrin binds iron(III), forming a stable ternary chelate-protein complex with a distorted octahedral coordination. In this complex, iron(III) is bound bidentately to the synergistic carbonate anion and monodentately to two tyrosine, one aspartic acid, and one histidine amino acid.6 The presence of the synergistic anion, like carbonate or oxalate, is critical for the formation of stable iron-transferrin complexes.7 Transferrin also forms complexes with Fe(II), though these are less stable.8 Four isoforms of hTf can be distinguished based on iron content: apo-hTf (no iron bound), FeN-hTf or FeC-hTf (one iron bound per hTf, in either lobe), and Fe2hTf (both binding sites occupied).
The proper binding of iron to transferrin, in terms of both thermodynamic and kinetic aspects, is essential for the normal functioning of the human organism. Unbound iron cations are hazardous as they can produce reactive and toxic oxygen species through the Fenton reaction, leading to significant cellular damage.9 The body maintains a tight regulation of iron, with only about 1% of total iron bound to transferrin, undergoing a considerable daily turnover of around 25 mg, 80% of which is used for haemoglobin synthesis in the bone marrow.10,11 In addition to iron, various cations can form more or less stable complexes with transferrin, some of which might be of physiological importance.12
The extent of transferrin-iron complexation, which is reflected in the values of the equilibrium constants, is pH-dependent. This is attributed to the release of protons during the iron binding process.13 The affinity of transferrin for iron decreases with decreasing pH, a property that is effectively utilized in iron release in endosomes at pH 5.6.14 The process of iron release is further facilitated by binding to the human transferrin receptors hTfR1 and hTfR2.15,16 Despite the notable difference in binding affinities between hTfR1 and hTfR2 for transferrin, the lower affinity of hTfR2 does not diminish its ability to facilitate iron endocytosis.16
Another important factor that can influence the iron binding affinity of transferrin is the extent of glycosylation.17 Transferrin exhibits microheterogeneity due to the varying degree of sialylation of its N-linked oligosaccharide chains, which can be bi- or triantennary and typically terminate with sialic acid residues.18 Different sialoforms can be distinguished by isoelectric focussing or chromatography, highlighting the importance of sialic acid content in determining the physicochemical properties and possibly biological functions of transferrin.19 In healthy individuals, approximately 80% of hTf is present as a tetrasialoform shown in Fig. 1.20 Deviations from normal sialylation patterns may indicate various pathological conditions or genetic diseases.21
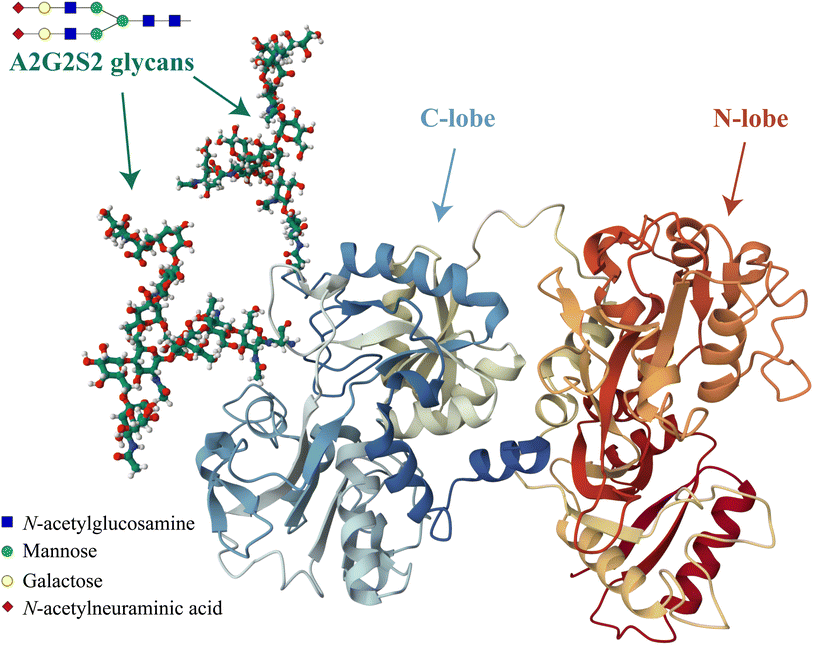 | ||
| Fig. 1 Visual representation of the predominant glycosylated variant of human serum transferrin based on the glycan-free structure identified by Yang et al.5 The structure was modified by adding two A2G2S2 glycans and by performing Molecular Dynamics (MD) optimization using the GLYCAM glycoprotein builder tool.40 The A2G2S2 glycans were determined to be the most abundant fraction of Tf+S by UHPLC N-glycan analyses reported in previous studies.17,39 Further details on the N-glycan analysis can be found in the ESI,† subsection 2.3. | ||
For example, during pregnancy, there is a progressive and gradual shift towards highly sialylated hTf, which is quickly reversed postpartum.22 In addition, the reduction in transferrin sialylation is observed as part of the acute phase response in septic patients, and a reduction in transferrin sialylation may be a predictor of severe sepsis and septic shock.23,24 In normal serum, glycosylated transferrin exhibits a half-life of 7 to 10 days.25 The half-life of desialylated hTf is significantly shorter, resulting in increased iron turnover and faster delivery of iron to hepatic stores.24 The degree of transferrin sialylation can also serve as a marker for chronic alcohol abuse by identifying elevated levels of carbohydrate-deficient transferrin isoforms.26
Over the past 45 years, the accurate determination of the equilibrium constants of transferrin-iron complexes has been the subject of numerous studies, which have been complicated by exceptionally high equilibrium constants and the potential hydrolysis of the hexaaquairon(III) cation. Under these circumstances, methods for iron exchange between transferrin and suitable iron chelators are required. This is due to the fact that direct application of solutions containing free Fe(III) ions has proven ineffective.12 Typically, either an iron chelator complex is added to unsaturated transferrin or, vice versa, saturated transferrin is treated with the chelator to remove the iron. Suitable chelators include nitrilotriacetic acid (NTA), ethylenediaminetetraacetic acid (EDTA), citrate, and others.27 In addition, kinetic considerations are crucial for iron exchange, as the time required to reach equilibrium varies greatly, depending on the experimental conditions.28
The formation of transferrin-iron complexes can be effectively monitored by UV-Vis spectroscopy, with a broad spectral peak around λ ≈ 460 nm indicating iron-saturated transferrin.29–31 However, this method requires relatively high protein concentrations due to the low molar absorption coefficients in this spectral range.31,32 Alternatively, fluorescence spectroscopy can be used to study transferrin-iron binding, which allows lower protein concentrations by monitoring the partial quenching of the intrinsic fluorescence of transferrin upon iron binding.33
In addition to spectroscopic techniques, isothermal titration calorimetry (ITC) and differential scanning calorimetry (DSC) have been successfully used to determine the equilibrium constants of transferrin-iron complexes.34,35 Our recent calorimetric study on the effect of sialylation and synergistic anion on the binding of iron to hTf suggests that desialylated hTf has a higher capacity for iron sequestration, suggesting possible effects on iron metabolism.17 Furthermore, we observed that decreasing the sialic acid content in hTf leads to more exothermic apparent binding enthalpies and increased apparent binding constants in the presence of carbonate for both iron binding sites.17 This emphasises the potentially important role of sialylation in modulating the iron-binding properties of transferrin.
Considering that the uptake and release of iron by hTf is pH-dependent (pH ≈ 7.4 in serum vs. pH ≈ 5.6 in the endosome),36 the aim of this study was to further investigate the pH dependence of the binding of ferric ions to native sialylated hTf (Tf+S) and enzymatically desialylated hTf (Tf−S) using a high-throughput method. First, we established a spectrofluorometric method to determine the thermodynamic equilibrium constants at serum pH by independently repeating the measurements on Tf+S performed 45 years ago by Aisen et al.37 The spectrofluorometric method was chosen because of its high sensitivity38 and suitability for high-throughput analysis using a microplate reader. After successfully benchmarking the iron binding process with Tf+S, we enzymatically removed the terminal sialic acids from Tf+S and performed detailed glycan characterisation of both Tf+S and Tf−S, as reported previously.17,39 We then examined the iron binding of Tf+S and Tf−S at five different pH values ranging from serum to endosome conditions (7.4, 6.9, 6.5, 6.2 and 5.9) to better understand the potential effects of different physiological pH values.
The emerging research on sialic acids underscores their role in cancer initiation, progression, and immune evasion, highlighting the broader biological significance of sialylation.41,42 The phenomenon of hypersialylation in cancer cells, resulting from increased metabolic flux of sialic acids and dysregulated enzyme expression, seems to align well with the investigation into transferrin sialylation reported herein. This relationship is particularly relevant, considering that alterations in sialic acid content on transferrin impact its primary function as an iron carrier with potential consequences in cellular management of oxidative stress associated with cancer or ferroptosis.43
As far as we know, prior to this and our other recent work,17,39 there was only one study addressing the possible effects of hTf sialic acid content on metal binding.44 This study showed a preference of iron for the N-site in hTf, with similar binding affinities observed for both native and asialo forms. The lack of significant differences was attributed to the inherently high affinity of iron for hTf and the relatively low sensitivity of the HPLC/ICP-MS method.
Experimental
Chemicals and instrumentation
The following chemicals were used in this study without further purification: hydrochloric acid, HCl (37%, CAS 7647-01-0, Carlo Erba, cat. no. 403871, lot no. V3A465153A), nitrilotriacetic acid trisodium salt, Na3NTA (≥98%, CAS 5064-31-3, Sigma, cat. no. N-0253, lot. no. 023K0126), sodium hydroxide, NaOH (≥98%, CAS 1310-73-2, Kemika, cat. no. 1452506), iron(III) chloride, FeCl3 (≥98%, CAS 7705-08-0, Riedel-de Haën, cat. no. 231-729-4, lot no. 50250), piperazine-N,N′-bis(2-ethanesulfonic acid) dipotassium salt, PIPES (≥97%, CAS 108321-27-3, AMRESCO, cat. no. E912-500G, lot no. 0795C478), 2-(N-morpholino) ethanesulfonic acid hydrate, MES (≥99.5%, CAS 1266615-59-1, Sigma-Aldrich, cat. no M8250-1006, lot no. 021M5406), potassium chloride, KCl (≥99.5%, CAS 7447-40-7, Sigma-Aldrich, cat. no. 60128-2506-F, lot no. BCCF7782), 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm iron ICP standard in 5% HNO3(aq) (9992 ± 30 μg mL−1, Inorganic Ventures, cat. no. CGFE10, lot no. P2-FE676240), and pISep Buffer Kit (CryoBioPhysica, cat. no. 20055). Human serum transferrin was purchased from Sigma-Aldrich, cat. no. T2036, lot no. SLCF3538. Water used for the experiments was double distilled in an all-glass apparatus.
000 ppm iron ICP standard in 5% HNO3(aq) (9992 ± 30 μg mL−1, Inorganic Ventures, cat. no. CGFE10, lot no. P2-FE676240), and pISep Buffer Kit (CryoBioPhysica, cat. no. 20055). Human serum transferrin was purchased from Sigma-Aldrich, cat. no. T2036, lot no. SLCF3538. Water used for the experiments was double distilled in an all-glass apparatus.
The following instrumentation and consumables were used in this study: UV-Vis spectrophotometer (Varian Cary 50 Bio with UV Scan application software, version: 3.00), ICP-MS instrument (Agilent 7900), titrator T70 (Mettler Toledo with LabX™ Titration Software, version 2.62), multimode microplate reader (Tecan Spark M10), pipetting robot (Opentrons OT-2), ÄKTA Purifier 10 FPLC system (GE Healthcare), SOURCE™ 15Q 4.6/100 PE anion exchange chromatographic column (Cytiva, cat. no. 17-5181-01), immobilized SialEXO® microspin columns (Genovis, cat. no. G1-SM6-050), Amicon® Ultra centrifugal filters (0.5 mL, MWCO 30 K, Merck Millipore, cat. no. UFC503096), and 96-well microplates (black, flat bottom, Greiner, cat. no. 655097).
Desialylated apo-transferrin (Tf−S) was prepared according to the modified SialEXO protocol,45 starting from a solution of native hTf (Tf+S) in 20 mM TRIS buffer, pH 6.8, γ = 2.5 mg mL−1. For desialylation, 800 μL of this solution was added to SialEXO® columns containing the enzyme and the mixture was incubated at 25 °C for 48 hours. The protein was then recovered by centrifugation, leaving the enzyme beads in the column, so that the process could be repeated with a new transferrin solution. The initial evaluation of the desialylation process was performed by FPLC.39,46 Detailed glycan profiling was carried out using UHPLC N-glycan analysis. Further details on the preparation of Tf−S and the subsequent analyses can be found in the ESI (section 2).†
Titration experiments
For the titration experiments, buffer solutions (25 mM PIPES, 0.2 M KCl, 0.01 M K2CO3) were prepared by dissolving exact amounts of solid substances in volumetric flasks, followed by a short ultrasonic treatment and careful pH adjustment. The transferrin solutions were then prepared by dissolving transferrin in these buffers, readjusting the pH as necessary. The protein concentration was determined spectrophotometrically at λ = 280 nm. The molar absorption coefficient for Tf+S solutions was redetermined using the modified Edelhoch method.47 The obtained value of ε280 nm = 84.4 ± 0.8 × 103 M−1 cm−1 agrees with our previous results (ε280 nm = 84.8 ± 0.2 × 103 M−1 cm−1)39 as well as literature values (ε280 nm = 84.0 ± 0.2 × 103 M−1 cm−1).48 The molar absorption coefficient for Tf−S solutions was ε280 nm = 88.2 ± 0.2 × 103 M−1 cm−1, as reported in our previous study.39Buffer solutions containing NTA chelator were prepared by the addition of a standardized NTA stock solution (c = 0.4703 M) to the buffer stock solutions.31 Excess NTA was present in all working solutions to ensure iron solubility and maintain the appropriate titration regime (see later). The FeNTA solutions used for iron loading were prepared by diluting a concentrated FeNTA stock solution (cNTA = 0.3043 M, cFe(III) = 0.1505 M, pH = 2.23) in a suitable buffer and then carefully adjusting the pH. The final FeNTA concentration was determined spectrophotometrically at λ = 260 nm (ε260 nm = 5.93 × 103 M−1 cm−1), as reported in our previous study.31 For the titration experiments, all samples were prepared using the OT-2 liquid handling robot. The final working solutions were first transferred to microcentrifuge tubes for incubation and then to 96-well microplates for fluorescence measurements, with samples randomly placed in the wells to minimize position effects and ensure unbiased analysis. A detailed description of all experimental procedures can be found in the ESI.†
Fluorescence and absorbance measurements
Single-wavelength fluorescence intensity and absorbance spectra were measured in UV-Vis-transparent 96-well microplates (Greiner, cat. no. 655097) using a Tecan Spark M10 multimode microplate reader. Absorbance spectra was collected from 200 to 1000 nm with 1 nm increments, and fluorescence was measured at an excitation wavelength of 280 nm and an emission wavelength of 335 nm, utilizing a custom optical filter for excitation (bandwidth 15 nm, Tecan cat. no. 30092080). The position of the optical element along the vertical axis (z-position) was optimized for each microplate to ensure consistent fluorescence intensity readings across different z-positions. Full details on the instrumental measurements are given in the ESI (sections 4 and 5).†The experimental design maintained a constant protein concentration in all measured samples to minimize the variability of the fluorescence signal due to the Inner Filter Effect (IFE), which can mainly be attributed to protein absorbance at λ = 280 nm. Despite the constant transferrin concentration, variations in IFE may result in measurement errors due to differences in the molar absorbance coefficients of iron-containing transferrin forms and due to the spectral contribution of FeNTA.31,48 Therefore, special care was taken to account for IFE artifacts, considering that the relative error in recorded fluorescence intensity is about 8% at an absorbance of A = 0.06, increasing further to 12% at A = 0.1 and 38% at A = 0.3.49,50 In our experiments, the maximum absorbance values were ≈0.33 at 280 nm (excitation) and ≈0.12 at 335 nm (emission).
IFE corrections were performed using the recently developed ZINFE method that takes advantage of the variable z-position of the optical element. The ZINFE correction is specifically suited for measurements in microplates since it requires no absorbance measurements.51 To evaluate the performance of the ZINFE method under the experimental conditions of this study, fluorescence measurements were adjusted using the established technique described by Lakowicz as a reference standard.52 Both correction procedures are detailed in the ESI (subsection 5.1).†
Binding model and data fitting
The dependence of the measured fluorescence on the concentration of added FeNTA was modelled according to the binding polynomial for two iron binding sites of hTf. The binding polynomial theory provides a general statistical thermodynamic framework for studying ligand binding to macromolecules. The modelling procedure consisted of the following steps: (i) define the binding polynomial for two binding sites; (ii) calculate the total concentration of the protein and iron(III) for each experimental point; (iii) solve analytically the mass conservation equation for iron(III) for each experimental point, assuming certain values of the macroscopic association constants; (iv) calculate the concentration of the different complexes for each experimental point, assuming certain values for the association constants; (v) calculate the expected signal, assuming certain values for the molar fluorescence of the contributing species, which can be floating parameters in the nonlinear least squares analysis; and (vi) obtain the optimal set of macroscopic association constants that reproduce the experimental data using an iterative method.53The interaction between free iron and transferrin, characterized by the equilibrium constants K1m and K2m, can be expressed as follows (charges were omitted for simplicity):
| Fe + apoTf ⇄ FeTf | (1) |
| Fe + FeTf ⇄ Fe2Tf | (2) |
The thermodynamic equilibrium constants K1m and K2m are then defined as:
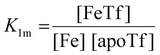 | (3) |
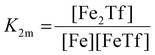 | (4) |
It follows that the value of [X] can be determined from the cubic equation:
| p[X]3 + q[X]3 + r[X] − Xt = 0 | (5) |
| p = K1mK2m | (6) |
| q = K1m(2K2mnPt − K2mXt + 1) | (7) |
| r = K1m(nPt − Xt) + 1 | (8) |
The values of Pt and Xt are the bulk concentrations of the protein and iron, respectively, and n is the average number of binding sites per protein molecule.
The relative concentrations of the apoTf, FeTf and Fe2Tf species for each data point were calculated53,54 as:
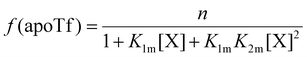 | (9) |
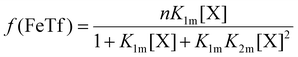 | (10) |
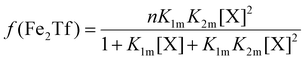 | (11) |
The measured fluorescence values were normalized as Fnorm = Fx/Fapo, where Fnorm is the normalized fluorescence, Fx is the measured fluorescence for the point x in the data set and Fapo is the measured fluorescence of the apo-transferrin without added iron. This allowed the use of relative molar fluorescence values for the calculation of total normalized relative fluorescence using relative concentrations of the apoTf, FeTf and Fe2Tf species. The total normalized relative fluorescence for each data point Fcalc corresponding to the model parameters was calculated as:
| Fcalc = f(apoTf) + (s + (1 − s)t)f(FeTf) + sf(Fe2Tf) | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FeTf
FeTf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe2Tf = 1.0
Fe2Tf = 1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6
0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2.55
0.2.55
According to Jarmoskaite et al., two steps are required for equilibrium binding measurements: (i) varying the incubation time to test for equilibration, and (ii) controlling for titration artifacts that can arise when the concentration of the constant limiting component is too high relative to the dissociation constant (KD).56 In our experiments, all working solutions were equilibrated at 25 °C for a period of ≥1 day before measurement. No further change in the fluorescence signal was observed with longer incubation times, which indicates that the proportion of the formed complex does not change further over time, thus ensuring that equilibrium has been reached. It is known that the kinetics of iron(III) uptake is strongly dependent on the type of chelator used. In the presence of the bicarbonate anion, the reaction with the FeNTA chelator shows a biphasic character and very fast kinetics, with the slower phase being completed in about 10 seconds (for c(hTf) ≈ 10−5 M, c(FeNTA) ≈ 10−4 M).28 This expected reaction time is significantly shorter than the incubation time we used. In all titrations, an excess of the competing ligand (NTA) was present in the solution to quench the apparent binding constants and ensure an appropriate concentration regime.
The value of s corresponding to the relative fluorescence of Fe2Tf was determined in a separate experiment without excess NTA, corresponding to the titration regime where essentially all added Fe is depleted from solution due to binding to hTf, until there is no free hTf left and a break in the titration curve can be observed.56 Consequently, the values of the relative fluorescence of Fe2Tf obtained in the titration regime (s = 0.174 for Tf+S and s = 0.183 for Tf−S) were used for fitting the titration data.
The obtained macroscopic binding constants K1m and K2m are apparent constants that correspond to the exchange of iron from the FeNTA complex to transferrin. For the calculation of the conditional thermodynamic binding constants from the apparent binding constants, the equilibria for the FeNTA complex must be considered.57 The pH-specific conditional thermodynamic binding constants K′1m and K′2m were calculated from the obtained values of K1m and K2m alongside the pH-dependent conditional constant K′110 which characterizes the interaction between iron(III) and NTA:
| log(K′1m) = log(K1m) + log(K′110) | (13) |
| log(K′2m) = log(K2m) + log(K′110) | (14) |
For additional details on the calculation of the binding constants and data fitting, see ESI, section 7.†
Statistical considerations
All results are expressed as means of at least 3 replicate measurements, with standard deviations in parentheses. The statistical significance of the differences between the native and desialylated protein for each pH value was evaluated using the Satterthwaite's approximate t-test, a method in the Behrens-Welch family based on the more robust t-statistic with approximate degrees of freedom.58 All values of p ≤ 0.05 were considered statistically significant. Further details on the statistical analyses can be found in the ESI, section 8.†Uncertainties in fitting parameters were obtained using the “jackknife” procedure by omitting a data point one by one from the calculation of the RSS and fitting all remaining points to obtain a new set of parameters.59 The standard deviations of the parameters were calculated as described in the ESI, subsection 7.3.† A custom VBA routine was written for automatic application of this procedure to all data sets.
Results and discussion
Iron binding at normal serum pH
The addition of FeNTA to the solution of apoTf leads to a decrease in the observed fluorescence due to the quenching of the intrinsic protein fluorescence upon binding of the paramagnetic Fe(III) ion.55 The decrease in fluorescence is proportional to the amount of iron-containing transferrin and thus allows the calculation of the apparent binding constants K1m and K2m according to the binding model (eqn (1)–(11)). A typical titration experiment and the calculated fluorescence, Fcalc, obtained by fitting the observed normalized fluorescence, Fnorm, using the Solver tool in Microsoft Excel are shown in Fig. 2. Table 1 shows the calculated binding constants for Tf+S and Tf−S at different pH levels. Additionally, data for all titrations can be found in the ESI, Fig. S7–S40.†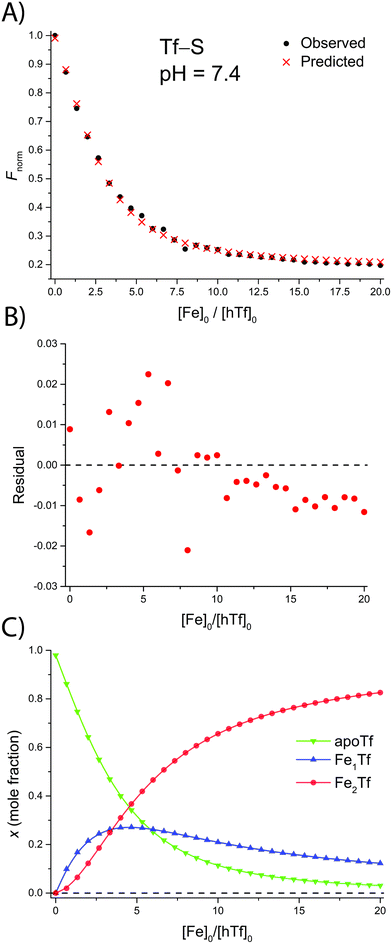 | ||
| Fig. 2 A typical spectrofluorometric titration of human serum transferrin with FeNTA: [Tf]0 = 3.84 μM, [PIPES] = 25 mM, [KCl] = 0.2 M, pH = 6.5, 25 °C. The parameters determined with the Solver tool in Microsoft Excel to calculate Fcalc defined in eqn (12) are: log(K1m) = 5.886 ± 0.026, log(R) = 1.175 ± 0.019, R2 = 0.9934. (A): Measured normalized fluorescence (Fobs) and calculated normalized fluorescence (Fcalc); (B): residuals of fit calculated as Fcalc − Fobs; (C): transferrin speciation according to eqn (9)–(11). | ||
| pH | Native apo-transferrin (Tf+S), IS = 127.79,a pI = 5.4 | Desialylated apo-transferrin (Tf−S), IS = 1.51, pI = 6.8 | ||||||
|---|---|---|---|---|---|---|---|---|
| log(K′1m) | log(K′2m) | log(K′1m) | log(K′2m) | |||||
a
IS is the index of sialylation defined as: 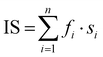 . n represents the N-glycan fraction number, fi denotes the percentage content of the specific N-glycan fraction, and si indicates the count of sialic acids within the structure of the corresponding N-glycan fraction.39
b Obtained by Aisen et al. for native hTf (Tf+S) by equilibrium dialysis at ambient p(CO2) = 3.6 × 104 atm, corresponding to the concentration of [HCO3−] = 0.14 mM.37 The original values of the conditional thermodynamic constants were subsequently recalculated and corrected by Martin et al.60
c Obtained by Martin et al. for native hTf (Tf+S) by UV/Vis spectroscopy and [HCO3−] = 5 mM.60
d Values obtained from ITC data for the reaction of FeNTA with apoTf at 25 °C in 0.1 M HEPES, pH 7.4, and [HCO3−] = 25 mM. Data were analysed using a model for two non-identical binding sites.17
e At pH = 6.8 we observed significant cooperative binding (i.e., K′1m ≪ K′2m) that can complicate the accurate determination of equilibrium constants.63 For clarity, these results were omitted from Fig. 2–5 and discussed separately (see text).
f Omitting a significant single-point outlier, the adjusted values become log(K′1m) = 20.216 (0.017), log(K′2m) = 18.837 (0.014). . n represents the N-glycan fraction number, fi denotes the percentage content of the specific N-glycan fraction, and si indicates the count of sialic acids within the structure of the corresponding N-glycan fraction.39
b Obtained by Aisen et al. for native hTf (Tf+S) by equilibrium dialysis at ambient p(CO2) = 3.6 × 104 atm, corresponding to the concentration of [HCO3−] = 0.14 mM.37 The original values of the conditional thermodynamic constants were subsequently recalculated and corrected by Martin et al.60
c Obtained by Martin et al. for native hTf (Tf+S) by UV/Vis spectroscopy and [HCO3−] = 5 mM.60
d Values obtained from ITC data for the reaction of FeNTA with apoTf at 25 °C in 0.1 M HEPES, pH 7.4, and [HCO3−] = 25 mM. Data were analysed using a model for two non-identical binding sites.17
e At pH = 6.8 we observed significant cooperative binding (i.e., K′1m ≪ K′2m) that can complicate the accurate determination of equilibrium constants.63 For clarity, these results were omitted from Fig. 2–5 and discussed separately (see text).
f Omitting a significant single-point outlier, the adjusted values become log(K′1m) = 20.216 (0.017), log(K′2m) = 18.837 (0.014).
|
||||||||
| 7.4 | 21.510 | (0.019) | 21.743 | (0.013) | 22.011 | (0.027) | 22.271 | (0.013) |
| 22.5 | (0.1)b | 21.3 | (0.1)b | |||||
| 22.3 | (0.1)c | 21.7 | (0.1)c | |||||
| 23.22 | (0.15)d | 21.06 | (0.12)d | 24.06 | (0.23)d | 22.31 | (0.15)d | |
| 6.8e | 15.302 | (0.010) | 24.833 | (0.017) | 15.407 | (0.043) | 24.863 | (0.046) |
| 6.5 | 20.589 | (0.033) | 19.414 | (0.015) | 20.791 | (0.033) | 20.657 | (0.014) |
| 6.2 | 19.915 | (0.065) | 18.395 | (0.027) | 20.233 | (0.161)f | 18.841 | (0.056)f |
| 5.9 | 18.937 | (0.016) | 17.396 | (0.012) | 19.933 | (0.050) | 18.369 | (0.015) |
The conditional thermodynamic constants for the binding of the first and second iron(III) ion determined at pH = 7.4 agree reasonably well with the earlier studies by Aisen et al. and Martin et al.37,60 This indicates the validity of the model and provides a basis for comparison with literature data and further comparison of Tf+S and Tf−S. To compare the results obtained at different solution HCO3− concentrations, the literature values were corrected by adding log(10 M/[HCO3−]) to the values of log(K′1m) and log(K′2m), where [HCO3−] = 10 mM (in all experiments).60,61 As noted by Harris and Pecoraro, this correction only applies at pH = 7.4, because all equilibria involved are pH-dependent.61
Protein sialic acid content appears to influence iron binding at normal human serum pH, with log(K′1m) and log(K′2m) values for desialylated transferrin, Tf−S, being approximately 0.5 log units higher, corresponding to an approximately 3-fold increase in iron binding affinity for both sites. This corresponds to a change in free energy of about 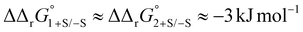 for binding of the first and second iron ion, respectively. Furthermore, at normal human serum pH, the two binding sites appear to have low positive cooperativity, i.e. K1m < K2m, for both Tf+S and Tf−S.
for binding of the first and second iron ion, respectively. Furthermore, at normal human serum pH, the two binding sites appear to have low positive cooperativity, i.e. K1m < K2m, for both Tf+S and Tf−S.
Based on the considerations of Thordarson54 the extent of cooperativity in binding can be quantified using the interaction parameter α, which is calculated as follows:
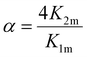 | (15) |
Positive cooperativity is indicated by α > 1, negative cooperativity by α < 1 and non-cooperative binding by α = 1. This corresponds to the parameter ρ2 in the work of Freire et al.,53 who equate the value of α = ρ2 with a cooperativity association constant κ, which reflects the energy loss or gain due to simultaneous binding of the ligand to both binding sites. Consequently, α > 1 in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding system corresponding to two iron binding sites of hTf indicates a preference for the formation of a 2
1 binding system corresponding to two iron binding sites of hTf indicates a preference for the formation of a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex over a 1
1 complex over a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, i.e. for equivalent degrees of saturation, the concentration of single liganded species is lower than in the case of independent binding.
1 complex, i.e. for equivalent degrees of saturation, the concentration of single liganded species is lower than in the case of independent binding.
The observed low positive cooperativity at pH 7.4 is consistent with the earlier recalculation of binding constants by Freire et al. using digitally extracted ITC titration data for hTf published by Lin et al.34 They also found a cooperative effect of α = 2.2 (expressed as the equivalent parameter ρ2), corresponding to a cooperative Gibbs energy of 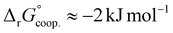 .53 Our results show slightly higher values for α, corresponding to Gibbs energies of
.53 Our results show slightly higher values for α, corresponding to Gibbs energies of 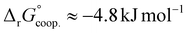 for Tf+S and
for Tf+S and 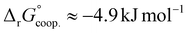 for Tf−S. Very similar values for Tf+S and Tf−S indicate that sialylation does not appear to affect the binding cooperativity at pH = 7.4 (p = 0.126, Table S6, ESI†).
for Tf−S. Very similar values for Tf+S and Tf−S indicate that sialylation does not appear to affect the binding cooperativity at pH = 7.4 (p = 0.126, Table S6, ESI†).
On the other hand, Aisen et al.37 and subsequently Martin et al.60 reported non-cooperative binding with values corresponding to log(K′1m) and log(K′2m), listed in Table 1 for reference. These values differ by more than 0.6 units, which is the expected statistical factor for binding to a two-sited protein with equal and independent binding sites (i.e., α = 1 and K′1m/K′2m = 4 ≈ 100.6).37 Methodological differences, such as buffer compositions and ionic strengths, between our study and those of Aisen et al. and Martin et al., may account for these discrepancies, highlighting the need for careful consideration of experimental conditions.
The results obtained by spectrofluorometric titrations in this study are also in some contrast to our results for the reaction of hTf with FeNTA obtained by ITC.17 These showed a difference of about two orders of magnitude in the values corresponding to the conditional thermodynamic constants log(K′1m) and log(K′2m), indicating sequential binding. In addition, desialylation was found to increase the binding of the first iron(III) ion by about 10-fold, while the effect on the binding of the second iron(III) ion was about 20-fold, which is much higher than observed in this study.
The differences in the binding constants observed between the fluorometric and ITC methods can be attributed, at least in part, to differences in the ionic strength and buffer composition of the samples. The fluorometric experiments reported here used solutions containing 0.2 M KCl and PIPES buffer, as opposed to the HEPES buffer used in the previous ITC study. This observation is consistent with the findings of Abdizadeh et al.,62 who showed that variations in salt concentration significantly affect the dynamics and conformation of transferrin, which in turn can affect its iron-binding affinity.
Importantly, our two studies both confirm the increased iron binding affinity for desialylated hTf. It seems reasonable to attribute the observed differences to the different experimental techniques and conditions. The results presented in this work were obtained under conditions with an excess of competing ligand (NTA) and long incubation time. On the other hand, the ITC experiments were performed by incremental addition of reactant aliquots and measuring the resulting heat change immediately after addition, which emphasizes the kinetic aspects of the interaction.
Therefore, under the conditions of the spectrofluorimetric titrations reported here, additional site-exchange reactions mediated by the competing ligand that occur at longer incubation times may be reflected in the results. Such observations are consistent with previous studies that have shown that iron binding site preference is determined by kinetic as well as thermodynamic factors.13,34,37
The pH-dependence of iron binding
A significant effect of sialylation can be observed on the pH-dependence of iron binding, as can be seen from the decreasing macroscopic binding constants K′1m and K′2m with decreasing pH for both Tf+S and Tf−S (Fig. 3). The shift in pH from 7.4 to 5.9 results in a change in free energy of approximately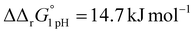 for the binding of the first iron cation to Tf+S and
for the binding of the first iron cation to Tf+S and 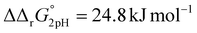 for the second, while for Tf−S the corresponding changes are
for the second, while for Tf−S the corresponding changes are 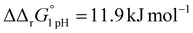 and
and 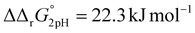 . This means that the binding affinity for Tf−S is increased about 10-fold compared to Tf+S at pH 5.9, while the binding affinity for Tf−S is only increased 3-fold compared to Tf+S at pH 7.4.
. This means that the binding affinity for Tf−S is increased about 10-fold compared to Tf+S at pH 5.9, while the binding affinity for Tf−S is only increased 3-fold compared to Tf+S at pH 7.4.
 | ||
| Fig. 3 The pH dependence of the apparent macroscopic binding constants K′1m and K′2m for different pH values at 25 °C (values are listed in Table 1): (A): log(K′1m) values for Tf+S and Tf−S; (B): log(K′1m) and log(K′2m) values for Tf+S; (C): log(K′2m) values for Tf+S and Tf−S; (D): log (K′1m) and log(K′2m) values for Tf−S. The statistical significance of the observed differences in panels (A) and (C) is coded as p < 0.001 (***), p < 0.01 (**), p < 0.025 (*), see Table S5, ESI.† The error bar and the estimated K′1m value, pH = 6.2, Tf−S, highlighted in yellow, were derived by omitting the outlier at the 21st titration point from the analysis. | ||
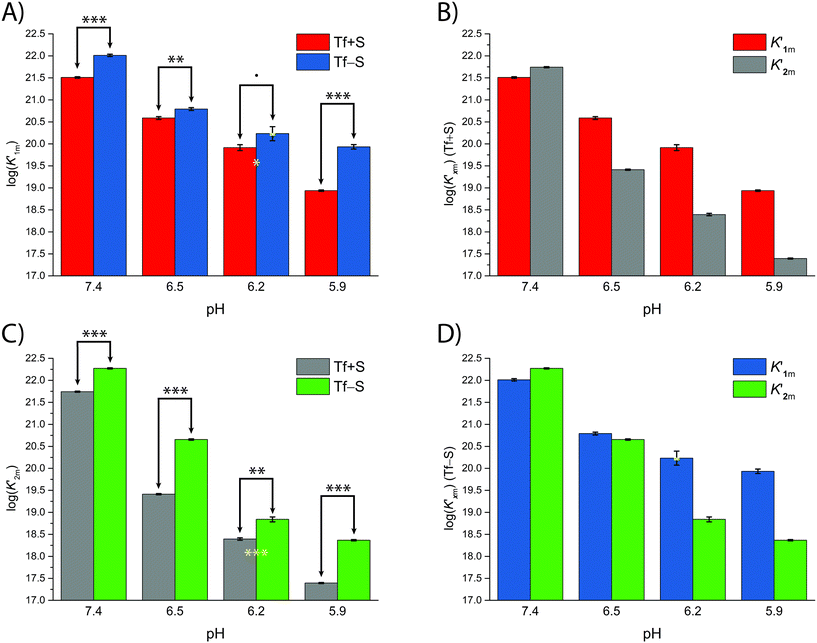
A mathematical model that can account for the observed pH-dependence of the binding constants was presented by Chasteen and Williams.13 Briefly, the metal-binding sites are affected by the apparent ionization of the functional groups of the protein according to the following model:
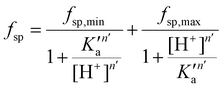 | (16) |
In their work, Chasteen and Williams found that the site preference factor of native transferrin is pH-dependent and is significantly affected by the presence of 0.5 M NaCl. Below a certain pH, referred to as the transition zone, iron binding shows a preference for the C-terminal site, independent of the presence of NaCl. Above this transition zone, the binding affinities for iron at both sites become similar in the absence of NaCl. However, in the presence of NaCl, the N-terminal site becomes more favourable, with a preference of almost 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Interestingly, the pH profiles between pH 6.0 and 6.5 are similar under both conditions.13
1. Interestingly, the pH profiles between pH 6.0 and 6.5 are similar under both conditions.13
The fsp values for Tf+S and Tf−S were calculated from log(K′1m) and log(K′2m), which are listed in Table 1. The results of fitting of these fsp values to the model described in eqn (16) using the Solver tool in Microsoft Excel are shown in Fig. 4 and in Table S8, ESI.† The results in Fig. 4 show that native hTf has a slightly higher pK′a value by about 0.2 units, implying that the site preference shifts to the first site at a less acidic pH compared to Tf−S. In other words, binding to the second site of the desialylated protein appears to be more resistant to an increase in acidity. This altered sensitivity of the second site to changes in solution pH seems to be mediated by the terminal sialic acids of the protein glycan chains.
 | ||
| Fig. 4 The pH-dependence of the site preference factor (K1m/K2m) defined by eqn (16) for different pH values at 25 °C. (A): Native hTf (Tf+S): pK′a = 6.47, fsp, min = 0.58, fsp, max = 34.8, n′ = 4.73, R2 > 0.999, (B): desialylated hTf (Tf−S): pK′a = 6.25, fsp, min = 0.55, fsp, max = 36.9, n′ = 6.45, R2 > 0.999. The values of fsp were calculated from the values of log(K′1m) and log(K′2m) obtained by fitting the titration data (Table 1). The numerical data are shown in Table S7, ESI.† The error bar and the estimated fsp value for Tf−S at pH = 6.2 (highlighted in cyan) result from omitting the outlier at the 21st titration point from the analysis. | ||
Considering that hTf undergoes significant conformational changes during the processes of iron uptake and release,3,64,65 the effect of the relatively large glycan structures (about 6% of hTf mass, see Fig. 1 for illustration) could have a significant impact on these processes. Moreover, the apparent number of protons increases from n′ ≈ 4.7 for Tf+S to n′ ≈ 6.4 for Tf−S, indicating a reduced pH-buffering capacity due to the sialic acid residues in Tf+S. The increase in proton exchange in desialylated transferrin suggests that the removal of sialic acids affects the protein conformation. This conformational change likely exposes more sites that can interact with protons, thus increasing the n′ value. The possible effect of the hTf sialylation pattern could therefore be in tuning the stability of the conformational state, which in turn contributes to the stability of the second site and decreases the value of the site-preference factor for Tf−S at pH 6.5 (Fig. 5).
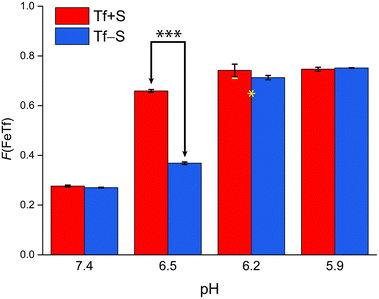 | ||
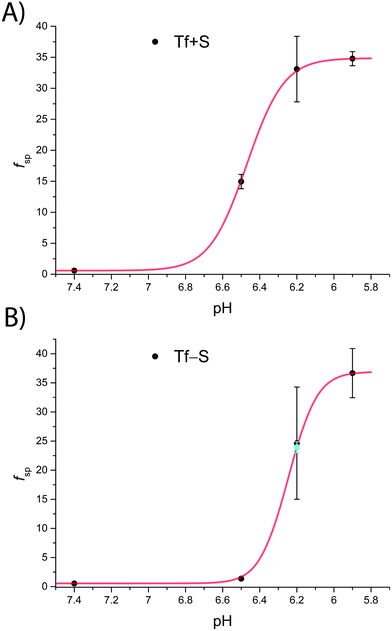
| Fig. 5 The pH-dependence of the fractional population of the intermediate complex at half saturation, F(FeTf), for experiments at 25 °C, at different pH values (values are shown in Tables S2 and S3, ESI†). Statistical significance of observed differences is coded as p < 0.001 (***), p < 0.01 (**), p < 0.025 (*), p < 0.1 (′) (Table S7, ESI†). The error bar and the estimated fsp value for Tf−S at pH = 6.2 (highlighted in yellow) result from omitting the outlier at the 21st titration point from the analysis. | ||
A recent study has highlighted a conformational stabilizing influence of sialic acids on hTf, suggesting a possible link to interactions between anionic sialic acid residues and cationic lysine residues within the N-lobe (e.g. Lys206 and Lys296).66 These lysine residues are involved in a pH-sensitive dilysine interaction that contributes to the stability of the N-site. Notably, the disruption of this dilysine pair has been found to trigger the release of Fe from the N-site.44,67
Furthermore, it has recently been shown that changes in the glycan composition of the human insulin receptor can alter long-range allosteric communication between protein residues. Specifically, removal of sialic acid residues resulted in increased flexibility of insulin-binding residues, accompanied by perturbations in glycan–protein interactions. Importantly, the same study has shown that even in the absence of significant changes in protein dynamics at the global level, changes in glycan composition induce perturbations at the local level.68 Our results seem to confirm a similar effect of sialic acid content on the iron binding dynamics of hTf.
Not surprisingly, the observed pH-dependence of the site preference factor translates directly into the fractional population of the intermediate complex at half saturation, F(FeTf), defined53 as:
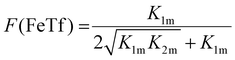 | (19) |
A reference value of F(FeTf) < 0.3 is observed for pH values close to 7.4 (Fig. 5), which corresponds to positive cooperativity, i.e. at equivalent saturation levels, the concentration of each liganded species is lower than for independent binding with a corresponding value of F(FeTf) = 0.5. Increasing the pH values led to an increase in the maximum value of F(FeTf) to higher values (above 0.7), corresponding to the values of the apparent acid dissociation constant pK′a. This means that for both Tf+S and Tf−S there is a much higher preference for FeTf over Fe2Tf at pH values closer to 5.9, which corresponds to conditions in the endosome, facilitating iron release.
However, the increased affinity of the second site of desialylated hTf maintains the value of F(FeTf) ≈ 0.37 at pH 6.5, followed by a sharp increase to above 0.7 at pH 6.2 and further to about 0.75 at pH 5.9. Fig. 5 shows very similar values of F(FeTf) for Tf+S and Tf−S at endosomal pH, which corresponds to the similar values of the site preference factor as shown in Fig. 4 (fsp ≈ 35 for Tf+S and fsp ≈ 37 for Tf−S). These overall differences in fsp values translate to differences in the free energy of 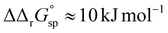 for both Tf+S and Tf−S, which is consistent with the results of Chasteen and Williams, who determined corresponding values of 7–9 kJ mol−1 for native hTf (Tf+S) under different experimental conditions (1 mM NaHCO3, pH range 7–9).13 Adding further context to these values, the absolute magnitude of the average change in free energy due to protein unfolding in water is
for both Tf+S and Tf−S, which is consistent with the results of Chasteen and Williams, who determined corresponding values of 7–9 kJ mol−1 for native hTf (Tf+S) under different experimental conditions (1 mM NaHCO3, pH range 7–9).13 Adding further context to these values, the absolute magnitude of the average change in free energy due to protein unfolding in water is 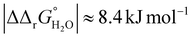 for a single amino acid mutation.69 This value is comparable to the
for a single amino acid mutation.69 This value is comparable to the 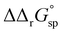 values determined for hTf, suggesting that sialylation as a post-translational modification can have a comparable impact on the stability and function of the protein without altering its primary structure.
values determined for hTf, suggesting that sialylation as a post-translational modification can have a comparable impact on the stability and function of the protein without altering its primary structure.
Again, these results contrast with our results for the same reaction obtained with ITC, due to the different values of K1m and K2m and the associated different values of fsp and F(FeTf). In particular, the values corresponding to the site preference factor in the ITC study can be calculated as fsp ≈ 170 for Tf+S and fsp ≈ 60 for Tf−S. This also resulted in a lower value of F(FeTf) for desialylated protein (F(FeTf) = 0.87 for Tf+S and F(FeTf) = 0.79 for Tf−S), indicating an increased proportion of Fe2Tf species due to the increased value of K′2m.17 Regardless of these differences, the general effect of desialylation, namely the increased stability of the second site to changes in pH, appears to be confirmed by both sets of experiments and may be reflected in the increased proportion of Fe2Tf species for Tf−S observable from the physiological pH of 7.4 to at least pH 6.5.
Physiological significance and other considerations
The observed influence of Tf sialylation may be related to the in vivo preference for iron binding to the N-lobe of the protein. In human serum, the average distribution of Tf iron variants was determined as follows: apoTf, 39.2%; FeCTf, 11.2%; FeNTf, 22.9%; and holoTf (Fe2Tf), 26.7%.67 The stabilization of the second binding site and the observed positive cooperativity at normal serum pH seem to be consistent with this distribution. The observed effect of transferrin desialylation could also influence the interaction with its receptors, hTfR1 and/or hTfR2. At pH 7.4, hTfR1 preferentially binds Fe2Tf, with about 5-fold lower affinity for FeTf species and about 30-fold lower affinity for apoTf.67 Therefore, the increased preference for Fe2Tf over FeTf for Tf−S at pH 6.5 may facilitate its binding to hTfR1. In the presence of the receptor, the rate of iron release from the C-lobe is increased, while the rate of release from the N-lobe is decreased. Furthermore, the interaction with the receptor favours the initial release of iron from the C-lobe at pH 5.6, which is reversed in the absence of hTfR1.67Molecular dynamics simulations performed at pH 5.6 and 7.4 showed that at the lower, endosomal pH, the cooperative interaction between the two domains of holo-transferrin decreases, facilitating iron release. The authors concluded that the pH-dependent change in hTf dynamics is due to the altered electrostatic potential distribution on the protein surface.70 This is consistent with our experimental results, where we found a lack of cooperativity at lower pH values. In addition, the ionic strength of the solution could play an important role in altering the electrostatic potential distribution around the protein surface. This in turn could contribute to the energetic pathways required for the protonation of tyrosine residues, a necessary precursor for iron release.62
The physiological significance of our results could also lie in understanding the behaviour of hTf in an acidic environment. Tissue acidosis is common in various pathological conditions such as cancer, inflammation, arthritis, stroke, ischemia, and others. Decreased tissue pH is the result of changes in cellular metabolism, often associated with hypoxia and impaired blood supply, leading to increased acid production through glycolysis.71 For example, in the tumour microenvironment, factors such as deregulated energy metabolism, insufficient perfusion, and uncontrolled proliferation collectively contribute to tissue acidity. Local pH values as low as 5.6 have been recorded in human tumours, with typical values between 6.4 to 7, which corresponds well to the experimental conditions in this study.72 As mentioned in the introduction, alterations in transferrin sialylation are also closely associated with various acute and chronic disease states. For example, acute pancreatitis has been shown to be associated with a rapid decrease in hTf sialylation from the first to the second day of illness, which has been shown to be a good prognostic marker.73
By demonstrating that Tf−S binds iron much more effectively under acidic conditions, our study suggests a possible mechanism by which iron availability and toxicity could be modulated in ischemic tissues. This modulation could influence the dynamics of the labile iron pool (LIP) and potentially impact the pathophysiological consequences of ischemic events. For example, transferrin-mediated iron transport has recently been shown to play an important role in increasing LIP during ischemia and to contribute to Fenton reaction-mediated lipid peroxidation in the early reperfusion phase of cardiac ischemia/reperfusion injury.74
Unexpectedly, we observed a pronounced positive cooperativity for both Tf+S and Tf−S at pH = 6.8, which was not observed at other pH values (Table 1 and Fig. S20–S22 and S35–S37, ESI†). Apparently, the initial binding of an iron ion to apo-transferrin significantly enhances the binding of the subsequent ion, resulting in a persistent scarcity of the monoferric form, as additional iron tends to further saturate the half-saturated monoferric transferrin. This suggests that the second iron ion binding event may dominate and possibly mask the effects of the first binding event, leading to incorrect values of the equilibrium constant.63 Our observations indicate that the pronounced cooperativity in the experiments at pH = 6.8 is likely due to a particular interplay between pH and ionic strength.
In the context of the high-throughput fluorescence measurements used in this study, a recently developed z-position inner filter effect correction method (ZINFE) was successfully used to correct the measured fluorescence in microplates51 and compared with the commonly used method proposed by Lakowicz.52 The two IFE correction methods are highly correlated, as can be observed by plotting the results of one correction against the other (Fig. S5 and S6, ESI†). This indicates that both methods are suitable for the range of absorbance values observed in this study. However, the ZINFE method does not require direct measurements of sample absorbance at the excitation and emission wavelengths. As previously reported, it is important to clarify that the high and constant IFE itself does not cause nonlinearity with respect to the fluorescence concentration response; rather, this is caused by the variation of IFE in the samples.75 To minimize the variation of the primary IFE, the experiments were designed to keep the transferrin concentration constant for all samples in each titration.
Conclusions
The intrinsic fluorescence quenching upon binding of iron to hTf was successfully modelled according to the binding polynomial for two independent iron binding sites. This provided a general solution to obtain both the apparent and conditional thermodynamic equilibrium constants by using only 2 parameters to fit the experimental data. The results obtained at pH = 7.4 for Tf+S were in good agreement with previous benchmark studies, confirming the validity of the model and allowing further measurements in a high-throughput format. Removal of the sialic acid residues resulted in an approximately 3-fold increase in iron binding affinity for both sites of desialylated hTf at pH 7.4. In general, this appears to be consistent with our previous ITC study, but the results reported here seem to emphasize the effects of excess competing ligand and a long incubation time on the obtained results.A significant effect is also observed in the pH-dependence of iron binding, with differences in the conditional thermodynamic equilibrium constants indicating a higher stability of the second binding site for the desialylated hTf down to pH = 6.5. Such an effect can possibly be attributed to the effects of sialic acid residues on the conformational state of hTf, leading to a tuning of the stability of the second site. This suggests that variations in the sialic acid content of the protein influence the iron binding dynamics of hTf through allosteric interactions. This could explain the distribution of hTf binding sites in vivo and also influence binding to the hTf receptor. Beyond the scope of this work, the obtained results could help to establish a correlation between the changes in hTf glycan structure associated with different conditions and the observed changes in iron binding equilibrium. This study demonstrates that desialylated hTf binds iron more efficiently under acidic conditions, highlighting the potential role of hTf in regulating iron availability and toxicity in ischemic tissues.
Furthermore, in this study we have developed an efficient template for the numerical calculation of chemical equilibrium problems using Microsoft Excel. This approach, which is based on the binding polynomial, serves as a basis for a comprehensive and model-independent investigation of binding experiments.53 The presented spreadsheet-based approach may be a practical addition to the tools available to researchers and educators alike. In our previous work,31 the distribution of FeNTA species obtained using the Jenkins–Traub algorithm in Excel showed excellent agreement with the species distribution from the HySS software, which uses the Newton–Raphson algorithm to solve mass balance equations with known equilibrium constants.76 These results outperform those of the original treatment of FeNTA equilibria by Hegenauer et al., which requires an iterative procedure that is difficult to implement in spreadsheet software and is only applicable to solutions with an excess of total NTA over total Fe.77 However, future studies applied to systems with well-characterized binding constants should further validate the accuracy of the approach.
Author contributions
Tomislav Friganović and Valentina Borko carried out the experiments under the supervision of Tin Weitner. Tin Weitner created the Excel template that was used for the equilibrium constants. Tomislav Friganović created the Python software utilized for the glycan analysis. All authors contributed to the writing of the manuscript.Data availability
Data for this paper, including all measurements, fitting results and statistical analyses are available at Zenodo at https://doi.org/10.5281/zenodo.10881688.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by funding from the Croatian Science Foundation grant UIP-2017-05-9537 – Glycosylation as a factor in the iron transport mechanism of human serum transferrin (GlyMech). Valentina Borko was additionally financed by the Croatian Science Foundation grant DOK-2018-09-1042. Additional support was provided by the European Regional Development Fund grants for ‘Strengthening of Scientific Research and Innovation Capacities of the Faculty of Pharmacy and Biochemistry at the University of Zagreb’ (KK.01.1.1.02.0021), ‘Development of methods for production and labelling of glycan standards for molecular diagnostics’ (KK.01.1.1.07.0055) and ‘Scientific center of excellence for personalized health care’ (KK.01.1.1.01.0010).References
- J. Parkkinen, L. Von Bonsdorff, F. Ebeling and L. Sahlstedt, Vox Sang., 2002, 83, 321–326 CrossRef CAS PubMed.
- Y. Yu, L. Jiang, H. Wang, Z. Shen, Q. Cheng, P. Zhang, J. Wang, Q. Wu, X. Fang, L. Duan, S. Wang, K. Wang, P. An, T. Shao, R. T. Chung, S. Zheng, J. Min and F. Wang, Blood, 2020, 136, 726–739 CrossRef CAS PubMed.
- R. Pakdaman and J.-M. E. H. Chahine, Eur. J. Biochem., 1996, 236, 922–931 CrossRef CAS PubMed.
- P. T. Gomme, K. B. McCann and J. Bertolini, Drug Discovery Today, 2005, 10, 267–273 CrossRef CAS PubMed.
- N. Yang, H. Zhang, M. Wang, Q. Hao and H. Sun, Sci. Rep., 2012, 2, 999 CrossRef PubMed.
- R. T. A. MacGillivray, S. A. Moore, J. Chen, B. F. Anderson, H. Baker, Y. Luo, M. Bewley, C. A. Smith, M. E. P. Murphy, Y. Wang, A. B. Mason, R. C. Woodworth, G. D. Brayer and E. N. Baker, Biochemistry, 1998, 37, 7919–7928 CrossRef CAS PubMed.
- M. R. Schlabach and G. W. Bates, J. Biol. Chem., 1975, 250, 2182–2188 CrossRef CAS PubMed.
- N. Kojima and G. W. Bates, J. Biol. Chem., 1981, 256, 12034–12039 CrossRef CAS PubMed.
- M. Wessling-Resnick, Crit. Rev. Biochem. Mol. Biol., 1999, 34, 285–314 CrossRef CAS PubMed.
- M. E. Conrad, J. N. Umbreit and E. G. Moore, Am. J. Med. Sci., 1999, 318, 213 CrossRef CAS PubMed.
- A. H. Schmaier, Cell Res., 2020, 30, 101–102 CrossRef PubMed.
- J. B. Vincent and S. Love, Biochim. Biophys. Acta, Gen. Subj., 2012, 1820, 362–378 CrossRef CAS PubMed.
- N. D. Chasteen and J. Williams, Biochem. J., 1981, 193, 717–727 CrossRef CAS PubMed.
- D. A. Lee and J. M. Goodfellow, Biophys. J., 1998, 74, 2747–2759 CrossRef CAS PubMed.
- P. Aisen, Ann. Neurol., 1992, 32 Suppl, S62–S68 CrossRef CAS PubMed.
- C. A. Worthen and C. A. Enns, Front. Pharmacol., 2014, 5 DOI:10.3389/fphar.2014.00034.
- V. Borko, T. Friganović and T. Weitner, J. Inorg. Biochem., 2023, 244, 112207 CrossRef CAS PubMed.
- J. Caslavska and W. Thormann, J. Sep. Sci., 2018, 41, 303–322 CrossRef CAS PubMed.
- G. De Jong and H. G. Van Eijk, Electrophoresis, 1988, 9, 589–598 CrossRef CAS PubMed.
- V. Sanz-Nebot, E. Balaguer, F. Benavente, C. Neusüβ and J. Barbosa, Electrophoresis, 2007, 28, 1949–1957 CrossRef CAS PubMed.
- M. Edwards, F. McKenzie, S. O'Callaghan, D. Somerset, P. Woodford, J. Spilsbury, M. Fietz and J. Fletcher, Prenatal Diagn., 2006, 26, 985–988 CrossRef CAS PubMed.
- G. De Jong, R. Feelders, W. L. Van Noort and H. G. Van Eijk, Glycoconjugate J., 1995, 12, 219–226 CrossRef CAS PubMed.
- M. Piagnerelli, K. Z. Boudjeltia, V. Nuyens, D. De Backer, F. Su, Z. Wang, J.-L. Vincent and M. Vanhaeverbeek, Shock, 2005, 24, 48–52 CrossRef CAS PubMed.
- O. Gornik, I. Gornik, I. Z. Kolednjak and G. Lauc, Intern. Med., 2011, 50, 861–869 CrossRef CAS PubMed.
- B.-J. Kim, J. Zhou, B. Martin, O. D. Carlson, S. Maudsley, N. H. Greig, M. P. Mattson, E. E. Ladenheim, J. Wustner, A. Turner, H. Sadeghi and J. M. Egan, J. Pharmacol. Exp. Ther., 2010, 334, 682–692 CrossRef CAS PubMed.
- M. E. del Castillo Busto, M. Montes-Bayón, E. Blanco-González, J. Meija and A. Sanz-Medel, Anal. Chem., 2005, 77, 5615–5621 CrossRef CAS PubMed.
- R. Aasa, B. G. Malmström, P. Saltman and T. Vänngaard, Biochim. Biophys. Acta, 1963, 75, 203–222 CrossRef CAS PubMed.
- G. W. Bates and J. Wernicke, J. Biol. Chem., 1971, 246, 3679–3685 CrossRef CAS.
- J. O. Jeppsson, H. Kristensson and C. Fimiani, Clin. Chem., 1993, 39, 2115–2120 CrossRef CAS.
- A. Levina, A. R. M. Chetcuti and P. A. Lay, Biomolecules, 2022, 12, 1319 CrossRef CAS PubMed.
- V. Borko, T. Friganović and T. Weitner, Anal. Methods, 2023, 15, 6499–6513 RSC.
- D. C. Harris, A. L. Rinehart, D. Hereld, R. W. Schwartz, F. P. Burke and A. P. Salvador, Biochim. Biophys. Acta, Gen. Subj., 1985, 838, 295–301 CrossRef CAS PubMed.
- N. G. James, C. L. Berger, S. L. Byrne, V. C. Smith, R. T. A. MacGillivray and A. B. Mason, Biochemistry, 2007, 46, 10603–10611 CrossRef CAS PubMed.
- L. N. Lin, A. B. Mason, R. C. Woodworth and J. F. Brandts, Biochemistry, 1993, 32, 9398–9406 CrossRef CAS PubMed.
- L. N. Lin, A. B. Mason, R. C. Woodworth and J. F. Brandts, Biochemistry, 1994, 33, 1881–1888 CrossRef CAS PubMed.
- N. G. James, S. L. Byrne and A. B. Mason, Biochim. Biophys. Acta, Proteins Proteomics, 2009, 1794, 532–540 CrossRef CAS PubMed.
- P. Aisen, A. Leibman and J. Zweier, J. Biol. Chem., 1978, 253, 1930–1937 CrossRef CAS PubMed.
- T. J. Egan, O. Zak and P. Aisen, Biochemistry, 1993, 32, 8162–8167 CrossRef CAS PubMed.
- T. Friganović, A. Tomašić, T. Šeba, I. Biruš, R. Kerep, V. Borko, D. Šakić, M. Gabričević and T. Weitner, Heliyon, 2021, 7, e08030 CrossRef PubMed.
- Woods Group. (2005–2024) GLYCAM Web. Complex Carbohydrate Research Center, University of Georgia, Athens, GA. (https://glycam.org).
- R. Wen, H. Zhao, D. Zhang, C.-L. Chiu and J. D. Brooks, Carbohydr. Res., 2022, 519, 108598 CrossRef CAS PubMed.
- G. Murugesan, B. Weigle and P. R. Crocker, Curr. Opin. Chem. Biol., 2021, 62, 34–42 CrossRef CAS PubMed.
- H. Yan, T. Zou, Q. Tuo, S. Xu, H. Li, A. A. Belaidi and P. Lei, Signal Transduction Targeted Ther., 2021, 6, 49 CrossRef CAS PubMed.
- M. Hamano Nagaoka and T. Maitani, Biochim. Biophys. Acta, Gen. Subj., 2001, 1526, 175–182 CrossRef CAS PubMed.
- T. Friganović, V. Borko and T. Weitner, Maced. Pharm. Bull., 2022, 68, 415–416 Search PubMed.
- T. Friganović, V. Borko, T. Šeba, R. Kerep and T. Weitner, Protocol for pH-gradient chromatofocusing of the native and desialylated human apo-transferrin, Zenodo, 2020 DOI:10.5281/zenodo.4006002.
- T. Šeba, T. Friganović and T. Weitner, Protocol for spectrophotometric determination of native and desialylated apo-transferrin molar absorption coefficients, Zenodo, 2020 DOI:10.5281/zenodo.4001959.
- N. G. James and A. B. Mason, Anal. Biochem., 2008, 378, 202–207 CrossRef CAS PubMed.
- A. V. Fonin, A. I. Sulatskaya, I. M. Kuznetsova and K. K. Turoverov, PLoS One, 2014, 9, e103878 CrossRef PubMed.
- M. Kubista, R. Sjöback, S. Eriksson and B. Albinsson, Analyst, 1994, 119, 417–419 RSC.
- T. Weitner, T. Friganović and D. Šakić, Anal. Chem., 2022, 94, 7107–7114 CrossRef CAS PubMed.
- Principles of Fluorescence Spectroscopy, ed. J. R. Lakowicz, Springer, US, Boston, MA, 2006, pp. 27–61 Search PubMed.
- E. Freire, A. Schön and A. Velazquez-Campoy, in Methods in Enzymology, Elsevier, 2009, vol. 455, pp. 127–155 Search PubMed.
- P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323 RSC.
- S. L. Byrne and A. B. Mason, JBIC, J. Biol. Inorg. Chem., 2009, 14, 771–781 CrossRef CAS PubMed.
- I. Jarmoskaite, I. AlSadhan, P. P. Vaidyanathan and D. Herschlag, eLife, 2020, 9, e57264 CrossRef CAS PubMed.
- R. J. Motekaitis and A. E. Martell, J. Coord. Chem., 1994, 31, 67–78 CrossRef CAS.
- P. Armitage, G. Berry and J. N. S. Matthews, Statistical Methods in Medical Research, Wiley, 1st edn, 2002 Search PubMed.
- D. C. Harris, J. Chem. Educ., 1998, 75, 119 CrossRef CAS.
- R. B. Martin, J. Savory, S. Brown, R. L. Bertholf and M. R. Wills, Clin. Chem., 1987, 33, 405–407 CrossRef CAS.
- W. R. Harris and V. L. Pecoraro, Biochemistry, 1983, 22, 292–299 CrossRef CAS PubMed.
- H. Abdizadeh, A. R. Atilgan and C. Atilgan, J. Phys. Chem. B, 2017, 121, 4778–4789 CrossRef CAS PubMed.
- J. Peacock and J. B. Jaynes, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 2789–2801 CrossRef CAS PubMed.
- S. L. Byrne, A. N. Steere, N. D. Chasteen and A. B. Mason, Biochemistry, 2010, 49, 4200–4207 CrossRef CAS PubMed.
- M. Hirose, Biosci., Biotechnol., Biochem., 2000, 64, 1328–1336 CrossRef CAS PubMed.
- G. Li, A. Phetsanthad, M. Ma, Q. Yu, A. Nair, Z. Zheng, F. Ma, K. DeLaney, S. Hong and L. Li, Anal. Chem., 2022, 94, 2142–2153 CrossRef CAS PubMed.
- A. M. N. Silva, T. Moniz, B. De Castro and M. Rangel, Coord. Chem. Rev., 2021, 449, 214186 CrossRef CAS.
- R. M. Rao, H. Wong, M. Dauchez and S. Baud, Glycobiology, 2021, cwab049 CrossRef PubMed.
- R. Nikam, A. Kulandaisamy, K. Harini, D. Sharma and M. M. Gromiha, Nucleic Acids Res., 2021, 49, D420–D424 CrossRef CAS PubMed.
- H. Abdizadeh and C. Atilgan, Phys. Chem. Chem. Phys., 2016, 18, 7916–7926 RSC.
- Y. K. Reshetnyak, A. Moshnikova, O. A. Andreev and D. M. Engelman, Front. Bioeng. Biotechnol., 2020, 8, 335 CrossRef PubMed.
- E. Boedtkjer and S. F. Pedersen, Annu. Rev. Physiol., 2020, 82, 103–126 CrossRef CAS PubMed.
- O. Gornik, I. Gornik, V. Gašparović and G. Lauc, Clin. Biochem., 2008, 41, 504–510 CrossRef CAS PubMed.
- D. Lee, E. Son and Y.-H. Kim, Free Radical Res., 2022, 56, 713–729 CrossRef CAS PubMed.
- T. Friganović and T. Weitner, Anal. Chem., 2023, 95, 13036–13045 CrossRef PubMed.
- L. Alderighi, P. Gans, A. Ienco, D. Peters, A. Sabatini and A. Vacca, Coord. Chem. Rev., 1999, 184, 311–318 CrossRef CAS.
- J. Hegenauer, P. Saltman and G. Nace, Biochemistry, 1979, 18, 3865–3879 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt01311e |
| This journal is © The Royal Society of Chemistry 2024 |
