Open Access Article
Open Access ArticleThermodynamics of spin crossover in a bis(terpyridine) cobalt(II) complex featuring a thioether functionality†
Lúcio
Ferraz Lobato
 a,
Samuele
Ciattini
b,
Angelo
Gallo
a,
Samuele
Ciattini
b,
Angelo
Gallo
 c,
Rafael A.
Allão Cassaro
c,
Rafael A.
Allão Cassaro
 a,
Lorenzo
Sorace
a,
Lorenzo
Sorace
 *d and
Giordano
Poneti
*d and
Giordano
Poneti
 *ae
*ae
aInstituto de Química, Universidade Federal do Rio de Janeiro, Rio de Janeiro, RJ 21941-909, Brazil
bInterdepartmental Center for Crystallography (CRIST), University of Florence, Via della Lastruccia 3–13, 50019 Sesto Fiorentino, Italy
cDepartment of Chemistry, University of Turin, Via Pietro Giuria 7, 10125 Torino, Italy
dDepartment of Chemistry “U. Schiff” and INSTM Research Unit, University of Florence, Via della Lastruccia 3–13, 50019 Sesto Fiorentino, Italy. E-mail: lorenzo.sorace@unifi.it
eDipartimento di Scienze Ecologiche e Biologiche, Università degli Studi della Tuscia, Largo dell'Università, 01100, Viterbo, Italy. E-mail: giordano.poneti@unitus.it
First published on 21st May 2024
Abstract
In this contribution, a terpyridine-based ligand bearing a thioether functionality is used to prepare a new cobalt(II) spin crossover complex: [Co(TerpyPhSMe)2](PF6)2 (1), where TerpyPhSMe is 4′-(4-methylthiophenyl)-2,2′:6′,2′′-terpyridine. Its structure, determined by single crystal X-ray diffraction, reveals a mer coordination of the tridentate terpyridine ligands, leading to a tetragonally compressed octahedron. Intermolecular interactions in the crystal lattice freeze the complex in the high spin state in the solid state at all temperatures, as indicated by magnetometry and Electron Paramagnetic Resonance (EPR) spectra. When dissolved in acetonitrile, however, temperature dependent electronic, 1H-NMR and EPR spectra highlight an entropy-driven spin crossover transition, whose thermodynamics parameters have been determined. This is the first report of a cobalt(II) SCO complex featuring a thioether group, allowing its implementation in chemically grown bistable monolayers and may open important perspectives for the use of such systems in molecular spintronics.
Introduction
Molecular materials with externally controllable physico-chemical properties1 are appealing candidates for sensors,2 mechanical actuators,3 units of storage4 or treatment5,6 of digital data. Complexes exhibiting Spin Crossover (SCO) are the most widely investigated class of switchable materials, featuring a transition between low spin and high spin electronic configurations, which is triggered by application of heat, pressure, magnetic field and other stimula.7–9 Albeit being mostly found for pseudo-octahedral iron(II) complexes,10 SCO has been observed also in coordination compounds based on different metal ions,11–13 being cobalt(II) one of them.11,14–17 Compared to iron(II) systems, cobalt(II) complexes are known to display more gradual entropy-driven SCO transitions.18 More recently, they attracted attention for their ability to show thermal hysteretic SCO behaviour19–21 and the possibility to act on their electronic state by electrochemical stimuli.19Deposition of switchable molecular materials on solid surfaces in a controlled and reproducible manner is a mandatory step for their implementation in devices. Moreover, it offers a potential way to control their electronic state externally using physical properties of the supporting layer.22 Indeed, the thioether,23,24 thioacetyl,25–27 or thiol28–30 functional groups have been frequently used, in the past, to functionalize magnetic molecular materials in order to graft them on top of noble metal surfaces. In this respect, due to its ability to bind transition metal ions and the ample possibilities of functionalization, the 2,2′:6′,2′′-terpyridine (tpy) molecular scaffold has proven to be a powerful building block for the development of discrete or supramolecular systems31–33 with potential gas absorption, photovoltaic, luminescent and magnetic applications.34–36 The 4′-position of the central pyridine ring is the most frequently encountered position for the derivatization of the terpyridine motif, yielding divergent molecular synthons for the preparation of coordination polymers.33 Furthermore, terpyridine-based ligands are the most frequently reported in literature to provide cobalt(II) SCO systems.11,17,37 By exploiting this approach, a complex where the cobalt(II) ion is coordinated by two terpyridine molecules functionalized in their 4′-position with a carboxylic acid recently revealed the persistence of SCO in a self-assembled monolayer on top of a silver surface.38 This is the only example, up to date, of a chemisorbed self assembled monolayer of a SCO complex, clearly evidencing the need to search for other potential candidates.
With this aim, we have here used the 4′ position to functionalize the terpyridine scaffold with a thioether functional group, separated from the terpyridine motif by a phenyl ring, to prepare the 4′-(4-methylthiophenyl)-2,2′:6′,2′′-terpyridine ligand (TerpyPhSMe hereafter – Scheme 1). The TerpyPhSMe ligand has been previously employed to prepare coordination compounds with different metal ions (ruthenium(II),39–41 iridium(III),42 zinc(II)43,44 and copper(II)45), but to the best of our knowledge, its potential for the preparation of switchable paramagnetic complexes is still unexplored.
The obtained ligand has been used to prepare a new cobalt-based complex, [Co(TerpyPhSMe)2](PF6)2 (1): its structure has been determined by single-crystal X-ray diffraction and its magnetic behaviour in the solid state has been evaluated with magnetometry and electron paramagnetic resonance. In solution, its SCO behaviour has been evaluated with temperature dependent electronic spectroscopy and nuclear (1H NMR) and electron (EPR) magnetic resonances.
Results and discussion
Synthesis
All manipulations were performed under aerobic conditions using materials as received. CoCl2·6H2O, 2-acetylpyridine, 4-methylthiobenzaldehyde and potassium hexafluorophosphate were purchased from Aldrich and used as received. The 4′-(4-methylthiophenyl)-2,2′:6′,2′′-terpyridine ligand (TerpyPhSMe) was synthesized according to a previously reported procedure.39 Compound 1 has been prepared by reacting a methanolic solution of CoCl2·6H2O (0.133 g, 0.56 mmol) with a stirring methanol suspension of TerpyPhSMe (0.452 g, 1.27 mmol) and left to react at room temperature for 4 hours. After this, the solution was filtrated to eliminate any undissolved, unreacted material, and an aqueous solution of KPF6 (0.207 g, 1.125 mmol) was added to the filtrate, causing the immediate separation of an orange precipitate. The obtained microcrystalline powder was subsequently recrystallized from a mixture of acetone and water. Mass spectrometry (Fig. S1†) and elemental analysis confirmed the expected structure of 1. Yield: 86%. Anal. Calcd for C44H34CoF12N6P2S2: C, 49.87; H, 3.23; N, 7.93. Found: C, 50.06; H, 3.17; N, 7.62%. Selected IR data (cm−1): 1599(m), 1479(w), 1419(w), 1248(w), 1079(w), 1017(w), 828(s), 650(w), 552(m), 503(w). 1H NMR (600.17 MHz, CD3CN) at 298 K δ (ppm): 92.36 (4H, s, 1), 54.35 (4H, s, 4), 43.6 (4H, s, 5), 32.27 (4H, s, 2), 13.77 (4H, s, 3), 9.14 (4H, s, 6), 9.09 (4H, s, 7), 3.55 (6H, s, 8).Solid state behaviour
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
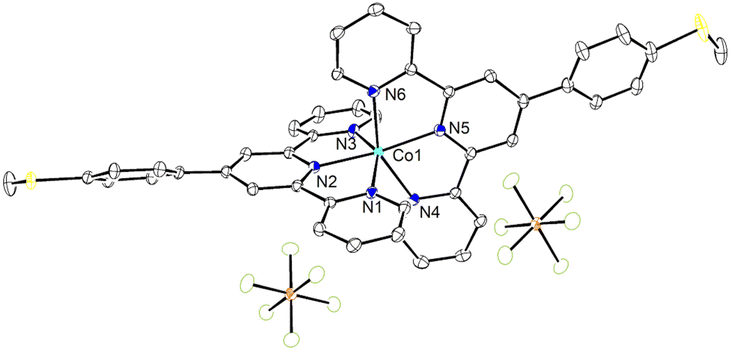
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 acetone/water solution at room temperature. The crystal structure of 1 has been determined at 99 K and its asymmetric unit is shown in Fig. 1. Details of the data collection and structure refinement are reported in Table S1.† Compound 1 crystallizes in the P21/c space group with 4 molecules per unit cell. The cobalt(II) ion is coordinated by the two terpyridine ligands in the classical bis-meridional fashion. The average Co–N bond length is 2.1285 Å, and the coordination environment can be described as an axially compressed octahedron, with Co–N2 and Co–N5 bond lengths being about 0.1 Å shorter than the average of the other four ones (see Table 1 selected bond lengths and angles). This is consistent with what previously observed for the high spin isomer of [Co(tpy-R)]2+ cations.16,20,21,46 In order to quantify the degree of distortion from ideal octahedral coordination of cobalt(II), Σ and ζ parameters were calculated using the OctaDist software,48 and Continuous Shape Measure analysis (CShM) was carried out using the SHAPE software.49 The ζ parameter describes the dispersion among the distances of the first coordination sphere (
50 acetone/water solution at room temperature. The crystal structure of 1 has been determined at 99 K and its asymmetric unit is shown in Fig. 1. Details of the data collection and structure refinement are reported in Table S1.† Compound 1 crystallizes in the P21/c space group with 4 molecules per unit cell. The cobalt(II) ion is coordinated by the two terpyridine ligands in the classical bis-meridional fashion. The average Co–N bond length is 2.1285 Å, and the coordination environment can be described as an axially compressed octahedron, with Co–N2 and Co–N5 bond lengths being about 0.1 Å shorter than the average of the other four ones (see Table 1 selected bond lengths and angles). This is consistent with what previously observed for the high spin isomer of [Co(tpy-R)]2+ cations.16,20,21,46 In order to quantify the degree of distortion from ideal octahedral coordination of cobalt(II), Σ and ζ parameters were calculated using the OctaDist software,48 and Continuous Shape Measure analysis (CShM) was carried out using the SHAPE software.49 The ζ parameter describes the dispersion among the distances of the first coordination sphere (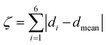 where di and dmean are Co–N bond lengths and average bond length, respectively), while Σ measures the deviation of the twelve cis-N–Co–N angles from 90° (
where di and dmean are Co–N bond lengths and average bond length, respectively), while Σ measures the deviation of the twelve cis-N–Co–N angles from 90° (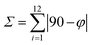 both are expected to be zero for a perfect octahedron. The obtained values of ζ = 0.25, Σ = 130.9 and CShM = 4.68 (see Table S2† for details) indicate that the octahedral coordination environment of cobalt(II) is significantly distorted. However, the ζ = 0.25 value obtained is in the expected range for high spin systems, while typically higher values are found for low-spin systems, due to Jahn–Teller distortions.16 Therefore, all of these structural parameters indicate that in the single crystal phase of 1, the cobalt(II) ion displays a high spin configuration at 99 K.
both are expected to be zero for a perfect octahedron. The obtained values of ζ = 0.25, Σ = 130.9 and CShM = 4.68 (see Table S2† for details) indicate that the octahedral coordination environment of cobalt(II) is significantly distorted. However, the ζ = 0.25 value obtained is in the expected range for high spin systems, while typically higher values are found for low-spin systems, due to Jahn–Teller distortions.16 Therefore, all of these structural parameters indicate that in the single crystal phase of 1, the cobalt(II) ion displays a high spin configuration at 99 K.
| Bond lengths (Å) | |||
| Co1–N1 | 2.1765(18) | Co1–N4 | 2.1637(19) |
| Co1–N2 | 2.0699(18) | Co1–N5 | 2.0624(18) |
| Co1–N3 | 2.1573(19) | Co1–N6 | 2.1415(18) |
| Bond angles (°) | |||
| N2–Co1–N1 | 75.21(7) | N2–Co1–N6 | 112.12(7) |
| N3–Co1–N1 | 149.39(7) | N3–Co1–N4 | 96.26(7) |
| N4–Co1–N1 | 95.93(7) | N5–Co1–N3 | 104.84(7) |
| N5–Co1–N1 | 105.31(7) | N6–Co1–N3 | 90.96(7) |
| N6–Co1–N1 | 91.54(7) | N5–Co1–N4 | 76.12(7) |
| N2–Co1–N3 | 75.61(7) | N6–Co1–N4 | 151.55(7) |
| N2–Co1–N4 | 96.33(7) | N5–Co1–N6 | 75.44(7) |
| N5–Co1–N2 | 172.44(7) | ||
In the case of 1, intermolecular π⋯π interactions are observed between pyridyl rings containing N4 and N6 and between pyridyl ring containing N4 and the phenyl ring of methylthiophenyl moiety of TerpyPhSMe ligand. Each molecule of the complex interacts with other three adjacent molecules leading to a two-dimensional network (Fig. S2†). The distances between centroids of pyridyl rings, and between centroids of pyridyl and phenyl rings are 3.718 and 4.004 Å, with the angle between planes being 15.4 and 17.8° and slippage of 1.614 and 1.244 Å, respectively. Other C–H⋯π and P–F⋯π interactions (not shown) were observed involving H3 and H43, with H⋯centroid distances of 2.76 and 2.99 Å, and C–H⋯centroid angles of 134 and 161°, respectively. The P2–F7⋯π (1 − x, −1/2 + y, 1/2 − z) intermolecular interaction involves the pyridyl moiety of TerpyPhSMe containing N5, with F7⋯centroid distance of 3.055 Å and P2–F7⋯centroid angle of 124.3°. These parameters are in the range found for π⋯π, C–H⋯π and P–F⋯π interactions in the literature.52–55 In addition, PF6− anions interact with the complex through non-classical C–H⋯F hydrogen bonds (Fig. S3†).56 The parameters found for the shortest H⋯F distances interactions are gathered in Table S3.† Many other weak intermolecular interactions with H⋯F distances spanning the range 2.45–2.54 Å were observed (not shown). These intermolecular interactions contribute to stabilization of crystal lattice and to the structural rigidity which locks 1 in the high spin state, in analogy to what was previously observed for other SCO complexes.11,50,51
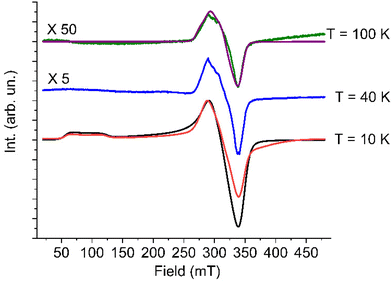
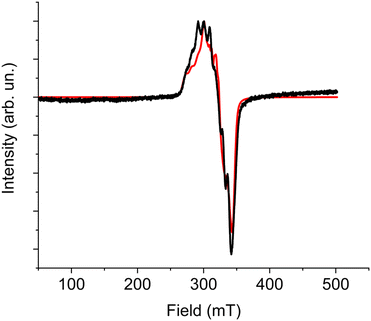
At low temperature the spectrum shows the typical features of a high spin cobalt(II) system, and can be interpreted by considering an effective S = 1/2 Spin Hamiltonian with largely anisotropic g tensor, resulting from the combined effect of distortions and spin–orbit coupling affecting the orbitally degenerate 4T1g state in purely octahedral symmetry.
In particular, the gzeff > gx,yeff feature is consistent with a tetragonal compression of the octahedron, resulting in an orbital ground doublet, further split by spin–orbit coupling.16 On increasing temperature the spectrum of the high spin species disappears as expected, due to the strong temperature dependence of the spin–lattice relaxation time of high-spin cobalt(II) in distorted octahedral environment. However, up to 100 K it remains a small trace of a broad and partially structured spectrum around g = 2.00, which we attribute to a fraction of low-spin cobalt(II) species.
A reliable simulation of the low temperature spectrum was obtained by using the following Spin Hamiltonian:57
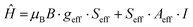 | (1) |
The observed pattern of effective g values for the high-spin species cannot be analyzed in the framework of an S = 3/2 Spin Hamiltonian58 and requires resorting to a description of the electronic structure of distorted octahedral cobalt(II) which explicitly takes into account the unquenched orbital angular momentum first proposed by Griffith:59,60
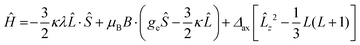 | (2) |
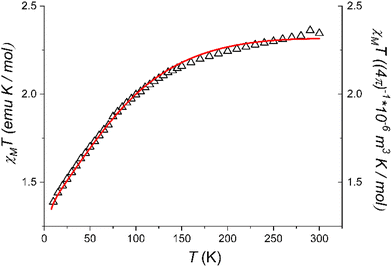 | ||
| Fig. 3 Temperature evolution of the χMT product of 1 and simulated curve obtained using the parameter-free model reported in the text. | ||
The χMT value at room temperature (2.35 emu K mol−1) is on the lower end of what expected for an octahedrally distorted high spin Co(II) centre, characterized by a relevant orbital contribution.60 On cooling, the χMT values lower steadily until about 150 K, then more steeply to reach 1.39 emu K mol−1 at 10.0 K. The observed values are consistent with those observed by EPR spectroscopy, and point to a high-spin cobalt(II) configuration for 1 in the whole investigated temperature range but with a fraction of low-spin cobalt(II) species. In line with the results from the crystallographic analysis, which evidenced a structural rigidity imposed by the intermolecular interactions, no spin crossover is observed in the whole investigated temperature range. The observed data could be reasonably reproduced by using for the high spin species the same set of parameters of the Griffith Hamiltonian (eqn (2)) which were used to interpret the low temperature EPR spectrum,61 and assuming the powder sample to contain a 25% fraction of low-spin cobalt(II) with a temperature independent χMT value of 0.4 emu K mol−1.
Thus, the combined investigation of solid state EPR spectrum and magnetometry unequivocally indicate that 1 maintains the high spin configuration down to low temperature, despite indicating the presence of a non-negligible amount of a temperature independent fraction of low-spin cobalt(II) species in the powder sample.
Solution behaviour
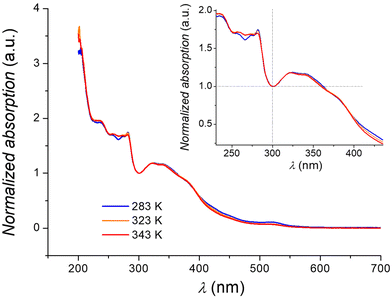 | ||
| Fig. 4 Temperature dependence of the electronic spectrum of an acetonitrile solution of 1. Inset: Zoom of the region around the isosbestic point at 300 nm. | ||
All spectra are dominated by charge-transfer bands in the ultra-violet region, while the absorption band observed at 520 nm can be ascribed to a d–d transition of the low spin isomer of 1 (2A1 → 2T1, 2T2), in analogy to what was previously inferred for the [Co(tpy)2]2+ cation.63 Upon heating from 283 K to 343 K, an evolution of the electronic spectrum is observed, with the bands at 236 and 255 nm becoming more intense, and the other absorptions (280 and 520 nm) losing intensity, giving rise to an isosbestic point (here located at 300 nm due to the normalization condition of the spectra). Such behaviour is in line with an entropy-driven SCO equilibrium for 1, with the high and low spin isomers coexisting in solution for every investigated temperature, due to the gradual nature of the transition in cobalt(II) SCO systems.
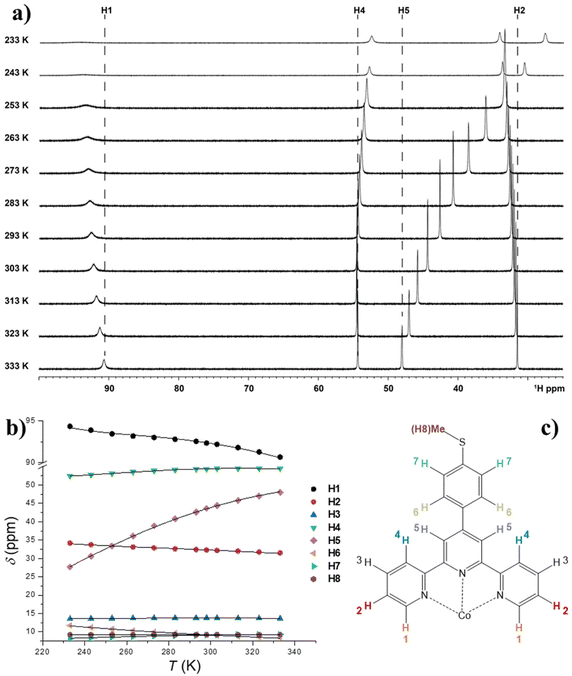
The spectrum consists of 8 paramagnetically shifted signals over a 90 ppm frequency range, indicating the presence of a significant magnetic anisotropy in the susceptibility of 1. The spectral attribution has been carried out on the basis of the relative integrals of the various signals, the D2d symmetry of the complex in solution and on a recent study of the 1H-NMR spectrum of a structurally related system, [Co(pytpy)2](OTf)2, where pytpy is the 4′-(4′′′-pyridyl)-2,2′:6′,2′′-terpyridine ligand.68
It is evident that the chemical shift of H4 and H5 signals increases upon heating; this cannot be explained by the temperature dependence of the susceptibility of 1 in the solid state, which undergoes a monotonic decrease upon heating (see Fig. S7†). Rather, considering the outcome of the UV-Vis spectroscopy and solution EPR study, this behaviour can be interpreted assuming the onset of SCO behaviour in solution. Moreover, the continuous shifting of the peaks suggests that the high spin/low spin equilibrium is fast on our NMR time scale. Under this condition, the temperature dependence of the chemical shifts of the ith signal can be fitted with eqn (3):64,67
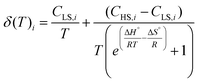 | (3) |
Conclusions
In this contribution, a terpyridine ligand functionalized with a thioether group, TerpyPhSMe, has been used to prepare a new cobalt(II) complex designed as a potential candidate to observe spin crossover on chemically grafted monolayers. The molecular structure of complex 1 obtained by X-ray diffractometry shows that TerpyPhSMe ligand binds in the usual meridional fashion to yield a mononuclear complex featuring the thioether moieties uncoordinated. The axial compression of the octahedron, the analysis of the bond lengths and distortion of the first coordination sphere shows that 1 is a high spin complex in the solid state at 99 K. We attribute the absence of a spin conversion in the solid state to the intramolecular π–π interactions and non-classic C–H⋯F hydrogen bonds, which lock the molecule in the high spin isomeric form. Magnetometry and EPR confirms that 1 is a high spin complex in the solid state independently of the temperature but powder sample contains a fraction of low spin cobalt(II). After dissolution in acetonitrile, however, EPR indicates the sole presence of low spin cobalt(II) at low temperature, and temperature-dependent electronic spectra suggest the onset of an entropy-driven spin crossover equilibrium above room temperature, which is indeed confirmed by the temperature evolution of 1H-NMR spectra. Fitting of the thermal dependencies of the chemical shifts using a Boltzmann distribution model allowed to extrapolate the thermodynamic quantities associated to it (ΔH° = 9.4(6) kJ mol−1 and ΔS° = 28(2) J K−1 mol−1). This is extremely relevant in the perspective of using this complex to obtain switchable monolayers, where the solid state effects which lock the molecule in high spin state can be neglected.30Conflicts of interest
There are no conflicts to declare.Acknowledgements
GP and RAAC gratefully acknowledge FAPERJ for funding through grants E-26/202.912/2019, SEI-260003/001167/2020, E-26/010.000978/2019 and E-26/203.033/2018. RAAC acknowledges CAPES-PrInt (23079.241056/2023-17) for a fellowship. The authors thank Prof. Roberta Sessoli (Dipartimento di Chimica “Ugo Schiff”, Università degli Studi di Firenze, Italy) and the Laboratório Multiusuário (Instituto de Física, Universidade Federal do Rio de Janeiro, Brazil) for providing access to the SQUID magnetometers. Dr Laura Chelazzi (CRIST, University of Florence) is acknowledged for single crystal X-ray diffraction data collection and processing, and Prof. Débora de Almeida Azevedo and Dr Thamara Andrade Barra (Instituto de Química, Universidade Federal do Rio de Janeiro) for the mass spectrometry analysis. Prof. Raffaele Saladino (Dipartimento di Scienze Ecologiche e Biologiche, University of Tuscia) is acknowledged for granting access to the electronic spectrometer. LS acknowledges the support of MUR through Progetto Dipartimenti di Eccellenza 2023–2027 (CUP B97G22000740001—DICUS 2.0).References
- O. Sato, Nat. Chem., 2016, 8, 644–656 CrossRef CAS PubMed.
- I.-R. Jeon, J. G. Park, C. R. Haney and T. D. Harris, Chem. Sci., 2014, 5, 2461–2465 RSC.
- H. J. Shepherd, I. A. Gural’skiy, C. M. Quintero, S. Tricard, L. Salmon, G. Molnar and A. Bousseksou, Nat. Commun., 2013, 4, 2607 CrossRef PubMed.
- T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada, P. Ohresser, E. Beaurepaire and W. Wulfhekel, Nat. Commun., 2012, 3, 938 CrossRef PubMed.
- A. Cornia and P. Seneor, Nat. Mater., 2017, 16, 505–506 CrossRef CAS PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS PubMed.
- P. Gütlich and H. A. Goodwin, in Spin Crossover in Transition Metal Compounds I, ed. P. Gütlich and H. A. Goodwin, Springer, Berlin Heidelberg, 2004, vol. 233, pp. 1–47 Search PubMed.
- P. Gutlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427 RSC.
- Spin-Crossover Materials: Properties and Applications, ed. M. A.Halcrow, Wiley and Sons, 2013 Search PubMed.
- P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054 CrossRef.
- H. A. Goodwin, in Spin Crossover in Transition Metal Compounds II, ed. P. Gütlich and H. A. Goodwin, Springer, Berlin, Heidelberg, 2004, pp. 23–47 Search PubMed.
- Y. Garcia and P. Gütlich, in Spin Crossover in Transition Metal Compounds II, ed. P. Gütlich and H. A. Goodwin, Springer, Berlin, Heidelberg, 2004, pp. 49–62 Search PubMed.
- D. J. Harding, P. Harding and W. Phonsri, Coord. Chem. Rev., 2016, 313, 38–61 CrossRef CAS.
- O. Drath and C. Boskovic, Coord. Chem. Rev., 2018, 375, 256–266 CrossRef CAS.
- S. Hayami, M. Nakaya, H. Ohmagari, A. S. Alao, M. Nakamura, R. Ohtani, R. Yamaguchi, T. Kuroda-Sowa and J. K. Clegg, Dalton Trans., 2015, 44, 9345–9348 RSC.
- I. Krivokapic, M. Zerara, M. L. Daku, A. Vargas, C. Enachescu, C. Ambrus, P. Tregenna-Piggott, N. Amstutz, E. Krausz and A. Hauser, Coord. Chem. Rev., 2007, 251, 364–378 CrossRef CAS.
- S. Hayami, Y. Komatsu, T. Shimizu, H. Kamihata and Y. H. Lee, Coord. Chem. Rev., 2011, 255, 1981–1990 CrossRef CAS.
- S. Brooker, P. G. Plieger, B. Moubaraki and K. S. Murray, Angew. Chem., Int. Ed., 1999, 38, 408–410 CrossRef CAS PubMed.
- M. G. Cowan, J. Olguín, S. Narayanaswamy, J. L. Tallon and S. Brooker, J. Am. Chem. Soc., 2012, 134, 2892–2894 CrossRef CAS PubMed.
- R. G. Miller, S. Narayanaswamy, J. L. Tallon and S. Brooker, New J. Chem., 2014, 38, 1932–1941 RSC.
- D. Shao, L. Shi, F.-X. Shen, X.-Q. Wei, O. Sato and X.-Y. Wang, Inorg. Chem., 2019, 58, 11589–11598 CrossRef CAS PubMed.
- X. Zhang, T. Palamarciuc, J.-F. Letard, P. Rosa, E. V. Lozada, F. Torres, L. G. Rosa, B. Doudin and P. A. Dowben, Chem. Commun., 2014, 50, 2255–2257 RSC.
- C. H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Westerström, C. Bulbucan, M. Studniarek, J. Dreiser, A. U. B. Wolter, B. Büchner and A. A. Popov, Nanoscale, 2018, 10, 11287–11292 RSC.
- L. Zobbi, M. Mannini, M. Pacchioni, G. Chastanet, D. Bonacchi, C. Zanardi, R. Biagi, U. Del Pennino, D. Gatteschi, A. Cornia and R. Sessoli, Chem. Commun., 2005, 1640–1642 RSC.
- F. Pineider, M. Mannini, C. Danieli, L. Armelao, F. M. Piras, A. Magnani, A. Cornia and R. Sessoli, J. Mater. Chem., 2010, 20, 187–194 RSC.
- L. Poggini, E. Tancini, C. Danieli, A. L. Sorrentino, G. Serrano, A. Lunghi, L. Malavolti, G. Cucinotta, A.-L. Barra, A. Juhin, M.-A. Arrio, W. Li, E. Otero, P. Ohresser, L. Joly, J. P. Kappler, F. Totti, P. Sainctavit, A. Caneschi, R. Sessoli, A. Cornia and M. Mannini, Adv. Mater. Interfaces, 2021, 8, 2101182 CrossRef CAS.
- L. Poggini, A. Lunghi, A. Collauto, A. Barbon, L. Armelao, A. Magnani, A. Caneschi, L. Sorace and M. Mannini, Nanoscale, 2021, 13, 7613–7621 RSC.
- D. Gatteschi, A. Cornia, M. Mannini and R. Sessoli, Inorg. Chem., 2009, 48, 3408–3419 CrossRef CAS PubMed.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M. A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed.
- G. Poneti, L. Poggini, M. Mannini, B. Cortigiani, L. Sorace, E. Otero, P. Sainctavit, A. Magnani, R. Sessoli and A. Dei, Chem. Sci., 2015, 6, 2268–2274 RSC.
- H. Hofmeier and U. S. Schubert, Chem. Soc. Rev., 2004, 33, 373–399 RSC.
- E. C. Constable, Chem. Soc. Rev., 2007, 36, 246–253 RSC.
- C. E. Housecroft, CrystEngComm, 2015, 17, 7461–7468 RSC.
- P. C. Mondal, V. Singh and M. Zharnikov, Acc. Chem. Res., 2017, 50, 2128–2138 CrossRef CAS PubMed.
- L. Fioravanti, L. Bellucci, L. Armelao, G. Bottaro, F. Marchetti, F. Pineider, G. Poneti, S. Samaritani and L. Labella, Inorg. Chem., 2022, 61, 265–278 CrossRef CAS PubMed.
- L. Bellucci, L. Fioravanti, L. Armelao, G. Bottaro, F. Marchetti, F. Pineider, G. Poneti, S. Samaritani and L. Labella, Chem. – Eur. J., 2023, 29, e202202823 CrossRef CAS PubMed.
- S. Brooker, Chem. Soc. Rev., 2015, 44, 2880–2892 RSC.
- V. García-López, N. Giaconi, L. Poggini, J. Calbo, A. Juhin, B. Cortigiani, J. Herrero-Martín, E. Ortí, M. Mannini, M. Clemente-León and E. Coronado, Adv. Funct. Mater., 2023, 33, 2300351 CrossRef.
- E. C. Constable, C. E. Housecroft, E. Medlycott, M. Neuburger, F. Reinders, S. Reymann and S. Schaffner, Inorg. Chem. Commun., 2008, 11, 518–520 CrossRef CAS.
- D. C. Wanniarachchi, M. J. Heeg and C. N. Verani, Inorg. Chem., 2014, 53, 3311–3319 CrossRef CAS PubMed.
- R. Dhiman, N. Singh, B. Ugale and C. M. Nagaraja, RSC Adv., 2017, 7, 39325–39333 RSC.
- E. C. Constable, C. E. Housecroft, G. E. Schneider, J. A. Zampese, H. J. Bolink, A. Pertegás and C. Roldan-Carmona, Dalton Trans., 2014, 43, 4653–4667 RSC.
- J. Jiang, J. Li, C. Liu, R. Liu, X. Liang, Y. Zhou, L. Pan, H. Chen and Z. Ma, J. Biol. Inorg. Chem., 2020, 25, 311–324 CrossRef CAS PubMed.
- J. Li, R. Liu, J. Jiang, X. Liang, L. Huang, G. Huang, H. Chen, L. Pan and Z. Ma, Molecules, 2019, 24, 4519 CrossRef CAS PubMed.
- J. Li, H. Yan, Z. Wang, R. Liu, B. Luo, D. Yang, H. Chen, L. Pan and Z. Ma, Dalton Trans., 2021, 50, 8243–8257 RSC.
- M. Nakaya, R. Ohtani, J. W. Shin, M. Nakamura, L. F. Lindoy and S. Hayami, Dalton Trans., 2018, 47, 13809–13814 RSC.
- M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119–4142 RSC.
- R. Ketkaew, Y. Tantirungrotechai, P. Harding, G. Chastanet, P. Guionneau, M. Marchivie and D. J. Harding, Dalton Trans., 2021, 50, 1086–1096 RSC.
- M. C. Llunell, D. Cirera, J. Alemany and P. Alvarez, SHAPE: Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Associated Tools, 2013 Search PubMed.
- N. Bridonneau, L. Rigamonti, G. Poneti, D. Pinkowicz, A. Forni and A. Cornia, Dalton Trans., 2017, 46, 4075–4085 RSC.
- B. J. C. Vieira, V. da Gama, I. C. Santos, L. C. J. Pereira, N. A. G. Bandeira and J. C. Waerenborgh, CrystEngComm, 2018, 20, 2465–2475 RSC.
- C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885–3896 RSC.
- M. Nishio, CrystEngComm, 2004, 6, 130–158 RSC.
- A. Di Santo, H. Pérez, G. A. Echeverría, O. E. Piro, R. A. Iglesias, R. E. Carbonio, A. Ben Altabef and D. M. Gil, RSC Adv., 2018, 8, 23891–23902 RSC.
- P. Li, J. M. Maier, E. C. Vik, C. J. Yehl, B. E. Dial, A. E. Rickher, M. D. Smith, P. J. Pellechia and K. D. Shimizu, Angew. Chem., Int. Ed., 2017, 56, 7209–7212 CrossRef CAS PubMed.
- E. D'Oria and J. J. Novoa, CrystEngComm, 2008, 10, 423–436 RSC.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- A. V. Palii, D. V. Korchagin, E. A. Yureva, A. V. Akimov, E. Y. Misochko, G. V. Shilov, A. D. Talantsev, R. B. Morgunov, S. M. Aldoshin and B. S. Tsukerblat, Inorg. Chem., 2016, 55, 9696–9706 CrossRef CAS PubMed.
- J. S. Griffith, The Theory of Transition-Metal Ions, Cambridge University Press, Cambridge, 1961 Search PubMed.
- F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- S. Kremer, W. Henke and D. Reinen, Inorg. Chem., 1982, 21, 3013–3022 CrossRef CAS.
- C. Enachescu, I. Krivokapic, M. Zerara, J. A. Real, N. Amstutz and A. Hauser, Inorg. Chim. Acta, 2007, 360, 3945–3950 CrossRef CAS.
- W. Klaeui, W. Eberspach and P. Guetlich, Inorg. Chem., 1987, 26, 3977–3982 CrossRef CAS.
- L. A. Yatsunyk and F. A. Walker, Inorg. Chem., 2004, 43, 757–777 CrossRef CAS PubMed.
- B. Weber and F. A. Walker, Inorg. Chem., 2007, 46, 6794–6803 CrossRef CAS PubMed.
- H.-J. Lin, D. Siretanu, D. A. Dickie, D. Subedi, J. J. Scepaniak, D. Mitcov, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2014, 136, 13326–13332 CrossRef CAS PubMed.
- A. A. Pavlov, G. L. Denisov, M. A. Kiskin, Y. V. Nelyubina and V. V. Novikov, Inorg. Chem., 2017, 56, 14759–14762 CrossRef CAS PubMed.
- S. E. Creutz and J. C. Peters, Inorg. Chem., 2016, 55, 3894–3906 CrossRef CAS PubMed.
- Y. Pankratova, D. Aleshin, I. Nikovskiy, V. Novikov and Y. Nelyubina, Inorg. Chem., 2020, 59, 7700–7709 CrossRef CAS PubMed.
- A. E. Thorarinsdottir, A. I. Gaudette and T. D. Harris, Chem. Sci., 2017, 8, 2448–2456 RSC.
- M. Zerara and A. Hauser, ChemPhysChem, 2004, 5, 395–399 CrossRef CAS PubMed.
- M. G. Simmons and L. J. Wilson, Inorg. Chem., 1977, 16, 126–130 CrossRef CAS.
- J. K. Beattie, R. A. Binstead, M. T. Kelso, P. Del Favero, T. G. Dewey and D. H. Turner, Inorg. Chim. Acta, 1995, 235, 245–251 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, mass spectra of 1, additional crystallographic information and spectroscopic data. CCDC 2335192 for 1. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00574k |
| This journal is © The Royal Society of Chemistry 2024 |