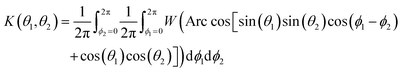Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conditions under which a natural iterative method for calculating the orientation distribution of rodlike particles decreases the free energy at each step†
Alan E.
Berger

Department of Surgery, Johns Hopkins University School of Medicine, Baltimore, MD 21287, USA. E-mail: aberger9@jhmi.edu
First published on 27th August 2024
Abstract
It is shown that under certain conditions the iterative method suggested by the calculus of variations for calculating a cylindrically symmetric orientation distribution function (ODF) for rodlike particles strictly decreases the free energy at each full step. This monotonic behavior has strong implications for convergence of the sequence, or a subsequence, of the calculated ODFs. The result is valid not only for the reference system of hard core particles with indistinguishable ends, but also for free energy functions of similar type. The effect of an applied field is also permitted. Since the behavior of the iteration is intrinsic to the general form of the free energy function it applies to rod mixtures and may extend to a wider class of free energy functions. Outside the conditions that guarantee a monotonically decreasing free energy, we find that the iteration can fail to converge.
1 Introduction
This paper concerns the spontaneous alignment of rodlike particles. Mean field studies in terms of excluded volume date back to Onsager,1 and have been extended to include long-range interparticle interactions (as reviewed by Franco-Melgar, Haslam and Jackson2). In calculating the orientation distribution functions (ODFs), an iterative procedure proposed in 19843 has proven widely effective on a case-by-case basis, e.g., ref. 4–11. The purpose of this paper is to identify the remarkably broad range of conditions under which this iteration is guaranteed to decrease the free energy at each step, which is a substantial indication for convergence. The presentation is divided into three major sections.The Background section develops necessary concepts and notation, beginning with a review of the origins of the iterative procedure for finding the free energy minima and concluding with a review of the expansion of the particle interactions and orientation distributions in terms of Legendre polynomials. Whereas the discussion in ref. 3 and 12 focused on excluded volume effects, while also noting possible application to long range interactions, the present analysis takes a general point of view, including long-range interactions and applied field effects, in addition to volume exclusion.
The subsequent Results and discussion section shows that for physically reasonable potentials, the iteration for cylindrically symmetric ODFs strictly decreases the free energy at each full step (unless one is already at a converged solution, i.e., a fixed point of the iteration). While Herzfeld et al.3 proved that each iterative step gives a descent direction (meaning that the free energy will decrease for a sufficiently small move in that direction), they provided only empirical evidence of the convergence of full steps in particular instances, as have others who have since used the method, e.g., ref. 4–11. The main benefit of the present analysis is in specifying when overshoot of the full step can be excluded. It also identifies conditions under which the iteration will converge to a “nearby” local minimum of the free energy function.
2 Background
2.1 The model
We consider a model for the orientation distribution function f(Ω) of identical rodlike particles, where the orientations are given in terms of spherical coordinates Ω = (θ,ϕ) with 0 ≤ θ ≤ π and 0 ≤ ϕ ≤ 2π, and f is required to be a continuous function of (θ,ϕ) and 2π-periodic in ϕ.An orientation distribution function (ODF) is, by definition, a continuous probability density function for the orientation of any given particle. Thus
| f(Ω) ≥ 0 | (1) |
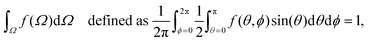 | (2) |
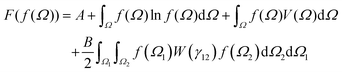 | (3) |
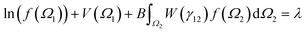 | (4) |
Notice that the mean field interactions between rodlike particles depend only on the angle γ12 in [0,π] between their two orientation vectors (i.e., between the vector from the origin to the point P1 on the unit sphere given by Ω1 = (θ1,ϕ1) and the vector from the origin to the point P2 on the unit sphere given by Ω2 = (θ2,ϕ2)). For future reference, we note that, according to the law of cosines on the triangle whose vertices are P1, the origin, and P2,
γ12 = Arc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[sin(θ1)sin(θ2)cos(ϕ1 − ϕ2) + cos(θ1)cos(θ2)] cos[sin(θ1)sin(θ2)cos(ϕ1 − ϕ2) + cos(θ1)cos(θ2)] | (5) |
| W(γ12) = sin(γ12) | (6) |
2.2 Properties of the solutions of the Euler–Lagrange equation
Other workers have shown that, even in the absence of an applied field (i.e., V = 0), eqn (4) has a wide variety of solutions. It is worthwhile to review those results in order to focus the rest of this paper on the solutions that are of primary physical interest, i.e., those that represent minima in the free energy.For the hard core reference system, Kayser and Raveché12 considered ODFs having cylindrical symmetry and found that there is a branch of anisotropic solutions of the Euler–Lagrange eqn (4) at B = 32/π (ρ = 4 in their normalization and notation) off of the isotropic solution (f(Ω) ≡ 1), and beyond that value of B the isotropic solution is no longer a local minimum of the free energy. Furthermore, ODFs from bifurcations off of the isotropic solution at larger values of B are also not local minima. Vollmer18 has done an extensive analysis of the general case where the kernel W(γ12) in the particle interaction term is a function of cos(γ12), while V = 0, and allowed for solutions of the Euler–Lagrange equation that are not necessarily cylindrically symmetric. In ref. 18 it is proven, in particular, that for W(γ12) equal the Onsager kernel sin(γ12), the solutions branching off the isotropic solution at B = 32/π are axisymmetric.
For W(γ12) equal to the Maier–Saupe kernel 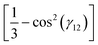 , Liu, Zhang, and Zhang,19 and Fatkullin and Slastikov20 proved that there is only one bifurcation from the isotropic solution, showed that the solutions of the Euler–Lagrange equation are all axisymmetric, and provided explicit formulas for the solutions. Fatkullin and Slastikov20 also proved the same holds for the dipolar kernel W(γ12) = −cos(γ12).
, Liu, Zhang, and Zhang,19 and Fatkullin and Slastikov20 proved that there is only one bifurcation from the isotropic solution, showed that the solutions of the Euler–Lagrange equation are all axisymmetric, and provided explicit formulas for the solutions. Fatkullin and Slastikov20 also proved the same holds for the dipolar kernel W(γ12) = −cos(γ12).
For the coupled dipolar/Maier–Saupe kernel W(γ12) = −σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(γ12) − κ
cos(γ12) − κ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(γ12) (with positive constants σ and κ), Zhou, Wang, Wang and Forest21 proved that solutions of the Euler–Lagrange equation that are local minima of F are axisymmetric. They also showed there are solutions that are not axisymmetric (but these are not local minima).
cos2(γ12) (with positive constants σ and κ), Zhou, Wang, Wang and Forest21 proved that solutions of the Euler–Lagrange equation that are local minima of F are axisymmetric. They also showed there are solutions that are not axisymmetric (but these are not local minima).
For more general W, Ball22 proved existence of non-axisymmetric solutions under certain conditions, and noted that it is an open question whether there exist non-axisymmetric solutions of eqn (4) (for general W, and particularly for the Onsager kernel) that are local minima of F.
Yin, Zhang and Zhang23 have conducted a wide ranging, and beautifully illustrated, numerical investigation of the solution landscape for the W kernels noted above, and found a rich variety of non-axisymmetric solutions of (4), but none were local minima of the free energy F. They point out that, as far as currently known, it is possible there could be a secondary bifurcation branch from an axisymmetric primary bifurcation that could lead to non-axisymmetric minima, however, all secondary bifurcation solutions that they observed were not minima.
2.3 Assumption of cylindrical symmetry
The upshot of the studies summarized in Section 2.2 is that, in the absence of an applied field, all known minima of F correspond to cylindrically symmetric ODFs. The same should be true in the presence of an applied field, as long as that field does not break cylindrical symmetry, i.e., as long as V(Ω) is independent of ϕ. Therefore, since the focus of this study is the behavior of the iterative method3 for finding solutions of the Euler–Lagrange eqn (4) that are minima of the free energy F, it will henceforth be assumed that V depends only on θ, and the orientation distribution functions f are cylindrically symmetric, i.e.,| f is independent of ϕ. | (7) |
| f(θ) ≥ 0 | (8) |
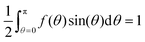 | (9) |
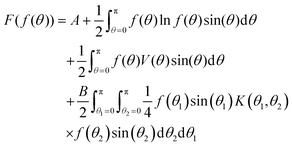 | (10) |
Since cos(ϕ1) is 2π periodic, the inner integral over ϕ1 in [0,2π] is independent of ϕ2, and K simplifies to
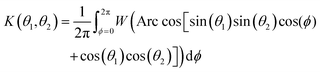 | (11) |
| K(θ2,θ1) = K(θ1,θ2) | (12) |
It will be useful in certain instances to express an orientation distribution function f(θ) as a linear combination of Legendre polynomials Pm(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), which is natural in the setting of spherical coordinates:
θ), which is natural in the setting of spherical coordinates:
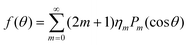 | (13) |
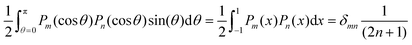 | (14) |
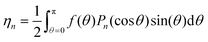 | (15) |
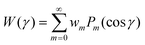 | (16) |
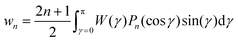 | (17) |
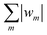 is finite (see Appendix 1 in ESI†). This is also the case for the dipolar kernel W(γ) = −P1(cos
is finite (see Appendix 1 in ESI†). This is also the case for the dipolar kernel W(γ) = −P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ), the Maier–Saupe kernel W(γ) = −(2/3)P2(cos
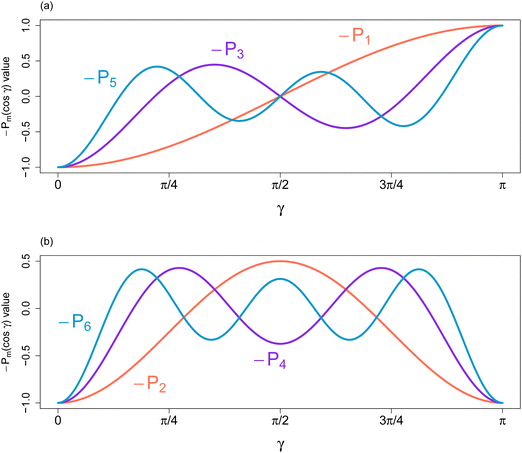
γ), the Maier–Saupe kernel W(γ) = −(2/3)P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ), as well as the coupled dipolar/Maier–Saupe kernel. Generally, it will be seen below that wm ≤ 0 for m > 0 plays an essential role in the proof that each iterative step strictly decreases the value of the free energy function (10) and (11) (unless one is already at a converged solution). The physical significance of this condition is illustrated in Fig. 1, which shows that each term wmPm(cos
γ), as well as the coupled dipolar/Maier–Saupe kernel. Generally, it will be seen below that wm ≤ 0 for m > 0 plays an essential role in the proof that each iterative step strictly decreases the value of the free energy function (10) and (11) (unless one is already at a converged solution). The physical significance of this condition is illustrated in Fig. 1, which shows that each term wmPm(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ) for m > 0 with a negative coefficient wm contributes to a minimum of W(γ) at γ = 0. This minimum favoring alignment counteracts the effect of entropy.
γ) for m > 0 with a negative coefficient wm contributes to a minimum of W(γ) at γ = 0. This minimum favoring alignment counteracts the effect of entropy.
In view of these features of the −Pm(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ) functions, it will henceforth be assumed that W(γ) has an expansion in terms of Legendre polynomials that satisfies these specific conditions on the coefficients:
γ) functions, it will henceforth be assumed that W(γ) has an expansion in terms of Legendre polynomials that satisfies these specific conditions on the coefficients:
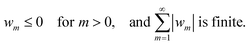 | (18) |
| K(π − θ1,θ2) = K(θ1,π − θ2) = K(θ1,θ2) | (19) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(−Z) = π − Arc
cos(−Z) = π − Arc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Z), whence replacing ϕ by ϕ + π in the integrand of eqn (11) gives the result.
cos(Z), whence replacing ϕ by ϕ + π in the integrand of eqn (11) gives the result.
2.4 The iteration suggested by the calculus of variations
To set the stage for the proof in Results and discussion, and have a key equation in hand, we now formally derive the iterative method given in ref. 3 and 12, extended to include a term for the possibility of an applied field. For the rest of this section, assume the ODF f(θ) is a local minimum of the free energy function and positive on [0,π] (to avoid problems with ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f). Then for any continuous function g(θ) on [0,π] for which max |g(θ)| is sufficiently small and
f). Then for any continuous function g(θ) on [0,π] for which max |g(θ)| is sufficiently small and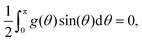 | (20) |
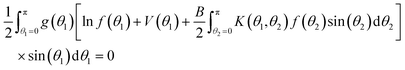 | (21) |
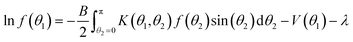 | (22) |
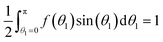 .
.
From eqn (22) we have
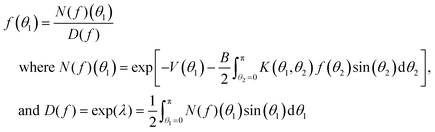 | (23) |
| fn+1(θ) = I(fn)(θ) = N(fn)(θ)/D(fn) | (24) |
Note that fn+1 and any function f that satisfies eqn (23) will be positive on [0,π].
Several special cases deserve particular attention: if V(π − θ) = V(θ) and the ODF f(θ) is a solution of eqn (23), then g(θ) defined to be f(π − θ) will also be a solution of eqn (23). This follows from the rotational invariance of γ12 and can be verified directly by employing eqn (22):
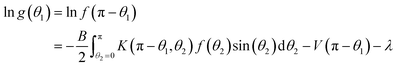 | (25) |
The same steps verify that if V(π − θ) = V(θ) and fn(π − θ) = fn(θ), then fn+1(π − θ) will equal fn+1(θ). Therefore, in cases where there may be a local minimum f of F that is not symmetric about θ = π/2, one should be sure to use initial ODFs f0 that are not symmetric about θ = π/2.
Similarly, if W(π − γ) = −W(γ) and there is no applied field (V(θ) = 0), when fn(π − θ) = fn(θ), 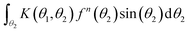 will be 0, and fn+1 will be the isotropic solution. Therefore, in this case one should thus also use initial ODFs that are not symmetric about π/2.
will be 0, and fn+1 will be the isotropic solution. Therefore, in this case one should thus also use initial ODFs that are not symmetric about π/2.
In addition, when W(π − γ) = W(γ) and V(π − θ) = V(θ), by eqn (19), fn+1 and any function satisfying eqn (23) will satisfy f(π − θ) = f(θ).
2.5 The expansion of K(θ1,θ2) in terms of Legendre polynomials
This expansion was developed in Kayser and Raveché;12 we summarize it here in terms of our notation and normalizations since it is a key part of the proof that the iteration decreases the free energy. As shown in Appendix 2 in ESI,† for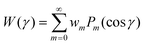 | (26) |
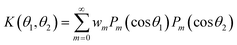 | (27) |
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) (f) is defined to be the last term (the particle interaction term) in eqn (10), and
(f) is defined to be the last term (the particle interaction term) in eqn (10), and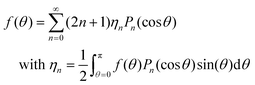 | (28) |
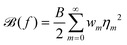 | (29) |
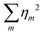 is finite. Note that for f to satisfy eqn (9), η0 must be 1. Furthermore, if g is the difference between two ODFs, then η0 for g is 0. Notice also that, if all the wm are ≤0 for m > 0, then
is finite. Note that for f to satisfy eqn (9), η0 must be 1. Furthermore, if g is the difference between two ODFs, then η0 for g is 0. Notice also that, if all the wm are ≤0 for m > 0, then ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) (g) ≤ 0. This plays a key role in the proof that the iteration decreases the free energy.
(g) ≤ 0. This plays a key role in the proof that the iteration decreases the free energy.
The result (27) together with the fact that the Legendre polynomials are orthogonal (14) shows that, when V = 0, the isotropic ODF f = 1 is always a solution of eqn (22) and (23).
When V = 0, the values of B that are potential locations of bifurcations of anisotropic solutions of the Euler–Lagrange equation off of the isotropic solution are Bm = (2m + 1)/(−wm) (see Appendix 5 in ESI†). The smallest of these Bm, denoted by B*, is the location at which one would generally expect to have a branch of anisotropic local minima of the free energy. If there is an odd number of the Bm equal to B*, then there will be such a branch at B* (Vollmer,18 Rabinowitz25).
3 Results and discussion
3.1 Critical relationships
To make the presentation of new results somewhat self-contained, this section repeats a few primary equations.Let S denote the set of orientation distribution functions (ODFs), i.e., functions f(θ) that are continuous on [0,π] and satisfy
| f(θ) ≥ 0 | (30) |
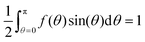 | (31) |
As noted after eqn (11), K(θ2,θ1) = K(θ1,θ2). By eqn (19), when W(π − γ) = W(γ), K(π − θ1,θ2) = K(θ1,π − θ2) = K(θ1,θ2).
The iterative method (as in Kayser and Raveché12 and Herzfeld et al.3) takes a function fn(θ) in S and produces the next iterate fn+1(θ) = I(fn)(θ) defined in terms of our normalization and notation by:
| fn+1(θ) = I(fn)(θ) = N(fn)(θ)/D(fn) | (32) |
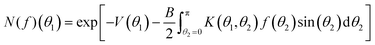 | (33) |
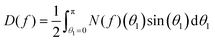 | (34) |
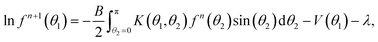 | (35) |
Note that if f0(θ) is any function in S (actually any continuous (or L1([0,π])) function), then, directly from its definition and the properties of K noted above, f1(θ) = I(f0)(θ) will be in S and in fact will be positive on [0,π]. In addition, if W(π − γ) = W(γ) and V(π − θ) = V(θ), then f1(π − θ) = f1(θ).
Now assume f0(θ) is in S, and for each non-negative integer n, define fn+1(θ) to be I(fn)(θ). For a given n, define
| g(θ) = fn+1(θ) − fn(θ) and fn(t)(θ) = fn(θ) + tg(θ) for t ∈ [0,1] | (36) |
3.2 The main result
| fn+1(θ) = fn(θ) | (37) |
| F(fn(t)) is a strictly decreasing function of t for t ∈ [0,1]; in particular, F(fn+1) < F(fn). | (38) |
Furthermore, from the result that F(fn(t)) is a strictly decreasing function of t for n = 0, 1, 2, 3,… (unless fn+1 = fn for some n) we will prove below that a subsequence of {fn(θ)} converges uniformly to a function f(θ) in S for which I(f) = f, and, with some further assumptions, that the entire sequence converges to f.
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) in (a,b) for which y(b) − y(a) = (b − a) × y′(
in (a,b) for which y(b) − y(a) = (b − a) × y′(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) )) shows F(fn(t)) is strictly decreasing for 0 ≤ t ≤ 1 completing the proof.
)) shows F(fn(t)) is strictly decreasing for 0 ≤ t ≤ 1 completing the proof.
In what follows, we write down the derivative; use the fact that 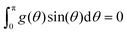 (since fn and fn+1 both satisfy eqn (31)); utilize eqn (35) as was done in eqn (17) of ref. 3 where it was shown that the derivative of F(fn(t)) is <0 at t = 0 (as long as fn(θ) > 0 on [0,π]); and employ eqn (29) (with f replaced by g), and the sentence below it to show that the contribution to the derivative of F(fn(t)) from the term involving
(since fn and fn+1 both satisfy eqn (31)); utilize eqn (35) as was done in eqn (17) of ref. 3 where it was shown that the derivative of F(fn(t)) is <0 at t = 0 (as long as fn(θ) > 0 on [0,π]); and employ eqn (29) (with f replaced by g), and the sentence below it to show that the contribution to the derivative of F(fn(t)) from the term involving ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) (g) is ≤0 so it needs no further consideration. This is the place where the signs of the {wm} in the expansion of Wm come into play.
(g) is ≤0 so it needs no further consideration. This is the place where the signs of the {wm} in the expansion of Wm come into play.
The first step is to write out explicitly what F(fn(t)) is, and then take its derivative with respect to t. For this we can take the derivative under the integral signs, since fn(t)(θ) is bounded away from 0 for any given t in (0,1] so x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(x) not being differentiable at x = 0 does not cause any problems.
ln(x) not being differentiable at x = 0 does not cause any problems.
Recalling that g(θ) = fn+1(θ) − fn(θ) and fn(t) = fn + tg, for t in [0,1] we have
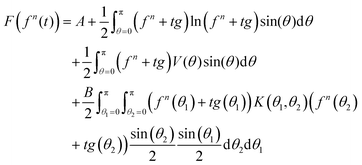 | (39) |
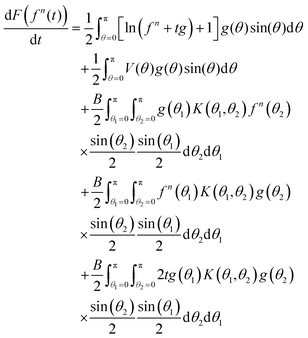 | (40) |
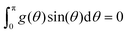 . Since K is symmetric (K(θ2,θ1) = K(θ1,θ2)) the third and fourth terms on the right side of eqn (40) are equal. The last term on the right side of eqn (40) equals 2t
. Since K is symmetric (K(θ2,θ1) = K(θ1,θ2)) the third and fourth terms on the right side of eqn (40) are equal. The last term on the right side of eqn (40) equals 2t![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) (g), which from eqn (29) and the sentence below it, is ≤0, so it needs no further treatment. We thus have
(g), which from eqn (29) and the sentence below it, is ≤0, so it needs no further treatment. We thus have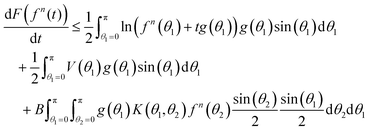 | (41) |
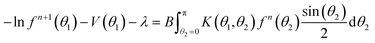 | (42) |
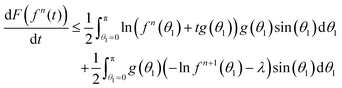 | (43) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ) is 0. Denote the right hand side of (43) by
sin(θ) is 0. Denote the right hand side of (43) by ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (t). Recalling that g = fn+1 − fn, we then have
(t). Recalling that g = fn+1 − fn, we then have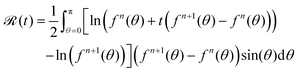 | (44) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (t) is well defined for t in (0,1] (and also for t = 0 if fn > 0 (which is always the case for n > 0), though we don't need
(t) is well defined for t in (0,1] (and also for t = 0 if fn > 0 (which is always the case for n > 0), though we don't need ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) defined at t = 0 for our proof).
defined at t = 0 for our proof).
Since ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x is a strictly increasing function, and here fn+1 ≠ fn; as was seen in eqn (17) of Herzfeld et al.,3
x is a strictly increasing function, and here fn+1 ≠ fn; as was seen in eqn (17) of Herzfeld et al.,3 ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (0) < 0 (as long as fn > 0). What really matters for our proof is that, by inspection, we have the striking result that
(0) < 0 (as long as fn > 0). What really matters for our proof is that, by inspection, we have the striking result that ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (1) = 0. Hence if we could show that
(1) = 0. Hence if we could show that ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (t) was a strictly increasing function for t in (0,1], we would have shown that
(t) was a strictly increasing function for t in (0,1], we would have shown that ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (t) < 0 for t in (0,1), and thereby dF(fn(t))/dt is <0 for t in (0,1) and (by the mean value theorem) the proof of the main result would be done. So let's look at the derivative of
(t) < 0 for t in (0,1), and thereby dF(fn(t))/dt is <0 for t in (0,1) and (by the mean value theorem) the proof of the main result would be done. So let's look at the derivative of ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) for t in (0,1):
for t in (0,1):
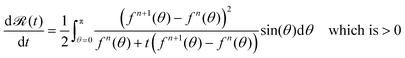 | (45) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (t) < 0 for t in (0,1), and the proof is complete.
(t) < 0 for t in (0,1), and the proof is complete.
This result, and the proof, seem to be intrinsic to the form of the free energy function, and the corresponding form of the iterative method suggested by the calculus of variations. As will be seen in the next subsection, F(fn(t)) being strictly decreasing for t in [0,1] has significant implications for convergence of the iteration. Note that the convergence results below depend on the form of the iteration (22)–(24), not just that F(fn(t)) is strictly decreasing (unless the iteration has converged). It may be the case that the approach used here to show that the iteration decreases the free energy is applicable in other settings.
3.3 Convergence consequences of F(fn(t)) being strictly decreasing (unless fn+1 = fn)
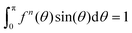 for each n, the magnitude of the argument of the exponential in eqn (33) is uniformly bounded by (B
for each n, the magnitude of the argument of the exponential in eqn (33) is uniformly bounded by (B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) max(|K(θ1,θ2)|) + max(|V(θ)|)), so N(fn)(θ) is uniformly bounded (i.e., by the same constant for all n), and, importantly, D(fn) is uniformly bounded away from 0, so {fn} is uniformly bounded. Since K and V are uniformly continuous, {fn} is equicontinuous, meaning given ε > 0 there is a δ > 0 such that |fn(θ1) − fn(θ2)| < ε whenever |θ1 − θ2| < δ and this holds for every n and every θ1, θ2 in [0,π] for which |θ1 − θ2| < δ. The Arzelà–Ascoli theorem (e.g., page 158 in Rudin26) then applies and every infinite subsequence of {fn} is conditionally compact (i.e., has a subsequence that converges uniformly to a continuous function on [0,π] which will be in S since each fn is).
max(|K(θ1,θ2)|) + max(|V(θ)|)), so N(fn)(θ) is uniformly bounded (i.e., by the same constant for all n), and, importantly, D(fn) is uniformly bounded away from 0, so {fn} is uniformly bounded. Since K and V are uniformly continuous, {fn} is equicontinuous, meaning given ε > 0 there is a δ > 0 such that |fn(θ1) − fn(θ2)| < ε whenever |θ1 − θ2| < δ and this holds for every n and every θ1, θ2 in [0,π] for which |θ1 − θ2| < δ. The Arzelà–Ascoli theorem (e.g., page 158 in Rudin26) then applies and every infinite subsequence of {fn} is conditionally compact (i.e., has a subsequence that converges uniformly to a continuous function on [0,π] which will be in S since each fn is).
The same reasoning shows that the set of functions {I(s)} for s ranging over the set of ODFs S is conditionally compact.
Proof: if not, then from eqn (38) in the main result, we have F(I(f)) < F(f) which will lead to a contradiction. Define f(t)(θ) as follows. Let t = n + r where n is a non-negative integer and 0 ≤ r ≤ 1. Then f(t)(θ) is defined as fn(r)(θ), as in eqn (36). This continuously “patches together” the fn(θ) functions, and by the main result, F(f(t)) is strictly decreasing for t in [0,∞) (unless for some n, fn+1 = fn, but then there would be nothing left to prove). From the discussion in the first paragraph of Section 3.3.1, {fn} is uniformly bounded, and so we have F(f(t)) is uniformly bounded over t, and so has a finite lower bound. Hence F(f(t)) converges monotonically “down to” a finite limit which we denote by β (which is the greatest lower bound for the values F(f(t))).
Now F is a continuous function on S (with ‖f1 − f2‖ = max(|f1(θ) − f2(θ)|)), so F(fni) must converge to F(f), which from the previous paragraph equals β. Since D(fn) is uniformly bounded away from 0, I(fni) must converge to I(f) and then F(I(fni)) must converge to F(I(f)). But by definition, I(fni) = fni+1 so F(I(fni)) must be ≥β. Hence F(I(f)) ≥ β, contradicting F(I(f)) < F(f).
Discussion: note in general, a subsequence {fni} from an iteration fn+1 = I(fn) might possibly converge to a solution of the calculus of variations eqn (22), or equivalently, (23) at which F has one or more directions of decrease, rather than a local minimum. However, in practice, that would be “unlikely” since the iteration strictly decreases F (unless fn+1 = fn for some n). Similarly, unless f0 is a local maximum, a subsequence {fni} can not converge to a local maximum, since f(t) is strictly decreasing (unless fn+1 = fn for some n).
We will see that with strong but natural assumptions, the full sequence {fn} will converge to a solution of I(f) = f.
The result below suggests (but does not prove) that if one starts with f0 “close enough” to an isolated local minimum f of F, then the full sequence {fn} will converge to f. Note Kayser and Raveché12 and Scheurle27 (which is ref. 6 in ref. 12) examine convergence using the spectral radius of the Fréchet derivative of the mapping under consideration which here is I(f), and bifurcation theory. Herzfeld, Berger and Wingate3 observed that computational results indicated that the mapping f → I(f) was Lipschitz continuous with a Lipschitz constant L below 1 near solutions of I(f) = f for the cases for which computations were carried out, with L (perforce) approaching 1 near bifurcation points.
What one would “like” (and might expect) to be the case (but is not proven here) is that one would often have the situation of an isolated local minimum f of F contained in an open set U on whose boundary ∂S, F is ≥ some constant k which is greater than F(f), and f is the only solution of I(f) = f in U. Note I have not yet specified what norm is to be used to define “open” and “boundary” and “local minimum”. Then if f0 is in U and F(f0) < k, one would have the full sequence {fn} converging to f, because these assumptions and the main result would show that f(t) can't “escape” U (since F(f(t)) is decreasing but would have to increase to “cross” the boundary of U), and the entire sequence fn would have to converge to f by the assumption that f was the only fixed point of I in U.
For this purpose, the appropriate (and natural) function space and norm to use is L2([0,π],dμ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθ), i.e., functions z for which the norm ‖z‖2 defined to be
θdθ), i.e., functions z for which the norm ‖z‖2 defined to be 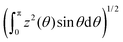 is finite. The maximum norm (‖z‖ = maximum over θ in [0,π] of |z(θ)|) on the set C[0,π] of continuous functions on [0,π] is too strong in that one can use the same type of construction as in Appendix 4 in ESI† with hat functions to show that if f was a local minimum of F then for any ε > 0 and ν > 0 there is a function fν in S with |F(fν) − F(f)| < ε and max |fν(θ) − f(θ)| = ν. The idea is that with narrow hat functions, one can construct a “perturbation” of f satisfying these conditions that is still in S. Note that while max |fν(θ) − f(θ)| = ν; ‖fν − f‖2 would be small if the “hat” functions were sufficiently narrow (had small support). This shows that the desired situation in the previous paragraph can not take place using the maximum norm to define “open” and “boundary”. Also note that if z is in C[0,π], then it will also be in L2([0,π],dμ = sin
is finite. The maximum norm (‖z‖ = maximum over θ in [0,π] of |z(θ)|) on the set C[0,π] of continuous functions on [0,π] is too strong in that one can use the same type of construction as in Appendix 4 in ESI† with hat functions to show that if f was a local minimum of F then for any ε > 0 and ν > 0 there is a function fν in S with |F(fν) − F(f)| < ε and max |fν(θ) − f(θ)| = ν. The idea is that with narrow hat functions, one can construct a “perturbation” of f satisfying these conditions that is still in S. Note that while max |fν(θ) − f(θ)| = ν; ‖fν − f‖2 would be small if the “hat” functions were sufficiently narrow (had small support). This shows that the desired situation in the previous paragraph can not take place using the maximum norm to define “open” and “boundary”. Also note that if z is in C[0,π], then it will also be in L2([0,π],dμ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθ), and
θdθ), and
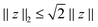 | (46) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθ) on S).
θdθ) on S).
A comment: let U be an open set in S and let β be the greatest lower bound for F(∂U). Note since closed bounded sets in L2([0,π],dμ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdθ) are not necessarily compact, there might not be a function b in ∂U for which F(b) = β (e.g., the set of orthonormal Legendre polynomials
θdθ) are not necessarily compact, there might not be a function b in ∂U for which F(b) = β (e.g., the set of orthonormal Legendre polynomials ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) n(cos
n(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) defined in eqn (S.21) in Appendix 3 in ESI† has no convergent subsequence).
θ) defined in eqn (S.21) in Appendix 3 in ESI† has no convergent subsequence).
Statement: under the conditions and definitions given in the previous 2 paragraphs; if f0 is in U and F(f0) < β it will be the case that the limit f of any uniformly convergent subsequence {fni} of fn (starting with f0) is in U (from the results above, there is at least one subsequence converging uniformly to some function ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) in S, i.e., ‖fni −
in S, i.e., ‖fni − ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ‖ converges to 0).
‖ converges to 0).
Proof: using the notation from above, let fni be a convergent subsequence of fn converging to some function ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) (which from the first convergence result satisfies I(
(which from the first convergence result satisfies I(![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ) =
) = ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ). We need to show
). We need to show ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is in U. Consider f(t), and F(f(t)) which is decreasing (actually strictly decreasing unless some fn+1 = fn). The idea is that the assumptions imply that U is “an energy well” from which f(t) can't “escape”, since to do so, f(t) would have to “cross” the boundary of U, where F ≥ β.
is in U. Consider f(t), and F(f(t)) which is decreasing (actually strictly decreasing unless some fn+1 = fn). The idea is that the assumptions imply that U is “an energy well” from which f(t) can't “escape”, since to do so, f(t) would have to “cross” the boundary of U, where F ≥ β.
Suppose ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is not in U. Now since F(f(t)) is continuous and decreasing and we assumed F(f(0)) < β it can not be the case that
is not in U. Now since F(f(t)) is continuous and decreasing and we assumed F(f(0)) < β it can not be the case that ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is in ∂U where F ≥ β. Let T be the least upper bound of the t values for which f(t) is in U for t in [0,t]. Since U is open, by continuity and eqn (46)T > 0. We next need to show T is finite. Since we are working with the assumption that
is in ∂U where F ≥ β. Let T be the least upper bound of the t values for which f(t) is in U for t in [0,t]. Since U is open, by continuity and eqn (46)T > 0. We next need to show T is finite. Since we are working with the assumption that ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is not in U, and we just noted that
is not in U, and we just noted that ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) can't be in ∂U, there must be an ε > 0 such that if u satisfies ‖u −
can't be in ∂U, there must be an ε > 0 such that if u satisfies ‖u − ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ‖2 < ε then u is not in U (otherwise we would have
‖2 < ε then u is not in U (otherwise we would have ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) in the boundary of U). However, we have f(ni) = fni converging uniformly to
in the boundary of U). However, we have f(ni) = fni converging uniformly to ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) , so (by eqn (46)) T must be finite. By the definition of T, and the same type of reasoning used above, f(T) must be in the boundary of U, which is a contradiction to F(f(t)) < β (if f(T) is not in U and not in ∂U then T would not be the least upper bound; if f(T) is in U then T would not be an upper bound). Thus we have shown
, so (by eqn (46)) T must be finite. By the definition of T, and the same type of reasoning used above, f(T) must be in the boundary of U, which is a contradiction to F(f(t)) < β (if f(T) is not in U and not in ∂U then T would not be the least upper bound; if f(T) is in U then T would not be an upper bound). Thus we have shown ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) is in U.
is in U.
Proof: from the second convergence result there is at least 1 subsequence converging uniformly to some function f and the limit of any uniformly convergent subsequence is in U (and from the first convergence result the limit satisfies I(f) = f). If the full sequence doesn't converge to f, then one could extract a second subsequence converging to another function f2 in U satisfying I(f2) = f2, contradicting the assumption that there was only one solution of I(f) = f in U. Suppose there was some function u ≠ f in U for which F(u) ≤ F(f). Then we could set f0 = u, and by the main result, either I(u) = u; or F(I(u)) < F(u) and there would be a convergent subsequence of the iterates starting with u converging to some function in U at which the free energy was <F(f), and so either way we would get the contradiction of a second solution of I(f) = f in U.
3.4 The behavior of the iteration
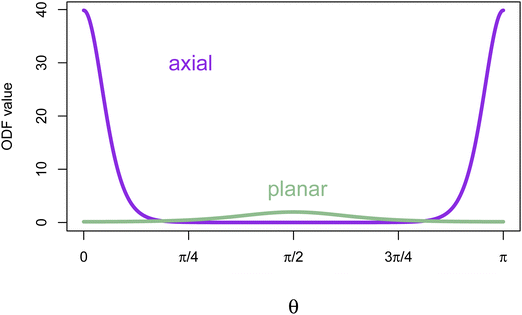
Representative results are illustrated in the next section. Unless otherwise noted, the iterative method was applied using trapezoidal numerical integration with 512 evenly spaced θ intervals on [0,π] and 2048 evenly spaced ϕ intervals on [0,2π]. Initial ODFs used in calculations for the hard core reference system were either “axial” (peaks at θ = 0 and θ = π and a trough at θ = π/2), or “planar” (peak at θ = π/2 and troughs at θ = 0 and θ = π). (Further details are available in ref. 28.) As noted below eqn (25), when there may be local minima of F that are not symmetric about π/2, one should include initial ODFs for the iteration that are not symmetric about π/2.
Our computational procedure avoids the approximations made in previous work. Earlier approaches for obtaining minima of the free energy (in the hard particle system where W(γ) = sin(γ) and V = 0) have included replacing the ODF f(θ) either by a finite expansion in terms of Legendre polynomials Pm(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) with even index m, and determining the coefficients that minimize the free energy (Lasher29), or by a function with just one optimizable parameter (Onsager,1 Baron and Gelbart30). Another approach replaced the particle interaction term in the free energy with the expansion (29) and used the resulting form of the Euler–Lagrange eqn (22) in terms of the unknown {ηm} (note η0 must be 1 for f to be an ODF):
θ) with even index m, and determining the coefficients that minimize the free energy (Lasher29), or by a function with just one optimizable parameter (Onsager,1 Baron and Gelbart30). Another approach replaced the particle interaction term in the free energy with the expansion (29) and used the resulting form of the Euler–Lagrange eqn (22) in terms of the unknown {ηm} (note η0 must be 1 for f to be an ODF):
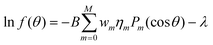 | (47) |
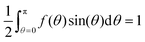 , together with the consistency requirement
, together with the consistency requirement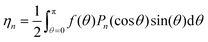 | (48) |
The iteration method studied here is complementary to the uniform sampling method of Yin, Zhang, Zhang.23 Both procedures will accurately determine ODFs that minimize the free energy. By its nature, the iterative method will in general not find ODFs that are solutions of the Euler–Lagrange eqn (22) but are not local minima of the free energy (such as were obtained by Kayser and Raveché12 using a different method). On the other hand, Yin, Zhang and Zhang23 give an extensive discussion of methods for exploring the landscape as B is varied of solutions of (22) that are not necessarily local minima of the free energy. In particular, their own uniform sampling method, while necessarily more complex than the iterative method, has the advantages that it searches over all ODFs (not just axisymmetric ODFs), and by design enables construction of the landscape and bifurcation branches of solutions of (22).
The iterative method studied here naturally converges to minima of the free energy as considered over the subset of axisymmetric ODFs. Since, as far as is known at present, minima of the free energy for models having the form of eqn (3) where W is a function of cos(γ12) are axisymmetric,18–23 the iterative method provides a robust straightforward way of determining minima of the free energy, i.e., the physically observed ODFs, only requiring the user to run the algorithm with a variety of starting values for the iteration to best determine the global minimum. As previously noted below eqn (12), if f is a saddle point but all directions of decrease in the free energy around f are non-axisymmetric ODFs, then f will be a local minimum over the set of axisymmetric ODFs and the iterative method will converge to it when started with a suitable ODF.
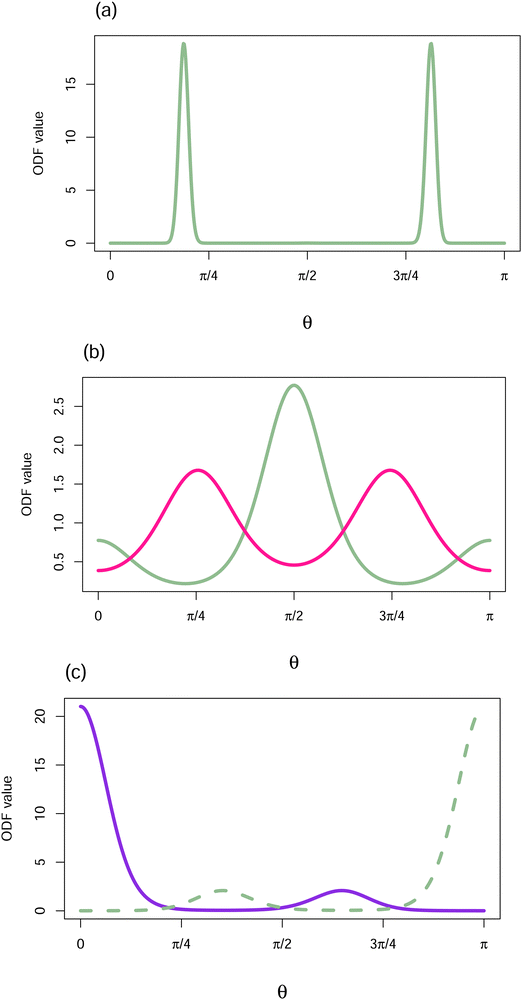
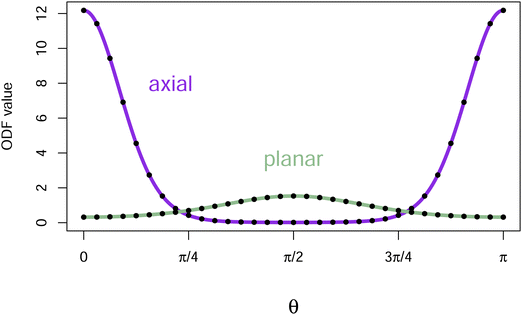
Fig. 2 displays the ODFs that are local minima of the free energy for the hard core reference system (W(γ) = sin(γ) and the applied field V = 0) with B = 14. Graphs of the axial and the planar minima for other values of B are given in ref. 3. The axial ODF is the global minimum of the free energy. The planar ODF is a local minimum with respect to the set of axisymmetric ODFs, but is a saddle point having a two dimensional set of directions of decrease over all ODFs (see Fig. 7 in Yin, Zhang and Zhang23 where they use the terminology oblate for planar ODFs and prolate for axial ODFs).
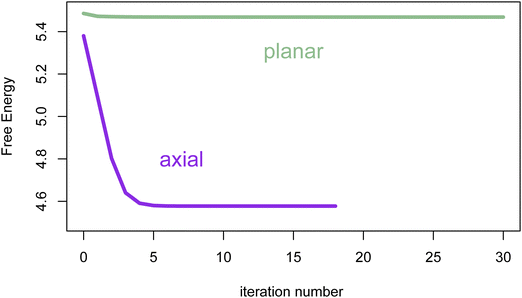
Fig. 3 illustrates that when all the coefficients wn for n > 0 in the expansion of the interparticle potential in terms of Legendre polynomials are ≤0, each iterative step decreases the free energy. This has been the case for all calculations that we have carried out (by trapezoidal numerical integration), up to computer finite precision.
Fig. 4 displays the dependence of particle order on the value of B in the hard core reference system (W(γ) = sin(γ) and V(θ) = 0) as obtained with initial axial (peaks at θ = 0 and θ = π) and planar (peak at θ = π/2) ODFs. The jump at approximately B = 8.883 is indicative of the known first order phase transition at this value of B, e.g., ref. 12 and 33–35.
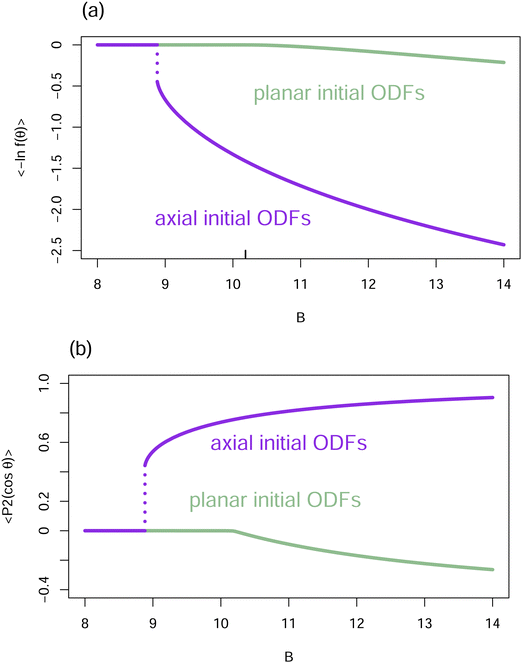 | ||
Fig. 4 Ordering in the hard core reference system. (a) The entropy 〈−ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f(θ)〉 vs. B for converged ODFs resulting from starting the iteration with axial (purple) and planar (green) ODFs. f(θ)〉 vs. B for converged ODFs resulting from starting the iteration with axial (purple) and planar (green) ODFs. 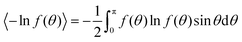 . The jump in this plot for the axial ODFs around B = 8.883 (delineated by dots) corresponds to the location ρb of Kayser and Ravaché.12 (Their ρ* = 4 corresponds to B = 32/π = 10.18592 (marked here with a short vertical black bar) where planar local minima bifurcate from the isotropic ODF.) (b) The order parameter 〈P2(cos . The jump in this plot for the axial ODFs around B = 8.883 (delineated by dots) corresponds to the location ρb of Kayser and Ravaché.12 (Their ρ* = 4 corresponds to B = 32/π = 10.18592 (marked here with a short vertical black bar) where planar local minima bifurcate from the isotropic ODF.) (b) The order parameter 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 vs. B for converged ODFs, resulting from initial axial (purple) and planar (green) ODFs. θ)〉 vs. B for converged ODFs, resulting from initial axial (purple) and planar (green) ODFs. 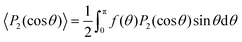 . Note the discontinuity around B = 8.883 (delineated by dots) and change in slope around B = 32/π = 10.18592. . Note the discontinuity around B = 8.883 (delineated by dots) and change in slope around B = 32/π = 10.18592. | ||
Fig. 5 plots the free energy as a function of B for the axial, planar and isotropic solutions of the Euler–Lagrange equation for the hard core reference system. Fig. 5a shows the free energy per particle for all the local minima. Fig. 5b shows the free energy per unit volume for the global minimum, as required to identify the boundaries for coexistence of the isotropic and planar phases by the common tangent construction. The number of θ intervals used here was increased to 1024, as the determination of the coexistence region is quite sensitive to the accuracy of the numerical approximation.34 The coexistence region depicted in Fig. 5b is consistent with results obtained by appropriate thermodynamic calculations in ref. 12, 32, 34 and 36. (Note the scale factor 8/π to go from endpoints of the coexistence region determined in these references to those depicted in Fig. 5b.)
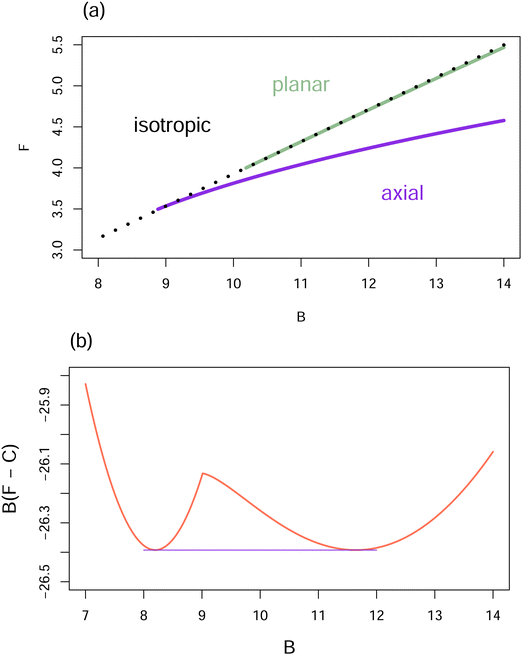 | ||
| Fig. 5 Free energy vs. B for the hard core reference system. (a) The free energy per particle, F, for the isotropic ODF is compared with F for local minima found using the iterative method, eqn (24). Note that the isotropic ODF is no longer a local minimum of F for B larger than the bifurcation value 32/π. The “unstable” bifurcation branch of ODFs that are not local minima, but lead to the axial ODFs that are local minima,12 will not be found using the present iteration procedure. (b) The common tangent construction in which the free energy per particle, F, is multiplied by B to give an energy per unit volume, with the zero of energy per particle adjusted to give a horizontal common tangent by choosing C = 6.4387. | ||
Fig. 6 plots results for the Maier–Saupe kernel W(γ) = 1/3 − cos2(γ) = −(2/3)P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ) = sin2(γ) − 2/3 with B = 9. The bifurcation point from the isotropic solution is at B = 7.5,19,20 Appendix 5 in ESI.† Note that some texts omit constants in the kernel because they have no effect on which ODFs are minima of the free energy or solutions of the Euler Lagrange equation. Yin, Zhang and Zhang23 report (see their Fig. 2) that for the Maier–Saupe kernel, the planar ODF when viewed in the set of all ODFs (not just the axisymmetric ODFs) is a 2-saddle, meaning there is a two dimensional set of descent directions at this ODF. With B = 9, the order parameter r in Fatkullin and Slastikov's eqn (27), where τ = 1/B, is −2.2412853 for the axial ODF and 0.5231352 for the planar ODF. The exact solutions are then given in their eqn (5) with Z the normalizing constant such that eqn (9) is satisfied.
γ) = sin2(γ) − 2/3 with B = 9. The bifurcation point from the isotropic solution is at B = 7.5,19,20 Appendix 5 in ESI.† Note that some texts omit constants in the kernel because they have no effect on which ODFs are minima of the free energy or solutions of the Euler Lagrange equation. Yin, Zhang and Zhang23 report (see their Fig. 2) that for the Maier–Saupe kernel, the planar ODF when viewed in the set of all ODFs (not just the axisymmetric ODFs) is a 2-saddle, meaning there is a two dimensional set of descent directions at this ODF. With B = 9, the order parameter r in Fatkullin and Slastikov's eqn (27), where τ = 1/B, is −2.2412853 for the axial ODF and 0.5231352 for the planar ODF. The exact solutions are then given in their eqn (5) with Z the normalizing constant such that eqn (9) is satisfied.
 | ||
| Fig. 6 Planar and axial ODFs from the iterative method for the Maier–Saupe kernel with B = 9, compared with exact values from the analytical solutions20 plotted as black dots. The Maier–Saupe kernel gives results qualitatively similar to the Onsager kernel (W(γ) = sin(γ)) while being more amenable to analysis, and this is reflected in the similarity between Fig. 2 and 6. | ||
The shape of ODFs minimizing the free energy will obviously depend on the form of the particle interaction W(γ). In particular, subject to the effect of entropy, ODFs will tend to have orientations around θ values that give rise to angles between orientations where W has minima. Several examples for V = 0 are shown in Fig. 7. Fig. 7a displays a free energy minimizing ODF obtained when W(γ) = sin(γ) − 8P6(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ). Fig. 7b exhibits a case where W is such that the first B at which there might be a branch of anisotropic solutions of the Euler–Lagrange equation off of the isotropic ODF is attained from 2 of the coefficients in the expansion of W in terms of Legendre polynomials (see Appendix 5 in ESI†). This results in a more complex group of local minima. Fig. 7c shows the pair of minima resulting from W(γ) = −(7π/32)P3(cos
γ). Fig. 7b exhibits a case where W is such that the first B at which there might be a branch of anisotropic solutions of the Euler–Lagrange equation off of the isotropic ODF is attained from 2 of the coefficients in the expansion of W in terms of Legendre polynomials (see Appendix 5 in ESI†). This results in a more complex group of local minima. Fig. 7c shows the pair of minima resulting from W(γ) = −(7π/32)P3(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ) which favors parallel particle alignment and disfavors antiparallel particle alignment.
γ) which favors parallel particle alignment and disfavors antiparallel particle alignment.
The foregoing behavior can be modulated by an applied field V(θ) superimposed on the particle interaction, as illustrated in Fig. 8a and b where W(γ) = sin(γ). In Fig. 8a, the applied field V(θ) = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ) favors particles having orientations toward θ = 0 or θ = π, relative to other orientations. In Fig. 8b, the applied field V(θ) = −cos(θ) favors particles having orientations around θ = 0, and disfavors those around θ = π. In both cases, the iteration obtains the same converged ODF from initial ODFs that are axial, planar or have one peak at either θ = 0 or θ = π.
sin(θ) favors particles having orientations toward θ = 0 or θ = π, relative to other orientations. In Fig. 8b, the applied field V(θ) = −cos(θ) favors particles having orientations around θ = 0, and disfavors those around θ = π. In both cases, the iteration obtains the same converged ODF from initial ODFs that are axial, planar or have one peak at either θ = 0 or θ = π.
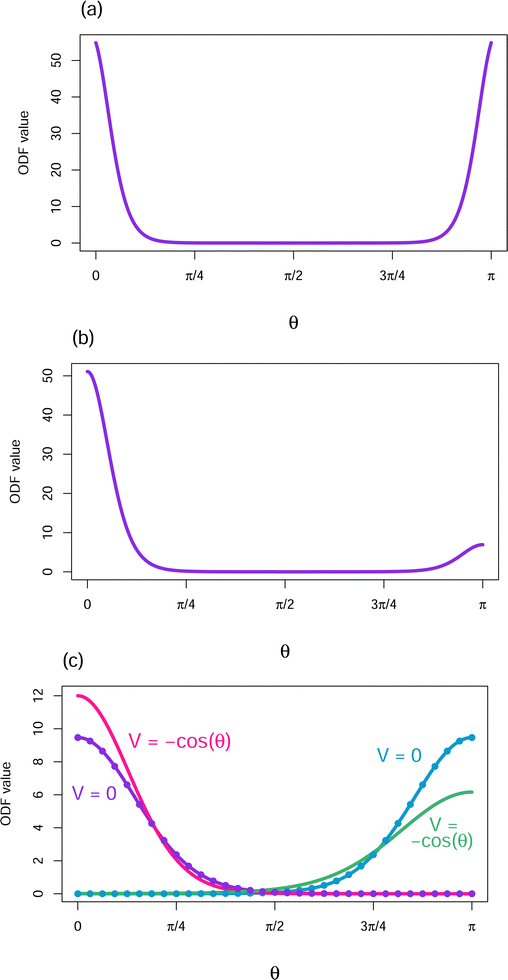 | ||
Fig. 8 ODF modulation by an external field. (a) Results for W(γ) = sin(γ) with B = 12, and an applied field V(θ) = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ) which favors orientations around both θ = 0 and π. The peak value of this ODF is even larger than that for the hard core reference system with B = 14 (cf.Fig. 2). (b) Results for W(γ) = sin(γ) with B = 12, and an applied field V(θ) = −cos(θ) which favors orientations around θ = 0 and disfavors orientations around θ = π. (c) The pair of minima of the free energy for the dipolar kernel with V = 0 and B = 6 (purple and cyan) were obtained from initial values for the iteration having either a peak at θ = 0 or a peak at θ = π. The dots are exact values.20 These ODFs are mirror images of each other about π/2 and are physically equivalent, since each can be obtained from the other by a rotation of spherical coordinates. In the presence of an applied field V(θ) = −cos(θ) which favors orientation toward θ = 0, for starting values with a peak close to θ = π the iteration converges to an ODF (green) that has attenuated orientation toward θ = π. For other starting values, the iteration converges to an ODF (magenta) that has accentuated orientation toward θ = 0. The ODF with the accentuated peak at θ = 0 has the lower free energy in the presence of the applied field. sin(θ) which favors orientations around both θ = 0 and π. The peak value of this ODF is even larger than that for the hard core reference system with B = 14 (cf.Fig. 2). (b) Results for W(γ) = sin(γ) with B = 12, and an applied field V(θ) = −cos(θ) which favors orientations around θ = 0 and disfavors orientations around θ = π. (c) The pair of minima of the free energy for the dipolar kernel with V = 0 and B = 6 (purple and cyan) were obtained from initial values for the iteration having either a peak at θ = 0 or a peak at θ = π. The dots are exact values.20 These ODFs are mirror images of each other about π/2 and are physically equivalent, since each can be obtained from the other by a rotation of spherical coordinates. In the presence of an applied field V(θ) = −cos(θ) which favors orientation toward θ = 0, for starting values with a peak close to θ = π the iteration converges to an ODF (green) that has attenuated orientation toward θ = π. For other starting values, the iteration converges to an ODF (magenta) that has accentuated orientation toward θ = 0. The ODF with the accentuated peak at θ = 0 has the lower free energy in the presence of the applied field. | ||
As expected, the Maier–Saupe kernel continues to give results qualitatively similar to those of the hard core reference system, under the influence of an applied field. When the fields V(θ) = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ) and V(θ) = −cos(θ) were applied with W(γ) equal the Maier–Saupe kernel and B = 9 (data not shown), the iteration obtained the same converged ODF from initial ODFs that were axial, planar or had one peak at either θ = 0 or θ = π.
sin(θ) and V(θ) = −cos(θ) were applied with W(γ) equal the Maier–Saupe kernel and B = 9 (data not shown), the iteration obtained the same converged ODF from initial ODFs that were axial, planar or had one peak at either θ = 0 or θ = π.
Fig. 8c shows results for the dipolar potential with B = 6. The pair of minima when V = 0 determined by the iterative method are displayed along with exact values from the analytical solution.20 (B = 6 corresponds to the order parameter r = ±4.73332.) When the field V(θ) = −cos(θ) is applied, one obtains a minimum with an attenuated peak at θ = π when the iteration is started with an ODF with a peak near θ = π. For other starting values, including an ODF with a peak just to the right of π/2, one obtains the global minimum ODF with an enhanced peak at θ = 0.
When there are wn > 0 for one or more n > 0, the iteration may not reduce the free energy F at some steps, and may not converge. This is illustrated in Fig. 9 for W(γ) = sin(γ) + P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ). When
γ). When 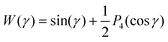 , the iteration does converge (albeit non-monotonically in free energy) from both axial and planar initial ODFs. Nevertheless, whenever there is a positive wn (n > 0), it is best to use an alternate method for finding local minima.
, the iteration does converge (albeit non-monotonically in free energy) from both axial and planar initial ODFs. Nevertheless, whenever there is a positive wn (n > 0), it is best to use an alternate method for finding local minima.
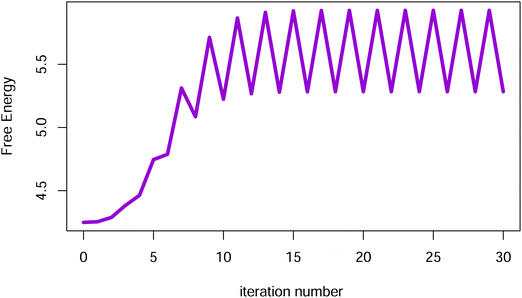 | ||
Fig. 9 The free energy vs. iteration number for W(γ) = sin(γ) + P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ), V = 0 and B = 10.8 starting from an axial ODF. This W does not satisfy the conditions in eqn (18) since w4 = 1 − 9π/256 > 0, and the iteration (24) fails to converge. The oscillation in the free energy that is established by iteration 30 was seen to continue through 3000 iterations. γ), V = 0 and B = 10.8 starting from an axial ODF. This W does not satisfy the conditions in eqn (18) since w4 = 1 − 9π/256 > 0, and the iteration (24) fails to converge. The oscillation in the free energy that is established by iteration 30 was seen to continue through 3000 iterations. | ||
4 Conclusions
The natural iterative method that the calculus of variations suggests for obtaining orientation distribution functions (ODFs) strictly decreases the free energy at each step (unless already at a fixed point of the iteration) under specific and physically appropriate conditions on the particle interaction term. This has significant implications for convergence. In numerical practice, when these conditions are satisfied, convergence is generally quite rapid. It is important to select a variety of initial ODFs in order for the computations to have a good chance to reach all the physically relevant minima of the free energy. The extent to which the behavior of the iteration considered as a dynamical system will represent all stable branches of bifurcations is an open question.When there are one or more positive coefficients in the expansion of the interparticle potential in terms of Legendre polynomials, the iterative method can fail to converge, and it is advisable to use alternative computational procedures for obtaining minima of the free energy function and/or solutions of the Euler–Lagrange equation, such as described in, for example.23
Data availability
There is no experimental data for this paper. Relevant code including examples of running the code and corresponding output is available as indicated in ref. 28 in the paper: A. Berger, R-code-for-calculating-orientation-distribution-functions-for-rodlike-particles, 7 Jan 2024. https://github.com/AlanBerger/R-code-for-calculating-orientation-distribution-functions-for-rodlike-particles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author thanks Judith Herzfeld for encouragement to extend the results to a wider class of interactions than the original hard core reference system, and for providing physical insight into the conditions for convergence and the computational results. The author also appreciates the excellent suggestions offered by the referees.References
- L. Onsager, The effects of shape on the interaction of colloidal particles, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- M. Franco-Melgar, A. J. Haslam and G. Jackson, Advances in generalized van der Waals approaches for the isotropic-nematic fluid phase equilibria of thermotropic liquid crystals-an algebraic equation of state for attractive anisotropic particles with the Onsager trial function, Mol. Phys., 2009, 107, 2329–2358, DOI:10.1080/00268970903352335.
- J. Herzfeld, A. E. Berger and J. W. Wingate, A highly convergent algorithm for computing the orientation distribution functions of rodlike particles, Macromolecules, 1984, 17, 1718–1723, DOI:10.1021/ma00139a014.
- R. Aliabadi, S. Nasirimoghadam and H. H. Wensink, Evidence of T-type structures of hard square boards in capillary confinement, Phys. Rev. E, 2023, 107, 054117-1, DOI:10.1103/PhysRevE.107.054117.
- R. Aliabadi, S. Nasirimoghadam and H. H. Wensink, Capillary-driven biaxial planar and homeotropic nematization of hard cylinders, Phys. Rev. E, 2022, 105, 064704-1, DOI:10.1103/PhysRevE.105.064704.
- V. I. Shmotolokha and M. F. Holovko, Effects of porous media on the phase behaviour of polypeptide solutions, Condens. Matter Phys., 2022, 25, 33602-1, DOI:10.5488/CMP.25.33602.
- I. Pihlajamma, R. de Bruijn and P. van der Schoot, Continuum percolation in colloidal dispersions of hard nanorods in external axial and planar fields, Soft Matter, 2021, 17, 10458–10468, 10.1039/D1SM01408K.
- S. M. Ghazi, F. Behzadi and R. Aliabadi, Second-Virial Onsager Theory and Its Limitations in the Prediction of the Ordering Transitions of Confined Hard Rods between Two Parallel Hard Walls, J. Phys. Soc. Jpn., 2020, 89, 114601-1, DOI:10.7566/JPSJ.89.114601.
- M. M. C. Tortora, G. Mishra, D. Prešern and J. P. K. Doye, Chiral shape fluctuations and the origin of chirality in cholesteric phases of DNA origamis, Sci. Adv., 2020, 6, eaaw8331-1, DOI:10.1126/sciadv.aaw8331.
- K. May, A. Eremin, R. Stannarius, S. D. Peroukidis, S. H. L. Klapp and S. Klein, Colloidal suspensions of rodlike nanocrystals and magnetic spheres under an external magnetic stimulus: experiment and molecular dynamics simulation, Langmuir, 2016, 32, 5085–5093, DOI:10.1021/acs.langmuir.6b00739.
- K. Slyusarenko, V. Reshetnyak and Y. Reznikov, Magnetic field control of the ordering of two-component suspension of hard rods, Philos. Trans. R. Soc., A, 2013, 371, 20120250, DOI:10.1098/rsta.2012.0250.
- R. F. Kayser Jr. and H. J. Raveché, Bifurcation in Onsager's model of the isotropic-nematic transition, Phys. Rev. A: At., Mol., Opt. Phys., 1978, 17, 2067–2072, DOI:10.1103/PhysRevA.17.2067.
- M. A. Cotter, Hard spherocylinders in an anisotropic mean field: a simple model for a nematic liquid crystal, J. Chem. Phys., 1977, 66, 1098–1106, DOI:10.1063/1.434044.
- M. A. Cotter, Generalized van der Waals theory of nematic liquid crystals: An alternative formulation, J. Chem. Phys., 1977, 66, 4710–4711, DOI:10.1063/1.433686.
- M. A. Cotter, Generalized van der Waals theory of nematic liquid crystals: Requirements for self-consistency, J. Chem. Phys., 1977, 67, 4268–4270, DOI:10.1063/1.435364.
- W. M. Gelbart and B. A. Baron, Generalized van der Waals theory of the isotropic-nematic phase transition, J. Chem. Phys., 1977, 66, 207–213, DOI:10.1063/1.433665.
- W. M. Gelbart and A. Gelbart, Mol. Phys., 1977, 33, 1387–1398, DOI:10.1080/00268977700101151.
- M. A. C. Vollmer, Critical points and bifurcations of the three-dimensional Onsager model for liquid crystals, Arch. Ration. Mech. Anal., 2017, 226, 851–922, DOI:10.1007/s00205-017-1146-8.
- H. Liu, H. Zhang and P. Zhang, Axial symmetry and classification of stationary solutions of Doi-Onsager equation on the sphere with Maier–Saupe potential, Commun. Math. Sci., 2005, 3, 201–218 CrossRef.
- I. Fatkullin and V. Slastikov, Critical points of the Onsager functional on a sphere, Nonlinearity, 2005, 18, 2565–2580, DOI:10.1088/0951-7715/18/6/008.
- H. Zhou, H. Wang, Q. Wang and M. G. Forest, Characterization of stable kinetic equilibria of rigid, dipolar rod ensembles for coupled dipole–dipole and Maier–Saupe potentials, Nonlinearity, 2007, 20, 277–297, DOI:10.1088/0951-7715/20/2/003.
- J. M. Ball, Axisymmetry of critical points for the Onsager functional, Philos. Trans. R. Soc., A, 2021, 379, 20200110, DOI:10.1098/rsta.2020.0110.
- J. Yin, L. Zhang and P. Zhang, Solution landscape of the Onsager model identifies non-axisymmetric critical points, Phys. D, 2022, 430, 133081, DOI:10.1016/j.physd.2021.133081.
- H. J. Weber and G. B. Arfken, Essential Mathematical Methods for Physicists, Elsevier Science, Amsterdam, 2004 Search PubMed.
- P. H. Rabinowitz, Some global results for nonlinear eigenvalue problems, J. Funct. Anal., 1971, 7, 487–513, DOI:10.1016/0022-1236(71)90030-9.
- W. Rudin, Principles of Mathematical Analysis, McGraw-Hill, New York, 3rd edn, 1976 Search PubMed.
- J. Scheurle, Selective Iteration and Applications, J. Math. Anal. Appl., 1977, 59, 596–616, DOI:10.1016/0022-247X(77)90084-1.
- A. Berger, R-code-for-calculating-orientation-distribution-functions-for-rodlike-particles, 2024. https://github.com/AlanBerger/R-code-for-calculating-orientation-distribution-functions-for-rodlike-particles.
- G. Lasher, Nematic ordering of hard rods derived from a scaled particle treatment, J. Chem. Phys., 1970, 53, 4141–4146, DOI:10.1063/1.1673914.
- B. A. Baron and W. M. Gelbart, Molecular shape and volume effects on the orientational ordering of simple liquid crystals, J. Chem. Phys., 1977, 67, 5795–5801, DOI:10.1063/1.434786.
- R. Alben, Pretransition Effects in Nematic Liquid Crystals: Model Calculations, Mol. Cryst. Liq. Cryst., 1971, 13, 193–231, DOI:10.1080/15421407108083541.
- H. N. W. Lekkerkerker, P. Coulon, R. van der Haegen and R. Deblieck, On the isotropic-liquid crystal phase separation in a solution of rodlike particles of different lengths, J. Chem. Phys., 1984, 80, 3427–3433, DOI:10.1063/1.447098.
- M. J. Freiser, Ordered States of a Nematic Liquid, Phys. Rev. Lett., 1970, 24, 1041–1043, DOI:10.1103/PhysRevLett.24.1041.
- G. J. Vroege and H. N. W. Lekkerkerker, Phase transitions in lyotropic colloidal and polymer liquid crystals, Rep. Prog. Phys., 1992, 55, 1241–1309, DOI:10.1088/0034-4885/55/8/003.
- C. Erignoux and A. Giuliani, Nematic first order phase transition for liquid crystals in the van der Waals–Kac limit, J. Math. Phys., 2020, 61, 103306-1, DOI:10.1063/5.0007613.
- R. van Roij, The isotropic and nematic liquid crystal phase of colloidal rods, Eur. J. Phys., 2005, 26, S57–S67, DOI:10.1088/0143-0807/26/5/S07.
Footnote |
| † Electronic supplementary information (ESI) available: Appendices for conditions for an iterative method for calculating the orientation distribution of rodlike particles to decrease the free energy. See DOI: https://doi.org/10.1039/d4cp02217c |
| This journal is © the Owner Societies 2024 |