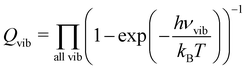Unraveling the interaction between singlet state atomic oxygen O(1D) and water: toward the formation of oxywater and hydrogen peroxide†
Received
5th March 2024
, Accepted 3rd May 2024
First published on 6th May 2024
Abstract
We performed high-level quantum mechanical calculations to explore the interaction of atomic oxygen in the ground triplet state, O(3P), and the excited singlet state, O(1D), with water. We reported the potential energy curves for a few lowest electronic states when an atomic oxygen approaches the oxygen of a water molecule. Our results predict the formation of a singlet oxywater species as the product of O(1D) and H2O which lies about 149.33 kJ mol−1 below the total energy of a singlet oxygen atom and a water molecule. Our calculations predict that an O(3P) atom interacting with a water molecule forms a triplet oxywater complex with a shallow minimum on the triplet potential energy surfaces. We examined the transition of the singlet state oxywater species to hydrogen peroxide through the unimolecular reaction pathway, a (1,2)-hydrogen shift. We reported the structural properties, vibrational frequencies, and dipole moments of oxywater species, the transition state, and hydrogen peroxide. We also reported the energy barrier for the transition, and we provided an estimate for the respective reaction rate constant. In addition, we investigated the impact of solvents on the reaction pathway using an implicit solvation model of water. We predict that a singlet state oxywater species has a longer lifetime in a water environment than in the gas phase.
1 Introduction
Electric gas discharge plasmas generated in oxygen, O2, containing gas mixtures, such as air or oxygen admixed with noble gases, produce atomic oxygen in either the ground triplet state, O(3P), or the excited singlet state, O(1D).1–3 In contact with humidity or with aqueous solutions, oxygen atoms may undergo reactions with water molecules or may dissolve in solutions and undergo reactions in the liquid phase.4–8 These reactions are crucial for the plasma processing of liquids and biological molecules for diverse applications in health and environmental remediation.9,10 In addition, these reactions are broadly involved in environmental chemistry and atmospheric chemistry.11 Despite their significance, the detailed reaction mechanisms involving oxygen atoms in the presence of water are not completely understood. This motivates us to explore the interaction mechanisms between oxygen atoms and water molecules, with a particular emphasis on singlet state atomic oxygen, O(1D).
Filatov et al.12 were the first to consider the formation of oxywater, O·OH2, theoretically by reaction of O(1D) with water molecules
The authors used the complete active space self-consistent field, CASSCF, method to find the structure of oxywater at equilibrium and of the transition states. They also computed the energy to remove the oxygen atom from oxywater as 101.2 kJ mol
−1 at the CASSCF level of theory and 107.16 kJ mol
−1 at the multi-reference configuration interaction, MRDCI, level of theory.
Prior to the work of Filatov et al.,12 a majority of experimental and theoretical studies on oxywater were focused on its potential existence as a structural isomer of hydrogen peroxide, H2O2, yielding controversial findings.13–21 Bain and Giguere13 made the first experimental reference to oxywater in which they concluded that any tautomeric form of hydrogen peroxide such as O·OH2 was unlikely because they failed to observe O–O stretching other than the one which characterizes hydrogen peroxide. Theoretical studies of Pople et al.16 suggested that oxywater does not exist as a stable minimum. However, theoretical studies of other authors in ref. 17–19 and 21 concluded that oxywater is a genuine minimum on the H2O2 potential energy hypersurface, and although oxywater may only have a transient existence in the gas phase, it is likely to be longer lived in protic solvents. Later, the experimental findings of Schröder et al.20 suggested that oxywater is a viable molecule in the gas phase. After the investigation by Filatov et al.,12 the rearrangement of oxywater into hydrogen peroxide with the assistance of water molecules was also studied by Okajima.22,23 Studies by Ignatov et al.24 suggested that the ice surface stabilizes the oxywater against the transition to hydrogen peroxide due to the formation of hydrogen bonds. In 2009, Franz et al.25 theoretically investigated the production of singlet oxygen atoms by photo-dissociation of singlet oxywater. They reported the energies of a few lowest electronic singlet states of oxywater along with dissociation of the oxygen–oxygen bond into water and singlet oxygen using multiscale multireference second-order Møller–Plesset perturbation theory. Accordingly, the energy to remove one oxygen atom in the lowest singlet state was predicted to be 89.12 kJ mol−1.25 More recently and in the context of plasma interaction with water, Yusupov et al.26 investigated the interaction of atomic oxygen with liquid water using ReaxFF molecular dynamics simulations wherein abstraction of a hydrogen atom from a water molecule was predicted with subsequent formation of two OH radicals. Verlackt et al.27 predicted the formation of oxywater as a result of interaction of singlet states oxygen atoms with water using density functional tight binding (DFTB)-based molecular dynamics simulations which was stable for a simulation time of 10 ps. Xu et al.28 predicted the formation of oxywater as the intermediate product in the interaction between the singlet state oxygen atom and water using density functional theory (DFT)-based molecular dynamics simulations. This was followed by the generation of hydrogen peroxide as the final product.28
In macroscopic fluid simulations of electric gas discharge plasmas,29,30 often the following reaction channels between singlet state atomic oxygen, O(1D), and water molecules have been considered:
| | | O(1D) + H2O → O(3P) + H2O, | (2) |
| | | O(1D) + H2O → OH + OH, | (3) |
| | | O(1D) + H2O → H2 + O2. | (4) |
Channel 2 is a physical quenching process which deactivates the excited oxygen atom without any chemical change. The rate coefficient for this reaction is reported to be
k1 = 1.2 × 10
−11 cm
3 molecule
−1 s
−1.
31 Channel 3 was suggested in ref.
32–36 with a rate coefficient of
k2 = (2.07 ± 0.18) × 10
−10 cm
3 molecule
−1 s
−1 at room temperature using laser-induced fluorescence spectroscopy.
36 The rate coefficient of channel 4 relative to the rate coefficient of channel 3 is reported to be
k3/
k2 ≤ 0.016.
37 The possibility of generating oxywater as a result of singlet state atomic oxygen interaction with water and its subsequent transition to a more stable product (
e.g., hydrogen peroxide) has not been considered in macroscopic simulations of electric gas discharge plasmas. In this work, we re-examined the mechanism of oxywater production as a result of atomic oxygen interaction with water molecules using high-level quantum mechanical calculations. We predict the production of a relatively stable singlet state oxywater species as a product of singlet state atomic oxygen interacting with water. We predict that the ground triplet state atomic oxygen interacting with a water molecule forms a triplet oxywater complex with a shallow minimum on the triplet potential energy curves. We also investigated the transition from the singlet state oxywater complex to hydrogen peroxide,
| | | O(1D) + H2O → O·OH2 → H2O2, | (5) |
and we provide an estimate of the respective reaction rate constant. Furthermore, we explored the impact of the solvent environment (
i.e., water) on the reaction path using an implicit solvent model of water. We predict that the lifetime of the singlet oxywater species in the water environment is longer than that in the gas phase.
The rest of this manuscript is organized as follows: the methods are described in Section 2. It is followed by the results and discussion in Section 3. Finally, concluding remarks are presented in Section 4.
2 Methodology
We first used the complete active space self consistent field with 10 active electrons in 8 orbitals, (10,8)CASSCF, and the strongly contracted N-electron valence state perturbation theory,38–40 SC-NEVPT2, to investigate the potential energy curve derived from atomic oxygen approaching the oxygen of a water molecule, commencing at a distance of 4.0 Å and gradually approaching the oxygen of the water (H2O ← O). We used the correlation-consistent polarized valence triple-zeta, cc-pVTZ, basis set of Dunning and coworkers.41,42 The molecular complex has C2v symmetry at all positions of the potential energy curve. We conducted two sets of calculations: in the first set, the geometry of H2O was held fixed at each oxygen–oxygen distance and all atoms were in one plane, while in the second set, the geometry of H2O was optimized for each oxygen–oxygen distance.
In addition, we used the (10,8)CASSCF method and the coupled cluster methods, namely CCSD (including single and double excitations) and CCSD(T) (including single, double, and perturbatively treated connected triple excitations), all with the correlation-consistent polarized triple-zeta, cc-pVTZ, basis sets to explore the unimolecular reaction pathway of the oxywater species to hydrogen peroxide through the (1,2)-hydrogen shift. We also examined the effect of the solvent (i.e., water) on the reaction pathway using an implicit solvation model of water with a dielectric constant of 80.4 and a refractive index of 1.33. The latter was only applied to the CCSD and CCSD(T) methods using the conductor-like polarizable continuum model.43 All the above procedures were carried out using the program ORCA44 version 5.0.4.
3 Results and discussion
3.1 Formation of oxywater
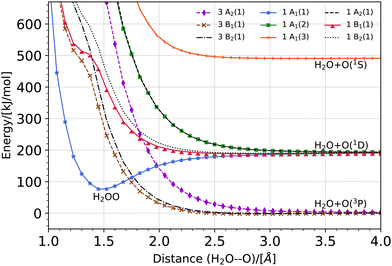
The potential energy curve for the O·OH2 complex along the oxygen–oxygen coordinate, from 1 Å to 4 Å, at the (10,8)CASSCF-SC-NEVPT2/cc-pVTZ level of theory is shown in Fig. 1. The lowest lying states on the triplet energy surface, 3P, on the singlet energy surface, 1D, and on the second excited energy surface, 1S, are shown. The energies are plotted with respect to the energy of a H2O molecule and an O(3P) atom at an oxygen–oxygen distance of 10 Å (see Fig. S1 of the ESI,† for the energy curves in the 1–10 Å region). Additionally, a zoom of the triplet potential energy curves around the 3 Å region is shown in Fig. 2. In all these calculations, the geometry of H2O at each oxygen–oxygen distance position was held fixed. The results wherein the geometry of H2O at each oxygen–oxygen distance position is optimized are shown in Fig. S2 and S3 of the ESI.† In the latter case, the potential energy curves shift toward lower energies, while the overall features of the energy curves remain consistent. This outcome is expected, given the optimization of H2O at each distance position. At an oxygen–oxygen distance of 10 Å, the energy gap between O(1D) and O(3P) is about 1.98 eV (about 191 kJ mol−1) according to our calculations. This is in good agreement with the reported energy gap from the NIST database, which is about 1.97 eV.45,46
 |
| | Fig. 1 Potential energy curve for the O·OH2 complex along the oxygen–oxygen coordinate at the (10,8)CASSCF-SC-NEVPT2/cc-pVTZ level of theory. The lowest lying states on the triplet energy surface, 3P, on the singlet energy surface, 1D, and on the second excited energy surface, 1S, are shown. The energies are plotted with respect to the energy of a H2O molecule and an O(3P) atom at an oxygen–oxygen distance of 10 Å (see Fig. S1 of the ESI,† for the energy curves in the 1–10 Å region). In these calculations, the geometry of H2O is held fixed at each distance position. | |
 |
| | Fig. 2 Potential energy curve for the O·OH2 complex along the oxygen−oxygen coordinate on the triplet energy surface, 3P, at the (10,8)CASSCF-SC-NEVPT2/cc-pVTZ level of theory. The potential energy curve is shifted with regard to the total energy of a H2O molecule and an O(3P) atom at an oxygen–oxygen distance of 10 Å (see Fig. S1 of the ESI†). A zoom of the potential energy around a 3 Å oxygen–oxygen distance is shown. In these calculations, the geometry of H2O is held fixed at each distance position. | |
The product of a triplet oxygen atom O(3P) and a H2O molecule has a shallow minimum on the 3B1 (1) and 3B2 (1) energy surfaces at an oxygen–oxygen distance of about 2.75 Å leading to the formation of a triplet oxywater species, 3O·OH2, as shown in Fig. 2. This species may be viewed as a cluster stabilized by a weak electrostatic interaction between the apical oxygen and the hydrogens of the water molecule. The relative energies of the triplet oxywater species are about 2.41 kJ mol−1 below the total energy of a triplet oxygen atom and a water molecule on the 3B1 (1) energy surface and 1.37 kJ mol−1 on the 3B2 (1) energy surface. The appearance of the triplet oxywater species in our study is in agreement with studies by Filatov et al.12 in which the triplet oxywater complex with an oxygen–oxygen distance of 3.002 Å at the (14,10)CASSCF/6-31G** level of theory was reported. Furthermore, the authors predicted that the relative energies of the triplet oxywater complex with respect to a triplet oxygen atom and a water molecule are 2.93 kJ mol−1 at the CASSCF level and 5.86 kJ mol−1 at the MR-(S)DCI level of theory.12 The authors indicated that the obtained minimum may be due to the basis set superposition error (BSSE), and therefore, it may be an artifact of calculations.12 It is challenging to determine the BSSE for such a complex using the CASSCF method as the complex as well as the isolate oxygen atom are in triplet states whereas the water molecule is in a singlet state. Therefore, the CASSCF space cannot be identical in different calculations needed for determining the BSSE. However, we examined the BSSE of the triplet complex at an oxygen–oxygen distance of 2.77 Å on the 3B1 (1) energy surface for which we adapted the CASSCF space for an isolate triplet oxygen atom to (6,6)CASSCF, and for H2O to (8,8)CASSCF while SC-NEVPT2 was still in use. With the calculated counterpoise correction, the binding energy was reduced by about 40% but it did not vanish. This suggests that the existence of a global minimum on the potential energy curve of the triplet complex may not be due to the BSSE. The 3A2 (1) triplet energy surface does not lead to formation of a triplet oxywater species as the curve has only a repulsive feature (see Fig. 2).
As shown in Fig. 1, the product of the singlet oxygen atom O(1D) and the H2O molecule has a minimum on the 1A1 (1) energy surface at an oxygen–oxygen distance of about 1.5 Å, leading to formation of a relatively stable singlet oxywater species, 1O·OH2. The singlet oxywater species lies about 114.17 kJ mol−1 below the total energy of a singlet oxygen atom and a water molecule. By optimizing the H2O molecule at each distance point, the singlet oxywater species lies about 149.33 kJ mol−1 below the total energy of a singlet oxygen atom and a water molecule (see Fig. S2 and S3 of the ESI†). In the latter calculation, by reducing the oxygen–oxygen distance from 1.1 Å to 1.0 Å, the energy of the singlet state, 1A1 (1), remains almost unchanged (see Fig. S2, ESI†). At an oxygen–oxygen distance of r(OO) = 1 Å, the oxygen–hydrogen distance is r(O2H) = 1.57 Å, the hydrogen–hydrogen distance is r(HH) = 1.98 Å, and the complex transitions to two separate hydrogen atoms while the two oxygen atoms are bonded (see Fig. 3 for the atomic numbering scheme used). Our results are in agreement with the studies of Filatov et al.12 where it was predicted that the energy of the singlet oxywater complex is about 101.25 kJ mol−1 below the total energy of a singlet oxygen atom and a water molecule. Furthermore, our findings are in agreement with the studies of Franz et al.25 who predicted a minimum on the singlet state energy curve at an oxygen–oxygen distance of about 1.64 Å with a depth of about 89.12 kJ mol−1 with respect to the total energy of a singlet oxygen atom and a water molecule at the MSMRMP2/TZVP level of theory. The remaining four singlet energy curves, 1A1 (2), 3B2 (1), 1A1 (2), and 1B2 (1), as well as the second excited state energy curve, 1A1 (3), have repulsive characters (see Fig. 1).
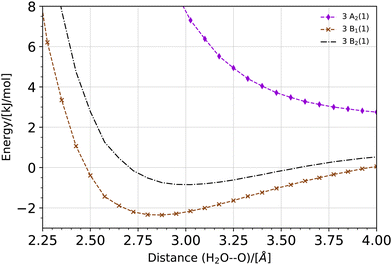
 |
| | Fig. 3 Reaction diagram of the oxywater transition to hydrogen peroxide through the (1,2)-hydrogen shift calculated on the singlet energy surface at three different levels of theory, (10,8)CASSCF/cc-pVTZ, CCSD/cc-pVTZ, and CCSD(T)/cc-pVTZ, in a vacuum and in implicit water. The energies are relative to the energy of the oxywater species. | |
In the following section, we explore the unimolecular reaction pathway of the singlet oxywater species to hydrogen peroxide through the (1,2)-hydrogen shift. We also provide an estimate of the respective reaction rate both in a vacuum and in an implicit water environment. While explicit water molecules provide a more accurate description of molecular processes in water, the substantial computational cost associated with our quantum mechanical calculations necessitates this pragmatic approach.
3.2 Oxywater transition to hydrogen peroxide
We calculated the reaction pathway of the singlet oxywater species, 1O·OH2, to hydrogen peroxide through the (1,2)-hydrogen shift, at three different levels of theory, (10,8)CASSCF/cc-pVTZ, CCSD/cc-pVTZ, and CCSD(T)/cc-pVTZ, in a vacuum and in implicit water using the nudged elastic band (NEB) method.47–49 The latter condition applies exclusively to the CCSD/cc-pVTZ and CCSD(T)/cc-pVTZ levels of theory. Fig. 3 depicts the energies of the transition state for (1,2)-hydrogen rearrangements, and the hydrogen peroxide relative to the energies of the oxywater species. The geometries of oxywater, hydrogen peroxide, and the transition state for the (1,2)-hydrogen shift were optimized at the three levels of theory in a vacuum and in implicit water, and are tabulated in Table 1. The atomic numbering scheme used in Table 1 is indicated in Fig. 3. The harmonic vibrational frequencies that are reported in Table 2 support our characterization of stationary points as minima and transition states on the potential energy surface. The predicted energies of hydrogen peroxide and the transition state relative to the energy of oxywater are provided in Table 4.
Table 1 Structural parameters of oxywater, the transition state, and hydrogen peroxide. Distances are in angstrom and angles in degree. The torsional angle, τ, is defined as H4–O2–O1–H3. The atomic numbering scheme used is indicated in Fig. 3
| Structural properties |
(10,8)CASSCF/cc-pVTZ |
CCSD/cc-pVTZ |
CCSD(T)/cc-pVTZ |
CCSD(T)/TZ2P+fa |
CCSD/cc-pVTZ implicit water |
CCSD(T)/cc-pVTZ implicit water |
|
Data from the study of Huang et al.21 for comparison.
|
| Oxywater |
|
r(OO) |
1.571 |
1.533 |
1.546 |
1.549 |
1.492 |
1.505 |
|
r(OH) |
0.971 |
0.964 |
0.967 |
0.967 |
0.969 |
0.972 |
| ∠HOO |
99.8 |
101.2 |
99.8 |
— |
105.3 |
104.5 |
| ∠H4O2H3 |
107.4 |
109.5 |
108.4 |
106.4 |
111.7 |
110.7 |
|
|
| Transition state |
|
r(OO) |
1.641 |
1.610 |
1.628 |
1.634 |
1.585 |
1.600 |
|
r(O2H4) |
0.972 |
0.964 |
0.967 |
0.968 |
0.969 |
0.972 |
|
r(O2H3) |
1.046 |
1.032 |
1.023 |
1.031 |
1.065 |
1.062 |
| ∠H4O2O1 |
96.5 |
98.5 |
97.0 |
97.4 |
101.1 |
100.5 |
| ∠H3O2O1 |
55.0 |
57.1 |
59.4 |
— |
54.4 |
55.4 |
| ∠H3O2H4 |
102.9 |
103.4 |
103.5 |
— |
101.5 |
101.6 |
|
|
| Hydrogen peroxide |
|
r(OO) |
1.477 |
1.441 |
1.458 |
1.461 |
1.438 |
1.455 |
|
r(OH) |
0.967 |
0.961 |
0.964 |
0.964 |
0.963 |
0.966 |
| ∠HOO |
98.9 |
100.3 |
99.5 |
99.7 |
101.3 |
100.7 |
|
τ
|
116.7 |
113.1 |
113.9 |
111.9 |
99.0 |
99.6 |
Table 2 Theoretical vibrational frequencies (in cm−1) for oxywater, the transition state for the hydrogen rearrangement, and hydrogen peroxide
| Symmetry |
(10,8)CASSCF/cc-pVTZ |
CCSD/cc-pVTZ |
CCSD(T)/cc-pVTZ |
CCSD(T)/TZ2P+fa |
|
CCSD/cc-pVTZ implicit water |
CCSD(T)/cc-pVTZ implicit water |
Assignment |
|
Theoretical data from the study of Huang et al.21
Experimental data from the study of Giguere and Srinivasan.54
Experimental data from the study of Hillman et al.55
|
| Oxywater |
|
a′ |
688 |
704 |
672 |
666 |
|
816 |
791 |
O–O stretch |
|
a′′ |
961 |
874 |
830 |
848 |
|
984 |
973 |
O–O–H bend |
|
a′ |
965 |
888 |
874 |
880 |
|
1024 |
993 |
Out-of-plane |
|
a′ |
1698 |
1644 |
1627 |
1626 |
|
1637 |
1620 |
H–O–H bend |
|
a' |
3751 |
3788 |
3749 |
3741 |
|
3731 |
3697 |
O–H stretch |
|
a′′ |
3833 |
3885 |
3847 |
3840 |
|
3806 |
3770 |
O–H stretch |
|
|
| Transition state |
|
a
|
1340i |
1217i |
1059i |
1103i |
|
1557i |
1439i |
Reaction coordinate |
|
a
|
698 |
698 |
680 |
670 |
|
756 |
738 |
O–O stretch |
|
a
|
971 |
963 |
913 |
925 |
|
1064 |
1033 |
O–O–H bend |
|
a
|
1510 |
1442 |
1467 |
1450 |
|
1346 |
1354 |
Out-of-plane |
|
a
|
2959 |
3035 |
3094 |
3001 |
|
2813 |
2803 |
O–H stretch |
|
a
|
3799 |
3840 |
3796 |
3788 |
|
3777 |
3734 |
O–H stretch |
|
|
| Hydrogen peroxide |
|
|
|
|
|
|
Exp |
|
|
|
|
a
|
435 |
383 |
372 |
392 |
317b |
371 |
354 |
Torsion |
|
a
|
851 |
974 |
912 |
891 |
863b, 864c |
977 |
916 |
O–O stretch |
|
b
|
1357 |
1357 |
1323 |
1322 |
1266b, 1265c |
1390 |
1355 |
O–O–H bend |
|
a
|
1459 |
1468 |
1436 |
1426 |
1393b |
1430 |
1397 |
O–O–H bend |
|
b
|
3790 |
3850 |
3808 |
3801 |
3607b |
3822 |
3782 |
O–H stretch |
|
a
|
3840 |
3851 |
3809 |
3803 |
3608b |
3829 |
3790 |
O–H stretch |
Structural properties.
Our theoretical predictions of the structural properties of oxywater, the transition state, and hydrogen peroxide in a vacuum are in good agreement with those of Huang et al.21 where the CCSD(T) methods with DZP and TZ2P+f basis sets were used, and those of Meredith et al.19 where SCF, CISD, and CCSD methods with DZP, and TZ2P+f basis sets, and the CCSD(T) method with the DZP basis set were used. We included the structural properties of Huang et al.21 at the CCSD(T)/TZ2P+f level of theory in Table 1 for comparison. To the best of our knowledge, oxywater has not been observed experimentally. However, hydrogen peroxide has been extensively studied, both experimentally and theoretically. Therefore, the extent to which our predictions for hydrogen peroxide align with experimental results can serve as an indicator of the potential success of our calculations in characterizing oxywater and the transition state. However, there has been a controversy over the equilibrium geometry of hydrogen peroxide due to its skew configuration which makes the determination of its four internal parameters from three rotational constants ambiguous. Therefore, a full set of internal parameters for hydrogen peroxide can only be obtained by selecting a value for one of the coordinates, which is usually the O–H bond length.19,50 According to the infrared spectral data of Redington et al.,50 the equilibrium geometry of hydrogen peroxide has a r(O–O) distance of 1.475 Å, an angle of ∠OOH of 94.8°, and a torsional angle of τ = 119.8° based on the assumption that the r(O–H) distance is 0.950 Å which is in agreement with the torsional angle from the work of Oelfke and Gordy.51 However, Koput52 obtained the following structure based on the assumption that the r(O–H) distance is 0.965 Å: r(O–O) = 1.464 Å, ∠OOH = 99.4°, and τ = 111.8°. The experimental results of Koput52 are in better agreement with our theoretical predictions. Additionally, our results for hydrogen peroxide are in good agreement with the theoretical predictions of Huang et al.21 (see Table 1) and with those of Harding53 using the ab initio anharmonic force field.
Theoretical vibrational frequencies.
Our theoretical predictions of the vibrational frequencies, in particular the results of the CCSD(T)/cc-pVTZ method, are in reasonable agreement with the theoretical predictions of Huang et al.21 at the CCSD(T)/TZ2P+f level of theory (see Table 2). In the case of hydrogen peroxide, the two methods demonstrate agreement within 1% for all frequencies, except for a 5% deviation in torsion and approximately 2% variance in the O–O stretch. Similarly, for oxywater, the two methods align within about 1% for all frequencies, except for a discrepancy of approximately 2% in the O–O–H asymmetric bend. Experimental vibrational frequencies for hydrogen peroxide are available, enabling us to obtain a rough estimate of the validity of our theoretical predictions. The experimental values for hydrogen peroxide are considerably lower than our theoretical predictions. Scaling of our theoretical frequencies at the CCSD(T)/cc-pVTZ level of theory by a factor of 0.95 brings the O–H stretch within 0.3% of the experimental values, the O–O stretch within 0.3% of the experimental values, O–O–H bends within 0.7%, and the torsion within 11% of the experimental values. This suggests that our unscaled theoretical predictions for oxywater are also higher than the possible experimental results.
Theoretical dipole moments.
Theoretical dipole moments (in Debye) for oxywater, the transition state, and hydrogen peroxide are presented in Table 3. Theoretical dipole moments are helpful in identifying these structures in experiments. The experimental dipole moment of hydrogen peroxide and the theoretical predictions by Huang et al.21 are presented for comparison. For the dipole moment of hydrogen peroxide, our theoretical prediction using the (10,8)CASSCF/cc-pVTZ method is in excellent agreement with the experimental value. Using the CCSD(T)/cc-pVTZ (or CCSD/cc-pVTZ) method, the predicted dipole moment of hydrogen peroxide is about 11% (or 12%) smaller than the experimental value. Our theoretical predictions at the CCSD(T)/cc-pVTZ level of theory is about 2% smaller than the predictions of Huang et al.21 at the CCSD(T)/TZ2P+f level of theory. The theoretical predictions of the dipole moment of oxywater are considerably large.
Table 3 Theoretical dipole moments (in Debye) for oxywater, the transition state for the unimolecular rearrangement, hydrogen peroxide, and the experimental dipole moment for hydrogen peroxide for comparison
| Species |
(10,8)CASSCF/cc-pVTZ |
CCSD/cc-pVTZ |
CCSD(T)/cc-pVTZ |
CCSD(T)/TZ2P+fa |
CCSD/cc-pVTZ implicit water |
CCSD(T)/cc-pVTZ implicit water |
Exp. |
|
Theoretical data from the study of Huang et al.21
Experimental data from the study of Cohen and Pickett.56
|
| Oxywater |
4.68 |
4.58 |
4.52 |
4.54 |
5.71 |
5.31 |
|
| Transition state |
3.25 |
3.17 |
3.24 |
3.15 |
3.70 |
3.74 |
|
| Hydrogen peroxide |
1.58 |
1.78 |
1.76 |
1.80 |
2.60 |
2.46 |
1.58b |
Energy barriers for oxywater transition to hydrogen peroxide.
The relative energy of the transition state and hydrogen peroxide with respect to the energy of oxywater is presented in Table 4. The theoretical predictions by Huang et al.21 at the CCSD(T)/TZ2P+f level of theory are shown for comparison. Hydrogen peroxide lies well below oxywater. Our results show that the activation barrier at the CCSD(T)/cc-pVTZ level of theory is about 3 kJ mol−1 smaller than those of Huang et al.21 at the CCSD(T)/TZ2P+f level of theory. Our calculations in the implicit water environment predict a relatively higher energy barrier for the transition than that for the predictions in a vacuum. This suggests that the oxywater species is more stable in the water environment than vacuum. This result is in agreement with the results of Ignatov et al.24 who suggested that the ice surface stabilizes the oxywater against the transition to hydrogen peroxide due to the formation of hydrogen bonds. A similar conclusion can be made from the studies of Okajima22,23 who theoretically investigated the formation of oxywater from hydrogen peroxide through the (1,2)-hydrogen shift mechanism and suggested that a protic solvent such as water can play a significant role in accelerating the formation of oxywater. Oxywater is a powerful oxidant against biomolecules especially in a hydrophilic environment.22,23
Table 4 Energies (kJ mol−1) of the transition state and hydrogen peroxide relative to the energy of oxywater
| Species |
(10,8)CASSCF/cc-pVTZ |
CCSD/cc-pVTZ |
CCSD(T)/cc-pVTZ |
CCSD(T)/TZ2P+fa |
CCSD/cc-pVTZ implicit water |
CCSD(T)/cc-pVTZ implicit water |
|
Theoretical data from the study of Huang et al.21
|
| Oxywater |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
| Transition state |
35.7 |
30.6 |
20.9 |
23.9 |
65.3 |
54.3 |
| Hydrogen peroxide |
−168.5 |
−200.9 |
−202.1 |
−195.8 |
−154.4 |
−155.5 |
Reaction rate.
We estimated the rate of the unimolecular reaction at room temperature (T = 298 K) using the following equation57–59| | 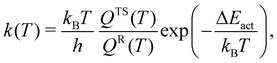 | (6) |
wherein kB is the Boltzmann constant, T is the temperature, h is the Planck constant, and ΔEact is the activation energy barrier. QTS and QR denote the total partition functions of the transition state and the reactant (i.e., oxywater for the forward reaction and hydrogen peroxide for the backward/reverse reaction), respectively. The total partition function includes contributions from all rotational states, Qrot, and all vibrational states, Qvib. In unimolecular reactions, the contribution from translational modes is not considered. Furthermore, at room temperature, the excited states remain unpopulated due to their relatively high excitation energies (see Fig. 1), allowing for the electronic contribution to be disregarded. Therefore, the total partition function is given by Q = Qrot × Qvib. The rotational partition function is given by| | 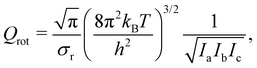 | (7) |
wherein T is the temperature, and σr is the rotational symmetry (here is 1 as there is no centre of symmetry). Ii (i = a, b, c) is the principal moments of inertia for each rotational axis, and is attributed to the respective rotational frequency, ωi, by 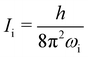 . The vibration partition function is given by
. The vibration partition function is given by| | 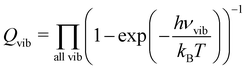 | (8) |
in which the product operator is over all vibrational frequencies, νvib. The results at T = 298 K are presented in Table 5. As expected, hydrogen peroxide is a stable molecule and the backward reaction is almost absent with rates that are of the order of 10−23 (s−1), 10−28 (s−1), and 10−27 (s−1) at the (10,8)CASSCF/cc-pVTZ, CCSD/cc-pVTZ, and CCSD(T)/cc-pVTZ levels of theory, respectively. The rates of the forward reaction for hydrogen peroxide production are about 3.02 × 106 (s−1), 2.72 × 107 (s−1), and 1.34 × 109 (s−1) at the (10,8)CASSCF/cc-pVTZ, CCSD/cc-pVTZ, and CCSD(T)/cc-pVTZ levels of theory, respectively. In general, the predicted rate is quite sensitive to the predicted value of the activation energy barrier. The rates of the forward reaction for hydrogen peroxide production in the implicit water environment reduce to 2.18 × 10 (s−1) and 1.91 × 103 (s−1) at the CCSD/cc-pVTZ and CCSD(T)/cc-pVTZ levels of theory, respectively. This suggests that oxywater is more stable in the water environment, which is in agreement with predictions of Ignatov et al.24 and Okajima22,23 that the oxywater species has a longer lifetime in water.
Table 5 Reaction constants, k (s−1), for the oxywater transition to hydrogen peroxide (forward) and the reverse (backward) reaction at T = 298 K
| (10,8)CASSCF/cc-pVTZ |
CCSD/cc-pVTZ |
CCSD(T)/cc-pVTZ |
CCSD/cc-pVTZ implicit water |
CCSD(T)/cc-pVTZ implicit water |
| Forward reaction |
| 3.02 × 106 |
2.72 × 107 |
1.34 × 109 |
2.18 × 101 |
1.91 × 103 |
|
|
| Backward reaction |
| 1.06 × 10−23 |
1.55 × 10−28 |
4.75 × 10−27 |
1.89 × 10−26 |
1.04 × 10−24 |
It is worth mentioning that because the three triplet potential energy curves arising from O3 (P), 3B1 (1), 3B2 (1), and 3A2 (1) cross the well of the singlet potential energy curve of the O·OH2 complex, 1A1 (1), there may be possible routes to deactivate the electronic excitation of the oxygen atom (see Fig. 1). In particular, the energy difference between the minimum of the singlet O·OH2 well, the 1A1 (1) state, and the 3B1 (1) state at the crossing point is about 21.5 kJ mol−1. The energy difference between the minimum of the singlet O·OH2 well, the 1A1 (1) state, and the 3B2 (1) state at the crossing point is about 45.8 kJ mol−1. These energy differences are within the range of the activation energy barrier toward hydrogen peroxide production (see Table 4) which suggests that there may be competition between production of the triplet oxygen atom and hydrogen peroxide formation if the spin–orbit coupling is strong enough.
4 Conclusions
Atomic oxygen either in the ground triplet state, O(3P), or in the excited singlet state, O(1D), can be produced by electric gas discharge plasmas generated in O2 containing gases. We explored the interaction of O(3P) and O(1D) with water molecules. In particular, we examined the formation of the oxywater species as the reaction product of atomic oxygen and water molecules. Our high-level quantum mechanical calculations predict the formation of a relatively stable oxywater species as the product of O(1D) and H2O. The energy of this singlet state oxywater complex is well below the total energy of a singlet O(1D) atom and a water molecule (about 114.17 kJ mol−1 or 149.33 kJ mol−1). We also predict a triplet oxywater complex as the product of the O(3P) atom and the water molecule. The energy of the triplet oxywater complex is about 2.41 kJ mol−1 or 1.37 kJ mol−1 below the total energy of O(3P) and H2O.
Considering the singlet state oxywater species as a stable complex, we examined its transition to hydrogen peroxide through the unimolecular reaction pathway, the (1,2)-hydrogen shift. Our predicted structural properties, vibrational frequencies, and dipole moments are consistent and are in agreement with those of Huang et al.21 The energy barriers for the transition to hydrogen peroxide are predicted to be about 35.7 kJ mol−1 at the (10,8)CASSCF/cc-PVTZ level, 30.6 kJ mol−1 at the CCSD/cc-pVTZ level, and 20.9 kJ mol−1 at the CCSD(T)/cc-pVTZ level. Performing the calculations in an implicit water environment results in relatively higher energy barriers which suggest a longer lifetime of the singlet oxywater species in the water environment. This is aligned well with the predictions of Ignatov et al.24 and Okajima.22,23
Although the oxywater species has not yet been detected experimentally, a reaction channel for the production of the oxywater species and thereby hydrogen peroxide in macroscopic models of electric gas discharge plasmas may be important for predicting the final concentration of hydrogen peroxide.
Data availability
The input files to perform the simulations are provided at DOI: https://zenodo.org/doi/10.5281/zenodo.10630824.
Author contributions
JS and BB carried out the simulations and data analysis. BB conceived and supervised the project. BB wrote the manuscript in collaboration with JS.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
BB thanks the strategic alliance between TU/e, Utrecht University, and University Medical Center Utrecht for financial support.
References
- T. Jaffke, M. Meinke, R. Hashemi, L. G. Christophorou and E. Illenberger, Chem. Phys. Lett., 1992, 193, 62–68 CrossRef CAS.
- R. Peyrous, Ozone: Sci. Eng., 1990, 12(1), 41–64 CrossRef CAS.
- S. Schröter, A. Wijaikhum, A. R. Gibson, A. West, H. L. Davies, N. Minesi, J. Dedrick, E. Wagenaars, N. De Oliveira and L. Nahon,
et al.
, Phys. Chem. Chem. Phys., 2018, 20, 24263–24286 RSC.
- J. Benedikt, M. M. Hefny, A. Shaw, B. R. Buckley, F. Iza, S. Schäkermann and J. Bandow, Phys. Chem. Chem. Phys., 2018, 20, 12037–12042 RSC.
- M. M. Hefny, C. Pattyn, P. Lukes and J. Benedikt, J. Phys. D: Appl. Phys., 2016, 49, 404002 CrossRef.
- V. Jirásek and P. Lukeš, Plasma Sources Sci. Technol., 2019, 28, 035015 CrossRef.
- Y. Gorbanev, J. Golda, V. Schulz-von der Gathen and A. Bogaerts, Plasma, 2019, 2, 316–327 CrossRef CAS.
- B. Myers, E. Barnat and K. Stapelmann, J. Phys. D: Appl. Phys., 2021, 54, 455202 CrossRef CAS.
- D. O’connell, L. J. Cox, W. B. Hyland, S. J. McMahon, S. Reuter, W. G. Graham, T. Gans and F. J. Currell, Appl. Phys. Lett., 2011, 98(4), 043701 CrossRef.
- X. Lu, G. V. Naidis, M. Laroussi, S. Reuter, D. B. Graves and K. Ostrikov, Phys. Rep., 2016, 630, 1–84 CrossRef CAS.
- J. M. Anglada, M. Martins-Costa, J. S. Francisco and M. F. Ruiz-Lopez, Acc. Chem. Res., 2015, 48, 575–583 CrossRef CAS PubMed.
- M. Filatov, W. Reckien, S. D. Peyerimhoff and S. Shaik, J. Phys. Chem. A, 2000, 104, 12014–12020 CrossRef CAS.
- O. Bain and P. A. Giguère, Can. J. Chem., 1955, 33, 527–545 CrossRef CAS.
- U. Kaldor and I. Shavitt, J. Chem. Phys., 1966, 44, 1823–1829 CrossRef CAS.
- D. Cremer, J. Chem. Phys., 1978, 69, 4440–4455 CrossRef CAS.
- J. A. Pople, K. Raghavachari, M. J. Frisch, J. S. Binkley and P. V. Schleyer, J. Am. Chem. Soc., 1983, 105, 6389–6399 CrossRef CAS.
- R. D. Bach, J. J. McDouall, A. L. Owensby and H. B. Schlegel, J. Am. Chem. Soc., 1990, 112, 7065–7067 CrossRef CAS.
- R. D. Bach, A. L. Owensby, C. Gonzalez, H. B. Schlegel and J. J. McDouall, J. Am. Chem. Soc., 1991, 113, 6001–6011 CrossRef CAS.
- C. Meredith, T. P. Hamilton and H. F. Schaefer III, J. Phys. Chem., 1992, 96, 9250–9254 CrossRef CAS.
- D. Schröder, C. A. Schalley, H. Schwarz, N. Goldberg and J. Hrûsák, Chem. – Eur. J., 1996, 2, 1235–1242 CrossRef.
- H. H. Huang, Y. Xie and H. F. Schaefer, J. Phys. Chem., 1996, 100, 6076–6080 CrossRef CAS.
- T. Okajima, Can. J. Chem., 2001, 79, 22–28 CAS.
- T. Okajima, J. Mol. Struct.: THEOCHEM, 2001, 572(1), 45–52 CrossRef CAS.
- S. K. Ignatov, P. G. Sennikov, H.-W. Jacobi, A. G. Razuvaev and O. Schrems, Phys. Chem. Chem. Phys., 2003, 5, 496–505 RSC.
- J. Franz, J. S. Francisco and S. D. Peyerimhoff, J. Chem. Phys., 2009, 130(8), 084304 CrossRef PubMed.
- M. Yusupov, E. Neyts, P. Simon, G. Berdiyorov, R. Snoeckx, A. Van Duin and A. Bogaerts, J. Phys. D: Appl. Phys., 2013, 47, 025205 CrossRef.
- C. Verlackt, E. Neyts and A. Bogaerts, J. Phys. D: Appl. Phys., 2017, 50, 11LT01 CrossRef.
- S. Xu, V. Jirasek and P. Lukes, J. Phys. D: Appl. Phys., 2020, 53, 275204 CrossRef CAS.
- Y. Sakiyama, D. B. Graves, H.-W. Chang, T. Shimizu and G. E. Morfill, J. Phys. D: Appl. Phys., 2012, 45, 425201 CrossRef.
- D. S. Stafford and M. J. Kushner, J. Appl. Phys., 2004, 96, 2451–2465 CrossRef CAS.
- J. C. Person and D. O. Ham, Int. J. Radiat. Appl. Instrum., Part C, 1988, 31, 1–8 CAS.
- G. Paraskevopoulos and R. Cvetanović, Chem. Phys. Lett., 1971, 9, 603–605 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1975, 62, 1893–1898 CrossRef CAS.
- G. Streit, C. J. Howard, A. Schmeltekopf, J. Davidson and H. Schiff, J. Chem. Phys., 1976, 65, 4761–4764 CrossRef CAS.
- E. J. Dunlea and A. Ravishankara, Phys. Chem. Chem. Phys., 2004, 6, 3333–3340 RSC.
- K. Takahashi, Y. Takeuchi and Y. Matsumi, Chem. Phys. Lett., 2005, 410, 196–200 CrossRef CAS.
- R. Zellner, G. Wagner and B. Himme, J. Phys. Chem., 1980, 84, 3196–3198 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- A. K. Wilson, T. van Mourik and T. H. Dunning Jr, J. Mol. Struct.: THEOCHEM, 1996, 388, 339–349 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152(22), 224108 CrossRef CAS PubMed.
- NIST, Basic Atomic Spectroscopic Data, https://physics.nist.gov/PhysRefData/Handbook/Tables/oxygentable5.htm [Accessed: (April 2024)].
-
J. Gallagher and C. E. Moore, Tables of spectra of hydrogen, carbon, nitrogen, and oxygen atoms and ions, CRC Press, 1993 Search PubMed.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
-
H. Jónsson, G. Mills, K. W. Jacobsen, B. Berne, G. Ciccotti and D. Coker, Classical and quantum dynamics in condensed phase simulations, 1998 Search PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- R. L. Redington, W. Olson and P. Cross, J. Chem. Phys., 1962, 36, 1311–1326 CrossRef CAS.
- W. C. Oelfke and W. Gordy, J. Chem. Phys., 1969, 51, 5336–5343 CrossRef CAS.
- J. Koput, J. Mol. Spectrosc., 1986, 115, 438–441 CrossRef CAS.
- L. B. Harding, J. Phys. Chem., 1989, 93, 8004–8013 CrossRef CAS.
- P. Giguere and T. Srinivasan, J. Raman Spectrosc., 1974, 2, 125–132 CrossRef CAS.
- J. Hillman, D. Jennings, W. Olson and A. Goldman, J. Mol. Spectrosc., 1986, 117, 46–59 CrossRef CAS.
- E. Cohen and H. Pickett, J. Mol. Spectrosc., 1981, 87, 582–583 CrossRef CAS.
- H. Eyring, Chem. Rev., 1935, 17, 65–77 CrossRef CAS.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1 shows the potential energy curves for the O·OH2 complex along the oxygen–oxygen coordinate from 1 Å to 10 Å for calculations wherein the geometry of H2O is held fixed at each distance position. Fig. S2 depicts potential energy curves as an oxygen atom approaches the oxygen of a water molecule in calculations where the H2O geometry is optimized at each distance position. In Fig. S3, the singlet potential energy curve is compared between calculations with H2O held fixed and those with H2O optimized at each distance position. See DOI: https://doi.org/10.1039/d4cp00969j |
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab


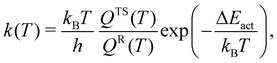
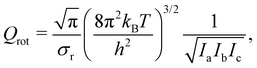
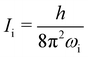 . The vibration partition function is given by
. The vibration partition function is given by