Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic properties and collision cross sections of AgOkHm± (k, m = 1–4) aerosol ionic clusters†
Mohsen
Doust Mohammadi
 a,
Somnath
Bhowmick
a,
Somnath
Bhowmick
 *a,
Anne
Maisser
*a,
Anne
Maisser
 a,
Andreas
Schmidt-Ott
a,
Andreas
Schmidt-Ott
 ab and
George
Biskos
ab and
George
Biskos
 *ac
*ac
aClimate & Atmosphere Research Centre, The Cyprus Institute, 20 Konstantinou Kavafi Street, Nicosia 2121, Cyprus. E-mail: s.bhowmick@cyi.ac.cy; g.biskos@cyi.ac.cy; Fax: +357 22208625; Tel: +357 22 208618
bFaculty of Applied Sciences, Delft University of Technology, Delft, 2629 HZ, The Netherlands
cFaculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, 2628 CN, The Netherlands
First published on 30th April 2024
Abstract
Experimental evidence shows that hydroxylated metal ions are often produced during cluster synthesis by atmospheric pressure spark ablation. In this work, we predict the ground state equilibrium structures of AgOkHm± clusters (k and m = 1–4), which are readily produced when spark ablating Ag, using the coupled cluster with singles and doubles (CCSD) method. The stabilization energy of these clusters is calculated with respect to the dissociation channel having the lowest energy, by accounting perturbative triples corrections to the CCSD method. The interatomic interactions in each of the systems have been investigated using the frontier molecular orbital (FMO), natural bond orbital (NBO) and quantum theory of atoms in molecules (QTAIM) methods. Many of the ground states of these ionic clusters are found to be stable, corroborating experimental observations. We find that clusters having singlet spin states are more stable in terms of dissociation than the clusters that have doublet or triplet spin states. Our calculations also indicate a strong affinity of the ionic and neutral Ag atom towards water and hydroxyl radicals or ions. Many 3-center, 4-electron (3c/4e) hyperbonds giving rise to more than one resonance structure are identified primarily for the anionic clusters. The QTAIM analysis shows that the O–H and O–Ag bonds in the clusters of both polarities are respectively covalent and ionic. The FMO analysis indicates that the anionic clusters are more reactive than the cationic ones. Using the cluster structures predicted by the CCSD method, we calculate the collision cross sections of the AgOkHm± family, with k and m ranging from 1 to 4, by the trajectory method. In turn, we predict the electrical mobilities of these clusters when suspended in helium at atmospheric pressure and compare them with experimental measurements.
1 Introduction
Positively and negatively charged hydroxylated atomic clusters are readily produced by aerosol-based synthesis techniques, such as spark ablation at atmospheric pressure,1 mainly due to the presence of trace amounts of O2 and H2O in the carrier gas.2 When ablating silver, in addition to pure silver clusters, stable species such as silver oxides (AgnOk±) and hydroxylated silver (AgnOkHm±) ionic clusters are also formed.2 Considering that such silver-based atomic clusters find applications in optical materials,3 medicine,4 catalysis,5,6 sensing and imaging,7,8etc., it is highly important to determine their structure and stability.A wide range of theoretical methods have been used to identify the structure and stability of neutral and charged silver clusters,9–19 whereas a number of experimental and theoretical studies have investigated silver-based ionic species that can form via direct interaction with oxygen.11,20–28 Most of these studies have employed standard density functional theory (DFT). More advanced ab initio methods, such as the coupled cluster (CC) with single (S), double (D), and perturbative triple (T) excitation (CCSD(T)) level of theory,29–32 have recently been shown to more accurately capture the ground state structures and stabilities of such clusters.28 For example, for the ground state of the Ag2O+ cluster, the DFT method predicts both bent11,26 and linear25 geometries depending on whether local, gradient-corrected, or hybrid functionals are used. On the other hand, less precise methods, such as the Hartree–Fock (HF) self-consistent field (SCF) theory, predict a linear structure for Ag2O+.20 Recently reported CCSD(T) calculations show that the ground state of the Ag2O+ cluster has a geometry that is very close to a linear structure (∠Ag–O–Ag = 172°).28 We should note here that CCSD(T) theory, which is often termed the “gold standard” in quantum chemistry for single-reference systems,33 has a better “chemical accuracy” (with errors much less than 0.05 eV for thermochemical calculations) compared to the standard DFT method (errors greater than 0.05 eV).34,35
Analysis of the interatomic interactions of clusters and molecules provides great insights into the nature of chemical bonding and reactivities of the AgOkHm± clusters. A number of different approaches, such as the frontier molecular orbitals (FMO),36 natural bond orbital (NBO),37 and quantum theory of atoms in molecules (QTAIM),38,39 can be used to achieve that. The reactivities of different chemical systems could be identified through the FMOs, primarily composed of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). In general, the energy difference between HOMO and LUMO serves as an important parameter from which many physio-chemical properties, such as stability, chemical hardness, reactivity, chemical potential, and electrophilicity, can be qualitatively predicted.40–43 For example, Fournier9 reported that the HOMO–LUMO energy gap (HLG) in neutral silver clusters can be linked to their relative stabilities. Dixon et al.19 also showed that the HLG of neutral silver clusters calculated by the B3LYP functional, is comparable to energy gaps between ground and excited states obtained by time-dependent DFT calculations. Albeit being efficient, the FMO approach cannot be used to capture the local bonding information due to the delocalized nature of the molecular orbitals (MOs).36 The local region of a molecule can be effectively described through Lewis-like structures, such as those incorporated in the NBO approach developed by Weinhold et al.44 Finally, the QTAIM method, introduced by Bader,38 provides an alternating route for evaluating and classifying the nature of chemical bonding and interatomic interactions through topological analysis of the electron density distribution.
Using the structure of the ionic clusters estimated by ab initio methods as described above, one can calculate the collision cross section (CCS) and, from that, the electrical mobility of the clusters.45,46 Maisser et al.47 have experimentally measured the electrical mobilities of both positively and negatively charged silver-based clusters produced by spark ablation at atmospheric pressure,48 containing their pure, oxide and hydroxide variants. Some of the unidentified peaks of the experimental mobility spectra were later attributed to a particular cationic silver oxide cluster, AgnOk+ (n = 1–4; k = 1–5), estimated by CCS calculations using the trajectory method (TM).28
In this work, we predict, for the first time to the best of our knowledge, the ground state equilibrium geometry, stabilization energy, collision cross section, and electrical mobility of both cationic and anionic AgOkHm clusters, where k and m range from 1 to 4. Further insights into the nature of bonding in the AgOkHm± clusters are provided through FMO, NBO, and QTAIM analysis. The rest of the paper is organized as follows: Section 2 describes details of the computational methods we used, Section 3 discusses our results, and Section 4 highlights the most important results.
2 Computational details
2.1 Electronic structure
We follow the same computational strategy as for the silver oxide cluster cations described in ref. 28 In brief, we employ the ABCluster program that uses the artificial bee colony algorithm to search for the minimum energy structures of AgOkHm± clusters.49–51 Full dimensional geometry optimization calculations on the initial structures generated by ABCluster were carried out at the M06 level of theory,52 as it provides results for charged silver clusters that are consistent with experimental observations.17 Once some of the low-energy isomers of a particular AgOkHm± cluster were identified, we optimized them at the CCSD level of theory29–31 using a tighter energy convergence criterium (2 × 10−9 hartree). At the CCSD level geometry optimization step, we considered all possible isomers which have ground state electronic energy less than 1.0 eV compared to that of the lowest energy isomer estimated at the M06 level for a particular AgOkHm± cluster. The M06 functional can capture all of the low-energy isomers of the charged silver clusters15 and provide energy differences among the isomers that have excellent agreement with those predicted by the CCSD(T) method (within ±0.1 eV difference).13 To estimate the ground state electronic energy, we carried out CCSD(T) single-point calculations on the optimized structures obtained at the CCSD level.In order to verify the local minima on the potential energy surfaces of the low-energy isomers, obtained from the geometry optimization by the CCSD method, harmonic frequency calculations were carried out at the M06 level. CCSD(T) ground state electronic energy was further corrected by considering the zero-point vibrational energy (ZPVE). The stabilization energy, ΔE, for the ionic clusters is calculated as the electronic energy difference between the products of the unimolecular dissociation of the AgOkHm± cluster and the cluster itself, E(AgOkHm±), and represented as follows:
| ΔE = E(AgOaHb±,0) + E(AgOc±,0) + E(AgHd±,0) + E(Ag±,0) + E(OeHf±,0) + E(Og±,0) + E(Hh±,0) − E(AgOkHm±) | (1) |
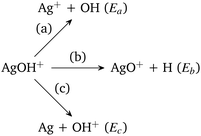
In Scheme 1, Ea is the sum of the electronic energies of the products Ag+ and OH, i.e., E(Ag+) + E(OH). Similarly, Eb = E(AgO+) + E(H) and Ec = E(Ag) + E(OH+). If Ea is less than Eb and Ec, then the reaction channel (a) is denoted as the lowest energy dissociation channel (LEDC) for the AgOH+ cluster. We should note that the stabilization energy defined in eqn (1) is a simplistic model for estimating the stability of a cluster only with respect to unimolecular dissociation, as it neglects a number of thermodynamic and kinetic factors.
For each cluster, the two lowest spin states (singlet and triplet for even numbers, or doublet and quartet for odd numbers of electrons) were considered. To study the closed-shell and open-shell systems, we employed spin-restricted and spin-unrestricted electronic structure theory (both DFT and CCSD), respectively. The standard Dunning's augmented correlation-consistent triple−ζ basis set (aug-cc-pVTZ)53,54 and the cc-pVTZ basis set were used respectively for the oxygen/hydrogen atoms and for the valence electrons of the silver atom. The core electrons of silver atoms are represented by the Stuttgart/Köln energy consistent pseudopotential (ECP28MDF).55,56 All electronic structure calculations were performed using the Gaussian 16 software.57
2.2 Interatomic interactions
The inter-atomic interactions in the AgOkHm± clusters were assessed by FMO (i.e., HOMO and LUMO), NBO, and QTAIM analysis. The density matrices required for the above analyses were obtained from the long-range corrected ωB97XD hybrid functional58 employing the same basis sets as the ones used for the CCSD(T) calculations. The reactivity of a molecular species can be effectively predicted from the morphologies and energies of the FMOs.36 To illustrate, if εHOMO and εLUMO are the energies of HOMO and LUMO, respectively, then from Koopmans' theorem,59 we obtain −εHOMO = IP and −εLUMO = EA. Here, IP and EA are the ionization potential and electron affinity of any chemical system. From the values of IP and EA, we can calculate important electronic properties such as chemical hardness40 (η), chemical potential40 (μ), and electrophilicity index42 (ω) as follows:| η = 1/2(IP − EA) | (2) |
| μ = − 1/2(IP + EA) | (3) |
| ω = μ2/2η | (4) |
Similarly to the energy difference in the FMO (HLG), the quantum chemical descriptors η, μ, and ω can provide valuable information about the stability and reactivity of a chemical species. For example, high HLG and η values indicate low chemical reactivity and high stability,41 whereas μ and ω can be used respectively to characterize the tendency of electrons to escape from a chemical system at equilibrium43 and the capability of a species to accept electrons.42 We should note that the above analyses were performed only for the closed-shell systems.
NBO analysis is a practical tool for describing localized Lewis-like chemical bonds in a molecule.37 We have calculated the second-order energy stabilization, ΔEi,j(2), from the NBO perspective as follows:37
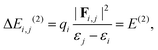 | (5) |
| ΓNRT = ωIΓI + ωIIΓII + ωIIIΓIII+ … | (6) |
Another effective approach to examine the interaction between atoms in a molecule is via QTAIM analysis, which takes the topological representation of a structure into consideration.38,39 In QTAIM, a critical point, such as the bond critical point (BCP), is defined as the turning point in a bond of physical contact at which the gradient of the electron density is zero, i.e., ∇ρ(r) = 0.62,63 A covalent atomic interaction is indicated by a negative value of ∇2ρ(r) at a BCP and a high value of ρ(r) (≥0.1 a.u.). In comparison, a non-substrate closed-shell form of interaction occurs if ∇2ρ(r) is positive, including ionic and hydrogen bonds, as well as van der Waals interactions.64 The virial theorem establishes the following connection between kinetic energy density, G(r), potential energy density, V(r), and ∇2ρ(r):39
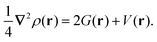 | (7) |
The balance between G(r) and V(r) can be used to classify the mode of interaction, so that the G(r)/|V(r)| ratio serves as a suitable indicator.39 A value of G(r)/|V(r)| greater than 1 indicates a non-covalent interaction, while a value less than 0.5 indicates a predominantly covalent bond. For the QTAIM analysis carried out here, we used the Multiwfn software.65
2.3 Collision cross section and electrical mobility
The CCS of the AgOkHm± clusters have been calculated by the IMoS package developed by Larriba-Andaluz et al.,66,67 and specifically, by the TM45 method. We should note that the results obtained by the TM method are considered more accurate than those obtained either with the exact hard sphere scattering or the projection approximation methods, since it considers the interaction potential between the ion and the carrier gas, which is usually represented by the 12–6 Lennard-Jones (LJ) potential.45 Helium is considered as the carrier gas in the calculations of CCSs and mobilities reported in this work. The optimized values of the LJ parameters in helium were obtained by fitting the predicted values with the measured values (using drift tube experiments) of CCS.68,69 Previous analysis has shown that the CCS calculations were less sensitive towards small changes in the LJ parameters (∼1 and ∼11% deviation in CCS for a 10% change in ε and σ, respectively).28 All calculations have been performed at 298.15 K and 1 atm pressure.The electrical mobilities of all ionic clusters investigated here were calculated based on the CCSs calculations described above, using the following formula:45
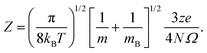 | (8) |
3 Results and discussion
3.1 Structure and stability
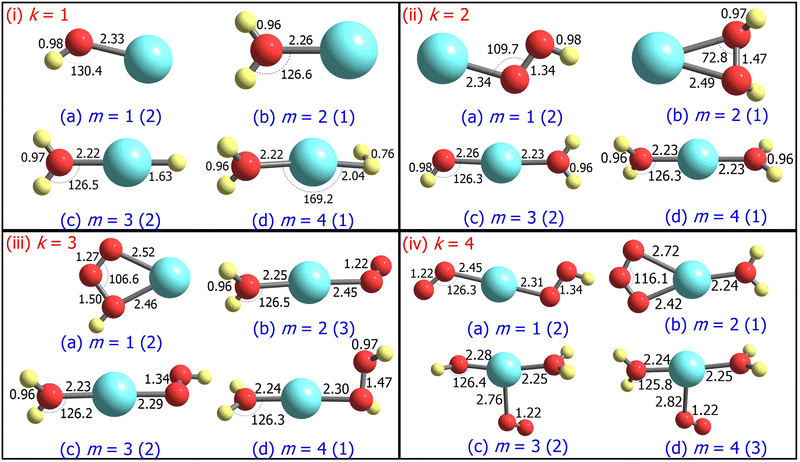
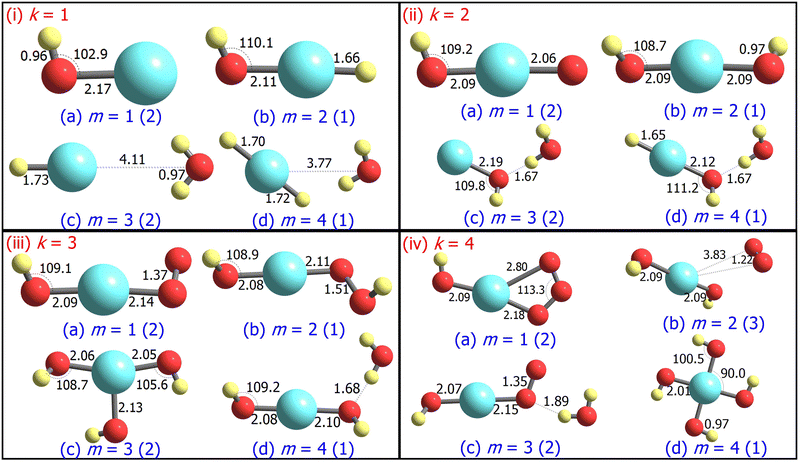
The ground state geometries of the AgOkHm+ clusters are depicted in Fig. 1, whereas those for their anionic counterparts are illustrated in Fig. 2. The optimized coordinates of both cationic and anionic clusters are also provided in Table S1 of the ESI.† The stabilization energy of the clusters, along with the LEDCs, is reported in Table 1 for cations and Table 2 for the anions. The ΔE values for all dissociation channels are also provided in Table S2 of the ESI.† In general, low spin states (singlet and doublet states) are primarily favoured in comparison to the high spin states, except for AgO3H2+, AgO4H4+ and AgO4H2−, where triplet states are more favourable over the singlet states (cf.Tables 1 and 2). This can be attributed to the presence of the weakly bonded triplet O2 molecule to the rest of the cluster that has a singlet spin. These results are different compared to those obtained for the AgOk+ clusters (with k = 1–5),28 where high-spin states are predominant. We should note here that a terminally attached O2 molecule is present in most of the AgOk+ clusters, which is not a dominant feature for the AgOkHm± clusters.| Species | 2S + 1 | PG | T1 | LEDC | ΔE | Ω | Z |
|---|---|---|---|---|---|---|---|
| AgOH+ | 2 | C s | 0.0104 | Ag+ + OH | 0.86 | 30.6 | 19.4 |
| AgOH2+ | 1 | C 2v | 0.0087 | Ag+ + H2O | 1.20 | 31.3 | 19.0 |
| AgOH3+ | 2 | C 2v | 0.0208 | AgOH2+ + H | 0.57 | 32.9 | 18.1 |
| AgOH4+ | 1 | C 2v | 0.0101 | AgOH2+ + H2 | 0.41 | 34.6 | 17.2 |
| AgO2H+ | 2 | C s | 0.0287 | Ag+ + HO2 | 1.02 | 33.7 | 17.6 |
| AgO2H2+ | 1 | C 2 | 0.0118 | Ag+ + H2O2 | 1.18 | 34.2 | 17.3 |
| AgO2H3+ | 2 | C s | 0.0130 | AgOH2+ + OH | 0.84 | 37.0 | 16.0 |
| AgO2H4+ | 1 | D 2d | 0.0108 | AgOH2+ + H2O | 1.14 | 37.8 | 15.7 |
| AgO3H+ | 2 | C s | 0.0409 | AgO2+ + OH | 0.77 | 35.6 | 16.7 |
| AgO3H2+ | 3 | C s | 0.0171 | AgOH2+ + O2 | 0.26 | 39.5 | 15.0 |
| AgO3H3+ | 2 | C s | 0.0260 | AgOH2+ + HO2 | 0.97 | 40.1 | 14.8 |
| AgO3H4+ | 1 | C 1 | 0.0125 | AgOH2+ + H2O2 | 1.08 | 41.2 | 14.4 |
| AgO4H+ | 2 | C s | 0.0226 | AgO2H+ + O2 | −1.13 | 41.9 | 14.1 |
| AgO4H2+ | 1 | C s | 0.0232 | AgOH2+ + O3 | 0.76 | 40.9 | 14.5 |
| AgO4H3+ | 2 | C 1 | 0.0124 | AgO2H3+ + O2 | −0.34 | 46.7 | 12.7 |
| AgO4H4+ | 3 | C 1 | 0.0146 | AgO2H4+ + O2 | 0.08 | 47.1 | 12.5 |
| Species | 2S + 1 | PG | T1 | LEDC | ΔE | Ω | Z |
|---|---|---|---|---|---|---|---|
| AgOH− | 2 | C s | 0.0285 | Ag + OH− | 1.68 | 34.0 | 17.5 |
| AgOH2− | 1 | C s | 0.0194 | AgH + OH− | 2.70 | 33.9 | 17.5 |
| AgOH3− | 2 | C 2v | 0.0229 | AgH− + H2O | 0.40 | 39.3 | 15.1 |
| AgOH4− | 1 | C s | 0.0151 | AgH2− + H2O | 0.47 | 37.4 | 15.9 |
| AgO2H− | 2 | C s | 0.0236 | AgOH + O − | 2.58 | 36.0 | 16.5 |
| AgO2H2− | 1 | C 2 | 0.0202 | AgOH + OH− | 3.12 | 38.2 | 15.5 |
| AgO2H3− | 2 | C 1 | 0.0235 | AgOH− + H2O | 0.73 | 40.1 | 14.8 |
| AgO2H4− | 1 | C 1 | 0.0170 | AgOH2− + H2O | 0.70 | 40.7 | 14.6 |
| AgO3H− | 2 | C 1 | 0.0294 | AgOH− + O2 | 1.55 | 38.4 | 15.4 |
| AgO3H2− | 1 | C 1 | 0.0216 | AgO2H− + OH | 2.58 | 41.0 | 14.4 |
| AgO3H3− | 2 | C 1 | 0.0322 | AgO2H2− + OH | 0.92 | 41.2 | 14.4 |
| AgO3H4− | 1 | C 1 | 0.0180 | AgO2H2− + H2O | 0.66 | 45.6 | 13.0 |
| AgO4H− | 2 | C s | 0.0389 | AgO2H− + O2 | 1.35 | 40.6 | 14.6 |
| AgO4H2− | 3 | C 1 | 0.0197 | AgO2H2− + O2 | 0.04 | 48.3 | 12.2 |
| AgO4H3− | 2 | C 1 | 0.0263 | AgO3H− + H2O | 0.40 | 46.6 | 12.7 |
| AgO4H4− | 1 | C 4h | 0.0253 | AgO3H3− + OH | 2.45 | 42.5 | 13.9 |
As mentioned in section 2.1, we have applied spin-unrestricted electronic structure theory for the open-shell systems. To verify the presence of spin contamination, we calculate the expectation value of the square of the total spin operator (〈Ŝ2〉). Except for the AgO4H+ and AgO4H3+ clusters, the calculated 〈Ŝ2〉 values after the annihilation of the first spin contaminant70 for each of the ionic clusters considered in this study has less than 0.2% deviation from the values of 0.75 (for doublet spin states) or 2.00 (for triplet spin states). In the cases of the doublet AgO4H+ and AgO4H3+ clusters, the maximum 〈Ŝ2〉 value calculated is 0.80, having a deviation from the eigenvalue of Ŝ2 is ca. 6.7%. Therefore, the spin contamination in the open-shell systems studied in this work can be considered negligible.
We have also examined the multireference character in the ground state of these clusters by inspecting the T1 diagnostics values obtained from the CCSD(T) calculations, which are provided in Table 1 (cations) and 2 (anions). Our calculations show that the T1 diagnostics values for the closed-shell systems fall within the range of 0.0087–0.0253, while that for the open-shell systems is 0.0104–0.0409. If the T1 value is predicted to be larger than 0.02 (for closed-shell systems) or 0.045 (for open-shell systems), then the results obtained from single-reference methods such as CC or DFT are less reliable.71,72 Therefore, except for AgO4H2+, AgO3H2− and AgO4H4− clusters, the multireference character in the ground state wavefunction of all other ionic clusters may be considered not predominant. The large T1 diagnostics values predicted for AgO4H2+, AgO3H2− and AgO4H4− clusters may be associated with considerable static correlation in its ground state wavefunction, as evidenced from their multiple dominating resonance structures (cf. section 3.2). That said, however, one should also note that the above-mentioned T1 thresholds are not rigorously defined and can be extended up to 0.05 for transition metal complexes.73,74
We should note that we did not use any symmetry constraint for geometry optimization, and as a result, with the exception of AgOH± and AgOH2− (Cs point group), we did not observe the AgOkHm± clusters studied in this work exhibiting symmetry. If a threshold of 0.01 in both bond distances (expressed in Ångstroms) and angles (expressed in degrees) is introduced so that the geometrical parameters are treated equal below this value, many symmetric structures can be identified for both positive and negative clusters (cf.Tables 1 and 2). Considering that, cationic clusters have more structures belonging to a particular point group other than the non-symmetric C1 compared to their anionic counterparts. Specifically, AgOkHm+ clusters possess 1 D2d, 3 C2v, 1 C2 and 8 Cs symmetric structures, whereas AgOkHm− clusters exhibit only 1 C4h, 1 C2v, 1 C2 and 5 Cs structures. Notably, all AgO3Hm− cluster geometries belong to the non-symmetric C1 point group. Among the most symmetric structures identified in this study are the cationic AgO2H4+ cluster (D2d) and the anionic AgO4H4− cluster (C4h).
For m ≥ 2, a general trend in the structure of the cationic AgOkHm+ clusters is observed, whereby a water moiety is directly attached to a silver atom through the oxygen atom. The interatomic Ag–O distance in these systems lies within the range of 2.22–2.28 Å, while the O–H distance is identical to that of the isolated water molecule (0.96 Å).75 One exception to this pattern is the AgO2H2+ cluster, where a hydrogen peroxide moiety is attached to the positively charged Ag atom. This structural feature is completely absent in the anionic AgOkHm− clusters, in which the most prevalent moiety interacting with the central and partially positive Ag atom is the OH− ion that has a slightly positive charge on H, rendering a stable system due to attractive Coulombic interaction. The Ag–O distances in the anions are marginally shorter (2.01–2.19 Å) than those obtained for the cations (2.22–2.28 Å). The O–H bond distance in the AgOkHm− clusters are in the range of 0.96–0.97 Å, which is very close to that of free OH− as reported by observations (i.e., 0.96 Å).76 We have also identified structures where two water molecules (i.e., in AgO2H4+ and AgO4H4+), or two and more hydroxyl ions (i.e., in AgO2H2−, AgO3H3−, AgO3H4−, AgO4H2− and AgO4H4−) are directly attached to the positively charged Ag atom. If the number of O and H atoms is the same (i.e., k = m), then the AgOkHm− clusters can be represented as Ag(OH)m−, where H is always attached to an O atom. From these observations, one can infer that Ag+ has a strong water affinity, while Ag and Ag− have a similar affinity towards OH− and OH radicals, given that they form stable complexes even if only trace amounts of them are available.
Both AgOH+ (Fig. 1.i.a) and AgOH− (Fig. 2.i.a) have similar structures, with the Ag atoms connected to the O atom of a hydroxyl moiety. The Ag–O bond length in AgOH− is shorter than in AgOH+ (2.17 and 2.33 Å, respectively). The Ag–O and O–H bond lengths in AgOH− are similar to those reported previously by the CCSD(T) method.77 The stabilization energy of the anion (1.68 eV) is higher than that of the cation (0.86 eV), as shown in Tables 1 and 2. Both the AgOH+ and AgOH− clusters preferably dissociate through the Ag–O bond, yielding a positively charged or neutral Ag atom and OH radical or OH− ion, respectively. The ΔE value for AgOH− reported here (1.68 eV) is in good agreement with those obtained through energy decomposition analysis (EDA) at BLYP/TZP level, reported by Zhang and co-workers (1.80 eV).77
The AgOH2+ cluster is the most stable cationic species (in terms of stabilization energy as calculated by eqn (1)) investigated in this work, having a ΔE value of 1.20 eV. The predicted bond dissociation energy between Ag+–OH2 is in good agreement with the experimental bond dissociation enthalpies at 298 K, independently determined by Holland et al.78,79 (1.44 ± 0.09 eV) and Koizumi et al.79,80 (1.38 ± 0.08 eV). We should note that the structure of AgOH2+ contains a positively charged Ag atom interacting with a negatively charged O atom of a water molecule (cf.Fig. 1.i.b). In contrast, the AgOH3+ and AgOH4+ clusters have comparatively low stabilities with ΔE values of 0.57 and 0.41 eV, respectively. This can be explained by the fact that in AgOH3+ and AgOH4+, H and H2, respectively, interact with the Ag atom of the AgOH2+ cluster from the opposite side of the H2O moiety (cf.Fig. 1.i.c and i.d). The H and H2 will readily split off from the AgOH3+ and AgOH4+ clusters, resulting in a stable AgOH2+ cluster. Similarly, the anionic AgOH2− cluster can be perceived as an H atom interacting with the Ag atom from the opposite side of the hydroxyl moiety of AgOH− (cf.Fig. 2.i.b). Interestingly, an energetically more favourable dissociation channel for the AgOH2− cluster is not obtained through the breaking of the Ag–H, but of the Ag–O bond. Finally, AgOH3− (Fig. 2.i.c) and AgOH4− (Fig. 2.i.d) clusters are sparingly stabilized by weak van der Waals forces (as will be discussed further below) between a water molecule and AgH− or AgH2− ions, respectively.
The ground state structures of AgO2H+ (Fig. 1.ii.a) and AgO2H2+ (Fig. 1.ii.b) include a hydroperoxy radical and hydrogen peroxide molecule, forming a bond with a positively charged Ag atom. The most favourable dissociation channel for both these complexes is the loss of the HO2 or H2O2 moieties. The ΔE value of AgO2H2+ (1.18 eV) is moderately larger than that of AgO2H+ (1.02 eV), probably due to the fact that the LEDC of AgO2H2+ requires breaking of two Ag–O bonds, rather than one in the case of AgO2H+. The larger clusters of the AgO2Hm+ family, i.e., AgO2H3+ (Fig. 1.ii.c) and AgO2H4+ (Fig. 1.ii.d), have one or two water molecules attached to the Ag atom. The ΔE values of these clusters are similar to those obtained for smaller clusters in the AgO2Hm+ series. Each of the AgO2Hm− clusters has at least one terminal hydroxyl anion bonded with the Ag atom (cf.Fig. 2.ii.a–d). The stabilization energies of the AgO2H− and AgO2H2− are considerably larger than those of the heavier clusters of AgO2Hm−, i.e., AgO2H3− and AgO2H4−. This is due to the fact that the ground state structure of AgO2H3− and AgO2H4− show weak hydrogen bonds between a water molecule and AgOH− and AgOH2−, respectively.
Geometrically, the AgO3H+ cluster (Fig. 1.iii.a) is very similar to the AgO3+,28 with the exception that an additional H atom is attached to one of the O atoms. On the other hand, the larger clusters of the AgO3Hm+ family have at least a water molecule and an O2, HO2, or H2O2 moiety attached directly to the central Ag atom (Fig. 1.iii.b–d). Interestingly, the geometrical parameters of O2, HO2, and H2O2 moieties are almost identical to their free form. The most favourable dissociation channel for these complexes is obtained by the release of these moieties, leading to the formation of the very stable AgOH2+ cluster. The ΔE values for the AgO3Hm+ clusters are similar, falling within the range of 0.77–1.08 eV, except for the AgO3H2+ cluster, in which the ΔE value along the LEDC is somewhat smaller (0.26 eV). Their anionic counterparts, AgO3Hm−, also show similar geometrical characteristics (cf.Fig. 2.iii.a–d). For example, in the cases of AgO3H− and AgO3H2−, a molecular oxygen and hydroperoxy radical is respectively attached to the Ag atom. In AgO3H3−, there are three OH moieties, as stated previously. One should note that in this cluster, one Ag–O bond is slightly more elongated than the other two (2.13 vs. 2.06 Å). Finally, AgO3H4− consists of two parts, AgO2H2− and H2O, interacting through a hydrogen bond, as discussed below.
The stabilization energies of most of the AgO4Hm+ clusters are either negative or close to zero, indicating that these clusters will promptly dissociate into more stable products (cf.Table 1). One can interpret these results by carefully inspecting the respective geometries shown in Fig. 1.iv.a, 1.iv.c and 1.iv.d. The O2 molecule that is released after the dissociation of these clusters has a comparatively long Ag–O bond distance (2.45 to 2.82 Å), so rupturing it to form the products (AgO2Hm+ + O2) will not consume a vast amount of energy. Only one relatively stable cluster has been found in the AgO4Hm+ family, i.e., the AgO4H2+ cluster. The enhanced stabilization energy (0.76 eV) of this cluster compared to others in its series can be attributed to the fact that an ozone molecule can be considered to be attached to the Ag atom by its two terminal O atoms. As a result, its dissociation will involve the breaking of two Ag–O bonds. Similar arguments can be put forward for the AgO4Hm− clusters, where the ground state is stabilized only by the van der Waals forces (e.g., for AgO4H2− and AgO4H3−). Last, one of the most symmetric structures found in this study is that of AgO4H4− (C4h), in which four hydroxyl ions are attached to a cationic Ag atom (cf.Fig. 2.iv.d) having the same Ag–O bond length. The high stabilization energy of this cluster may be attributed to electronic charge delocalization over the four O atoms, as discussed below. Spectral measurements already confirm the high stability of this ion in solution.81
There is an apparent correlation between spin multiplicity of the cluster and ΔE. For both ionic clusters, the closed-shell system (i.e., singlet spin state) exhibits the largest ΔE value for a particular k in the AgOkHm± (m = 1–4) family. This suggests that the ionic clusters that have a singlet spin state at their ground state equilibrium geometry are more stable than those with either doublet or triplet spin states along the LEDCs for a particular series of AgOkHm±. Interestingly, for the majority of the cases, the AgOkH2± cluster has the largest ΔE in a AgOkHm± family. Moreover, it is also evident that for a specific k, the singlet AgOkHm± cluster has larger ΔE values than the preceding doublet AgOkHm−1± cluster. This phenomenon is more prevalent in the cationic clusters. Notable exceptions being the AgOH4+, AgO2H4−, and AgO3H4− clusters.
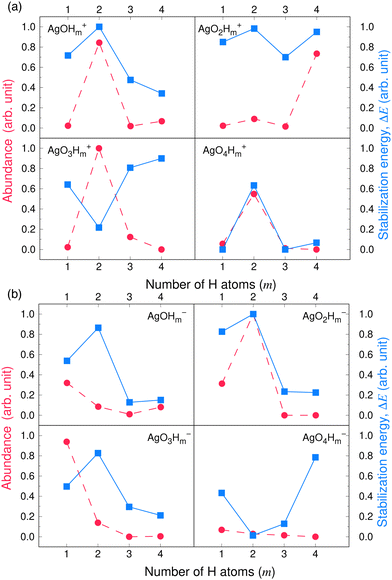
Fig. 3 and 4 compare the signal strength of the mass spectra reported by Maisser et al.2 with the stabilization energies, ΔE 's, calculated here. The signal strengths and ΔE values provided in these plots were normalized with respect to the highest values (scaled to 1.0) of signal strengths measured in the mass spectra (obtained at 157.17 Da for the cationic and 140.91 Da for the anionic mass spectrum) with respect to the largest ΔE value (scaled to 1.0) for the calculated stabilization energy (1.20 eV for the cations and 3.12 eV for the anions), respectively. Since in this work, we are only tracking the variation in the calculated stabilization energies and the signal strengths of mass spectra with respect to the number of H or O atoms in the cluster, analyzing the signals of the mass spectra and the ΔE values as described above will not affect the analysis. The change in stabilization energies and signal strengths with respect to the addition of an H or O atom in the studied systems are shown in Fig. 3a and b or Fig. 4a and b, respectively.
 | ||
| Fig. 3 Stabilization energies calculated theoretically by the CCSD(T) method (blue lines and square symbols) and abundance of the species determined experimentally by mass spectrometry provided by Maisser et al. (ref. 2) (red dashed lines and circle symbols) as a function of the number of H atoms in the (a) AgOkHm+ (b) AgOkHm− clusters, where, k, m = 1–4. ΔE values and the mass spectra peaks are normalized respectively with respect to the largest ΔE calculated for the (a) AgOkHm+ and (b) AgOkHm− clusters in this study and maximum signal strength among the investigated species found in ref. 2 | ||
 | ||
| Fig. 4 Stabilization energies calculated theoretically by the CCSD(T) method (blue lines and square symbols) and abundance of the species determined experimentally by mass spectrometry provided by Maisser et al. (ref. 2) (red dashed lines and circle symbols) as a function of the number of O atoms in the (a) AgOkHm+ (b) AgOkHm− clusters, where, k, m = 1–4. ΔE values and the mass spectra peaks are normalized respectively with respect to the largest ΔE calculated for the (a) AgOkHm+ and (b) AgOkHm− clusters in this study and maximum signal strength among the investigated species found in ref. 2 | ||
Overall, there is a good correspondence in the nature of the variations between the calculations carried out in this study and the experimental results reported by Maisser et al.2 That said, we should note that the assumptions used to determine the experimental signal intensity for the two different isotopes of Ag might not hold for all species, and therefore the differences observed for the normalized ΔE values and the signal strengths of the mass spectra may be the results of the sequential addition of an H or O atom. Apparently, the variation in ΔE with respect to the number of H atoms in the clusters has a better agreement with the experimental results than those obtained for O atoms. This is particularly true for the AgOkH+ and AgOkH3+ clusters. For example, in the AgOkH+ cluster series (where k = 1–3), their signals in the mass spectra are very weak, but their corresponding ΔE values are relatively large. This may be due to the fact that with the addition of each O atom, there is a substantial increase in its mass. Since transmission of an ionic cluster in a mass spectrometer depends ultimately on its mass-to-charge ratio, the signal strengths in the mass spectrum could vary significantly depending upon that.84 To expand the above statement, when two clusters are only differentiated by a single H atom (for example, AgOH+ and AgOH2+ clusters), their transmission in mass spectra should be similar. In contrast, when two clusters are varied by a much heavier atom, such as O (for example, AgOH+ and AgO2H+ clusters), the transmissions of the two clusters in the mass spectrometer can be different. Furthermore, the LEDC for each of these clusters involves the breaking of the Ag–O bond (cf.Table 1). These dissociation channels could involve low-lying intermediates/transition states on the potential energy surface.
Apparently, except for AgO3H2+, the theoretical and the experimental results have a very good agreement for each of the AgOkHm+ cluster series when varying the number of H atoms, as shown in Fig. 3a. The calculated stabilization energy for the AgO3H2+ indicates that this cluster is not very stable and has a low-energy dissociation channel (0.26 eV). This is in contrast to the observations, where a very strong signal in the mass spectrum has been observed for AgO3H2+, indicating that its abundance and, consequently, its high stability. Indeed, the recorded signal strength for AgO3H2+ exhibits the highest value among the cations in the mass spectrum. As mentioned earlier, the AgO3H2+ cluster undergoes dissociation by cleaving an Ag–O bond, resulting in the formation of an O2 molecule and a highly stable (in terms of ΔE) AgOH2+ ion. It is plausible to assume that the transition state leading to the rupture of the Ag–O bond is situated at a notably elevated energy barrier, offering a potential explanation for the observed experimental outcomes. To explore this further, an examination of the reaction kinetics would be necessary to provide a more precise understanding of the stability of AgO3H2+. This, however, is beyond the scope of this study.
Similarly, reasonably good agreement between predictions and measurements is obtained for the anionic AgOkHm− clusters, with k and m ranging from 1 to 4 (cf.Fig. 3b). The largest contradiction between calculations and observations is observed for the AgO3H− and AgO4H4− ions. AgO3H− has a comparatively moderate ΔE value (1.55 eV), but exhibits a strong signal in the mass spectrum. Similarly to AgO3H2+, AgO3H− preferably dissociates by the breaking of the Ag–O bond, releasing an O2 molecule. Likewise, a dynamical study on this reactive pathway can shed some light on its stability. For AgO4H4−, on the other hand, the calculated ΔE value suggests a high stability (2.45 eV), but in the mass spectrum, this ionic cluster shows a very weak signal. The AgO4H4− ion is stabilized by electron delocalization, as discussed below.
3.2 Interatomic interactions
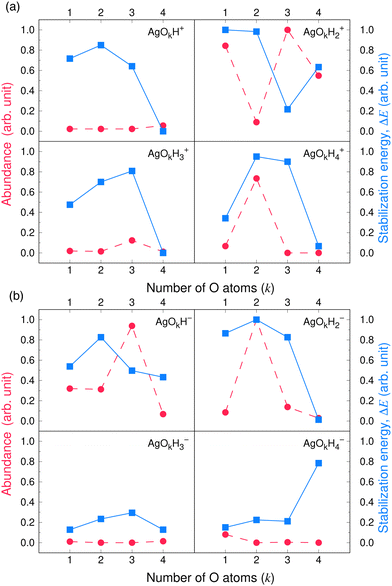
Valuable information can be obtained on the electronic structure and stability of the clusters by examining their HLG. For example, a small HLG may suggest a higher reactivity or instability of the cluster and vice versa.85 The HLG values for each of the closed-shell AgOkHm± clusters are reported in Table S3 of ESI.† In general, the HLG and η values for the cations are slightly larger than those obtained for the corresponding anionic clusters. These results suggest that the AgOkHm+ clusters are less reactive than the AgOkHm− clusters. However, one can also infer from the negative LUMO orbital energies and μ values, along with higher electrophilicity indices, that AgOkHm+ clusters would readily accept an electron in its LUMO orbitals. As expected, the opposite holds true for the anionic clusters. The HOMO–LUMO diagrams (Fig. S1 to S8 in ESI†) are generated to gain a better understanding of the bonding in the charged silver hydroxide clusters. The topology of the HOMOs could be utilized to interpret the high and low ΔE values to a degree. To illustrate this, we take two examples, AgO2H2− and AgOH4−. As mentioned above, AgO2H2− was found to have a high stabilization energy with an ΔE of 3.12 eV, while AgOH4− is very weakly bounded by van der Waals forces (ΔE = 0.47 eV). In AgO2H2−, the HOMO is formed by the constructive overlap between valence 5s and 4d hybrid orbitals of the Ag atom and 2px and 2pz orbitals of both O atoms (cf.Fig. 5a). Therefore, to obtain the most favourable product (AgOH + OH−), one has to overcome the 5s + 4d + 2px +2pz positive overlaps. On the other hand, in AgOH4−, the weakly bounded H2O molecule has a very small contribution to the HOMO, which is primarily composed of 5s, 4dz2 and 4dx2−y2 hybrid orbital of Ag and 1s orbital of the H atoms attached to it (cf.Fig. 5b). We should note that the actual bond that breaks and leads to the energetically most favourable dissociated products may not always be represented by the HOMO since the corresponding MO could have a smaller energy. | ||
| Fig. 5 The highest occupied molecular orbitals (HOMO) of (a) AgO2H2− (b) AgOH4− with isovalues of 0.03 obtained at the ω B97XD level of theory. | ||
From NPA analysis (cf. Table S4 of ESI†), we find that the numerical values of partial charges for the oxygen atoms are either negative or marginally positive for each of the AgOkHm± clusters. This small partial positive charge on the O atom arises when it is connected with another O atom. The asymmetry in the linkages of the two O atoms may inflict a small positive charge on one of the O atoms. On the other hand, the partial charges on both Ag and H atoms are always positive in the cationic clusters and can be both positive or negative in AgOkHm− clusters, depending on their bonding. For example, in AgOH3+, the Ag atom has a net positive charge of 0.92, while the same is partially negative (−0.37 a.u.) in AgOH3−. This can be explained by the fact that the Ag atom in AgOH3+ is directly bonded to an O atom having a net negative charge, and therefore, the pair is stabilized by a Coulombic interaction (cf.Fig. 1.i.c). On the other hand, in AgOH3−, the Ag atom is weakly interacting (at a large distance) with the O atom (of water) and is only practically bonded with an H atom (cf.Fig. 2.i.c). Since the electron affinity of Ag is higher than that of H (1.30 eV and 0.75 eV, respectively),86 the Ag atom attains a partial negative charge. Similarly, both of the H atoms are partially positive (0.52 a.u.) in AgOH2+ since they are part of a water moiety (cf.Fig. 1.i.b). In contrast, in AgOH2−, the H atom, which is bonded with an Ag atom (cf.Fig. 2.i.b), has a negative partial charge (−0.52 a.u.), due to a partial positive charge on Ag. Finally, in the AgOkHm+ clusters, usually, as the number of H atoms increases (keeping the number of O atoms constant), the partial charges on the O atoms increase. This is due to the fact that the H atom could efficiently hold on to a partial positive charge. For example, adding an H to AgOH+ (i.e., AgOH+ and AgOH2+, respectively) increases the induced negative partial charge from −0.44 a.u. to −1.02 a.u. on the O atom. However, even for anionic clusters, the oxidation state of O atoms never attains −2.
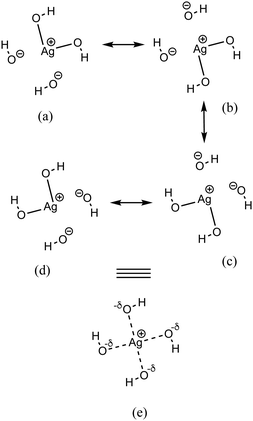
The second-order perturbation theory is a framework that can be employed to estimate the charge delocalization from Lewis to non-Lewis NBOs with a relatively high accuracy. Donor–acceptor pairs and corresponding second-order perturbation energies, E(2) 's, for all clusters investigated here have been calculated, and the most dominant ones are listed in Table S5 of ESI.† The results show that there are many clusters that have a lone pair on one O atom (or to a lesser extent on H atom) and empty Ag–O (or Ag–H) σ* orbital donor–acceptor pair interactions. The three atoms involved in this donor–acceptor interaction usually lie in a straight line, in which the Ag atom is situated close to the center. This type of donor–acceptor interaction may be a fingerprint of a 3-center, 4-electron (3c/4e) “hyperbonds” (ω-bonds).87–92 A 3c/4e bond is primarily composed of a triad of atoms B′, A, B, and has a strong resonance hybrid of two localized Lewis structures: B′–A:B ↔ B′:A–B. The leading factor for the formation of a ω -bond is the charge delocalization arising from the donor–acceptor interaction between valence lone pair of B (respectively B′), i.e., nB (respectively 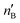 ), and σ* antibonds of AB′ (respectively AB), i.e.,
), and σ* antibonds of AB′ (respectively AB), i.e., 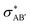 (respectively
(respectively 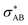 ).
).
For the AgOkHm± ions studied in this work, there are many clusters that forms 3c/4e bonds (cf.Fig. 6a and Fig. S9a–S18a). Corresponding donor–acceptor pair interacting NBOs and the dominant resonating structures are illustrated in plot (b) and (c) of the same figures and in Fig. 7. It is evident that the 3c/4e bonds are more abundant in the anionic clusters (nine) than the cationic clusters (one, AgO4H2+). In AgO4H2+, the 3c/4e bond originates within the O3 fragment through donor–acceptor interactions between a lone pair of terminal O and an empty π* orbital of the remaining two oxygen atoms (cf. Fig. S18b, ESI†). The formation of such 3c/4e π bonding in free ozone molecule has already been reported by DeBlase et al.93
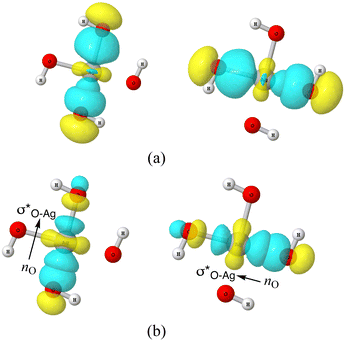 | ||
| Fig. 6 (a) 3-d surface views of leading 3c/4e Lewis-type NBOs in AgO4H4− cluster (b) lone-pair NBO of O (nO) and empty σ* NBO of Ag–O donor–acceptor pairs in AgO4H4− cluster. | ||
As discussed above, the AgO4H4− cluster is highly stable as inferred from a relatively large ΔE value (2.45 eV) and experimental observation.81 The stability of this cluster could be attributed to the substantial electron delocalization over the whole cluster. More specifically, one can find two 3c/4e bondings, each one formed between two O atoms (Ag being at the center) that are directly opposite to each other in this cluster (cf.Fig. 6a). The donor–acceptor pairs associated are lone pairs of O (nO) and empty σ* orbitals of Ag and the O atoms in the opposite end (cf.Fig. 6b). The donor–acceptor stabilization energies for these interactions are ca. 6.6 eV (cf. Table S5 of ESI†). These two 3c/4e bonding results in four resonating structures (cf.Fig. 7), each having equal weights (wα) of more than 21% with the Ag–O bond order of 0.43.
In the AgOHm− series, there is only one cluster, AgOH4−, that has a 3c/4e bonding (cf. Fig. S9 of ESI†). In AgOH4−, the donor–acceptor pair is the negatively charged H atom and the σ* orbital of Ag and H. The negatively charged H atoms in the AgOH4− cluster can also be verified by NPA analysis (cf. Table S4 of ESI†). In the AgO2Hm− series, there are two clusters with such multi-center bondings, viz., AgO2H− and AgO2H2− (cf. Fig. S10 and S11 of ESI†). In both these clusters, the associated donor–acceptor pairs are nO and σ* of Ag–O. Similarly, in the AgO3Hm− series, there are three clusters exhibiting the 3c/4e bonding (AgO3H−, AgO3H2−, and AgO3H4−), all associated with the nO and σ* of Ag–O donor–acceptor pairs (cf. Fig. S12–S14 in ESI†). More interestingly, each of the four AgO4Hm− clusters studied in this work shows the presence of 3c/4e bonds (cf. Fig. S15–S17 in ESI†). It should be noted that in a few of the clusters that exhibit 3c/4e bonds, the resonance weights (wα 's) of the resonating structures are very different. This is either due to the dissimilar bonding of the two participating terminal atoms (e.g., AgO2H− and AgO4H−) or close proximity to a water moiety (e.g., AgOH4−, AgO3H4−, and AgO4H3−).
There are a few other anionic clusters, viz., AgOH2− and AgO2H4−, in which there are significant donor–acceptor pair stabilizations (≈2.8–3.1 eV) and have at least two dominating resonance structures (cf. Fig. S19 and S20 in ESI†). In both these cases, the donor is a nO, while the acceptor is the empty σ* orbital of Ag and H. However, these donor–acceptor interactions do not lead to 3c/4e bonding, since the two terminal atoms (O and H) have substantially different electronegativities. Another interesting case is the AgO3H3− cluster, in which two of Ag–O bonds are of similar length (2.05 Å), while the other Ag–O bond (along the vertical axis) is slightly elongated (2.13 Å) (cf.Fig. 2.iii.c). In AgO3H3−, there is a strong donor–acceptor interaction (E(2) ≈ 2.5 eV) between nO and σ* of Ag and O, resulting in two resonating structures of almost equal weights (cf. Fig. S21 of ESI†). Quite surprisingly, this cluster does not have any 3c/4e bond, as one may expect, since the two participating O atoms have very similar chemical environments (both attached to a hydrogen atom). The absence of the 3c/4e bond may be due to the fact that the σ* orbital exclusively resides on the Ag, with negligible contribution arising from the O atom (cf. Fig. S21a, ESI†) and therefore, the O atom does not participate in multi-center bonding. Finally, we have also tried to interpret the H-bonding in terms of donor–acceptor stabilization. As discussed in section 3.1, the AgO2H3−, AgO2H4−, AgO3H4−, and AgO4H3− clusters have intra-molecular H-bonds. The donor–acceptor pair to establish such H-bonds are nO of an O atom attached to an Ag atom (donor) and empty σ* orbital (acceptor) formed by H and O of a neighbouring water moiety (cf. Fig. S22, ESI†). The E(2) stabilization energies for these donor–acceptor interactions fall within the range of 0.5–1.1 eV.
The results of the QTAIM calculations are reported in Table S6, whereas the BCPs are illustrated in Fig. S23 to S26 of ESI.† The numerical values of each of the QTAIM parameters, as described in section 2.2, at each desired BCP are provided in Table S6 (ESI†). Evidently, all O–H interatomic bonds are covalent since their ∇2ρ(r) values are all negative (∼2.8). Moreover, these BCPs are also accompanied by G(r)/|V(r)| ratios that are smaller than 0.5 (∼ 0.1). Similarly, in almost all cases, the O–Ag bonds are characterized by large positive values of ∇2ρ(r), indicating an ionic bond. However, since they also have G(r)/|V(r)| ratios marginally smaller than unity, the O–Ag bonds can be classified as having more ionic character than co-valency. On the other hand, the weak O–Ag interactions, such as in AgO4H3+, AgO4H4+, AgOH3−, and AgO3H−, have small positive values of ∇2ρ(r) (less than 0.1). Interestingly, for such van der Waals-type interactions, the G(r)/|V(r)| ratio is greater than unity for cationic clusters and slightly less than unity for the anions. Moreover, we can also define the Ag–H bonds in a few of the clusters as more covalent than ionic due to the G(r)/|V(r)| ratio values being very close to 0.5. Finally, one can attempt to identify the intramolecular hydrogen bonds by looking at the corresponding O–H BCP that have ρ(r) ≈ 0.05, ∇2ρ(r) ≈ 0.1, and G(r)/|V(r)| ratio ≈ 0.75. Some examples include AgO2H3−, AgO2H4−, and AgO3H4− clusters; although in AgO4H3−, these values are slightly larger.
3.3 Collision cross section and electrical mobility
Since pure, oxides, and hydroxylated silver clusters are often very difficult to resolve in the mobility spectra, it is useful to calculate their electrical mobilities theoretically and subsequently label the experimental spectra.28 The numerical values of the TM-calculated CCS and electrical mobilities (Z) of the AgOkHm± clusters suspended in helium are provided in Tables 1 and 2. In general, and as expected, by adding H or O atoms to the clusters, we observe an increase in the CCS and a decrease in Z. However, there are some cases where the addition of an H atom to a cluster leads to a decrease in the CCS and, consequently, an increase of Z. This phenomenon is more prevalent for the anionic than the cationic clusters. For example, in AgOH−, AgOH3−, AgO4H2−, and AgO4H3−, the addition of an H atom decreases the corresponding CCSs. On the other hand, only one cationic cluster, viz., AgO4H+, has been found to show analogous behavior.Only one cluster (i.e., AgO3H4−) has been found in this study, where the addition of an O atom decreases the CCS values. Since CCS is proportional to the molecular surface area, one can analyze the trend in CCS values by comparing the molecular surface area of the related structures.28 For example, the Connolly molecular area94 of AgO3H4− is 90.5 Å2, while that of AgO4H4− is 86.4 Å2. It should be noted that AgO4H4− has a more compact geometry while the structure of AgO3H4− is more broad due to H bonding between AgO2H2− and H2O moieties. Therefore, it is not surprising that the CCS of AgO3H4− (45.6 Å2) is greater than that of AgO4H4− (42.5 Å2). Another interesting example is the AgOH− and AgOH2− pair. Although AgOH− has a smaller Connolly molecular area (60.2 Å2) than AgOH2− (66.7 Å2), the CCS of AgOH− was found to be larger than that of AgOH2− (34.0 Å2 and 33.9 Å2, respectively). This is a combined effect of the negligible contribution of the H atom to the CCS and a marginally longer Ag–O bond length in AgOH− (cf.Fig. 2.i.a and i.b).
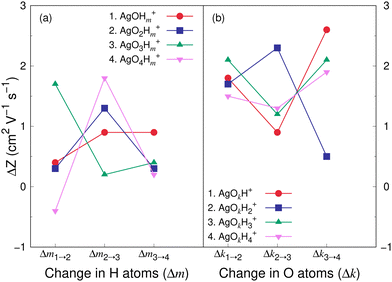
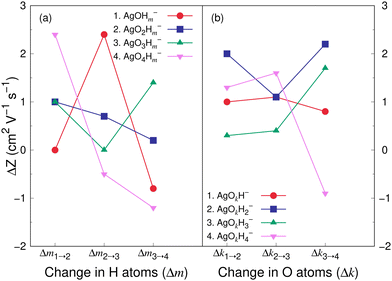
Fig. 8 and 9 show the variation in the Z value difference (ΔZ) as a function of the change in the number of H and O atoms in the clusters for the cations and anions, respectively. It is interesting to note that for both the cations or anions, the relationship between Z and the number of H or O atoms in a cluster is not linear. This is in contrast to what was observed for cationic silver oxides.28 In the AgOkHm+ clusters, the addition of an H atom does not change the mobility values significantly and falls within 0.2–1.8 cm2 V−1 s−1. When varying the number of O atoms in the clusters, the changes in the mobility vary from 0.5 to 2.6 cm2 V−1 s−1 for the cationic clusters and from 0.3 to 2.2 cm2 V−1 s−1 for the anions. This is, in general, larger than what we obtained for the H atoms (0.2–1.8 cm2 V−1 s−1 for the cations and up to 2.4 cm2 V−1 s−1 for the anions). It should be noted that the largest change in the Z values with H atom addition is obtained for the AgOH− and AgO4H2− clusters, whereas the same is observed for the AgOH3+ cluster with the addition of O atom.
4 Conclusions
We have theoretically estimated the ground state structures, stabilization energies, bonding, collisions cross sections, and electrical mobilities of both cationic and anionic hydroxylated silver clusters, AgOkHm±, where k and m = 1–4. Full dimensional geometry optimization of the clusters was performed using the highly-accurate CCSD method, while the single-point energies were calculated by the CCSD(T) method, including zero-point vibrational energy corrections.Our results show that the ground state of most of the ionic clusters of both polarities has a low spin state, whereas the cations tend to have more structural symmetry than the anions. We find that at the equilibrium geometry, the closed-shell systems tend to be more stable than the open-shell systems with respect to unimolecular dissociation. For the AgOkHm+ clusters with m ≥ 2, a water molecule is always directly attached to the positively charged Ag atom, with the exception of AgO2H2+. In contrast, each AgOkHm− cluster has at least one hydroxyl ion (OH−) attached to a partially positive Ag atom. There are many cases where two (or more) water molecules or OH− ions are attached to an Ag atom in cationic and anionic clusters, respectively, indicating a strong affinity of the ionic and neutral Ag atoms towards these two species. Other species, such as hydrogen (H2), oxygen (O2), hydroperoxy radical (HO2), ozone (O3) and hydrogen peroxide (H2O2), have been found to be attached to the Ag atom. These molecules may preferably split off from the rest of the Ag-containing cluster, giving rise to low to moderate stabilization of the original cluster.
Few of the clusters have been found to be bounded by weak van der Waals forces and, therefore, could dissociate promptly. Reasonably good agreement has been found when the stabilization energies calculated in this work are compared to the mass spectra obtained experimentally.2 HOMO–LUMO energy gap analysis and calculated chemical hardness values show that, in general, the anionic clusters are more reactive than the cationic ones. We have found that the 3c/4e “hyperbonds” (ω -bonds) are abundant in the anionic clusters that primarily result from donor–acceptor stabilization between a valence lone pair of an O atom and an empty σ* anti-bonding orbital of Ag and another O atom. These 3c/4e bonding results in at least two dominating resonance structures. The relatively high stability of the AgO4H4− cluster, as confirmed experimentally,81 could be explained in terms of electron delocalization through four dominating resonance structures resulting from two 3c/4e hyperbonds. QTAIM showed that the O–H bonds are covalent, while the O–Ag bonds are mostly ionic. Finally, through both donor–acceptor interactions and QTAIM analysis, we have identified the intramolecular hydrogen bonds in some of the anionic clusters.
The CCS and corresponding electrical mobility values of the AgOkHm± clusters in helium gas have been calculated by the trajectory method. We found that a sequential increase in the number of H (for e.g., AgOH−) or O (for e.g., AgO3H4−) atoms in the ionic hydroxylated silver clusters does not necessarily increase the CCS or decreases mobility values due to the shrinkage of the molecular surface area as well as the small contribution of H atoms towards the CCS.
Author contributions
Mohsen Doust Mohammadi: investigation, data curation, visualization. Somnath Bhowmick: conceptualization, methodology, investigation, formal analysis, data curation, validation, supervision, writing – original draft, writing – review & editing, visualization. Anne Maisser: formal analysis, writing – review & editing, resources. Andreas Schmidt-Ott: resources. George Biskos: conceptualization, supervision, formal analysis, funding acquisition, validation, writing – original draft, writing – review & editing, resources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support of the European Regional Development Fund and the Republic of Cyprus through the Research and Innovation Foundation project ML-NANOCAT (CODEVELOP-GT/0322/0093). This research was also supported by the EMME-CARE project that has received funding from the European Unions Horizon 2020 Research and Innovation Program, under Grant Agreement No. 856612, as well as co-funding by the Government of the Republic of Cyprus. The authors thank the Cyclone High Performance Computing Facility of The Cyprus Institute for computational resources (Cyclone project number: pro22a111).Notes and references
- Spark Ablation: Building Blocks for Nanotechnology, ed. A. Schmidt-Ott, Jenny Stanford Publishing, New York, 1st edn, 2020 Search PubMed.
- A. Maisser, K. Barmpounis, S. Holm, M. Attoui, A. Schmidt-Ott, J. Kangasluoma and G. Biskos, J. Aerosol Sci., 2021, 156, 105780 CrossRef CAS.
- W.-M. He, Z. Zhou, Z. Han, S. Li, Z. Zhou, L.-F. Ma and S.-Q. Zang, Angew. Chem., Int. Ed., 2021, 60, 8505–8509 CrossRef CAS PubMed.
- M. Pereiro, D. Baldomir, J. Botana, J. E. Arias, K. Warda and L. Wojtczak, J. Appl. Phys., 2008, 103, 07A315 CrossRef.
- G. M. Koretsky and M. B. Knickelbein, J. Phys. Chem., 1997, 107, 10555–10566 CrossRef CAS.
- Z. Chang, X. Jing, C. He, X. Liu and C. Duan, ACS Catal., 2018, 8, 1384–1391 CrossRef CAS.
- V. Bonačić-Koutecký, A. Kulesza, L. Gell, R. Mitrić, R. Antoine, F. Bertorelle, R. Hamouda, D. Rayane, M. Broyer, T. Tabarin and P. Dugourd, Phys. Chem. Chem. Phys., 2012, 14, 9282–9290 RSC.
- S. Biswas, A. K. Das, A. Nath, S. Paul, M. Suheshkumar Singh and S. Mandal, Nanoscale, 2021, 13, 17325–17330 RSC.
- R. Fournier, J. Chem. Phys., 2001, 115, 2165–2177 CrossRef CAS.
- P. Weis, T. Bierweiler, S. Gilb and M. M. Kappes, Chem. Phys. Lett., 2002, 355, 355–364 CrossRef CAS.
- M. Schmidt, P. Cahuzac, C. Bréchignac and H. P. Cheng, J. Chem. Phys., 2003, 118, 10956–10962 CrossRef CAS.
- M. L. Tiago, J. C. Idrobo, S. Öğüt, J. Jellinek and J. R. Chelikowsky, Phys. Rev. B, 2009, 79, 155419 CrossRef.
- M. Chen, J. E. Dyer, K. Li and D. A. Dixon, J. Phys. Chem. A, 2013, 117, 8298–8313 CrossRef CAS PubMed.
- G. U. Gamboa, A. C. Reber and S. N. Khanna, New J. Chem., 2013, 37, 3928–3935 RSC.
- K. Duanmu and D. G. Truhlar, J. Phys. Chem. C, 2015, 119, 9617–9626 CrossRef CAS.
- J. Van Der Tol, D. Jia, Y. Li, V. Chernyy, J. M. Bakker, M. T. Nguyen, P. Lievens and E. Janssens, Phys. Chem. Chem. Phys., 2017, 19, 19360–19368 RSC.
- M. L. McKee and A. Samokhvalov, J. Phys. Chem. A, 2017, 121, 5018–5028 CrossRef CAS PubMed.
- P. Ahuja, M. Molayem and S. R. Gadre, J. Phys. Chem. A, 2019, 123, 7872–7880 CrossRef CAS PubMed.
- R. R. Persaud, M. Chen and D. A. Dixon, J. Phys. Chem. A, 2020, 124, 1775–1786 CrossRef CAS PubMed.
- R. A. Flurer and K. L. Busch, J. Am. Chem. Soc., 1991, 113, 3656–3663 CrossRef CAS.
- V. Bonacic-Koutecky, M. Boiron, J. Pittner, P. Fantucci and J. Koutecký, Eur. Phys. J. D, 1999, 9, 183–187 CrossRef CAS.
- M. J. Manard, P. R. Kemper and M. T. Bowers, Int. J. Mass Spectrom., 2003, 228, 865–877 CrossRef CAS.
- R. Snyders, M. Wautelet, R. Gouttebaron, J. Dauchot and M. Hecq, Surf. Coat. Technol., 2003, 174–175, 1282–1286 CrossRef CAS.
- T. M. Bernhardt, Int. J. Mass Spectrom., 2005, 243, 1–29 CrossRef CAS.
- J. Roithová and D. Schröder, J. Am. Chem. Soc., 2007, 129, 15311–15318 CrossRef PubMed.
- Y. Wang and X. G. Gong, J. Nanosci. Nanotechnol., 2010, 10, 5500–5506 CrossRef CAS PubMed.
- E. V. Trushin and I. L. Zilberberg, Chem. Phys. Lett., 2013, 560, 37–41 CrossRef CAS.
- S. Bhowmick, A. Maisser, Y. V. Suleimanov, A. Schmidt-Ott and G. Biskos, J. Phys. Chem. A, 2022, 126, 6376–6386 CrossRef CAS PubMed.
- J. Čížek, Adv. Chem. Phys., 1969, 35–89 CrossRef.
- R. J. Bartlett, Annu. Rev. Phys. Chem., 1981, 32, 359–401 CrossRef CAS.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- J. D. Watts and R. J. Bartlett, Int. J. Quantum Chem., 1993, 48, 51–66 CrossRef.
- R. O. Ramabhadran and K. Raghavachari, J. Chem. Theory Comput., 2013, 9, 3986–3994 CrossRef CAS PubMed.
- J. Erhard, P. Bleiziffer and A. Görling, Phys. Rev. Lett., 2016, 117, 143002 CrossRef PubMed.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed.
- J. Yu, N. Q. Su and W. Yang, JACS Au, 2022, 2, 1383–1394 CrossRef CAS PubMed.
- C. R. Landis and F. Weinhold, The NBO View of Chemical Bonding, John Wiley & Sons, Ltd, 2014, pp. 91–120 Search PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990 Search PubMed.
- P. L. A. Popelier, The Chemical Bond, John Wiley & Sons, Ltd, 2014, pp. 271–308 Search PubMed.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Parr and Z. Zhou, Acc. Chem. Res., 1993, 26, 256–258 CrossRef CAS.
- R. G. Parr, L. v Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082–16086 CrossRef CAS.
- A. A. Shvartsburg and M. F. Jarrold, Chem. Phys. Lett., 1996, 261, 86–91 CrossRef CAS.
- A. Maisser, K. Barmpounis, M. B. Attoui, G. Biskos and A. Schmidt-Ott, Aerosol Sci. Technol., 2015, 49, 886–894 CrossRef CAS.
- J. Fernández de la Mora and J. Kozlowski, J. Aerosol Sci., 2013, 57, 45–53 CrossRef.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010 RSC.
- J. Zhang, V.-A. Glezakou, R. Rousseau and M.-T. Nguyen, J. Chem. Theory Comput., 2020, 16, 3947–3958 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296 Search PubMed.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- T. Koopmans, Physica, 1934, 1, 104–113 CrossRef.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Am. Chem. Soc., 2019, 141, 4156–4166 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Ree, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0, 2018 Search PubMed.
- R. F. W. Bader, S. G. Anderson and A. J. Duke, J. Am. Chem. Soc., 1979, 101, 1389–1395 CrossRef CAS.
- S. R. Gadre, C. H. Suresh and N. Mohan, Molecules, 2021, 26, 3289 CrossRef CAS PubMed.
- P. S. V. Kumar, V. Raghavendra and V. Subramanian, J. Chem. Sci., 2016, 128, 1527–1536 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- C. Larriba and C. J. Hogan, J. Comput. Phys., 2013, 251, 344–363 CrossRef CAS.
- V. Shrivastav, M. Nahin, C. J. Hogan and C. Larriba-Andaluz, J. Am. Soc. Mass Spectrom., 2017, 28, 1540–1551 CrossRef CAS PubMed.
- I. Campuzano, M. F. Bush, C. V. Robinson, C. Beaumont, K. Richardson, H. Kim and H. I. Kim, Anal. Chem., 2012, 84, 1026–1033 CrossRef CAS PubMed.
- P. Weis, O. Welz, E. Vollmer and M. M. Kappes, J. Chem. Phys., 2004, 120, 677–684 CrossRef CAS PubMed.
- H. B. Schlegel, J. Chem. Phys., 1986, 84, 4530–4534 CrossRef CAS.
- J. C. Rienstra-Kiracofe, W. D. Allen and H. F. Schaefer, J. Phys. Chem. A, 2000, 104, 9823–9840 CrossRef CAS.
- S. R. Miller, N. E. Schultz, D. G. Truhlar and D. G. Leopold, J. Chem. Phys., 2009, 130, 024304 CrossRef PubMed.
- W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460–468 CrossRef CAS PubMed.
- J. Wang, S. Manivasagam and A. K. Wilson, J. Chem. Theory Comput., 2015, 11, 5865–5872 CrossRef CAS PubMed.
- A. Hoy and P. Bunker, J. Mol. Spectrosc., 1979, 74, 1–8 CrossRef CAS.
- N. H. Rosenbaum, J. C. Owrutsky, L. M. Tack and R. J. Saykally, J. Chem. Phys., 1986, 84, 5308–5313 CrossRef CAS.
- J. Zhang, Z. Qin, C. Jiao and Z. Tang, J. Quant. Spectrosc. Radiat. Transfer, 2019, 233, 52–56 CrossRef CAS.
- P. M. Holland and A. W. Castleman, Jr., J. Chem. Phys., 1982, 76, 4195–4205 CrossRef CAS.
- Y.-R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, 2007 Search PubMed.
- H. Koizumi, M. Larson, F. Muntean and P. B. Armentrout, Int. J. Mass Spectrom., 2003, 228, 221–235 CrossRef CAS.
- L. J. Kirschenbaum and L. Mrozowski, Inorg. Chem., 1978, 17, 3718–3719 CrossRef CAS.
- A. W. Castleman and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10552–10553 CrossRef CAS PubMed.
- J. R. De Laeter, J. K. Böhlke, P. De Bièvre, H. Hidaka, H. S. Peiser, K. J. R. Rosman and P. D. P. Taylor, Pure Appl. Chem., 2003, 75, 683–800 CAS.
- H. Junninen, M. Ehn, T. Petäjä, L. Luosujärvi, T. Kotiaho, R. Kostiainen, U. Rohner, M. Gonin, K. Fuhrer, M. Kulmala and D. R. Worsnop, Atmos. Meas. Tech., 2010, 3, 1039–1053 CrossRef CAS.
- S. Prabha, A. C. Reber and S. N. Khanna, Chem. Phys. Lett., 2019, 720, 76–82 CrossRef CAS.
- J. C. Rienstra-Kiracofe, G. S. Tschumper, H. F. Schaefer, S. Nandi and G. B. Ellison, Chem. Rev., 2002, 102, 231–282 CrossRef CAS PubMed.
- R. E. Rundle, J. Am. Chem. Soc., 1947, 69, 1327–1331 CrossRef CAS.
- R. E. Rundle, J. Chem. Phys., 1949, 17, 671–675 CrossRef CAS.
- G. C. Pimentel, J. Chem. Phys., 1951, 19, 446–448 CrossRef CAS.
- C. A. Coulson, J. Chem. Soc., 1964, 1442–1454 RSC.
- J. I. Musher, Angew. Chem., Int. Ed. Engl., 1969, 8, 54–68 CrossRef CAS.
- C. R. Landis and F. Weinhold, Inorg. Chem., 2013, 52, 5154–5166 CrossRef CAS PubMed.
- A. DeBlase, M. Licata and J. M. Galbraith, J. Phys. Chem. A, 2008, 112, 12806–12811 CrossRef CAS PubMed.
- M. L. Connolly, J. Appl. Crystallogr., 1983, 16, 548–558 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05499c |
| This journal is © the Owner Societies 2024 |