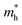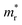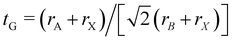Open Access Article
Open Access ArticleFirst-principles study on the optoelectronic and mechanical properties of all-inorganic lead-free fluoride perovskites ABF3 (A = Na, K and B = Si, Ge)†
Chol-Jin
Pak
,
Un-Gi
Jong
 *,
Chung-Jin
Kang
,
Yun-Sim
Kim
,
Yun-Hyok
Kye
and
Chol-Jun
Yu
*,
Chung-Jin
Kang
,
Yun-Sim
Kim
,
Yun-Hyok
Kye
and
Chol-Jun
Yu
 *
*
Chair of Computational Materials Design (CMD), Faculty of Materials Science, Kim Il Sung University, PO Box 76, Pyongyang, Democratic People's Republic of Korea. E-mail: ug.jong@ryongnamsan.edu.kp; cj.yu@ryongnamsan.edu.kp
First published on 1st September 2023
Abstract
In spite of extensive studies on halide perovskites for advanced photovoltaic applications, little attention has been paid to fluoride perovskites so far. Here, we present a systematic investigation of not only the electronic and optical properties but also the mechanical and chemical stabilities of all-inorganic lead-free fluoride perovskites ABF3 (A = Na, K and B = Si, Ge) in the cubic phase using first-principles calculations. We provide a reliable prediction of their lattice constants, band gaps, effective masses and exciton binding energies, revealing variation tendencies according to the selection of A- and B-site cations. Between the two different B-site fluoride perovskites, the silicon-based compounds ASiF3 (A = Na, K) are highlighted as being more suitable for a light absorber of perovskite solar cells, due to their appropriate band gaps, remarkably low exciton binding energies, and ultrahigh spectroscopic limited maximum efficiency reaching ∼34% with a layer thickness over 1 μm. Through the calculations of elastic constants, phase decomposition energies and phonon dispersion curves, we further find that the all-inorganic lead-free fluoride perovskites ABF3 are mechanically stable but only KGeF3 is chemically stable against phase decomposition into its chemical reactants and is also thermodynamically stable. This work highlights that all-inorganic lead-free fluoride perovskites have high potentiality to be used as a promising light absorber in less toxic and high-performance perovskite solar cells.
1 Introduction
Over the past decade, metal halide perovskites have triggered an enormous research interest in various fields such as solar cells, photodetectors, X-ray detectors, lasers and light emitting diodes.1 In particular, perovskite solar cells (PSCs) have emerged as the most promising alternative to the conventional silicon-based solar cells, due to their high power conversion efficiency (PCE) exceeding 25.5%2 and low cost of their scalable fabrication.3 However, there still exist some challenges that need to be addressed for widespread commercialization of PSCs, such as poor stability4–6 and toxicity of perovskite thin films.7,8 Here, the poor stability is attributed to the intrinsic volatility of organic components in organic–inorganic hybrid halide perovskites such as MAPbI3 (MA = CH3NH3), while the toxicity originates from lead (Pb).9–11 To address such problems and find alternatives to MAPbI3, extensive studies have been performed by replacing the organic component with inorganic monovalent cations like alkali cations and toxic lead with nontoxic elements such as Sn and Ge in the same group.12–18In particular, all-inorganic halide perovskites have been proved to exhibit long-term stability of PSCs against dampness, ultraviolet light and heat, concurrently providing an efficient pathway for removing toxicity.19,20 As a typical example, all-inorganic cesium lead iodide CsPbI3 has been found to significantly improve the stability of PSCs compared with the organic–inorganic hybrid counterpart MAPbI3 while maintaining high PCE comparable to that of hybrid PSCs.21–25 In 2015, a CsPbI3-based PSC was fabricated for the first time with an efficiency of 2.9% by Eperon and co-workers,25 and soon after, a certified high efficiency of over 18% and excellent operational stability were achieved by using surface passivation and quantum dot engineering.24 Moreover, Chang et al.21 recently reported high-performance printable CsPbI3 solar cells with an efficiency of 19% via a scalable manufacturing technique under ambient conditions. They synthesized high quality CsPbI3 films by using a combination of air-flow-assisted drying and the addition of organic Lewis acid Zn(C6F5)2, demonstrating that the PSC degrades by only ∼2% after 700 h under air conditions without any encapsulation. However, perovskite CsPbI3 in the cubic phase has an intrinsic instability problem caused by phase transition, promoting the development of various methods such as nanostructuring,26–28 ion substitution29 and hybridization (e.g., (CsMA)PbI3)12,30.
On the other hand, to mitigate the toxicity of lead halide perovskites, great research efforts have been devoted to replacing Pb with Sn or Ge, which has resulted in the development all-inorganic Sn- or Ge-based perovskites CsSnI3 or CsGeI3 and their solid solutions with tunable band gaps of around 1.3 eV, which are suitable for single-junction solar cells.31–34 Promising progress has been reported with the solid-solution CsSn0.5Ge0.5I3 perovskite by Padture and co-workers.33 They demonstrated that a native-oxide layer with full coverage can encapsulate and passivate the CsSn0.5Ge0.5I3 perovskite surface leading to a promising efficiency of up to 7.1% and high stability with less than 10% decay in efficiency after 500 h of continuous operation under ambient conditions. Recently, Lanzetta et al.4 reported new mechanistic insights into the degradation of tin-based perovskites, proposing that dark hole withdrawal from the perovskite can delay the formation of SnI4 and its evolution to highly aggressive I2 and thus lead to improved stability of the tin perovskite film. In addition to the substitution of Pb with the same group elements of Sn and Ge, the replacement of Pb with monovalent and trivalent ions results in a double perovskite structure (e.g., Cs2AgBiBr6)35,36 which is a compositional variation within the perovskite lattice. So far, more than 350 all-inorganic lead-free double perovskites have been synthesized with good phase stabilities and a wide range of tunable optoelectronic properties, but they exhibited relatively lower PCEs below 5%.18
Despite extensive research on all-inorganic lead-free halide perovskites, little attention has been paid to fluoride perovskites. Berastegui et al.37 reported the relatively low temperature of cubic phase transition as 187 K for CsPbF3. Li et al.38 found that when X decreases from I to F in ABX3 the temperature of cubic phase transition decreases from 634 K to 187 K, indicating that the perovskites with lower halogen element need less thermal energy to lift the symmetry to the cubic phase. Using the first-principles calculation, Yang et al.39 confirmed the experimental finding that cubic CsBX3 perovskites (B = Sn, Pb) show improved stability with decreasing X. For all-inorganic fluoride perovskites, challenges may arise from the synthesis process and especially very large band gaps of over 4 eV,40 hindering their use as solar absorbers. In this work, we propose another lead-free all-inorganic fluoride perovskite ABF3 (A = Na, K and B = Si, Ge) in order to address the band gap issue. Houari et al.41 reported the theoretical work for the structural and optoelectronic properties of KGeF3 but not for electronic and dynamical properties. Here, we report a systematic investigation of the structural, electronic, and optical properties and mechanical and thermodynamic stabilities of fluoride perovskites ABF3 using first-principles calculations.
2 Computational methods
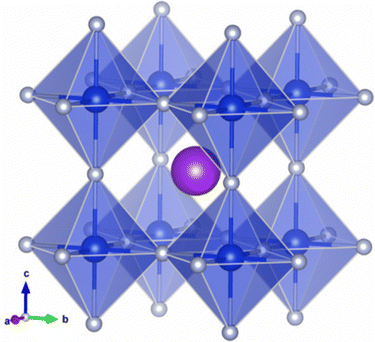
All the DFT calculations in this work were carried out by applying the pseudopotential plane wave method as implemented in the Vienna ab initio simulation package (VASP).42,43 For a description of the Coulomb interaction between the ionic cores and the valence electrons, we employed the projector augmented wave (PAW) potentials44,45 provided in the package. The valence electronic configurations of atoms are F-2s22p5, K-3p64s1, Na-2p63s1, Ge-4s24p2 and Si-3s23p2. The Perdew–Burke–Ernzerhof (PBE) functional46 within the generalized gradient approximation (GGA) was used to describe the exchange–correlation (XC) interaction among the valence electrons. For the cubic phase (see Fig. 1), structural optimizations and electronic structure calculations were performed with a plane-wave cutoff energy of 800 eV and a Γ-centered k-point mesh of 8 × 8 × 8. These computational parameters provided an accuracy of total energy as 1 meV per formula unit (see Fig. S1, ESI†). We carried out variable cell structural optimizations until the atomic forces and pressures became less than 10−4 eV Å−1 and 0.003 GPa, respectively. The total energy convergence threshold was set to 10−8 eV.For the calculations of electronic density of states (DOS), a denser k-point mesh of 12 × 12 × 12 was adopted by imposing the partial occupancy on each orbital using the tetrahedra approach with Blöchl correction. To obtain more reliable band gaps, we also performed electronic structure calculations with the Heyd–Scuseria–Ernzerhof (HSE06) hybrid XC functional.47 Here, 20% of the PBE functional was replaced with the exact Hartree–Fock exchange functional, which has been proven to yield band gaps in good agreement with the experimental values for inorganic halide perovskites.48,49 The spin–orbit coupling (SOC) effect was taken into account only for electronic structure calculations, resulting in negligible contribution to the band gap as the relativistic effect is very small for light atoms.
We applied the density functional perturbation theory (DFPT) method50 and solved the Bethe-Salpeter equation within the GW method (BSE/GW)51–56 to calculate the macroscopic frequency-dependent dielectric functions, ε(ω) = ε1(ω) + iε2(ω), and estimated the light-absorption coefficients α(ω) as follows:13,57
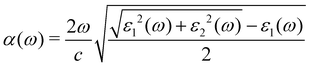 | (1) |
 and holes
and holes 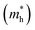 were calculated by numerically processing the refined energy band structure around the R point of the Brillouin zone, at which both the valence band maximum (VBM) and the conduction band minimum (CBM) were found. Then, we estimated the exciton binding energy (Eb) by using the following formula:13,57
were calculated by numerically processing the refined energy band structure around the R point of the Brillouin zone, at which both the valence band maximum (VBM) and the conduction band minimum (CBM) were found. Then, we estimated the exciton binding energy (Eb) by using the following formula:13,57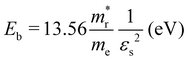 | (2) |
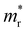 is the reduced effective mass
is the reduced effective mass 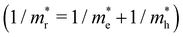 and εs is the static dielectric constant.
and εs is the static dielectric constant.
We calculated the spectroscopic limited maximum efficiency (SLME),58,59 which is regarded as a good metric for determining the maximum efficiency that an absorber material can reach in a single-junction solar cell. Because it takes into account the nature of the band gap, the shape of absorption spectra, and the material-dependent non-radiative recombination losses,59 SLME is an improved version of the Shockley and Queisser (SQ) efficiency.60 Usually, the SLME is calculated as the ratio between the maximum power density and the incident power density, exceeding the Shockley–Queisser limit within the detailed balance framework. The standard solar spectrum, the energy band gap and the light-absorption coefficient were used as inputs for SLME calculation. In calculations, we employed the SL3ME package59 for implementing SLME analysis of solar absorbers in Python3.
The mechanical stability of a polycrystalline solid can be estimated using elastic constants such as bulk (B), shear (G) and Young's (E) moduli, which are determined from the elastic stiffness (Cij) and compliance (Sij) constants for a single crystal.61 For a cubic structure, there exist three independent elastic constants (ij = 11, 12 and 44), from which B, G and E are calculated within the Voigt and Reuss approximation as follows:
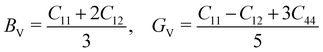 | (3) |
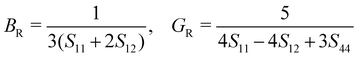 | (4) |
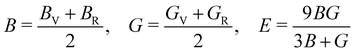 | (5) |
For a direct estimation of material stability of fluoride perovskites ABF3, we calculated the cohesive energy ΔEc and formation energy ΔEf of ABF3 with respect to the chemical reaction ABF3 → AF + BF2 (see Fig. S2, ESI†) as follows:57,63
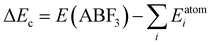 | (6) |
| ΔEf = E(ABF3) − [E(AF) + E(BF2)] | (7) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and orthorhombic BF2 with the P212121 space group,64 respectively, while Eatomi is for the isolated atom of i-th species. The positive or negative formation energy ΔEf directly indicates whether the phase decomposition of ABF3 into AB and BF2 is thermodynamically favorable or unfavorable.
m space group and orthorhombic BF2 with the P212121 space group,64 respectively, while Eatomi is for the isolated atom of i-th species. The positive or negative formation energy ΔEf directly indicates whether the phase decomposition of ABF3 into AB and BF2 is thermodynamically favorable or unfavorable.
To proceed with calculations of phonon dispersion curves and the corresponding phonon DOS, we utilized the supercell method, as implemented in the ALAMODE code.65 We applied the finite displacement approach by the use of 3 × 3 × 3 supercells including 135 atoms (see Fig. S4, ESI†). For these supercell calculations, a reduced k-point mesh of 3 × 3 × 3 and a cutoff energy of 400 eV were used in accordance with the larger size of the supercell. A q-point mesh of 50 × 50 × 50 was used for the calculations of phonon DOS. For the harmonic and quartic interatomic force constants (IFCs), we prepared 5 and 60 different configurations where all atoms were randomly displaced by 0.01 and over 0.06 Å from their equilibrium positions, and then computed the atomic forces for each displaced configuration by performing precise DFT calculations. In these calculations, the VASP code was used as a force calculator and IFCs were extracted by performing the compressive sensing lattice dynamics (CSLD),66 as implemented in the ALAMODE code.65 Using these IFCs, the atomic forces were reproduced within the relative errors less than 3% compared to the DFT-calculated ones (see Fig. S3, ESI†). With the harmonic and quartic IFCs, we finally calculated the phonon dispersion curves, and total and atom-projected phonon DOSs at 0 K and finite temperatures ranging from 100 to 900 K with a step of 100 K.
3 Results and discussion
First we assessed the possibility of fluoride perovskite ABF3 formation in the cubic phase by evaluating the geometric factors such as the Goldschmidt tolerance factor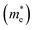 and the octahedral factor to = rB/rX, where ri is the ionic radius of the i-th species.71,72 In fact, the Goldschmidt tolerance factor tG is used to check whether the A-site cation can fit between the BX6 octahedra, while the octahedral factor to is used to assess whether the BX6 octahedron is stable. According to the empirical criteria, a cubic perovskite structure is formed when 1.0 ≥ tG ≥ 0.8 and to ≥ 0.41.71,72 These factors have been widely applied to check the formability of oxide and halide perovskites.73–78Table 1 lists the evaluated geometric factors of fluoride perovskites ABF3 (A = Na, K and B = Si, Ge) using the ionic radii of rNa = 1.39 Å, rK = 1.64 Å, rSi = 0.55 Å, rGe = 0.73 Å, and rF = 1.285 Å. Except KSiF3, all the compounds under study were found to have tG values in the range of 1.0 ≥ tG ≥ 0.8 for a stable cubic phase, while the to values ranged from 0.43 to 0.57, indicating that BF6 octahedra are stable in these compounds. Therefore, the fluoride compounds ABF3 considered in this work are expected to crystallize in a stable perovskite structure. Based on such analysis of geometrical factors, we supposed that the fluoride perovskites ABF3 stabilize in the cubic phase with the Pm
and the octahedral factor to = rB/rX, where ri is the ionic radius of the i-th species.71,72 In fact, the Goldschmidt tolerance factor tG is used to check whether the A-site cation can fit between the BX6 octahedra, while the octahedral factor to is used to assess whether the BX6 octahedron is stable. According to the empirical criteria, a cubic perovskite structure is formed when 1.0 ≥ tG ≥ 0.8 and to ≥ 0.41.71,72 These factors have been widely applied to check the formability of oxide and halide perovskites.73–78Table 1 lists the evaluated geometric factors of fluoride perovskites ABF3 (A = Na, K and B = Si, Ge) using the ionic radii of rNa = 1.39 Å, rK = 1.64 Å, rSi = 0.55 Å, rGe = 0.73 Å, and rF = 1.285 Å. Except KSiF3, all the compounds under study were found to have tG values in the range of 1.0 ≥ tG ≥ 0.8 for a stable cubic phase, while the to values ranged from 0.43 to 0.57, indicating that BF6 octahedra are stable in these compounds. Therefore, the fluoride compounds ABF3 considered in this work are expected to crystallize in a stable perovskite structure. Based on such analysis of geometrical factors, we supposed that the fluoride perovskites ABF3 stabilize in the cubic phase with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group like the inorganic iodide perovskites.
m space group like the inorganic iodide perovskites.
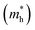 and holes
and holes 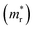 , reduced mass
, reduced mass 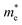 , static dielectric constant (εs), and exciton binding energy (Eb) in fluoride perovskites ABF3 (A = Na, K and B = Si, Ge), calculated with PBE and HSE06 XC functionals. For comparison, those for typical all-inorganic halide perovskites such as CsPbI3, CsGeI3, RbGeI3 and KGeI3 are provided
, static dielectric constant (εs), and exciton binding energy (Eb) in fluoride perovskites ABF3 (A = Na, K and B = Si, Ge), calculated with PBE and HSE06 XC functionals. For comparison, those for typical all-inorganic halide perovskites such as CsPbI3, CsGeI3, RbGeI3 and KGeI3 are provided
| Compound | Geometric factor | Lattice constant (Å) | Band gap (eV) | Effective mass (me) | ε s | E b (meV) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t G | t o | This | Prev. | PBE | HSE06 | Prev. | ||||||
| a The lattice constant and band gap were calculated with PBE functional.41 b The band gap were calculated with HSE06 functional.67 c Our previous first-principles work using Quantum ESPRESSO code.68 d Our previous first-principles work using VASP code.69 e Our previous first-principles work for tetragonal phase using VASP code.70 | ||||||||||||
| NaSiF3 | 1.03 | 0.43 | 4.27 | — | 0.81 | 1.24 | 1.15b | 0.26 | 0.41 | 0.16 | 16.23 | 8.50 |
| NaGeF3 | 0.94 | 0.57 | 4.39 | — | 1.93 | 2.57 | — | 0.54 | 0.65 | 0.29 | 21.10 | 9.02 |
| KSiF3 | 1.13 | 0.43 | 4.34 | — | 0.85 | 1.37 | — | 0.35 | 0.44 | 0.19 | 15.28 | 11.19 |
| KGeF3 | 1.02 | 0.57 | 4.45 | 4.46a | 1.97 | 2.61 | 2.00a | 0.58 | 0.89 | 0.35 | 20.94 | 10.98 |
| CsPbI3c | 0.85 | 0.54 | 6.30 | 1.76 | 2.24 | 1.73 | 0.15 | 0.20 | 4.7 | 54 | ||
| CsGeI3d | 0.93 | 0.40 | 5.94 | 1.19 | 1.64 | 1.63 | 0.15 | 0.16 | 0.08 | 19.82 | 19.24 | |
| RbGeI3d | 0.90 | 0.40 | 5.91 | 1.31 | 1.78 | 0.16 | 0.17 | 0.08 | 23.01 | 13.49 | ||
| KGeI3e | 0.87 | 0.34 | 0.85 | 1.24 | 0.60 | 0.13 | 0.11 | |||||
Through variable-cell structural optimization by using the PBE functional, we determined the equilibrium lattice constants of these lead-free inorganic fluoride perovskites ABF3 (A = Na, K and B = Si, Ge). The calculated lattice constants are given in Table 1. To the best of our knowledge, there are no experimental data for lattice constants of these fluoride perovskites. Only for the case of KGeF3, Houari et al.41 reported a lattice constant of 4.46 Å calculated with the same PBE functional, which coincides with our lattice constant of 4.45 Å. As the ionic radii of A- and B-site cations increase, we found a slight increase in the lattice constant in accordance with common knowledge.
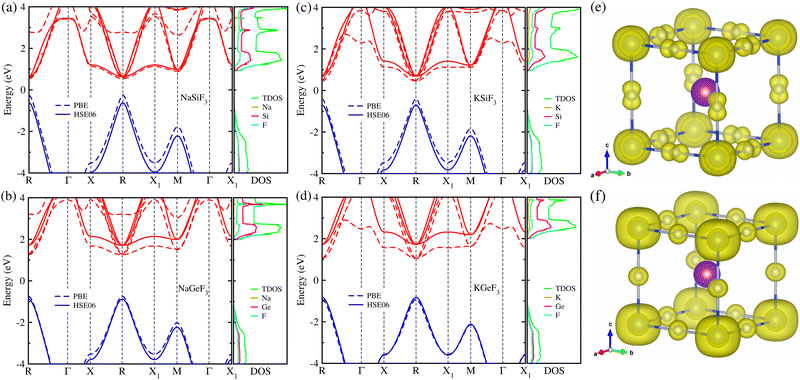
Using the optimized structures, we then calculated their electronic band structures and atomic-resolved DOS by the use of both PBE and HSE06 XC functionals. It was established that the GGA-PBE functional could yield band gaps in good agreement with the experimental values for organic–inorganic hybrid iodide perovskite MAPbI3 due to a fortuitous error cancellation between the GGA underestimation and overestimation by ignoring the spin–orbit coupling (SOC) effect.57,79 For all-inorganic halide perovskites, however, the PBE functional underestimated the band gaps compared to the experimental data, whereas the HSE06 hybrid functional without SOC provided precise band gaps in line with experiments.68,69 Based on the previously established facts, we adopted the HSE06 hybrid functional without the SOC effect to obtain sufficiently reliable band gaps, being the most important material property of light absorbers to assess the light-to-electricity conversion efficiency of solar cells, and also the PBE functional only for comparison. Fig. 2 shows the electronic band structures and atom-projected DOSs calculated with HSE06 (solid lines) and PBE (dashed lines) functionals for the fluoride perovskites ABF3 under study.
Our calculations indicate that the electron excitation from the valence band maximum (VBM) to the conduction band minimum (CBM) occurs in a direct way at the edge point R (0.5, 0.5, 0.5) of the Brillouin zone (BZ), similar to other halide perovskites in the cubic phase. Obviously, such direct transition is useful for the generation of charge carriers including electrons in the conduction band and holes in the valence band by absorbing light compared with indirect way. We also confirmed that the HSE06 hybrid functional yielded remarkably larger band gaps compared to the PBE functional for the fluoride perovskites due to a upward shift of conduction bands and a downward shift of valence bands. Experimental and theoretical data are not yet available for these fluoride perovskites, except KGeF3 (NaSiF3), for which the band gap was calculated to be 2.00 (1.15) eV with the PBE (HSE06) functional41,67 in accordance with our calculation of 1.97 (1.24) eV with the same XC functional (see Table 1). As far as believing the HSE06 calculations, the Si-based fluoride perovskites ASiF3 (A = Na, K) were found to be suitable for visible light absorber applications because of their appropriate band gaps of 1.24 eV (A = Na) and 1.37 eV (A = K). These values are comparable to those of CsPbI3 (1.76 eV),68 CsGeI3 (1.19 eV) and RbGeI3 (1.31 eV),69 which have been widely used as light absorbers for PSCs. Meanwhile, Ge-based fluoride perovskites AGeF3 have a significantly larger band gap over 2.5 eV, implying their other possible applications such as charge carrier conductors and light emitting diodes. It is worth noting that in accordance with the lattice constant analysis, the larger the ionic radii of A- and B-site cations are, the larger band gaps the fluoride perovskites ABF3 provide, which is similar to the halide perovskites.68,69 Through the analysis of atom-projected DOS, we found that the valence bands are dominated by F-p states coupling with the B-s state while the conduction bands are dominated by F-p and A-p states with negligible contribution from the A-site cations. Moreover, we observed that the VBM is characterized by B-s and F-p states and the CBM has characteristics of B-s and F-s states, as shown in Fig. 2(e) and (f). Similar findings were observed for the all-inorganic and organic–inorganic hybrid halide perovskites, demonstrating that fluoride perovskites have the same electronic mechanism as the halide perovskite.
In order to see how charge carriers such as electrons and holes behave after being generated by absorbing photons, we evaluated their effective masses, dielectric constants, and exciton binding energies by using the PBE functional. Such optical properties are the key quantities for the qualitative assessment of charge carrier mobility. As listed in Table 1, the Si-based compounds ASiF3 (A = Na and K) have much lighter effective masses of electrons and holes than the Ge-based compounds AGeF3. In accordance with the band gaps, this indicates that the former is more favourable for light absorbers than the latter. In particular, NaSiF3 exhibits the lightest effective masses of electrons and holes as 0.26me and 0.41me among the four fluoride perovskites under study, implying the highest mobilities of charge carriers. These values are slightly larger than those of ABI3 (A = Cs, Rb and B = Pb, Ge),68,69 but comparable with those of tetragonal KGeI3.70 We note that the effective masses in AGeF3 are still small enough for applications as charge carrier conductors.
Also, the static dielectric constants εs of Si-based fluoride perovskites, calculated using the DFPT approach while considering the atomic displacement effect, are smaller than those of the Ge-bases ones (see Table 1). The calculated values range from 15.28 for KSiF3 to 21.10 for NaGeF3, which are considerably larger than those of organic–inorganic hybrid MA-based perovskites (3–5).57,63 This indicates that these fluoride perovskites are expected to have much smaller exciton binding energies than the hybrid chloride perovskites as the exciton binding energy is inversely proportional to the square of the static dielectric constant, which is favourable for solar cell performance.
Then, using the calculated effective masses and static dielectric constants, we determined the exciton binding energies Eb with eqn (2), which is a crucial quantity to estimate whether the electrons and holes recombine or behave as free charge carriers. The calculated exciton binding energies in fluoride perovskites ABF3 are provided in Table 1. We found that the Eb values are very low, below 12 meV, which can be attributed to very light effective masses and relatively large static dielectric constants. When compared with other halide perovskites, these values are comparable to those of all-inorganic Ge-based perovskites AGeX3 (A = Cs, Rb and X = I, Br, Cl),69 while distinctly lower than those of hybrid perovskite MAPbX3 (40–300 meV).57,63 We also note that the calculated exciton binding energy has the similar variation tendency according to the selection of A- and B-site cations as the effective mass and band gap. To sum up the calculated band gaps and charge transport properties, we emphasize that the Si-based fluoride perovskites ASiF3 (A = Na, K) are promising light-absorber materials for PSCs because of their suitable band gaps (1.2–1.4 eV) and low exciton binding energies (8.5–11.2 meV).
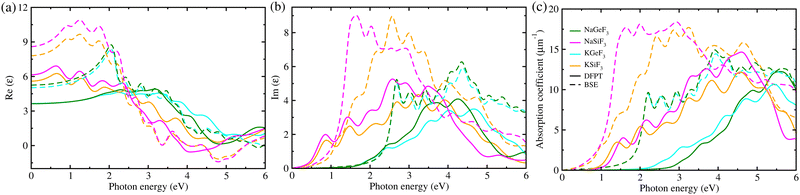
Subsequently, we considered the light-absorption coefficients α(ω) as a function of frequency ω, which were calculated using the frequency-dependent dielectric functions ε(ω) with eqn (1). Fig. 3 displays the real and imaginary parts of ε(ω), calculated with DFTP (solid) and BSE/GW (dashed) approaches, and the α(ω) value for four fluoride perovskites. The BSE/GW calculations provided higher peak values of ε(ω) compared with the DFPT calculations. With reference to α(ω), the highest peaks were estimated to range from 11 (15) to 15 (18) μm−1 for DFPT (BSE/GW) calculations, which are lower than ∼20 μm−1 in MAPbX357,63 but higher than 2–4 μm−1 in AGeX3 (A = Cs, Rb and X = I, Br, Cl)69, indicating that the fluoride perovskites conceived in this work can exhibit reasonable light harvesting capability. In accordance with the band gaps, the Si-based fluoride perovskites ASiF3 (A = Na, K) show an absorption onset at a lower photon energy than the Ge-based ones. Moreover, we found that the light absorption of the Si-based perovskites spans the whole visible light spectrum, which is clearly beneficial for enhancing the efficiency of solar cells. Such findings provide strong evidence that the Si-based fluorides are a promising absorber for solar cell applications.
Using the calculated band gaps and light-absorption coefficients as input, we estimated the SLME values for PSCs employing fluoride perovskites as a light absorber, providing the maximum efficiency for a single-junction solar cell. Fig. 4 shows the calculated SLME as a function of absorber thickness in fluoride perovskites ABF3 (A = Na, K and B = Si, Ge). We found that the SLMEs become saturated to nearly constant over a layer thickness of ∼1 μm for the four fluoride perovskites. The resulting SLME values were found to be 34% and 13% for Si- and Ge-based fluoride perovskites, respectively. Therefore, the solar cells using Si-based fluoride perovskites ASiF3 (A = Na, K) as a light-absorber are sufficiently competitive compared with other PSCs and the conventional Si-based solar cells. Meanwhile, the calculated SLME (∼34%) of Si-based fluoride perovskites is larger than the theoretical calculations (∼30%) of chalcogenide perovskites AZrS3 (A = Ca, Sr, and Ba),59 indicating that the Si-based fluoride perovskite is superior to the chalcogenide perovskite for solar cell applications.
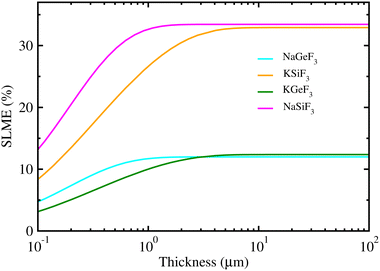 | ||
| Fig. 4 Spectroscopic limited maximum efficiency (SLME) as a function of thickness in lead-free all-inorganic fluoride perovskites ABF3 (A = Na, K and B = Si, Ge). | ||
Finally, we estimated the mechanical, chemical and thermodynamical stabilities of the fluoride perovskites based on the analysis of their elastic constants, and cohesive and formation energies. The elastic stiffness and compliance constants were obtained from the DFPT calculations to investigate the mechanical stability of the fluoride perovskites ABF3 (A = Na, K and B = Si, Ge). As listed in Table 2, for all the fluoride perovskites, the three independent elastic stiffness constants of C11, C12 and C44 satisfy the well-known Born stability criteria for cubic crystals,80 expressed as C11 > 0, C44 > 0, C11 − C12 > 0 and C11 + 2C12 > 0, therefore implying their mechanical stability at zero pressure. Furthermore, it was found that all the fluoride perovskites ABF3 are ductile materials in accordance with the Pugh criteria62 because the calculated values of Pugh's ratio B/G and Poisson's ratio ν are larger than the threshold values of 1.75 and 0.26, respectively. On the other hand, the cohesive energies ΔEc were found to be negative for all the fluoride perovskites, but the formation energy ΔEf was estimated to be negative only for KGeF3, thereby indicating that only the KGeF3 exhibits a good chemical stability against the chemical decomposition into its chemical reactants. It should be noted that although ASiF3 perovskites have suitable band gaps and low exciton binding energy, they show poor chemical stability, which means that these materials are unstable and can be decomposed quickly. In order to address the thermodynamical stability of the mechanically and chemically stable KGeF3, we calculated its phonon dispersions at 0 K and finite temperatures. As shown in Fig. 5(a), anharmonic phonon modes with negative phonon energies were observed in the dispersion curves at 0 K, which are so-called soft phonon modes, a typical characteristic of halide and oxide perovskites in the cubic phase. The atom-projected phonon DOS reveals that the soft phonon modes are mainly attributed to the atomic vibrations of F atoms with a small contribution from K and Ge atoms. However, the anharmonic phonon modes were all renormalized by considering the finite temperature effects, demonstrating that the cubic phase of KGeF3 is dynamically stable (Fig. 5(b)). To sum up, only KGeF3 is stable in mechanic, chemical and thermodynamic aspects among the four lead-free fluoride perovskites, together with a moderate SLME of ∼13%, making it a suitable and promising light-absorber for nontoxic, long-term stable and high-performance solar cells.
| Compound | C ij (GPa) | S ij (TPa−1) | Elastic moduli (GPa) | Ratio | ΔE (eV per atom) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C 11 | C 12 | C 44 | S 11 | S 12 | S 44 | B | G | E | B/G | ν | ΔEc | ΔEf | |
| NaSiF3 | 173.65 | 63.45 | 35.96 | 0.72 | −0.19 | 2.78 | 100.14 | 22.64 | 63.17 | 4.42 | 0.39 | −4.25 | 0.28 |
| NaGeF3 | 177.62 | 51.34 | 34.62 | 0.65 | −0.14 | 2.88 | 93.54 | 23.86 | 65.97 | 3.92 | 0.38 | −4.19 | 0.13 |
| KSiF3 | 164.85 | 62.85 | 43.48 | 0.77 | −0.21 | 2.29 | 96.87 | 24.17 | 66.95 | 4.00 | 0.38 | −4.33 | 0.13 |
| KGeF3 | 168.29 | 50.92 | 40.05 | 0.69 | −0.16 | 2.49 | 89.94 | 24.67 | 67.82 | 3.64 | 0.37 | −4.29 | −0.04 |
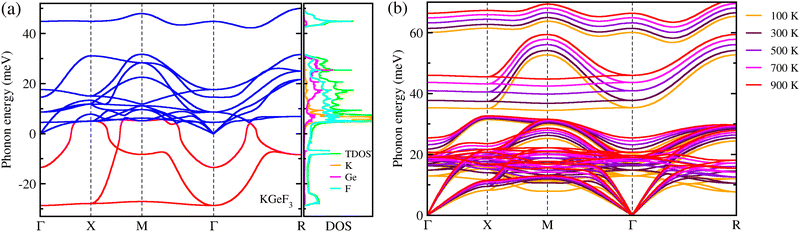 | ||
| Fig. 5 Phonon dispersion curves calculated at 0 K (a) and finite temperatures ranging from 100 to 900 K with a step of 100 K (b) for KGeF3. | ||
4 Conclusions
In this work, we have systematically investigated the structural, electronic and optical properties, and mechanical and chemical stabilities of all-inorganic lead-free fluoride perovskites ABF3 (A = Na, K and B = Si, Ge) using first-principles calculations. From the assessment of geometric factors such as Goldschmidt tolerance and octahedral factors, we confirmed that ABF3 could stabilize in the cubic perovskite structure. Our calculations illustrated that their material properties, such as lattice constants, band gaps, effective masses of electrons and holes, exciton binding energies, exhibit a similar increasing tendency according to the increase in ionic radii of A- and B-site cations. We emphasize that the band gaps and exciton binding energies of the Si-based perovskites ASiF3 were calculated to be 1.24 eV and 8.50 meV for A = Na, and 1.37 eV and 11.19 meV for A = Si, respectively, which are suitable for absorbing visible light and transferring charge carriers. Moreover, the calculated spectroscopic limited maximum efficiency for the Si-based fluoride perovskites reaches ∼34% with a layer thickness over 1 μm, indicating a competitiveness of solar cells. Through the analysis of calculated elastic constants, formation energies and phonon dispersion curves, we revealed that all the fluoride perovskites ABF3 (A = Na, K and B = Si, Ge) are mechanically stable in the cubic phase, whereas only KGeF3 is chemically stable, not decomposing back into its precursor materials due to a negative formation energy, and also thermodynamically stable. Finally, we concluded that KGeF3 is the most suitable and promising light-absorber for solar cells due to its moderate material properties combined with good mechanical, chemical and thermodynamic stabilities among the four compounds, highlighting the potentiality of using all-inorganic lead-free fluoride perovskites for nontoxic and high-performance solar cells.Author contributions
Chol-Jin Park and Un-Gi Jong developed the original project, performed the calculations and drafted the first manuscript. Chung-Jin Kang, Yun-Sim Kim, and Yun-Hyok Kye assisted in DFT calculations and the post-processing of calculation results, and contributed to useful discussions. Chol-Jun Yu supervised the work. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported as part of the basic research project “Design of New Energy Materials” (no. 2021-12) funded by the State Commission of Science and Technology, DPR Korea. Computations have been performed on the HP Blade System C7000 managed by the Faculty of Materials Science, Kim Il Sung University.References
- W. Xiang and W. Tress, Adv. Mater., 2019, 31, 1902851 CrossRef CAS PubMed.
- M. Green, E. Dunlop, J. Hohl-Ebinger, M. Yoshita, N. Kopidakis and X. Hao, Prog. Photovoltaics, 2021, 29, 3–15 Search PubMed.
- Z. Li, T. R. Klein, D. H. Kim, M. Yang, J. J. Berry, M. F. A. M. van Hest and K. Zhu, Nat. Rev. Mater., 2018, 3, 18017 CrossRef CAS.
- L. Lanzetta, T. Webb, N. Zibouche, X. Liang, D. Ding, G. Min, R. J. E. Westbrook, B. Gaggio, T. J. Macdonald, M. S. Islam and S. A. Haque, Nat. Commun., 2021, 12, 2853–2863 CrossRef CAS PubMed.
- T. A. Berhe, W.-N. Su, C.-H. Chen, C.-J. Pan, J.-H. Cheng, H.-M. Chen, M.-C. Tsai, L.-Y. Chen, A. A. Dubaleb and B.-J. Hwang, Energy Environ. Sci., 2016, 9, 323–356 RSC.
- G. Niu, W. Li, J. Li, X. Liang and L. Wang, RSC Adv., 2017, 7, 17473–17479 RSC.
- A. Urbina, J. Phys.: Energy, 2020, 2, 022001 CAS.
- M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Grätzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122–7127 CrossRef CAS PubMed.
- Y.-H. Kye, C.-J. Yu, U.-G. Jong, Y. Chen and A. Walsh, J. Phys. Chem. Lett., 2018, 9, 2196–2201 CrossRef CAS PubMed.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Nano Lett., 2014, 14, 2584–2590 CrossRef CAS PubMed.
- G. Niu, X. Guo and L. Wang, J. Mater. Chem. A, 2015, 3, 8970–8980 RSC.
- Y.-H. Kye, C.-J. Yu, C.-H. Kim, Y.-S. Kim and U.-G. Jong, J. Phys. Chem. C, 2021, 125, 13195–13211 CrossRef CAS.
- U.-G. Jong, C.-J. Yu and Y.-H. Kye, RSC Adv., 2020, 10, 201–209 RSC.
- M. Li, W. W. Zuo, Y. G. Yang, M. H. Aldamasy, Q. Wang, S. H. T. Cruz, S. L. Feng, M. Saliba, Z. K. Wang and A. Abate, ACS Energy Lett., 2020, 5, 1923–1929 CrossRef CAS.
- Z. Zhang, G. Yang, C. Zhou, C. C. Chung and I. Hany, RSC Adv., 2019, 9, 23459–23464 RSC.
- M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldtd and M. Grätzel, Energy Environ. Sci., 2016, 9, 1989–1997 RSC.
- D. Sabba, H. K. Mulmudi, R. R. Prabhakar, T. Krishnamoorthy, T. Baikie, P. P. Boix, S. Mhaisalkar and N. Mathews, J. Phys. Chem. C, 2015, 119, 1763–1767 CrossRef CAS.
- F. Giustino and H. J. Snaith, ACS Energy Lett., 2016, 1, 1233–1240 CrossRef CAS.
- J. Wang, J. Zhang, Y. Zhou, H. Liu, Q. Xue, X. Li, C.-C. Chueh, H.-L. Yip, Z. Zhu and A. K. Jen, Nat. Commun., 2020, 11, 177–185 CrossRef CAS PubMed.
- Z. Guo, S. Teo, Z. Xu, C. Zhang, Y. Kamata, S. Hayase and T. Ma, J. Mater. Chem. A, 2019, 7, 1227–1232 RSC.
- X. Chang, J. Fang, Y. Fan, T. Luo, H. Su, Y. Zhang, J. Lu, L. Tsetseris, T. D. Anthopoulos, S. Liu and K. Zhao, Adv. Mater., 2020, 32, 2001243 CrossRef CAS PubMed.
- U.-G. Jong, C.-J. Yu, Y.-H. Kye, Y.-S. Kim, C.-H. Kim and S.-G. Ri, J. Mater. Chem. A, 2018, 6, 17994–18002 RSC.
- Y.-H. Kye, C.-J. Yu, U.-G. Jong, K.-C. Ri, J.-S. Kim, S.-H. Choe, S.-N. Hong, S. Li, J. N. Wilson and A. Walsh, J. Phys. Chem. C, 2019, 123, 9735–9744 CrossRef CAS.
- Y. Wang, M. I. Dar, L. K. Ono, T. Zhang, M. Kan, Y. Li, L. Zhang, X. Wang, Y. Yang, X. Gao, Y. Qi3, M. Gratzel and Y. Zhao, Science, 2019, 365, 591–595 CrossRef CAS PubMed.
- G. E. Eperon, G. M. Paternó, R. J. Sutton, A. Zampetti, A. A. Haghighirad, F. Cacialli and H. J. Snaith, J. Mater. Chem. A, 2015, 3, 19688–19695 RSC.
- A. D. Shpatz, S. Rahmany, F. Marion, T. Binyamin, A. Hoell, A. Abate and L. Etgar, Mater. Adv., 2022, 3, 1737–1746 RSC.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- S.-T. Ha, R. Su, J. Xing, Q. Zhang and Q. Xiong, Chem. Sci., 2017, 8, 2522–2536 RSC.
- W. Zhang, H. Liu, X. Qi, Y. Yu, Y. Zhou, Y. Xia, J. Cui, Y. Shi, R. Chen and H.-L. Wang, Adv. Sci., 2022, 9, 2106054 CrossRef CAS PubMed.
- D. Dong, H. Deng, C. Hu, H. Song, K. Qiao, X. Yang, J. Zhang, F. Cai, J. Tang and H. Song, Nanoscale, 2017, 9, 1567–1574 RSC.
- K. P. Marshall, R. I. Walton and R. A. Hatton, J. Mater. Chem. A, 2015, 3, 11631–11640 RSC.
- X. Qiu, B. Cao, S. Yuan, X. Chen, Z. Qiu, Y. Jiang, Q. Ye, H. Wang, H. Zeng, J. Liu and M. G. Kanatzidis, Sol. Energy Mater. Sol. Cells, 2017, 159, 227–234 CrossRef CAS.
- M. Chen, M.-G. Ju, H. F. Garces, A. D. Carl, L. K. Ono, Z. Hawash, Y. Zhang, T. Shen, Y. Qi, R. L. Grimm, D. Pacifici, X. C. Zeng, Y. Zhou and N. P. Padture, Nat. Commun., 2019, 10, 16–23 CrossRef CAS PubMed.
- K. P. Marshall, S. Tao, M. Walker, D. S. Cook, J. Lloyd-Hughes, S. Varagnolo, A. Wijesekara, D. Walker, R. I. Walton and R. A. Hatton, Mater. Chem. Front., 2018, 2, 1515–1522 RSC.
- A. C. Dakshinamurthy and C. Sudakar, Mater. Adv., 2022, 3, 5813–5817 RSC.
- L. Chen, H. Jiang, Z. Luo, G. Liu, X. Wu, Y. Liu, P. Sun and J. Jiang, Mater. Adv., 2022, 3, 4381–4386 RSC.
- P. Berastegui, S. Hull and S. Eriksson, J. Phys.: Condens. Matter, 2001, 13, 5077–5088 CrossRef CAS.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702–707 CrossRef CAS PubMed.
- R. X. Yang, J. M. Skelton, E. L. da Silva, J. M. Frost and A. Walsh, J. Phys. Chem. Lett., 2017, 8, 4720–4726 CrossRef CAS PubMed.
- C.-J. Yu, I.-C. Ri, H.-M. Ri, J.-H. Jang, Y.-S. Kim and U.-G. Jong, RSC Adv., 2023, 13, 16012–16022 RSC.
- M. Houari, B. Bouadjemi, S. Haid, M. Matougui, T. Lantri, Z. Aziz, S. Bentata and B. Bouhafs, Indian J. Phys., 2020, 94, 455–467 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- T. Krishnamoorthy, H. Ding, C. Yan, W. L. Leong, T. Baikie, L. Zhang, M. Sherburne, S. Li, M. Asta, N. Mathews and S. G. Mhaisalkar, J. Mater. Chem. A, 2015, 3, 23829–23832 RSC.
- Z. G. Lin, L. C. Tang and C. P. Chou, Opt. Mater., 2008, 31, 28–34 CrossRef CAS.
- S. Sharma, J. K. Dewhurst and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 165332 CrossRef.
- S. R. Kumavat, Y. Sonvane and S. K. Gupta, Appl. Phys. Lett., 2016, 109, 133108 CrossRef.
- A. C. Ulpe and T. Bredow, ChemPhysChem, 2020, 21, 546–551 CrossRef CAS PubMed.
- P. Mishra, D. Singh, Y. Sonvane and R. Ahuja, Opt. Mater., 2020, 110, 110476 CrossRef CAS.
- E. Oyeniyi, Solid State Commun., 2022, 355, 114927 CrossRef CAS.
- P. Mishra, D. Singh, Y. Sonvane and R. Ahuja, Mater. Today Energy, 2022, 27, 101026 CrossRef CAS.
- Y. Cho and T. C. Berkelbach, J. Phys. Chem. Lett., 2019, 10, 6189–6196 CrossRef CAS PubMed.
- U.-G. Jong, C.-J. Yu, J.-S. Ri, N.-H. Kim and G.-C. Ri, Phys. Rev. B, 2016, 94, 125139 CrossRef.
- L. Yu and A. Zunger, Phys. Rev. Lett., 2012, 108, 068701–068707 CrossRef PubMed.
- M. Kumar, A. Singh, D. Gill and S. Bhattacharya, J. Phys. Chem. Lett., 2021, 12, 5301–5307 CrossRef CAS PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- C.-J. Yu, U.-S. Hwang, Y.-C. Pak, K. Rim, C. Ryu, C.-R. Mun and U.-G. Jong, New J. Chem., 2020, 44, 21218–21227 RSC.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
- U.-G. Jong, C.-J. Yu, Y.-M. Jang, G.-C. Ri, S.-N. Hong and Y.-H. Pae, J. Power Sources, 2017, 350, 65–72 CrossRef CAS.
- J. Trotter, M. Akhtar and N. Bartlett, Phase Trans., 1992, 38, 127–220 CrossRef.
- T. Tadano, Y. Gohda and S. Tsuneyuki, J. Phys.: Condens. Matter, 2014, 26, 225402 CrossRef CAS PubMed.
- F. Zhou, W. Nielson, Y. Xia and V. Ozolins, Phys. Rev. Lett., 2014, 113, 185501 CrossRef PubMed.
- N. Rahman, M. Husain, M. Sohail, R. Khan, T. Zaman, R. Neffati, G. Murtaza, A. Khan, A. A. Khan and Z. Igbal, Phys. Scr., 2023, 98, 065929–065938 CrossRef.
- C.-J. Yu, U.-H. Ko, S.-G. Hwang, Y.-S. Kim, U.-G. Jong, Y.-H. Kye and C.-H. Ri, Phys. Rev. Mater., 2020, 4, 045402–045410 CrossRef CAS.
- U.-G. Jong, C.-J. Yu, Y.-H. Kye, Y.-G. Choe, W. Hao and S. Li, Inorg. Chem., 2019, 58, 4134–4140 CrossRef CAS PubMed.
- C.-H. Ri, Y.-S. Kim, U.-G. Jong, Y.-H. Kye, S.-H. Ryang and C.-J. Yu, RSC Adv., 2021, 11, 26432–26443 RSC.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC.
- Z. Li, M. Yang, J. Park, S. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292 CrossRef CAS.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- J. Yang, Q. Yuan and B. I. Yakobson, J. Phys. Chem. C, 2016, 120, 24682–24687 CrossRef CAS.
- S. R. Kumavat, G. Sachdeva, Y. Sonvane and S. K. Gupta, RSC Adv., 2022, 12, 25924–25931 RSC.
- E. Shi, Y. Gao, B. P. Finkenauer, Akriti, A. H. Coffey and L. Dou, Chem. Soc. Rev., 2018, 47, 6046–6072 RSC.
- S. R. Kumavat, Y. Sonvane, D. Singh and S. K. Gupta, J. Phys. Chem. C, 2019, 123, 5231–5239 CrossRef CAS.
- S. R. Kumavat, Y. Sonvane and S. K. Gupta, J. Appl. Phys., 2020, 128, 114304 CrossRef CAS.
- J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999–3005 CrossRef CAS.
- B. Max and H. Kun, Dynamical theory of crystal lattices, Clarendon, Oxford, UK, 1956 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Total energy convergence tests according to the kinetic energy cutoff and k-point mesh, comparison of the atomic forces, crystalline structures of cubic AF and orthorhombic BF2 and convergence of phonon dispersion curves according to the size of the supercell. See DOI: https://doi.org/10.1039/d3ma00457k |
| This journal is © The Royal Society of Chemistry 2023 |