Open Access Article
Open Access ArticleIncorporation of protons and hydroxide species in BaZrO3 and BaCeO3
Andrew J. E.
Rowberg
 *a,
Meng
Li
*a,
Meng
Li
 b,
Tadashi
Ogitsu
b,
Tadashi
Ogitsu
 a and
Joel B.
Varley
a and
Joel B.
Varley
 a
a
aQuantum Simulations Group (QSG) and Laboratory for Energy Applications for the Future (LEAF), Lawrence Livermore National Laboratory, Livermore, California 94550, USA. E-mail: rowberg1@llnl.gov
bEnergy and Environmental Science and Technology, Idaho National Laboratory, Idaho Falls, ID 83415, USA
First published on 18th October 2023
Abstract
Barium zirconate (BaZrO3 or BZO) and barium cerate (BaCeO3 or BCO) are among the best-performing proton-conducting oxides used as electrolytes in all-solid-state fuel and/or electrolysis cells. During synthesis, they are seeded with oxygen vacancies (V2+O), which charge-compensate with acceptor dopants such as yttrium (Y−Zr) and, upon exposure to water vapor, are replaced by interstitial protons (H+i). Here, we investigate this and alternative processes for protonation by calculating defect formation energies, concentrations, and migration barriers for several relevant species, including H+i, V2+O, interstitial oxygen (O2−i), and interstitial hydroxide (OH−i), using density functional theory. We confirm that V2+O are favorable under typical operating conditions, although at lower partial pressures of H2 gas and wet conditions, H+i becomes the dominant donor species. Higher H+i concentrations in BCO than in BZO under comparable conditions help to explain the higher conductivity measured in BCO. OH−i species are present in low concentrations in the bulk (particularly in BZO; they may incorporate in BCO under wet conditions), and their migration is slow; however, they may form at surfaces and help seed materials with H+i. Alloying BZO and BCO improves ionic conduction in general, although the presence of native defects tends to impede kinetics. Our results show that high ionic conductivity can be achieved through optimizing synthesis conditions to maximize the concentrations of H+i, as well as reducing defect-rich regions such as grain boundaries.
1. Introduction
Proton-conducting oxides (PCOs) are widely studied as solid-state electrolytes in ceramic fuel and/or electrolysis cells, on account of their favorable proton kinetics and ease of hydrogen incorporation.1–5 Two ABO3 perovskite oxides, barium zirconate (BaZrO3 or BZO) and barium cerate (BaCeO3 or BCO), are among the most attractive of these materials, and they are often alloyed together to merge BZO's superior chemical stability with BCO's higher proton conductivity.6–11It is generally accepted that acceptor doping (e.g., with yttrium, Y−Zr/Ce) is necessary to incorporate protons (H+i) into PCOs, as they initially seed the materials with oxygen vacancies (V2+O), which serve as intermediaries for protonation upon water exposure:1
| 2Y−Zr/Ce + V2+O + H2O → 2Y−Zr/Ce + 2H+i. | (1) |
It is therefore of interest to consider other routes for protonation that do not require oxygen vacancies. Direct exposure to dry H2 during synthesis with an acceptor species is one option:
| BaO(s) + {Zr/Ce}O2(s) + H2+ 2Y(s) → Ba{Zr/Ce}O3 + 2H+i+ 2Y−Zr/Ce. | (2) |
Another alternative is that exposure to water could give rise to H+i in addition to an interstitial hydroxide (OH−i) via the following reaction:
| H2O → OH−i + H+i. | (3) |
Whether or not these pathways are relevant is unclear. For one thing, the formation energy of OH−i in the bulk has not previously been calculated, to our knowledge. However, previous computational studies have suggested that hydroxide migration may be relevant for protonation, particularly when moving from the surface to the bulk. Polfus et al. found adsorbed OH−i to be favorable on surfaces of BZO, even more so than adsorbed O2−i.15 Jing et al. calculated hydroxide migration barriers to be one-third as large as those for protons at the surface of SrZrO3, another perovskite proton conductor, which suggests that hydroxide migration is key for protons to migrate into the bulk.16 Halwidl et al. also showed that interstitial hydroxide species created through the dissociation of water are very mobile at the surface of perovskite-like Sr2RuO4 and Sr3Ru2O7.17
In addition to considering migration of other proton-related species, it is important to consider the effect of local chemical environments on proton diffusion. Grain boundaries, for instance, exhibit environments characterized by different concentrations of defects (such as vacancies) than in the bulk.18–22 Several studies have shown that ions are less mobile near grain boundaries than in the bulk, meaning that grain boundaries limit the overall proton conductivity in polycrystalline samples of BZO and BCO.23–30 Furthermore, the importance of BZO–BCO alloys means that ionic migration should also be considered in the presence of alloy impurities, i.e., Ce on a Zr site in BZO (CeZr) or Zr on a Ce site in BCO (ZrCe).
In this work, we use density functional theory (DFT) calculations to study the properties of protons, oxide ions, and hydroxide ions in BZO and BCO, as well as their mobility in the presence of cation vacancies and alloy impurities. To begin, we calculate defect formation energies for each of the relevant species, using a hybrid exchange–correlation functional to capture electronic properties accurately. Using these results, we compute concentrations of defects and H-related impurities in Y-doped BCO and BZO. V2+O will be the most prevalent native point defect; however, H+i can replace it very easily, particularly under wet conditions. Their presence reduces the concentration of free charge carriers, which implies that proton-rich samples will exhibit less electrical leakage. OH−i species will not typically be present in large concentrations, although they will be slightly more common in BCO than in BZO.
Subsequently, we calculate migration barriers for these defects and impurities. We calculate barriers for H+i, V2+O, O2−i, and OH−i in the bulk, which we then compare with values calculated in the presence of an alloy impurity (i.e., CeZr in BZO or ZrCe in BCO) or an intrinsic vacancy. Comparing these values gives us a sense for how migration pathways will be affected by alloying and the presence of defect-rich regions such as grain boundaries. Unsurprisingly, H+i has the fastest kinetics, though other species will also be fairly mobile. Alloying generally reduces migration barriers, while the presence of cation vacancies increases barriers due to Coulombic binding. As such, defect-rich regions like grain boundaries should be limited in order to optimize ionic conductivity.
2. Computational methods
We perform DFT calculations31,32 using the Vienna ab initio simulation package (VASP).33 We use the hybrid exchange–correlation functional of Heyd, Scuseria, and Ernzerhof (HSE06)34 with 25% mixing of exact exchange in order to obtain accurate results for defect formation energies. For the calculation of migration barriers, we use the nudged elastic band (NEB) method with climbing images.35,36 The generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) is used for NEB calculations for computational efficiency.37 We apply projector augmented wave (PAW) potentials38,39 with a plane-wave cutoff of 500 eV. The Ba 5s2 5p6 6s2, Zr 4s2 4p6 5s2 4d2, Ce 5s2 5p6 6s2 5d1 4f1, Y 4s2 4p6 5s2 4d1, and O 2s2 2p4 electrons are treated explicitly as valence. Spin polarization is included for all of our calculations. Supercells are constructed for defect formation and migration calculations; these consist of eight unit cells of BCO (2a × 2b × 2c in terms of the lattice vectors, 160 atoms) and 27 unit cells of BZO (3a × 3b × 3c, 135 atoms). The bulk properties we calculate for unit cells are described in our previous work.40 For supercell calculations, a single special k point is used.As a word of caution, we note that while our supercells are appropriately sized for defect calculations, they may be insufficient for studying global defect migration, particularly in highly disordered materials. As such, our results for defect migration provide relative trends, but our calculated migration barriers may not fully explain experimental measurements for these systems. Furthermore, as demonstrated in several review articles, experimental measurements of proton conductivity show significant variability, even in certain cases for materials with ostensibly the same composition.3,41 As such, it is challenging to match computed barriers with experimental results.
2.1 Defect formation
We calculate the formation energy Ef(Dq) of a defect D in charge state q as:42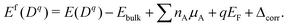 | (4) |
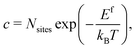 | (5) |
For defect complexes, we can use formation energies to calculate a binding energy for a complex (AB) relative to its constituent, isolated defects (A and B):
| Ebind(AB) = Ef(A) + Ef(B) − Ef(AB). | (6) |
The chemical potential μA reflect the energetic preference for a specific element present in the system. We define it in terms of a deviation ΔμA from a reference energy as:
| μA = EA + ΔμA, | (7) |
| ΔμBa + Δμ{Zr,Ce} + 3ΔμO = ΔHf(Ba{Zr,Ce}O3), | (8) |
Additional bounds are placed on ΔμBa and Δμ{Zr,Ce} to ensure that limiting phases such as BaO, ZrO2, and CeO2 do not precipitate. For Ba, this condition is expressed as:
| ΔμBa + ΔμO ≤ ΔHf(BaO). | (9) |
| Δμ{Zr,Ce} + 2ΔμO ≤ ΔHf({Zr,Ce}O2). | (10) |
We treat impurity chemical potentials (e.g., for H and Y) in a similar fashion. As for eqn (9) and (10), we establish an upper limit on Δμ by ensuring that a limiting phase does not precipitate. For yttrium, that phase is Y2O3, leading to the condition:
| 2ΔμY + 3ΔμO ≤ ΔHf(Y2O3). | (11) |
| 2ΔμH + ΔμO = ΔμH2O ≤ ΔGf(H2O), | (12) |
Note that ΔGf(H2O) is the upper limit here, rather than ΔHf as with our other limiting phases. Strictly speaking, the free energies ΔGf are the proper limits in each case and are reflective of conditions at finite temperatures. However, the entropic contribution is most pronounced for gaseous species such as water vapor, so while we can approximate the upper limits in eqn (8)–(11) with DFT-calculated ΔHf values, we necessarily need to consider the temperature-dependent ΔGf in this case. To that end, we use tabulated values for ΔGf(T).46
Finally, for elements with a gas-phase reference state, such as oxygen and hydrogen (and also water vapor), the Δμ values can be connected to experimentally measurable partial pressures using the expression:
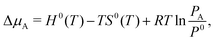 | (13) |
2.2 Defect concentrations
Using eqn (5), we can identify how defect concentrations change under different operating conditions. Specifically, by enforcing charge neutrality among all the defects we calculate, we can determine the concentrations for each species and the position of the Fermi level for certain conditions. This procedure requires two additional parameters, namely, the electron and hole concentrations, which we determine by integrating the calculated densities of states (DOS). We determine electron concentrations by integrating the calculated DOS near the CBM, using the expression:47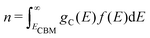 | (14) |
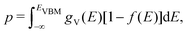 | (15) |
3. Results
3.1 Defect formation
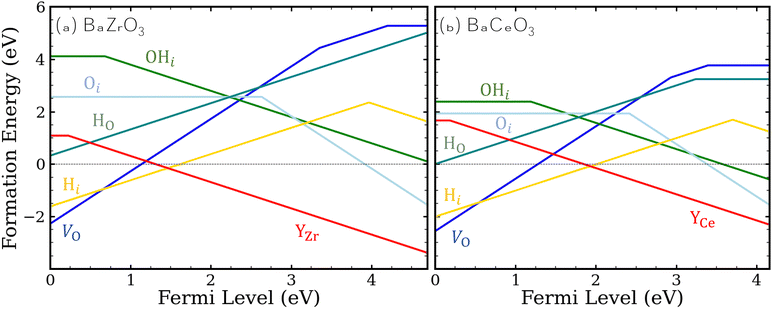 | ||
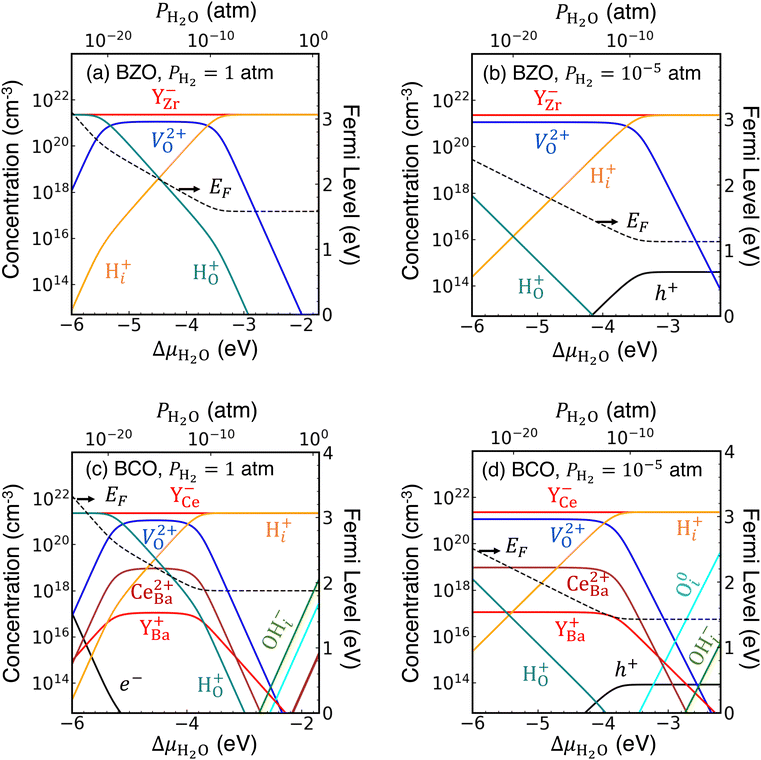
| Fig. 1 Formation energies of hydrogen- and oxygen-related defects and impurities in (a) BaZrO3 and (b) BaCeO3. ΔμO is set at −2.42 eV, which corresponds to sintering conditions at 1650 °C,49 and equilibrium with H2O is assumed. Ba-rich conditions and the Y solubility limit are assumed for calculating the formation energies of YZr and YCe. | ||
Our defect formation energies allow us to comment on the relative energetics of eqn (1) and (3), which describe possible routes toward protonation in BZO and BCO, by comparing the formation energies of products and reactants. For eqn (1), the enthalpy of the reaction will be related to 2Ef[H+i] − Ef[V2+O], while for eqn (3), the enthalpy is related to Ef[H+i] + Ef[OH−i]. The difference between these two quantities (2Ef[H+i] − Ef[V2+O] and Ef[H+i] + Ef[OH−i]) provides an estimate of the relative favorability of the two reactions; notably, this quantity is independent both of chemical potentials and the Fermi level position. In BZO, we find eqn (1) to be 4.14 eV lower in energy than eqn (3), while for BCO, we find eqn (1) to be 3.02 eV lower in energy. In both cases, these relative energies suggest that the widely proposed V2+O-mediated reaction of eqn (1) will proceed much more favorably, although the process described by eqn (3), whereby V2+O are not required and OH−i species are created, will be more competitive in BCO. Most likely, this result extends qualitatively to surfaces and interfaces, where OH−i are most likely to form initially.
In each of our concentration plots, we maintain a fixed value of ΔμH and vary ΔμO from −5 eV to 0 eV, which in turn yields a range of ΔμH2O that we use as our x-axis. Using eqn (13), we can connect ΔμH2O to partial pressures of water (PH2O), which we show on the upper x-axis of our concentration plots. We consider two choices of PH2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 atm (corresponding to ΔμH = −0.625 eV) and 10−5 atm (ΔμH = −1.071 eV), to compare H-rich and H-poor conditions. Otherwise, we use intermediate chemical potentials halfway between the Ba-rich and Ba-poor limits. An upper limit on our x-axis is set by ΔGf(H2O), which at 900 K is −2.05 eV, although we extend slightly beyond this limit for illustrative purposes in the case of PH2 = 1 atm. We include certain defect formation energies calculated previously13,40,45,52 to generate these plots.
1 atm (corresponding to ΔμH = −0.625 eV) and 10−5 atm (ΔμH = −1.071 eV), to compare H-rich and H-poor conditions. Otherwise, we use intermediate chemical potentials halfway between the Ba-rich and Ba-poor limits. An upper limit on our x-axis is set by ΔGf(H2O), which at 900 K is −2.05 eV, although we extend slightly beyond this limit for illustrative purposes in the case of PH2 = 1 atm. We include certain defect formation energies calculated previously13,40,45,52 to generate these plots.
To start, we plot concentrations of defects and impurities in BZO in Fig. 2(a) and (b). In panel (a), for which PH2 = 1 atm, we identify three distinct regimes based on which donor species compensates with Y−Zr. At dry conditions, below approximately PH2O = 10−20 atm, the substitutional hydride H+O will be the dominant donor. On the other hand, for wet conditions of PH2O ≥ 10−10 atm, interstitial protons H+i will dominate. In between those two extremes, V2+O will have the highest concentration among donor species. The situation is similar in Fig. 2(b), for PH2 = 10−5 atm, with the main difference being that H+O concentrations will be significantly less competitive with V2+O for dry conditions.
We note two more significant results for BZO. First, the Fermi level positions will be higher than those we calculated in previous work for BZO absent any hydrogen exposure,40 spanning a range of about 1.6–3.1 eV above the VBM for PH2 = 1 atm [Fig. 2(a)], and about 1.2–2.4 eV above the VBM for PH2 = 10−5 atm [Fig. 2(b)]. Under the more H-poor conditions in panel (b), free hole (h+) concentrations are noticeably higher than under the H-rich conditions in panel (a); however, they plateau just above 1014 cm−3. Free electron (e−) concentrations do not even appear in the plotted range in either case. In general, these results suggest that the presence of H+i will minimize harmful electrical leakage in these materials by limiting the presence of free carriers and/or polarons. This result is consistent with a previous report that proton conductivity will significantly exceed electrical conductivity in BZO at high PH2O.53 Second, we find that the hydroxide species, OH−i, does not appear on our concentration plots; as such, we do not expect measurable concentrations of OH−i in bulk BZO.
Next, in Fig. 2(c) and (d) we plot defect concentrations in bulk BCO. The trends are generally similar to those we observed in BZO. For PH2 = 1 atm, shown in panel (c), the dominant compensating donor species varies from H+O under dry conditions (PH2O ≤ 10−20 atm), to V2+O for intermediate conditions (10−18 atm ≤ PH2O ≤ 10−12 atm), to H+i under wet conditions (PH2O ≥ 10−10 atm). In comparison with BZO, BCO has higher concentrations of cation antisites (CeBa2+) and wrong-site Y donors (YBa+). CeBa2+ in particular will compete with V2+O, with a more pronounced effect under more Ba-poor conditions than those shown here. In addition, OH−i concentrations are noticeably higher than in BZO, particularly under wet conditions, where they approach concentrations of 1018 cm−3. For PH2 = 10−5 atm, shown in panel (d), V2+O is the dominant donor for PH2O ≤ 10−12 atm (again accompanied by CeBa2+), and H+i takes its place for wetter conditions. These H-poor conditions are less amenable to OH−i formation; instead, O0i concentrations will become increasingly sizeable with increasing ΔμH2O.
Once again, as with BZO, we observe relatively high Fermi levels, ranging from 1.9–3.4 eV above the VBM for PH2 = 1 atm, and 1.4–2.4 eV for PH2 = 10−5 atm. Correspondingly, h+ concentrations are significantly lower than those we found in our previous study,40 although e− concentrations can be high under extremely dry/H2-rich conditions.
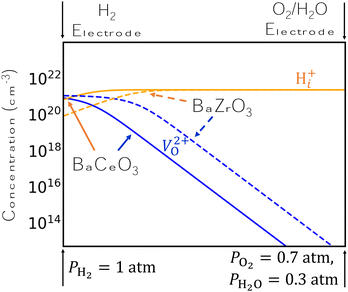
The results of Fig. 2 suggest a possible explanation for BCO's superiority to BZO as a proton conductor. Specifically, the concentration of H+i is higher in BCO than in BZO under comparable conditions, and H+i is preferred over V2+O over a wider range of chemical potentials in BCO. We demonstrate this finding schematically in Fig. 3, which plots the concentrations of H+i and V2+O side-by-side for analogous conditions in BZO and BCO. Specifically, we choose conditions that are typical of the two electrodes in an electrolysis cell under open-circuit conditions and change the chemical potentials linearly between these two extremes. We use H-rich conditions at the H2 electrode, with PH2 = 1 atm and PO2 = 7 × 10−20 atm, and O-rich conditions at the O2/H2O electrode, with PO2= 0.7 atm and PH2O = 0.3 atm. As our results indicate, H+i concentrations are dominant over most of the electrolyte, with V2+O only beginning to displace H+i very close to the H2 electrode. However, this crossover point between H+i and V2+O occurs more quickly for BZO than for BCO, implying a lower proton conductivity due to limited H+i concentrations in BZO. Tuning the precise conditions at the two electrodes may be a viable strategy to keep H+i concentrations high.
Finally, we note that the concentrations we plot in Fig. 2 and 3 evolve slightly with increasing temperature. While our assumed temperature of 900 K is typical for electrolysis applications, other use cases for these materials (such as in oxide ion conduction) require higher temperatures. The most noticeable impact of higher temperatures is to increase the free carrier concentration, which can increase the degree of electrical leakage, as has been observed experimentally.54,55 This rise in carrier concentrations is accompanied by a decrease in H+i concentrations and an increase in V2+O concentrations for analogous conditions. Increasing temperature appears to depress OH−i concentrations, however. Thus, to the extent that water can be directly converted into H+i and OH−iviaeqn (3), we expect that process to be most favorable at the lower temperatures most characteristic of electrolysis.
3.2 Defect migration
| BaZrO3 (eV) | ||||||
|---|---|---|---|---|---|---|
| Species | Pathway | Bulk | BZO:Ce | V2−Ba | V4−Zr | V2+O |
| a This barrier is simply the change in energy between the initial (O2−i separated from V4−Zr) and final (O2−i near V4−Zr) states. The reverse process proceeds spontaneously. | ||||||
| H+i | Hop | 0.21 | 0.13–0.36 | 0.64 | 0.43 | 0.22–0.23 |
| Rotate | 0.18 | 0.10–0.28 | 0.21–0.93 | 0.06–1.89 | 0.22–0.28 | |
| V2+O | Hop | 0.72 | 0.42–0.96 | 0.59–1.00 | 0.75–2.25 | 0.21–0.99 |
| O2−i | Hop | 0.58 | 0.16–0.55 | 0.48 | 1.37a | — |
| Rotate | 1.28 | 0.78–1.23 | 0.78–0.95 | 0.33–1.02 | — | |
| OH−i | Hop | 0.55 | 0.24–0.85 | 0.57–1.69 | 0.85 | — |
| Rotate | 1.67 | 1.54–1.68 | 0.24–2.17 | 0.61–1.52 | — | |
| BaCeO3 (eV) | ||||||
|---|---|---|---|---|---|---|
| Species | Pathway | Bulk | BCO:Zr | V2−Ba | VCe4− | V2+O |
| H+i | Hop | 0.21–0.39 | 0.13–0.55 | 0.26–1.00 | 0.21–1.57 | 0.21–0.38 |
| Rotate | 0.07–0.14 | 0.06–0.22 | 0.11–0.58 | 0.13–1.60 | 0.12–0.20 | |
| V2+O | Hop | 0.45–0.50 | 0.32–0.81 | 0.30–1.08 | 0.30–1.51 | 0.05–0.72 |
| O2−i | Hop | 0.22–0.27 | 0.20–0.64 | 0.30–0.50 | 0.85–0.93 | — |
| Rotate | 0.58–0.64 | 0.53–0.87 | 0.66–0.74 | 0.21–0.22 | — | |
| OH−i | Hop | 0.37–0.46 | 0.09–0.73 | 0.24–1.10 | 0.78–0.84 | — |
| Rotate | 0.80–0.95 | 0.72–1.10 | 0.53–1.31 | 0.34–0.98 | — | |
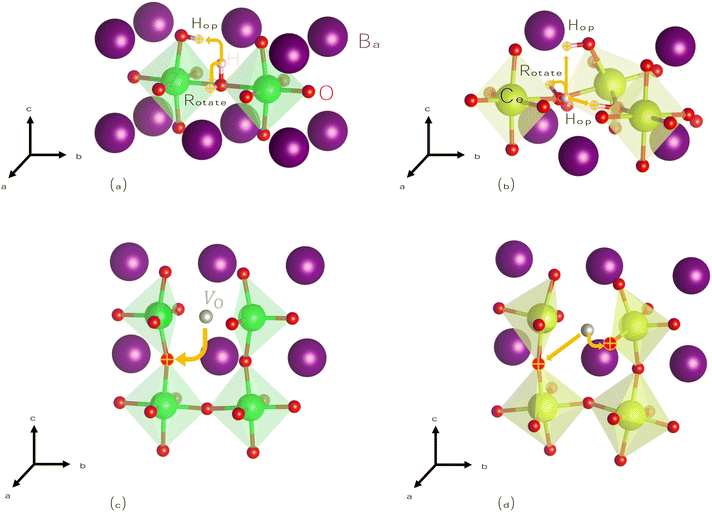
To begin, we calculate barriers for H+i migration. We consider two pathways, summarized visually in Fig. 4(a) and (b): hopping, whereby H+i moves from its host oxygen atom to another nearby oxygen, and rotation, where H+i simply changes its orientation while remaining attached to the same oxygen atom. Our results compare well to those of previous calculations on proton migration in BZO58 and BCO,59 exclusively considering regions far from dopants like Y−Zr where additional interactions can be neglected. We compute nearly identical barriers for proton hopping in both materials, although due to its lower symmetry, BCO has more possible pathways, some of which are slightly higher in energy.
Next, we calculate barriers for V2+O migration, which proceeds via a hopping mechanism as shown in Fig. 4(c) and (d). For a reaction such as that described by eqn (1) to drive protonation, V2+O must necessarily be mobile in order to replace vacancies filled by water at the surface. Oxygen diffusion has been observed in BZO and BCO,60–63 particularly at elevated temperatures.64,65 We calculate a barrier of 0.72 eV in BZO, similar to the value of 0.66 eV recently calculated in another study.66 For BCO, we calculate barriers ranging from 0.45–0.50 eV. We are unaware of previous NEB calculations on V2+O migration in BCO, and experimental activation energies are higher (0.69–0.90 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,67,68). However, when adding our calculated migration barriers to the energy contribution from thermal activation of the mobile species (namely, their formation energies), our results are consistent with these values.
1,67,68). However, when adding our calculated migration barriers to the energy contribution from thermal activation of the mobile species (namely, their formation energies), our results are consistent with these values.
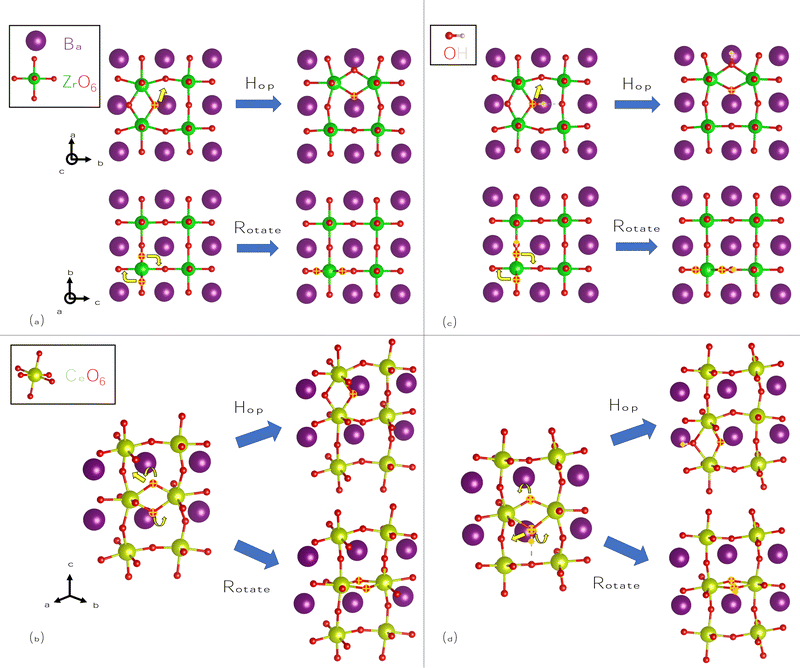
We also consider the migration of O2−i, despite the higher formation energies of these species, as it is closely related to OH−i. We identify pathways for hopping and rotation, shown for BZO in Fig. 5(a), and for BCO in Fig. 5(b). In the hopping pathway, migration proceeds via an interstitialcy (“kick-out”) process, meaning that the migrating species replaces a lattice O atom after “kicking it out” of its lattice site. Hopping is favored over rotation in both materials; in fact, in BCO, its barrier is roughly equal to that of H+i hopping. These hopping barriers are lower than those of V2+O; nonetheless, the markedly lower formation energy of V2+O will ensure that any oxygen conductivity will be predominately vacancy mediated. We attribute the larger barriers for rotation to the mobile O atoms moving too close to large Ba atoms.
Finally, we consider OH−i migration, using the same approximate pathways as O2−i, as shown in Fig. 5(c) for BZO and in Fig. 5(d) for BCO. As for O2−i, hopping proceeds via an interstitialcy process; however, there is an additional step of rotation and transfer of hydrogen to complete the movement. As such, OH−i migration can be considered to be a composite of H+i and O2−i migration. Hopping pathways for OH−i generally proceed more favorably than for O2−i, while rotation is less favorable, again due to the close proximity of Ba cations at the saddle point configuration. These barriers suggest that OH−i will be mobile if it is present, and due to its large binding energy, it will be favored over O2−i if hydrogen is present. OH−i migration also proceeds more favorably in BCO than in BZO; as we showed earlier, OH−i will also have much higher concentrations in BCO.
In Table 1, we list the range of barriers computed for the hopping and rotation pathways discussed above. In each case, certain placements of the impurity reduce the energetic barrier for migration. This improvement is generally most pronounced in BZO:Ce, which follows from the lower barriers we identify in bulk BCO; however, BCO:Zr can also exhibit slightly improved kinetics for ion migration.
However, certain pathways in alloyed systems also have larger barriers than in the bulk materials for almost every mobile species we consider. This mixed behavior likely arises from alloy impurities breaking the local symmetry in such a way as to create additional space for certain migration pathways, while at the same time constricting other pathways. As such, it is not entirely clear what the overall impact of alloying will be on large-scale ion migration. Presumably, in highly heterogeneous alloys, species will be able to migrate along more energetically favorable pathways, whereas in a phase-separated system, migration would be slower in Zr-rich (BZO-like) than in Ce-rich (BCO-like) regions. It is also possible that alloying may create higher-energy corridors that serve as bottlenecks for ion transport; however, a detailed examination of this possibility is beyond the scope of this work.
In Table 2, we list the binding energies (determined using eqn (6)) for complexes involving a mobile defect and an alloy impurity. These binding energies represent a coulombic barrier that must be overcome—in addition to the migration barrier—for a mobile species to break away from the complex. The values we list reflect the most energetically favored configurations of the complexes, which suggests a worst-case-scenario for migration. It is evident that alloy species exhibit some amount of Coulombic binding with V2+O and O2−i, thereby limiting their mobility, while the negative binding energies for complexes between H+i and alloy species suggest that they will not inhibit proton mobility. The effect on OH−i is more complicated, as our results suggest that Ce-alloying in BZO will bind OH−i, while Zr-alloying in BCO will repel OH−i. Of course, it is unlikely that alloy impurities will be present at the dilute limit, as they are in our simulation cells; for a near equal mix of Zr and Ce atoms, our results suggest very little net impact on OH−i migration.
| Mobile species | Binding energy (eV) | ||||
|---|---|---|---|---|---|
| Material | CeZr/ZrCe | V2−Ba | V4−Zr/Ce | V2+O | |
| H+i | BaZrO3 | −0.09 | 0.77 | 1.53 | −0.09 |
| BaCeO3 | −0.02 | 0.75 | 1.29 | −0.18 | |
| V2+O | BaZrO3 | 0.28 | 0.36 | 1.74 | −0.10 |
| BaCeO3 | 0.20 | 0.69 | 1.38 | 0.06 | |
| O2−i | BaZrO3 | 0.43 | −0.48 | −0.45 | — |
| BaCeO3 | 0.21 | −0.32 | −0.39 | — | |
| OH−i | BaZrO3 | 0.52 | 0.91 | 0.33 | — |
| BaCeO3 | −0.29 | 0.33 | 0.16 | — | |
Tables 1 and 2 list migration barriers and binding energies, respectively, for mobile species in proximity to native vacancies. For each mobile species, we include both its preferred charge state (+1 for H+i, +2 for V2+O, −2 for O2−i, and −1 for OH−i), as well as that of the nearby vacancies (−2 for V2−Ba, −4 for V4−Zr/Ce, and +2 for V2+O). Note that for O2−i and OH−i, we do not include results in the vicinity of V2+O, as the interstitial O atom in both cases will spontaneously fill the vacancy. Several of the combinations have multiple pathways that we consider; in these cases, we list a representative range of migration barriers. Binding energies are computed using the most energetically stable complexes among those we identify.
The presence of cation vacancies has a significant impact on proton migration, with V2−Ba and V4−{Zr,Ce} giving rise to larger H+i migration barriers in general. Additionally, protons have large, positive binding energies with cation vacancies (particularly with V4−Zr/Ce), which will severely hamper proton migration in their vicinity. Furthermore, if cation vacancies dominate the defect chemistry in disordered regions, as may occur in space charge layers due to dopant segregation to grain boundary cores,18,76 the concentration of protons will drop precipitously due to an increase in their formation energy. If we simply approximate the concentration of H+i by assuming equilibrium with V2−Ba, the concentrations will decrease by as much as six orders of magnitude compared with the results presented in Fig. 2. These large barriers and binding energies, and decreased proton concentrations, may help to explain the observation of higher activation energies for proton migration in grain boundaries compared to bulk regions.30 V2+O migration is similarly affected by the presence of cation vacancies, with V4−Zr/Ce again leading to larger migration barriers and binding energies than V2−Ba.
Bringing a V2+O defect into proximity with H+i does not significantly affect the migration barriers. However, having two V2+O defects in close proximity does appear to enhance V2+O diffusion along certain directions, with barriers as small as 0.21 eV in BZO and 0.05 eV in BCO. As both V2+O and H+i are positively charged, Coulombic trapping is not a concern, as evidenced by the small (and in most cases negative) binding energies.
Cation vacancies can have either a beneficial or harmful impact on O2−i and OH−i migration, depending on the placement of the vacancy relative to the mobile species. Rotation, as we have discussed, is limited in bulk systems by the presence of large Ba cations; removing these cations will therefore make rotation significantly easier along pathways including the vacancy. Hopping barriers, on the other hand, are generally increased slightly by the presence of vacancies (particularly V4−Zr/Ce).
Interestingly, O2−i has negative binding energies in complexes with cation vacancies, while OH−i has positive binding energies. This discrepancy reflects the nature of OH−i as a complex between H+i and O2−i; as such, the binding energies with cation vacancies are generally intermediate between the binding energies for isolated H+i and O2−i. The stronger Coulombic attraction between cation vacancies and H+i may cause dissociation of OH−i, as H+i will be drawn to the vacancies while O2−i are repelled. Such an effect might be observable near grain boundaries, where we expect cation vacancies to be most prevalent.
4. Conclusion
In conclusion, we have investigated the formation energies, concentrations, and migration barriers of H+i, V2+O, O2−i, and OH−i in BZO and BCO. Our formation energies suggest that it will be difficult to dissociate water and protonate BZO and BCO without oxygen vacancies (slightly more so in BZO than in BCO), lending credence to the widely accepted notion that V2+O are needed for protonation. When doped with an element like yttrium, three donor species can be stabilized based on the partial pressure of water vapor: H+O at extremely dry conditions, V2+O at intermediate conditions, and H+i under wet conditions. Decreasing the partial pressure of H2 makes V2+O favored over H+O at extremely dry conditions, while leaving H+i mostly unaffected. The presence of H+i limits the concentration of free carriers and polarons, which has advantages for avoiding electrical leakage. O2−i and OH−i will have very low concentrations in bulk regions, although OH−i should have measurable concentrations in BCO under wet conditions. Considering both kinetics and thermodynamics of proton incorporation in BZO and BCO, our results indicate that the tendency for higher conductivities in BCO is likely attributed to the greater relative solubility of protons under the same conditions.The precise effect of alloying on ionic mobility in BZO and BCO is highly dependent on the position of alloy impurity states relative to the mobile species, meaning that certain ionic pathways may be more favored in alloys, and the ordering of Ce and Zr atoms may impact kinetics. The presence of vacancies has a mixed effect on migration for H+i, V2+O, O2−i, and OH−i, which has implications for understanding diffusion in disordered or off-stoichiometric regions (e.g. surfaces, interfaces, and grain boundaries). Cation vacancies hinder H+i and V2+O conduction due to Coulombic binding, while additional V2+O defects have little impact. For O2−i and OH−i migration, cation vacancies reduce energetic barriers for rotation if they lie in the path of motion; otherwise, they tend to increase migration barriers. In addition, OH−i will be bound to cation vacancies, perhaps leading to the dissociation of OH−i into H+i and O2−i. Overall, these results suggest that in order to maximize the conductivity of the most mobile species in these systems (H+i and V2+O), defect-rich regions such as grain boundaries should be avoided as much as possible.
Author contributions
Andrew J. E. Rowberg: formal analysis, investigation, methodology, visualization, writing – original draft, writing – review & editing. Meng Li: resources, writing – review & editing. Tadashi Ogitsu: funding acquisition, project administration, writing – review & editing. Joel B. Varley: conceptualization, methodology, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the HydroGEN Advanced Water Splitting Materials Consortium, established as part of the Energy Materials Network under the U.S. Department of Energy (DOE), the Office of Energy Efficiency and Renewable Energy (EERE), the Hydrogen and Fuel Cell Technologies Office (HFTO). Part of this work was performed under the auspices of the DOE by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. M. Li additionally acknowledges support from the DOE Idaho Operations Office under contract no. DE-AC07-05ID14517. The research was performed using computational resources sponsored by the DOE's EERE and located at the National Renewable Energy Laboratory.Notes and references
- K.-D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- T. Norby, Solid State Ionics, 1999, 125, 1–11 CrossRef CAS.
- N. Kochetova, I. Animitsa, D. Medvedev, A. Demin and P. Tsiakaras, RSC Adv., 2016, 6, 73222–73268 RSC.
- S. Rajendran, N. K. Thangavel, H. Ding, Y. Ding, D. Ding and L. M. Reddy Arava, ACS Appl. Mater. Interfaces, 2020, 12, 38275–38284 CrossRef CAS PubMed.
- C. Duan, J. Huang, N. Sullivan and R. O’Hayre, Appl. Phys. Rev., 2020, 7, 011314 CAS.
- K. H. Ryu and S. M. Haile, Solid State Ionics, 1999, 125, 355 CrossRef CAS.
- K. Katahira, Y. Kohchi, T. Shimura and H. Iwahara, Solid State Ionics, 2000, 138, 91–98 CrossRef CAS.
- J. Lü, L. Wang, L. Fan, Y. Li, L. Dai and H. Guo, J. Rare Earths, 2008, 26, 505–510 CrossRef.
- W. Bian, W. Wu, B. Wang, W. Tang, M. Zhou, C. Jin, H. Ding, W. Fan, Y. Dong, J. Li and D. Ding, Nature, 2022, 604, 479–485 CrossRef CAS PubMed.
- S. Choi, C. J. Kucharczyk, Y. Liang, X. Zhang, I. Takeuchi, H.-I. Ji and S. M. Haile, Nat. Energy, 2018, 3, 202–210 CrossRef CAS.
- L. Yang, S. Wang, K. Blinn, M. Liu, Z. Liu, Z. Cheng and M. Liu, Science, 2009, 326, 126–129 CrossRef CAS PubMed.
- T. Norby, M. Widerøe, R. Glöckner and Y. Larring, Dalton Trans., 2004, 3012–3018 RSC.
- A. J. E. Rowberg, L. Weston and C. G. Van de Walle, ACS Appl. Ener. Mater., 2019, 2, 2611–2619 CrossRef CAS.
- S. Fop, K. S. McCombie, E. J. Wildman, J. M. Skakle and A. C. Mclaughlin, Chem. Commun., 2019, 55, 2127–2137 RSC.
- J. M. Polfus, T. S. Bjørheim, T. Norby and R. Bredesen, J. Mater. Chem. A, 2016, 4, 7437–7444 RSC.
- Y. Jing, H. Matsumoto and N. R. Aluru, Chem. Mater., 2018, 30, 138–144 CrossRef CAS.
- D. Halwidl, B. Stöger, W. Mayr-Schmölzer, J. Pavelec, D. Fobes, J. Peng, Z. Mao, G. S. Parkinson, M. Schmid, F. Mittendorfer, J. Redinger and U. Diebold, Nat. Mater., 2016, 15, 450–455 CrossRef CAS PubMed.
- J. M. Polfus, K. Toyoura, F. Oba, I. Tanaka and R. Haugsrud, Phys. Chem. Chem. Phys., 2012, 14, 12339–12346 RSC.
- M. Vollmann, R. Hagenbeck and R. Waser, J. Am. Ceram. Soc., 1997, 80, 2301–2314 CrossRef CAS.
- R. A. De Souza, Z. A. Munir, S. Kim and M. Martin, Solid State Ionics, 2011, 196, 1–8 CrossRef CAS.
- G. L. Burton, S. Ricote, B. J. Foran, D. R. Diercks and B. P. Gorman, J. Am. Ceram. Soc., 2020, 103, 3217–3230 CrossRef CAS.
- S. Haile, G. Staneff and K. Ryu, J. Mater. Sci., 2001, 36, 1149–1160 CrossRef CAS.
- F. Iguchi, N. Sata, T. Tsurui and H. Yugami, Solid State Ionics, 2007, 178, 691–695 CrossRef CAS.
- J.-H. Yang, B.-K. Kim and Y.-C. Kim, Solid State Ionics, 2015, 279, 60–65 CrossRef CAS.
- B. Joakim Nyman, E. E. Helgee and G. Wahnström, Appl. Phys. Lett., 2012, 100, 4355 CrossRef.
- A. Lindman, E. E. Helgee, B. Joakim Nyman and G. Wahnström, Solid State Ionics, 2013, 230, 27–31 CrossRef CAS.
- A. Lindman, E. E. Helgee and G. Wahnström, Chem. Mater., 2017, 29, 7931–7941 CrossRef CAS.
- S. Yue, Y. Jing, Y. Sun, J. Zhao and N. Aluru, Ceram. Int., 2022, 48, 2097–2104 CrossRef CAS.
- M. Shirpour, R. Merkle, C. Lin and J. Maier, Phys. Chem. Chem. Phys., 2012, 14, 730–740 RSC.
- R. Pornprasertsuk, O. Kosasang, K. Somroop, S. Jinawath and F. B. Prinz, ECS Trans., 2010, 25, 367 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. E. Heyd, J. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. J. E. Rowberg, M. Li, T. Ogitsu and J. B. Varley, Phys. Rev. Mater., 2023, 7, 015402 CrossRef CAS.
- C. Y. R. Vera, H. Ding, D. Peterson, W. T. Gibbons, M. Zhou and D. Ding, J. Phys.: Energy, 2021, 3, 032019 CAS.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253 CrossRef.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Status Solidi B, 2011, 248, 1067–1076 CrossRef CAS.
- A. J. E. Rowberg, M. W. Swift and C. G. Van de Walle, Phys. Chem. Chem. Phys., 2021, 23, 14205–14211 RSC.
- M. W. Chase Jr, J. Phys. Chem. Ref. Data, Monograph, 1998, 9, 1 Search PubMed.
- B. J. Van Zeghbroeck, Principles of Semiconductor Devices, University of Colorado, Boulder, 2011 Search PubMed.
- K. Hoang, C. Latouche and S. Jobic, J. Am. Ceram. Soc., 2022, 105, 4242–4249 CrossRef CAS.
- T. Yajima, H. Suzuki, T. Yogo and H. Iwahara, Solid State Ionics, 1992, 51, 101–107 CrossRef CAS.
- P. G. Sundell, M. E. Björketun and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104112 CrossRef.
- M. E. Björketun, P. G. Sundell and G. Wahnström, Faraday Discuss., 2007, 134, 247–265 RSC.
- M. W. Swift, A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214114 CrossRef.
- D. Han, K. Toyoura and T. Uda, ACS Appl. Energy. Mater., 2021, 4, 1666–1676 CrossRef CAS.
- J. Exner, T. Nazarenus, J. Kita and R. Moos, Int. J. Hydrog. Energy, 2020, 45, 10000–10016 CrossRef CAS.
- F. J. Loureiro, D. Pérez-Coll, V. C. Graça, S. M. Mikhalev, A. F. Ribeiro, A. Mendes and D. P. Fagg, J. Mater. Chem. A, 2019, 7, 18135–18142 RSC.
- K. Toyoura, W. Meng, D. Han and T. Uda, J. Mater. Chem. A, 2018, 6, 22721–22730 RSC.
- T. Fujii, K. Toyoura, T. Uda and S. Kasamatsu, Phys. Chem. Chem. Phys., 2021, 23, 5908–5918 RSC.
- M. E. Björketun, P. G. Sundell and G. Wahnström, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054307 CrossRef.
- J. Hermet, M. Torrent, F. Bottin, G. Dezanneau and G. Geneste, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104303 CrossRef.
- R. Glöckner, M. Islam and T. Norby, Solid State Ionics, 1999, 122, 145–156 CrossRef.
- K. Kreuer, E. Schönherr and J. Maier, Solid State Ionics, 1994, 70, 278–284 CrossRef.
- S. J. Stokes and M. S. Islam, J. Mater. Chem., 2010, 20, 6258–6264 RSC.
- H. Zhu, S. Ricote, C. Duan, R. P. O'Hayre, D. S. Tsvetkov and R. J. Kee, J. Electrochem. Soc., 2018, 165, F581–F588 CrossRef CAS.
- V. Gorelov, V. Balakireva and A. Kuz’min, Russian J. Inorg. Chem., 2018, 63, 930–937 CrossRef CAS.
- F. Zhao, Q. Liu, S. Wang, K. Brinkman and F. Chen, Int. J. Hydrog. Energy., 2010, 35, 4258–4263 CrossRef CAS.
- F. M. Draber, J. R. Denninger, P. C. Müller, I. K. Sommerfeld and M. Martin, Adv. Energy. Sustain. Res., 2022, 3, 2200007 CrossRef CAS.
- R. De Souza, J. Kilner and C. Jeynes, Solid State Ionics, 1997, 97, 409–419 CrossRef CAS.
- T. He, K. Kreuer, Y. M. Baikov and J. Maier, Solid State Ionics, 1997, 95, 301–308 CrossRef CAS.
- X. Xu, Y. Liu, J. Wang, D. Isheim, V. P. Dravid, C. Phatak and S. M. Haile, Nat. Mater., 2020, 19, 887–893 CrossRef CAS PubMed.
- S. M. Haile, D. L. West and J. Campbell, J. Mater. Res., 1998, 13, 1576–1595 CrossRef CAS.
- M. Shirpour, R. Merkle and J. Maier, Solid State Ionics, 2012, 216, 1–5 CrossRef CAS.
- T. Bondevik, J. M. Polfus and T. Norby, Solid State Ionics, 2020, 353, 115369 CrossRef CAS.
- M. Shirpour, R. Merkle and J. Maier, Solid State Ionics, 2012, 225, 304–307 CrossRef CAS.
- F. Iguchi, N. Sata and H. Yugami, J. Mater. Chem., 2010, 20, 6265–6270 RSC.
- C. Kjølseth, H. Fjeld, Ø. Prytz, P. I. Dahl, C. Estournès, R. Haugsrud and T. Norby, Solid State Ionics, 2010, 181, 268–275 CrossRef.
- M. Shirpour, B. Rahmati, W. Sigle, P. A. van Aken, R. Merkle and J. Maier, J. Phys. Chem. C, 2012, 116, 2453–2461 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |