Open Access Article
Open Access ArticleExploring the hygroscopicity, water diffusivity, and viscosity of organic–inorganic aerosols – a case study on internally-mixed citric acid and ammonium sulfate particles†
Craig S.
Sheldon
a,
Jack M.
Choczynski
a,
Katie
Morton
b,
Teresa
Palacios Diaz
b,
Ryan D.
Davis
 bc and
James F.
Davies
bc and
James F.
Davies
 *a
*a
aDepartment of Chemistry, University of California Riverside, Riverside, CA 92521, USA. E-mail: jfdavies@ucr.edu
bTrinity University, Department of Chemistry, San Antonio, TX 78212, USA
cSandia National Laboratories, Materials Reliability Department, Albuquerque, NM 87123, USA
First published on 27th October 2022
Abstract
Internally-mixed aerosol particles containing organic molecules and inorganic salts are prevalent in the atmosphere, arising from direct emission (e.g., from the ocean) or indirect production by condensation of organic vapors onto existing inorganic particle seeds. Aerosol particles co-exist with water vapor and, under humid conditions, will exist as dilute aqueous solution particles that can be well described by thermodynamic models. Under low humidity conditions, the increase in solute concentrations leads to molecular interactions and significant non-ideality effects that drive changes in important physical properties, such as viscosity and phase state, that are not predicted using simple models. Here, we explore a model system containing ammonium sulfate (AS) and citric acid (CA). We measure the hygroscopicity, viscosity, and rate of water diffusion in particles across a range of RH conditions and organic fractions to better understand the influence of organic–inorganic mixtures on particle properties. We report the RH dependence of these properties and explore the applicability of commonly used methods that connect them together, such as the Stokes–Einstein relationship and thermodynamic modelling methods. We show that at low RH, the addition of AS to CA leads to a reduction in the amount of water as indicated by the radial growth factor at a fixed RH, while observing an increase in the viscosity over several orders of magnitude. Contrary to the viscosity, only minor changes in water diffusion were measured, and analysis with the fractional Stokes–Einstein relationship indicates that changes in the molecular matrix due to the presence of AS could explain the observed phenomena. This work reveals that small additions of electrolytes can drive large changes in particle properties, with implications for chemical reactivity, lifetime, and particle phase that will influence the environmental impacts and chemistry of aerosol particles.
Environmental significanceInternally-mixed aerosol particles containing organic molecules and inorganic salts are prevalent in the atmosphere, arising from direct emission (e.g., from the ocean) or indirect production by condensation of organic vapors onto existing inorganic particle seeds. Aerosol particles co-exist with water vapor and, under humid conditions, will exist as dilute aqueous solution particles. As the humidity decreases, water is lost and the solute concentration increases, leading to potentially significant changes in particle properties as ion–molecule interactions begin to dominate and large changes in rheological properties can occur. Here, we explore a model system containing ammonium sulfate and citric acid and measure the hygroscopicity, viscosity, and rate of water diffusion in particles across a range of RH conditions and organic fractions. This work reveals that molecular interactions in internally-mixed organic–inorganic aerosol systems can give rise to deviations in physical properties that may have profound effects on the environmental impacts and chemistry of aerosol particles. |
1. Introduction
Aerosols in the atmosphere play an important role in regulating climate through their interactions with solar radiation and ability to nucleate clouds.1,2 In urban and indoor environments, aerosols contribute to reduced air quality and are strongly implicated in the spread of diseases via bacteria and viruses entrained within respiratory particles.3–6 In engineered applications, aerosols are used as a means of producing dry powders by spray drying,7 and aerosol methods are increasingly being used in spray-assisted nanoparticle formation.8,9 Central to the role of aerosols in all these fields are the physical and chemical properties of the constituent particles, such as their hygroscopicity, viscosity, and phase morphology, which all depend on the composition.10 Interactions with water vapor and other gas-phase chemical species play an important role in the evolving chemical composition of aerosol particles. In aerosol containing hygroscopic compounds, the extent of water at equilibrium is controlled by the environmental relative humidity (RH), which in turn controls the phase state of the particles, their rheological properties, such as viscosity, and the rate of molecular diffusion in the condensed phase.11–17The hygroscopicity of aerosols is typically measured from the size response of particles to changes in RH. Many methods have been developed that probe hygroscopicity on sub-micron and super-micron particles, and these studies have supported thermodynamic modelling efforts to predict hygroscopic growth based on the chemical composition.18–21 Frameworks have been developed to simplify the hygroscopic growth of aerosol particles into single parameters to allow predictions of the cloud-forming ability of an aerosol based on reduced composition metrics, such as the oxygen-to-carbon ratio of constituent organic molecules, which is easily measured using established aerosol mass spectrometry methods.22,23 While the hygroscopic growth of aerosols at high RH is the most reflective of cloud-forming ability, the hygroscopic growth at low RH (typically less than 50%) plays a more important role in regulating the physical properties of aerosol particles, such as viscosity and phase morphology. Phase transitions due to decreasing RH encompass liquid–liquid phase separation, efflorescence, and the formation of highly viscous and semi-solid amorphous states such as glasses and gels.
In bulk samples, viscosity can be measured using rheometric and flow-based techniques. However, bulk samples cannot generally represent the physical state adopted by the same material when in an aerosol due to the formation of supersaturated amorphous states at low RH. Unfortunately, measuring the viscosity of aerosol particles is much more challenging. Methods have been established to determine the viscosity of aerosols via coalescence,24 impaction,25 and fluorescence imaging.26 Single-particle levitation methods that allow the controlled coalescence of two particles have shown that the viscosity of an aerosol droplet can be measured over many orders of magnitude from the timescale for the particles to fully coalesce.27,28 These measurements and methods have contributed to our understanding of the formation of ultra-viscous and glassy states in organic aerosol particles found in the atmosphere. Recently, single-particle levitation methods have shown that, in particles containing both organic and inorganic materials, the molecular interactions can lead to significant changes in the viscosity compared to the predictions based on the individual components.29 This motivates a broader exploration of how the viscosity of organic–inorganic mixtures that represent atmospheric aerosols varies.
An important consequence of the increase in viscosity is that diffusion typically slows. The rate of diffusion of molecules within viscous aerosol particles regulates the timescales for equilibration with changing environmental conditions as it controls the rate of uptake and loss of volatile and semi-volatile species. Diffusion is also a major factor in the rate of chemical reactions, in particular heterogeneous reactions where oxidants impinge on the particle surface and diffuse inwards.30–32 The mixing of reactants and products by diffusion will impact the composition and phase morphology of the particle.33 There are several methods for probing diffusion in aerosol materials, although most have focused on the diffusion of water,16,34–38 and measurements of the rate of diffusion of other molecules in viscous media are much more limited.39–41 Measuring the rate of water diffusion is challenging because the viscosity, and therefore diffusion coefficient, is a strong function of the amount of water, and methods that perturb the number of water molecules to infer diffusivity must account for this concentration-dependent diffusivity. To get around this, isotope exchange methods have been used that maintain a constant water activity and measure the switch between H2O and D2O or other isotopically labelled compounds,16,36 although these methods may introduce other complications.
The rate of molecular diffusion is inversely related to the viscosity. The simplest relationship between these properties is the Stokes–Einstein (S–E) equation, formulated based on the assumption of a large sphere diffusing in a continuum. With small molecule diffusion, such as water, the S–E equation has been shown to be unreliable in predicating the diffusion coefficients due to the mismatch of the diffusing molecule size to the size of molecules in the matrix.36,40 Modifications to the S–E equation, such as the fractional S–E equation, attempt to resolve the limitations of the S–E approach, with generally successful outcomes across a wide range of chemical species.42,43 However, given the recent identification of highly viscous and gel states formed in simple mixtures of organic and inorganic components,29 the validity of S–E and a fractional S–E approach needs to be further tested.
In our earlier work measuring the diffusivity of water in mixed citric acid and ammonium sulfate particles, we showed that the addition of ammonium sulfate slowed the rate of diffusion at low humidity.38 The effect was small, around a factor of 2 to 3× at most, and was broadly rationalized by a predicted decrease in mole fraction of water present as the inorganic fraction increased. The measurements supporting these results involved determining the half-life for the response of a levitated particle to step changes in RH of 10, 20, and 30%. A diffusive mass transport model was used to infer the diffusivity as a function of composition over this range. While this method has been shown to be effective, the requirement for a time and spatially-resolved model to fully interpret the results limits its general applicability. In this work, we revisit the citric acid and ammonium sulfate system and provide a more comprehensive analysis of the physical properties of particles across a range of RH conditions. Firstly, we measure the rate of diffusion once again, in this case using a much smaller step change in RH. Compared to previous methods, a smaller step change will result in a much smaller perturbation of the particle. This leads to more difficulties in performing the measurements and interpreting the data (accuracy is improved, but precision is lessened), but will provide a more direct measure of the diffusivity of water at specific RH under conditions. Secondly, we measure the hygroscopic growth of mixed particles using single-particle levitation coupled with the dual-droplet method discussed in our earlier work.44 This allows small differences in hygroscopic growth to be resolved. Finally, we measure the viscosity of these particles across a range of compositions and RHs. The connection between diffusivity and viscosity has been explored and questioned in the literature, and the measurements we report here show additional complications by using viscosity to infer diffusion, at least for small molecules. Overall, this case study presents the first comprehensive analysis of three physicochemical properties in the same system under the same experimental conditions, allowing the connections between the properties to be investigated.
2. Methods
2.1 Sample preparation and chemicals
All chemicals in this study were purchased and utilized without additional purification. Hygroscopic growth, diffusion, and viscosity measurements were conducted on sample particles containing ammonium sulfate (AS) and citric acid (CA), using probe particles containing lithium chloride (LC) as a measure of the RH. Particles were generated following solvent evaporation from droplets produced using a microdroplet dispenser, as described in our previous work. Briefly, dilute aqueous solutions of total solute concentration in the range 4 to 6 g L−1 were prepared and transferred to a microdroplet dispenser. Solutions were made with molar mixing ratios of citric acid to ammonium sulfate of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 3
1, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, yielding organic mole fractions, xorg, of 0.5, 0.67, and 0.75, respectively. Individual droplets with diameters on the order of 50 μm were generated, and evaporation of excess solvent yielded particles of a size from 3 to 8 μm. A charge was induced on the droplets during their formation leading to a net charge on the resulting particles that allowed them to be levitated using electric fields.
1, yielding organic mole fractions, xorg, of 0.5, 0.67, and 0.75, respectively. Individual droplets with diameters on the order of 50 μm were generated, and evaporation of excess solvent yielded particles of a size from 3 to 8 μm. A charge was induced on the droplets during their formation leading to a net charge on the resulting particles that allowed them to be levitated using electric fields.
2.2 Particle levitation
Particles were levitated in a linear quadrupole electrodynamic balance (LQ-EDB) for extended periods of time using electric fields, as described previously and briefly here.45 Sample droplets were generated from a microdroplet dispenser in the presence of an induction electrode (operational voltage 200 to 500 V) to impart a net charge of 10 to 100 fC on the droplet as it was introduced to the LQ-EDB. A 532 nm laser with a 0.9 mm beam width and operating power of <5 mW was used to visually verify the trapping of droplets. Once the charged droplet was introduced into the quadrupole electrodes, the electric field generated by applied AC voltages confined the droplet to the central axis. The downward acting gravitational force and the drag force from an air flow (at 200 sccm) were balanced by a repulsive electrostatic force generated by an applied DC voltage (10 to 300 V) to a disk electrode in the center of the chamber. A CMOS camera was used to image the particles and stabilize the vertical position by varying the DC voltage through a PID feedback loop, programmed using LabVIEW software.The RH in the chamber was controlled by introducing a mixture of dry and humidified nitrogen. The RH was monitored using the dual-droplet method with LC as a probe particle. This method has been described in detail in our previous work.44 The probe acts as an accurate in situ measurement of the RH in the chamber and reflects both the magnitude of the RH and the time dependence of any changes. To achieve the dual-droplet configuration, two dispensers and two induction electrodes were used to introduce the sample and probe droplets into the LQ-EDB simultaneously. The probe and sample particles were periodically moved up and down in the trap to measure the broadband scattering spectra of both particles in a consecutive manner.
2.3 Broadband spectroscopy
A red LED was used to illuminate a single particle and the backscattered spectrum was collected by optical fibers and delivered to a spectrometer (Ocean Insight HR4000). Spectra were collected with a 1 s exposure time consecutively from both the probe and sample particles, with the particles switched every 10 s over the course of the experiment. Spectra contain reflected light from the LED and resonant light scattered by the spherical particle, at wavelengths commensurate with a standing wave propagating around the circumference. The wavelength position of these resonant peaks or whispering gallery modes depends on the size and optical properties of the particle. The spectra were analyzed offline to determine the wavelength positions of the peaks and were compared with Mie theory predictions using the algorithms of Preston and Reid to find the radius and real part of the complex refractive index (RI).46,47 To validate the size and RI results, full spectra were simulated using Mie theory and compared by eye to the experimental data allowing additional factors, such as peak width, to be used.2.4 Water diffusion measurements
To measure water transport within the sample, the particle was brought to the target RH and allowed to equilibrate. The equilibration time was determined based on the measured response times of the sample, which depends on the composition and size. Once the particle was fully equilibrated, the RH was raised or lowered in a 1% step, initiating either water uptake or loss, and the particle responded accordingly. To measure the response of a particle, the time dependence of single peaks in the Mie resonance spectrum was found and the half-life was determined by fitting a stretched-exponential function to the response using eqn (1):48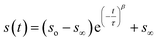 | (1) |
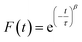 | (2) |
The numerical values of τ and β from either eqn (1) or (2) were used to find the half-life of the response according to:
t1/2 = |τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(0.5)β| ln(0.5)β| | (3) |
The half-life is directly related to the diffusion rate of water in the particle according to:34
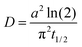 | (4) |
During these measurements and our previous work on this and similar chemical systems,38 it was noticed that over long periods of time, small upward changes in the wavelength of a resonance peak would occur. In our previous work, due to the larger RH change, the magnitude of the upward response was insignificant and could be reliably ignored. In this work, due to the smaller RH perturbation of 1%, measurements performed at low RH show a significant contribution to this upward change (Fig. S1A†). Although it is unclear what causes this effect, we speculate that it may be due to uptake of gas-phase basic compounds; the overall change to the particle composition is very small and we do not expect chemical changes to influence any of the results herein. To account for this effect and reveal the response of the particle due to RH changes alone, a linear function was fit to the wavelength versus time after the RH response was complete. This linear region was subtracted from the data to yield the RH response of the particle for subsequent analysis (Fig. S1B†).
2.5 Hygroscopic growth analysis
Hygroscopic growth measurements were performed to compare the relative composition of pure and mixed particles under experimental RH conditions. In these measurements, the dual-droplet approach, detailed in our earlier work, was used to establish the radial growth factor as a function of RH.44 Sample droplets were exposed to various RHs from dry conditions (0% RH) up to 50% across all particle compositions, in addition to pure CA. Selected mixing ratios were measured over a broader range of RHs, up to around 85%. Since all mixtures studied remained amorphous at 0% RH, the equilibrium radius measured at 0% was used as the reference dry radius to determine the radial growth factor. The equilibration time was sufficient to reduce the uncertainty in this value to no more than a few nm based on the trajectory of the size change with time.These measurements were performed using an RH probe droplet of LiCl, which deliquesces at 11% RH and has a known growth curve. The sample and probe were dried to effloresce the LiCl and establish the dry size of the sample droplet. The RH was then slowly raised up to the deliquescence RH of LiCl. This size of the LiCl particle at this point allows a precise measurement of the RH from the size of the LiCl particle under any RH condition and informs the chamber RH with an uncertainty <1%. The chamber RH was then increased in steps of 10%, and the size evolution of the probe and sample particles was recorded.
2.6 Viscosity characterization
To measure viscosity, two droplets of opposite polarity were simultaneously levitated and equilibrated at a fixed RH for a minimum of ten minutes. Droplets were subsequently merged by removing the top DC balance voltage, allowing the uppermost particle, charged with opposite polarity, to fall and coalesce with the lower particle. The merging process was captured using bright field and far-field imaging, as described in greater detail elsewhere.28 Brightfield images were binarized and the aspect ratio, which is the ratio of the long to short axis of the merged dimer, was tracked as a function of time. The viscosity of the merged dimer is directly proportional to the timescale of coalescence, which is determined from the characteristic e-folding time determined from an exponential fit to the plot of aspect ratio versus time.28 The time constant, τ, associated with coalescence is related to viscosity, η, according to:13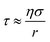 | (5) |
3. Results and discussion
3.1 Water transport in AS and CA particles
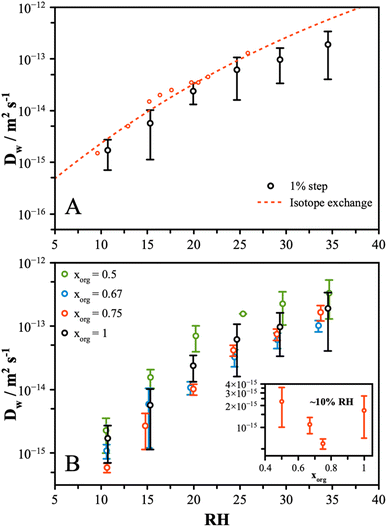
Water transport measurements were performed by tracking the particle response to a change in RH by 1%. The response of the particle was measured from the change in wavelength of a resonant peak in the Mie resonance spectrum. This method was applied to particles in the size range 5 to 7 μm and resulted in changes in peak positions of up to 1 nm. A typical normalized response curve is shown in Fig. S2A† for a 1% increase and decrease for pure CA at around 20% RH. The stretched exponential described by eqn (2) is fit to both transitions, and the half-life is determined by solving for t1/2 using eqn (3). Measurements were typically performed with an additional LiCl particle in the trap as a means of determining the RH and establishing the timescale for the step change in RH, which was found to occur with a half-life of ∼3 to 5 s (Fig. S2B†). This leads to an upper value for the diffusion coefficient that we can measure of approximately 5 × 10−13 m2 s−1, with faster rates of diffusion leading to particle responses that are limited by the rate of change of the RH in the gas phase.To compare this method and validate the results against previous measurements, we performed a rigorous set of measurements on pure CA particles. The diffusion coefficients were determined from the average of 5 repeat measurements at each RH, and the results are shown in Fig. 1A. The large standard deviation, on the order of ±50%, is attributed to random error associated with measuring such a small change in particle state during the 1% transition. However, the trend with RH is clearly captured, and a good agreement compared to the earlier isotope exchange measurements is observed.16 Other measurements of this system, reported by Preston et al.35 and Wallace et al.,50 also agree within error, although these are not shown to preserve clarity. These measurements indicate much faster water diffusion than early data reported by Lienhard et al.;37 however, these were extrapolated from low-temperature data and may not be fully comparable to the present measurements. Compared to similar methods that measure the response to a large step change in RH, this method allows for a more direct measure of diffusivity at a single-valued RH. For a large step change in RH, the half-life will be skewed to shorter times compared to a smaller change as a larger proportion of the change in the particle state will occur at a faster rate of diffusion. Thus, inferring the rate of diffusion from these kinds of experiments has limitations and necessitates a more in-depth modelling approach to extract information. The measurements and interpretation we present here, while simplified relative to earlier work, provide a useful set of data for comparing the changes across different conditions and particle compositions.
Having validated the approach, further measurements were performed on AS/CA mixtures with organic mole fractions, xorg, of 0.5, 0.67, and 0.75. Repeat measurements were performed showing the standard deviation to be broadly consistent with the pure CA measurements. The inferred diffusion coefficients are shown in Fig. 1B for each mixture and pure CA. While the measured values span up to an order of magnitude at each RH, the differences in D across the range of composition are small. At 10% RH, the rate of diffusion of water in the pure CA particle is faster than in mixtures containing small amounts of AS (see inset of Fig. 1B), with a “V”-shaped dependence. At the highest AS content, the diffusion rate is observed to be faster than pure CA. The slowest diffusion is consistently observed in the xorg of 0.67 and 0.75 mixtures and, although the uncertainties overlap, this behavior was seen for all measurements. To explore the differences between particle compositions more closely, instead of trapping a sample particle alongside a LiCl probe particle, measurements were made with pure CA and a mixture particle, with an xorg of 0.5 and 0.67. The 1% step change was initiated, and the response of the particles directly compared. Fig. S2† shows the resulting diffusion coefficient calculated from these measurements. These measurements confirm that at ∼10% RH, the pure CA particles respond at approximately same rate as the xorg = 0.5 mixture and slightly faster than the xorg = 0.67 mixture.
In our earlier work, the diffusivity was assessed using the Maxwell–Stefan framework and the experimental data were used, alongside the mixing rules and thermodynamic data derived from the AIOMFAC model, to infer the diffusivity.21,50,51 This decouples the diffusion of water from the diffusion of other species in the particle. However, it was concluded that the timescale for equilibration depends on the parameter D12, which does not show a strong dependence on the composition at a fixed RH. This agrees with our measurements, which show a variation only within the uncertainty of the measurement. When modelling the diffusion coefficient using the Maxwell–Stefan framework, the amount of water present plays an important role. However, the hygroscopic growth of these mixtures has not previously been measured. In the next section, we present new measurements of hygroscopic growth to compare against the modelling predictions of AIOMFAC. Furthermore, diffusion is typically correlated with viscosity, although many studies point towards how the Stokes–Einstein relationship breaks down when considering water diffusion. To explore how rheological properties of the particle connect with the rate of diffusion and hygroscopic growth, Section 3.3 will discuss new measurements using coalescence to determine the viscosity of AS/CA mixture.
3.2 Hygroscopic growth of AS and CA particles
The hygroscopic growth of AS/CA particles will influence the physicochemical properties due to the strong dependence diffusivity and viscosity on water content. Previously, the AIOMFAC model was used to predict the hygroscopicity of these mixtures.50,51 Here, we report measurements for the hygroscopic growth of mixed particles and compare these data to AIOMFAC predictions across the full RH range and, specifically, at low RH.Using the dual-droplet method with a LiCl particle as an RH probe, the radius of AS/CA particles was measured as a function of RH. To derive the dry size, particles were left under dry conditions for an extended period and the measured size was used to determine the radial growth factor. Measurements were performed on particles with xorg = 0.5, 0.67, and 0.75, with data reported in our earlier work used for pure CA.44Fig. 2A shows the radial growth factor as a function of RH. As expected, the radial GF increases more strongly with RH as the composition of the particle tends towards ammonium sulfate. Mixtures had similar growth factors at lower RH, namely, 10 and 20%. Above 20%, however, differences in hygroscopicity between mixtures gradually deviate from one another as AS becomes a more significant contribution to water uptake due to its greater hygroscopicity. We can determine the effective κ parameter, from κ-Kohler theory,23 from these data, and the results are shown in Fig. S4.† These data show that a fixed value of κeff is not able to capture the full dependence, although the general trend towards larger κeff with more AS is reproduced, at least at high RH. The volume-additive prediction of κeff using a value of 0.55 for AS and 0.23 for CA is shown for comparison.22 A trend towards an increased κeff as the RH decreases is not unusual, having been reported for a range of systems.22,44,53 The value of κeff reaches a maximum at around 40% RH and then decreases as the RH falls further. At low RH, the κeff decreases, indicating that the mixture is less hygroscopic than a simple mixing rule would predict. This is consistent with an increase in the extent of inter-molecular interactions due to more favorable solute–solute interactions than solute–solvent interactions.
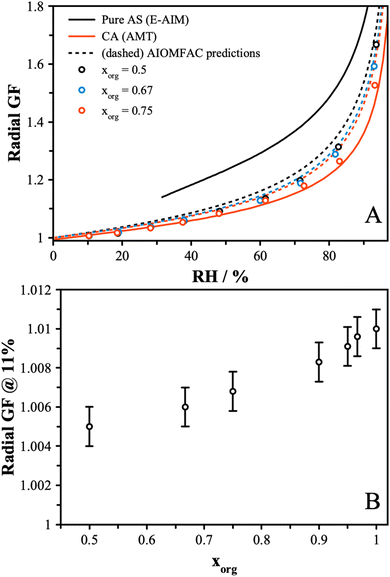 | ||
| Fig. 2 (A) Radial growth factors for mixed AS/CA and pure components. Points were measured in this study, while the solid lines represent pure CA hygroscopicity from our previous work and pure AS from the E-AIM model.44,52 The dashed lines represent the AIOMFAC predicted hygroscopicity of the mixtures, assuming a volume-additive density. (B) Radial growth factors of different mixing ratios of AS/CA particles at the deliquescence RH of LC (11%). The error bars reflect the uncertainty in particle size. A trend towards increasing hygroscopic size with increasing organic fraction is observed. | ||
We further compare our results to the output from the AIOMFAC model, as shown in Fig. 2A. While the measurements and model agree well for pure CA, when AS is added, the AIOMFAC predictions indicate a slightly larger growth factor at high RH. This may arise from how the density is treated to convert the AIOMFAC model output to a size-based parameter. To convert from the mass growth factor model output to a radial growth factor, a volume-additive density approach was used. The density of AS was taken to be 1.55 g cm−3 and the density of CA was 1.58 g cm−3. These values reflect the fact that the solutes are not in a crystalline form and are thus smaller than the respective crystalline densities.54 In general, the trend towards increased hygroscopic growth at high RH is observed and is consistent across both the model and measurement. At low RH, the AIOMFAC model also predicts that the radial GF will be larger as the amount of AS is increased. However, our measurements show a trend towards a smaller radial GF with increasing AS contribution. To show this more clearly, additional measurements were performed at a single RH equal to the deliquescence RH of LiCl (∼11% RH). The growth factor was determined for a finer range of mixing ratios of CA and AS, yielding the data shown in Fig. 2B. Here, a clear increase in the radial growth factor at 11% RH is observed as the organic fraction is increased. These results highlight the challenges of converting the mole fraction output of AIOMFAC to a radial growth factor, requiring assumptions of the aqueous density and the density of the dry particle state. Further unknowns in how the density varies with composition limit the applicability of a direct quantitative comparison between AIOMFAC and experimental observations.
In general, due to the larger value of the hygroscopicity parameter of AS compared to CA, an increase in radial growth factor would be expected when xorg decreases, which is counter to the observed behavior at low RH. The implications of this dependence on the particle properties will be discussed considering diffusion measurements in the prior section and viscosity measurements in the next section.
3.3 Viscosity of AS and CA particles
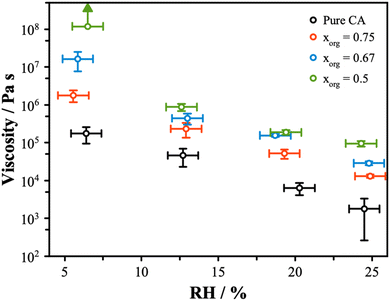
The viscosity is related to the composition and the amount of water present. Water acts as a plasticizer and will reduce viscosity, leading to a strong RH dependence on viscosity. The viscosity is related to the diffusivity, with the rates of diffusion predicted to be slower in highly viscous material from the Stokes–Einstein equation. Given our measurements of diffusion, a significant change in diffusivity is not expected. However, the hygroscopic growth data at low RH indicate that viscosity might show a change, as mixtures with lower xorg have less water. Using the coalescence method, measurements of the viscosity were obtained for the AS/CA mixtures across the RH range from ∼5% to 25%, as shown in Fig. 3. There is an increase in the coalescence timescale as the RH is decreased, consistent with an increase in viscosity. Furthermore, there is a clear increase in viscosity as xorg is reduced, with at least 3 orders of magnitude separating the viscosity of pure CA from the xorg = 0.5 mixture. This significant variation is unexpected based on diffusion measurements but correlates with the trend in radial growth factor at low RH, with less water correlated with increased viscosity.Recently, Jeong et al.55 described viscosity measurements of sucrose and ammonium sulfate mixtures, showing a decrease in viscosity observed as the organic fraction was reduced. This trend is opposite to our observations for the AS and CA systems and indicates that the unique behavior may be due to the molecular interactions that can result between carboxylic acid and carboxylate groups and electrolytes. Previous work has shown that the addition of certain electrolytes, in particular divalent cations, to organic solutions can result in significant increases in viscosity.29 This effect is attributed to the formation of a two-phase gel structure and typically coincides with a slowing of the rate of water transport as diffusion is limited to percolation of water through channels in the solid gel network. In the case of AS/CA, we do not observe clear evidence for a gel structure, as particles do eventually undergo full coalescence and Newtonian flow was observed in all instances. In gel particles, the rigid structure prevents full coalescence. Instead, we surmise that the reduction in the water content at low RH compared to pure CA contributes to an increased viscosity. Richards et al. showed that mixtures of other organic molecules with AS can show an increase in viscosity.28 In the case of AS/CA mixtures, interactions between NH4+ and negatively charged citrate may result in the expulsion of water from the particle, while also increasing the viscosity due to the more tightly bound molecules. While we see no evidence for long-range solid networks in this system, it is likely that ion–molecule interactions are still responsible for the observed increased viscosity with increasing inorganic content in AS/CA mixtures.
3.4 Connecting viscosity and diffusion
The amount of water plays an important role in defining the phase state and resulting properties of aerosol particles. However, based on the data we have presented here, under low RH conditions, there are non-linear changes that make empirical relationships between these properties challenging to derive and difficult to use. Traditionally, the Stokes–Einstein (S–E) relationship has been used to connect the viscosity and the diffusion coefficient: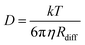 | (6) |
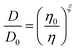 | (7) |
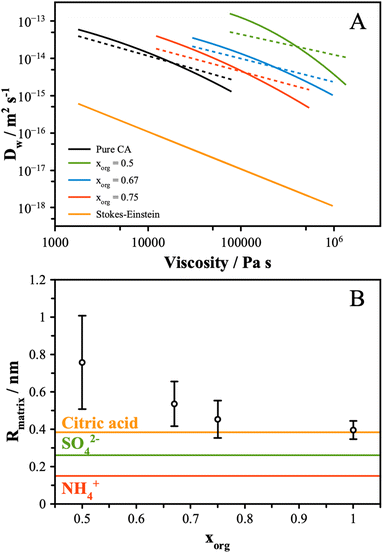 | ||
| Fig. 4 (A) The experimental data from Fig. 1B and 3 were interpolated and plot together (solid lines). The Stokes–Einstein prediction from eqn (6) is shown for reference. Using the fractional Stokes–Einstein approach (eqn (7)), a single-valued exponential factor, ξ, was determined and used to predict D versus viscosity (dash lines). (B) Eqn (8) was solved using the values of ξ reported in the text. The uncertainty reflects the range of ξ values that best fit the data. The molecular and ionic radii of citric acid and sulfate and ammonium ions, respectively, are indicated. | ||
These data indicate a couple of things regarding the AS/CA system at low RH. Firstly, as more AS is added and the viscosity gets larger, the deviation from S–E becomes more significant, as indicated by ξ getting smaller. We can relate ξ to the properties of the matrix in which water is diffusing using the expression:
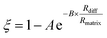 | (8) |
4. Conclusions
The physical properties of aerosol particles in the atmosphere at low RH control many of their impacts and chemical evolution. The hygroscopicity, viscosity, and rate of molecular diffusion in particles influence equilibration timescales, heterogeneous reaction kinetics, and phase morphology, which in turn influence their optical properties and chemical composition. Understanding how these properties are connected is vital towards applying simplified models to predict aerosol behavior. In this work, we have demonstrated a comprehensive approach using single-particle levitation to quantify the hygroscopic growth, viscosity, and rate of water diffusion in internally-mixed particles containing ammonium sulfate and citric acid across a range of mixing ratios. For a range of AS and CA mixtures, the rate of water diffusion was quantified from ∼10% to 35% RH and revealed that the addition of small amounts of AS led to a slowing of the rate of diffusion, while larger amount of AS led to a diffusion rate similar to that in pure CA. To explore these observations further, we have shown that the hygroscopic growth of CA is reduced due to the addition of small amount of AS at low RH, opposite to the trend observed in conditions above the deliquescence RH of AS, but consistent with the observed slowing of the rate of diffusion. Finally, we measured the viscosity in these mixtures, revealing significant changes due to the addition of AS, with orders of magnitude increases in viscosity seen with the addition of AS. Using the fractional Stokes–Einstein approach, an established framework for correcting for the assumptions of Stokes–Einstein, we have shown that the observations are consistent with the formation of molecular clusters likely formed due to favorable molecular interactions between citric acid and ammonium ions. While the molecular details cannot be resolved purely from these experiments, they motivate further studies to identify the molecular dynamics in this system to fully explain the observations.More broadly, this study points towards the necessity of treating aerosol systems containing both organic molecules and electrolytes with much more care than required for organic or inorganic aerosols alone. Along with recent studies showing the formation of semi-solid gel states, this work provides evidence that molecular interactions are responsible for significant diversions from the expected behavior that cannot be explained using simplified mixing rules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J.F.D. acknowledges the support of the NSF through grant CHE-2108004. R.D.D. acknowledges the support of the NSF through grant CHE-2107690. The authors thank Andreas Zuend for assistance in working with the AIOMFAC output analysis. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.References
- U. Lohmann and J. Feichter, Global Indirect Aerosol Effects: A Review, Atmos. Chem. Phys., 2005, 5(3), 715–737, DOI:10.5194/acp-5-715-2005.
- J. Haywood and O. Boucher, Estimates of the Direct and Indirect Radiative Forcing Due to Tropospheric Aerosols: A Review, Rev. Geophys., 2000, 38(4), 513–543, DOI:10.1029/1999rg000078.
- F. J. Kelly and J. C. Fussell, Air Pollution and Public Health: Emerging Hazards and Improved Understanding of Risk, Environ. Geochem. Health, 2015, 37(4), 631–649, DOI:10.1007/s10653-015-9720-1.
- C. C. Wang, K. A. Prather, J. Sznitman, J. L. Jimenez, S. S. Lakdawala, Z. Tufekci and L. C. Marr, Airborne Transmission of Respiratory Viruses, Science, 2021, 373(6558), eabd9149, DOI:10.1126/science.abd9149.
- K. A. Prather, L. C. Marr, R. T. Schooley, M. A. McDiarmid, M. E. Wilson and D. K. Milton, Airborne Transmission of SARS-CoV-2, Science, 2020, 370(6514), 303–304, DOI:10.1126/science.abf0521.
- W. Yang, S. Elankumaran and L. C. Marr, Relationship between Humidity and Influenza A Viability in Droplets and Implications for Influenza's Seasonality, PLoS One, 2012, 7(10), e46789, DOI:10.1371/journal.pone.0046789.
- R. Vehring, W. R. Foss and D. Lechuga-Ballesteros, Particle Formation in Spray Drying, J. Aerosol Sci., 2007, 38(7), 728–746, DOI:10.1016/j.jaerosci.2007.04.005.
- B. Buesser and S. E. Pratsinis, Design of Nanomaterial Synthesis by Aerosol Processes, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 103–127, DOI:10.1146/annurev-chembioeng-062011-080930.
- W. Wei, F. Bai and H. Fan, Surfactant-Assisted Cooperative Self-Assembly of Nanoparticles into Active Nanostructures, iScience, 2019, 11, 272–293, DOI:10.1016/j.isci.2018.12.025.
- B. R. Bzdek and J. P. Reid, Perspective: Aerosol Microphysics: From Molecules to the Chemical Physics of Aerosols, J. Chem. Phys., 2017, 147(22), 220901, DOI:10.1063/1.5002641.
- M. A. Freedman, Phase Separation in Organic Aerosol, Chem. Soc. Rev., 2017, 46(24), 7694–7705, 10.1039/c6cs00783j.
- C. Marcolli and U. K. Krieger, Relevance of Particle Morphology for Atmospheric Aerosol Processing, Trends Chem., 2020, 2(1), 1–3, DOI:10.1016/j.trechm.2019.11.008.
- J. P. Reid, A. K. Bertram, D. O. Topping, A. Laskin, S. T. Martin, M. D. Petters, F. D. Pope and G. Rovelli, The Viscosity of Atmospherically Relevant Organic Particles, Nat. Commun., 2018, 9(1), 956, DOI:10.1038/s41467-018-03027-z.
- F. H. Marshall, R. E. H. Miles, Y.-C. Song, P. B. Ohm, R. M. Power, J. P. Reid and C. S. Dutcher, Diffusion and Reactivity in Ultraviscous Aerosol and the Correlation with Particle Viscosity, Chem. Sci., 2016, 7(2), 1298–1308, 10.1039/c5sc03223g.
- J. F. Davies and K. R. Wilson, Nanoscale Interfacial Gradients Formed by the Reactive Uptake of OH Radicals onto Viscous Aerosol Surfaces, Chem. Sci., 2015, 6(12), 7020–7027, 10.1039/c5sc02326b.
- J. F. Davies and K. R. Wilson, Raman Spectroscopy of Isotopic Water Diffusion in Ultra-Viscous, Glassy and Gel States in Aerosol Using Optical Tweezers, Anal. Chem., 2016, 88(4), 2361–2366, DOI:10.1021/acs.analchem.5b04315.
- S. Bastelberger, Ra, U. K. Krieger, B. Luo and T. Peter, Diffusivity Measurements of Volatile Organics in Levitated Viscous Aerosol Particles, Atmos. Chem. Phys., 2017, 17(13), 8453–8471, DOI:10.5194/acp-17-8453-2017.
- C. Denjean, P. Formenti, B. Picquet-Varrault, E. Pangui, P. Zapf, Y. Katrib, C. Giorio, A. Tapparo, A. Monod, B. Temime-Roussel, P. Decorse, C. Mangeney and J. F. Doussin, Relating Hygroscopicity and Optical Properties to Chemical Composition and Structure of Secondary Organic Aerosol Particles Generated from the Ozonolysis of α-Pinene, Atmos. Chem. Phys., 2015, 15(6), 3339–3358, DOI:10.5194/acp-15-3339-2015.
- J. Duplissy and P. DeCarlo, Relating Hygroscopicity and Composition of Organic Aerosol Particulate Matter, Atmos. Chem. Phys., 2011, 11(3), 1155–1165, DOI:10.5194/acp-11-1155-2011.
- S. L. Clegg, J. H. Seinfeld and P. Brimblecombe, Thermodynamic Modelling of Aqueous Aerosols Containing Electrolytes and Dissolved Organic Compounds, J. Aerosol Sci., 2001, 32, 713–738 CrossRef CAS.
- A. Zuend, C. Marcolli, B. P. Luo and T. Peter, A Thermodynamic Model of Mixed Organic-Inorganic Aerosols to Predict Activity Coefficients, Atmos. Chem. Phys., 2008, 8(16), 4559–4593, DOI:10.5194/acp-8-4559-2008.
- A. M. J. Rickards, R. E. H. Miles, J. F. Davies, F. H. Marshall and J. P. Reid, Measurements of the Sensitivity of Aerosol Hygroscopicity and the κ Parameter to the O/C Ratio, J. Phys. Chem. A, 2013, 117, 14120–14131, DOI:10.1021/jp407991n.
- M. D. Petters and S. M. Kreidenweis, A Single Parameter Representation of Hygroscopic Growth and Cloud Condensation Nucleus Activity, Atmos. Chem. Phys., 2007, 7(8), 1961–1971, DOI:10.5194/acp-7-1961-2007.
- R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, The Transition from Liquid to Solid-like Behaviour in Ultrahigh Viscosity Aerosol Particles, Chem. Sci., 2013, 4(6), 2597–2604, 10.1039/c3sc50682g.
- A. Virtanen, J. Joutsensaari, T. Koop, J. Kannosto, P. Yli-Pirilä, J. Leskinen, J. M. Mäkelä, J. K. Holopainen, U. Pöschl, M. Kulmala, D. R. Worsnop and A. Laaksonen, An Amorphous Solid State of Biogenic Secondary Organic Aerosol Particles, Nature, 2010, 467(7317), 824–827, DOI:10.1038/nature09455.
- N. A. Hosny, C. Fitzgerald, C. Tong, M. Kalberer, M. K. Kuimova and F. D. Pope, Fluorescent Lifetime Imaging of Atmospheric Aerosols: A Direct Probe of Aerosol Viscosity, Faraday Discuss., 2013, 165, 343–356, 10.1039/c3fd00041a.
- R. M. Power and J. P. Reid, Probing the Micro-Rheological Properties of Aerosol Particles Using Optical Tweezers, Rep. Prog. Phys., 2014, 77(7), 074601, DOI:10.1088/0034-4885/77/7/074601.
- D. S. Richards, K. L. Trobaugh, J. Hajek-Herrera and R. D. Davis, Dual-Balance Electrodynamic Trap as a Microanalytical Tool for Identifying Gel Transitions and Viscous Properties of Levitated Aerosol Particles, Anal. Chem., 2020, 92(4), 3086–3094, DOI:10.1021/acs.analchem.9b04487.
- D. S. Richards, K. L. Trobaugh, J. Hajek-Herrera, C. L. Price, C. S. Sheldon, J. F. Davies and R. D. Davis, Ion-Molecule Interactions Enable Unexpected Phase Transitions in Organic-Inorganic Aerosol, Sci. Adv., 2020, 6(47), eabb5643, DOI:10.1126/sciadv.abb5643.
- A. M. Arangio, J. H. Slade, T. Berkemeier, U. P'oschl, D. A. Knopf and M. Shiraiwa, Multiphase Chemical Kinetics of OH Radical Uptake by Molecular Organic Markers of Biomass Burning Aerosols: Humidity and Temperature Dependence, Surface Reaction, and Bulk Diffusion, J. Phys. Chem. A, 2015, 119(19), 4533–4544, DOI:10.1021/jp510489z.
- M. Shiraiwa, M. Ammann, T. Koop and U. Pöschl, Gas Uptake and Chemical Aging of Semisolid Organic Aerosol Particles, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(27), 11003–11008, DOI:10.1073/pnas.1103045108.
- A. A. Wiegel, M. J. Liu, W. D. Hinsberg, K. R. Wilson and F. A. Houle, Diffusive Confinement of Free Radical Intermediates in the OH Radical Oxidation of Semisolid Aerosols, Phys. Chem. Chem. Phys., 2017, 19, 6814–6830, 10.1039/c7cp00696a.
- F. A. Houle, A. A. Wiegel and K. R. Wilson, Changes in Reactivity as Chemistry Becomes Confined to an Interface. The Case of Free Radical Oxidation of C30H62 Alkane by OH, J. Phys. Chem. Lett., 2018, 9(5), 1053–1057, DOI:10.1021/acs.jpclett.8b00172.
- D. L. Bones, J. P. Reid, D. M. Lienhard and U. K. Krieger, Comparing the Mechanism of Water Condensation and Evaporation in Glassy Aerosol, Proc. Natl. Acad. Sci, 2012, 109(29), 11613–11618, DOI:10.1073/pnas.1200691109.
- T. C. Preston, J. F. Davies and K. R. Wilson, The Frequency-Dependent Response of Single Aerosol Particles to Vapour Phase Oscillations and Its Application in Measuring Diffusion Coefficients, Phys. Chem. Chem. Phys., 2017, 19(5), 3922–3931, 10.1039/c6cp07711k.
- H. C. Price, B. J. Murray, J. Mattsson, D. O'Sullivan, T. W. Wilson, K. J. Baustian and L. G. Benning, Quantifying Water Diffusion in High-Viscosity and Glassy Aqueous Solutions Using a Raman Isotope Tracer Method, Atmos. Chem. Phys., 2014, 14(8), 3817–3830, DOI:10.5194/acp-14-3817-2014.
- D. M. Lienhard, A. J. Huisman, D. L. Bones, Y.-F. Te, B. P. Luo, U. K. Krieger and J. P. Reid, Retrieving the Translational Diffusion Coefficient of Water from Experiments on Single Levitated Aerosol Droplets, Phys. Chem. Chem. Phys., 2014, 16(31), 16677–16683, 10.1039/c4cp01939c.
- B. J. Wallace and T. C. Preston, Water Uptake and Loss in Viscous Aerosol Particles with Concentration-Dependent Diffusivities, J. Phys. Chem. A, 2019, 123(15), 3374–3382, DOI:10.1021/acs.jpca.9b00907.
- F. H. Marshall, T. Berkemeier, M. Shiraiwa, L. Nandy, P. B. Ohm, C. S. Dutcher and J. P. Reid, Influence of Particle Viscosity on Mass Transfer and Heterogeneous Ozonolysis Kinetics in Aqueous–Sucrose–Maleic Acid Aerosol, Phys. Chem. Chem. Phys., 2018, 20(22), 15560–15573, 10.1039/C8CP01666F.
- Y. Chenyakin, A. D. Ullmann, E. Evoy, L. Renbaum-Wolff, S. Kamal and K. A. Bertram, Diffusion Coefficients of Organic Molecules in Sucrose-Water Solutions and Comparison with Stokes-Einstein Predictions, Atmos. Chem. Phys., 2017, 17, 2423–2435, DOI:10.5194/acp-17-2423-2017.
- H. C. Price, J. Mattsson and B. J. Murray, Sucrose Diffusion in Aqueous Solution, Phys. Chem. Chem. Phys., 2016, 18, 19207–19216, 10.1039/c6cp03238a.
- E. Evoy, A. M. Maclean, G. Rovelli, Y. Li, A. P. Tsimpidi, V. A. Karydis, S. Kamal, J. Lelieveld, M. Shiraiwa, J. P. Reid and A. K. Bertram, Predictions of Diffusion Rates of Organic Molecules in Secondary Organic Aerosols Using the Stokes-Einstein and Fractional Stokes-Einstein Relations, Atmos. Chem. Phys., 2019, 1–24, DOI:10.5194/acp-2019-191.
- E. Evoy, S. Kamal, G. N. Patey, S. T. Martin and A. K. Bertram, Unified Description of Diffusion Coefficients from Small to Large Molecules in Organic–Water Mixtures, J. Phys. Chem. A, 2020, 124(11), 2301–2308, DOI:10.1021/acs.jpca.9b11271.
- J. M. Choczynski, R. Kaur Kohli, C. S. Sheldon, C. L. Price and J. F. Davies, A Dual-Droplet Approach for Measuring the Hygroscopicity of Aqueous Aerosol, Atmos. Meas. Tech., 2021, 1–24, DOI:10.5194/amt-2021-108.
- J. F. Davies, Mass, Charge, and Radius of Droplets in a Linear Quadrupole Electrodynamic Balance, Aerosol Sci. Technol., 2019, 53, 309–320, DOI:10.1080/02786826.2018.1559921.
- T. C. Preston and J. P. Reid, Accurate and Efficient Determination of the Radius, Refractive Index, and Dispersion of Weakly Absorbing Spherical Particle Using Whispering Gallery Modes, J. Opt. Soc. Am. B, 2013, 30(8), 2113–2122, DOI:10.1364/josab.30.002113.
- C. L. Price, A. Bain, B. J. Wallace, T. C. Preston and J. F. Davies, Simultaneous Retrieval of the Size and Refractive Index of Suspended Droplets in a Linear Quadrupole Electrodynamic Balance, J. Phys. Chem. A, 2020, 124(9), 1811–1820, DOI:10.1021/acs.jpca.9b10748.
- A. M. J. Rickards, Y.-C. Song, R. E. H. Miles, T. C. Preston and J. P. Reid, Variabilities and Uncertainties in Characterising Water Transport Kinetics in Glassy and Ultraviscous Aerosol, Phys. Chem. Chem. Phys., 2015, 17(15), 10059–10073, 10.1039/c4cp05383d.
- A. Rafferty, K. Gorkowski, A. Zuend and T. C. Preston, Optical Deformation of Single Aerosol Particles, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(40), 19880–19886, DOI:10.1073/pnas.1907687116.
- B. J. Wallace, C. L. Price, J. F. Davies and T. C. Preston, Multicomponent Diffusion in Atmospheric Aerosol Particles, Environ. Sci.: Atmos., 2021, 1(1), 45–55, 10.1039/D0EA00008F.
- A. Zuend, C. Marcolli, A. M. Booth, D. M. Lienhard, V. Soonsin, U. K. Krieger, D. O. Topping, G. McFiggans, T. Peter and J. H. Seinfeld, New and Extended Parameterization of the Thermodynamic Model AIOMFAC: Calculation of Activity Coefficients for Organic-Inorganic Mixtures Containing Carboxyl, Hydroxyl, Carbonyl, Ether, Ester, Alkenyl, Alkyl, and Aromatic Functional Groups, Atmos. Chem. Phys., 2011, 11(17), 9155–9206, DOI:10.5194/acp-11-9155-2011.
- S. L. Clegg, P. Brimblecombe and A. S. Wexler, A Thermodynamic Model of the System H-NH4-Na-SO4-NO3-Cl-H2O at at 298.15 K, J. Phys. Chem. A, 1998, 102, 2155–2171 CrossRef CAS.
- P. Zhao, S. Ge, J. Su, J. Ding and Y. Kuang, Relative Humidity Dependence of Hygroscopicity Parameter of Ambient Aerosols, J. Geophys. Res.: Atmos., 2022, 127(8), e2021JD035647, DOI:10.1029/2021JD035647.
- D. M. Lienhard, D. L. Bones, A. Zuend, U. K. Krieger, J. P. Reid and T. Peter, Measurements of Thermodynamic and Optical Properties of Selected Aqueous Organic and Organic-Inorganic Mixtures of Atmospheric Relevance, J. Phys. Chem. A, 2012, 116(40), 9954–9968, DOI:10.1021/jp3055872.
- R. Jeong, J. Lilek, A. Zuend, R. Xu, M. N. Chan, D. Kim, H. G. Moon and M. Song, Viscosity and Physical State of Sucrose Mixed with Ammonium Sulfate Droplets, Atmos. Chem. Phys., 2022, 22(13), 8805–8817, DOI:10.5194/acp-22-8805-2022.
- S. K. Kumar, G. Szamel and J. F. Douglas, Nature of the Breakdown in the Stokes-Einstein Relationship in a Hard Sphere Fluid, J. Chem. Phys., 2006, 124, 214501, DOI:10.1063/1.2192769.
Footnote |
| † Electronic supplementary information (ESI) available: Additional data figures demonstrating the methodology and analysis approach, data for the direct comparison of diffusion coefficient between mixtures of AS/CA, and hygroscopicity parameters for the mixtures. See DOI: https://doi.org/10.1039/d2ea00116k |
| This journal is © The Royal Society of Chemistry 2023 |