Open Access Article
Open Access ArticleSynthesis and structural, magnetic and spectroscopic characterization of iron(III) complexes with in situ formed ligands from methyl-2-pyridyl ketone transformations†‡
Sofia
Tzani
a,
Michael
Pissas
a,
Vassilis
Psycharis
 a,
Dimitrios A.
Pantazis
a,
Dimitrios A.
Pantazis
 b,
Yiannis
Sanakis
*a and
Catherine P.
Raptopoulou
b,
Yiannis
Sanakis
*a and
Catherine P.
Raptopoulou
 *a
*a
aInstitute of Nanoscience and Nanotechnology, NCSR “Demokritos”, 15310 Aghia Paraskevi, Athens, Greece. E-mail: i.sanakis@inn.demokritos.gr; c.raptopoulou@inn.demokritos.gr
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany
First published on 11th January 2023
Abstract
Reactions of methyl-2-pyridyl ketone, pyCOMe, with FeCl3·6H2O in various solvents gave complexes [Fe4Cl6(OMe)2(L1)2]·0.7MeCN·0.4MeOH (1·0.7MeCN·0.4MeOH) and [Fe3Cl4(bicine)(L2)]·Me2CO·0.2H2O (2·Me2CO·0.2H2O). The ligands (L1)2− = pyCO(Me)CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COpy (in 1) and (L2)2− = pyCO(Me)CH2CO(OMe)py (in 2) are formed in situ, through an aldol reaction-type mechanism between the carbanion pyC(O)CH2− (formed by the nucleophilic attack of the MeO− in pyCOMe) and pyCOMe which results in the formation of a new C–C bond. The intermediate compound undergoes attack in the –CH2– or –C
COpy (in 1) and (L2)2− = pyCO(Me)CH2CO(OMe)py (in 2) are formed in situ, through an aldol reaction-type mechanism between the carbanion pyC(O)CH2− (formed by the nucleophilic attack of the MeO− in pyCOMe) and pyCOMe which results in the formation of a new C–C bond. The intermediate compound undergoes attack in the –CH2– or –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O– group by a MeO− group, and the new ligands (L1)2− and (L2)2−, respectively, are formed. The molecular structure of 1 consists of three corner-sharing [Fe2O2] rhombic units in cis-arrangement. The two terminal FeIII ions display distorted square pyramidal geometry and the two central FeIII ions are distorted octahedral. The molecular structure of 2 consists of two corner-sharing [Fe2O2] rhombic units, with the two terminal FeIII ions in distorted square pyramidal geometry and the central FeIII in distorted octahedral. The differentiation in the coordination environment of the FeIII ions in 1–2 is reflected in the values of the Mössbauer hyperfine parameters. In agreement with theoretical calculations, the square pyramidal sites exhibit a smaller isomer shift value in comparison to the octahedral sites. Magnetic studies indicate antiferromagnetic interactions leading to an S = 0 ground state in 1 and to an S = 5/2 ground state in 2, consistent with Electron Paramagnetic Resonance spectroscopy. Mössbauer spectra of 2 indicate the onset of relaxation effects below 80 K. At 1.5 K the spectrum of 2 consists of magnetic sextets. The determined hyperfine magnetic fields are consistent with the exchange coupling scheme imposed by the crystal structure of 2. Theoretical calculations shed light on the differences in the electronic structure between the square pyramidal and the octahedral sites.
O– group by a MeO− group, and the new ligands (L1)2− and (L2)2−, respectively, are formed. The molecular structure of 1 consists of three corner-sharing [Fe2O2] rhombic units in cis-arrangement. The two terminal FeIII ions display distorted square pyramidal geometry and the two central FeIII ions are distorted octahedral. The molecular structure of 2 consists of two corner-sharing [Fe2O2] rhombic units, with the two terminal FeIII ions in distorted square pyramidal geometry and the central FeIII in distorted octahedral. The differentiation in the coordination environment of the FeIII ions in 1–2 is reflected in the values of the Mössbauer hyperfine parameters. In agreement with theoretical calculations, the square pyramidal sites exhibit a smaller isomer shift value in comparison to the octahedral sites. Magnetic studies indicate antiferromagnetic interactions leading to an S = 0 ground state in 1 and to an S = 5/2 ground state in 2, consistent with Electron Paramagnetic Resonance spectroscopy. Mössbauer spectra of 2 indicate the onset of relaxation effects below 80 K. At 1.5 K the spectrum of 2 consists of magnetic sextets. The determined hyperfine magnetic fields are consistent with the exchange coupling scheme imposed by the crystal structure of 2. Theoretical calculations shed light on the differences in the electronic structure between the square pyramidal and the octahedral sites.
Introduction
The role of organic ligands in coordination chemistry is of prime importance, because of the chemical nature of their donor atoms and/or binding groups which, in addition to the chemical properties of the metal ions, determine the stereochemical characteristics of the derived complexes. The complexation of an organic ligand around a metal ion affects its chemical properties, such as acidity, redox behaviour, electrophilic or nucleophilic character etc.1 In some cases, the organic ligands undergo chemical reactivity at specific active sites/groups upon coordination to metal ions, resulting in the formation, and therefore coordination, of new organic molecules, which would not be isolated without the presence of the metal ions. Thus, in these cases, the role of the metal ion is catalytic and the reaction of the in situ transformation of the organic precursor is metal-ion assisted. There are many factors that affect the reactivity of the ligands, which mainly depend on the electronic properties of the metal and the ligands, as well as the presence of co-ligands. Among metal-ion assisted chemical reactivity of organic ligands, the nucleophilic addition to the carbonyl group –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–, is very common. The difference in electronegativity between the C and O carbonyl atoms results in the polarization of the C
O–, is very common. The difference in electronegativity between the C and O carbonyl atoms results in the polarization of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond. Upon coordination of the carbonyl oxygen to a metal ion, the δ+ character of the carbonyl carbon atom is enhanced, and nucleophilic addition reactions by nucleophilic reagents, such as bases, are observed.
O double bond. Upon coordination of the carbonyl oxygen to a metal ion, the δ+ character of the carbonyl carbon atom is enhanced, and nucleophilic addition reactions by nucleophilic reagents, such as bases, are observed.
Carbonyl compounds of general formula R–CO–R′, have been widely used in coordination chemistry due to the rich chemical reactivity and coordination versatility of the carbonyl group. The size of the R and R′ groups play an important role because large groups impose steric hindrance and therefore make nucleophilic addition difficult. The chemical nature and the presence of donor atoms in the R and R′ groups also influence the coordination ability of the carbonyl compounds and their behaviour as ligands. The coordination chemistry of carbonyl compounds with R and R′ groups containing donor atoms, such as di-2-pyridyl ketone and 2,6-bis(2-pyridylcarbonyl)pyridine, with transition metal ions, has been extensively studied as they afford polynuclear complexes with interesting chemical and physical properties. In most of the cases, the ligands have been transformed due to nucleophilic addition reactions on the carbonyl group.2–4
Carbonyl compounds possessing only one substituent with donor atoms, such as phenyl-2-pyridyl ketone, pyCOPh, and methyl-2-pyridyl ketone, pyCOMe, have gained great attention also, because the electron-releasing and electron-withdrawing character of the methyl and phenyl groups, respectively, may affect their reactivity. Moreover, the methyl α-hydrogens adjacent to the carbonyl group in pyCOMe are polar and they are potential reaction sites, whereas pyCOPh lacks this possibility. Complexes which contain the ligand pyCOPh, such as the organometallic [FeII(pyCOPh)(CH3)2(Me3P)2] and [CoI(pyCOPh)(CH3)(Me3P)2],5 the trinuclear [MnII3(O2CPh)6 (pyCOPh)2],6 and the mononuclear [ZnIIX2(pyCOPh)2] (X = CF3SO3, Cl, Br, NCS),7 [CuII(pyCOPh)2(ClO4)2] and [CuII(pyCOPh)2(H2O)2](NO3)2,8 have been reported. Also complexes which contain in situ formed ligands due to nucleophilic addition reactions on the carbonyl group of pyCOPh, such as [CuII2(pyCOPh)2(pyC(OH)(O)Ph)2(H2O)](ClO4)2,9 [CuII4(OMe)2(NO3)4(pyCOPh)2(pyC(OMe)(O)Ph)2], [CuII2(NO3)2(pyC (OEt)(O)Ph)2(EtOH)] and [CuII2(NO3)2(pyC (CH2NO2)(O)Ph)2],1 [NiII(pyC(CH2CN)(O)Ph)2],10 and [ReVOX2(pyCH(O)Ph)(PPh3)] (X = Cl, Br),11 have been reported.
The coordination chemistry of pyCOMe with transition metal ions has been also investigated in detail and yielded complexes which contain the ligand in its present form, such as the mononuclear [MII(pyCOMe)2(H2O)2](NO3)2 (MII = Co, Ni, Cd),12 [CuI(pyCOMe)2] (ClO4),13 and [CuII(pyCOMe)2Cl2],14 and the coordination polymer [MnII(N3)2(pyCOMe)]n with 3D diamandoid network.15 Interesting in situ transformations of pyCOMe were observed in [CuII2{pyCOCH2C(CH3)(OH)py}2](ClO4)2 and [CuII4{pyCOCH2C (CH3)(O)py}2Cl4].13,14 The heptanuclear complex [CoIIICoII6(OH)6{pyC (CH3)(O)CH2COCH3}6](ClO4)3 contains another in situ formed ligand from the nucleophilic addition of the carbanion CH3COCH2− to pyCOMe. The carbanion is formed from the acetone solution due to the presence of the strong base NBun4OMe in the reaction. The heptanuclear complex displays single-molecule magnet behaviour and magnetization hysteresis loops below 0.04 K.16 Two in situ formed ligands from transformations of pyCOMe are reported in [CuII2Cl2{pyCOCH2C(CH3)(OH)py}2](ClO4)2 and [CuII2Cl2(L′)2(ClO4)2], where L′ is the zwitterionic-type molecule 3-hydroxy-1-methyl-3-(pyridine-2-yl)-3H-indolizin-4-ium.1
Inspired by the rich coordination chemistry of pyridyl ketone ligands and the variety of transformations leading to the in situ formation of new ligands, we have embarked into the investigation of the chemistry of these ligands in reactions with iron(III) sources. We present herein our results on the coordination chemistry of methyl-2-pyridyl ketone, pyCOMe, with iron(III) salts, complexes [Fe4Cl6(OMe)2(L1)2]·0.7MeCN·0.4MeOH (1·0.7MeCN·0.4MeOH) and [Fe3Cl4(bicine)(L2)]·Me2CO·0.2H2O (2·Me2CO·0.2H2O), where (L1)2− = pyCO(Me)CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COpy and (L2)2− = pyCO(Me)CH2CO(OMe)py were formed in situ from transformations of pyCOMe during the reactions. We present the synthesis, crystallographic characterization, magnetic studies and spectroscopic properties of 1 and 2 supported by theoretical calculations. These compounds give the opportunity to elaborate on the effect of factors such as the coordination mode on the electronic properties of a high spin FeIII ion.
COpy and (L2)2− = pyCO(Me)CH2CO(OMe)py were formed in situ from transformations of pyCOMe during the reactions. We present the synthesis, crystallographic characterization, magnetic studies and spectroscopic properties of 1 and 2 supported by theoretical calculations. These compounds give the opportunity to elaborate on the effect of factors such as the coordination mode on the electronic properties of a high spin FeIII ion.
Results and discussion
Synthesis and infrared characterization
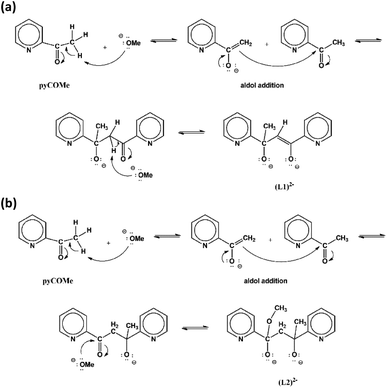
The equimolar reaction of FeCl3·6H2O with pyCOMe in the simultaneous presence of MeONa in MeCN/MeOH under reflux gave a red solution, which was layered with mixture of Et2O/n-hexane to afford compound [Fe4Cl6(OMe)2(L1)2]·0.7MeCN·0.4MeOH (1·0.7MeCN·0.4MeOH). The ligand (L1)2− = pyCO(Me)CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) COpy is formed in situ according to a simplified mechanism shown in Scheme 1a. According to a mechanism proposed recently,1 the strong electron-withdrawing character of the carbonyl double bond of pyCOMe polarizes the adjacent C–H bonds, therefore the methyl α-hydrogens become weakly acidic and are susceptible to attack by a strong base, such as MeO− which are present in the solution. The so-formed carbanion, pyC(O)CH2−, attacks the positive (δ+) carbonyl carbon of another pyCOMe molecule through an aldol reaction-type mechanism, resulting in the formation of a new C–C bond. The intermediate formed product contains one carbonyl group which polarizes the adjacent C–H bonds of the –CH2– group, and one of these methylene α-hydrogens is attacked by the strong base MeO− resulting in the formation of (L1)2−. Compound 1 can be prepared by the equimolar reaction of FeCl3·6H2O with pyCOMe in MeOH under reflux (Method B), i.e. in the absence of base MeONa. Therefore, the source of the MeO− which is important during the first stage for the formation of the carbanion pyC(O)CH2− is possibly the solvent of the reaction.
COpy is formed in situ according to a simplified mechanism shown in Scheme 1a. According to a mechanism proposed recently,1 the strong electron-withdrawing character of the carbonyl double bond of pyCOMe polarizes the adjacent C–H bonds, therefore the methyl α-hydrogens become weakly acidic and are susceptible to attack by a strong base, such as MeO− which are present in the solution. The so-formed carbanion, pyC(O)CH2−, attacks the positive (δ+) carbonyl carbon of another pyCOMe molecule through an aldol reaction-type mechanism, resulting in the formation of a new C–C bond. The intermediate formed product contains one carbonyl group which polarizes the adjacent C–H bonds of the –CH2– group, and one of these methylene α-hydrogens is attacked by the strong base MeO− resulting in the formation of (L1)2−. Compound 1 can be prepared by the equimolar reaction of FeCl3·6H2O with pyCOMe in MeOH under reflux (Method B), i.e. in the absence of base MeONa. Therefore, the source of the MeO− which is important during the first stage for the formation of the carbanion pyC(O)CH2− is possibly the solvent of the reaction.
The ligand (L1)2− has been reported previously during the synthesis of [Cu8Ln9(NO3)2(OH)10(L1)4(O2CMe)18(H2O)4](NO3)2(OH)3 (LnIII = Gd, Dy) from the in situ transformation of pyCOMe in MeCN/MeOH solutions. The proposed mechanism involves the nucleophilic attack of OH− to the methyl α-hydrogens of pyCOMe to yield the intermediate carbanion pyC(O)CH2−, followed by an aldol reaction-type mechanism to another molecule of pyCOMe which resulted in new C–C bond formation.17
The synthesis of H2L1 = 1,3-di(pyridine-2-yl)but-1-ene-1,3-diol, was reported by the reaction of 2-bromopyridine with pyCOMe in Et2O under nitrogen atmosphere at 0 °C. The ligand H2L1 was isolated as a yellow oil and characterized by microanalysis, 1H and 13C-NMR in CDCl3 solutions. Subsequent reaction of H2L1 with trans-[ReOCl3(PPh3)2] gave the complex [Re2O2Cl4(PPh3)2(L1)].18
The equimolar reaction of FeCl3·6H2O with pyCOMe in the simultaneous presence of bicine, N(CH2CH2OH)2CH2COOH, and MeONa in Me2CO/MeOH under reflux gave a red solution, which was layered with mixture of Et2O/n-hexane to afford compound [Fe3Cl4(bicine)(L2)]·Me2CO·0.2H2O (2·Me2CO·0.2H2O). The ligand (L2)2− = pyCO(Me)CH2CO(OMe)py is formed in situ according to a simplified mechanism shown in Scheme 1b. The carbanion pyC(O)CH2− formed by the nucleophilic addition of MeO− to pyCOMe attacks a neutral pyCOMe molecule according to the aldol reaction mechanism described above and affords the same intermediate product after the formation of the C–C bond. The intermediate compound contains one carbonyl group whose carbon atom is susceptible to nucleophilic attack by a MeO− resulting in the formation of (L2)2−.
The fully deprotonated ligand (L2)2− was reported previously in the study of complex [Cu4Cl4(L2)2] and it was formed in situ during the reaction of pyCOMe with CuCl in MeOH,13 and in the synthesis of the analogous complex [Cu4Br4(L2)4] from the in situ transformation of pyCOMe in MeOH in the presence of CuBr2 and cyclopentylamine.19
The ligand (HL2)− has been previously found in a dicopper complex, [Cu2(HL2)2](ClO4)2; it was suggested that the in situ formation of the ligand is facilitated by the oxidation of the metal ion from CuI to CuII.13,20
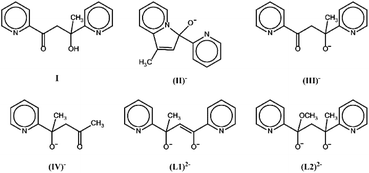
The new ligands derived from transformations of pyCOMe which are reported in the literature so far are shown in Scheme 2; the derived complexes are listed in Table 1.
In the infrared spectra of complexes 1–2 the strong bands at 1600–1400 cm−1 are attributed to the vibrations ν(C⋯C) and ν(C⋯N) of the pyridine rings of the ligands (L1)2− and (L2)2−. Pyridines have four ring breathing vibrations in the range 1600–1400 cm−1, at 1615–1585 cm−1, 1588–1560 cm−1, 1520–1465 cm−1 and 1438–1410 cm−1. In the infrared spectra of complexes 1–2 strong bands appear at ∼1600, ∼1565, ∼1480 and ∼1430 cm−1. In the infrared spectra of 2 and in the range 1600–1400 cm−1, the bands due to νas(COO) and νs(COO) stretching vibration of the coordinated carboxylato group of the ligand (bicine)3− are also expected; therefore, the assignment of the bands in the range 1600–1400 cm−1 is not completely feasible. The strong band at ∼1300–1290 cm−1 and the medium (1) or strong (2) band at ∼1020 cm−1 in the spectra of 1–2 are attributed to in plane hydrogen bending modes and ring vibration of the pyridine rings, respectively. The strong bands at ∼780 and ∼755 cm−1 in the spectra of 1–2 are attributed to the CH deformation of the o-substituted pyridine rings of the ligands. In the spectrum of 2, the medium intensity bands at 2964 and 2883 cm−1 are attributed to the asymmetric and symmetrical stretching vibration of the CH3 group, and the band at 2934 cm−1 is attributed to the CH2 group, of the ligand (L2)2− and/or (bicine)3−.21
Description of the structures
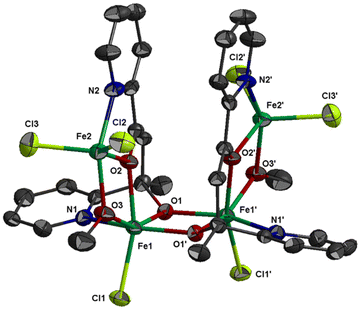
The molecular structure of 1 is shown in Fig. 1; selected bond distances are listed in Table 2. The complex crystallizes in the hexagonal space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c. The structure consists of tetranuclear entities [FeIII4Cl6(OMe)2(L1)2] and solvate molecules. The asymmetric unit cell contains half of the tetranuclear entity and partially occupied solvate molecules; the latter will not be discussed further due to disorder. The structure of 1 consists of three corner-sharing [FeIII2(OR)2] rhombic units in cis orientation as imposed by the C2 axis which is vertical to the central rhombic unit defined by atoms Fe(1)/O(1)/Fe(1′)/O(1′) (symmetry code (′) = −2/3 + y, 2/3 + x, 1/6 − z, two-fold axis within the ab plane). The interatomic FeIII⋯FeIII distance within each [FeIII2(OR)2] rhombic unit is Fe(1)⋯Fe(2) = 3.228(1) and Fe(1)⋯Fe(1′) = 3.165(1) Å. Each [FeIII2(OR)2] rhombic unit is coplanar within experimental error. The central rhombic unit defined by atoms Fe(1)/O(1)/Fe(1′)/O(1′) is almost perpendicular to the two terminal rhombic units defined by atoms Fe(1)/O(2)/Fe(2)/O(3) and their symmetric counterparts forming a dihedral angle between the best mean planes of 79.8°. The dihedral angle between the two terminal rhombic units is 20.3°. The interatomic distance between the two terminal FeIII ions is Fe(2)⋯Fe(2′) = 6.164 Å.
c. The structure consists of tetranuclear entities [FeIII4Cl6(OMe)2(L1)2] and solvate molecules. The asymmetric unit cell contains half of the tetranuclear entity and partially occupied solvate molecules; the latter will not be discussed further due to disorder. The structure of 1 consists of three corner-sharing [FeIII2(OR)2] rhombic units in cis orientation as imposed by the C2 axis which is vertical to the central rhombic unit defined by atoms Fe(1)/O(1)/Fe(1′)/O(1′) (symmetry code (′) = −2/3 + y, 2/3 + x, 1/6 − z, two-fold axis within the ab plane). The interatomic FeIII⋯FeIII distance within each [FeIII2(OR)2] rhombic unit is Fe(1)⋯Fe(2) = 3.228(1) and Fe(1)⋯Fe(1′) = 3.165(1) Å. Each [FeIII2(OR)2] rhombic unit is coplanar within experimental error. The central rhombic unit defined by atoms Fe(1)/O(1)/Fe(1′)/O(1′) is almost perpendicular to the two terminal rhombic units defined by atoms Fe(1)/O(2)/Fe(2)/O(3) and their symmetric counterparts forming a dihedral angle between the best mean planes of 79.8°. The dihedral angle between the two terminal rhombic units is 20.3°. The interatomic distance between the two terminal FeIII ions is Fe(2)⋯Fe(2′) = 6.164 Å.
| Symmetry operation: (′) −2/3 + y, 2/3 + x, 1/6 − z. | |||
|---|---|---|---|
| Fe(1)–O(3) | 1.981(3) | Fe(2)–O(2) | 1.962(3) |
| Fe(1)–O(1′) | 1.987(3) | Fe(2)–O(3) | 1.965(3) |
| Fe(1)–O(1) | 2.021(3) | Fe(2)–N(2) | 2.146(4) |
| Fe(1)–O(2) | 2.085(3) | Fe(2)–Cl(3) | 2.204(2) |
| Fe(1)–N(1) | 2.144(4) | Fe(2)–Cl(2) | 2.212(2) |
| Fe(1)–Cl(1) | 2.266(1) | Fe(1)⋯Fe(1′) | 3.165(1) |
| Fe(1)⋯Fe(2) | 3.228(1) | Fe(2)⋯Fe(1′) | 5.444(1) |
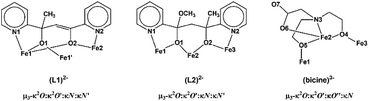
The four metal ions are held through the bridging provided by the oxygen atoms of two (L1)2− and two MeO− ligands, and the coordination of the ligands is characterized by the fact that the molecule possesses two-fold axis symmetry. Each (L1)2− ligand binds three metal ions, Fe(1), Fe(2) and Fe(1′), and adopts coordination mode described as μ3–κ2O:κ2O′:κN:κN′ (Scheme 3). The (L1)2− ligands chelate around Fe(1) and Fe(2) through the pyridine nitrogen and deprotonated alkoxo oxygen atoms, N(1)/O(1) and N(2)/O(2), respectively. Atoms O(1) and O(2) also bind Fe(1′) and Fe(1), respectively. The mean planes of the two pyridine rings of each (L1)2− ligand are almost vertical to each other forming a dihedral angle of 88.7°. The MeO− ligands bridge atoms Fe(1) and Fe(2). Therefore, the terminal rhombic units are formed via the bridging of the MeO− ligand (O(3)) and the deprotonated alkoxo atom O(2) whilst the central rhombic unit is formed via the bridging of the deprotonated alkoxo oxygen atoms O(1) and O(1′) belonging to two (L1)2− ligands. The coordination sphere of Fe(1′) and Fe(2′) has the same characteristics as Fe(1) and Fe(2), respectively, due to symmetry equivalence.
The coordination geometry of the central metal ions Fe(1) and Fe(1′) is distorted octahedral and consists of atoms N(1)/O(1)/O(2) of one (L1)2− ligand, atom O(1′) of the second (L1)2− ligand, atom O(3) of the MeO− ligand, and a chloro ligand, Cl(1). The Fe–O bond distances are in the range 1.981(3)–2.085(3) Å. The Fe–N and Fe–Cl distance are much longer at 2.144(4) and 2.266(1) Å, respectively. The two terminal metal ions, Fe(2) and Fe(2′), are five coordinated to atoms N(2)/O(2)/O(3) from a (L1)2− ligand and two chloro ligands, Cl(2) and Cl(3). The Fe–O bond distances are ∼1.96 Å, shorter than the respective bond lengths around the six coordinated Fe(1) and Fe(1′). The Fe–N and Fe–Cl bond distances are longer, 2.146(4) and ∼2.20 Å, respectively, as in the case of the central metal ions. The coordination geometry around Fe(2) and Fe(2′) is distorted square pyramidal with trigonality index, τ = 0.29 (τ is 0 for perfect sp and 1 for perfect tbp).22 The equatorial plane is defined by atoms N(2)/O(2)/O(3)/Cl(2) (largest deviation 0.40 Å for N(2)); the metal ion is displaced at 0.68 Å towards the apical atom Cl(3) which lies 2.89 Å above the equatorial plane.
The molecular structure of 1 is stabilized through the intramolecular π–π interactions developed between the almost parallel pyridine rings defined by atoms N(2) and N(2′) which belong to the two symmetry related (L1)2− ligands. The inter-centroid distance between the two rings is 3.634 Å and the dihedral angle between their mean planes is 7.3°. The tetranuclear entities are linked through intermolecular π–π interactions developed between the pyridine rings defined by N(1) and form chains extending parallel to the crystallographic c axis (the inter-centroid distance between the parallel rings is 4.086 Å, Fig. S1‡).
The molecular structure of 2 is shown in Fig. 2; selected bond distances are listed in Table 3. The complex consists of trinuclear entities [FeIII3Cl4(bicine)(L2)] and solvate molecules; the latter will not be discussed. The structure of 2 consists of two corner-sharing [FeIII2(OR)2] rhombic units defined by atoms Fe(1)/O(1)/Fe(2)/O(5) and Fe(2)/O(2)/Fe(3)/O(4). The interatomic FeIII⋯FeIII distance within each [FeIII2(OR)2] rhombic unit is Fe(1)⋯Fe(2) = 3.141(1) and Fe(2)⋯Fe(3) = 3.140(1) Å. Each [FeIII2(OR)2] rhombic unit is coplanar within experimental error. The interatomic distance between the two terminal metal ions is Fe(1)⋯Fe(3) = 5.690 Å. The three metal ions form an angle of 129.9°. The mean planes of the two corner-sharing [FeIII2(OR)2] rhombic units form dihedral angle 61.3°.
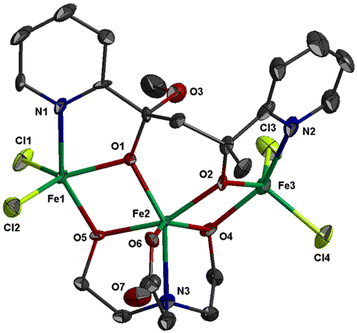 | ||
| Fig. 2 Thermal ellipsoid plot of 2 at 50% probability. Colour code: Fe, green; Cl, lime; O, red; N, blue; C, dark grey. Hydrogen atoms are omitted for clarity. | ||
| Fe(1)–O(5) | 1.958(4) | Fe(2)–O(2) | 2.011(4) |
| Fe(1)–O(1) | 1.970(4) | Fe(2)–N(3) | 2.217(6) |
| Fe(1)–N(1) | 2.121(6) | Fe(3)–O(2) | 1.950(4) |
| Fe(1)–Cl(1) | 2.215(2) | Fe(3)–O(4) | 1.995(5) |
| Fe(1)–Cl(2) | 2.223(2) | Fe(3)–N(2) | 2.098(6) |
| Fe(2)–O(6) | 1.950(5) | Fe(3)–Cl(4) | 2.214(2) |
| Fe(2)–O(4) | 1.987(4) | Fe(3)–Cl(3) | 2.224(2) |
| Fe(2)–O(1) | 2.004(4) | Fe(1)⋯Fe(2) | 3.141(1) |
| Fe(2)–O(5) | 2.007(5) | Fe(2)⋯Fe(3) | 3.140(1) |
The three metal ions are bridged through the deprotonated alkoxo oxygen atoms of one (L2)2− ligand, O(1) and O(2), and through the deprotonated alkoxo oxygen atoms of one bicine(3-) ligand, O(4) and O(5). Ligand (L2)2− binds the three metal ions and adopts coordination mode described as μ3–κ2O:κ2O′:κN:κN′ (Scheme 3). (L2)2− chelates around Fe(1) and Fe(3) through the pyridine nitrogen and deprotonated alkoxo oxygen atoms, N(1)/O(1) and N(2)/O(2), respectively. The oxygen atoms also bind the central metal ion Fe(2). The mean planes of the two pyridine rings of (L2)2− form dihedral angle 36.3°. The bicine(3-) ligand also binds the three metal ions and adopts coordination mode described as μ3–κ2O:κ2O′:κO′′:κN (Scheme 3).
The coordination geometry of the central metal ion, Fe(2), is distorted octahedral and consists of atoms N(3)/O(4)/O(5)/O(6) of the bicine(3-) ligand and atoms O(1)/O(2) of (L2)2− ligand. The Fe–O bond distances are in the range 1.950(5)–2.011(4) Å, whilst the Fe(2)–N(3) distance is much longer, 2.217(6) Å. The terminal metal ions, Fe(1) and Fe(3), are five coordinated and each binds two chloro ligands, one pyridine nitrogen and one alkoxo oxygen atoms of (L2)2− and one alkoxo oxygen atom of bicine(3-). The Fe–O bond distances are in the range 1.950(4)–1.995(5) Å, whilst the Fe–N and Fe–Cl are much longer, ∼2.11 and ∼2.22 Å, respectively. The coordination geometry around Fe(1) and Fe(3) is distorted square pyramidal with trigonality index τ = 0.33 and τ = 0.21, respectively. The equatorial plane around Fe(1) is formed via atoms N(1)/O(1)/O(5)/Cl(2) (largest deviation 0.40 Å for N(1)); the metal ion is displaced at 0.71 Å towards the apical atom Cl(1) which lies 2.93 Å above the equatorial plane. For Fe(3), the equatorial plane is formed via atoms N(2)/O(2)/O(4)/Cl(3) (largest deviation 0.32 Å for N(2)) with the metal ion being 0.63 Å above their mean plane towards the apical Cl(4) which is displaced at 2.84 Å.
The molecular structure of 2 is similar to the cation [Fe3Cl4{pyC(ph)O}4]+ which consists of two V-shaped corner-sharing [FeIII2(OR)2] rhombic units with Fe⋯Fe⋯Fe angle of ∼130°. Complexes 2 and [Fe3Cl4{pyC(ph)O}4][FeCl4] consist of two terminal FeIII ions with square pyramidal NO2Cl2 chromophore and one central FeIII ion with octahedral O5N chromophore in 2 and O4N2 chromophore in [Fe3Cl4{pyC(ph)O}4][FeCl4].23,24
In the lattice structure of 2, two centrosymmetrically related trinuclear entities are loosely held together due to π–π interactions developed between the pyridine rings with inter-centroid distance ∼4.41 Å and inter-planar angle 36.3°. Weak C–H⋯Cl interactions are also developed between the dimers (H(3)⋯Cl(3) (−x, 1 − y, 2 − z) = 3.136 Å, C(3)⋯Cl(3) = 4.072 Å, C(3)–H(3)⋯Cl(3) = 168.6°; Fig. S3‡).
Magnetic measurements
Variable-temperature magnetic dc-susceptibility studies of 1 and 2 were carried out. The χMT product from powder samples of 1 at 300 K is 8.04 cm3 K mol−1, significantly lower than the theoretically expected value for four non-interacting FeIII (S = 5/2) ions (∼17.5 cm3 K mol−1). When the temperature decreases, the χMT product decreases and reaches a value of 0.17 cm3 K mol−1 at 2 K. This overall behaviour is indicative of relatively strong antiferromagnetic exchange with diamagnetic ground state (Fig. 3). This behaviour is further corroborated by magnetization measurements at 2 K under 0–5 T applied magnetic field. The measured magnetization reaches the value of only 0.20μB at 5 T (Fig. S5‡) whereas the expected saturation molar magnetization, per formula unit, (fully aligned iron moments) is M = 4gSFe = 20μB (SFe = 5/2).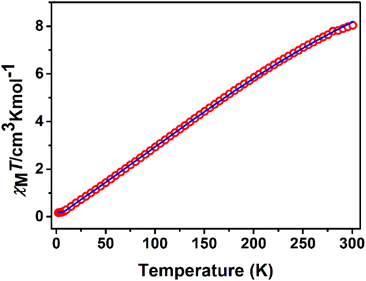 | ||
| Fig. 3 χ M T vs. T plot of 1 at 1 kOe. The solid line represents the best fit according to 2J model, see text for the fit parameters. | ||
The crystal structure of 1 consists of three corner-sharing rhombic units [FeIII2(OR)2] in cis orientation due to the crystallographic C2 axis passing through the central rhombic unit. The intramolecular Fe⋯Fe distances are Fe(1)⋯Fe(2) = 3.228(1) Å, Fe(1)⋯Fe(1′) = 3.165(1) Å and Fe(2)⋯Fe(1′) = Fe(1)⋯Fe(2′) = 5.444(1) Å. On the basis of this topology the data were fitted according to the spin Hamiltonian:
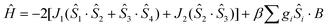 | (1) |
Broken-symmetry density functional theory (DFT) calculations gave J1 = −25.4 cm−1, J2 = −8.8 cm−1, in good agreement with the values determined by the analysis of the experimental magnetic data and compared to those observed in similar [FeIII4] complexes with O-bridges.25–29
The χMT product from powder samples of 2 at 300 K is 6.50 cm3 K mol−1, significantly lower than the theoretically expected value for three non-interacting FeIII (S = 5/2) ions (∼13.1 cm3 K mol−1). When the temperature decreases, the χMT product decreases reaching the value of 3.78 cm3 K mol−1 at 60 K, and then increases slightly to reach a maximum of 4.03 cm3 K mol−1 at 8 K. Below that temperature, the χMT product decreases rapidly to the value of 2.68 cm3 K mol−1 at 2.5 K (Fig. 4). The field-dependence of the magnetization was measured at 0–8 T applied magnetic field at 2.5 K (inset in Fig. 4). The magnetization curve shows a rapid increase up to ∼2 T and then increases smoothly to ∼4μB at 8 T. The crystal structure of 2 consists of two corner-sharing rhombic units [FeIII2(OR)2] with Fe⋯Fe interatomic distances Fe(1)⋯Fe(2) ≅ Fe(2)⋯Fe(3) ≅ 3.14 Å and Fe(1)⋯Fe(3) = 5.690 Å; the terminal ions Fe(1) and Fe(3) are bridged through the (L2)2− ligand. The experimental susceptibility and magnetization data were fitted by considering the magnetic exchange depicted in Scheme 4 and also the magnetic anisotropy (zero field splitting, zfs) of the FeIII ions, Di, according to the spin Hamiltonian:
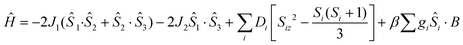 | (2) |
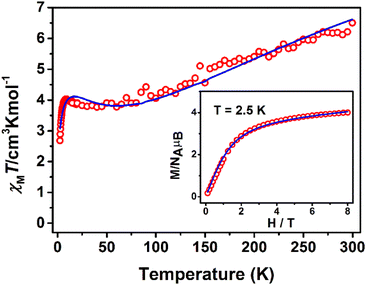 | ||
| Fig. 4 χ M T vs. T plot at 1 kOe and M vs. H at 2.5 K (inset) for 2. The solid lines represent the best fit according to 2J model, see text for the fit parameters. | ||
EPR spectroscopy
The X-band EPR spectrum of a powder sample of 2 at 4.2 K is shown in Fig. 5. The spectrum comprises a strong derivative like feature at 1500 G which corresponds to an effective g-value of 4.3. This feature is accompanied by a weak shoulder at ca. 700 G (geff = 9.0). This set of signals is compatible with an S = 5/2 spin system, in agreement with the analysis of the magnetic data. In this spin manifold the following spin Hamiltonian is applied: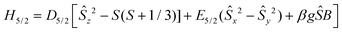 | (3) |
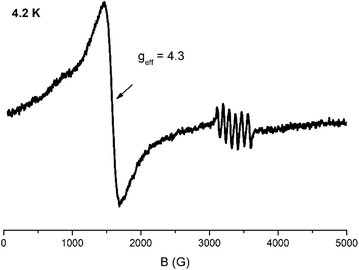 | ||
| Fig. 5 X-band EPR spectrum of a powder sample of 2 at 4.2 K. Microwave power 2 mW, modulation amplitude 25 Gpp, microwave frequency 9.42 GHz. | ||
Mössbauer spectroscopy
57Fe Mössbauer spectra from powdered samples of 1 and 2 were recorded at several temperatures in the range 1.5–295 K. The spectrum of 1 at 4.2 K consists of an asymmetric quadrupole doublet which can be simulated considering two sites with ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
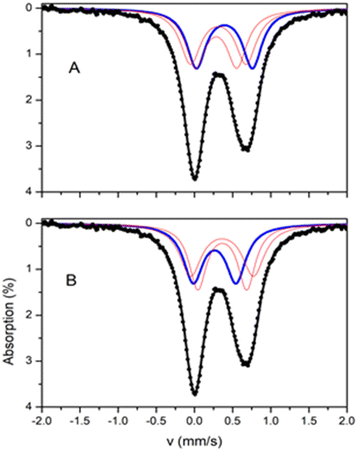
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 6). The two doublets agree with the presence of two different ferric sites [Fe(1)/Fe(1′)] and [Fe(2)/Fe(2′)] in terms of coordination environment and geometry. The Mössbauer parameters for sites I (red) and II (blue) are δ = 0.37 mm s−1 and ΔEQ = 0.51 mm s−1 for site I, and δ = 0.51 mm s−1 and ΔEQ = 0.56 mm s−1 for site II. These values are consistent with high-spin ferric ions (S = 5/2) in N/O/Cl coordination environment. The two sites differ significantly in the values of the isomer shift. DFT calculations were used in order to properly assign the doublets to the two different ferric ions based on the molecular structure. For the isomer shifts, the calculations yield a value of 0.368 mm s−1 for Fe(1), Fe(1′) and 0.465 mm s−1, for Fe(2), Fe(2′). Therefore, site I is assigned to the square pyramidal ions whereas site II is assigned to the octahedral ions. The smaller isomer shift values for the square pyramidal sites, indicate a more covalent character for these ions in comparison to the octahedral ions.32
1 (Fig. 6). The two doublets agree with the presence of two different ferric sites [Fe(1)/Fe(1′)] and [Fe(2)/Fe(2′)] in terms of coordination environment and geometry. The Mössbauer parameters for sites I (red) and II (blue) are δ = 0.37 mm s−1 and ΔEQ = 0.51 mm s−1 for site I, and δ = 0.51 mm s−1 and ΔEQ = 0.56 mm s−1 for site II. These values are consistent with high-spin ferric ions (S = 5/2) in N/O/Cl coordination environment. The two sites differ significantly in the values of the isomer shift. DFT calculations were used in order to properly assign the doublets to the two different ferric ions based on the molecular structure. For the isomer shifts, the calculations yield a value of 0.368 mm s−1 for Fe(1), Fe(1′) and 0.465 mm s−1, for Fe(2), Fe(2′). Therefore, site I is assigned to the square pyramidal ions whereas site II is assigned to the octahedral ions. The smaller isomer shift values for the square pyramidal sites, indicate a more covalent character for these ions in comparison to the octahedral ions.32
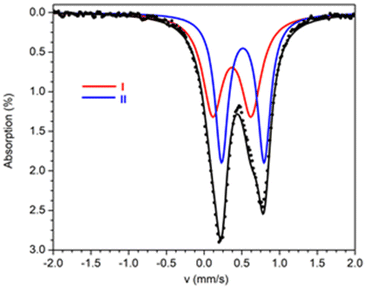 | ||
| Fig. 6 Mössbauer spectra from powdered samples of 1 at 4.2 K. The solid lines above the spectra are theoretical simulations. | ||
The 57Fe Mössbauer spectrum of 2 at room temperatures (Fig. 7) consists of an asymmetric quadrupole doublet with an average isomer shift of ∼0.33 mm s−1 which is indicative for high spin ferric ions. The crystal structure analysis showed that Fe(2) is octahedral with an [O5N] environment, whereas Fe(1) and Fe(3) are square pyramidal with an [NO2Cl2] environment. Moreover, the coordination for Fe(1) and Fe(2) slightly differ. On the basis of this differentiation the spectrum was simulated assuming three distinct sites at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Two different models, A and B, can be used in order to simulate the spectrum, with parameters listed in Table 4. The isomer shift depends on the type of ligands, therefore, Fe(1) and Fe(3) should have similar isomer shift values, distinct from this of Fe(2). The difference in the symmetry between Fe(1) and Fe(3) should be reflected in the values of the quadrupole splitting. For both fitting models, this differentiation is reflected on the results of the fitting procedure. For the two models, two doublets are characterized by almost equal δ and the third doublet has a distinctly different value with δmax − δmin ∼ 0.10 mm s−1. The two sites with equal δ have different ΔEQ. On the basis of these arguments the tentative assignment of the doublets to the specific iron sites, for each model, is this given in Table 4.
1 ratio. Two different models, A and B, can be used in order to simulate the spectrum, with parameters listed in Table 4. The isomer shift depends on the type of ligands, therefore, Fe(1) and Fe(3) should have similar isomer shift values, distinct from this of Fe(2). The difference in the symmetry between Fe(1) and Fe(3) should be reflected in the values of the quadrupole splitting. For both fitting models, this differentiation is reflected on the results of the fitting procedure. For the two models, two doublets are characterized by almost equal δ and the third doublet has a distinctly different value with δmax − δmin ∼ 0.10 mm s−1. The two sites with equal δ have different ΔEQ. On the basis of these arguments the tentative assignment of the doublets to the specific iron sites, for each model, is this given in Table 4.
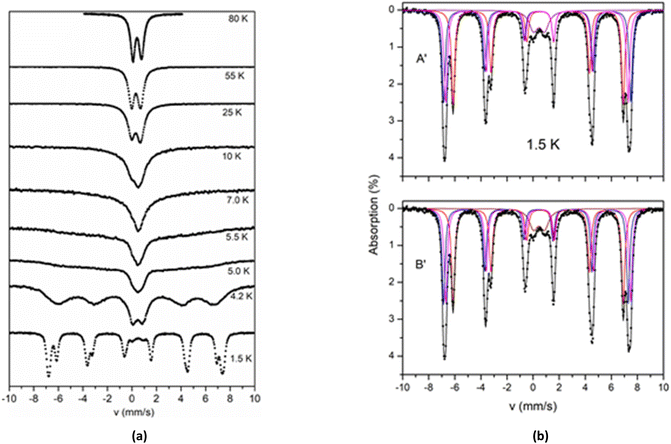
The spectra of 2 above 80 K exhibit similar behaviour apart from an increase of the average isomer shift due to the second order Doppler effect and an increase in the absorption due to the expected increase in the recoilless fraction f. The Mössbauer spectra of 2 collected at temperatures 1.5–80 K are shown in Fig. 8a. As the temperature decreases the spectra exhibit a characteristic broadening of the lines. The broadening is more severe below 10 K and at 4.2 K a six-line pattern is observed. This behaviour is indicative of magnetic relaxation effects.
In the 1.5 K spectrum, two well resolved sextets are observed. At this temperature a quadruple doublet is also present accounting for around 7% of total iron. This component is attributed to fast relaxing species (probably from excited states, still thermally occupied at 1.5 K) and is not discussed further. The crystal structure of 2 shows two kinds of ferric sites with ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The observation of two magnetic sextets at a 2
1. The observation of two magnetic sextets at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in the spectrum at 1.5 K indicates that the two different kinds of ferric sites are also magnetically non-equivalent. The simulation of the spectrum at 1.5 K was performed by assuming two models, A′ and B′, with parameters listed in Table 5. According to model A′, the major sextet can be simulated as the overlay of two sextets (II and III), with isomer shift δ = 0.38 mm s−1 and effective hyperfine fields that differ by around 1 T. According to model B′, the isomer shift of sextet II, δ = 0.46 mm s−1, is significantly larger than the value δ = 0.31 mm s−1 of the sextet III, and almost equal with the isomer shift of the minor sextet I (δ ∼ 0.46 mm s−1). The isomer shift of sextet III is remarkably smaller (0.31 mm s−1). The Mössbauer spectra at 1.5 K and the simulations according to models A′ and B′ are shown in Fig. 8b.
1 ratio in the spectrum at 1.5 K indicates that the two different kinds of ferric sites are also magnetically non-equivalent. The simulation of the spectrum at 1.5 K was performed by assuming two models, A′ and B′, with parameters listed in Table 5. According to model A′, the major sextet can be simulated as the overlay of two sextets (II and III), with isomer shift δ = 0.38 mm s−1 and effective hyperfine fields that differ by around 1 T. According to model B′, the isomer shift of sextet II, δ = 0.46 mm s−1, is significantly larger than the value δ = 0.31 mm s−1 of the sextet III, and almost equal with the isomer shift of the minor sextet I (δ ∼ 0.46 mm s−1). The isomer shift of sextet III is remarkably smaller (0.31 mm s−1). The Mössbauer spectra at 1.5 K and the simulations according to models A′ and B′ are shown in Fig. 8b.
| Model | Site | δ (mm s−1) |
B
eff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (T) b (T) |
2εa,c (mm s−1) | Γ , (mm s−1) | Areae (%) | Assignment |
|---|---|---|---|---|---|---|---|
a ±0.01 mm s−1.
b ±0.1 T.
c 2ε = (1/4)eQVzz(3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1 + η θ − 1 + η![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2φ) where e is the proton charge, Q is the 57Fe nuclear quadrupole moment, and Vzz and η are the principal component and the asymmetry parameter of the electric field gradient tensor. θ and φ are the polar and azimuthal angles that the hyperfine field makes with the principal axes of the electric field gradient tensor.
d Full width at half maximum.
e ±2.0%.
f ΔEQ = 0.84 ± 0.02 mm s−1. 2φ) where e is the proton charge, Q is the 57Fe nuclear quadrupole moment, and Vzz and η are the principal component and the asymmetry parameter of the electric field gradient tensor. θ and φ are the polar and azimuthal angles that the hyperfine field makes with the principal axes of the electric field gradient tensor.
d Full width at half maximum.
e ±2.0%.
f ΔEQ = 0.84 ± 0.02 mm s−1.
|
|||||||
| A′ | I | 0.47 | 40.6 | −0.16 | 0.31 | 31 | Fe(2) |
| II | 0.38 | 44.7 | −0.13 | 0.30 | 31 | Fe(1)/Fe(3) | |
| III | 0.38 | 43.6 | −0.18 | 0.30 | 31 | Fe(1)/Fe(3) | |
| IVf | 0.46 | — | — | 0.79 | 7 | ||
| B′ | I | 0.47 | 40.6 | −0.16 | 0.31 | 31 | Fe(2) |
| II | 0.46 | 44.2 | −0.13 | 0.29 | 31 | Fe(1)/Fe(3) | |
| III | 0.31 | 44.1 | −0.19 | 0.28 | 31 | Fe(1)/Fe(3) | |
| IVf | 0.45 | — | 0.79 | 7 | |||
The results from the analyses of the spectra at 295 and 1.5 K indicate that models A and A′ provide a consistent combination that accounts for the observations. According to this approach, the isomer shift of all sites increases at an amount of ca. 0.08 mm s−1, which is close to the increase expected because of the second order Doppler effect. In all other combinations, the isomer shift of at least one site does not decrease from room to liquid helium temperatures.
Theoretical calculations give the values δ = 0.466 mm s−1 for Fe(2) and δ = 0.378/0.371 mm s−1 for Fe(1)/Fe(3). These results corroborate the arguments presented above in support of the assumption that the octahedral site is characterized by the largest isomer shift in comparison with the isomer shift of the square pyramidal sites. The same results were obtained for the ferric sites of cluster 1.
The magnetic susceptibility data and X-band EPR spectroscopy of 2 indicate a ground state with S = 5/2. This is a consequence of the particular exchange coupling scheme imposed by the specific arrangement of the iron sites according to which the terminal iron sites, Fe(1) and Fe(3), are antiferromagnetically coupled to the central site Fe(2) leading to an S = 5/2 ground state. In the case that JFe1–Fe2 = JFe3–Fe2, and by application of standard spin coupling techniques,33,34 the effective hyperfine fields in the three sites are given by the relationships:
| Beff1,3 = 6/7B0,1,3 | (4) |
| Beff2 = −5/7B0,2 | (5) |
B 0,i (i = 1,2,3) is the internal field for the isolated ferric ion and relates to the ligand field environment.
On the basis of the above analysis according to model A′, site I is readily attributed to Fe(2). Considering the average value of Beff1,3, eqn (4) gives an average B0,1,3 = 51.5 T, whereas eqn (5) gives B0,2 = 56.9 T. The B0,i values are in the range expected for high spin ferric ions in an octahedral environment. The coordination environments of Fe(1) and Fe(3) are similar and distinct from this of Fe(2). Therefore, it can be anticipated that B0,1 ∼ B0,3 ≠ B0,2. DFT results suggest that B0,1,3ave < B0,2 with B0,1,3ave/B0,2 = 0.95. The calculated ratio B0,1,3ave/B0,2 is very close to the experimentally determined Beff1,3ave/Beff2 (= 0.90). The trend in B0,i parallels to the trend observed in the values of the isomer shift for which δ1,3 < δ2. This denotes the more covalent character for the square pyramidal ferric ions with respect to the octahedral in the present case.
For model A′ the effective fields Beff,1 and Beff,3 differ by 1.1 T. In the following we discuss possible reasons for this differentiation.
I. In the case of equal exchange coupling constants, JFe1–Fe2 and JFe3–Fe2, the coefficient 6/7 in eqn (4) is common for both Fe(1) and Fe(3) sites. If, however, the two exchange coupling constants differ, then the coefficients are not equal anymore; nevertheless, for small differences between JFe1–Fe2 and JFe3–Fe2, the average value is, still, 6/7. Such small differences between JFe1–Fe2 and JFe3–Fe2 cannot be revealed in the analysis of the magnetic susceptibility data (see above) that are insensitive on small variations.
II. On the other hand, if the environments of Fe(1) and Fe(3) are different (even slightly), then B0,1 ≠ B0,3 and subsequently Beff,1 ≠ Beff,3. The theoretical calculations yield B0,1 > B0,3 with |B0,1 − B0,3|/B0,1,3ave = 0.028. This value is very close to the value of 0.023 found for |Beff1 − Beff3|/Beff1,3ave as determined from the analysis of the Mössbauer spectra. On the basis of these calculations, in the model A′ approach (Table 5), sextet II with the largest magnetic field is attributed to Fe(1) and sextet III to Fe(3).
Therefore, the major contribution to the difference of 1.1 T in the effective hyperfine magnetic fields of the two square pyramidal sites stems from the differences in the internal magnetic fields B0,1 and B0,3 and not from possible differentiation of the exchange coupling constants, JFe1–Fe2 and JFe3–Fe2.
Concluding comments
The reaction of FeCl3·6H2O with methyl-2-pyridyl ketone, pyCOMe, in MeCN/MeOH gave complex [Fe4Cl6(OMe)2(L1)2] (1), whereas the same reaction mixture, in Me2CO/MeOH, in the simultaneous presence of bicine, gave complex [Fe3Cl4(bicine)(L2)] (2). The ligands (L1)2− and (L2)2− are formed in situ. A simplified mechanism involves the nucleophilic attack of the MeO− group in pyCOMe and the formation of the carbanion pyC(O)CH2−, which then reacts with pyCOMe and through an aldol-type reaction results in the formation of a new C–C bond. The intermediate formed is then attacked by a MeO− group in its –CH2– or –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O– group, thus leading to ligands (L1)2− and (L2)2−, respectively. X-ray crystal structure analysis of 1–2 revealed the presence of corner-sharing [Fe2O2] rhombic units and two types of FeIII ions based on their coordination geometry, i.e. five- and six-coordinate FeIII ions with distorted square pyramidal and distorted octahedral geometry, respectively.
O– group, thus leading to ligands (L1)2− and (L2)2−, respectively. X-ray crystal structure analysis of 1–2 revealed the presence of corner-sharing [Fe2O2] rhombic units and two types of FeIII ions based on their coordination geometry, i.e. five- and six-coordinate FeIII ions with distorted square pyramidal and distorted octahedral geometry, respectively.
The two distinct coordination environments for the ferric ions are reflected in the values of the Mössbauer hyperfine parameters, isomer shift, δ, (for 1 and 2) and internal hyperfine field, B0 (2). These parameters reflect the degree of covalency of the metal–ligand bonds and Mössbauer spectroscopy, corroborated by theoretical calculations, indicate that the two kinds of sites differ in this respect. The high spin FeIII sites in a square pyramidal environment are more covalent in comparison to the FeIII sites in an octahedral environment for both complexes. This agrees with the general trend that the covalency increases upon decrease of the coordination number.32
The strength of the antiferromagnetic exchange interactions in the FeIII dimers encountered in 1 and 2 is within the range found for such pairs. In the case of 2, the present work indicates that non-negligible exchange coupling can be mediated by the in situ formed (L2)2− and (bicine)3− ligands. For 2, the specific exchange coupling scheme, determined by the analysis of the magnetic data, is also reflected in the low temperature Mössbauer spectra that reveal two magnetically distinct ferric sites at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Further, theoretical calculations facilitated the clarification of the factors that may affect the fine details of the specific exchange coupling scheme.
1 ratio. Further, theoretical calculations facilitated the clarification of the factors that may affect the fine details of the specific exchange coupling scheme.
The coordination chemistry of pyCOMe has been proven very rich. In most of the cases, pyCOMe undergoes transformations due to the addition of nucleophiles to the carbonyl group, followed by aldol condensation reactions, which finally lead to new ligands. So far, six new ligands have been reported in the literature as a result of pyCOMe transformations, which probably occur after its complexation around the metal ions.1,13,14,16–20 Attempts to synthesize the new ligands in the absence of the metal ions, under strongly basic conditions, by varying several reaction parameters (e.g. reaction times, temperatures, solvents, reactant ratios and concentrations of the reaction solutions) have failed.1,16 A possible explanation might be that the metal ions are excellent electron acceptors which stabilize the coordinated intermediates thus facilitating the transformation reactions.14 Therefore, it appears that pyCOMe is an excellent pro-ligand which can be activated under various reaction conditions, in the presence of metal ions and combinations of them, in order to afford new types of ligands and complexes with novel metal topologies and physical properties. These perspectives are currently under investigation in our lab.
Experimental
General methods
All manipulations were performed under aerobic conditions using materials as received (Aldrich Co). All chemicals and solvents were of reagent grade. Elemental analysis for carbon, hydrogen, and nitrogen was performed on a PerkinElmer 2400/II automatic analyser. Infrared spectra were recorded at room temperature from powdered samples using the Attenuated Total Reflection (ATR) technique with a PerkinElmer Spectrum 100 FTIR spectrometer (4000–400 cm−1). Variable-temperature magnetic susceptibility and field dependent magnetization measurements were carried out on polycrystalline samples of 1 by using a SQUID magnetometer (Quantum Design MPMS 5.5) and of 2 by using the extraction method of ACMS option of the Quantum Design PPMS 9T. Diamagnetic corrections were estimated by using Pascal's constants. The program PHI was used to fit the magnetic data. Mössbauer spectra from powdered samples of 1 and 2 were recorded with a constant-acceleration conventional spectrometer with a source of 57Co (Rh matrix). Spectra in the 1.5–300 K range were obtained using a Janis cryostat. The spectra were analysed by using the program WMOSS (Web Research, Edina, MN). Isomer shift values (δ) are reported relative to iron foil at 293 K. X-band EPR measurements from powdered sample of 2 were carried out on an upgraded Bruker ER-200D spectrometer equipped with an Oxford ESR 9000 cryostat, an Anritsu MF76A frequency counter, and a Bruker 035 NMR Gaussmeter with the perpendicular mode standard cavity 4102ST, in the 4.2–65 K temperature range.Compound preparations
Method A. Methyl-2-pyridyl ketone, pyCOMe, (0.5 mmol, 56 μl) was added to a colourless solution of MeONa (0.5 mmol, 0.027 g) in MeCN/MeOH (20/5 mL) and stirred for 10 min. Solid FeCl3·6H2O (0.5 mmol, 0.1352 g) was added and the red solution was refluxed for 1 h. The final dark red solution was filtered off and layered with mixture of Et2O/n-hexane. Crystals of 1·0.7MeCN·0.4MeOH suitable for crystal structure determination were obtained after three weeks. The crystals were filtered off, dried in vacuo and analysed as solvent free. (Yield: 0.070 g, ∼60% based on the metal). C30H30Cl6Fe4N4O6 (1) fw = 978.68 requires C, 36.82; H, 3.09; N, 5.72%. Found: C, 36.72; H, 3.07; N, 5.69%. FT-IR (ATR, cm-1): 3360 (br), 1635(sh), 1601(vs), 1567(m), 1470(vs), 1452(vs), 1377(m), 1343(s), 1290(s), 1271(m), 1258(m), 1230(m), 1178(m), 1156(s), 1147(m), 1107(vs), 1094(vs), 1067(m), 1050(s), 1018(m), 934(m), 906(s), 886(m), 852(w), 785(s), 755(s), 710(m), 635(vs), 575(vs), 538(w), 493(m), 458(m).
Method B. Methyl-2-pyridyl ketone, pyCOMe, (0.5 mmol, 56 μl) was added to an orange solution of FeCl3·6H2O (0.5 mmol, 0.1352 g) in MeOH (20 mL). The red solution was refluxed for 1 h. X-ray quality crystals were obtained in closed vial after one week. The crystals were identified as 1 by unit cell determination (a = b = 34.147(5) Å, c = 21.902(3) Å, α = β = 90°, γ = 120°, V = 22116.43 Å3, see Table 6).
| 1·0.7MeCN·0.4MeOH | 2·Me2CO·0.2H2O | |
|---|---|---|
a w = 1/[σ2(Fo2) + (αP)2 + bP] and P = (max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fo2,0 + 2Fc2)/3, R1 = ∑(|Fo| − |Fc|)/∑(|Fo|) and wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2. Fo2,0 + 2Fc2)/3, R1 = ∑(|Fo| − |Fc|)/∑(|Fo|) and wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2.
|
||
| Formula | C31.8H33.7Cl6Fe4N4.7O6.4 | C24H32.4Cl4Fe3N3O8.2 |
| Fw | 1020.23 | 803.48 |
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| a (Å) | 34.0344(2) | 11.0768(2) |
| b (Å) | 34.0344(2) | 12.9640(2) |
| c (Å) | 21.8653(3) | 13.9148(3) |
| α (°) | 90.00 | 112.906(1) |
| β (°) | 90.00 | 101.930(1) |
| γ (°) | 120.00 | 105.515(1) |
| V (Å3) | 21934.2(4) | 1661.21(6) |
| Z | 18 | 2 |
| T (°C) | −103 | −113 |
| Radiation | Cu Kα 1.54178 | Cu Kα 1.54178 |
| ρ calcd, g cm−3 | 1.390 | 1.606 |
| μ, mm−1 | 12.726 | 13.743 |
| Reflections with I > 2σ(I) | 3032 | 3356 |
R
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0.0553 | 0.0557 |
wR2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0.1346 | 0.1115 |
Single crystal X-ray crystallography
Crystals of 1·0.7MeCN·0.4MeOH (0.07 × 0.12 × 0.64 mm) and 2·Me2CO·0.2H2O (0.13 × 0.17 × 0.34 mm) were taken from the mother liquor and immediately cooled to −103 °C (1) or −113 °C (2). Diffraction measurements were made on a Rigaku R-AXIS SPIDER Image Plate diffractometer using graphite monochromated Cu Kα radiation. Data collection (ω-scans) and processing (cell refinement, data reduction and Empirical/Numerical absorption correction) were performed using the CrystalClear program package.35 The structures were solved by direct methods using SHELXS v.2013/1 and refined by full-matrix least-squares techniques on F2 with SHELXL ver.2014/6.36 Important crystallographic and refinement data are listed in Table 6. Further experimental crystallographic details for 1·0.7MeCN·0.4MeOH: 2θmax = 130°; reflections collected/unique/used, 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 103/4124 [Rint = 0.1231]/4124; 287 parameters refined; (Δ/σ)max = 0.001; (Δρ)max/(Δρ)min = 0.586/−0.679 e Å−3; R1/wR2 (for all data), 0.0784/0.1583. Further experimental crystallographic details for 2·Me2CO·0.2H2O: 2θmax = 125°; reflections collected/unique/used, 21
103/4124 [Rint = 0.1231]/4124; 287 parameters refined; (Δ/σ)max = 0.001; (Δρ)max/(Δρ)min = 0.586/−0.679 e Å−3; R1/wR2 (for all data), 0.0784/0.1583. Further experimental crystallographic details for 2·Me2CO·0.2H2O: 2θmax = 125°; reflections collected/unique/used, 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930/5011 [Rint = 0.0830]/5011; 384 parameters refined; (Δ/σ)max = 0.002; (Δρ)max/(Δρ)min = 0.836/−0.981 e Å−3; R1/wR2 (for all data), 0.0911/0.1591. Hydrogen atoms were either located by difference maps and were refined isotropically or were introduced at calculated positions as riding on bonded atoms. All non-hydrogen atoms were refined anisotropically, except of the partially occupied solvate molecules which were refined isotropically with H-atoms not included in the refinement. Plots of the structure were drawn using the Diamond 3 program package.37
930/5011 [Rint = 0.0830]/5011; 384 parameters refined; (Δ/σ)max = 0.002; (Δρ)max/(Δρ)min = 0.836/−0.981 e Å−3; R1/wR2 (for all data), 0.0911/0.1591. Hydrogen atoms were either located by difference maps and were refined isotropically or were introduced at calculated positions as riding on bonded atoms. All non-hydrogen atoms were refined anisotropically, except of the partially occupied solvate molecules which were refined isotropically with H-atoms not included in the refinement. Plots of the structure were drawn using the Diamond 3 program package.37
Computational details
Quantum chemical calculations were used to probe the electronic structure and compute the magnetic and spectroscopic properties of the synthesized complexes. All calculations were performed with ORCA 5.38 The crystallographic models were employed directly, maintaining the coordinates of heavy atoms but optimizing the positions of hydrogens, which are crystallographically ill-defined. These calculations used the B3LYP functional39 in combination with the def2-TZVP basis sets for all atoms except C and H, for which def2-SVP was used.40 The resolution of the identity for Coulomb integrals was used in combination with SARC/J auxiliary basis sets (fully decontracted versions of def2/J for the present elements)41 and the chain-of-spheres approximation was applied for the treatment of exact exchange.42 Increased integration grids (DefGrid2 keyword in ORCA) and TightSCF settings were used for the geometry optimizations. Property calculations described in the following employed even finer grids (DefGrid3) and VeryTightSCF settings. Exchange coupling constants were computed using the broken-symmetry DFT approach.43–49 Appropriate broken-symmetry Kohn–Sham determinants were constructed with the FlipSpin keyword and the convergence to the correct solution was confirmed by inspection of the local spin populations of Fe ions. Extraction of pairwise exchange coupling constants followed standard established protocols described previously for complexes with three,50,51 and four,52,53 spin sites, with and without assumption of exchange pathway equivalence due to molecular symmetry. Antiferromagnetic coupling pathways were analysed by utilizing the corresponding orbital transformation and associated overlap integrals.54 For the calculation of core properties (Mössbauer and hyperfine parameters) the CP(PPP) basis set was used for Fe. Isomer shifts were deduced from the density at a given Fe nucleus following relationships described in the literature, adopting the published parameters that are appropriate for the present combination of functional and basis set.55Author contributions
Sofia Tzani: Investigation. Michael Pissas: Investigation, methodology, writing. Vassilis Psycharis: Investigation, methodology, writing. Dimitris A. Pantazis: Investigation, methodology, writing. Yiannis Sanakis: Investigation, methodology, writing-review and editing. Catherine P. Raptopoulou: Investigation, methodology, writing-review and editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
VP would like to thank the Special Account of NCSR “Demokritos” for financial support regarding the operation of the X-ray facilities at INN through the internal program entitled “Structural study and characterization of crystalline materials” (NCSR “Demokritos”, ELKE #10813). DAP acknowledges support by the Max Planck Society.References
- A. A. Kitos, C. G. Efthymiou, M. J. Manos, A. J. Tasiopoulos, V. Nastopoulos, A. Escuer and S. P. Perlepes, Dalton Trans., 2016, 45, 1063–1077 RSC.
- G. S. Papaefstathiou and S. P. Perlepes, Comments Inorg. Chem., 2002, 23, 249–274 CrossRef CAS.
- T. C. Stamatatos, C. G. Efthymiou, C. S. Stoumpos and S. P. Perlepes, Eur. J. Inorg. Chem., 2009, 3361–3391 CrossRef CAS.
- C. Stamou, W. Papawassiliou, J. P. Carvalho, K. F. Konidaris, V. Bekiari, P. Dechambenoit, A. J. Pell and S. P. Perlepes, Inorg. Chem., 2021, 60, 4829–4840 CrossRef CAS PubMed.
- R. Beck, U. Flörke and H.-F. Klein, Inorg. Chim. Acta, 2009, 362, 1984–1990 CrossRef CAS.
- C. Milios, T. C. Stamatatos, P. Kyritsis, A. Terzis, C. P. Raptopoulou, R. Vicente, A. Escuer and S. P. Perlepes, Eur. J. Inorg. Chem., 2004, 2885–2901 CrossRef CAS.
- C. Sudbrake and H. Vahrenkamp, Inorg. Chim. Acta, 2001, 318, 23–30 CrossRef CAS.
- S. Dey, S. Sarkar, E. Zangrando, H. Evans, J.-P. Sutter and P. Chattopadhyay, Inorg. Chim. Acta, 2011, 367, 1–8 CrossRef CAS.
- Y. Li and L. Jin, J. Cluster Sci., 2011, 22, 41–47 CrossRef CAS.
- A. Kitos, D. P. Giannopoulos, C. Papatriantafyllopoulou, L. Cuhna-Silva and S. P. Perlepes, Inorg. Chem. Commun., 2016, 64, 53–55 CrossRef CAS.
- B. Machura, J. Milek, R. Kruszynski, J. Kusz and J. Mrozinski, Polyhedron, 2008, 27, 1262–1269 CrossRef CAS.
- M. Tatucu, A. Kriza, C. Maxim and N. Stanica, J. Coord. Chem., 2008, 62, 1067–1075 CrossRef.
- M. G. B. Drew, J. P. Naskar, S. Chowdhury and D. Datta, Eur. J. Inorg. Chem., 2005, 4834–4839 CrossRef CAS.
- L. Álvarez-Miguel, I. Álvarez-Miguel, J. M. Martín-Álvarez, C. M. Álvarez, G. Rogez, R. García-Rodríguez and D. Miguel, Dalton Trans., 2019, 48, 17544–17555 RSC.
- R. Vicente, B. Bitschnau, A. Egger, B. Sodin and F. A. Mautner, Dalton Trans., 2009, 5120–5126 RSC.
- A. Kitos, C. Efthymiou, C. Papatriantafyllopoulou, V. Nastopoulos, A. Tasiopoulos, M. Manos, W. Wernsdorfer, G. Christou and S. P. Perlepes, Polyhedron, 2011, 30, 2987–2996 CrossRef CAS.
- J.-L. Liu, W.-Q. Lin, Y.-C. Chen, S. Gómez-Coca, D. Aravena, E. Ruiz, J.-D. Leng and M.-L. Tong, Chem. – Eur. J., 2013, 19, 17567–17577 CrossRef CAS PubMed.
- P. Mayer, E. Hosten, T. I. A. Gerber and A. Abrahams, Bull. Korean Chem. Soc., 2009, 30, 1204–1206 CrossRef CAS.
- X. Zhou, X.-F. Meng, W.-N. Li, C. Li and J.-J. Ma, Synth. React. Inorg., Met.-Org., Nano-Met. Chem., 2016, 46, 202–205 CrossRef CAS.
- C. Li, X.-F. Meng, W.-N. Li, X. Zhou and J.-J. Ma, Synth. React. Inorg., Met.-Org., Nano-Met. Chem., 2016, 46, 185–188 CrossRef CAS.
- L. J. Bellamy, The Infrared Spectra of Complex Molecules, Chapman and Hall, London, 1975 Search PubMed.
- A. W. Addison, N. T. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356 RSC.
- W.-Q. Chen, Y.-M. Chen, T. Lei, W. Liu and Y. Li, Inorg. Chem. Commun., 2012, 19, 4–9 CrossRef CAS.
- F. Di Salvo, M. Y. Tsang, F. Teixidor, C. Viñas, J. G. Planas, J. Crassous, N. Vanthuyne, N. Aliaga-Alcalde, E. Ruiz, G. Coquerel, S. Clevers, V. Dupray, D. Choquesillo-Lazarte, M. E. Light and M. B. Hursthouse, Chem. – Eur. J., 2014, 20, 1081–1090 CrossRef CAS PubMed.
- R. Herchel, I. Nemec, M. Machata and Z. Trávníček, Inorg. Chem., 2015, 54, 8625–8638 CrossRef CAS PubMed.
- E. N. Chygorin, O. V. Nesterova, J. A. Rusanova, V. N. Kokozay, V. V. Bon, R. Boča and A. Ozarowski, Inorg. Chem., 2012, 51, 386–396 CrossRef CAS PubMed.
- T. Weyhermüller, R. Wagner, B. Biswas and P. Chaudhuri, Inorg. Chim. Acta, 2011, 374, 140–146 CrossRef.
- T. Taguchi, T. C. Stamatatos, K. A. Abboud, C. M. Jones, K. M. Poole, T. A. O'Brien and G. Christou, Inorg. Chem., 2008, 47, 4095–4108 CrossRef CAS PubMed.
- A. K. Boudalis, F. Dahan, A. Bousseksou, J.-P. Tuchagues and S. P. Perlepes, Dalton Trans., 2003, 3411–3418 RSC.
- S. Tanase, E. Bouwman, G. J. Long, A. M. Shahin, R. de Gelder, A. M. Mills, A. L. Spek and J. Reedijk, Polyhedron, 2005, 24, 41–48 CrossRef CAS.
- U. Beckmann, E. Bill, T. Weyhermüller and K. Wieghardt, Eur. J. Inorg. Chem., 2003, 1768–1777 CrossRef CAS.
- N. N. Greenwood and T. C. Gibb, Mössbauer Spectroscopy, Chapman and Hall Ltd, London, 1971, pp. 1–660 Search PubMed.
- M. C. Kennedy, T. A. Kent, M. Emptage, H. Merkle, H. Beinert and E. Munck, J. Biol. Chem., 1984, 259, 14463–14471 CrossRef PubMed.
- E. Bill, C. Krebs, M. Winter, M. Gerdan, A. X. Trautwein, U. Flörke, H.-J. Haupt and P. Chaudhuri, Chem. – Eur. J., 1997, 3, 193–201 CrossRef CAS PubMed.
- Rigaku/MSC (2005), CrystalClear. Rigaku/MSC Inc., The Woodlands, Texas, USA Search PubMed.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed; (b) G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- DIAMOND – Crystal and Molecular Structure Visualization, Ver. 3.1, Crystal Impact, Rathausgasse 30, 53111, Bonn, Germany Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef.
- K. Yamaguchi, Chem. Phys. Lett., 1975, 33, 330–335 CrossRef CAS.
- K. Yamaguchi, M. Okumura, W. Mori, J. Maki, K. Takada, T. Noro and K. Tanaka, Chem. Phys. Lett., 1993, 210, 201–210 CrossRef CAS.
- M. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, Chem. Phys. Lett., 2006, 432, 343–347 CrossRef CAS.
- M. Orio, D. A. Pantazis and F. Neese, Photosynth. Res., 2009, 102, 443–453 CrossRef CAS PubMed.
- M. Orio and D. A. Pantazis, Chem. Commun., 2021, 57, 3952–3974 RSC.
- C. Baffert, M. Orio, D. A. Pantazis, C. Duboc, A. G. Blackman, G. Blondin, F. Neese, A. Deronzier and M.-N. Collomb, Inorg. Chem., 2009, 48, 10281–10288 CrossRef CAS PubMed.
- V. Krewald, F. Neese and D. A. Pantazis, J. Am. Chem. Soc., 2013, 135, 5726–5739 CrossRef CAS PubMed.
- D. A. Pantazis, M. Orio, T. Petrenko, S. Zein, E. Bill, W. Lubitz, J. Messinger and F. Neese, Chem. – Eur. J., 2009, 15, 5108–5123 CrossRef CAS PubMed.
- D. A. Pantazis, M. Orio, T. Petrenko, S. Zein, W. Lubitz, J. Messinger and F. Neese, Phys. Chem. Chem. Phys., 2009, 11, 6788–6798 RSC.
- F. Neese, J. Phys. Chem. Solids, 2004, 65, 781–785 CrossRef CAS.
- F. Neese, Inorg. Chim. Acta, 2002, 337, 181–192 CrossRef.
Footnotes |
| † This article is dedicated to our precious friend and colleague Prof. Spyros P. Perlepes on the occasion of his retirement. This article is part of the Spotlight collection entitled “Inorganic Chemistry in Greece”. |
| ‡ Electronic supplementary information (ESI) available: Intermolecular interactions in the structures of 1–2, and magnetization data of 1 (Fig. S1–S3). CCDC 2225058 and 2225059 for 1–2, respectively. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt03944c |
| This journal is © The Royal Society of Chemistry 2023 |