Open Access Article
Open Access ArticleCarbon vacancy-assisted stabilization of individual Cu5 clusters on graphene. Insights from ab initio molecular dynamics†
Lenard L.
Carroll
 a,
Lyudmila V.
Moskaleva
a,
Lyudmila V.
Moskaleva
 *a and
María Pilar
de Lara-Castells
*a and
María Pilar
de Lara-Castells
 *b
*b
aDepartment of Chemistry, University of the Free State, PO Box 339, Bloemfontein 9300, South Africa. E-mail: lyudmila.moskaleva@gmail.com
bInstitute of Fundamental Physics (AbinitSim Unit), Consejo Superior de Investigaciones Científicas (CSIC), E-28006 Madrid, Spain. E-mail: Pilar.deLara.Castells@csic.es
First published on 8th May 2023
Abstract
Recent advances in synthesis and characterization methods have enabled the controllable fabrication of atomically precise metal clusters (AMCs) of subnanometer size that possess unique physical and chemical properties, yet to be explored. Such AMCs have potential applications in a wide range of fields, from luminescence and sensing to photocatalysis and bioimaging, making them highly desirable for further research. Therefore, there is a need to develop innovative methods to stabilize AMCs upon surface deposition, as their special properties are lost due to sintering into larger nanoparticles. To this end, dispersion-corrected density functional theory (DFT-D3) and ab initio molecular dynamics (AIMD) simulations have been employed. Benchmarking against high-level post-Hartree–Fock approaches revealed that the DFT-D3 scheme describes very well the lowest-energy states of clusters of five and ten atoms, Cu5 and Cu10. AIMD simulations performed at 400 K illustrate how intrinsic defects of graphene sheets, carbon vacancies, are capable of confining individual Cu5 clusters, thus allowing for their stabilization. Furthermore, AIMD simulations provide evidence on the dimerization of Cu5 clusters on defect-free graphene, in agreement with the ab initio predictions of (Cu5)n aggregation in the gas phase. The findings of this study demonstrate the potential of using graphene-based substrates as an effective platform for the stabilization of monodisperse atomically precise Cu5 clusters.
1 Introduction
Atomically precise metal clusters (AMCs) of subnanometer size have attracted considerable attention in recent years, due to their molecule-like electronic structures that give rise to unique properties and quantum confinement effects. This makes them interesting materials for applications in nano- and bio-technology, including luminescence,1 sensing,2 bioimaging,3,4 theranostics,5–7 energy conversion,8,9 catalysis,10–13 and photocatalysis14 (see, e.g., ref. 15 and 16 for recent reviews). Furthermore, from a more fundamental point of view, it has been demonstrated how modification of popular materials such as TiO2 with AMCs can serve to investigate surface polaron properties, such as the photo-induced conversion of a small polaron into a large polaron, and to stabilize multiple surface polarons.17–19 Among the AMCs with less than 10 atoms, subnanometric copper clusters have been particularly well studied by different groups.20–22 For instance, it has been shown that these small clusters composed of only a few metal atoms are able to catalyze a range of chemical transformations; examples include the oxidation of CO,23,24 selective hydrogenation of olefins and carbonyl groups,25,26 C–X (X = C, N, S, P) cross-coupling reactions,27 partial oxidation of methane to methanol,28 and oxidative dehydrogenation of cyclohexene on Cu–Pd alloy clusters.22 Additionally, it has been observed21 that atomically precise copper clusters display remarkable chemical and thermodynamical stability in solution over a broad pH range, are resistant to irreversible oxidation,29 and are capable of enhancing the solar absorption of TiO2 and extending it into the visible region.30To reach their full potential for practical applications and widespread use as functional materials, AMCs must be fabricated reproducibly with simple and robust synthetic protocols. For certain applications, such as catalysis, as well as for fundamental studies of reactivity, it is desirable to produce AMCs without strongly binding ligands. In this case, the clusters can be stabilized, for example, by depositing them on solid supports. Highly oriented pyrolytic graphite (HOPG) has been widely used as an atomically flat and chemically inert substrate for growth or deposition of atomically precise metal clusters. Due to its very smooth surface and electrical conductivity, HOPG is an ideal support for specimens to be studied using electron spectroscopy and scanning tunneling microscopy (STM) techniques. For instance, HOPG has recently been used as a chemically-inert substrate to assist experimental measurements that have been interpreted as evidence on the reversible oxidation of HOPG-supported Cu5 clusters.29 In this work, we have considered a single graphene sheet supporting two Cu5 clusters as a model system of interacting AMCs adsorbed onto HOPG.
The relevance of graphene itself in nanomaterials research is well-established thanks to its remarkable properties such as the large surface area, high charge-carrier mobility, optical transparency, elasticity, and thermal conductivity.31 Based on some of these properties, such as the high conductivity and high specific surface area, excellent chemical stability and mechanical strength, graphene has been proposed as a material capable of improving the catalytic efficiency of supported metal nanoparticles.31 However, it is well known that potential applications of surface-supported small metal clusters (e.g., subnanometric metal clusters and even single-atom catalysts) can be compromised by their tendency to sinter into larger nanoparticles.32,33 Strategies to stabilize single atoms and clusters have been recently discussed in literature. In addition to anchoring them on suitable supports via strong particle-support interactions, other approaches have been applied, such as confinement (or encapsulation) in zeolites, MOFs, graphene and related 2D materials where AMCs can be coordinated with supports by covalent bonds but remain coordinatively unsaturated and active in catalysis.33–35 In one of the recently proposed methods, single metal atoms or clusters can be attached to the support by a so-called ‘nanoglue’ composed of oxide nanoparticles (e.g. ceria, titania) of less than 2 nm which themselves are dispersed on a suitable large surface area support (e.g. alumina, silica). The effectiveness of this method in confining and stabilizing single-atom Pt catalysts in SiO2-supported CeOx nanoglues has recently been demonstrated.36
Whereas strong metal–oxide interactions are beneficial for immobilization of the metal clusters and help protect them from sintering, strong interactions with the support modify physical and chemical properties of the AMCs, such as geometric shape, charge state, and reactivity.18,22,37–39 In the quest of achieving the stabilization of substrate-supported AMCs, here we investigate if intrinsic defects of graphene (carbon vacancies) are capable to confine and stabilize individual Cu5 clusters, while still leaving most of the metal atoms available for participating in reactive processes with environmental species. In fact, it has been previously shown that carbon vacancies alter the properties of graphene, leading to enhanced stability of supported metals.40–42 Previous works have proposed that graphene vacancies may be used to stabilize isolated metal clusters by notably increasing the adsorption energy of metal atoms and small metal clusters.43–47
This work also aims to investigate whether two Cu5 monomers can form Cu10 dimers on defect-free graphene above room temperature, as has recently been shown for gas-phase Cu5 clusters at zero temperature.48 To this end, we have conducted ab initio molecular dynamics (AIMD) simulations at 400 K on the interaction of two Cu5 clusters on defect-free and carbon-vacancies-containing monolayers of graphene. We utilize the dispersion-corrected DFT-D3 ansatz,49,50 which has previously been shown to provide good results for surface-supported coinage metal clusters when compared to high-level ab initio treatments and experimental data. For instance, its good performance was demonstrated for characterizing the interaction of an Ag2 cluster with graphene and TiO2 rutile (110) surface in ref. 51 and 52. The DFT-D3 approach has also been applied to optimize the structures of Cu5/TiO2(110) and Ag5/TiO2(110) supported clusters in order to calculate UV-Vis spectra of the AMCs-modified surfaces, with good agreement to diffuse reflectance spectroscopic measurements (see ref. 17 and 30). To further assess the DFT-D3 scheme's ability to account for ACM–ACM interactions, this work compares the energetic and structural aspects of gas-phase Cu5 and Cu10 clusters using the DFT-D3 scheme and higher levels of ab initio theory.
The article is structured as follows. In Section 2 we provide a detailed description of the computational methods. Results are presented in Section 3 as follows: first, we compare basic structural and energetic aspects of gas-phase Cu5 and Cu10 clusters at zero temperature obtained with the DFT-D3 scheme, multireference Rayleigh Schrödinger (second-order) perturbation theory53 denoted as RS2C, the domain-based pair natural orbital coupled-cluster approach DLPNO-CCSD(T),54 and Møller–Plesset perturbation theory (MP2). Second, we discuss the ab initio molecular dynamics (AIMD) simulations on the dimerization process of two Cu5 clusters on defect-free graphene at 400 K. Third, AIMD simulations are presented to evidence the stabilization of individual Cu5 clusters on a graphene sheet containing carbon vacancies at 400 K. Finally, our findings are summarized and conclusions are presented in Section 4.
2 Methods
2.1 Electronic structure calculations on unsupported and circumpyrene-supported Cu5 monomer and the Cu10 dimer
To account for dispersion interaction forces in DFT, the dispersion-corrected DFT-D3(BJ) ansatz has been chosen,49,50 given its good performance in describing the adsorption of the silver dimer (Ag2) on graphene.51 Specifically, this scheme involves applying the Perdew–Burke–Ernzerhof (PBE) density functional55 and the Becke-Johnson (BJ) damping50 for the D3 dispersion correction. DFT-D3 calculations have been carried out using density-fitting (DF) as implemented in the last version of the MOLPRO code.56 Based on previous benchmarking on the adsorption of the Ag2 dimer on benzene and coronene,51 the atom-centered (augmented) polarized correlation-consistent triple-ζ cc-pVTZ-PP basis set (denoted as AVTZ-PP) has been chosen for copper atoms,57 including a small (10-valence-electron) relativistic pseudopotential. As a point of comparison, the cc-pVTZ-PP basis set (denoted as VTZ-PP) has also been used following a previous study,48 as well as the all electron def2-TZVPP and def2-QZVPP58 basis sets.In order to assess the performance of the DFT-D3 approach, we have applied an ab initio multireference perturbation theory method. Specifically, density-fitting single-state multi-configurational self-consistent-field (DF-CASSCF) calculations have been carried out to account for the most important non-dynamical correlation effects. Next, the (density-fitting) internally contracted multireference Rayleigh Schrödinger (second-order) perturbation theory DF-RS2C method53 has been applied to cover the dynamical correlation. The RS2C method is a modified version of CASPT2 (complete active space with second-order perturbation theory) developed by Celani and Werner,53 using CASSCF wave functions as a reference in the RS2C calculations. For density-fitting (DF), JKFIT and MP2FIT basis sets have been used in DF-CASSCF and subsequent DF-RS2C calculations. Based on a previous study applying the DF-RS2C method with the VTZ-PP basis set on optimized structures at the DF-CASSCF lvel,48 an active space of 7 electrons in 7 orbitals [denoted as (7,7)] has been chosen in our DF-RS2C calculations of Cu5 clusters, using the AVTZ-PP basis set on structures optimized at the DF-RS2C level. This active space has been enlarged to 10 electrons in 10 orbitals [denoted as (10,10)] in order to characterize the Cu10 dimer. These active spaces included the 4s orbitals of all Cu atoms.
Relative energies of the different Cu5 isomers and interaction energies between two Cu5 clusters have been estimated considering fully optimized structures at the same level of theory. The interaction energy was calculated as the difference between the energy of the Cu10 dimer in the energetically most favored structure and two times that calculated for the lowest-energy Cu5 isomer. Additionally, for comparison, the domain-based pair natural orbital coupled-cluster approach DLPNO-CCSD(T),54 as implemented in the ORCA suite of programs59–61 (version 5.0.1), was used to perform single-point energy calculations on the geometries optimized at the second order Møller–Plesset perturbation theory (MP2) and DFT-D3 levels with the ORCA code.
Preliminary DLPNO-CCSD(T) calculations were also carried out to assess the performance of the DFT-D3 approach in describing the interaction between the copper cluster and the carbon support. For this purpose, circumpyrene was selected as a molecular model of graphene, using the VTZ-PP and AVTZ-PP basis sets.
2.2 Electronic structure calculations on the interaction between graphene-supported Cu5 clusters
Periodic electronic structure calculations were performed using spin-polarized DFT implemented in the Vienna Ab initio Simulation Package (VASP 5.4.4),62,63 following a similar computational approach to that reported in previous work on the Ag2–graphene interactions51 as well as in a systematic analysis of noble-gas atoms on the same surface.64 Electron-ion interactions were described by the projector augmented-wave method,63,65 using PAW–PBE pseudopotentials as implemented in the VASP code (treating C 2s2p and Cu 3d4s orbitals as valence electrons). A plane-wave basis set with a kinetic energy cutoff of 415 eV was used. The Methfessel-Paxton order 1 smearing scheme66 was employed with a smearing of 0.05 eV to account for partial occupancies, and the Brillouin zone was sampled using a 5 × 5 × 1 Monkhorst–Pack mesh.67 The convergence threshold criterion was set to 10−6 eV for the self-consistent electronic minimization. Geometries were relaxed with a force threshold of 0.02 eV Å−1.The graphene substrate was modelled using a p(6 × 10) supercell characterizing a single graphene sheet, with 12 Å of vacuum above it. Interaction energies between two surface-supported Cu5 clusters (Einter) were calculated as,
| Einter = {ECu10/graphene}Min − 2{ECu5/graphene}Min + Egraphene |
2.3 Ab initio molecular dynamics simulations on the interaction between graphene-supported Cu5 clusters
Ab initio molecular dynamics (AIMD) simulations have been carried out using the open-source MD simulation package, CP2K.68 AIMD simulations allow for the exploration of the time-evolution of a process at a given temperature and to quickly find interesting or low-energy reaction pathways. A single p(6 × 10) supercell graphene sheet was used in this work, with two Cu5 clusters (adsorbed on top of it) separated by at least 8.5 Å, with a large vacuum space of around 12 Å. The entire graphene sheet and all Cu atoms were allowed to relax freely. Both defect-free graphene and graphene sheets containing two double carbon vacancies have been modelled. We selected double carbon vacancies as they are more stable than the more reactive single vacancies and, therefore, occur more commonly in graphene than single vacancies.69 The initial frame/geometry of the AIMD simulation was obtained from the geometry optimization of the structure via electronic-structure computations from CP2K. Dispersion corrections were applied to all computations and simulations, while spin-polarization was added to the Cu5 cluster in the gas-phase. The PBE functional was used to compute the exchange–correlation energy.55 Furthermore, the Goedecker–Teter–Hutter, Perdew, Burke and Ernzerhof (GTH–PBE) pseudopotential,70 Gaussian and plane-wave (GPW) basis sets,71 and a multigrid cutoff energy of 500 Rydberg were chosen for this work. CP2K's own double-zeta basis sets were employed to minimize basis set superposition errors, as they have been optimized for use with GTH pseudopotentials and are suitable for both solid and molecular calculations.72 For the Brillouin zone integration, only a Γ point was chosen, and for the ensemble and thermostat, the Langevin ensemble with the adaptive-Langevin thermostat were selected.73 A small γ damping parameter of 0.01 fs−1 for the Langevin ensemble and reduced thermostat time constants were selected to improve thermostatting during heating and equilibration phases.74 During our benchmarking of the CP2K code, we further found that this combination of ensemble and thermostat typically leads to an improved average ensemble temperature, is significantly more cost effective, and produced similar results to other ensemble-thermostat combinations. Our choice was also further justified by the Langevin thermostat maintaining the correct canonical distribution,75 while also resulting in a faster temperature equilibration. Furthermore, to attain reliable results that properly describe the system under thermal equilibrium conditions, it is crucial to have the correct kinetic energy distribution between the graphene support and copper clusters. If the effective temperature of the cluster is too low or too high, this leads to correspondingly too low or too high isomerization and diffusion rates and the biased kinetic energy distribution can skew the observed cluster ensemble. The same is true when considering the graphene support, focusing on the movement of the support system and the opening of the vacancies on the sheet. According to our own benchmark tests and the 2022 study by Korpelin et al.,74 the Langevin ensemble with adaptive-Langevin thermostat is one of the better combinations in terms of kinetic energy distribution. The Langevin/adaptive-Langevin ensemble-thermostat combination also allows for an increased time-step, with us opting for a time step of 2 fs, but printing out every 20 fs. To rapidly explore a large phase space volume of configurations and to significantly speed up the simulation, a statistical sampling was performed at an elevated temperature of 400 K, but temperatures of 300 K and 600 K are also considered for pristine graphene in the ESI† (see videos S3 and S4). Fermi-Dirac smearing was also employed, selecting an electronic temperature of 300 K. Lastly, the convergence threshold criterion was set to 10−6 eV for the self-consistent electronic minimization.Note that the CP2K and VASP results are comparable given the chosen computational settings. This is illustrated by a comparison study of the adsorption and interaction energies calculated with the two codes, presented in the ESI.†
3 Results and discussion
3.1 Assessment of the dispersion-corrected DFT in the characterization of the Cu5 monomer and the Cu10 dimer
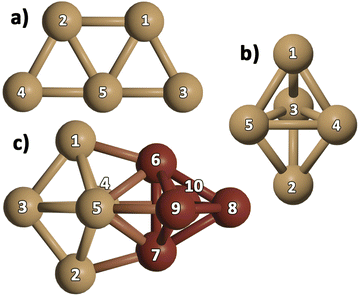
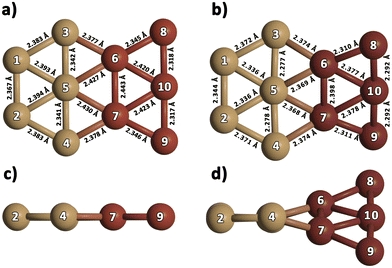
We optimized gas-phase Cu5 cluster geometries considering the two main structural arrangements identified by electronic structure calculations48,76,77 (Fig. 1a and b): planar trapezoidal two-dimensional (further referred to as 2D–Cu5) and trigonal bipyramidal three-dimensional (denoted as 3D–Cu5) shapes. In agreement with a recent ab initio study, using the VTZ-PP and the Def2-TZVP basis sets,48 as well as with previous works (see, e.g., ref. 27, 77 and 78), the 2D–Cu5 structure is found to be the most stable configuration and two energy minima are identified for the 3D–Cu5 structure corresponding to doublet and quartet spin configurations. As it is well-known for the case of Cu3 clusters,79 however, a closely lying transition state exists for the doublet spin state. It can be observed from Table 1 that when enlarging the basis set (either from VTZ-PP to AVTZ-PP or from Def2-TZVPP to Def2-QZVPP), the values of the Cu–Cu bond lengths change by less than 0.03 Å for all considered methods. Note also that the values of the Cu–Cu distances calculated with the DF-RS2C and DF-DFT-D3 methods differ very little (by 3.4% at most using the AVTZ-PP basis set) and the same holds true when comparing the Cu–Cu bond lengths calculated with the MP2 and DF-DFT-D3 treatments (by 4% at most using the Def2-QZVPP basis set). Relative energies are converged to within 0.1 eV using the AVTZ-PP basis set. Applying the DF-RS2C treatment, the energy difference between the energetically most favored 2D–Cu5 and 3D–Cu5 structures (ca. 0.1 eV) is below that predicted using DF-DFT-D3 and DLPNO-CCSD(T) methods (ranging from 0.2 to 0.4 eV). The dispersion D3 correction hardly favors the 2D–Cu5 structure: the difference between relative energies with and without a D3 correction is just 0.03 eV when using the AVTZ-PP basis set. The same holds true if dynamical correlation effects are estimated using second-order perturbation theory. This outcome is reflected in the quasi-degeneracy found for 2D– and 3D–Cu5 isomers at the MP2 level using both the def2-TZVPP and def2-QZVPP basis sets. Our findings underlie the role of non-dynamical correlation effects in the energy difference between 2D– and 3D–Cu5 isomers in the doublet spin state. A multi-state multi-reference treatment accounting for both non-dynamical and dynamical correlation should be necessary to describe the Jahn–Teller effects which might be responsible for reducing the molecular symmetry of the cluster from D3h to C2v in the doublet spin state. Altogether, however, based on the comparison with the results of three different ab initio methods [RS2C, MP2, and DLPNO-CCSD(T)], the single-reference DF-DFT-D3 performance for relative energies and structures can be considered quite good. In spite of having used different basis sets and DFT schemes, our results have a sensible agreement with the DFT-based ones recently reported for 2D–Cu5 and 3D–Cu5 clusters in the lowest doublet states.78 In particular, a C2v structure has been predicted for the 3D–Cu5 cluster, being 0.44 eV higher in energy than the 2D–Cu5 structure.| Method | Cu5, unsupported | |||
|---|---|---|---|---|
| DF-RS2C(7,7) | DF-DFT-D3 | DF-DFT-D3 | [DLPNO-CCSD(T)] MP2 | |
| Basis set | AVTZ-PP | VTZ-PP/AVTZ-PP | Def2-TZVPP/Def2-QZVPP | Def2-TZVPP/Def2-QZVPP |
| Planar, doublet | 0.0 | 0.0 | 0.0 | 0.0/0.0 |
| Bipyramidal, quartet | 1.1 | 0.7/0.8 | 0.7/0.8 | [1.1] 0.6/0.6 |
| Bipyramidal, doublet | 0.1 | 0.3/0.3 | 0.2/0.2 | [0.4] 0./0.03 |
| Planar, doublet | ||||
| Cu1–Cu2 | 2.35 | 2.39/2.38 | 2.42/2.41 | 2.43/2.44 |
| Cu1–Cu3 | 2.32 | 2.36/2.35 | 2.39/2.38 | 2.36/2.36 |
| Cu3–Cu5 | 2.32 | 2.34/2.33 | 2.37/2.36 | 2.35/2.34 |
| Bipyramidal, quartet | ||||
| Cu1–Cu3 | 2.34 | 2.38/2.37 | 2.40/2.40 | 2.38/2.38 |
| Cu3–Cu4 | 2.40 | 2.53/2.51 | 2.54/2.53 | 2.43/2.44 |
| Cu4–Cu5 | 2.41 | 2.53/2.51 | 2.54/2.53 | 2.43/2.44 |
| Bipyramidal, doublet | ||||
| Cu1–Cu3 | 2.39 | 2.43/2.41 | 2.46/2.43 | 2.41/2.40 |
| Cu3–Cu5 | 2.28 | 2.33/2.32 | 2.36/2.35 | 2.30/2.30 |
| Cu4–Cu5 | 2.50 | 2.58/2.55 | 2.58/2.57 | 2.47/2.47 |
Analyzing the case of the Cu10 dimer in Table 2, it can be seen that all considered methods consistently predict a D2d-symmetry structure as the energetically favored configuration, in agreement with previous ab initio work48 and DFT studies.80–83 Panel c of Fig. 1 shows that this Cu10 geometry is composed of two trigonal bipyramidal 3D–Cu5 structures rotated by ca. 90 degrees with respect to each other. The DF-DFT-D3/AVTZ-PP values of the Cu–Cu bond lengths differ by at most 2.5% from those obtained with the DF-RS2C/AVTZ-PP ansatz, while the interaction energy is estimated to be 8% lower (−5.2 eV) when using the DFT-D3/AVTZ-PP treatment. The RS2C-based structures are clearly more compacted, with the average Cu--Cu distances up to 0.08 Å shorter than those obtained with the DF-DFT-D3 ansatz. The interaction energy calculated with the DLPNO-CCSD(T) method depends significantly on the considered geometry. Using the VTZ-PP basis, the DLPNO-CCSD(T) estimate is 6.3 eV when geometries optimized at either RS2C or DFT-D3 levels are considered. As can be observed in Table 2, this value (−6.3 eV) remains unchanged when the AVTZ-PP basis set is used in the DLPNO-CCSD(T) single-point calculation with the geometry optimized at the DFT-D3/AVTZ-PP level. The value is in very good agreement with the literature value, −6.1 eV, calculated at the CCSD(T)-F12b level.77
| Cu10, singlet | Unsupported | Supported | ||||
|---|---|---|---|---|---|---|
| Method | DF-RS2C(10,10) | DF-DFT-D3 | DF-DFT-D3 | MP2 | DFT-D3 | DFT-D3 |
| Basis set | VTZ-PP/AVTZ-PP | VTZ-PP/AVTZ-PP | Def2-TZVPP/Def2-QZVPP | Def2-TZVPP/Def2-QZVPP | PAW–PBE | PAW–PBE |
| E int, eV | [−6.3]−6.1/−6.2 | [−6.3]/[−6.3]−5.3/−5.2 | −5.5/−5.2 | −6.9/−6.7 | −5.4 | −4.3 |
| Cu1–Cu3, Å | 2.44/2.42 | 2.46/2.45 | 2.48/2.48 | 2.47/2.47 | 2.45 | 2.46 |
| Cu1–Cu4, Å | 2.41/2.34 | 2.40/2.40 | 2.42/2.42 | 2.37/2.37 | 2.40 | 2.41 |
| Cu3–Cu4, Å | 2.43/2.41 | 2.49/2.49 | 2.51/2.51 | 2.45/2.44 | 2.49 | 2.49 |
| Cu4–Cu5, Å | 2.41/2.40 | 2.55/2.54 | 2.56/2.55 | 2.42/2.42 | 2.54 | 2.57 |
| Cu5–Cu6, Å | 2.41/2.39 | 2.49/2.48 | 2.50/2.50 | 2.42/2.42 | 2.48 | 2.51 |
In addition to the lowest-energy 3D structure of the Cu10 dimer shown in panel c of Fig. 1, we have compared the energy of a Cu10 isomer built from two planar 2D–Cu5 fragments (see Fig. 2)). As noted in ref. 48, as opposed to the Cu5 monomer case, the Cu10 isomer built from two planar 2D–Cu5 fragments is energetically less favored than the D2d structure composed of two 3D–Cu5 clusters (by 1.5 and 2.2 eV at DF-DFT-D3 and DF-RS2C levels of theory, respectively). The dispersion correction accounts for only 0.1 eV of their energy difference at the DFT-D3 level. Dynamical correlation effects might be responsible for the stabilization of the 3D structure since, including just the non-dynamical correlation with the DF-CASSCF/AVTZ-PP treatment, the energy difference between the two structures of the Cu10 dimer is reduced to just 0.1 eV. It can be also observed in Fig. 2 that the structures predicted via DF-RS2C and DF-DFT-D3 methods are very similar, with the differences in the values of Cu–Cu bond-lengths not exceeding 3%. However, note that the DFT method predicts a perfect 2D planar structure whereas in the DF-RS2C-based geometry, the planes containing the 2D–Cu5 fragments are rotated by about 45 degrees with respect to each other. Preference for planar structures shown by the smallest coinage metal and Pt clusters at least up to hexamers is a well-known phenomenon discussed in several theoretical studies and attributed to the hybridization of the ns-(n − 1) d orbitals, which is especially pronounced for gold due to relativistic effects.32 While for Aun clusters, the transition from planar to 3D structures occurs at n = 10 or 11,84–86 for Cun, it happens already at n = 7 according to several DFT-based studies80–83,87–89 and a computational work at the CCSD(T)//MP2 level.87 As the cluster size increases, 3D shapes become energetically more favorable, while in most cases there are several low-lying isomers with only slightly different stability.32
Before comparing the interaction energies of two Cu5 components in the gas-phase Cu10 and in the graphene-supported Cu10 dimer, we note that the DFT-D3 values for the former calculated by using the non-periodic and periodic computational set-ups agree very well with each other (to within 3.4%). As can be seen in Table 2, the graphene support causes a decrease in the pair interaction by 0.5 eV, while the values of the Cu–Cu distances in unsupported and supported dimers differ by 0.03 Å at most. This outcome can be explained by considering that graphene tends to stabilize to a larger extent radical species such as Cu5 clusters (in a doublet spin state) than closed-shell systems including the Cu10 dimer (in a singlet spin state). Altogether, from the results presented in Tables 1 and 2, it can be concluded that the DFT-D3 scheme delivers estimations of basic energetic and structural aspects of the lowest-energy states for either the Cu5 monomer or the Cu10 dimer in very good agreement with the results of high-level correlated ab initio methods.
As for the Cu5–graphene interaction, our calculations using circumpyrene as a molecular model of graphene, along with the VTZ-PP and AVTZ-PP basis sets, show that the DLPNO-CCSD(T) adsorption energies (−1.64 eV for the 3D–Cu5 isomer) are smaller (to within 21%) than those obtained with the DFT-D3 approach. However, the energy difference between circumpyrene-supported 2D–Cu5 and 3D–Cu5 isomers has the same value (0.12 eV) with the two approaches.
3.2 Ab initio molecular dynamics simulations
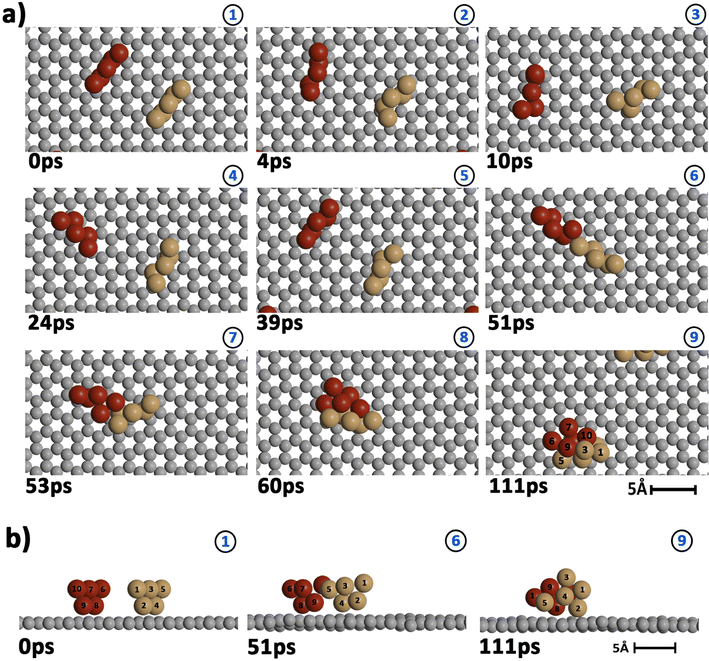
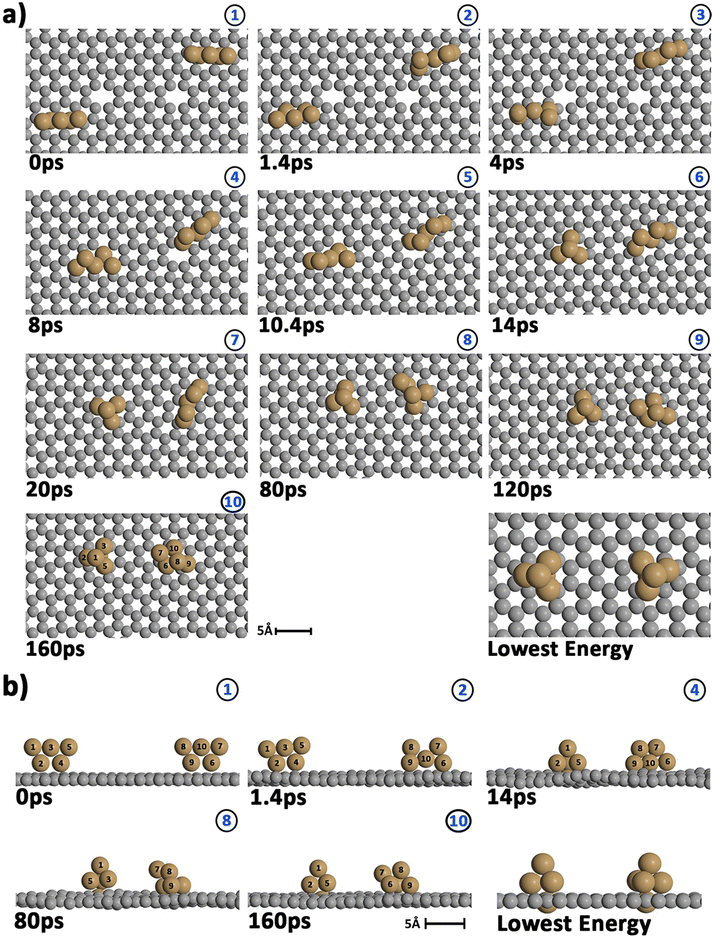
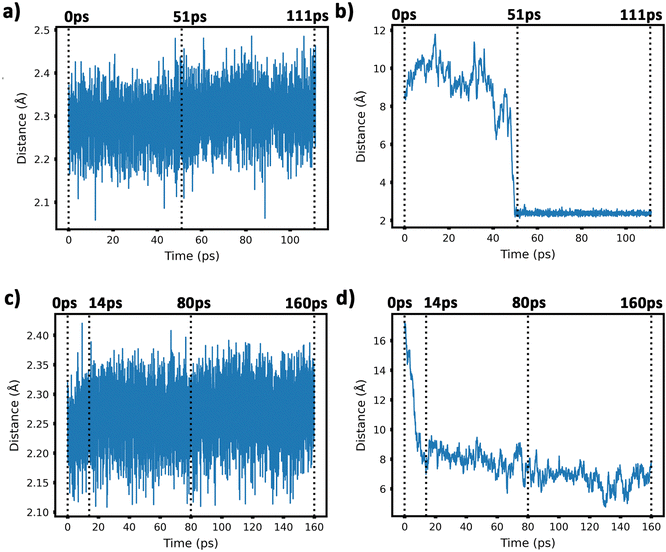
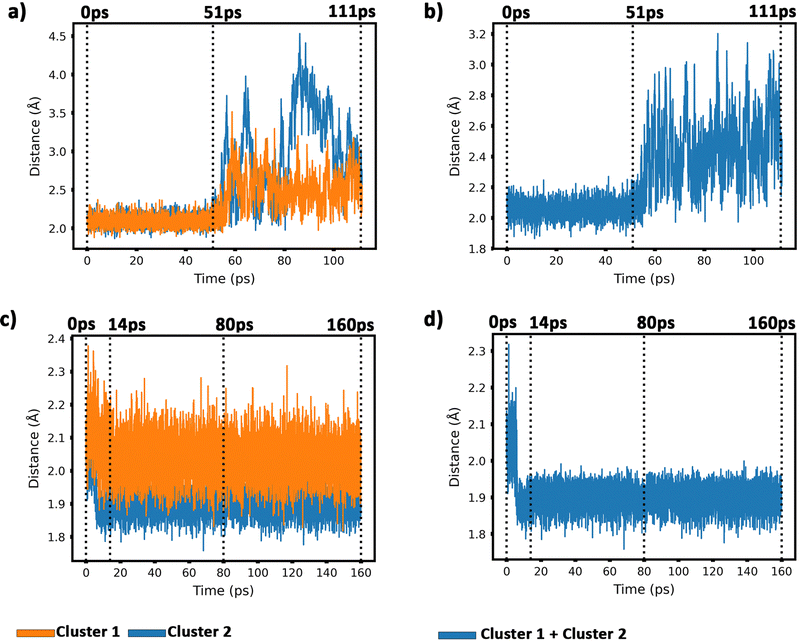
To get insight into the interaction between two Cu5 clusters supported on defect-free or defected graphene (with carbon double vacancies), ab initio molecular dynamics simulations were carried out for several picoseconds. Fig. 3 and 4 show snapshots of the structural evolution of supported clusters on perfect and defected graphene, respectively. The minimum intra-cluster and inter-cluster Cu–Cu distances of the supported Cu5 clusters are presented in Fig. 5 while the time-dependent evolution of the root mean square deviations (RMSDs) of individual Cu atoms are depicted in Fig. 6. These RMSDs have been defined as: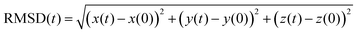 | (1) |
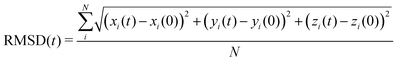 | (2) |
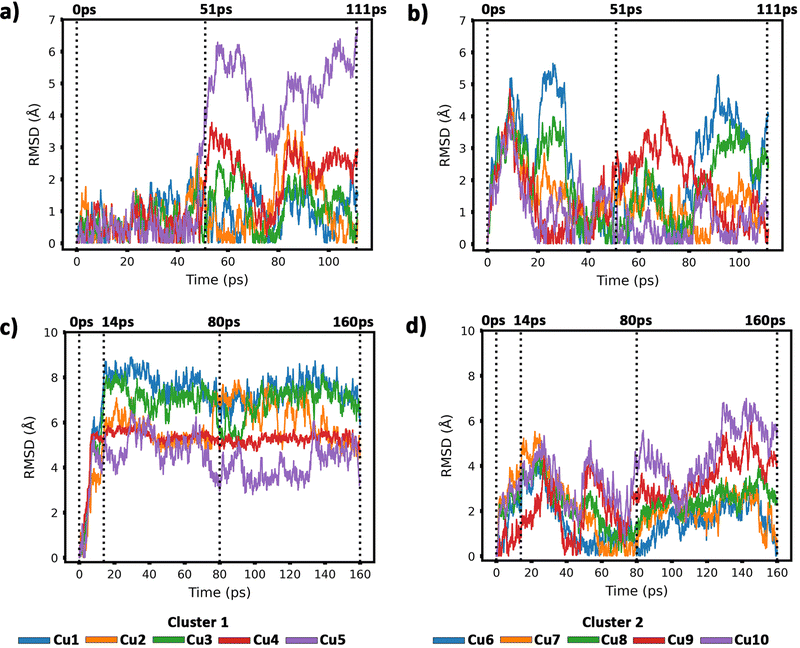 | ||
| Fig. 6 Root-mean-square deviations (RMSDs) of copper atomic positions for the two Cu5 clusters supported on defect-free graphene [panels (a) and (b)] and supported on defected graphene [panels (c) and (d)] (see also Fig. 4 and 5). | ||
3.3 Interaction of two Cu5 clusters on a defect-free graphene sheet. Dimerization
Our AIMD simulation started with two 2D–Cu5 clusters deposited onto a defect-free graphene sheet, with a distance of ca. 8 Å from one cluster to the other (Fig. 5b). A video animation of the entire AIMD simulation has also been uploaded as ESI,† see Video S1. It can be observed from the shapshots at 4 and 10 ps that the structure of one Cu5 cluster becomes slightly distorted from the initial planar structure. During the next 30 ps, the two Cu5 clusters show a diffusive behaviour on the graphene sheet. In fact, the very similar values of the RMSDs for all Cu atoms within each cluster reflect a collective motion of the Cu atoms since the Cu5 clusters are moving ‘as a whole’ (Fig. 6a and b), except between 20 and 30 ps for cluster 2 in which there is a collective motion but also rotation of the cluster, as reflected by the RMSD values for all the Cu atoms being spread out in this interval. During this 10 ps period, cluster 2 sees a rotation of more than 90° at first, then a back rotation returning roughly to the same position again. However starting at ca. 46 ps, the Cu atoms within the same Cu5 cluster start acquiring very different RMSDs values. This outcome reflects that the Cu5 clusters are experiencing a mutual attraction and are rotating as a result of this interaction (with both clusters in Fig. 3 rotating by 90 degrees between 46 and 51 ps). Formation of a complex made of quasi-planar Cu5 structures becomes apparent in the snapshot at 51 ps (Fig. 3). The formation of such a complex is consistent with the gas-phase results (Section 3.1) where a planar local minimum formed by two connected 2D–Cu5 structures was identified (see also ref. 48). As mentioned in Section 3.1, however, the interaction between the two Cu5 clusters in that configuration is 1.5 eV less attractive at the DFT-D3 level than in the structure composed of anchored 3D–Cu5 clusters. Hence, it is understandable that in the last part of the simulation (from 51 to 111 ps), the structure evolves towards the latter more energetically stable complex (see Fig. 1c for an enlarged view).Summarizing, three steps can be distinguished in the dimerization of two 2D–Cu5 clusters into a highly stable Cu10 dimer formed by two anchored 3D–Cu5 structures: (1) step 1, from 0 to 46 ps, cluster diffusion; (2) step 2, from 46 to 51 ps, Cu5–Cu5 attraction and aggregation into a structure made of two planar fragments; (3) step 3, from 51 to 111 ps, geometrical transformation into the final structure composed of two anchored 3D–Cu5 bipyramidal arrangements. These three distinct steps are naturally reflected in the time-evolution of the RMSDs of the copper atomic positions (see Fig. 6). Cluster 1 shows more restricted motion than cluster 2 in the first 46 ps of the simulation, with cluster 2 experiencing significant rotation. The attraction, aggregation, and geometrical transformation steps (step 2 and step 3), however, are marked by wide and uneven amplitude motions of the Cu atoms, acquiring very different RMSDs. When the clusters start to rotate from 46 ps onwards, the RMSDs of the different Cu atoms (specifically cluster 1) significantly spread apart. The two planar clusters first align parallel to each other and then start to interact with their side edges. The onset of step 3 (transformation from 2D to 3D) can also be well distinguished in the evolution of the minimum inter-cluster Cu–Cu distance. At around 50 ps it features an abrupt drop to an almost constant value (Fig. 5b), indicating that there exists at least one Cu–Cu bond between the two Cu5 fragments from this point onward. The geometrical transformation is accompanied by a slight lifting of the Cu10 dimer from the graphene surface (see Fig. 7a and b). This is probably due to a weaker interaction of the closed-shell Cu10 species with the graphene substrate compared to that of open-shell Cu5 clusters.
Preliminary calculations of the same dimerization process have also been carried out on multi-layered graphene-supported clusters using the LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulation) package90 and a computational set-up closely following that presented in ref. 91. For this purpose, the interaction potential obtained via the embedded atom method (EAM) of Foiles et al.92 was used to describe the Cu–Cu pair interactions. In order to characterize the interaction between the graphene carbon atoms, the adaptive intermolecular reactive bond order (AIREBO) potential was used instead.93 Finally, the effective Cu–C interactions were extracted from Cu5–graphene interaction potentials calculated with the DFT-D3/PAW-PBE scheme (see also ref. 94 for the details). These LAMMPS simulations were carried out by considering a surface of four graphene sheets (i.e., representing graphite) and a broad temperature range (from 0.1 K to 1000 K). In order to relax the graphite substrate, the lowest sheet was created to represent bulk graphite and the other sheets were allowed to relax at the corresponding temperature, i.e., representing the surface levels as well as the Cu5 cluster that was previously deposited on the upper sheet. According to these exploratory calculations, two planar (2D) Cu5 clusters aggregate into a Cu10 dimer already at 1 K if the initial distance between the two interacting Cu5 clusters is below 5 Å. This key result is reconfirmed in our AIMD simulations in spite of the very different computational set-up used in LAMMPS simulations. However, due probably to the different Cu–Cu potentials in AIMD and LAMMPS simulations, the latter show that a single graphene-supported 2D–Cu5 cluster transforms spontaneously into a bypiramidal 3D–Cu5 cluster at temperatures as low as 1 K. As pointed out by preliminary high-level ab initio calculations, the energy difference between surface-supported 2D and 3D structures is so small (ca. 0.1 eV) that both isomers could coexist.
Before starting the dynamical simulation, the two 2D–Cu5 clusters were placed onto the graphene sheet containing two double C vacancies per unit cell and the initial structure was optimized with full relaxation of all atoms. According to Fig. 4a and b, within the first 1.4 ps of the simulation, one of the Cu5 clusters, cluster 2 (cluster 2 is always on the right in these snapshots), undergoes a small structural change, whereby it transitions from adsorbing via two Cu atoms to adsorbing via three Cu atoms. From this point forward both clusters head towards the carbon vacancies, with cluster 1 (left cluster) reaching a vacancy first at 4 ps, before entering the vacancy at 8 ps.
Cluster 2 arrives at another vacancy at 8 ps. From 8 ps to 14 ps, the vacancy at cluster 1 opens up more, allowing cluster 1 to get locked into the vacancy and then undergo a geometrical transformation from planar to trigonal bipyramidal. At 14 ps, we can observe this trigonal bipyramidal geometry. Our calculations indicate that the adsorption energy of the 3D–Cu5 structure on a graphene sheet with two C-divacancies is 0.75 eV lower than of the 2D–Cu5 counterpart (Fig. S11, ESI†). Thus, the 2D-to-3D transformation of the individual Cu5 clusters is due to the interaction with the defect sites of the support.
Cluster 2 covers the right-side vacancy by 14 ps, but the vacancy is not opening up further. For the next 70 ps, cluster 2 is only rotating over the vacancy until at 80 ps, when a geometrical transformation occurs to a distorted trigonal bipyramidal geometry. For the next 40 ps cluster 2 once again rotates (back and forth) over the vacancy. As shown in Fig. S12 of the ESI,† the structure at 120 ps in Fig. 4a and b is not the most stable. The most stable structure involves both clusters locked into their respective vacancies and having a trigonal bipyramidal geometry. In particular, there is a nearly 2 eV difference between these two structures. At this point, it appears that either the structure is stuck in a local minimum, or the energy required to open up the vacancy and for the cluster to move into it is too high to be overcome with the thermal energy available in this simulation. To confirm that it is not the former case, we used the NVT ensemble with the Nosé–Hoover thermostat from 120 ps to 160 ps. This has been known to spread out the kinetic energy between the surface and adsorbates in a biased manner,74 potentially allowing for the graphene sheet to take up more kinetic energy from the copper clusters, which could help the vacancy to open up further. Despite small transformations of the cluster during the 40 ps period, including a speed up of the graphene support system (see Video S2 in the ESI†), ultimately the trigonal bipyramidal isomer remained and the cluster kept rotating back and forth over the vacancy, without the vacancy opening up further. Increasing the temperature with both ensemble-thermostat combinations beyond 160 ps (not shown here) just results in a speed up of the graphene sheet and copper clusters. Ultimately, our hypothesis is that, since we are dealing with a single graphene sheet and have no constrained (fixed) sheets underneath it, the graphene sheet is free to move in all three directions, so the thermal energy is used rather to move the sheet and clusters around, moving as much as 10 Å (relative to its initial position) in the z direction over the 160 ps, instead of using the energy to open up the vacancy. If a fixed graphene sheet layer was placed underneath the relaxed one, this would not happen, as the relaxed graphene sheet would be less capable of moving around. Using fixed graphene only, as shown in the ESI† (Fig. S2), we see that when the vacancies are both open, the Cu5 clusters easily fall into the vacancies and undergo geometrical transformations.
From 14 ps to 160 ps, cluster 1 which is locked into the vacancy as a trigonal bipyramidal geometry, undergoes frustrated rotational motion, as evidenced by the RMSD plots being spread out and fluctuating over a range of values in Fig. 6c. Additionally, Fig. 7c shows a decrease in the minimum C–Cu distance from cluster 1 to graphene over the 14 ps period. For cluster 2 as per Fig. 6d, the RMSD values for each Cu atom increase up to 14 ps as all the Cu atoms move towards the vacancy, after which the RMSD plots are generally spread out due to the back and forth rotation of the cluster. After the geometrical transformation at 80 ps, the RMSD plots are spread out once again as the cluster rotates back and forth over the vacancy. Furthermore, while cluster 1 remains confined within a graphene vacancy, cluster 2 also observes a decrease in the minimum C–Cu distance (see Fig. 7c), decreasing to a lower value than cluster 1 at a similar rate. That is, cluster 2 is positioned closer to at least one carbon atom (from graphene) compared to cluster 1. From Fig. 5c, we can observe the minimum intra-cluster Cu–Cu distance increasing over the first 14 ps of the simulation, coinciding with a decrease in the C–Cu distance. Beyond this point, there is no general increase or decrease. For the inter-cluster distance, there is a sharp decrease in the cluster–cluster distance in the first 14 ps as the clusters approach the vacancies. Beyond 14 ps, there is a further decrease of the distance up until 80 ps, where cluster 2 undergoes a geometrical transformation. Beyond this point, we observe fluctuating values for the distance as the two clusters rotate about.
It should be stressed that although the 3D–Cu5 clusters rotate around or on the cavity, with the anchored Cu atom experiencing minimal displacement (Fig. 6c), cluster geometries exhibit a stable behaviour during the rest of the simulation of 160 ps. Wider amplitude Cu–Cu motions (to within 0.5 Å) have been found when 3D–Cu5 clusters interact with environmental O2 molecules (see, for example, ref. 94). Previous studies have explained the small change in minimum intra-cluster distance going from 2D– to 3D–Cu5 in terms of the fluxional nature of atomic metal clusters (see, e.g., ref. 15, 38, 95 and 96).
To summarize, this simulation involves several steps. Step 1 entails the displacement of the Cu5 clusters, particularly as they approach the vacancy. Step 2 entails the opening up of one of the vacancies as cluster 1 moves into the vacancy, getting locked into the vacancy and eventually transforming to the trigonal bipyramidal geometry. Step 3 sees cluster 2 rotate back-and-forth over the still “closed” vacancy on the graphene sheet, while cluster 1 rotates in another vacancy it has been “locked” into. Step 4 sees cluster 2 undergoing a geometrical transformation to trigonal bipyramidal, but still not being able to enter the vacancy, but only rotating about the vacancy. Although cluster 2 never enters the vacancy, it also does not approach cluster 1 to dimerize with it, but only rotates back and forth over the vacancy. As can be learned from Fig. S2 in the ESI,† if this vacancy would be more opened, cluster 2 would be able to enter and also get locked into it.
4 Conclusions
Recent research has shown that atomically precise clusters possess interesting chemical and physical properties making them relevant in applications such as catalysis. One major concern is the sintering of these clusters upon dispersion onto a given substrate. A critical step in making them efficient requires their stabilization on solid supports. In the quest of finding ways to stabilize substrate-supported AMCs, we have provided an ab initio molecular dynamics (AIMD) evidence that carbon vacancies of graphene are capable to confine and stabilize individual AMCs above room temperature. While most Cu atoms in these clusters still show frustrated rotational motion, for the confined cluster, a Cu atom is strongly anchored into a graphene vacancy site, thus ‘locking’ the cluster ‘in place’ into the vacancies. The reliability of our DFT-based predictions is supported by the assessment of the electronic structure method applied in the AIMD simulations (the DFT-D3 scheme50) with ab initio methods based on multireference Rayleigh–Schrödinger perturbation,53 second-order Møller–Plesset perturbation, and coupled-cluster theory in the domain-based pair natural approach,54 using all-electron and pseudo-potential-based electronic basis sets of increasing size. Future work will address a deeper analysis of the interaction of the Cu5 cluster with both perfect and vacancies-containing graphene by applying high-level correlated ab initio methods which is especially important in the latter case due to the radical nature of the interacting open-shell species.The strategy of using carbon vacancies to confine AMCs is general. As a follow-up study, it would be interesting to study atomic bi-metallic clusters in which one metal atomic species could anchor the clusters to vacancy sites, allowing other metal atoms to be available for catalytic processes. It would be also interesting to theoretically study the stability of these pushpin-like cluster structures when exposed to oxidizing and reducing conditions above room temperature. In this regard, it is worth mentioning that recent experimental and theoretical studies have pointed out to the possibility of reversible oxidation of HOPG-supported atomic copper clusters at different conditions of temperature and oxygen gas pressure.29,76,89,94,97,98
Author contributions
All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Ricardo Fernández-Perea for having shared the results from preliminary simulations using the LAMMPS code. This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) under Grant No. PID2020-117605GB-I00. This publication is also based upon work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). One of the authors (M. P. d. L. C.) is also greatly thankful for the support of the EU Doctoral Network PHYMOL 101073474 (project call reference HORIZON-MSCA-2021-DN-01). L. V. M. acknowledges the support from the South African National Research Foundation (NRF), grant 148775. The CESGA supercomputer center (Spain), the Spanish Supercomputing Network (RES), and the Centre for High Performance Computing (CHPC), South Africa, are acknowledged for having provided computational resources. We also acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).Notes and references
- H.-T. Sun and Y. Sakka, Sci. Technol. Adv. Mater., 2014, 15, 014205 CrossRef CAS PubMed.
- L. Zhang and E. Wang, Nano Today, 2014, 9, 132–157 CrossRef CAS.
- V. Bonaci-Koutecký and R. Antoine, Nanoscale, 2019, 11, 12436–12448 RSC.
- M. V. Romeo, E. López-Martínez, J. Berganza-Granda, F. Goñi-de Cerio and A. L. Cortajarena, Nanoscale Adv., 2021, 3, 1331–1341 RSC.
- G. F. Combes, A.-M. Vuckovic, M. Peric Bakulic, R. Antoine, V. Bonacic-Koutecky and K. Trajkovic, Cancers, 2021, 13, 4206 CrossRef CAS PubMed.
- K. Zheng and J. Xie, Trends Chem., 2020, 2, 665–679 CrossRef CAS.
- Q. Zhang, M. Yang, Y. Zhu and C. Ma, Curr. Med. Chem., 2018, 25, 1379–1396 CrossRef CAS PubMed.
- R. S. Dhayal, W. E. van Zyl and C. W. Liu, Dalton Trans., 2019, 48, 3531–3538 RSC.
- Y. Lykhach, A. Bruix, S. Fabris, V. Potin, I. Matolínová, V. Matolín, J. Libuda and K. M. Neyman, Catal. Sci. Technol., 2017, 7, 4315–4345 RSC.
- A. Halder, C. Lenardi, J. Timoshenko, A. Mravak, B. Yang, L. K. Kolipaka, C. Piazzoni, S. Seifert, V. Bonacic-Koutecký, A. I. Frenkel, P. Milani and S. Vajda, ACS Catal., 2021, 11, 6210–6224 CrossRef CAS.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef CAS.
- R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088 CrossRef CAS PubMed.
- L. Vega, H. A. Aleksandrov, R. Farris, A. Bruix, F. Viñes and K. M. Neyman, Mater. Adv., 2021, 2, 6589–6602 RSC.
- L. Zhou, J. M. P. Martirez, J. Finzel, C. Zhang, D. F. Swearer, S. Tian, H. Robatjazi, M. Lou, L. Dong, L. Henderson, P. Christopher, E. A. Carter, P. Nordlander and N. J. Halas, Nat. Energy, 2020, 5, 61–70 CrossRef CAS.
- M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759 CrossRef CAS PubMed.
- J. Juraj, A. Fortunelli and S. Vajda, Phys. Chem. Chem. Phys., 2022, 24, 12083–12115 RSC.
- P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853 RSC.
- P. López-Caballero, S. Miret-Artés, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Chem. Phys., 2020, 153, 164702 CrossRef PubMed.
- M. P. de Lara-Castells and S. Miret-Artés, Europhys. News, 2022, 53, 7–9 CrossRef.
- P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568 CrossRef.
- S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908 CrossRef CAS.
- J. Jašik, S. Valtera, M. Vaidulych, M. Bunian, Y. Lei, A. Halder, H. Tarábková, M. Jindra, L. Kavan, O. Frank, S. Bartling and S. Vajda, Faraday Discuss., 2023, 242, 70–93 RSC.
- A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901 CrossRef PubMed.
- S. Hirabayashi and M. Ichihashi, Phys. Chem. Chem. Phys., 2014, 16, 26500–26505 RSC.
- B. Yang, C. Liu, A. Halder, E. C. Tyo, A. B. F. Martinson, S. Seifert, P. Zapol, L. A. Curtiss and S. Vajda, J. Phys. Chem. C, 2017, 121, 10406–10412 CrossRef CAS.
- P. Maity, S. Yamazoe and T. Tsukuda, ACS Catal., 2013, 3, 182–185 CrossRef CAS.
- J. Oliver-Messeguer, L. Liu, S. García-García, C. Canós-Giménez, I. Domínguez, R. Gavara, A. Doménech-Carbó, P. Concepción, A. Leyva-Pérez and A. Corma, J. Am. Chem. Soc., 2015, 137, 3894–3900 CrossRef PubMed.
- M. Gallego, A. Corma and M. Boronat, J. Phys. Chem. A, 2022, 126(30), 4941–4951 CrossRef CAS PubMed.
- D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. Lóopez-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. Calvino, M. Lopez-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, Outstanding nobility observed in Cu5 clusters reveals the key role of collective quantum effects, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv.13661081.v1.
- M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500 RSC.
- K. Geim, Science, 2009, 324, 1530 CrossRef PubMed.
- E. Fernández and M. Boronat, J. Phys.: Condens. Matter, 2018, 31, 013002 CrossRef PubMed.
- L. Liu and A. Corma, Trends Chem., 2020, 2, 383–400 CrossRef CAS.
- Y. Wang, J. Mao, X. Meng, L. Yu, D. Deng and X. Bao, Chem. Rev., 2019, 119, 1806–1854 CrossRef CAS PubMed.
- Y. Chen, J. Lin, B. Jia, X. Wang, S. Jiang and T. Ma, Adv. Mater., 2022, 34, 2201796 CrossRef CAS PubMed.
- X. Li, X. I. Pereira-Hernández, Y. Chen, J. Xu, J. Zhao, C.-W. Pao, C.-Y. Fang, J. Zeng, Y. Wang, B. C. Gates and J. Liu, Nature, 2022, 611(7935), 284–288 CrossRef CAS PubMed.
- A. Sanchez, S. Abbet, U. Heiz, W.-D. Schneider, H. Häkkinen, R. N. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573–9578 CrossRef CAS.
- P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074 CrossRef PubMed.
- H. Tao, Y. Li, X. Cai, H. Zhou, Y. Li, W. Lin, S. Huang, K. Ding, W. Chen and Y. Zhang, J. Phys. Chem. C, 2019, 123, 24118–24132 CrossRef CAS.
- M. D. Bhatt, H. Kim and G. Kim, RSC Adv., 2022, 12, 21520–21547 RSC.
- F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26–41 CrossRef CAS PubMed.
- Q. Tang, Z. Zhou and Z. Chen, Nanoscale, 2013, 5, 4541–4583 RSC.
- R. E. Palmer, S. Pratontep and H.-G. Boyen, Nat. Mater., 2003, 2, 443–448 CrossRef CAS PubMed.
- G. Kim, S.-H. Jhi, S. Lim and N. Park, Appl. Phys. Lett., 2009, 94, 173102 CrossRef.
- M. J. López, I. Cabria and J. A. Alonso, J. Phys. Chem. C, 2014, 118, 5081–5090 CrossRef.
- C. M. Ramos-Castillo, J. U. Reveles, M. E. Cifuentes-Quintal, R. R. Zope and R. de Coss, J. Phys. Chem. C, 2016, 120, 5001–5009 CrossRef CAS.
- B. K. Medasani, J. Liu and M. L. Sushko, MRS Commun., 2017, 7, 891–895 CrossRef CAS.
- B. Fernández and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 26992–26997 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804 CrossRef PubMed.
- M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119 RSC.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557 CrossRef CAS.
- A. Kubas, D. Berger, H. Oberhofer, D. Maganas, K. Reuter and F. Neese, J. Phys. Chem. Lett., 2016, 7, 4207–4212 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253 CrossRef CAS; H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, III, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef PubMed; H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, version 2021.2, a package of ab initio programs, see https://www.molpro.net.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, WIREs Computational Molecular Science, 2012, 2, 73–78 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- M. P. de Lara-Castells, M. Bartolomei, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 194701 CrossRef PubMed.
- P. E. Blöch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- T. Kühne, M. Iannuzzi, M. D. Ben, V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- M. Batt, H. Kim and G. Kim, RSC Adv., 2022, 12, 21520–21547 RSC.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- https://github.com/misteliy/cp2k/blob/master/tests/QS/BASIS_MOLOPT accessed on 8 Dec. 2022.
- D. A. McQuarrie, Statistical Mechanics. Harper and Row, 2000, p. 452, ISBN 06-044366-9 Search PubMed.
- https://manual.cp2k.org/trunk/CP2K_INPUT/MOTION/MD/THERMOSTAT/AD_LANGEVIN.html accessed on 8 Dec. 2022.
- N. Goga, A. Rzepiela, A. de Vries, S. Marrink and H. Berendsen, J. Chem. Theory Comput., 2012, 8, 3637–3649 CrossRef CAS PubMed.
- P. Concepción, et al. , ACS Catal., 2017, 7, 3560–3568 CrossRef.
- R. R. Persaud, M. Chen and D. A. Dixon, J. Phys. Chem. A, 2020, 124, 1775–1786 CrossRef CAS PubMed.
- Q. Wu, S. Hou, D. Buceta, H. J. Ordoñez, M. Arturo López-Quintela and C. J. Lambert, Appl. Surf. Sci., 2022, 594, 153455 CrossRef CAS.
- R. R. Persaud, M. Chen, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2019, 123, 1198–1207 CrossRef CAS PubMed.
- A. S. Chaves, G. G. Rondina, M. J. Piotrowski, P. Tereshchuk and J. L. F. Da Silva, J. Phys. Chem. A, 2014, 118, 10813–10821 CrossRef CAS PubMed.
- G. Guzmán-Ramírez, F. Aguilera-Granja and J. Robles, Eur. Phys. J. D, 2010, 57, 49–60 CrossRef.
- C.-G. Li, Z.-G. Shen, Y.-F. Hu, Y.-N. Tang, W.-G. Chen and B.-Z. Ren, Sci. Rep., 2017, 7, 1345 CrossRef PubMed.
- H. A. Hussein, M. Gao, Y. Hou, S. L. Horswell and R. L. Johnston, Z. Phys. Chem., 2019, 233, 813–843 CrossRef CAS.
- B. Assadollahzadeh and P. Schwerdtfeger, J. Chem. Phys., 2009, 131, 064306 CrossRef PubMed.
- M. P. Johansson, I. Warnke, A. Le and F. Furche, J. Phys. Chem. C, 2014, 118, 29370–29377 CrossRef CAS.
- P. V. Nhat, N. T. Si, N. T. N. Hang and M. T. Nguyen, Phys. Chem. Chem. Phys., 2022, 24, 42–47 RSC.
- H. Nakashima, H. Mori, M. S. Mon and E. Miyoshi, Proceedings of the 1st WSEAS International Conference on Computational Chemistry, Stevens Point, Wisconsin, USA, 2007, 11–13.
- P. Jaque and A. Toro-Labbé, J. Mol. Model., 2014, 20, 2410 CrossRef PubMed.
- E. Fernández, M. Boronat and A. Corma, J. Phys. Chem. C, 2015, 119, 19832–19846 CrossRef.
- S. Plimpton, J. Comp. Phys., 1995, 117, 1–19 CrossRef CAS.
- R. Fernández-Perea, L. F. Gómez, C. Cabrillo, M. Pi, A. O. Mitrushchenkov, A. F. Vilesov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 22248–22257 CrossRef.
- S. M. Foiles, M. I. Baskes and M. S. Daw, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7983–7991 CrossRef CAS PubMed.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- J. Garrido-Aldea and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 24810–24822 RSC.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef CAS.
- Q.-Y. Fan, Y. Wang and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 3891–3897 CrossRef CAS PubMed.
- A. Zanchet, P. López-Caballero, A. O. Mitrushchenkov, D. Buceta, M. A. López-Quintela, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 27064–27072 CrossRef CAS PubMed.
- A. O. Mitrushchenkov, A. Zanchet, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. A, 2021, 125, 9143–9150 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Results of AIMD simulations on graphene with constrained (fixed) positions of C atoms at 400 K, as well as on unconstrained (relaxed) graphene at 300 K and 600 K. Tests comparing VASP and CP2K relative energies. Tests of convergence with respect to the k-point mesh size. Structural comparisons of various Cu5 isomers adsorbed on pristine and defective graphene surfaces. Six movies showing ab initio molecular dynamics simulations on the interaction of Cu5 clusters on defect-free (VideoS1.mp4) and carbon vacancies-containing (VideoS2.mp4) graphene sheets at 400 K, on defect-free graphene at 600 K (VideoS3.mp4) and 300 K (VideoS4.mp4), as well as constrained defect-free graphene at 400 K (VideoS5.mp4) and constrained defective graphene at 400 K (VideoS6.mp4). See DOI: https://doi.org/10.1039/d2cp05843j |
| This journal is © the Owner Societies 2023 |