Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New insights into the competition between antioxidant activities and pro-oxidant risks of rosmarinic acid†
Dinh Hieu Truongab,
Thi Chinh Ngo ab,
Nguyen Thi Ai Nhung
ab,
Nguyen Thi Ai Nhung c,
Duong Tuan Quangc,
Thi Le Anh Nguyen
c,
Duong Tuan Quangc,
Thi Le Anh Nguyen ab,
Dorra Khirid,
Sonia Taamalli
ab,
Dorra Khirid,
Sonia Taamalli d,
Florent Louisd,
Abderrahman El Bakalid and
Duy Quang Dao
d,
Florent Louisd,
Abderrahman El Bakalid and
Duy Quang Dao *ab
*ab
aInstitute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam. E-mail: daoduyquang@duytan.edu.vn
bFaculty of Natural Sciences, Duy Tan University, Da Nang 550000, Vietnam
cDepartment of Chemistry, University of Sciences, Hue University, Hue 530000, Vietnam
dDepartment of Chemistry, University of Education, Hue University, Hue 530000, Vietnam
eUniversité de Lille, CNRS, UMR 8522 – PC2A – PhysicoChimie des Processus de Combustion et de l'Atmosphère, 59000 Lille, France
First published on 10th January 2022
Abstract
Direct and indirect antioxidant activities of rosmarinic acid (RA) based on HOO˙/CH3OO˙ radical scavenging and Fe(III)/Fe(II) ion chelation were theoretically studied using density functional theory at the M05-2X/6-311++G(2df,2p) level of theory. First, four antioxidant mechanisms including hydrogen atom transfer (HAT), radical adduct formation (RAF), proton loss (PL) and single electron transfer (SET) were investigated in water and pentyl ethanoate (PEA) phases. Regarding the free radical scavenging mechanism, HAT plays a decisive role with overall rate coefficients of 1.84 × 103 M−1 s−1 (HOO˙) and 4.49 × 103 M−1 s−1 (CH3OO˙) in water. In contrast to PL, RAF and especially SET processes, the HAT reaction in PEA is slightly more favorable than that in water. Second, the [Fe(III)(H2O)6]3+ and [Fe(II)(H2O)6]2+ ion chelating processes in an aqueous phase are both favorable and spontaneous especially at the O5, site-1, and site-2 positions with large negative ΔrG0 values and great formation constant Kf. Finally, the pro-oxidant risk of RA− was also considered via the Fe(III)-to-Fe(II) complex reduction process, which may initiate Fenton-like reactions forming reactive HO˙ radicals. As a result, RA− does not enhance the reduction process when ascorbate anions are present as reducing agents, whereas the pro-oxidant risk becomes remarkable when superoxide anions are found. The results encourage further attempts to verify the speculation using more powerful research implementations of the antioxidant activities of rosmarinic acid in relationship with its possible pro-oxidant risks.
Introduction
Oxidative stress (OS) resulting from free radical action is one of the reasons for the serious decline in human health.1,2 Free radicals damage biological compounds that make up human cells (i.e. lipid and protein) or carry genetic information (i.e. DNA and RNA).1,3,4 This causes several diseases such as cancers, heart diseases, and Alzheimer's disease.5–11 Many methods have been used to protect human health from OS. Among them, the use of antioxidant compound supplementary provided from natural products or diets is one of the most effective ways.1,12 Phenolic compounds that are ubiquitously distributed phytochemicals found in most fruits and vegetables have widely been investigated as potent antioxidants towards different free radicals, mostly peroxyl radicals including HOO˙, CH3OO˙, and C2H5OO˙. For example, fraxetin can scavenge HOO˙/CH3OO˙ with overall rate constants (koverall) of 3.99 × 108 M−1 s−1/2.76 × 109 M−1 s−1 and 2.43 × 104 M−1 s−1/2.81 × 103 M−1 s−1 in aqueous and pentyl ethanoate (PEA), respectively.13 Ellagic acid is also reported to be able to react with HOO˙ radicals via a hydrogen transfer (HT) mechanism with koverall values of 1.57 × 105 M−1 s−1 and 4.29 × 102 M−1 s−1 in water and PEA media, respectively.14 Similarly, different phenolic compounds have also been analyzed for evaluating their scavenging activities towards peroxyl radicals: propyl gallate,15 esculetin,16 trans-resveratrol,17 capsaicin,18 sinapinic acid,19 piceatannol,20 genistein, daidzein, glycitein, equol, 6-hydroxydaidzein, 8-hydroxiglycitein,21 and dihydroxybenzoic acids.22The hydroxycinnamic acids, a class of polyphenol compounds, have already demonstrated their benefits to human health, including antioxidant,9,12,23 anticancer,7,24 anti-inflammatory,25,26 and antiviral27 activities. The antioxidant activity of hydroxycinnamic acids and their derivatives has attracted the attention of many researchers.5–12,23,28 Owing to the presence of phenolic hydroxyl groups and the participation of large conjugated systems, many hydroxycinnamic acids are expected to have high free radical scavenging activities based on the H-atom transfer from the –OH group.5,6 In addition, the secondary antioxidant activity via transition metal ion chelation of hydroxycinnamic acids has also been well reported.9,10 Normally, these acids contain –COOH and –OH groups and sometimes have the ester or ether groups that allow the complexation with metal ions.9,29–31
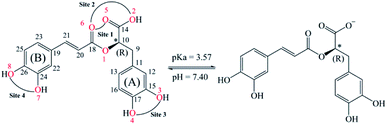
Rosmarinic acid (RA, Fig. 1) is one of the hydroxycinnamic acids, and was initially isolated and purified from the extract of rosemary, a member of mint family (Lamiaceae), in 1958 by Scarpati and Oriente.32,33 With an acid dissociation constant Ka of 10−3,57 mono-anionic RA− is the main form of RA existing in the physiological environment (pH ranging from 7.35 to 7.45).34 Rosmarinic acid also shows a large number of biological and pharmacological activities including anti-myotoxic,35 antioxidant,36–40 anti-inflammatory,26 antimicrobial,41 anti-mutagenic,42 anti-cancer,43 antibacterial,44 and antiviral27 functions. Moreover, RA is able to interact with several high-molecular weight compounds such as proteins and lipids.40,45–47 In a research study by Xin Peng et al., the interaction of RA with bovine serum albumin (BSA) was investigated by combining experiments and molecular docking.46 The experimental results indicate that BSA has a high affinity towards RA with a binding constant of 4.18 × 104 mol L−1. Meanwhile, the docking results show that RA is bound to the site-1 (subdomain IIA) of BSA, at Leu-209, Val-239, Leu-196, Trp-212, Ala-289 and Leu-236 amino acids.
Among the biological activities of RA, its antioxidant activity has been investigated via both experimental and computational approaches.36–40 For example, Fadel et al. experimentally studied the antioxidant activity of RA in preventing lipid peroxidation.36 The authors measured the peroxidation of liposomes of 1,2-dilinoleoyl-sn-glycero-3-phosphocholine (DLPC) at 37 °C with a hydrophilic radical generator, namely, 2,2′-azo-bis(2-amidinopropane)dihydrochloride (AAPH). The results indicate that DLPC is fully peroxidized at a RA concentration of 0.25 μM, whereas the peroxidation level is lower than 20% for a RA concentration greater than 2 μM after 60 min. Popov et al. conducted a comparative study on the radical scavenging properties of RA in a system of 2,2′-azo-bis(2-methylpropionamidin)dihydrochloride/luminol and hemoglobin/hydrogen peroxide/luminol to determine its protective potential in preventing peroxidation of linoleic acid.40 The antioxidant activity of RA in this studied system is remarkably higher than that of trolox, ascorbic acid and taxifolin. Additionally, Cao et al. evaluated the antioxidant activity of RA via a DFT approach at the B3LYP/6-311G(d) level of theory.37 Their results indicated the BDE values of O7–H, O8–H, and O4–H bonds (see Fig. 1) are 325.7, 314.9, and 316.5 kJ mol−1, respectively. Furthermore, the radical resulting from the H-abstraction of O7–H is more stable than that of the remaining O–H bonds. Besides, Świsłocka et al. combined DFT calculations at the B3LYP/6-311+G(d,p) level of theory and experiments to investigate the structures and antioxidant properties of rosmarinic acid and its alkali metal salts.48 In this work, the antioxidant activities of RA and its lithium, sodium, and potassium salts were determined by their ability to scavenge 1,1-diphenyl-2-picrylhydrazyl (DPPH˙) radicals and to reduce the ferric complex in the ferric reducing antioxidant power (FRAP) assay. The results indicate that all of these salts have better antioxidant properties than that of initial RA. Moreover, the IC50 values in the DPPH˙ assay are very similar for all the studied salts, whereas sodium rosmarinate shows the highest antioxidant activity in the FRAP assay. There has been scare study on the pro-oxidant activities of rosmarinic acid in the literature. Muñoz-Muñoz et al. experimentally investigated the intrinsic pro-oxidant activity of RA via generation of H2O2 and free radicals by the action of peroxidase in competition with its antioxidant properties based on consumption of H2O2 and free radicals.49 In balancing between the pro-oxidant and antioxidant activities, the authors concluded that RA can be considered as a net antioxidant.
Although there are some experimental and computational works dedicated for the antioxidant and pro-oxidant activities of rosmarinic acid, systematic study of its chemical kinetics in free radical scavenging mechanisms is still lacking, and hence, further detailed studies are needed. Furthermore, the secondary antioxidant properties based on the transition metal chelating ability, and the pro-oxidant activity based on redox processes that may initiate Fenton-like reactions yielding reactive HO˙ radicals, have not been reported in the literature yet.
Thus, the main goal of this study is to evaluate the free radical scavenging activities of rosmarinic acid (RA) towards the ROO˙ radical family including HOO˙ and CH3OO˙ in aqueous and pentyl ethanoate (PEA) phases. Density functional theory (DFT) was used to optimize the structures and to calculate vibrational frequencies for different forms of RA including neutral, mono-anion, radicals, and metal complexes. The intrinsic thermochemical parameters including bond dissociation energy (BDE), proton affinity (PA) and ionization potential (IP) were first calculated. The standard enthalpies (ΔrH0) and Gibbs free energies (ΔrG0) of reactions between RA and HOO˙/CH3OO˙ at potential positions were estimated and the kinetics of these reactions were also computed using the conventional transition state theory (TST) and quantum mechanics-based tests for the overall free radical scavenging activity (QM-ORSA) method. In addition, the secondary antioxidant properties of RA based on the chelation towards Fe(III) and Fe(II) ions to prevent the Harber–Weiss reaction50–52 forming harmful radicals were investigated. Moreover, the reactions between the Fe(III) complexes and the reducing agents, i.e., ascorbate anion and superoxide anion, were studied to evaluate the pro-oxidant activity of RA. The reaction enthalpies (ΔrH0) and Gibbs free energies (ΔrG0) of these reactions were finally calculated. Hopefully, the obtained results can explain whether there is a competition between the antioxidant and pro-oxidant properties of rosmarinic acid in the studied conditions.
Computational method
All geometry optimizations and vibrational frequency calculations were performed using Gaussian 16 Rev. A.03 package53 in water and pentyl ethanoate (PEA) phases at the M05-2X/6-311++G(2df,2p) level of theory. The hybrid meta exchange–correlation GGA M05-2X functional was recommended for the thermodynamic and kinetic calculation by their developers54 and has widely been used in the kinetics of free radical scavenging reactions.4,55 The structures of [Fe(H2O)6]2+ and [Fe(H2O)6]3+ were respectively employed as ferrous and ferric ion models in the aqueous phase, as recommended by several previous research studies.9,31,56–58 In these models, the Fe ion interacted with six water molecules via the Fe–O bonds in an octahedral fashion with quintet spin for Fe(II) complexes and sextet one for Fe(III) complexes. Four main direct antioxidant mechanisms of RA including formal hydrogen transfer (FHT), proton loss (PL), single electron transfer (SET) and radical adduct formation (RAF) were evaluated.First, the intrinsic thermochemical parameters including bond dissociation energies (BDE), proton affinities, and adiabatic ionization potentials (IP) characterizing respectively for FHT, PL, and SET mechanisms were calculated using the following equations:
| BDE (R–H) = H(R˙) + H(H˙) − H(R–H); | (1) |
| PA = H(R−) + H(H+) − H(RH˙+); | (2) |
| IP = H(RH˙+) + H(e−) − H(R–H); | (3) |
The peroxyl radicals including HOO˙ and CH3OO˙ were chosen in order to evaluate the influence of free radicals' nature on the primary antioxidant activities of RA. A large number of works reported in the literature have recommended the use of the peroxyl radicals (ROO˙) as major reaction partners for evaluating the relative scavenging activity of different compounds.4,63–65 These radicals have not too short half-lives, which is required for the efficient interception by phenolic compounds.67 The HOO˙ is the simplest of the ROO˙ radicals that is among the free radicals of biological relevance. An excess amounts of HOO˙ in a physiological environment need to be removed to retard oxidative stress.66 HOO˙ and CH3OO˙ were therefore chosen to evaluate the influence of free radicals' nature on the primary antioxidant activities of RA.
The standard Gibbs free energies of reaction (ΔrG0) with free radicals, HOO˙ as an example, were calculated using equations (eqn (5), (7), (9) and (11)) for four mechanisms including FHT, PL, RAF and SET as follows:
| - FHT: R–H + HOO˙ → R˙ + HOOH; | (4) |
| ΔrG0FHT = [G(R˙) + G(HOOH)] − [G(R–H) + G(HOO˙)]; | (5) |
| - PL: R–H + HOO˙ → R− + HOOH+˙; | (6) |
| ΔrG0PL = [G(R−) + G(HOOH+˙)] − [G(R–H) + G(HOO˙)]; | (7) |
| - RAF: R–H + HOO˙ → [RH–OOH]˙; | (8) |
| ΔrG0RAF = G([RH–OOH]˙) − [G(R–H) + G(HOO˙)]; | (9) |
| - SET: R–H + HOO˙ → R–H+˙ + HOO−; | (10) |
| ΔrG0SET = [G(R–H+˙) + G(HOO−)] − [G(R–H) + G(HOO˙)]; | (11) |
The energy values for the CH3OO˙ radical scavenging reactions were similarly determined.
The rate constants (k) of three reactions FHT, RAF and SET, which may be in concurrence were calculated via the conventional transition state theory (TST) approach68,69 as follows:4
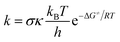 | (12) |
For the single electron transfer (SET) process, ΔG≠ was determined using the Marcus theory.71,72 The ΔG≠ quantity in this approach was calculated using equation (eqn (13)):
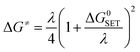 | (13) |
| λ = ΔESET − ΔG0SET | (14) |
In the Collins–Kimball theory,73 the apparent rate constant (kapp) should include the diffusion limit, which is the close to or higher than the diffusion limit of the solution. The kapp value was calculated as follows:
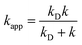 | (15) |
| kD = 4πRABDABNA | (16) |
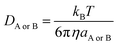 | (17) |
When all rate constants of possible free radical scavenging reactions have been estimated, the total or overall rate coefficient (ktot)4,78 which characterizes the reaction rate of each antioxidant compound was calculated using equation (eqn (18)):
| ktot = ∑kFHT + ∑kRAF + ∑kSET | (18) |
Furthermore, the indirect antioxidant activity of RA was evaluated based on its chelating ability towards Fe(II) and Fe(III) ions. The complexation reactions of RA with [Fe(H2O)]2+ and [Fe(H2O)]3+ were estimated using reaction enthalpies (ΔrH0), standard Gibbs free energies (ΔrG0), and formation constants (Kf) (eqn (19)):
| Lx + [Fe(H2O)6]y → [FeL(H2O)6−n]x+y + nH2O; | (19) |
| ΔrH0 = H([FeL(H2O)6−n]x+y) + nH(H2O) − H(Lx) − H([Fe(H2O)6]y); | (20) |
| ΔrG0 = G([FeL(H2O)6−n]x+y) + nG(H2O) − G(Lx) − G([Fe(H2O)6]y); | (21) |
Stability constant (K) is the important parameter for the investigation of equilibrium in solutions. For the complexation reactions of metal ions with different ligands, this parameter commonly called the formation constant (Kf) is widely studied to evaluate the concentration of each existing form of the complexes in the solution.79–81 The Kf values82 were calculated using equation (eqn (22)):
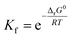 | (22) |
The pro-oxidant activity of RA was estimated through the reduction reactions of Fe(III) to Fe(II) complexes, which are involved in Fenton-like reactions producing reactive hydroxyl (HO˙) radicals. Following previous research,9,83 a superoxide anion radical (O2˙−) and an ascorbate anion (Asc−) were chosen as reductive agents. The reactions between the complexes of Fe(III) and two reducing agents occur as follows (reactions (23) and (24)):
| [Fe(III)L(H2O)6−n]x+3 + (O2˙−) → [Fe(II)L(H2O)6−n]x+2 + O2; | (23) |
| [Fe(III)L(H2O)6−n]x+3 + (Asc−) → [Fe(II)L(H2O)6−n]x+2 + Asc˙; | (24) |
The corresponding redox reactions of aqueous complexes occur as follows (reactions (25) and (26)):
| [Fe(III)(H2O)6]3+ + (O2˙−) → [Fe(II)(H2O)6]2+ + O2; | (25) |
| [Fe(III)(H2O)6]3+ + (Asc−) → [Fe(II)(H2O)6]2+ + Asc˙; | (26) |
The standard reaction enthalpies (ΔrH0) and Gibbs free energies (ΔrG0) of the reactions (23) and (24) were also determined by the difference in the total enthalpies (H) and Gibbs free energy (G), respectively, between the products and the reactants as follows (eqn (27)–(30)):
For superoxide anion radical (O2˙−):
| ΔrH0 = H([Fe(II)L(H2O)6−n]x+2) + H(O2) − H([Fe(III)L(H2O)6−n]x+3) − H(O2˙−); | (27) |
| ΔrG0 = G([Fe(II)L(H2O)6−n]x+2) + G(O2) − G([Fe(III)L(H2O)6−n]x+3) − G(O2˙−); | (28) |
For ascorbate anion (Asc−):
| ΔrH0 = H([Fe(II)L(H2O)6−n]x+2) + H(Asc˙) − H([Fe(III)L(H2O)6−n]x+3) − H(Asc−); | (29) |
| ΔrG0 = G([Fe(II)L(H2O)6−n]x+2) + G(Asc˙) − G([Fe(III)L(H2O)6−n]x+3) − G(Asc−); | (30) |
The energy values for the redox reactions of aqueous complexes were similarly determined.
SEAGrid (http:www.seagrid.org)84–87 is acknowledged for computational resources and services for the selected results used in this publication.
Results and discussion
Direct antioxidant potential: intrinsic thermochemical properties
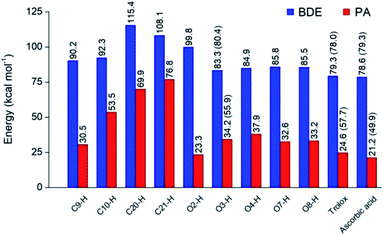
Optimized structures of rosmarinic acid in neutral and mono-anionic forms in the water phase at 298.15 K calculated at the M05-2X/6-311++G(2df,2p) level of theory are presented in Fig. S1 (ESI file†). An intrinsic reactivity-based strategy, which only focuses on the chemical nature of the studied compound itself, is a helpful approach to quickly screen potential antioxidants. The intrinsic thermochemical parameters including BDE, PA, and IP values were first calculated to determine the antioxidant potential of RA via three mechanisms FHT, PL (Fig. 2), and SET (Fig. S2, ESI file†), respectively.It can be seen in Fig. 2 that the phenolic O–H bonds (i.e. O3–H, O4–H, O7–H, and O8–H) have lower BDE values ranging from 83.3 to 85.8 kcal mol−1 than that of other bonds from 90.2 to 115.4 kcal mol−1. Therefore, the FHT reactions on the RA molecule may probably involve O–H sites. The two weakest O–H bonds are found at the O3–H (83.3 kcal mol−1) and O4–H (84.9 kcal mol−1) sites of the A ring (Fig. 1). These values are higher than the BDEs of trolox and ascorbic acid calculated at the same level of theory, 79.3 and 78.6 kcal mol−1, respectively. When compared with several other antioxidants in previous studies obtained by the same M05-2X method, the BDE value at the O3–H of RA is lower than that in water of 2-(sec-butyl)-7,8-dimethoxybenzo[de]imidazo[4,5,1-ij][1,6]-naphthyridin-10(9H)-one (84.9 kcal mol−1),61 xanthyletin (87.1 kcal mol−1),62 trans-p-coumaric acid (85.0 kcal mol−1)6 and protocatechuic acid (83.9 kcal mol−1).88 Furthermore, the hydrogen dissociation in the PEA solvent is slightly more favorable than that in water with a lower BDE value, for example, a BDE (O3–H) of 80.4 kcal mol−1 as compared to 83.3 kcal mol−1 in water. This value is also slightly higher than those of trolox and ascorbic acid in the same medium.
The PA values characterize the deprotonation process of molecules involved in the first step of SPL-ET or SPL-HAT two-step mechanisms.1 The second step of SPL-ET mechanism is related to the electron transfer from the deprotonated antioxidant to the free radical, whereas the second transferred species in SPL-HAT is a hydrogen atom. Thus, the PA parameter allows characterizing the preponderance of these mechanisms. The lower the PA value, the higher the deprotonation potential of molecules. The PA values of different C–H and O–H bonds present in Fig. 2 vary from 23.3 to 76.8 kcal mol−1. The PA values of O–H bonds (from 23.3 to 37.9 kcal mol−1) are generally lower than the ones of C–H (from 53.5 to 76.8 kcal mol−1), except a quite low value of the C9–H bond (30.5 kcal mol−1). Furthermore, the PA value observed at the C9–H bond (30.5 kcal mol−1) is quite lower than that of C20–H (69.9 kcal mol−1) and C21–H (76.8 kcal mol−1). The lower PA value of the C9–H bond is due to the cleavage of the C10–O1 bond resulting from the proton dissociation at the C9–H position (Fig. S2, ESI file†). In addition, it is expected that a non-polar solvent like PEA is not favorable for transition of a charged particle like a proton. In fact, PA (C3–H) is equal to 55.9 kcal mol−1 that is remarkably higher than that in water (i.e. 34.2 kcal mol−1). Thus, the first step of SPL-ET or SPL-HAT mechanisms is expected to occur at the O2–H or C9–H of the RA molecule. The relatively low PA value at O2–H of the COOH group (23.3 kcal mol−1) probably indicates the presence of the mono-anionic form generated from the deprotonation at this position in water. This PA value is quite lower than that of piperidine[3,2-b]demethyl(oxy)aaptamine (60.2 kcal mol−1),61 pandanusin A (54.6 kcal mol−1), and 5-hydroxynoracronycin (36.5 kcal mol−1)62 (obtained at the M05-2X/6-311++G(d,p) level of theory).
The adiabatic IP value is the minimum energy required to remove an electron from a studied compound. Thus, the lower IP value represents the easier electron transferring ability and the higher antioxidant activity via the SET mechanism. As shown in Fig. S3 (ESI file†), the IP value in water of RA being 121.2 kcal mol−1 is lower than that of trolox (128.8 kcal mol−1), but higher than that of ascorbic acid (108.5 kcal mol−1). It is noteworthy that the PEA solvent is also unfavorable to the transfer of an electron particle from RA to free radical with IP in PEA (138.5 kcal mol−1) higher than that in water (121.2 kcal mol−1). In addition, RA presents an IP value in PEA higher than that of trolox (122.1 kcal mol−1) but lower than that of ascorbic acid (148.7 kcal mol−1).
Kinetics of scavenging reactions towards HOO˙/CH3OO˙ radicals
Evaluating the antioxidant activities based on the thermochemical strategy allows considering the influence of the free radical nature by predicting reaction enthalpies (ΔrH0) and standard Gibbs free energies (ΔrG0) at 298.15 K. As discussed above, the RA− mainly exists in a physiological environment under the mono-anionic form, RA−. Thus, in this section, we evaluate the standard Gibbs free energies of the FHT, PL, RAF and SET reactions of the RA− towards HOO˙ and CH3OO˙ radicals as recommended by several previous studies1,4 (Table 1).| Pos. | HOO˙ | CH3OO˙ | ||||||
|---|---|---|---|---|---|---|---|---|
| FHT | PL | RAF | SET | FHT | PL | RAF | SET | |
| 30.8 (64.1) | 32.5 (64.8) | |||||||
| C9H | 1.2 | 44.4 | — | 2.2 | 48.4 | — | ||
| C10H | 6.1 | 92.4 | — | 7.2 | 96.4 | — | ||
| C20 | 25.6 | 87.2 | 2.4 (−3.4) | 26.7 | 91.2 | 9.8 (9.0) | ||
| C21 | 18.3 | 96.8 | 9.7 | 19.4 | 100.8 | 10.4 | ||
| O3H | −5.0 (−5.2) | 51.3 | — | −3.9 (−3.5) | 55.3 | — | ||
| O4H | −3.9 | 55.3 | — | −2.8 | 59.2 | — | ||
| O7H | −2.5 (−3.4) | 49.5 (103.6) | — | −1.4 (−1.7) | 53.5 (88.8) | — | ||
| O8H | −3.0 | 50.4 | — | −1.9 | 54.4 | — | ||
| Trolox | −8.7 (−7.3) | 40.7 (94.9) | 19.4 (59.0) | −7.6 (−5.6) | 44.7 (80.1) | 21.1 (59.6) | ||
| Ascorbic acid | −9.4 (−5.8) | 36.4 (86.8) | 40.0 (86.1) | −8.3 (−4.1) | 40.3 (72.0) | 41.7 (86.8) | ||
The ΔrG0 values of the FHT reaction between RA− towards HOO˙ and CH3OO˙ at the phenolic O–H positions are all negative, and thus, the FHT reactions occurring at these positions are all favorable and spontaneous. The most favorable reactions in water are expected at the O3–H site with the ΔrG0 value being −5.0 and −3.9 kcal mol−1 for the reaction towards HOO˙ and CH3OO˙ radicals, respectively. Moreover, ΔrG0 values of these reactions are less negative than that of trolox and ascorbic acid being −8.7 and −9.4 kcal mol−1 for the reactions with HOO˙, and −7.6 and −8.3 kcal mol−1 for the ones with CH3OO˙, respectively. Besides, the lowest ΔrG0 value of FHT between RA− and HOO˙ is very close to those obtained by the DFT/M05-2X method for piperidine[3,2-b]demethyl(oxy)aaptamine (−5.0 kcal mol−1),61 pandanusin (−5.0 kcal mol−1), citrusinine-I (−4.9 kcal mol−1),62 and 5-hydroxynoracronycin (−4.6 kcal mol−1)62 and remarkably lower than those of 9-amino-2-ethoxy-8-methoxy-3H-benzo[de][1,6]naphthyridine-3-one (7.1 kcal mol−1)61 and tryptamine (−3.8 kcal mol−1).78 In contrast, the reactions occurring at the C–H positions are all unfavorable with positive ΔrG0 values ranging from 1.2 to 25.6 kcal mol−1 for the HOO˙ radical and from 2.2 to 26.7 kcal mol−1 for the CH3OO˙ one. Furthermore, the FHT process occurs in the PEA solvent more favorably than in the aqueous phase. In fact, ΔrG0 values in PEA of the reactions with HOO˙ obtained at O3–H and O7–H are −5.2 and −3.4 kcal mol−1, which are slightly lower than those in water (i.e. −5.0 and −2.5 kcal mol−1, respectively).
Regarding the PL mechanism, it is observed that all the reactions towards both the radicals show large positive ΔrG0 values. The lowest ΔrG0 value of PL reactions was found at the C9–H bond with the values in water as 44.4 and 48.4 kcal mol−1 for HOO˙ and CH3OO˙ radicals, respectively. In addition, the ΔrG0 values of these reactions are higher than those of trolox (i.e. 40.7 kcal mol−1 for HOO˙ and 44.7 kcal mol−1 for CH3OO˙) and ascorbic acid (i.e. 36.4 kcal mol−1 for HOO˙ and 40.3 kcal mol−1 for CH3OO˙). As mentioned above, the PEA medium largely increases the ΔrG0 value of the PL process. For example, the ΔrG0 values obtained in PEA at O7–H (103.6 and 88.8 kcal mol−1) is higher than that in water (49.5 and 53.5 kcal mol−1 for HOO˙ and CH3OO˙, respectively).
The RAF reactions of RA− were examined at the C20![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C21 double bond. Similar to the PL reactions, the ΔrG0 values of the RAF reactions are all positive. It is noteworthy that the reactions of HOO˙ and CH3OO˙ radicals with RA− at the C20 position are more favorable than those at the C21 one. Indeed, the ΔrG0 values of the RAF reaction at C20 are 2.4 and 9.8 kcal mol−1 for HOO˙ and CH3OO˙ radicals, respectively, whereas the ones at C21 are 9.7 and 10.4 kcal mol−1, in turn. In addition, the lowest ΔrG0 of RAF reactions between RA− and HOO˙ is lower than those obtained by the DFT/M05-2X method for 9-amino-2-ethoxy-8-methoxy-3H-benzo[de][1,6]naphthyridine-3-one (5.2 kcal mol−1)61 and tryptamine (2.5 kcal mol−1).78 In contrast to FHT and PL, the ΔrG0 value of the RAF reaction in the PEA solvent is slightly lower than that in water. Indeed, ΔrG0 (C20) values in PEA are equal to −3.4 and 9.0 kcal mol−1 that are lower than those in water, which are 2.4 and 9.8 kcal mol−1 for HOO˙ and CH3OO˙ radical, respectively (Table 1).
C21 double bond. Similar to the PL reactions, the ΔrG0 values of the RAF reactions are all positive. It is noteworthy that the reactions of HOO˙ and CH3OO˙ radicals with RA− at the C20 position are more favorable than those at the C21 one. Indeed, the ΔrG0 values of the RAF reaction at C20 are 2.4 and 9.8 kcal mol−1 for HOO˙ and CH3OO˙ radicals, respectively, whereas the ones at C21 are 9.7 and 10.4 kcal mol−1, in turn. In addition, the lowest ΔrG0 of RAF reactions between RA− and HOO˙ is lower than those obtained by the DFT/M05-2X method for 9-amino-2-ethoxy-8-methoxy-3H-benzo[de][1,6]naphthyridine-3-one (5.2 kcal mol−1)61 and tryptamine (2.5 kcal mol−1).78 In contrast to FHT and PL, the ΔrG0 value of the RAF reaction in the PEA solvent is slightly lower than that in water. Indeed, ΔrG0 (C20) values in PEA are equal to −3.4 and 9.0 kcal mol−1 that are lower than those in water, which are 2.4 and 9.8 kcal mol−1 for HOO˙ and CH3OO˙ radical, respectively (Table 1).
Moreover, the SET reactions of RA− toward HOO˙ and CH3OO˙ radicals also show positive ΔrG0 values of 30.8 and 32.5 kcal mol−1, in sequence. Additionally, the ΔrG0 values are comparable with the ones of trolox (i.e. 19.4 and 21.1 kcal mol−1 for HOO˙ and CH3OO˙ radicals, respectively) and ascorbic acid (i.e. 40.0 and 41.7 kcal mol−1 for HOO˙ and CH3OO˙ radicals). The non-polar PEA solvent is shown to be unfavorable for the electron transfer reaction as compared to the one in a polar solvent like water. Overall, the FHT and RAF reactions of RA− toward HOO˙ and CH3OO˙ radicals are likely more favorable than that of the PL and SET reactions.
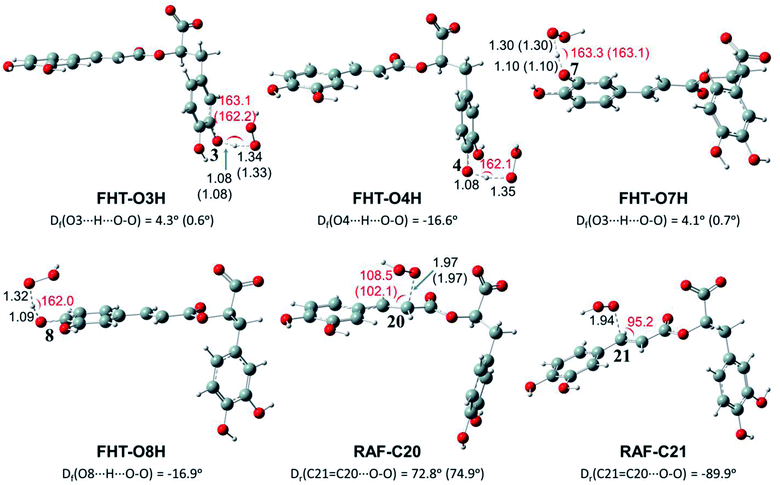
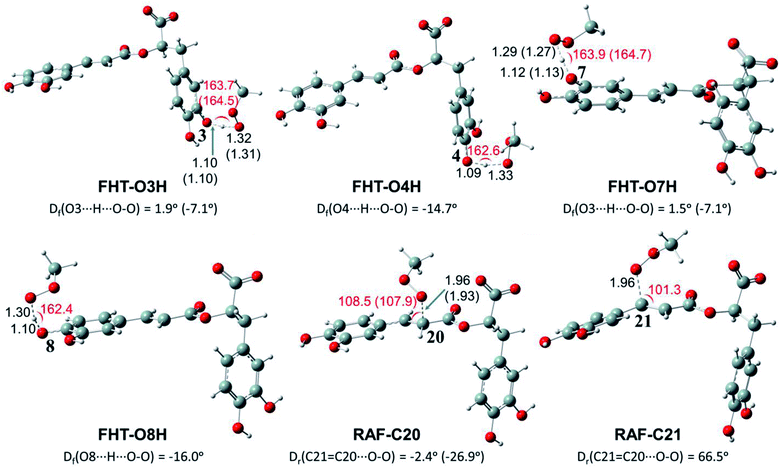
Depending on the chemical structure of the potential antioxidant, the RAF reaction may be in competition with the FHT one.1,61,62,78 In this work, the kinetic calculations were considered for the FHT reactions at the O–H sites showing negative ΔrG0 values, also for all RAF and SET reactions. Optimized structures of the transition states (TSs) for FHT and RAF reactions of RA− toward HOO˙ and CH3OO˙ radicals in water are presented in Fig. 3 and 4, respectively. The corresponding Cartesian coordinates and thermochemistry data are also presented in Tables S1 and S2 (ESI file†). The similar data for the reactions occurring in pentyl ethanoate (PEA) that mimics lipid media are also resumed in Table S3 (ESI file†).
As can be seen in Fig. 3 and 4, the O–H bond lengths at the TSs of FHT vary from 1.08 to 1.09 Å and from 1.10 to 1.18 Å for HOO˙ and CH3OO˙ radicals, respectively. Meanwhile, the distances between the shifting H-atom and the reacted O-atom of the radical are noticeably longer ranging from 1.30 to 1.35 Å for HOO˙ and from 1.29 to 1.33 Å for CH3OO˙. The bent angles for H⋯O⋯H in FHT reactions vary from 162.0 to 164.0°. For RAF reactions, the bond distances between the oxygen atom of the radical and the C-sp2 atom range from 1.94 to 1.97 Å, whereas the interactive O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C angles change from 95.2 to 108.5°.
C angles change from 95.2 to 108.5°.
In order to evaluate the kinetics of HOO˙ and CH3OO˙ scavenging reactions for RA−, the Gibbs free energy of activation (ΔG≠), diffusion rate constant (kD), TST thermal rate constant (kT), Eckart-tunneling-corrected rate constants (keck), diffusion-corrected apparent rate constants (kapp), and branching ratio (Γ) for FHT, RAF and SET reactions were calculated at 298.15 K in water and PEA using conventional transition state theory (TST). The kinetics data are shown in Table 2 for the reactions of HOO˙ radicals and Table 3 for the reactions of CH3OO˙ radicals.
| Position | ΔG≠ | kD | kT | keck | kapp | Γ |
|---|---|---|---|---|---|---|
| FHT | ||||||
| O3H | 18.6 (17.1) | 2.41 × 109 (2.55 × 109) | 4.73 × 102 (8.25 × 103) | 6.44 × 104 (1.39 × 105) | 4.73 × 102 (8.25 × 103) | 25.70 |
| O4H | 18.8 | 2.41 × 109 | 3.44 × 102 | 4.26 × 104 | 3.44 × 102 | 18.67 |
| O7H | 18.8 (17.6) | 2.39 × 109 (2.53 × 109) | 8.73 × 102 (7.05 × 103) | 2.72 × 105 (2.58 × 105) | 8.73 × 102 (7.05 × 103) | 47.41 |
| O8H | 20.2 | 2.40 × 109 | 1.51 × 102 | 8.44 × 104 | 1.51 × 102 | 8.21 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| RAF | ||||||
| C20 | 21.4 (23.8) | 1.98 × 109 (2.10 × 109) | 9.76 × 10−2 (8.01 × 10−3) | 1.36 × 10−1 (1.12 × 10−2) | 9.76 × 10−2 (8.01 × 10−3) | 0.01 |
| C21 | 23.7 | 1.95 × 109 | 2.65 × 10−3 | 4.42 × 10−3 | 2.65 × 10−3 | 0.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| SET | ||||||
| 36.1 (103.1) | 8.36 × 109 (8.93 × 109) | 5.03 × 10−13 (4.10 × 10−62) | — | 5.03 × 10−13 (4.41 × 10−62) | 0.00 | |
| Position | ΔG≠ | kD | kT | keck | kapp | Γ |
|---|---|---|---|---|---|---|
| FHT | ||||||
| O3H | 19.1 (18.0) | 2.41 × 109 (2.36 × 109) | 3.52 × 102 (3.74 × 103) | 8.10 × 104 (1.34 × 105) | 3.52 × 102 (3.74 × 103) | 7.84 |
| O4H | 18.6 | 2.40 × 109 | 8.61 × 102 | 2.07 × 105 | 8.61 × 102 | 19.17 |
| O7H | 18.3 (19.0) | 2.39 × 109 (2.35 × 109) | 3.22 × 103 (1.73 × 103) | 1.72 × 106 (1.65 × 105) | 3.22 × 103 (1.73 × 103) | 71.60 |
| O8H | 21.1 | 2.40 × 109 | 6.20 × 101 | 7.07 × 104 | 6.20 × 101 | 1.38 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| RAF | ||||||
| C20 | 22.3 (25.9) | 1.97 × 109 (1.94 × 109) | 2.39 × 10−2 (2.70 × 10−4) | 3.42 × 10−2 (4.24 × 10−4) | 2.39 × 10−2 (2.7 × 10−4) | 0.00 |
| C21 | 24.4 | 1.92 × 109 | 8.79 × 10−4 | 1.65 × 10−3 | 8.79 × 10−4 | 0.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| SET | ||||||
| 40.4 (104.5) | 7.88 × 109 (8.59 × 109) | 3.41 × 10−16 (3.77 × 10−63) | — | 3.41 × 10−16 (3.77 × 10−63) | 0.00 | |
As observed in Table 2, FHT reactions demonstrate lower activation energies (i.e. from 18.6 for O3–H to 20.2 kcal mol−1 for O8–H) than those of RAF reactions (i.e. 21.4 and 23.7 kcal mol−1 for C20 and C21 positions, respectively) as well as than that of the SET reaction (i.e. 36.1 kcal mol−1). As a result, FHT reactions have high diffusion-corrected apparent rate constants (kapp), and thus, the products of HOO˙ radical scavenging of RA− almost result from these reactions with a total branching ratio (Γ) of 99.99%. It is noteworthy that the FHT reaction occurring at O7–H is the fastest with a kapp value of 8.73 × 102 M−1 s−1 and it accounts for the highest Γ value of 47.41%. In contrast, RAF and SET reactions occur with very low rate constants; especially, the kapp value of the SET reaction is only 5.03 × 10−13 M−1 s−1 and, therefore, this reaction hardly contributes to HOO˙ radical scavenging of RA−. Regarding two RAF reactions, the one occurring at the C20 position with a kapp value of 9.76 × 10−2 M−1 s−1 is more dominant than that at the C21 one showing kapp of 2.65 × 10−3 M−1 s−1.
Furthermore, the overall rate coefficient, ktot, for radical scavenging of RA− towards HOO˙ is 1.84 × 103 M−1 s−1, which is close to those obtained by the DFT/M05-2X method for guaiacol (1.55 × 103 M−1 s−1),89 1-methyluric acid (1.08 × 103 M−1 s−1)90 and about 100 times higher than those of vanillin (9.75 × 101 M−1 s−1),89 caffeine (3.19 × 101 M−1 s−1),91 and N(1)-acetyl-N(2)-formyl-5-methoxykynuramine (4.57 × 101 M−1 s−1).92
Regarding the CH3OO˙ scavenging reactions, the FHT mechanism is also the main process in forming approximately 100% product. The Gibbs free energies of activation (ΔG≠) vary from 18.3 to 21.1 kcal mol−1, while the ones of RAF are 22.3 and 24.4 kcal mol−1 for the reactions at the C20 and C21 positions, respectively. The ΔG≠ value of SET is also the highest one being 40.4 kcal mol−1. Besides, the most potential position for the FHT process is found at the –O7H position with a kapp value of 3.22 × 103 M−1 s−1 and Γ value of 71.60%. The RAF reactions at the C20 and C21 positions show lower kapp values (i.e. 2.39 × 10−2, 8.79 × 10−4, respectively) than the ones of FHT reactions. The SET reaction is also negligible with a kapp value of 3.41 × 10−16 M−1 s−1. The CH3OO˙ radical scavenging of RA− has ktot of 4.49 × 103 M−1 s−1. Therefore, the CH3OO˙ radical scavenging reaction by RA− is slightly more favorable and spontaneous than that of HOO˙ (i.e. 1.84 × 103 M−1 s−1).
It is noteworthy that the PEA solvent shows different influences on the scavenging processes. In fact, the FHT reactions towards both HOO˙ and CH3OO˙ radicals are favored in the PEA solvent with lower ΔG≠ and kapp values, whereas the RAF and especially SET processes are all less favorable than those that occurred in the aqueous phase (Tables 2 and 3). The differences in reactivity of RA− with HOO˙ and CH3OO˙ radicals via FHT and RAF reactions can be explained by different dipole moment values at their transition states (Table S4, ESI file†). As observed in Table S4,† the higher the dipole moment value of TS, the lower the Gibbs free energy of activation value, and thus the more favorable the reaction occurs.
Overall, the FHT reactions of RA− towards both HOO˙ and CH3OO˙ radicals are more preponderant than those of RAF and SET reactions. The non-polar PEA solvent slightly enhances FHT reactions, while it is unfavorable to RAF and especially to SET reactions.
Chemical nature of formal hydrogen transfer (FHT) reactions
Understanding the chemical nature of the formal hydrogen transfer (FHT) process plays an important role in the potential applications of RA in chemical and biological fields. The FHT may occur via two different pathways, i.e. hydrogen atom transfer (HAT) or proton-coupled electron transfer (PCET), which have similar initial reactants and final products. For that reason, distinguishing these two processes is always a challenging task that needs multiple supplementary calculations and analyses, e.g. single occupied molecular orbital (SOMO) distributions (Fig. 5), natural bond orbital (NBO) analyses (Table S5, ESI file†), natural population analysis (NPA) charges, atomic spin densities (ASD), and natural electron configuration (NEC) at the transition states (TSs) of FHT reactions (Table S6, ESI file†).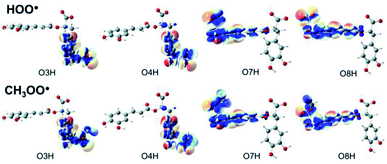 | ||
| Fig. 5 SOMO distributions of the transition states (TSs) for FHT reactions between RA− with HOO˙ and CH3OO˙ radicals in the aqueous phase. | ||
Fig. 5 represents the SOMO distributions at the TSs for FHT reactions with HOO˙ and CH3OO˙ radicals at all four hydroxyl groups of RA−. Generally, the SOMO of HAT TSs is distributed along the H transition vector between the donor and the acceptor, whereas the one of PCET TSs is orthogonal to the transition vector.61,93 As can be seen in Fig. 5, the 2p orbitals of the acceptor (O atoms of hydroxyl group) and the ones of the donor (O atoms of the radicals) are interacted and distributed along the H-shifting vector. This observation is the first signal of the HAT process.
To provide more insights into the electron density interaction at the TSs of FHT reactions, we also performed the NBO analyses (Table S5, ESI file†). It is generally noted that the electron densities are essentially transferred from the lone pairs of the reactive oxygen atom on HOO˙ or CH3OO˙, i.e., O41 or O42, to the first unoccupied anti-bonding orbitals of the shifted H from the –OH groups. The stabilization energies of these processes vary from 66.0 to 79.0 kcal mol−1 and from 71.2 to 85.8 kcal mol−1 for the reactions with HOO˙ and CH3OO˙ radicals, respectively. In the reverse trend, the electron densities are also donated from the electron lone pairs on the reactive oxygen atom of the studied radicals to the first unoccupied anti-bonding orbital of the shifted-H.
Furthermore, NPA charge and 1s occupancy of the mitigating H and two involved O atoms at the TSs of the FHT reactions are presented in Table S6 (ESI file†). The results indicate that the NPA charges of the mitigating H are all positive varying from 0.37 to 0.38 e−. These charges are similar to that reported in the literature for the HAT mechanism (i.e. 0.31 to 0.4 e−).94 Meanwhile, the NPA charges of two oxygen atoms involved in the FHT reaction are all negative ranging from −0.42 to −0.44 e− and from −0.47 to −0.56 e− for the reactive O atom of the radical and for the one of RA−, respectively. Moreover, the 1s occupancy show that the mitigating H is characterized by 1s0.51–0.52 orbital configuration, which corresponds to one H atom with the 1s1.0 configuration. In addition, the spin densities are all located at the H-donor, (i.e. 0.12286–0.14291) and -acceptor atoms (i.e. 0.28294–0.34933); thus, the ones at the mitigating-H are slightly negative (i.e. about −0.02). All the above-mentioned signals allow confirming that the shifting-H represents an atom-like species rather than a proton-like species. It means that the FHT processes at all four –OH groups have the chemical nature of the HAT mechanism.
Preventive antioxidant potential based on iron ion-chelating activities
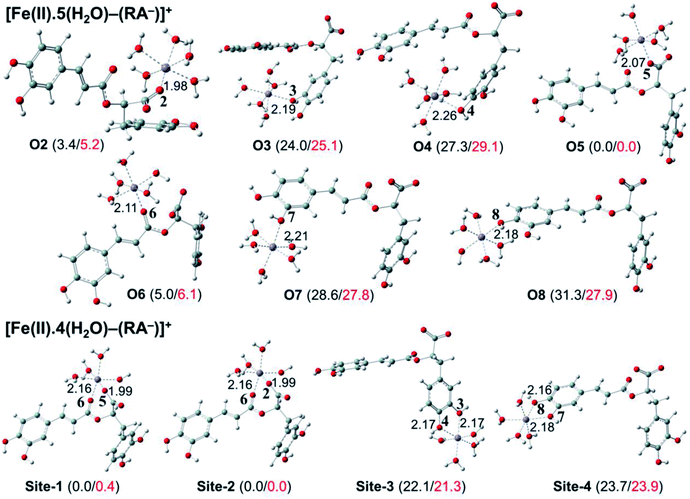
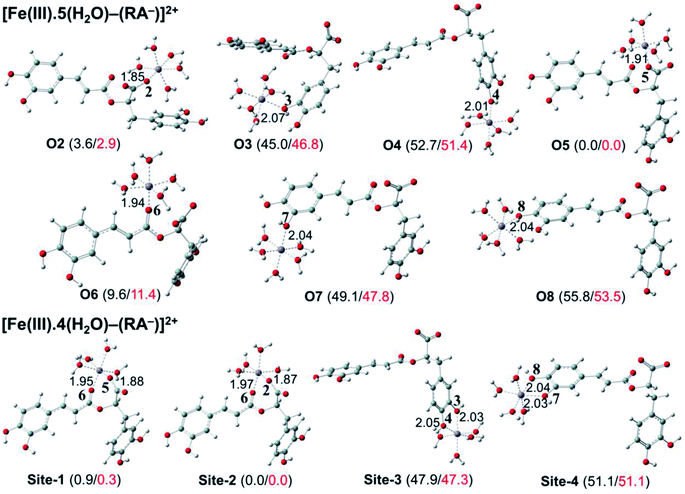
The secondary antioxidant activities of rosmarinic acid based on its ferrous and ferric ion chelation in preventing the formation of the reactive hydroxyl radical (HO˙) via the Haber–Weiss reaction1,95,96 were evaluated. The hydrated Fe(II) and Fe(III) ions existed in the octahedral-coordinated structures with six water molecules, as largely proposed in the literature9,82,97,98 in which the Fe(II) or Fe(III) ion is located at the center and H2O in the corner.The optimized structures and the relative energies of complexes between RA− and [Fe(II)(H2O)6]3+ and [Fe(III)(H2O)6]3+ ions are shown in Fig. 6 and 7, respectively. Their Cartesian coordinates and thermochemistry data are resumed in Tables S7 and S8 (ESI file†). Table 4 presents the reaction enthalpies (ΔrH0), standard Gibbs free energies (ΔrG0), and formation constants (Kf) of the chelating reactions for RA− towards the hydrated Fe(II) and Fe(III) ions at 298.15 K. The similar data for the complexation processes between the neutral RA and the [Fe(II)(H2O)6]2+ and [Fe(III)(H2O)6]3+ ions are shown in Tables S9 and S10 (ESI file†), respectively. Since the mono-anionic form RA− is the main existing form of rosmarinic acid in a physiological medium; thus, only the data related to the RA− are presented in this section. Table S11 (ESI file†) resumes Cartesian coordinates and thermochemistry properties of ascorbate mono-anions, ascorbate radicals, superoxide anion radicals, oxygen molecules, neutral rosmarinic, mono-anion rosmarinate and aqueous iron complexes in water.
| Chelating position | Fe(II) complexes | Fe(III) complexes | ||||
|---|---|---|---|---|---|---|
| ΔrH0 | ΔrG0 | Kf | ΔrH0 | ΔrG0 | Kf | |
| O2 | −24.2 | −14.6 | 5.32 × 1010 | −42.4 | −37.1 | 1.57 × 1027 |
| O3 | −4.3 | 4.6 | 4.44 × 10−4 | −1.1 | 6.6 | 1.34 × 10−5 |
| O4 | −0.6 | 8.9 | 2.85 × 10−7 | 7.1 | 11.8 | 2.27 × 10−9 |
| O5 | −28.4 | −20.6 | 1.31 × 1015 | −46.1 | −40.1 | 2.65 × 1029 |
| O6 | −24.1 | −15.3 | 1.64 × 1011 | −37.1 | −29.3 | 3.00 × 1021 |
| O7 | −0.5 | 6.4 | 1.90 × 10−5 | 3.0 | 7.6 | 2.65 × 10−6 |
| O8 | 2.0 | 6.4 | 1.96 × 10−5 | 10.1 | 13.8 | 8.04 × 10−11 |
| Site-1 | −16.3 | −21.7 | 8.12 × 1015 | −33.1 | −38.3 | 1.23 × 1028 |
| Site-2 | −16.3 | −22.1 | 1.61 × 1016 | −33.6 | −38.4 | 1.29 × 1028 |
| Site-3 | 5.3 | −1.1 | 6.71 × 100 | 13.7 | 8.4 | 7.34 × 10−7 |
| Site-4 | 6.9 | 1.4 | 9.88 × 10−2 | 16.9 | 12.3 | 1.04 × 10−9 |
As can be seen in Fig. 6 and 7, the RA− can chelate [Fe(II)(H2O)6]2+ and [Fe(III)(H2O)6]3+ ions via 7 oxygen atom positions including O2, O3, O4, O5, O6, O7, and O8 to form mono-dentate complexes. Besides, the bi-dentate complexes are formed at the two nearby oxygen atom positions, including site-1 (O5 and O6), site-2 (O2 and O6), site-3 (O3 and O4), and site-4 (O7 and O8) (Fig. 1). Regarding the Fe(II) complexes, the Fe–O distances of the mono-dentate complexes vary from 1.98 to 2.26 Å, while the ones of the bi-dentate complexes vary from 1.91 to 2.18 Å (Fig. 6). In the case of Fe(III) complexes, the Fe–O lengths vary from 1.84 to 2.06 Å for the mono-dentate complexes and from 1.88 to 2.05 Å for the bidentate ones (Fig. 7). These bond lengths are slightly shorter than those of Fe(II)–RA− complexes.
Furthermore, it is noteworthy that RA− represents strong chelating ability towards both Fe(II) and Fe(III) ions compared to its neutral form RA (see Table S12, ESI file†). Indeed, Table 4 shows that the mono-dentate complexes formed at the O5 position have large negative ΔrG0 values of −20.6 and −40.1 kcal mol−1 for the Fe(II) and Fe(III) complexes, respectively. Therefore, the complexation reactions of RA− with the hydrated iron ions at this site have the highest formation constants Kf of 1.31 × 1015 and 2.65 × 1029, respectively. Besides, the mono-dentate complexes formed at the O2 and O6 positions also show large negative ΔrG0 of −14.6/−15.3 kcal mol−1 for the Fe(II) complexes, and −37.1/−29.3 kcal mol−1 for the Fe(III) ones, respectively. Their Kf values vary from 5.32 × 1010 to 1.57 × 1027, respectively. Thus, the mono-dentate complexes of RA− at the O2, O5, and O6 positions are all significantly favorable and exergonic, and hence, they account for high formation constants compared to other forms.
Regarding the bi-dentate complexes, all the complexes formed at the site-1 and site-2 positions have significantly large negative ΔrG0 values for the [Fe(II)(H2O)6]2+ ion (i.e. −16.3 kcal mol−1 for both) and the [Fe(III)(H2O)6]3+ ion (i.e. −38.3 and −38.4 kcal mol−1, respectively) (Table 4). These complexes are also favorable and spontaneous with high Kf values ranging from 8.12 × 1015 to 1.29 × 1028; thus, they are abundant in an aqueous environment. In contrast, the other bi-dentate complexes of RA− are unstable with positive ΔrG0 and low Kf values.
Moreover, the chelating ability of RA− towards the [Fe(III)(H2O)6]3+ ion is better than the one towards the [Fe(II)(H2O)6]2+ ion. For example, the ΔrG0 and Kf values for Fe(III) complexes at the site-2 position are equal to −38.4 kcal mol−1 and 1.29 × 1028, respectively, which are higher than those for Fe(II) complexes being −22.1 kcal mol−1 and 1.61 × 1016, respectively.
Overall, since the mono-anion form RA− is the main existing form of rosmarinic acid under physiological conditions, RA− plays the main role in the secondary antioxidant activity of rosmarinic acid via its chelation towards the iron ions. The most favorable chelating sites of RA− constituted the O2, O5, O6, site-1, and site-2 positions. The coordination of RA− with the [Fe(III)(H2O)6]3+ ion is likely to be more favorable and stable than the one with [Fe(II)(H2O)6]2+.
Pro-oxidant activities of rosmarinic acid
The reduction reactions of Fe(III)-to-Fe(II) complexes involved in Fenton-like reactions that produce reactive hydroxyl (HO˙) radical9,83 are used to estimate the pro-oxidant risks of rosmarinic acid. The used reducing agents are ascorbate anion (Asc−) and superoxide anion (O2˙−).Tables 5 and 6 represent the reaction enthalpies (ΔrH0) and standard Gibbs free energies (ΔrG0) of Fe(III)-to-Fe(II) reactions and mono-anion rosmarinate (RA−) complexes by Asc− and O2˙−, respectively. The similar data of reduction processes of Fe(III)-to-Fe(II) complexes by two reducing agents for the iron complexes of neutral-rosmarinic form (RA) are shown in Table S13 (ESI file†).
| Position | ΔrH0 | ΔrG0 | λ | ΔG≠ | kD | kT | kapp |
|---|---|---|---|---|---|---|---|
| [Fe(III)(H2O)6]3+ + O2˙− → [Fe(II)(H2O)6]2+ + O2 (eqn (25)) | |||||||
| −38.2 | −41.3 | 27.3 | 1.8 | 7.63 × 109 | 7.30 × 1012 | 7.63 × 109 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| [Fe(III)L(H2O)6−n]x+3 + O2˙− → [Fe(II)L(H2O)6−n]x+2 + O2 (eqn (23)) | |||||||
| O2 | −20.4 | −19.2 | 26.8 | 0.5 | 8.47 × 109 | 6.12 × 1013 | 8.47 × 109 |
| O3 | −41.2 | −43.2 | 27.0 | 2.4 | 8.54 × 109 | 2.46 × 1012 | 8.51 × 109 |
| O4 | −45.7 | −43.9 | 25.6 | 3.3 | 8.43 × 109 | 6.25 × 1011 | 8.43 × 109 |
| O5 | −20.2 | −21.4 | 24.5 | 0.1 | 8.58 × 109 | 1.31 × 1014 | 8.58 × 109 |
| O6 | −24.8 | −26.9 | 28.6 | 0.0 | 8.56 × 109 | 1.45 × 1014 | 8.56 × 109 |
| O7 | −42.0 | −42.8 | 25.6 | 2.5 | 8.51 × 109 | 2.39 × 1012 | 8.47 × 109 |
| O8 | −46.6 | −47.1 | 24.4 | 5.3 | 8.64 × 109 | 2.15 × 1010 | 6.16 × 109 |
| Site-1 | −20.5 | −23.7 | 27.1 | 0.1 | 8.54 × 109 | 1.45 × 1014 | 8.54 × 109 |
| Site-2 | −18.8 | −18.3 | 22.3 | 0.2 | 8.50 × 109 | 1.12 × 1014 | 8.50 × 109 |
| Site-3 | −45.5 | −49.7 | 25.1 | 6.0 | 8.62 × 109 | 5.67 × 109 | 3.42 × 109 |
| Site-4 | −47.1 | −51.0 | 25.3 | 6.6 | 8.43 × 109 | 2.35 × 109 | 1.84 × 109 |
| Position | ΔrH0 | ΔrG0 | λ | ΔG≠ | kD | kT | kapp |
|---|---|---|---|---|---|---|---|
| [Fe(III)(H2O)6]3+ + Asc− → [Fe(II)(H2O)6]2+ + Asc˙ (eqn (26)) | |||||||
| −39.3 | −43.5 | 24.5 | 1.1 | 7.44 × 109 | 2.22 × 1013 | 7.44 × 109 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| [Fe(III)L(H2O)6−n]x+3 + Asc− → [Fe(II)L(H2O)6−n]x+2 + Asc˙ (eqn (24)) | |||||||
| O2 | −21.4 | −21.3 | 24.0 | 0.5 | 7.58 × 109 | 1.35 × 1013 | 7.57 × 109 |
| O3 | −42.2 | −45.4 | 24.2 | 4.7 | 7.60 × 109 | 5.77 × 1010 | 6.72 × 109 |
| O4 | −46.7 | −46.1 | 22.8 | 5.9 | 7.60 × 109 | 6.84 × 109 | 3.60 × 109 |
| O5 | −21.3 | −23.7 | 21.7 | 0.0 | 7.62 × 109 | 1.4 × 1014 | 7.62 × 109 |
| O6 | −25.8 | −29.1 | 25.8 | 0.1 | 7.61 × 109 | 1.28 × 1014 | 7.61 × 109 |
| O7 | −41.7 | −43.6 | 22.8 | 4.8 | 7.59 × 109 | 4.78 × 1010 | 6.55 × 109 |
| O8 | −45.7 | −49.3 | 21.6 | 8.8 | 7.64 × 109 | 5.04 × 107 | 5.00 × 107 |
| Site-1 | −21.6 | −25.9 | 24.3 | 0.0 | 7.60 × 109 | 1.45 × 1014 | 7.60 × 109 |
| Site-2 | −19.8 | −20.5 | 19.5 | 0.0 | 7.58 × 109 | 1.49 × 1014 | 7.58 × 109 |
| Site-3 | −46.5 | −51.9 | 22.3 | 9.8 | 7.63 × 109 | 9.23 × 106 | 9.22 × 106 |
| Site-4 | −48.1 | −53.2 | 22.5 | 10.5 | 7.56 × 109 | 2.93 × 106 | 2.92 × 106 |
It can be seen that all the reaction enthalpies (ΔrH0) and standard Gibbs free energies of reactions (ΔrG0) for the reduction process of the Fe(III) to Fe(II) complexes by both Asc− (Table 5) and O2˙− (Table 6) are largely negative; thus, these reactions are spontaneous and exergonic. Especially, the reactions between Asc− and O2˙− with mono-dentate complexes at the O8 position and with the bi-dentate complexes at the site-3, site-4 have significantly negative ΔrG0 values being −49.3 and −47.1 kcal mol−1, −51.9 and −49.7 kcal mol−1, and −53.2 and −51.0 kcal mol−1, respectively. These values are noticeably lower than those of the similar reaction for [Fe(III)(H2O)6]3+ to [Fe(II)(H2O)6]2+ complexes (i.e. −43.5 and −41.3 kcal mol−1, respectively). Furthermore, the ΔrG0 value of the reduction process between the mono-dentate complexes with the two studied reducing agents at O3, O4, and O7 are all lower than those of [Fe(III)(H2O)6]3+ complexes. Therefore, these complexes are expected to have risk to promote the Fenton reactions. However, it is noted that all three mono-dentate Fe(III) complexes have low Kf values (Table 4); thus, their formation in aqueous solutions can be considered to be negligible, and their pro-oxidant risk is limited.
On the contrary, the main existing complexes, including the ones at the O2, O5, O6, site-1, and site-2 positions, do not enhance the Fenton reactions. Indeed, the ΔrG0 values of their reduction reactions with the Asc− and O2˙− agents are all higher than −29.1 and −26.9 kcal mol−1, respectively, which are significantly higher than those of the reduction reaction for [Fe(III)(H2O)6]3+ complexes (−43.5 and 41.3 kcal mol−1, respectively). Thus, the reduction processes of Fe(III)-to-Fe(II) complexes are less favorable than that of the Fe(III) complexes in the aqueous phase. Consequently, the pro-oxidant risks of these complexes are not taken into account.
In order to evaluate the rate of the reduction reactions for Fe(III)-to-Fe(II) complexes by the Asc− and the O2˙− values, the kinetics data for these SET processes were calculated using the Marcus theory.71,72 These kinetic parameters including reorganization energy (λ), Gibbs free energy of activation (ΔG≠, kcal mol−1), diffusion rate constant (kD, M−1 s−1), TST thermal rate constant (kT, M−1 s−1), and diffusion-corrected apparent rate constants (kapp, M−1 s−1) are shown in Tables 5 and 6 for the superoxide anion (O2˙−) and the ascorbate anion (Asc−), respectively.
Regarding the reactions between the [Fe(III)(H2O)6]3+ ion and the Fe(III)–RA− complexes with O2˙− (Table 5), almost the complexes have higher reaction rates than that of the [Fe(III)(H2O)6]3+ ion. Indeed, the reactions for all the Fe(III)–RA− complexes, except the ones formed at O8, site-3 and site-4, have a kapp value varying from 8.43 × 109 to 8.58 × 109 M−1 s−1. These values are higher than that of the [Fe(III)(H2O)6]3+ ion (i.e. 7.63 × 109 M−1 s−1). This means that these complexes have high risk to the reduction of Fe(III)-to-Fe(II) complexes and thus enhance the Fenton-like reactions. Conversely, the kapp values of the redox reactions between O2˙− and the Fe(III)–RA− complexes obtained at the O8, site-3 and site-4 (i.e. 6.16 × 109, 3.42 × 109 and 1.84 × 109 M−1 s−1, respectively) are smaller than that of the [Fe(III)(H2O)6]3+ ion. These complexes have high potential to prevent the reduction of the Fe(III)-to-Fe(II) complexes by the O2˙− agent. However, it is noteworthy that the Fe(III)–RA− complexes formed at O8, site-3 and site-4 positions are quite negligible (Table 4). Thus, when O2˙− is the reducing agent, the Fe(III)-to-Fe(II) complex reduction processes are enhanced, and the pro-oxidant risks may be remarkable.
Regarding the redox reaction between the Asc− and Fe(III) complexes (Table 6), it can be seen that all reactions are fast and favorable with the kapp value ranging from 2.92 × 106 to 7.62 × 109 M−1 s−1 for the ones of the Fe(III)–RA− complexes, which are generally lower or similar to the reaction of the [Fe(III)(H2O)6]3+ ion (i.e. 7.44 × 109 M−1 s−1). The kapp value of the reaction of Fe(III)–RA− complexes formed at O2, O5, O6, site-1, and site-2 are slightly higher than that of the [Fe(III)(H2O)6]3+ ion, and thus, these reactions occur slightly faster. Meanwhile, the reactions for the other complexes especially the ones at site-3 and site-4 have lower reaction rates. Indeed, the rates of the Fe(III)–RA− complexes at site-3 and site-4 are approximately 800 and 3000 times lower than that for the reaction of the [Fe(III)(H2O)6]3+ ion. As a result, these complexes are able to prevent Fe(III)-to-Fe(II) reduction processes by the Asc− agent. Therefore, the pro-oxidant risks of these complexes are insignificant.
Overall, the RA− does not enhance the Fe(III)-to-Fe(II) reduction process by the ascorbate anion, but it slightly promotes this process when the superoxide anion is considered as the reducing agent. Thus, the RA− may express the pro-oxidant risk depending on the reducing agent present in the environment.
Conclusions
Based on the direct and indirect antioxidant activities of rosmarinic acid and its pro-antioxidant risks in an aqueous phase using the DFT approach, there are multiple conclusions as follows:(i) Rosmarinic acid has an antioxidant potential via FHT and SET mechanisms with the smallest BDE (O3–H) value being 83.3 kcal mol−1 and the IP being 121.2 kcal mol−1. These values are similar or lower than several popular antioxidant compounds.
(ii) HAT is the responsible mechanism for HOO˙ and CH3OO˙ radical scavenging activities of mono-anion rosmarinate (RA−) in the aqueous phase with the negative Gibbs free energies and high rate constants at all –OH positions. Especially, the HAT reaction occurring at O7H represents the most preponderant one with branching ratios of 47.41% for HOO˙ and 71.60% for CH3OO˙ radical. In addition, RA− has demonstrated its good antioxidant capacity to HOO˙ and CH3OO˙ radicals in comparison to other popular antioxidants with ktot values of 1.84 × 103 and 4.49 × 103 M−1 s−1, respectively. The non-polar pentyl ethanoate solvent slightly enhances FHT reactions, while it is unfavorable to RAF and especially to SET ones compared to the ones in the aqueous phase.
(iii) RA− has remarkable potential to chelate both Fe(III) and Fe(II) ions, especially at the O5 position for the mono-dentate complexes and the site-1, site-2 ones for the bi-dentate complexes. Moreover, the chelation process towards Fe(III) ions is more favorable and spontaneous than that for Fe(II) ions.
(iv) Reduction processes of Fe(III)-to-Fe(II) complexes by Asc− and O2˙− agents, which may be an initial step for Fenton-like reactions forming reactive HO˙ radicals were considered in comparison with the self-reduction process of [Fe(III)(H2O)6]3+ ions. Consequently, RA− may enhance the pro-oxidant risk when O2˙− is present in the reactive media; however, this phenomenon is not observed if Asc− is available.
Hopefully, the actual work may provide a multi-facet point of view into the antioxidant potential of rosmarinic acid before further chemical and biological applications.
Author contributions
Dinh Hieu Truong: investigation – writing. Thi Chinh Ngo: investigation, review & editing. Nguyen Thi Ai Nhung: review & editing. Duong Tuan Quang: conception, review & editing. Thi Le Anh Nguyen: review & editing. Dorra Khiri: writing – review & editing. Sonia Taamalli: review & editing. Abderrahman El Bakali: review & editing. Florent Louis: investigation – review & editing. Duy Quang Dao: conceptualization – project administration – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.01-2019.380. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575. Dorra Khiri, Sonia Taamalli, Florent Louis, and Abderrahman El Bakali appreciated the support from the LABEX CaPPA (Chemical and Physical Properties of the Atmosphere), which is funded by the French National Research Agency (ANR) through the PIA (Programme d'Investissement d'Avenir) under contract ANR-11-LABX-0005-01 and also the Regional Council “Hauts de France” and the “European Funds for Regional Economic Development”.References
- A. Galano, J. Mex. Chem. Soc., 2017, 59, 231–262 CrossRef.
- G. J. Burton and E. Jauniaux, Best Pract. Res. Clin. Obstet. Gynaecol., 2011, 25, 287–299 CrossRef PubMed.
- B. Moosmann, T. Skutella, K. Beyer and C. Behl, Biol. Chem., 2001, 382, 1601–1612 CAS.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2013, 34, 2430–2445 CrossRef CAS PubMed.
- H. Y. Zhang, Y. M. Sun and D. Z. Chen, Quant. Struct.-Act. Relat., 2001, 20, 148–152 CrossRef CAS.
- A. Urbaniak, M. Molski and M. Szeląg, Computational Methods in Science and Technology, 2012, 18, 117–128 CrossRef.
- L. Tabrizi, T. L. A. Nguyen, H. D. T. Tran, M. Q. Pham and D. Q. Dao, J. Chem. Inf. Model., 2020, 60, 6185–6203 CrossRef CAS PubMed.
- D. K. Maurya and T. P. A. Devasagayam, Food Chem. Toxicol., 2010, 48, 3369–3373 CrossRef CAS PubMed.
- D. H. Truong, N. T. A. Nhung and D. Q. Dao, Comput. Theor. Chem., 2020, 1185, 112905 CrossRef CAS.
- A. Beneduci, E. Furia, N. Russo and T. Marino, New J. Chem., 2017, 41, 5182–5190 RSC.
- G. Mazzone, N. Russo and M. Toscano, Comput. Theor. Chem., 2016, 1077, 39–47 CrossRef CAS.
- J. Teixeira, A. Gaspar, E. M. Garrido, J. Garrido and F. Borges, BioMed Res. Int., 2013, 2013, 1–11 Search PubMed.
- M. E. Medina, C. Iuga and J. R. Álvarez-Idaboy, RSC Adv., 2014, 4, 52920–52932 RSC.
- A. Galano, M. Francisco Marquez and A. Pérez-González, Chem. Res. Toxicol., 2014, 27, 904–918 Search PubMed.
- M. E. Medina, C. Iuga and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2013, 15, 13137 RSC.
- M. E. Medina, A. Galano and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2014, 16, 1197–1207 RSC.
- C. Iuga, J. R. Alvarez-Idaboy and N. Russo, J. Org. Chem., 2012, 77, 3868–3877 CrossRef CAS PubMed.
- A. Galano and A. Martínez, J. Phys. Chem. B, 2012, 116, 1200–1208 CrossRef CAS PubMed.
- A. Galano, M. Francisco-Márquez and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2011, 13, 11199 RSC.
- M. Cordova-Gomez, A. Galano and J. R. Alvarez-Idaboy, RSC Adv., 2013, 3, 20209–20218 RSC.
- C. Caicedo, C. Iuga, R. Castañeda-Arriaga and J. R. Alvarez-Idaboy, RSC Adv., 2014, 4, 38918–38930 RSC.
- A. Pérez-González, A. Galano and J. R. Alvarez-Idaboy, New J. Chem., 2014, 38, 2639 RSC.
- E. Graf, Free Radic. Biol. Med., 1992, 13, 435–448 CrossRef CAS PubMed.
- G. Mariappan, N. Sundaraganesan and S. Manoharan, Spectrochim. Acta, Part A, 2012, 97, 340–351 CrossRef CAS PubMed.
- H. Zhu, Q.-H. Liang, X.-G. Xiong, J. Chen, D. Wu, Y. Wang, B. Yang, Y. Zhang, Y. Zhang and X. Huang, Evid. base Compl. Alternative Med., 2014, 2014, 1–10 Search PubMed.
- N. Chockalingam and S. Muruhan, Int. J. Res. Pharm. Sci., 2017, 8, 656–662 CAS.
- V. Swarup, J. Ghosh, S. Ghosh, A. Saxena and A. Basu, Antimicrob. Agents Chemother., 2007, 51, 3367–3370 CrossRef CAS PubMed.
- A. Amić, Z. Marković, J. M. Dimitrić Marković, D. Milenković and V. Stepanić, Phytochemistry, 2020, 170, 112218 CrossRef PubMed.
- E. Palierse, C. Przybylski, D. Brouri, C. Jolivalt and T. Coradin, Int. J. Mol. Sci., 2020, 21, 1–14 Search PubMed.
- E. Furia, A. Beneduci, N. Russo and T. Marino, New J. Chem., 2018, 42, 11006–11012 RSC.
- G. Mazzone, J. Phys. Chem. A, 2019, 123, 9560–9566 CrossRef CAS PubMed.
- M. Petersen, Phytochemistry, 2003, 62, 121–125 CrossRef CAS PubMed.
- S. Y. Lee, H. H. Kim and S. U. Park, EXCLI J., 2015, 14, 199–203 Search PubMed.
- B. Sik, V. Kapcsándi, R. Székelyhidi, E. L. Hanczné and Z. Ajtony, Nat. Prod. Commun., 2019, 14, 1934578X1986421 CrossRef.
- F. K. Ticli, L. I. S. Hage, R. S. Cambraia, P. S. Pereira, Â. J. Magro, M. R. M. Fontes, R. G. Stábeli, J. R. Giglio, S. C. França, A. M. Soares and S. V. Sampaio, Toxicon, 2005, 46, 318–327 CrossRef CAS PubMed.
- O. Fadel, K. El Kirat and S. Morandat, Biochim. Biophys. Acta Biomembr., 2011, 1808, 2973–2980 CrossRef CAS PubMed.
- H. Cao, W.-X. Cheng, C. Li, X.-L. Pan, X.-G. Xie and T.-H. Li, J. Mol. Struct.: THEOCHEM, 2005, 719, 177–183 CrossRef CAS.
- Z. Liang, L. Wu, X. Deng, Q. Liang, Y. Xu, R. Deng, L. Lv, M. Ji, Z. Hao and J. He, Inflammation, 2020, 43, 1902–1912 CrossRef CAS PubMed.
- A. Khojasteh, M. H. Mirjalili, M. A. Alcalde, R. M. Cusido, R. Eibl and J. Palazon, Antioxidants, 2020, 9, 1273 CrossRef CAS PubMed.
- A. M. Popov, A. N. Osipov, E. A. Korepanova, O. N. Krivoshapko and A. A. Artyukov, Biophysics, 2013, 58, 607–615 CrossRef CAS.
- D. Benedec, D. Hanganu, I. Oniga, B. Tiperciuc, N.-K. Olah, O. Raita, C. Bischin, R. Silaghi-Dumitrescu and L. Vlase, Pak. J. Pharm. Sci., 2015, 28, 2297–2303 CAS.
- M. A. Furtado, L. C. F. de Almeida, R. A. Furtado, W. R. Cunha and D. C. Tavares, Mutat. Res., Genet. Toxicol. Environ. Mutagen., 2008, 657, 150–154 CrossRef CAS PubMed.
- R. Bhatt, N. Mishra and P. K. Bansal, J. Pharm. Sci. Innovation, 2013, 2, 28–34 CrossRef CAS.
- S. P. Ekambaram, S. S. Perumal, A. Balakrishnan, N. Marappan, S. S. Gajendran and V. Viswanathan, J. Intercult. Ethnopharmacol., 2016, 5, 358–363 CrossRef CAS PubMed.
- F. Geller, C. Schmidt, M. Göttert, M. Fronza, V. Schattel, B. Heinzmann, O. Werz, E. M. M. Flores, I. Merfort and S. Laufer, J. Ethnopharmacol., 2010, 128, 561–566 CrossRef CAS PubMed.
- X. Peng, X. Wang, W. Qi, R. Huang, R. Su and Z. He, Food Funct., 2015, 6, 2712–2726 RSC.
- H. Highland, M. Thakur, P. Pandya, A. Mankad and L.-B. George, J. Drug Delivery Ther., 2019, 9, 159–166 CrossRef.
- R. Świsłocka, E. Regulska, J. Karpińska, G. Świderski and W. Lewandowski, Molecules, 2019, 24, 2645 CrossRef PubMed.
- J. L. Muñoz-Muñoz, F. Garcia-Molina, E. Ros, J. Tudela, F. García-Canovas and J. N. Rodríguez-López, J. Food Biochem., 2013, 37, 396–408 CrossRef.
- W. H. Koppenol, J. Butler and J. W. V. Leeuwen, Photochem. Photobiol., 1978, 28, 655–658 CrossRef CAS.
- G. García-Díez, R. Ramis and N. Mora-Diez, ACS Omega, 2020, 5, 14502–14512 CrossRef PubMed.
- N. Mora-Diez, R. Monreal-Corona, J. Biddlecombe and A. Ippolito, Antioxidants, 2020, 9, 1–21 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussion 16 Rev. A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382 CrossRef PubMed.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS PubMed.
- O. Boukar, J. J. Fifen, M. Nsangou, H. Ghalila and J. Conradie, New J. Chem., 2021, 45, 10693–10710 RSC.
- A. A. Jarzęcki, A. D. Anbar and T. G. Spiro, J. Phys. Chem. A, 2004, 108, 2726–2732 CrossRef.
- J. Ortega-Castro, J. Frau, R. Casasnovas, D. Fernández, J. Donoso and F. Muñoz, J. Phys. Chem. A, 2012, 116, 2961–2971 CrossRef CAS PubMed.
- J. E. Bartmess, J. Phys. Chem., 1994, 98, 6420–6424 CrossRef CAS.
- Z. Marković, J. Tošović, D. Milenković and S. Marković, Comput. Theor. Chem., 2016, 1077, 11–17 CrossRef.
- T. L. A. Nguyen, T. H. N. Doan, D. H. Truong, N. T. Ai Nhung, D. T. Quang, D. Khiri, S. Taamalli, F. Louis, A. El Bakali and D. Q. Dao, RSC Adv., 2021, 11, 21433–21446 RSC.
- T. C. Ngo, T. V. T. Mai, T. T. Pham, S. Jeremic, Z. Markovic, L. K. Huynh and D. Q. Dao, Chem. Phys. Lett., 2020, 746, 137312 CrossRef CAS.
- R. C. Rose and A. M. Bode, FASEB J., 1993, 7, 1135–1142 CrossRef CAS.
- A. Galano, D. X. Tan and R. J. Reiter, J. Pineal Res., 2011, 51, 1–16 CrossRef CAS PubMed.
- D. Q. Dao, T. T. T. Phan, T. L. A. Nguyen, P. T. H. Trinh, T. T. Van Tran, J. S. Lee, H. J. Shin and B.-K. Choi, J. Chem. Inf. Model., 2020, 60, 1329–1351 CrossRef CAS PubMed.
- P. Terpinc and H. Abramovič, Food Chem., 2010, 121, 366–371 CrossRef CAS.
- H. Sies, Exp. Physiol., 1997, 82, 291–295 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664–2682 CrossRef CAS.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- R. A. Marcus, Pure Appl. Chem., 1997, 69, 13–30 CAS.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425–437 CrossRef CAS.
- M. v. Smoluchowski, Z. Phys. Chem., 1918, 92U, 129–168 CrossRef.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 322, 891–921 CrossRef.
- G. G. Stokes, Mathematical and Physical Papers, Cambridge University Press, Cambridge, 2009 Search PubMed.
- E. N. Bentz, R. M. Lobayan, H. Martínez, P. Redondo and A. Largo, J. Phys. Chem. B, 2018, 122, 6386–6395 CrossRef CAS PubMed.
- S. Muthaiah, A. Bhatia and M. Kannan, in Stability and Applications of Coordination Compounds, IntechOpen, 2020 Search PubMed.
- R. Golbedaghi and F. Khajavi, Bull. Chem. Soc. Ethiop., 2014, 28, 1 CrossRef CAS.
- E.-I. Ochiai and R. Morand, J. Coord. Chem., 1985, 14, 83–86 CrossRef CAS.
- G. García-Díez and N. Mora-Diez, Antioxidants, 2020, 9, 1–18 CrossRef PubMed.
- R. Castañeda-Arriaga, A. Pérez-González, J. R. Alvarez-Idaboy and A. Galano, Int. J. Quantum Chem., 2018, 118, 1–15 CrossRef.
- S. Pamidighantam, S. Nakandala, E. Abeysinghe, C. Wimalasena, S. R. Yodage, S. Marru and M. Pierce, Procedia Comput. Sci., 2016, 80, 1927–1939 CrossRef.
- N. Shen, Y. Fan and S. Pamidighantam, J. Comput. Sci., 2014, 5, 576–589 CrossRef.
- R. Dooley, K. Milfeld, C. Guiang, S. Pamidighantam and G. Allen, J. Grid Comput., 2006, 4, 195–208 CrossRef.
- K. Milfeld, C. Guiang, S. Pamidighantam and J. Giuliani, Proc. 2005 Linux Clust. HPC Revolut, 2005 Search PubMed.
- A. Amić, B. Lučić, V. Stepanić, Z. Marković, S. Marković, J. M. Dimitrić Marković and D. Amić, Food Chem., 2017, 218, 144–151 CrossRef PubMed.
- A. Galano, J. R. León-Carmona and J. R. Alvarez-Idaboy, J. Phys. Chem. B, 2012, 116, 7129–7137 CrossRef CAS PubMed.
- J. R. León-Carmona and A. Galano, J. Phys. Chem. B, 2011, 115, 15430–15438 CrossRef PubMed.
- J. R. León-Carmona and A. Galano, J. Phys. Chem. B, 2011, 115, 4538–4546 CrossRef PubMed.
- A. Galano, D. X. Tan and R. J. Reiter, J. Pineal Res., 2013, 54, 245–257 CrossRef CAS PubMed.
- A. Martínez, A. Galano and R. Vargas, J. Phys. Chem. B, 2011, 115, 12591–12598 CrossRef PubMed.
- L. Tabrizi, T. L. A. Nguyen and D. Q. Dao, RSC Adv., 2019, 9, 17220–17237 RSC.
- W. H. Koppenol, Redox Rep., 2001, 6, 229–234 CrossRef CAS PubMed.
- F. Haber and J. Weiss, Naturwissenschaften, 1932, 20, 948–950 CrossRef CAS.
- R. V. Listyarini, D. S. Gesto, P. Paiva, M. J. Ramos and P. A. Fernandes, Front. Chem., 2019, 7, 1–12 CrossRef PubMed.
- E. Miliordos and S. S. Xantheas, J. Chem. Theory Comput., 2015, 11, 1549–1563 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07599c |
| This journal is © The Royal Society of Chemistry 2022 |